Abstract
In order to solve the problem of false recycling, where the real recycling volume does not match the theoretical one, blockchain is widely used in practice due to its characteristics of transparency, traceability, and tamper resistance. To study its value in academics, this paper focuses on a closed-loop supply chain (CLSC) consisting of a manufacturer and an online platform. This paper discusses the implementation conditions of blockchain, the impact on enterprise decision making, and manufacturer recycling channel selection, and the triple benefits of economy, environment, and society in the CLSC with blockchain empowerment are achieved. Because of the nontransparency of the supply chain, the problem of false recycling is always present. To further solve the problem of false recycling, the recycler decides whether to implement blockchain or not. Through analysis and numerical examples, it is concluded that the greater the difference between real and theoretical recycling volumes, the greater the need for blockchain implementation. At the same time, three major effects of blockchain implementation are defined as decision incentive effect, marketing leverage effect, and incentive alignment effect, which reveal the impact of blockchain on increasing the motivation of CLSC members to make efforts, expanding the market size by improving brand goodwill, and avoiding the inconsistency between the manufacturer and the platform in the preference of the recycling channel. In addition, under blockchain empowerment, a cost range of blockchain implementation is defined, where both the manufacturer and the platform are better off, as well as the optimal recycling channel, which achieves the triple benefits of the CLSC.
1. Introduction
The rapid development of online platforms has further promoted the upgrading of products and shortened their life cycle, and the number of waste products has continued to increase. It is reported that between 2014 and 2019, the world produced a record 53.6 million tons of e-waste in 2019; the global amount of e-waste increased by 21%, and it is expected to reach 74 million tons by 2030. In 2021, the global electronic waste and electrical equipment waste exceeded 57.4 million tons (https://baijiahao.baidu.com/s?id=1714299926895059962&wfr=spider&for=pc, accessed on 25 December 2022). By 2050, the world will generate 32 billion tons of garbage annually. Experts say that every ton of unrecycled e-waste produces 2 tons of carbon impact. However, the cost of remanufacturing the usable parts in waste products is only 50% of the cost of new products, which can save 60% of energy and 70% of materials (https://auto.ifeng.com/usecar/news/20090910/101940.shtml, accessed on 25 December 2022). The negative impact on the environment is significantly reduced compared with manufacturing new products. However, in practice, due to the nontransparency of the recycling process and weak consumer awareness of recycling, it is difficult to carry out waste product recycling activities, and the real recycling volume of recyclers does not match the theoretical recycling volume of consumers, which leads to false recycling problems. Considering the value of reusable components in waste products and the potential pollution and waste of resources caused by improper treatment, recycling of waste products has become more important and urgent than ever in the era of continuous product improvement [1,2,3].
Driven by legislation and the economics of resource conservation and reuse, corporate recycling activities have become very common [4]. Hewlett Packard (HP) separates used equipment into components that can be reused in new manufacturing systems [5]. For the benefit of consumers and the environment, Apple’s proposed trade-in and recycling process requires that every refurbished product meet Apple’s official new product testing standard. In addition, well-known companies such as Xerox and Epson have incorporated the recycling and remanufacturing plan of waste products into their daily operating plan [6]. In the process of enterprise recycling activities, due to the inability to monitor the whole recycling process with the existing methods, the real recycling volume of waste products is far away from the theoretical recycling volume, and the problem of false recycling is gradually exposed, which has become a bottleneck problem restricting the development of circular economy (https://baijiahao.baidu.com/s?id=1703519650356222772&wfr=spider&for=pc, accessed on 25 December 2022). In the textile industry, more than 70% of used clothing recycling is illegally dumped in other used clothing markets in Africa and China every year, and about 20% of the waste clothing has unclear final flow direction. The real recycling volume is less than 10% of the theoretical one (http://news.cyol.com/, accessed on 25 December 2022). In addition, the data disclosed in the White Paper on the Development of China’s Lithium-Ion Battery Recycling, Disassembly, and Echelon Utilization Industry shows that in 2020, the theoretical recovery of lithium-ion batteries in the Chinese market reached 478,000 tons, but the actual recovery was 196,000 tons, accounting for only 41% (http://www.xevcar.com/, accessed on 25 December 2022). This phenomenon, where the actual recycling volume of waste products is much lower than the theoretical recycling volume, is called false recycling. Therefore, the consumer’s awareness is gradually improved. The existence of false recycling not only reduces the efficiency of recycling investment, but also leads to consumer distrust, which greatly damages the company’s image and further reduces consumers’ willingness to return waste products.
The lack of transparency and effective monitoring of the entire recycling process is at the root of false recycling. In recent years, the continuous development of blockchain technology and practical feedback have brought new hope for solving false recycling. Blockchain was born along with bitcoin and has been applied to finance, government, people’s livelihood, and medical care due to its technical characteristics, such as transparency, trustworthiness, traceability, and tamper-proofing [7,8]. In recent years, blockchain has proven to play an important role in enabling information sharing, maintaining supply chain traceability, and effectively improving operational efficiency [9,10,11]. Given the technical advantages of blockchain in achieving end-to-end traceability and improving supply chain transparency, companies have used it to monitor the recycling of waste products. China’s Hainan Green Technology and Thunder Chain cooperate to recycle waste textiles, which realized effective supervision of the whole recycling process and increased the amount of textile recycling. By developing the JD Chain Tracking System to track the recycling process of recycled mobile phones and other recycled electronic products, JD & AI Recycling has won consumers’ trust in recycling and greatly improved the company’s reputation. Laiyue’s recycling platform applies blockchain technology to the recycling industry to verify the authenticity of recycling operations. The “battery home” service platform in Guangdong Province, China, uses blockchain to establish a battery recycling system, which realizes the supervision of the recycling process of waste batteries. We can see that the application of blockchain increases the transparency of the recycling process, enables the supervision of the whole recycling process, and increases the trust of consumers. This not only enhances a company’s image, but also promotes the sustainable recycling of waste products, laying the foundation for a circular economy. However, considering the trade-off between the cost of implementation and the effectiveness of blockchain, when to use blockchain to monitor the recycling process and solve the problem of false recycling is one of the important issues considered in this paper.
In addition, the rapid development of the platform economy has not only enabled manufacturers to develop their online sales channels and expand the market scale with the help of the “platform power”, but also made online recycling using the platform an important recycling channel other than manufacturer-independent recycling [12,13]. The innovative recycling mode of “Internet + Recycling” has become increasingly popular. On the one hand, the platform has a large amount of online traffic and consumer data. It can accurately locate consumer groups through big data analytics technology, increase brand exposure, and improve sales conversion rate through live online broadcasting and other marketing activities [12,14,15]. On the other hand, in the “Internet + Recycling” mode, by tracking consumers’ product usage, the platform will remind consumers to return the waste products after a certain period of time, and the platform will bear the cost of recycling the waste products [16]. JD & Aihuishou provides consumers with one-click online ordering and door-to-door pickup. It has cooperated with many manufacturers to realize the recycling of waste products. In China, online recycling platforms, such as taolv.com, Lehuishou, and Huishoubao, have grown rapidly, providing a convenient channel for online recycling of waste products. Therefore, weighing the convenience and cost of online recycling, manufacturers still face the problem of selecting recycling channels in the current recycling process under the background of platform economy. Not only that, but considering the issue of false recycling, how the implementation of blockchain will affect the platform’s original operational strategy, the manufacturer’s choice of recycling channels, and the economic, environmental, and social benefits of a CLSC is also a very challenging and valuable issue that needs to be further explored theoretically.
To this end, this paper focuses on a CLSC system consisting of a manufacturer engaged in manufacturing and remanufacturing and an online platform that sells products as a marketplace. Considering that blockchain can regulate the whole recycling process of waste products, improve consumer trust, and boost the recycling volume, this paper aims to answer the following three questions to fill the gap between blockchain adoption and recycling channel selection in the CLSC:
Q1: What are the optimal conditions for implementing blockchain in the waste recycling process?
Q2: What impact will the adoption of blockchain technology in the recycling process have on corporate decisions, recycling rate, and manufacturer recycling channel selection?
Q3: How to optimize the combination of blockchain implementation and recycling channel selection to further enhance the economic, environmental, and social triple benefits of the CLSC?
In order to answer the above questions, four differential game models are developed, namely, manufacturer recycling channel without blockchain (model ), platform recycling channel without blockchain (model ), manufacturer recycling channel with blockchain (model ), and platform recycling channel with blockchain (model ). With the help of Bellman’s dynamic programming theory, the firm’s decisions, the recycling rate of waste products, the firm’s profits, the consumer surplus, and the social welfare under the four models are obtained. By comparing the economic benefits of blockchain implementation under different recycling channels, the conditions for blockchain implementation are clarified. A comparative analysis illustrates the value of blockchain implementation. It also defines the scope that enables the triple benefits of CLSC with blockchain empowerment. The main conclusions are: (1) Blockchain can effectively solve the phenomenon of false recycling and realize the supervision of the whole recycling process by its transparency, traceability, and tamper-proofing. Under a certain cost range, the blockchain will be adopted by the recycler. Moreover, the greater the difference between the real and theoretical volume of recovery, the greater the need for blockchain implementation. (2) By analyzing decision making, performance, and manufacturer recovery channel selection before and after blockchain implementation, this study summarizes three main effects of blockchain implementation: decision incentive effect, marketing leverage effect, and incentive alignment effect, which reveal the impact of blockchain on increasing the motivation of CLSC members to exert effort, expanding the market size by improving brand goodwill, and enabling both the manufacturer and the platform to be better off from the manufacturer recycling channel under certain conditions. (3) When blockchain is not implemented, the manufacturer’s choice is the manufacturer recycling channel, a finding consistent with the previous research. Under blockchain empowerment, we define a cost range for blockchain implementation, i.e.,, where the manufacturer and the platform reach an agreement on manufacturer recycling with blockchain, and the triple benefits of the CLSC are optimally realized. Furthermore, to illustrate the robustness of the results, we perform an extension with the unit cost of the blockchain implementation. The recycler partners with an established blockchain technology service company. Thus, the cost of implementing blockchain is no longer a fixed cost, as it was in the baseline model, but a variable cost per unit. The results of the extended model are consistent with the baseline model, and the robustness of the results of this paper is tested. The main contributions of this paper are as follows:
First of all, the adoption of blockchain to avoid false recycling fills the gap between blockchain implementation and backward supply chain management. In addition, it is worth noting that we introduced blockchain from the perspective of avoiding false recycling, which explores the application of blockchain only in the backward chain. The analysis results demonstrated that the implementation of blockchain in the recycling process of waste products can not only build consumer trust in the recycling chain and promote the recycling of waste products, but also play its marketing leverage function by improving brand goodwill, which can further promote the demand with the improvement of brand premium capacity in forward sales. Therefore, this paper studies blockchain in a CLSC considering forward and backward interactions and proposes corresponding management insights, which will be of great value to both forward sales and reverse recycling.
Second, a growing body of research shows that platforms with platform power act as online marketplaces in online marketing, a sales format that allows brand manufacturers more flexibility in pricing power while avoiding order fulfillment costs and operational risk for the platform. Most of the existing studies explore the static operational strategies in the forward supply chain when the platform acts as a market intermediary. On the one hand, the impact of online marketing on the dynamic change of brand goodwill is not extremely considered on the long-term benefits of the supply chain. On the other hand, given that platforms are closer to consumers, more and more platforms are acting as recyclers. In contrast, few theoretical studies have been reported that consider platforms as recyclers and explore manufacturers’ motivations for recycling channel selection. Therefore, in response to these two current situations, the contribution of this paper is to consider the dynamic impact of blockchain implementation, recycling efforts, and platform online marketing on brand goodwill and its long-term impact on the triple economic, environmental, and social performance in a dynamic CLSC system. At the same time, the platform is involved in the selection of recyclers to explore the optimal recycling channel selection of the manufacturer under blockchain empowerment and its impact on the triple benefits of CLSC.
Finally, one of the outstanding contributions of this paper is the discovery of the inconsistency between the manufacturer and the platform caused by the false recycling status when the blockchain is not implemented. The important contribution of this paper to the study of blockchain is that the research defines the three main effects of the blockchain by analyzing the implementation value of the blockchain. The results confirm the coordinating role of the blockchain in the equilibrium recycling channel selection of the CLSC. The cost range of the blockchain implementation that benefits both the manufacturer and the platform at the same time is clarified. Furthermore, the triple benefit of the entire CLSC has been shown to be improved within this range. Therefore, our research results can further deepen the research scope of blockchain in the supply chain and make an important contribution to the optimization of CLSC operations considering the recycling of waste products.
In order to explore the above issues and draw conclusions and insights, the remainder of the paper is organized as follows: in Section 2, we will review the relevant literature; in Section 3 and Section 4, we will make assumptions about the relevant models and analyze optimal corporate decisions and social performance. In Section 5, we will clarify the conditions for blockchain adoption and illustrate the impact of blockchain implementation on corporate decisions and the triple benefits of CLSC. In Section 6, we will further verify the robustness of the results obtained in the benchmark model by developing extended models in which the recycler cooperates with a blockchain service company. In Section 7, we will draw the main conclusions and management insights of the paper.
2. Materials and Methods
Our paper is closely related to three main streams: blockchain implementation in the supply chain, recycling channel selection, and platform operations.
2.1. Blockchain Implementation in Supply Chain
Blockchain, as a distributed, shared database, with characteristics such as transparency, tamper-proofing, and traceability, has been proven to be an emerging technology to alleviate the difficult problems of regulation and traceability in supply chain management [9]. Blockchain can be used to record, track, monitor, and transact, and has applied in the financial, legal, physical, and other industries [7]. Using cobalt mining and pharmaceuticals as a research context, Hasting and Sodhi [17] summarized seven business requirements and seven critical success factors for blockchain implementation, providing a basis for empirical research. Babich and Hilary [8] summarized five advantages and five disadvantages of technological characteristics, and illustrated the research topic from classical inventory management to industrial organization. Dutta et al. [18] provided a brief overview of the supply chain architecture and its characteristics by summarizing 178 relevant papers. Many theoretical studies proved to us that blockchain has a wide development prospect and research value due to its transparency and trust, tamper-proofing, and traceability [19]. Research on blockchain implementation has mostly focused on the operational process of one-way supply chain. Chod et al. [20] solved the financing challenges of information asymmetry in the supply chain, and helped companies obtain favorable financing terms using blockchain. Cui et al. [21] leveraged the traceability of the blockchain to enable the study of supply chain quality and supply chain contracts. Shen et al. [22] combated counterfeit products using a permitted blockchain platform and achieved full process control for manufacturers and consumers by utilizing the transparency, trust, and traceability of the blockchain. Pun et al. [23] used the tamper-proofing and traceability features of the blockchain to effectively reveal the authenticity of products and combat deceptive counterfeiting. Choi [24] proved that the implementation of blockchain will greatly improve the trust between consumers and manufacturers. In addition, Xu et al. [25] demonstrated that blockchain can record the production process of products, which will help consumers understand the authenticity of product information and increase their willingness to buy.
In related research, many studies have also shown that blockchain has great potential for solving the problem of false recycling by improving the traceability of recycling processes, which will also promote the sustainable development of supply chains. Saberi et al. [9] showed that blockchain, as a transparent, immutable, and trusted distributed database, is one of the most effective means to solve the complex problems faced in achieving the triple benefits of ESS. Centobelli et al. [11] believed that blockchain technology will improve the traceability and transparency of the recycling link in the supply chain, and increase consumer confidence in recycling. However, to date, there has been no theoretical research on how to solve the problem of false recycling and what impact blockchain will have on the operation and management of the CLSC. This paper fills this gap by using a game theory model to explore the implementation conditions of blockchain in the face of the false recycling problem and the impact of blockchain implementation on manufacturers’ recycling channel selection and closed-loop supply chain operation strategies.
2.2. Recycling Channel Selection
The economic and environmental performance of product recycling has been widely recognized in theory and practice [26]. The evolution of the CLSC’s management over the years has repeatedly demonstrated the importance of proper recycling channels to improve the triple bottom line of economy, environment and society. Savaskan et al. [26] considered the problem of selecting three recycling channels: manufacturer recycling, retailer recycling, and third-party recycling, and found that retailer recycling is more efficient than others by establishing a decentralized channel and a centralized channel. On this basis, by introducing competition between two retailers to reduce the retail price, Savaskan et al. [27] found that the retailer recycling would be the manufacturer’s first choice for goods where competition is determined by price. Huang et al. [28] examined how the intensity of competition determines the choice of recycling channel when retailers and third parties compete to recycle waste products. De Giovanni et al. [29] investigated the optimal choice of both manufacturers and retailers investing in recycling programs using incentive strategies in a dynamic closed-loop supply chain. Ji et al. [30] explored the closed-loop supply chain game model of manufacturer and retailer recycling channels, and found the optimal performance of the supply chain under different hypothetical models. Recycling of used electronics has been the focus of recycling research. Liu et al. [31] considered quality-based price competition models in a qualified sector and unqualified sector setting and analyzed the impact of retail price and government subsidies. For offline recycling channels and online recycling channels, two-part contracts and revenue-sharing contracts can coordinate reverse recycling systems and create a win–win situation [4].
Most of the above studies focus on the choice of traditional recycling channels, and there are few studies that consider online platform recycling, which is becoming more popular in practice, as a choice of recycling channels. However, the economy of the platform has grown rapidly in recent years, the platform aggregates and stores huge data about consumers, and traditional offline recyclers do not have an advantage [14]. Related empirical studies have shown that the promotional knowledge of waste products posted by platforms can increase consumers’ willingness to recycle online [19]. Unlike previous studies on recycling channels [32], we consider the inclusion of a platform in the recycling selection and adopt the new technology of blockchain to monitor the entire recycling process and solve the problem of inconsistency between the real recycling volume and the theoretical recycling volume of waste products. Considering the role of blockchain in solving the false recycling problem, this paper investigates the channel selection of direct recycling by manufacturers and online recycling by platforms.
2.3. Platform Operations
In the era of booming platform economy, more and more attention has been paid to platform operation, and most of the research focuses on the platform sales format. The marketplace (agency selling) sales format is becoming more popular as the number of independent online sellers increases with the development of Internet technology. Unlike the traditional reselling format, the marketplace acts as an intermediary, providing a trading platform and shared access to information for manufacturers and consumers, and receives commissions [33]. Although the platform loses pricing power, it saves on order fulfillment costs, such as inventory and transportation, and effectively mitigates the double marginal effect in the reseller [34].
Chiang et al. [35] found that the new direct channel results in lower wholesale prices for manufacturers in the indirect channel; it will reduce double marginality and help manufacturers benefit. Retailers can benefit from lower wholesale prices. When manufacturers sell their products through platforms, Arya et al. [36] demonstrated that suppliers can increase efficiency and ensure Pareto improvements by selling products directly to consumers through online stores. Zheng et al. [37] argued that information sharing strategies influence online retailers’ decision to open a commission channel. Tan and Carrillo [38] found that the marketplace is more suitable for the sale of digital goods; the members of the supply chain will make more profits if the publishers set the prices of the products. Abhishek et al. [39] found that the marketplace sells products at lower prices and in higher demand. Guo et al. [40] investigated the conditions under which two independent products are bundled and sold in the marketplace, and found that the price of the products set by the manufacturer in the marketplace influences the platform’s bundling decisions. In addition, Ha et al. [41] found that the appearance of the marketplace will affect the wholesale price under the reseller. In recent years, manufacturers and online platforms have been actively exploring the need for a marketplace to drive sales. Hagiu and Wright [42] showed that a marketplace format is appropriate for long-tail products. Shi et al. [43] found that the choice of marketplace is also related to the intensity of competition; the appearance of the marketplace benefits manufacturers when there is little prior competition for the products. Recently, some studies have concluded that the characteristic of platform operations that distinguishes them from traditional physical retailers is “platform power”, which is defined as the ability to expand market scale and promote positive demand [12]. Moreover, considering that the platform in practice begins to play the recycling function outside the marketing, there is little discussion on the operation strategy of the platform as an online recycling channel in theory. Based on this, this paper will not only discuss the operation strategy of the platform as the marketing party, but also consider the operating strategy of the platform as a recycling party.
In summary, the research on the application of blockchain is mostly focused on the positive sales; however, there has been little research to investigate blockchain in the recycling process to solve the false recycling problems and the whole CLSC management, including recycling channel selection. In this paper, we aim to fill this gap by applying blockchain to the recycling process of waste products, using blockchain characteristics such as authenticity to improve reverse supply chain transparency and prevent false recycling issues that can damage a company’s reputation. The adoption of blockchain will further strengthen the regulation of recycling, increase trust in recycling, and improve the willingness to recycle. Meanwhile, taking the platform as one of the important recycling channels, we are exploring the optimal recycling channel from the triple benefits of economy, environment, and society. To further compare this study with existing studies and to highlight the theoretical contributions of this study, the studies related to this study are listed in Table 1.

Table 1.
Comparison among related studies.
Although we introduce blockchain from the perspective of avoiding false recycling of waste products, which seems to explore the application of blockchain only in the backward chain, it is demonstrated that the implementation of blockchain in the recycling process of waste products will not only build consumer trust in the recycling chain and promote the recycling of waste products, but also play its marketing leverage function by improving brand goodwill, which can further promote the demand with the improvement of brand premium capacity in forward sales. Therefore, this paper investigates blockchain in a CLSC by considering forward and backward interactions, and proposes corresponding management insights, which will be of great value to both forward sales and reverse recycling, and the contribution scope of the study is both forward sales chain and reverse recycling chain.
3. Model Framework
This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, and the experimental conclusions that can be drawn.
This paper investigates a dynamic CLSC system consisting of a manufacturer () and an online platform (), where the manufacturer is responsible for production and remanufacturing, and the platform is responsible for online marketing. In the forward supply chain, the manufacturer sets the retail price of the product and sells it on the platform, which acts as a marketplace. This agency selling format of direct pricing and sales by manufacturers is widely used by online platforms. For instance, it is used when Amazon sells personal computers with ASUStek, Lenovo, and other brands. In this case, the platform charges a commission from the manufacturer; the commission rate is . In this paper, we assume that the commission rate is an exogenous variable; this assumption has been adopted in several studies [34,42,44]. In the actual operation of enterprises, the platform’s commission rate for selling the same type of products is basically fixed. For example, when manufacturers’ products are sold on Amazon as a marketplace, Amazon charges a percentage of the retail price as a commission, depending on the category of the item, such as 15% for shoes, 6% for computers, 20% for jewelry, and 8% for electronics and cameras (http://www.amazon.com, accessed on 25 December 2022). In addition, in order to give scope to “platform power” and expand the potential market demand, the platform will make online marketing efforts , such as webcast and APP home page recommendation, to target customers with the help of big data and so on.
In the backward supply chain, the recycler(M or P)sets recycling efforts , including door-to-door pickup, recycling logistics, recycling packaging, and other efforts, to increase the volume of waste products recycled. Then, this paper uses the characteristics of blockchain, such as transparency and traceability, to regulate the entire recycling process. It not only solves the phenomenon of false recycling, where the real recycling volume is less than the theoretical recycling volume, increases the real recycling rate of waste products, but also improves the brand goodwill of products and enhances consumers’ recycling confidence through the brand. Finally, we consider the benefits of combining blockchain with an appropriate recycling channel to improve the triple bottom line of economy, environment, and society in the CLSC. Thus, the optimal recycling channel selection with blockchain empowerment is achieved.
In this section, we focus on modeling and analyzing four differential game models: manufacturer recycling channel without blockchain (model ), platform recycling channel without blockchain (model ), manufacturer recycling channel with blockchain (model ), and platform recycling channel with blockchain (model ). The structure of the CLSC and the decision content of the members under the above four models are shown in Figure 1. In the CLSC without blockchain adoption, the theoretical volume of consumers is defined as , but the recyclers only receive the real volume . of recycling is loss. It can be seen from Figure 1 In the CLSC with blockchain adoption, thanks to the transparency and traceability of blockchain, the theoretical and real volume of recovery is consistent, that is . In addition, is defined as the sales volume in the forward chain. The finance flow, recycle flow, product flow, service flow, and technology flow are labeled in detail. The other notations are defined in Table 2.
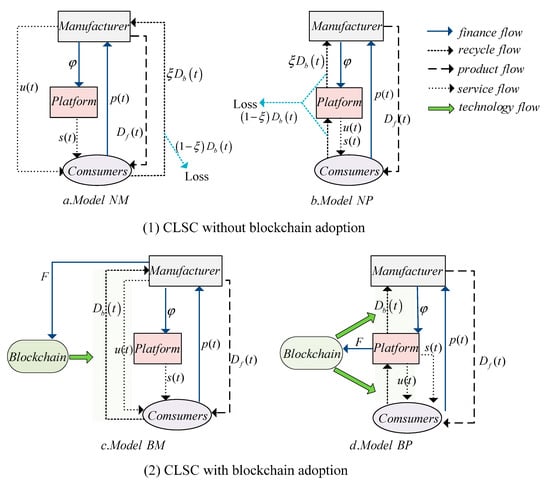
Figure 1.
Model structure.

Table 2.
Notations and definition.
One of the main points used to measure the implementation effect of blockchain in this paper is brand goodwill, which is considered to be an important indicator reflecting the image of enterprises in the minds of consumers, and also an important factor influencing demand. Brand goodwill depends on many aspects, such as high product quality, good company image, perfect management system, and so on. We assume that brand goodwill is affected by both marketing activities and recycling activities and depends on the entire history, not just the current level of marketing and recycling activities. In this case, a common assumption is that is the continuous weighted average of past marketing and recycling efforts, and the weight function decays exponentially. This assumption is very intuitive, because brand goodwill is related to consumers’ perception of the brand, which is the “ psychological state “ that consumers acquire over time rather than overnight [45]. This is also an important consideration for this paper to adopt continuous time dynamic programming theory. This process is captured by defining as a state variable, and its evolution is controlled by the following linear differential equation:
where Equation (1a) represents the situation where the recycler does not implement blockchain for recycling. It reflects the impact of online marketing on brand goodwill. Based on previous studies, we assume that the platform’s marketing effort plays an advertising role by increasing product exposure and consumer awareness of products, which has a positive impact on brand goodwill [12,46,47]. is the coefficient of the platform’s marketing effort on the brand goodwill. is the initial goodwill of the brand when no effort is made. represents the rate of decline in brand goodwill caused by the change in consumer attitude toward the brand. This assumption comes from the advertising goodwill model of Nerlove–Arrow [48]. The study points out that a company’s goodwill will naturally decline as consumers forget the brand or switch to other competing brands, and represents the natural rate of decline. The impact of changes in consumers’ brand attitudes during the recycling process is shown as , where is the percentage of real recycling compared with theoretical recycling. Accordingly, the proportion of false recycling is characterized. We assume that consumers who observe false recycling will directly distrust the brand and accelerate the decline of brand goodwill, which is consistent with our observation in practice. However, if the recycler adopts blockchain, the tracking and tracing of the entire recycling process of blockchain and the technical characteristics of data that is difficult to tamper with will make the real recovery rate infinitely closer to the theoretical recovery rate. We assume that the implementation of blockchain makes the two consistent, thus avoiding false recycling, that is, . The entire recycling process can be presented transparently to consumers who participate in recycling, avoiding brand distrust caused by false recycling. Brand goodwill with blockchain is represented as
Considering the positive impact of goodwill on market demand, in the forward supply chain, the research assumes that the market demand at every moment is positively correlated with brand goodwill and negatively correlated with product retail price [49]:
where is the basic demand of the market, which reflects the basic appeal of the brand to consumers [47]. is the basic market power of the product. represents the potential expansion of market size through “platform power” [25,50]. is the ability to expand the potential market size of the platform. The second root of brand goodwill reflects the saturation effect of brand goodwill on market demand [45]. is the coefficient of price sensitivity of consumers [38]. is the retail price of every unit of product.
In the reverse recycling chain, it is assumed that the theoretical volume returned by consumers is positively influenced by the recycling effort of the recycler (manufacturer/platform) [51], which is assumed as
where is the basic theoretical recycling volume without any recycling efforts, and represents the impact of recycling effort on theoretical recycling volume. Without the adoption of blockchain, the recycling process of waste products is not transparent and regulated, leading to false recycling. We assume the real recycling volume without blockchain as , which shows that the real recycling volume is lower than the theoretical one as . While the recycler implements the blockchain in the recycling process, we assume that the real recycling volume is equal to the theoretical recycling volume as . To ensure that the forward sales volume of the product is greater than the reverse recycling volume, it is assumed that .
It is also believed that recycling waste products can reduce unit cost (unit value of waste products–unit remanufacturing cost) for new products [45]. To build a blockchain system, recyclers must pay a fixed cost [22]. In the extended model, we will further consider the case where the recycler collaborates with a blockchain service company, rather than developing it by itself, and the cost of the blockchain is portrayed as a unit cost . The cost of the recycling effort is [29], the cost of the marketing effort is [52], all cost functions satisfy the law of diminishing marginal returns [51], and is the cost coefficient for the recycling effort and the marketing effort, respectively. Meanwhile, we need to note that the manufacturer signs a residual value sharing contract with the platform in order to motivate the platform to recycle when the manufacturer recycles through the platform, and the platform receives a proportion of the residual value.
In addition, we assume that both the manufacturer and the platform in the CLSC operate over an infinite planning horizon, profit maximization is the decision objective, and the discount rate is . For clarity, the notations used in the article are shown in Table 2.
4. Model Development
This section focuses on further analyzing the optimal decisions of the retail price, the platform’s marketing effort, the recycling effort, and optimal profits under the four models, including manufacturer recycling channel without blockchain (model ), platform recycling channel without blockchain (model ), manufacture recycling channel with blockchain (model ), and platform recycling channel with blockchain (model ). For the sake of clarity, the four recycling models are denoted by superscripts, and the supply chain subjects are denoted by subscripts. The subscript represents the stable value of each decision variable. All the relevant proofs are listed in Appendix A.
4.1. Manufacturer Recycling Channel without Blockchain (Model )
Under the model , the manufacturer first determines the retail price of the products and the recycling effort , and the platform determines the marketing effort . The manufacturer and the platform adopt a manufacturer-driven Stackelberg differential game, where the decision sequence is pricing and recycling decisions by the manufacturer and marketing decisions by the platform on this basis. The differential game model is represented as:
Proposition 1.
The time trajectory of brand goodwill is: ; the stable value of brand goodwill under model is: ; and the retail price of the products, the marketing efforts of the platform, and the recycling efforts of the manufacturer are: , , and . The optimal functions of the manufacturer and the platform are, respectively:
From the optimal decisions under the model in Proposition 1, we know that: (1) Brand market power and “platform power” have a very important impact on corporate decisions and social performance. Brand goodwill, retail price, the profits of supply chain, and social performance are positively correlated with brand market power and “platform power”. That is, if a product has high market power and the platform has made marketing efforts through advertising and other activities, both the manufacturer and the platform can make more profits. (2) Analyzing the impact of the real recycling rate of waste products, it is found that the real recycling rate has a positive effect on brand goodwill and recycling effort, and the higher the real recycling rate, the higher the brand goodwill of the products, and the higher the retail price of the products. The recycler’s recycling effort is incentivized by the real recycling rate, and the higher the real recycling rate, the higher the reward for the recycler’s recycling effort. In addition, supply chain profits and social performance are positively correlated with the real recycling rate, and supply chain members strive to increase the real recycling rate for optimal profits.
4.2. Platform Recycling Channel without Blockchain (Model )
Under the model , the manufacturer first sets the retail price of the products, and then, the platform sets the marketing effort and the recycling effort . The platform gives the waste products to the manufacturer for remanufacturing and receives a proportional share of the residual value. The manufacturer and the platform adopt a manufacturer-driven Stackelberg differential game, and the decision sequence is: the manufacturer makes the pricing decision, and the platform makes the marketing and recycling decisions. The differential game model of the manufacturer and the platform is represented as
Proposition 2.
The time trajectory of brand goodwill is: ; the stable value of brand goodwill under model is: ; and the retail price of the products, the marketing effort, and the recycling effort of the platform are: , , and . The optimal functions of the manufacturer and the platform are, respectively:
The optimal decisions under the model in Proposition 2 are similar to the optimal decisions under the model . (1) The platform’s brand goodwill, retail price, and marketing efforts are consistent; these are , , and . Brand market power and “platform power” have a positive impact on corporate decisions and social performance, while the real recycling rate of waste products has a positive impact on brand goodwill, recycling effort, and supply chain profits and social performance. (2) The platform will return the waste products to the manufacturer for disposal and remanufacturing when the platform recycles, and the platform will share a proportion of the residual value. The platform’s recycling effort is positively correlated with the proportion. The higher the profits the platform receives from the residual value, the more willing the platform is to make an effort to recycle. At the same time, the proportion of waste products affects the volume of reverse recycling, which has a positive impact on supply chain profits and social performance.
Corollary 1.
If the recycler does not implement blockchain to monitor the recycling process, the manufacturer’s recycling channel of choice is manufacturer recycling.
Comparing the profits of the manufacturer between the model and the model , there is always . This illustrates that the manufacturer is always better off collecting the waste products without the blockchain implementation. Compared with the platform-recycling channel, the manufacturer can obtain all the profits of the waste products under the manufacturer recycling channel so that the manufacturer will choose to recycle the waste products. Additionally, when comparing the profits of the platform under the model and the model without blockchain, there is always . The model is better than the model for the platform. That is, the platform prefers to recycle the waste products in order to obtain a share of the residual value of the waste products. Compared with the manufacturer recycling channel, it is clear that the platform makes more profit from recycling.
If the recycler does not implement blockchain, there is a conflict in the choice of recycling channels: both the manufacturer and the platform tend to recycle waste products themselves, without blockchain, in order to keep the residual profits. While the manufacturer makes the choice of recycling channel in its favor, it does not make the platform better off. Therefore, the manufacturer and the platform cannot reach a stable willingness to cooperate on this recycling channel for waste products when blockchain is not implemented.
4.3. Manufacturer Recycling Channel with Blockchain (Model )
Under the model , the manufacturer will invest in building a blockchain system with a fixed cost, and the decision sequence is this: the manufacturer first makes pricing and recycling decisions and determines the retail price of the products and the recycling effort , and the platform makes marketing decisions to determine the marketing effort . The manufacturer and the platform take a manufacturer-driven Stackelberg differential game. The differential game model for the manufacturer and the platform is represented as
Proposition 3.
The time trajectory of brand goodwill is: ; the stable value of brand goodwill under the model is: ; and the retail price of the products, the platform’s marketing effort, and the manufacturer’s recycling effort are: , , and . The optimal functions of the manufacturer and the platform are, respectively:
The analysis of optimal decisions and optimal profits under the model in Proposition 3 shows this: (1) Brand market power and “platform power” will have a positive impact on brand goodwill, the retail price, and the platform’s marketing effort, and corporate decisions and social performance, which is the same as the recycling channel without blockchain. The difference in the intensity of the impact can be observed in particular in Section 6. (2) Members of the supply chain can monitor the entire recycling process through blockchain, effectively solving the problem of false recycling. The theoretical recycling volume is equal to the real recycling volume; that is, the real recycling rate is . The manufacturer needs to build a blockchain system to monitor the recycling process under the model . We assume that the construction of the blockchain system requires a fixed cost , which will determine whether or not the manufacturer proceeds with the construction of the blockchain system; that is, has an inverse effect on the manufacturer’s profits, the manufacturer will not establish a blockchain system if the costs are greater than the profits and vice versa, and the manufacturer may choose to adopt blockchain. The manufacturer’s recycling channel will not affect the platform’s profits, but will conversely affect social welfare.
4.4. Platform Recycling Channel with Blockchain (Model )
Under the model , the platform establishes a blockchain system to monitor the recycling process, which will invest a fixed cost , and at the same time, the platform gives the waste products to the manufacturer for remanufacturing, and obtains a proportion of the revenue. Since the residual value of the waste products cannot be shared, the manufacturer pays the platform its share of the revenue up front. The manufacturer and the platform adopt a manufacturer-driven Stackelberg differential game; the decision sequence is: the manufacturer makes pricing decisions, and the platform makes marketing and recycling decisions based on those decisions. The manufacturer determines the retail price of the products, and the platform sets the marketing effort and the recycling effort. The differential game model is expressed as
Proposition 4.
The time trajectory of brand goodwill is: ; the stable value of brand goodwill under the model is: ; and the products’ retail price, the platform’s marketing effort, and the platform’s recycling effort are: , , and . The optimal functions of the manufacturer and the platform are, respectively:
In Proposition 4, the optimal decisions under the model are similar to the optimal decisions under the model . From that: (1) , , , the stable value of brand goodwill, the retail price, and the marketing effort are consistent; and the brand market power and “platform power” positively influence corporate decisions and social performance. (2) The real recycling rate is under the model . The platform returns the waste products to the manufacturer for disposal and remanufacturing, and receives a proportion of the residual value. Therefore, the recycling effort is positively correlated with the share of residual value, and the higher the residual value profits received by the platform, the more willing it is to make recycling efforts. In addition, the construction of the blockchain system requires a fixed cost , has an inverse effect on the platform’s profits, and the platform will not establish a blockchain system if the cost is higher than the profit. The cost of blockchain will not have a direct impact on the manufacturer’s profits, but it will have an impact on social welfare.
Corollary 2.
The optimal recycling channel for manufacturers with blockchain implementation is the manufacturer recycling channel if . If , the result will be the platform recycling channel. Additionally, if , the two recycling channels make no difference to the manufacturer, while .
From Corollary 2, it is concluded that the selection of recycling channel is related to the fixed cost of establishing the blockchain system. In other words, if the profit obtained by the manufacturer from the establishment of the blockchain system is higher than the profit obtained by the platform, the manufacturer will choose to establish the blockchain for the recycling of waste products; otherwise, the choice of the platform recycling channel will be more appropriate. Comparing the profits of the platform under the models and , the platform will benefit from the manufacturer recycling channel if , and the platform recycling channel if . Additionally, there is no difference for the platform if , while . A key finding is that if , the manufacturer will choose the manufacturer recycling channel, and the platform can benefit from it at the same time. At this point, the platform does not need to invest in blockchain to recycle waste products, but it can reap the additional benefits of the manufacturer’s investment in blockchain in the forward sales process: the blockchain implementation drives forward demand by increasing the manufacturer’s incentive to invest in recycling efforts and reducing the brand goodwill decay caused by brand goodwill.
5. Value Analysis of Blockchain Implementation
Based on the hypothesis analysis of the four models, this section will further compare the corporate decisions and social performance under the two different recycling channels with and without blockchain adoption, thus investigating the value of blockchain implementation.
5.1. The Condition of Blockchain Adoption
Proposition 5.
In the manufacturer recycling channel, the manufacturer will use blockchain technology to track the recycling process if ; in the platform recycling channel, the platform will implement blockchain technology if , while
From Proposition 5, we can see that the recycler’s choice of different recycling channels is related to the fixed cost of blockchain implementation. Besides, the cost threshold for blockchain adoption varies across recycling channels. The common denominator is that the cost threshold is related to the difference between the real and theoretical volume of the waste recycled. The greater the difference, the higher the cost of blockchain implementation acceptable to recyclers; that is, the greater the need for blockchain implementation in the waste recycling process. The difference is that the cost threshold for the recycler of the blockchain implementation under different recycling channels is affected to a different extent by the platform’s commission rate and the residual value of the waste products. This suggests that recyclers should also consider the type of product and the value of the waste products to determine the conditions for blockchain adoption. The comparison between and reveals that
This means that when the commission rate is relatively low, the manufacturer can accept higher blockchain implementation costs to facilitate the real recycling of waste products. Additionally, the situation will be reversed when the commission rate is relatively high.
Further analysis of the impact of blockchain implementation on the interests of other members in the CLSC under different recycling channels shows that: the implementation of blockchain in both recycling channels can effectively increase the profitability of other members of the CLSC. The reasons are obvious. The adoption of blockchain avoids the discrepancy between the real recycling volume of waste products and the theoretical recycling volume, and maximizes the real recycling volume. In addition, it also reduces the decay rate of brand goodwill.
5.2. Impact of Blockchain Implementation on Corporate Decision Making and Performance
Proposition 6.
(Impact of blockchain implementation on retail price, recycling effort, marketing effort, brand goodwill, and demand) Comparison of the retail price, recycling effort, marketing effort, brand goodwill, and demand across four recycling channels. Analysis of the impact of blockchain implementation.
- (1)
- In the manufacturer recycling model, there are , , , , , and .
- (2)
- In the platform recycling model, there are , , , , , and .
The results show that the implementation of blockchain under different recycling channels can incentivize the platform to increase online marketing efforts, while incentivizing the recycler to increase recycling efforts. We call this impact of blockchain on increasing the motivation of business inputs the “decision incentive effect.” As the level of decision making increases, so does brand goodwill and, consequently, retail prices. As a result, the real recycling volume of waste products in both recycling channels and the demand in the positive chain are increased. We call this cascading effect of blockchain the “marketing leverage effect.” It is demonstrated that the implementation of blockchain in the recycling process of waste products can not only build consumer trust in the recycling chain and promote the recycling of waste products, but also play its marketing leverage function by improving brand goodwill, which can further promote the demand with the improvement of brand premium capacity in forward sales. Therefore, it can be concluded that the implementation of blockchain on the recycling side of the CLSC has the dual function of promoting recycling in the backward direction and promoting demand in the forward direction.
Proposition 7.
(Impact of blockchain implementation on corporate profits, consumer surplus, and social welfare) Within the feasible range of the blockchain adoption, that is, in the manufacturer recycling channel and in the platform recycling channel, the results are: , , , , , and . Besides, if , , and if , , while
Comparing corporate profits, consumer surplus, and social welfare with and without blockchain, it is shown that the cost of building the blockchain is critical to the performance of the CLSC. What can be proven is that the implementation of blockchain in different recycling models will effectively increase the profits of the CLSC companies and consumer surplus, if the cost of blockchain implementation is within a certain range. To further define the cost range, the social welfare under both recycling channels will also be enhanced with the implementation of blockchain. Additionally, observing the comparison results, it can be seen that the larger the difference between the real recycling volume and the theoretical recycling volume, the more effective the blockchain implementation will be in improving the overall performance.
Proposition 8.
(Impact of blockchain adoption on recycling channel selection) By comparing corporate decisions and performance with and without blockchain implementation, an interesting finding is that blockchain implementation coordinates CLSC channel selection. Specifically, when blockchain is not implemented, manufacturers and platforms tend to collect the waste themselves. The manufacturer chooses the optimal recycling channel, but not the platform. Additionally, the overall performance of the CLSC does not improve across the board. When blockchain is implemented, both the manufacturer and the platform are better off in the manufacturer’s recycling within a certain range of blockchain implementation cost, that is, . Therefore, within this cost range, the platform benefits from the manufacturer investing in the blockchain for recycling through the free-rider effect, and a balanced recycling channel exists in the CLSC that allows both to be better off. We call this blockchain-enabled equilibrium, which allows both the manufacturer and the platform to agree and benefit from the same recycling channel, the “incentive alignment effect.” Furthermore, the balanced recycling channel with blockchain enables the triple benefits of economy, environment, and society in the CLSC.
Proposition 9.

Considering the impact of each parameter on each optimal decision, such as brand goodwill, retail price, recycling effort, and marketing effort, we analyze the key parameters under four recycling channels, as shown in Table 3.

Table 3.
Sensitivity of key parameters for manufacturer and platform recycling with and without blockchain.
This can be concluded from the sensitivity analysis of the key parameters shown in Table 3: (1) The increase in the brand’s market power can positively increase brand goodwill and further promote the retail price by promoting the brand’s premium power. The greater the brand’s market power, the higher the retail price, and the marketing effort is positively influenced by the brand’s market power. (2) Brand goodwill and retail price are positively related to the commission rate. The higher the commission rate set by the platform, the higher the brand goodwill and the retail price will be. Meanwhile, the platform’s marketing effort is positively influenced by the commission rate; the higher the commission rate, the more revenue the platform receives and the more it will increase its marketing effort for the product. (3) The brand goodwill, the retail price, and the platform’s marketing effort are inversely related to the price sensitivity coefficient. (4) The brand goodwill of the product, retail price, marketing effort, and recycling effort are positively associated with the real recycling rate of waste products without blockchain. For products with higher recycling rate and higher brand goodwill, consumers will trust them more; meanwhile, the platform is willing to make more marketing effort to promote product sales, and the recycler is willing to make more recycling effort. This is a virtuous cycle mechanism of recycling. (5) If the platform performs recycling, the platform’s recycling effort is positively correlated with the proportion of waste products; the higher the proportion, the higher the platform’s benefit, and the more the platform is willing to pay for more recycling effort. (6) The cost coefficient of marketing effort negatively affects brand goodwill, retail price, and marketing effort, while the coefficient of recycling effort also negatively affects recycling effort.
6. Numerical Analysis
This section uses numerical examples to verify the analytical conclusions reached in the previous sections. Through linear analysis of key exogenous variables, such as real recycling rate and “platform power”, we obtain the trajectories of optimal decisions of brand goodwill, the retail price, supply chain members’ profits, and social welfare under different values. Based on the actual situation (Amazon charges a percentage of the retail price as commission according to the item’s category, such as 15% for shoes, 6% for computers, 20% for jewelry, and 8% for electronics and cameras) and referring to some literature [22,53], we set the specific parameters as follows: ; ; ; ; ; ; ; ; ; ; ; ; ; ; .
The manufacturer’s choice and the platform’s willingness to engage in the recycling channel are examined by comparing the changes in the manufacturer’s and platform’s profits with blockchain, as shown in Figure 2.
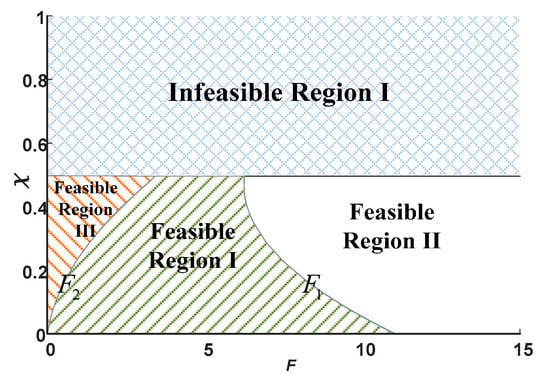
Figure 2.
The choice of the model and the model .
As shown in Figure 2, and represent the boundaries, where the manufacturer and the platform choose the same recycling channel. Infeasible Region Ι indicates a completely infeasible region (does not conform to the sales profits being greater than the residual value of the waste products). Feasible Region Ι indicates that the manufacturer chooses the model in this region, from which the platform can benefit from forward sales; that is, both the manufacturer and the platform can be optimized under the model . Feasible Region ΙΙ is that neither the manufacturer nor the platform can benefit from blockchain. Feasible Region ΙΙΙ indicates that the manufacturer chooses the model , from which the platform cannot benefit, but he can benefit from the model ; they will benefit from different recycling channels. Therefore, in order to maximize the benefits, the manufacturer and the platform will choose the recycling channel that can generate revenue to coordinate the profits, and both the manufacturer and the platform will prefer Feasible Region Ι.
In order to compare the impact on corporate decisions and social performance under four recycling channels, we analyze the changes in supply chain profits and social welfare by numerical analysis and derive the following figure of recycling channel selections, and the manufacturer and the platform achieve their optimal interests, respectively, as shown in Figure 3.
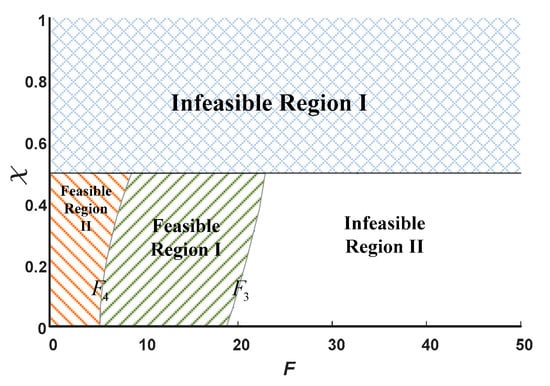
Figure 3.
The choice of models for corporate decisions and social performance of the manufacturer and the platform.
Figure 3 shows: and represent the boundaries, where all the social performance can benefit from this. Infeasible Region Ι represents the infeasible region (does not satisfy the condition that the profit of the new product is greater than the residual value of the waste products). Infeasible Region ΙΙ indicates that social welfare and supply chain profits are not improved under two models with blockchain. Feasible Region Ι indicates that supply chain profits and social welfare can be increased in platform recycling with blockchain. Feasible Region Ι + Feasible Region ΙΙ indicates that the supply chain profits and social welfare under the model are better than the model . Therefore, the analysis shows that the goal of recycling with blockchain can be better achieved than without blockchain, for both corporate decisions and social performance, whether for platform recycling or for manufacturer recycling, in Feasible Region Ι.
The selection of recycling channel of the platform is related to the proportion of residual value, when examining the triple benefits of economy, environment, and society in the CLSC under platform recycling, as shown in Figure 4, Figure 5 and Figure 6 below based on numerical analysis.
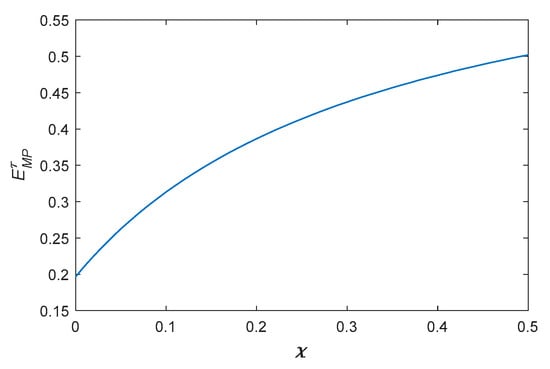
Figure 4.
The change of platform recycling environmental efficiency.
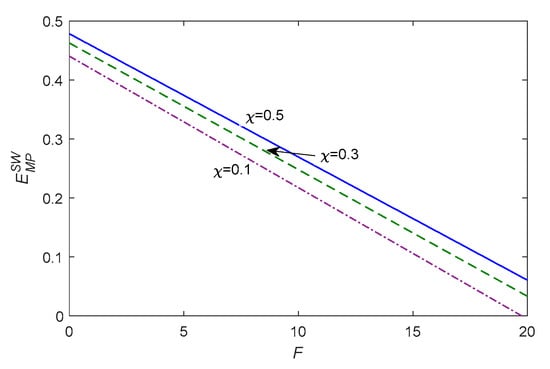
Figure 5.
The change in the growth rate of supply chain profits.

Figure 6.
The change in the growth rate of social welfare.
Figure 4, Figure 5 and Figure 6 represent the environmental efficiency, the growth rate of supply chain profits, and the growth rate of social welfare of the model compared with the model . From Figure 4, it can be seen that the environmental efficiency is positively related to the proportion; as the proportion obtained by the platform increases, the platform will be more willing to carry out recycling activities. The platform takes its own interests as a starting point, and the additional profits it gains will enhance its higher sense of social responsibility. According to Figure 5 and Figure 6, we can see that the growth rate of supply chain profits and social welfare are negatively related to the fixed cost of blockchain; that is, if the fixed cost increases, both the profits and social performance will decrease, and if their growth rate is less than zero, the members of the supply chain will not choose to establish a blockchain system.
By examining the patterns of products’ price under different initial prices, we analyze the patterns of change over time. The specific trajectory is shown in Figure 7.

Figure 7.
Time trajectory of products’ retail price.
From Figure 7, it can be observed that if the initial retail price is higher than the stable retail price, the retail price will gradually decrease until it eventually converges to the steady price; if the initial retail price is lower than the stable retail price, the retail price will gradually increase until it eventually converges to the stable price over time. In addition, by observing the linear variation, we find that the retail price of the product gradually converges to, but never reaches, the stable price. Then the price in the model and the model is the same, and the price in the model and the model is same. The stable price with blockchain is higher than it without blockchain, while the change rate of the price with blockchain is lower than the change rate of the price without blockchain. The reason for this change may be the cost of establishing the blockchain, and in order to make more profits, the manufacturer will increase the retail price.
According to Figure 8 and Figure 9, we can find that the steady goodwill and retail price are positively influenced by the real recycling rate; ultimately, it is because the real recycling rate affects the change in steady price. In this paper, we assume that the real recycling rate affects the speed of the consumer forgetting about the brand without blockchain; the forgetting coefficient of brand goodwill is larger if is smaller. The steady goodwill and steady price without blockchain gradually converge to them with blockchain as increases. If , it reaches the stable value.

Figure 8.
The steady-state goodwill with real recycling rate.
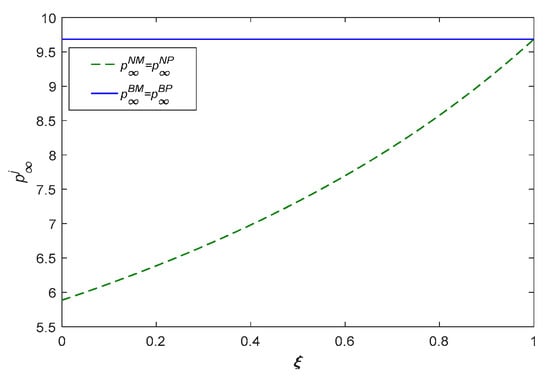
Figure 9.
The steady price with real recycling rate.
From Figure 10 and Figure 11, we can see that the demand for forward sales and reverse recycling and the growth rate of recycling are positively correlated with the real recycling rate in the CLSC. First, it can be seen that the forward sales of products are greater than the reverse recycling, which means that the manufacturer is not able to recycle all the waste products after selling new products. There are many reasons for this, such as the lack of residual value or the reluctance of consumers to recycle. Second, the amount of forward demand and reverse recycling with blockchain is greater than it without blockchain, and the real recycling rate limits the amount of forward demand and reverse recycling without blockchain. In addition, manufacturer recycling rates are higher than platform reuse rates, regardless of whether blockchain is used.
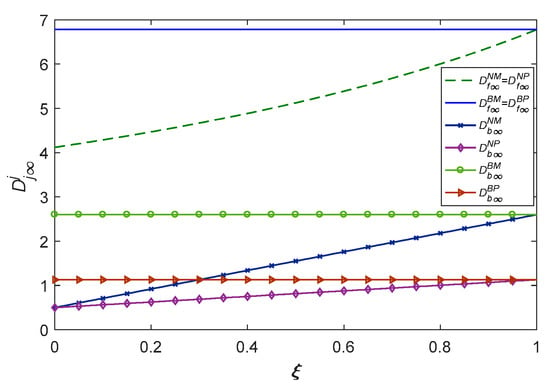
Figure 10.
The demand with real recycling rate.
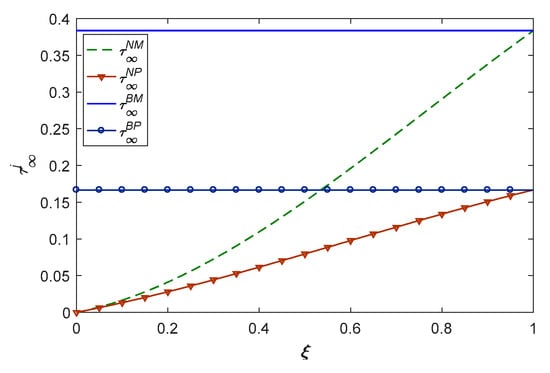
Figure 11.
The growth rate of recycling with real recycling rate.
As shown in Figure 12, Figure 13, Figure 14 and Figure 15, optimal decisions such as supply chain profits, manufacturer and platform profits, and social welfare are positively related to the real recycling rate of waste products. We can see that supply chain profits and social welfare are higher in manufacturer recycling than in platform recycling. As the real recycling rate increases, the manufacturer’s recycling rate is higher than that of the platform without blockchain; it is better for the profits, corporate decisions, and social performance for the manufacturer to recycle directly without secondary transportation. Under this assumption, the manufacturer can obtain more profit if it chooses to establish its blockchain system; if the platform obtains less profit establishing the blockchain system than the manufacturer recycling, both the platform and the manufacturer will choose the model .
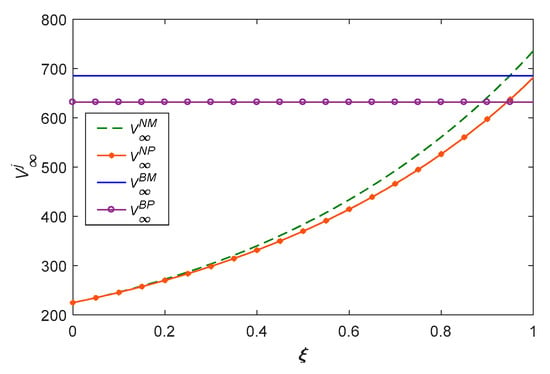
Figure 12.
The profits of supply chain with real recycling rate.

Figure 13.
The manufacturer’s profits with real recycling rate.
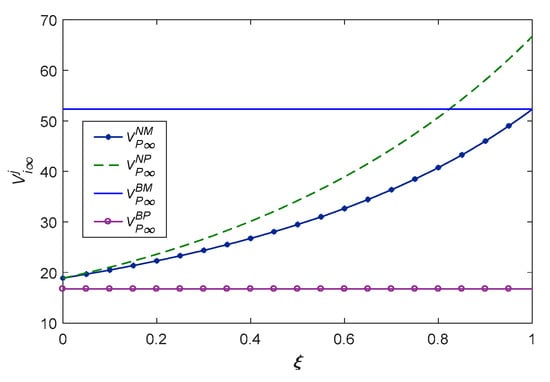
Figure 14.
The platform’s profits with real recycling rate.

Figure 15.
The social welfare with real recycling rate.
As shown in Figure 16 and Figure 17, the stable price and brand goodwill are positively influenced by “platform power” for four models. The stable goodwill and price with blockchain are always greater than them without blockchain. Additionally, the growth rate with blockchain is higher than that without blockchain.
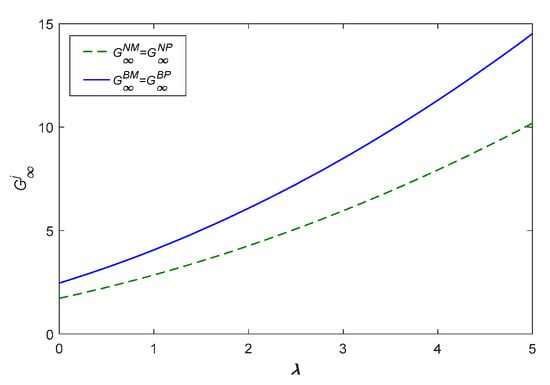
Figure 16.
The brand goodwill with platform power.
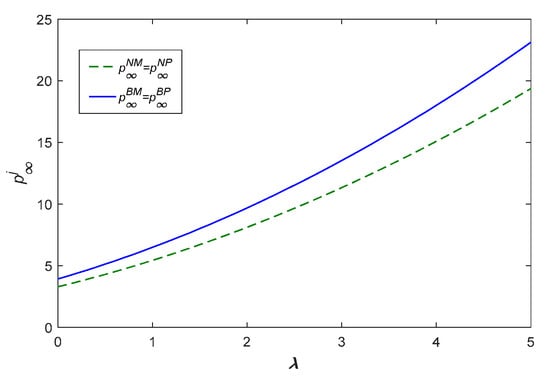
Figure 17.
The retail price with platform power.
From Figure 18, Figure 19 and Figure 20, we can see that there are equal growth rates of manufacturer profit, platform profit, and social welfare under two channels with blockchain. Similarly, the manufacturer’s profits, platform’s profits, and social welfare grow at the same rate under two channels without blockchain. The figure shows that the profits and social welfare of the manufacturer with blockchain are better than those without blockchain, and the model is always better than the model . However, for the platform’s profits, the model is better than the model ; the platform recycling channel is better than the manufacturer recycling channel without blockchain.
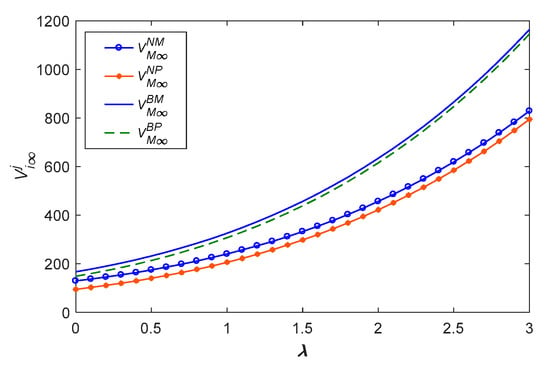
Figure 18.
The manufacturer’s profits with platform power.

Figure 19.
The platformer’s profits with platform power.
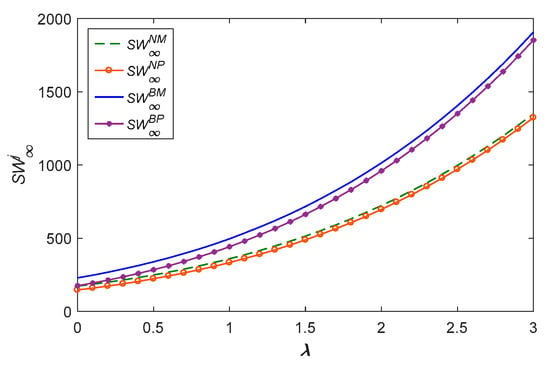
Figure 20.
The social welfare with platform power.
7. Extension with Unit Cost of Blockchain Implementation
7.1. Manufacturer Recycling Channel with Unit Cost of Blockchain (Model )
In the extended model, we consider the adoption of blockchain through a third-party blockchain service company. In this way, the manufacturer and the platform do not have to pay a fixed cost for the blockchain, but only pay a marginal cost per unit based on the number of waste products. The manufacturer is involved in the recycling and disposal of products, so the manufacturer pays the marginal cost of recording the recycling process. If the platform recycles waste products, the platform must return them to the manufacturer for disposal, so both the manufacturer and the platform must keep records, and both must pay a marginal cost . Similar to the benchmark model, we use superscript and to represent manufacturer recycling and platform recycling, respectively, and subscript and to represent CLSC members, the manufacturer, and the online platform, respectively.
Under the model , the manufacturer and the platform adopt a manufacturer-driven Stackelberg differential game: The manufacturer first determines the retail price and the recycling effort , while the manufacturer is required to pay a third-party company the unit marginal cost . Then, the platform determines the marketing efforts . The differential Stackelberg game model can be summarized as
Proposition 10.
The time trajectory of brand goodwill is: ; is the stable value of brand goodwill under the model ; and the products’ retail price, platform’s marketing effort, and manufacturer’s recycling effort are: , , and . The optimal functions of the manufacturer and the platform are, respectively:
7.2. Platform Recycling Channel with Unit Cost of Blockchain (Model )
Under the model , the manufacturer and the platform also adopt a manufacturer-driven Stackelberg differential game: The manufacturer first determines the retail price ; then the platform determines the marketing decisions and the recycling effort . In addition, in order to record the data of all links of recycling, both the platform and the manufacturer need to pay a marginal blockchain cost under the platform recycling mode. The differential game model is described as
Proposition 11.
The time trajectory of brand goodwill is: ; is the stable value of brand goodwill under the model ; and the products’ retail price, platform’s marketing effort, and platform’s recycling effort are: , , and . The optimal functions of the manufacturer and the platform are
7.3. The Condition of Blockchain Adoption
Proposition 12.
In the model , the manufacturer will pay a unit cost per product to a third-party blockchain technology service company. The manufacturer will use blockchain technology to track the recycling process if . In the model , the platform will implement blockchain technology if , while
Using numerical examples, we specifically describe the choice of blockchain technology by the manufacturer and the platform and the relationship between the proportion of the residual value and a unit blockchain cost.
As shown in Figure 21, Infeasible Region represents a completely infeasible region in a reality. Feasible Region Ι indicates that both the manufacturer and the platform can benefit under the model . Feasible Region ΙΙ and Feasible Region ΙΙΙ indicate that the manufacturer chooses the model ; the platform does not benefit from this choice.
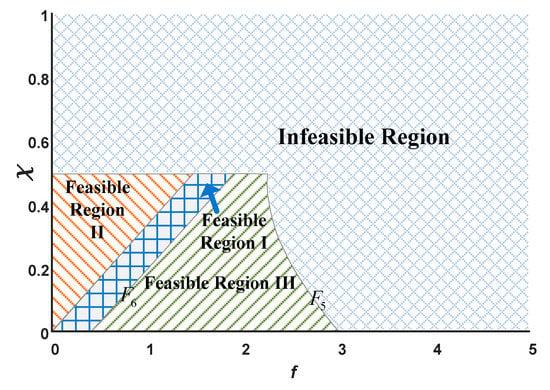
Figure 21.
Recycling channel selection with a marginal cost of blockchain.
We can see that, as in the benchmark model, the adoption of the blockchain system coordinates the selection of recycling channels by the manufacturer and the platform, resulting in the improvement of benefits for both the manufacturer and the platform. This is related to the marginal cost of the blockchain. If the manufacturer’s profit without blockchain is less than the profit with blockchain, the manufacturer chooses to use blockchain for recycling, and if the platform benefits from it and does not need to recycle waste products, the manufacturer and the platform reach an agreement on the benefits; that is, they choose the model . Conversely, in other recycling channels, the adoption of blockchain does not benefit both the manufacturer and the platform, and the interests of the manufacturer and the platform cannot be optimized at the same time.
8. Conclusions and Management Insights
8.1. Conclusions
In recent years, platforms have increasingly acted as online marketplaces in online commerce. Unlike the reseller format, where online platforms must bear the costs of order fulfillment, such as inventory and transportation, platforms act as intermediaries and receive a commission from manufacturers in the marketplace, greatly reducing operational costs and risk. In addition, to promote environmental performance, the state strongly emphasizes energy conservation and promotes the separation and recycling of waste products nationwide. Recycling of waste products has become a necessary link for the supply chain to actively respond to the national call for sustainability. This paper considers a CLSC consisting of a manufacturer and an online platform. In the forward chain, the manufacturer sells products through the platform, which acts as a marketplace. In the backward chain, the manufacturer chooses the appropriate recycling channel to collect waste products. To further solve the problem of false recycling where the real recycling volume does not match the theoretical recycling volume as well as consumer distrust, the recycler can decide to implement blockchain to monitor the entire recycling process of waste products. Considering the dynamic evolution of brand goodwill and the game relationship between the manufacturers and the platform, four differential game models are developed under manufacturer recycling and platform recycling with and without blockchain. Using the Bellman dynamic programming theory, the dynamic pricing decisions of the manufacturer, the online marketing efforts of the platform, the recycling efforts of the recycler, and the brand goodwill and triple benefits of the economy, environment, and society in the CLSC are solved under four models. Through comparative analysis, we answered the three questions raised earlier: we clarified the conditions for blockchain implementation, obtained the three main effects of blockchain implementation, and explored the optimal combination of blockchain and a recycling channel that can simultaneously improve the triple benefits of the CLSC. The main conclusions are as follows:
- (1)
- Blockchain can effectively solve the phenomenon of false recycling and realize the supervision of the whole recycling process through its transparency, traceability, and tamper-proofing. Weighing the implementation costs and effectiveness of blockchain, cost thresholds for implementing blockchain under different recycling channels are clarified. According to the numerical analysis, we obtained the optimal conditions for the implementation of blockchain. The analysis results show that the recycler is motivated to implement blockchain within a certain range of a fixed cost. The cost thresholds under different recycling models are related to the platform commission rate and the salvage sharing ratio. Additionally, the results show that manufacturers can accept higher blockchain implementation costs in the category of lower platform commission rates, and conversely, platforms will invest more. Furthermore, the greater the difference between the real and theoretical volume of recovery, the greater the need for blockchain implementation.
- (2)
- By analyzing decision making, performance, and manufacturer recovery channel selection before and after blockchain implementation, this study summarizes three major effects of blockchain implementation: (1) Decision incentive effect, that is, the implementation of blockchain under different recycling channels, incentivizes the platform to increase its online marketing efforts, while incentivizing the recycler to increase its recycling efforts. (2) Marketing leverage effect, that is, the implementation of blockchain in the recycling process of waste products, can not only build consumer trust in the recycling chain and promote the recycling of waste products, but also play its marketing leverage function by improving brand goodwill, which can further promote the demand with the improvement of brand premium capacity in forward sales. (3) Incentive alignment effect, that is, if blockchain is not implemented, the manufacturer and the platform cannot improve together under the same recycling channel. Using blockchain, the manufacturer and the platform agree to recycle within a certain cost range. In this state, the platform benefits from the manufacturer’s investment in the blockchain for recycling through the free-rider effect, and there is a balanced recycling channel in the CLSC that allows both to be better off.
- (3)
- When blockchain is not implemented, the manufacturer’s choice is the manufacturer recycling channel, a finding consistent with those in previous studies, such as De Giovanni et al. [26]. This result is also consistent with the intuition that the manufacturer will capture the full salvage value of the waste products by recycling them on its own, without having to share the salvage value with the platform. However, the analysis reveals that this recycling channel choice does not make the platform more profitable and even frustrates its online marketing, which is not beneficial to the sustainability of the CLSC in the long run. Additionally, the blockchain implementation shows that the adoption of blockchain on the recycling side of the CLSC has the dual function of promoting recycling in the backward direction and promoting demand in the forward direction. Furthermore, the manufacturer implementing blockchain for used product recycling can coordinate the platform according to its recycling program. We define a cost range for blockchain implementation, that is, , where the manufacturer and the platform reach an agreement on manufacturer recycling with blockchain, and the triple benefits of the CLSC are optimally realized. Additionally, the more efficient the manufacturer’s recycling, the greater the scope of stable cooperation. What is more, research shows that the implementation of blockchain amplifies the potential market scale expansion capacity of the platform power, allowing the platform to act as an online marketplace to achieve stable cooperation with the manufacturer and further promote the sustainable development of the CLSC. Compared with the recycling without blockchain, the implementation of blockchain can effectively regulate the contradiction between recyclers, improve consumers’ awareness, and motivate consumers’ recycling behavior.
To demonstrate the reliability and robustness of the above findings, we further extend the model by replacing the fixed implementation cost of blockchain in the benchmark model with the unit implementation cost of blockchain. The results show that whether or not the recycler builds the underlying blockchain technology itself, the results of the study do not qualitatively change (corresponding to the fixed cost of blockchain in the benchmark model), or the recycler may work with a blockchain technology service company to implement the blockchain (corresponding to the unit cost of blockchain in the extended model).
Of course, to study the impact of blockchain on the recycling of waste products, we only focused on the choice of recycling channels and did not study the differences in sales modes. At the same time, we have adopted the dynamic game theory from a long-term perspective; there are limitations in parameter setting, which is a problem we will overcome in the future.
8.2. Management Insights
In this paper, we gain some management insights on blockchain implementation from the perspective of used product recycling and CLSC management by examining the combination of blockchain adoption and recycling channel selection. First, the need and value of blockchain implementation lies in the difference between the real recycling volume and the theoretical recycling volume. For example, BASF AG in Canada is using its blockchain platform, “reciChain”, to increase the recycling of plastic products and improve the circularity of its supply chain, which currently has a recycling rate of less than 11%. China’s Hainan green technology unlocks the value of 6.5 billion used clothes in China with blockchain. The bigger the difference, the more necessary and better the implementation of blockchain by the recycler will be. Second, because of the information advantage and platform power, we intuitively believe that the platform recycling channel will be better than a traditional retailer and even be more effective than manufacturer recycling. However, the counterintuitive conclusion is that while the platform tends to recycle waste products, the current situation of false recycling of waste products cannot make the platform recycling bring more benefits to the CLSC or even make the CLSC members agree on a certain recycling channel. The implementation of blockchain reconciles inconsistencies in channel selection and can enable the platform and the manufacturer to better recycle within a certain cost range, even achieving the triple benefit of the CLSC. From the results of the above analysis, we place the management insights obtained in Table 4.

Table 4.
Management insights.
From the management insights in Table 4, we need to give some suggestions to governments and companies; that is, considering the recycling of waste products from the perspective of environmental protection and resource conservation, the government should adopt policies to encourage recyclers to implement blockchain and give them more compensation. Enterprises should also contribute to the development of circular economy on the basis of securing profits; various enterprises should do what they can to build blockchain.
Author Contributions
Conceptualization, D.-Q.M. and J.-S.H.; methodology, X.-Q.W.; software, X.-Q.W. and X.W.; validation, D.-Q.M.; formal analysis, X.-Q.W.; writing—original draft preparation, X.-Q.W.; writing—review and editing, J.-S.H.; supervision, J.-S.H.; funding acquisition, D.-Q.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number 72202113, and Natural Science Foundatin of Shandong Province, grant number ZR2022QG017.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendix A
Proof of Proposition 1.
According to the backward induction, we first solve the marketing decisions of the platform. Then according to the Bellman dynamic programming theory, the continuous differentiable function satisfies the Hamilton–Jacobi–Bellman equation (HJB equation):
where is the optimal value function for the platform under the model ; that is, the optimal total profits of the platform, , represents the first-order partial derivative of the optimal value function of the platform about the state variable . The optimal marketing effort for the platform is . Bringing the optimal marketing effort into the manufacturer’s functional, the manufacturer’s Hamilton–Jacobi–Bellman equation is built as:
where is the optimal value function for the manufacturer under the model , and the manufacturer’s pricing decision and recycling decision are: . Bringing into the HJB equations of the manufacturer and the platform, we can obtain:
Based on the functional of the right side of the equations, we assume that the value functionals of the left side of the equations are .
The corresponding first-order partial derivatives are , bringing them into the HJB equations; the set of equations is obtained as
Based on the constant relationship between the two sides of the set of equations, the following results are solved:
Proposition 1 has been certified. □
Proof of Proposition 2.
The solution process uses the backward induction; we first solve the marketing and recycling decisions of the platform. According to the Bellman dynamic programming principle, the continuous differentiable function satisfies the Hamilton–Jacobi–Bellman equation:
where is the optimal value function for the platform under the model , represents the first-order partial derivative of the optimal value function of the platform about the state variable . The optimal marketing effort and recycling effort for the platform are, respectively, . Bringing the optimal marketing effort and recycling effort into the manufacturer’s functional, the manufacturer’s Hamilton–Jacobi–Bellman equation is:
where is the optimal value function for the manufacturer under the model , and the manufacturer’s pricing decision is: . Bringing , , and into the HJB equations of the manufacturer and platform, we can obtain:
Based on the functionals of the right side of the equations, we assume that the value functionals of the left side of the equation are .
The corresponding first-order partial derivatives about the state variable are . Bringing them into the HJB equations, the set of equations is obtained as
Based on the constant relationship between the two sides of the set of equations, the following results are solved:
Proposition 2 has been certified. □
Proof of Corollary 1.
Comparing the profits of the manufacturer and the platform under the model and the model .
- (1)
- ,
- (2)
- .
Corollary 1 has been certified. □
Proof of Proposition 3.
First, according to the backward induction, we obtain the marketing decisions of the platform. According to the Bellman dynamic programming principle, the continuous differentiable function satisfies the Hamilton–Jacobi–Bellman equation:
where is the optimal value function for the platform under the model ; represents the first-order partial derivative of the optimal value function of the platform about the state variable . The optimal marketing effort for the platform is . Substitute the optimal marketing effort into the manufacturer’s Functional (2); the manufacturer’s Hamilton–Jacobi–Bellman equation is:
where is the optimal value function for the manufacturer under the model , and the manufacturer’s pricing decision and recycling decision are: . Substitute into the HJB equations of the manufacturer and platform; we can obtain:
Based on the functionals of the right side of Equation (A13), we assume that the value functionals of the left side of the equations are .
The corresponding first-order partial derivatives about the state variable are . Bringing them into the HJB equations, the set of equations is obtained as
Based on the constant relationship between the two sides of the set of equations, the following results are solved:
Proposition 3 has been certified. □
Proof of Proposition 4.
According to the backward induction, we first obtain the marketing and recycling decisions of the platform. According to the Bellman dynamic programming principle, the continuous differentiable function satisfies the Hamilton–Jacobi–Bellman equation:
where is the optimal value function for the platform under the model , and represents the first-order partial derivative of the optimal value function of the platform about the state variable . The optimal marketing effort and recycling effort for the platform are, respectively, , Bringing the optimal marketing effort and recycling effort into the manufacturer’s functional, the manufacturer’s Hamilton–Jacobi–Bellman equation is:
where is the optimal value function for the manufacturer under the model , and the manufacturer’s pricing decision is: . Substitute , , and into the HJB equations of the manufacturer and platforms (A16) and (A17), and the following is obtained:
Based on the functionals of the right side of the equations, we assume that the value functionals of the left side of the equations are .
The corresponding first-order partial derivatives about the state variable are . Bringing them into the HJB equations, the set of equations is obtained as
Based on the constant relationship between the two sides of the set of equations, the following results are solved:
Proposition 4 has been certified. □
Proof of Corollary 2.
Comparing the profits of the manufacturer and the platform under the model and the model .
- (1)
- ,
- (2)
Corollary 2 has been certified. □
Proof of Proposition 5.
Comparing the profits of the manufacturer and the platform under the model and the model .
- (1)
- (2)
Proposition 5 has been certified. □
Proofs of Propositions 6, 7, and 8 are easy to obtain; they are not explained here.
Proof of Proposition 9.
Comparing the optimal decisions and analyzing the sensitivity of key parameters.Comparing brand goodwill, pricing decision, and marketing effort under the model and the model , we find , , and and obtain the sensitivity analysis of the stable value of each decision variable.
- (1)
- The sensitivity analysis of the stable value of brand goodwill for the model and the model is performed as follows:
- (2)
- The sensitivity analysis of the stable value of retail price for the model and the model is performed as follows:
- (3)
- The sensitivity analysis of the stable value of marketing effort of the platform for the model and the model is performed as follows:
- (4)
- The sensitivity analysis of the stable value of recycling effort of the platform for the model and the model is performed as follows:
- 1.
- Comparing brand goodwill, pricing decision, and marketing effort under the model and the model , we find , , and and obtain the sensitivity analysis of the stable value of each decision variable.
- (1)
- The sensitivity analysis of the stable value of brand goodwill for the model and the model is performed as follows:
- (2)
- The sensitivity analysis of the stable value of retail price for the model and the model is performed as follows:
- (3)
- The sensitivity analysis of the stable value of marketing effort of the platform for the model and the model is performed as follows:
- (4)
- The sensitivity analysis of the stable value of recycling effort of the platform for the model and the model is performed as follows:
Proposition 9 has been certified. □
Proof of Proposition 10.
According to the backward induction, we first solve the marketing decisions of the platform. According to the Bellman dynamic programming principle, for any state , the continuous differentiable function satisfies the Hamilton–Jacobi–Bellman equation (HJB equation):
of which is the optimal value function for the platform under the model ; that is, the optimal total profits of the platform, , represents the first-order partial derivative of the optimal value function of the platform about the state variable . It can be seen as the contribution of the change in brand goodwill to the total profits of the platform. The optimal marketing effort for the platform is . Bringing the optimal marketing effort into the manufacturer’s functional, the manufacturer’s Hamilton–Jacobi–Bellman equation is built as:
where is the optimal value function for the manufacturer under the model , and the manufacturer’s pricing decision and recycling decision are: and . Bringing , , and into the HJB equations of the manufacturer and platform, we can obtain:
Based on the functionals of the right side of the equations, we assume that the value functionals of the left side of the equations are .
The corresponding first-order partial derivatives are . Bringing them into the HJB equations, the set of equations is obtained as
Based on the constant relationship between the two sides of the set of equations, the following results are solved:
Proposition 10 has been certified. □
Proof of Proposition 11.
The solution process uses the backward induction; we first solve the decisions of the platform. According to the Bellman dynamic programming principle, the continuous differentiable function satisfies the Hamilton–Jacobi–Bellman equation:
where is the optimal value function for the platform under the model , and represents the first-order partial derivative of the optimal value function of the platform about the state variable . The optimal marketing effort and recycling effort for the platform are, respectively, . Bringing the optimal marketing effort and recycling effort into the manufacturer’s functional, the manufacturer’s Hamilton–Jacobi–Bellman equation is:
where is the optimal value function for the manufacturer under the model , and the manufacturer’s pricing decision is: . Bringing , , and into the HJB equations of the manufacturer and platform, we can obtain:
Based on the functionals of the right side of the equations, we assume that the value functionals of the left side of the equations are .
The corresponding first-order partial derivatives about the state variable are . Bringing them into the HJB equations, the set of equations is obtained as
Based on the constant relationship between the two sides of the set of equations, the following results are solved:
Proposition 11 has been certified. □
References
- Guide, V.D.R., Jr.; Van Wassenhove, L.N. OR FORUM—The evolution of closed-loop supply chain research. Oper. Res. 2009, 57, 10–18. [Google Scholar] [CrossRef]
- Souza, G.C. Closed-loop supply chains: A critical review, and future research. Decis. Sci. 2013, 44, 7–38. [Google Scholar] [CrossRef]
- Rahmani, M.; Gui, L.; Atasu, A. The Implications of Recycling Technology Choice on Extended Producer Responsibility. Prod. Oper. Manag. 2021, 30, 522–542. [Google Scholar] [CrossRef]
- Feng, L.; Govindan, K.; Li, C. Strategic planning: Design and coordination for dual-recycling channel reverse supply chain considering consumer behavior. Eur. J. Oper. Res. 2017, 260, 601–612. [Google Scholar] [CrossRef]
- Govindan, K.; Popiuc, M.N. Reverse supply chain coordination by revenue sharing contract: A case for the personal computers industry. Eur. J. Oper. Res. 2014, 233, 326–336. [Google Scholar] [CrossRef]
- Martin, P.; Guide, V.D.R., Jr.; Craighead, C.W. Supply chain sourcing in remanufacturing operations: An empirical investigation of remake versus buy. Decis. Sci. 2010, 41, 301–324. [Google Scholar] [CrossRef]
- Walport, M. Distributed ledger technology: Beyond blockchain. UK Gov. Off. Sci. 2016, 1, 1–88. [Google Scholar]
- Babich, V.; Hilary, G. OM Forum—Distributed Ledgers and Operations: What Operations Management Researchers Should Know About Blockchain Technology. Manuf. Serv. Oper. Manag. 2020, 22, 223–240. [Google Scholar] [CrossRef]
- Saberi, S.; Kouhizadeh, M.; Sarkis, J.; Shen, L. Blockchain technology and its relationships to sustainable supply chain management. Int. J. Prod. Res. 2019, 57, 2117–2135. [Google Scholar] [CrossRef]
- Lim, M.K.; Li, Y.; Wang, C.; Tseng, M.L. A literature review of blockchain technology applications in supply chains: A comprehensive analysis of themes, methodologies and industries. Comput. Ind. Eng. 2021, 154, 107133. [Google Scholar] [CrossRef]
- Centobelli, P.; Cerchione, R.; Del Vecchio, P.; Oropallo, E.; Secundo, G. Blockchain technology for bridging trust, traceability and transparency in circular supply chain. Inf. Manag. 2021, 59, 103508. [Google Scholar] [CrossRef]
- Xu, X.; Choi, T.M. Supply chain operations with online platforms under the cap-and-trade regulation: Impacts of using blockchain technology. Transp. Res. Part E 2021, 155, 102491. [Google Scholar] [CrossRef]
- Shen, Y.; Willems, S.P.; Dai, Y. Channel Selection and Contracting in the Presence of a Retail Platform. Prod. Oper. Manag. 2019, 28, 1173–1185. [Google Scholar] [CrossRef]
- Liu, C.Y.; Wang, H.; Tang, J.; Chang, C.T.; Liu, Z. Optimal recovery model in a used batteries closed-loop supply chain considering uncertain residual capacity. Transp. Res. Part E 2021, 156, 102516. [Google Scholar] [CrossRef]
- Pu, X.; Sun, S.; Shao, J. Direct selling, reselling, or agency selling? Manufacturer’s online distribution strategies and their impact. Int. J. Electron Comm. 2020, 24, 232–254. [Google Scholar] [CrossRef]
- Wang, B.; Ren, C.; Dong, X.; Zhang, B.; Wang, Z. Determinants shaping willingness towards on-line recycling behaviour: An empirical study of household e-waste recycling in China. Resour. Conserv. Recycl. 2019, 143, 218–225. [Google Scholar] [CrossRef]
- Hastig, G.M.; Sodhi, M.M.S. Blockchain for supply chain traceability: Business requirements and critical success factors. Prod. Oper. Manag. 2020, 29, 935–954. [Google Scholar] [CrossRef]
- Dutta, P.; Choi, T.-M.; Somani, S.; Butala, R. Blockchain technology in supply chain operations: Applications, challenges and research opportunities. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102067. [Google Scholar] [CrossRef]
- Wang, Y.; Singgih, M.; Wang, J.; Rit, M. Making sense of blockchain technology: How will it transform supply chains? Int. J. Prod. Econ. 2019, 211, 221–236. [Google Scholar] [CrossRef]
- Chod, J.; Trichakis, N.; Tsoukalas, G.; Aspegren, H.; Weber, M. On the Financing Benefits of Supply Chain Transparency and Blockchain Adoption. Manag. Sci. 2020, 66, 4378–4396. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, M.; Liu, J. Value and Design of Traceability-Driven Blockchains. Manuf. Serv. Oper. Manag. 2023. [Google Scholar] [CrossRef]
- Shen, B.; Dong, C.; Minner, S. Combating Copycats in the Supply Chain with Permissioned Blockchain Technology. Prod. Oper. Manag. 2022, 31, 138–154. [Google Scholar] [CrossRef]
- Pun, H.; Swaminathan, J.M.; Hou, P. Blockchain Adoption for Combating Deceptive Counterfeits. Prod. Oper. Manag. 2021, 30, 864–882. [Google Scholar] [CrossRef]
- Choi, T.M. Blockchain-technology-supported platforms for diamond authentication and certification in luxury supply chains. Transp. Ret. Part E 2019, 128, 17–29. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, M.; Dou, G.; Yu, Y. Coordination of a supply chain with an online platform considering green technology in the blockchain era. Int. J. Prod. Res. 2021, 1–18. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, D.J.; Zhang, F. Information Sharing on Retail Platforms. Manuf. Serv. Oper. Manag. 2021, 23, 606–619. [Google Scholar] [CrossRef]
- Savaskan, R.C.; Van Wassenhove, L.N. Reverse channel design: The case of competing retailers. Manag. Sci. 2006, 52, 1–14. [Google Scholar] [CrossRef]
- Huang, M.; Song, M.; Lee, L.H.; Ching, W.K. Analysis for strategy of closed-loop supply chain with dual recycling channel. Int. J. Prod. Econ. 2013, 144, 510–520. [Google Scholar] [CrossRef]
- De Giovanni, P.; Reddy, P.V.; Zaccour, G. Incentive strategies for an optimal recovery program in a closed-loop supply chain. Eur. J. Oper. Res. 2016, 249, 605–617. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, H.; Qu, S.; Nabe, M. Optimal Strategy for a Closed-Loop Supply Chain Considering Recycling and Warranty Channels. Arab. J. Sci. Eng. 2020, 46, 1585–1601. [Google Scholar] [CrossRef]
- Liu, H.; Lei, M.; Deng, H.; Leong, G.K.; Huang, T. A dual channel, quality-based price competition model for the WEEE recycling market with government subsidy. Omega 2016, 59, 290–302. [Google Scholar] [CrossRef]
- Li, C.; Feng, L.; Luo, S. Strategic introduction of an online recycling channel in the reverse supply chain with a random demand. J. Clean. Prod. 2019, 236, 117683. [Google Scholar] [CrossRef]
- Wang, L.; Chen, J.; Song, H. Marketplace or reseller? Platform strategy in the presence of customer returns. Transp. Res. Part E Logist. Transp. Rev. 2021, 153, 102452. [Google Scholar] [CrossRef]
- Tian, L.; Vakharia, A.J.; Tan, Y.; Xu, Y. Marketplace, reseller, or hybrid: Strategic analysis of an emerging e-commerce model. Prod. Oper. Manag. 2018, 27, 1595–1610. [Google Scholar] [CrossRef]
- Chiang, W.K.; Chhajed, D.; Hess, J.D. Direct marketing, indirect profits: A strategic analysis of dual-channel supply-chain design. Manag. Sci. 2003, 49, 1–20. [Google Scholar] [CrossRef]
- Arya, A.; Mittendorf, B.; Sappington, D.E.M. The Bright Side of Supplier Encroachment. Mark. Sci. 2007, 26, 651–659. [Google Scholar] [CrossRef]
- Zheng, H.; Li, G.; Guan, X.; Sethi, S.; Li, Y. Downstream information sharing and sales channel selection in a platform economy. Transp. Res. Part E Logist. Transp. Rev. 2021, 156, 102512. [Google Scholar] [CrossRef]
- Tan, Y.; Carrillo, J.E. Strategic analysis of the agency model for digital goods. Prod. Oper. Manag. 2017, 26, 724–741. [Google Scholar] [CrossRef]
- Abhishek, V.; Jerath, K.; Zhang, Z.J. Agency Selling or Reselling? Channel Structures in Electronic Retailing. Manag. Sci. 2016, 62, 2259–2280. [Google Scholar] [CrossRef]
- Guo, X.; Zheng, S.; Yu, Y.; Zhang, F. Optimal Bundling Strategy for a Retail Platform Under Agency Selling. Prod. Oper. Manag. 2021, 30, 2273–2284. [Google Scholar] [CrossRef]
- Ha, A.Y.; Tong, S.; Wang, Y. Channel structures of online retail platforms. Manuf. Serv. Oper. Manag. 2022, 24, 1547–1561. [Google Scholar] [CrossRef]
- Hagiu, A.; Wright, J. Marketplace or reseller? Manag. Sci. 2015, 61, 184–203. [Google Scholar] [CrossRef]
- Shi, D.; Wang, M.; Li, X. Strategic introduction of marketplace platform and its impacts on supply chain. Int. J. Prod. Econ. 2021, 242, 108300. [Google Scholar] [CrossRef]
- Jia, D.; Li, S. Optimal decisions and distribution channel choice of closed-loop supply chain when e-retailer offers online marketplace. J. Clean. Prod. 2020, 265, 121767. [Google Scholar] [CrossRef]
- De Giovanni, P. Closed-loop supply chain coordination through incentives with asymmetric information. Ann. Oper. Res. 2017, 253, 133–167. [Google Scholar] [CrossRef]
- Xiang, Z.; Xu, M. Dynamic cooperation strategies of the closed-loop supply chain involving the internet service platform. J. Clean. Prod. 2019, 220, 1180–1193. [Google Scholar] [CrossRef]
- Pnevmatikos, N.; Vardar, B.; Zaccour, G. When should a retailer invest in brand advertising? Eur. J. Oper. Res. 2018, 267, 754–764. [Google Scholar] [CrossRef]
- Nerlove, M.; Arrow, K.J. Optimal advertising policy under dynamic conditions. Economica 1962, 129–142. [Google Scholar] [CrossRef]
- De Giovanni, P. An optimal control model with defective products and goodwill damages. Ann. Oper. Res. 2020, 289, 419–430. [Google Scholar] [CrossRef]
- Yi, Z.; Li, F.; Ma, L. The impact of distribution channels on trial-version provision with a positive network effect. Omega 2019, 85, 115–133. [Google Scholar] [CrossRef]
- Minner, S.; Kiesmüller, G.P. Dynamic product acquisition in closed loop supply chains. Int. J. Prod. Res. 2012, 50, 2836–2851. [Google Scholar] [CrossRef]
- Buratto, A.; Cesaretto, R.; De Giovanni, P. Consignment contracts with cooperative programs and price discount mechanisms in a dynamic supply chain. Int. J. Prod. Econ. 2019, 218, 72–82. [Google Scholar] [CrossRef]
- Wang, X.; Ma, D.; Hu, J. Recycling Model Selection for Electronic Products Considering Platform Power and Blockchain Empowerment. Sustainability 2022, 14, 6136. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).