Numerical Study of Resistance Loss and Erosive Wear during Pipe Transport of Paste Slurry
Abstract
:1. Introduction
2. Computational Model
2.1. Mixture Laminar Flow Model
2.2. Particle Flow Tracking Model
2.3. Flow Domain and Boundary Conditions
2.4. Simulation Scenarios
2.5. Model Validation
3. Results and Discussion
3.1. Resistance Loss Characteristics of CPB Slurry in Pipes
3.1.1. Variation of Flow Rate and Pressure Patterns
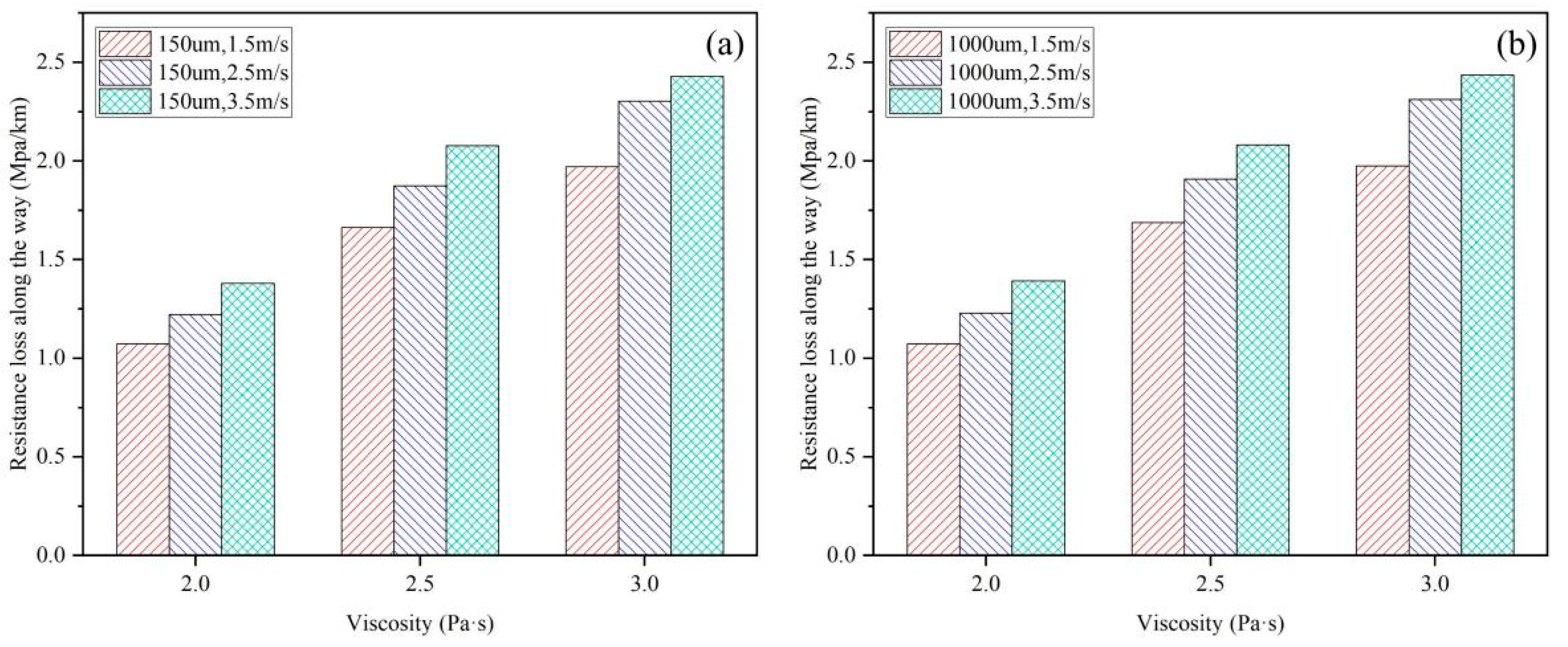
3.1.2. The Impact of Inlet Velocity and Viscosity on Resistance Loss
3.1.3. The Impact of Particle Size on Resistance Loss
3.1.4. Resistance Loss at Bends
3.2. Erosion Wear Characteristics of the Pipe Wall
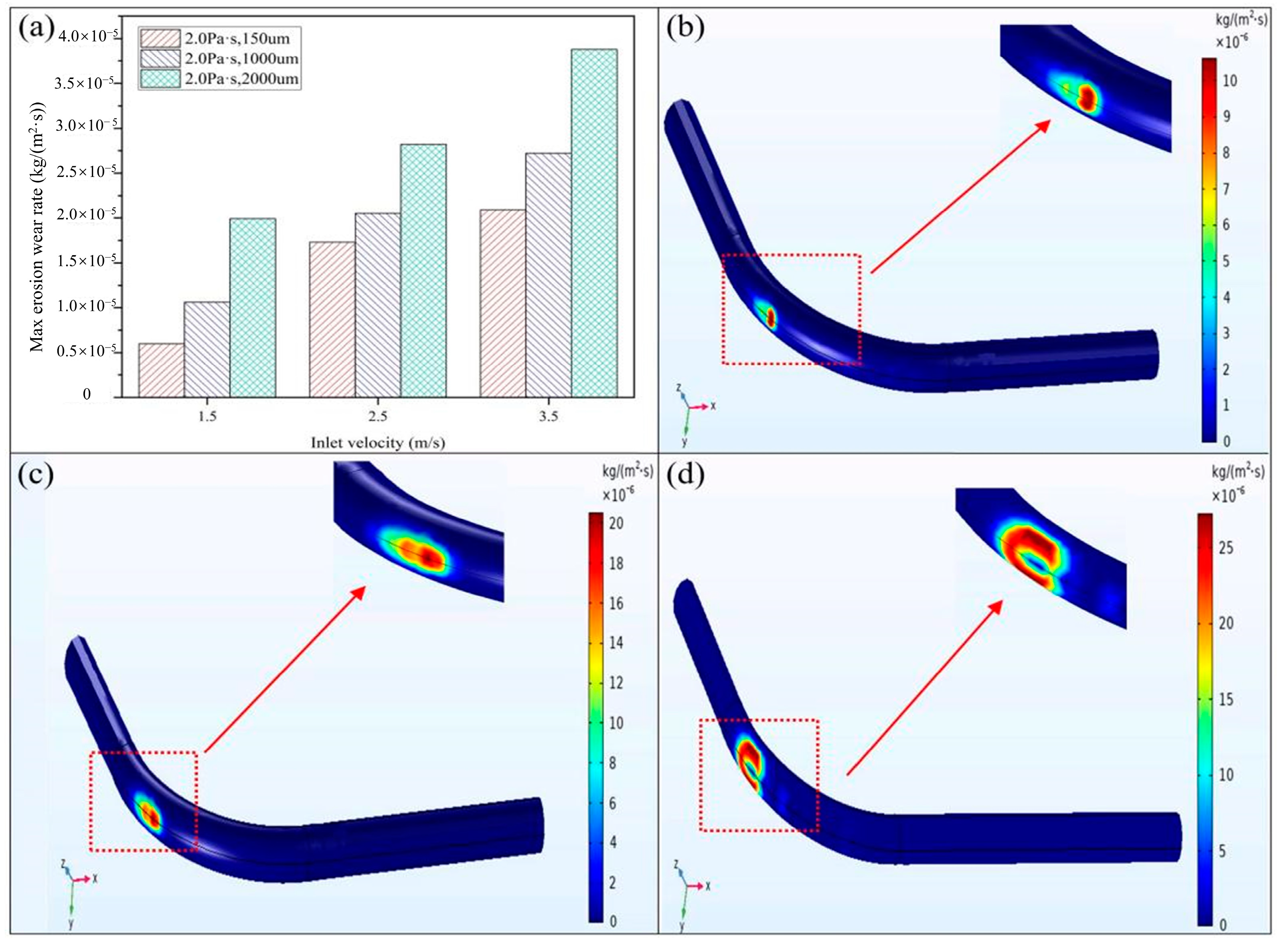
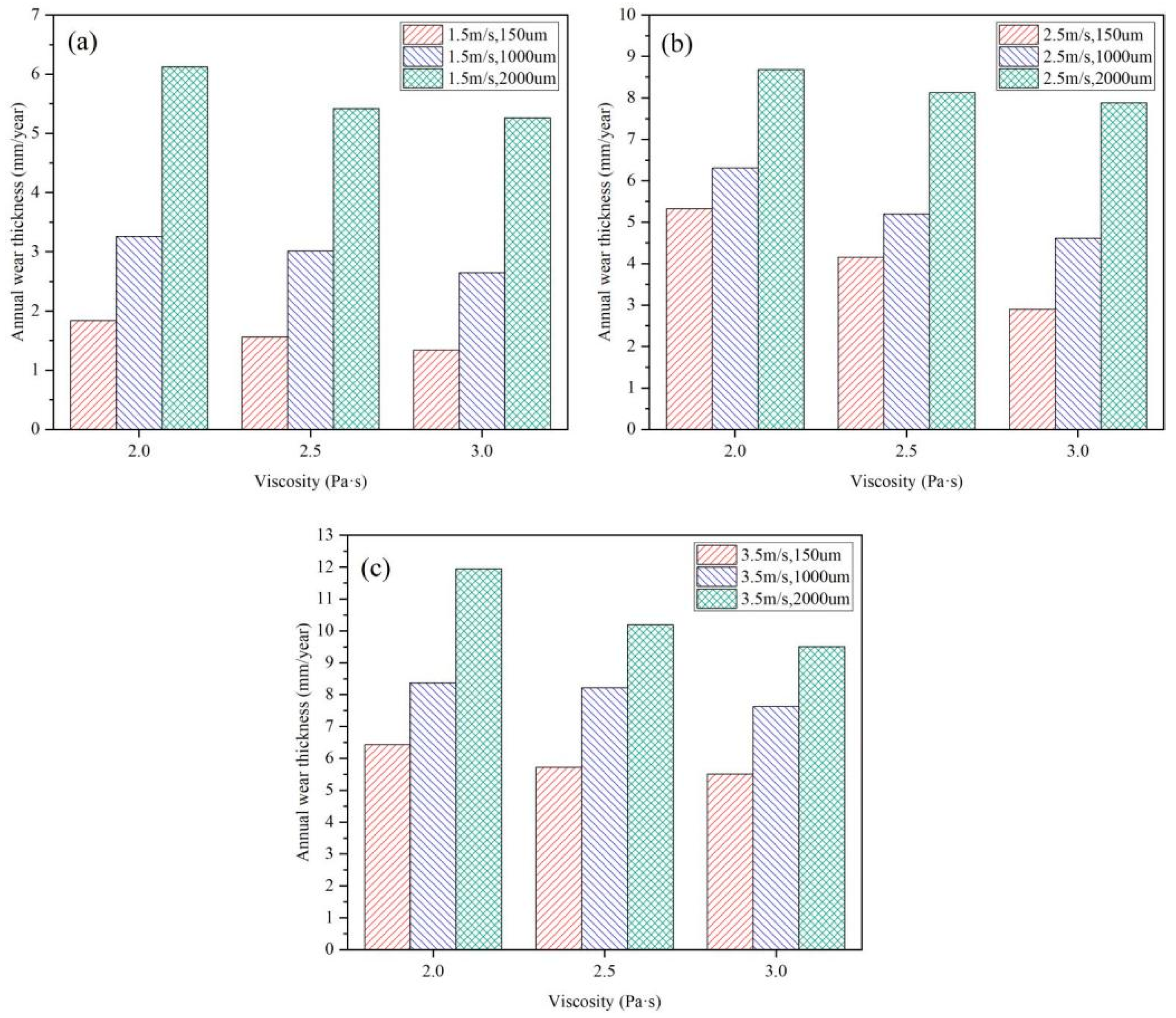
3.2.1. Effect of Inlet Velocity on Erosion Wear
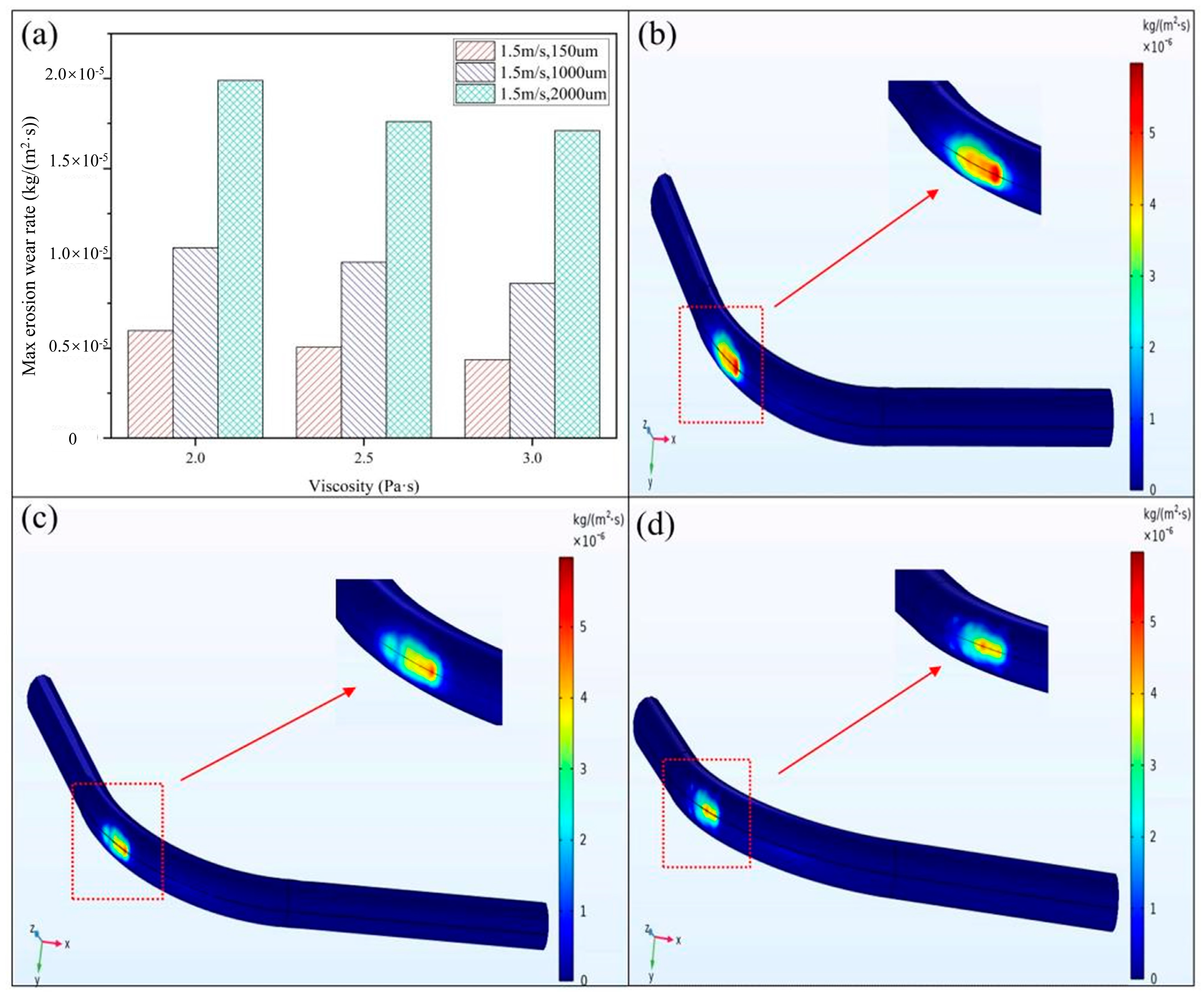
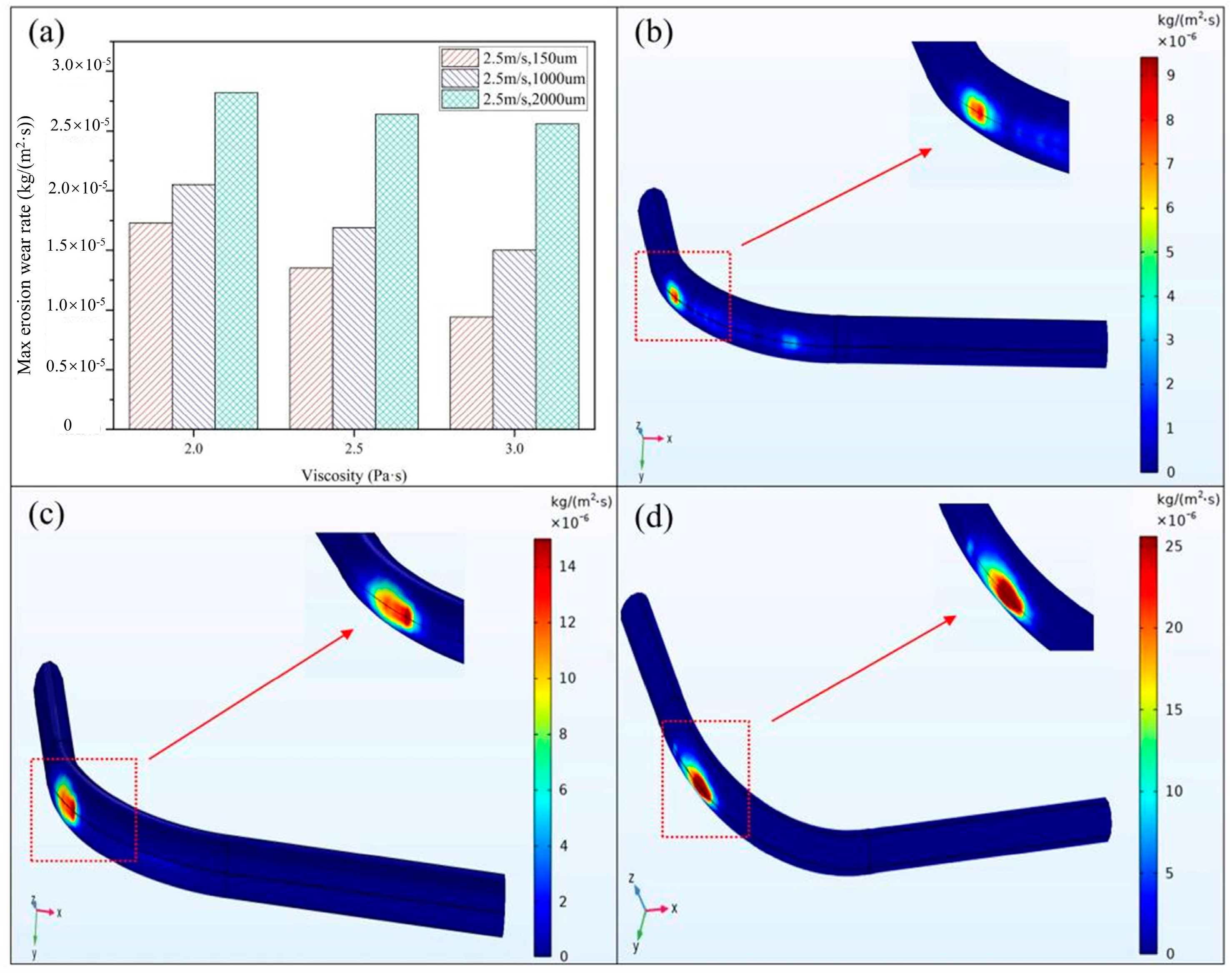
3.2.2. Effect of Viscosity on Erosion Wear
3.2.3. Effect of Particle Size on Erosion Wear
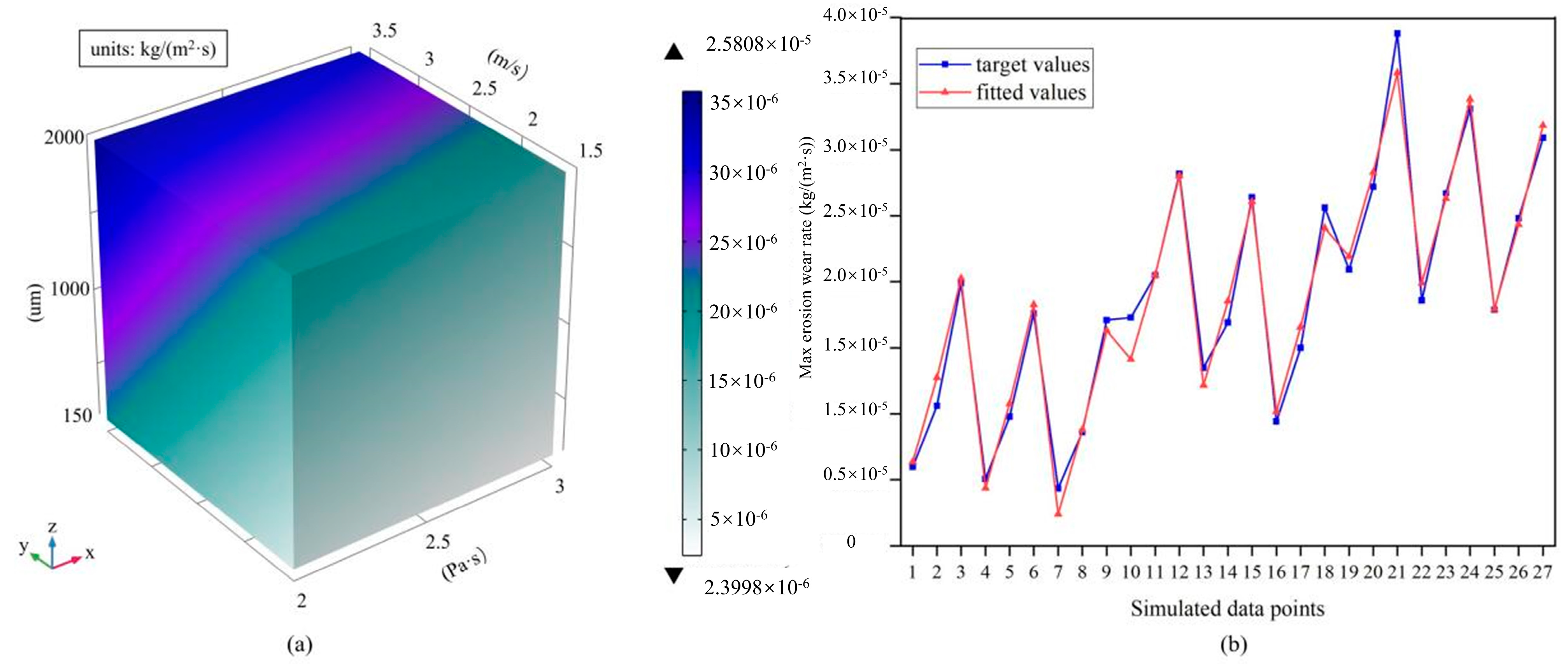
3.3. Calculation Model of Resistance Loss and Erosion Wear
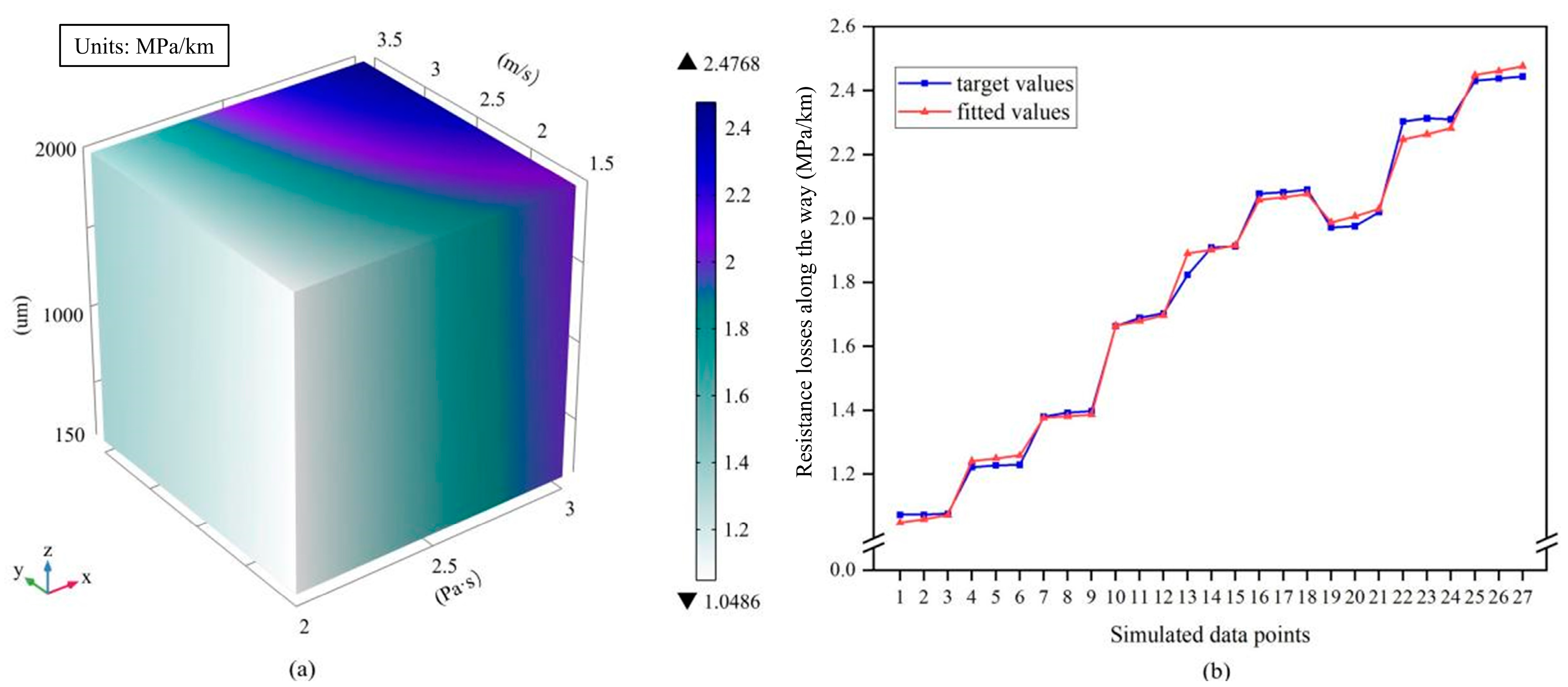
3.3.1. The Regression Function of Resistance Loss
3.3.2. The Regression Function of Maximum Erosion Wear Rate
4. Conclusions
- The resistance loss of CPB slurry during pipeline transportation is positively correlated with the inlet velocity, particle size, and viscosity. The resistance losses of the CPB slurry were minimized at an inlet velocity of 1.5 m/s, a particle size of 150 μm, and a slurry viscosity of 2.0 Pa·s.
- The resistance loss of CPB slurry at pipeline bends is high, therefore the number of bends should be minimized when designing mine backfill piping systems.
- In the process of transporting the CPB slurry, the outer wall of the bend is the most severely eroded and worn part of the pipe; therefore, it is important to focus on regular care of the bend, as well as to strengthen it through thickening the inner wall of the pipe and using better quality materials. In addition, the pipe should be replaced periodically to prevent it from failing.
- The maximum erosion wear rate at the outer wall of the bend is positively correlated with the slurry inlet velocity and particle size and negatively correlated with viscosity. Here, the maximum erosion wear rate was lowest at an inlet velocity of 1.5 m/s, a particle size of 150 μm, and a slurry viscosity of 3.0 Pa·s.
- Based on the data obtained from the simulations, formulae for the resistance losses and the maximum erosion wear rate of the pipe wall as functions of slurry inlet velocity, particle size, and viscosity were fitted, which may be of guidance for real-world mining applications.
- The CPB slurry’s particle size was assumed to be homogenous, and the effects of cement hydration, temperature, and chemical degradation of the pipe wall by the CPB slurry were not considered. Thus, the model will be expanded in subsequent studies to consider the pipeline transit of CPB slurry for unclassified tailing sand.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CBRM | Creep behavior of the rock mass |
| CVISC | Burger-creep visco-plastic model |
| CPB | Cemented paste backfill |
| FIT | Filling interval time |
| VCL | Vertical central line |
| MC | Mohr–Coulomb model |
| ρ | Density |
| G | Shear modulus |
| η | Viscosity |
| K | Bulk modulus |
| E | Young’s modulus |
| φ | Interface friction angle |
| μ | Poisson’s ratio |
| c | Cohesion |
| ψ | Dilation angle |
References
- Ma, D.; Zhang, J.; Duan, H.; Huang, Y.; Li, M.; Sun, Q.; Zhou, N. Reutilization of gangue wastes in underground backfilling mining: Overburden aquifer protection. Chemosphere 2021, 264, 128400. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Ji, K.; Wang, J.; Wang, S.; Zhang, P.; Hu, Y. Determination of the Required Strength of Artificial Roof for the Underhand Cut-and-Fill Mine Using Field Measurements and Theoretical Analysis. Sustainability 2023, 15, 189. [Google Scholar] [CrossRef]
- Li, H.; Ji, K.; Tao, Y.; Tang, C. Modelling a Novel Scheme of Mining Geothermal Energy from Hot Dry Rocks. Appl. Sci. 2022, 12, 11257. [Google Scholar] [CrossRef]
- Worlanyo, A.S.; Jiangfeng, L. Evaluating the environmental and economic impact of mining for post-mined land restoration and land-use: A review. J. Environ. Manag. 2021, 279, 111623. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhang, S.; Liu, H.; Zhao, Y. Disposal of mine tailings via geopolymerization. J. Clean. Prod. 2021, 284, 124756. [Google Scholar] [CrossRef]
- Qiu, J.; Zhao, Y.; Long, H.; Guo, Z.; Xing, J.; Sun, X. Low-Carbon Binder for Cemented Paste Backfill: Flowability, Strength and Leaching Characteristics. Minerals 2019, 9, 707. [Google Scholar] [CrossRef] [Green Version]
- Bull, A.J.; Fall, M. Curing temperature dependency of the release of arsenic from cemented paste backfill made with Portland cement. J. Environ. Manag. 2020, 269, 13. [Google Scholar] [CrossRef]
- Belem, T.; Benzaazoua, M. Design and application of underground mine paste backfill technology. Geotech. Geol. Eng. 2008, 26, 147–174. [Google Scholar] [CrossRef]
- Abdul-Hussain, N.; Fall, M. Thermo-hydro-mechanical behaviour of sodium silicate-cemented paste tailings in column experiments. Tunn. Undergr. Space Technol. 2012, 29, 85–93. [Google Scholar] [CrossRef]
- Ercikdi, B.; Kuekci, G.; Yilmaz, T. Utilization of granulated marble wastes and waste bricks as mineral admixture in cemented paste backfill of sulphide-rich tailings. Constr. Build Mater. 2015, 93, 573–583. [Google Scholar] [CrossRef]
- Behera, S.K.; Mishra, D.P.; Singh, P.; Mishra, K.; Mandal, S.K.; Ghosh, C.N.; Kumar, R.; Mandal, P.K. Utilization of mill tailings, fly ash and slag as mine paste backfill material: Review and future perspective. Constr. Build Mater. 2021, 309, 125120. [Google Scholar] [CrossRef]
- Chen, Q.; Tao, Y.; Zhang, Q.; Qi, C. The rheological, mechanical and heavy metal leaching properties of cemented paste backfill under the influence of anionic polyacrylamide. Chemosphere 2022, 286, 131630. [Google Scholar] [CrossRef] [PubMed]
- Qi, C.; Fourie, A. Cemented paste backfill for mineral tailings management: Review and future perspectives. Miner Eng. 2019, 144, 106025. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Q.; Feng, Y.; Chen, Q.; Xiao, C.; Li, H.; Xiang, Y.; Qi, C. Hydration and Mechanical Properties of Blended Cement with Copper Slag Pretreated by Thermochemical Modification. Materials 2022, 15, 3477. [Google Scholar] [CrossRef] [PubMed]
- Cui, L.; Fall, M. A coupled thermo–hydro-mechanical–chemical model for underground cemented tailings backfill. Tunn. Undergr. Space Technol. 2015, 50, 396–414. [Google Scholar] [CrossRef]
- Yin, S.; Shao, Y.; Wu, A.; Wang, H.; Liu, X.; Wang, Y. A systematic review of paste technology in metal mines for cleaner production in China. J. Clean. Prod. 2020, 247, 119590. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, G.; Wang, X. Hydraulic calculation of gravity transportation pipeline system for backfill slurry. J. Cent. South Univ. Technol. 2008, 15, 645–649. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Q.; Chen, Q.; Qi, C.; Feng, Y.; Xiao, C. Temperature variation characteristics in flocculation settlement of tailings and its mechanism. Int. J. Miner. Metall. Mater. 2020, 27, 1438–1448. [Google Scholar] [CrossRef]
- Singh, G.; Kumar, S.; Mohapatra, S.K. Erosion Wear in A Slurry Pipe With Multisized Coal And Bottom-Ash Slurries. Mater. Today Proc. 2017, 4, 3565–3571. [Google Scholar] [CrossRef]
- Li, M.; He, Y.; Liu, W.; Liu, Y.; Huang, C.; Jiang, R. Effect of adding finer particles on the transport characteristics of updates coarse-particle slurries in pipelines. Ocean Eng. 2020, 218, 108160. [Google Scholar] [CrossRef]
- More, S.R.; Bhatt, D.V.; Menghani, J.V. Failure analysis of coal bottom ash slurry pipeline in thermal power plant. Eng. Fail. Anal. 2018, 90, 489–496. [Google Scholar] [CrossRef]
- More, S.R.; Bhatt, D.V.; Menghani, J.V.; Jagtap, R.K. CFD Simulation and Experimental Results Validation of Slurry Erosion Wear using Slurry Pot Test Rig. Trends Sci. 2022, 19, 4524. [Google Scholar] [CrossRef]
- Kaushal, D.R.; Thinglas, T.; Tomita, Y.; Kuchii, S.; Tsukamoto, H. CFD modeling for pipeline flow of fine particles at high concentration. Int. J. Multiph Flow 2012, 43, 85–100. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, D.; Zhang, Q.; Zhao, B. Pipeline self-flowing transportation property of paste based on FLOW-3D software in deep mine. J. Cent. South Univ. Sci. Technol. 2011, 25, 141–150. [Google Scholar]
- Wu, D.; Yang, B.; Liu, Y. Pressure drop in loop pipe flow of fresh cemented coal gangue–fly ash slurry: Experiment and simulation. Adv. Powder Technol. 2015, 26, 920–927. [Google Scholar] [CrossRef]
- Bandyopadhyay, T.K.; Das, S.K. Non-Newtonian Liquid Flow through Small Diameter Piping Components: CFD Analysis. J. Inst. Eng. Ser. E 2016, 97, 131–141. [Google Scholar] [CrossRef]
- Yang, D.; Xia, Y.; Wu, D.; Chen, P.; Zeng, G.; Zhao, X. Numerical investigation of pipeline transport characteristics of slurry shield under gravel stratum. Tunn. Undergr. Space Technol. 2018, 71, 223–230. [Google Scholar] [CrossRef]
- Bansal, A.; Goyal, D.K.; Singh, P.; Singla, A.K.; Gupta, M.K.; Bala, N.; Kolte, J.; Setia, G. Erosive wear behaviour of HVOF-sprayed Ni-20Cr2O3 coating on pipeline materials. Int. J. Refract. Met. Hard Mater. 2020, 92, 105332. [Google Scholar] [CrossRef]
- Zhang, J.; Kang, J.; Fan, J.; Gao, J. Study on erosion wear of fracturing pipeline under the action of multiphase flow in oil & gas industry. J. Nat. Gas Sci. Eng. 2016, 32, 334–346. [Google Scholar] [CrossRef]
- Parsi, M.; Agrawal, M.; Srinivasan, V.; Vieira, R.E.; Torres, C.F.; McLaury, B.S.; Shirazi, S.A. CFD simulation of sand particle erosion in gas-dominant multiphase flow. J. Nat. Gas Sci. Eng. 2015, 27, 706–718. [Google Scholar] [CrossRef]
- Calderon-Hernandez, J.W.; Sinatora, A.; de Melo, H.G.; Chaves, A.P.; Mano, E.S.; Filho, L.S.L.; Paiva, J.L.; Braga, A.S.; Pinto, T.C.S. Hydraulic convey of iron ore slurry: Pipeline wear and ore particle degradation in function of pumping time. Wear 2020, 450–451, 203272. [Google Scholar] [CrossRef]
- Hewitt, D.; Allard, S.; Radziszewski, P. Pipe lining abrasion testing for paste backfill operations. Miner. Eng. 2009, 22, 1088–1090. [Google Scholar] [CrossRef]
- Hunacek, M. An invitation to applied mathematics. Math. Gaz. 2018, 102, 571–572. [Google Scholar] [CrossRef]
- Liu, L.; Fang, Z.; Qi, C.; Zhang, B.; Guo, L.; Song, K.I.-I.L. Numerical study on the pipe flow characteristics of the cemented paste backfill slurry considering hydration effects. Powder Technol. 2019, 343, 454–464. [Google Scholar] [CrossRef]
- Chhabra, R.; Shankar, V. Chapter 5—Flow of Multiphase Mixtures. In Coulson Richardson’s Chemical Engineering, 7th ed.; Chhabra, R., Shankar, V., Eds.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 215–284. [Google Scholar] [CrossRef]
- Chen, Q.; Zhou, H.; Wang, Y.; Li, X.; Zhang, Q.; Feng, Y.; Qi, C. Resistance Loss in Cemented Paste Backfill Pipelines: Effect of Inlet Velocity, Particle Mass Concentration, and Particle Size. Materials 2022, 15, 3339. [Google Scholar] [CrossRef] [PubMed]
- Song, H. Engineering Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 192–193. [Google Scholar]
- Zhang, Y.; Reuterfors, E.P.; McLaury, B.S.; Shirazi, S.A.; Rybicki, E.F. Comparison of computed and measured particle velocities and erosion in water and air flows. Wear 2007, 263, 330–338. [Google Scholar] [CrossRef]
- Kaushal, D.R.; Sato, K.; Toyota, T.; Funatsu, K.; Tomita, Y. Effect of particle size distribution on pressure drop and concentration profile in pipeline flow of highly concentrated slurry. Int. J. Multiph. Flow 2005, 31, 809–823. [Google Scholar] [CrossRef]
- Wichterle, K.; Večeř, M. The balance of mass and of mechanical energy in a flow tube. In Transport and Surface Phenomena; Wichterle, K., Večeř, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 121–126. [Google Scholar] [CrossRef]
- Li, M.; He, Y.; Liu, Y.; Huang, C. Hydrodynamic simulation of multi-sized high concentration slurry transport in pipelines. Ocean Eng. 2018, 163, 691–705. [Google Scholar] [CrossRef]
- Gupta, P.K.; San, N.A.; Bhramara, P. Numerical prediction of near-wall flow field of dense slurry flow in pipe bends. Mater. Today Proc. 2021, 45, 3201–3206. [Google Scholar] [CrossRef]
- Wu, A.; Ruan, Z.; Wang, Y.; Yin, S.; Wang, S.; Wang, J. Simulation of long-distance pipeline transportation properties of whole-tailings paste with high sliming. J. Cent. South Univ. 2018, 25, 141–150. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Xiao, Z.; Xiao, W. Rheological properties of tailing paste slurry. J. Cent. South Univ. Technol. Ed. 2004, 11, 75–79. [Google Scholar] [CrossRef]
- Gao, R.G.; Zhou, K.P.; Zhou, Y.L.; Yang, C. Research on the fluid characteristics of cemented backfill pipeline transportation of mineral processing tailings. Alex. Eng. J. 2020, 59, 4409–4426. [Google Scholar] [CrossRef]
- Li, G.; Sun, Y.; Qi, C. Machine learning-based constitutive models for cement-grouted coal specimens under shearing. Int. J. Min. Sci. Technol. 2021, 31, 813–823. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, W.; Li, K.; Lou, C.; Gong, J. Flow Patterns Transition Law of Oil-Water Two-Phase Flow under a Wide Range of Oil Phase Viscosity Condition. J. Appl. Math. 2013, 8, 291217. [Google Scholar] [CrossRef] [Green Version]
- Al-Dogail, A.S.; Gajbhiye, R.N. Effects of density, viscosity and surface tension on flow regimes and pressure drop of two-phase flow in horizontal pipes. J. Pet. Sci. Eng. 2021, 205, 108719. [Google Scholar] [CrossRef]
- Liu, M.; Chen, L.; Duan, Y. A Study of Resistance Characteristics of Coal-water Slurry Passing Through a Tube Bend with a Small Curvature Radius. J. Eng. Therm. Energy Power 2008, 4, 425–428+445–446. [Google Scholar]
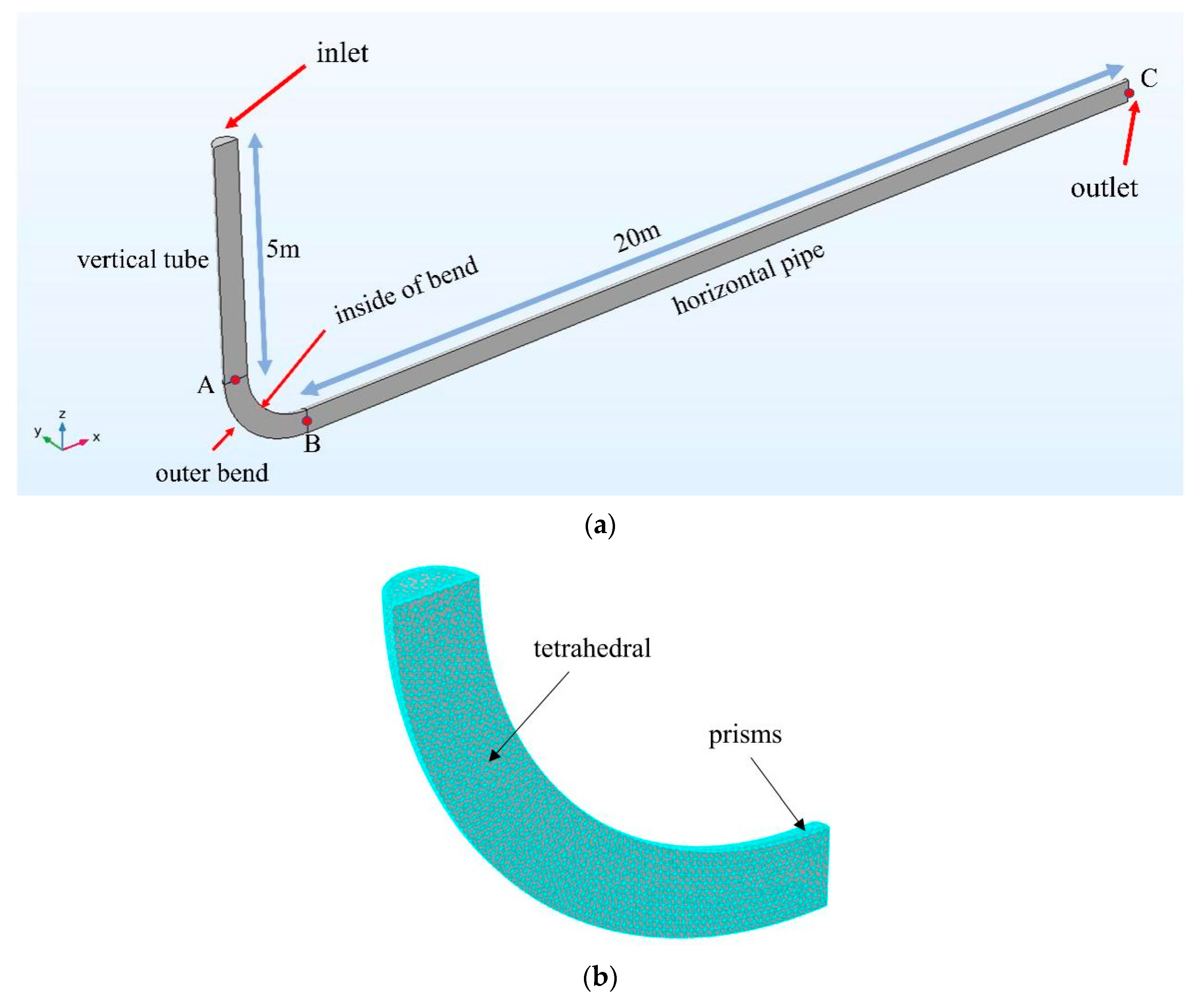

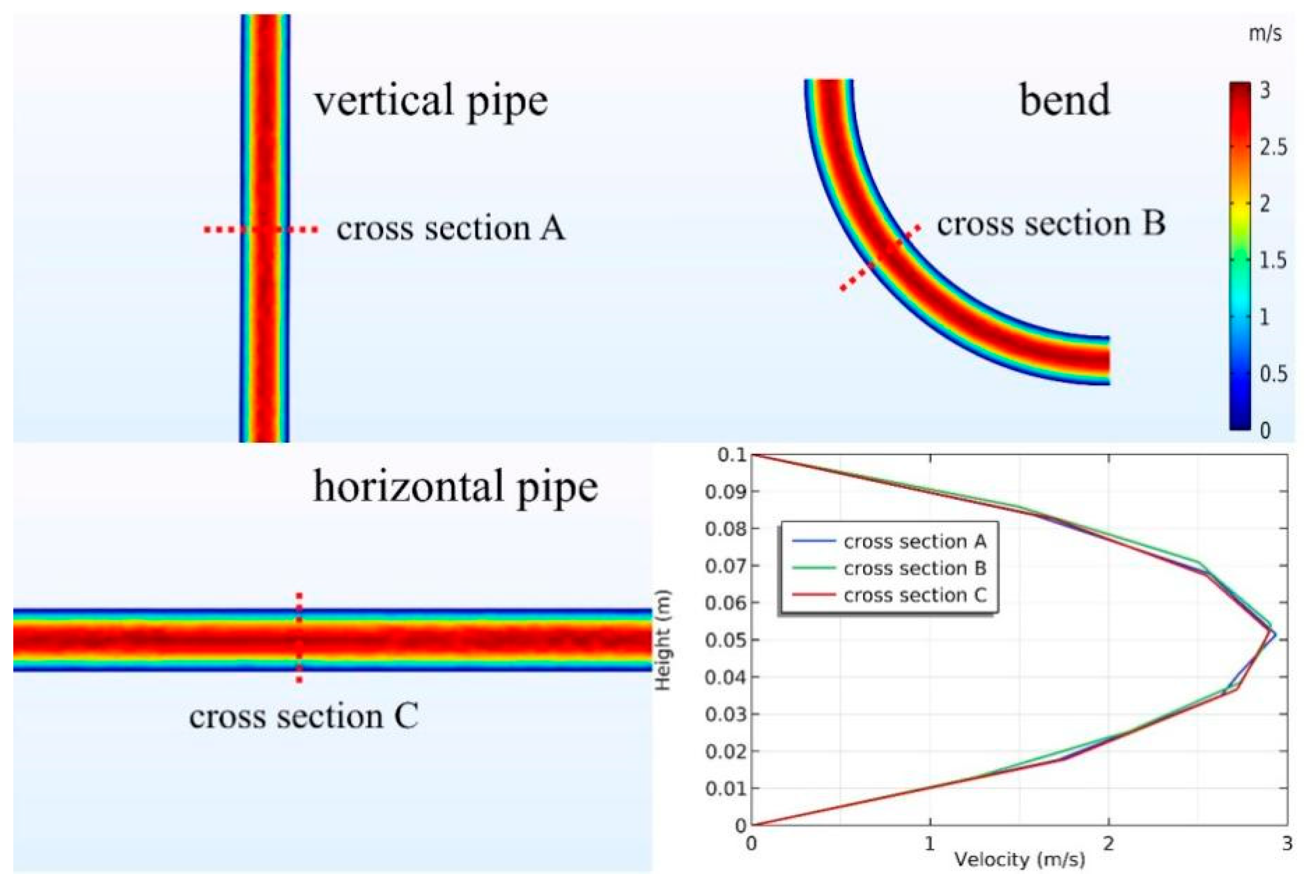
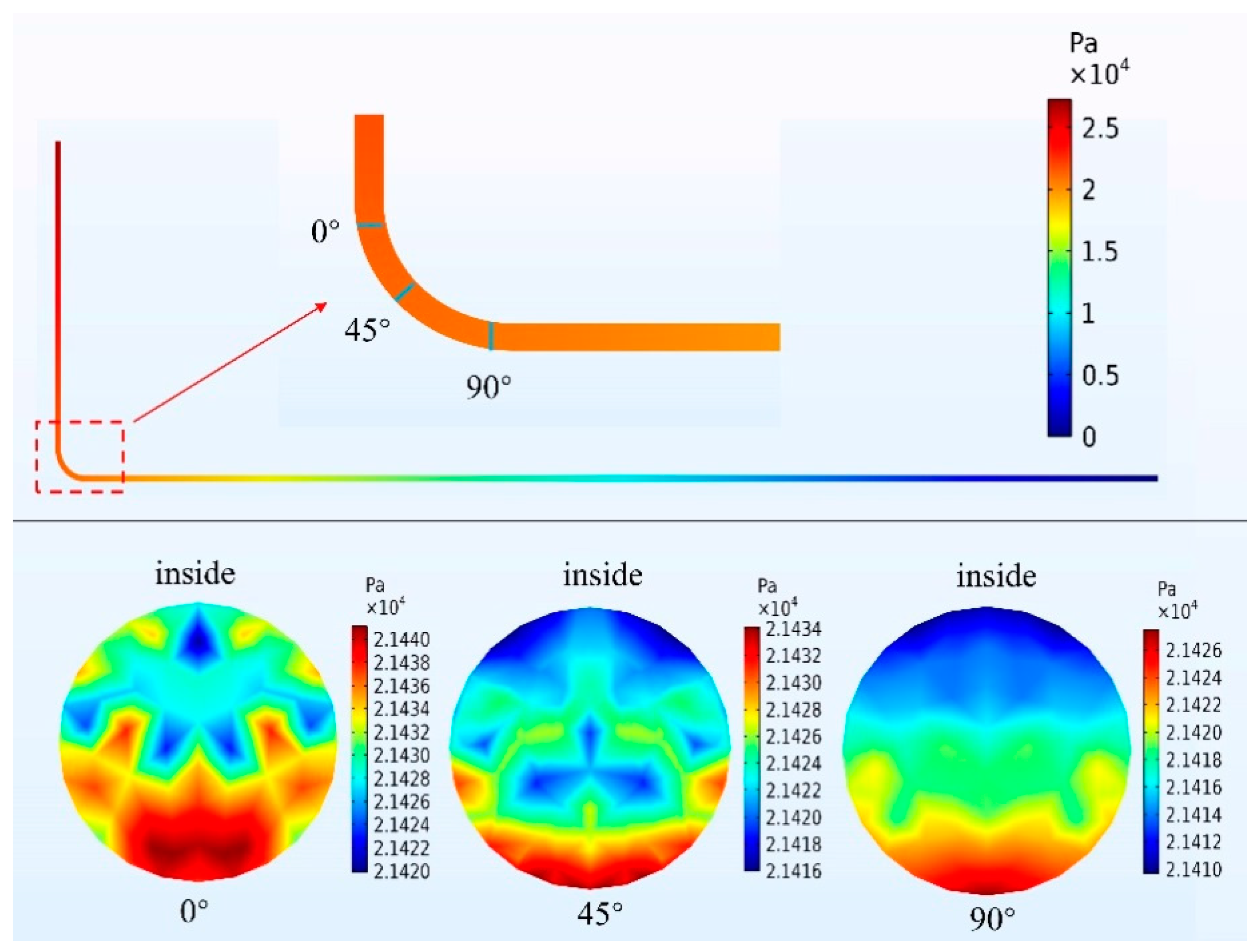


| Total Number of Grids | Bend Center Point Speed(m/s) | |
|---|---|---|
| grid 1 | 608,172 | 2.813 |
| grid 2 | 883,868 | 2.854 |
| grid 3 | 1,380,673 | 2.967 |
| grid 4 | 1,439,210 | 3.041 |
| grid 5 | 1,553,938 | 3.042 |
| CPB slurry concentration (%) | 70 |
| Fluid density (kg/m3) | 1850 |
| Particle density (kg/m3) | 2879 |
| Iron wall surface density (kg/m3) | 7860 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, J.; Tian, M.; Zhu, D.; Xiao, C.; Wen, B.; Bin, F.; Chen, H.; Wang, D. Numerical Study of Resistance Loss and Erosive Wear during Pipe Transport of Paste Slurry. Sustainability 2023, 15, 11890. https://doi.org/10.3390/su151511890
Qiu J, Tian M, Zhu D, Xiao C, Wen B, Bin F, Chen H, Wang D. Numerical Study of Resistance Loss and Erosive Wear during Pipe Transport of Paste Slurry. Sustainability. 2023; 15(15):11890. https://doi.org/10.3390/su151511890
Chicago/Turabian StyleQiu, Jianhui, Minghua Tian, Debin Zhu, Chongchun Xiao, Bin Wen, Feng Bin, Hao Chen, and Daolin Wang. 2023. "Numerical Study of Resistance Loss and Erosive Wear during Pipe Transport of Paste Slurry" Sustainability 15, no. 15: 11890. https://doi.org/10.3390/su151511890
APA StyleQiu, J., Tian, M., Zhu, D., Xiao, C., Wen, B., Bin, F., Chen, H., & Wang, D. (2023). Numerical Study of Resistance Loss and Erosive Wear during Pipe Transport of Paste Slurry. Sustainability, 15(15), 11890. https://doi.org/10.3390/su151511890







