Stability of Unsaturated Soil Slope Considering Stratigraphic Uncertainty
Abstract
1. Introduction
2. Methodology
2.1. Enhanced CMC Model for Simulating Stratigraphic Uncertainty
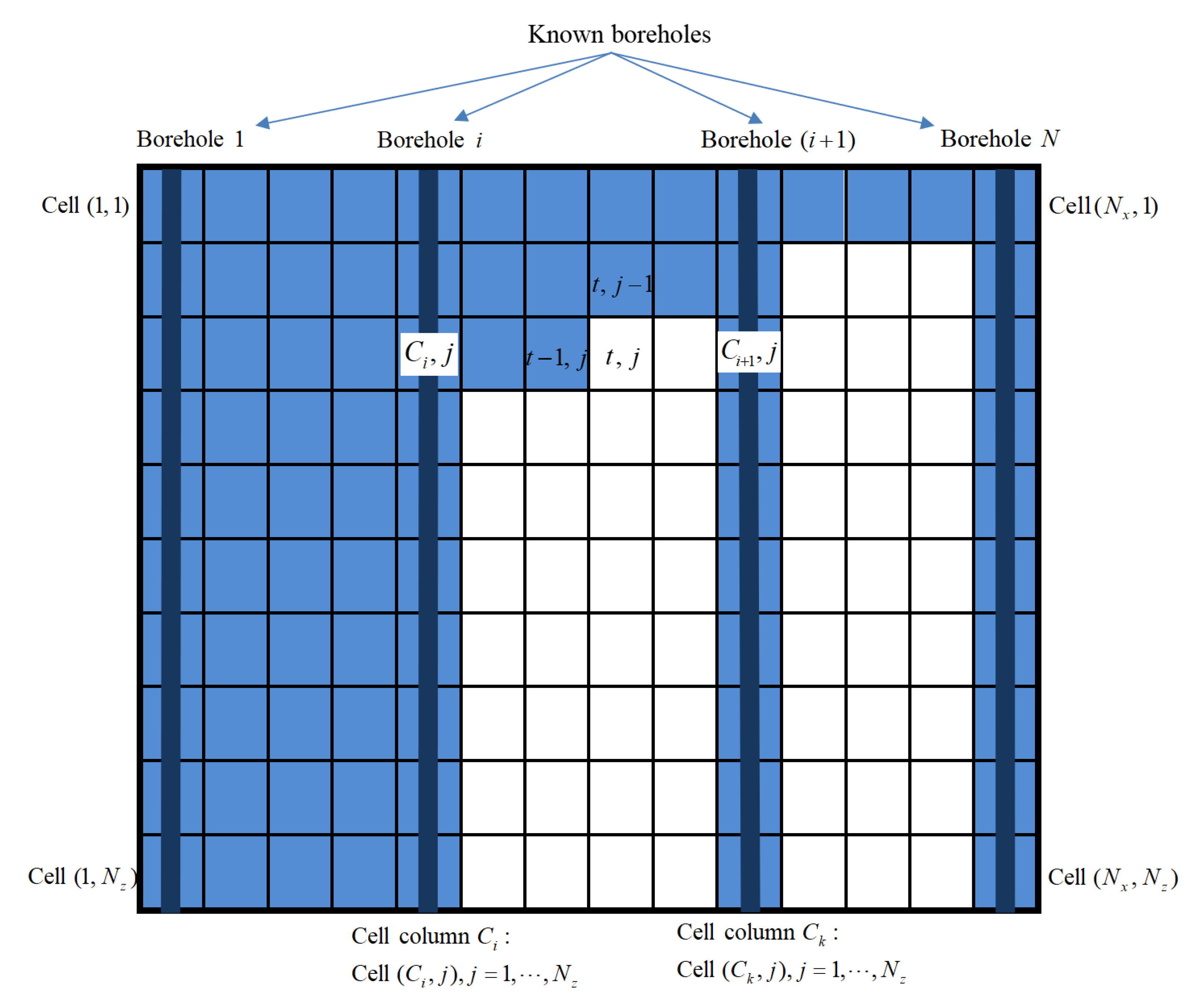
2.2. Mapping the Simulated Strata into the FEM Model of Slope
2.3. Coupled Pore Fluid Flow and Stress Analysis
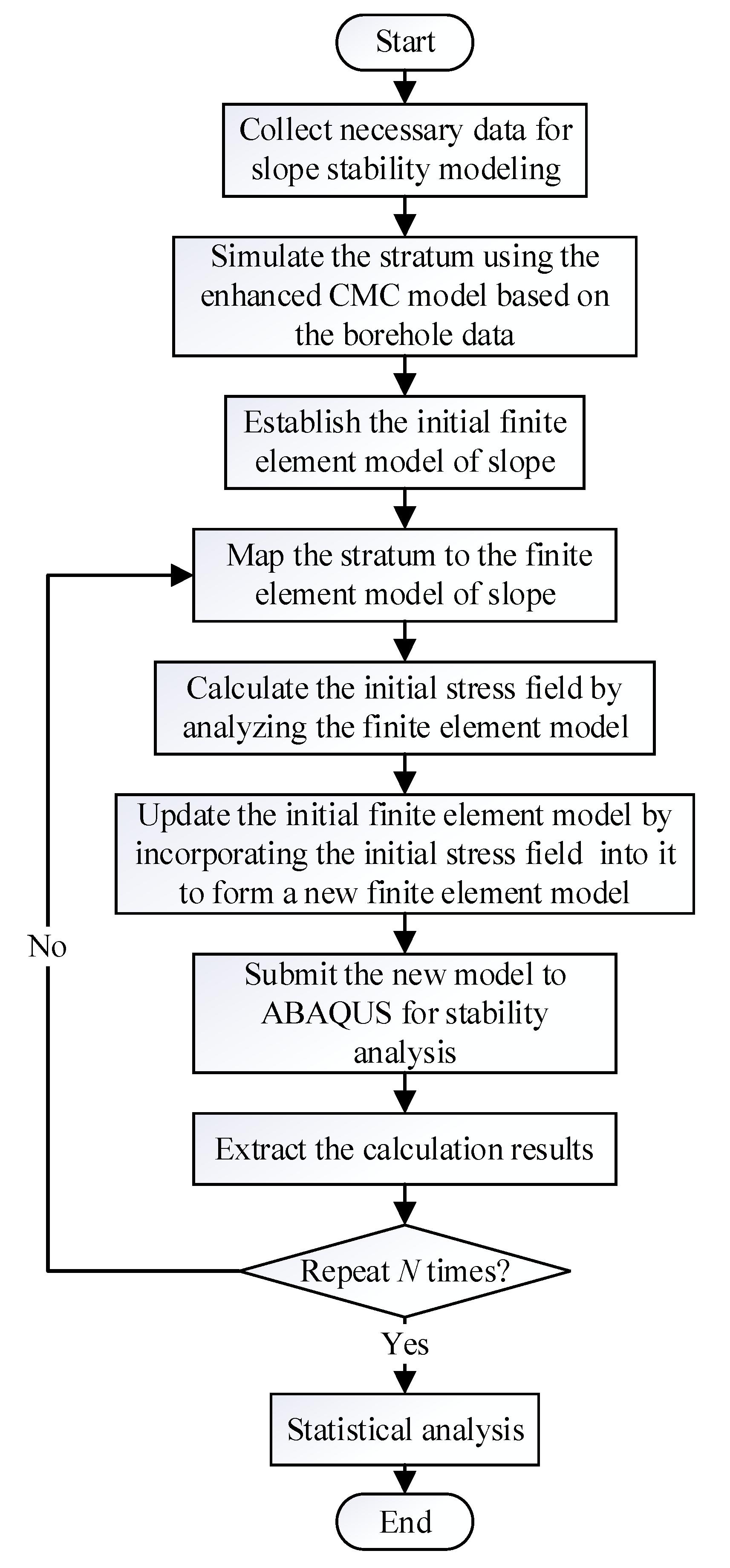
2.4. Algorithm Development for Automatically Calculating the Safety Factor of Unsaturated Soil Slope
- (1)
- Collect the necessary data for slope stability modeling including the borehole data of the stratum, the parameters of various types of soil, the slope geometric parameters, the boundary conditions of slope and other information contained in the site.
- (2)
- Discretize the stratigraphic profile into cells of appropriate size. Estimate the VTPM and HTPM based on the borehole data. Determine the simulation sequence according to the estimated values of KLR and KRL, and then use the enhanced CMC model introduced in Section 2.1 to generate the stratum.
- (3)
- Establish the initial FEM model of slope in ABAQUS software based on the information collected in Step 1 including the geometry and the boundary conditions of slope.
- (4)
- Map the simulated stratum into the FEM model of slope through python script and generate the input file named “Slope.inp”.
- (5)
- Calculate the initial stress field under the action of gravity by submitting the input file “Slope.inp” to analysis in ABAQUS. The initial stress field is saved in the “Slope.odb” file.
- (6)
- Incorporate the initial stress field into the FEM model of slope and modify the finite element model by editing the “Slope.inp” file. The input file of the modified model is named “Slope-New.inp”.
- (7)
- Submit the “Slope-New.inp” file to the ABAQUS solver through python script. The safety factor of slope is calculated using the strength reduction method, and the results are stored in the file named “Slope-New.odb”.
- (8)
- Extract the calculation results such as safety factor and groundwater table of slope from the “Slope-New.odb” file using python script.
- (9)
- Perform Monte Carlo simulation. Repeat steps 1–7 until the required N times are reached.
- (10)
- Conduct statistical analysis based on the results containing the slope safety factor and the groundwater table.
3. Case Study
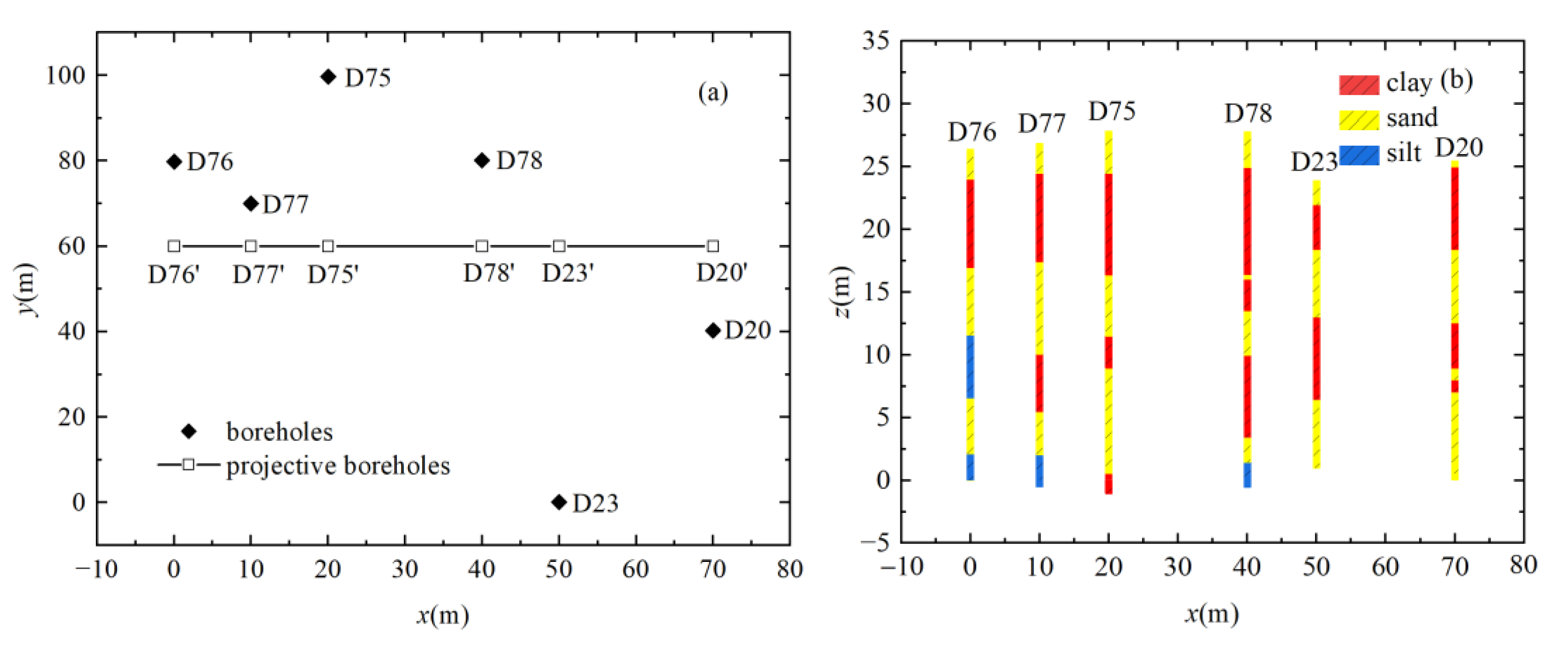
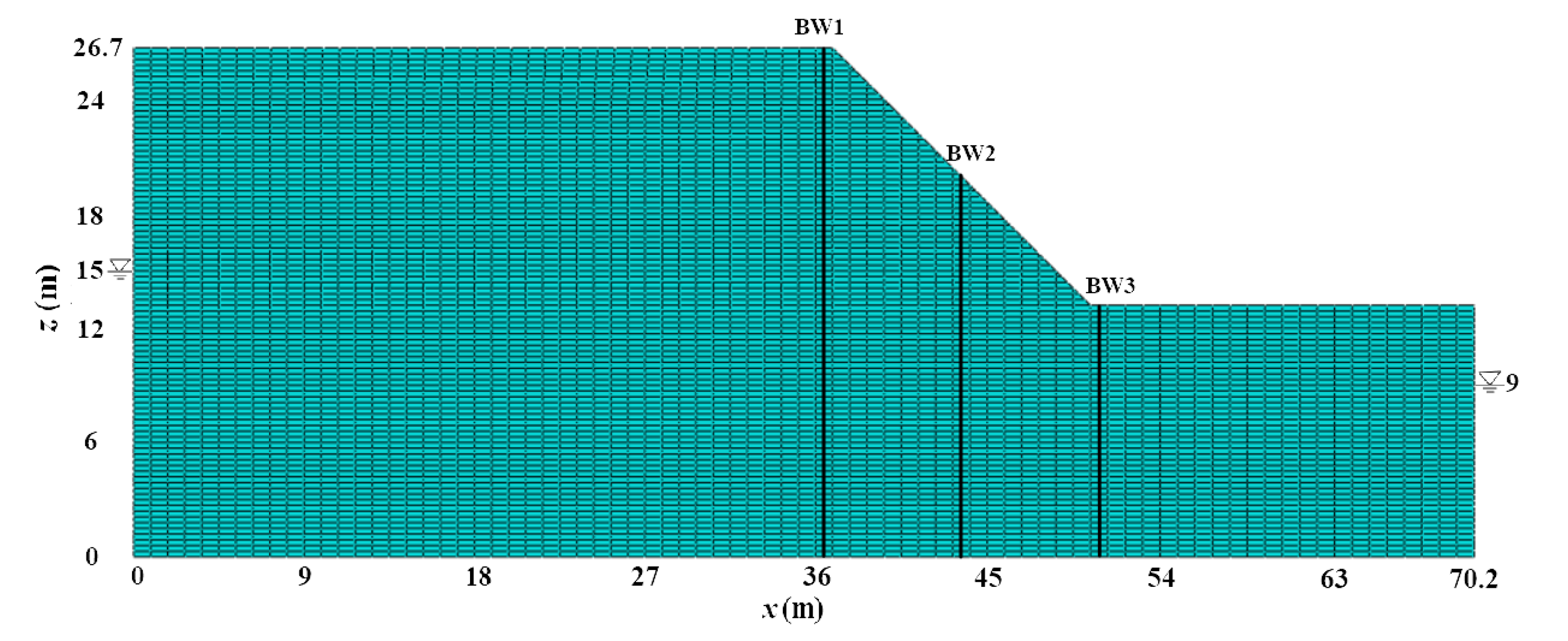
3.1. Borehole Data
3.2. Simulation and Evaluation of Stratigraphic Uncertainty for Different Borehole Schemes
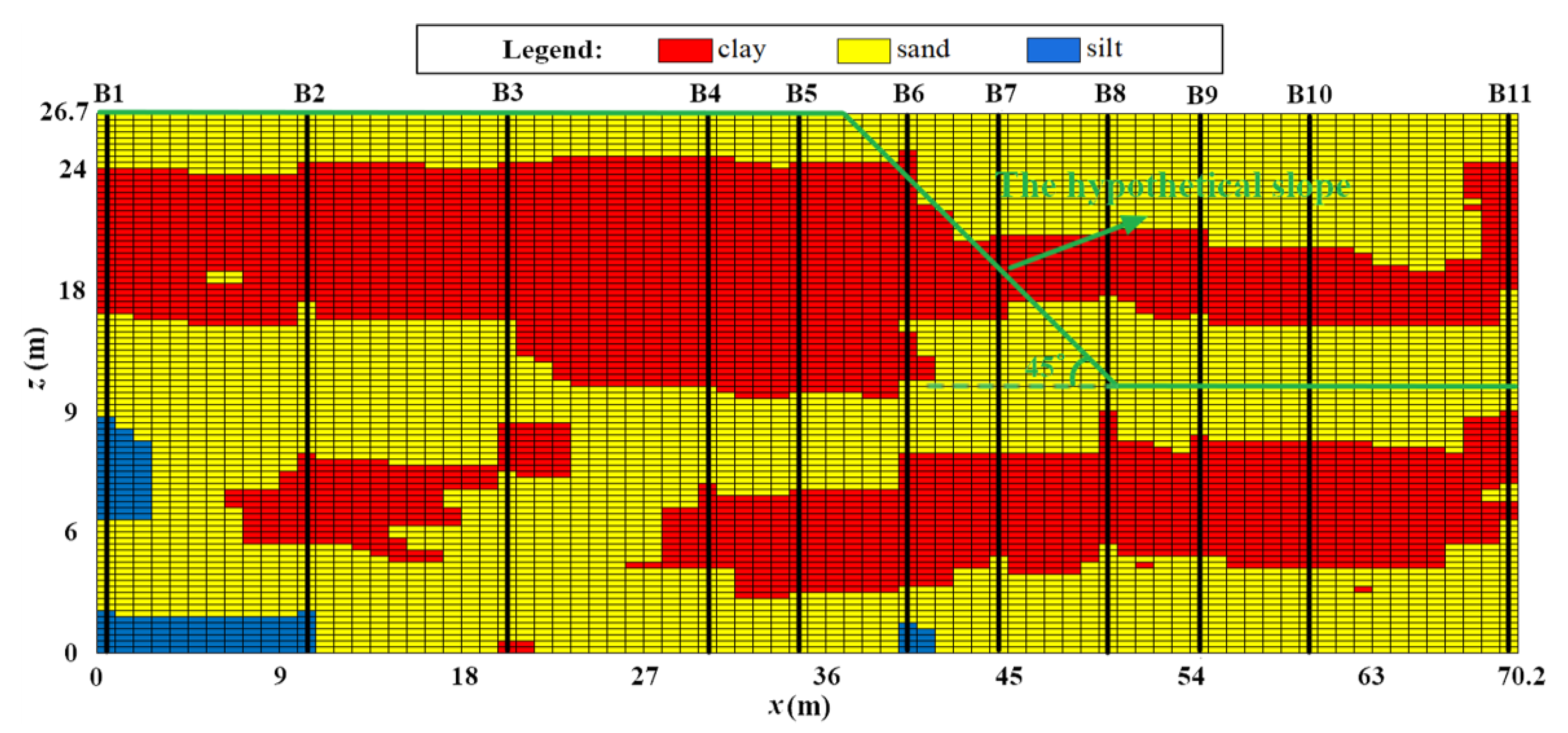
3.2.1. The “Real” Stratum
3.2.2. Borehole Schemes
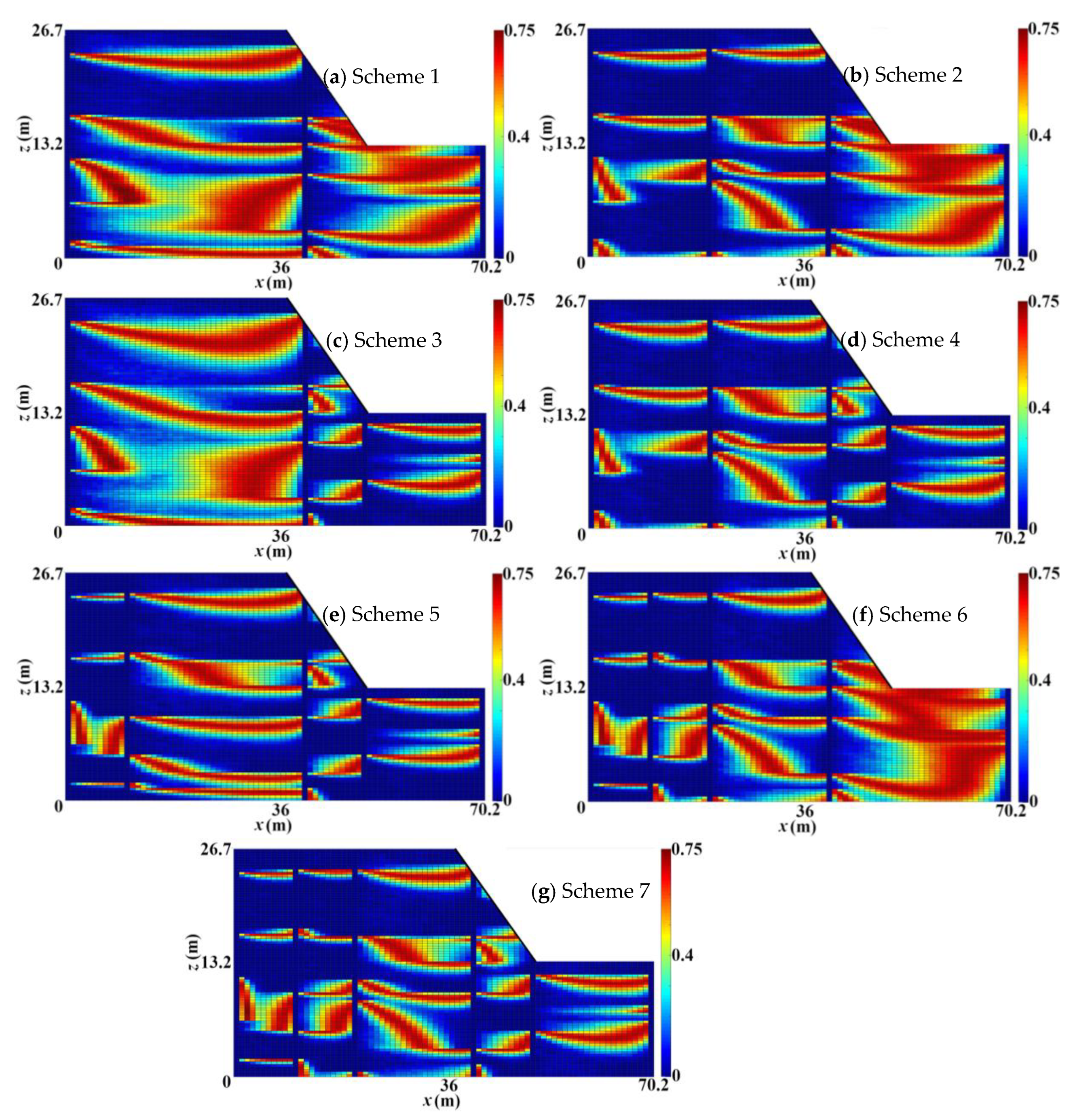
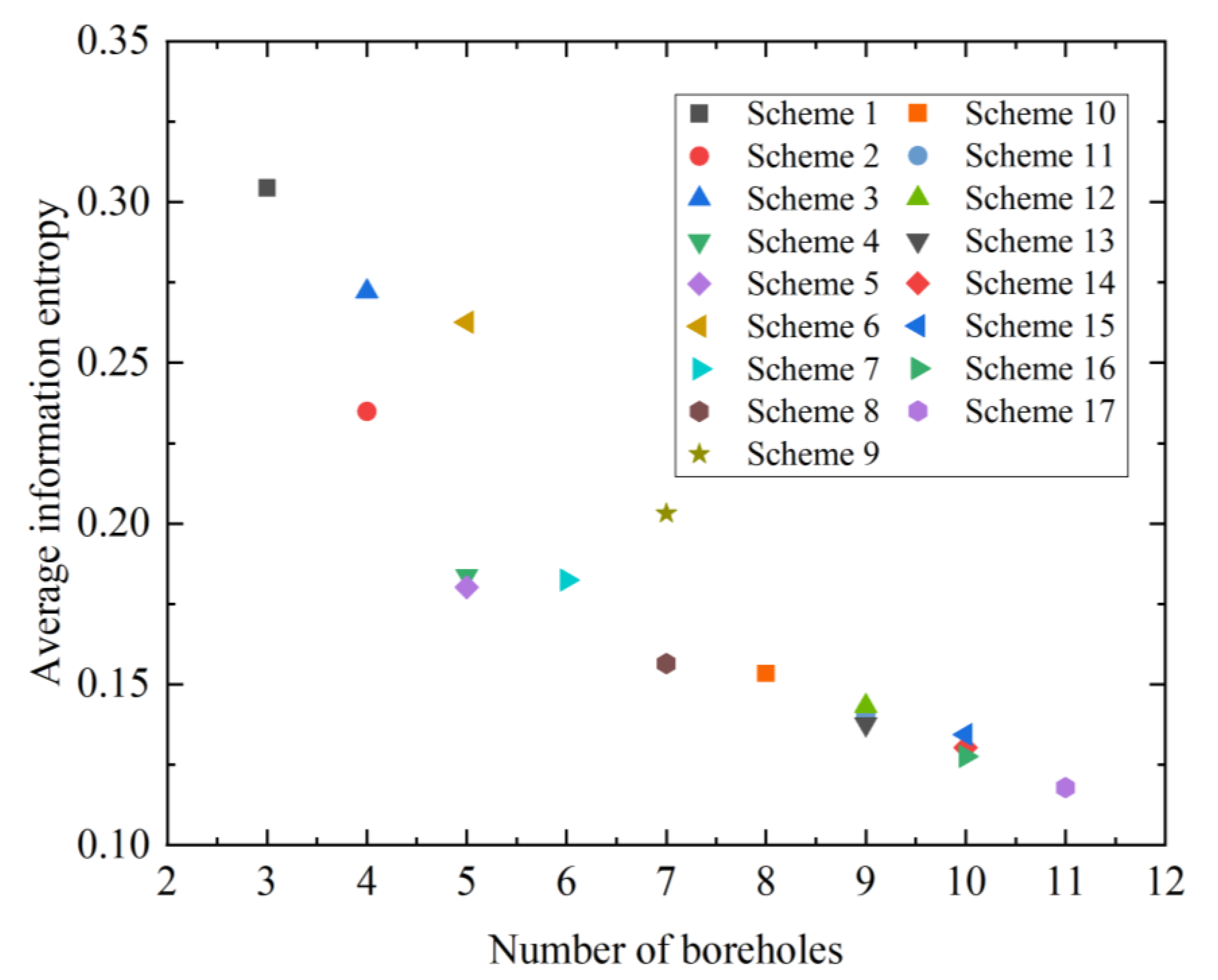
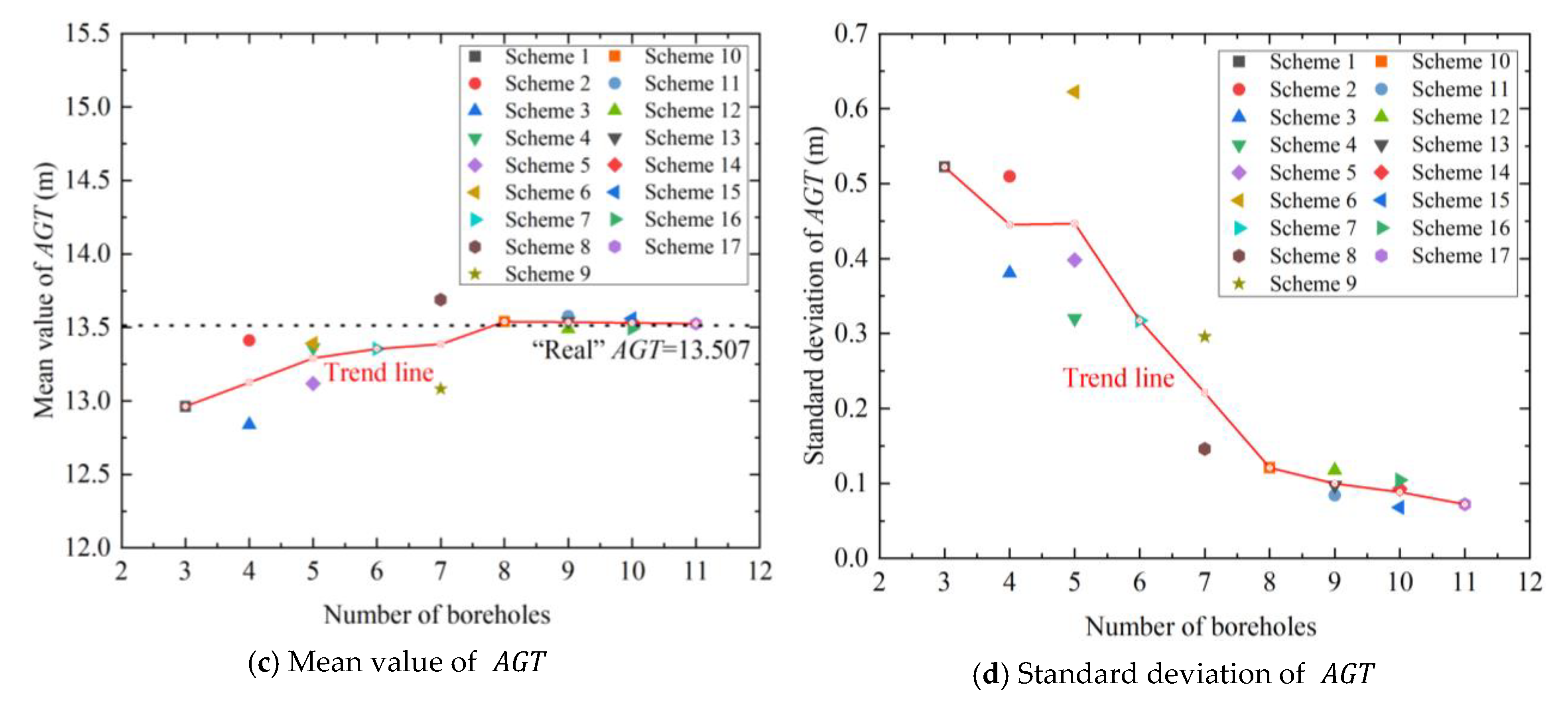
3.2.3. Stratigraphic Uncertainty for Different Borehole Schemes
3.3. Stability Analysis of Unsaturated Soil Slope Considering Stratigraphic Uncertainty
3.3.1. FEM Model of Slope
3.3.2. Stability of Unsaturated Soil Slope for Different Borehole Schemes
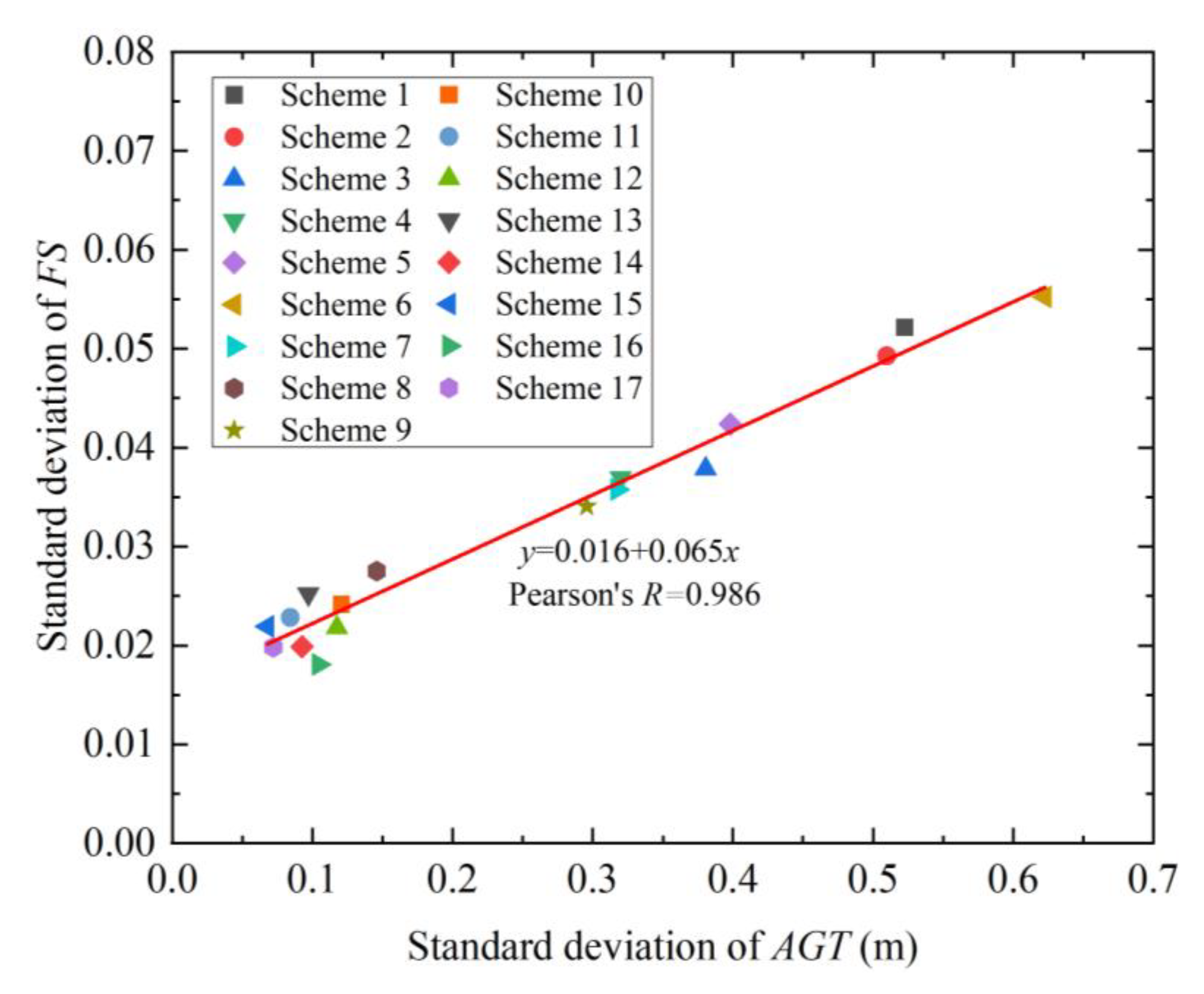
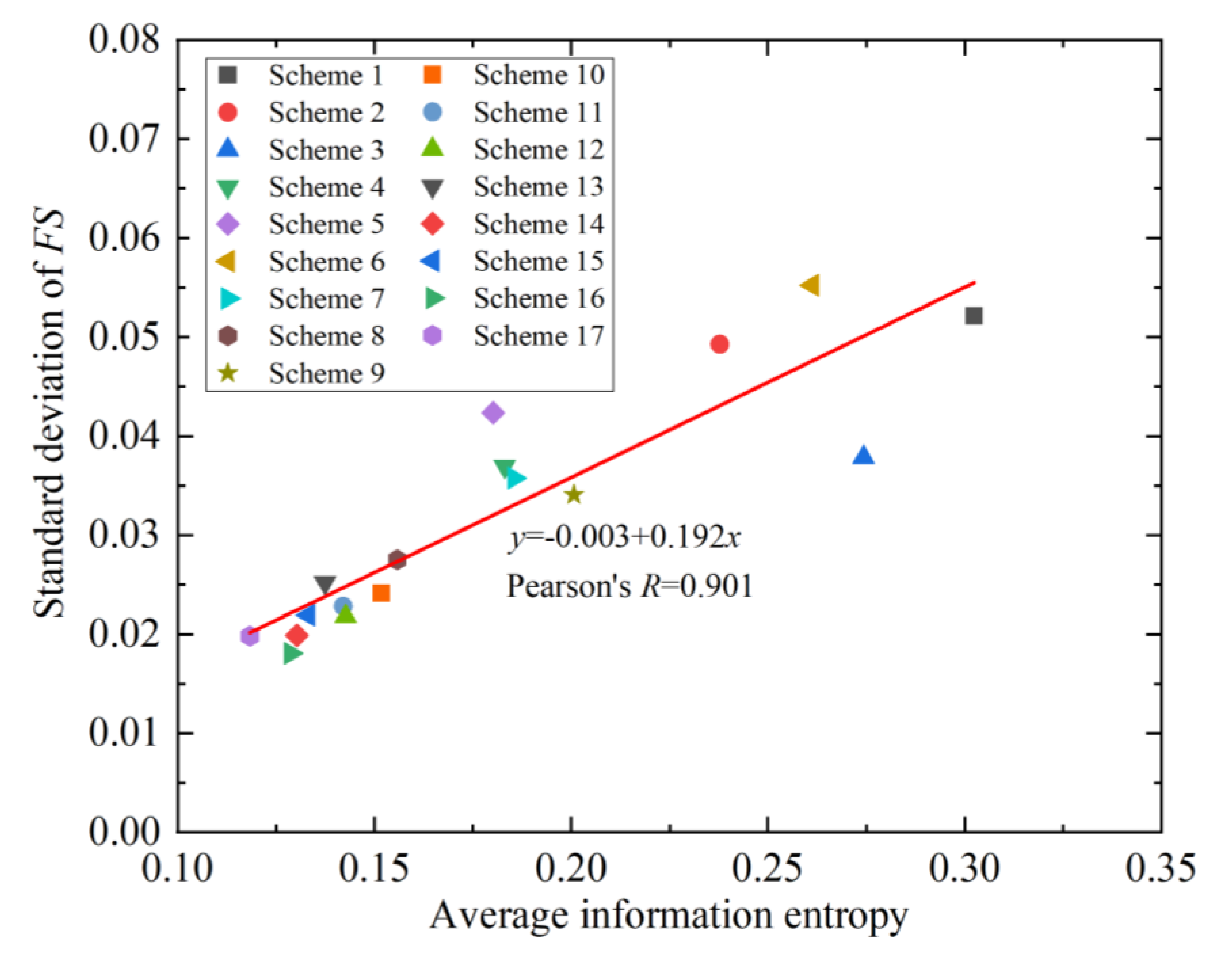
3.3.3. Relationship between the Standard Deviation of (or ) and the Average Information Entropy
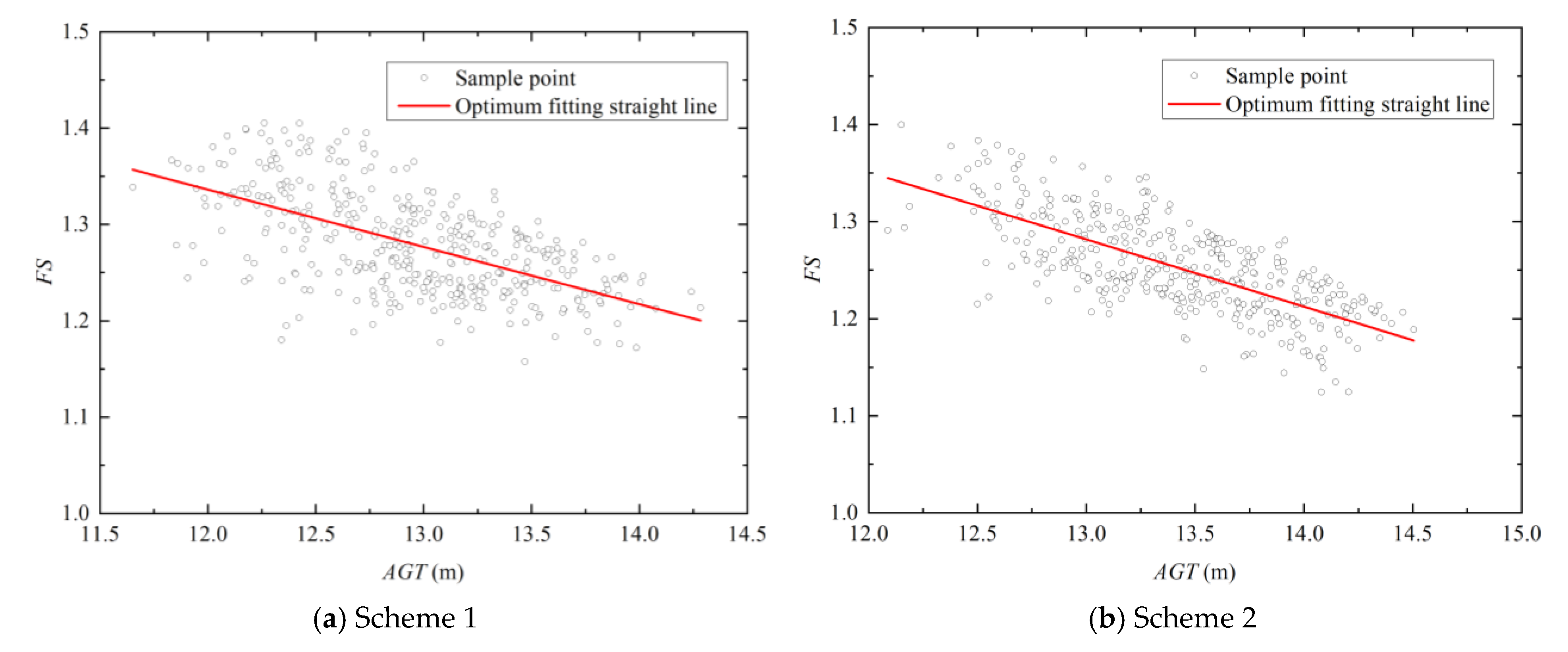
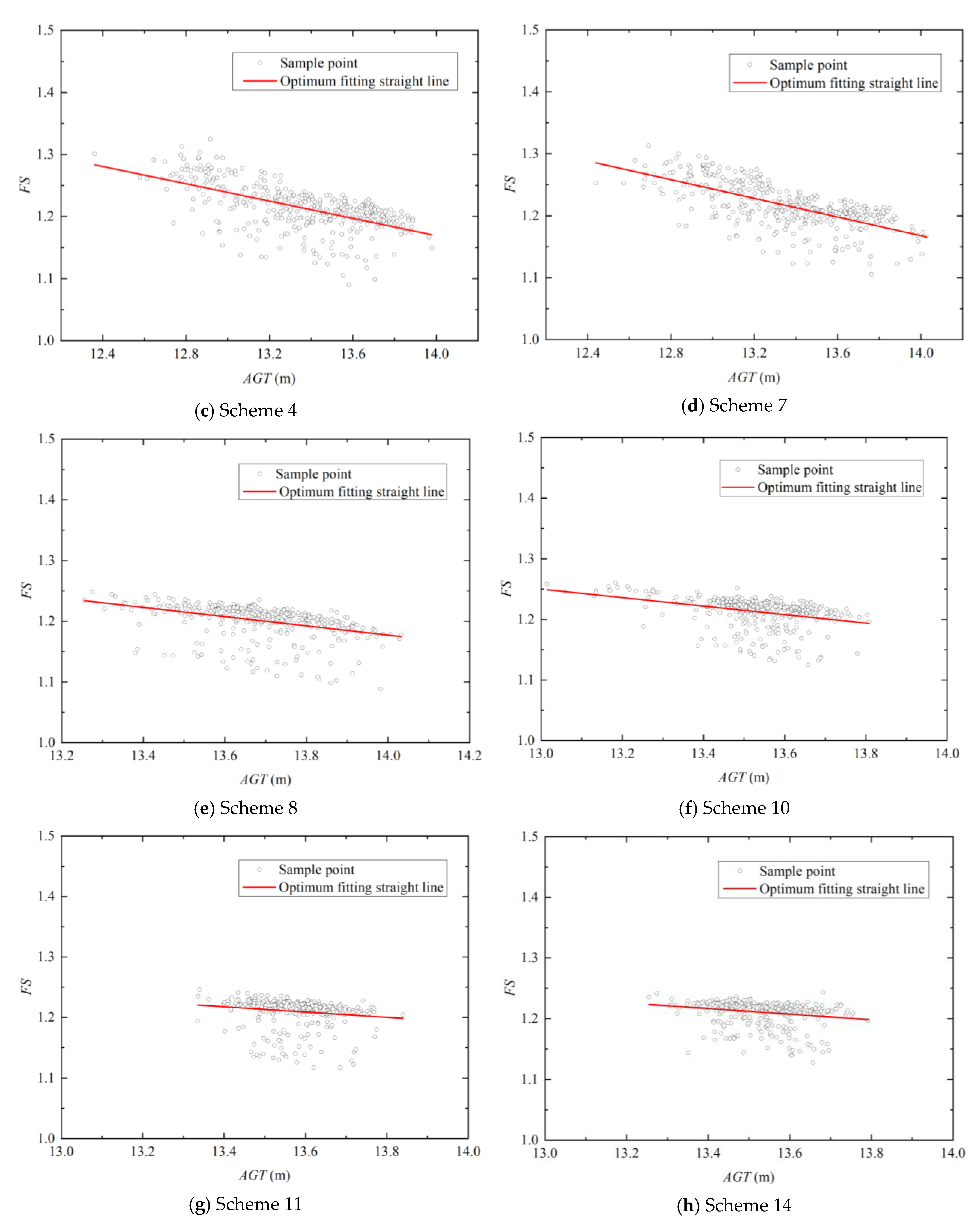
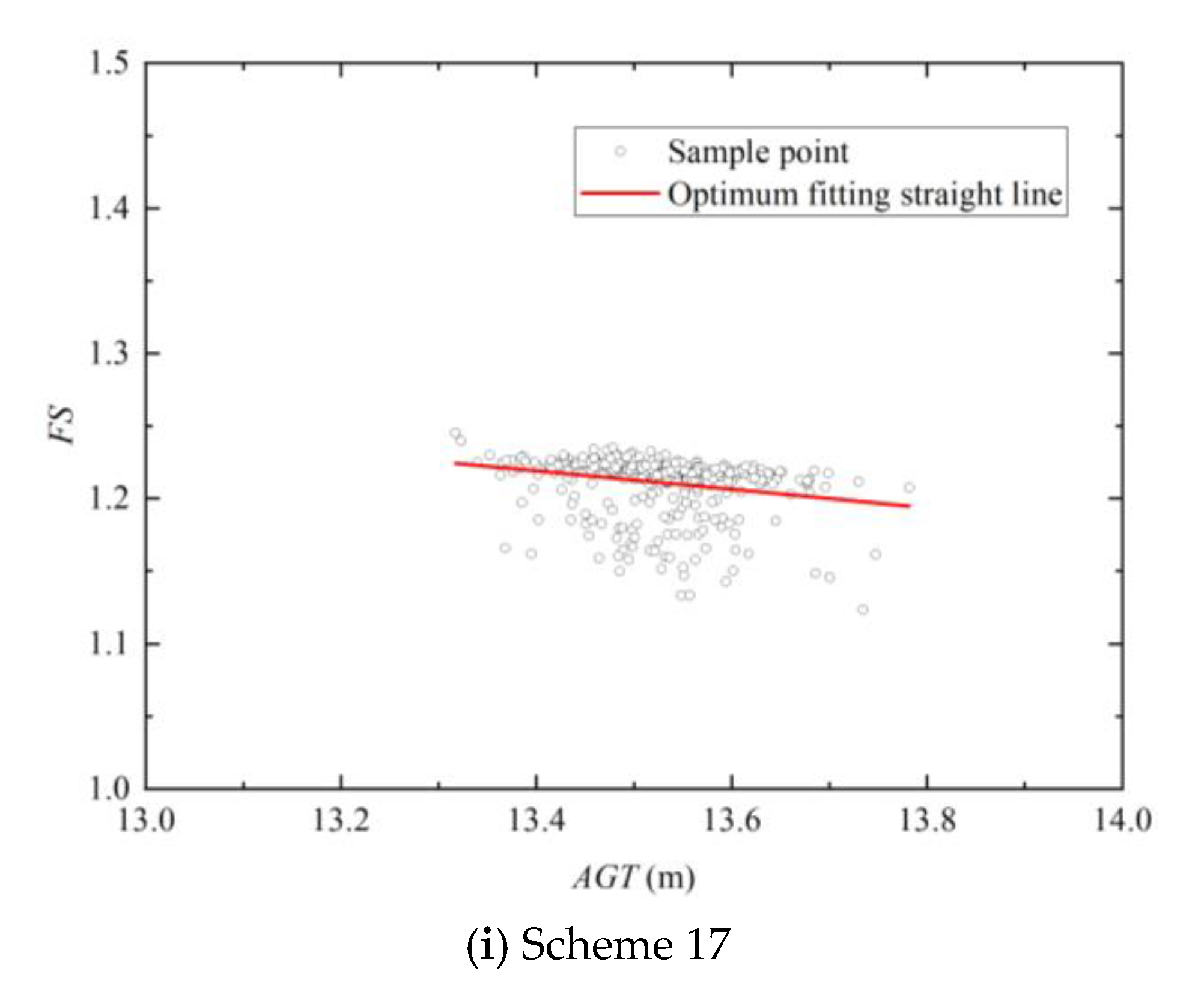
3.3.4. Relationship between and for Different Schemes
4. Conclusions
- (1)
- Information entropy can well quantify the overall and local uncertainty of strata. There is a linear relationship between the standard deviation of the (or ) and the average information entropy. Since the calculation of information entropy is simple and fast, the variation of and can be estimated by information entropy in practical engineering.
- (2)
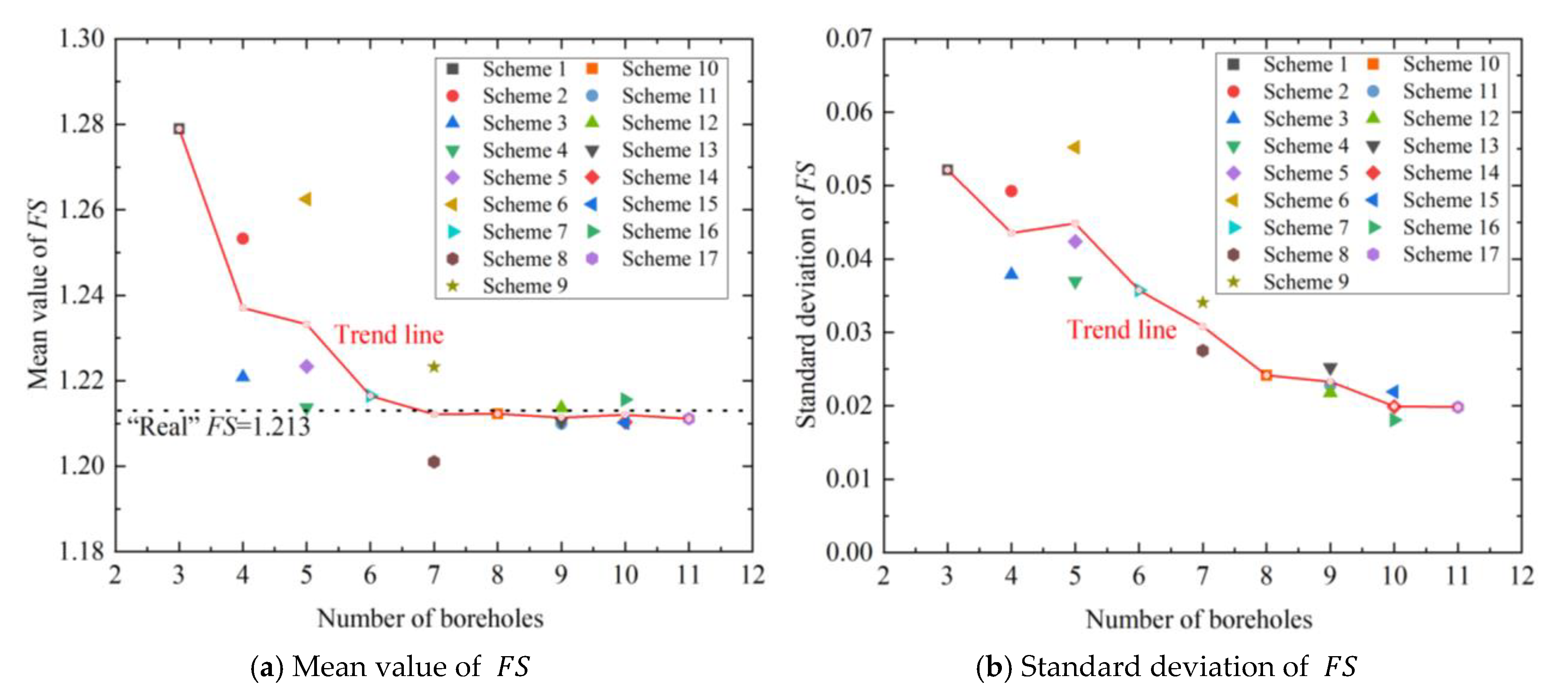
- When the number of boreholes is 11, the mean values of and are close to the “real” values, which proves that the proposed algorithm can accurately calculate the and . The statistics of and will not monotonically increase or decrease with the increase in the borehole number. But the trend is that the mean values of and gradually approach and eventually converge to the real values and the standard deviations of and decrease. Therefore, when there are more known boreholes, the mean value of (or ) is more likely to be close to the real value, and the standard deviation of (or ) is more likely to be small. Although some additional boreholes may be “bad” data and increase the deviation between the estimated values of and and the true values, the overall trend is still that the more boreholes are drilled, the more accurate the estimation is. Increasing boreholes is beneficial in practical engineering.
- (3)
- The sample points with and as abscissa and ordinate, respectively, are centralized and distributed in a downward inclined band, and some scattered sample points are distributed below the band, especially for the borehole schemes with more than six boreholes. The widths of the bands are related to the uncertainty of the stratum. The and the are negatively correlated considering stratigraphic uncertainty. In practical engineering, the of slope can be roughly estimated by observing the groundwater table according to this negative correlation property. However, the estimated results are not deterministic, have probabilistic properties and have a certain level of credibility.
- (4)
- The influence of stratigraphic uncertainty on the stability of unsaturated soil slopes is investigated in this paper. In the future, we will consider both the stratigraphic uncertainty and uncertainty of soil parameters and study their influence on the stability of unsaturated soil slopes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Phoon, K.K.; Kulhawy, F.H. Characterization of geotechnical variability. Can. Geotech. J. 1999, 36, 612–624. [Google Scholar] [CrossRef]
- Elkateb, T.; Chalaturnyk, R.; Robertson, P.K. An overview of soil heterogeneity: Quantification and implications on geotechnical field problems. Can. Geotech. J. 2003, 40, 1–15. [Google Scholar] [CrossRef]
- Deng, Z.P.; Li, D.Q.; Qi, X.H.; Cao, Z.J.; Phoon, K.K. Reliability evaluation of slope considering stratigraphic uncertainty and inherent variability of soil parameters. Comput. Geotech. 2017, 92, 121–131. [Google Scholar] [CrossRef]
- Gong, W.; Zhao, C.; Juang, C.H.; Zhang, Y.; Tang, H.; Lu, Y. Coupled characterization of stratigraphic and geo-properties uncertainties–a conditional random field approach. Eng. Geol. 2021, 294, 106348. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Probabilistic slope stability analysis by finite elements. J. Geotech. Geoenviron. Eng. 2004, 130, 507–518. [Google Scholar] [CrossRef]
- Jiang, S.H.; Huang, J. Modeling of non-stationary random field of undrained shear strength of soil for slope reliability analysis. Soils Found 2018, 58, 185–198. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, L.M. Characterizing geotechnical anisotropic spatial variations using random field theory. Can. Geotech. J. 2013, 50, 723–734. [Google Scholar] [CrossRef]
- Johari, A.; Fooladi, H. Comparative study of stochastic slope stability analysis based on conditional and unconditional random field. Comput. Geotech. 2020, 125, 103707. [Google Scholar] [CrossRef]
- Tang, W.H.; Sidi, I.; Gilbert, R.B. Average property in random two-state medium. J. Eng. Mech. 1989, 115, 131–144. [Google Scholar] [CrossRef]
- Kohno, S.; Ang, H.S.; Tang, W.H. Reliability evaluation of idealized tunnel systems. Struct. Saf. 1992, 11, 81–93. [Google Scholar] [CrossRef]
- Elfeki, A.; Dekking, M. A Markov chain model for subsurface characterization: Theory and applications. Math. Geol. 2001, 33, 569–589. [Google Scholar] [CrossRef]
- Elfeki, A.; Dekking, F.M. Modelling subsurface heterogeneity by coupled Markov chains: Directional dependency, Walther’s law and entropy. Geotech. Geol. Eng. 2005, 23, 721–756. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; Wang, H.; Liang, R.Y. Quantifying stratigraphic uncertainties by stochastic simulation techniques based on markov random field. Eng. Geol. 2016, 201, 106–122. [Google Scholar] [CrossRef]
- Wang, X. Uncertainty quantification and reduction in the characterization of subsurface stratigraphy using limited geotechnical investigation data. Under. Space 2020, 5, 125–143. [Google Scholar] [CrossRef]
- Wang, X.; Wang, H.; Liang, R.Y.; Zhu, H.; Di, H. A hidden markov random field model based approach for probabilistic site characterization using multiple cone penetration test data. Struct. Saf. 2018, 70, 128–138. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, K.; Cao, Z. Probabilistic identification of underground soil stratification using cone penetration tests. Can. Geotech. J. 2013, 50, 766–776. [Google Scholar] [CrossRef]
- Cao, Z.J.; Zheng, S.; Li, D.Q.; Phoon, K.K. Bayesian identification of soil stratigraphy based on soil behaviour type index. Can. Geotech. J. 2019, 56, 570–586. [Google Scholar] [CrossRef]
- Alshboul, O.; Shehadeh, A.; Almasabha, G.; Almuflih, A.S. Extreme gradient boosting-based machine learning approach for green building cost prediction. Sustainability 2022, 14, 6651. [Google Scholar] [CrossRef]
- Alshboul, O.; Almasabha, G.; Shehadeh, A.; Mamlook, R.E.A.; Almuflih, A.S.; Almakayeel, N. Machine learning-based model for predicting the shear strength of slender reinforced concrete beams without stirrups. Buildings 2022, 12, 1166. [Google Scholar] [CrossRef]
- Gong, W.; Zhao, C.; Juang, C.H.; Tang, H.; Hu, X. Stratigraphic uncertainty modelling with random field approach. Comput. Geotech. 2020, 125, 103681. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Y. Non-parametric and data-driven interpolation of subsurface soil stratigraphy from limited data using multiple point statistics. Can. Geotech. J. 2021, 58, 261–280. [Google Scholar] [CrossRef]
- Qi, X.H.; Li, D.Q.; Phoon, K.K.; Cao, Z.J.; Tang, X.S. Simulation of geologic uncertainty using coupled Markov chain. Eng. Geol. 2016, 207, 129–140. [Google Scholar] [CrossRef]
- Deng, Z.P.; Jiang, S.H.; Niu, J.T.; Pan, M.; Liu, L.L. Stratigraphic uncertainty characterization using generalized coupled Markov chain. B. Eng. Geol. Environ. 2020, 79, 5061–5078. [Google Scholar] [CrossRef]
- Cao, W.; Zhou, A.; Shen, S.L. An analytical method for estimating horizontal transition probability matrix of coupled Markov chain for simulating stratigraphic uncertainty. Comput. Geotech. 2021, 129, 103871. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Liu, Z.Q.; Zhang, D.M.; Huang, H.W.; Phoon, K.K.; Xue, Y.D. Improved coupled Markov chain method for simulating geological uncertainty. Eng. Geol. 2022, 298, 106539. [Google Scholar]
- Qi, X.H.; Li, D.Q.; Zhou, C.; Phoon, K.K. Estimation of horizontal transition probability matrix for coupled Markov chain based on borehole data. J. Basic Sci. Eng. 2017, 25, 967–984. [Google Scholar]
- Li, J.; Cai, Y.; Li, X.; Zhang, L. Simulating realistic geological stratigraphy using direction-dependent coupled Markov chain model. Comput. Geotech. 2019, 115, 103147. [Google Scholar] [CrossRef]
- Cho, S.E.; Lee, S.R. Instability of unsaturated soil slopes due to infiltration. Comput. Geotech. 2001, 28, 185–208. [Google Scholar] [CrossRef]
- Cho, S.E.; Lee, S.R. Evaluation of surficial stability for homogeneous slopes considering rainfall characteristics. J. Geotech. Geoenviron. Eng. 2002, 128, 756–763. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Lu, N. Unsaturated slope stability analysis with steady infiltration or evaporation using elasto-plastic finite elements. Int. J. Numer. Anal. Met. 2005, 29, 249–267. [Google Scholar] [CrossRef]
- Ray, R.L.; Jacobs, J.M.; Alba, P.D. Impacts of unsaturated zone soil moisture and groundwater table on slope instability. J. Geotech. Geoenviron. Eng. 2010, 136, 1448–1458. [Google Scholar] [CrossRef]
- Li, W.C.; Lee, L.M.; Cai, H.; Li, H.J.; Dai, F.C.; Wang, M.L. Combined roles of saturated permeability and rainfall characteristics on surficial failure of homogeneous soil slope. Eng. Geol. 2013, 153, 105–113. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Perna, A.; Martinelli, M. Modelling the spatio-temporal evolution of a rainfall-induced retrogressive landslide in an unsaturated slope. Eng. Geol. 2021, 294, 106371. [Google Scholar] [CrossRef]
- Yan, T.; Xiong, J.; Ye, L.; Gao, J.; Xu, H. Field investigation and finite element analysis of landslide-triggering factors of a cut slope composed of granite residual soil: A case study of Chongtou Town, Lishui City, China. Sustainability 2023, 15, 6999. [Google Scholar] [CrossRef]
- Jia, J.; Pei, X.; Liu, G.; Cai, G.; Guo, X.; Hong, B. Failure mechanism of anti-dip layered soft rock slope under rainfall and excavation conditions. Sustainability 2023, 15, 9398. [Google Scholar] [CrossRef]
- Santoso, A.M.; Phoon, K.K.; Quek, S.T. Effects of soil spatial variability on rainfall-induced landslides. Comput. Geotech. 2011, 89, 893–900. [Google Scholar] [CrossRef]
- Ali, A.; Huang, J.; Lyamin, A.V.; Sloan, S.W.; Griffiths, D.V.; Cassidy, M.J.; Li, J.H. Simplified quantitative risk assessment of rainfall-induced landslides modelled by infinite slopes. Eng. Geol. 2014, 179, 102–116. [Google Scholar] [CrossRef]
- Cho, S.E. Probabilistic stability analysis of rainfall-induced landslides considering spatial variability of permeability. Eng. Geol. 2014, 171, 11–20. [Google Scholar] [CrossRef]
- Dou, H.Q.; Han, T.C.; Gong, X.N.; Qiu, Z.Y.; Li, Z.N. Effects of the spatial variability of permeability on rainfall-induced landslides. Eng. Geol. 2015, 192, 92–100. [Google Scholar] [CrossRef]
- Zhou, A.; Li, C.Q.; Huang, J. Failure analysis of an infinite unsaturated soil slope. Geotech. Eng. 2016, 169, 410–420. [Google Scholar] [CrossRef]
- Johari, A.; Gholampour, A. A practical approach for reliability analysis of unsaturated slope by conditional random finite element method. Comput. Geotech. 2018, 102, 79–91. [Google Scholar] [CrossRef]
- Masoudian, M.S.; Afrapoli, M.; Tasalloti, A.; Marshall, A.M. A general framework for coupled hydro-mechanical modelling of rainfall-induced instability in unsaturated slopes with multivariate random fields. Comput. Geotech. 2019, 115, 103162. [Google Scholar] [CrossRef]
- Srivastava, A.; Babu, G.; Haldar, S. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis. Eng. Geol. 2010, 110, 93–101. [Google Scholar] [CrossRef]
- Jiang, S.H.; Li, D.Q.; Zhou, C.B.; Zhang, L.M. Reliability analysis of unsaturated slope considering spatial variability. Rock Soil Mech. 2014, 35, 2569–2578. [Google Scholar]
- Le, T.; Gallipoli, D.; Sanchez, M.; Wheeler, S. Stability and failure mass of unsaturated heterogeneous slopes. Can. Geotech. J. 2015, 52, 1747–1761. [Google Scholar] [CrossRef]
- Le, T.; Sanchez, M.; Gallipoli, D.; Wheeler, S. Probabilistic study of rainfall-triggered instabilities in randomly heterogeneous unsaturated finite slopes. Transport Porous Med. 2019, 126, 199–222. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Qu, C.; Ni, J.; Guo, H. Three-dimensional reliability analysis of unsaturated soil slope considering permeability rotated anisotropy random fields. Comput. Geotech. 2022, 151, 104944. [Google Scholar]
- Rotaru, A.; Bejan, F.; Almohamad, D. Sustainable slope stability analysis: A critical study on methods. Sustainability 2022, 14, 8847. [Google Scholar] [CrossRef]
- Li, D.Q.; Qi, X.H.; Cao, Z.J.; Tang, X.S.; Phoon, K.K.; Zhou, C.B. Evaluating slope stability uncertainty using coupled markov chain. Comput. Geotech. 2016, 73, 72–82. [Google Scholar] [CrossRef]
- Liu, L.L.; Cheng, Y.M.; Pan, Q.J.; Dias, D. Incorporating stratigraphic boundary uncertainty into reliability analysis of slopes in spatially variable soils using one-dimensional conditional Markov chain model. Comput. Geotech. 2019, 118, 103321. [Google Scholar] [CrossRef]
- Gong, W.; Tang, H.; Wang, H.; Wang, X.R.; Juang, H. Probabilistic analysis and design of stabilizing piles in slope considering stratigraphic uncertainty. Eng. Geol. 2019, 259, 105162. [Google Scholar]
- Ghadrdan, M.; Dyson, A.P.; Shaghaghi, T.; Tolooiyan, A. Slope stability analysis using deterministic and probabilistic approaches for poorly defined stratigraphies. Geomech. Geophys. Geo-Energ. Geo-Resour. 2021, 7, 4. [Google Scholar] [CrossRef]
- Deng, Z.P.; Pan, M.; Niu, J.T.; Jiang, S.H. Full probability design of soil slopes considering both stratigraphic uncertainty and spatial variability of soil properties. Bull. Eng. Geol. Environ. 2022, 81, 195. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Huang, H.W.; Zhang, D.M.; Phoon, K.K.; Tang, C. Quantitative evaluation of stratigraphic uncertainty and its influence on tunnel structural performance using improved coupled Markov chain. Acta Geotech. 2021, 16, 3709–3724. [Google Scholar] [CrossRef]
- Cao, W.; Zhou, A. An improved coupled Markov chain model for simulating geological uncertainty. In Proceedings of the 8th International Symposium on Geotechnical Safety and Risk (ISGSR), Newcastle, Australia, 14–16 December 2022. [Google Scholar]







| Borehole Scheme | Number of Boreholes | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 | B11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scheme 1 | 3 | √ | √ | √ | ||||||||
| Scheme 2 | 4 | √ | √ | √ | √ | |||||||
| Scheme 3 | 4 | √ | √ | √ | √ | |||||||
| Scheme 4 | 5 | √ | √ | √ | √ | √ | ||||||
| Scheme 5 | 5 | √ | √ | √ | √ | √ | ||||||
| Scheme 6 | 5 | √ | √ | √ | √ | √ | ||||||
| Scheme 7 | 6 | √ | √ | √ | √ | √ | √ | |||||
| Scheme 8 | 7 | √ | √ | √ | √ | √ | √ | √ | ||||
| Scheme 9 | 7 | √ | √ | √ | √ | √ | √ | √ | ||||
| Scheme 10 | 8 | √ | √ | √ | √ | √ | √ | √ | √ | |||
| Scheme 11 | 9 | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||
| Scheme 12 | 9 | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||
| Scheme 13 | 9 | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||
| Scheme 14 | 10 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |
| Scheme 15 | 10 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |
| Scheme 16 | 10 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |
| Scheme 17 | 11 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Soil Type | Unit Weight, (kN/m3) | Elastic Modulus, E (MPa) | Poisson’s Ratio, | Effective Cohesion, (kPa) | Effective Friction Angle, (Degree) | Fully Saturated Hydraulic Conductivity, k (m/s) | (kPa) | |
|---|---|---|---|---|---|---|---|---|
| Clay | 20 | 30 | 0.3 | 18 | 25 | 5 × 10−5 | 100 | 1.5 |
| Sand | 20 | 50 | 0.3 | 2 | 33 | 5 × 10−4 | 10 | 2.5 |
| Silt | 20 | 30 | 0.3 | 6 | 28 | 1 × 10−4 | 20 | 2.0 |
| Borehole Schemes | Borehole Number | Intercept A | Slope B | Pearson’s R | Residual Sum of Squares |
|---|---|---|---|---|---|
| 1 | 3 | 2.050 | −0.059 | −0.596 | 0.700 |
| 2 | 4 | 2.182 | −0.069 | −0.717 | 0.471 |
| 4 | 5 | 2.146 | −0.070 | −0.604 | 0.346 |
| 7 | 6 | 2.223 | −0.075 | −0.669 | 0.282 |
| 8 | 7 | 2.256 | −0.077 | −0.410 | 0.251 |
| 10 | 8 | 2.162 | −0.070 | −0.351 | 0.204 |
| 11 | 9 | 1.801 | −0.044 | −0.161 | 0.202 |
| 14 | 10 | 1.835 | −0.046 | −0.217 | 0.150 |
| 17 | 11 | 2.068 | −0.063 | −0.231 | 0.148 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.; Wan, Z.; Li, W. Stability of Unsaturated Soil Slope Considering Stratigraphic Uncertainty. Sustainability 2023, 15, 10717. https://doi.org/10.3390/su151310717
Cao W, Wan Z, Li W. Stability of Unsaturated Soil Slope Considering Stratigraphic Uncertainty. Sustainability. 2023; 15(13):10717. https://doi.org/10.3390/su151310717
Chicago/Turabian StyleCao, Wei, Zheng Wan, and Wenjing Li. 2023. "Stability of Unsaturated Soil Slope Considering Stratigraphic Uncertainty" Sustainability 15, no. 13: 10717. https://doi.org/10.3390/su151310717
APA StyleCao, W., Wan, Z., & Li, W. (2023). Stability of Unsaturated Soil Slope Considering Stratigraphic Uncertainty. Sustainability, 15(13), 10717. https://doi.org/10.3390/su151310717






