Power and Frequency Band Allocation Mechanisms for WPT System with Logarithmic-Based Nonlinear Energy Harvesting Model

Abstract

Wireless power transmission (WPT) is expected to play a crucial role in supporting the perpetual operations of Internet of Things (IoT) devices, thereby contributing significantly to IoT services. However, the development of efficient power allocation algorithms has remained a longstanding challenge. This paper addresses the aforementioned challenge by proposing a novel strategy, called energy poverty-based device selection (EPDS), in conjunction with energy beamforming, where orthogonal frequency bands are allocated to energy harvesting IoT devices (EHIs). To solve two power allocation problems, a logarithmic-based nonlinear energy harvesting model (NEHM) is introduced. The first problem tackled is the total received power maximization (TRPM), which is initially presented and, then, solved optimally in closed-form by incorporating Karush–Kuhn–Tucker (KKT) conditions with the modified water-filling algorithm. The second problem formulated is the common received power maximization (CRPM), which takes into account energy fairness considerations. To assess the proposed algorithms and gain insights into the effects of mobility, the mobility of EHIs is modeled as a one-dimensional random walk. Extensive numerical results are provided to validate the advantages of the proposed algorithms. Both the TRPM and CRPM algorithms exhibit exceptional performance in terms of total and minimum received energy, respectively. Furthermore, in comparison to round-robin scheduling, the EPDS demonstrates superior performance in terms of minimum received energy. This paper highlights the impact of the proposed energy harvesting (EH) model, demonstrating 12.68% and 3.69% higher values than the linear model for the minimum and total received energy, respectively.

1. Introduction

With the emergence of the IoT as a promising technology for a hyper-connected society, a significant number of IoT sensors have been deployed in various application domains, including smart cities and smart homes [1,2,3,4,5,6,7]. The pervasive nature of IoT technology is expected to encompass every aspect of our lives. However, a major challenge arises as most IoT sensors operate on battery power, leading to an energy poverty issue [8,9,10,11,12,13,14]. To address this challenge, the concept of radio-frequency (RF) wireless power transfer technology has been extensively explored. This technology enables wireless power transmission to mobile IoT sensors, which are often difficult to power through conventional cable connections. Consequently, this approach has garnered significant interest from researchers [15,16,17,18,19,20,21,22].

One of the practical areas of research related to RF–WPT is the Cota technology of the company Ossia [23]. The Cota technology utilizes a beacon signal to detect energy-absorbing objects, such as humans, and employs beamforming technology to transmit power wirelessly to specific objects, while avoiding energy-absorbing objects. Ossia successfully achieved the transmission of 1 W (Watt) of RF energy at a distance of 30 feet using the 2.4 GHz or 5.8 GHz ISM band through Cota technology. Another company, Energous, introduced a technology called WattUp, which utilizes the Wi-Fi frequency band from 5.7 GHz to 5.8 GHz to simultaneously transmit 4 W to twelve devices located 20 feet away from the power transmitter [24]. As mentioned above, WPT technology is actively studied by numerous technology companies for real-world applications, and various RF–WPT studies have also been conducted in academia. Two representative research topics related to WPT are simultaneous wireless information and power transfer (SWIPT) networks and wireless powered communication networks (WPCNs).

In SWIPT, the power transmitter simultaneously provides both power and information to multiple receivers by integrating a WPT system with a wireless communication system. Numerous studies on SWIPT have been reported, including studies on separated SWIPT [25,26,27,28,29], co-located SWIPT with a power splitting (PS) mechanism [29,30,31,32,33,34,35,36], and co-located SWIPT with a time splitting (TS) mechanism [28,29,30,37].

The other application technology of WPT, in which receivers are initially powered by WPT and then use the harvested energy for their information signal transmission, is referred to as WPCN.

Regarding the antenna technology in WPCN, a limited number of studies have been reported, including single-input single-output (SISO) WPCN [38,39,40], multiple-input single-output (MISO) WPCN [41,42,43,44,45], and multiple-input multiple-output (MIMO) WPCN [46]. In recent works, Goktas et al. [47] considered a time-switching-based WPT with two phases. In the first phase, WPT devices perform energy harvesting using signals from a base station and then, in the second phase, utilize the harvested energy to transmit uplink signals. They formulated an optimization problem to maximize the uplink data rate, while minimizing the interference effects from the transmission.

These WPT technologies offer user-friendliness, convenience, and flexibility to IoT applications, eliminating the need to replace the batteries of IoT sensors [48]. However, since WPT technology utilizes an RF signal for power transmission, dealing with signal power attenuation, which heavily depends on the distance from the wireless power transmitter, has been a significant challenge.

For instance, when IoT sensors are distributed at different distances from the power transmitter, there is a considerable difference in the received RF power strength among the sensors. This discrepancy leads to varying lifetimes and varied amounts of available energy for IoT sensors in the WPT system. IoT sensors closer to the wireless power transmitter can harvest significantly more energy than those located far away. As a result, IoT sensors with less available energy experience lower throughput when transmitting their data in the uplink. H. Ju et al. [38] addressed this “doubly near–far” problem as the common user throughput maximization problem, while L. Liu et al. [43] solved the problem of maximizing the minimum throughput among all users by jointly designing the downlink and uplink time allocations. Driven by the increasing interest in harnessing federated learning within wireless networks, Wu et al. [49] investigated the utilization of WPT to power edge devices for their data transmission and local training in each round of the federated learning process. They minimized the system-wise cost, that included the total energy consumption and the overall latency for the federated learning convergence, by optimizing the WPT durations for the edge devices and processing rates, etc.

However, since the IoT network lifetime depends on the minimum energy among all IoT sensors, addressing energy fairness issues among the sensors is crucial to prolonging the IoT network lifetime [33,50,51]. P. V. Tuan and I. Koo [33] solved the max–min fair harvested energy problem considering transmission power and required signal-to-interference-plus-noise ratio constraints by combining semidefinite relaxation with the bisection search method. In [52], the max–min energy harvesting fairness problem was formulated in the MISO–WPT system. Zhou et al. [52] jointly designed secure beamforming and the power splitting (PS) ratio under imperfect channel state information (CSI) to maximize the minimum harvested energy of EH receivers.

Although previous studies aimed to address the energy fairness problem, they solely focused on the linear energy harvesting (EH) model. The linear EH model is widely adopted in existing works, due to its simplicity and effectiveness in capturing energy harvesting characteristics. However, given its idealized nature, it is crucial to consider a more realistic nonlinear EH model [53,54,55,56,57]. E. Boshkovska et al. [54] introduced a practical nonlinear EH model, based on a logistic function, and explored the maximization of total harvested power at energy harvesting receivers. In a similar vein, X. Liu et al. [44] tackled the problem of maximizing secrecy throughput in wireless-powered communication networks by considering a nonlinear EH model under both perfect and imperfect CSIs. However, the nonlinear EH model mentioned above adds complexity to the optimization problem, due to the presence of the logistic function. As a result, there has been a growing interest among researchers in developing resource allocation algorithms that address both energy fairness among IoT sensors and simplified nonlinear EH characteristics.

In this paper, we consider a MISO–WPT system comprising a multi-antenna power transmitter (PT) and multiple single-antenna energy harvesting IoT devices. The main contributions of this paper are summarized below:

• Energy harvesting models are typically characterized by logistic behavior, yet most research studies have relied on linear models. In our study, however, we employ a logarithmic function-based nonlinear model. While previous research [53,54,55,56,57] utilized a logistic function-based nonlinear model, its form was considerably complex, posing challenges for optimization techniques. In contrast, we simplify the model based on the logistic function, resulting in even better alignment with the actual dataset. Thus, for future energy harvesting studies that employ a logistic function-based nonlinear EH model, researchers can adopt the model proposed in our study, offering a simpler and more accurate representation.
• In this study, we introduce two power transmission algorithms, namely the Total Received Power Maximization (TRPM) algorithm and the Common Received Power Maximization (CRPM) algorithm, within the framework of a logarithmic-based nonlinear EH model. The TRPM algorithm aims to maximize the overall received power by intelligently directing the power transmission. On the other hand, the CRPM algorithm addresses the issue of power imbalance among devices under the TRPM algorithm, offering an alternative approach that ensures fair energy distribution, while mitigating excessive inefficiency. Depending on the specific requirements of power transmission scenarios, these algorithms can be effectively selected and deployed.
• To solve the optimization problem in the TRPM algorithm, we propose a closed-form solution by combining KKT conditions with a modified water-filling algorithm. This integration brings the benefits of ease of implementation and applicability. For the somewhat complex CRPM problem, we propose a novel method that constrains the solution space, enabling the derivation of optimal transmission power through bisection search. This approach effectively addresses the challenges posed by the CRPM problem.
• Furthermore, considering the frequent mobility of EH devices, we incorporate mobility using a one-dimensional random walk model. We adopt the one-dimensional approach due to the significant influence of the “distance” between EH devices and the PT on our proposed model and algorithms. To demonstrate the advantages of our algorithms in mobile environments, we provide detailed numerical results comparing their performance with existing benchmark algorithms. Notably, our findings reveal that our proposed algorithms outperform the benchmark algorithms when mobility is taken into account. This paper particularly demonstrates the effect of the proposed logarithmic-based nonlinear EH model by showing higher values than the linear model, at 12.68% and 3.69% for the minimum and total received energy, respectively.

This paper is organized as follows: Section 3 discusses the system model for the WPT mechanism proposed in this paper; Section 4 formulates the total received power maximization and common received power maximization problems and derives the optimal solutions; the numerical results of the proposed algorithms are provided in Section 5; Section 6 and Section 7 provide a discussion of our work’s strengths and weaknesses and the conclusion of this paper, respectively.

Notation: The following notation is used in this paper. The uppercase bold $\mathit{A}$ represents a matrix, the lowercase bold $\mathit{a}$ represents a vector, the uppercase A for set, and the lowercase a for scalar. For a square matrix $\mathit{S}$, tr($\mathit{S}$) denotes the trace of $\mathit{S}$, ${\mathit{S}}^H$ means Hermitian, which denotes a conjugate transpose of $\mathit{S}$, $\lambda \left(\mathit{S}\right)$ denotes eigenvalues of $\mathit{S}$, and $v_{\lambda }$ means the eigenvector of eigenvalue $\lambda$. $n\left(A\right)$ denotes the cardinality of a set A and $\parallel \mathit{a}\parallel$ denotes the magnitude of a vector $\mathit{a}.$

2. Preliminary

We provide a brief introduction to the KKT optimality conditions that are widely used. It is a methodology for finding the optimal point when a real-valued function f has both equality and inequality constraints. Consider the following optimization problem.

$$\begin{array}{l}f:{\mathbb{R}}^n\to \mathbb{R}\\ g_i:{\mathbb{R}}^n\to \mathbb{R},i\in \{1,\cdots ,m\}\\ h_j:{\mathbb{R}}^n\to \mathbb{R},j\in \{1,\cdots ,l\}\\ \mathrm{minimize}f\left(x\right)\mathit{s}.\mathit{t}.g_i\left(x\right)\le 0,i\in \{1,\cdots ,m\}\mathrm{and}{h}_j\left(x\right)=0,j\in \{1,\cdots ,l\}\end{array}$$

(1)

The optimal solution satisfies the following necessary conditions, which are referred to as the KKT conditions.

$$\begin{array}{ll}\nabla f\left(x\right)+{\displaystyle \sum _{i=1}^m}{\mu }_i\nabla g_i\left(x\right)+{\displaystyle \sum _{j=1}^l}{\lambda }_j\nabla h_j\left(x\right)=0& \left(\mathrm{Stationarity}\right)\\ g_i\left(x\right)\le 0,h_j\left(x\right)=0& (\mathrm{Primal}\mathrm{Feasibility})\\ {\mu }_i\ge 0& (\mathrm{Dual}\mathrm{Feasibility})\\ {\mu }_i{g}_i\left(x\right)=0& (\mathrm{Complementary}\mathrm{Slackness})\end{array}$$

(2)

Detailed proof of the conditions is provided in [58]. Based on the aforementioned proof, the primary objective of this paper is to describe the process of obtaining a solution for the formulated optimization problem.

3. System Model

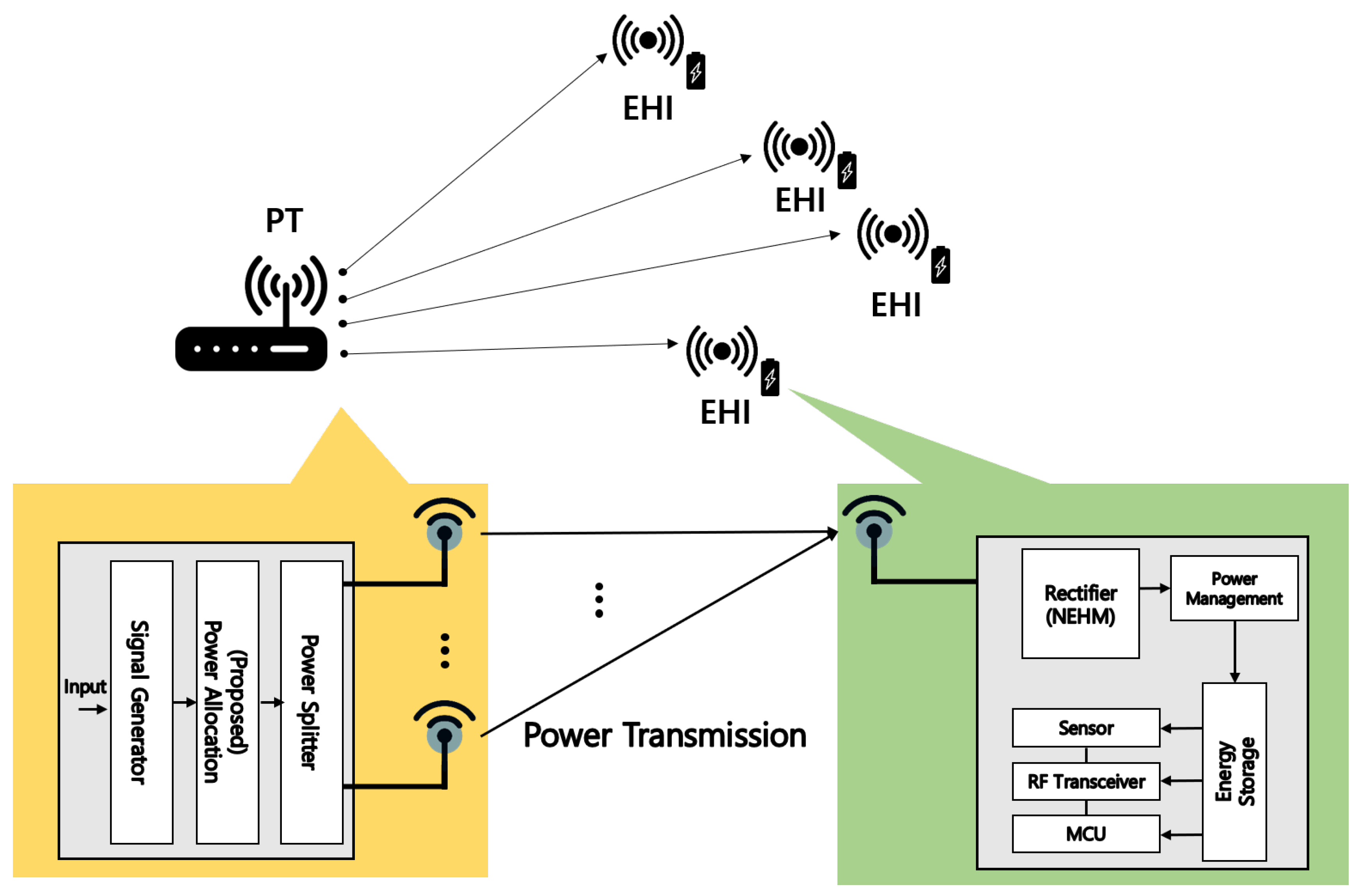
As depicted in Figure 1, this paper considered a MISO–WPT system consisting of an $n_t$-antenna PT and a set $\mathcal{K}=\{1,\cdots ,K\}$ of single-antenna EHIs. In the PT, the wireless power symbol is initially generated through the signal generator.

Subsequently, the proposed power allocation algorithm strives to optimize the transmission power of the power symbol assigned to each EHI. Then, the power splitter efficiently distributes the transmission power of the power symbol across the individual antennas. Lastly, leveraging the $n_t$-antenna, the PT is capable of transmitting the power to the EHIs, effectively and simultaneously. The EHI converts the AC power of the received signal into DC power by using the rectifier and utilizes the received transmission power for another purpose, such as charging the battery, through power management. Meanwhile, it is assumed that the wireless channel gains for all EHIs are perfectly known at the PT. In this system, a set of orthogonal frequency bands is denoted by $\mathrm{\Gamma }=\{1,2,\cdots ,n_c\}$. We considered a quasi-static flat fading channel where the wireless channel gain on each sub-channel stays constant at each uniform transmission time slot.

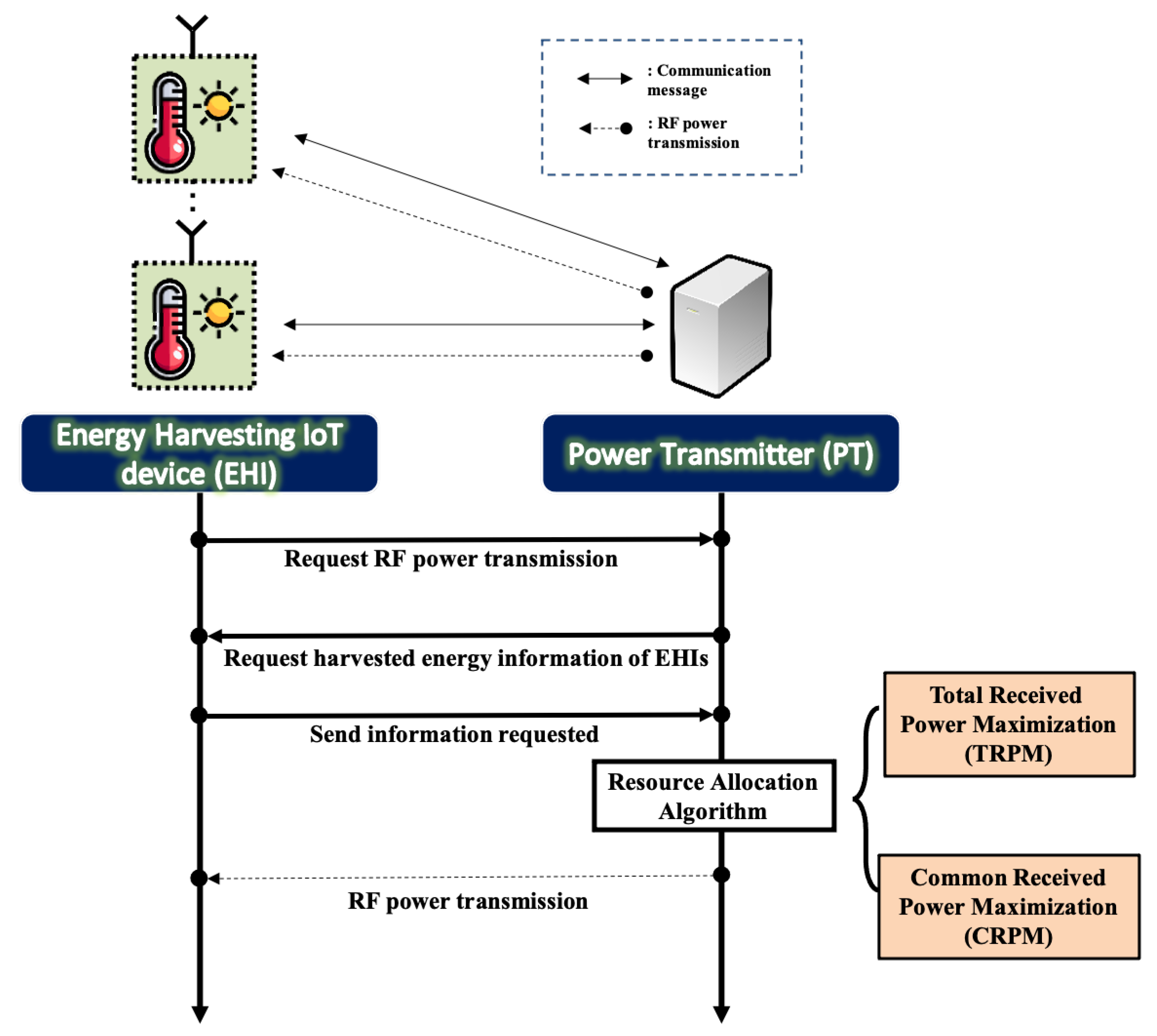
Figure 2 describes the overall process of wireless power transmission. Assuming that each EHI requires power transmission to the PT, the PT requests relevant information for transmitting RF power to each EHI. Upon receiving the requested information from the EHIs, the PT utilizes the proposed resource allocation algorithms, such as TRPM and CRPM, to transmit the RF power accordingly. In particular, this paper focuses on the analysis and optimization of harvested energy for EHIs in the context of the harvest-then-storage protocol (Therefore, optimizing the power consumption of wireless units is not of concern in this paper). This protocol entails EHIs saving the received energy and leveraging the harvested energy for tasks beyond communication purposes.

3.1. Energy Poverty-Based Device Selection (EPDS)

Each of the EHIs can receive power from the PT wirelessly as long as the condition $n_c\ge m$ is satisfied. However, concurrently transmitting power to all of the EHIs from the PT becomes infeasible in the case where $m>n_c$. It is vital to note that the number of IoT devices today is, in most instances, beyond the number of orthogonal frequency bands, since a tremendous amount of IoT devices have been deployed in various IoT application domains. Thus, this paper presents an orthogonal band assignment rule whereby the EHIs with less energy are given priority in assigning an orthogonal band and, subsequently, in receiving power from the PT at each transmission time slot. The whole procedure is expressed in Algorithm 1, where ${\mathcal{K}}_{n_c}$ represents a set of EHIs elected to receive power.

Algorithm 1 Energy Poverty-Based Device Selection (EPDS)

1: Initialization The total received energy $U_k$ of ${\mathrm{EHI}}_k$, $\forall k\in \mathcal{K}$, and the number of orthogonal bands $n_c$. 2: Obtain an index set $\mathcal{I}$ = $\left\{k_i\right|i\in \mathcal{K},U_{k_i}\le U_{k_{i+1}}\},$ by arranging EHIs in ascending order with respect to the total received energy. 3: Select $n_c$ indexes of EHIs sequentially ${\mathcal{K}}_{n_c}=\left\{i\right|i\in \mathcal{I}\}$, where the length of the ${\mathcal{K}}_{n_c}$ is $n_c$. 4: return Order the set ${\mathcal{K}}_{n_c}$, which has $n_c$ indexes of EHIs with less total received energy.

3.2. Energy Beamforming

Utilizing orthogonal frequency bands in the MISO system allows the PT to communicate with multiple EHIs at the same time [59]. Therefore, in this paper, to transmit wireless power optimally to multiple EHIs, we considered an energy beamforming scheme within each orthogonal frequency band [60]. First, the transmitted baseband signal of k-th EHI (${\mathrm{EHI}}_k$) for $k=1,\cdots ,K$ is defined as

$$\begin{array}{c}\hfill {\mathit{s}}_{\mathit{k}}={\mathit{w}}_{\mathit{k}}{s}_0,\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

(3)

where ${\mathit{w}}_{\mathit{k}}\in {\mathbb{C}}^{n_t\times 1}$ represents the beamforming weight vector for ${\mathrm{EHI}}_k$ and $s_0$ denotes the power symbol. Assuming $s_0$ is a random variable with zero mean and unit variance, the amount of transmission power from the PT to ${\mathrm{EHI}}_k$ can be expressed as $p_k^t=E[\parallel {\mathit{s}}_{\mathit{k}}{\parallel }^2]=\parallel {\mathit{w}}_{\mathit{k}}{\parallel }^2=$ tr$\left({\mathit{w}}_{\mathit{k}}{\mathit{w}}_{\mathit{k}}^H\right)$. Considering that all channels follow an independent quasi-static flat fading [61], ${\mathit{h}}_{\mathit{k}}\in {\mathbb{C}}^{n_t\times 1}$, which is the channel gain vector of ${\mathrm{EHI}}_k$, is uniform within each power transmission time slot. The received baseband signal of ${\mathrm{EHI}}_k$ is then expressed as follows:

$$\begin{array}{c}\hfill {\mathit{y}}_{\mathit{k}}={\mathit{h}}_{\mathit{k}}^T{\mathit{s}}_{\mathit{k}}+{ϵ}_k,\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

(4)

where ${ϵ}_k\sim N(0,{\sigma }_k^2)$ is additive Gaussian noise. Assuming that the noise power is negligible to all EHIs [60,62], the received power of ${\mathrm{EHI}}_k$ is described as

$$\begin{array}{c}\hfill p_k^r=\mathrm{tr}\left({\mathit{G}}_{\mathit{k}}{\mathit{W}}_{\mathit{k}}\right),\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

(5)

where ${\mathit{G}}_{\mathit{k}}={\mathit{h}}_{\mathit{k}}{\mathit{h}}_{\mathit{k}}^H\in {\mathbb{C}}^{n_t\times n_t}$ is a channel gain matrix for ${\mathrm{EHI}}_k$ and ${\mathit{W}}_{\mathit{k}}={\mathit{w}}_{\mathit{k}}{\mathit{w}}_{\mathit{k}}^H\in {\mathbb{C}}^{n_t\times n_t}$ indicates a beamforming weight matrix. To maximize the received power of ${\mathrm{EHI}}_k$, the authors in [60] expressed the optimal energy beamforming vector as

$$\begin{array}{c}\hfill {\mathit{w}}_{\mathit{k}}^{\ast }={\mathit{v}}_{max}\left({\mathit{h}}_{\mathit{k}}{\mathit{h}}_{\mathit{k}}^H\right),\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

(6)

where ${\mathit{v}}_{max}$ denotes the eigenvector corresponding to the maximum eigenvalue. Since the rank of the channel gain matrix $G_k$ is one, there exists only one eigenvalue. Thereby, the power allocated to ${\mathrm{EHI}}_k$ through the energy beamforming scheme becomes

$$\begin{array}{c}\hfill p_k^r={\lambda }_k{p}_k^t,\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

(7)

where ${\lambda }_k=\lambda \left({\mathit{h}}_{\mathit{k}}{\mathit{h}}_{\mathit{k}}^H\right)$ and $p_k^t$ denote the eigenvalue of ${\mathit{h}}_{\mathit{k}}{\mathit{h}}_{\mathit{k}}^H$ and the transmission power for ${\mathrm{EHI}}_k$, respectively.

Therefore, this paper assumed that, when PT transmits power wirelessly, optimal power transmission is achievable by employing the described energy beamforming scheme within each partitioned orthogonal band.

3.3. Logarithmic-Based Nonlinear EH Model (NEHM)

When the RF power signal is transmitted from the PT to EHIs, EHIs should convert the power signal into DC power that can be utilized for other purposes, such as charging the battery. At this time, EHIs need a rectifier that converts AC power into DC power. In this subsection, considering the nonlinear rectifier model operating in the 900 MHz frequency band, we propose a newly logarithmic-based nonlinear EH model (NEHM) as follows:

$$\begin{array}{c}\hfill r\left(x\right)=a_{k}log(1+b_{k}x),\mathit{s}.\mathit{t}.0\le x\le c_k,\end{array}$$

(8)

where $a_k,b_k$, and $c_k$ are the parameters (The parameters $a_k,b_k$ are calculated by minimizing the RMSE) that vary depending on the detailed circuit characteristics of the rectifiers, such as the capacitor and diode. From [63,64], we extracted experimentally measured data using Engauge Digitizer [65], and compared the matching accuracy between the three analytical rectifier models, which are the linear EH model, the logistic-based nonlinear EH model [54], and lastly the proposed NEHM. The $a_k$ and $b_k$ are manipulated by minimizing the root mean square error (RMSE) between the extracted data and the considered models, and $c_k$, which is the operation limit of the rectifier, could be easily detected by checking the extracted data.

4. Problem Formulation and Solution

4.1. Total Received Power Maximization (TRPM)

Considering the above-mentioned energy beamforming and the logarithmic-based nonlinear EH model, the PT should decide how much transmission power should be transmitted for each EHI. In this section, we focus on maximizing the total received power of all ${\mathrm{EHI}}_k$, $k\in {\mathcal{K}}_{n_c}$. The following total received power maximization (TRPM) problem can be mathematically formulated as:

Problem 1.

$$\begin{array}{c}\hfill \underset{{\mathit{p}}^{\mathit{t}}}{max}\sum _{k\in {\mathcal{K}}_{n_c}}r\left(p_k^t\right)=\sum _{k\in {\mathcal{K}}_{n_c}}{a}_k\mathit{log}(1+b_k{\lambda }_k{p}_k^t)\end{array}$$

(9)

$$\begin{array}{c}\hfill \mathit{s}.\mathit{t}.0\le p_k^t\le min\left(\frac{c_k}{{\lambda }_k},P_c\right),\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

(10)

$$\begin{array}{c}\hfill \sum _{k\in {\mathcal{K}}_{n_c}}{p}_k^t\le E_c,\end{array}$$

(11)

where $E_c$ is the transmission power budget the PT has, $P_c$ is the transmission power constraint under each orthogonal band, and $c_k$ is the rectifier’s operation limit of ${\mathit{EHI}}_k$. The constraints (10) and (11) delineate that the PT should determine the amount of transmission power to the ${\mathit{EHI}}_k$ by taking into account the transmission power constraint under each orthogonal band and total power budget, respectively.

By solving the optimization problem through the KKT conditions, we can obtain the closed-form solution of the TRPM problem, given by the following theorem:

Theorem 1.

The optimal power value $p_k^{t\ast }$ to be sent to ${\mathit{EHI}}_k$ in the TRPM problem is expressed as follows:

$$p_k^{t\ast }=\{\begin{array}{cc}h{a}_k-\frac{1}{b_k{\lambda }_k},& \mathit{if}\mathit{this}\mathit{is}>0\mathit{or}<min({\mathit{P}}_{\mathit{c}},\frac{{\mathit{c}}_{\mathit{k}}}{{\lambda }_{\mathit{k}}}),\\ \frac{c_k}{{\lambda }_k},& \mathit{if}\mathit{the}\mathit{above}\mathit{value}\mathit{is}\ge min({\mathit{P}}_{\mathit{c}},\frac{{\mathit{c}}_{\mathit{k}}}{{\lambda }_{\mathit{k}}}),\\ 0,& \mathit{Otherwise},\end{array}$$

(12)

where h is a Lagrange multiplier satisfying ${\sum }_{k\in {\mathcal{K}}_{n_c}}{p}_k^{t\ast }=E_r$.

Proof of Theorem 1. 

See the Appendix A.    □

Through the Theorem 1, the optimal power value $p_k^{t\ast }$ for ${\mathrm{EHI}}_k$ was obtained. The Lagrange multiplier h could be obtained by Algorithm 2, wherein this parameter was computed, based on the modified water-filling algorithm, which is proposed in [66]. If the PT transmits power $p_k^{t\ast }$ to ${\mathrm{EHI}}_k,$$\forall k\in {\mathcal{K}}_{n_c}$, then the total received power for all ${\mathrm{EHI}}_k,$$\forall k\in {\mathcal{K}}_{n_c},$ is maximized. In Algorithm 2, the time complexity is dominated by $\mathcal{O}\left(\right|{\mathcal{K}}_{n_c}|log(|{\mathcal{K}}_{n_c}\left|\right))$. This complexity arises from the sorting operation typically required in the proposed algorithm, which is often implemented using efficient sorting algorithms, such as quicksort or mergesort.

Algorithm 2 TRPM

1: Initialization Arrange the set of ${\mathrm{EHI}}_k$, $\forall k\in {\mathcal{K}}_{n_c}$ by the value of $\frac{1}{a_i{b}_i{\lambda }_i}$ in ascending order, the parameter indexes $j=1,k=2$, the water-filling width $C_w=a_1$, the remaining energy $E_r=E_c$, the energy height $h=\frac{1}{a_1{b}_1{\lambda }_1}$, the allocated power vector of EHIs ${\mathit{p}}^{\mathit{t}}=0$, $a_{n_c+1},b_{n_c+1}=1$,    and    ${\lambda }_{n_c+1}=\infty$.   2: while$E_r>0$do   3:    if $\left(\frac{min\left(\frac{c_k}{{\lambda }_k},P_c\right)}{a_j}>\frac{1}{a_k{b}_k{\lambda }_k}\right)\&\left(C_w\left(\frac{1}{a_k{b}_k{\lambda }_k}-h\right)<E_r\right)$ then   4:      Update $E_r=E_r-C_w\left(\frac{1}{a_k{b}_k{\lambda }_k}-h\right),C_w=C_w+a_k,h=\frac{1}{a_k{b}_k{\lambda }_k},$ and $k=k+1.$   5:      Rearrange the set of EHIs {j, j + 1, ..., k} $\in {\mathcal{K}}_{n_c}$ by the value of $\frac{min\left(\frac{c_k}{{\lambda }_k},P_c\right)}{a_j}$ in ascending order.   6: else if$\left(\frac{min\left(\frac{c_k}{{\lambda }_k},P_c\right)}{a_j}\le \frac{1}{a_k{b}_k{\lambda }_k}\right)\&\left(C_w\left(\frac{min\left(\frac{c_k}{{\lambda }_k},P_c\right)}{a_j}-h\right)<E_r\right)$then   7:      Update $E_r=E_r-C_w\left(\frac{min\left(\frac{c_k}{{\lambda }_k},P_c\right)}{a_j}-h\right),C_w=C_w-a_j,h=\frac{c_k}{{\lambda }_k{a}_j},$ and $j=j+1.$   8:      Set $p_j^t=\frac{min\left(\frac{c_k}{{\lambda }_k},P_c\right)}{a_j}.$   9:    else 10:      Set $h=h+\frac{E_r}{C_w}$ and $E_r=0.$ 11:      for $i=j:k$ do 12:         Set $p_i^t=a_i\left(h-\frac{1}{a_i{b}_i{\lambda }_i}\right).$ 13:      end for 14:    end if 15: end while 16: return Set of allocated transmission powers of EHIs ${\mathit{p}}^{\mathit{t}}$, after being re-aggregated in the original order.

4.2. Common Received Power Maximization (CRPM)

Although the PT could utilize the TRPM algorithm to optimize the total received power of all ${\mathrm{EHI}}_k,$$\forall k\in {\mathcal{K}}_{n_c}$, it can cause a severe energy imbalance problem among EHIs. For instance, through the EPDS algorithm, EHIs with less received energy are given the opportunity to receive power, but, according to the TRPM algorithm, most of the transmission power should be transmitted to the EHI that is deployed in the nearest position to the PT. Therefore, a sophisticated resource allocation algorithm is required that does not cause any energy imbalance among EHIs.

The Common Received Power Maximization (CRPM) problem was considered as a means to solve the energy imbalance problem. It can be formulated as:

Problem 2.

$$\begin{array}{c}\hfill \underset{{\mathit{p}}^{\mathit{t}}}{max}\underset{k}{min}{U}_k+a_{k}log(1+b_k{\lambda }_k{p}_k^t)\end{array}$$

(13)

$$\begin{array}{c}\hfill \mathit{s}.\mathit{t}.0\le p_k^t\le min\left(\frac{c_k}{{\lambda }_k},P_c\right),\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

(14)

$$\begin{array}{c}\hfill \sum _{k\in {\mathcal{K}}_{n_c}}{p}_k^t\le E_c,\end{array}$$

(15)

where $U_k$ denotes the total received energy of ${\mathit{EHI}}_k$.

In the CRPM problem, the problem of maximizing the minimum harvested energy of all EHIs, which could solve the energy imbalance problem among EHIs, was considered. Since the CRPM problem is a non-convex formulation in its current form, we reformulated this problem as an equivalent convex problem as follows:

Problem 3.

$$\begin{array}{c}\hfill \underset{{\mathit{p}}^{\mathit{t}},\overline{P}}{max}\overline{P}\end{array}$$

(16)

$$\begin{array}{c}\hfill \mathit{s}.\mathit{t}.U_k+a_{k}log(1+b_k{\lambda }_k{p}_k^t)\ge \overline{P},\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

(17)

$$\begin{array}{c}\hfill 0\le p_k^t\le min\left(\frac{c_k}{{\lambda }_k},P_c\right),\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

(18)

$$\begin{array}{c}\hfill \sum _{k\in {\mathcal{K}}_{n_c}}{p}_k^t=E_c,\end{array}$$

(19)

where $\overline{P}$ is the common received power for all EHIs. Here, the transmission power budget condition (19) has an equal value to the constraint $E_c$. It is natural to consume all of the transmission power budget at the PT because it can improve the performance of common received power $\overline{P}$ of all EHIs. Since the constraint (17) increases with $p_k^t$, when all these conditions have equal value, the optimal solution of CRPM problem can be obtained as follows:

$$\begin{array}{c}\hfill U_k+a_{k}log(1+b_k{\lambda }_k{p}_k^t)=\alpha ,\forall k\in {\mathcal{K}}_{n_c}.\end{array}$$

(20)

$$\begin{array}{c}\hfill \mathit{Then}, p_k^t=\frac{1}{b_k{\lambda }_k}\left(exp\left(\frac{\alpha -U_k}{a_k}\right)-1\right).\end{array}$$

(21)

We can find the solution $\alpha$ by using the exhaustive search in [67], which enumerates and checks all possible candidates for the solution. However, since the exhaustive search is computationally unrealistic [68], we propose a novel way of limiting the scope of the solution (LSS). The LSS is defined by the following Lemma:

Lemma 1.

The solution α satisfying the condition (19) exists in the following interval $\alpha \in$$\left[{\alpha }_{min},{\alpha }_{max}\right]$ where

$$\begin{gathered} {\alpha }_{min}={min}_{k\in {\mathcal{K}}_{n_c}}\left(U_k+a_{k}log(1+\frac{b_k{\lambda }_k{E}_c}{n\left({\mathcal{K}}_{n_c}\right)})\right), \\ {\alpha }_{max}={max}_{k\in {\mathcal{K}}_{n_c}}\left(U_k+a_{k}log(1+\frac{b_k{\lambda }_k{E}_c}{n\left({\mathcal{K}}_{n_c}\right)})\right). \end{gathered}$$

where, $n(·)$ denotes the cardinality of a set $(·)$.

Proof of Lemma 1. 

See the Appendix B.    □

Since $p_k^t$ is an increasing and continuous function over $\alpha$, we can adopt the bisection search algorithm, which is more computationally efficient than an exhaustive search [69], to find the solution $\alpha$. The Algorithm 3 describes the bisection search algorithm for common received power $\alpha$. Here, we considered the bisection search algorithm, not Newton’s method, because Newton’s method requires the function to be differentiable and, also, an initial guess should be close to the root. Considering these limitations, we utilized the bisection method in this paper, which is more robust than Newton’s method [70].

To meet the constraints concerning $p_k^t$, such as (18) and (19), the bisection search algorithm was applied iteratively to obtain the solution of the CRPM problem. The whole procedure is summarized in Algorithm 4. In Algorithm 4, the time complexity is dominated by the bisection search method, having time complexity $\mathcal{O}\left(\frac{{\alpha }_{\max }-{\alpha }_{\min }}{ϵ}\right)$. Lemma 1 provides the values of ${\alpha }_{\min }$ and ${\alpha }_{\max }$. As a result, the CRPM can be easily solved by using computationally efficient parameter settings, such as $ϵ$.

Algorithm 3 Bisection Search Method for the Common Received Power $\alpha$

1: Initialization The rectifier parameters $a_k,b_k$ for $k\in {\mathcal{K}}_{n_c}$, the allocated eigenvalue ${\lambda }_k$ for $k\in {\mathcal{K}}_{n_c}$, the total received power $U_k$ for $k\in {\mathcal{K}}_{n_c}$, the remaining energy $E_r$, ${\alpha }_{min}={min}_k\left(U_k+a_{k}log(1+\frac{b_k{\lambda }_k{E}_r}{|{\mathcal{K}}_{n_c}|})\right)$, ${\alpha }_{max}={max}_k\left(U_k+a_{k}log(1+\frac{b_k{\lambda }_k{E}_r}{|{\mathcal{K}}_{n_c}|})\right)$, $ϵ$ = stopping criterion,    and    $\alpha =\frac{{\alpha }_{min}+{\alpha }_{max}}{2}$.   2: while$\left\{\right|{\sum }_k\frac{1}{b_k{\lambda }_k}\left(exp\left(\frac{\alpha -U_k}{a_k}\right)-1\right)-E_r|\ge ϵ\}$do   3:    if ${\sum }_k\frac{1}{b_k{\lambda }_k}\left(exp\left(\frac{\alpha -U_k}{a_k}\right)-1\right)>E_r$ then   4:      ${\alpha }_{max}\leftarrow \frac{{\alpha }_{min}+{\alpha }_{max}}{2}.$   5:    else   6:      ${\alpha }_{min}\leftarrow \frac{{\alpha }_{min}+{\alpha }_{max}}{2}.$   7:    end if   8:    $\alpha \leftarrow \frac{{\alpha }_{min}+{\alpha }_{max}}{2}.$   9: end while 10: return The parameter $\alpha$ satisfying the condition ${\sum }_k\frac{1}{b_k{\lambda }_k}\left(exp\left(\frac{\alpha -U_k}{a_k}\right)-1\right)=E_r$.

Algorithm 4 CRPM

1: Initialization The number of iteration I = 0, the limit of Iteration $I^{\lim }$, the remaining energy $E_r=E_c$, the allocated power vector ${\mathit{p}}^{\mathit{t}}=0$, and the index set of EHIs, ${\mathcal{K}}_{n_c}.$   2: while$\{E_r>0\}$ and $\{I<I^{\lim }\}$ do   3:    Calculate $\alpha$ by Algorithm 3   4:    for $k\in {\mathcal{K}}_{n_c}$ do   5:      Set $p_k^t=p_k^t+\frac{1}{b_k{\lambda }_k}\left(exp\left(\frac{\alpha -U_k}{a_k}\right)-1\right).$   6:    end for   7:    Set $E_r$ = 0.   8:    for $k\in {\mathcal{K}}_{n_c}$ do   9:      if $p_k^t>min\left(\frac{c_k}{{\lambda }_k},P_c\right)$ then 10:         Set $E_r\leftarrow E_r+p_k^t-min\left(\frac{c_k}{{\lambda }_k},P_c\right),p_k^t\leftarrow min\left(\frac{c_k}{{\lambda }_k},P_c\right)$, and ${\mathcal{K}}_{n_c}\leftarrow {\mathcal{K}}_{n_c}\setminus k.$ 11:      end if 12:    end for 13:    $I=I+1.$ 14: end while 15: return Allocated transmission power vector ${\mathit{p}}^{\mathit{t}}$.

5. Numerical Results

In this section, we provide extensive numerical results to identify the performance of the proposed logarithmic-based nonlinear EH model, EPDS and two power allocation algorithms (TRPM and CRPM). Since adequately designing the power allocation algorithms for the mobile EHIs in the WPT system is a significant issue to be handled [71], the mobility of EHIs as a one-dimensional random walk model in the numerical results is also considered.

5.1. Benchmarks

We conducted a performance analysis by comparing the following methods with the proposed methods. In relation to the frequency band allocation, power allocation, and the effect of the energy harvesting model, we considered the following three benchmark models:

• Frequency Band Allocation

  -

  Round-robin (RR): The orthogonal frequency bands are assigned to each of the EHIs in equal portions without priority, the fairness for the number of the power receiving opportunities among EHIs is guaranteed [72].

• Power Allocation Algorithm

  -

  Equal power distribution (EPD): The transmission power is divided equally on each orthogonal frequency band [73].

• The Effect of the Energy Harvesting Model

  -

  Linear EH model: It simply and efficiently models the energy harvesting characteristics using a linear function.

To ensure a fair comparison, we adopted the same parameter setup for our proposed algorithm as well as the benchmarks.

5.2. Simulation Setup

The considered MISO–WPT system parameters were determined as described in

Table 1. The parameters of the considered system model.

Parameter	Value
The number of antennas $n_t$	4
The number of orthogonal bands	8
The number of EHIs	16
Total number of wireless power transmissions	10,000
Maximum transmission power $E_c$	4 W
Transmission power constraint $P_c$	4 W
$a_k,b_k$, and $c_k$ from [63]	0.0319, 3.6169, 3 mW
$a_k,b_k$, and $c_k$ from [64]	0.2411, 0.4566, 3 mW
Initial position of EHIs	uniformly distributed within 5 to 15 m

. Here, both the maximum transmission power $E_c$ of the PT and the transmission power constraint $P_c$ under each orthogonal band were assumed to be 4 W, which was defined in compliance with the power regulation of the 900 MHz bands. The logarithmic-based nonlinear EH model parameters $a_k,b_k$ of ${\mathrm{EHI}}_k$ were determined as one of the following two paired values, a = 0.0319, b = 3.6169 and a = 0.2411 and b = 0.4566 from [64]. The paired values in $a_k,b_k$ were obtained by minimizing the RMSE between the NEHM and extracted data. $c_k$, which denotes the operation limit of the rectifier, was fixed to 3 mW for both options. Each of the EHIs was uniformly distributed within 5 to 15 m from the PT and randomly moved with fixed-length walking steps in each iteration. All EHI were, thus, randomly placed within the simulation area, along with having a fixed moving speed. We considered the mobility of EHIs as a one-dimensional independent and identically distributed (i.i.d.) random walking case [74], which had three options, based on the PT, having equal probability: to stop, to move forward, and to move backward. Two fixed-length walking steps in the one-dimensional i.i.d. random walking case were considered: 0.03 m/iteration and 0.2 m/iteration (This configuration was determined by the fact that the proposed algorithms demonstrated an average running time of 0.15 s. As a result, the corresponding mobility of 0.03 m per iteration and 0.2 m per iteration would translate to velocities of 0.2 m/s and 1.3 m/s, respectively. These velocities assumed importance as parameters for evaluating the mobility characteristics of IoT devices [75]).

The distance-dependent signal path-loss model is described as the following equation:

$$\begin{array}{c}\hfill L_k=L_0{\left(\frac{d_k}{d_0}\right)}^{-\beta },\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

where $L_0$ is set to be ${10}^{-3}$, $d_k$ denotes the distance between the PT and ${\mathrm{EHI}}_k$, $\forall k\in {\mathcal{K}}_{n_c}$, $d_0$ is a reference distance, which was 1 m, and $\beta$ is the path loss exponent, set to be 3. The channel vector ${\mathit{h}}_{\mathit{k}}$ was defined as an i.i.d. Rayleigh fading channel obtained by averaging over 1000 randomized channel generations and the average power of ${\mathit{h}}_{\mathit{k}}$ was normalized by $L_k$.

5.3. Considered Linear EH Model-Based Power Allocation Algorithms

To explore the effect of the logarithmic-based nonlinear EH model, we compared the performance of the proposed NEHM with the linear EH model, under the proposed two power allocation algorithms. Therefore, we considered the Linear EH-based Total Received Power Maximization (LTRPM) problem and the Linear EH-based Common Received Power Maximization (LCRPM) problem.

• the LTRPM problem formulation:

  $$\begin{array}{c}\hfill \underset{{\mathit{p}}^{\mathit{t}}}{max}\sum _{k\in \mathrm{\Gamma }}{l}_k{\lambda }_k{p}_k^t\end{array}$$

  (22)

  $$\begin{array}{c}\hfill \mathit{s}.\mathit{t}.0\le p_k^t\le min\left(\frac{c_k}{{\lambda }_k},P_c\right),\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

  (23)

  $$\begin{array}{c}\hfill \sum _{k\in {\mathcal{K}}_{n_c}}{p}_k^t=E_c,\end{array}$$

  (24)

  where $l_k$ is a linear rectifier parameter of ${\mathrm{EHI}}_k$, derived by minimizing the RMSE between the extracted data and linear rectifier model. Since this is a linear optimization problem, it can be solved by applying the sequential power allocation method. First, the $l_k{\lambda }_k$ are sorted by descending order, and then power $p_k^t=min(P_c,\frac{c_k}{{\lambda }_k},E_r)$, $\forall k\in {\mathcal{K}}_{n_c}$, is allocated in sequential order until the remaining energy $E_r$ equals zero. It can be expressed as the Algorithm 5 in Appendix C.
• the LCRPM problem formulation:

  $$\begin{array}{c}\hfill \underset{{\mathit{p}}^{\mathit{t}},\overline{P}}{max}\overline{P}\end{array}$$

  (25)

  $$\begin{array}{c}\hfill \mathrm{s}.\mathrm{t}{U}_k+l_k{\lambda }_k{p}_k^t\ge \overline{P},\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

  (26)

  $$\begin{array}{c}\hfill 0\le p_k^t\le min\left(\frac{c_k}{{\lambda }_k},P_c\right),\forall k\in {\mathcal{K}}_{n_c},\end{array}$$

  (27)

  $$\begin{array}{c}\hfill \sum _{k\in {\mathcal{K}}_{n_c}}{p}_k^t=E_c.\end{array}$$

  (28)
  The LCRPM problem can also be solved by following the same process in the CRPM problem as follows:

  $$\begin{array}{c}\hfill l_k{\lambda }_k{p}_k^t=\alpha ⟺p_k^t=\frac{\alpha }{l_k{\lambda }_k},\forall k\in {\mathcal{K}}_{n_c}.\end{array}$$

  (29)
  As described in Algorithm 4, the optimal solution of the LCRPM problem can also be obtained by applying the bisection search algorithm repeatedly, until ${\sum }_{k\in {\mathcal{K}}_{n_c}}{p}_k^t=E_c$. The whole procedure is summarized as Algorithm A2 in Appendix D.

5.4. Performance Comparison of EH Models

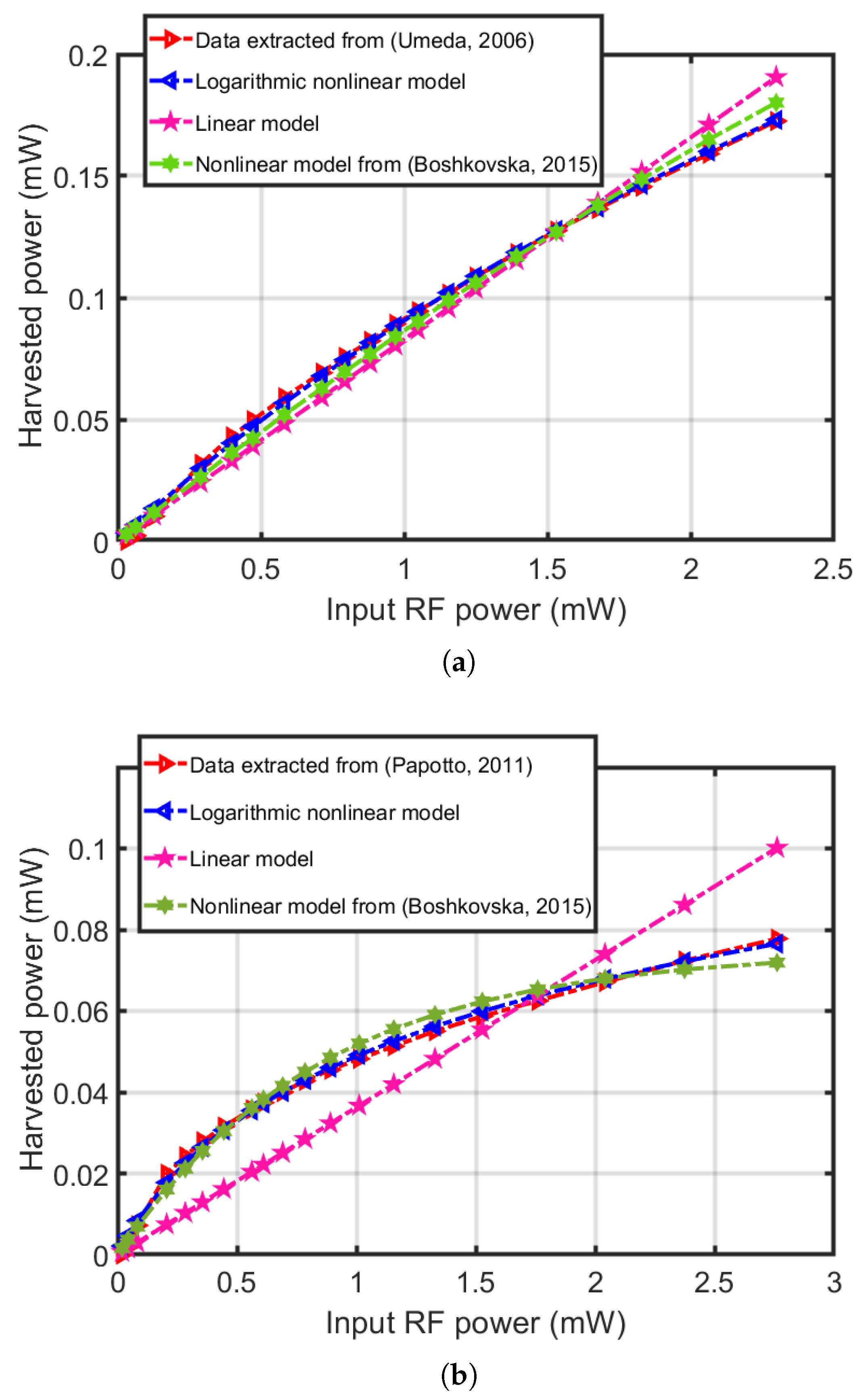
We compared the matching accuracy between the EH models and experimental data.

Table 2. An RMSE comparison between the linear, nonlinear models from [54], and the proposed NEHM.

Rectifier Model	RMSE from Data [63]	RMSE from Data [64]
Linear model	0.0067	0.0098
Nonlinear model from [54]	0.0042	0.0027
Proposed NEHM	0.0027	0.0020

shows how accurately the EH models matched the experimental data by comparing the RMSE value, and, as can be seen from the results, the linear EH model did not properly reflect the practical operating performance of the rectifier. Furthermore, based on the RMSE, when comparing the matching accuracy between the models in detail, the proposed NEHM best matched the extracted data.

As shown in Figure 3, it can be observed that the linear model failed to accurately capture the nonlinear relationship between input RF power and harvested power. This was due to the fact that the energy harvesting circuits from [63,64] consist of nonlinear components, such as a diode and capacitor, which the linear model cannot adequately represent. Moreover, it was visually evident that the proposed NEHM outperformed the logistic-based nonlinear model [54] in terms of accurately approximating extracted data.

5.5. Performance Comparison with Walk-Step: 0.03 m/iteration

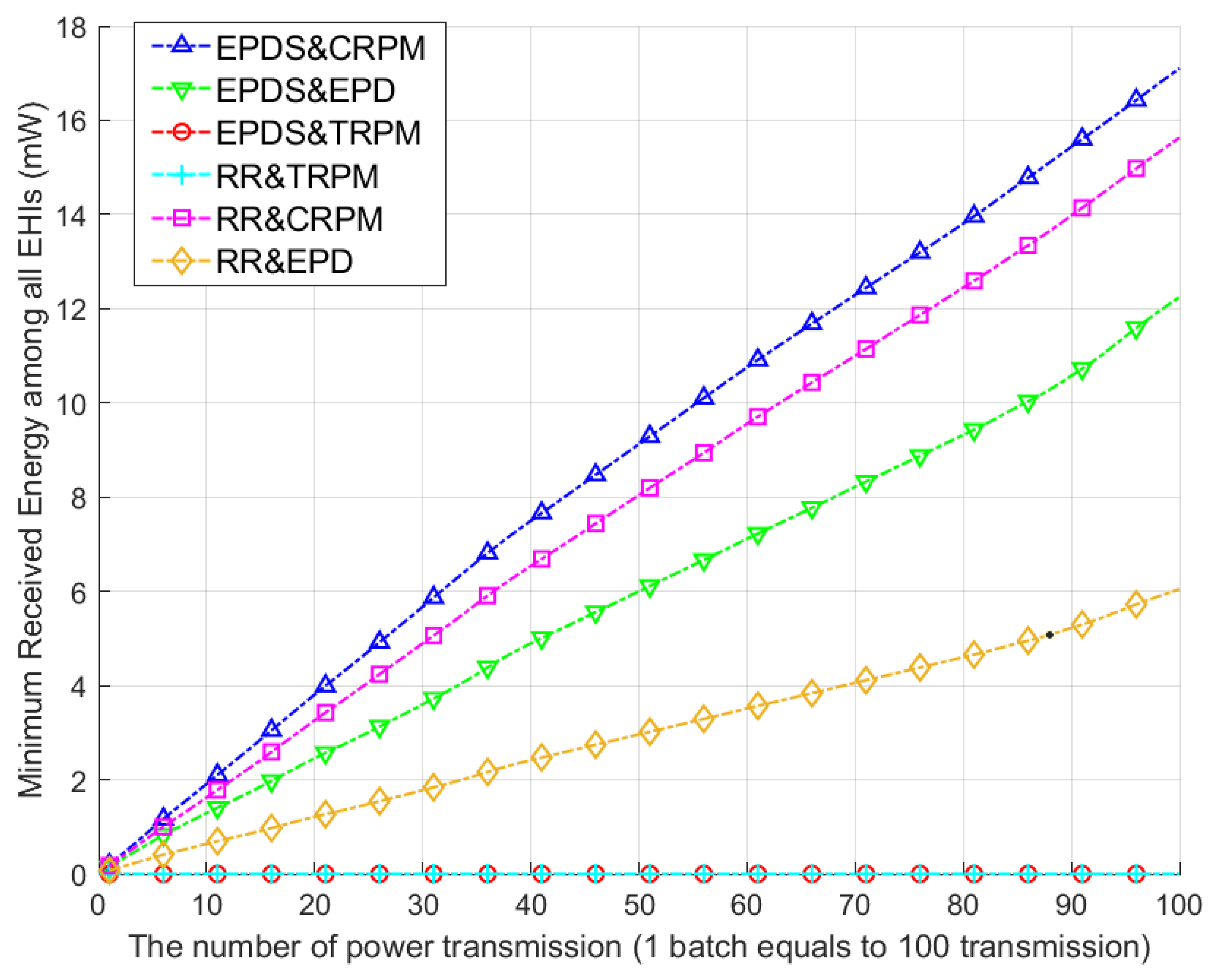
In this subsection, while considering the mobility of EHIs as a one-dimensional random walking model with 0.03m/iteration walking step, the performance of the EPDS algorithm, logarithmic-based nonlinear EH model, and two transmission power allocation algorithms were investigated. Here, the following algorithm naming structure was employed to distinguish them from one another: (the orthogonal band allocation algorithm & EH model & transmission power allocation algorithm). For example, if the EPDS, NEHM, and TRPM algorithm were jointly deployed for transmitting power to EHIs, this was denoted as (EPDS&NEHM&TRPM).

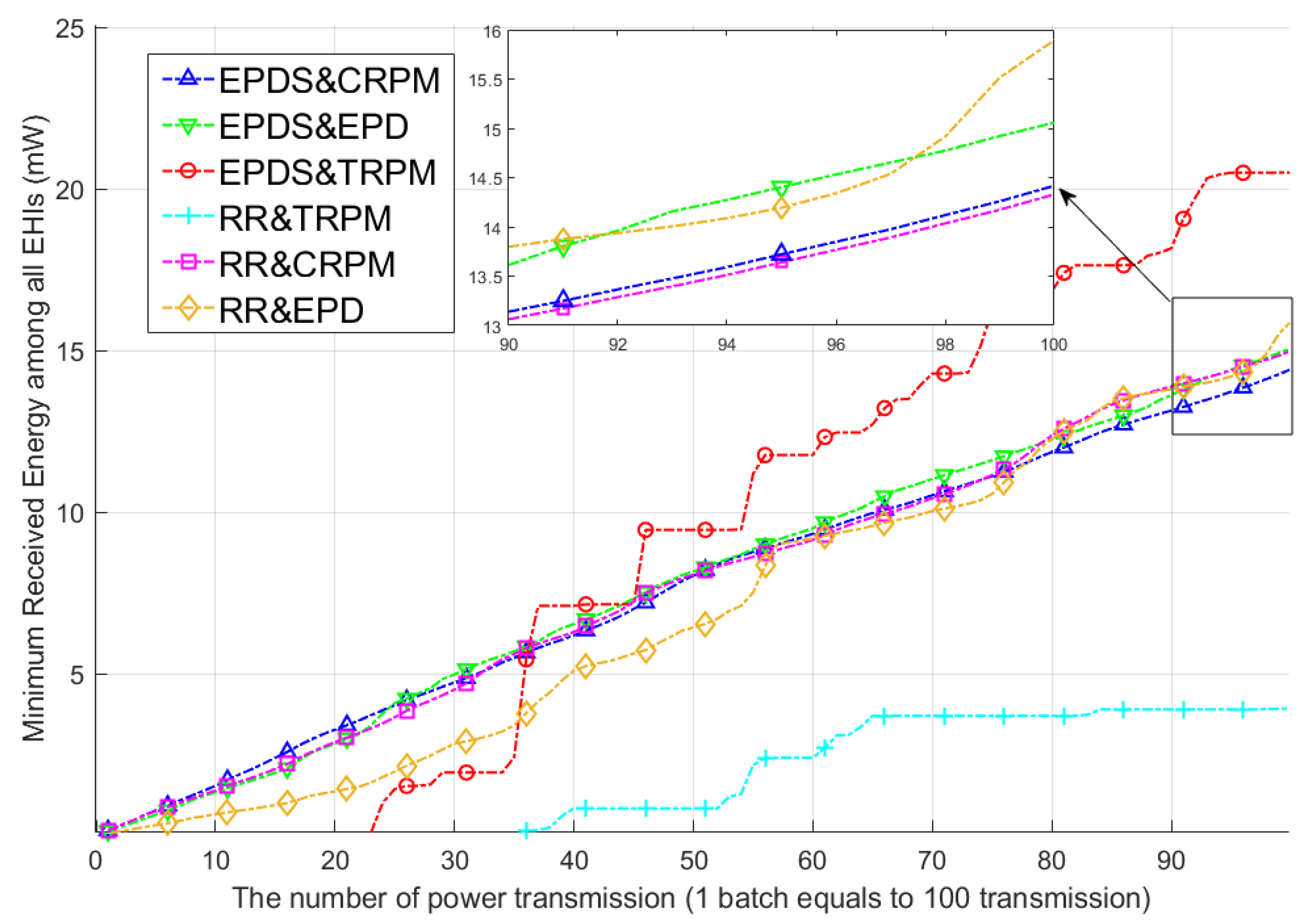
Figure 4 shows the minimum received energy of the power allocation algorithms versus the iteration of the power transmission, under the NEHM. It was observed that the EPDS and CRPM always had a higher minimum received energy value than the other schemes, respectively, within the same conditions. Therefore, the EPDS&CRPM showed the best performance in terms of the minimum received energy. The reason for this result was that EPDS&CRPM provoked the allocation of more resources, such as transmission power and the number of received orthogonal bands, to the EHIs with poor wireless link states. In the TRPM, regardless of whether the EPDS or RR was accommodated, the minimum received energy value equaled zero. This outcome disclosed that the wireless power had not been transmitted to several EHIs with a poor channel condition to maximize the total received power. In the CRPM and EPD, the minimum received energy value increased stably without significant changes, since both algorithms could dispense transmission power to all EHIs, regardless of the channel state.

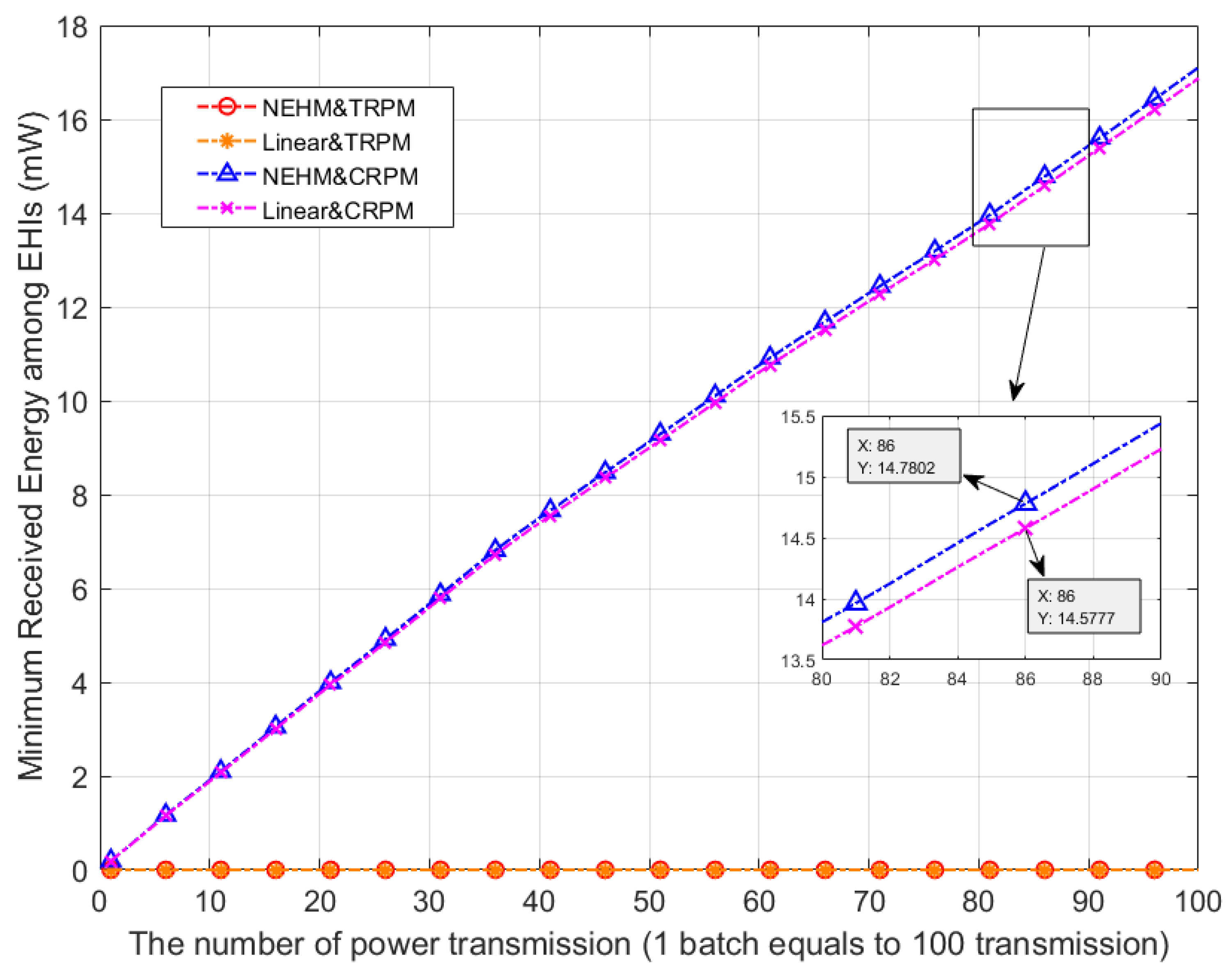
Figure 5 illustrates a quantitative comparison of the proposed CRPM and TRPM by taking into account the linear EH model and the NEHM, respectively. In the case of CRPM, the NEHM achieved a 1.39% higher minimum received energy value than the linear model at the 86-th batch iteration. As the number of power transmissions increased, the performance gap between the NEHM and the linear model widened slightly, because the NEHM exhibited the practical energy harvesting performance more precisely. In the TRPM cases, the performance between EH models was not comparable, since an EHI that had not received transmission power existed.

Table 3. Received energy comparison with walking step: 0.03 m.

Method	Total Received Energy	Minimum Received Energy
RR&NEHM&CRPM	277.3 mW	15.63 mW
RR&NEHM&EPD	591.1 mW	6.05 mW
RR&NEHM&TRPM	1123 mW	0 mW
EPDS&Linear&CRPM	270 mW	16.87 mW
EPDS&Linear&TRPM	458.1 mW	0 mW
EPDS&NEHM&CRPM	273.7 mW	17.1 mW
EPDS&NEHM&EPD	288.7 mW	12.25 mW
EPDS&NEHM&TRPM	533.1 mW	0 mW

depicts the overall outcomes of the total and minimum energy received in all considered algorithms. In the TRPM algorithm, the largest total received energy value was obtained from the RR&NEHM&TRPM among the transmission power allocation algorithms, whereas the smallest value was also attained regarding the minimum received energy value from the RR&NEHM&TRPM. It is noteworthy that several EHIs should be sacrificed to maximize the total received energy of all EHIs in the TRPM algorithm. In the outcomes of the CRPM algorithm, although the smallest total received energy value is represented, the largest value in the minimum received energy is noticed from the EPDS&NEHM&CRPM, in contrast to the TRPM results. Regarding the performance comparison between orthogonal bands allocation schemes (EPDS and RR) when the CRPM was employed, the EPDS was 9.4% higher and 1.31% lower in minimum and total received energy values than the RR, respectively. This result was due to the RR equally distributing the number of power transmission iterations to EHIs. Although this property enlarges the probability of gaining large total received energy compared to the EPDS, it could not elaborately consider EHIs with poor wireless link states. When comparing the NEHM and the linear model under the same EPDS&CRPM scheme, the minimum received energy of the NEHM was 1.36% higher than the linear model and the total energy was 1.37% higher. Therefore, these results demonstrated that RR&NEHM&TRPM achieved the highest efficiency in terms of the total received energy, while EPDS&NEHM&CRPM excelled in energy fairness.

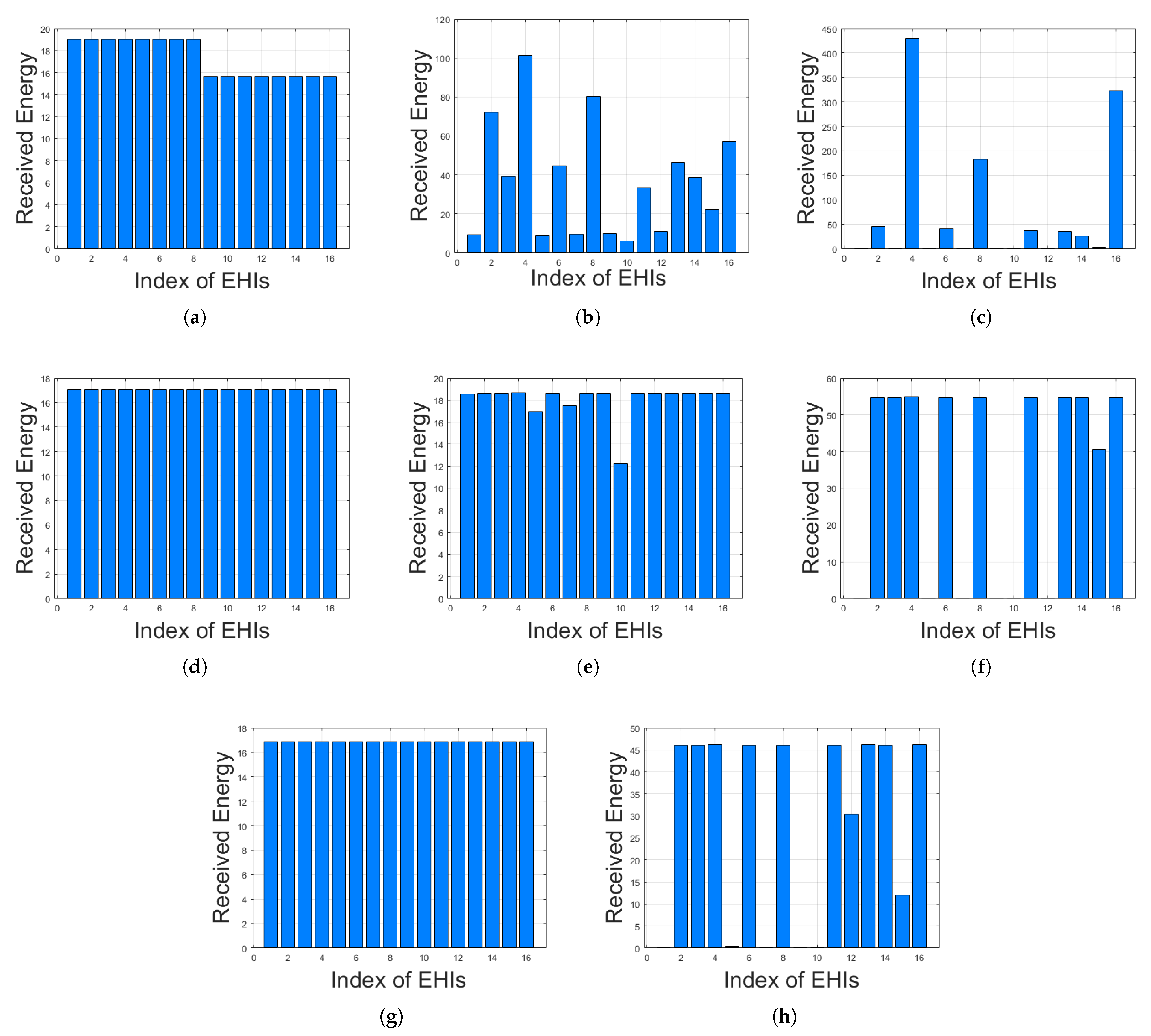
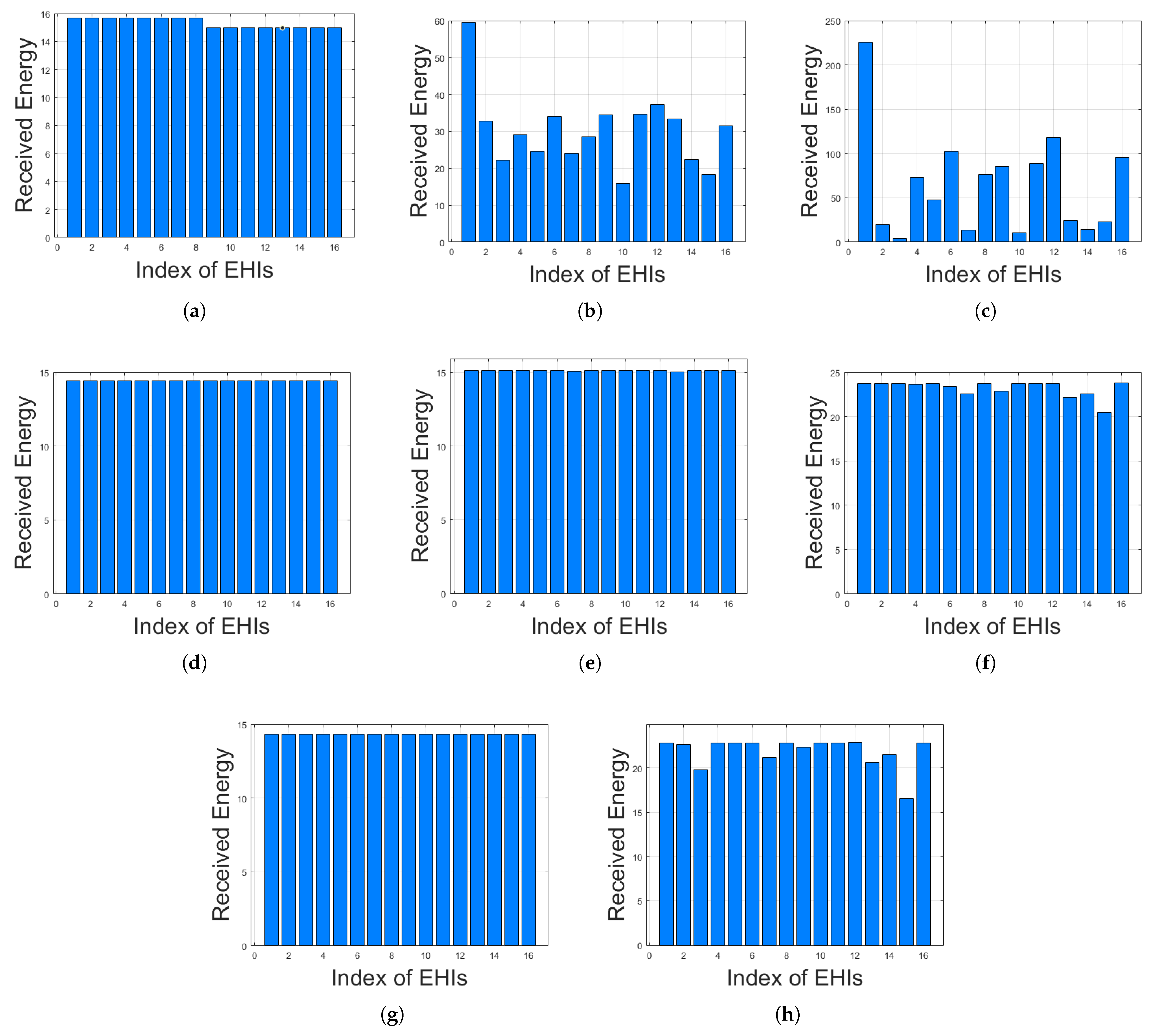
Figure 6 displays the total received energy of each EHI. In the RR&NEHM&CRPM, since the EHIs were grouped into the number of orthogonal bands and the grouped EHIs received the same amount of power, two visible received energy patterns were observed, as shown in Figure 6a. In the TRPM, a huge difference in the total received energy value between EHIs was discovered to maximize the total received energy of all EHIs. Figure 6f,h show that the 12-th EHI could not receive the power on the NEHM, but it received a certain amount of power in the linear model. This result may have been caused by misleading optimized power allocation, due to the inaccurate energy harvesting modeling in the linear model. Nevertheless, when comparing the NEHM and linear EH model in the CRPM case, significant performance degradation was not observed in the linear EH model.

5.6. Performance Comparison with Walk-Step: 0.2 m/Iteration

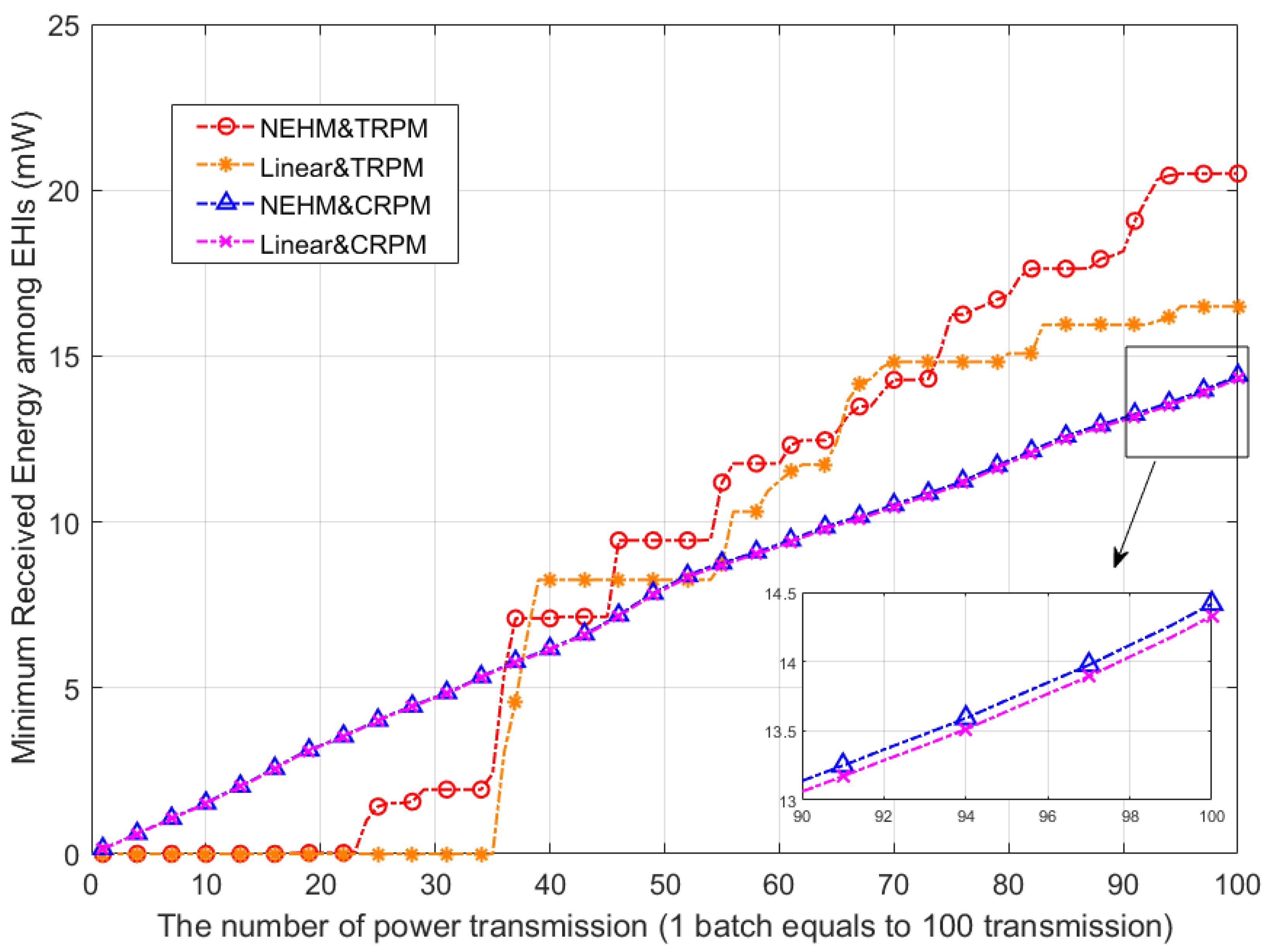
This subsection explores the effect of the proposed algorithms under the random walking model with 0.2m/iteration walking step. Figure 7 compares the performance of the power allocation schemes, in terms of the minimum received energy versus the iteration of the power transmission. Differing from Figure 4, in the TRPM, the minimum received energy value ascended step-wise as the number of power transmissions increased. In particular, unlike the outcomes of the 0.03 m/iteration walking step, the CRPM algorithm had the lowest minimum received energy value of all transmission power allocation algorithms, under the circumstances in which the EPDS was applied. The reason for this consequence was that the EHIs with the poor wireless channel states could gain improved wireless channel states by moving more dynamically than the 0.03 m/iteration walking step and this likely enhanced the probability of receiving substantial transmission power.

We further conducted a performance comparison between the linear and the NHEM models, with the CRPM and TRPM algorithms. As shown in Figure 8, in the CRPM, although the performance of the NEHM was similar to that of the linear EH model, it always slightly outperformed the linear EH model. In the 85-th batch iteration, the minimum received energy of EDPS&NEHM&CRPM was about 0.6% higher than the EDPS&linear&CRPM case. Furthermore, in both the NEHM and linear EH model of the TRPM algorithm, the minimum received energy value ascended stepwise, owing to the mobility of the EHIs. As the number of power transmissions increased, the NEHM gradually outperformed the linear model.

Table 4. Total received energy comparison with walking step: 0.2 m.

Method	Total Received Energy	Minimum Received Energy
RR&NEHM&CRPM	245.5 mW	14.98 mW
RR&NEHM&EPD	482.7 mW	15.89 mW
RR&NEHM&TRPM	1021 mW	3.93 mW
EPDS&Linear&CRPM	229.3 mW	14.33 mW
EPDS&Linear&TRPM	350 mW	16.5 mW
EPDS&NEHM&CRPM	230.7 mW	14.42 mW
EPDS&NEHM&EPD	241.9 mW	15.06 mW
EPDS&NEHM&TRPM	371.3 mW	20.5 mW

shows the overall outcomes of the total and minimum energy received values in all considered algorithms. When the EPDS was employed, TRPM exhibited the largest received energy values among all proposed transmission power allocation algorithms, which were 42% and 61% higher than the CRPM algorithm, in the minimum and total received energy values, respectively. Although the RR&NEHM&TRPM was approximately 175% higher than the EPDS&NEHM&TRPM in the total received energy value, the EPDS&NEHM&TRPM achieved about a 422% higher minimum received energy value than the RR&NEHM&TRPM at the expense of the total received energy. EPDS&NEHM&TRPM was approximately 24% and 6% higher in the minimum and total received energy values than the EPDS&linear&TRPM.

This appropriately depicted that both performance improvements were realized by employing the proposed NEHM. Hence, the findings indicate that RR&NEHM&TRPM attains superior efficiency in total received energy for a walking step of 0.2 m, while EPDS&NEHM&TRPM emerges as the most efficient approach in terms of energy fairness.

Figure 9 represents the total received energy of each EHI. In the EPDS, although some performance variations among EHIs appeared when EPDS&NEHM&TRPM was used, the variation was relatively smaller in scale than that with the round robin, as shown in Figure 9c,f. In particular, when EPDS&NEHM&TRPM was utilized, all EHIs received a similar amount of energy, as opposed to the case of the 0.03 m/iteration walking step. This indicated that the EHIs with poor wireless link-states might move closer to the PT occasionally, giving them opportunities to receive a substantial amount of energy. Therefore, when EPDS&NEHM&TRPM was employed, all EHIs could receive energy in a balanced way, even in the case of the TRPM.

6. Discussion and Future Work

The optimal allocation of transmission power is a major challenge in wireless power transmission technology, as it can lead to critical failures during emergencies. Consequently, a substantial body of literature has been devoted to this topic.

In this paper, we propose a new nonlinear energy harvesting model based on the logarithmic function to capture the practical characteristics of energy harvesting circuits. Leveraging this EH model, two transmission power allocation algorithms (TRPM and CRPM) are proposed. Furthermore, this paper demonstrates the benefits of the proposed two power allocation algorithms based on minimum and total received energy in WPT systems. Specifically, numerical results are presented to validate the merits of the proposed algorithms for powering up IoT devices in a practical system that considers the mobility of IoT devices.

However, there are a few potential drawbacks or disadvantages of the proposed approach. Firstly, we considered the mobility of EHIs as a one-dimensional random walking model in the numerical results. In practice, EHIs may dynamically move around in two-dimensional or three-dimensional space, makinf it necessary to consider more complex mobility models of EHIs.

Secondly, it would be fascinating to extend the considered TRPM and CRPM algorithms by considering random factors, such as imperfect CSI and mobility of EHIs. These factors could contribute to enhancing the performances of the proposed algorithms in the practical WPT system.

Thirdly, this study primarily addressed the power allocation algorithms of the WPT system. Evaluating performances with other statistical parameters, or using statistical analysis, would be fascinating to support our performance results.

Lastly, it would be fascinating to extend the considered system model to other practical configurations, such as the effect of inter-cell interference in the multi-cell scenario and multiple PTs.

7. Conclusions

In this paper, we investigated various power allocation schemes in a MISO–WPT system, consisting of a single power transmitter and multiple energy harvesting IoT devices. We examined the energy poverty-based IoT device selection scheme for orthogonal frequency band allocation, utilizing energy beamforming in each band. Moreover, we addressed two transmission power allocation problems by incorporating the practical logarithmic-based nonlinear energy harvesting model. Firstly, we presented the Total Received Power Maximization problem and obtained its optimal solution by combining the well-known Karush–Kuhn–Tucker conditions with a modified water-filling algorithm. Secondly, we formulated the Common Received Power Maximization problem and derived the optimal solution using an iterative bisection search method. To apply the bisection search method to the CRPM problem, we proposed a novel method to specify the solution scope. The extensive numerical results, including those from EPDS, the logarithmic-based nonlinear EH model, TRPM, and CRPM, confirmed the superiority of the proposed schemes. By comparing with the round-robin scheduling algorithm, we demonstrated the advantages of our proposed EPDS scheme in terms of the minimum received energy of all EHIs. Furthermore, through a comparison with the equal power distribution algorithm, we validated the excellent performance of the proposed power allocation algorithms, TRPM and CRPM. Considering the mobility of EHIs using a one-dimensional random walking model, we present the effects of EHI mobility on the minimum and total received energy. Surprisingly, the TRPM algorithm achieved the best performance for both the minimum and total received energy of all EHIs with a 0.2 m walking step. Additionally, we showcase the effectiveness of the logarithmic-based nonlinear EH model by comparing it with the linear EH model. In the EPDS–NEHM–TRPM case, the logarithmic-based model yielded an average increase of 12.68% and 3.69% in the minimum and total received energy, respectively, compared to the EPDS–linear-TRPM approach.