Wavelet Packet-Fuzzy Optimization Control Strategy of Hybrid Energy Storage Considering Charge–Discharge Time Sequence
Abstract
1. Introduction
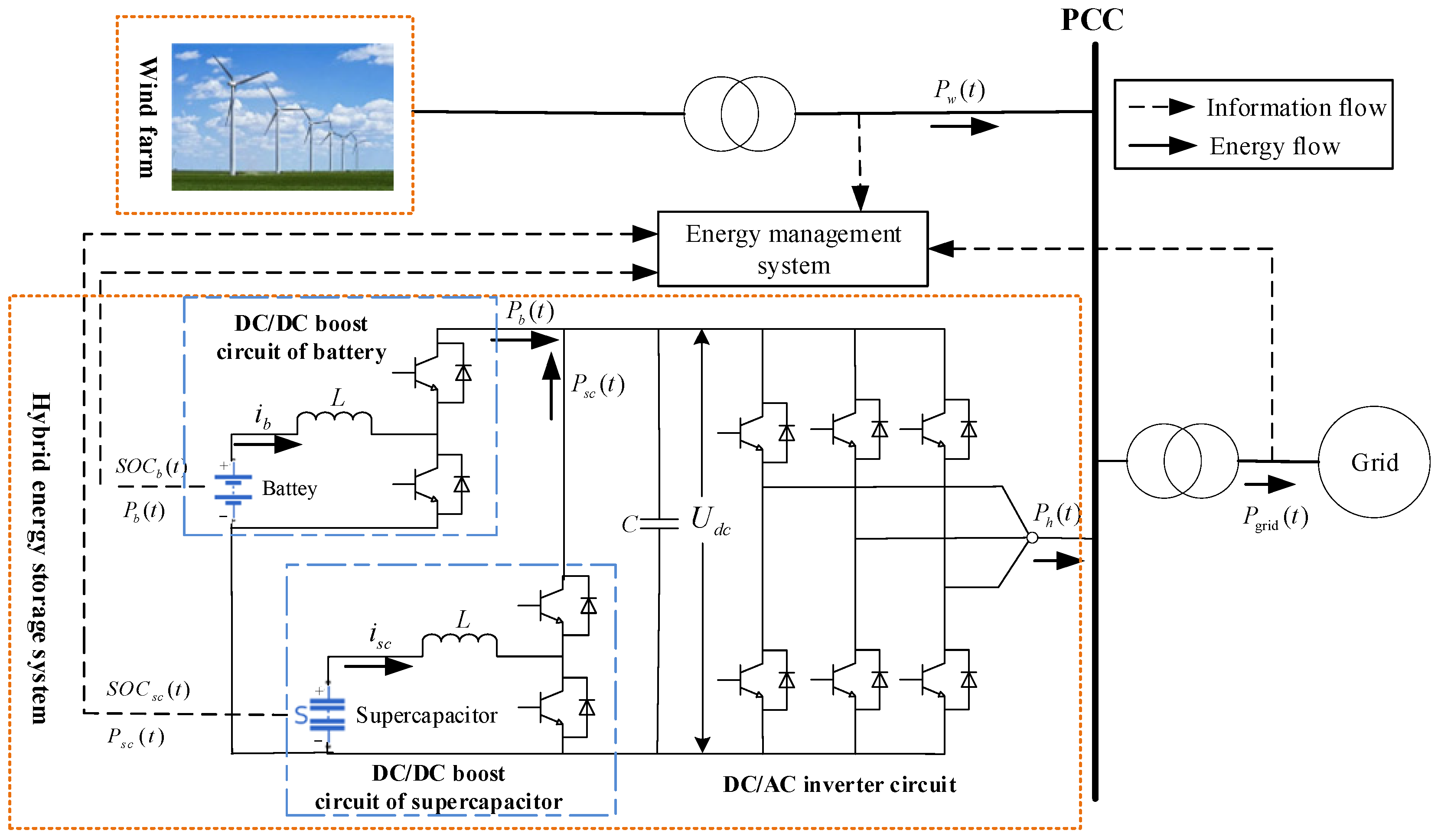
2. Wind Storage System Structure and Grid-Connected Power Acquisition
2.1. Wind Storage System Structure
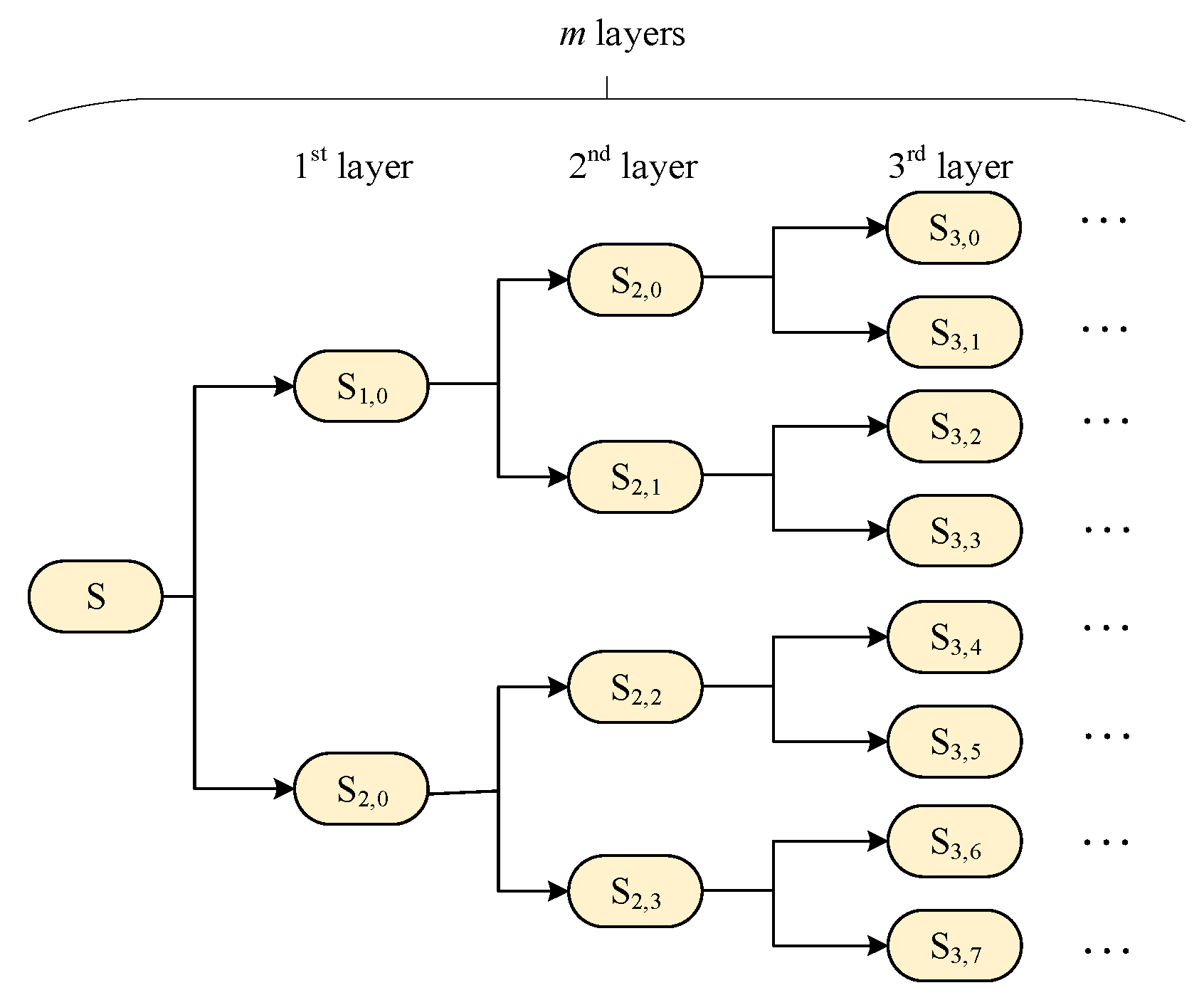
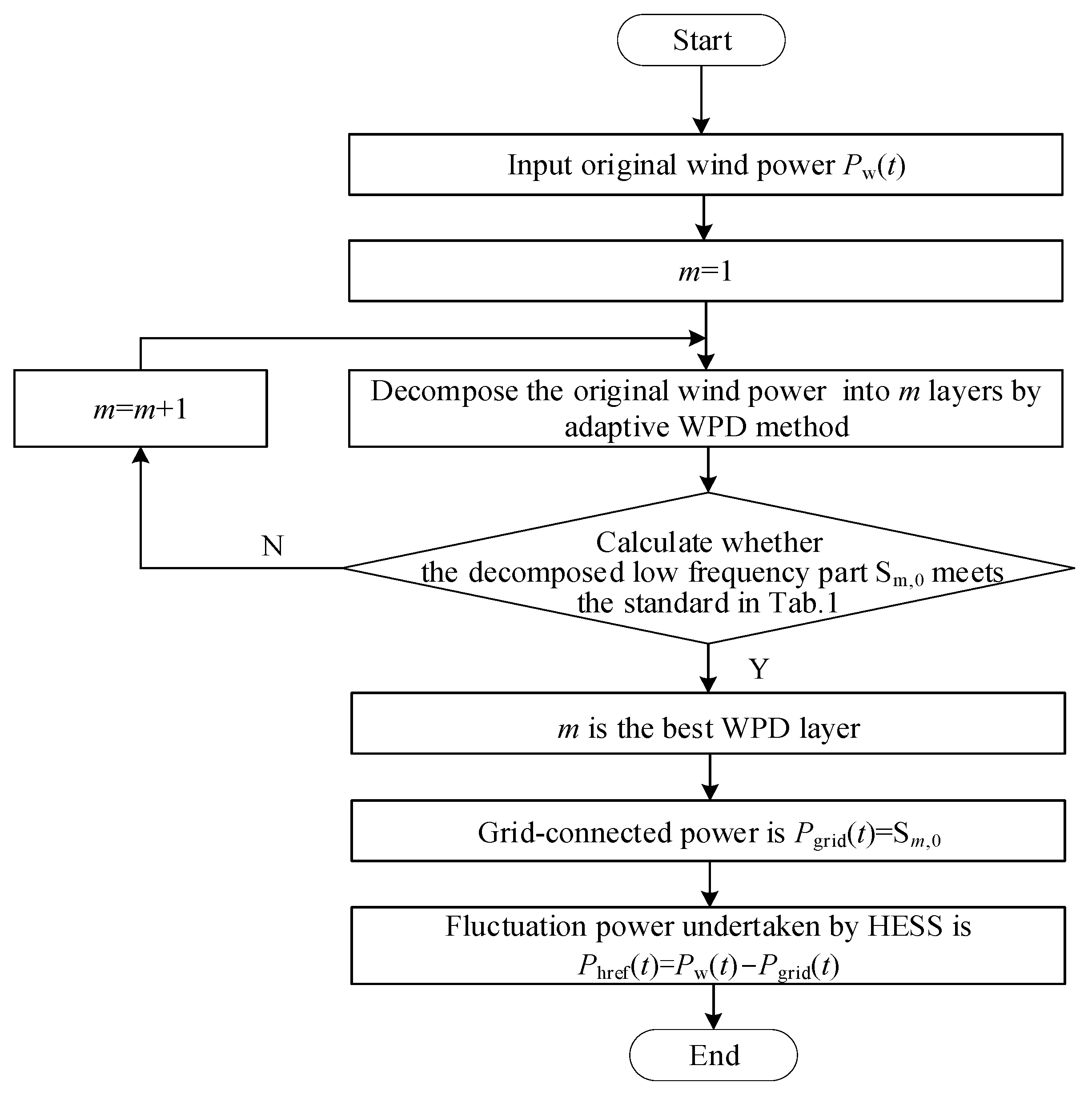
2.2. Grid-Connected Power Acquisition of Wind Storage System Based on Adaptive WPD
- (1)
- Let m = 1 and then decompose the original wind power;
- (2)
- Calculate whether the decomposed low-frequency part Sm,0 meets the standard in Table 1;
- (3)
- If the standard in Table 1 is not met, let m = m + 1, continue to decompose the original wind power and step (2) is repeated; If the standard in Table 1 is met, m is the best WPD layer, then let Pgrid(t) = Sm,0. In this way, the grid-connected power is acquired. The difference between Pgrid(t) and Pw(t) is the reference output power Phref(t) of HESS.
3. Initial Power Distribution and Charge–Discharge States Analysis of HESS
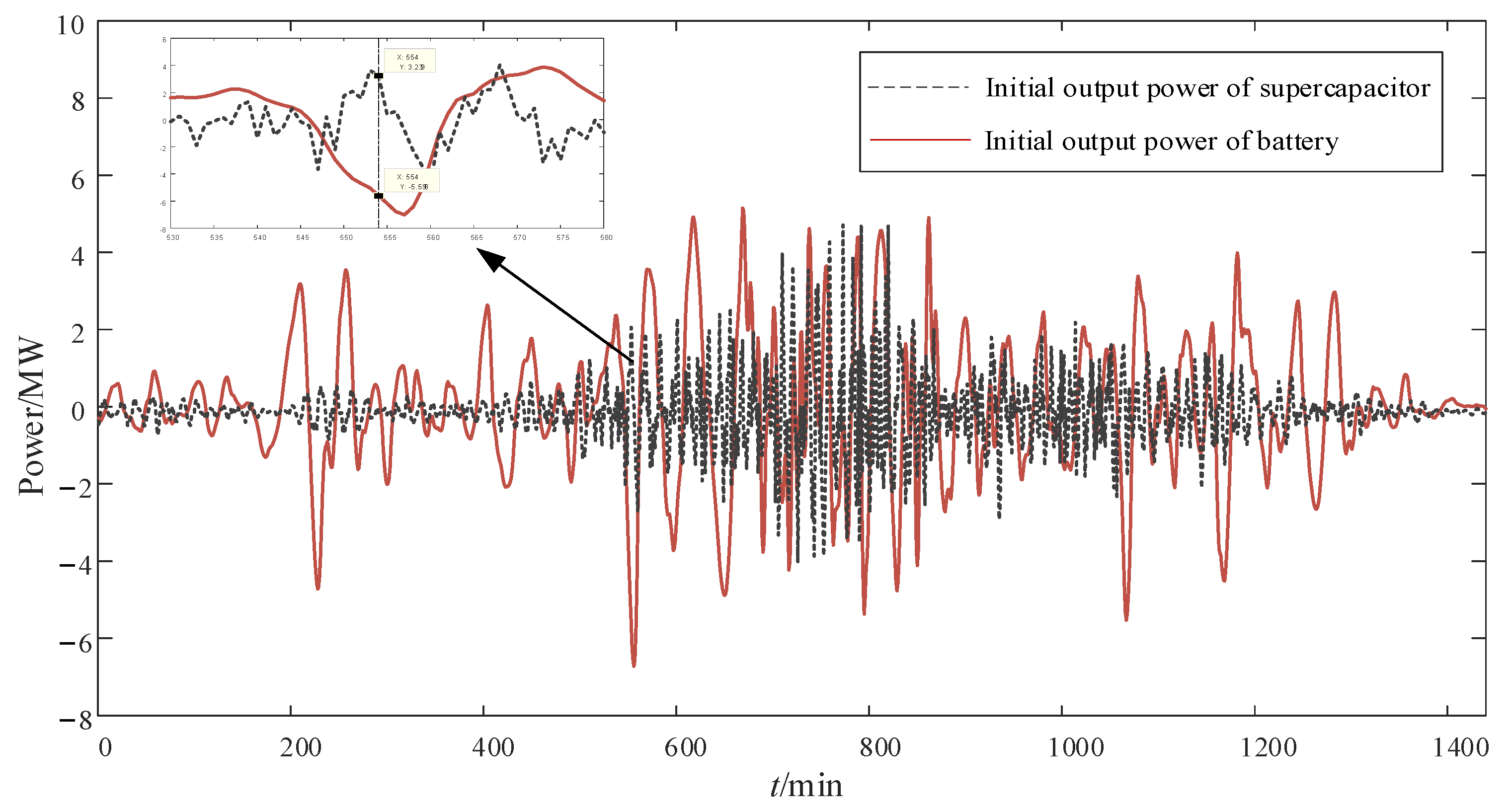
3.1. Initial Power Distribution of BESS Based on Adaptive WPD
3.2. Charge–Discharge States Analysis of HESS Based on Adaptive WPD
4. HESS Fuzzy Optimal Control Considering Charge-Discharge Time Sequence
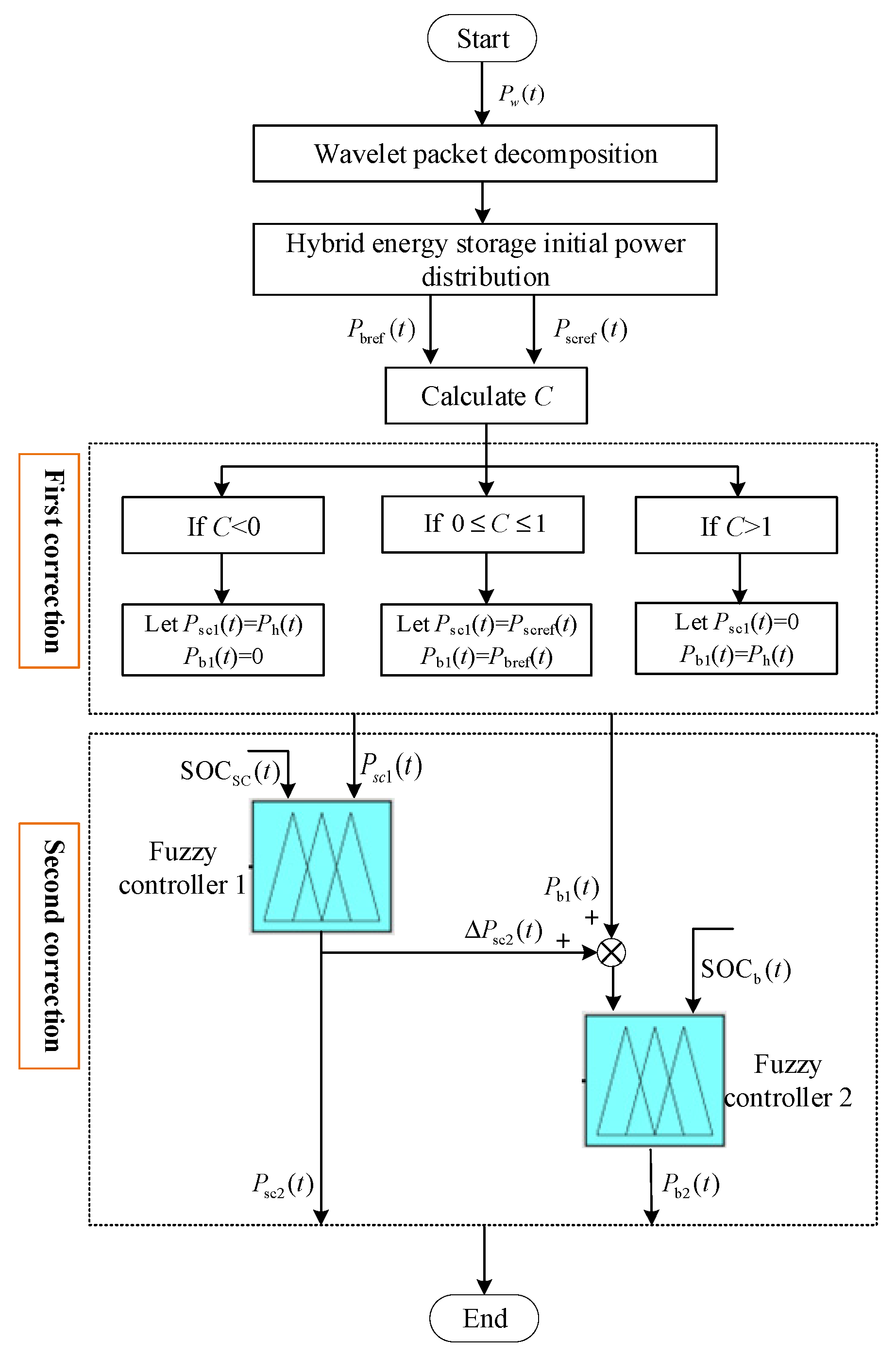
4.1. Charge–Discharge Time Sequence Optimization Based on Consistency Index
- (1)
- If , keep the original charge–discharge strategies of the battery and supercapacitor unchanged.
- (2)
- If C < 0, that is, |Psc(t)| > |Ph(t)|, which indicates that the HESS and supercapacitor are both in charge or discharge state, while the battery is in discharge or charge state, resulting in inconsistent charge–discharge states of different energy storage technologies in the same time sequence. In this case, let Psc1(t) = Ph(t), Pb1(t) = 0.
- (3)
- If C > 1, that is, |Psc(t)| < |Ph(t)|, which indicates that the HESS and battery are both in charge or discharge state, while the supercapacitor is in discharge or charge state. In this case, let Pb1(t) = Ph(t), Psc1(t) = 0.
4.2. Fuzzy Optimization of HESS Based on SOC
- (1)
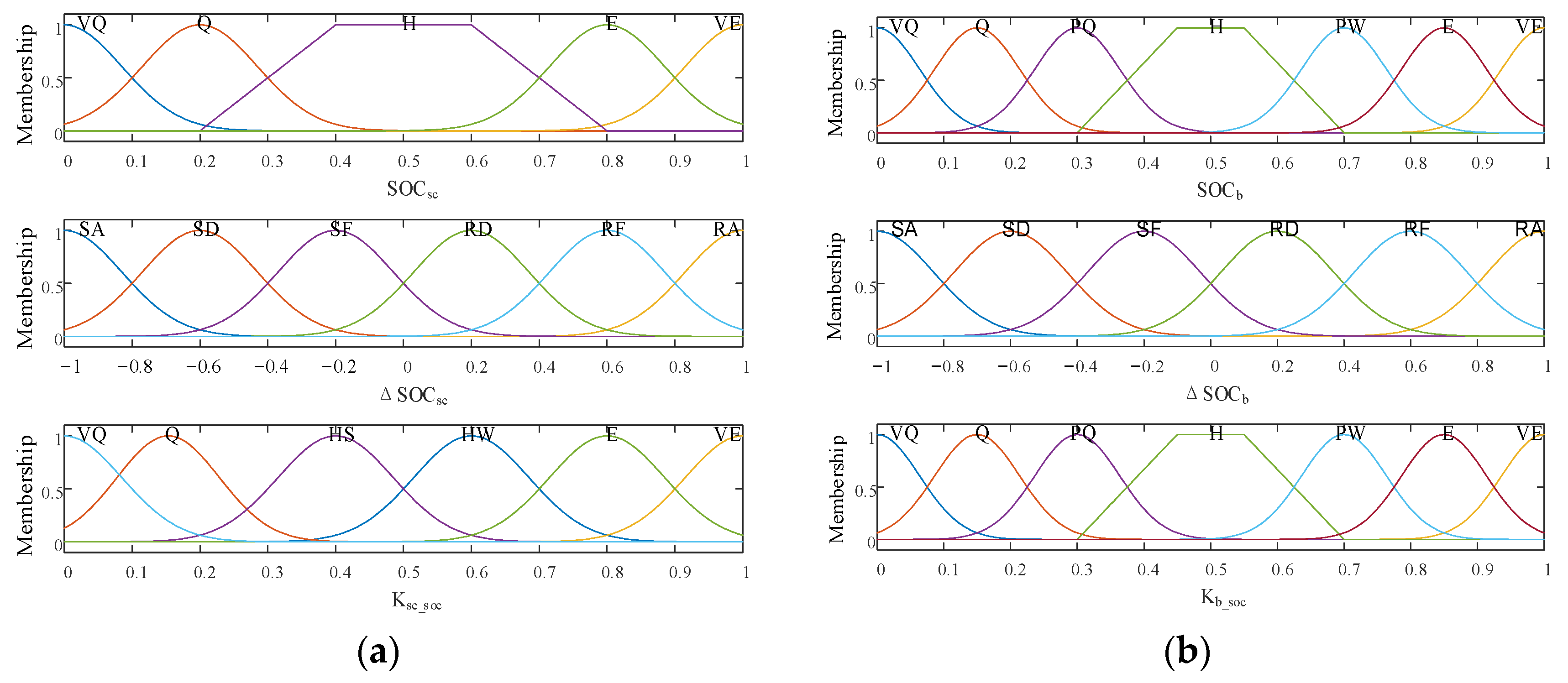
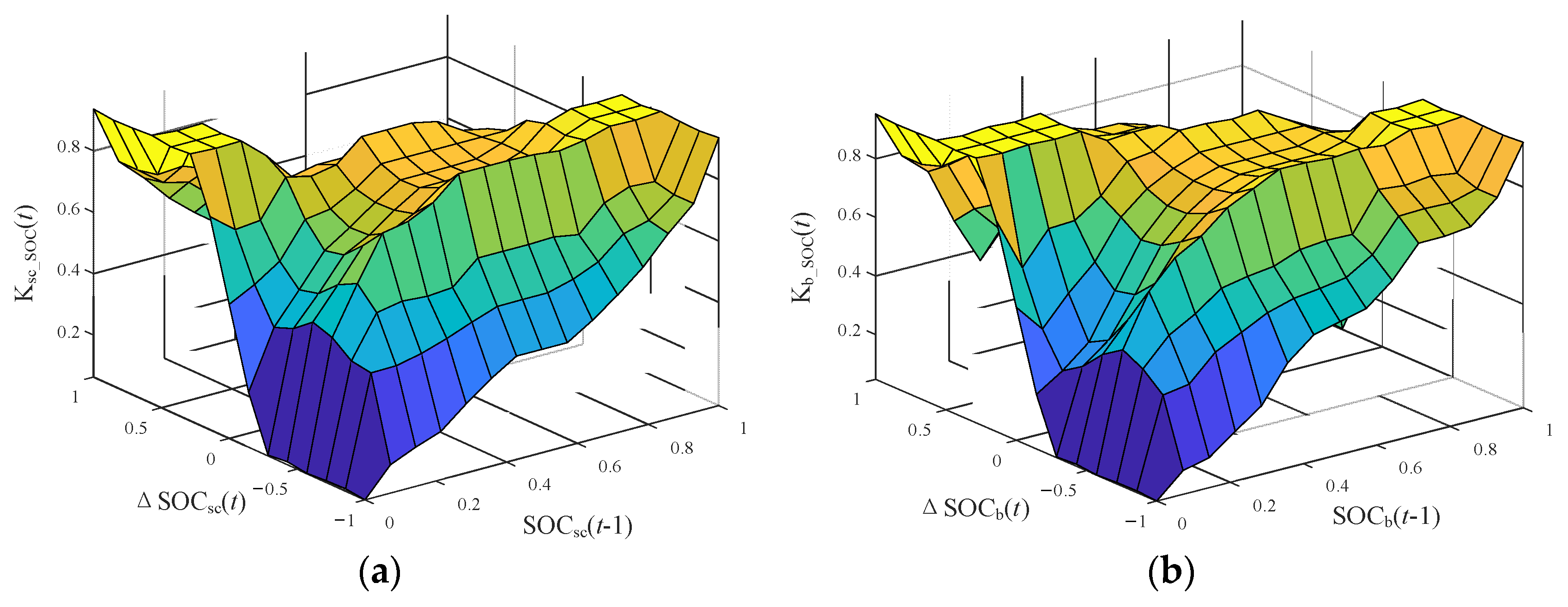
- Calculate the SOCSC(t) of the supercapacitor after the first correction; If SOCSC(t) is appropriate, keep the charge–discharge strategy of the supercapacitor after the first correction unchanged; If SOCSC(t−1) is too large and ΔSOCSC(t) > 0, or SOCSC(t−1) is too small and ΔSOCSC(t) < 0, it is necessary to make a second correction to the output power of supercapacitor. The output of the first fuzzy controller is the correction coefficient KSC_SOC(t). The supercapacitor power command after the second correction is Psc2(t) = KSC_SOC(t)·PSC1(t). In order to obtain a good control effect, the following principles should be followed when designing the fuzzy control rules between input and output variables in the first fuzzy controller: when ΔSOCSC(t) > 0, the larger the SOCSC(t−1) and ΔSOCSC(t), the smaller the output variable KSC_SOC(t); Similarly, when ΔSOCSC(t) < 0, the smaller the SOCSC(t−1) and ΔSOCSC(t), the smaller the output variable KSC_SOC(t). KSC_SOC(t)∈[0, 1]. So the membership functions and fuzzy rules for the first fuzzy controller are shown in Figure 7a and Table 2.
- (2)
- The difference between the power command of the supercapacitor before and after the second correction ΔPsc2(t) is supplemented by the battery, that is, ΔPsc2(t) = Psc1(t) − Psc2(t). The second fuzzy controller optimizes the SOCb1(t) of the battery based on the same strategy as step (1). The output of the second fuzzy controller is Kb-SOC(t). The battery power command after second correction is Pb2(t) = Kb_SOC(t)·(Pb1(t) + ΔPsc2(t)). The fuzzy design principles of the second fuzzy controller are the same as that of the first fuzzy controller. The membership functions and fuzzy rules for the second fuzzy controller are shown in Figure 7b and Table 3.
5. Case Study
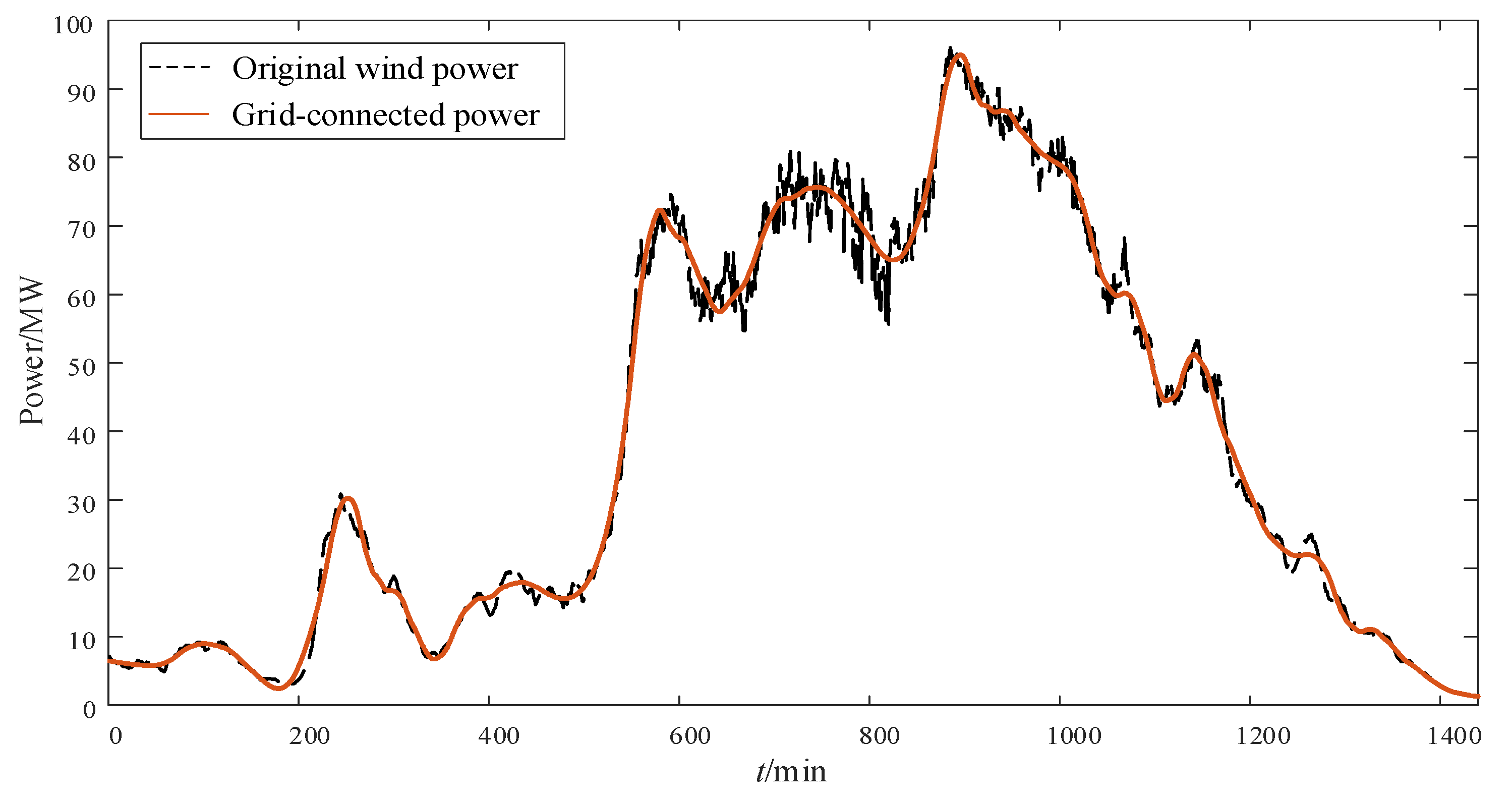
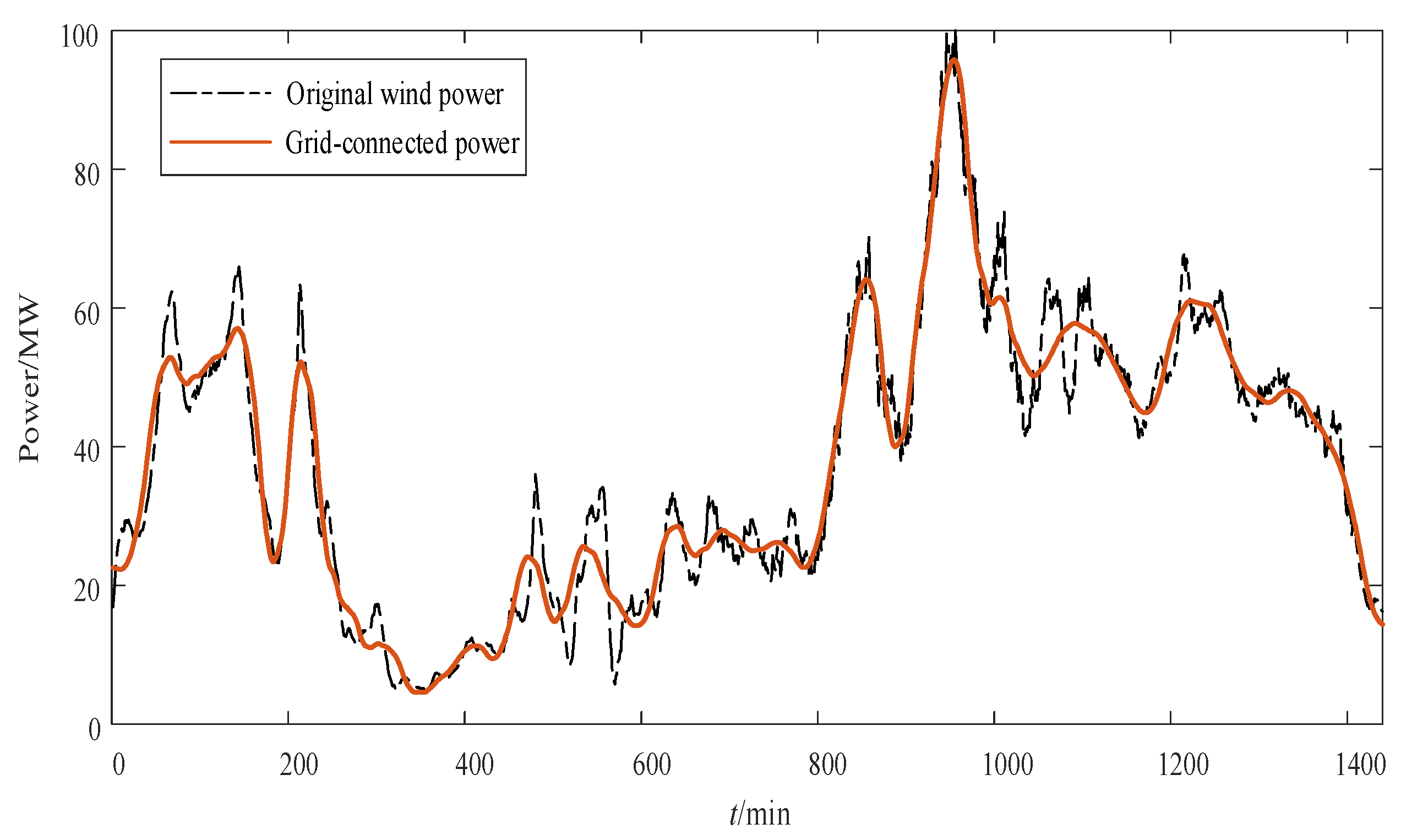
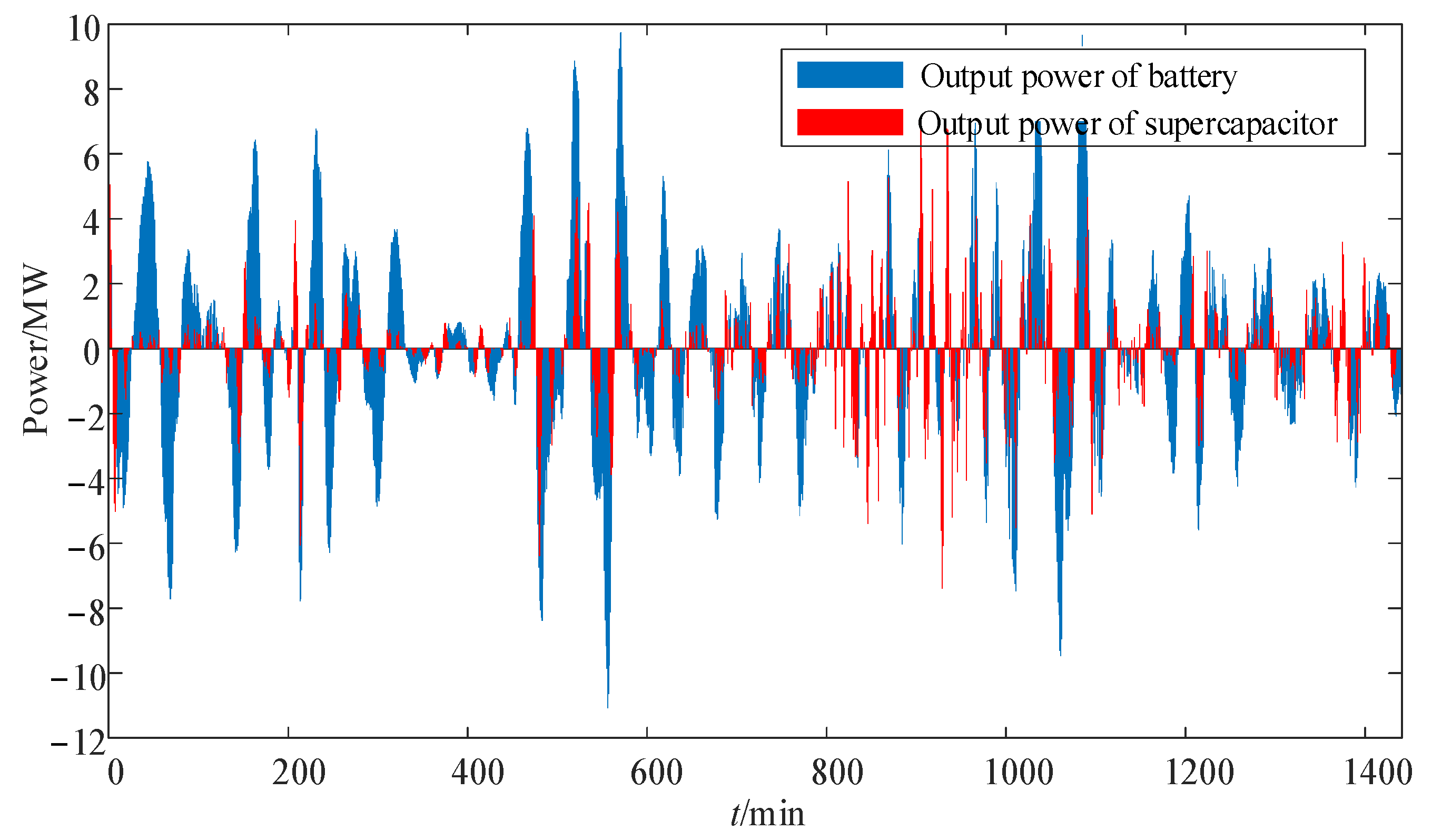
5.1. Analysis of Suppression Effect of Wind Power Fluctuation
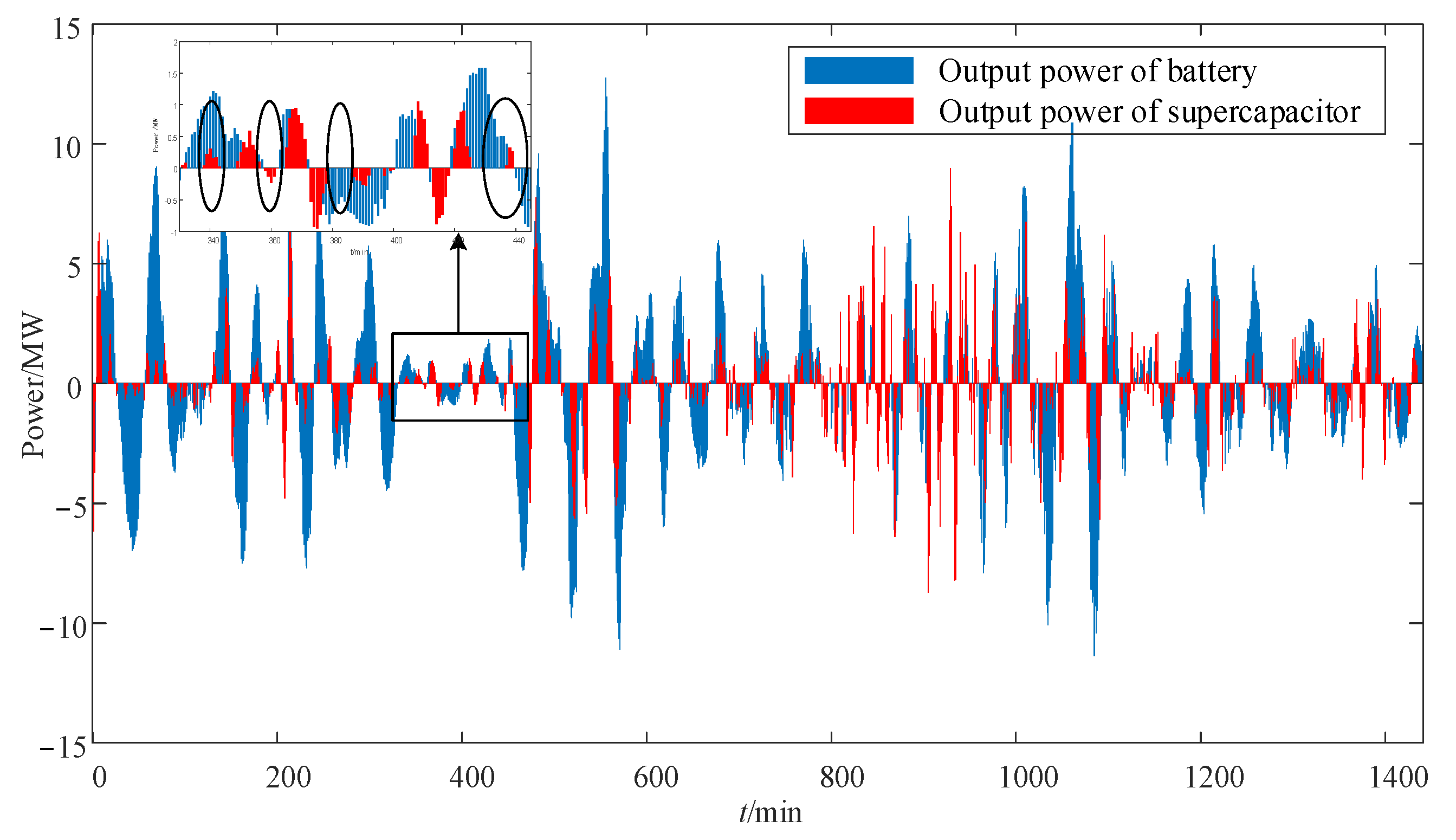
5.2. Analysis of Charge–Discharge Time Sequence Optimization of HESS
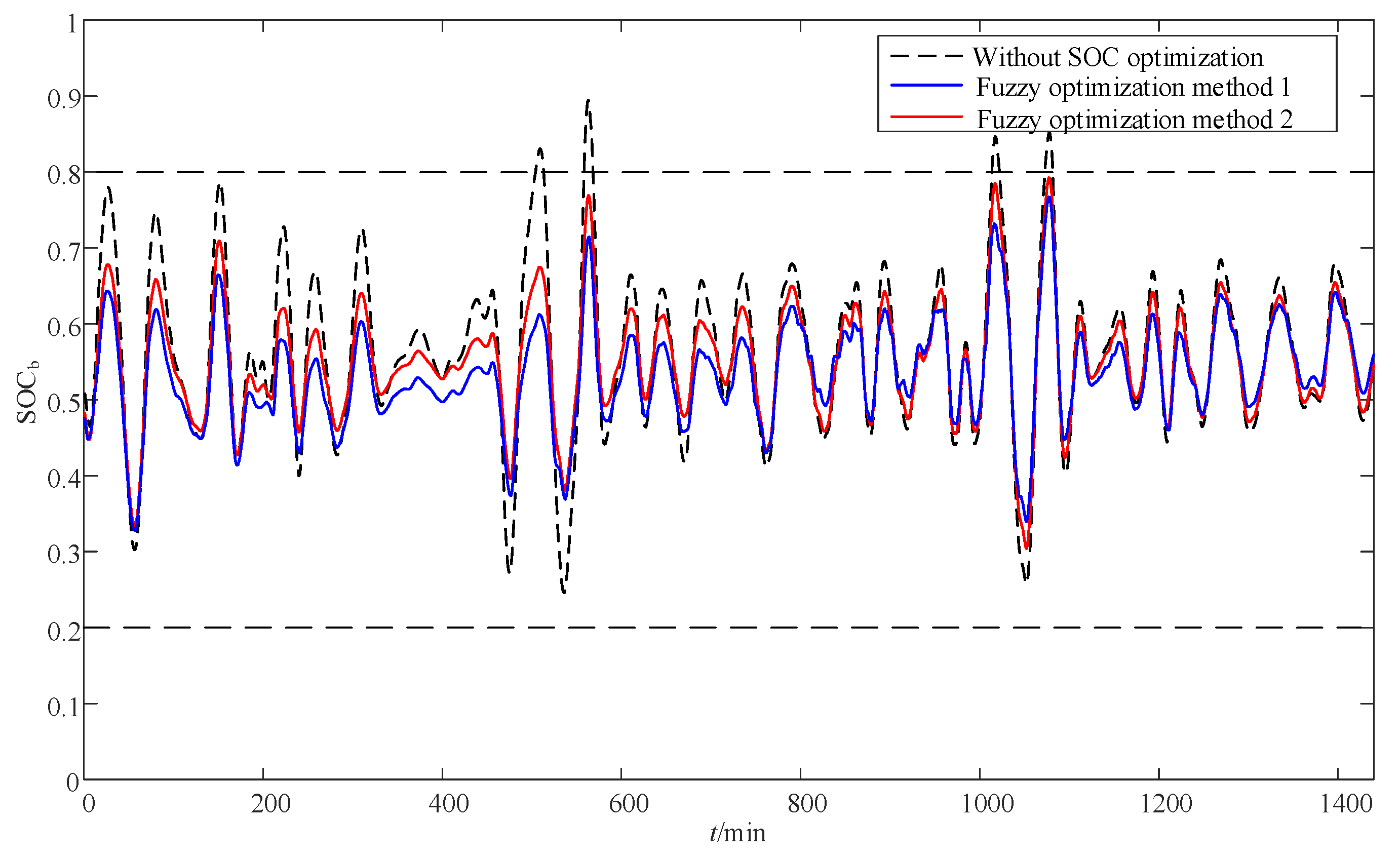
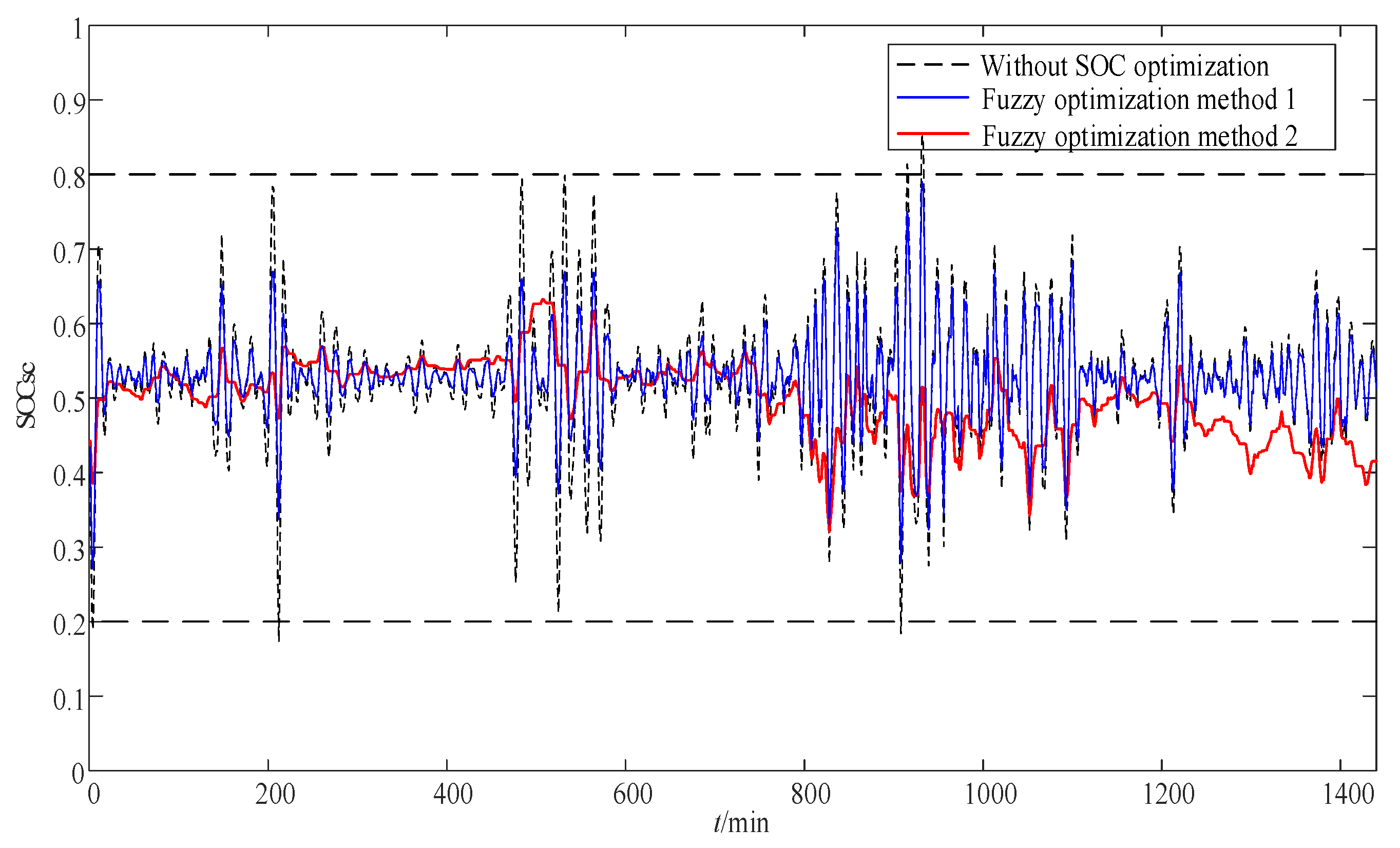
5.3. Analysis of SOC Optimization Effect of HESS
5.4. Sensitivity Analysis of Different Frequency Division Points on Optimization Results
6. Conclusions
- (1)
- By comprehensively analyzing the properties of wind power fluctuation and HESS, the grid-connected power that meets the GB/T 19963-2011 standard is obtained, and the initial power distribution of HESS is realized by the adaptive WPD method; The adaptive WPD method has a good suppression effect on the original wind power fluctuation, and it can be applied to different wind power fluctuation scenarios.
- (2)
- The proposed power optimization distribution method for HESS considering charge–discharge time sequence can enable the battery and supercapacitor to charge or discharge synchronously in the same time sequence, thus greatly reducing the charge–discharge conversion times and accumulated charge–discharge energy. Moreover, the fuzzy control method considering the charge–discharge time sequence proposed in this study can effectively reduce the charge–discharge depth of the energy storage system and prevent excessive charge–discharge, which is conducive to improving the lifetime and economy of the HESS.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Tang, X.; Sun, X.; Jia, D.; Cao, Z.; Pan, J.; Xu, B. Model predictive control and improved low-pass filtering strategies based on wind power fluctuation mitigation. J. Mod. Power Syst. Clean Energy 2019, 7, 512–524. [Google Scholar] [CrossRef]
- Xie, H.; Jiang, M.; Zhang, D.; Goh, H.H.; Ahmad, T.; Liu, H.; Liu, T.; Wang, S.; Wu, T. IntelliSense technology in the new power systems. Renew. Sustain. Energy Rev. 2023, 177, 113229. [Google Scholar] [CrossRef]
- Zhang, D.; Zhu, H.; Zhang, H.; Goh, H.H.; Liu, H.; Wu, T. Multi-Objective Optimization for Smart Integrated Energy System Considering Demand Responses and Dynamic Prices. IEEE Trans. Smart Grid 2022, 13, 1100–1112. [Google Scholar] [CrossRef]
- Nadeem, F.; Hussain, S.M.S.; Tiwari, P.K.; Goswami, A.K.; Ustun, T.S. Comparative review of energy storage systems, their roles, and impacts on future power systems. IEEE Access 2019, 7, 4555–4585. [Google Scholar] [CrossRef]
- Meng, L.; Zafar, J.; Khadem, S.K.; Collinson, A.; Murchie, K.C.; Coffele, F.; Burt, G.M. Fast frequency response from energy storage systems-a review of grid standards, projects and technical Issues. IEEE Trans. Smart Grid. 2019, 11, 1566–1581. [Google Scholar] [CrossRef]
- Ren, Y.; Xue, Y.; Yun, P. Multi-objective optimal energy storage system for reducing power fluctuation of wind farm via markov prediction. Power Syst. Autom. 2020, 44, 67–74. (In Chinese) [Google Scholar]
- Barelli, L.; Ciupageanu, D.-A.; Ottaviano, A.; Pelosi, D.; Lazaroiu, G. Stochastic power management strategy for hybrid energy storage systems to enhance large scale wind energy integration. J. Energy Storage 2020, 31, 101650. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Output power smoothing of wind power plants using self-tuned controlled SMES units. Electr. Power Syst. Res. 2020, 178, 106056. [Google Scholar] [CrossRef]
- Shi, J.; Wang, L.; Lee, W.-J.; Cheng, X.; Zong, X. Hybrid Energy Storage System (HESS) optimization enabling very short-term wind power generation scheduling based on output feature extraction. Appl. Energy 2019, 256, 113915. [Google Scholar] [CrossRef]
- Zou, J.; Dai, B.; Peng, C.; Xin, X.; Luo, W. Wind power smoothing method using hybrid energy storage system based on SOC hierarchical optimization. Power Syst. Autom. 2013, 37, 1–6. (In Chinese) [Google Scholar]
- Sun, Y.; Tang, X.; Sun, X.; Jia, D.; Wang, P.; Zhang, G. Research on multi-type energy storage coordination control strategy based on MPC-HHT. Proc. CSEE 2018, 38, 2580–2588. (In Chinese) [Google Scholar]
- Rasool, S.; Muttaqi, K.M.; Sutanto, D. A multi-filter based dynamic power sharing control for a hybrid energy storage system integrated to a wave energy converter for output power smoothing. IEEE Trans. Sustain. Energy 2022, 13, 1693–1706. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, X.; Yang, M.; Cao, Y.; Li, P. Capacity determination of hybrid energy storage system for smoothing wind power fluctuations with maximum net benefit. Trans. China Electrotech. Soc. 2016, 31, 40–48. (In Chinese) [Google Scholar]
- Han, X.; Tian, C.; Cheng, C. Power allocation method of hybrid energy storage system based on empirical mode decomposition. Acta Energ. Sol. Sinca 2014, 35, 1889–1896. [Google Scholar]
- Jiang, Q.; Hong, H. Wavelet-Based Capacity Configuration and Coordinated Control of Hybrid Energy Storage System for Smoothing Out Wind Power Fluctuations. IEEE Trans. Power Syst. 2013, 28, 1363–1372. [Google Scholar] [CrossRef]
- Trung, T.T.; Ahn, S.-J.; Choi, J.-H.; Go, S.-I.; Nam, S.-R. Real-Time Wavelet-Based Coordinated Control of Hybrid Energy Storage Systems for Denoising and Flattening Wind Power Output. Energies 2014, 7, 6620–6644. [Google Scholar] [CrossRef]
- Wu, J.; Ding, M. Wind power fluctuation smoothing strategy of hybrid energy storage system using self-adaptive wavelet packet decomposition. Power Syst. Autom. 2017, 41, 7–12. (In Chinese) [Google Scholar]
- Krim, Y.; Abbes, D.; Krim, S. Control and fuzzy logic supervision of a wind power system with battery/supercapacitor hybrid energy storage. In Proceedings of the 2018 7th International Conference on Systems and Control (ICSC), Valencia, Spain, 24–26 October 2018; pp. 180–187. [Google Scholar]
- Cohen, I.J.; Wetz, D.A.; McRee, B.J.; Dong, Q.; Heinzel, J.M. Fuzzy logic control of a hybrid energy storage module for use as a high rate prime power supply. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3887–3893. [Google Scholar] [CrossRef]
- Miao, F.; Tang, X.; Qi, Z. Fluctuation feature extraction of wind power. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Tianjin, China, 21–24 May 2012; pp. 1–5. [Google Scholar]
- GB/T 19963-2011; Technical Rule for Connecting Wind Farm to Power System. China Quality and Standards Publishing & Media Co., Ltd.: Beijing, China, 2011.
- Jia, W.; Ren, Y.; Xue, Y. Wavelet packet-fuzzy control of hybrid energy storage for power fluctuation smoothing of large wind farm. Acta Energ. Sol. Sin. 2021, 42, 357–363. [Google Scholar]

| Installation Capacity of Wind Farm (MW) | Maximum Power Variation in 1 Min (MW) | Maximum Power Variation in 10 Min (MW) |
|---|---|---|
| <30 | 3 | 10 |
| 30–150 | Installation capacity/10 | Installation capacity/3 |
| >150 | 15 | 50 |
| ΔSOCSC(t) | SOCSC(t − 1) | ||||
|---|---|---|---|---|---|
| VQ | Q | H | E | VE | |
| SA | VQ | Q | HS | HW | VE |
| SD | VQ | HW | E | VE | VE |
| SF | VQ | E | VE | VE | VE |
| RD | VE | VE | VE | E | VQ |
| RF | VE | VE | HW | HW | VQ |
| RA | VE | HW | HS | Q | VQ |
| ΔSOCb(t) | SOCb(t − 1) | ||||||
|---|---|---|---|---|---|---|---|
| VQ | Q | PQ | H | PW | E | VE | |
| SA | VQ | Q | PQ | H | PW | PW | VE |
| SD | VQ | PQ | PW | E | E | VE | VE |
| SF | VQ | PW | E | VE | VE | VE | VE |
| RD | VE | VE | VE | VE | VE | E | VQ |
| RF | VE | VE | VE | E | PW | PW | VQ |
| RA | VE | PW | PQ | PW | H | Q | VQ |
| Capacity of Wind Farm (MW) | Maximum Power Variation in 1 Min in the Original Wind Power Signal (MW) | Maximum Power Variation in 1 Min in the Grid-Connected Power Signal (MW) | Number of Decomposition Layers |
|---|---|---|---|
| 25 | 3.63 | 1.59 | 3 |
| 60 | 7.06 | 3.48 | 5 |
| 100 | 12.04 | 4.83 | 6 |
| Signal Component after Adaptive WPD | Frequency Range (Hz) |
|---|---|
| Sm,1 | 3.91 × 10−3–5.86 × 10−3 |
| Sm,2 | 5.86 × 10−3–7.81 × 10−3 |
| Sm,3 | 7.81 × 10−3–1.17 × 10−2 |
| Sm,4 | 1.17 × 10−2–1.56 × 10−2 |
| Sm,5 | 1.56 × 10−2–1.95 × 10−2 |
| Sm,6 | 1.95 × 10−2–2.34 × 10−2 |
| … | … |
| Response Time Boundary of HESS (Min) | Dividing Frequency of HESS (Hz) | Frequency Division Point of HESS | Proportion of Inconsistent Charge–Discharge States before Correction | Charge– Discharge Conversion Times of Battery before and after Correction | Charge– Discharge Conversion Times of Supercapacitor before and after Correction | Charge– Discharge Energy Reduction after Correction (MWh) |
|---|---|---|---|---|---|---|
| 1 | 1.67 × 10−2 | k = 4 | 49.8% | 71, 14 | 390, 61 | 12.12 |
| 2 | 8.33 × 10−3 | k = 2 | 50.1% | 69, 10 | 425, 69 | 13.11 |
| 3 | 5.56 × 10−3 | k = 1 | 52.4% | 61, 8 | 464, 75 | 13.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Zhang, Y.; Cui, X.; Wan, L.; Qiu, J.; Shang, E.; Zhang, Y.; Zhao, H. Wavelet Packet-Fuzzy Optimization Control Strategy of Hybrid Energy Storage Considering Charge–Discharge Time Sequence. Sustainability 2023, 15, 10412. https://doi.org/10.3390/su151310412
Zhao X, Zhang Y, Cui X, Wan L, Qiu J, Shang E, Zhang Y, Zhao H. Wavelet Packet-Fuzzy Optimization Control Strategy of Hybrid Energy Storage Considering Charge–Discharge Time Sequence. Sustainability. 2023; 15(13):10412. https://doi.org/10.3390/su151310412
Chicago/Turabian StyleZhao, Xinyu, Yunxiao Zhang, Xueying Cui, Le Wan, Jinlong Qiu, Erfa Shang, Yongchang Zhang, and Haisen Zhao. 2023. "Wavelet Packet-Fuzzy Optimization Control Strategy of Hybrid Energy Storage Considering Charge–Discharge Time Sequence" Sustainability 15, no. 13: 10412. https://doi.org/10.3390/su151310412
APA StyleZhao, X., Zhang, Y., Cui, X., Wan, L., Qiu, J., Shang, E., Zhang, Y., & Zhao, H. (2023). Wavelet Packet-Fuzzy Optimization Control Strategy of Hybrid Energy Storage Considering Charge–Discharge Time Sequence. Sustainability, 15(13), 10412. https://doi.org/10.3390/su151310412








