Modeling and Dynamic Simulation of a Phase-Change Material Tank for Powering Chiller Generators in District Cooling Networks
Abstract
1. Introduction
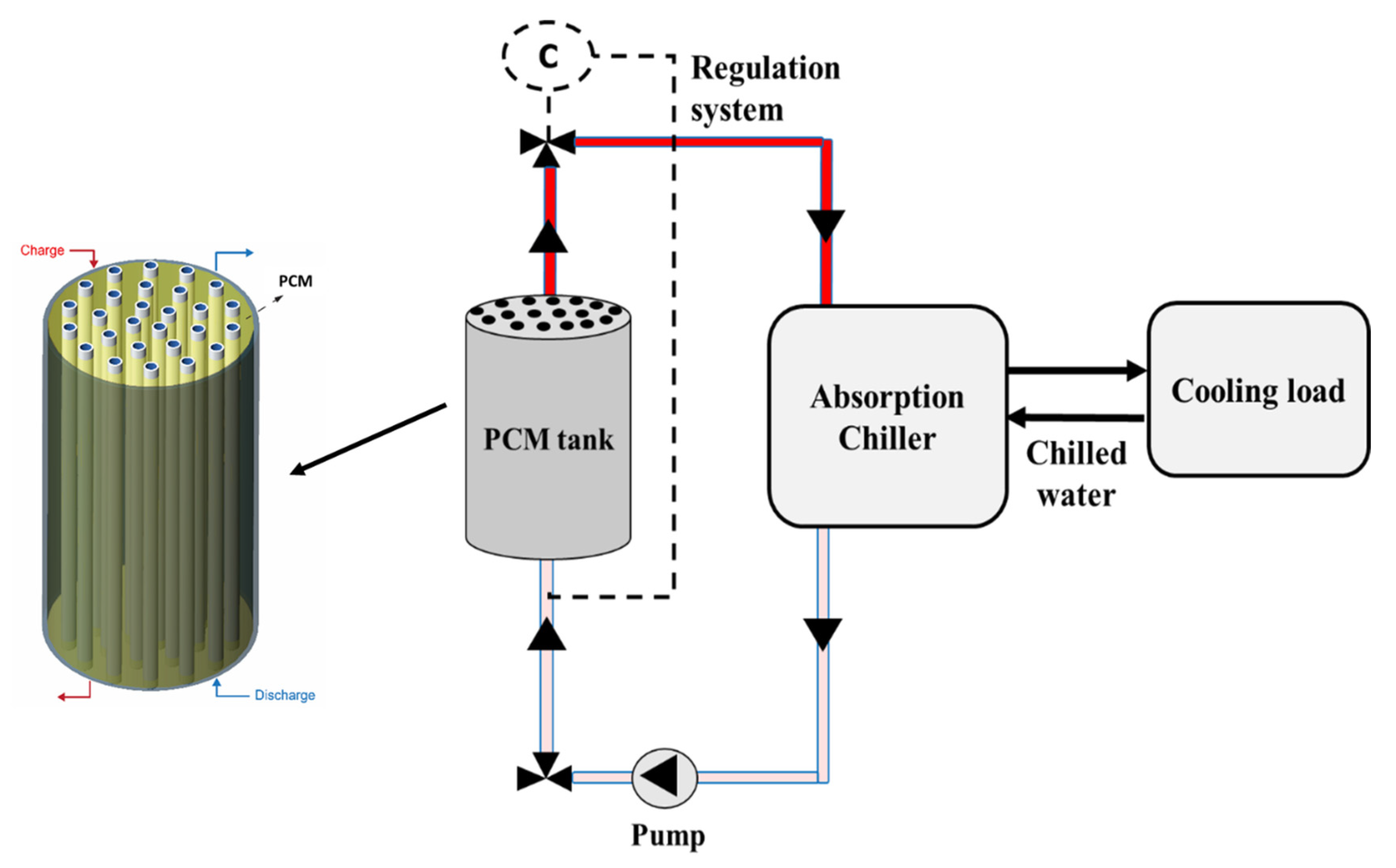
2. System Description
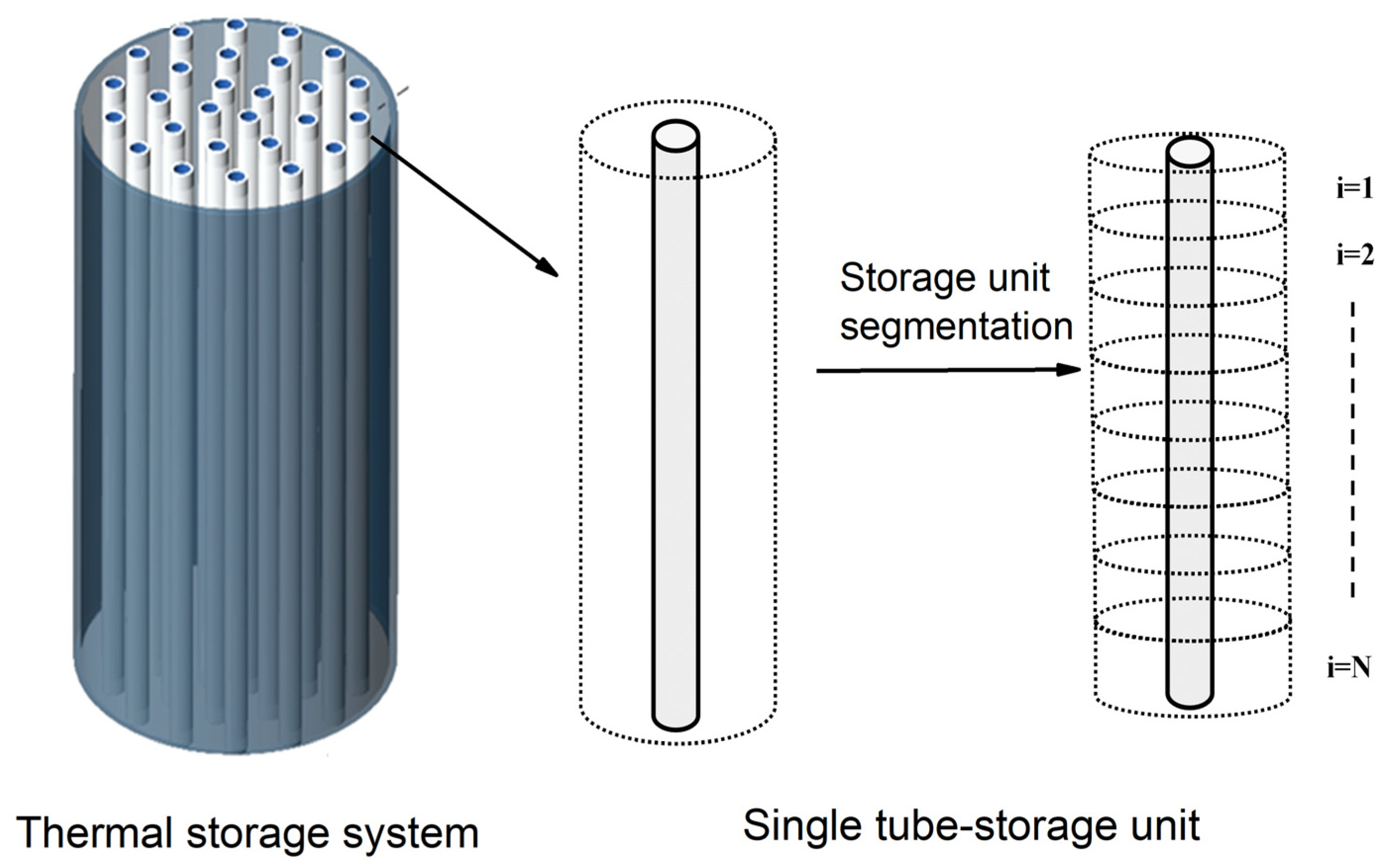
3. Modelling and Verification
- For the HTF medium:
- For the PCM storage medium:
4. Results and Discussion
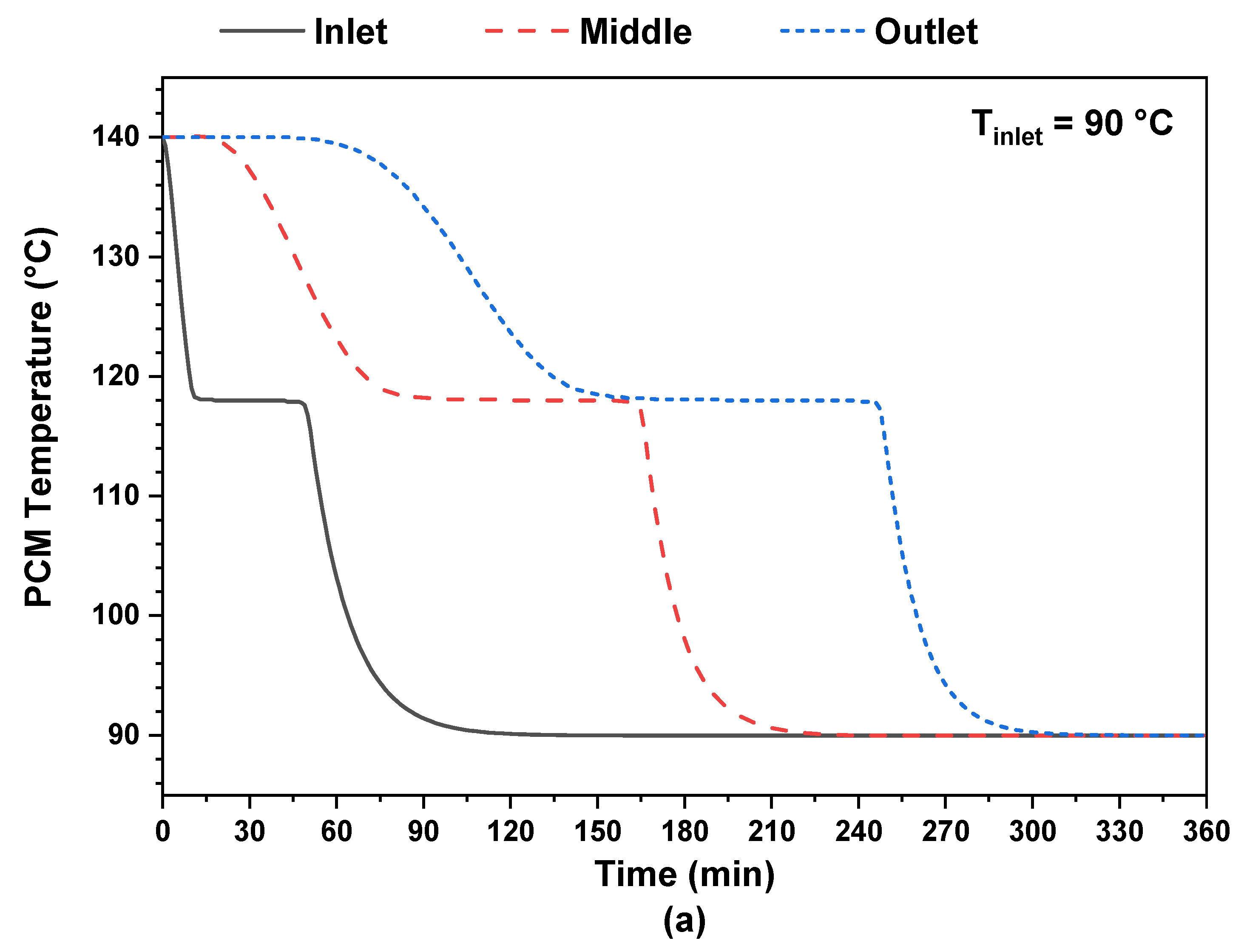
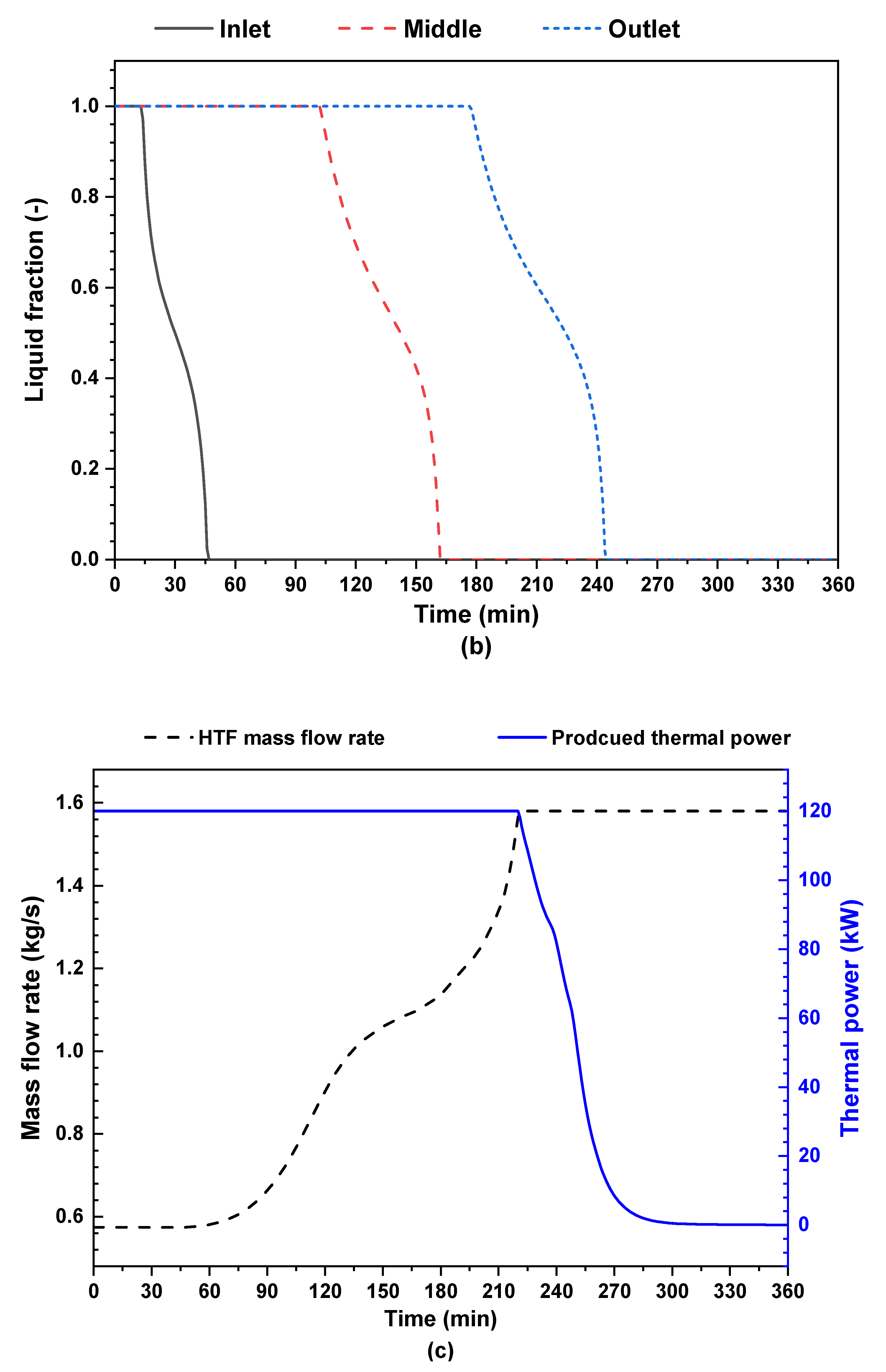
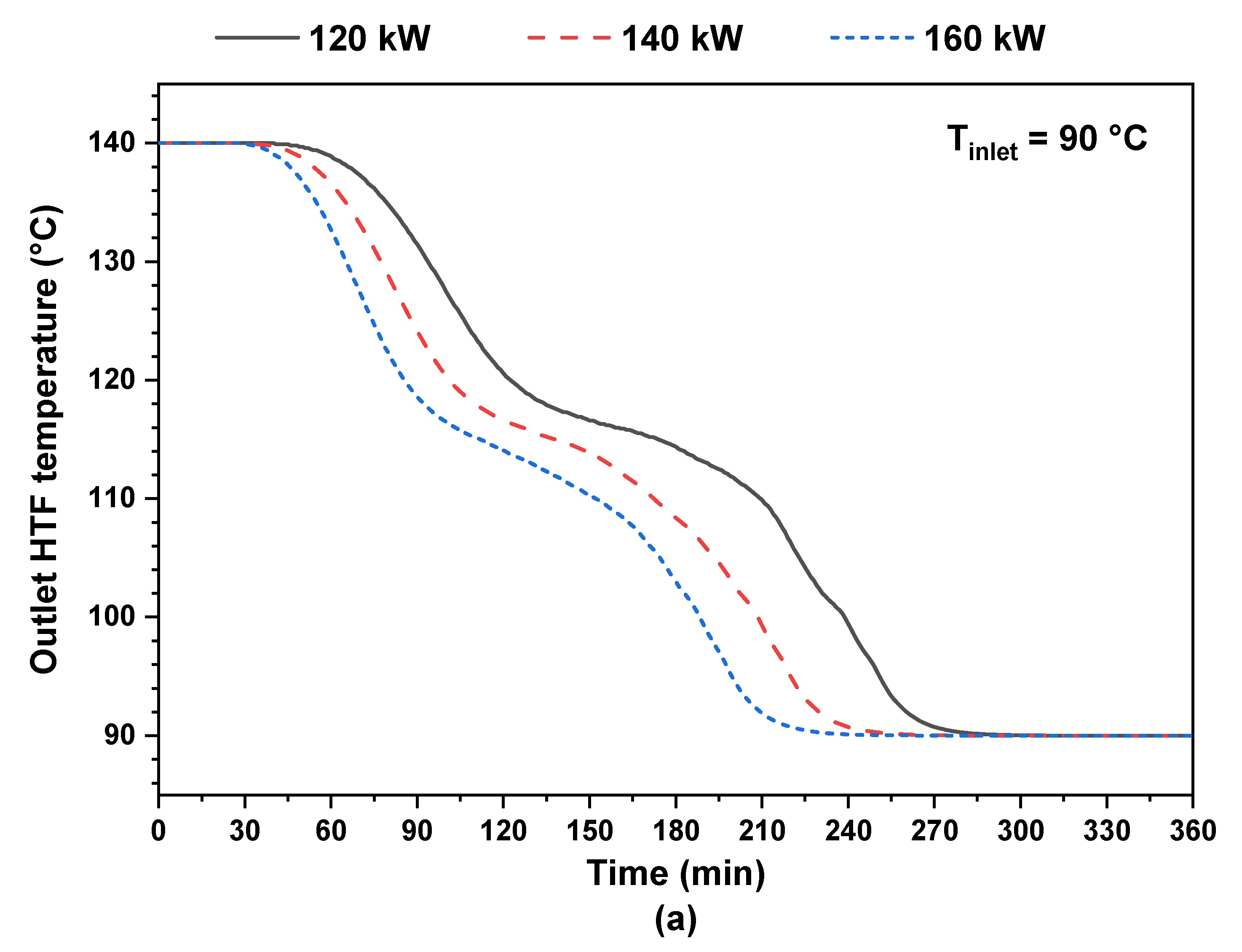
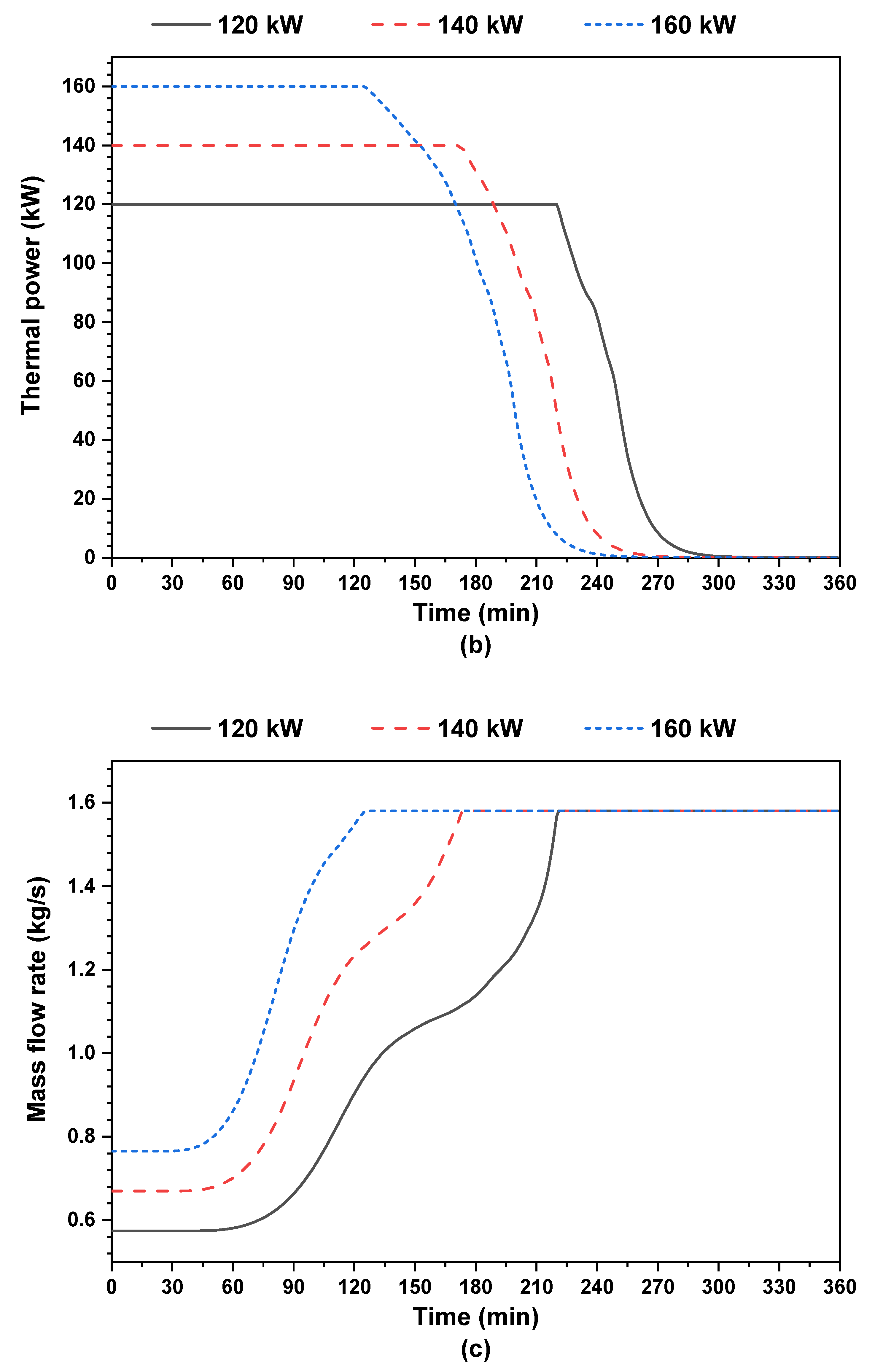
4.1. Influence of Generator Thermal Load
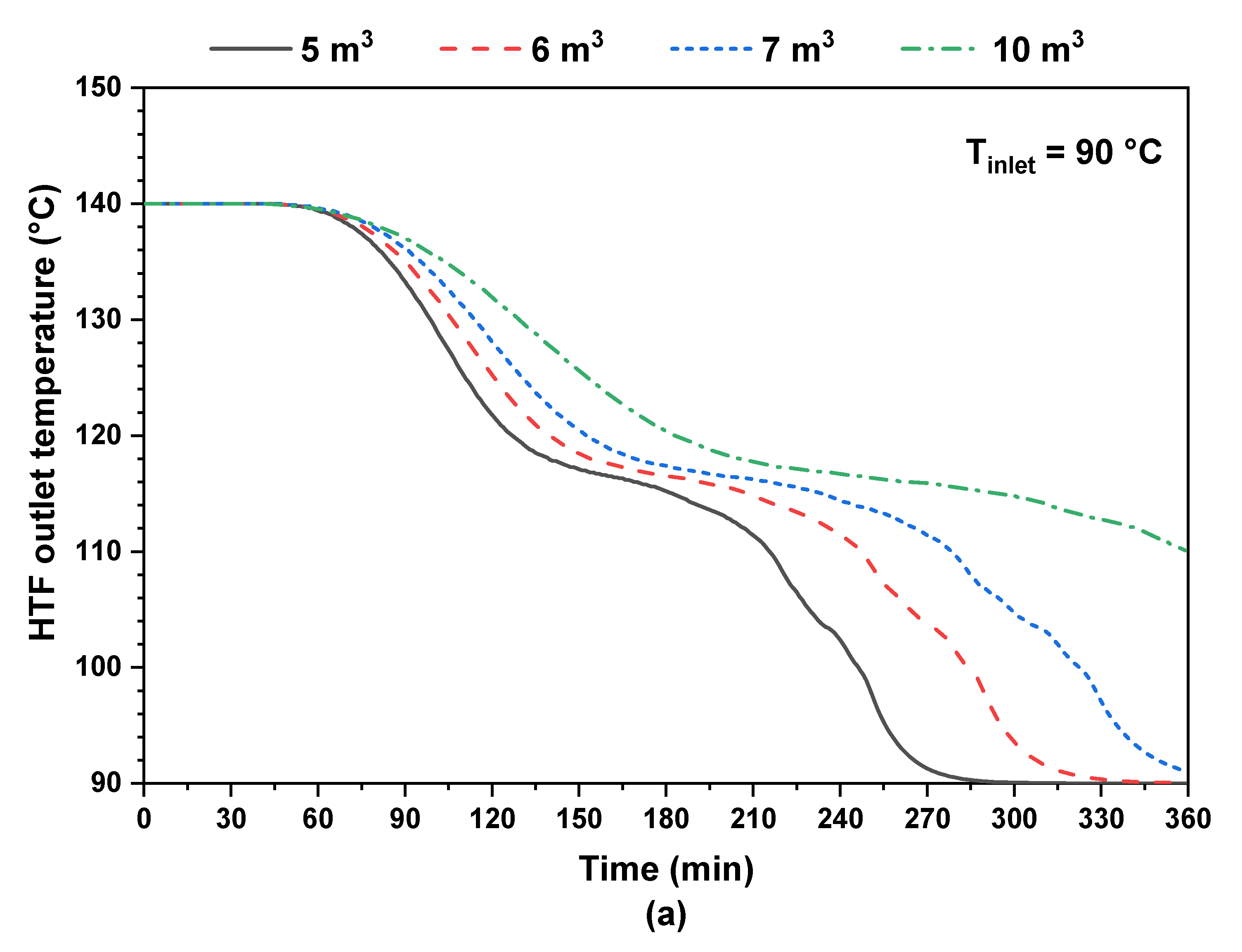
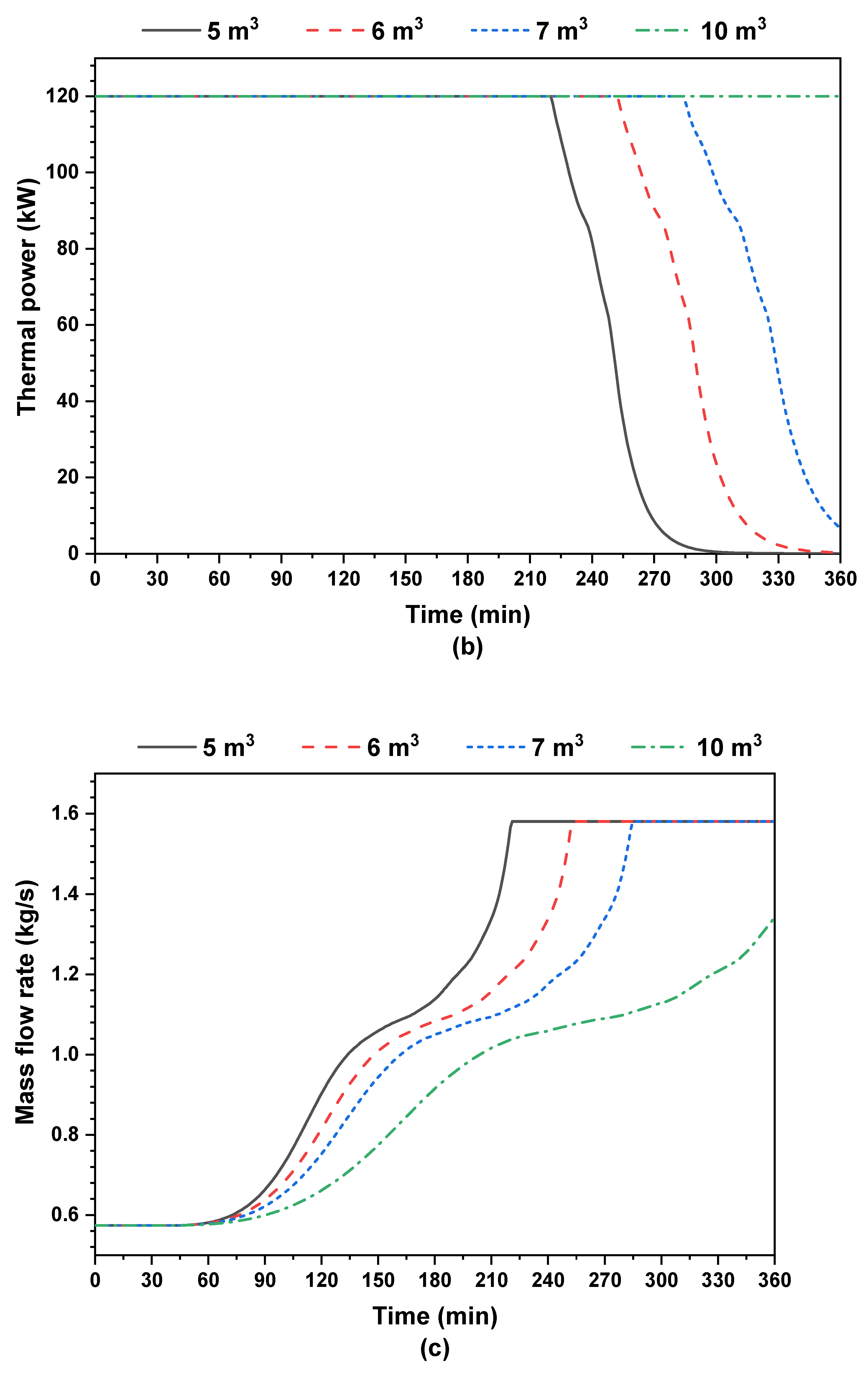
4.2. Effect of PCM Tank Volume
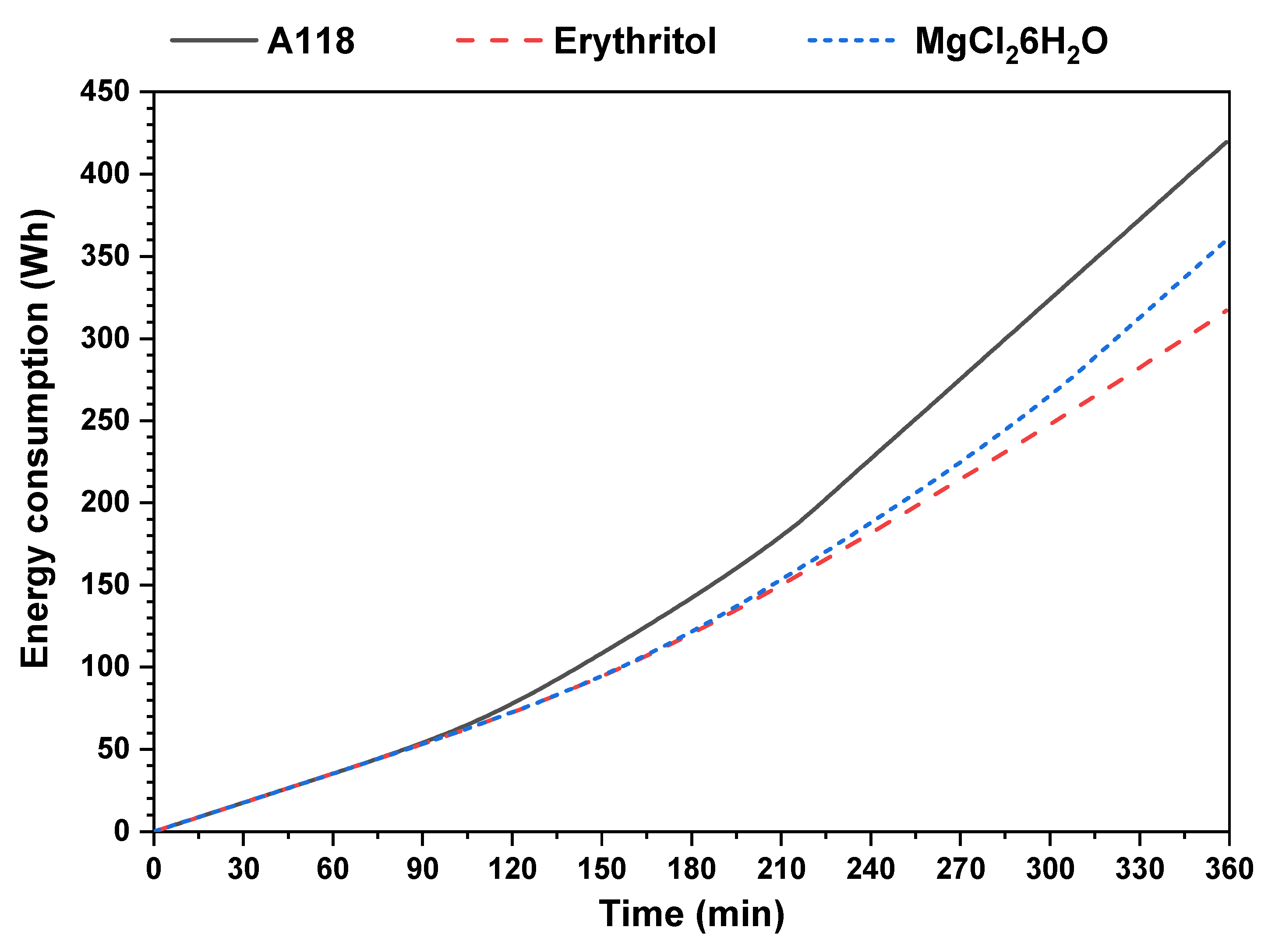
4.3. Effect of PCM Type
5. Conclusions
- The suggested PCM storage tank can produce a continuous heat rate of 120 kW within 3.6 h, which is advantageous and reduces the chiller generator’s energy consumption during this period.
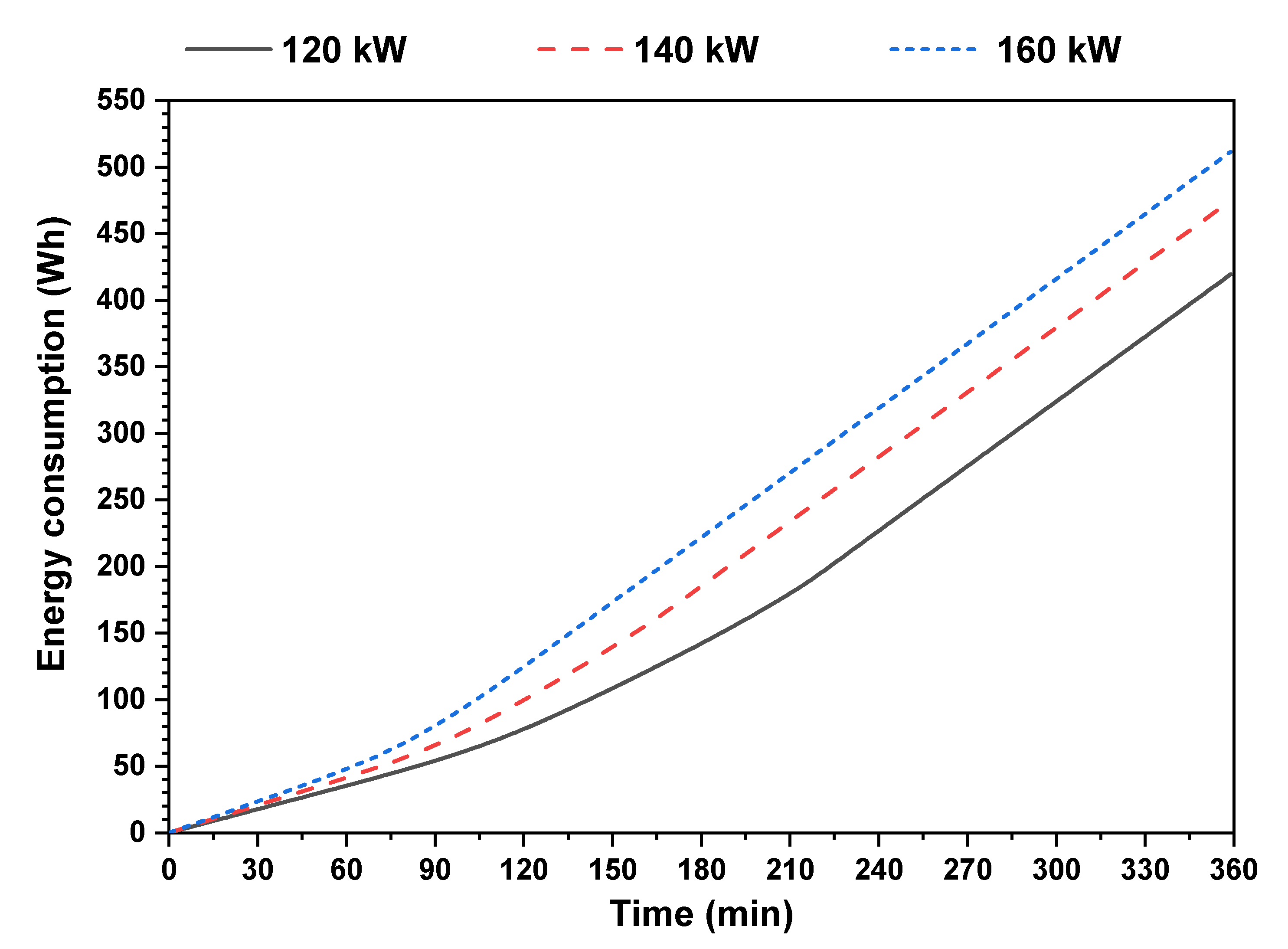
- Through increasing the thermal power needed by the generator cooling system from 120 kW to 160 kW, the duration of the PCM tank discharging process is decreased by about 20%, and the pump energy consumption is increased from 420 Wh to 512 Wh.
- The duration of 120 kW of constant power production from the tank is enhanced by about 62% when the PCM tank volume is increased from 5 m3 to 10 m3.
- The PCM tank volume variation has a small effect on the pump energy consumption. The latter is increased only by 23% when the tank volume is increased from 5 m3 to 10 m3.
- The utilization of erythritol as a medium for storage process is preferable to both PCMs A118 and MgCl2·6H2O.
- The period of continuous thermal power generation of 120 kW is increased by about 67% when erythritol is used as PCM instead of PCM A118.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Santos, F.D.; Ferreira, P.L.; Pedersen, J.S.T. The Climate Change Challenge: A Review of the Barriers and Solutions to Deliver a Paris Solution. Climate 2022, 10, 75. [Google Scholar] [CrossRef]
- Gjoka, K.; Rismanchi, B.; Crawford, R.H. Fifth-Generation District Heating and Cooling Systems: A Review of Recent Advancements and Implementation Barriers. Renew. Sustain. Energy Rev. 2023, 171, 112997. [Google Scholar] [CrossRef]
- Mortadi, M.; El Fadar, A. Performance, Economic and Environmental Assessment of Solar Cooling Systems under Various Climates. Energy Convers. Manag. 2022, 252, 114993. [Google Scholar] [CrossRef]
- Jahanger, A.; Ozturk, I.; Chukwuma Onwe, J.; Joseph, T.E.; Razib Hossain, M. Do Technology and Renewable Energy Contribute to Energy Efficiency and Carbon Neutrality? Evidence from Top Ten Manufacturing Countries. Sustain. Energy Technol. Assess. 2023, 56, 103084. [Google Scholar] [CrossRef]
- Zafar, M.W.; Saeed, A.; Zaidi, S.A.H.; Waheed, A. The Linkages among Natural Resources, Renewable Energy Consumption, and Environmental Quality: A Path toward Sustainable Development. Sustain. Dev. 2021, 29, 353–362. [Google Scholar] [CrossRef]
- Eveloy, V.; Ayou, D.S. Sustainable District Cooling Systems: Status, Challenges, and Future Opportunities, with Emphasis on Cooling-Dominated Regions. Energies 2019, 12, 235. [Google Scholar] [CrossRef]
- Alajmi, A.; Zedan, M. Energy, Cost, and Environmental Analysis of Individuals and District Cooling Systems for a New Residential City. Sustain. Cities Soc. 2020, 54, 101976. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Werner, S.; Dyrelund, A.; Lund, H.; Arabkoohsar, A.; Sorknæs, P.; Gudmundsson, O.; Thorsen, J.E.; Mathiesen, B.V. The Four Generations of District Cooling—A Categorization of the Development in District Cooling from Origin to Future Prospect. Energy 2022, 253, 124098. [Google Scholar] [CrossRef]
- Gong, Y.; Ma, G.; Jiang, Y.; Wang, L. Research Progress on the Fifth-Generation District Heating System Based on Heat Pump Technology. J. Build. Eng. 2023, 71, 106533. [Google Scholar] [CrossRef]
- Sulzer, M.; Werner, S.; Mennel, S.; Wetter, M. Vocabulary for the Fourth Generation of District Heating and Cooling. Smart Energy 2021, 1, 100003. [Google Scholar] [CrossRef]
- García-Céspedes, J.; Herms, I.; Arnó, G.; de Felipe, J.J. Fifth-Generation District Heating and Cooling Networks Based on Shallow Geothermal Energy: A Review and Possible Solutions for Mediterranean Europe. Energies 2023, 16, 147. [Google Scholar] [CrossRef]
- Li, G.; Zheng, X. Thermal Energy Storage System Integration Forms for a Sustainable Future. Renew. Sustain. Energy Rev. 2016, 62, 736–757. [Google Scholar] [CrossRef]
- Nie, B.; Palacios, A.; Zou, B.; Liu, J.; Zhang, T.; Li, Y. Review on Phase Change Materials for Cold Thermal Energy Storage Applications. Renew. Sustain. Energy Rev. 2020, 134, 110340. [Google Scholar] [CrossRef]
- Abd Majid, M.A.; Muhammad, M.; Hampo, C.C.; Akmar, A.B. Analysis of a Thermal Energy Storage Tank in a Large District Cooling System: A Case Study. Processes 2020, 8, 1158. [Google Scholar] [CrossRef]
- Dincer, I.; Rosen, M.A. Energetic, Environmental and Economic Aspects of Thermal Energy Storage Systems for Cooling Capacity. Appl. Therm. Eng. 2001, 21, 1105–1117. [Google Scholar] [CrossRef]
- Fiorentini, M.; Heer, P.; Baldini, L. Design Optimization of a District Heating and Cooling System with a Borehole Seasonal Thermal Energy Storage. Energy 2023, 262, 125464. [Google Scholar] [CrossRef]
- Tang, H.; Yu, J.; Geng, Y.; Liu, X.; Lin, B. Optimization of Operational Strategy for Ice Thermal Energy Storage in a District Cooling System Based on Model Predictive Control. J. Energy Storage 2023, 62, 106872. [Google Scholar] [CrossRef]
- Todorov, O.; Alanne, K.; Virtanen, M.; Kosonen, R. A Method and Analysis of Aquifer Thermal Energy Storage (ATES) System for District Heating and Cooling: A Case Study in Finland. Sustain. Cities Soc. 2020, 53, 101977. [Google Scholar] [CrossRef]
- Guelpa, E.; Verda, V. Thermal Energy Storage in District Heating and Cooling Systems: A Review. Appl. Energy 2019, 252, 113474. [Google Scholar] [CrossRef]
- Lamrani, B.; Belcaid, A.; Lebrouhi, B.E.; Khodadadi, J.M.; El Rhafiki, T. Dynamic Thermal Analysis of a Coupled Solar Water Heaters-Thermal Storage Tank for Solar Powered District Heating Networks. J. Energy Storage 2023, 61, 106793. [Google Scholar] [CrossRef]
- Abánades, A.; Rodríguez-Martín, J.; Roncal, J.J.; Caraballo, A.; Galindo, F. Proposal of a Thermocline Molten Salt Storage Tank for District Heating and Cooling. Appl. Therm. Eng. 2023, 218, 119309. [Google Scholar] [CrossRef]
- Hlimi, M.; Lebrouhi, B.E.; Belcaid, A.; Lamrani, B.; Balli, L.; Ndukwu, M.C.; El Rhafiki, T.; Kousksou, T. A Numerical Assessment of a Latent Heat Storage System for District Heating Substations. J. Energy Storage 2023, 57, 106210. [Google Scholar] [CrossRef]
- Soh, A.; Huang, Z.; Chen, W.; Islam, M.R.; Chua, K.J. Design Optimization of Low-Temperature Latent Thermal Energy Storage for Urban Cooling Applications. Appl. Therm. Eng. 2023, 230, 120711. [Google Scholar] [CrossRef]
- Bastida, H.; De la Cruz-Loredo, I.; Ugalde-Loo, C.E. Effective Estimation of the State-of-Charge of Latent Heat Thermal Energy Storage for Heating and Cooling Systems Using Non-Linear State Observers. Appl. Energy 2023, 331, 120448. [Google Scholar] [CrossRef]
- Shirazi, A.; Taylor, R.A.; Morrison, G.L.; White, S.D. Solar-Powered Absorption Chillers: A Comprehensive and Critical Review. Energy Convers. Manag. 2018, 171, 59–81. [Google Scholar] [CrossRef]
- Lamrani, B.; Kousksou, T. Numerical Investigation of a Shell-and-Tube Latent Heat Thermal Energy Storage System for Urban Heating Network. J. Energy Storage 2021, 43, 103216. [Google Scholar] [CrossRef]
- Lamrani, B.; Kuznik, F.; Draoui, A. Thermal Performance of a Coupled Solar Parabolic Trough Collector Latent Heat Storage Unit for Solar Water Heating in Large Buildings. Renew. Energy 2020, 162, 411–426. [Google Scholar] [CrossRef]
- Lamrani, B.; Draoui, A. Modelling and Simulation of a Hybrid Solar-Electrical Dryer of Wood Integrated with Latent Heat Thermal Energy Storage System. Therm. Sci. Eng. Prog. 2020, 18, 100545. [Google Scholar] [CrossRef]
- Wang, J.; Yan, R.; Wang, Z.; Zhang, X.; Shi, G. Thermal Performance Analysis of an Absorption Cooling System Based on Parabolic Trough Solar Collectors. Energies 2018, 11, 2679. [Google Scholar] [CrossRef]
- PlusICE®. Available online: www.pcmproducts.net (accessed on 3 March 2023).
- Agyenim, F. The Use of Enhanced Heat Transfer Phase Change Materials (PCM) to Improve the Coefficient of Performance (COP) of Solar Powered LiBr/H2O Absorption Cooling Systems. Renew. Energy 2016, 87, 229–239. [Google Scholar] [CrossRef]
- Mostafavi, S.S.; Taylor, R.A.; Saberi, P.; Diarce, G. Design and Feasibility of High Temperature Shell and Tube Latent Heat Thermal Energy Storage System for Solar Thermal Power Plants. Renew. Energy 2016, 96, 120–136. [Google Scholar] [CrossRef]
- Elbahjaoui, R.; El Qarnia, H. Thermal Performance of a Solar Latent Heat Storage Unit Using Rectangular Slabs of Phase Change Material for Domestic Water Heating Purposes. Energy Build. 2019, 182, 111–130. [Google Scholar] [CrossRef]
- Lamrani, B.; Khouya, A.; Zeghmati, B.; Draoui, A. Mathematical Modeling and Numerical Simulation of a Parabolic Trough Collector: A Case Study in Thermal Engineering. Therm. Sci. Eng. Prog. 2018, 8, 47–54. [Google Scholar] [CrossRef]
- Gnielinski, V. On Heat Transfer in Tubes. Int. J. Heat Mass Transf. 2013, 63, 134–140. [Google Scholar] [CrossRef]
- Bentivoglio, F.; Rouge, S.; Soriano, O.; Tempass de Sousa, A. Design and Operation of a 180 kWh PCM Heat Storage at the Flaubert Substation of the Grenoble Urban Heating Network. Appl. Therm. Eng. 2021, 185, 116402. [Google Scholar] [CrossRef]
- Medved, I.; Trník, A.; Vozár, L. Modeling of Heat Capacity Peaks and Enthalpy Jumps of Phase-Change Materials Used for Thermal Energy Storage. Int. J. Heat Mass Transf. 2017, 107, 123–132. [Google Scholar] [CrossRef]
- Halimov, A.; Lauster, M.; Müller, D. Validation and Integration of a Latent Heat Storage Model into Building Envelopes of a High-Order Building Model for Modelica Library AixLib. Energy Build. 2019, 202, 109336. [Google Scholar] [CrossRef]
- El Ouali, A.; Khattari, Y.; Lamrani, B.; El Rhafiki, T.; Zeraouli, Y.; Kousksou, T. Apparent Heat Capacity Method to Describe the Thermal Performances of a Latent Thermal Storage System during Discharge Period. J. Energy Storage 2022, 52, 104960. [Google Scholar] [CrossRef]
- Feustel, H. Simplified Numerical Description of Latent Storage Characteristics for Phase Change Wallboard; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1995.
- Lamrani, B.; Lebrouhi, B.E.; Khattari, Y.; Kousksou, T. A Simplified Thermal Model for a Lithium-Ion Battery Pack with Phase Change Material Thermal Management System. J. Energy Storage 2021, 44, 103377. [Google Scholar] [CrossRef]
- Höhlein, S.; König-Haagen, A.; Brüggemann, D. Thermophysical Characterization of MgCl2·6H2O, Xylitol and Erythritol as Phase Change Materials (PCM) for Latent Heat Thermal Energy Storage (LHTES). Materials 2017, 10, 444. [Google Scholar] [CrossRef]
- Al-Yasiri, Q.; Szabó, M.; Arıcı, M. A Review on Solar-Powered Cooling and Air-Conditioning Systems for Building Applications. Energy Rep. 2022, 8, 2888–2907. [Google Scholar] [CrossRef]




| Properties | A118 | Erythritol | MgCl2·6H2O |
|---|---|---|---|
| PCM thermal conductivity (W/m·K) | 0.22 | 0.3 (L)/0.7 (s) | 0.6 (L)/0.7 (s) |
| PCM density (kg/m3) | 900 | 1340 (L)/1380 (s) | 1450 (L)/1570 (s) |
| PCM melting temperature (°C) | 118 | 117.7 | 116.7 |
| PCM heat capacity (J/g·K) | 2.2 | 2.8 (L)/1.4 (s) | 2.6 (L)/2.3 (s) |
| PCM heat of fusion (kJ/kg) | 195 | 339.8 | 168.6 |
| Properties | Value |
|---|---|
| Volume of PCM tank (m3) | 5, 6, 7 |
| Length of PCM tank (m) | 5 |
| Tube number in PCM tank (-) | 400 |
| Diameter of one tube (m) | 0.036 |
| Case | Discharging Duration (h) | Constant Power Production Period (h) | Pumping Energy Consumption (Wh) |
|---|---|---|---|
| 120 kW | 5.2 | 3.7 | 420 |
| 140 kW | 4.75 | 2.9 | 475 |
| 160 kW | 4.4 | 2.1 | 512 |
| Case | Discharging Duration (h) | Constant Power Production Period (h) | Pumping Energy Consumption (Wh) |
|---|---|---|---|
| 5 m3 | 5.2 | 3.7 | 420 |
| 6 m3 | 6 | 4.2 | 400 |
| 7 m3 | 6.5 | 4.75 | 380 |
| 10 m3 | 9 | 6 | 323 |
| Case | Discharging Duration (h) | Constant Power Production Period (h) | Pumping Energy Consumption (Wh) |
|---|---|---|---|
| A 118 | 5.2 | 3.7 | 420 |
| Erythritol | 6 | 6 | 317 |
| MgCl2·6H2O | 6 | 5.2 | 360 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, E.; Ajbar, A.; Lamrani, B. Modeling and Dynamic Simulation of a Phase-Change Material Tank for Powering Chiller Generators in District Cooling Networks. Sustainability 2023, 15, 10332. https://doi.org/10.3390/su151310332
Ali E, Ajbar A, Lamrani B. Modeling and Dynamic Simulation of a Phase-Change Material Tank for Powering Chiller Generators in District Cooling Networks. Sustainability. 2023; 15(13):10332. https://doi.org/10.3390/su151310332
Chicago/Turabian StyleAli, Emad, Abdelhamid Ajbar, and Bilal Lamrani. 2023. "Modeling and Dynamic Simulation of a Phase-Change Material Tank for Powering Chiller Generators in District Cooling Networks" Sustainability 15, no. 13: 10332. https://doi.org/10.3390/su151310332
APA StyleAli, E., Ajbar, A., & Lamrani, B. (2023). Modeling and Dynamic Simulation of a Phase-Change Material Tank for Powering Chiller Generators in District Cooling Networks. Sustainability, 15(13), 10332. https://doi.org/10.3390/su151310332






