Evaluation the Resistance Growth of Aged Vehicular Proton Exchange Membrane Fuel Cell Stack by Distribution of Relaxation Times
Abstract
:1. Introduction
2. Materials and Methods
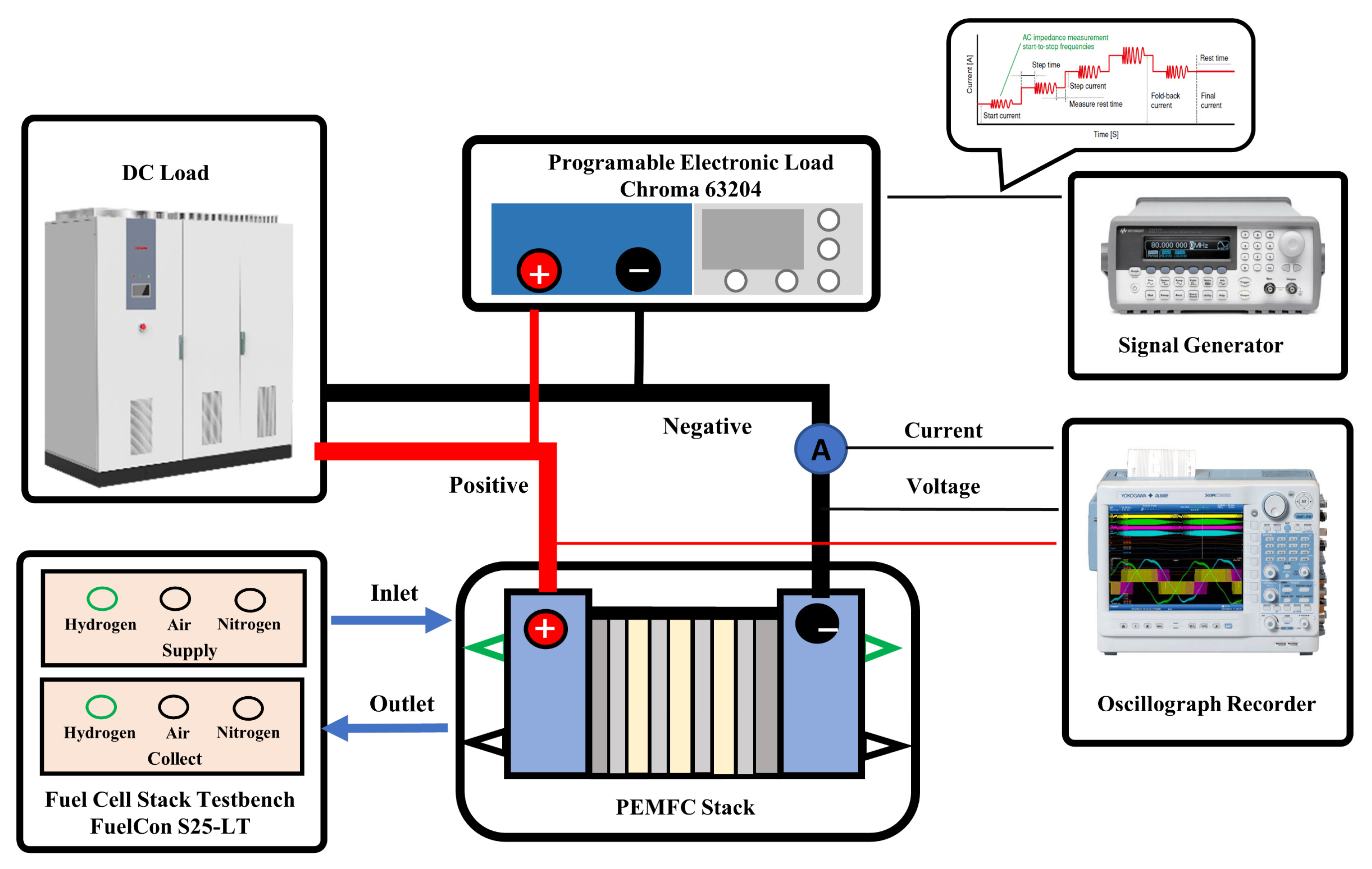
2.1. The PEMFC Stack and Test Bench
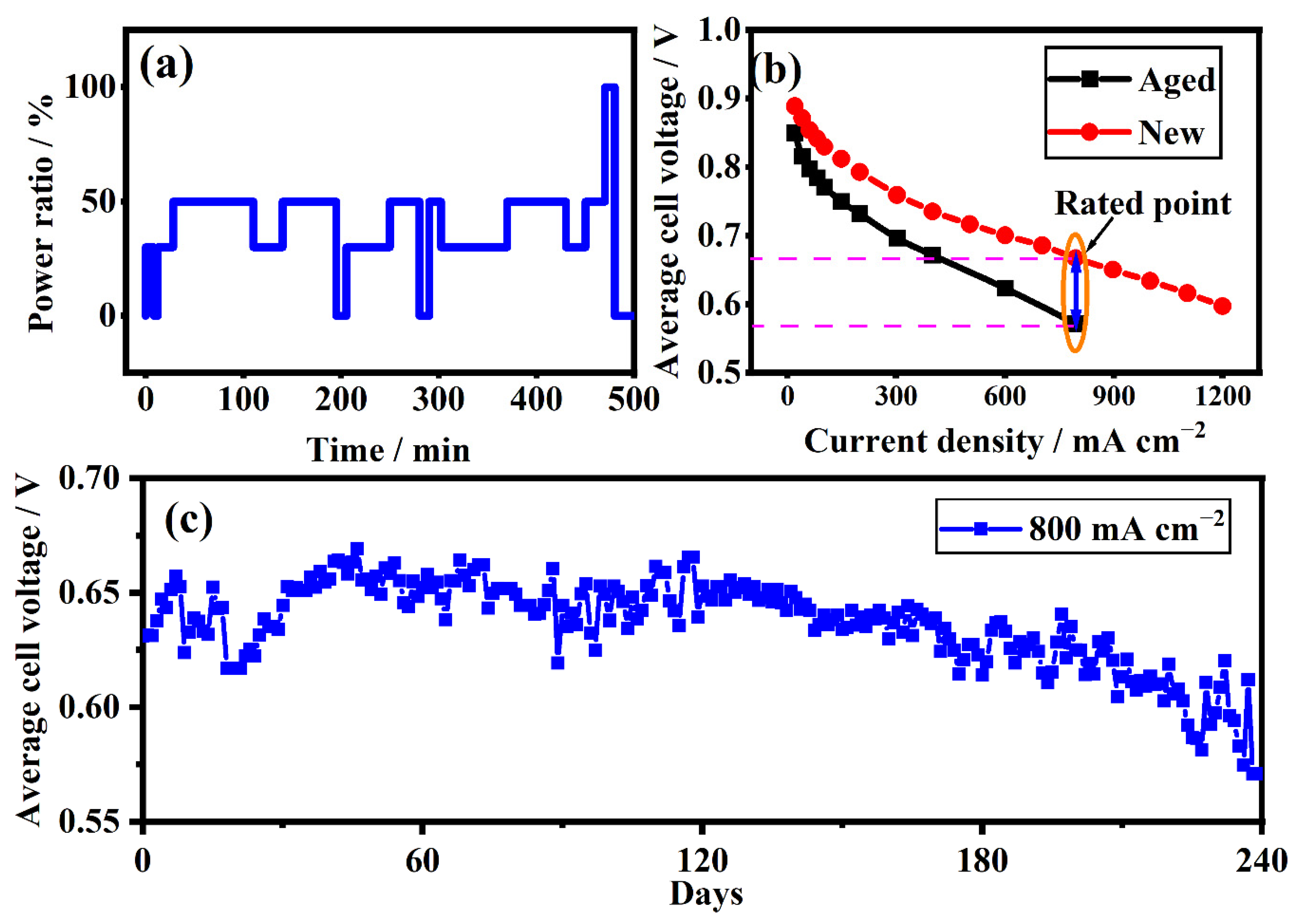
2.2. Procedure of the Experimental Test
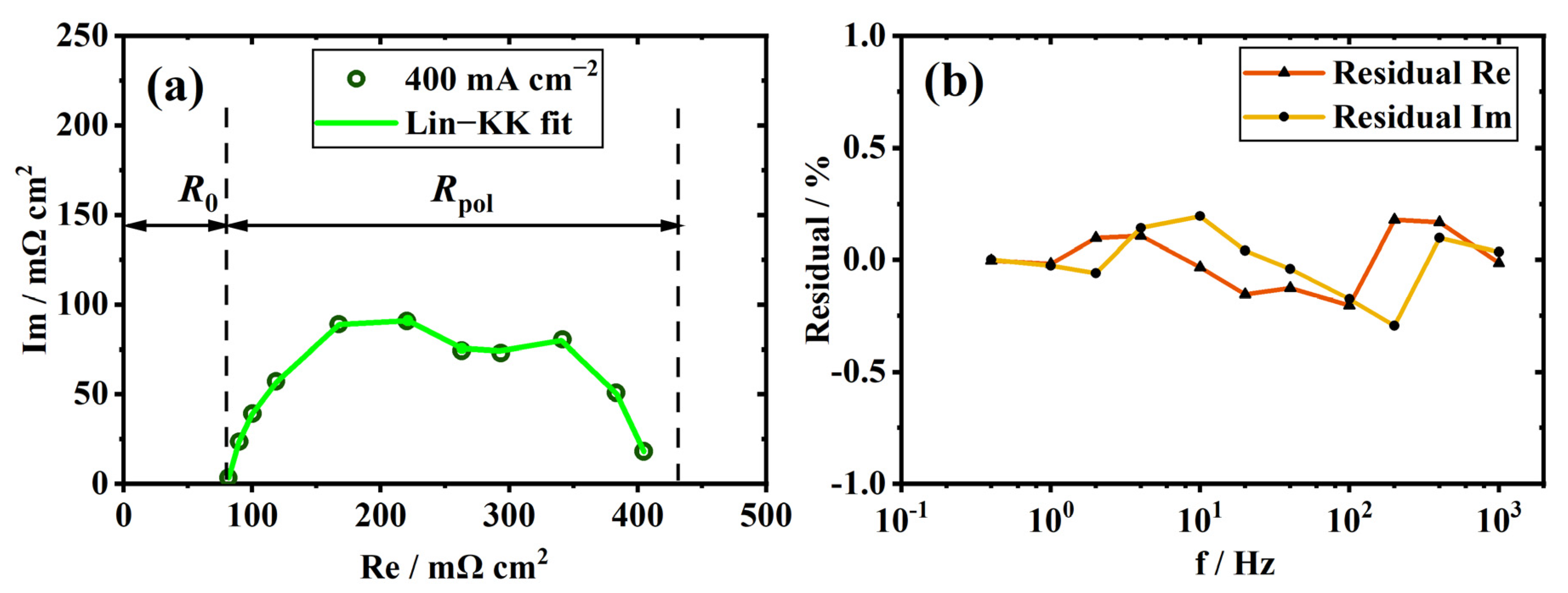
2.3. Kramers–Kronig Validity Test
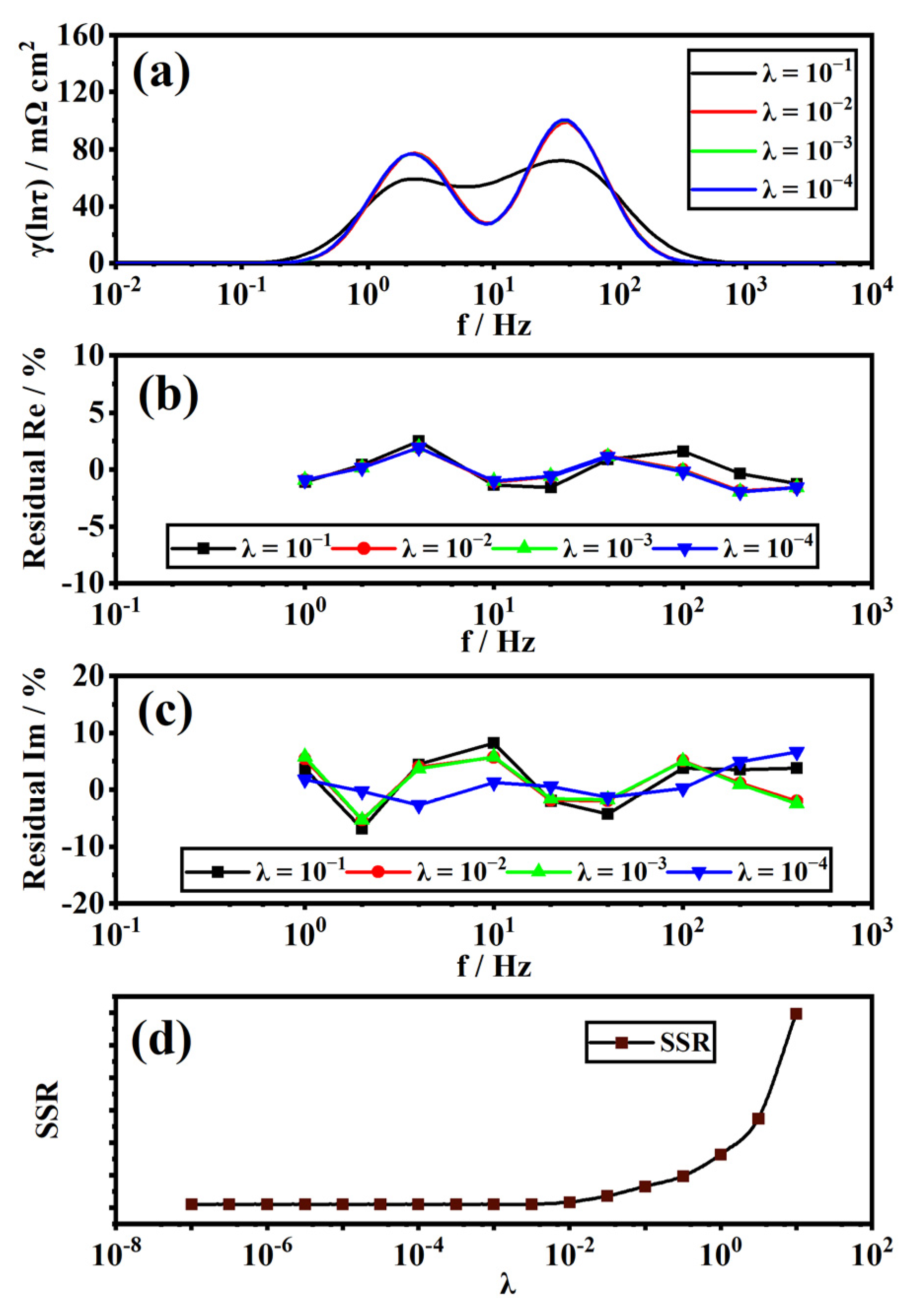
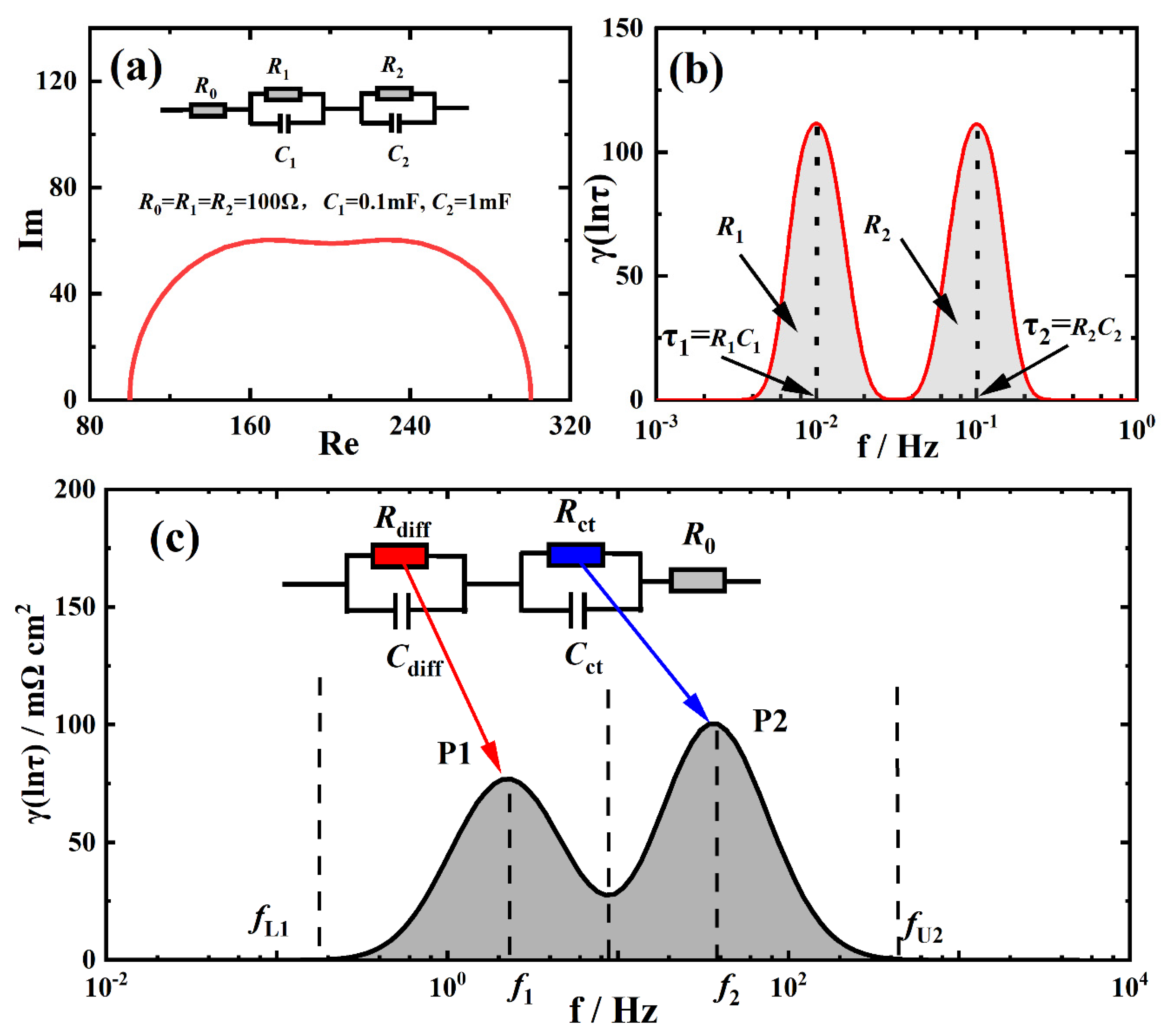
2.4. Distribution of Relaxation Times
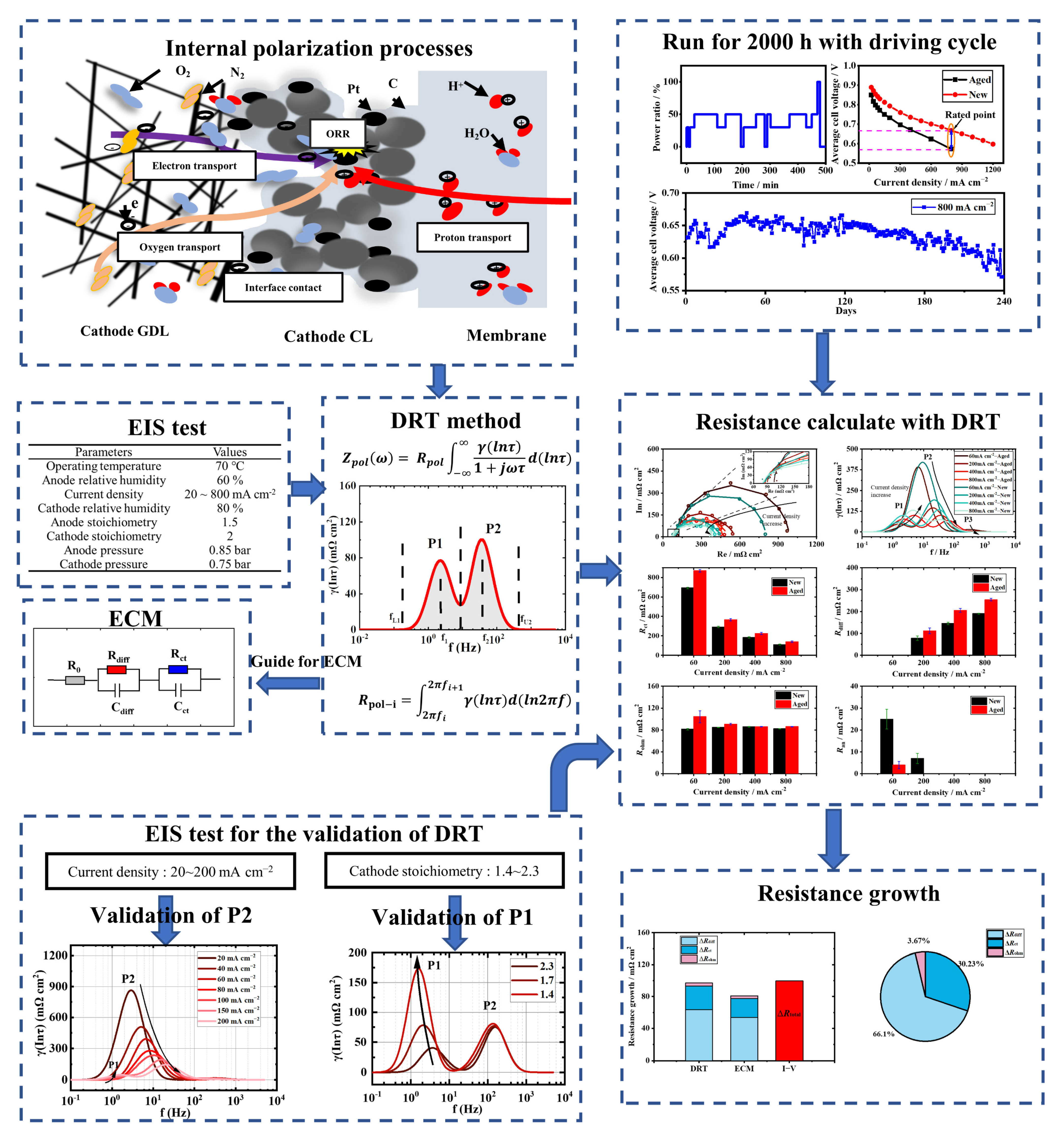
3. Results and Discussion
3.1. Validity and Analysis of Measured EIS Data
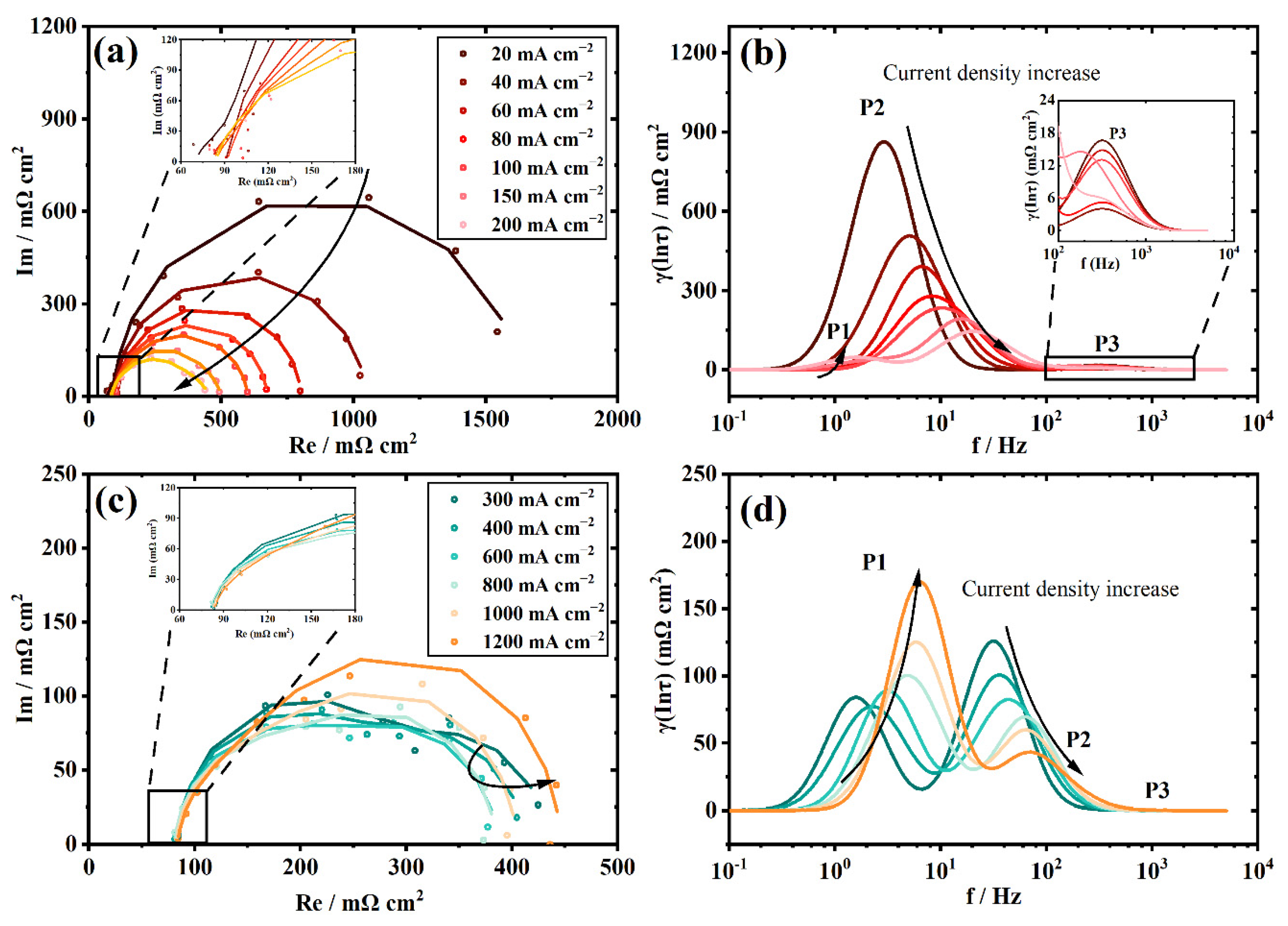
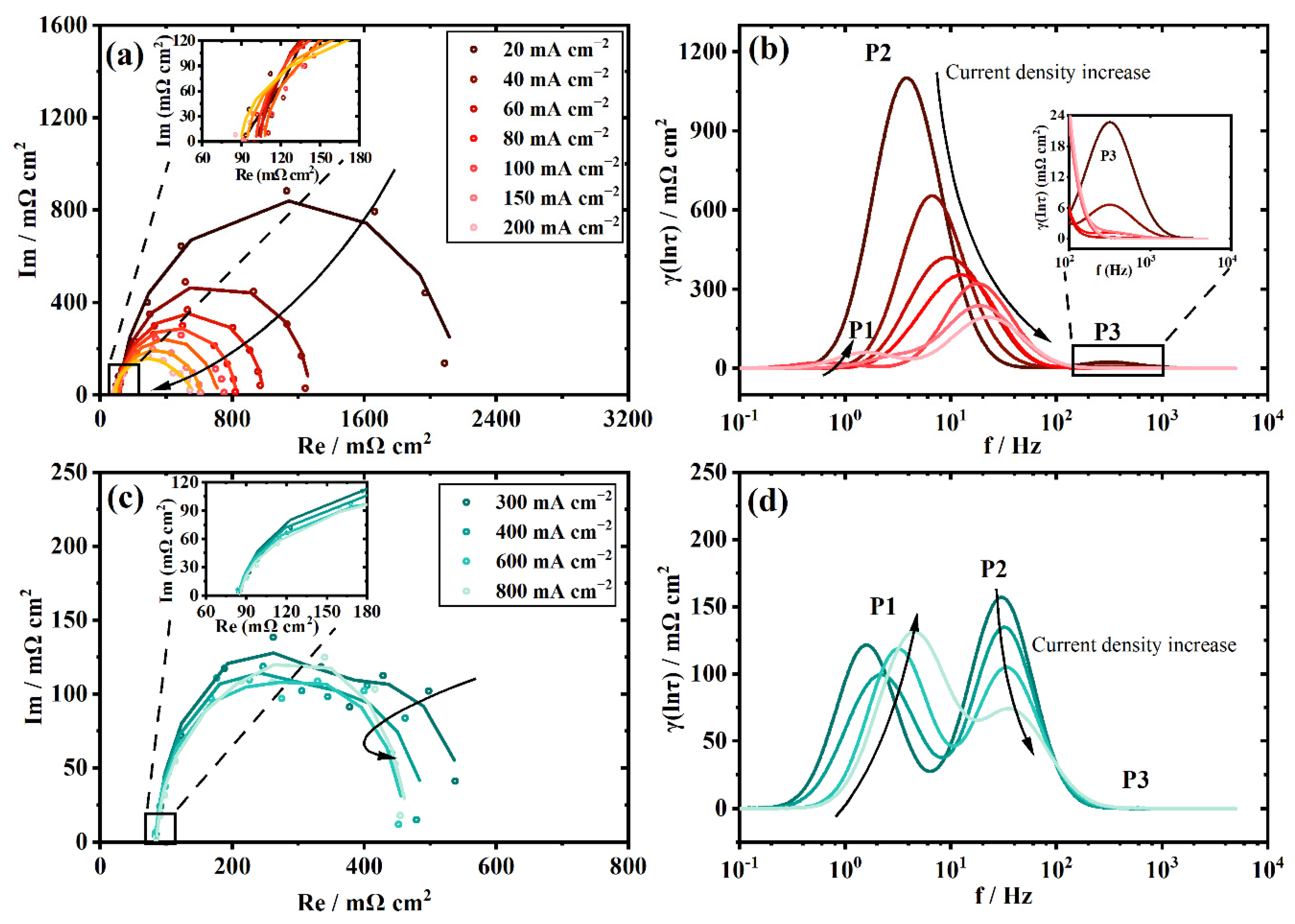
3.2. The Polarization Process Analysis of a New Stack with DRT
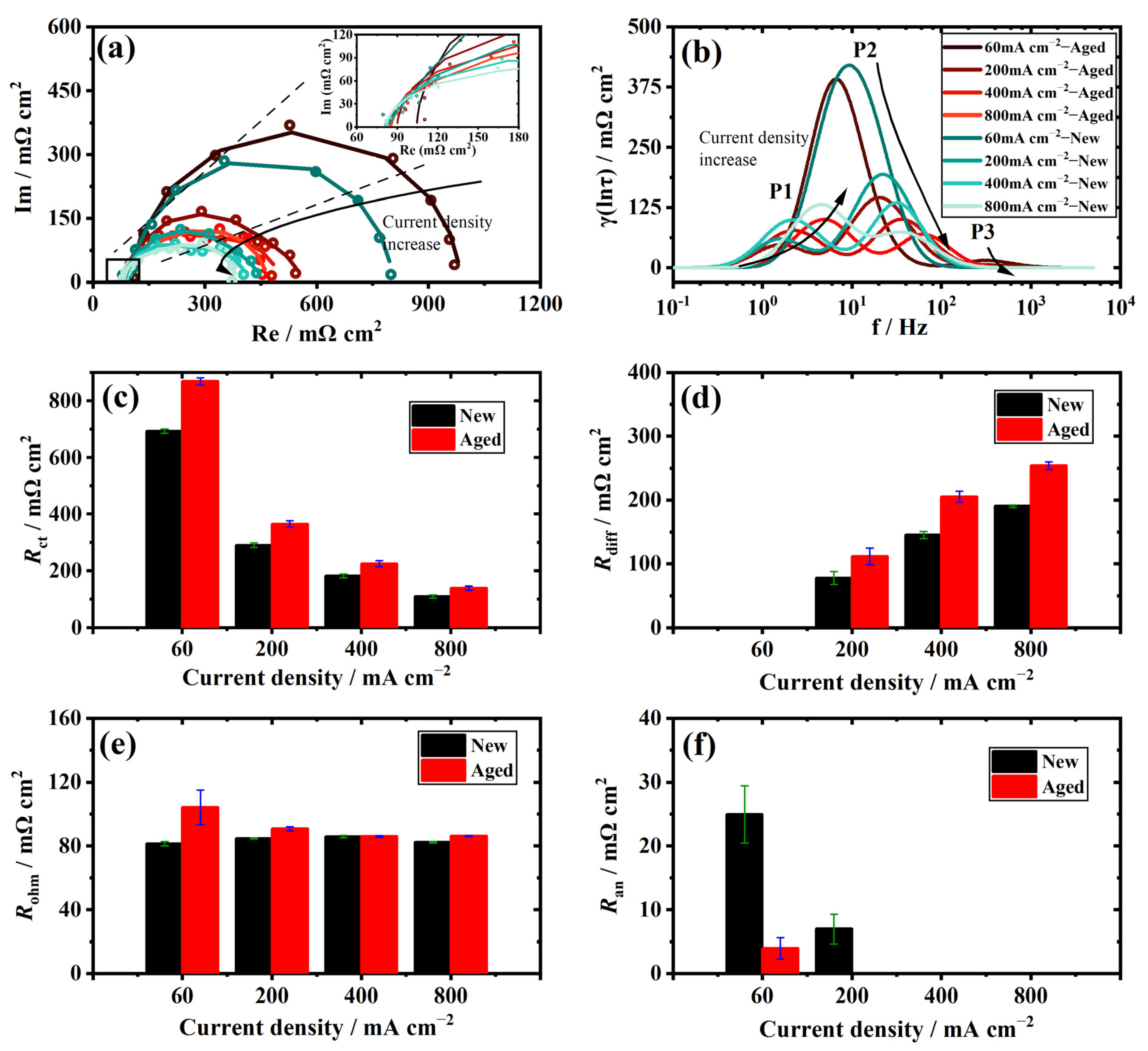
3.3. The Polarization Process Analysis of the Aged Stack with DRT
3.4. Individual Resistance Growth of the Aged Stack
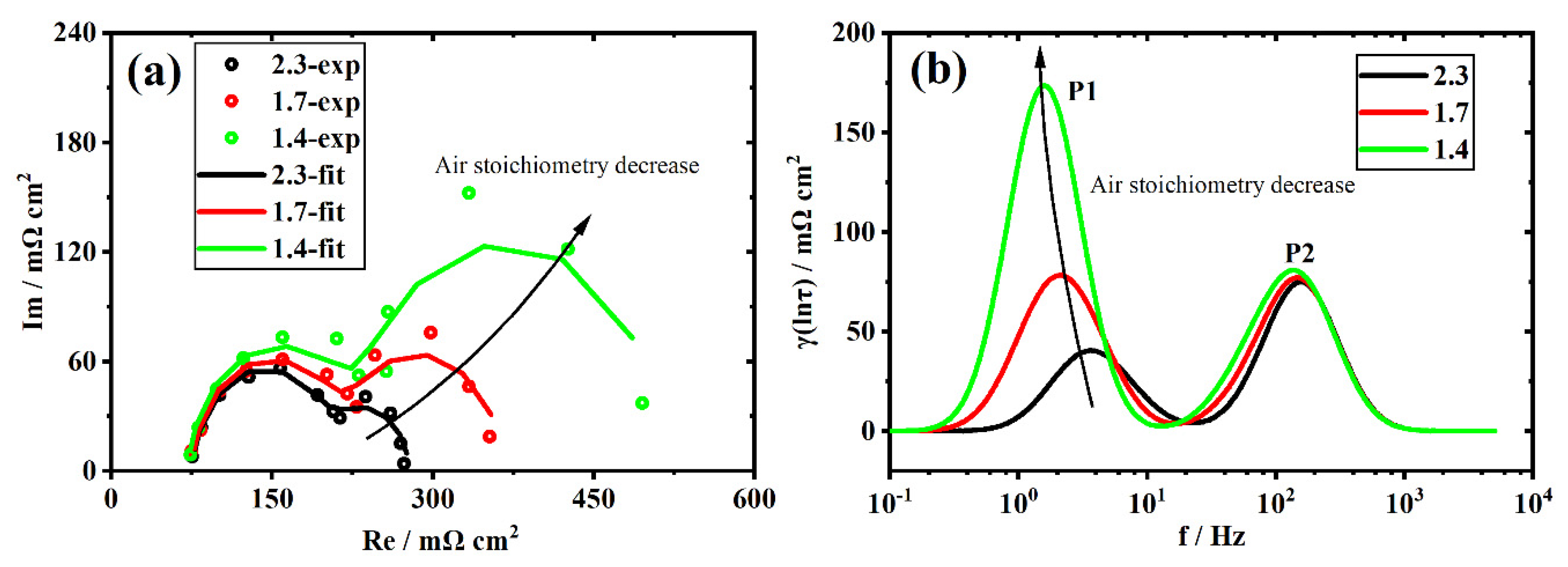
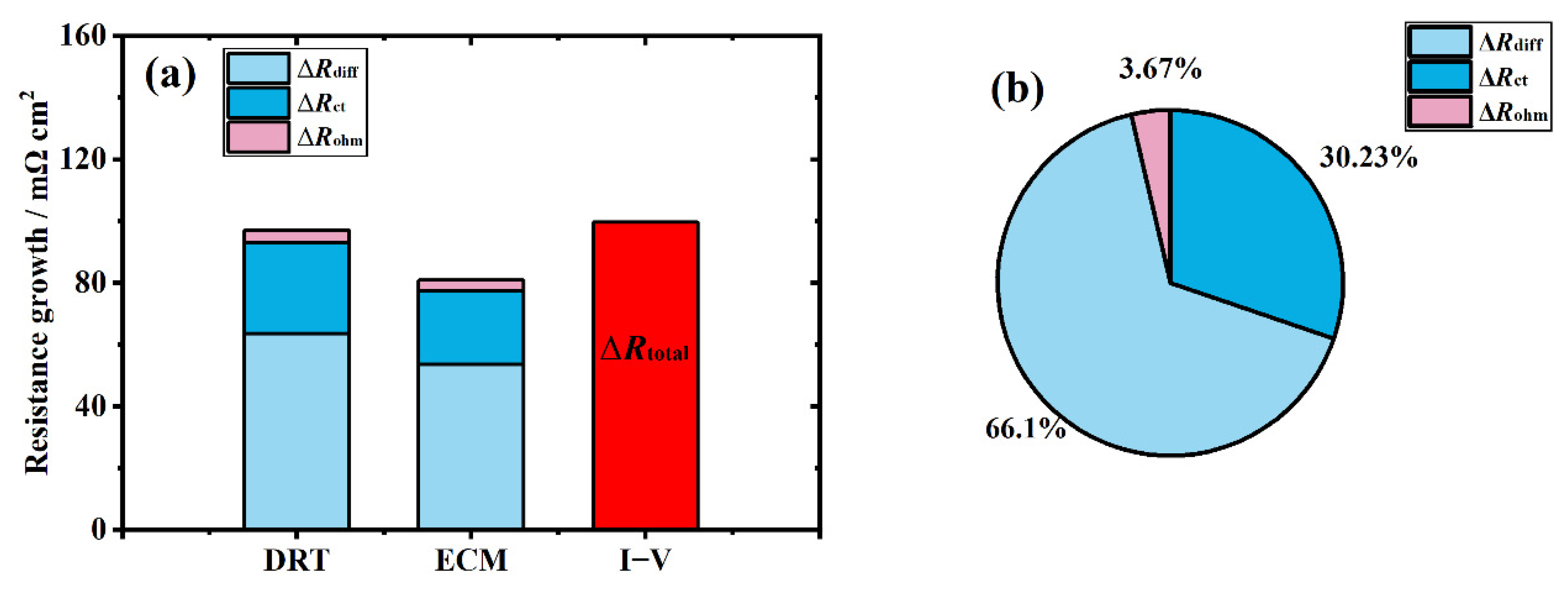
3.5. Recession Analysis of the Aged Stack
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shan, J.; Lin, R.; Xia, S.; Liu, D.; Zhang, Q. Local resolved investigation of PEMFC performance degradation mechanism during dynamic driving cycle. Int. J. Hydrog. Energy 2016, 41, 4239–4250. [Google Scholar] [CrossRef]
- Pei, P.; Chen, H. Main factors affecting the lifetime of Proton Exchange Membrane fuel cells in vehicle applications: A review. Appl. Energy 2014, 125, 60–75. [Google Scholar] [CrossRef]
- Yu, Y.; Tu, Z.; Zhang, H.; Zhan, Z.; Pan, M. Comparison of degradation behaviors for open-ended and closed proton exchange membrane fuel cells during startup and shutdown cycles. J. Power Sources 2011, 196, 5077–5083. [Google Scholar] [CrossRef]
- Al Amerl, A.; Oukkacha, I.; Camara, M.B.; Dakyo, B. Real-Time Control Strategy of Fuel Cell and Battery System for Electric Hybrid Boat Application. Sustainability 2021, 13, 8693. [Google Scholar] [CrossRef]
- Hu, D.; Wang, Y.; Li, J.; Yang, Q.; Wang, J. Investigation of optimal operating temperature for the PEMFC and its tracking control for energy saving in vehicle applications. Energy Convers Manag. 2021, 249, 114842. [Google Scholar] [CrossRef]
- Shen, J.; Xu, L.; Chang, H.; Tu, Z.; Chan, S.H. Partial flooding and its effect on the performance of a proton exchange membrane fuel cell. Energy Convers Manag. 2020, 207, 112537. [Google Scholar] [CrossRef]
- Ozden, A.; Shahgaldi, S.; Li, X.; Hamdullahpur, F. The impact of ionomer type on the morphological and microstructural degradations of proton exchange membrane fuel cell electrodes under freeze-thaw cycles. Appl. Energy 2019, 238, 1048–1059. [Google Scholar] [CrossRef]
- Yu, Y.; Li, H.; Wang, H.J.; Yuan, X.Z.; Wang, G.J.; Pan, M. A review on performance degradation of proton exchange membrane fuel cells during startup and shutdown processes: Causes, consequences, and mitigation strategies. J. Power Sources 2012, 205, 10–23. [Google Scholar] [CrossRef] [Green Version]
- Bose, A.; Babburi, P.; Kumar, R.; Myers, D.; Mawdsley, J.; Milhuff, J. Performance of individual cells in polymer electrolyte membrane fuel cell stack under-load cycling conditions. J. Power Sources 2013, 243, 964–972. [Google Scholar] [CrossRef]
- Ren, P.; Pei, P.; Li, Y.; Wu, Z.; Chen, D.; Huang, S. Degradation mechanisms of proton exchange membrane fuel cell under typical automotive operating conditions. Prog. Energy Combust. Sci. 2020, 80, 100859. [Google Scholar] [CrossRef]
- Galbiati, S.; Baricci, A.; Casalegno, A.; Marchesi, R. Degradation in phosphoric acid doped polymer fuel cells: A 6000 h parametric investigation. Int. J. Hydrog. Energy 2013, 38, 6469–6480. [Google Scholar] [CrossRef]
- Kim, J.-R.; Yi, J.S.; Song, T.-W. Investigation of degradation mechanisms of a high-temperature polymer-electrolyte-membrane fuel cell stack by electrochemical impedance spectroscopy. J. Power Sources 2012, 220, 54–64. [Google Scholar] [CrossRef]
- Lee, K.-S.; Lee, B.-S.; Yoo, S.J.; Kim, S.-K.; Hwang, S.J.; Kim, H.-J.; Cho, E.; Henkensmeier, D.; Yun, J.W.; Nam, S.W.; et al. Development of a galvanostatic analysis technique as an in-situ diagnostic tool for PEMFC single cells and stacks. Int. J. Hydrog. Energy 2012, 37, 5891–5900. [Google Scholar] [CrossRef]
- Gazdzick, P.; Mitzel, J.; Garcia Sanchez, D.; Schulze, M.; Friedrich, K.A. Evaluation of reversible and irreversible degradation rates of polymer electrolyte membrane fuel cells tested in automotive conditions. J. Power Sources 2016, 327, 86–95. [Google Scholar] [CrossRef] [Green Version]
- Cadet, C.; Jemeï, S.; Druart, F.; Hissel, D. Diagnostic tools for PEMFCs: From conception to implementation. Int. J. Hydrog. Energy 2014, 39, 10613–10626. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, T.; Chen, H.; Cao, Y. A review of online electrochemical diagnostic methods of on-board proton exchange membrane fuel cells. Appl. Energy 2021, 286, 116481. [Google Scholar] [CrossRef]
- Pavlisic, A.; Jovanovic, P.; Selih, V.S.; Sala, M.; Hodnik, N.; Gaberscek, M. Platinum Dissolution and Redeposition from Pt/C Fuel Cell Electrocatalyst at Potential Cycling. J. Electrochem. Soc. 2018, 165, F3161–F3165. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, Z.; Lin, W.; Cong, M.; Yang, Y. Impedance prediction model based on convolutional neural networks methodology for proton exchange membrane fuel cell. Int. J. Hydrog. Energy 2021, 46, 18534–18545. [Google Scholar] [CrossRef]
- Rezaei Niya, S.M.; Hoorfar, M. Study of proton exchange membrane fuel cells using electrochemical impedance spectroscopy technique—A review. J. Power Sources 2013, 240, 281–293. [Google Scholar] [CrossRef]
- Tang, Z.; Huang, Q.-A.; Wang, Y.-J.; Zhang, F.; Li, W.; Li, A.; Zhang, L.; Zhang, J. Recent progress in the use of electrochemical impedance spectroscopy for the measurement, monitoring, diagnosis and optimization of proton exchange membrane fuel cell performance. J. Power Sources 2020, 468, 228361. [Google Scholar] [CrossRef]
- Ma, T.; Lin, W.; Zhang, Z.; Kang, J.; Yang, Y. Research on electrochemical impedance spectroscope behavior of fuel cell stack under different reactant relative humidity. Int. J. Hydrog. Energy 2021, 46, 17388–17396. [Google Scholar] [CrossRef]
- Lu, H.; Chen, J.; Yan, C.; Liu, H. On-line fault diagnosis for proton exchange membrane fuel cells based on a fast electrochemical impedance spectroscopy measurement. J. Power Sources 2019, 430, 233–243. [Google Scholar] [CrossRef]
- Yuan, H.; Dai, H.; Wei, X.; Ming, P. Internal polarization process revelation of electrochemical impedance spectroscopy of proton exchange membrane fuel cell by an impedance dimension model and distribution of relaxation times. Chem. Eng. J. 2021, 418, 129358. [Google Scholar] [CrossRef]
- Rezaei Niya, S.M.; Phillips, R.K.; Hoorfar, M. Process modeling of the impedance characteristics of proton exchange membrane fuel cells. Electrochim. Acta 2016, 191, 594–605. [Google Scholar] [CrossRef] [Green Version]
- Danzer, M.A.; Hofer, E.P. Analysis of the electrochemical behaviour of polymer electrolyte fuel cells using simple impedance models. J. Power Sources 2009, 190, 25–33. [Google Scholar] [CrossRef]
- Dhirde, A.M.; Dale, N.V.; Salehfar, H.; Mann, M.D.; Han, T. Equivalent Electric Circuit Modeling and Performance Analysis of a PEM Fuel Cell Stack Using Impedance Spectroscopy. IEEE Trans. Energy Convers. 2010, 25, 778–786. [Google Scholar] [CrossRef]
- Macdonald, D.D. Reflections on the history of electrochemical impedance spectroscopy. Electrochim. Acta 2006, 51, 1376–1388. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Liaw, B.Y.; Zhang, J. Graphical analysis of electrochemical impedance spectroscopy data in Bode and Nyquist representations. J. Power Sources 2016, 309, 82–98. [Google Scholar] [CrossRef]
- Leonide, A.; Apel, Y.; Ivers-Tiffee, E. SOFC Modeling and Parameter Identification by Means of Impedance Spectroscopy. ECS Trans. 2009, 19, 81–109. [Google Scholar] [CrossRef]
- Leonide, A.; Sonn, V.; Weber, A.; Ivers-Tiffee, E. Evaluation and Modelling of the Cell Resistance in Anode Supported Solid Oxide Fuel Cells. ECS Trans. 2007, 7, 521–531. [Google Scholar] [CrossRef]
- Ivers-Tiffee, E.; Weber, A. Evaluation of electrochemical impedance spectra by the distribution of relaxation times. J. Ceram. Soc. Jpn. 2017, 125, 193–201. [Google Scholar] [CrossRef] [Green Version]
- Guo, D.; Yang, G.; Zhao, G.; Yi, M.; Feng, X.; Han, X.; Lu, L.; Ouyang, M. Determination of the Differential Capacity of Lithium-Ion Batteries by the Deconvolution of Electrochemical Impedance Spectra. Energies 2020, 13, 915. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Huang, J.; Pan, Z.; Ouyang, M. Impedance characterization of lithium-ion batteries aging under high-temperature cycling: Importance of electrolyte-phase diffusion. J. Power Sources 2019, 426, 216–222. [Google Scholar] [CrossRef]
- Kulikovsky, A. PEM fuel cell distribution of relaxation times: A method for the calculation and behavior of an oxygen transport peak. Phys. Chem. Chem. Phys. 2020, 22, 19131–19138. [Google Scholar] [CrossRef]
- Heinzmann, M.; Weber, A.; Ivers-Tiffée, E. Advanced impedance study of polymer electrolyte membrane single cells by means of distribution of relaxation times. J. Power Sources 2018, 402, 24–33. [Google Scholar] [CrossRef]
- Weiß, A.; Schindler, S.; Galbiati, S.; Danzer, M.A.; Zeis, R. Distribution of Relaxation Times Analysis of High-Temperature PEM Fuel Cell Impedance Spectra. Electrochim. Acta 2017, 230, 391–398. [Google Scholar] [CrossRef]
- Boukamp, B.A. A Linear Kronig-Kramers Transform Test for Immittance Data Validation. J. Electrochem. Soc. 1995, 142, 1885–1894. [Google Scholar] [CrossRef]
- Agarwal, P.; Crisalle, O.D.; Orazem, M.E.; Garcia-Rubio, L.H. Application of Measurement Models to Impedance Spectroscopy: II Determination of the Stochastic Contribution to the Error Structure. J. Electrochem. Soc. 1995, 142, 4149–4158. [Google Scholar] [CrossRef]
- Schönleber, M.; Ivers-Tiffée, E. Approximability of impedance spectra by RC elements and implications for impedance analysis. Electrochem. Commun. 2015, 58, 15–19. [Google Scholar] [CrossRef]
- Schönleber, M.; Klotz, D.; Ivers-Tiffée, E. A Method for Improving the Robustness of linear Kramers-Kronig Validity Tests. Electrochim. Acta 2014, 131, 20–27. [Google Scholar] [CrossRef]
- Saccoccio, M.; Wan, T.H.; Chen, C.; Ciucci, F. Optimal Regularization in Distribution of Relaxation Times applied to Electrochemical Impedance Spectroscopy: Ridge and Lasso Regression Methods—A Theoretical and Experimental Study. Electrochim. Acta 2014, 147, 470–482. [Google Scholar] [CrossRef]
- Boukamp, B.A.; Rolle, A. Analysis and Application of Distribution of Relaxation Times in Solid State Ionics. Solid State Ion. 2017, 302, 12–18. [Google Scholar] [CrossRef]
- Boukamp, B.A. Fourier transform distribution function of relaxation times; application and limitations. Electrochim. Acta 2015, 154, 35–46. [Google Scholar] [CrossRef]
- Horlin, T. Deconvolution and maximum entropy in impedance spectroscopy of noninductive systems. Solid State Ion. 1998, 107, 241–253. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Li, M.; Yan, M.; Ni, M.; Xia, C. A high-precision approach to reconstruct distribution of relaxation times from electrochemical impedance spectroscopy. J. Power Sources 2016, 308, 1–6. [Google Scholar] [CrossRef]
- Ciucci, F.; Chen, C. Analysis of Electrochemical Impedance Spectroscopy Data Using the Distribution of Relaxation Times: A Bayesian and Hierarchical Bayesian Approach. Electrochim. Acta 2015, 167, 439–454. [Google Scholar] [CrossRef]
- Wan, T.H.; Saccoccio, M.; Chen, C.; Ciucci, F. Influence of the Discretization Methods on the Distribution of Relaxation Times Deconvolution: Implementing Radial Basis Functions with DRTtools. Electrochim. Acta 2015, 184, 483–499. [Google Scholar] [CrossRef]
- Tuncer, E.; Gubanski, S.M. On dielectric data analysis—Using the Monte Carlo method to obtain relaxation time distribution and comparing non-linear spectral function fits. IEEE Trans. Dielectr. Electr. Insul. 2001, 8, 310–320. [Google Scholar] [CrossRef]
- Tesler, A.B.; Lewin, D.R.; Baltianski, S.; Tsur, Y. Analyzing results of impedance spectroscopy using novel evolutionary programming techniques. J. Electroceram. 2009, 24, 245–260. [Google Scholar] [CrossRef]
- Schlüter, N.; Ernst, S.; Schröder, U. Finding the Optimal Regularization Parameter in Distribution of Relaxation Times Analysis. ChemElectroChem 2019, 6, 6027–6037. [Google Scholar] [CrossRef] [Green Version]
- Setzler, B.P.; Fuller, T.F. A Physics-Based Impedance Model of Proton Exchange Membrane Fuel Cells Exhibiting Low-Frequency Inductive Loops. J. Electrochem. Soc. 2015, 162, F519–F530. [Google Scholar] [CrossRef]
- Roy, S.K.; Orazem, M.E.; Tribollet, B. Interpretation of Low-Frequency Inductive Loops in PEM Fuel Cells. J. Electrochem. Soc. 2007, 154, B1378. [Google Scholar] [CrossRef]
- Schiefer, A.; Heinzmann, M.; Weber, A. Inductive Low-Frequency Processes in PEMFC-Impedance Spectra. Fuel Cells 2020, 20, 499–506. [Google Scholar] [CrossRef] [Green Version]
- Kulikovsky, A.A. PEM Fuel Cell Impedance at Open Circuit. J. Electrochem. Soc. 2016, 163, F319–F326. [Google Scholar] [CrossRef] [Green Version]
- Kulikovsky, A.A.; Eikerling, M. Analytical solutions for impedance of the cathode catalyst layer in PEM fuel cell: Layer parameters from impedance spectrum without fitting. J. Electroanal. Chem. 2013, 691, 13–17. [Google Scholar] [CrossRef]
- Kim, B.; Cha, D.; Kim, Y. The effects of air stoichiometry and air excess ratio on the transient response of a PEMFC under load change conditions. Appl. Energy 2015, 138, 143–149. [Google Scholar] [CrossRef]
- Niblett, D.; Niasar, V.; Holmes, S. Enhancing the Performance of Fuel Cell Gas Diffusion Layers Using Ordered Microstructural Design. J. Electrochem. Soc. 2019, 167, 013520. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Case, S. Durability study of proton exchange membrane fuel cells under dynamic testing conditions with cyclic current profile. J. Power Sources 2006, 162, 521–531. [Google Scholar] [CrossRef]
- Wood, D.; Davey, J.; Atanassov, P.; Borup, R. PEMFC Component Characterization and Its Relationship to Mass-Transport Overpotentials during Long-Term Testing. ECS Trans. 2006, 3, 753–763. [Google Scholar] [CrossRef]
- Williams, M.V.; Kunz, H.R.; Fenton, J.M. Influence of Convection Through Gas-Diffusion Layers on Limiting Current in PEM FCs Using a Serpentine Flow Field. J. Electrochem. Soc. 2004, 151, A1617. [Google Scholar] [CrossRef]
- Yuan, H.; Dai, H.; Ming, P.; Zhao, L.; Tang, W.; Wei, X. Understanding dynamic behavior of proton exchange membrane fuel cell in the view of internal dynamics based on impedance. Chem. Eng. J. 2022, 431, 134035. [Google Scholar] [CrossRef]
- Ma, T.; Zhu, D.; Xie, J.; Lin, W.; Yang, Y. Investigation on a parking control strategy for automotive proton exchange membrane fuel cell. Fuel Cells 2021, 21, 390–397. [Google Scholar] [CrossRef]
| Parameters | Values |
|---|---|
| Specification | S2 |
| Pitch number | 216 |
| Electrochemical active area | 195 cm2 |
| Cathode/anode Pt loading | 0.4 mg cm−2/0.1 mg cm−2 |
| Rated output power of stack | 22.6 kW |
| Rated current of stack (0.67 V) | 156 A |
| Maximum output power of stack | 30.3 kW |
| Maximum current of stack (0.6 V) | 234 A |
| Working temperature | 70~80 °C |
| Bipolar plate | Metal |
| Flow field | Counter flow |
| Parameters | Values |
|---|---|
| Operating temperature | 70 °C |
| Anode relative humidity | 60% |
| Current density | 20~800 mA cm−2 |
| Cathode relative humidity | 80% |
| Anode stoichiometry | 1.5 |
| Cathode stoichiometry | 2 |
| Anode pressure | 0.85 bar |
| Cathode pressure | 0.75 bar |
| Current Density | Type | New Stack | Aged Stack | Growth Rate |
|---|---|---|---|---|
| 60 mA cm−2 | 693 mΩ cm2 | 854 mΩ cm2 | 23% | |
| 0 | 0 | - | ||
| 81.5 mΩ cm2 | 104 mΩ cm2 | 22% | ||
| 24.3 mΩ cm2 | 6 mΩ cm2 | −75% | ||
| 200 mA cm−2 | 292 mΩ cm2 | 372 mΩ cm2 | 27% | |
| 78 mΩ cm2 | 105 mΩ cm2 | 35% | ||
| 84.8 mΩ cm2 | 90 mΩ cm2 | 6% | ||
| 4.7 mΩ cm2 | 0 | - | ||
| 400 mA cm−2 | 183 mΩ cm2 | 220 mΩ cm2 | 20% | |
| 146 mΩ cm2 | 195 mΩ cm2 | 34% | ||
| 83 mΩ cm2 | 85.4 mΩ cm2 | 3% | ||
| 0 | 0 | - | ||
| 800 mA cm−2 | 109 mΩ cm2 | 139 mΩ cm2 | 28% | |
| 190 mΩ cm2 | 254 mΩ cm2 | 34% | ||
| 82 mΩ cm2 | 86 mΩ cm2 | 4% | ||
| 0 | 0 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, D.; Yang, Y.; Ma, T. Evaluation the Resistance Growth of Aged Vehicular Proton Exchange Membrane Fuel Cell Stack by Distribution of Relaxation Times. Sustainability 2022, 14, 5677. https://doi.org/10.3390/su14095677
Zhu D, Yang Y, Ma T. Evaluation the Resistance Growth of Aged Vehicular Proton Exchange Membrane Fuel Cell Stack by Distribution of Relaxation Times. Sustainability. 2022; 14(9):5677. https://doi.org/10.3390/su14095677
Chicago/Turabian StyleZhu, Dong, Yanbo Yang, and Tiancai Ma. 2022. "Evaluation the Resistance Growth of Aged Vehicular Proton Exchange Membrane Fuel Cell Stack by Distribution of Relaxation Times" Sustainability 14, no. 9: 5677. https://doi.org/10.3390/su14095677
APA StyleZhu, D., Yang, Y., & Ma, T. (2022). Evaluation the Resistance Growth of Aged Vehicular Proton Exchange Membrane Fuel Cell Stack by Distribution of Relaxation Times. Sustainability, 14(9), 5677. https://doi.org/10.3390/su14095677







