Abstract
The growth in e-commerce that our society has faced in recent years is changing the view companies have on last-mile logistics, due to its increasing impact on the whole supply chain. New technologies are raising users’ expectations with the need to develop customized delivery experiences; moreover, increasing pressure on supply chains has also created additional challenges for suppliers. At the same time, this phenomenon generates an increase in the impact on the liveability of our cities, due to traffic congestion, the occupation of public spaces, and the environmental and acoustic pollution linked to urban logistics. In this context, the optimization of last-mile deliveries is an imperative not only for companies with parcels that need to be delivered in the urban areas, but also for public administrations that want to guarantee a good quality of life for citizens. In recent years, many scholars have focused on the study of logistics optimization techniques and, in particular, the last mile. In addition to traditional optimization techniques, linked to the disciplines of operations research, the recent advances in the use of sensors and IoT, and the consequent large amount of data that derives from it, are pushing towards a greater use of big data and analytics techniques—such as machine learning and artificial intelligence—which are also in this sector. Based on this premise, the aim of this work is to provide an overview of the most recent literature advances related to last-mile delivery optimization techniques; this is to be used as a baseline for scholars who intend to explore new approaches and techniques in the study of last-mile logistics optimization. A bibliometric analysis and a critical review were conducted in order to highlight the main studied problems, the algorithms used, and the case studies. The results from the analysis allow the studies to be clustered into traditional optimization models, machine learning approaches, and mixed methods. The main research gaps and limitations of the current literature are assessed in order to identify unaddressed challenges and provide research suggestions for future approaches.
1. Introduction
Last-mile logistics is a steadily increasing phenomenon, mainly due to the ongoing urbanization and changes in consumer habits, with the strong growth in online retailing and the consequent increase in e-groceries and e-commerce activities. The most recent figures show that in the EU the share of online shoppers equaled 64% of all individuals aged 16–74 [1]. This growing pressure of freight traffic in urban areas brings with it a series of externalities that undermine the sustainability and liveability of our cities. It increases congestion and emissions in urban areas, due to the additional traffic generated by vehicles for deliveries that often have overlapping routes (25% of CO2, and 30 to 50% of PM and NOx); moreover, it reduces road safety due to the presence of heavy vehicles [2]. The restriction measures associated with the COVID-19 pandemic further accelerated the increase in online purchasing, while being a “rare catalyst” for logistic innovations [3]. However, notwithstanding the recent efforts made to improve the sustainability of the logistics, the issues related to the whole process are still debated. New technologies can play a key role in improving the impact of last-mile deliveries in urban areas. Aside from the already well-known smart technologies associated with online purchasing, the entire logistics supply chain can also take advantage of innovative processes, being a fertile ground for automation. More specifically, artificial intelligence (AI) and machine learning (ML) approaches have become a hot topic in literature and practice, and they are interfacing more and more with the traditional vehicle routing optimization (VRO) models present in the literature; their algorithms are in fact able to give exact predictions—based on historic data—on the efficiency problems common to supply chains, e.g., demand forecasting, routing, and tracking, while being able to detect anomalies during the process [4]. These algorithms are constantly evolving, and, thanks to recent disruptions, the last few years have been crucial for this research field and its development.
Based on these premises, this study presents an overview of the most recent literature advances in last-mile logistics optimization techniques, starting from the results of the SENATOR project (www.senatorproject.eu (accessed on 15 March 2022)), whose aim is to produce governance schemes on user-demand planning, transport planning, freight and logistics planning, and city infrastructure. The overview includes a bibliometric analysis and a critical review of the main studies and results presented by scholars on the subject and considers traditional VRO models, ML models, and mixed approaches. The studies were therefore classified according to the problem considered, the methodology adopted, and the case study, and the main research gaps and limitations were assessed. The final aim is to provide an overview of the topic to be considered, as a baseline for scholars who intend to explore new topics in the study of last-mile logistics optimization. The main research questions the paper is willing to answer are the following: (1) what are the most authoritative academic works to refer to in the study of urban logistics operations? (2) What problems have been investigated in the sector in recent years? (3) What are the main methods and algorithms that emerge from the analysis of these studies and to which problems are they applied?
The remainder of the paper is organized as follows. Section 2 describes the methodology adopted for the selection of the studies and their clustering. Section 3 presents the results of the analysis, both in terms of the critical review and the bibliometric analysis, and describes current limitations and gaps in the state of the art. Finally, Section 4 presents the conclusions.
2. Methodology
The methodology is based on the following steps: (i) the selection of scientific studies and clustering; (ii) the bibliometric analysis; (iii) the critical review; and (iv) the discussion.
The papers have been selected from the document “State of the art in optimization and machine learning algorithms applied to last-mile logistics” [5] developed in the SENATOR project. This analysis was published in June 2021; so, the papers published after that date are not included in the analysis. The document included a total of 165 references; for the purpose of this work, the selection of the studies was conducted considering only papers published and indexed in the Scopus database. Moreover, we excluded references which were not related to logistics. A classification of the resulting papers was conducted using the VOSviewer software. VOSviewer is a software tool for constructing and visualizing bibliometric networks, offering text mining functionality that can be used to construct and visualize networks of words extracted from a body of scientific literature [6]. The software allows the performance of a co-occurrence analysis, and this feature was used to cluster the reviewed studies in different groups according to the main keywords indicated by the authors.
The software VOSviewer was then used for a deeper bibliometric analysis of the studies, considering the citations for each document, in order to identify papers which might be considered as cornerstones, and analysing co-authorship and the authors’ scientometrics to highlight the role of the main scholars and experts in the field. A critical review was then conducted on the topics dealt with in the selected papers, in order to analyse the main problems in the studies, the methods applied, the case studies, and the efficiency of the proposed approaches. The following section describes in detail the result of the performed analyses.
3. Results
3.1. Selection of Papers
Of the 77 papers analysed, 17 are review papers, while the others are research articles. The temporal analysis in Figure 1 shows that the literature on the subject began to flourish in the early 2000s and has been growing in recent years; this is in line with the trend of city logistics.
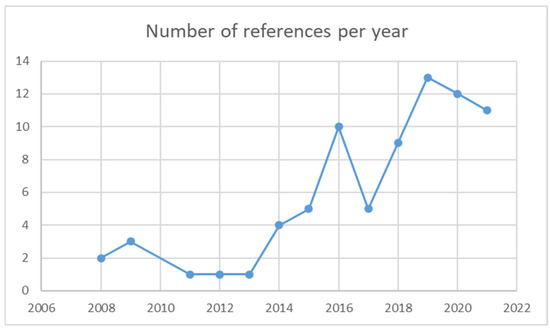
Figure 1.
Temporal analysis of publications (own elaboration).
3.2. Paper Clustering
The bibliometric network of the selected paper was then analysed through VOSviewer. The software is able to use as input a Scopus list of papers, exported in csv format. Its algorithm performs word mining of the keywords included by the authors and automatically assigned by the indexing database with a procedure called “co-occurrence”. For a first analysis, we decided to include as a unit only the authors’ keywords and set the minimum number of occurrences of a keyword to five. Of the 240 keywords, only 5 met this threshold. The five resulting words were city logistics, routing, vehicle routing, vehicle routing problem, and machine learning. In order to create a keyword network, the software computes for each keyword the total link strength, i.e., the number of publications in which two keywords occur together. The results of the co-occurrence analysis are reported in Table 1.

Table 1.
Keywords co-occurrence analysis (own elaboration from VOSviewer software results).
The results of the co-occurrence analysis allow the performance of some considerations:
- The item vehicle routing has a total link strength equal to 0; this is probably due to the presence of the full vehicle routing problem keyword.
- For the purposes of our analysis, three of the five keywords may be considered as synonyms, namely vehicle routing problem, vehicle routing, and routing.
- This leads us to consider that the three main keywords that can be considered are: city logistics, machine learning, and vehicle routing problem.
Based on these considerations, and on the fact that we are only considering papers including considerations on city logistics, we decided to consider three clusters for our analysis: Machine Learning Models, Vehicle Routing Optimization Models, and Mixed Approaches.
Citation analysis, i.e., the number of citations for each document and their related connection, was conducted through the VOSviewer software. For this analysis, we considered studies with at least 1 citation, resulting in a total of 72 papers. The citation values and the links in the selected network for the first 10 papers are reported in Table 2. It is worth noticing that, although predictable, the most cited studies are review papers.

Table 2.
Citation analysis (own elaboration from VOSviewer software results).
The largest set of connected papers in the selected network resulted in 40 items. The network of citations is reported in Figure 2; it is interesting to notice that although Figure 1 showed that the literature on the topic has been increasing in the last few years, the most cited papers within the network are the reviews dating back to before 2016. This justifies the need for a more recent study of the state of the art on the subject.
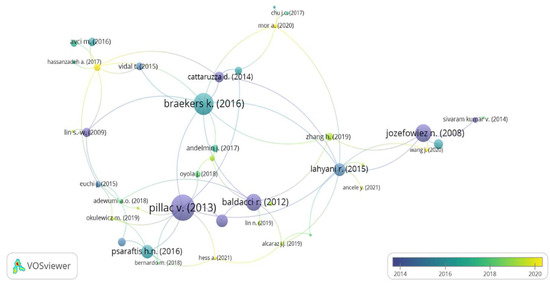
Figure 2.
Citation network (source: VOSviewer).
The software also allows the performance of a co-authorship analysis. For this analysis, we included the authors who wrote at least two of the documents in the network and were cited at least once; of the 253 authors, 17 met the threshold. In particular, only three authors have three documents within the network, and, among them, Semet F. is the most cited. Only 5 out of the 17 authors are connected to each other; the resulting network is shown in Figure 3 and Table 3. It is worth noticing that the connected authors are the most cited.
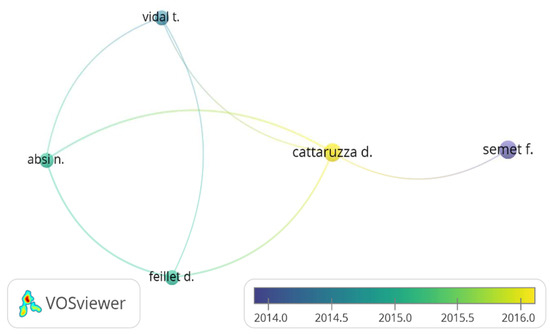
Figure 3.
Co-authorship network (source: VOSviewer).

Table 3.
Co-authorship analysis (own elaboration from VOSviewer software results).
In the following, a critical review of the selected papers, according to the three clusters, is proposed.
3.3. Critical Review
3.3.1. Machine Learning Models
ML algorithms find several research applications in logistics; the main topics that are drawn from the literature analysis are: warehouse issues, the predictions of traffic flows and demand, the supply chain process, and customer satisfaction.
Self-learning ML techniques are common in the case of the warehouse cluster. The algorithms are used to read handwritten documents and to detect frequent events. In this respect, Guermazi et al. [17] propose an entity-matching approach to validate logistics entities by matching names and addresses, using word embedding and supervised learning techniques, with good accuracy results. More recently, Bricher and Müller [18] trained deep neural networks to fully automate the control process for container logistics, allowing operators to add new container types with automatically labelled images from the observed container-routing workflow. Wojtusiak et al. [19] apply the Inferential Theory of Learning in multiagent-based simulation environments in the case of autonomous logistics to predict future traffic flows, showing that agents with learning abilities are more efficient than inexperienced agents in their tasks.
One of the applications of ML that is spreading the most in logistics is the one related to the forecasting of demand trends. This is important and needed for manufacturers (to predict production levels, e.g., [20]), transport operators (for vehicle capacity optimization), and retailers (to plan their stock) to reduce risks at an early stage of the supply chain. In 2009, Gao and Feng [21] developed a model based on support vector machine regression with a self-adaptive parameter-adjust iterative algorithm, enhancing the convergence rate and the forecasting accuracy. More recently Hess et al. [22] tested both classical forecasting and machine learning methods, adapting the models to the typical demand (intermittent with a double-seasonal pattern). With the results from the case study with a limited demand history (less than 2 months), machine learning performs better than traditional methods. Albadrani et al. [23] explored the use of k-nearest neighbours together with random forests (RF) and support vector machine (SVM) to support inbound logistics planning. Another recent work is the one by Lickert et al. [24], who proposed a set of criteria to compare supervised learning algorithms for classification tasks in reverse logistics.
Another debated issue is the one of customer satisfaction. Tamayo et al. [25] used social media content to test the public perception of city logistics, using unsupervised learning and natural language processing to perform content and sentiment analysis. The results showed that the overall view of city logistics is more positive than negative. Tian et al. [26] propose a blockchain-based evaluation approach, using the long short-term memory algorithm, with four criteria affecting customer satisfaction in urban logistics: the cargo damages rate; the on-time delivery rate; cost performance; and information transparency.
Several studies address the topic of anomaly detection (AD) in logistics. Rosen and Medvedev [27] developed an algorithm for AD in vehicle trajectories and proved its effectiveness with an application on a real dataset containing the trajectories of cargo vessels. Feng and Timmermans [28] dealt with the use of three ML algorithms (Bayesian belief network, decision tree, and random forest) to analyse anomalies in GPS traces. In 2018, Sarikan and Ozbayoglu [29] applied the k-nearest neighbour algorithm for unsupervised learning and image processing to detect vehicular flow directions; the method proved to be reliable in the case of a single-lane road. Recently, Savic et al. [30] embedded autoencoder-based AD modules into the 3GPP mobile cellular IoT architecture; they custom-designed a novel NB-IoT device platform for a smart logistics case study, where the NB-IoT devices were connected to shipping containers in a factory supply chain to collect data and deploy and test the modules, with successful AD results.
A growing demand leads to a growing request of spaces for urban logistics; a solution is the locating of consolidation centres outside the urban area to ensure the readiness of the delivery while reducing the impact of the heavy vehicle presence inside the city. El Ouadi et al. [31] developed an ML algorithm for the dimensioning of the centre, considering the proximity and logistics-demand behaviour; they applied the algorithm to experimental data, showing its usefulness.
The topic of safety and security has been addressed using ML algorithms by Zhao et al. [32], who used the generalized regression neural network (GRNN) combined with particle swarm optimization (PSO) to predict accidents and the a priori algorithm to analyse the combination of high-frequency risk factors in the whole process, including pick up, warehouse storage, transport, and the end distribution.
ML algorithms can play a key role when it comes to innovative technological solutions. In their study, Marcucci et al. [33] discussed the digital twin concept, suggesting the joint use of behavioral and simulation models within a living lab approach so as to stimulate effective, well-informed, and participated planning processes; they also forecast both behaviour and reactions to structural changes and policy measure implementations. The use of electric vehicles has been investigated by Kretzschmar et al. [34] using an ML-based range prediction model, including routing, traffic, and weather data, which is able to reproduce consumption levels (with an error level below 10%). Another explanatory example is the study of Sindhwani et al. [35], which proposes an anomaly-detection framework for a fleet of drones to perform parcel pickup and delivery tasks. The unsupervised algorithm can fit predictive flight dynamics models while identifying and discarding abnormal flight missions from the training set, outperforming alternative robust detection methods on synthetic benchmark problems.
3.3.2. Vehicle Routing Optimization Models
Optimization models have long been used in operational research and, consequently, in logistics in the travelling salesman problem (TSP) and the vehicle routing problem (VRP) [9]. The objective of the TSP is to find a route that, starting and ending at the same point, visits once every node, minimizing the total cost of the trip [36]. In addition, in the VRP the total demand of customers visited on a route should not exceed the capacity of the vehicle that performs it. Both problems are combinatorial optimization and NP-hard problems, whose optimal solution becomes computationally intractable to obtain once the size of the graph increases [8,37].
More recently, several variants of the VRP have been studied. A first class of variants is the one of the rich vehicle routing problems (RVRPs) [13], which deal with realistic optimization functions, uncertainty, dynamism, and other real-life constraints related to time, distances, and fleet size. Other models considering demand uncertainty are the ones developed by Sumalee et al. [38] and Chu et al. [39], where the actual demand is revealed at the customer location and sometimes cannot be met, so that the vehicles have to return to the depot for replenishment. These types of models are also known as VRP with split deliveries [40]. Another variant of the VRP, quite common in last-mile logistics, is the one where pick-up and delivery happen both at the depot and at the customer location [41]. Pick-up and deliveries can also be simultaneous, i.e., they are served with a single stop by the supplier [42] or through cross-dock facilities or intermediate depots [43]. In particular, last-mile logistics have increased the interest towards outsourcing and split deliveries [44,45], with the birth of VRP with outsourcing, in which a customer can be served using the owned facilities and fleet or by an external (outsourced) carrier.
Last-mile logistics usually needs a heterogeneous fleet; the heterogeneous VRP (HVRP) [46] assumes that a mixed fleet of vehicles, having distinct capacities, fixed costs, and travel costs, is used to serve a set of customers, minimizing the total costs or VRP with load-specific capacity [47], which can only accommodate one or more specific loads (e.g., multi-compartment vehicles where each compartment is dedicated to a specific type of freight). More recently, variants of the HVRP that incorporate these greener vehicles have been studied [48,49].
The stochastic VRP (SVRP) is a variant of the VRP where one or more parameters are stochastic, i.e., it incorporates uncertainty in some parameters whose value is not known, using random variables with a known probability distribution [50]. This means that routes cannot always be followed as planned and the solution cost must be minimized by taking into account an expected value. Among the SVRPs, we can find the VRP with stochastic demand, the VRP with stochastic customers, the VRP with stochastic demands and customers, and the VRP with stochastic travel and service times [50,51,52,53].
The dynamic routing of vehicles comes into play in different situations occurring in last-mile logistics (e.g., vehicle accidents and re-scheduling), and it may reduce operational costs, environmental impact, and improve customer satisfaction. The family of problems called the dynamic VRP (DVRP) takes into account the time factor, i.e., variations in services and travel times [7]; travel time is a dynamic component of most real-world applications [7,54]. The most common issue in the DVRP is the online customer requests during the operation; the DVRP models are gaining popularity due to their ability to model just-in-time supply systems and to the diffusion of recent technological advancements, such as mobile devices or sensors, that allow drivers to dynamically change their routing [54]. An interesting example is the emergence of new customers at an unknown location when the vehicles are already on route; the objective in this case is to maximize the probability that these additional customers can be served without violating time constraints [54]. A dynamism in service times is commonly related to the variation in demand [55], but it can also be attributed to the availability of resources in the customer premises [56]. A very recent, similar issue in last-mile logistics is the one related to the delivery or pick-up of small parcels in the so-called parcel locker system; examples of these types of problems can be found in Grabenschweiger et al. [57] and Orenstein et al. [58].
When solving the VRP in real-world last-mile logistics, there are several objective or performance measures which are often conflicting; in some sectors, (e.g., delivery of perishable foods) customer satisfaction and timely delivery are more important than minimizing the distance travelled. The multi-objective VRP (MOVRP) deals with these real-life instances [10,59]. Some of examples of performance measures can be the driver workload, customer satisfaction, GHG emissions, etc. [15,60]. An important difference with the classic VRP is that this family of problems has several optimal solutions, i.e., a set of non-dominated solutions called the Pareto set or Pareto front. The Pareto front is a set of non-dominated solutions which fulfil the Pareto optimality property, i.e., no individual objective can be better off without making at least one individual objective worse. Some examples of the objectives used in the MOVRP are those which are [61] tour-related, expressed in terms of total travel distance, the number of customers visited, and time needed [59,62]; resource-related, with both economic and sustainability meaning [63,64]; and node/arc-related, which imply the minimization of the violated time window constraints [65,66].
The class of algorithms used to solve the VRP variants varies with their degree of realism [14,37,67]. The classical VRP and all the subvariants are NP-hard, i.e., there is no deterministic algorithm that ensures the finding of the optimal solution for big size instances.
Several authors [11,68] used the branch-and-cut method to solve the VRPs; this is a more detailed [69], defined set of partitioning formulations that are exact methods to solve VRPs, associating a binary variable with each feasible route to search for optimal solutions. Another simple algorithm used to solve the TSP and VRPs is 2-opt, which takes a route that crosses over itself and reorders the sequence of nodes so that it avoids crossing, comparing every possible valid combination of the swapping mechanism [11].
Metaheuristics are among the most efficient approaches for VRPs, and they are strongly used in large-scale, real-life applications. Some examples of the use of metaheuristics in VRPs are reported in the following. Simulated annealing (SA) is often used when the search space is discrete (e.g., all tours that visit a given set of cities). The variable neighbourhood search is used when a change of the neighbourhood structure is needed within the search to find a local minimum [54,67]. In the ant colony optimization (ACO), a population-based metaheuristic approach, agents build solutions by moving on a graph-based representation of the problem, with a probabilistic model [70]. One of the metaheuristic approaches most commonly implemented in software libraries for the VRP is the large neighbourhood Search (LNS), in which the neighbourhood of a solution is built by “destroying and repairing” part of the solution (usually with a randomness component); the opportunity to enlarge the neighbourhoods to be visited made this method very popular in VRP solving [12,33,70,71].
More recently, hybrid metaheuristics have emerged as efficient methods to solve VRPs and the complex variants [67,72]; hybridization can be performed with metaheuristics or with other operational research or artificial intelligence techniques. Several authors used hybrid metaheuristics to solve VRP problems. In their study, [73] proposed a hybrid of metaheuristics combining simulated annealing and tabu search; the resulting effect allows movement in the solution space, which results in increasing objective function. Vidal et al. [74] combined a genetic search metaheuristic with three components of assignment, sequencing, and route evaluation. Cattaruzza et al. [60] presented a route decomposition technique for chromosome decoding and a local search to solve the multi-trip VRP with time windows and release dates. Liu et al. [75] proposed an iteration of the particle swarm algorithm and the large Neighbourhood search to escape from local optima. Avci et al. [76] developed a hybrid local search algorithm in which a non-monotone threshold adjusting strategy was integrated with tabu search. Jabir et al. [77] used ant colony optimization (ACO) integrated with the variable neighbourhood search for solving large scale instances and proposed integer linear programming models for a multi-depot vehicle routing problem. Later in 2018, Liu et al. [78] presented the hybridization of ant colony optimization and tabu search; ant colony optimization is used to search for a globally promising area, and then tabu search continues to optimize it to obtain a high-quality solution, with the initial solution of tabu search being provided by the final solution of ant colony optimization. In 2019, Hosseinabadi et al. [79] proposed a hybridization of gravitational emulation local search and the genetic algorithm (GA), using three standard benchmarks found in the literature and comparing the results with other metaheuristic algorithms, with competitive results. Lin et al. [80] created an initialization algorithm solution that combines a genetic algorithm with random components; they propose a specific crossover operator that generates feasible solutions, checks the constraints of the problem, and integrates with a neighbourhood search heuristic.
3.3.3. Mixed Approaches
A particular mention is deserved by the class of hybrid algorithms which combine metaheuristics with operational research or artificial intelligence methods. Yet, in 2009, Kheirkhahzadeh and Barforoush [81] combined a hybrid ACO algorithm for solving vehicle routing problems heuristically with an exact algorithm to improve both the performance and the quality of the solutions. Euchi et al. [82] developed an artificial ant colony based on the 2-opt to solve dynamic pickup and delivery VRPs; the success of this combination is due to the intelligent exploitation of the problem structure and in an effective interplay between the search space and the solution space, elaborating with the local search. More recently, Gutierrez-Rodríguez et al. [83] presented a method to solve VRPs with time windows, based on selecting metaheuristics via meta-learning, using a multilayer perceptron classifier for the prediction task; the experimental results show that this approach can effectively predict the best metaheuristics for each problem type.
3.4. Discussion and Lessons Learnt
Of the 77 papers analysed, 19 belong to the cluster of machine learning models and 56 to the one related to vehicle routing optimization models, and 3 propose mixed approaches. This is mainly due to the novelty of the ML approaches. More specifically, all the papers belonging to the ML cluster and to the mixed cluster can be classified as research articles, while 17 studies of the VRO cluster can be classified as review papers.
A schematization of the papers belonging to the ML cluster can be found in Table 4. In particular, it is interesting to see that the main problems analysed through the ML techniques are related to anomaly detection, forecasting, and planning. The studies mainly adopt supervised learning techniques, while only Tamayo et al. [25] and Tian et al. [26] adopt unsupervised algorithms; the case studies treated are varied, and this might be due to the novelty of the approach. There is not always a verification of the accuracy of the algorithm, which is essential as it justifies the relationship between the variables of the input data. Low accuracy is often due to the lack of additional data, the unwanted presences of outliers in the training samples, or the wrong selection of features. Industrial AI applications today yield accuracy values of 99% and above to meet especially high safety demands.
Table 5 shows the articles belonging to the VRO cluster. The methods used are mostly metaheuristics, often of their own elaboration, or well-known optimization algorithms, in particular PSO, ACO, LNS, MIP, and GA. The case studies are mainly the synthetic ones, which are usually analysed in the traditional literature on the VRP. The innovative use of algorithms or their own ones are often compared with the existing ones to verify their effectiveness.
The three articles proposing hybrid approaches [81,82,83] all deal with variants of the VRP problem and analyse synthetic case studies.
Finally, as already mentioned, the 17 review papers all deal with the topic of the VRP. While some articles provide an overview of the generic approach [8,9,67], others deal with specific problems. Some examples are those of Baldacci et al. [11], who analyse the variants of the VRP under capacity and time-window constraints; Costa et al. [68], who focus on branch-price-and-cut algorithms; and Jozefowiez et al. [1], who focus on MOVRP. The literature on the DVRP is reviewed by Pillac et al. [7] and Psaraftis et al. [12], while the SVRP is the core of the overviews conducted by Berhan et al. [50] and Oyola et al. [45,46]; finally, Caceres-Cruz et al. [14], Goel et al. [72], and Lahyani et al. [13] conduct a deep analysis of the RVRP studies.

Table 4.
Articles belonging to the ML cluster (source: own elaboration).
Table 4.
Articles belonging to the ML cluster (source: own elaboration).
| Problem | Author | Method/Algorithm | Case Study | Efficiency Highlights |
|---|---|---|---|---|
| Anomaly Detection | Feng and Timmermans, 2015 [28] | Bayesian belief network, Decision Tree, RF | Trip purposes by GPS traces | Accuracy >96% |
| Rosen and Medvedev, 2012 [27] | Own elaboration | Trajectories of freight ships | - | |
| Sarikan and Ozbayoglu, 2018 [29] | K-nearest neighbour | Vehicular flow directions | Reliable in the case of a single- lane road | |
| Savic et al., 2021 [30] | Deep Learning | Container-carrying vehicles | Autoencoders are adequate for IoT | |
| Sindhwani et al., 2020 [35] | Own elaboration | Drones flight | Successfully filters out anomalies from the training set | |
| Classification Tasks | Lickert et al., 2021 [24] | Supervised Learning | Reverse Logistics | - |
| Demand Forecasting | Gao and Feng, 2009 [21] | SVM and Radial Basis Function Neural Network | Synthetic | SVM has higher stability |
| Hess et al., 2021 [22] | RF and Support Vector Regression | Urban delivery platform | Min accuracy >70% | |
| Wojtusiak et al., 2012 [19] | Inferential Theory of Learning | Autonomous logistics | - | |
| Entity matching | Bricher and Müller, 2020 [18] | Deep Neural Network | Container labelling | - |
| Guermazi et al., 2020 [7] | Word Embedding and Supervised Learning | Validate logistics entities | - | |
| Forecasting | Albadrani et al., 2021 [23] | K-nearest neighbours, RF, SVM | Inbound logistics | Accuracy >96% |
| Kretzschmar et al., 2016 [34] | Own elaboration | E-vehicles | - | |
| Multicriteria analysis | Tian et al., 2021 [26] | Long Short-Term Memory | Customer satisfaction | Blockchain into sustainability in urban logistics |
| Planning | Knoll et al., 2016 [20] | Framework | Inbound logistics | - |
| Marcucci et al., 2020 [33] | Framework | Digital Twins | - | |
| El Ouadi et al., 2020 [31] | Hybrid ML | Dimensioning of UCC | Close to 100% | |
| Risk analysis | Zhao et al., 2020 [32] | GRNN, PSO | Safe operation of urban logistics | Accuracy = 80% |
| Sentiment analysis | Tamayo et al., 2020 [25] | Unsupervised Learning, Natural Language Processing | Opinions on city logistics | Positive feelings |

Table 5.
Articles belonging to the VRO cluster (source: own elaboration).
Table 5.
Articles belonging to the VRO cluster (source: own elaboration).
| Problem | Author | Method/Algorithm | Case Study | Efficiency Highlights |
|---|---|---|---|---|
| Capacitated VRP | Hosseinabadi et al., 2019 [79] | Gravitational Emulation Local Search and GA | Synthetic | Competitive with existing algorithms |
| DVRP | Grabenschweiger et al., 2021 [57] | Own elaboration | Parcel locker | - |
| Liu et al., 2019 [55] | Stochastic predictive control | Demand uncertainty | Small- up to medium-scale real-world routing problems | |
| Okulewicz and Mańdziuk, 2019 [54] | PSO and Differential Evolution (DE), discrete encoding utilizing GA | Demand uncertainty | Both PSO and DE outperform GA | |
| Orenstein et al., 2019 [58] | Savings heuristic, petal method and tabu search | Parcel locker | Outperforms existing algorithms | |
| Yan et al., 2019 [56] | MIP and dynamic neighbourhood search | Variation in supply | - | |
| MOVRP | Cattaruzza et al., 2016 [60] | Hybrid metaheuristics | City distribution centres | Competitive with existing algorithms |
| Cattaruzza et al., 2014 [15] | Memetic algorithm | Synthetic | Outperforms existing algorithms | |
| Ganji et al., 2020 [63] | PSO, Non-dominated Sorting GA II, and ACO | Supply chain scheduling | NSGAII outperforms PSO and ACO | |
| Hassanzadeh and Rasti-Barzoki, 2017 [64] | Own elaboration | Supply chain scheduling | Outperforms other algorithms | |
| Qin et al., 2019 [66] | Own elaboration | Cold chain logistics | - | |
| Sivaram Kumar et al., 2018 [62] | Fitness Aggregated Genetic Algorithm (FAGA) | Synthetic | - | |
| Wang et al., 2016 [42] | Multi-objective local search (MOLS) and multi-objective memetic algorithm (MOMA) | Reverse logistics | MOLS outperforms MOMA | |
| Wang et al., 2020 [59] | Own elaboration | Synthetic | Outperforms existing algorithms | |
| Zhang et al., 2019 [65] | ACO | Synthetic and real case (food distribution logistics) | Competitive with existing algorithms | |
| Periodic inventory RP | Liu et al., 2016 [75] | PSO and LNS | Synthetic | Outperforms existing algorithms |
| RVRP | Alcaraz et al., 2019 [44] | Own elaboration | Synthetic | - |
| Ancele et al., 2021 [43] | SA | Synthetic | - | |
| Chu et al., 2017 [39] | Two-stage heuristic solution | Demand uncertainty | - | |
| Gu et al., 2019 [40] | LNS | Split deliveries | Competitive with existing algorithms | |
| Jabir et al., 2017 [77] | ACO, Variable Neighbourhood Search, and Integer Linear Programming | Multi-depot | Solves both small- and large-scale problem instances in reasonable amount of time | |
| Sumalee et al., 2011 [38] | Stochastic multi-modal network model | Demand uncertainty | - | |
| SVRP | Bernardo et al., 2018 [51] | Sampling strategies | Synthetic | - |
| Two-echelon VRP | Caggiani et al., 2021 [49] | MILP model | Use of green modes | - |
| Grangier, et al., 2016 [16] | LNS | Synthetic | - | |
| VRP | Andelmin and Bartolini, 2017 [69] | Own elaboration | Synthetic | Instances with up to ∼110 customers |
| Avci et al., 2016 [76] | Hybrid metaheuristics | Reverse logistics | Competitive with existing algorithms | |
| Baller et al., 2020 [45] | Own elaboration | Synthetic | - | |
| Ghilas et al., 2016 [71] | LNS | Pickup and delivery with time windows | High-quality routing solutions for relatively large instances in a reasonable amount of time | |
| Lagos et al., 2018 | PSO | Reverse logistics | Competitive with existing algorithms | |
| Lin et al., 2009 [73] | SA and Tabu Search | Synthetic | Competitive with existing algorithms | |
| Lin et al., 2019 [80] | Hybrid metaheuristics | Synthetic | - | |
| Liu et al., 2018 [78] | ACO and Tabu Search | Cold-chain products (compatibility constraints) | Instances with up to 80 customers and 10 good types | |
| Mavrovouniotis and Yang, 2015 [70] | ACO | Synthetic | Immigrants schemes improve the performance of ACO | |
| Sivaram Kumar et al., 2014 [61] | Fitness Aggregated Genetic Algorithm (FAGA) | Synthetic | Competitive with existing algorithms | |
| Vidal et al., 2015 [74] | Hybrid metaheuristics | Synthetic | Pre-processing phase may become time-consuming for instances with large clusters |
4. Limitation of the Study and Future Research
The analysis conducted does not claim to be fully inclusive of all the studies relating to urban logistics in recent years; it gives, rather, a baseline for the definition of the state of the art on operations relating to urban logistics, with the aim of answering the three research questions defined in Section 1. The study, therefore, has some unavoidable limitations. The most evident is related to the need to refer only to works already published and indexed, in particular those on the Scopus database. As already detailed in Section 2, the analysis refers to studies published and indexed before June 2021. This does not exclude the potential existence of new authoritative studies that can be identified in subsequent analyses (see, e.g., [84,85]), bearing in mind the rapid evolution of the scientific publications related to this topic. From the analysis conducted, it emerges that future research still has room to focus on improving the efficiency of existing algorithms but, above all, on the application of the methods based on artificial intelligence and machine learning to improve the automation of logistics operation.
5. Conclusions
In recent years, we have been witnessing an increase in the phenomenon of urban logistics, mainly due to the digitization of purchases and the consequent increase in online sales. However, last-mile logistics brings with it various externalities, and scholars and companies are always looking for solutions to improve their efficiency, both by relying on traditional methods and by resorting to recently developed methodologies, linked to artificial intelligence. This study offers an overview of the main scientific approaches proposed by scholars in recent years for improving the performance of urban logistics, focusing, on the one hand, on traditional techniques related to operational research and, on the other, on new methodologies related to machine learning.
The results of the review of the main published and indexed articles show an increase in research in the sector in the last few years. In particular, the main techniques used in the case of the ML approaches include supervised learning, with a variety of case studies analysed. Particular attention is paid to the problems of demand forecasting and anomaly detection. The analysis paves the way for the development and testing of innovative unsupervised learning techniques for last-mile logistics.
The classic optimization techniques linked to operational research focus on the VRP and its variants, with particular attention to the issues of demand forecasting, reverse logistics, and the multimodal fleet. Moreover, the review shows that new models have been developed that adapt the classic models to real problems and that most of the case studies focus on urban last-mile logistics. It can be seen that due to high customer demand and the need to improve environmental quality in cities, there is a tendency to create collaborative models between logistics operators, which is one of the main challenges in last-mile logistics today.
Although the manuscript cannot be considered a systematic literature review as it does not include all the potential sources, it can be considered a baseline publication for other authors who want to further develop research on the topic.
In summary, the analysis conducted can help to identify the best methods and algorithms to be applied for each problem and case study and can serve as a basis for future studies aiming at developing innovative solutions in last-mile logistics.
Author Contributions
Conceptualization, N.G., J.F.-C., A.D.M., F.W., M.S. and F.P.; methodology, N.G., J.F.-C., A.D.M., F.W., M.S. and F.P.; software, N.G.; data curation, N.G., J.F.-C., A.D.M., F.W., M.S. and F.P.; writing—original draft preparation, N.G., J.F.-C., A.D.M., F.W., M.S. and F.P.; writing—review and editing, N.G., J.F.-C., A.D.M., F.W., M.S. and F.P. All authors have read and agreed to the published version of the manuscript.
Funding
This article was partially funded by the European Commission through the SENATOR project (H2020MG-2018-2020, RIA, project n. 861,540).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be available from the corresponding author upon request.
Acknowledgments
The authors would like to thank the contributions of the different partners of the SENATOR project (https://www.senatorproject.eu/ (accessed on 15 March 2022)).
Conflicts of Interest
The authors declare no conflict of interest.
References
- EC. E-Commerce Statistics for Individuals. 2021. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php/E-commerce_statistics_for_individuals (accessed on 15 March 2022).
- Interreg Europe. Sustainable Urban Logistics. A Policy Brief from the Policy Learning Platform on Low-Carbon Economy. 2020. Available online: http://www.interregeurope.eu/fileadmin/user_upload/plp_uploads/policy_briefs/Sustainable_urban_logistics.pdf (accessed on 15 March 2022).
- DHL. Logistics Trend Radar 5th Edition. 2021. Available online: https://www.dhl.com/global-en/home/insights-and-innovation/insights/logistics-trend-radar.html (accessed on 15 March 2022).
- Zhao, M.; Ji, S.; Wei, Z. Risk prediction and risk factor analysis of urban logistics to public security based on PSO-GRNN algorithm. PLoS ONE 2020, 15, e0238443. [Google Scholar] [CrossRef] [PubMed]
- SENATOR, 2021. [D2.1] State of the Art in Optimization and Machine Leaning Algorithms Applied to Last Mile Logistics. Available online: https://www.senatorproject.eu/wp-content/uploads/2021/10/D2.1-SotA-in-optimization-and-machine-leaning-algorithms-applied-to-last-mile-logistics-Public.pdf (accessed on 19 February 2022).
- Van Eck, N.J.; Waltman, L. Text mining and visualization using VOSviewer. ISSI Newsl. 2011, 7, 50–54. [Google Scholar]
- Pillac, V.; Gendreau, M.; Guéret, C.; Medaglia, A.L. A review of dynamic vehicle routing problems. Eur. J. Oper. Res. 2013, 225, 1–11. [Google Scholar] [CrossRef]
- Braekers, K.; Ramaekers, K.; Van Nieuwenhuyse, I. The vehicle routing problem: State of the art classification and review. Comput. Ind. Eng. 2016, 99, 300–313. [Google Scholar] [CrossRef]
- Golden, B.L.; Raghavan, S.; Wasil, E.A. The Vehicle Routing Problem: Latest Advances and New Challenges; Springer: New York, NY, USA, 2008. [Google Scholar]
- Jozefowiez, N.; Semet, F.; Talbi, E.G. Multi-objective vehicle routing problems. Eur. J. Oper. Res. 2008, 189, 293–309. [Google Scholar] [CrossRef]
- Baldacci, R.; Mingozzi, A.; Roberti, R. Recent exact algorithms for solving the vehicle routing problem under capacity and time window constraints. Eur. J. Oper. Res. 2012, 218, 1–6. [Google Scholar] [CrossRef]
- Psaraftis, H.N.; Wen, M.; Kontovas, C.A. Dynamic vehicle routing problems: Three decades and counting. Networks 2016, 67, 3–31. [Google Scholar] [CrossRef]
- Lahyani, R.; Khemakhem, M.; Semet, F. Rich vehicle routing problems: From a taxonomy to a definition. Eur. J. Oper. Res. 2015, 241, 1–14. [Google Scholar] [CrossRef]
- Caceres-Cruz, J.; Arias, P.; Guimarans, D.; Riera, D.; Juan, A.A. Rich vehicle routing problem: Survey. ACM Comput. Surv. 2014, 47, 1–28. [Google Scholar] [CrossRef]
- Cattaruzza, D.; Absi, N.; Feillet, D.; Vidal, T. A memetic algorithm for the Multi Trip Vehicle Routing Problem. Eur. J. Oper. Res. 2014, 236, 833–848. [Google Scholar] [CrossRef]
- Grangier, P.; Gendreau, M.; Lehuédé, F.; Rousseau, L.M. An adaptive large neighborhood search for the two-echelon multiple-trip vehicle routing problem with satellite synchronization. Eur. J. Oper. Res. 2016, 254, 80–91. [Google Scholar] [CrossRef]
- Guermazi, Y.; Sellami, S.; Boucelma, O. Address Validation in Transportation and Logistics: A Machine Learning Based Entity Matching Approach. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Ghent, Belgium, 14–18 September 2020; Springer: Cham, Switzerland, 2020; pp. 320–334. [Google Scholar]
- Bricher, D.; Müller, A. A Supervised Machine Learning Approach for Intelligent Process Automation in Container Logistics. J. Comput. Inf. Sci. Eng. 2020, 20, 031006. [Google Scholar] [CrossRef]
- Wojtusiak, J.; Warden, T.; Herzog, O. Machine learning in agent-based stochastic simulation: Inferential theory and evaluation in transportation logistics. Comput. Math. Appl. 2012, 64, 3658–3665. [Google Scholar] [CrossRef]
- Knoll, D.; Prüglmeier, M.; Reinhart, G. Predicting future inbound logistics processes using machine learning. Procedia CIRP 2016, 52, 145–150. [Google Scholar] [CrossRef]
- Gao, M.; Feng, Q. Modeling and Forecasting of Urban Logistics Demand Based on Support Vector Machine. In Proceedings of the 2009 Second International Workshop on Knowledge Discovery and Data Mining, Moscow, Russia, 23–25 January 2009; pp. 793–796. [Google Scholar]
- Hess, A.; Spinler, S.; Winkenbach, M. Real-time demand forecasting for an urban delivery platform. Transp. Res. Part E Logist. Transp. Rev. 2021, 145, 102147. [Google Scholar] [CrossRef]
- Albadrani, A.; Alghayadh, F.; Zohdy, M.A.; Aloufi, E.; Olawoyin, R. Performance and Predicting of Inbound Logistics Processes Using Machine Learning. In Proceedings of the 2021 IEEE 11th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 27–30 January 2021; pp. 790–795. [Google Scholar]
- Lickert, H.; Wewer, A.; Dittmann, S.; Bilge, P.; Dietrich, F. Selection of Suitable Machine Learning Algorithms for Classification Tasks in Reverse Logistics. Procedia CIRP 2021, 96, 272–277. [Google Scholar] [CrossRef]
- Tamayo, S.; Combes, F.; Gaudron, A. Unsupervised machine learning to analyze City Logistics through Twitter. Transp. Res. Procedia 2020, 46, 220–228. [Google Scholar] [CrossRef]
- Tian, Z.; Zhong, R.Y.; Vatankhah Barenji, A.; Wang, Y.T.; Li, Z.; Rong, Y. A blockchain-based evaluation approach for customer delivery satisfaction in sustainable urban logistics. Int. J. Prod. Res. 2021, 59, 2229–2249. [Google Scholar] [CrossRef]
- Rosen, O.; Medvedev, A. An on-line algorithm for anomaly detection in trajectory data. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 1117–1122. [Google Scholar]
- Feng, T.; Timmermans, H.J.P. Detecting activity type from GPS traces using spatial and temporal information. Eur. J. Transp. Infrastruct. Res. 2015, 15, 662–674. [Google Scholar] [CrossRef]
- Sarikan, S.S.; Ozbayoglu, A.M. Anomaly detection in vehicle traffic with image processing and machine learning. Procedia Comput. Sci. 2018, 140, 64–69. [Google Scholar] [CrossRef]
- Savic, M.; Lukic, M.; Danilovic, D.; Bodroski, Z.; Bajovic, D.; Mezei, I.; Vukobratovic, D.; Skrbic, S.; Jakovetic, D. Deep Learning Anomaly Detection for Cellular IoT with Applications in Smart Logistics. IEEE Access 2021, 9, 59406–59419. [Google Scholar] [CrossRef]
- El Ouadi, J.; Errousso, H.; Benhadou, S.; Medromi, H.; Malhene, N. A Machine-Learning Based Approach for Zoning Urban Area in Consolidation Schemes Context. In Proceedings of the 2020 IEEE 13th International Colloquium of Logistics and Supply Chain Management (LOGISTIQUA), Fez, Morocco, 2–4 December 2020; pp. 1–7. [Google Scholar]
- Zhao, S.; Sheng, Y.; Dong, Y.; Chang, E.I.; Xu, Y. Maskflownet: Asymmetric feature matching with learnable occlusion mask. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 6278–6287. [Google Scholar]
- Marcucci, E.; Gatta, V.; Le Pira, M.; Hansson, L.; Bråthen, S. Digital Twins: A Critical Discussion on Their Potential for Supporting Policy-Making and Planning in Urban Logistics. Sustainability 2020, 12, 10623. [Google Scholar] [CrossRef]
- Kretzschmar, J.; Gebhardt, K.; Theiß, C.; Schau, V. Range prediction models for e-vehicles in urban freight logistics based on machine learning. In International Conference on Data Mining and Big Data, Bali, Indonesia, 25–30 June 2016; Springer: Cham, Switzerland, 2016; pp. 175–184. [Google Scholar]
- Sindhwani, V.; Sidahmed, H.; Choromanski, K.; Jones, B. Unsupervised Anomaly Detection for Self-flying Delivery Drones. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 186–192. [Google Scholar]
- Mor, A.; Speranza, M.G. Vehicle routing problems over time: A survey. 4OR 2020, 18, 129–149. [Google Scholar] [CrossRef]
- Adewumi, A.O.; Adeleke, O.J. A survey of recent advances in vehicle routing problems. Int. J. Syst. Assur. Eng. Manag. 2018, 9, 155–172. [Google Scholar] [CrossRef]
- Sumalee, A.; Uchida, K.; Lam, W.H.K. Stochastic multi-modal transport network under demand uncertainties and adverse weather condition. Transp. Res. Part C: Emerg. Technol. 2011, 19, 338–350. [Google Scholar] [CrossRef]
- Chu, J.C.; Yan, S.; Huang, H.J. A Multi-Trip Split-Delivery Vehicle Routing Problem with Time Windows for Inventory Replenishment Under Stochastic Travel Times. Netw. Spat. Econ. 2017, 17, 41–68. [Google Scholar] [CrossRef]
- Gu, W.; Cattaruzza, D.; Ogier, M.; Semet, F. Adaptive large neighborhood search for the commodity constrained split delivery VRP. Comput. Oper. Res. 2019, 112, 104761. [Google Scholar] [CrossRef]
- Lagos, C.; Guerrero, G.; Cabrera, E.; Moltedo-Perfetti, A.S.; Johnson, F.; Paredes, F. An improved particle swarm optimization algorithm for the VRP with simultaneous pickup and delivery and time windows. IEEE Lat. Am. Trans. 2018, 16, 1732–1740. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, Y.; Wang, Y.; Zhang, J.; Chen CL, P.; Zheng, Z. Multiobjective Vehicle Routing Problems with Simultaneous Delivery and Pickup and Time Windows: Formulation, Instances, and Algorithms. IEEE Trans. Cybern. 2016, 46, 582–594. [Google Scholar] [CrossRef]
- Ancele, Y.; Hà, M.H.; Lersteau, C.; Matellini, B.D.; Nguyen, T.T. Toward a more flexible VRP with pickup and delivery allowing consolidations. Transp. Res. Part C Emerg. Technol. 2021, 128, 103077. [Google Scholar] [CrossRef]
- Alcaraz, J.J.; Caballero-Arnaldos, L.; Vales-Alonso, J. Rich vehicle routing problem with last-mile outsourcing decisions. Transp. Res. Part E: Logist. Transp. Rev. 2019, 129, 263–286. [Google Scholar] [CrossRef]
- Baller, A.C.; Dabia, S.; Dullaert, W.E.H.; Vigo, D. The vehicle routing problem with partial outsourcing. Transp. Sci. 2020, 54, 1034–1052. [Google Scholar] [CrossRef]
- Simeonova, L.; Wassan, N.; Salhi, S.; Nagy, G. The heterogeneous fleet vehicle routing problem with light loads and overtime: Formulation and population variable neighbourhood search with adaptive memory. Expert Syst. Appl. 2018, 114, 183–195. [Google Scholar] [CrossRef]
- Eshtehadi, R.; Demir, E.; Huang, Y. Solving the vehicle routing problem with multi-compartment vehicles for city logistics. Comput. Oper. Res. 2020, 115, 104859. [Google Scholar] [CrossRef]
- Perboli, G.; Rosano, M.; Saint-Guillain, M.; Rizzo, P. Simulation–optimisation framework for City Logistics: An application on multimodal last-mile delivery. IET Intell. Transp. Syst. 2018, 12, 262–269. [Google Scholar] [CrossRef]
- Caggiani, L.; Colovic, A.; Prencipe, L.P.; Ottomanelli, M. A green logistics solution for last-mile deliveries considering e-vans and e-cargo bikes. Transp. Res. Procedia 2021, 52, 75–82. [Google Scholar] [CrossRef]
- Berhan, E.; Beshah, B.; Kitaw, D.; Abraham, A. Stochastic Vehicle Routing Problem: A Literature Survey. J. Inf. Knowl. Manag. 2014, 13, 9848104. [Google Scholar] [CrossRef]
- Bernardo, M.; Pannek, J. Robust Solution Approach for the Dynamic and Stochastic Vehicle Routing Problem. J. Adv. Transp. 2018, 2018, 9848104. [Google Scholar] [CrossRef]
- Oyola, J.; Arntzen, H.; Woodruff, D.L. The stochastic vehicle routing problem, a literature review, Part II: Solution methods. EURO J. Transp. Logist. 2017, 6, 349–388. [Google Scholar] [CrossRef]
- Oyola, J.; Arntzen, H.; Woodruff, D.L. The stochastic vehicle routing problem, a literature review, part I: Models. EURO J. Transp. Logist. 2018, 7, 193–221. [Google Scholar] [CrossRef]
- Okulewicz, M.; Mańdziuk, J. A metaheuristic approach to solve Dynamic Vehicle Routing Problem in continuous search space. Swarm Evol. Comput. 2019, 48, 44–61. [Google Scholar] [CrossRef]
- Liu, K.; Li, N.; Kolmanovsky, I.; Girard, A. A vehicle routing problem with dynamic demands and restricted failures solved using stochastic predictive control. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 1885–1890. [Google Scholar] [CrossRef]
- Yan, X.; Xiao, B.; Xiao, Y.; Zhao, Z.; Ma, L.; Wang, N. Skill Vehicle Routing Problem with Time Windows Considering Dynamic Service Times and Time-Skill-Dependent Costs. IEEE Access 2019, 7, 77208–77221. [Google Scholar] [CrossRef]
- Grabenschweiger, J.; Doerner, K.F.; Hartl, R.F.; Savelsbergh, M.W.P. The vehicle routing problem with heterogeneous locker boxes. Cent. Eur. J. Oper. Res. 2021, 29, 113–142. [Google Scholar] [CrossRef]
- Orenstein, I.; Raviv, T.; Sadan, E. Flexible parcel delivery to automated parcel lockers: Models, solution methods and analysis. EURO J. Transp. Logist. 2019, 8, 683–711. [Google Scholar] [CrossRef]
- Wang, J.; Ren, W.; Zhang, Z.; Huang, H.; Zhou, Y. A Hybrid Multiobjective Memetic Algorithm for Multiobjective Periodic Vehicle Routing Problem with Time Windows. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4732–4745. [Google Scholar] [CrossRef]
- Cattaruzza, D.; Absi, N.; Feillet, D. The multi-trip vehicle routing problem with time windows and release dates. Transp. Sci. 2016, 50, 676–693. [Google Scholar] [CrossRef]
- Kumar, S.V.; Thansekhar, M.R.; Saravanan, R.; Amali, M.J.S. Solving multi-objective vehicle routing problem with time windows by FAGA. Procedia Eng. 2014, 97, 2176–2185. [Google Scholar] [CrossRef][Green Version]
- Kumar, S.V.; Thansekhar, M.R.; Saravanan, R.; Amali, M.J.S. Demonstrating the importance of using total time balance instead of route balance on a multi-objective vehicle routing problem with time windows. Int. J. Adv. Manuf. Technol. 2018, 98, 1287–1306. [Google Scholar] [CrossRef]
- Ganji, M.; Kazemipoor, H.; Hadji Molana, S.M.; Sajadi, S.M. A green multi-objective integrated scheduling of production and distribution with heterogeneous fleet vehicle routing and time windows. J. Clean. Prod. 2020, 259, 120824. [Google Scholar] [CrossRef]
- Hassanzadeh, A.; Rasti-Barzoki, M. Minimizing total resource consumption and total tardiness penalty in a resource allocation supply chain scheduling and vehicle routing problem. Appl. Soft Comput. J. 2017, 58, 307–323. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Q.; Ma, L.; Zhang, Z.; Liu, Y. A hybrid ant colony optimization algorithm for a multi-objective vehicle routing problem with flexible time windows. Inf. Sci. 2019, 490, 166–190. [Google Scholar] [CrossRef]
- Qin, G.; Tao, F.; Li, L. A vehicle routing optimization problem for cold chain logistics considering customer satisfaction and carbon emissions. Int. J. Environ. Res. Public Health 2019, 16, 576. [Google Scholar] [CrossRef]
- Elshaer, R.; Awad, H. A taxonomic review of metaheuristic algorithms for solving the vehicle routing problem and its variants. Comput. Ind. Eng. 2020, 140, 106242. [Google Scholar] [CrossRef]
- Costa, L.; Contardo, C.; Desaulniers, G. Exact branch-price-and-cut algorithms for vehicle routing. Transp. Sci. 2019, 53, 946–985. [Google Scholar] [CrossRef]
- Andelmin, J.; Bartolini, E. An exact algorithm for the green vehicle routing problem. Transp. Sci. 2017, 51, 1288–1303. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Yang, S. Ant algorithms with immigrants schemes for the dynamic vehicle routing problem. Inf. Sci. 2015, 294, 456–477. [Google Scholar] [CrossRef]
- Ghilas, V.; Demir, E.; Van Woensel, T. An adaptive large neighborhood search heuristic for the Pickup and Delivery Problem with Time Windows and Scheduled Lines. Comput. Oper. Res. 2016, 72, 12–30. [Google Scholar] [CrossRef]
- Goel, R.K.; Bansal, S.R. Hybrid algorithms for rich vehicle routing problems: A survey. In Smart Delivery Systems: Solving Complex Vehicle Routing Problems; Elsevier: Amsterdam, The Netherlands, 2020; pp. 157–184. [Google Scholar] [CrossRef]
- Lin, S.W.; Lee, Z.J.; Ying, K.C.; Lee, C.Y. Applying hybrid meta-heuristics for capacitated vehicle routing problem. Expert Syst. Appl. 2009, 36, 1505–1512. [Google Scholar] [CrossRef]
- Vidal, T.; Battarra, M.; Subramanian, A.; Erdoʇan, G. Hybrid metaheuristics for the Clustered Vehicle Routing Problem. Comput. Oper. Res. 2015, 58, 87–99. [Google Scholar] [CrossRef]
- Liu, S.C.; Lu, M.C.; Chung, C.H. A hybrid heuristic method for the periodic inventory routing problem. Int. J. Adv. Manuf. Technol. 2016, 85, 2345–2352. [Google Scholar] [CrossRef]
- Avci, M.; Topaloglu, S. A hybrid metaheuristic algorithm for heterogeneous vehicle routing problem with simultaneous pickup and delivery. Expert Syst. Appl. 2016, 53, 160–171. [Google Scholar] [CrossRef]
- Jabir, E.; Panicker, V.V.; Sridharan, R. Design and development of a hybrid ant colony-variable neighbourhood search algorithm for a multi-depot green vehicle routing problem. Transp. Res. Part D Transp. Environ. 2017, 57, 422–457. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Z.; Su, X.; Qin, H. A hybrid algorithm for the vehicle routing problem with compatibility constraints. In Proceedings of the 2018 IEEE 15th International Conference on Networking, Sensing and Control (ICNSC), Zhuhai, China, 27–29 March 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Hosseinabadi, A.A.; Slowik, A.; Sadeghilalimi, M.; Farokhzad, M.; Babazadeh Shareh, M.; Sangaiah, A.K. An Ameliorative Hybrid Algorithm for Solving the Capacitated Vehicle Routing Problem. IEEE Access 2019, 7, 175454–175465. [Google Scholar] [CrossRef]
- Lin, N.; Shi, Y.; Zhang, T.; Wang, X. An Effective Order-Aware Hybrid Genetic Algorithm for Capacitated Vehicle Routing Problems in Internet of Things. IEEE Access 2019, 7, 86102–86114. [Google Scholar] [CrossRef]
- Kheirkhahzadeh, M.; Barforoush, A.A. A hybrid algorithm for the vehicle routing problem. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, CEC 2009, Trondheim, Norway, 18–21 May 2009; pp. 1791–1798. [Google Scholar] [CrossRef]
- Euchi, J.; Yassine, A.; Chabchoub, H. The dynamic vehicle routing problem: Solution with hybrid metaheuristic approach. Swarm Evol. Comput. 2015, 21, 41–53. [Google Scholar] [CrossRef]
- Gutierrez-Rodríguez, A.E.; Conant-Pablos, S.E.; Ortiz-Bayliss, J.C.; Terashima-Marín, H. Selecting meta-heuristics for solving vehicle routing problems with time windows via meta-learning. Expert Syst. Appl. 2019, 118, 470–481. [Google Scholar] [CrossRef]
- Kiba-Janiak, M.; Marcinkowski, J.; Jagoda, A.; Skowrońska, A. Sustainable last mile delivery on e-commerce market in cities from the perspective of various stakeholders. Literature review. Sustain. Cities Soc. 2021, 71, 102984. [Google Scholar] [CrossRef]
- Calabrò, G.; Le Pira, M.; Giuffrida, N.; Fazio, M.; Inturri, G.; Ignaccolo, M. Modelling the dynamics of fragmented vs. consolidated last-mile e-commerce deliveries via an agent-based model. Transp. Res. Procedia 2022, 62, 155–162. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).