Correlation of Climatic Factors with the Weight of an Apis mellifera Beehive
Abstract
:1. Introduction
2. Materials and Methods
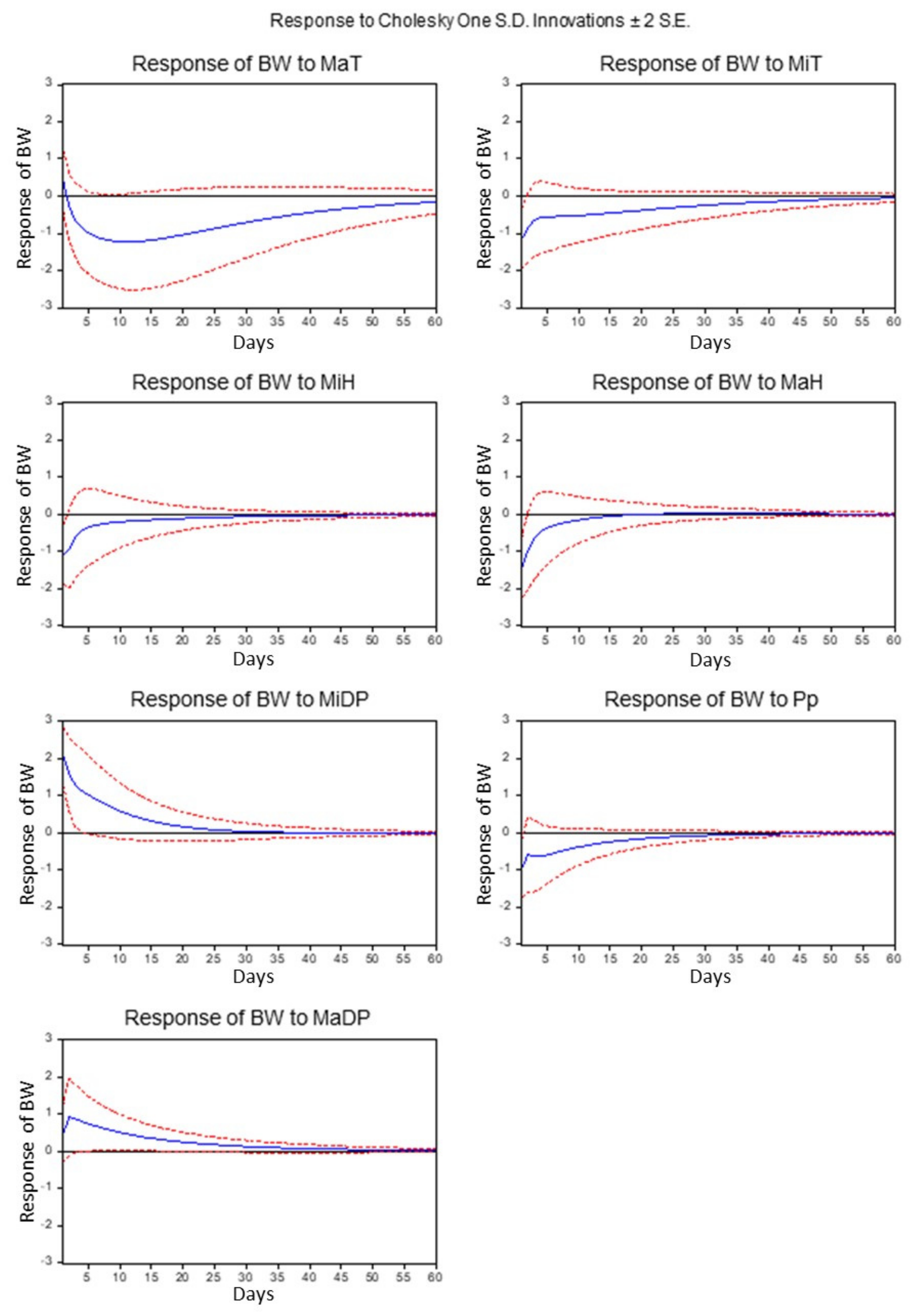
3. Results and Discussion
0.0082.MiDPt−1 + 0.7018.Ppt−1 + 0.1939.MaDPt−1 + 0.9029.BWt−1 + 19.5323
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| MaT | MiT | MiH | MaH | MiDP | Pp | MaDP | BW | |
|---|---|---|---|---|---|---|---|---|
| MaTt−1 | 0.8614 | 0.4367 | −0.3370 | 0.1458 | 0.2655 | 0.0006 | 0.7371 | −0.1968 |
| (0.0865) | (0.0714) | (0.2107) | (0.1058) | (0.1348) | (0.0057) | (0.0854) | (0.1274) | |
| [9.9588] | [6.1098] | [−1.5993] | [1.3781] | [1.9696] | [0.1111] | [8.6265] | [−1.5440] | |
| MiTt−1 | 0.2777 | 0.5086 | 0.1096 | 0.0831 | 0.2547 | 0.0090 | 0.4033 | −0.0545 |
| (0.0773) | (0.0638) | (0.1883) | (0.0945) | (0.1204) | (0.0051) | (0.0763) | (0.1139) | |
| [3.5931] | [7.9617] | [0.5819] | [0.8785] | [2.1142] | [1.7708] | [5.2823] | [−0.4791] | |
| MiHt−1 | 0.0123 | 0.0738 | 0.2420 | 0.0501 | −0.0187 | 0.0138 | 0.1729 | −0.0327 |
| (0.0453) | (0.0374) | (0.1105) | (0.0555) | (0.0707) | (0.0030) | (0.0448) | (0.0668) | |
| [0.2728] | [1.9711] | [2.1896] | [0.9030] | [−0.2657] | [4.6231] | [3.8607] | [−0.4891] | |
| MaHt−1 | 0.0144 | 0.0227 | 0.1153 | 0.3419 | −0.0083 | 0.0015 | 0.2281 | −0.0175 |
| (0.0512) | (0.0423) | (0.1249) | (0.0627) | (0.0799) | (0.0033) | (0.0506) | (0.0755) | |
| [0.2825] | [0.5361] | [0.9233] | [5.4505] | [−0.1050] | [0.4425] | [4.5045] | [−0.2326] | |
| MiDPt−1 | −0.0065 | 0.0436 | 0.3509 | 0.0527 | 0.6126 | −0.0134 | −0.0638 | 0.0082 |
| (0.0572) | (0.0473) | (0.1395) | (0.0700) | (0.0892) | (0.0037) | (0.0565) | (0.0844) | |
| [−0.1138] | [0.9212] | [2.5142] | [0.7523] | [6.8628] | [−3.5446] | [−1.1289] | [0.0972] | |
| Ppt−1 | 0.5510 | −1.2784 | −3.1818 | −1.9231 | −0.9684 | 0.0184 | −1.9094 | 0.7018 |
| (0.6641) | (0.5489) | (1.6184) | (0.8127) | (1.0351) | (0.0439) | (0.6561) | (0.9789) | |
| [0.8295] | [−2.3290] | [−1.9660] | [−2.3663] | [−0.9355] | [0.4201] | [−2.9102] | [0.7169] | |
| MaDPt−1 | −0.2124 | −0.0495 | 0.0124 | −0.0680 | −0.0851 | 0.0041 | −0.1881 | 0.1939 |
| (0.0975) | (0.0805) | (0.2375) | (0.1193) | (0.1519) | (0.0064) | (0.0963) | (0.1437) | |
| [−2.1794] | [−0.6154] | [0.0525] | [−0.5701] | [−0.5602] | [0.6447] | [−1.9537] | [1.3495] | |
| BWt−1 | −0.0012 | −0.0246 | −0.0037 | 0.0204 | −0.0037 | −0.0007 | −0.0098 | 0.9029 |
| (0.0136) | (0.0113) | (0.0333) | (0.0167) | (0.0213) | (0.0009) | (0.0135) | (0.0201) | |
| [−0.0916] | [−2.1763] | [−0.1122] | [1.2186] | [−0.1752] | [−0.8242] | [−0.7250] | [44.7572] | |
| C | 5.4877 | −7.3191 | 28.6454 | 43.7979 | −7.6936 | −0.6836 | −32.1226 | 19.5323 |
| (6.4125) | (5.2996) | (15.6257) | (7.8467) | (9.9945) | (0.4239) | (6.3346) | (9.4513) | |
| [0.8557] | [−1.3810] | [1.8332] | [5.5816] | [−0.7697] | [−1.6124] | [−5.0709] | [2.0666] |
References
- Hülsmann, M.; von Wehrden, H.; Klein, A.-M.; Leonhardt, S.D. Plant diversity and composition compensate for negative effects of urbanization on foraging bumble bees. Apidologie 2015, 46, 760–770. [Google Scholar] [CrossRef]
- Potts, S.G.; Imperatriz-Fonseca, V.; Ngo, H.T.; Aizen, M.A.; Biesmeijer, J.C.; Breeze, T.D.; Dicks, L.V.; Garibaldi, L.A.; Hill, R.; Settele, J.; et al. Safeguarding pollinators and their values to human well-being. Nature 2016, 540, 220–229. [Google Scholar] [CrossRef] [PubMed]
- Christ, L.; Dreesmann, D.C. SAD but True: Species Awareness Disparity in Bees Is a Result of Bee-Less Biology Lessons in Germany. Sustainability 2022, 14, 2604. [Google Scholar] [CrossRef]
- FAO Pollinators Vital to Our Food Supply under Threat. Available online: https://www.fao.org/news/story/pt/item/384726/icode/ (accessed on 13 February 2022).
- Leonhardt, S.D.; Gallai, N.; Garibaldi, L.A.; Kuhlmann, M.; Klein, A.M. Economic gain, stability of pollination and bee diversity decrease from southern to northern Europe. Basic Appl. Ecol. 2013, 14, 461–471. [Google Scholar] [CrossRef]
- Verboven, H.A.F.; Uyttenbroeck, R.; Brys, R.; Hermy, M. Different responses of bees and hoverflies to land use in an urban–rural gradient show the importance of the nature of the rural land use. Landsc. Urban Plan. 2014, 126, 31–41. [Google Scholar] [CrossRef]
- Kuchling, S.; Kopacka, I.; Kalcher-Sommersguter, E.; Schwarz, M.; Crailsheim, K.; Brodschneider, R. Investigating the role of landscape composition on honey bee colony winter mortality: A long-term analysis. Sci. Rep. 2018, 8, 12263. [Google Scholar] [CrossRef]
- Wintermantel, D.; Odoux, J.; Decourtye, A.; Henry, M.; Allier, F.; Bretagnolle, V. Neonicotinoid-induced mortality risk for bees foraging on oilseed rape nectar persists despite EU moratorium. Sci. Total Environ. 2019, 704, 135400. [Google Scholar] [CrossRef]
- Van Engelsdorp, D.; Evans, J.D.; Saegerman, C.; Mullin, C.; Haubruge, E.; Nguyen, B.K.; Frazier, M.; Frazier, J.; Cox-Foster, D.; Chen, Y.; et al. Colony Collapse Disorder: A Descriptive Study. PLoS ONE 2009, 4, e6481. [Google Scholar] [CrossRef]
- Ziegler, C.; Sinigaglia, T.; Martins, M.E.S.; Souza, A.M. Technological Advances to Reduce Apis mellifera Mortality: A Bibliometric Analysis. Sustainability 2021, 13, 8305. [Google Scholar] [CrossRef]
- Switanek, M.; Crailsheim, K.; Truhetz, H.; Brodschneider, R. Modelling seasonal effects of temperature and precipitation on honey bee winter mortality in a temperate climate. Sci. Total Environ. 2017, 579, 1581–1587. [Google Scholar] [CrossRef]
- Oliver Hernández, C.; Li, S.; Merino Rivera, M.D.; Mateo Rodríguez, I. Does Postural Feedback Reduce Musculoskeletal Risk?: A Randomized Controlled Trial. Sustainability 2022, 14, 583. [Google Scholar] [CrossRef]
- Van Dooremalen, C.; Gerritsen, L.; Cornelissen, B.; van der Steen, J.J.; van Langevelde, F.; Blacquiere, T. Winter Survival of Individual Honey Bees and Honey Bee Colonies Depends on Level of Varroa destructor Infestation. PLoS ONE 2012, 7, e36285. [Google Scholar] [CrossRef] [Green Version]
- Ratnieks, F.L.W.; Carreck, N.L. Clarity on Honey Bee Collapse? Science 2010, 327, 152–153. [Google Scholar] [CrossRef]
- Osborne, J.L. Bumblebees and pesticides. Nature 2012, 491, 43–45. [Google Scholar] [CrossRef]
- Braga, A.R.; Gomes, D.G.; Freitas, B.M.; Cazier, J.A. A cluster-classification method for accurate mining of seasonal honey bee patterns. Ecol. Inform. 2020, 59, 101107. [Google Scholar] [CrossRef]
- Meikle, W.G.; Holst, N. Application of continuous monitoring of honeybee colonies. Apidologie 2015, 46, 10–22. [Google Scholar] [CrossRef] [Green Version]
- Gil-Lebrero, S.; Quiles-Latorre, F.; Ortiz-López, M.; Sánchez-Ruiz, V.; Gámiz-López, V.; Luna-Rodríguez, J. Honey Bee Colonies Remote Monitoring System. Sensors 2017, 17, 55. [Google Scholar] [CrossRef] [Green Version]
- Meikle, W.G.; Weiss, M.; Maes, P.W.; Fitz, W.; Snyder, L.A.; Sheehan, T.; Mott, B.M.; Anderson, K.E. Internal hive temperature as a means of monitoring honey bee colony health in a migratory beekeeping operation before and during winter. Apidologie 2017, 48, 666–680. [Google Scholar] [CrossRef] [Green Version]
- Meikle, W.G.; Holst, N.; Mercadier, G.; Derouané, F.; James, R.R. Using balances linked to dataloggers to monitor honey bee colonies. J. Apic. Res. 2006, 45, 39–41. [Google Scholar] [CrossRef]
- Hambleton, J.I. The Effect of Weather upon the Change in Weight of a Colony of Bees during the Honey Flow; United States Department of Agriculture: Washington, DC, USA, 1925.
- Flores, J.M.; Gil-Lebrero, S.; Gámiz, V.; Rodríguez, M.I.; Ortiz, M.A.; Quiles, F.J. Effect of the climate change on honey bee colonies in a temperate Mediterranean zone assessed through remote hive weight monitoring system in conjunction with exhaustive colonies assessment. Sci. Total Environ. 2019, 653, 1111–1119. [Google Scholar] [CrossRef]
- Lecocq, A.; Kryger, P.; Vejsnæs, F.; Bruun Jensen, A. Weight Watching and the Effect of Landscape on Honeybee Colony Productivity: Investigating the Value of Colony Weight Monitoring for the Beekeeping Industry. PLoS ONE 2015, 10, e0132473. [Google Scholar] [CrossRef]
- Meikle, W.G.; Rector, B.G.; Mercadier, G.; Holst, N. Within-day variation in continuous hive weight data as a measure of honey bee colony activity. Apidologie 2008, 39, 694–707. [Google Scholar] [CrossRef] [Green Version]
- Cecchi, S.; Spinsante, S.; Terenzi, A.; Orcioni, S. A Smart Sensor-Based Measurement System for Advanced Bee Hive Monitoring. Sensors 2020, 20, 2726. [Google Scholar] [CrossRef]
- Zacepins, A.; Brusbardis, V.; Meitalovs, J.; Stalidzans, E. Challenges in the development of Precision Beekeeping. Biosyst. Eng. 2015, 130, 60–71. [Google Scholar] [CrossRef]
- Rodrigues, S.D.; Ueda, R.M.; Barreto, A.C.; Zanini, R.R.; Souza, A.M. How atmospheric pollutants impact the development of chronic obstructive pulmonary disease and lung cancer: A var-based model. Environ. Pollut. 2021, 275, 116622. [Google Scholar] [CrossRef]
- Ueda, R.M.; Souza, A.M. An effective approach to detect the source(s) of out-of-control signals in productive processes by vector error correction (VEC) residual and Hotelling’s T2 decomposition techniques. Expert Syst. Appl. 2022, 187, 115979. [Google Scholar] [CrossRef]
- Basile, R.; Pirk, C.W.W.; Tautz, J. Trophallactic activities in the honeybee brood nest—Heaters get supplied with high performance fuel. Zoology 2008, 111, 433–441. [Google Scholar] [CrossRef]
- Becher, M.A.; Scharpenberg, H.; Moritz, R.F.A. Pupal developmental temperature and behavioral specialization of honeybee workers (Apis mellifera L.). J. Comp. Physiol. A 2009, 195, 673–679. [Google Scholar] [CrossRef] [PubMed]
- Braga, A.R.; Gomes, D.G.; Rogers, R.; Hassler, E.E.; Freitas, B.M.; Cazier, J.A. A method for mining combined data from in-hive sensors, weather and apiary inspections to forecast the health status of honey bee colonies. Comput. Electron. Agric. 2020, 169, 105161. [Google Scholar] [CrossRef]
- de Mattos, I.M.; Souza, J.; Soares, A.E.E. Analysis of the effects of climate variables on Apis mellifera pollen foraging performance. Arq. Bras. Med. Vet. Zootec. 2018, 70, 1301–1308. [Google Scholar] [CrossRef] [Green Version]
- Gillott, C. Entomology, 3rd ed.; Springer: Dordrecht, The Netherlands, 2005; ISBN 1-4020-3184-X. [Google Scholar]
- Chittka, L.; Geiger, K. Can honey bees count landmarks? Anim. Behav. 1995, 49, 159–164. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, M.; Zhang, S.; Bidwell, N. Visually mediated odometry in honeybees. J. Exp. Biol. 1997, 200, 2513–2522. [Google Scholar] [CrossRef]
- Hilário, S.D.; de Fátima Ribeiro, M.; Imperatriz-Fonseca, V.L. Impacto da precipitação pluviométrica sobre a atividade de vôo de Plebeia remota (Holmberg, 1903) (Apidae, Meliponini). Biota Neotrop. 2007, 7, 135–143. [Google Scholar] [CrossRef] [Green Version]
- He, X.-J.; Tian, L.-Q.; Wu, X.-B.; Zeng, Z.-J. RFID monitoring indicates honeybees work harder before a rainy day. Insect Sci. 2016, 23, 157–159. [Google Scholar] [CrossRef]
- Boyles, R.; Raman, S. Analysis of climate trends in North Carolina (1949–1998). Environ. Int. 2003, 29, 263–275. [Google Scholar] [CrossRef] [Green Version]
- Bellido-Jiménez, J.A.; Estévez Gualda, J.; García-Marín, A.P. Assessing new intra-daily temperature-based machine learning models to outperform solar radiation predictions in different conditions. Appl. Energy 2021, 298, 117211. [Google Scholar] [CrossRef]
- Joslyn, C.A.; Charles, L.; DePerno, C.; Gould, N.; Nowak, K.; Praggastis, B.; Purvine, E.; Robinson, M.; Strules, J.; Whitney, P. A Sheaf Theoretical Approach to Uncertainty Quantification of Heterogeneous Geolocation Information. Sensors 2020, 20, 3418. [Google Scholar] [CrossRef]
- Oakman, E.C.; Hagan, D.L.; Waldrop, T.A.; Barrett, K. Understory Vegetation Responses to 15 Years of Repeated Fuel Reduction Treatments in the Southern Appalachian Mountains, USA. Forests 2019, 10, 350. [Google Scholar] [CrossRef] [Green Version]
- Montgomery, D.C. Introduction to Statistical Quality Control, 6th ed.; John Wiley & Sons: New York, NY, USA, 2009; ISBN 0470169923. [Google Scholar]
- Devore, J.L. Probabilidade e Estatística para Engenharia e Ciências, 9th ed.; Cengage: São Paulo, Brazil, 2018; ISBN 9788522128037. [Google Scholar]
- Said, S.E.; Dickey, D.A. Testing for unit roots in autoregressive-moving average models of unknown order. Biometrika 1984, 71, 599–607. [Google Scholar] [CrossRef]
- Phillips, P.C.B.; Perron, P. Testing for a unit root in time series regression. Biometrika 1988, 75, 335–346. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- da Bueno, R.D.S. Econometria de Séries Temporais, 2nd ed.; Cengage Learning: São Paulo, Brazil, 2018; ISBN 9788522111572. [Google Scholar]
- Granger, C.W.J. Developments in the study of cointegrated economic variables. Oxf. Bull. Econ. Stat. 1986, 48, 213–228. [Google Scholar] [CrossRef]
- De Senna, V.; Souza, A.M. Assessment of the relationship of government spending on social assistance programs with Brazilian macroeconomic variables. Phys. A Stat. Mech. Its Appl. 2016, 462, 21–30. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Pan, C. Tourism–Growth Nexus in the Presence of Instability. Sustainability 2022, 14, 2170. [Google Scholar] [CrossRef]
- Ueda, R.M.; Souza, A.M.; Menezes, R.M.C.P. How macroeconomic variables affect admission and dismissal in the Brazilian electro-electronic sector: A VAR-based model and cluster analysis. Phys. A Stat. Mech. Its Appl. 2020, 557, 124872. [Google Scholar] [CrossRef]
- Sims, C.A. Macroeconomics and Reality. Econometrica 1980, 48, 1. [Google Scholar] [CrossRef] [Green Version]
- Hill, R.C.; Griffiths, W.E.; Judge, G.G. Econometria, 3rd ed.; Saraiva: São Paulo, Brazil, 2010; ISBN 9788502078826. [Google Scholar]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Second International Symposium on Information Theory; Springer: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Schwarz, G. Estimating the dimensional of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Hannan, E.J.; Quinn, B.G. The Determination of the Order of an Autoregression. J. R. Stat. Soc. 1979, 41, 190–195. [Google Scholar] [CrossRef]
- Aho, K.; Derryberry, D.; Peterson, T. Model selection for ecologists: The worldviews of AIC and BIC. Ecology 2014, 95, 631–636. [Google Scholar] [CrossRef] [PubMed]
- Brooks, C. Introductory Econometrics for Finance, 2nd ed.; Cambridge University Press: New York, NY, USA, 2008; ISBN 9780511841644. [Google Scholar]
- De Souza Ramser, C.A.; Souza, A.M.; Souza, F.M.; da Veiga, C.P.; da Silva, W.V. The importance of principal components in studying mineral prices using vector autoregressive models: Evidence from the Brazilian economy. Resour. Policy 2019, 62, 9–21. [Google Scholar] [CrossRef]
- Brahmasrene, T.; Huang, J.-C.; Sissoko, Y. Crude oil prices and exchange rates: Causality, variance decomposition and impulse response. Energy Econ. 2014, 44, 407–412. [Google Scholar] [CrossRef]
- Gordon, D.M.; Dektar, K.N.; Pinter-Wollman, N. Harvester Ant Colony Variation in Foraging Activity and Response to Humidity. PLoS ONE 2013, 8, e63363. [Google Scholar] [CrossRef] [Green Version]
- Mahdavi, M.; Mehdizadeh, E.; Pourkamali, S. Piezoelectric MEMS resonant dew point meters. Sens. Actuators A Phys. 2018, 276, 52–61. [Google Scholar] [CrossRef]
- Sasagawa, Y. Internal environment of footwear is a risk factor for tinea pedis. J. Dermatol. 2019, 46, 940–946. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Xu, X.; Zhu, X.; Chen, L.; Zhou, S.; Huang, Z.Y.; Zhou, B. Low-Temperature Stress during Capped Brood Stage Increases Pupal Mortality, Misorientation and Adult Mortality in Honey Bees. PLoS ONE 2016, 11, e0154547. [Google Scholar] [CrossRef]
- Nürnberger, F.; Härtel, S.; Steffan-Dewenter, I. The influence of temperature and photoperiod on the timing of brood onset in hibernating honey bee colonies. PeerJ 2018, 6, e4801. [Google Scholar] [CrossRef]
- Damos, P.; Savopoulou-Soultani, M. Temperature-Driven Models for Insect Development and Vital Thermal Requirements. Psyche A J. Entomol. 2012, 2012, 123405. [Google Scholar] [CrossRef]
- Jones, J.C.; Oldroyd, B.P. Nest Thermoregulation in Social Insects. In Advances in Insect Physiology; Elsevier: Amsterdam, The Netherlands, 2006; Volume 33, pp. 153–191. ISBN 012373715X. [Google Scholar]
- Southwick, E.E.; Heldmaier, G. Temperature Control in Honey Bee Colonies. Bioscience 1987, 37, 395–399. [Google Scholar] [CrossRef]
- Jones, J.C.; Myerscough, M.R.; Graham, S.; Oldroyd, B.P. Honey Bee Nest Thermoregulation: Diversity Promotes Stability. Science 2004, 305, 402–404. [Google Scholar] [CrossRef] [Green Version]
- Winston, M.L. The Biology of the Honey Bee; Harvard University Press: Cambridge, UK, 1987; ISBN 0674074084. [Google Scholar]
- Southwick, E.E.; Moritz, R.F.A. Social control of air ventilation in colonies of honey bees, Apis mellifera. J. Insect Physiol. 1987, 33, 623–626. [Google Scholar] [CrossRef]
- Heinrich, B.; Esch, H. Thermoregulation in Bees. Am. Sci. 1994, 82, 164–170. [Google Scholar]
- Goulson, D. Effects of Introduced Bees on Native Ecosystems. Annu. Rev. Ecol. Evol. Syst. 2003, 34, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Schmaranzer, S. Thermoregulation of water collecting honey bees (Apis mellifera). J. Insect Physiol. 2000, 46, 1187–1194. [Google Scholar] [CrossRef]
- Sánchez-Echeverría, K.; Castellanos, I.; Mendoza-Cuenca, L.; Zuria, I.; Sánchez-Rojas, G. Reduced thermal variability in cities and its impact on honey bee thermal tolerance. PeerJ 2019, 7, e7060. [Google Scholar] [CrossRef]
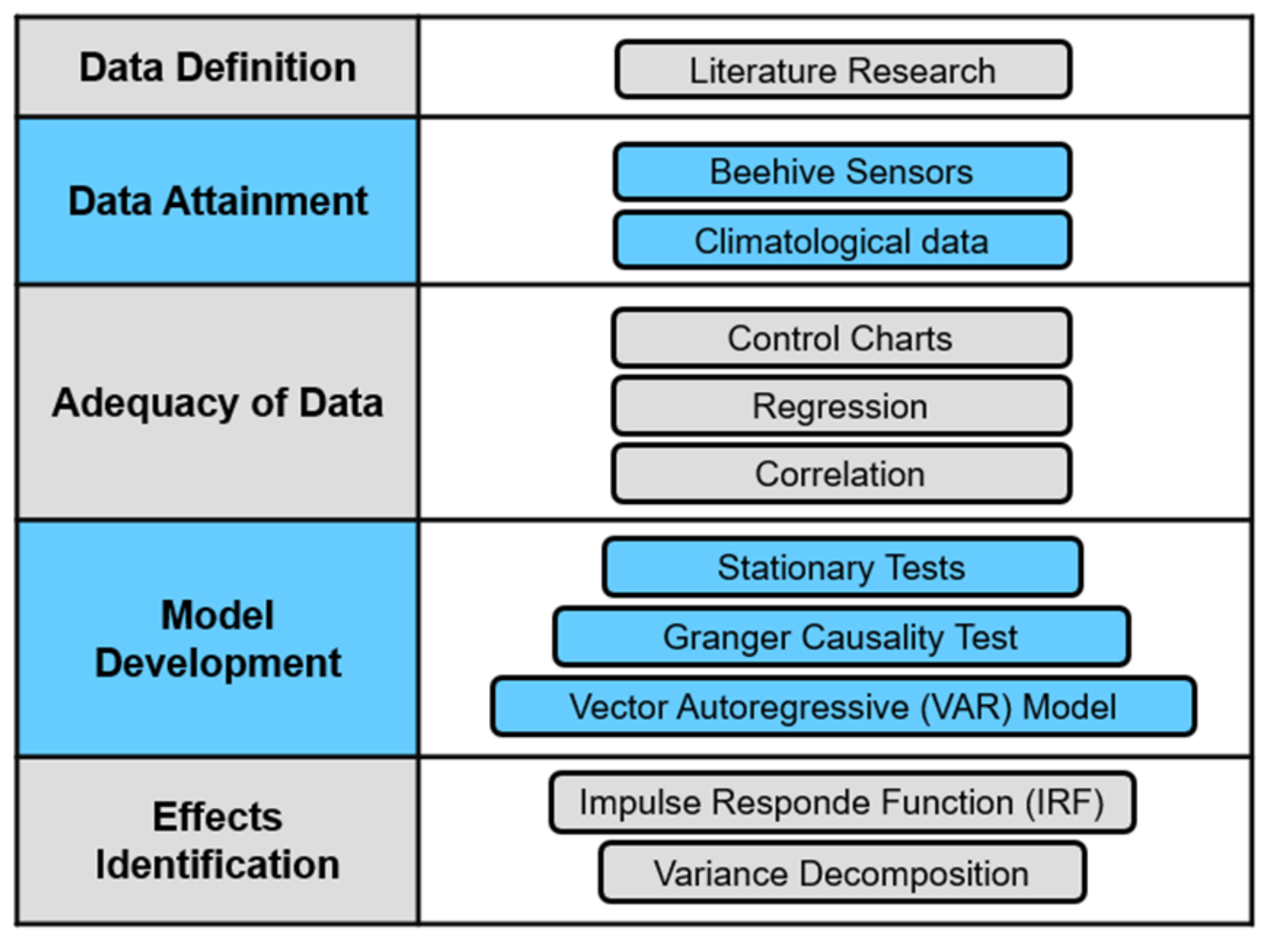

| Name | Unit of Measurement | Abbrev. | Origin |
|---|---|---|---|
| Maximum Temperature | °F | MaT | Climatological Historical Data |
| Minimum Temperature | °F | MiT | |
| Maximum Dew Point | °F | MaDP | |
| Minimum Dew Point | °F | MiDP | |
| Maximum Humidity | % | MaH | |
| Minimum Humidity | % | MiH | |
| Maximum Wind Speed | mph | MaWS | |
| Minimum Wind Speed | mph | MiWS | |
| Precipitation | In | Pp | |
| Beehive Weight | Lb | BW | Anastasia Beehive Data |
| Variable | Correlation | p-Value |
|---|---|---|
| MiT | −0.3313 | 0.0001 |
| MaDP | −0.3132 | 0.0001 |
| MaT | −0.2541 | 0.0001 |
| MiDP | −0.2468 | 0.0001 |
| MaH | −0.1739 | 0.0001 |
| Pp | −0.1727 | 0.0001 |
| MiH | −0.1489 | 0.0010 |
| MiWS | 0.0594 | 0.1890 |
| MaWS | 0.0162 | 0.7210 |
| Variable | ADF | KPSS | PP | |
|---|---|---|---|---|
| tcalculated | tcalculated | tcalculated | ||
| In Level | In Level | d = 1 | In Level | |
| BW | 3.8473 | 2.3153 | 0.0676 | 4.2575 |
| MaT | 3.4444 | 0.5364 | 0.1105 | 4.0552 |
| MiT | 3.1402 | 0.5682 | 0.1081 | 3.6572 |
| MaDP | 3.7213 | 0.5642 | 0.0892 | 4.7388 |
| MiDP | 4.2747 | 0.5414 | 0.1364 | 5.7227 |
| MaH | 5.0612 | 0.5222 | 0.0828 | 12.3431 |
| MiH | 12.4964 | 0.2555 | - | 12.3887 |
| Pp | 18.4703 | 0.1903 | - | 18.4649 |
| Granger Causality | F-Stat. | p-Value |
|---|---|---|
| (MaT) ↔ (MaDP) | 73.5540 | 0.0001 |
| (MiT) ↔ (MaT) | 58.2526 | 0.0001 |
| (MiDP) → (MaH) | 38.8462 | 0.0001 |
| (MaT) → (MiDP) | 37.7328 | 0.0001 |
| (MiT) → (MaH) | 36.7529 | 0.0001 |
| (MiH) → (Pp) | 35.9899 | 0.0001 |
| (MiT) ↔ (MiDP) | 34.9817 | 0.0001 |
| (MiT) ↔ (MaDP) | 32.6592 | 0.0001 |
| (MaH) ↔ (MaDP) | 30.7836 | 0.0001 |
| (MiDP) ↔ (MaDP) | 30.4254 | 0.0001 |
| (MaH) ↔ (MaT) | 29.9600 | 0.0001 |
| (MiH) ↔ (MiDP) | 27.9657 | 0.0001 |
| (Pp) ↔ (MaDP) | 17.7474 | 0.0001 |
| (MiT) ↔ (Pp) | 17.6224 | 0.0001 |
| (MiH) ↔ (MaDP) | 15.2420 | 0.0001 |
| (MiH) ↔ (MiT) | 12.9488 | 0.0001 |
| (MaH) ↔ (Pp) | 9.9353 | 0.0001 |
| (MaT) → (MiH) | 7.6596 | 0.0005 |
| (MiDP) → (Pp) | 7.0307 | 0.0010 |
| (MaDP) → (BW) | 6.4782 | 0.0017 |
| (MiT) → (BW) | 5.7810 | 0.0033 |
| (MiH) ↔ (MaH) | 4.0992 | 0.0172 |
| (MaT) → (BW) | 3.9215 | 0.0204 |
| (BW) → (Pp) | 3.8442 | 0.0221 |
| (MaT) → (Pp) | 3.7287 | 0.0247 |
| Lag | AIC | BIC | HQ |
|---|---|---|---|
| 0 | 50.9926 | 51.0620 | 51.0199 |
| 1 | 46.0895 | 46.7136 * | 46.3348 * |
| 2 | 46.0821 * | 47.2610 | 46.5454 |
| 3 | 46.0858 | 47.8194 | 46.7671 |
| 4 | 46.1391 | 48.4275 | 47.0385 |
| 5 | 46.2197 | 49.0628 | 47.3371 |
| 6 | 46.3365 | 49.7343 | 47.6718 |
| 7 | 46.4982 | 50.4508 | 48.0516 |
| 8 | 46.5729 | 51.0803 | 48.3444 |
| Period (Days) | MaT | MiT | MiH | MaH | MiDP | Pp | MaDP | BW |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.2253 | 1.6962 | 1.4516 | 2.6090 | 5.3370 | 1.1593 | 0.2551 | 87.2661 |
| 10 | 2.4654 | 1.2289 | 0.8005 | 1.0850 | 3.6508 | 0.9304 | 1.2852 | 88.5534 |
| 20 | 5.1490 | 1.5053 | 0.7281 | 0.9324 | 3.3695 | 0.9296 | 1.3800 | 86.0058 |
| 30 | 6.5876 | 1.6572 | 0.7148 | 0.8998 | 3.2655 | 0.9195 | 1.3992 | 84.5560 |
| 40 | 7.1944 | 1.7194 | 0.7109 | 0.8917 | 3.2300 | 0.9142 | 1.4029 | 83.9361 |
| 50 | 7.4235 | 1.7424 | 0.7096 | 0.8895 | 3.2182 | 0.9121 | 1.4035 | 83.7009 |
| 60 | 7.5054 | 1.7505 | 0.7091 | 0.8888 | 3.2142 | 0.9113 | 1.4035 | 83.6167 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziegler, C.; Ueda, R.M.; Sinigaglia, T.; Kreimeier, F.; Souza, A.M. Correlation of Climatic Factors with the Weight of an Apis mellifera Beehive. Sustainability 2022, 14, 5302. https://doi.org/10.3390/su14095302
Ziegler C, Ueda RM, Sinigaglia T, Kreimeier F, Souza AM. Correlation of Climatic Factors with the Weight of an Apis mellifera Beehive. Sustainability. 2022; 14(9):5302. https://doi.org/10.3390/su14095302
Chicago/Turabian StyleZiegler, Cristiano, Renan Mitsuo Ueda, Tiago Sinigaglia, Felipe Kreimeier, and Adriano Mendonça Souza. 2022. "Correlation of Climatic Factors with the Weight of an Apis mellifera Beehive" Sustainability 14, no. 9: 5302. https://doi.org/10.3390/su14095302
APA StyleZiegler, C., Ueda, R. M., Sinigaglia, T., Kreimeier, F., & Souza, A. M. (2022). Correlation of Climatic Factors with the Weight of an Apis mellifera Beehive. Sustainability, 14(9), 5302. https://doi.org/10.3390/su14095302






