Abstract
Aviation incident is a crucial approach for accident prevention and safety improvement. It is of remarkable practical significance to clarify the relationship between aviation incidents and airline capacity. In the present study, time-series analysis methods, such as cross-correlation, co-integration, and causality analysis are employed to explore the longitudinal relationship between airline capacity (measured by flight hours) and aviation incidents in seven different categories in China from 1994 to 2020. The obtained results indicate the existence of a substantial positive correlation between the total number of incidents and flight hours in China’s civil aviation. Among the incidents with various categories, there exists a remarkably positive correlation between flight hours and incidents caused by environmental factors, ground support, and other factors. Additionally, the maximum degree of positive correlation is detected between incidents caused by environmental factors and flight hours. However, a negative correlation between flight hours and incidents caused by aircrew, air traffic control, and aircraft maintenance is carefully displayed and discussed. More investigations reveal that there would be no co-integration relationship between the total number of incidents and flight hours. Among the incidents with different categories, a co-integration relationship between the number of incidents caused by ground support and flight hours is also reported, demonstrating a long-term equilibrium relationship between them. There is no Granger causality between the total number of incidents and flight hours; nevertheless, there is a one-way Granger causality between flight hours and incidents resulting from ground support and environmental factors. It implies that the flight hours can be exploited to explain and predict the variations of these two categories of incidents. This study clarifies the relationship between incidents and airline capacity from a statistical point of view and provides a solid reference for policymakers to implement safety management.
1. Introduction
Aviation safety is a key factor that determines the sustainable development of the civil aviation system. Aviation accidents have a huge negative impact on economic development, social stability, and national image [1]. Therefore, all countries, international organizations, and aircraft manufacturers have paid great attention to the safety level of civil aviation operations and have made great efforts to avoid aviation accidents [2]. In recent years, the overall safety record of commercial aircraft continues to be improved [3]. According to the statistics of the international civil aviation organization (ICAO), in 2020, only 22 accidents of scheduled commercial transport airlines (i.e., aircraft with a weight greater than 5.7 t) were reported, including four fatal accidents, indicating the lowest in history [4]. By the end of 2021, China’s 121 scheduled passenger flights have operated safely without a fatal accident for 11 years, and China’s civil aviation has established excellent safety records.
Although aviation accidents rarely occur, the rapid development of China’s air transport market brings new challenges for accident prevention and safety improvement. In 2005, China became the second-largest aviation market [5]. According to the international aviation association, China will overtake the United States as the world’s largest aviation market by 2024 [6]. Facing the rapid growth of airline capacity, namely the sharp increase in flight hours and flight frequencies, the number of incidents in China’s civil aviation presents an increasing trend year by year. In 2016, the annual number of incidents in China’s civil aviation has exceeded 500 cases, bringing new hidden dangers to the safety of civil aviation operations. Generally, incidents are considered as the precursors of accidents [7]. The accident pyramid model states that the control and reduction of a large number of non-injurious events and incidents are highly required to prevent fatal and serious accidents [8]. These events are related to the unsafe states of objects and workers’ unsafe behaviors, often identified as the source of accidents [9]. It is worth mentioning that it is necessary to give full play to the role of the fuse of incidents in civil aviation operation: an incident is similar to the fuse of the operation system blowing, and dealing with incidents and learning from them is equivalent to checking the cause of system failure and replacing the fuse. Therefore, scientific monitoring and timely dealing with incidents can avoid further damage to the operating system in the future. Although the concept of Safety-II points out that accidents cannot be prevented only from the accidents and incidents that have occurred, it is necessary to take a more proactive approach to avoid accidents, such as analyzing operation data [10]. At present, incidents are still a crucial and effective means to prevent accidents.
From the industry level, the airline capacity is generally taken into account as a vital factor affecting the number of incidents [11]. Given the obvious upward trend in the airline capacity and the number of incidents in China’s civil aviation, one cannot help wondering: what is the relationship between airline capacity and incidents? The clarification of the relationship between the airline capacity and incidents, as well as the macrovariation law, is a critical measure and breakthrough point for accident prevention. This issue will surely help managers improve the foresight of accident prevention and implement more scientific safety management. Therefore, it has very prominent practical significance for the continuous improvement of civil aviation safety levels.
2. Literature Review
Few research works have been focused on the longitudinal variation of the number of aviation accidents and incidents in China. As the number of aviation accidents in China is limited and has apparent discontinuous characteristics on a time scale, it is difficult to carry out in-depth scrutiny by statistical means. Although the number of incidents is larger, the data collection is extremely challenging. The following is a brief overview of the research on the law of accidents in other countries.
In the field of aviation safety, Raghavan and Rhoades [12] analyzed the relationship between airlines’ profitability and accident rates in the US airline industry from 1955 to 2002. The regression results exhibited an inverse relationship between the profitability and the rate of air carrier accidents, particularly for small regional air carriers.
Bazargan and Guzhva [13] collected general aviation accidents in the US within the time interval 1983–2002 and assessed the influences of gender, age, and the experience of pilots on general aviation accidents. The employed Chi-square tests and logistic regression models revealed that male pilots, those older than 60 years, and with more experience, were more likely to be involved in a fatal accident.
Di Gravio et al. [14] scrutinized the safety of the Italian air traffic management system, the safety indices included accidents, events, and relevant issues. They exploited historical fit, time-series analysis, and causal fit to forecast the safety performance of the air traffic management system. The obtained results suggested that the causal fit analysis provides the best forecasting power.
Aguiar et al. [15] analyzed the rates and causes of general aviation accidents that occurred in mountainous terrain and high elevation terrain (MEHET) from 2001 to 2014. By employing the Pearson chi-square test, the study indicated that the MEHET-related accident rate declined by 57% in the US; however, the high proportion of fatal accidents showed little reduction, and controlled flight into terrain and wind gusts and shear were the most frequent causes of and factor categories for MEHET-related accidents.
Gao et al. [16] examined the co-integration relationship between aviation safety reports, traffic volume, and aviation accidents in the US throughout 1998–2019. The obtained results proposed a significant and stable long-run relationship between the number of accidents and the number of safety reports. Nevertheless, there is no evidence to support the inference from the traffic volume to either the number of accidents or the number of safety reports.
Due to the frequent occurrence of accidents in other fields (i.e., road and occupational accidents), many scholars have conducted extensive research on accident trends in these fields, and the relationship between accidents and their associated factors has been cultivated. SONG et al. [17] investigated the relationship between economic development and occupational accidents in China from 1953 to 2008. The obtained results indicated that there would be no causal relationship between economic scale and occupational accidents during the planning economy period (before 1978); however, after 1979, the economic speed considerably caused the occupational accidents fatality rate.
Yannis et al. [18] exploited mixed linear models to examine the relationship between the GDP growth and road traffic fatalities of 27 European countries during the time interval 1975–2011. Their study revealed that the GDP per capita has positive contributions to mortality rates and these effects are statistically significant overall, as well as in various groups of countries. Li et al. [19] applied a dynamic time-series approach to address the relationship between social-economic development and the number of road accidents in Hong Kong from 1984 to 2015. The analysis confirmed a long-run relationship between four social-economic variables, GDP, population, road network length, and private car ownership, and road accidents frequency. Specifically, it was shown that the increase in the population could lead to a long-run increment in road accidents, while an increase in licensed private car ownership yields more road accidents in both short-run and long-run terms.
As can be concluded from the above research works, time-series analysis methodologies, such as regression, co-integration analysis, and Granger causality, are employed to scrutinize the longitudinal relationship between accidents and related factors. The incident is a crucially developed approach to enhance operation safety [20] based on the growth of the incidents and airline capacity. A brief literature survey indicates that a particular empirical study on the relationship between airline capacity and incidents in China civil aviation is not available now. In this view, the following important questions are raised:
- (1)
- What is the relationship between airline capacity and incidents?
- (2)
- Is there a long-term equilibrium relationship between airline capacity and incidents? In other words, is there a co-integration relationship between them?
- (3)
- Is there a statistical causality between airline capacity and incidents?
In line with the research questions above, this paper aims to fill these scientific gaps by utilizing cross-correlation, co-integration, and causality analyses. The vital final goal is to systematically explore the relationship between airline capacity and incidents in China’s civil aviation. Since incidents have different categories, they have different causations. This study will also reveal the statistical relationship between airline capacity and incidents caused by various causes.
3. Data and Method
3.1. Data Description
The data used in this study are the annual airline capacity data and 6357 incidents of China’s civil aviation from 1994 to 2020. In general, the airline capacity can be represented by two indicators: flight frequency and flight hours. However, the CAAC did not officially publish flight frequency data before 2005; the airline capacity data is represented by flight hours in the present work. In addition, for China’s civil aviation, the average time of a single flight from 2005 to 2020 is about 2 h, and flight hours can be converted to flight frequency according to this relationship. Flight hour data are collected from the civil aviation industry development statistics bulletin that is published annually on the official website of the China civil aviation administration. The incident data are collected from the statistical analysis report of the China civil aviation safety information issued by the China civil aviation safety office.
According to the China civil aviation incident standard, the incident is defined as an event related to an aircraft that occurs during the aircraft operation phase or in the airport activity area, which does not constitute an accident but may affect operation safety [21]. This definition is consistent with that given in Annex 13 accident and incident investigation of the international civil aviation convention [22]. Generally, aviation incidents are classified into seven categories according to the direct causes accounting for the incident attributes and the characteristics based on the CAAC. These are flight crew, air traffic control, maintenance, machinery (or mechanical failure), ground support, environment, and other causes. Table 1 displays the meaning of incidents with various causes and gives illustrative examples of typical incidents due to each cause.

Table 1.
Definition of incident cause and typical incidents.
By the end of 2020, the China civil aviation incident standard has been revised six times. Each version, validity period, and the number of incidents cited in the standard are listed in Table 2. It should be noted that in each version, there exist about eighty definition terms or examples of incidents. In the present study, the incidents are based on the effective standard of the actual occurrence time. Therefore, during the handover period between old and new standards, the data inevitably fluctuates.

Table 2.
The CAAC incident standard.
Table 3 presents the descriptive statistics of flight hours and incident data. In order to ensure that the magnitude difference between flight hours and incidents is not too large, the unit of flight hours is taken as 104 h in the following analysis. According to Table 3, most of the incidents, about 4032 of them, are caused by environmental factors which account for about 63.4% of the total incidents. The numbers of incidents caused by machinery and flight crew in order are 781 and 732, accounting for about 12.3% and 11.5%. The number of incidents caused by ground support, other causes, maintenance, and air traffic control is less than 500. Additionally, the minimum value of incidents caused by air traffic control, maintenance, and other reasons is equal to zero, indicating the discontinuous characteristics of the aforementioned incidents on the annual scale.

Table 3.
Descriptive statistics of various variables.
The time-series plots of the flight hours and incidents are provided in Figure 1. The demonstrated graphs can more intuitively present the changing trends and characteristics of flight hours and incidents in the time dimension.
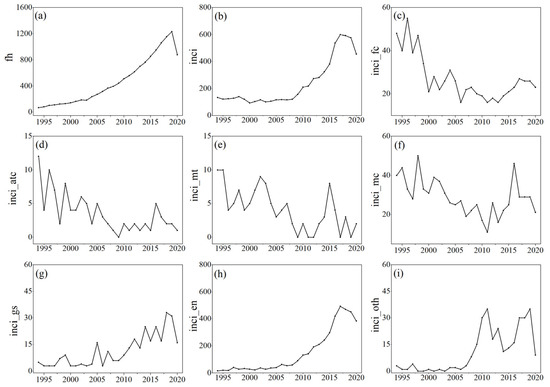
Figure 1.
The time-series plots: (a) fh, (b) inci, (c) inci_fc, (d) inci_atc, (e) inci_mt, (f) inci_mc, (g) inci_gs, (h) inci_en and (i) inci_oth.
It can be seen from Figure 1a,b that the flight hours (fh) and incidents (inci) generally show an upward trend. In particular, the incidents before 2017 show an exponential trend and then decrease in 2018 and after, which reflects that the safety situation of China’s civil aviation has improved. This is because the number of incidents is sometimes affected by factors other than airline capacity. In May 2018, a non-fatal aviation incident occurred in China that shocked the whole country. Sichuan Airlines flight 3U8633 was en route in a high altitude area, when the front windshield of the cockpit suddenly ruptured, causing the co-pilot to be sucked out of the cockpit and the aircraft cabin to lose pressure. Fortunately, no one was killed on this flight. After this incident, CAAC immediately invested a lot of effort to improve flight safety, strictly reduce operational risks in harsh environments, and improve flight personnel’s operational skills under adverse weather conditions and environmental disturbances. Therefore, 2018 became a pivot point for the number of incidents.
From Figure 1c–i, it can be seen that all the incidents with different causes, except the environmental factors, show apparent fluctuation characteristics. The incidents produced by environmental factors accounted for a large proportion compared with incidents of other causes. Therefore, the variation trend of this type of incident is similar to that of the total number of incidents. The incidents caused by the crew, air traffic control, and maintenance generally demonstrate a downward trend; however, the trend of incidents caused by mechanical reasons is not obvious. Further, the incidents generated by ground support and other reasons exhibit an upward trend.
3.2. Statistical Methods
In order to analyze the relationship between flight hours and incidents more comprehensively, it is necessary to exploit a variety of statistical methods to assess the time series of flight hours and incidents based on various analysis perspectives. The macro-relationship between flight hours and incidents in China’s civil aviation can be analyzed from three aspects: cross-correlation, co-integration, and the causality relationship. The flight hours, incidents, and incidents caused by environmental factors all have a similar exponential variation trend. The current mainstream statistical analysis methods are more often applied to linear models to describe the relationship between variables. Therefore, herein, natural logarithms are taken into account for all data to linearize the nonlinear variation trend.
3.2.1. Cross-Correlation
The cross-correlation is based on Pearson’s correlation coefficient [23] to describe the correlation between two time-series data with different time lag lengths. For two time series x(t) and y(t) with the same length T where 1 < t < T, the cross-correlation coefficient Cor(x(t − d), y(t)) between y(t) and x(t − d) with the time lag d is defined by:
where mx and my represent the mean values of the corresponding time series. If t − d < 0, the value of x(t − d) would be equal to zero. In the present study, x(t) corresponds to lnfh(t), y(t) corresponds to lninci(t), lninci_fc(t), …, lninci_oth(t). The lag length values of x(t) (i.e., d) is 0, 1, …, 6, respectively.
The value of the cross-correlation coefficient is between +1 and −1, and the correlation coefficient symbol represents the change direction between the two variables. The positive correlation coefficient indicates that the change direction of the two variables is the same, and the negative correlation coefficient represents the opposite direction of the consisting variables. The larger the absolute value of the correlation coefficient, the higher the linear correlation between the two variables. Additionally, if the corresponding value of d is not equal to 0 when Cor(x(t − d), y(t)) reaches the maximum value, it indicates that x(t) has a leading relationship to y(t). It implies that the current x(t) is more related to y(t + d) with lag length d.
3.2.2. Engle–Granger Co-Integration Test
As most of the macroscopic variables associated with the socio-economic system are non-stationary, we will arrive at the spurious-regression problem for the regression model. Therefore, co-integration has become a powerful approach to examining non-stationary time series. Generally, if two or more non-stationary time series can be transformed into stationary time series through some linear combinations, it denotes that there exists a co-integration relationship between these non-stationary time series [24]. The co-integration means that there is a long-term equilibrium relationship between time series, and the regression results between them have high reliability.
It should be noticed that the co-integration test requires that the under-analyzed time series have the same order of integration (i.e., the non-stationary time series can be transformed into stationary time series after the difference processing with the same order). Therefore, first of all, the stationary and integration order of time series should be identified by the unit root test. The most commonly applied unit root test is the Dickey–Fuller (DF) test [25] and the augmented Dickey–Fuller (ADF) test. The null hypothesis of the ADF test is that the time series has a unit root (i.e., the series is non-stationary). If the null hypothesis is rejected, the series can be considered as stationary. The ADF test contains three test models, which in order are marked as None, Intercept, and Trend, as presented in Equations (2)–(4). Three models are exploited to test the time series, and an optimal test model can be selected according to the sequential t rule or AIC information criterion.
The Engle–Granger co-integration test [24] is generally utilized to test the co-integration relationship between two time series with the same order of integration. Compared with another co-integration test, the Johansen co-integration rank test [26], the Engle–Granger co-integration test is more suitable for small samples. The basic steps of the Engle–Granger co-integration test are commonly divided into two steps:
- (1)
- The linear regression model between independent and dependent variables is established by the least square method. In the present scrutiny, the only independent variable is lnfh, and the dependent variables are lninci, lninci_fc, …, lninci_oth.
- (2)
- The ADF test is carried out on the residual sequence of the regression model.
If the residual sequence is stationary, it can be considered that there exists a co-integration relationship between the two variables. According to the null hypothesis of the Engle–Granger co-integration test, if prob < 0.1, it can be considered that there is a co-integration relationship between the two variables at the 10% significance level.
3.2.3. Toda and Yamamoto (1995) Causality Test
Generally, statistical causality refers to Granger causality [27]. X is said to Granger-cause Y if Y can be better predicted using the histories of both X and Y than that based on the history of Y alone. The null hypothesis of the Granger causality test is that X is not the Granger-cause of Y.
A prerequisite for performing the Granger causality test is that the time series should be stationary. For non-stationary time series, it is generally necessary to transform the time series into stationary series by differential processing and then perform the Granger causality test. Since the meaning of time series is considerably different after differentiating, the persuasiveness of the causal test on difference series may lessen. Toda and Yamamoto [28] proposed a simple but robust Granger causality test method on the basis of the vector autoregressive (VAR) model. This approach relaxes the restriction on the stationarity of time series and can construct a VAR-based model for the causality test on the time series integrated of arbitrary order.
A general VAR(p) model without adding exogenous variables can be stated as:
where represents a variable composed of endogenous variables. In the present study, eight VAR-based models are constructed, in which the values of in order are set to (lnfh,lninci), (lnfh,lninci_fc), …, (lnfh,lninci_oth) for these suggested models; α denotes a intercept vector; represents the parameter matrix of lagged variable with ith order, and denotes the corresponding error vector of .
Herein, the steps of the causality test proposed by Toda and Yamamoto can be briefly stated as:
- (1)
- Determine the integration order of all the time series in the VAR system. Record the highest integration order as n. In the present study, we set n = 1 (see Section 3.2).
- (2)
- Select a larger lag order, which is set equal to 6 in this work, and the VAR model is established by the level value of the time series.
- (3)
- According to the information criteria (such as AIC, FPPE, SBIC, and HQIC) and the obtained results of the residuals auto-correlation test, the optimal lag order p of the VAR-based model can be determined, and the stability of the characteristic roots of the VAR(p)-based models can be tested.
- (4)
- Establish the VAR model with the lag order of (p + n), and the additional nth order lag quantity is taken as an exogenous variable.
- (5)
- Granger causality test is performed on the VAR model of order (p + n). In this step, the additional n lag coefficients should be ignored.
4. Results
4.1. Cross-Correlation between Flight Hours and Incidents
The correlation between the flight hours and the total number of incidents, as well as incidents with seven categories, should be systematically assessed. To this end, the obvious lag effects of flight hours on incidents with different categories are analyzed, and the corresponding cross-correlation diagrams have been demonstrated in Figure 2. The abscissa of the consisting subfigures in Figure 2 represents flight hours with various lag lengths, and the maximum lag length is set equal to 6. Figure 2 clearly displays the correlation between the total number of incidents, the incidents with seven categories, and flight hours at different lag lengths. It implies that the total incidents as well as the incidents with seven categories are more related to the flight hours at lag 0. The contemporaneous correlations are larger than the correlations at lags. Therefore, more attention should be paid to the variable correlation in the current period.
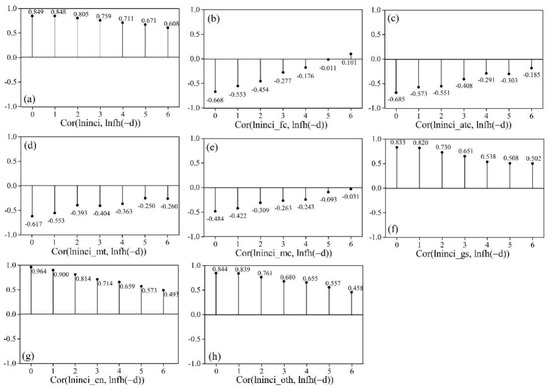
Figure 2.
The cross-correlation diagrams: (a) Cor(lninci, lnfh(−d)), (b) Cor(lninci_fc, lnfh(−d)), (c) Cor(lninci_atc, lnfh(−d)), (d) Cor(lninci_mt, lnfh(−d)), (e) Cor(lninci_mc, lnfh(−d)), (f) Cor(lninci_gs, lnfh(−d)), (g) Cor(lninci_en, lnfh(−d)) and (h) Cor(lninci_oth, lnfh(−d)).
In general, if the absolute value of the correlation coefficient is higher than 0.5, it can be rationally considered that there exists a significant correlation between the variables. From Figure 2b, the correlation coefficient between lninci and lnfh is +0.849, and the apparent positive correlation indicates that the change trend between them is the same. The correlations between incidents with different causes and flight hours are then analyzed carefully. The factors lninci_gs, lninci_en, and lninci_oth are all positively correlated with lnfh, among which the correlation coefficient between lninci_en and lnfh is the highest, whose corresponding value would be 0.964 (see Figure 2g). The correlations between lninci_fc, lninci_atc, lninci_mt, and lnfh are meaningfully negative, which are obtained as −0.668, −0.685 and −0.617, respectively. The obtained results clarify that the change trend of these three category incidents is opposite to that of flight hours. The correlation coefficient between lninci_mc and lnfh is only −0.484; however, the negative correlation is not obvious.
4.2. The Co-Integration between Flight Hours and Incidents
Before performing the co-integration test, it is necessary to test the unit root or stationary of each variable since the premise of the co-integration test is that the variable should be integrated with the same order. Table 4 shows the results of the ADF unit root test. It is worth mentioning that the level value of lninci_mc rejects the null hypothesis at the significance level of 5%, that is, lninci_mc is a stationary process without a unit root. The level value of lninci_gs also rejects the null hypothesis at a 5% significance level, but the test model contains trend items, and lninci_gs is not stationary. All the other variables cannot reject the null hypothesis at the significance level of 10%, showing that the time series contains unit roots and is non-stationary.

Table 4.
The ADF unit root test results on the understudy variables.
After performing the first-order difference on all variables, the ADF test is performed again. All variables reject the null hypothesis within the 10% significance level. It is indicating that the first-order differences of lninci, lninci_fc, lninci_atc, lninci_mt, lninci_gs, and lninci_oth are all stationary.
According to the obtained results of correlation analysis in Section 3.1, there exists a significant negative correlation between lnfh and the variables lninci_fc, lninci_atc, and lninci_mt. Logically, the reduction in lninci_fc, lninci_atc, and lninci_mt should not be attributed to the growth of flight hours. Therefore, the significant negative correlation between lnfh and the abovementioned three dependent variables is expected to be a spurious correlation, and it is meaningless to perform the co-integration test. Table 5 summarizes the Engle–Granger co-integration test results of lnfh as well as lninci, lninci_gs, lninci_en, and lninci_oth.

Table 5.
The Engle–Granger co-integration test results.
The Engle–Granger co-integration test can be divided into two steps. In the first step, lnfh is taken as an independent variable to conduct the regression on the dependent variable. The second step is to test the stationarity of the regression residual. If the residual is stationary, there would exist a co-integration relationship between the two variables. As displayed in Table 4, the significance level of the coefficient of lnfh in the given four regression equations is less than 1%. In the regression equation with lninci as the dependent variable, the constant term C represents 5% significance, and the significance level of the constant term in the other three regression equations is less than 1%. The parameters lnfh and C are taken as independent variables to conduct the regression on lninci_gs, and the standard errors of the regression coefficient are fairly small, which are 0.102 and 0.604, respectively. Through the ADF test of the regression residual, it is found that the regression residual corresponding to lninci_gs would be stable at the significance level of 1%. Therefore, there is a co-integration relationship between lninci_gs and lnfh. The regression residuals corresponding to lninci, lninci_en, and lninci_oth cannot reject the null hypothesis at the level of 10% significance; hence, there is no co-integration relationship between lninci, lninci_en, lninci_oth, and lnfh.
The obtained results show that there is a co-integration relationship between lninci_gs and lnfh, which means that there is a long-term equilibrium relationship between incidents caused by the ground support and flight hours. Therefore, flight hours can be exploited as a crucial factor to predict incidents caused by ground support. The regression equation between lninci_gs and lnfh is also known as a co-integration equation. According to this relation, lnfh increases about 0.813% when lninci_gs increases by 1%. As there is no co-integration relationship between lninci, lninci_en, lninci_oth, and lnfh, the regression equation between these variables and lnfh will not be reliable, and the prediction and interpretation capability of the regression coefficients in their corresponding equations cannot be guaranteed.
4.3. Casual Relation between Flight Hours and Incidents
The bivariate VAR models between lninci, lninci_fc, lninci_atc, lninci_mt, lninci_mc, lninci_gs, lninci_en, lninci_oth, and lnfh are appropriately established. According to the AIC, FP, HQIC, SBIC, and other information criteria, the optimal lag order of the eight VAR-based models is set equal to 1. Additionally, the Portmanteau test [29] results indicate that the residuals of the VAR (1) models are not subject to serial auto-correlation. The stability of the VAR model is tested, revealing that VAR (1) models satisfy the eigenvalue stability condition.
Based on the test method proposed by Toda and Yamamoto [28], one additional lag (n = 1) to VAR (1) models is added, and the Wald test is utilized to check (non-) Granger causalities. The results of the Toda and Yamamoto causality test have been summarized in Table 6.

Table 6.
The predicted results by Toda and Yamamoto (1995) causality test.
As shown in Table 6, we can reject the null hypothesis of lnfh that does not Granger-cause lninci_gs and lninci_en at the significance levels of 5.8% and 9.4%, respectively. It indicates that there exists a unidirectional causality from flight hours to incidents caused by the ground support or the environment factor. Table 6 also displays that there is no statistical causal relationship between flight hours and the total number of incidents. Further, there is no causal relationship between the flight hours and incidents caused by the crew, air traffic control, aircraft maintenance, machinery, and other reasons. The Granger causality basically represents a statistical causality. The causality test results indicate that the capability of predicting the number of occurred incidents due to the ground support and environmental factors can be remarkably enhanced by employing the historical data of flight hours. For the total number of incidents and the number of incidents associated with the other five causes, flight hours cannot help to explain the increasing trend. In other words, flight hours used to explain and predict the total number of incidents and the number of incidents pertaining to the other five causes would be unreliable.
5. Discussion
There is an exciting finding in the cross-correlation analysis. Generally speaking, we intuitively assume that the more flight hours, the more the number of incidents with different causation. It means that there is a positive correlation between flight hours and incidents with different causation. However, the correlation between the number of incidents due to the crew, air traffic control, maintenance, and flight hours is considerably negative, indicating that an increase in the flight hours might lead to a reduction in the number of incidents caused by the crew, air traffic control, and maintenance. The civil aviation operation system is a complex man-made system, and this negative correlation reflects the strong intervention of civil aviation authorities on operation safety. The civil aviation administration of China has invested a lot of effort in skills training and safety education for front-line operators, and implemented strict safety management in the whole process of operation. Thus, in the whole industry, the caused incidents due to human factors of front-line operators have been effectively controlled and reduced. There is a significant positive correlation between the incidents caused by the other four causes and the flight hours. For instance, for the highest positive correlation between the incidents caused by the environment and the flight hours, a value of 0.964 is observed. Therefore, in the face of the increase in flight hours, it is necessary to pay more attention to the incidents caused by environmental factors and prevent and control the number of such incidents.
The co-integration test results show that there is a long-term equilibrium relationship between incidents caused by the ground support and flight hours such that the regression residual between them is stationary. Additionally, the co-integration relationship between the two variables can be understood from a more intuitive perspective, that is, through regression and residual plots. The scatter diagrams of lninci, lninci_gs, lninci_en, lninci_oth, and lnfh are plotted, and the corresponding regression lines are added to the plots (see Figure 3). It is observable in Figure 3c that lninci_en and lnfh demonstrate a very significant linear trend, and the regression line has the highest fitting degree, followed by that of lninci_gs, lninci_oth, and lninci. However, as displayed in Figure 4c, the regression residual corresponding to lninci_en presents a down and then uptrend, which does not satisfy the characteristics of the stationary sequence. Similarly, the residual plots corresponding to lninci_oth and lninci cannot pass the stationarity test because of their obvious trends. The regression residual graph associated with lninci_gs is stable near zero (see Figure 4b), which meets the requirement of stationarity. Therefore, the conclusion of the co-integration test was rationally verified by the residual diagrams.
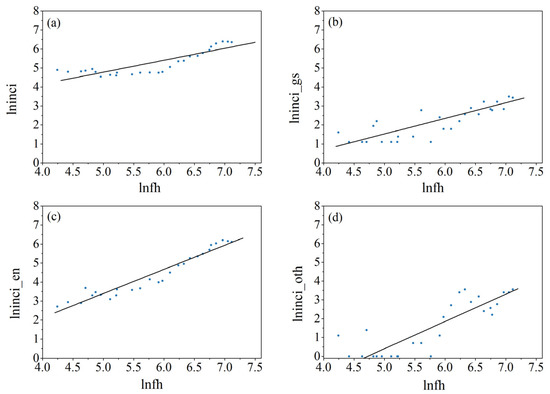
Figure 3.
The scatter diagrams and regression lines: (a) (lninci, lnfh), (b) (lninci_gs, lnfh), (c) (lninci_en, lnfh) and (d) (lninci_oth, infh).
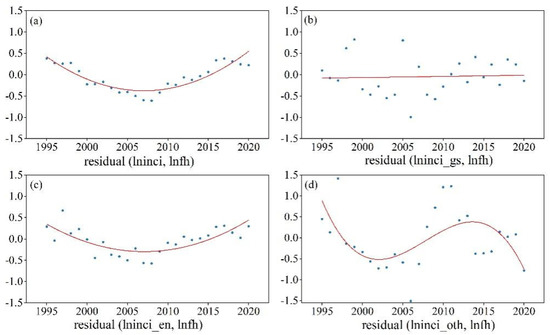
Figure 4.
The residual diagrams of the regression model: (a) (lninci, lnfh), (b) (lninci_gs, lnfh), (c) (lninci_en, lnfh) and (d) (lninci_oth, lnfh).
The stationarity of regression residuals also indicates some new enlightenment. The unstable regression residual between lninci, ninci_en, lninci_oth, and lnfh indicates that there may be a problem with missing variables in their regression model. For some categories of incidents, their corresponding numbers are not only related to the airline capacity (flight hours in this study), but also directly affected by other macro variables, such as the safety input of civil aviation authorities. In the follow-up study, if the macro variables that affect the number of incidents in each year can be effectively quantified to establish a multivariable system including incidents, airline capacity, and related macro factors, the residual of their regression model may be stable, resulting in a co-integration relationship. Through the study of the co-integration relationship, a more accurate prediction of the number of incidents can be achieved to carry out a forward-looking layout of the accident prevention work.
In the analysis of the causality relationship between incidents and flight hours, it is noted that there is no statistical causality relationship between the total number of incidents and flight hours. The one-way causal relationship only exists between flight hours and incidents caused by environments and ground support. This is a very important finding because, for the fast-growing aviation market of CAAC, both managers and researchers are always easy to attribute the rising trend of incidents directly to the growth of airline capacity. Determining the causality relationship is a complex process. Correct and reliable causality needs to be verified by both logical reasoning and statistical data. In the case of the increase in airline capacity (flight hours) and the number of incidents, the number of incidents is affected by many factors. Thus, it is not comprehensive and reasonable to attribute the growth of incidents only to the growth of airline capacity. As flight hours are the Granger-cause of incidents caused by ground support and environmental factors, in the face of the increase in flight hours, policymakers should pay special attention to the high trend of these two categories of incidents, and do their best in preventing incidents and accidents.
6. Conclusions
Through the time-series analysis method, this paper reveals the cross-correlation, co-integration and causality relationship between aviation incidents and airline capacity in China from 1994 to 2020.
The cross-correlation analysis indicates that the incidents are more related to the number of flight hours in the current period, that is, historical capacity conditions do not affect the current number of incidents. There is a significant positive correlation between the total number of incidents and flight hours, that is, there is a co-directional relationship between their variations. Among the incidents of various causes, there is a significant positive correlation between the incidents caused by environmental factors, ground support, other factors, and flight hours. The obtained results indicate that the maximum positive correlation between incidents caused by environmental factors and flight hours is observed. Therefore, as the number of flight hours increases, specific attention should be paid to controlling the number of such incidents. There is an apparent negative correlation between the number of incidents caused by the crew, air traffic control, aircraft maintenance, and the number of flight hours. Such a fact reflects that the CAAC has achieved remarkable results in the operation safety work in terms of human factors.
The co-integration analysis shows that there would be no co-integration relationship between the total number of incidents and flight hours. Among the incidents of various causes, the highest co-integration relationship is only observed between the incidents caused by the ground support and flight hours, indicating a long-term equilibrium relationship. The stationarity of the regression residual in the co-integration test shows that there is a problem of missing variables in the regression model between the total number of incidents or incidents caused by environmental factors, or other factors, and flight hours. As a result, it is necessary to introduce relevant macro variables, such as safety input into the co-integration regression, to find the co-integration relationship. The co-integration relationship is helpful in accurately predicting all kinds of incidents and achieving the forward-looking layout of accident prevention.
The causality analysis shows that there is no Granger causality between the total number of incidents and flight hours. Among the incidents of different causes, only the incidents caused by ground support and environmental factors have a one-way causal relationship with flight hours. It suggests that the historical data of flight hours can be employed to interpret and predict these two incidents. Therefore, when the number of flight hours shows an increasing trend, more attention should be paid to the high incidence of incidents caused by ground support and environmental factors, and accident prevention should be accomplished.
The incident is a crucial approach to preventing accidents and enhancing safety. By examining the longitudinal relationship between incidents and flight hours, this study may have a particular guiding significance for safety management at the industry level. The correlation, co-integration, and causality analysis can clarify the relationship between incidents and their influencing factors, so as to provide solid references for policymakers to implement scientific safety management.
There are strengths and limitations in the present scrutiny, suggesting the future research path. In terms of the number of incidents, in addition to the most important factor of airline capacity, the safety investment of airlines and the supervision of civil aviation authorities also have a certain influence on the number of incidents. However, due to the availability of data, the analysis of such factors was not included in this study. For complex civil aviation systems, these factors will be considered in future studies, leading to providing accurate data support for civil aviation safety management.
Author Contributions
Conceptualization, P.H. and R.S.; methodology, P.H.; software, P.H.; validation, P.H. and R.S.; formal analysis, R.S.; investigation, P.H.; resources, R.S.; data curation, P.H.; writing—original draft preparation, P.H.; writing—review and editing, P.H. and R.S.; visualization, P.H.; supervision, R.S.; project administration, P.H.; funding acquisition, P.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Tianjin Research Innovation Project for postgraduate students under Contract No. 2021YJSB241.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, upon reasonable request.
Acknowledgments
The authors would like to thank Tianjin Municipal Education Commission for their financial support to this research, and the authors would also like to thank the data support of Civil Aviation Authority of China.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cui, Q.; Li, Y. The change trend and influencing factors of civil aviation safety efficiency: The case of Chinese airline companies. Saf. Sci. 2015, 75, 56–63. [Google Scholar] [CrossRef]
- Oster, C.V.; Strong, J.S.; Zorn, K.C. Analyzing aviation safety: Problems, challenges, opportunities. Res. Transp. Econ. 2013, 43, 148–164. [Google Scholar] [CrossRef]
- Zhou, T.; Zhang, J.; Baasansuren, D. A Hybrid HFACS-BN Model for Analysis of Mongolian Aviation Professionals’ Awareness of Human Factors Related to Aviation Safety. Sustainability 2018, 10, 4522. [Google Scholar] [CrossRef] [Green Version]
- ICAO (International Civil Aviation Organization). Global Aviation Safety Snapshot. 2021. Available online: https://www.icao.int/Pages/default.aspx (accessed on 30 November 2021).
- Lei, Z.; O’Connell, J.F. The evolving landscape of Chinese aviation policies and impact of a deregulating environment on Chinese carriers. J. Transp. Geogr. 2011, 19, 829–839. [Google Scholar] [CrossRef]
- IATA (International Air Transport Association). IATA Forecasts Passenger Demand to Double Over 20 Years. Available online: https://www.iata.org/en/pressroom/pr/2016-10-18-02 (accessed on 30 November 2021).
- Wiegmann, D.A.; Thaden, T.L.V. Using schematic aids to improve recall in incident reporting: The Critical Event Reporting Tool (CERT). Int. J. Aviat. Psychol. 2003, 13, 153–171. [Google Scholar] [CrossRef]
- Heinrich, H.; Petersen, D.; Ross, N. Industrial Accident Prevention, 5th ed.; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Reason, J. Safety in the operating theatre part 2: Human error and organisational failure. Qual. Saf. Health Care 2005, 14, 56–61. [Google Scholar] [CrossRef] [Green Version]
- Hollnagel, E. Safety-I and Safety-II; CRC-Press: London, UK, 2014. [Google Scholar]
- Balicki, W.; Głowacki, P.; Loroch, L. Large aircraft reliability study as important aspect of the aircraft systems’ design changes and improvements. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 235, 138–147. [Google Scholar] [CrossRef]
- Raghavan, S.; Rhoades, D.L. Revisiting the relationship between profitability and air carrier safety in the US airline industry. J. Air Transp. Manag. 2005, 11, 283–290. [Google Scholar] [CrossRef]
- Bazargan, M.; Guzhva, V.S. Impact of gender, age and experience of pilots on general aviation accidents. Accid. Anal. Prev. 2011, 43, 962–970. [Google Scholar] [CrossRef]
- Di Gravio, G.; Mancini, M.; Patriarca, R.; Costantino, F. Overall safety performance of Air Traffic Management system: Forecasting and monitoring. Saf. Sci. 2015, 72, 351–362. [Google Scholar] [CrossRef]
- Aguiar, M.; Stolzer, A.; Boyd, D.D. Rates and causes of accidents for general aviation aircraft operating in a mountainous and high elevation terrain environment. Accid. Anal. Prev. 2017, 107, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Hao, Y.; Wang, S.; Wu, H. The dynamics between voluntary safety reporting and commercial aviation accidents. Saf. Sci. 2021, 141, 105351. [Google Scholar] [CrossRef]
- Song, L.; He, X.; Li, C. Longitudinal relationship between economic development and occupational accidents in China. Accid. Anal. Prev. 2011, 43, 82–86. [Google Scholar] [CrossRef] [PubMed]
- Yannis, G.; Papadimitriou, E.; Folla, K. Effect of GDP changes on road traffic fatalities. Saf. Sci. 2014, 63, 42–49. [Google Scholar] [CrossRef]
- Li, X.; Wu, L.; Yang, X. Exploring the impact of social economic variables on traffic safety performance in Hong Kong: A time series analysis. Saf. Sci. 2018, 109, 67–75. [Google Scholar] [CrossRef]
- Griffin, T.G.C.; Young, M.A.; Stanton, N.A. Human Factors Models for Aviation Accident Analysis and Prevention; Ashgate: Aldershot, UK, 2015. [Google Scholar]
- CAAC (Civil Aviation Administration of China). MH/T 2001-2018 Civil Aircraft Incident. 2018. Available online: http://www.caac.gov.cn/XXGK/XXGK/BZGF/HYBZ/201902/P020190218522047031827.pdf (accessed on 30 November 2020).
- ICAO (International Civil Aviation Organization). Annex 19: Safety Management, 2nd ed.; International Civil Aviation Organization: Montreal, QC, Canada, 2016; Available online: https://www.icao.int/training/NASP_iPack/Forms/AllItems.aspx?RootFolder=%2ftraining%2fNASP%5fiPack%2fAnnex%5f19&FolderCTID=0x0120009A316302EB2CA1469A0AB4C3A55B71FE (accessed on 30 November 2021).
- Pearson, E.S. An appreciation of some aspects of his life and work. Biometrika 1938, 28, 193–257. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W. Co-integration and error correction: Representation, estimation, and testing. Econometrica 1987, 55, 251–276. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [CrossRef]
- Johansen, S. Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models. Econometrica 1991, 59, 1551. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Toda, H.Y.; Yamamoto, T. Statistical inference in vector autoregressions with possibly integrated processes. J. Economet. 1995, 66, 225–250. [Google Scholar] [CrossRef]
- Ljung, G.M.; Box, G.E.P. On a measure of lack of fit in time series models. Biometrika 1978, 65, 297. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).