Abstract
Before the transaction data in the blockchain is successfully linked, its signature must be publicly verified by a large number of nodes in the blockchain, which is also one of the ways to leak transaction information. To alleviate the contradiction between the public verifiability of signatures and the protection of transaction privacy, we introduce a verifiably encrypted signature scheme into the blockchain. A verifiably encrypted signature scheme contains two parts of signature information: the encrypted signature is used for public verification, and the ordinary signature is used for internal verification. To reach this goal even better, we design a new lattice-based verifiably encrypted signature scheme, which separates the parameter settings of the signer and the adjudicator, and replaces the Gaussian sampling algorithm with a small range of uniform random sampling, achieving better efficiency and security.
1. Introduction
1.1. Verifiably Encrypted Signature
A verifiably encrypted signature was first given by Asokan et al. [1] in 1997, which is used to ensure the fairness of the exchange process in a distributed network [2]. Compared with the ordinary signature, the verifiably encrypted signature has an adjudicator besides the signer and verifier. The signer encrypts the ordinary signature using the adjudicator’s public key, and the verifier uses the public keys of the signer and the adjudicator to verify the authenticity of the signature ciphertext. If there is a dispute, the adjudicator recovers the signer’s ordinary signature from the signature ciphertext. A verifiably encrypted signature is the core of fair contract signing protocols. When the party signing the online contract repudiates, the adjudicator can take the extracted signature as evidence of the signer’s signing behavior. In addition to the above applications, a verifiably encrypted signature has many important applications in other fields. Jae Hong Seo et al. [3] have implemented the accumulable optimistic fair exchange using a verifiably encrypted signature. Yujue Wang et al. [4] have introduced a cascading instantiable blank signature on the basis of a verifiably encrypted signature, which realizes the protection of progressive decision management. Therefore, the research on a verifiably encrypted signature has great practical impetus.
A verifiably encrypted signature has achieved good results under the assumption of traditional number theory, such as [5,6,7]. In pace with the rapid growth of quantum algorithms, verifiably encrypted signatures that can strive against quantum algorithm attacks become more pressing. As the most powerful branch of post-quantum cryptography, lattice-based cryptography has a good degree of performance in the construction of various cryptographic primitives. A lattice-based verifiably encrypted signature includes [8,9,10]. To successfully complete the adjudication function of the adjudicator, these schemes have one thing in common: the signer’s key depends on the adjudicator’s public key. Then, the signer’s key will change with the change of the adjudicator, which forms a restriction for the signer to choose the adjudicator. It is of great significance to remove the binding relationship between the key of the signer and the adjudicator in a lattice-based verifiably encrypted signature scheme.
Beyond the above point, as a basic algorithm in lattice-based cryptography [11,12], the Gaussian sampling algorithm has more computational complexity [13] and is vulnerable to side-channel attacks [14,15]. Thomas Prest [13] mentions the following facts. The existing algorithms cannot use discrete Gaussian distribution directly; they have to sample from a statistically approximate distribution. It is generally required that the statistical distance between the sampling distribution and the expected discrete Gaussian distribution is less than . To achieve it, a floating-point operation with a precision of at least 100 bits is required. Any precomputation means storing the variable values with the same precision. This may seriously affect the sampling performance on the computer, or even make it impractical to implement on a limited device. With regard to the security, Léo Ducas et al. [16] emphasize the potential side-channel attack risk of Gaussian sampling and suggest replacing Gaussian sampling with random sampling. As for small-range random sampling, the sampling rejection algorithm ensures that the algorithm output will not disclose the signature private key by filtering the output value.
In the wake of the post-quantum cryptography standard collection activities, the efficiency and security of lattice-based cryptosystems have attracted many researchers’ attention, and more and more work has been performed to implement the lattice-based cryptosystems, which promotes lattice-based cryptography from the theoretical stage to the practical stage. So far, it is an important research direction to design a secure lattice-based verifiably encrypted signature scheme with better efficiency.
1.2. Application
Blockchain is a research field that many cryptographers have recently been paying close attention to, and it is widely used in financial payments such as Bitcoin. At present, digital signature technology is used in the authentication link of blockchain. Specifically, when payer Alice uses Bitcoin or other digital currency to pay payee Bob, she needs to sign the transaction content and broadcast it throughout the whole network, to verify the transaction in the network without an authority center.
Blockchain is an open network, and it is an important demand for privacy protection for traders to complete the public verification of transactions without disclosing the sensitive information of transactions. Transaction information can appear on the blockchain network in the form of a hash digest, but corresponding digital signatures can still disclose sensitive information. Gustavus J. Simmons [17] tell us that sensitive information can be embedded in the random value of the digital signature and transmitted with the message signature pair, which leads to a situation: in the process of signing a transaction, the digital signature may involve sensitive information, and Alice does not want anyone other than Bob to obtain the signature. Some people may think that this is simple: encrypting Alice’s signature with Bob’s public key and sending the result to Bob. However, we say that this idea is naive: because if the public key encryption scheme is adopted, other participants in the network will no longer be able to publicly verify transactions and signatures, which goes against the original intention of the decentralized blockchain.
We introduce verifiably encrypted signatures into the blockchain, which will solve the problem that signatures need to be publicly verified and that signatures need to avoid the disclosure of transaction information. The verifiably encrypted signature scheme designed in this paper can reduce privacy leakage in the blockchain. In addition, our scheme can also be used in other environments with privacy protection requirements for information authentication, such as image encryption authentication privacy protection [18,19].
1.3. Our Contribution
- Taking the verifiably encrypted signature in a lattice as the research object, we investigate the limitations caused by the correlation between the parameters of the signer and the adjudicator, the important role of the Gaussian sampling algorithm in lattice signatures, and the fact that the Gaussian sampling algorithm is vulnerable to side-channel attacks. On this basis, a new and verifiably encrypted signature scheme based on the assumption of the lattice difficulty problem is designed. The new scheme realizes the relative independence of the keys of the signer and the adjudicator and avoids the pre-set communication between the two parties. We replace the Gaussian sampling algorithm with a small range of uniform random sampling, which enhances the scheme’s security and efficiency.
- We analyze the double needs of blockchain for the authentication and privacy of signatures and interpret verifiably encrypted signatures in a manner suitable for the blockchain environment. We regard the transaction’s initiator as the signer, the transaction’s receiver as the adjudicator, and the verifier who can verify the encrypted signature as other public nodes in the blockchain. We embed verifiably encrypted signatures into the blockchain environment and realize the public authentication and privacy protection of transactions with the public verification and arbitration verification functions of verifiably encrypted signatures.
1.4. Paper Outline
The subsequent content of this paper includes the following six aspects. In Section 2, we display some notations and facts, as well as the module short integer solution problem and the computational ring-LWR assumption. In Section 3, we describe the verifiably encrypted signature’s definition and security model, and the basic structure of the blockchain. In Section 4, we design the verifiably encrypted signature scheme without Gaussian sampling from a lattice, which is suitable for blockchain scenarios. Our scheme’s correctness analysis is also here. In Section 5, we analyze our scheme’s security, including strong unforgeability, strong opacity, and extractability. In Section 6, we make a comparison between the previous related schemes and point out the application mode and the special role of our scheme in the blockchain. Lastly, a conclusion is given in Section 7.
2. Preliminaries
2.1. Notations
The symbols in the paper mainly come from [16,20].
and are two polynomial rings.
For integer , . For , . For , .
denotes uniform distribution in , , .
For , w is a polynomial with coefficients that are less than or equal to in , and .
.
For , integer x, , floor rounding function is defined as: , function is defined as: .
Reconciliation rounding function , reconciliation cross-rounding function: .
The algorithm rec, with input and , output , where x is the element with the smallest distance from y, such as .
The randomized doubling function , where e samples from with probabilities .
Functions : , denote that there exist two constants such that for all .
At the end of this subsection, we summarize the basic symbols used in the text into Table 1 for easy searching.

Table 1.
Symbol Description.
2.2. Lattice Problems and Facts
Definition 1
([21]). is defined as follows: Given , which are uniform and independent, find , such that and , where .
The module short integer solution problem (M-SIS) is a generalization of the short integer solution problem (SIS) and the ring short integer solution problem (R-SIS), whose hardness is based on the module shortest independent vectors problem (Mod-SIVP).
Definition 2
([20]). s is selected from a distribution χ over R. Let be the distribution of , where , and let be the distribution of , where . Denote and , . For a challenger , is the probability for an adversary to win with ; is the probability for an adversary to win with .
The computational ring-LWR assumption with respect to a secret distribution χ says that for all challengers , if is negligible for any adversary , does so.
The computational ring-LWR assumption with respect to a secret distribution , also as , is based on the approximate shortest independent vectors problem (app-SIVP).
Lemma 1
([20]). If is odd and , then .
Lemma 2
([22]). and are two positive integers, is a fixed integer, and . If is negligible, then the statistical distance between the distribution of and the distribution of is also negligible.
3. General Model of the Verifiably Encrypted Signature and Blockchain
3.1. Definition of Verifiably Encrypted Signature
For the verifiably encrypted signature’s definition and security model, we refer to Kee Sung Kim and Ik Rae Jeong [10]. A verifiably encrypted signature scheme involves three parties: the signer, verifier, and adjudicator. The signer is responsible for generating the ordinary signature and the verifiably encrypted signature of the message, the verifier is responsible for the verification of two kinds of signatures, and the adjudicator is responsible for the ordinary signature extraction of the verifiably encrypted signature to prevent the signer’s malicious repudiation. The three parties work together to complete the following algorithms.
- Setup (): is the security parameter as input; this algorithm outputs as the system public parameter.
- AKeyGen (): The adjudicator provides public key and secret key , which are used to generate the signature ciphertext and extract an ordinary signature.
- KeyGen (): The signer provides a secret signing key and a public verification key , which are used to generate and verify the ordinary signature, respectively.
- Sign (): With the signing key , the signer provides an ordinary signature for message M.
- Verify (): Given message M and its signature associated with the verification key , the verifier and the adjudicator determine whether the ordinary signature provides legal authentication for the message M. If the answer is yes, they output 1, indicating approval of the authentication; otherwise, they output 0, indicating a denial of the authentication.
- VES-Sign (): With signing key , message M and the adjudicator’s public key , the signer provides the verifiably encrypted signature .
- VES-Verify (): Given the signer’s verification key , the adjudicator’s public key , and message M, as well as its verifiably encrypted signature , the verifier and the adjudicator determine whether the signature provides legal authentication for the message M. If the answer is yes, they output 1, indicating approval of the authentication; otherwise, they output 0, indicating denial of the authentication.
- Adju (): With the adjudicator’s secret key , the signer’s verification key and message M, as well as its verifiably encrypted signature , the adjudicator extracts an ordinary signature from for message M.
The correctness of the scheme includes two aspects.
- , the output of algorithm VES-Sign (), needs to be verified by algorithm VES-Verify ().
- , the output of algorithm Adju (), needs to be verified using algorithm Verify ().
3.2. Security Model of the Verifiably Encrypted Signature
A verifiably encrypted signature scheme should satisfy strong unforgeability, strong opacity, extractability, and abuse-freeness. Because strong unforgeability implies abuse-freeness, we only consider three security definitions.
3.2.1. Strong Unforgeability
- Initialization: Challenger executes the algorithms Setup, AKeyGen, and KeyGen, and obtains the public parameters , the adjudicator’s secret key , and the public key , as well as the signer’s signing key and verification key . Then, challenger provides the public parameters , the adjudicator’s secret key and public key , and the signer’s verification key to adversary .
- Verifiably Encrypted Signature Queries: Adversary adaptively performs verifiably encrypted signature queries with a polynomial bound.Adversary selects message M and sends it to challenger for the associated verifiably encrypted signature. Challenger invokes the VES-Sign algorithm, and returns the result to adversary . Adversary can adaptively execute the query polynomial.
- Forgery: When adversary finishes the queries, he gives a fresh message and its verifiably encrypted signature .
If a message–signature pair can pass the VES-Verify algorithm, and it is not the result of some verifiably encrypted signature query, adversary wins the game.
Theorem 1.
A verifiably encrypted signature scheme owns strong unforgeability, if, for every adversary with polynomial bounded computational resources, the probability of him winning the above game is negligible.
3.2.2. Strong Opacity
- Initialization: Challenger executes algorithms Setup, AKeyGen, and KeyGen, obtains public parameters , and the adjudicator’s secret key and public key , as well as the signer’s signing key and verification key . Then, challenger provides public parameters , the adjudicator’s public key , and the signer’s verification key to adversary .
- Queries: Adversary adaptively performs verifiably encrypted signature queries and adjudication queries with a polynomial bound.
- VES-Sign Query: Adversary selects message M, and sends it to challenger for the associated verifiably encrypted signature. Challenger invokes the VES-Sign algorithm and returns the result to adversary . Adversary can adaptively execute the query polynomial.
- AdjuQuery: Adversary sends to challenger for the associated ordinary signature. Challenger invokes the Adju algorithm, and returns the result to adversary . Adversary can adaptively execute the query polynomial.
- Forgery: When adversary finishes the queries, he gives a fresh message and its ordinary signature .
If a message–signature pair can pass the Verify algorithm and it is not the result of some adjudication query, adversary wins the game.
Theorem 2.
A verifiably encrypted signature scheme owns strong opacity if, for every adversary with polynomial bounded computational resources, the probability of him winning the above game is negligible.
3.2.3. Extractability
- Initialization: Challenger executes the algorithms Setup and AKeyGen, and obtains public parameters , the adjudicator’s secret key , and public key . Then, challenger provides the public parameters and the adjudicator’s public key to adversary .
- AdjuQueries: Adversary adaptively performs adjudication queries with a polynomial bound.Adversary sends to challenger for the associated ordinary signature. Challenger invokes the Adju algorithm and returns the result to adversary . Adversary can adaptively execute the query polynomial.
- Forgery: When adversary finishes the queries, he gives a message and its verifiably encrypted signature , as well as a signer’s key pair .
If the message–signature pair can pass the VES-Verify algorithm, and the result of algorithm Adju () is invalid, adversary wins the game.
Theorem 3.
A verifiably encrypted signature scheme owns extractability, if, for every adversary with polynomial bounded computational resources, the probability of him winning the above game is negligible.
3.3. The Structure of Blockchain
The blockchain is a chain composed of a large number of blocks. Blocks are generated via an enormous number of distributed network nodes through a consensus algorithm. Each block records different transaction contents. In a blockchain, each node can be considered a user. Each user has a unique address information identification, the address information comes from the user’s public key, and the private key is held locally by the user. When user A attempts to initiate a transaction with user B, he signs the transaction. The transaction will lock a payout and claim that only recipients who meet the lockup conditions will be the owner of the money. To be specific, user A signs the transaction using his private key, claiming that the money can only be spent by providing recipient B’s legitimate signature. User A marks B with user B’s address, which can be a string of numbers. Because this condition is met, the only user who can provide B’s signature is B himself, and so funds are safely transferred from A to B. Each node in the blockchain performs the following tests after receiving a transaction:
- Check whether the signature in the transaction is valid or not, and reject it if the signature is invalid.
- Check whether the delivery address has sufficient funds to complete the transaction, and reject the transaction if the balance is insufficient.
- Update the blockchain ledger based on the consensus mechanism.
The decentralized design not only reduces the risk of network congestion and collapse, but also protects the privacy and freedom of users. However, for some specific focus events, such as a huge transaction on the blockchain during the time period when a company or an individual needs to pay a huge amount of money, even if there is no identity information of both parties in the transaction, people will associate the possible link between them and obtain the property distribution of the parties through the public transaction information. Identity anonymity is far from enough for real life, where identity can be locked through multiple channels. If transaction information and corresponding signatures can obtain more privacy protection, the blockchain can give people more of a sense of security.
4. Lattice-Based Verifiably Encrypted Signature Scheme without Gaussian Sampling
Our scheme is based on Fiat–Shamir style lattice-based signature schemes [23]; we use the construction framework of the scheme [23] and the optimization algorithm of the scheme [16] is also applicable. In our scheme, the signer’s key generation algorithm and the adjudicator’s key generation algorithm are relatively independent, which avoids the interaction between the signer and the adjudicator in the key generation phase. We use a small range of uniform random sampling algorithms instead of a Gaussian sampling algorithm to reduce the impact of side-channel attacks and the computational complexity of the scheme.
4.1. Design
- Setup (n): The system parameters, sets, and functions involved in the scheme are defined as follows.
- = 8,380,417, , , , , = 523,776, , is odd, , .
- Function is defined as in [20].
- Functions and are collision-resistant hash functions.
- AKeyGen (n): The adjudicator selects , and computes , . Then, he provides a public key and a secret key .
- KeyGen (n): The signer samples , , and computes . Then, verification key , and signing key .
- Sign (): The signer obtains the ordinary signature with respect to the signing key and the message .
- Sample , , and compute , , .
- If , repeatedly sample , and compute , , .
- If , return as the signature of message .
- Verify (): Given message and its signature associated with verification key , the verifier make the following judgment. If and holds, the signature is valid and output 1; otherwise, the signature is invalid and output 0.
- VES-Sign (): With signing key , message , and the adjudicator’s public key , the signer computes the verifiably encrypted signature .
- Sample , , and compute , , , .
- If or , repeatedly sample , and compute , , , . The operations end when and .
- Compute and construct the corresponding non-interactive zero-knowledge proof due to [24].
- Sample , and let , , .
- Let , , .
Then, verifiably encrypted signature . - VES-Verify(): Given , , and message , as well as its verifiably encrypted signature , the verifier makes the following judgment.
- Judge the legality of . If the result is no, output 0 and reject the signature; otherwise, continue.
- If and holds, the signature is valid and output 1; otherwise, the signature is invalid and output 0.
- Adju (): With , and message M, as well as its verifiably encrypted signature , the adjudicator extracts an ordinary signature from for message M.
- Compute and .
- Let .
Then, output the ordinary signature .
4.2. Correctness Analysis
The correctness analysis of the scheme includes the correctness of the ordinary signature, the correctness of the verifiably encrypted signature, and the correctness of the adjudication algorithm. We will elaborate on them separately.
4.2.1. The Correctness of the Ordinary Signature
According to the analysis in reference [16], in the ordinary signing algorithm, when the recommended parameters are used, the average number of iterations is
so that the signing algorithm can be effectively terminated, and satisfying the condition can be obtained easily. In addition, because and , we have ; therefore, .
4.2.2. The Correctness of the Verifiably Encrypted Signature
In the verifiably encrypted signing algorithm, the probability of is about . When , the probability of is no more than the probability of , so that the probability of both and is about . Therefore, in the verifiably encrypted signing algorithm, when the recommended parameters are used, the average number of iterations is =, so that the verifiably encrypted signing algorithm can be effectively terminated, and , satisfying the condition and can be obtained easily. Moreover, because and , we have ; therefore, .
4.2.3. The Correctness of the Adjudication Algorithm
When , , , , =, . Due to , , , and , , , we have and , so that with overwhelming probability.
According to Lemma 1, . Due to , ; hence, .
According to the verifiably encrypted signing algorithm, , , , and . From the analysis of Section 4.2.1, is a valid ordinary signature.
5. Security Analysis of Our Scheme
5.1. Strong Unforgeability of Our Scheme
Theorem 4.
If there exists adversarywho can attack the strong unforgeability of our scheme with a probability that cannot be ignored, then challengercan find a solution to an M-SIS problem instance with a non-negligible probability by using his ability. In other words, because the M-SIS problem is difficult to solve, our scheme is strongly unforgeable.
Proof.
Suppose that adversary can forge a verifiably encrypted signature with probability , and the maximum number of times he executes hash queries is ; the maximum number of times that he executes the verifiably encrypted signature queries is . By interacting with adversary , challenger can find the non-zero vector satisfying the condition and , with probability for the M-SIS problem instance .
- Initialization: Challenger gives system parameters according to the algorithms Setup, and provides the adjudicator’s public key and secret key according to algorithms AKeyGen. He also samples , computes , and sets the verification key and signing key . Then, the challenger provides the system parameters, the adjudicator’s public key and secret key , and the signer’s public verification key to adversary .
- Queries: Adversary adaptively performs the following queries with a polynomial bound.
- Query: Challenger maintains a list for queries. When adversary sends message to challenger , samples , . Then, he selects , such that . computes , lets , saves in list , and returns . When adversary sends message for the query again, returns directly.
- VES-Sign Query: Adversary selects message and sends it to challenger for the associated verifiably encrypted signature. Challenger searches list for and constructs the non-interactive zero-knowledge proof for . Then, Challenger samples and computes , , , , , . Finally, Challenger returns to adversary .If does not exist in list , challenger executes query for message firstly.
- Forgery: When adversary finishes the queries, he gives a new message and its verifiably encrypted signature , which satisfies and .
Because adversary can make at most hash queries and verifiably encrypted signature queries, the number of is, at most, . For an undocumented , adversary has only probability of producing c, such that . Therefore, comes from with probability . In addition, adversary forges a valid verifiably encrypted signature with probability , so that comes from the valid forgery and with probability . Let , it comes from some query or verifiably encrypted signature query.
If comes from some query, interacts with adversary to execute queries and verifiably encrypted signature queries again. According to [25], adversary generates a new verifiably encrypted signature for message with probability , where . This is because , , so that . Due to , , , , so that . If , is a solution. If , there exists such as and with overwhelming probability, then is a solution. For adversary , the occurrence probabilities of and are equal, so that is obtained with a probability of at least .
If comes from some verifiably encrypted signature query, . If or , then adversary finds a preimage of . Therefore, and , then . Due to , . Moveover, , , then . Therefore, is a solution.
In short, whether comes from query or a verifiably encrypted signature query, challenger can find a non-zero vector satisfying and with a probability of . □
5.2. The Strong Opacity of Our Scheme
In our scheme, message ’s verifiably encrypted signature is , and the strong opacity of our scheme equals that will not divulge information about .
For , according to Lemma 2, and are statistically indistinguishable, and has nothing to do with , so that will not divulge information about .
According to the hardness of the module short integer solution problem, will not divulge information about , and then also will not divulge information about .
is the zero-knowledge proof of , so will not divulge information about .
In conclusion, will not divulge information about , so that cannot be obtained merely by ; hence, our scheme owns strong opacity. For a more rigorous description of strong opacity, see Theorem 5.
Theorem 5.
If there exists an adversary who can break the strong opacity of our scheme with probability ϵ, then challenger can construct an algorithm that can solve the M-SIS problem with a probability of at least , where is the maximum number of queries to .
Proof.
Given an instance of M-SIS problem , challenger needs to find a non-zero short satisfying .
- Initialization: Challenger executes the algorithms Setup, AKeyGen, and KeyGen, and sends the public key , , and to the the adversary .
- Queries: Allowed queries include H queries, VES-Sign queries and Adju-Queries. When finishes the queries, and with probability outputs a forged ordinary signature for some message, Challenger can solve the M-SIS problem.
- H Query: first examines the list L for this query . If it has not existed in the list L, randomly chooses , records the corresponding relationship between and c in the table, and sends c to . If the query has existed in the list L, returns its corresponding c to directly.
- VES-Sign Query: adaptively chooses message , and sends it to the challenger . executes the VES-Sign algorithm, and returns to .
- AdjuQuery: Assume that has queried to H before Adju-Queries. When receiving the Adju-Queries to the verifiably encrypted signature , returns the ordinary signature .
Hence, finally proposes a valid ordinary signature with probability . If c is a response of the VES-Sign query, there exists another signature for some message , such that
Hence, , and . That is, . Note that successfully forges a new and valid signature; thus, . Because , thus there exists a non-zero vector , such that , and . That is, challenger solves the M-SIS problem instance with probability . If c is not a response of the VES-Sign query, may sign the same message again, and the situation is similar. □
5.3. Extractability of Our Scheme
For a verifiably encrypted signature associated with message , if is valid, we can extract an ordinary signature . Proof guarantees the existence of the short vector in . With the adjudicator’s secret key , we can compute , ; let , then is an ordinary signature for message .
6. Comparison of Related Work and Our Scheme’s Application in the Blockchain
So far, there has been a lot of work on verifiably encrypted signatures. We mainly compare some of the main schemes in terms of application scenarios, key features, difficulties basis, and resistance to quantum attack. Table 2 shows the details of the comparison. Due to space, some abbreviations are used in Table 2, which are explained as follows. “Resistance to Quantum Attack” is abbreviated as RQA, “cascade-instantiable blank signature” is abbreviated as CBS, “adjudicator public key binding” is abbreviated as APKB, “inhomogeneous small integer solution problem” is abbreviated as ISIS, and “Module short integer solution problem” is abbreviated as M-SIS.

Table 2.
Comparison of Related Work.
According to the analysis in Table 2, schemes in the literature [8,9,10] and our scheme are all lattice-based schemes against quantum algorithm attacks. We further analyze the efficiency of these four schemes in Table 3.

Table 3.
Comparisons of the Schemes in Lattice.
Table 3 lists the comparisons of different verifiably encrypted signature schemes in lattices. m and n represent the dimension and rank of the lattice used in the scheme [8,9,10], respectively, and k and l represent the dimension and rank of the modular lattice in our scheme, respectively. These four parameters play a decisive role in the verification key size, signing key size, and signature size. Our scheme is based on module lattices, and the values of the corresponding parameters are smaller than that of in general lattices. Thus, the scheme in our work has advantages in terms of signature and key sizes. Furthermore, our construction does not require Gaussian sampling, and it is much simpler to implement it securely against side-channel attacks.
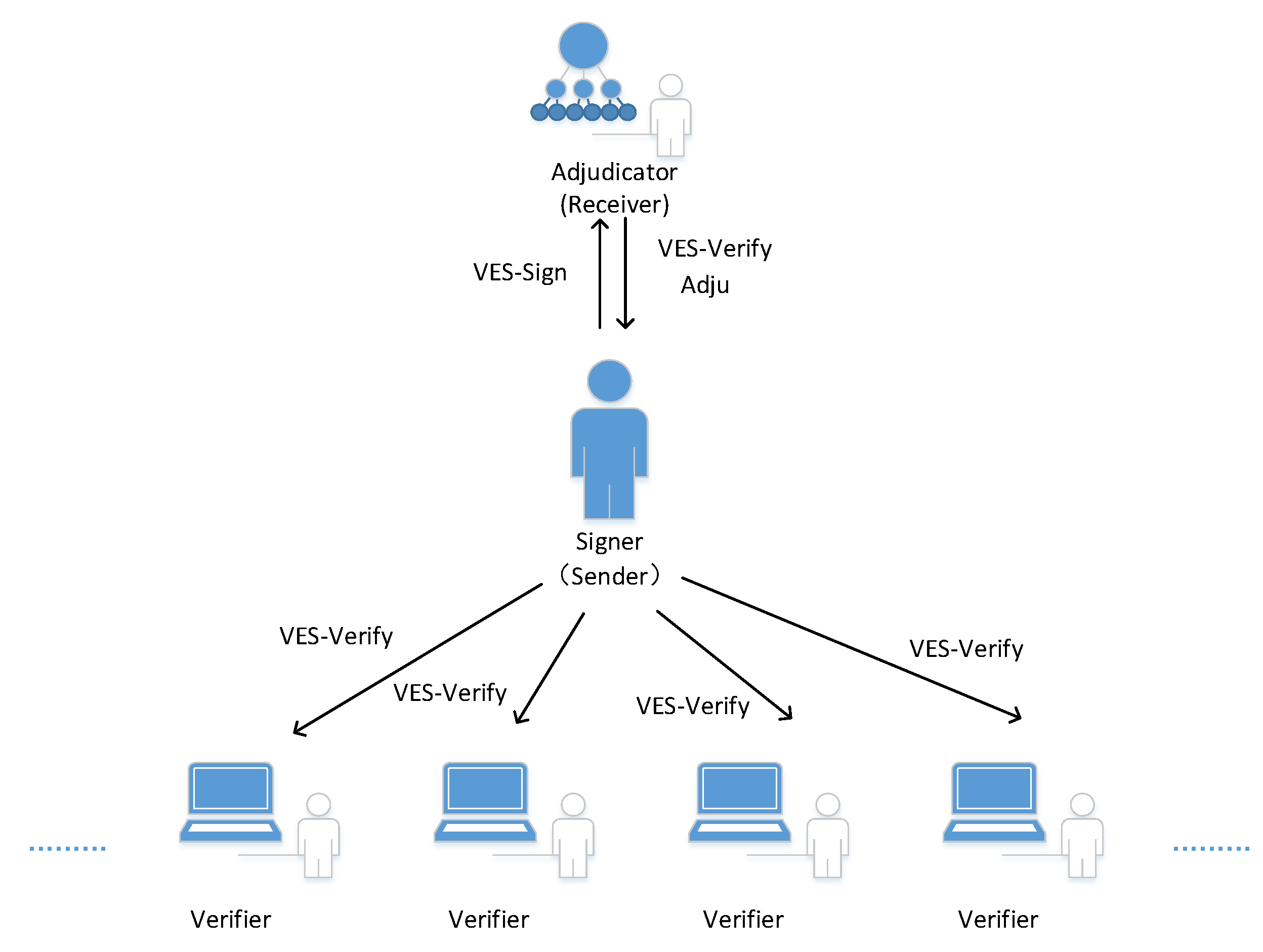
When our scheme is applied to the blockchain scenario, there are three participants: the payer Alice (signer), the payee Bob (digital signature receiver), and the verifier (miner in the blockchain). More precisely, these three parties are nodes in the blockchain network. After generating a transaction between Alice and Bob, Alice signs the transaction with her private key, associates Bob’s public key with the signature to obtain the verifiably encrypted signature, then broadcasts the result to the blockchain network. The miner in charge of keeping a ledger verifies the signature and records it. Each miner can verify the verifiably encrypted signature to prove the real existence of the transaction, but they cannot obtain more information about the transaction and both parties from the signature. The payee Bob has the private key used for the encrypted signature and is able to obtain the common signature of the transaction for further confirmation of the transaction, and as evidence to avoid disputes with the payer Alice. Figure 1 shows the basic framework.
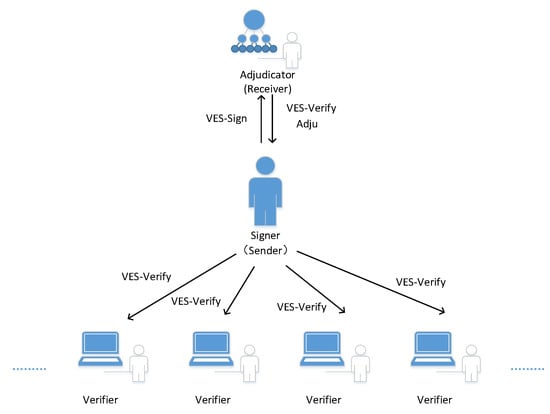
Figure 1.
The Framework of Our Scheme.
Introducing verifiably encrypted signatures into the blockchain has two functions. First, publicly verifiable signatures are encrypted. Verifiably encrypted signatures prevent blockchain nodes from obtaining transaction information through this signature while ensuring the signature authentication function. Second, for the recipient of the transaction, he still obtains the ordinary signature of the transaction, so that the displayed authentication of the transaction information under his control is realized. A verifiably encrypted signature balances the public verification demand of the signature, the privacy demand of the transaction party, and the controllability of the arbitration demand, to a certain extent.
7. Conclusions
We construct a new and verifiably encrypted signature scheme in the lattice; the scheme realizes the relative independence of the signer and adjudicator, eliminates dependence on the Gaussian sampling algorithm, simplifies the parameter setting process of the participants, enhances the security, and improves the operation efficiency, which is a better choice for the actual applications. We integrate this signature scheme into the blockchain environment, which not only realizes the public verification requirements of the blockchain for transactions, but also reduces the disclosure of information about the privacy of transactions from the disclosure of signatures in the blockchain to a certain extent. Our scheme provides a good choice for blockchain transaction authentication. In our environment, the initiator and receiver of a transaction need to consult with each other about the transaction information, which is a natural situation in real life. If message recoverability is added to the signature, this restriction is no longer necessary. The last thing we want to say is that, in the blockchain environment, we have given the signer, verifier, and adjudicator a new role and a new idea for the verifiably encrypted signature scheme’s application. We believe that this idea can be extended to more application environments that are sensitive to signature privacy.
Author Contributions
Conceptualization, X.L.; methodology, X.L.; validation, X.L., W.Y. and P.Z.; formal analysis, X.L. and P.Z.; writing—original draft preparation, X.L. and W.Y.; writing—review and editing, X.L. and W.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Cryptography Development Fund, grant number MMJJ20180110; the National Natural Science Foundation of China, grant number 62102300; Shandong Social Science Planning Project, grant number 21CSDJ30; and Key Research Project of Higher Education Institutions of Henan Province, grant number 23A520012.
Institutional Review Board Statement
Our study does not involve humans or animals, nor state secrets or confidential projects. The names “Alice” and “Bob” used in our study are two commonly used personas in cryptography. They do not refer to specific characters and do not have infringement attributes.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Thank reviewers and the editorial department for their suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Asokan, N.; Schunter, M.; Waidner, M. Optimistic protocols for fair exchange. In Proceedings of the CCS ’97: Proceedings of the 4th ACM Conference on Computer and Communications Security, Zurich, Switzerland, 1–4 April 1997; pp. 7–17. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Yu, J.; Xian, H. Blockchain-based two-party fair contract signing scheme. Inf. Sci. 2020, 535, 142–155. [Google Scholar] [CrossRef]
- Seo, J.H.; Emura, K.; Xagawa, K.; Yoneyama, K. Accumulable optimistic fair exchange from verifiably encrypted homomorphic signatures. Int. J. Inf. Secur. 2018, 17, 193–220. [Google Scholar] [CrossRef]
- Wang, Y.; Pang, H.; Deng, R.H. Verifiably encrypted cascade-instantiable blank signatures to secure progressive decision management. Int. J. Inf. Secur. 2018, 17, 347–363. [Google Scholar] [CrossRef]
- Yang, X.; Liu, M.; Au, M.H.; Luo, X.; Ye, Q. Efficient Verifiably Encrypted ECDSA-Like Signatures and Their Applications. IEEE Trans. Inf. Forensics Secur. 2022, 17, 1573–1582. [Google Scholar] [CrossRef]
- Shao, Z.; Gao, Y. Practical verifiably encrypted signatures based on discrete logarithms. Secur. Commun. Netw. 2016, 9, 5996–6003. [Google Scholar] [CrossRef]
- Nishimaki, R.; Xagawa, K. Verifiably encrypted signatures with short keys based on the decisional linear problem and obfuscation for encrypted VES. Des. Codes Cryptogr. 2015, 77, 61–98. [Google Scholar] [CrossRef]
- Wang, F.; Shi, S. Lattice-Based Encrypted Verifiably Encryption Signature Scheme for the Fair and Private Electronic Commence. IEEE Access 2019, 7, 147481–147489. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, Y. A New Verifiably Encrypted Signature Scheme from Lattices. J. Comput. Res. Develop. 2017, 54, 305–312. [Google Scholar] [CrossRef]
- Kim, K.S.; Jeong, I.R. Efficient verifiably encrypted signatures from lattices. Int. J. Inf. Secur. 2014, 13, 305–314. [Google Scholar] [CrossRef]
- Gentry, C.; Peikert, C.; Vaikuntanathan, V. Trapdoors for Hard Lattices and New Cryptographic Constructions. In Proceedings of the Fortieth Annual ACM Symposium on Theory of Computing, Victoria, BC, Canada, 17–20 May 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 197–206. [Google Scholar] [CrossRef]
- Micciancio, D.; Peikert, C. Trapdoors for Lattices: Simpler, Tighter, Faster, Smaller. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Pointcheval, D., Johansson, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 700–718. [Google Scholar] [CrossRef]
- Prest, T. Gaussian Sampling in Lattice-Based Cryptography. Ph.D. Thesis, École Normale Supérieure, Paris, France, 2015. [Google Scholar]
- Bootle, J.; Delaplace, C.; Espitau, T.; Fouque, P.A.; Tibouchi, M. LWE Without Modular Reduction and Improved Side-Channel Attacks Against BLISS. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, Austrilia, 2–6 December 2018; Peyrin, T., Galbraith, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 494–524. [Google Scholar] [CrossRef]
- Mujdei, C.; Beckers, A.; Mera, J.M.B.; Karmakar, A.; Wouters, L.; Verbauwhede, I. Side-Channel Analysis of Lattice-Based Post-Quantum Cryptography: Exploiting Polynomial Multiplication. Cryptology ePrint Archive, Paper 2022/474. 2022. Available online: https://eprint.iacr.org/2022/474 (accessed on 20 September 2022).
- Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schwabe, P.; Seiler, G.; Stehlé, D. Crystals-dilithium: A lattice-based digital signature scheme. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2018, 238–268. [Google Scholar] [CrossRef]
- Simmons, G.J. The Prisoners’ Problem and the Subliminal Channel. In Proceedings of the Advances in Cryptology, Santa Barbara, CA, USA, 19–22 August 1984; pp. 51–67. [Google Scholar] [CrossRef]
- Masood, F.; Ahmad, J.; Shah, S.A.; Jamal, S.S.; Hussain, I. A Novel Hybrid Secure Image Encryption Based on Julia Set of Fractals and 3D Lorenz Chaotic Map. Entropy 2020, 22, 274. [Google Scholar] [CrossRef] [PubMed]
- Masood, F.; Masood, J.; Zhang, L.; Jamal, S.S.; Boulila, W.; Rehman, S.U.; Khan, F.A.; Ahmad, J. A new color image encryption technique using DNA computing and Chaos-based substitution box. Soft Comput. 2022, 26, 7461–7477. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Z.; Zhang, Z. On the Hardness of the Computational Ring-LWR Problem and Its Applications. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, Austrilia, 2–6 December 2018; Peyrin, T., Galbraith, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 435–464. [Google Scholar] [CrossRef]
- Langlois, A.; Stehlé, D. Worst-case to average-case reductions for module lattices. Des. Codes Cryptogr. 2015, 75, 565–599. [Google Scholar] [CrossRef]
- Asharov, G.; Jain, A.; López-Alt, A.; Tromer, E.; Vaikuntanathan, V.; Wichs, D. Multiparty Computation with Low Communication, Computation and Interaction via Threshold FHE. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Pointcheval, D., Johansson, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 483–501. [Google Scholar] [CrossRef]
- Lyubashevsky, V. Lattice Signatures Without Trapdoors. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Pointcheval, D., Johansson, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 738–755. [Google Scholar] [CrossRef]
- Bootle, J.; Lyubashevsky, V.; Seiler, G. Algebraic Techniques for Short(er) Exact Lattice-Based Zero-Knowledge Proofs. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 17–21 August 2019; pp. 176–202. [Google Scholar] [CrossRef]
- Bellare, M.; Neven, G. Multi-signatures in the plain public-Key model and a general forking lemma. In Proceedings of the Proceedings of the ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 30 October–3 November 2006; pp. 390–399. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).