Optimization of Hydrokinetic Swept Blades
Abstract
1. Introduction
2. Blade Element Momentum Theory for Swept Blades
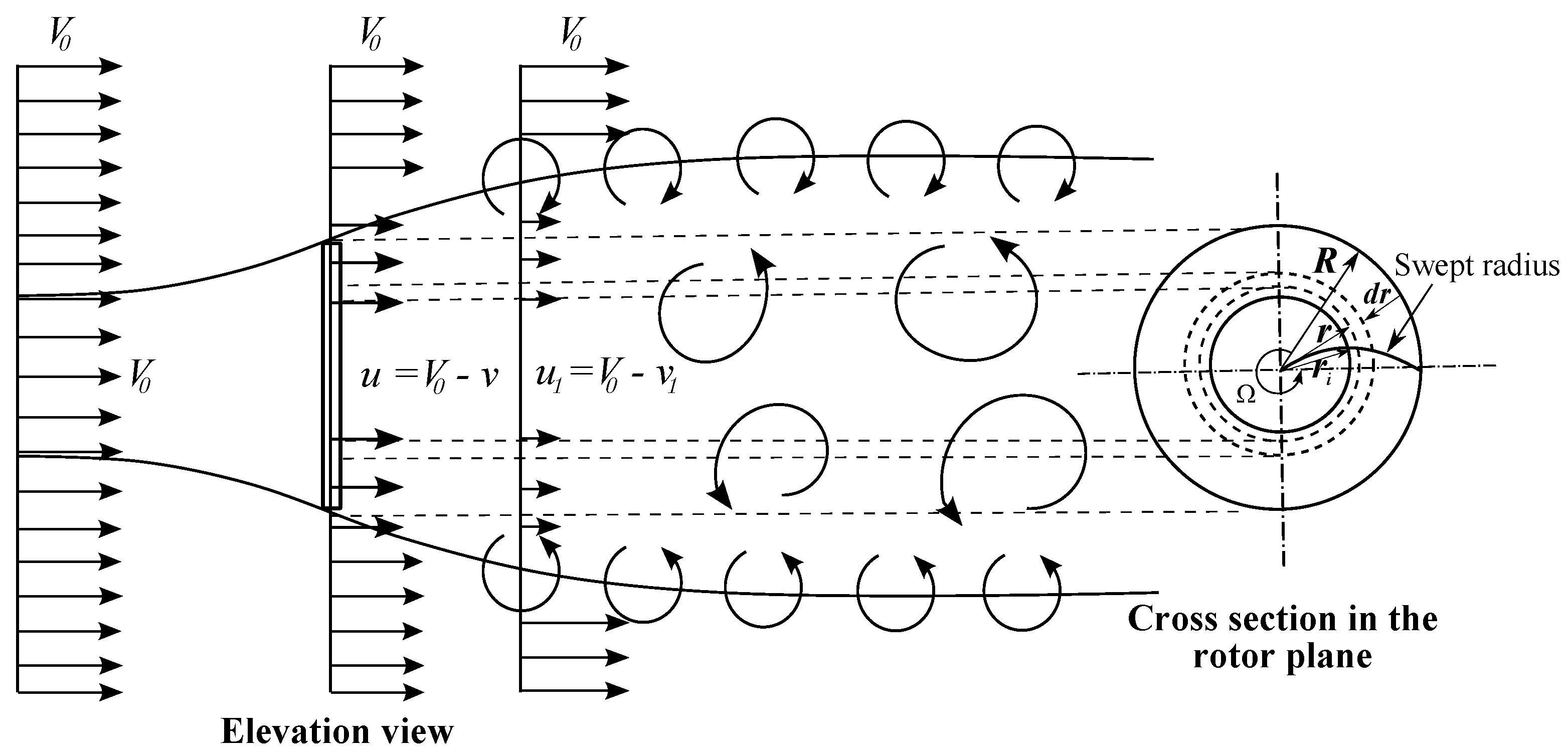
2.1. Axial Momentum Theory with Sweep Effect
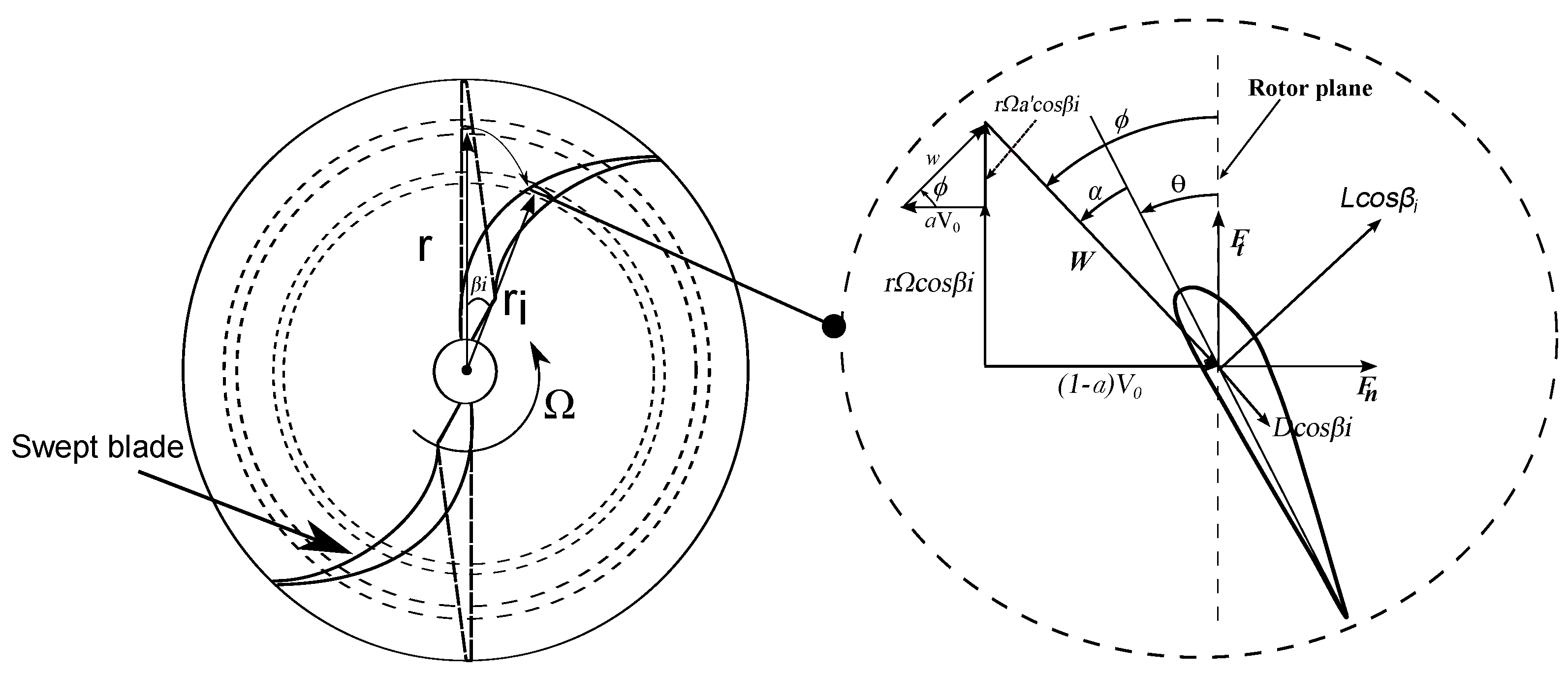
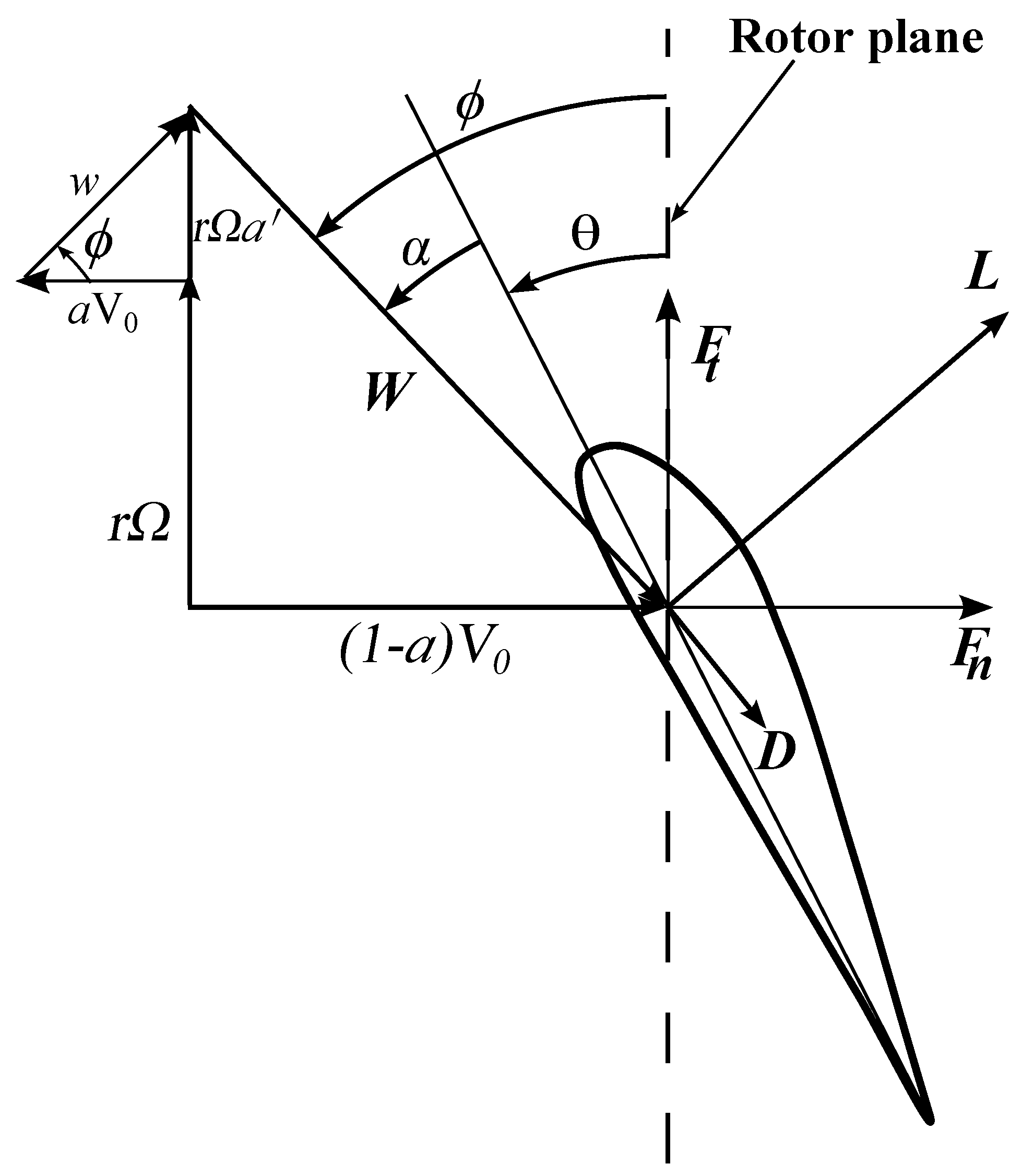
2.2. Blade Element Momentum Theory for Turbines with Swept Blades
2.3. Optimization Model for the Turbine Swept Blade
3. Results and Discussion
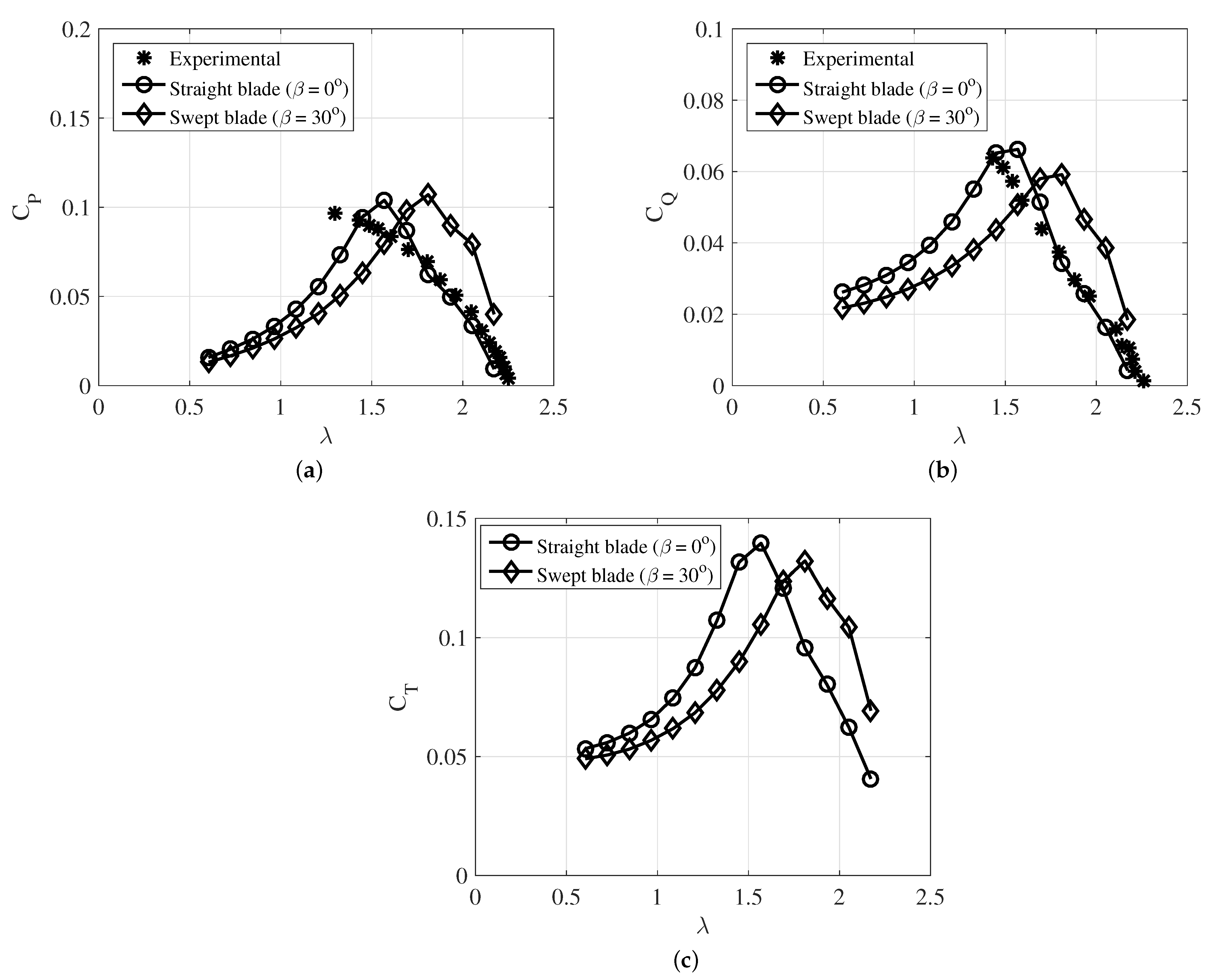
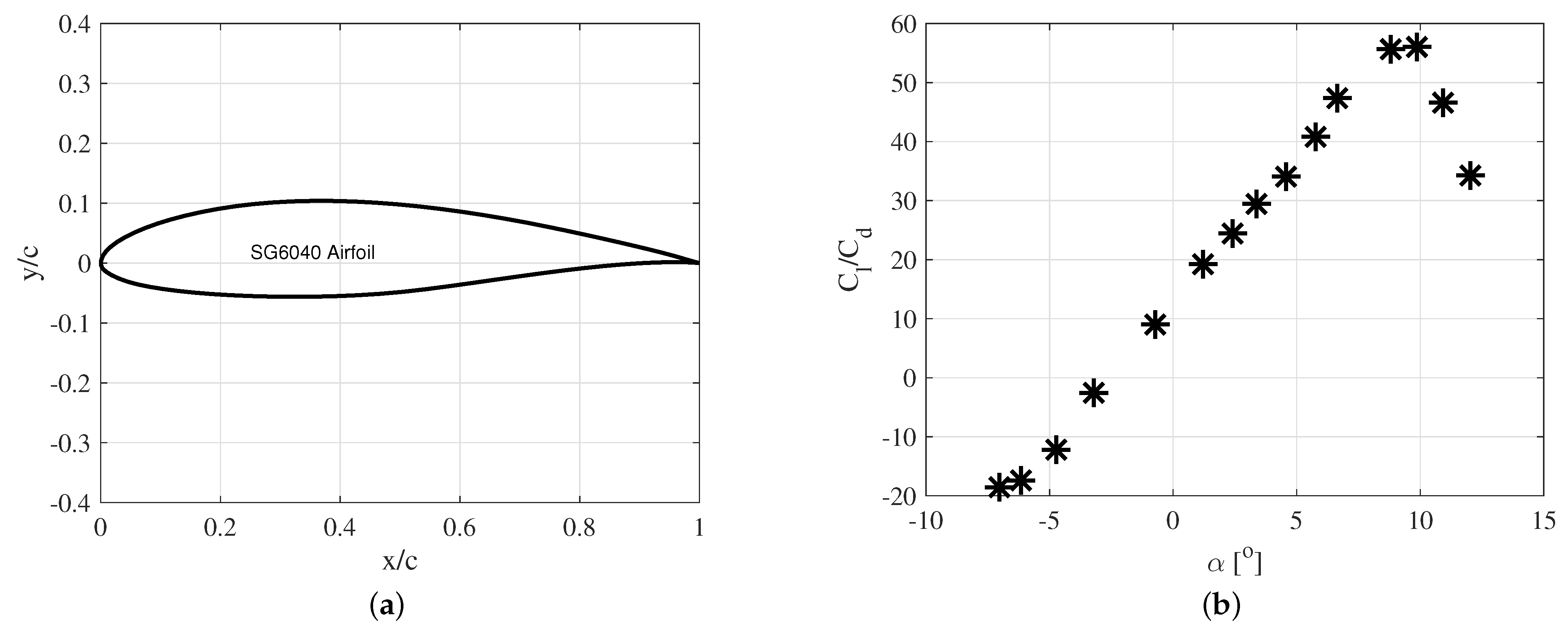
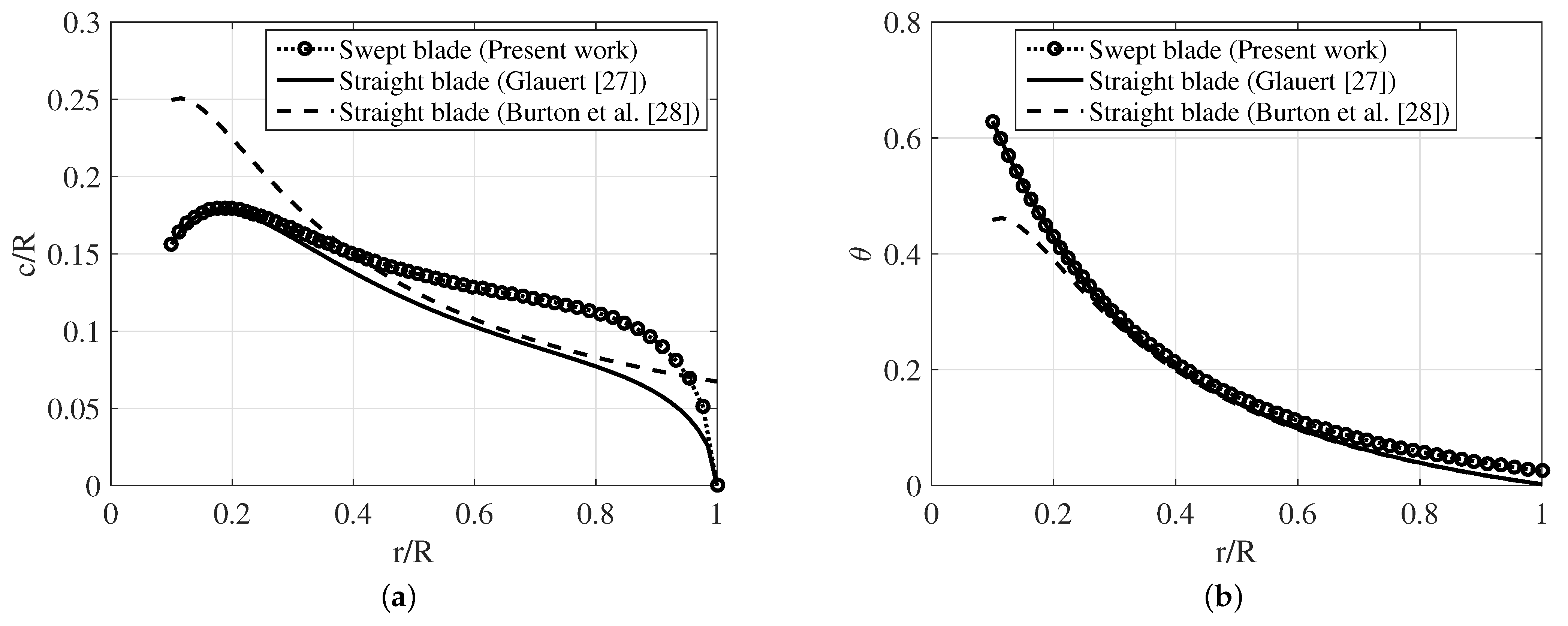
3.1. Validation
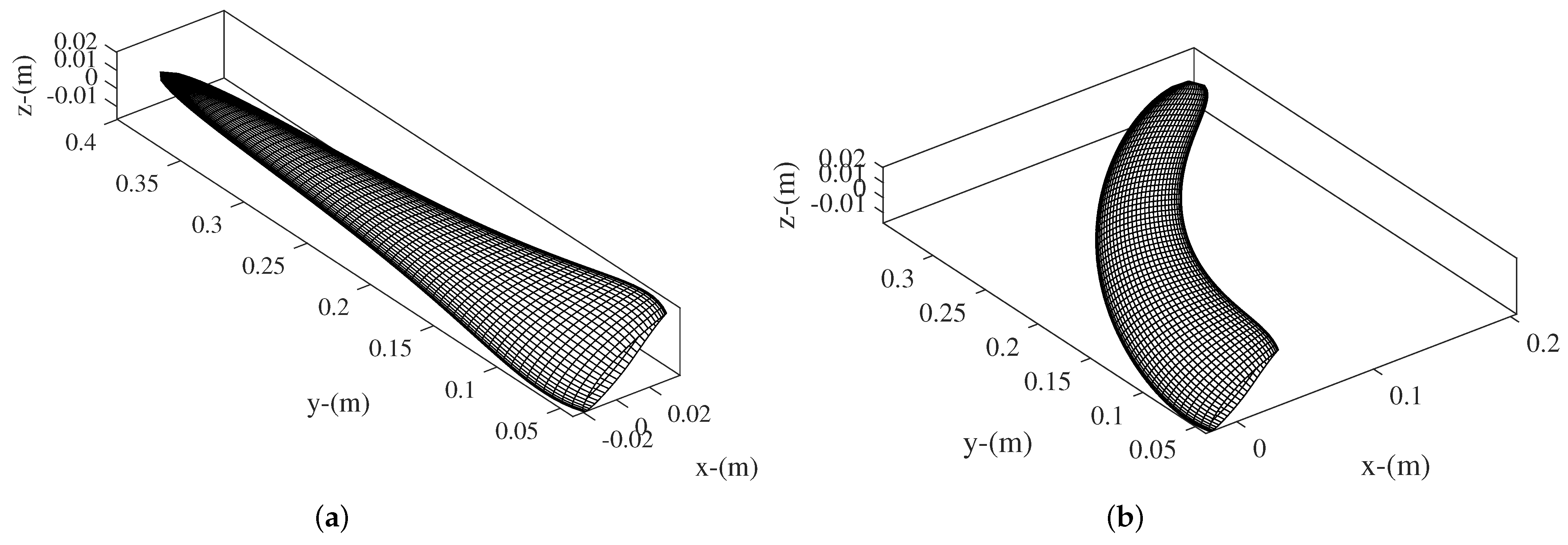
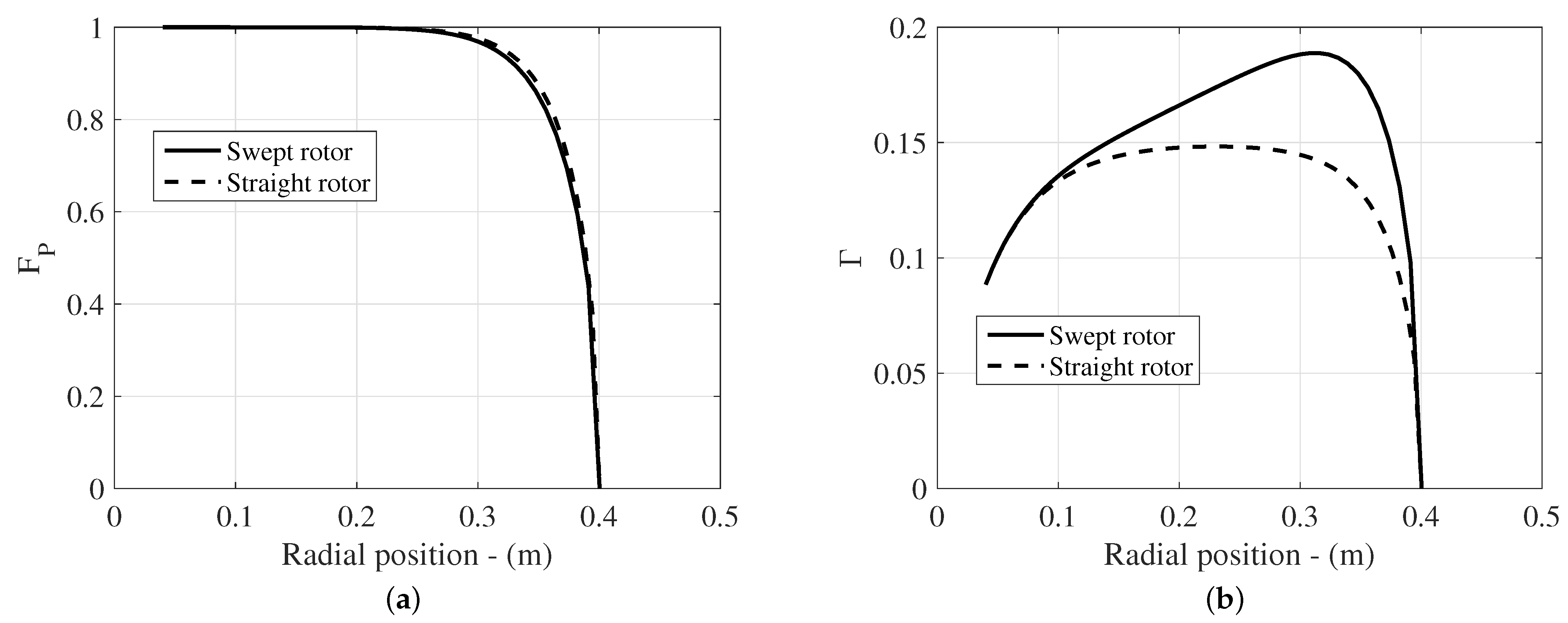
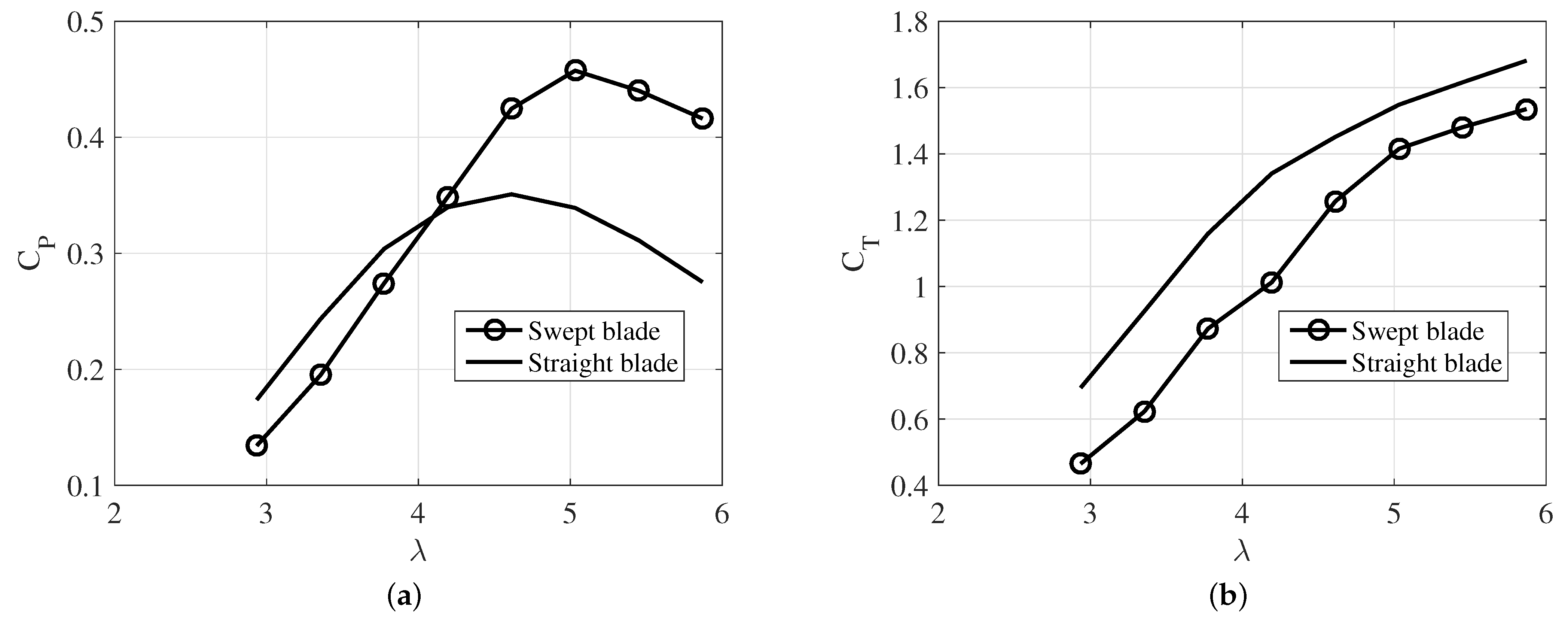
3.2. Performance Analysis of the Proposed Optimization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin Symbols | |
| a, | Axial and tangential induction factors at the rotor |
| Optimal axial induction factor | |
| B | Number of blades |
| c | Chord (m) |
| Drag coefficient | |
| Lift coefficient | |
| Torque coefficient | |
| Normal force coefficient | |
| Power coefficient | |
| Optimal power coefficient | |
| Tangential force coefficient | |
| Thrust coefficient | |
| Elementary area (m2) | |
| F | Prandtl tip-loss factor |
| Pressure in the external flow (Pa) | |
| Pressure at the turbine upstream (Pa) | |
| Pressure at the diffuser outlet (Pa) | |
| P | Output power (W) |
| r | Radial position at the rotor plane (m) |
| R | Radius of the rotor (m) |
| Freestream wind velocity (m/s) | |
| Axial velocity at the diffuser outlet (m/s) | |
| w | Total induced velocity (m/s) |
| W | Relative velocity (m/s) |
| x | Local speed ratio |
| Greek Symbols | |
| Angle of attack (rad) | |
| Twist angle (rad) | |
| Tip speed ratio | |
| Density of the fluid (kg/m3) | |
| Solidity of the turbine | |
| Flow angle (rad) | |
| Angular speed of the turbine (rad/s) |
References
- do Rio Vaz, D.A.; Vaz, J.R.; Silva, P.A. An approach for the optimization of diffuser-augmented hydrokinetic blades free of cavitation. Energy Sustain. Dev. 2018, 45, 142–149. [Google Scholar] [CrossRef]
- Betz, A. Introduction to the Theory of Flow Machines; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- da Silva, P.A.S.F.; Shinomiya, L.D.; de Oliveira, T.F.; Vaz, J.R.P.; Mesquita, A.L.A.; Junior, A.C.P.B. Design of hydrokinetic turbine blades considering cavitation. Energy Procedia 2015, 75, 277–282. [Google Scholar] [CrossRef]
- Muratoglu, A.; Tekin, R.; Ertuğrul, Ö.F. Hydrodynamic optimization of high-performance blade sections for stall regulated hydrokinetic turbines using Differential Evolution Algorithm. Ocean. Eng. 2021, 220, 108389. [Google Scholar] [CrossRef]
- Larwood, S.; Van Dam, C.P.; Schow, D. Design studies of swept wind turbine blades. Renew. Energy 2014, 71, 563–571. [Google Scholar] [CrossRef]
- Sessarego, M.; Ramos-García, N.; Shen, W.Z. Analysis of winglets and sweep on wind turbine blades using a lifting line vortex particle method in complex inflow conditions. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2018; Volume 1037, p. 022021. [Google Scholar]
- Zuo, H.M.; Liu, C.; Yang, H.; Wang, F. Numerical Study on the Effect of Swept Blade on the Aerodynamic Performance of Wind Turbine at High Tip Speed Ratio. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2016; Volume 753, p. 102010. [Google Scholar]
- Bora, B.J.; Dai Tran, T.; Shadangi, K.P.; Sharma, P.; Said, Z.; Kalita, P.; Nguyen, X.P. Improving combustion and emission characteristics of a biogas/biodiesel-powered dual-fuel diesel engine through trade-off analysis of operation parameters using response surface methodology. Sustain. Energy Technol. Assess. 2022, 53, 102455. [Google Scholar] [CrossRef]
- Zahedi, R.; Zahedi, A.; Ahmadi, A. Strategic study for renewable energy policy, optimizations and sustainability in Iran. Sustainability 2022, 14, 2418. [Google Scholar] [CrossRef]
- Rajamoorthy, R.; Arunachalam, G.; Kasinathan, P.; Devendiran, R.; Ahmadi, P.; Pandiyan, S.; Sharma, P. A novel intelligent transport system charging scheduling for electric vehicles using Grey Wolf Optimizer and Sail Fish Optimization algorithms. Energy Sources Part A Recover. Util. Environ. Eff. 2022, 44, 3555–3575. [Google Scholar] [CrossRef]
- Sadollah, A.; Nasir, M.; Geem, Z.W. Sustainability and optimization: From conceptual fundamentals to applications. Sustainability 2020, 12, 2027. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, X. An optimal design method of swept blades for HAWTs. J. Renew. Sustain. Energy 2016, 8, 043303. [Google Scholar] [CrossRef]
- Fei, C.W.; Li, H.; Lu, C.; Han, L.; Keshtegar, B.; Taylan, O. Vectorial surrogate modeling method for multi-objective reliability design. Appl. Math. Model. 2022, 109, 1–20. [Google Scholar] [CrossRef]
- Fei, C.; Wen, J.; Han, L.; Huang, B.; Yan, C. Optimizable Image Segmentation Method with Superpixels and Feature Migration for Aerospace Structures. Aerospace 2022, 9, 465. [Google Scholar] [CrossRef]
- Han, L.; Li, P.; Yu, S.; Chen, C.; Fei, C.; Lu, C. Creep/fatigue accelerated failure of Ni-based superalloy turbine blade: Microscopic characteristics and void migration mechanism. Int. J. Fatigue 2022, 154, 106558. [Google Scholar] [CrossRef]
- Pavese, C.; Kim, T.; Murcia, J.P. Design of a wind turbine swept blade through extensive load analysis. Renew. Energy 2017, 102, 21–34. [Google Scholar] [CrossRef]
- Kaya, M.N.; Kose, F.; Ingham, D.; Ma, L.; Pourkashanian, M. Aerodynamic performance of a horizontal axis wind turbine with forward and backward swept blades. J. Wind. Eng. Ind. Aerodyn. 2018, 176, 166–173. [Google Scholar] [CrossRef]
- Ning, A.; Hayman, G.; Damiani, R.; Jonkman, J.M. Development and validation of a new blade element momentum skewed-wake model within AeroDyn. In 33rd Wind Energy Symposium; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2015; p. 0215. [Google Scholar]
- Vaz, J.R.; Wood, D.H. Effect of the diffuser efficiency on wind turbine performance. Renew. Energy 2018, 126, 969–977. [Google Scholar] [CrossRef]
- Vaz, J.R.P.; Wood, D.H. Aerodynamic optimization of the blades of diffuser-augmented wind turbines. Energy Convers. Manag. 2016, 123, 35–45. [Google Scholar] [CrossRef]
- Wood, D. Small Wind Turbines: Analysis, Design, and Application; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hansen, M. Aerodynamics of Wind Turbines, 2nd ed.; Earthscan: London, UK, 2008. [Google Scholar]
- Clifton-Smith, M.J. Wind Turbine Blade Optimisation with Tip Loss Corrections. Wind. Eng. 2009, 33, 477496. [Google Scholar] [CrossRef]
- Wood, D.H. Maximum wind turbine performance at low tip speed ratio. J. Renew. Sustain. Energy 2015, 7, 053126. [Google Scholar] [CrossRef]
- John, I.H.; Vaz, J.R.; Wood, D. Aerodynamic performance and blockage investigation of a cambered multi-bladed windmill. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1618, p. 042003. [Google Scholar]
- Bruining, A. Aerodynamic Characteristics of a Curved Plate Airfoil Section at Reynolds Numbers 60,000 and 100,000 and Angles of Attack From-10 to+ 90 Degrees; Report LR-281; Delft University of Technology, Department of Aerospace Engineering: Delft, The Netherlands, 1979. [Google Scholar]
- Glauert, H. Aerodynamic Theory; Durand, W.F., Ed.; Division L. Airplanes Propellers: NewYork, NY, USA, 1963; Chapter XI; Volume 4, pp. 191–195. [Google Scholar]
- Jenkins, N.; Burton, T.L.; Bossanyi, E.; Sharpe, D.; Graham, M. Wind Energy Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Picanço, H.P.; Kleber Ferreira de Lima, A.; Dias do Rio Vaz, D.A.T.; Lins, E.F.; Pinheiro Vaz, J.R. Cavitation Inception on Hydrokinetic Turbine Blades Shrouded by Diffuser. Sustainability 2022, 14, 7067. [Google Scholar] [CrossRef]
- Vaz, J.R.; Okulov, V.L.; Wood, D.H. Finite blade functions and blade element optimization for diffuser-augmented wind turbines. Renew. Energy 2021, 165, 812–822. [Google Scholar] [CrossRef]
- Wood, D.H.; Okulov, V.L.; Vaz, J.R.P. Calculation of the induced velocities in lifting line analyses of propellers and turbines. Ocean. Eng. 2021, 235, 109337. [Google Scholar] [CrossRef]
| Parameters | Value |
|---|---|
| Turbine diameter, m | 0.8 |
| Hub diameter, m | 0.08 |
| Number of blades | 4 |
| Stream velocity, m/s | 1.0 |
| water density, kg/m3 (1) | 997 |
| Angular velocity, rad/s | 10.5 |
| Swept angle, degrees | 30 |
| Swept Blades | Straight Blades | |
|---|---|---|
| 0.13 | 0.11 | |
| 0.529 | 0.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gemaque, M.L.A.; Vaz, J.R.P.; Saavedra, O.R. Optimization of Hydrokinetic Swept Blades. Sustainability 2022, 14, 13968. https://doi.org/10.3390/su142113968
Gemaque MLA, Vaz JRP, Saavedra OR. Optimization of Hydrokinetic Swept Blades. Sustainability. 2022; 14(21):13968. https://doi.org/10.3390/su142113968
Chicago/Turabian StyleGemaque, Miriam L. A., Jerson R. P. Vaz, and Osvaldo R. Saavedra. 2022. "Optimization of Hydrokinetic Swept Blades" Sustainability 14, no. 21: 13968. https://doi.org/10.3390/su142113968
APA StyleGemaque, M. L. A., Vaz, J. R. P., & Saavedra, O. R. (2022). Optimization of Hydrokinetic Swept Blades. Sustainability, 14(21), 13968. https://doi.org/10.3390/su142113968








