Cavitation Inception on Hydrokinetic Turbine Blades Shrouded by Diffuser
Abstract
1. Introduction
2. The Optimization for Hydrokinetic Blades Shrouded by Diffuser
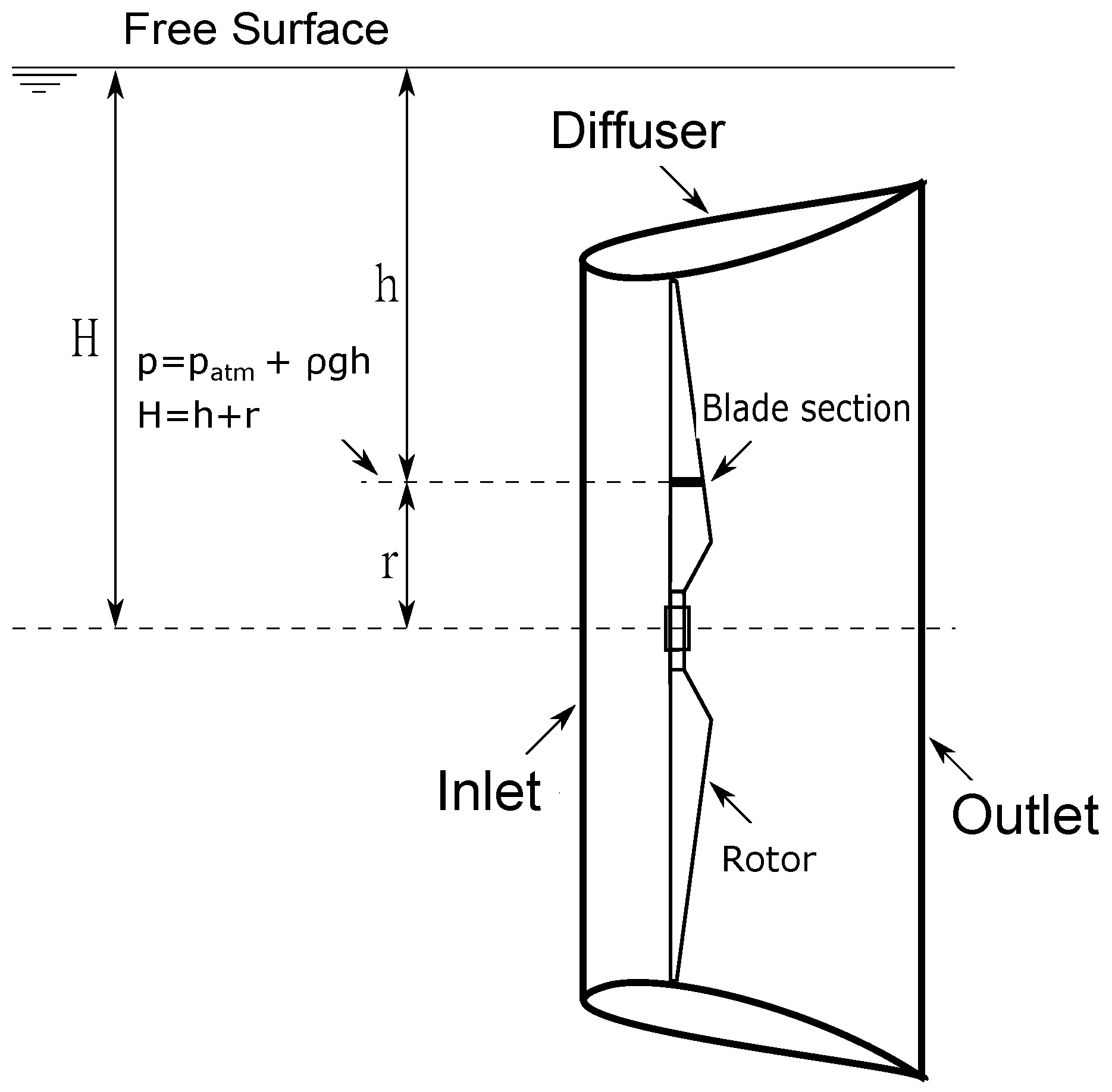
2.1. Cavitation Criterion on Hydrokinetic Rotors
2.2. The Optimization Model
| Algorithm 1 Chord and twist angle optimization |
| Require:
r, , , and for to (Number of sections) do Compute using Equation (16) for and ; Compute , calculated for obtained from maximum ; Compute the relative velocity, W; Compute , using Equation (18) and ; Compute , using Equation (4); if then end if end for Compute blade geometry. |
3. Computational Fluid Dynamics Methodology
3.1. Diffuser Geometry
3.2. Cavitating Flow Simulation
3.3. Numerical Setup
4. Results and Discussion
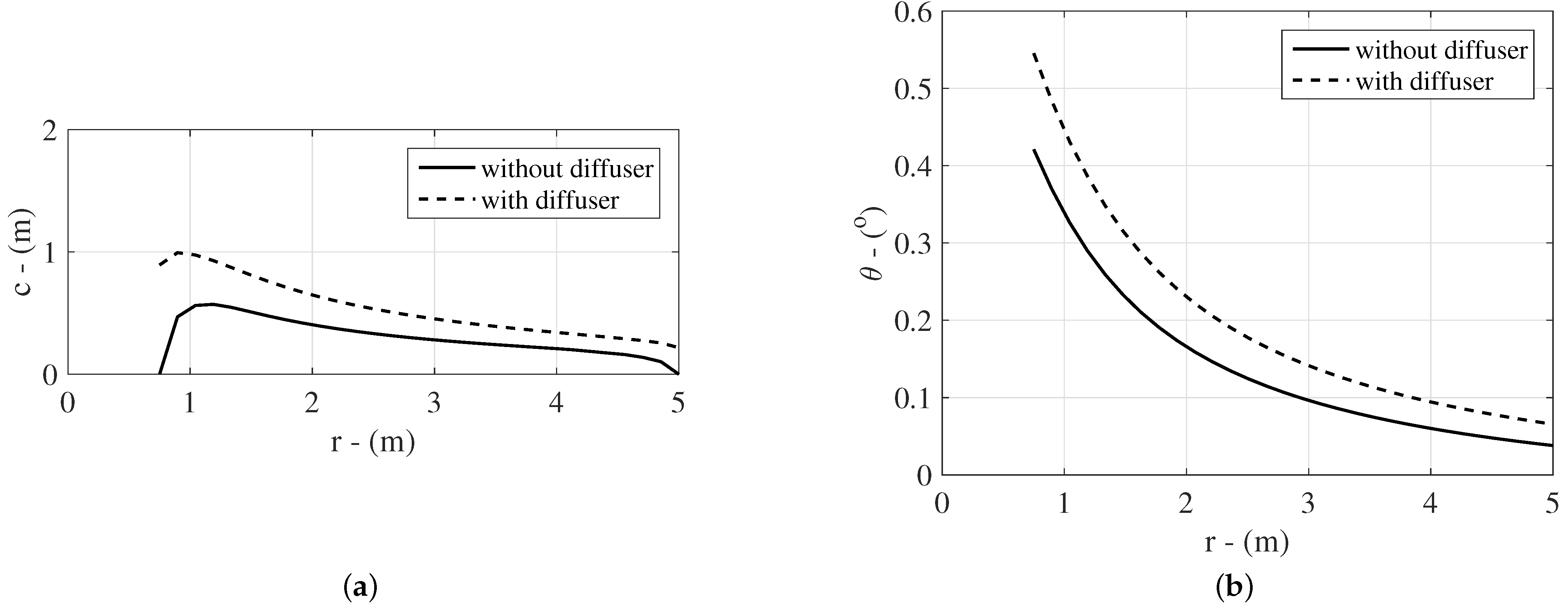
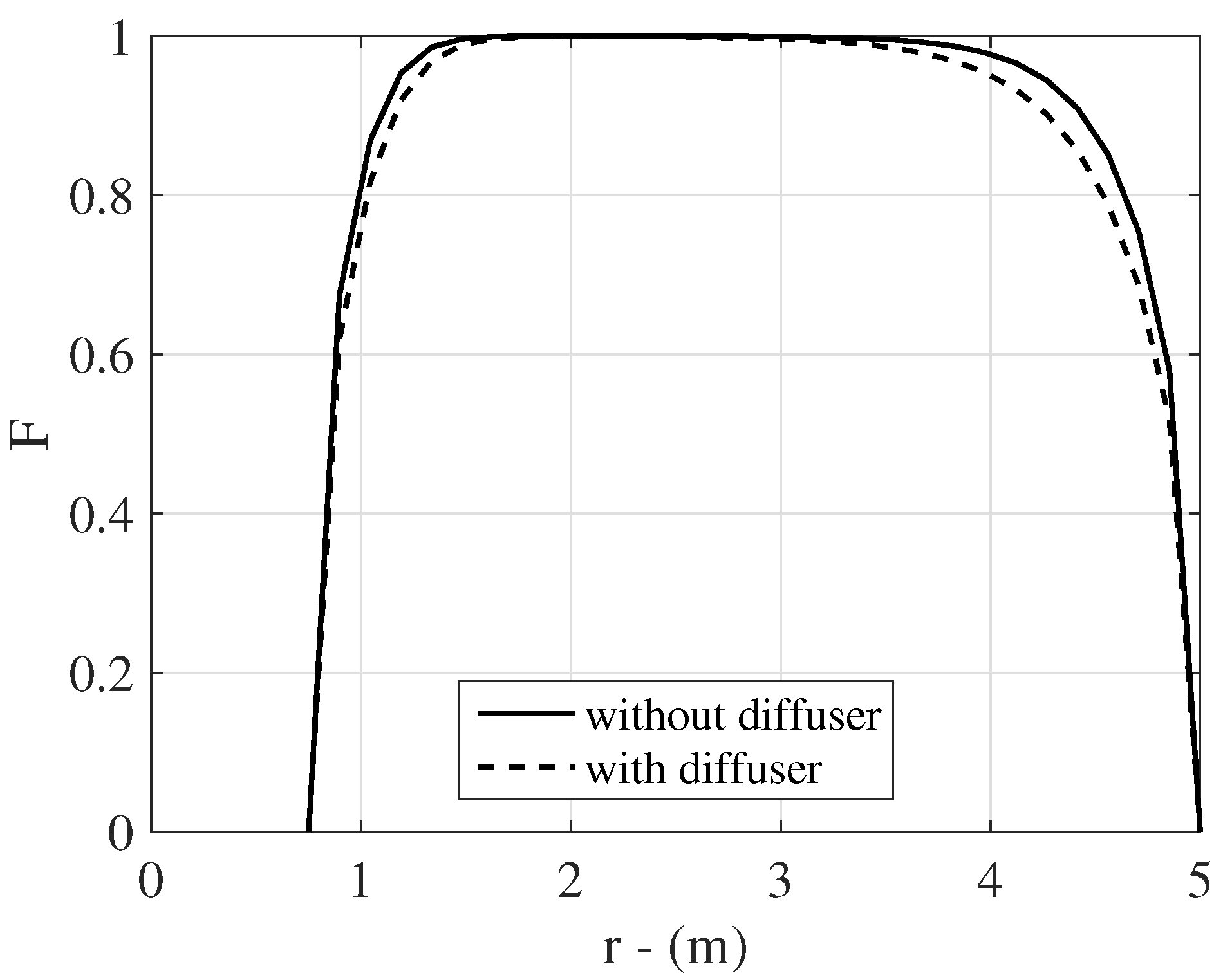
4.1. The Optimization Model
4.2. CFD Simulations and Validation
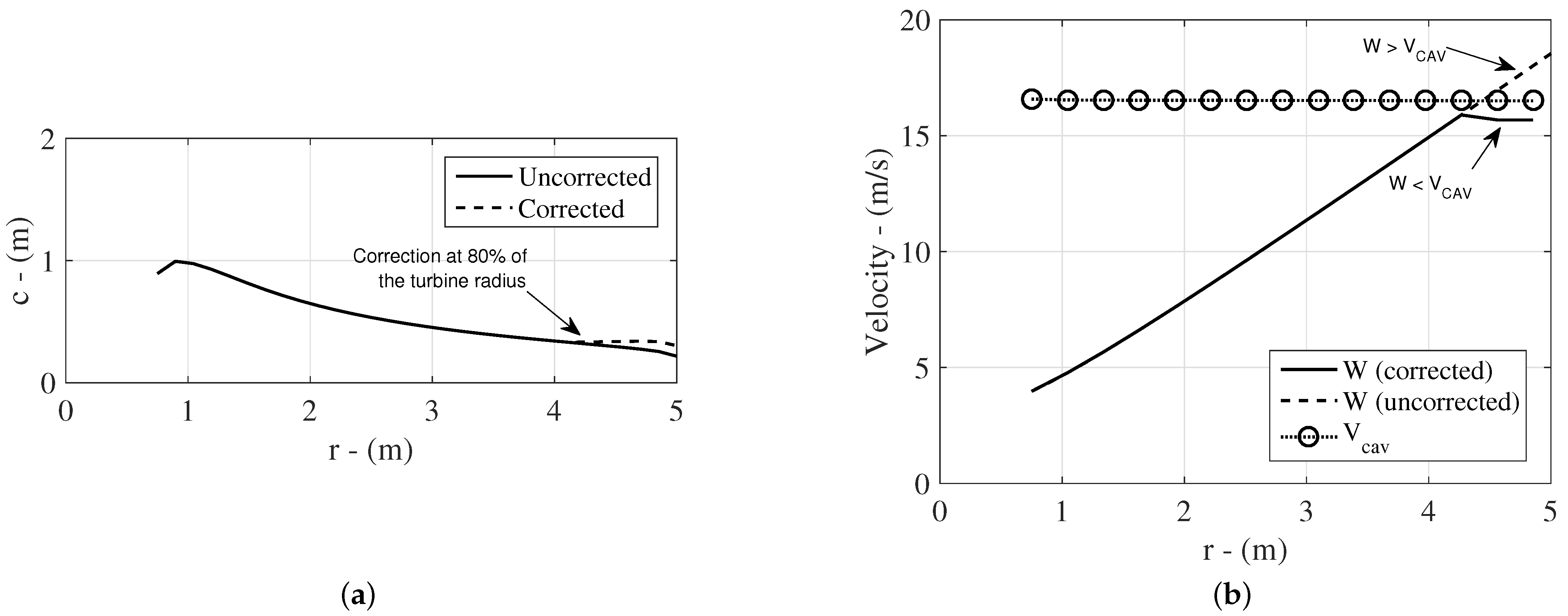
4.2.1. Verification of Optimal Point of Rotor Position and Mesh Independence Study
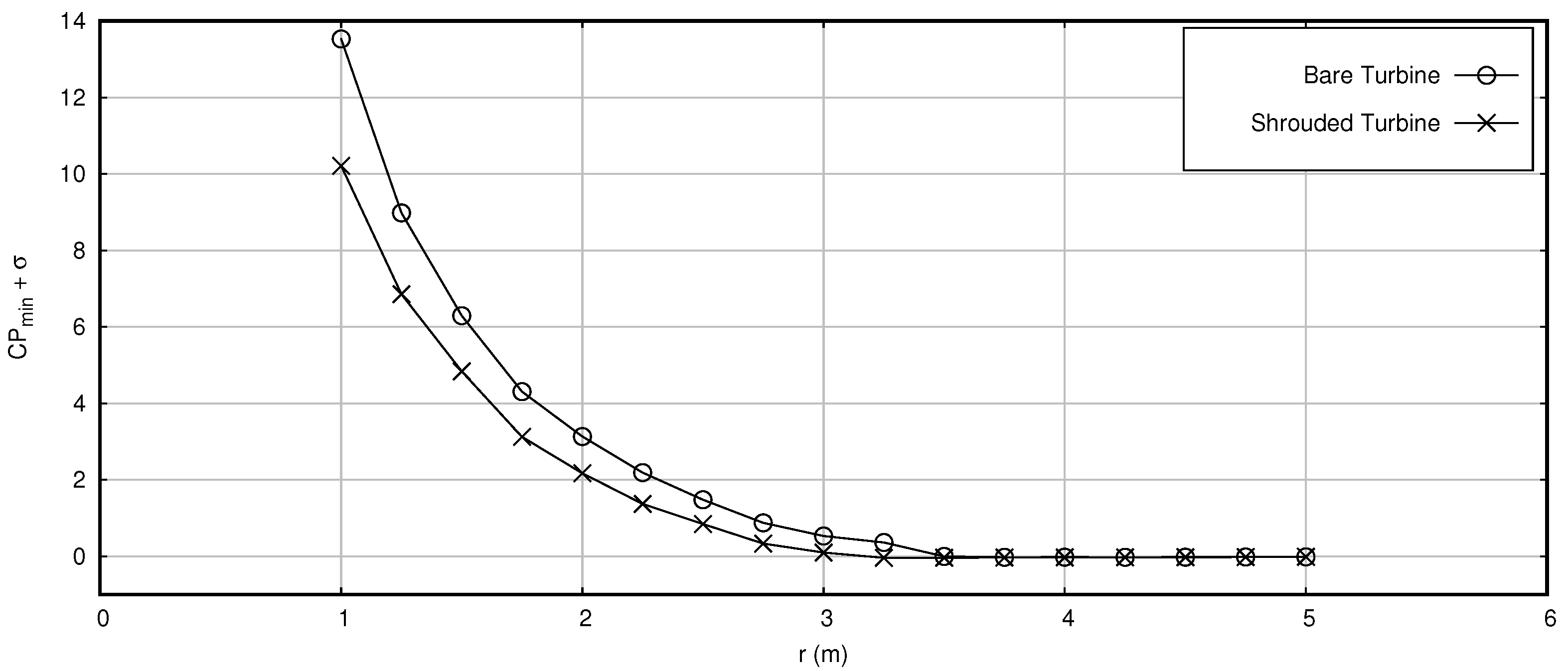
4.2.2. Numerical Simulation of Cavitation Effect on Diffuser-Augmented Hydrokinetic Blades
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BET | Blade Element Theory |
| CFD | Computational Fluid Dynamics |
| DAHT | Diffuser-augmented Hydrokinetic Turbine |
| DNS | Direct Numeric Simulation |
| HT | Hydrokinetic Turbine |
| MRF | Moving Reference Frame |
| LES | Large Eddy Simulation |
| RANS | Reynolds-Averaged Navier–Stokes |
| VOF | Volume Of Fluid Technique |
| Arabic Symbols | |
| a, | Streamtube average axial and tangential induction factors |
| , | Axial and tangential induction factors at the blade |
| A | Area of the Disc () |
| Cross section at the diffuser outlet () | |
| c | Chord (m) |
| , | Uncorrected and corrected chord (m) |
| , | Lift and drag coefficients |
| Power coefficient | |
| Pressure coefficient at the diffuser outlet | |
| Minimum pressure coefficient | |
| Normal force coefficient | |
| , | Thrust coefficient and diffuser thrust coefficient |
| D | Turbine Diameter (m) |
| , | Inlet and outlet diffuser diameters (m) |
| Elementary power (W) | |
| f | Additional momentum source () |
| Safety factor | |
| F | Prandtl’s tip loss factor |
| Empirical constant of the cavitation model | |
| g | Gravity () |
| h,H | Distance between free surface and turbine radial or center position (m) |
| , | Rate of change mass per unit of volume for liquid and vapor phases |
| , | Upstream and downstream diffuser lengths relative to rotor center plane (m) |
| Diffuser total length (m) | |
| N | Number of blades |
| Number of bubbles per unit of mixture volume | |
| p | Local pressure (Pa) |
| Atmospheric pressure (Pa) | |
| Pressure in the external flow (Pa) | |
| Pressure in the turbine upstream (Pa) | |
| Pressure in the diffuser outlet (Pa) | |
| Vapor pressure (Pa) | |
| r | Radial position at the rotor plane (m) |
| R | Radius of the rotor (m) |
| Dimensionless radial position | |
| , | liquid and vapor volume fractions |
| Nucleation volume fraction | |
| Bubble radius (m) | |
| Symmetric part of the velocity gradient tensor | |
| , | Mean velocity and flutuations components () |
| Reynolds Stress Tensor () | |
| Diffuser thickness (m) | |
| X-component of the flow velocity at the diffuser centerline () | |
| Freestream flow velocity () | |
| Axial velocity at the rotor () | |
| , | Axial velocity at the diffuser outlet and at the wake () |
| Minimum cavitating flow velocity () | |
| X | Longitudinal position at the diffuser centerline () |
| W | Relative velocity of fluid |
| Greek Symbols | |
| Angle of attack () | |
| Cross sectional area ratio | |
| Wall distance () | |
| Velocity ratio | |
| Far-wake velocity ratio | |
| Diffuser efficiency | |
| Diffuser speed-up ratio | |
| Dynamic viscosity () | |
| Kinematic viscosity () | |
| Angular velocity of turbine () | |
| Fluid density () | |
| Liquid, vapor and mixture densities () | |
| Cavitation number | |
| Local solidity | |
| Surface tension coefficient | |
| Flow angle () | |
| Diffuser opening angle | |
| Reynolds stress tensor () | |
| Twist angle () |
References
- Mesquita, A.L.A.; Mesquita, A.L.A.; Palheta, F.C.; Vaz, J.R.P.; de Morais, M.V.G.; Gonçalves, C. A methodology for the transient behavior of horizontal axis hydrokinetic turbines. Energy Convers. Manag. 2014, 87, 1261–1268. [Google Scholar] [CrossRef]
- Vaz, J.R.; Wood, D.H. Aerodynamic optimization of the blades of diffuser-augmented wind turbines. Energy Convers. Manag. 2016, 123, 35–45. [Google Scholar] [CrossRef]
- Zhu, F.w.; Ding, L.; Huang, B.; Bao, M.; Liu, J.T. Blade design and optimization of a horizontal axis tidal turbine. Ocean Eng. 2020, 195, 106652. [Google Scholar] [CrossRef]
- Silva, P.A.; Vaz, D.A.R.; Britto, V.; de Oliveira, T.F.; Vaz, J.R.; Junior, A.C.B. A new approach for the design of diffuser-augmented hydro turbines using the blade element momentum. Energy Convers. Manag. 2018, 165, 801–814. [Google Scholar] [CrossRef]
- do Rio Vaz, D.A.; Vaz, J.R.; Silva, P.A. An approach for the optimization of diffuser-augmented hydrokinetic blades free of cavitation. Energy Sustain. Dev. 2018, 45, 142–149. [Google Scholar] [CrossRef]
- Batten, W.; Bahaj, A.; Molland, A.; Chaplin, J. The prediction of the hydrodynamic performance of marine current turbines. Renew. Energy 2008, 33, 1085–1096. [Google Scholar] [CrossRef]
- Silva, P.A.S.F.; Shinomiya, L.D.; de Oliveira, T.F.; Vaz, J.R.P.; Mesquita, A.L.A.; Junior, A.C.P.B. Analysis of cavitation for the optimized design of hydrokinetic turbines using BEM. Appl. Energy 2017, 185, 1281–1291. [Google Scholar] [CrossRef]
- Taskar, B.; Steen, S.; Eriksson, J. Effect of waves on cavitation and pressure pulses of a tanker with twin podded propulsion. Appl. Ocean. Res. 2017, 65, 206–218. [Google Scholar] [CrossRef]
- Pennings, P.; Bosschers, J.; Westerweel, J.; van Terwisga, T. Dynamics of isolated vortex cavitation. J. Fluid Mech. 2015, 778, 288–313. [Google Scholar] [CrossRef]
- Wang, D.; Sampson, R. An experimental investigation on cavitation, noise, and slipstream characteristics of ocean stream turbines. J. Power Energy 2015, 221, 219–231. [Google Scholar] [CrossRef]
- Morgut, M.; Nobile, E.; Bilus, I. Comparison of mass transfer models for the numerical prediction of sheet cavitation around a hydrofoil. Int. J. Multiph. Flow 2011, 37, 620–626. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, X.; Gong, Z.; Li, J.; Lu, C. Numerical investigation on the dynamic behavior of sheet/cloud cavitation regimes around hydrofoil. Appl. Math. Model. 2016, 40, 5833–5857. [Google Scholar] [CrossRef]
- Movahedian, A.; Pasandidehfard, M.; Roohi, E. LES investigation of sheet-cloud cavitation around a 3-D twisted wing with a NACA 16012 hydrofoil. Ocean Eng. 2019, 192, 106547. [Google Scholar] [CrossRef]
- Pendar, M.R.; Esmaeilifar, E.; Roohi, E. LES study of unsteady cavitation characteristics of a 3-D hydrofoil with wavy leading edge. Int. J. Multiph. Flow 2020, 132, 103415. [Google Scholar] [CrossRef]
- Adhikari, R.C.; Vaz, J.; Wood, D. Cavitation inception in crossflow hydro turbines. Energies 2016, 9, 237. [Google Scholar] [CrossRef]
- Goundar, J.N.; Ahmed, M.R.; Lee, Y.H. Numerical and experimental studies on hydrofoils for marine current turbines. Renew. Energy 2012, 42, 173–179. [Google Scholar] [CrossRef]
- Lauterborn, W.; Ohl, C.D. Cavitation bubble dynamics. Ultrason. Sonochem. 1997, 4, 65–75. [Google Scholar] [CrossRef]
- Vaz, J.R.; Wood, D.H. Effect of the diffuser efficiency on wind turbine performance. Renew. Energy 2018, 126, 969–977. [Google Scholar] [CrossRef]
- Phillips, D.G. An Investigation on Diffuser Augmented wind Turbine Design. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 2003. [Google Scholar]
- do Rio, D.A.T.D.; Mesquita, A.L.A.; Vaz, J.R.P.; Blanco, C.J.C.; Pinho, J.T. An extension of the blade element momentum method applied to diffuser augmented wind turbines. Energy Convers. Manag. 2014, 87, 1116–1123. [Google Scholar]
- Hansen, M.O.L.; Sørensen, N.N.; Flay, R. Effect of placing a diffuser around a wind turbine. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 2000, 3, 207–213. [Google Scholar] [CrossRef]
- Sørensen, J.N. General Momentum Theory for Horizontal Axis Wind Turbines; Springer: Berlin/Heidelberg, Germany, 2016; Volume 4. [Google Scholar]
- Bontempo, R.; Manna, M. Effects of the duct thrust on the performance of ducted wind turbines. Energy 2016, 99, 274–287. [Google Scholar] [CrossRef]
- Barbosa, D.; Vaz, J.; Figueiredo, S.; E Silva, M.; Lins, E.; Mesquita, A. An investigation of a mathematical model for the internal velocity profile of conical diffusers applied to DAWTs. Ann. Braz. Acad. Sci. 2015, 87, 1133–1148. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Plesset, M.; Prosperetti, A. Bubble dynamics and cavitation. Annu. Rev. Fluid Mech. 1977, 9, 145–185. [Google Scholar] [CrossRef]
- Vaz, J.R.; Wood, D.H.; Bhattacharjee, D.; Lins, E.F. Drivetrain resistance and starting performance of a small wind turbine. Renew. Energy 2018, 117, 509–519. [Google Scholar] [CrossRef]
- Igra, O. Research and Development for Shrouded Wind Turbines. Energy Convers. Manag. 1981, 21, 13–48. [Google Scholar] [CrossRef]
- Bet, F.; Grassmann, H. Upgrading conventional wind turbines. Renew. Energy 2003, 28, 71–78. [Google Scholar] [CrossRef]
- Ohya, Y.; Karasudania, T.; Sakurai, A.; Abeb, K.I.; Inoue, M. Development of a shrouded wind turbine with a flanged diffuser. J. Wind. Eng. 2008, 96, 524–539. [Google Scholar] [CrossRef]
- Benjanirat, S.; Sankar, L.; Xu, G. Evaluation of turbulence models for the prediction of wind turbine aerodynamics. In Proceedings of the ASME 2003 Wind Energy Symposium, Reno, NV, USA, 6–9 January 2003; Paper number WIND2003-517. pp. 73–83. [Google Scholar]
- Jo, C.; Yim, J.; Lee, K.; Rho, Y. Performance of horizontal axis tidal current turbine by blade configuration. Renew. Energy 2012, 42, 195–206. [Google Scholar] [CrossRef]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Menter, F. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Gerber, A. Two-equation eddy-viscosity turbulence models for engineering applications. In Proceedings of the ASME International Mechanical Engineering Congress & Exposition, New Orleans, LA, USA, 17–22 November 2002. Paper number IMECE2002-39315. [Google Scholar]
- Morgut, M.; Nobile, E. Numerical Predictions of Cavitating flow around model scale propellers by CFD and advanced model calibration. Int. J. Rotating Mach. 2012, 2012, 618180. [Google Scholar] [CrossRef]
- Bakir, F.; Rey, R.; Gerber, A.G.; Belamri, T.; Hutchinson, B. Numerical and experimental investigations of the cavitating behaviour of an inducer. Int. J. Rotating Mach. 2004, 10, 15–25. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; DCW Industries, Inc.: La Canada, CA, USA, 2006. [Google Scholar]
- Vaz, J.R.; Okulov, V.L.; Wood, D.H. Finite blade functions and blade element optimization for diffuser-augmented wind turbines. Renew. Energy 2020, 165, 812–822. [Google Scholar] [CrossRef]
- Moreira, J.L.; Mesquita, A.L.; Araujo, L.F.; Galhardo, M.A.; Vaz, J.R.; Pinho, J.T. Experimental investigation of drivetrain resistance applied to small wind turbines. Renew. Energy 2020, 153, 324–333. [Google Scholar] [CrossRef]


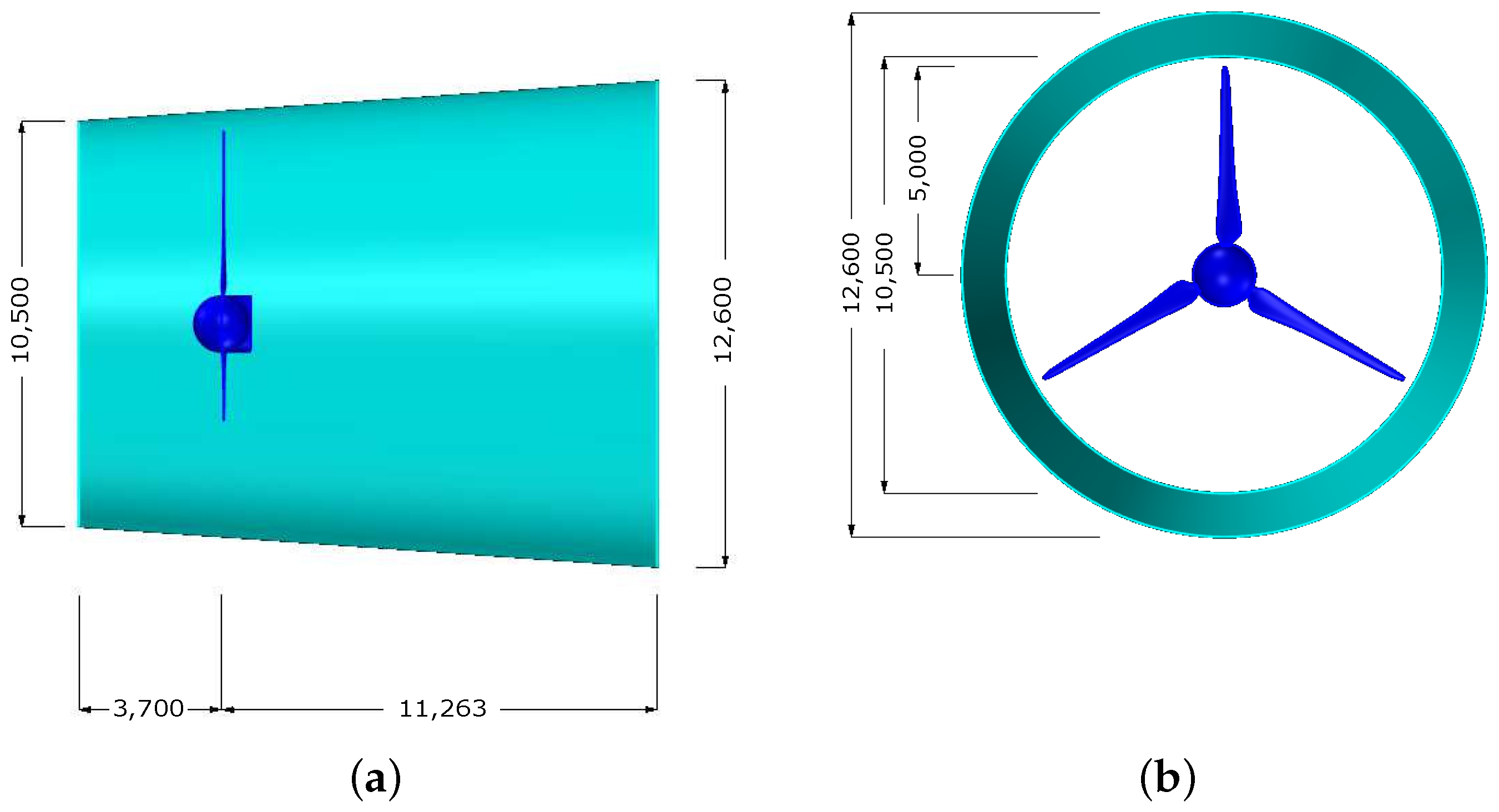
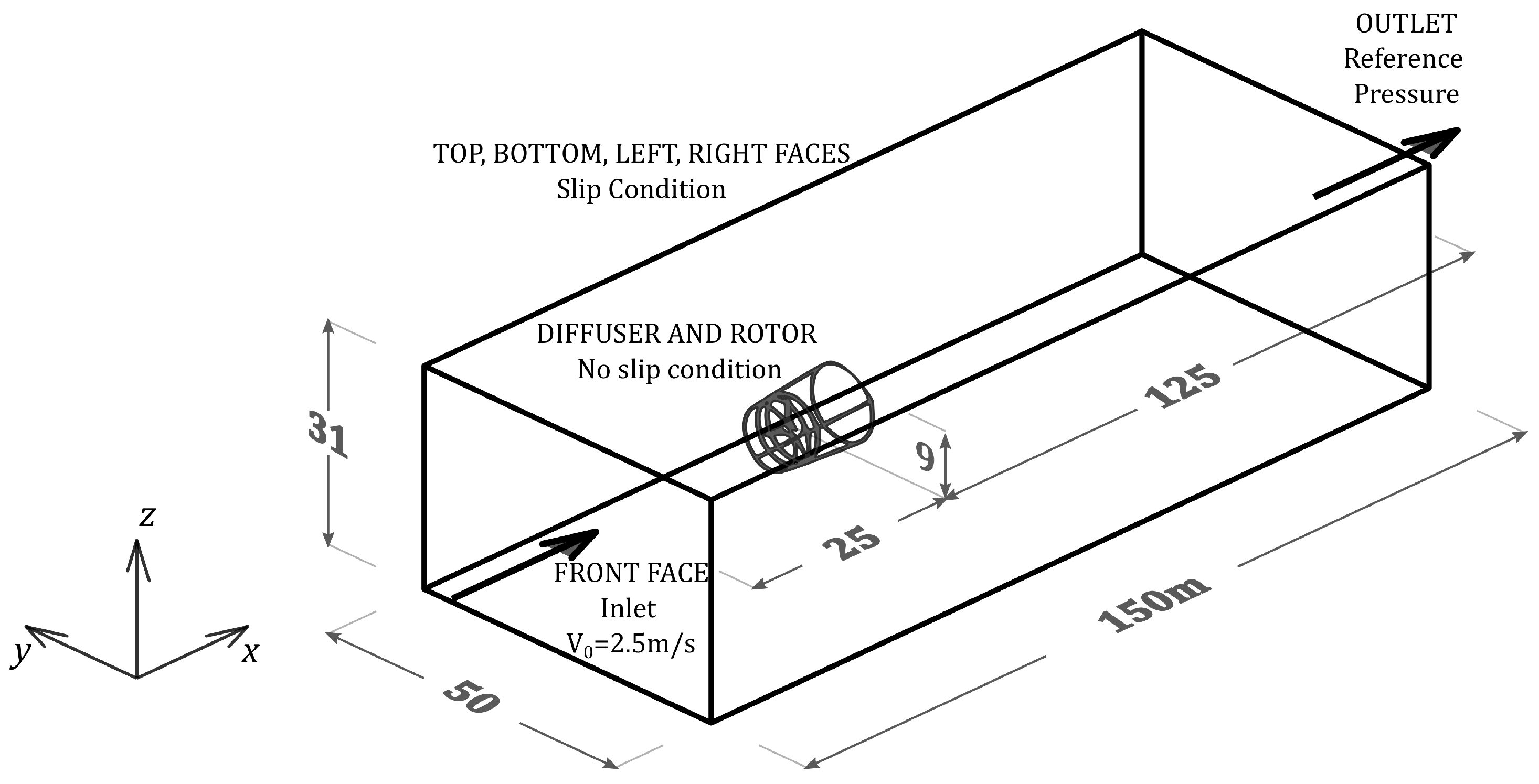


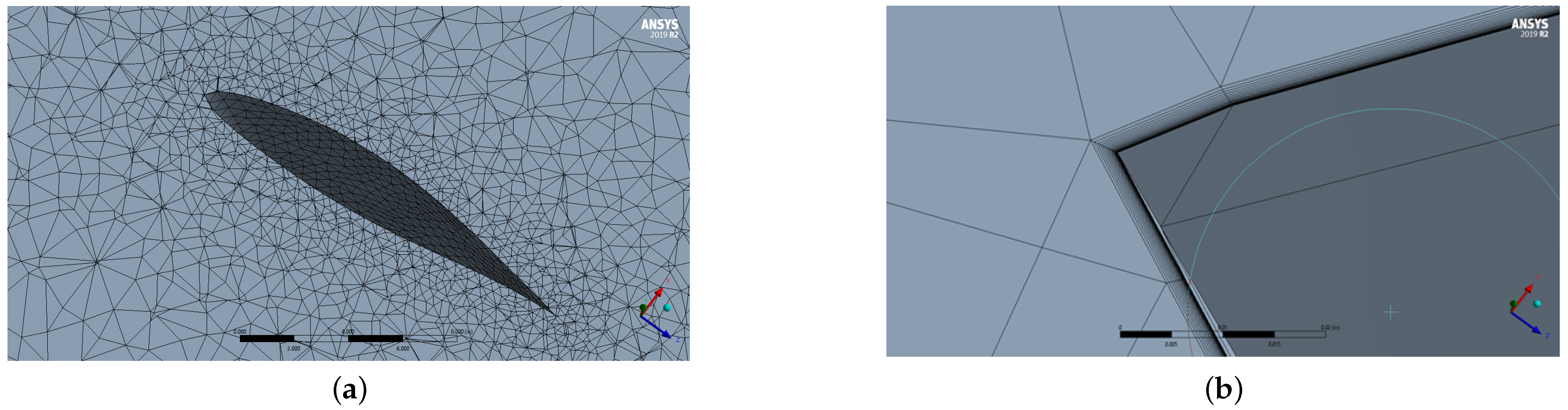


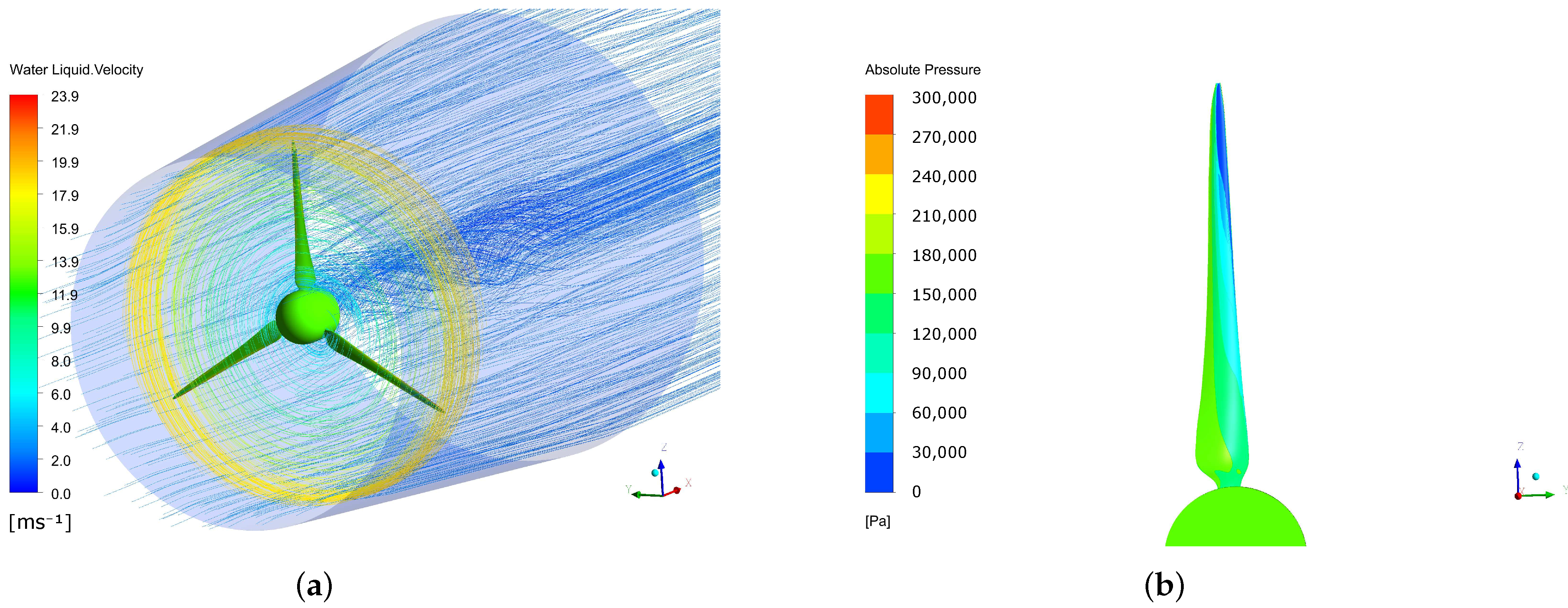

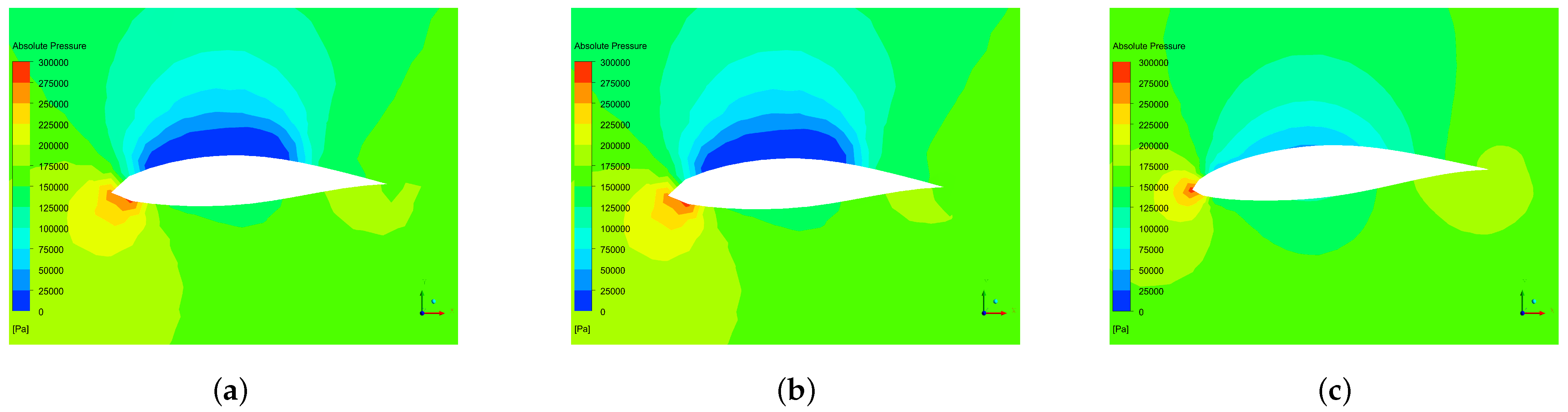

| Parameter | Value |
|---|---|
| Inlet diffuser diameter () | m |
| Outlet diffuser diameter () | m |
| Diffuser upstream length () | m |
| Diffuser downstream length () | m |
| Diffuser total length () | m |
| Diffuser thickness () | mm |
| Opening angle () | deg |
| Quantity | Value |
|---|---|
| (Condensation) and 50 (Vaporization) | |
| 997 kg/m | |
| kg/m | |
| Mean bubble diameter () | m |
| Pressure of vapor () | 3.170 kPa |
| Radial Distance | Span Station | Chord Length | Twist | Twist Axis |
|---|---|---|---|---|
| [m] | [m] | [deg.] | [% chord] | |
| 0.793 | 0.148 | 0.27 | 24 | 30 |
| 0.949 | 0.189 | 0.56 | 20 | 30 |
| 1.185 | 0.237 | 0.55 | 16 | 30 |
| 1.400 | 0.280 | 0.51 | 13 | 30 |
| 1.635 | 0.327 | 0.47 | 11 | 30 |
| 1.860 | 0.372 | 0.43 | 10 | 30 |
| 2.086 | 0.417 | 0.39 | 8 | 30 |
| 2.311 | 0.462 | 0.35 | 7 | 30 |
| 2.536 | 0.507 | 0.33 | 6 | 30 |
| 2.761 | 0.552 | 0.30 | 5 | 30 |
| 2.985 | 0.597 | 0.28 | 5 | 30 |
| 3.210 | 0.642 | 0.26 | 4 | 30 |
| 3.432 | 0.686 | 0.26 | 4 | 30 |
| 3.657 | 0.731 | 0.26 | 3 | 30 |
| 3.880 | 0.776 | 0.26 | 3 | 30 |
| 4.101 | 0.820 | 0.25 | 2 | 30 |
| 4.328 | 0.865 | 0.26 | 2 | 30 |
| 4.550 | 0.910 | 0.26 | 2 | 30 |
| 4.776 | 0.955 | 0.26 | 2 | 30 |
| 5.000 | 1.000 | 0.11 | 1 | 30 |
| Parameter | Value |
|---|---|
| Turbine diameter (D) | 10 m |
| Hub diameter | m |
| Number of blades (N) | 3 |
| Free stream velocity | m/s |
| Water density at 25 C | 997 kg/m |
| Submergence of the turbine (H) | 9 m |
| Pa | |
| Pa | |
| Gravity (g) | m/s |
| Angular velocity () | 35 rpm |
| Foil type | NACA -618 |
| Region | Condition |
|---|---|
| Inlet | m/s |
| Outlet | |
| Blade surface | No-slip |
| Rotor surface | No-slip |
| Top, bottom and lateral surfaces | Slip |
| Rotatory domain | Frozen rotor |
| Turbulence intensity |
| Parameter | Value |
|---|---|
| Mesh | Cells [×10] | Power | |
|---|---|---|---|
| Mesh A | 16.2 | 1.32 | 388 kW |
| Mesh B | 17.6 | 1.01 | 337 kW |
| Mesh C | 18.9 | 1.15 | 333 kW |
| Mesh D | 19.4 | 1.10 | 325 kW |
| Mesh E | 20.5 | 1.11 | 324 kW |
| Bare Turbine | Shrouded Turbine | |||||
|---|---|---|---|---|---|---|
| [m] | [m/s] | [m/s] | ||||
| 1.00 | 4.4366 | 17.9746 | −4.4438 | 4.8882 | 14.8072 | −4.5960 |
| 1.25 | 5.2192 | 12.8085 | −3.8261 | 5.6089 | 11.0903 | −4.2369 |
| 1.50 | 6.0395 | 9.4309 | −3.1398 | 6.3809 | 8.4489 | −3.6099 |
| 1.75 | 6.8841 | 7.1554 | −2.8491 | 7.1868 | 6.5652 | −3.4404 |
| 2.00 | 7.7450 | 5.5713 | −2.4387 | 8.0165 | 5.2003 | −3.0272 |
| 2.25 | 8.6173 | 4.4344 | −2.2454 | 8.8635 | 4.1915 | −2.8229 |
| 2.50 | 9.4979 | 3.5959 | −2.1149 | 9.7230 | 3.4313 | −2.5876 |
| 2.75 | 10.3847 | 2.9625 | −2.0876 | 10.5926 | 2.8474 | −2.5156 |
| 3.00 | 11.2762 | 2.4740 | −1.9430 | 11.4700 | 2.3911 | −2.2933 |
| 3.25 | 12.1714 | 2.0904 | −1.7277 | 12.3537 | 2.0292 | −2.0685 |
| 3.50 | 13.0695 | 1.7843 | −1.7887 | 13.2425 | 1.7379 | −1.7737 |
| 3.75 | 13.9700 | 1.5365 | −1.5611 | 14.1354 | 1.5008 | −1.5322 |
| 4.00 | 14.8724 | 1.3336 | −1.3559 | 15.0299 | 1.3058 | −1.3339 |
| 4.25 | 15.7764 | 1.1654 | −1.1897 | 15.9229 | 1.1441 | −1.1691 |
| 4.50 | 16.6818 | 1.0247 | −1.0465 | 16.8117 | 1.0089 | −1.0314 |
| 4.75 | 17.5882 | 0.9060 | −0.9224 | 17.6833 | 0.8963 | −0.9166 |
| 5.00 | 18.4957 | 0.8049 | −0.8194 | 18.5221 | 0.8026 | −0.8180 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Picanço, H.P.; Kleber Ferreira de Lima, A.; Dias do Rio Vaz, D.A.T.; Lins, E.F.; Pinheiro Vaz, J.R. Cavitation Inception on Hydrokinetic Turbine Blades Shrouded by Diffuser. Sustainability 2022, 14, 7067. https://doi.org/10.3390/su14127067
Picanço HP, Kleber Ferreira de Lima A, Dias do Rio Vaz DAT, Lins EF, Pinheiro Vaz JR. Cavitation Inception on Hydrokinetic Turbine Blades Shrouded by Diffuser. Sustainability. 2022; 14(12):7067. https://doi.org/10.3390/su14127067
Chicago/Turabian StylePicanço, Hamilton Pessoa, Adry Kleber Ferreira de Lima, Déborah Aline Tavares Dias do Rio Vaz, Erb Ferreira Lins, and Jerson Rogério Pinheiro Vaz. 2022. "Cavitation Inception on Hydrokinetic Turbine Blades Shrouded by Diffuser" Sustainability 14, no. 12: 7067. https://doi.org/10.3390/su14127067
APA StylePicanço, H. P., Kleber Ferreira de Lima, A., Dias do Rio Vaz, D. A. T., Lins, E. F., & Pinheiro Vaz, J. R. (2022). Cavitation Inception on Hydrokinetic Turbine Blades Shrouded by Diffuser. Sustainability, 14(12), 7067. https://doi.org/10.3390/su14127067







