Abstract
The indicators of student success at higher education institutions are continuously analysed to increase the students’ enrolment in multiple scientific areas. Every semester, the students respond to a pedagogical survey that aims to collect the student opinion of curricular units in terms of content and teaching methodologies. Using this information, we intend to anticipate the success in higher-level courses and prevent dropouts. Specifically, this paper contributes with an interpretable student classification method. The proposed solution relies on (i) a pedagogical survey to collect student’s opinions; (ii) a statistical data analysis to validate the reliability of the survey; and (iii) machine learning algorithms to classify the success of a student. In addition, the proposed method includes an explainable mechanism to interpret the classifications and their main factors. This transparent pipeline was designed to have implications in both digital and sustainable education, impacting the three pillars of sustainability, i.e.,economic, social, and environmental, where transparency is a cornerstone. The work was assessed with a dataset from a Portuguese higher-level institution, contemplating multiple courses from different departments. The most promising results were achieved with Random Forest presenting 98% in accuracy and F-measure.
1. Introduction
There are more than 20 million students in higher education institutions (heis) in the European Union. However, according to Vossensteyn et al. (2015) [1], around seven million (36%) will not finish their studies. Shapiro et al. (2015) [2] present a similar picture where out of 20.5 million existing students, around 39% will interrupt their studies.
The Organisation for Economic Co-operation and Development (oecd) [3] reports that other countries show similar behaviours in higher education (Australia and New Zealand (20%), Israel (25%), and Brazil (52%)). In addition, it is still possible to observe interesting remarks regarding school dropouts. In the United Kingdom, students who start higher education at 21 years old have more probability of dropout during the first year than those who had a higher education enrolment after high school (11.8% vs. 7.2%, respectively). The success of students may depend on students’ characteristics and the conditions provided by heis. Specifically, students with a lower ranking in hei admissions tend to underperform compared to the remaining students. By using both the students’ characteristics and hei information, it is possible to predict the success of students employing appropriate tools [4]. The advent of information technologies has dramatically increased the amount of data generated within heis. It is important to extract useful knowledge from data in multiple hei dimensions, i.e., administrative, financial, and educational. It requires intelligent mechanisms to manipulate and extract relevant patterns for effective decision making [5]. In this context, several solutions have been raised to increase not only the performance of students but essentially avoid or decrease the dropout rate [6,7]. Learning analysis (la), together with statistical analysis and predictive modelling, have been identified as relevant mechanisms to extract meaningful information from academic data [8,9]. The prediction of student performance is an indicator for students, professors, and hei administration who can adapt the learning processes accordingly [10]. According to Kolo and Adepoju (2015) [11], one of the most complex tasks is to find a set of rules to predict student performance. However, embedding la with machine learning (ml) and data mining (dm) mechanisms [12,13,14,15] makes it possible to explore relevant patterns. Specifically for higher education, the emergence of educational data mining (edm), which relies on decision trees (DT), k-nearest neighbours (knn), naive Bayes (nb), association rule mining (arm), and neural networks (nn), allows to obtain predictions, association rules, classifications, and clusters. These edm solutions support intelligent decision making in heis [16,17] concerning students success or other academic problems.
The existing solutions still do not embrace the desired accountability, responsibility, and transparency to underline the concept of sustainable education. Sustainable education is defined as “the active academic participation to create economic, social, and environmental programs improving life standards, generating empowerment and respecting interdependence” [18]. Therefore, an artificial intelligence (ai)-based system that helps to understand the student performance may support sustainable education. ai enables to anticipate factors which have a high impact on student dropout, supporting the three pillars of sustainability: (i) economic, by providing good professionals to the labour market early; (ii) social, by decreasing the percentage of dropouts in heis; and (iii) environmental, by decreasing the mean time spent to finish a course [19,20,21,22]. In this context, this paper contributes an interpretable student success classification, aiming to approach the three pillars of sustainable education.
This work aims to analyse the information collected from pedagogical surveys during the last eight years. The purpose of the pedagogical surveys is to evaluate opinions and processes on three dimensions. The unit of analyses include students, teachers, and curricular units. To do so, every year, heis use pedagogical surveys to collect the students’ opinions concerning the curricular unit and the corresponding teacher. The results are analysed by department, by course, and by curricular unit, allowing to detect the main problems occurred during the semester. The analysis enables to understand which measures are required to overcome the problems. The pedagogical surveys used in this work contemplate, on average, 2000 students, 40 teachers, and 10 curricular units per year. On average, each teacher has 3 curricular units and 50 students. However, the absence rate is approximately 25%.
The pedagogical surveys are provided to students using a web platform which allows the automatic and anonymous collection of information. The survey covers questions to evaluate three categories: (i) teaching activity; (ii) curricular unit (cu); and (iii) student performance. Using this data, this paper aims to classify and interpret student performance. The proposed method encompasses: (i) a statistical analysis; (ii) ml algorithms for classification; and (iii) explainability mechanisms to interpret the results. The questions have been adapted over the years, according to the pedagogical challenges of each school year. The experiments were conducted with a dataset with 87,752 valid responses of four courses from different departments. The proposed method presents macro- and microclass classification accuracy and an F-measure of 98%.
The rest of this paper is organised as follows. Section 2 overviews the relevant related work concerning student performance classification. Section 3 introduces the proposed method, detailing the data pre-processing, classification, explainability, and evaluation metrics. Section 4 describes the experimental set-up and presents the empirical evaluation results, considering the data analysis, classification, and explanation. Finally, Section 5 concludes and highlights the achievements and future work.
2. Related Work
heis are evaluated either by the labour market or by national higher education assessment agencies. In addition, the universities’ rankings are based on their students’ success (academic and professional). To improve student progress, the data generated within academic activities can be used to recognise patterns and make suggestions to boost student performance. Despite the concern about reducing the number of dropouts, it is also essential to understand which decisions need to be implemented at the strategic level, concerning policies, strategies, and actions that institutions carry out as a whole.
Abdallah and Abdullah (2020) [23] and Rastrollo-Guerrero et al. (2020) [24] provide an extensive literature review of intelligent techniques used to predict student performance. In particular, Abdallah and Abdullah (2020) analyse three perspectives: (i) the learning results predicted; (ii) the predictive models developed; and (iii) the features which influence student performance. Both reviews conclude that most of the proposed methods focus on predicting students’ grades. Regression models and supervised machine learning are the most used approaches to classify student performance.
The current literature review contemplates recent works that classify student performance by analysing both methods and data. Therefore, to predict the student success:
- Hamoud et al. (2018) [25] use a questionnaire encompassing health, social activity, relationships, and academic performance information. The proposed solution employs tree-based algorithms to predict student performance in heis.
- Yuri et al. (2019) [26] employ classification algorithms to predict graduation rates from real grades of under-graduated engineering students.
- Akour et al. (2020) [27] explore deep learning to predict whether the student will be able to finish the course. The proposed model relies on demographic, student behaviour, and academic-related data.
- Salah et al. (2020) [28] propose a method to predict student performance on final examinations. The proposed method identifies demographic, academic background, and behavioural features as important for the final results. As ml algorithms, the authors compare DT, nb, logistic regression (lr), Support Vector Machine (svm), knn, and nn.
- Muhammad et al. (2022) [29] predict the students who might fail final exams. The proposed model employs the course details and the students’ grades. As ml classifiers, they compare nb, nn, svm, and dt.
In addition to the face-to-face environment, other models provide learning conditions, without spatial and temporal restrictions, through online learning platforms, such as Massive Open Online Course (mooc), Virtual Learning Environments (vles), and Learning Management Systems (lms). Although it gives students more autonomy, online learning has raised multiple challenges, such as a lack of interest and motivation and low engagement and outcomes. In this context, a blended learning methodology is seen as an alternative because it combines face-to-face and online learning approaches [30]. In the literature, the student success classification has been explored by:
- Muhammad et al. (2021) [31], which aims to predict at-risk students. The proposed model uses machine learning and deep learning algorithms to identify important variables to classify the students’ behaviour in online learning. Student assessment scores and the intensity of engagement (e.g., clickstream data or time-dependent variables) are essential factors in online learning. The experiments were conducted with Random Forest (rf), svm, knn, Extra Tree (et), Ada Boost (ab), and Gradient Boosting (gb).
- Mubarak et al. (2020) [32] present a predictive model for the early prediction of at-risk students.The authors believe that the dropout prediction is a time-series problem. In this context, the proposed solution encompasses logistic regression models and the Hidden Markov Model (hmm), using demographic data and vle logs.
- Gomathy et al. (2022) [33], who developed a predictive model to identify at-risk students across a wide variety of courses. The proposed method relies on courses details as well as actions logs Moodle to apply CatBoost (cb), rf, nb, lr, and knn classifiers.
Table 1 compares the reviewed classification models concerning the success/failure or dropouts in heis. A significant number of research proposals explore the students’ grades and demographic information, excluding the student’s opinions concerning the course organisation. In addition, the ml models leave users with no clue about why those classification has been generated.

Table 1.
Comparison of student success prediction methods.
Interpretability and explainability are essential to understand ml-generated outputs. According to Berchin et al. (2021) [34], transparency promotes a change towards sustainability. Explainability and interpretability can often be used interchangeably [35]. Specifically, interpretability is “loosely defined as the science of comprehending what a model did (or might have done)” [36], implying a determination of cause and effect. A model is interpretable when a human can understand without further resources. However, ml incorporates both self-explainable and opaque models. While opaque models behave as black boxes, interpretable mechanisms are self-explainable. Naser (2021) [37] details the level of explainability of the models depicted in Table 2.

Table 2.
Interpretability of models [37].
Interpretability and explainability have been explored to explain predictions [38], recommendations [39], or classifications [40]. In this context, several solutions were developed to be coupled with ml models [39,41,42,43] to provide explanations. However, scant research has been addressed to incorporate those explainable models in dropout prediction or success classification in heis. Wang and Zhan (2021) [44] identify interpretability as the main limitation related to artificial intelligence technologies in higher education. To address this vacuity, the current work concentrates on: (i) employing the student’s opinion via pedagogical questionnaires; (ii) implementing a transparent classification method with explanations; and (iii) using a face-to-face environment. Therefore, we propose a method which promotes transparency in higher-level education, supporting the three pillars of sustainability, i.e., economic, social, and environmental.
3. Proposed Method
This paper proposes an explainable method to classify the success of hei courses using pedagogical questionnaires. Figure 1 introduces the proposed solution which adopts ml classification algorithms to generate interpretable success classification. The proposed method encompasses: (i) as inputs, the pedagogical questionnaire (Section 3.1); (ii) a data analysis module to assess the reliability of the data (Section 3.2); (iii) a classification method (Section 3.3) to automatically classify the success; and (iv) an interpretability mechanism to describe and explain the outputs (Section 3.4). The transparency of the solution supports the concept of sustainability in heis. The effectiveness of the proposed method is evaluated using standard classification metrics (Section 3.5). Figure 1 depicts the different modules of the proposed solutions.

Figure 1.
Interpretable student classification using pedagogical questionnaires.
3.1. Pedagogical Questionnaire
The proposed solution relies on a pedagogical questionnaire of a Portuguese hei. The importance of pedagogical questionnaires among students has increased, contributing to improving and adapting the teaching system continuously in heis.
The questionnaire is equal to all cu, covering 3 categories: (i) teaching activity (not included in this study); (ii) cu (); and (iii) student’s performance in the cu (). Each category encompasses 4 different questions using a 7-level Likert scale (level 1 represents the lowest value, and 7—the highest). Table 3 details the questionnaire composition and the content of the questions. We used eight consecutive academic years (2013/2014 to 2020/2021) and four courses from three different departments.

Table 3.
Questionnaire description.
3.2. Data Analysis
The current work employs quantitative research to analyse the student’s opinions using structured questionnaires [45]. According to the most adopted approaches, i.e., power analysis [46] and rules of thumb by Hair [47], the used sample size is enough for this study. Specifically, data analysis is a three-phase stage composed of:
- Cronbach’s alpha reliability analysis [48] which was used to verify whether the variability of the answers effectively resulted from differences in students’ opinions.
- Descriptive analysis which was conducted employing univariate and multivariate analysis. It uses descriptive and association measures, e.g., Pearson and Spearman correlations, graphical representations, and categorical principal component analysis (catpca). While Pearson’s correlation coefficient measures the intensity and direction of a linear relation among two quantitative variables, Spearman’s measures the dependence between ordinal variables using rankings [49]. In a positive correlation, two variables tend to follow the same direction, i.e., one variable increases as the other variable increases. In a negative scenario, the behaviour is the opposite, i.e., an increase in one variable is associated with a decrease in the other.Principal component analysis (pca) can transform a set of p-correlated quantitative variables into a smaller set of independent variables denominated by principal components. Because the pedagogical survey is expressed in a 7-level Likert scale, the optimal scaling procedure was used to assign numeric quantifications to categorical variables, i.e., catpca.
- Inferential analysis employs t-test for means and Levene’s for variances.t-test is used to verify whether two populations are significantly different. This test requires the validation of normality assumptions of two groups and the homogeneity of variances (Kolmogorov–Smirnov and Levene’s test, respectively). Therefore, for two populations 1 and 2, where Y follows a normal distribution, the hypotheses to be tested are: : vs.: . The hypothesis is rejected if p-value where is the significance level adopted (5% or 1%). When the population variances are not homogeneous, the test statistic used to assess the equality of means is Welch t-Student.
3.3. Classification
This work employs batch ml classification. The experiments involve multiple classification algorithms to analyse the most promising results. The binary classification algorithms selected from scikit-learn (available at https://scikit-learn.org/stable, accessed on 12 April 2022) are well-known interpretable models with good performance:
- nb is a probabilistic classifier based on Bayes’ theorem [50].
- dt can be employed in prediction or classification tasks. The model is based on a tree structure which embeds decision rules inferred from data features. Decision trees are self-explainable algorithms easy to understand and interpret [51].
- CF is an ensemble learning model which combines multiple dt classifiers [52] to provide solutions for complex problems.
- Boosting Classifier (bc) is an ensemble of weak predictive models which allows the optimisation of a differentiable loss function [53].
- knn determines the nearest neighbours using feature similarity to solve classification and regression problems [54].
3.4. Interpretability
Interpretability and explainability are relevant to describing and understanding the outputs generated by ml models.
The proposed solution adopts local interpretable model-agnostic explanations (lime) [42], which determine the output impact of an input feature variation. lime will allow to understand the impact of the pedagogical survey variables in the success or failure scenarios. Therefore, for each classification, lime generates the corresponding explanations promoting the transparency and, consequently, the sustainability of the method.
3.5. Evaluation
The model evaluation will allow to assess the feasibility and effectiveness of the solution. The proposed method employs offline processing to learn the behaviour of the students. Specifically, the data are partitioned into training, used to build an initial model, and testing is used to assess the quality of the classifications. The quality of classifications is assessed using the evaluation standard metrics:
- Classification accuracy indicates the performance of ml model. As a binary classification, it uses the number of positives and negatives in the classification.
- F-measure in macro- and micro-averaging computing scenarios assesses the effectiveness of the model employing the precision and recall. While precision concentrates the percentage of correct classifications, recall is the ability of a model to find all relevant cases in the dataset. The combination of macro- and micro-average provides an overall evaluation of the models across all target classes (assigning the same weight to each class) or individually.
4. Experiments and Results
We conducted several offline experiments using the results obtained from pedagogical questionnaires to evaluate the proposed method. Our system holds the following hardware specifications:
- Operating System: Windows 64 bits.
- Processor: Intel(R) Core(TM) i7-8565U CPU .
- RAM: 16 GB.
- Disk: 500 GB SSD.
The experiments comprise: (i) data analysis; (ii) classification; and (iii) explainability. The data collected were statistically treated using the IBM SPSS Statistics 27.0 and R software. The classification models rely on scikit-learn (https://scikit-learn.org/stable/, accessed on 15 April 2022) from Python.
4.1. Dataset
The dataset was built from pedagogical surveys in a Portuguese hei. The data collected encompass: (i) two semesters; (ii) eight consecutive academic years (2013/2014 to 2020/2021); (iii) four courses (of 3 or 4 years); and (iv) three different departments. The dataset contains 87,752 valid responses to eight questions of two categories (Section 3.1).
Table 4 describes the content of the dataset. In particular, the target was defined considering the median of failed students, i.e., it is considered a success if the failed percentage is lesser than the median. The distribution of classes is balanced where 44,089 were marked as success and 43,636 failure.

Table 4.
Description of the dataset.
4.2. Data Analysis
A feature analysis identifies the most promising independent features to predict the target variables. Therefore, we start employing a descriptive and exploratory analysis of the dataset.
- Cronbach’s alpha reliability analysis verifies the variability of the answers. The eight questions of and present a Cronbach’s alpha of 0.953, revealing excellent reliability. To assess whether students consciously responded to the questionnaire, the percentage of students that attributed the same value to the eight questions was explored. The results indicate that only 1.4% of the answers have the same value, being a very positive aspect of the dataset.
- The descriptive analysis starts with the mean, median, mode, standard deviation (sd), and coefficient of variation (cv), depicted in Table 5. The three location measures, i.e., mean, median, and mode, tend to be good and similar in all the questions except . In the remaining questions, the most frequent answer is 7, while in question Q7, it is 5, i.e., the classification tends to be lower. The variability measured by cv shows moderate dispersion, indicating some lack of homogeneity in the responses. Therefore, the most appropriate location measure is the median used to create the target variable in the dataset.
 Table 5. Descriptive statistics for questions Q1 to Q8.
Table 5. Descriptive statistics for questions Q1 to Q8.
In terms of correlations, we started to employ Spearman’s correlation coefficient, illustrated in Figure 2. The results show that the variables are highly positively correlated, i.e., the student’s opinion in all questions tends to follow the same direction. The highest correlations ( > 0.7) are observed among variables from (Student’s opinion about cu). All correlations are statistically significant at 1%.
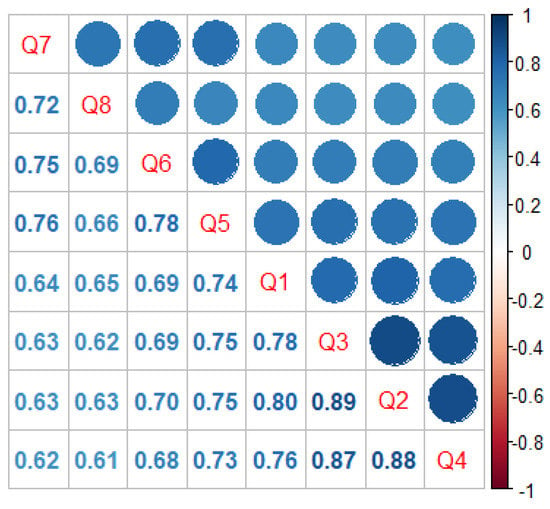
Figure 2.
Spearman correlation coefficient between questions Q1 to Q8.
Because the courses used in the dataset have different sizes, we have employed the same analysis for the two groups, i.e., small courses (<200 students) and big courses (≥400 students). The results point to a favourable opinion of students enrolled in small courses in terms of motivation () and student subjects ().
Regarding the behaviour of students in both semesters, it is interesting to highlight that motivation (Q5) and frequent study of subjects (Q7) decrease from the 1st to the 2nd semester. The accumulated tiredness can explain this scenario over the academic year. Additionally, the 2nd semester is composed of several academic breaks and activities, which can decrease the amount of time spent studying.
In addition to the information collected using pedagogical questionnaires, we associate for each cu the number of enrolled students (# students), the number of those who failed (# students failed), the number of students who suspended/annulled the cu (# suspended), and the mean of the cu. In this context, assessing the correlation between the mean and the remaining variables is relevant. Because, in terms of enrolled students, the real data encompass the number of enrolled students per cu; the correlations were calculated with the number of students instead of percentages (Table 6). The results indicate a strong positive correlation between # students and # suspended or # students failed of and , respectively. It is also worth noting the existence of a strong negative correlation between the cu mean and # students failed (), i.e., increasing the number of failures, the mean decreases.

Table 6.
Correlations between the variables associated to the cus.
Given these high values for the correlations, we chose to build new variables to represent the percentages of students who cancelled/suspended and the number of students who failed.
- An inferential analysis with t-test was used to validate the hypothesis that the size of the courses has an impact on the mean. Specifically, t-test determines whether there are significant differences between the means of the two groups.
The normality and the homogeneity of variances in the two groups were evaluated, with the Kolmogorov–Smirnov test (p-value = 0.06 for group 1 and p-value = 0.04 for group 2) and with the Levene test (p-value = 0.000), respectively.
Although group 2 does not follow a normal distribution because the asymmetry and kurtosis values ( and , respectively) are not very high, we can proceed with the test. On the other hand, once the hypothesis of equality of variance is rejected, the test statistic used for the equality of means is Welch’s t-Student (Table 7).

Table 7.
Independent samples t-test.
The differences between means are considered statistically significant because p-value = 0.00 leads to the rejection of the hypothesis : . In short, small courses have higher mean grades than big courses. In this context, it is important to measure the dependence of the dataset variables concerning the size of the courses, i.e., small courses (S) or big courses (B). In addition, the answers in small courses are more homogeneous, (i.e., the cv in small and big courses is 21.5% and 26%, respectively).
- catpca multivariate statistical analysis will explore the principal components concerning S and B. The component criterion used was the eigenvalue rule greater than 1.
Table 8 presents the Cronbach’s alpha and the variance account for the total. According to the rule of an eigenvalue greater than 1, it is possible to summarise the relational information between the variables in two orthogonal components (dimensions 1 and 2). The total variance of the 11 variables is explained by more than 80%. The internal consistency of each component was measured with Cronbach’s alpha. No further components were retained as the very low Cronbach’s alpha values indicate unreliability. Specifically, the Cronbach’s alpha of dimensions 1 and 2 is 0.919 and 0.571, respectively. These values represent the reliability of each dimension, and it is not cumulative. The total value (0.965) represents the reliability of the general model composed of dimensions 1 and 2.

Table 8.
Model Summary—Cronbach’s alpha and eigenvalues.
Table 9 presents the weights of the variables for each component, i.e., the component loadings. We have selected the variables for each dimension with component loadings greater than 0.5 in absolute value. Therefore, while dimension one is determined by variables to , dimension two uses the mean per cu, percentage of students who failed (% Failed cu), and percentage of students who suspended/annulled (% Suspended cu). We can conclude that defines the “Students’ opinion about the cus” and the “cus performance”.

Table 9.
Component loadings extracted from catpca analysis.
Figure 3 illustrates graphically the principal components provided by catpca.
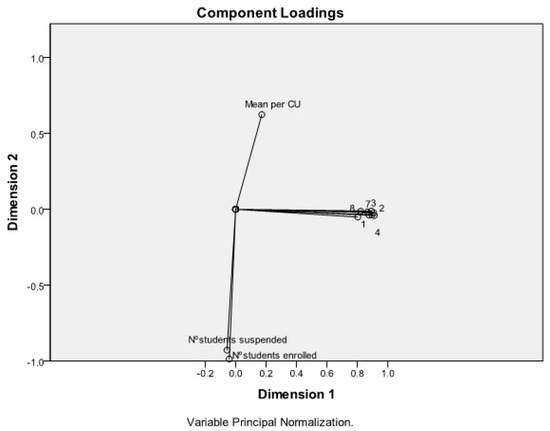
Figure 3.
Principal components (Appendix A) extracted from catpca analysis.
Furthermore, in general, we can conclude that small courses present, in dimension 1, higher averages and a lower percentage of failures and dropouts than big courses. Therefore, the results obtained by the catpca analysis reinforce the preliminary descriptive study. In the attachment, we include further results concerning the catpca with objects labelled by course size.
4.3. Classification
The proposed method estimates if the student will succeed using the flag target feature. While class #0 represents the students who failed, class #1 stands for success. Based on the data analysis results using the entire dataset, the experiments have been performed employing three different sets:
- Complete dataset combining small and big courses;
- Big courses;
- Small courses.
Table 10 contains the macro and micro classification results. The values obtained are consistent in most cases for all classifiers, increasing the accuracy according to the set used. In addition, the proposed solution provides promising results with the differentiation of courses with distinct amounts of students. The best classifiers in all the experiments are rf and ab with approximated results. When compared with ab, rf requires less computation effort. Therefore, to explain the classifications, the proposed method focuses on the rf algorithm.

Table 10.
Performance of the classification with the entire dataset.
4.4. Explanations
The rf classifier provides promising results, being based on decision trees, which are interpretable models. The proposed method employs lime to each subset to understand the impact of the multiple features in the final classifications. The final explanation is generated via decision tree visualisation.
4.4.1. Features Impact
- Subset 1 encompasses the answers of courses with different dimensions. Figure 4 displays the lime explanations for a success scenario. The classification of this student was predicted with a probability of success of 78% based on the features , , , , , and . From the lime explanations, we can conclude that the variables which most contribute to the classifications are the percentage of students who failed and the mean of the cu. In terms of questions, the questions from are associated with failure classifications in this subset.
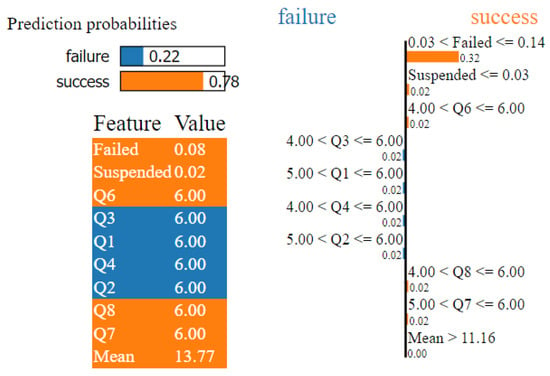 Figure 4. lime explanations for subset 1.
Figure 4. lime explanations for subset 1.
- Subset 2 encompasses the answers of courses with a higher number of students. Figure 5 displays the lime explanations for a failure scenario in big courses. The classification of this student was predicted with a probability of 99% based on the features , , , and . From the lime explanations, we can conclude that the variables which most contribute to the classifications are the percentage of students who failed and the mean of the cu. In terms of questions, in this subset which integrates big courses, the classifications in the questions tend to be lower. In addition, the questions from appear to be associated with the success classification.
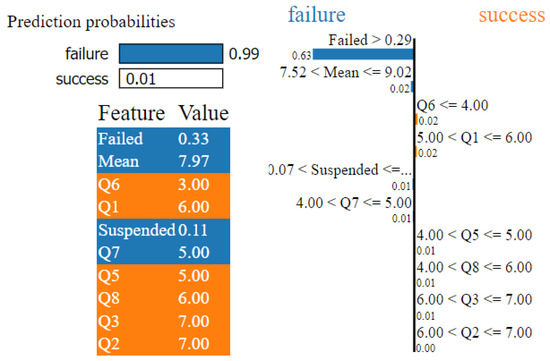 Figure 5. lime explanations for subset 2.
Figure 5. lime explanations for subset 2.
- Subset 3 encompasses the answers of courses with a smaller number of students. Figure 6 displays the lime explanations for a failure scenario in small courses. The classification of this student was predicted with a probability of 99% based on the features , , , and .
 Figure 6. lime explanations for subset 3.
Figure 6. lime explanations for subset 3.
4.4.2. Visualisation
For the proposed method, the rf classifier provides the best results. It is based on decision trees, which are interpretable models. Therefore, in addition to the lime explanations, we generate automatic sentences from the tree which cover the relevant subset of branches, namely from the root to the classification leaf, using the categories of the pedagogical survey (cu and Student performance in the cu).
Figure 7 depicts the decision tree extracted from subset 1. For this tree, we generate an explanation to understand why a student has failed using only the leafs with questions: “At cu level, the program was not adapted to the skills of the student (Q3). Concerning the student’s performance, the tasks proposed in the class were not achieved (Q6) because the student was not motivated for the cu (Q5)”. With these explanations, the cu can be adapted in order to minimise the failed rate.
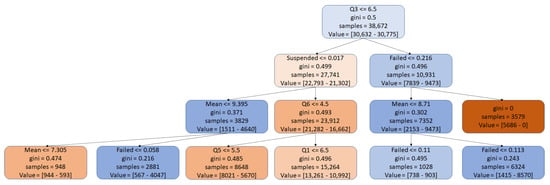
Figure 7.
Partial decision tree visualisation.
5. Conclusions
An hei aims to increase its ranking by seeking to provide up-to-date teaching and research methodologies and, consequently, provide good professionals to the labour market. In this regard, an hei will collect and analyse indicators related to the students’ performance. In particular, every semester, students respond to a pedagogical survey to manifest their opinion concerning the cu content and teaching methodology.
Emphasising the student opinion, this work proposes a transparent method to predict the student’s success. Particularly, the designed solution includes: (i) a data analysis to validate and explore statistically the collected dataset; (ii) ml classification; and (iii) the integration of an explainable mechanism to generate explanations for classifications.
The experiments were performed with a balanced dataset with 87,752 valid responses. The data analysis identified relevant differences between small and big courses. Small courses have higher mean grades in the cu, being more homogeneous than big courses. Furthermore, it can be concluded that courses with a high score in the mean of the cu have a lower percentage of failures or dropouts.
The proposed method was evaluated using standard classification metrics, achieving a 98% classification accuracy and F-measure. This result shows that it is possible to explain and classify student performance using pedagogical questionnaires. The proposed method allows to take pre-emptive actions and avoid early cancellations or dropouts. Specifically, the proposed method provides explanations which help to understand the reasons of the success or failure for each curricular unit. With this knowledge, the curricular unit can be adapted to avoid failures, early cancellations, or dropouts. The explanations provide information at both levels, curricular unit and students’ efforts being a starting point to improve the pedagogical method in the next school year. In addition, the proposed solution aims to support the three pillars of sustainability, i.e., economic, social, and environmental.
We plan to integrate more information about student behaviour and enhance the explanations in future work. Moreover, we intend to analyse the performance of deep learning models and integrate more explainable mechanisms. In addition, we intend to create an environment-agnostic model for student performance prediction, i.e., adapting dynamically the ml model, independent of it being face-to-face, online, or blended.
Author Contributions
Author Contributions: Conceptualisation, C.S.P., N.D., B.V., F.L., F.M. and N.J.S.; methodology, C.S.P., N.D., B.V., F.L., F.M. and N.J.S.; investigation, C.S.P., N.D., B.V., F.L., F.M. and N.J.S.; data curation, C.S.P., N.D., B.V., F.L., F.M. and N.J.S.; writing—original draft preparation, C.S.P., N.D., B.V., F.L., F.M. and N.J.S.; writing—review and editing, C.S.P., N.D., B.V., F.L., F.M. and N.J.S.; visualisation, C.S.P., N.D., B.V., F.L., F.M. and N.J.S.; supervision, C.S.P., N.D., B.V., F.L., F.M. and N.J.S.; funding acquisition, C.S.P., N.D., B.V., F.L., F.M. and N.J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the FCT—Fundação para a Ciência e a Tecnologia, I.P. [Project UIDB/05105/2020].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HEI | Higher Education Institution |
| OECD | Economic Co-operation and Development |
| LA | Learning Analytics |
| ML | Machine Learning |
| DM | Data Mining |
| EDM | Educational Data Mining |
| DT | Decision Tree |
| KNN | K-Nearest Neighbours |
| NB | Naive Bayes |
| ARM | Association Rule Mining |
| NN | Neural Networks |
| AI | Artificial Intelligence |
| LR | Logistic Regression |
| SVM | Support Vector Machines |
| MOOC | Massive Open Online Course |
| VLE | Virtual Learning Environments |
| LMS | Learning Management Systems |
| RF | Random Forest |
| ET | Extra Tree |
| ab | Ada Boost |
| GB | Gradient Boosting |
| HMM | Hidden Markov Model |
| CB | CatBoost |
| CU | Curricular Unit |
| CATPCA | Categorical Principal Component Analysis |
| PCA | Principal Component Analysis |
| BC | Boosting Classifier |
| LIME | Local interpretable model-agnostic explanations |
| SD | Standard Deviation |
| SV | Coefficient of Variation |
| S | Small courses |
| B | Big courses |
Appendix A
Figure A1 plots the weights of each variable in each component, i.e., the set of answers, and of the corresponding component loadings. In the figure, the small courses are identified as S and big courses as B. We can observe the relationships between objects and variables. We can conclude that, in general, small courses present, in dimension 1, higher averages and a lower percentage of failures and dropouts than big courses.
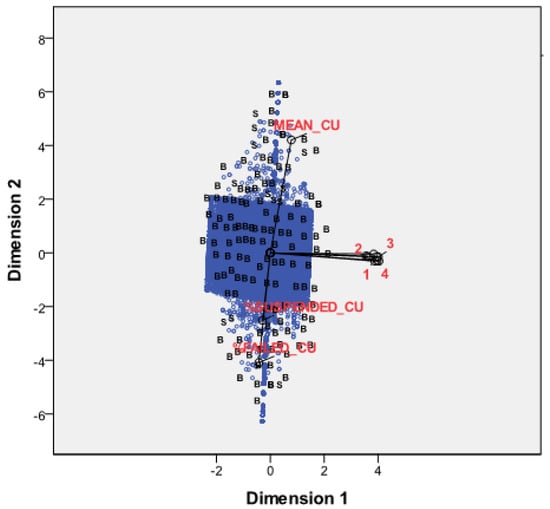
Figure A1.
Representation of objects labelled by course size, i.e., small courses (S) and big courses (B).
References
- Vossensteyn, J.J.; Kottmann, A.; Jongbloed, B.W.; Kaiser, F.; Cremonini, L.; Stensaker, B.; Hovdhaugen, E.; Wollscheid, S. Dropout and Completion in Higher Education in Europe: Main Report; European Union: Luxembourg, 2015. [Google Scholar]
- Shapiro, D.; Dundar, A.; Wakhungu, P.; Yuan, X.; Harrell, A. Completing College: A State-Level View of Student Attainment Rates; Signature Report; National Student Clearinghouse: Herdon, VA, USA, 2015. [Google Scholar]
- Indicators, O. Education at a Glance 2016. Editions OECD; OECD: Paris, France, 2012; Volume 90. [Google Scholar]
- Fancsali, S.E.; Zheng, G.; Tan, Y.; Ritter, S.; Berman, S.R.; Galyardt, A. Using Embedded Formative Assessment to Predict State Summative Test Scores. In Proceedings of the 8th International Conference on Learning Analytics and Knowledge, Sydney, Australia, 7–8 March 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 161–170. [Google Scholar] [CrossRef]
- Yehuala, M.A. Application of data mining techniques for student success and failure prediction (The case of Debre Markos university). Int. J. Sci. Technol. Res. 2015, 4, 91–94. [Google Scholar]
- Abaidullah, A.M.; Ahmed, N.; Ali, E. Identifying Hidden Patterns in Students’ Feedback through Cluster Analysis. Int. J. Comput. Theory Eng. 2015, 7, 16. [Google Scholar] [CrossRef]
- Goyal, M.; Vohra, R. Applications of data mining in higher education. Int. J. Comput. Sci. Issues (IJCSI) 2012, 9, 113. [Google Scholar]
- Na, K.S.; Tasir, Z. Identifying at-risk students in online learning by analysing learning behaviour: A systematic review. In Proceedings of the 2017 IEEE Conference on Big Data and Analytics (ICBDA), Kuching, Malaysia, 16–17 November 2017; pp. 118–123. [Google Scholar] [CrossRef]
- Williams, P. Squaring the circle: A new alternative to alternative-assessment. Teach. High. Educ. 2014, 19, 565–577. [Google Scholar] [CrossRef]
- Bekele, R.; Menzel, W. A bayesian approach to predict performance of a student (bapps): A case with ethiopian students. Algorithms 2005, 22, 24. [Google Scholar]
- Kolo, D.; Adepoju, S.A. A decision tree approach for predicting students academic performance. International. J. Educ. Manag. Eng. 2015, 5, 12–19. [Google Scholar]
- Luan, J. Data mining applications in higher education. SPSS Exec. 2004, 7. Available online: http://www.insol.lt/software/modeling/modeler/pdf/Data%20mining%20applications%20in%20higher%20education.pdf (accessed on 29 May 2022). [CrossRef]
- Baker, R.S. Educational Data Mining: An Advance for Intelligent Systems in Education. IEEE Intell. Syst. 2014, 29, 78–82. [Google Scholar] [CrossRef]
- Hamoud, A.; Humadi, A.; Awadh, W.A.; Hashim, A.S. Students’ success prediction based on Bayes algorithms. Int. J. Comput. Appl. 2017, 178, 6–12. [Google Scholar]
- Hamound, A.K. Classifying Students’ Answers Using Clustering Algorithms Based on Principle Component Analysis. J. Theor. Appl. Inf. Technol. 2018, 96, 1813–1825. [Google Scholar]
- Mohamad, S.K.; Tasir, Z. Educational Data Mining: A Review. Procedia Behav. Sci. 2013, 97, 320–324. [Google Scholar] [CrossRef]
- Berland, M.; Baker, R.S.; Blikstein, P. Educational data mining and learning analytics: Applications to constructionist research. Technol. Knowl. Learn. 2014, 19, 205–220. [Google Scholar] [CrossRef]
- Palmer, D.E. Handbook of Research on Business Ethics and Corporate Responsibilities; IGI Global: Hershey, PA, USA, 2015. [Google Scholar]
- Doan, T.T.T. The effect of service quality on student loyalty and student satisfaction: An empirical study of universities in Vietnam. J. Asian Financ. Econ. Bus. 2021, 8, 251–258. [Google Scholar]
- Alamri, M.M.; Almaiah, M.A.; Al-Rahmi, W.M. Social media applications affecting students’ academic performance: A model developed for sustainability in higher education. Sustainability 2020, 12, 6471. [Google Scholar] [CrossRef]
- Brito, R.M.; Rodríguez, C.; Aparicio, J.L. Sustainability in teaching: An evaluation of university teachers and students. Sustainability 2018, 10, 439. [Google Scholar] [CrossRef]
- Olmos-Gómez, M.d.C.; Luque Suarez, M.; Ferrara, C.; Olmedo-Moreno, E.M. Quality of Higher Education through the Pursuit of Satisfaction with a Focus on Sustainability. Sustainability 2020, 12, 2366. [Google Scholar] [CrossRef]
- Namoun, A.; Alshanqiti, A. Predicting student performance using data mining and learning analytics techniques: A systematic literature review. Appl. Sci. 2020, 11, 237. [Google Scholar] [CrossRef]
- Rastrollo-Guerrero, J.L.; Gómez-Pulido, J.A.; Durán-Domínguez, A. Analyzing and predicting students’ performance by means of machine learning: A review. Appl. Sci. 2020, 10, 1042. [Google Scholar] [CrossRef]
- Hamoud, A.; Hashim, A.S.; Awadh, W.A. Predicting student performance in higher education institutions using decision tree analysis. Int. J. Interact. Multimed. Artif. Intell. 2018, 5, 26–31. [Google Scholar] [CrossRef]
- Nieto, Y.; Gacía-Díaz, V.; Montenegro, C.; González, C.C.; Crespo, R.G. Usage of machine learning for strategic decision making at higher educational institutions. IEEE Access 2019, 7, 75007–75017. [Google Scholar] [CrossRef]
- Akour, M.; Alsghaier, H.; Al Qasem, O. The effectiveness of using deep learning algorithms in predicting students achievements. Indones. J. Elect. Eng. Comput. Sci 2020, 19, 387–393. [Google Scholar] [CrossRef]
- Hashim, A.S.; Awadh, W.A.; Hamoud, A.K. Student performance prediction model based on supervised machine learning algorithms. IOP Conf. Ser. Mater. Sci. Eng. 2020, 928, 032019. [Google Scholar] [CrossRef]
- Sudais, M.; Safwan, M.; Khalid, M.A.; Ahmed, S. Students’ Academic Performance Prediction Model Using Machine Learning; Research Square: Durham, NC, USA, 2022; Available online: https://www.researchsquare.com/article/rs-1296035/v1 (accessed on 29 May 2012). [CrossRef]
- Clark, I.; James, P. Blended learning: An approach to delivering science courses on-line. In Proceedings of the Australian Conference on Science and Mathematics Education, Sydney, Autralia, 26–28 September 2012; Volume 11. [Google Scholar]
- Adnan, M.; Habib, A.; Ashraf, J.; Mussadiq, S.; Raza, A.A.; Abid, M.; Bashir, M.; Khan, S.U. Predicting at-risk students at different percentages of course length for early intervention using machine learning models. IEEE Access 2021, 9, 7519–7539. [Google Scholar] [CrossRef]
- Mubarak, A.A.; Cao, H.; Zhang, W. Prediction of students’ early dropout based on their interaction logs in online learning environment. Interact. Learn. Environ. 2020, 1–20. [Google Scholar] [CrossRef]
- Ramaswami, G.; Susnjak, T.; Mathrani, A. On Developing Generic Models for Predicting Student Outcomes in Educational Data Mining. Big Data Cogn. Comput. 2022, 6, 6. [Google Scholar] [CrossRef]
- Berchin, I.I.; de Aguiar Dutra, A.R.; Guerra, J.B.S.O.d.A. How do higher education institutions promote sustainable development? A literature review. Sustain. Dev. 2021, 29, 1204–1222. [Google Scholar] [CrossRef]
- Došilović, F.K.; Brčić, M.; Hlupić, N. Explainable artificial intelligence: A survey. In Proceedings of the 2018 41st International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 21–25 May 2018; pp. 0210–0215. [Google Scholar]
- Gilpin, L.H.; Bau, D.; Yuan, B.Z.; Bajwa, A.; Specter, M.; Kagal, L. Explaining explanations: An overview of interpretability of machine learning. In Proceedings of the 2018 IEEE 5th International Conference on Data Science and Advanced Analytics (DSAA), Turin, Italy, 1–3 October 2018; pp. 80–89. [Google Scholar]
- Naser, M. An engineer’s guide to eXplainable Artificial Intelligence and Interpretable Machine Learning: Navigating causality, forced goodness, and the false perception of inference. Autom. Constr. 2021, 129, 103821. [Google Scholar] [CrossRef]
- Zhang, D.; Xu, Y.; Peng, Y.; Du, C.; Wang, N.; Tang, M.; Lu, L.; Liu, J. An Interpretable Station Delay Prediction Model Based on Graph Community Neural Network and Time-Series Fuzzy Decision Tree. IEEE Trans. Fuzzy Syst. 2022. [Google Scholar] [CrossRef]
- Leal, F.; García-Méndez, S.; Malheiro, B.; Burguillo, J.C. Explanation Plug-In for Stream-Based Collaborative Filtering. In Proceedings of the Information Systems and Technologies; Rocha, A., Adeli, H., Dzemyda, G., Moreira, F., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 42–51. [Google Scholar]
- García-Méndez, S.; Leal, F.; Malheiro, B.; Burguillo-Rial, J.C.; Veloso, B.; Chis, A.E.; González–Vélez, H. Simulation, modelling and classification of wiki contributors: Spotting the good, the bad, and the ugly. Simul. Model. Pract. Theory 2022, 120, 102616. [Google Scholar] [CrossRef]
- Molnar, C.; Casalicchio, G.; Bischl, B. iml: An R package for interpretable machine learning. J. Open Source Softw. 2018, 3, 786. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Association for Computing Machinery, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Wang, J.; Zhan, Q. Visualization Analysis of Artificial Intelligence Technology in Higher Education Based on SSCI and SCI Journals from 2009 to 2019. Int. J. Emerg. Technol. Learn. (iJET) 2021, 16, 20–33. [Google Scholar] [CrossRef]
- Malhotra, N.; Nunan, D.; Birks, D. Marketing Research: An Applied Approach; Pearson: London, UK, 2017. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: Oxfordshire, UK, 2013. [Google Scholar]
- Hair, J.F. Multivariate Data Analysis; Pearson: London, UK, 2009. [Google Scholar]
- Pestana, M.H.; Gageiro, J.N. Análise de Dados para Ciências Sociais: A Complementaridade do SPSS. 2008. Available online: https://silabo.pt/catalogo/informatica/aplicativos-estatisticos/livro/analise-de-dados-para-ciencias-sociais/ (accessed on 29 May 2012).
- Marôco, J. Análise Estatística com o SPSS Statistics.: 7ª edição; ReportNumber, Lda: Lisbon, Portugal, 2018. [Google Scholar]
- Berrar, D. Bayes’ Theorem and Naive Bayes Classifier. In Encyclopedia of Bioinformatics and Computational Biology; Elsevier: Amsterdam, The Netherlands, 2019; Volume 1–3, pp. 403–412. [Google Scholar] [CrossRef]
- Trabelsi, A.; Elouedi, Z.; Lefevre, E. Decision tree classifiers for evidential attribute values and class labels. Fuzzy Sets Syst. 2019, 366, 46–62. [Google Scholar] [CrossRef]
- Parmar, A.; Katariya, R.; Patel, V. A Review on Random Forest: An Ensemble Classifier. In Proceedings of the International Conference on Intelligent Data Communication Technologies and Internet of Things; Springer: New York, NY, USA, 2019; pp. 758–763. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Goldberger, J.; Hinton, G.E.; Roweis, S.; Salakhutdinov, R.R. Neighbourhood components analysis. Adv. Neural Inf. Process. Syst. 2004, 17, 1–8. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).