1. Introduction
Pavement performance is the ability of pavement to remain in an acceptable condition to serve the intended users over a period of time. High-quality pavement contributes towards the sustainability of pavement by reducing costs and pollution and the impact on the community due to noise during repair or construction. There are several principal, combined factors that affect flexible pavement performance such as environmental conditions, pavement materials, and traffic loads. Pavement deterioration modeling is one of the key elements of any pavement management system (PMS) within which pavement maintenance, rehabilitation, or reconstruction plans can be efficiently predicted. A full account of surrounding pavement systems is necessary to prolong the life of the pavement and to improve the sustainability of pavements by conserving virgin materials and energy, providing quieter and smoother riding surfaces, and reducing noise impacts on the surrounding area. A wide variety of methodological approaches have been used for improving the prediction accuracy in estimating pavement performance measures. These methods can be classified into two main distinct categories: deterministic and stochastic approaches.
Most of the deterministic models are mainly based on regression analysis (including linear and nonlinear models). The pavement performance or condition can be predicted as a single mean value in a certain period when dealing with the aggregated impacts of various contributing independent predictors. The deterministic approach in pavement deterioration modeling includes mechanistic models, mechanistic-empirical models, and regression models [
1]. In 1987, Paterson developed a nonlinear regression model for flexible pavement roughness progression using data from Brazil [
2]. He found that the initial rate of pavement roughness IRI progression depends on the relative relationship between pavement strength and traffic loading. In 2004, Prozzi and Madanat [
3] developed a relationship between flexible pavement roughness performance and several contributing factors using a nonlinear multivariate regression model with the use of both field survey data and accelerated pavement test data to estimate riding quality. The study revealed that the initial IRI decreases with an increase in asphalt layer thickness. In addition, Prozzi and Hong [
4] used a seemingly unrelated regression estimation (SURE) model to estimate rutting depth and IRI of the pavement surface while accounting for the correlation between the two variables. In 2013, Luo [
5] used the autoregression method in pavement performance modeling to improve the accuracy of predictions. A non-linear mixed effects model using different pavement sections and climatic factors to quantify the contribution of these factors to pavement evolution was developed [
6]. Also a multi-input prediction model for flexible asphalt pavements specific to four different climatic conditions and two classes of road was proposed [
7]. It was found that the deterministic approaches fail to explain the randomness of environmental conditions and traffic loads, the bias from subjective evaluations of pavement conditions, and the measurement errors related to pavement conditions [
8].
The stochastic models, which are alternatives to the deterministic approach, expect different lifetime or pavement states distribution of such events [
9,
10]. In 1997, Li et al. [
11] proposed a stochastic model of pavement performance curve that is represented by the Markov transition process. Other stochastic models use the Bayesian inference which uses a combination of prior knowledge and information from historical data to capture uncertainty in performance modeling [
12,
13]. The Monte Carlo simulation technique is also extensively used in the pavement-related field. Alsherri and George [
14] implemented the Monte Carlo simulation technique to estimate the expected life of different pavement sections based on the present serviceability index (PSI). In 2011, Coleri and Harvey [
15] used Monte Carlo simulation to predict rut depths for different reliability levels.
Most of these deterioration models are used to predict the amount of a given type of distress after a given period of time as a function of a set of covariates. However, the time duration or the number of applied loads until pavement serviceability performance reaches the terminal value (i.e., the failure threshold) is an important parameter. Survival time analysis is one of the most popular methods for estimating the remaining service life of pavements. The survival analysis models the survival time of an event and quantifies the effect of predictors (independent variables) on the survival time [
16]. In 2015, Anastasopoulos and Mannering used survival analysis to evaluate the impact of various factors on pavement service life [
17]. Estimating the service life can produce sustainable pavement and contribute to the health of the highway sector. Mamlouk and Souliman [
18] stated that the design of sustainable asphalt pavement without accumulation of fatigue cracking is an important goal of transportation agencies and should produce good, long-term performance. Loizos and Karlaftis [
19] used the log-logistic proportional-hazard model to evaluate the initiation of pavement cracking. The study revealed that the initiation rate is affected by annual average freezing, annual equivalent single axle load, days where the temperature is below 0 °C, and pavement type. In addition, Auiar-Moya et al. [
20] used the Weibull proportional-hazard model to evaluate the time to rutting failure of flexible pavements. They found that the failure time is affected by freezing index, air void, binder content, layer thickness, and annual equivalent single axle load (ESAL).
With the continuous growth of freight transportation, vehicle overloading is considered one of the most significant causes of accelerating flexible pavement deterioration, reducing the life span of vehicles and increasing fuel consumption and crash accident rates. This will affect the United Nations in meeting the sustainable development goals. Several researchers have studied the impact of traffic loads and overweight vehicles on pavement performance and the relationship between excess overweight in the transportation network and pavement maintenance. In order to obtain a sustainable pavement, a system dynamics model (SD) was used in order to enable the assessment of the relationship between overweight vehicles and the costs associated with the operational cost of transportation and social costs due to pavement maintenance and traffic accidents [
21]. Hasim et al. [
22] indicated that the rate of deterioration is dependent on the quantity and variability of traffic loads. Barraj et al. [
23] showed that thick pavement structure is recommended if default axle load spectra is used in mechanistic empirical pavement design guide (MEPDG) for areas suffering from scarcity of traffic data. Dey et al. [
24] pointed out that fatigue cracking was more sensitive to overweight trucks compared to other pavement distresses such as rutting and roughness. Sebaaly et al. [
25] studied the impact of heavy vehicles on low-volume roads. Rys et al. [
26] showed that the presence of overweight vehicles will significantly reduce the service life of flexible pavements. Wu et al. [
27] assessed the damage to Texas highways due to oversize and overweight loads considering climatic factors. The results indicated that in the early age of a road, higher oversize and overweight loading would bring a faster deterioration rate. The study conducted by Pais et al. [
28] found that the pavement life-cycle costs may increase by about 30% due to overweight vehicles, thus affecting the long-term performance and sustainability of pavement. Another study conducted by Sadeghi and Fathali [
29] presented some models that describe the behavior of asphalt pavements under overloaded vehicles. Wang et al. [
30] concluded that there was a linear relationship between the percentage of overweight trucks and the reduction ratio of pavement life, despite how the pavement structure and traffic loading changed. Zhang et al. [
31] used accelerated failure time models to identify the most critical overweighting characteristics. They pointed out that the average pavement rutting life and fatigue life would be extended by about 29% and 43%, respectively, in the absence of overweight vehicles, thereby extending the lifespan and sustainability of pavement.
The use of processed reclaimed asphalt mixes in HMA is another significant factor that could affect the performance of pavement. RAP is considered a useful alternative to virgin materials because it reduces the use of virgin asphalt binder and aggregate and conserves energy required to obtain quality virgin materials. Zhao et al. [
32] stated that a key element to generating sustainable pavement designs is the use of RAP material that saves natural resources and reduces energy, greenhouse gas emissions, and costs. Previous evaluations of the fatigue performance of recycled asphalt mixes have shown some controversial findings. In this context, Barros et al. [
33], Shu et al. [
34], and Noferini et al. [
35] reported a decline in the fatigue resistance of recycled asphalt mixes compared to standard hot mix asphalt (HMA), whereas recent studies by Al Qadi et al. [
36], Poulikokas et al. [
37] and Baraj et al. [
38] experimentally found that the fatigue behavior of recycled asphalt mixes is similar to that of HMA.
The long-term pavement performance program, known as LTPP, is the largest pavement performance research program ever undertaken. It was established in 1987 as part of the first Strategic Highway Research Program (SHRP) to collect and store performance data for more than 2400 monitored pavement test sections in different climatic regions of the United States and Canada. The data collection started in 1989. After 25 years, these data are available to the public via the Web through the data portal system: LTPPInfoPave
TM [
39]. The LTPP data is usually collected and uploaded periodically on a six-month cycle by four regional contractors. The information management system, where the LTPP database is stored, consists of 16 general data modulus with 430 tables in a simple row-column format in which the columns are referred to as fields and the rows contains records. The main objective of the LTPP program of collecting and storing performance data is to support analysis and develop usable engineering products relevant to pavement management, construction, maintenance and design. Zhang and Wang [
40] developed decision tree models using LTPP data to provide enhanced decision-making information in pavement maintenance and design. Wang et al. [
41] developed an AdaBoost regression model to improve the prediction ability of international roughness index (IRI) for roads using records from LTPP program. Another research study was conducted by Rezapour et al. [
42] to investigate factors contributing to pavement skid resistance using LTPP data. El Ashwah et al. [
43] used the LTPP data to calibrate transfer functions used in developing and implementing a simplified Mechanistic Empirical (M-E) pavement design method.
There are several potential issues in the existing pavement deterioration models. The first issue is that most of the regression models that have been developed do not consider correlations between the independent variables. The second issue is related to the input variables selection that would affect the performance of pavement for which the variables in most existing models may not reflect the effect of overweight axles with other potentially influential factors. The third issue is that the pavement failures that occur during the given monitoring period are only considered in model development and the observations in which the time-to-event is unknown, are dropped from the analysis.
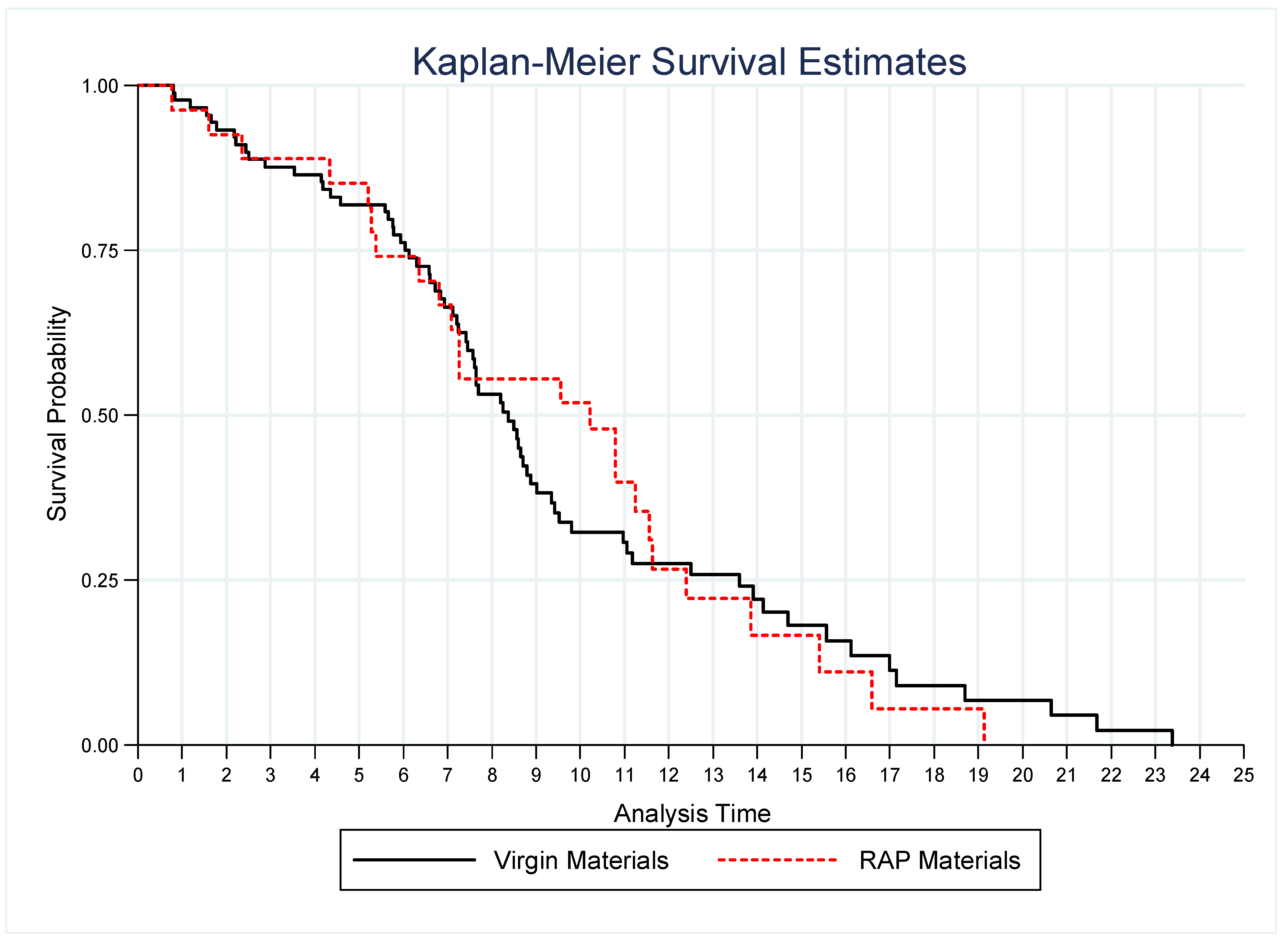
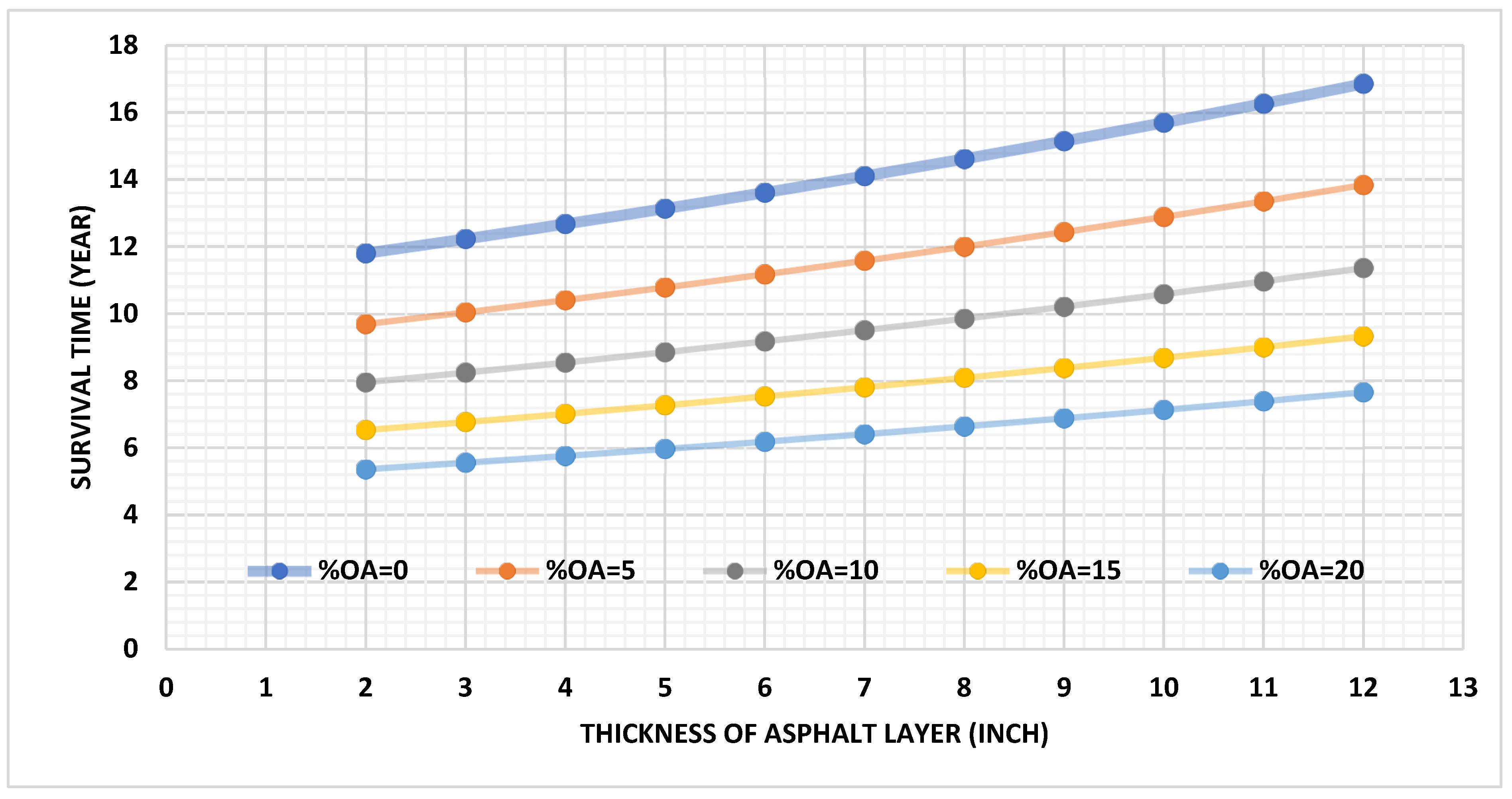
Using data extracted from the long-term pavement performance (LTPP) program, this study aims to conduct a non-parametric and parametric survival analysis for the selected flexible pavement test sections and to indicate the most significant subset of risk factors (covariates) under various pavement distresses. The selected distresses for this study are fatigue cracking, longitudinal wheel path and non-wheel path cracking, and transverse cracking, as shown in
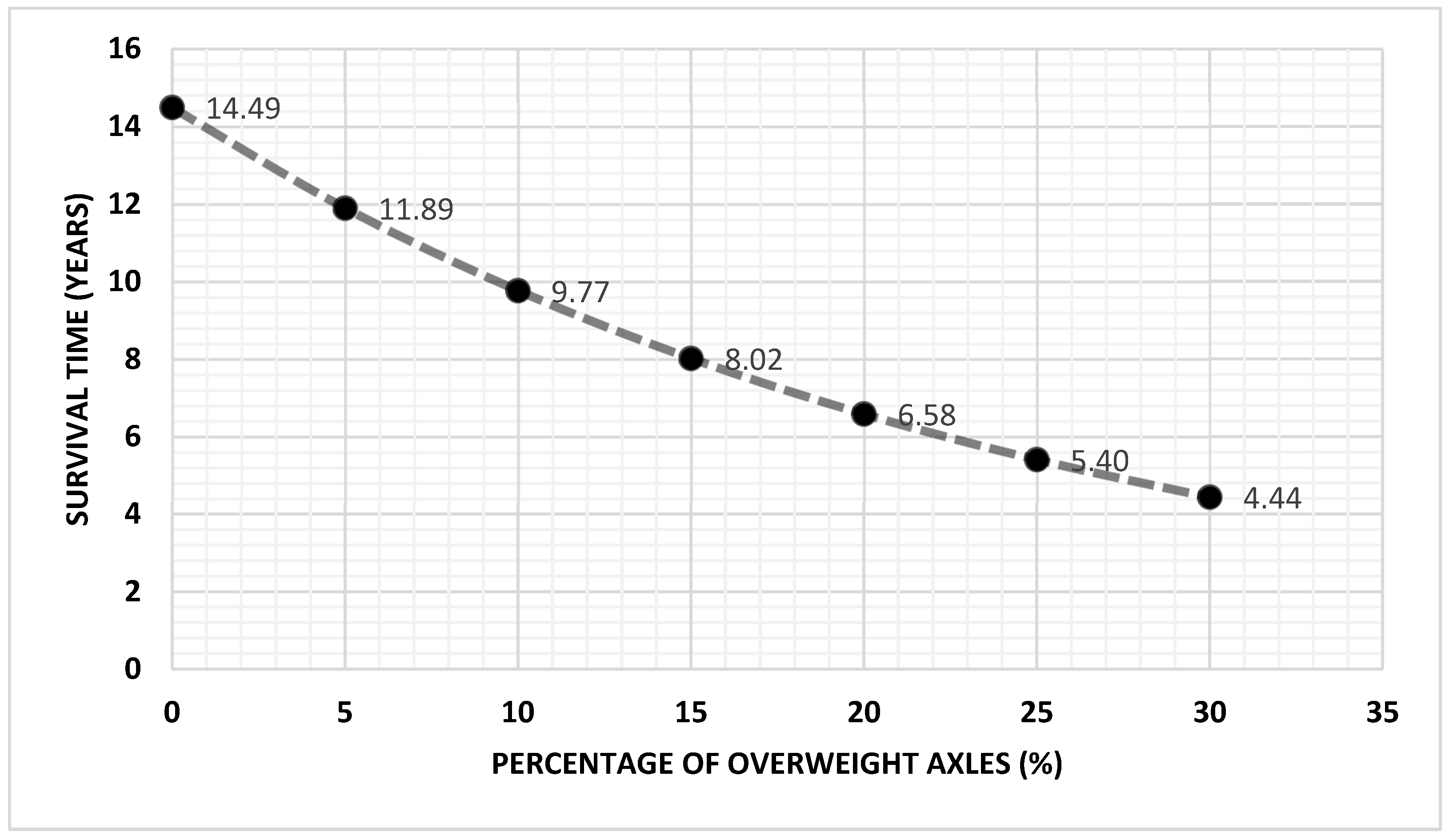
Figure 1. The non-parametric Kaplan–Meier method was used to assess the influence of using RAP vs standard HMA in asphalt mixes. For fatigue pavement cracking, the most appropriate parametric model was specified to predict the survival times and to evaluate the relationship between fatigue deterioration cracking and its potential influential factors. The percentages of overweight axles in the test section lane were considered to evaluate the impact of overweight vehicles on fatigue cracking and to investigate the relations with other factors. Thus, researchers can reach a good understanding of the relationship between these factors and the pavement systems to define the most appropriate sustainability practices. The outcomes of this research should contribute towards increasing the service life and sustainability of pavement.
2. Methodology
2.1. Survival Analysis
Generally, survival analysis or time-to-event analysis is a collection of statistical procedures used for data analysis. The outcome variable is referred to as the survival time (in year, months, weeks, or days) from the beginning of follow-up of an individual until the occurrence of the event of interest. In this research, the event of interest refers to the pavement failure when the measured pavement deterioration indicator drops below the acceptable threshold level.
Table 1 lists the used mechanistic empirical pavement design guide (MEPDG) pavement failure thresholds for each failure distress mode separately.
Survival analysis is considered a “censored regression”. Censored is defined as the incomplete observed responses during the observation period of an experiment when some information is available about a subject’s event time, but we do not know the exact survival time. The exclusion of these censored data can cause bias in the analyzed results according to SAS Institute Inc. [
46].
In summary, there are three different types of censoring used in this analysis:
Left-censored: data can occur when the pavements section’s true survival time is less than or equal to that pavements section’s observed survival time. In other words, if a pavement is left censored at time “t”, the failure event occurs between time 0 and t before the study began, but the exact time of occurrence is not known.
Right-censored: most survival data used in this study is right-censored. Data can occur when the event has not occurred during the study or before the termination of data collection. In this case, the true survival time is equal to or greater than the observed survival time.
Interval-censored: the pavement failed within a certain specified time interval but the exact true failure time is unknown.
In this study, the percentages and the numbers of censored data for the extracted data are indicated in
Table 2.
2.2. Survival Function:
The survival function, S(t), defines the probability (P) that the pavement section failure has not occurred at time t, which can be expressed as:
where
T is the pavement service life,
F(t) is the cumulative distribution function of the pavement service life, and
f(u) is the density function of the pavement failure [
47].
The hazard function,
h(t), defines the instantaneous potential per unit time for the failure event to occur, given that the pavement section has survived up to time
t. The hazard function can be expressed as:
The Kaplan–Meier (KM) Method or the product-limit method [
48] is the most popular nonparametric modal. It does not assume an underlying failure distribution of the data and it is often used to develop survival curves. In Kaplan–Meier method, it defines survival probability S(t) as follows:
where t
i is the time of ith pavement failure, d
i is the number of pavement sections that failed at time t
i, and n
i is the number of pavement sections that survived just before time t
i.
The 95% confidence interval (CI) for the KM and for the median survival time, when the time point at which the probability of survival equals 50%, is calculated using Greenwood’s formula.
2.3. Parametric Survival Analysis
In a parametric survival model, the survival time is assumed to follow several distributions. The most commonly used distributions that are applied in this study are the Gompertz, the generalized gamma, the Weibull, the log-logistic, and the log-normal.
These models are used to investigate the influence of predictors on the survival time or hazard rate. The maximum likelihood estimation method and the likelihood ratio test are used to estimate the survival model and to test the significance of each independent variable, respectively. The accelerated failure-time (AFT) and the proportional hazards (PH) are two models which are often used for adjusting survivor functions for the effects of predictors. Specifically, the underlying assumption for PH models is that the effect of predictors is proportional with respect to hazard, whereas the underlying assumption of AFT models is that the effect of predictors is proportional with respect to the survival time.
2.4. Model Selection Criterion
The corrected Akaike information criterion (AIC) is an approach that can be applied to compare the fit of models with different underlying distributions. The model with the smaller AIC value is considered to be closer to the true distribution. The following formula was used to calculate the AIC value:
where
LL is the likelihood,
c is the number of model covariates and
p is the number of model-specific ancillary parameters [
49].
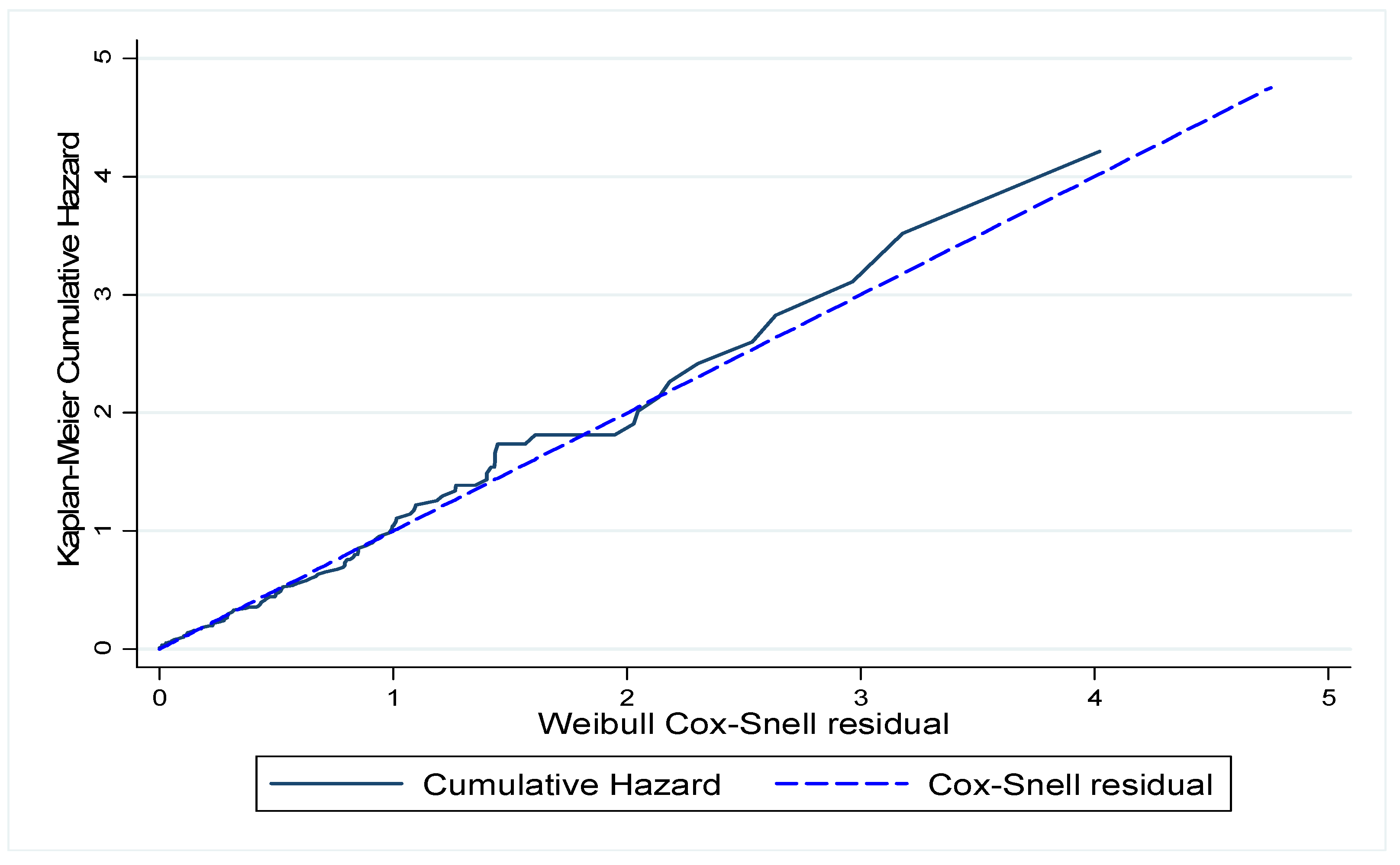
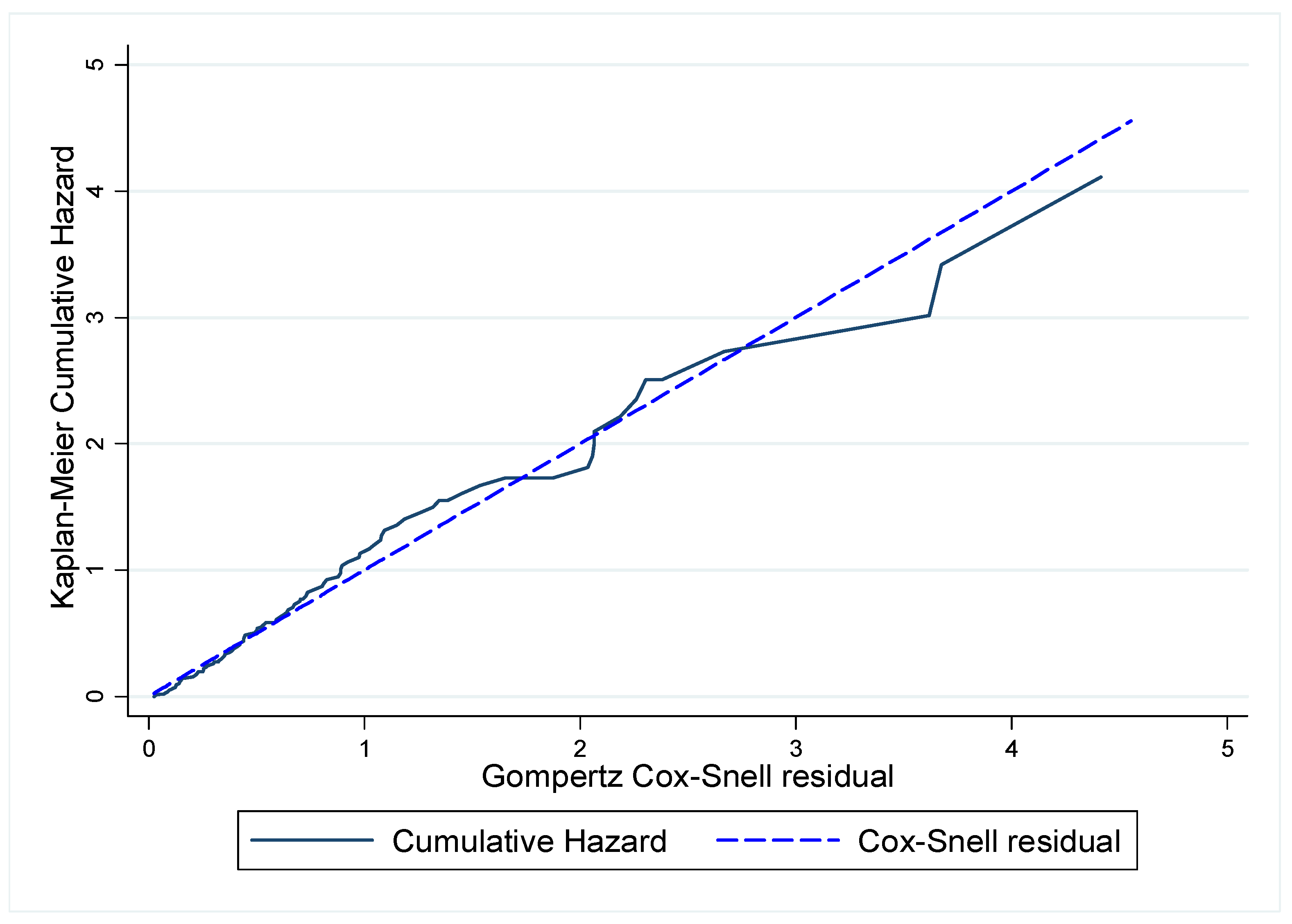
In addition to the AIC criteria method, the Cox-Snell residuals are also applied to select the most appropriate parametric model by graphically assessing which model would generate a plot that lies directly on top of the diagonal line [
50]. The residuals “r
ci”, that were reported by Cox and Snell [
51] and Hosmer and Lemeshow [
52], are formed by using the model-based estimate of the empirical cumulative hazard function
(t
i) or the survival empirical hazard function
(t
i) where:
Stata MP/13 software package [
53] was chosen to conduct the underlying nonparametric and parametric survival analysis and to provide the analysis needed for this study. A
p-value of less than 0.05 was considered statistically significant.
2.5. Preparation of Data
The data extracted for this study were selected from the GPS-1 and GPS-2 experiments in LTPP. The GPS-1 and GPS-2 are commonly constructed pavement types that refer to an asphalt concrete (AC) layer on unbound and bound bases, respectively.
The potential influential predictors and the pavement performance indicators used in this study with its source table in the LTPP database are listed in
Table 3 and
Table 4, respectively. These explanatory variables are briefly summarized as follows:
There are two types of LTPP traffic data: historical and monitored traffic data [
39]. The historical traffic data provide traffic data for the period of time from the original date of pavement construction to the beginning of traffic monitoring in 1990; while the monitoring traffic data provide data for each year after 1990, computed from raw data or estimated by the highway agencies [
54]. The traffic data are stored in Traffic Data Module (TRF) of the LTPP database. The potentially influential traffic data extracted for this research to depict the effect of traffic loads and overweighting in the lane of the LTPP test section are:
The annual average daily truck traffic (AADTT), in trucks/day, extracted from LTPP table (TRF_MEPDG_AADTT_LTPP_LN) according to specific state and section ID.
The annual average cumulative single axle load (KESAL) extracted from two sources. The first table (TRF_HIST_EST_ESAL) contains estimates of 80 KN (18 kips) ESALs for sections with historical traffic data and the second table (TRF_MON_EST_ESAL) contains annual estimate of ESAL during the period when pavement monitoring measurements were conducted.
The total axle weights (W) for the 13-bin classified vehicles according to FHWA (federal highway administration)
The total overweight axles (OW) for the weight of the axles exceed the federal trucks axle weight limit listed in
Table 5. The total axle weights and overweight axles are extracted from table (TRF_MEPDG_AX_DIST_ANL), which contains the annual normalized axle distribution by class and axle group and from table (TRF_MONITOR_LTPP_LN), which contains information about the estimated annual volumes of trucks and axles per LTPP lane (LN).
The total axles volume (V) and the total overweight axles volume (OV) for all the vehicle classes and axle group. These data are also extracted from table (TRF_MONITOR_LTPP_LN).
The total percentage of overweight axles (%OA) is calculated using the normalized axle distribution by vehicle class and axle group type. The data are extracted from table (TRF_MEPDG_AX_DIST_ANL) and from table (TRF_MEPDG_AX_PER_TRUCK), which contains the annual average number of axles number by vehicle class and axle type per year.
The cross-correlations and the scatterplot matrix for the extracted traffic variables are shown in
Figure 2 with the calculated Pearson correlated coefficients, located above the diagonal of the plot matrix, and were used to verify the multicollinearity of these variables. All the
p-values were smaller than the significance level (a = 0.05) so that the correlations were statistically significant. The results revealed that many correlations were quite high. There was no significant evidence of a relationship between the AADTT and the KESAL values, while the AADTT and KESAL were strongly interdependent with the other extracted variables, with the exception of the total percentage of overweight (%OA).
Climatic factors also have a significant effect on pavement deterioration. The climate-related variables chosen for this study were the average annual precipitation, freezing indices (FI), temperatures, and snowfall for the test sections, the average number of days when maximum temperature is above 32 °C (89 °F), and the average number of days when the maximum temperature is below 0 °C (32 °F).
The multicollinearity was also tested for the environmental data and the results are shown in
Table 6.
The pavement materials-related variables used in this study are the subgrade material resilient modulus (Mr) to characterize the subgrade material stiffness, the thicknesses of surface, base, and subbase layers, and the type of materials used in asphalt mixes (RAP or standard HMA). The subgrade resilient modulus was extracted from TST (test modulus), specifically from table (TST_UG07_SS07_WKSHT_SUM), which contains the average resilient modulus data for unbound granular materials.
The other pavement material data available in the LTPP data such as the percentage of asphalt content and air void in the mix were excluded from the selected data due to the high percentage of the missing values for the selected test sections.
2.6. Pavement Performance
The four pavement performance indicators selected for this study were alligator cracks or bottom-up fatigue cracking, non-wheel path longitudinal cracks, wheel path longitudinal cracks, and thermal or transverse cracks. The pavement deterioration data in each test section was examined to identify any incomplete historical data, outliers in data, or any abnormal data due to technical and mechanical errors. The data were extracted from the (MON_DIS_AC_REV) table, which contains distress survey information obtained by manual inspection for asphalt concrete surfaces and this table belongs to the monitoring (MON) module.
2.7. Descriptive Analysis
A univariate analysis was performed to establish the descriptive data of the selected independent variables and the values are shown in
Table 7.