The Description and Application of BRDF Based on Shape Vectors for Typical Landcovers
Abstract
1. Introduction
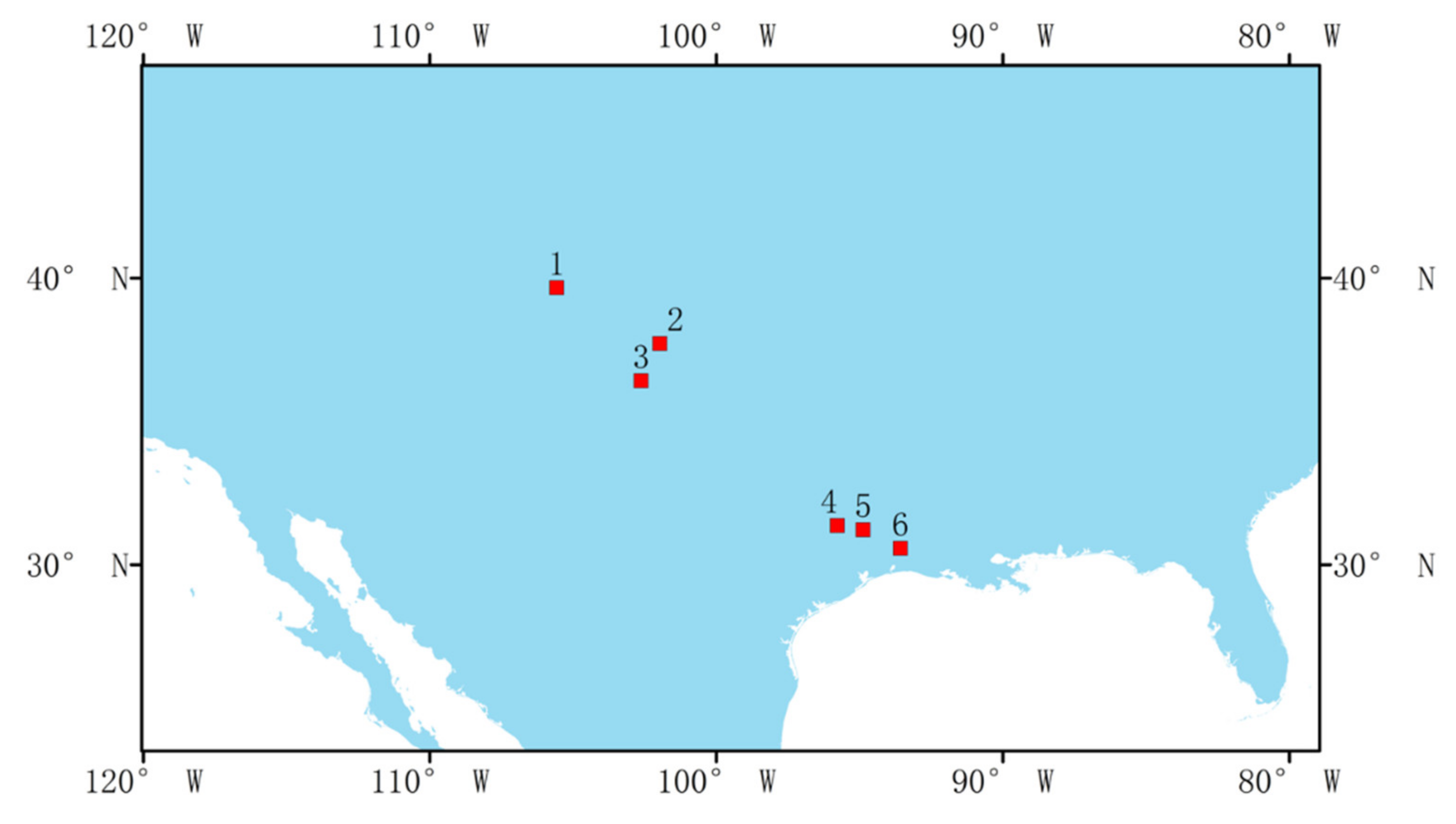
2. Data
2.1. MODIS Classification Dataset
2.2. MODIS BRDF Dataset
2.3. CDL Dataset
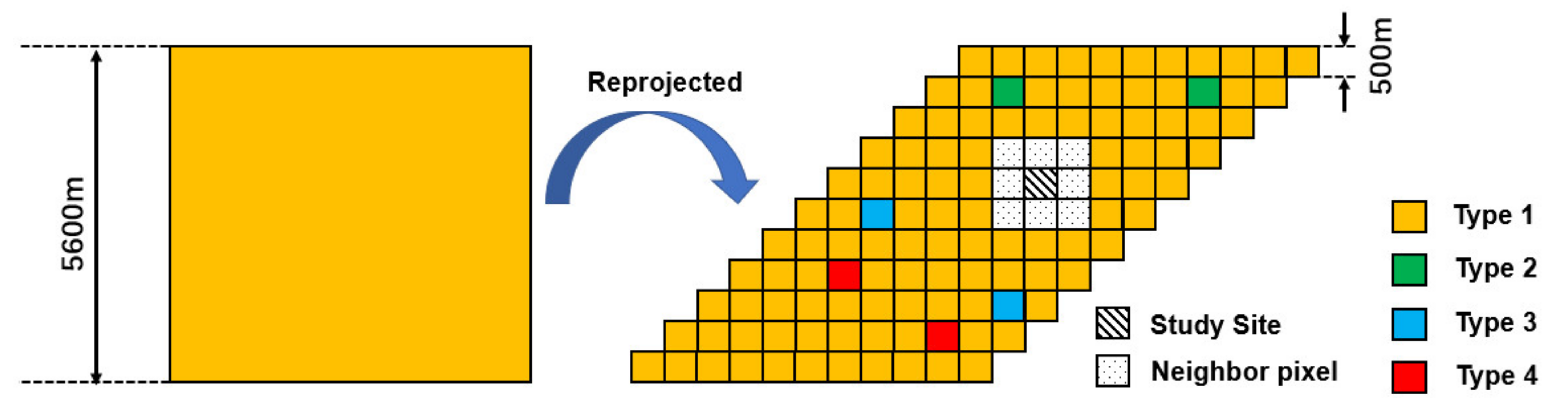
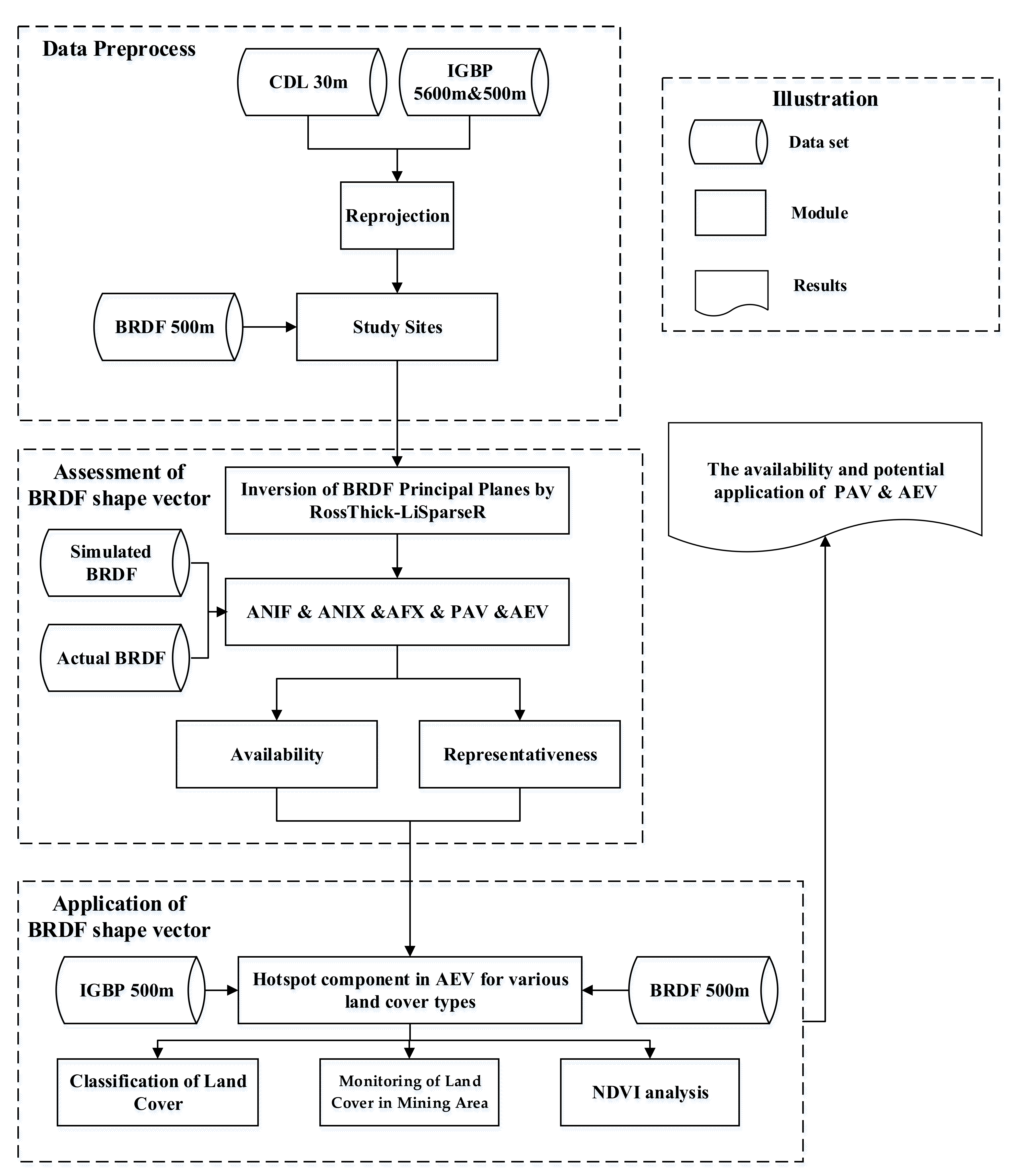
2.4. Data Preprocessing
3. Method
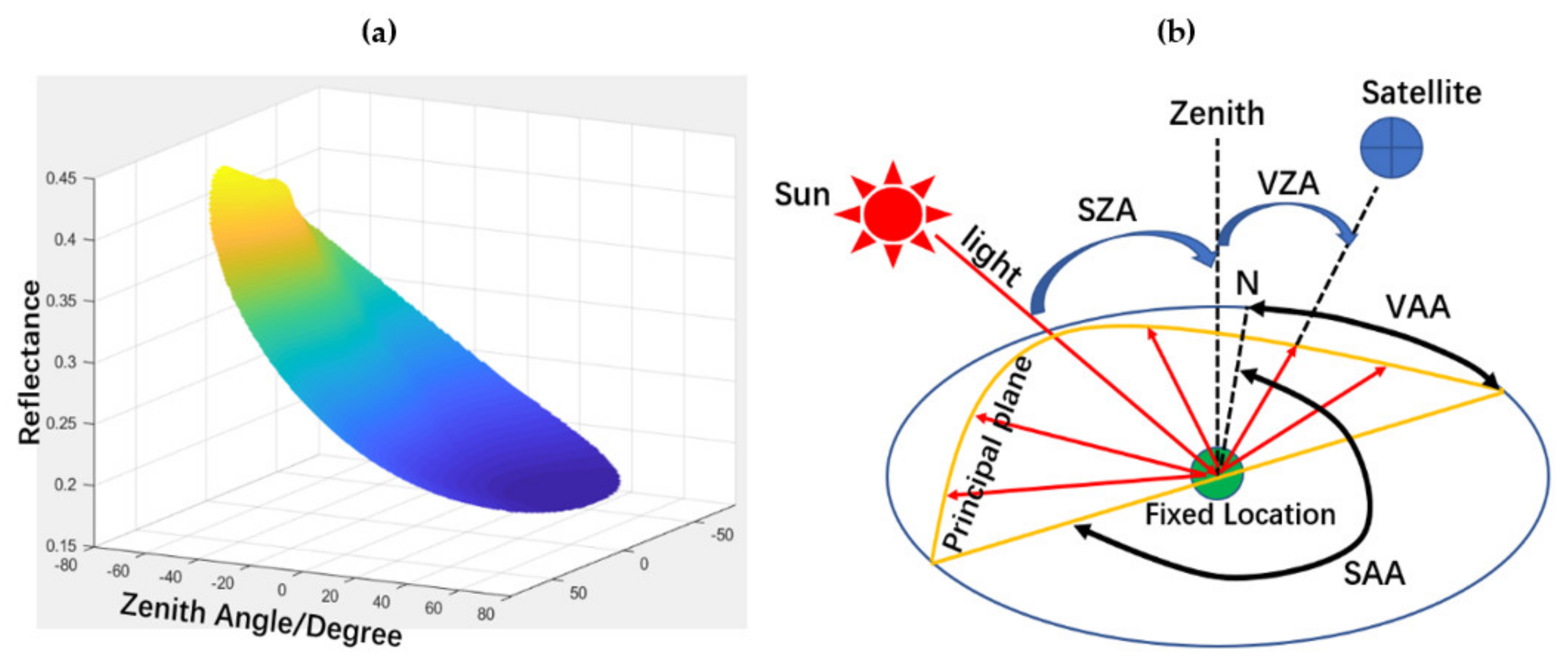
3.1. The Retrieval of BRDF Principal Planes
3.2. Classic BRDF Shape Indicators
3.3. 6-Component Partial Anisotropic Vector
3.4. Three-Component Angular Effect Vector
3.5. Cosine Similarity
3.6. Error Transfer Function
3.7. Coefficient of Variation
4. Results and Analysis
4.1. Effectiveness of Shape Vectors
4.2. Representativeness of Shape Vectors
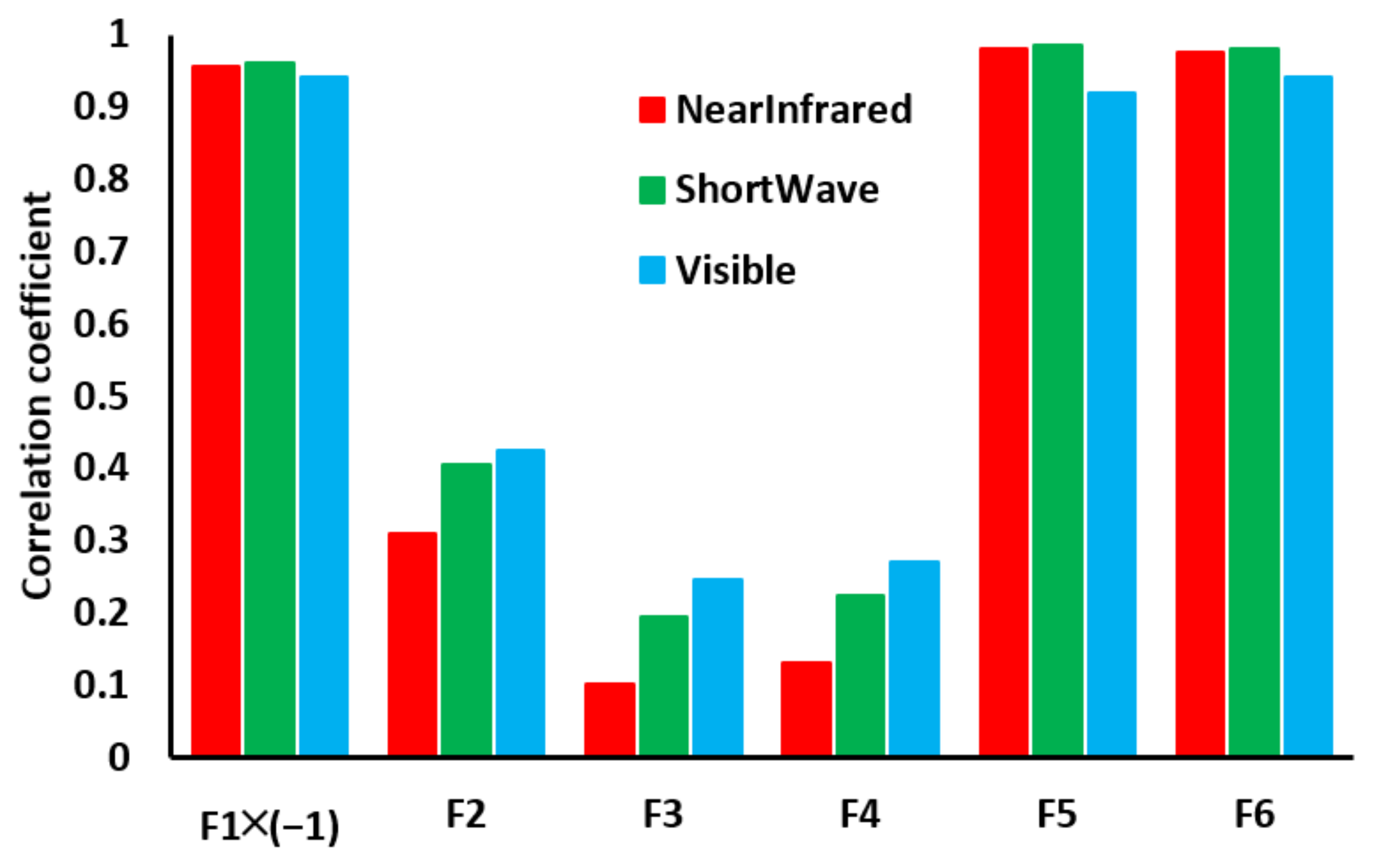
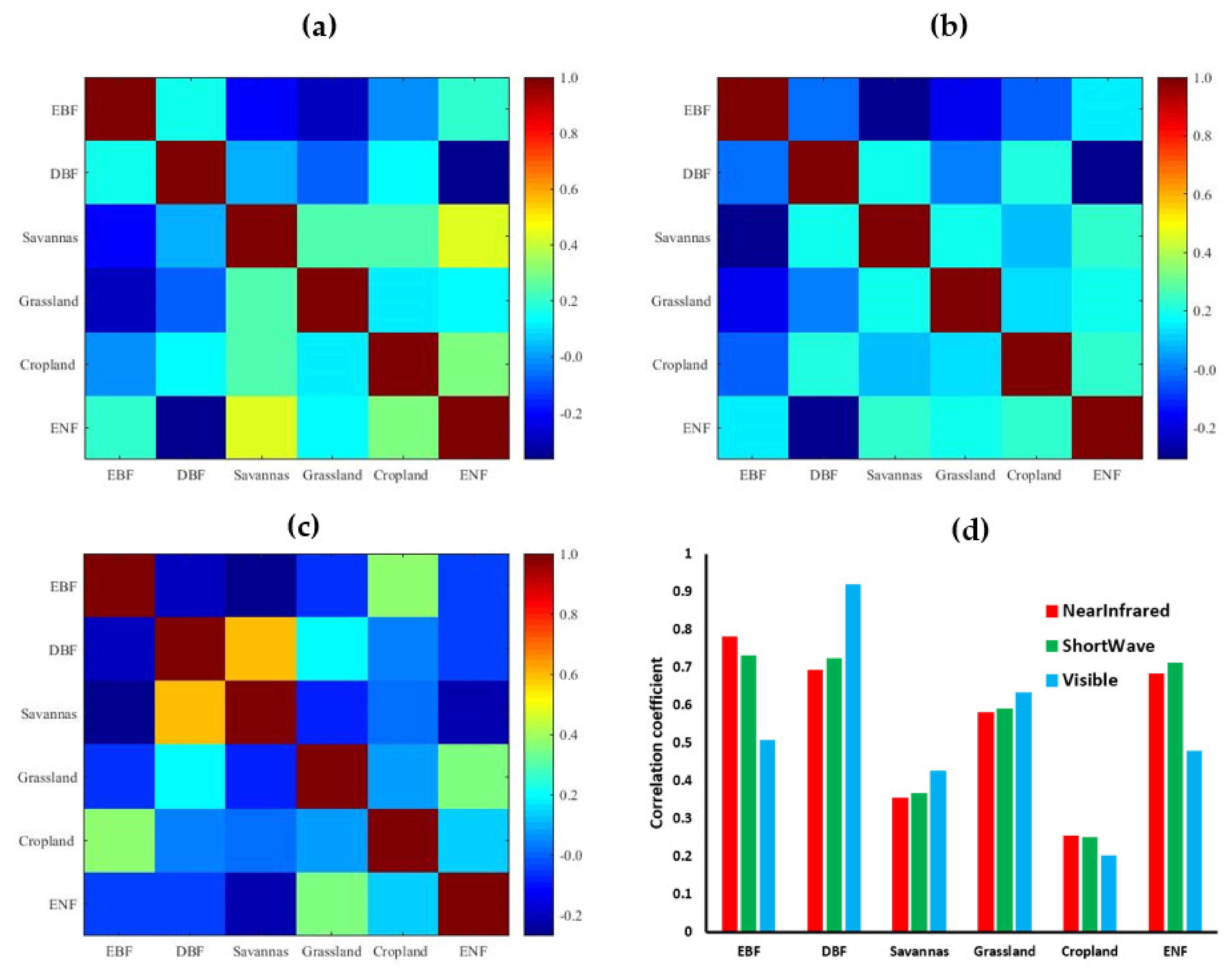
4.2.1. Representativeness of PAV
4.2.2. Representativeness of AEV
4.3. Shape Vectors and AFX
4.4. Application of Shape Vectors
4.4.1. Land Cover Classification
4.4.2. NDVI and BRDF Shape Vector
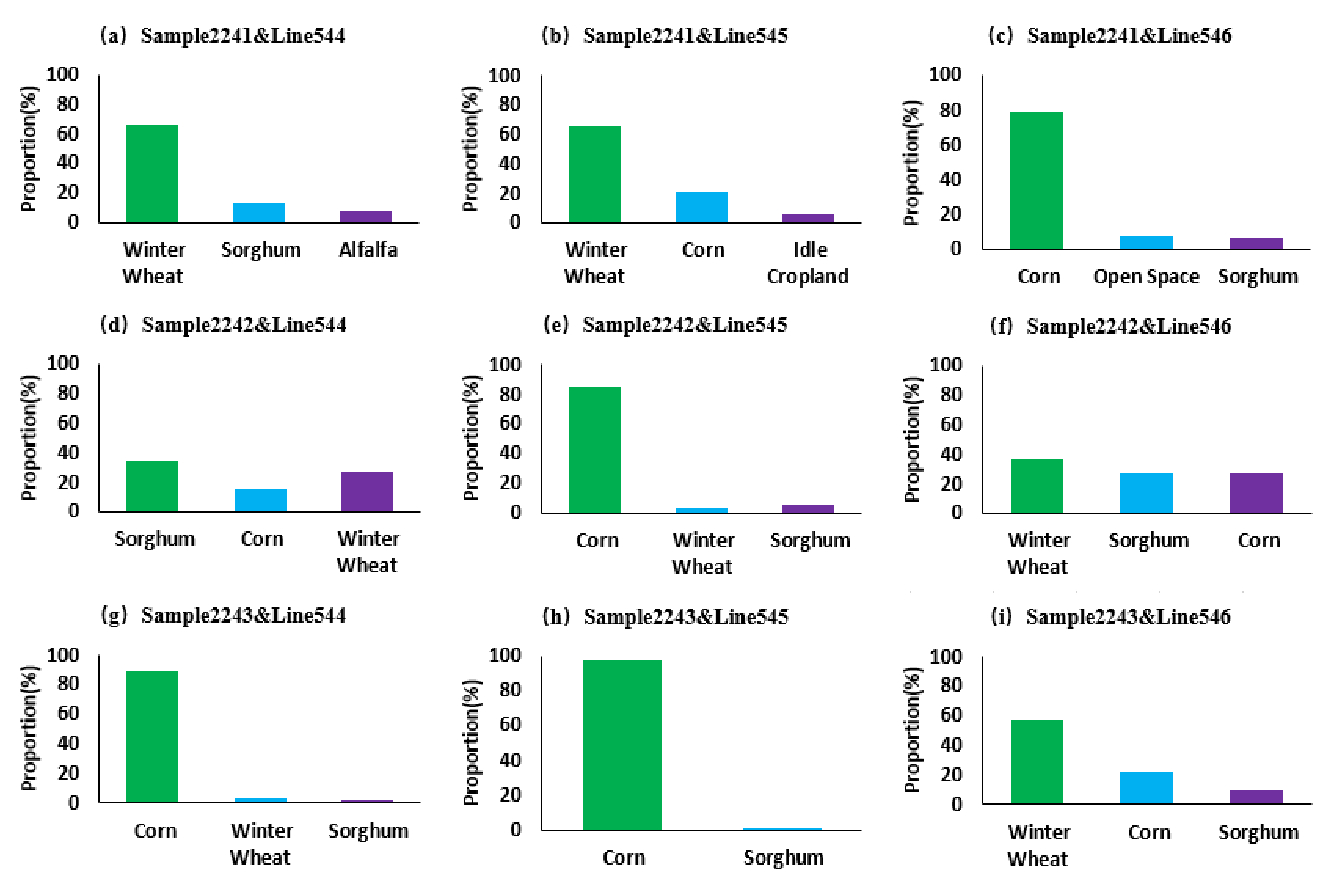
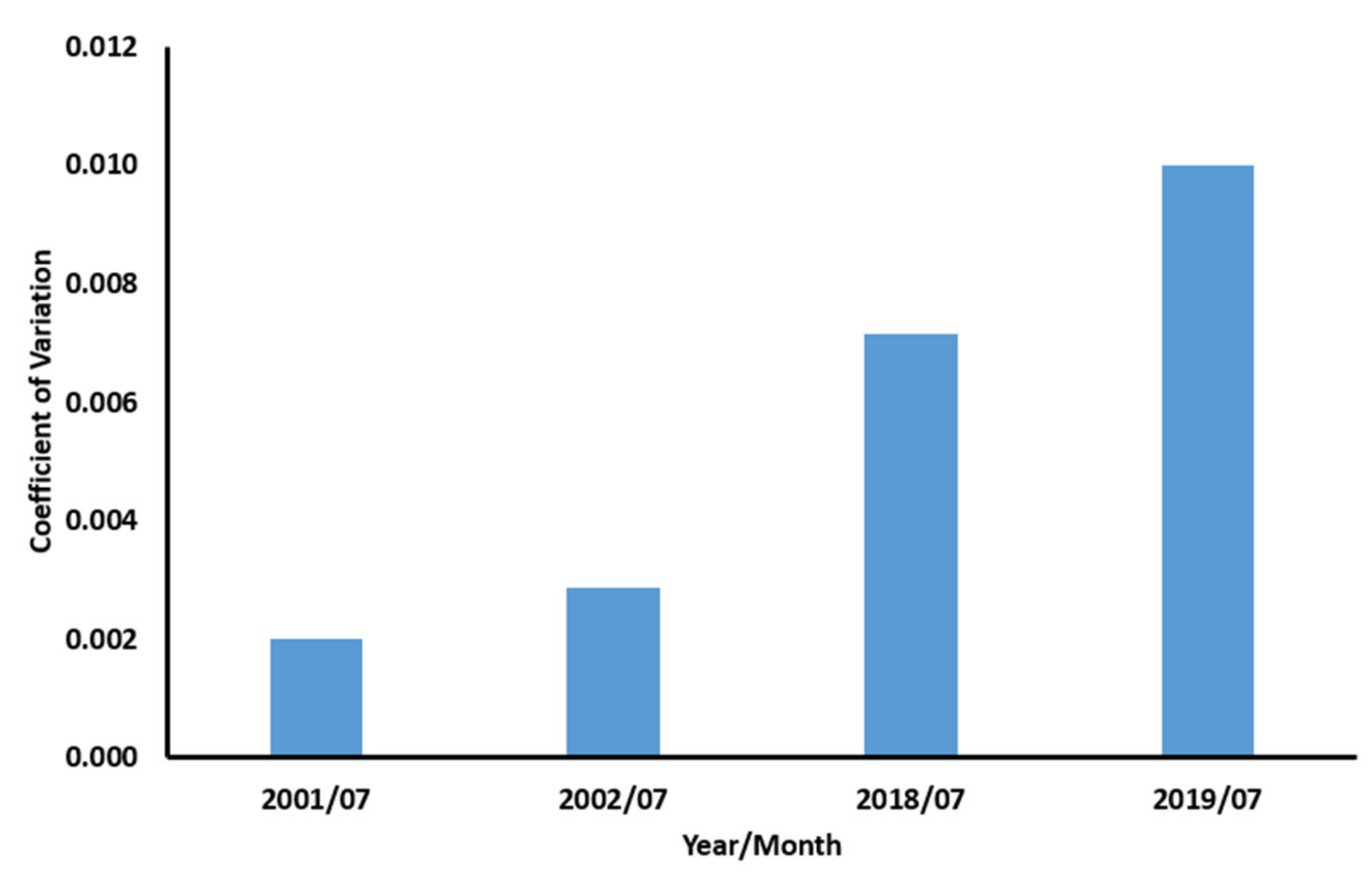
4.4.3. Monitoring of Land Cover in Mining Area
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Song, F.; Fan, W.; Liu, Q.; Xu, X. A Method of Acquiring BRDF of Objects in the Field. J. Remote Sens. 2007, 11, 296–302. [Google Scholar] [CrossRef]
- Zhu, G.L.; Ju, W.M.; Chen, J.M.; Liu, Y.B.; Zhu, J.F.; Xing, B.L. Validation of MODIS BRDF model parameters product and the Ross-Li model with POLDER data. J. Remote Sens. 2011, 15, 875–894. [Google Scholar] [CrossRef]
- He, D.D.; Jiao, Z.T.; Dong, Y.D.; Zhang, X.N.; Ding, A.X.; Yin, S.Y.; Cui, L.; Chang, Y.X. Preliminary verification of Landsat satellite albedo from airborne WIDAS data. J. Remote Sens. 2019, 23, 53–61. [Google Scholar] [CrossRef]
- Wang, Q.F.; Li, J.Y.; Chen, B.M. Land Cover Classification System Based on Spectrum in Poyang Lake Basin. Acta Geogr. Sin. 2006, 61, 359–368. [Google Scholar] [CrossRef]
- Li, C.C.; Wang, J.; Wang, L.; Hu, L.Y.; Gong, P. Comparison of classification algorithms and training sample sizes in urban land classification with landsat thematic mapper imagery. Remote Sens. 2014, 6, 964–983. [Google Scholar] [CrossRef]
- Yu, L.; Liang, L.; Wang, J.; Zhao, Y.; Cheng, Q.; Hu, L.; Liu, S.; Yu, L.; Wang, X.; Zhu, P.; et al. Meta-discoveries from a synthesis of satellite-based land-cover mapping research. Int. J. Remote Sens. 2014, 35, 4573–4588. [Google Scholar] [CrossRef]
- DeFries, R.S.; Townshend, G. NDVI-derived land cover classifications at a global scale. Int. J. Remote Sens. 1994, 15, 3567–3586. [Google Scholar] [CrossRef]
- Loveland, T.R.; Belward, A.S. The IGBP-DIS global 1 km land cover data set, DISCover: First results. Int. J. Remote Sens. 1997, 18, 3289–3295. [Google Scholar] [CrossRef]
- Friedl, M.; McIver, D.; Hodges, J.; Zhang, X.; Muchoney, D.; Strahler, A.; Woodcock, C.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Qi, J.; Moran, M.S.; Cabot, F.; Dedieu, G. Normalization of sun/view angle effects using spectral albedo-based vegetation indices. Remote Sens. Environ. 1995, 52, 207–217. [Google Scholar] [CrossRef]
- Gu, L.; Shuai, Y.; Shao, C.; Xie, D.; Zhang, Q.; Li, Y.; Yang, J. Angle Effect on Typical Optical Remote Sensing Indices in Vegetation Monitoring. Remote. Sens. 2021, 13, 1699. [Google Scholar] [CrossRef]
- Shuai, Y.M.; Yang, J.; Wu, H.; Shao, C.Y.; Xu, X.C.; Liu, M.Y.; Liu, T.; Liang, J. Variation of multi-angle reflectance collected by UAV over quadrats of paddy-field canopy. Remote Sens. Technol. Appl. 2021, 36, 342–352. [Google Scholar] [CrossRef]
- Petri, C.A.; Lênio, S.G. Sensitivity of Seven MODIS Vegetation Indices to BRDF Effects during the Amazonian Dry Season. Remote. Sens. 2019, 11, 1650. [Google Scholar] [CrossRef]
- Bhandari, S.; Phinn, S.; Gill, T. Assessing viewing and illumination geometry effects on the MODIS vegetation index (MOD13Q1) time series: Implications for monitoring phenology and disturbances in forest communities in Queensland, Australia. Int. J. Remote Sens. 2011, 32, 7513–7538. [Google Scholar] [CrossRef]
- Gao, F.; Schaaf, C.B.; Strahler, A.H.; Jin, Y.; Li, X. Detecting Vegetation Structure using a Kernel-based BRDF Model. Remote Sens. Environ. 2003, 86, 198–205. [Google Scholar] [CrossRef]
- Wang, Q.; Ni-Meister, W. Forest Canopy Height and Gaps from Multiangular BRDF, Assessed with Airborne LiDAR Data. Remote. Sens. 2019, 11, 2566. [Google Scholar] [CrossRef]
- Yao, Y.; Yan, G.; Wang, J. The Approach on Leaf Area Index Inversion Using Multiangular and Multispectral Data Sets. J. Remote Sens. 2005, 9, 117–122. [Google Scholar] [CrossRef]
- Yang, G.J.; Huang, W.J.; Wang, J.H.; Xing, Z.R. Inversion of forest leaf area index calculated from multi-source and multi-angle remote sensing data. Chin. Bull. Bot. 2010, 45, 566–578. [Google Scholar] [CrossRef]
- Yang, X.F.; Wang, X.M. Classification of MISR multi- angle imagery based on decision tree classifier. J. Geo-Inf. Sci. 2016, 18, 416–422. [Google Scholar] [CrossRef]
- Dickinson, R.E. Land surface processes and climate-Surface albedos and energy balance. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 1983; Volume 25, pp. 305–353. [Google Scholar] [CrossRef]
- Kimes, D.S.; Sellers, P.J. Inferring hemispherical reflectance of the earth’s surface for global energy budgets from remotely sensed nadir or directional radiance values. Remote Sens. Environ. 1985, 18, 205–223. [Google Scholar] [CrossRef]
- Nicodemus, F.E.; Richmond, J.C.; Hsia, J.J.; Ginsberg, I.W.; Limperis, T. Geometrical Considerations and Nomenclature for Reflectance; Nation Bur. Stand.: Washington, DC, USA, 1977; pp. 1–50. [Google Scholar] [CrossRef]
- Walthall, C.L.; Norman, J.M.; Welles, G.C.; Blad, B.L. Simple equation to approximate the bidirectional reflectance from vegetation canopies and bare soil surfaces. Appl. Opt. 1985, 24, 383–387. [Google Scholar] [CrossRef] [PubMed]
- Nilson, T.; Kuusk, A. A reflectance model for the homogeneous plant canopy and its inversion. Remote Sens. Environ. 1989, 27, 157–167. [Google Scholar] [CrossRef]
- Liang, S.; Strahler, A.H. Retrieval of surface BRDF from multiangle remotely sensed data. Remote Sens. Environ. 1994, 50, 18–30. [Google Scholar] [CrossRef]
- Allen, W.A.; Gayle, T.V.; Richardson, A.J. Plant-Canopy Irradiance Specified by the Duntley Equations. J. Opt. Soc. Am. 1970, 60, 372–376. [Google Scholar] [CrossRef]
- Suits, G.H. The calculation of the directional reflectance of a vegetative canopy. Remote Sens. Environ. 1972, 2, 117–125. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Marshak, A.L. The effect of the hot spot on the transport equation in plant canopies. J. Quant. Spectrosc. Radiat. Transf. 1989, 42, 615–630. [Google Scholar] [CrossRef]
- Qin, W.; David, L.B. An analytical and computationally efficient reflectance model for leaf canopies. Agric. For. Meteorol. 1993, 66, 31–64. [Google Scholar] [CrossRef]
- Liang, S.; Strahler, A.H. An analytic BRDF model of canopy radiative transfer and its inversion. IEEE Trans. Geosci. Remote Sens. 1993, 31, 1081–1092. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-Optical Modeling of a Conifer Forest Canopy. IEEE Trans. Geosci. Remote Sens. 1985, 23, 705–721. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-Optical Bidirectional Reflectance Modeling of a Conifer Forest Canopy. IEEE Trans. Geosci. Remote Sens. 1986, 24, 906–919. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-optical bidirectional reflectance modeling of the discrete crown vegetation canopy: Effect of crown shape and mutual shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–292. [Google Scholar] [CrossRef]
- Rahman, H.; Pinty, B.; Verstraete, M.M. Coupled Surface-Atmosphere Reflectance (CSAR) Model 2. Semiempirical Surface Model Usable with NOAA Advanced Very High Resolution Radiometer Data. J. Geophys. Res. Atmos. 1993, 98, 20791–20801. [Google Scholar] [CrossRef]
- Lucht, W.; Schaaf, C.; Strahler, A. An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote Sens. 2000, 38, 977–998. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Diner, D.; Beckert, J.; Reilly, T.; Bruegge, C.; Conel, J.; Kahn, R.; Martonchik, J.; Ackerman, T.; Davies, R.; Gerstl, S.; et al. Multiangle Imaging Spectro Radiometer (MISR) description and experiment overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1072–1087. [Google Scholar] [CrossRef]
- Deschamps, P.Y.; Bréon, F.M.; Leroy, M.; Podaire, A.; Bricaud, A.; Buriez, J.C.; Seze, G. The POLDER mission: Instrument characteristics and scientific objectives. IEEE Trans. Geosci. Remote Sens. 1994, 32, 598–615. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and Product Vision for Terrestrial Global Change Research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Yang, A.; Zhong, B.; Lv, W.; Wu, S.; Liu, Q. Cross-Calibration of GF-1/WFV over a Desert Site Using Landsat-8/OLI Imagery and ZY-3/TLC Data. Remote Sens. 2015, 7, 10763–10787. [Google Scholar] [CrossRef]
- Shuai, Y.; Masek, J.; Gao, F.; Schaaf, C. An algorithm for the retrieval of 30-m snow-free albedo from Landsat surface reflectance and MODIS BRDF. Remote Sens. Environ. 2011, 115, 2204–2216. [Google Scholar] [CrossRef]
- Shuai, Y.; Masek, J.; Gao, F.; Schaaf, C.; He, T. An Approach for the Long-Term 30-m Land Surface Snow-Free Albedo Retrieval from Historic Landsat Surface Reflectance and MODIS-based A Priori Anisotropy Knowledge. Remote Sens. Environ. 2014, 152, 467–479. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.; Claverie, M. Intercomparison of Landsat albedo retrieval techniques and evaluation against in situ measurements across the US SURFRAD network. Remote Sens. Environ. 2014, 152, 627–637. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Bréon, F. Towards a Generalized Approach for Correction of the BRDF Effect in MODIS Directional Reflectances. IEEE Trans. Geosci. Remote Sens. 2009, 47, 898–908. [Google Scholar] [CrossRef]
- Jiao, Z.; Zhang, H.; Li, X. To derive a prior database of archetypal BRDF shapes from ground measurements using anisotropic flat index (AFX). In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 6753–6756. [Google Scholar] [CrossRef]
- Jiao, Z.; Michael, J.H.; Crystal, S.; Zhang, H.; Wang, Z.; Li, X. An Anisotropic Flat Index (AFX) to derive BRDF archetypes from MODIS. Remote Sens. Environ. 2014, 141, 168–187. [Google Scholar] [CrossRef]
- Jiao, Z.; Li, X.; Wang, J.; Zhang, H. Assessment of MODIS BRDF shape indicators. J. Remote Sens. 2011, 15, 432–456. [Google Scholar] [CrossRef]
- Sandmeier, S.R.; Muller, C.; Hosgood, B.; Andreoli, G. Physical Mechanisms in Hyperspectral BRDF Data of Grass and Watercress. Remote Sens. Environ. 1998, 66, 222–233. [Google Scholar] [CrossRef]
- Sandmeier, S.R.; Deering, D.W. Structure Analysis and Classification of Boreal Forest Using Airborne Hyperspectral BRDF Data from ASAS. Remote Sens. Environ. 1999, 69, 281–295. [Google Scholar] [CrossRef]
- Chen, J.M.; Menges, C.H.; Leblanc, S.G. Global mapping of foliage clumping index using multi-angular data. Remote Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.M.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Yang, J.; Shuai, Y.; Duan, J.; Xie, D.; Zhang, Q.; Zhao, R. Impact of BRDF Spatiotemporal Smoothing on Land Surface Albedo Estimation. Remote. Sens. 2022, 14, 2001. [Google Scholar] [CrossRef]
- Boryan, C.; Yang, Z.; Mueller, R.; Craig, M. Monitoring US agriculture: The US Department of Agriculture, National Agricultural Statistics Service, Cropland Data Layer Program. Geocarto Int. 2011, 26, 341–358. [Google Scholar] [CrossRef]
- Wickham, J.D.; Stehman, S.V.; Gass, L.; Dewitz, J.; Sorenson, D.G.; Granneman, B.; Poss, R.V.; Baer, L.A. Thematic accuracy assessment of the 2011 National Land cover Database (NLCD). Remote Sens. Environ. 2017, 191, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Wolfe, R.; Roy, D.; Vermote, E. MODIS land data storage, gridding, and compositing methodology: Level 2 grid. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1324–1338. [Google Scholar] [CrossRef]
- Yang, K.; Wolfe, R. MODIS level 2 grid with the ISIN map projection. In Proceedings of the IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, Australia, 9–13 July 2001; pp. 3291–3293. [Google Scholar] [CrossRef]
- Gao, F. MODIS bidirectional reflectance distribution function and albedo Climate Modeling Grid products and the variability of albedo for major global vegetation types. J. Geophys. Res. Atmos. 2005, 110, D01104. [Google Scholar] [CrossRef]
- Wanner, W.; Li, X.; Strahler, A.H. On the derivation of kernels for kernel-driven models of bidirectional reflectance. J. Geophys. Res. Atmos. 1995, 100, 21077–21089. [Google Scholar] [CrossRef]
- Wanner, W.; Strahler, A.H.; Hu, B.; Lewis, P.; Muller, J.P.; Li, X.; Barker Schaaf, C.L.; Barnsley, M.J. Global retrieval of bidirectional reflectance and albedo over land from EOS MODIS and MISR data: Theory and algorithm. J. Geophys. Res. 1997, 102, 17143–17162. [Google Scholar] [CrossRef]
- Yan, G.J.; Jiang, H.L.; Yan, K.; Cheng, S.; Song, W.; Tong, Y.; Liu, Y.; Qi, J.; Mu, X.; Zhang, W.M.; et al. Review of optical multi-angle quantitative remote sensing. Natl. Remote Sens. Bull. 2021, 25, 83–108. [Google Scholar] [CrossRef]
- Chang, Y.X.; Jiao, Z.T.; Dong, Y.D.; Zhang, X.N.; He, D.D.; Yin, S.Y.; Cui, L.; Ding, A.X. Parameterization and correction of hotspot parameters of Ross-Li kernel driven models on POLDER dataset. J. Remote Sens. 2019, 23, 661–672. [Google Scholar] [CrossRef]
- Cui, L.; Jiao, Z.; Dong, Y.; Zhang, X.; Sun, M.; Yin, S.; Chang, Y.; He, D.; Ding, A. Forest Vertical Structure from MODIS BRDF Shape Indicators. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 23 July 2018. [Google Scholar] [CrossRef]

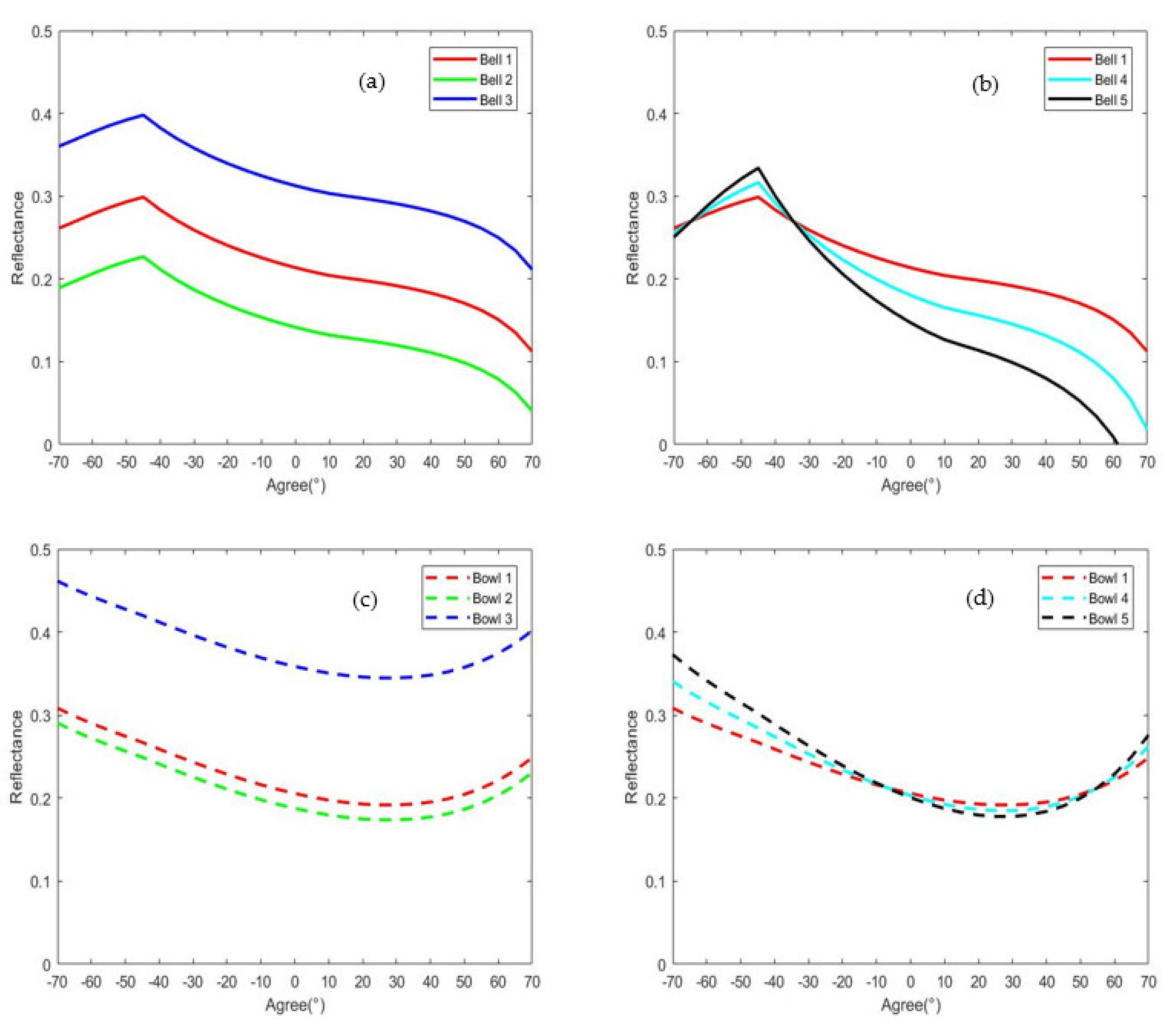
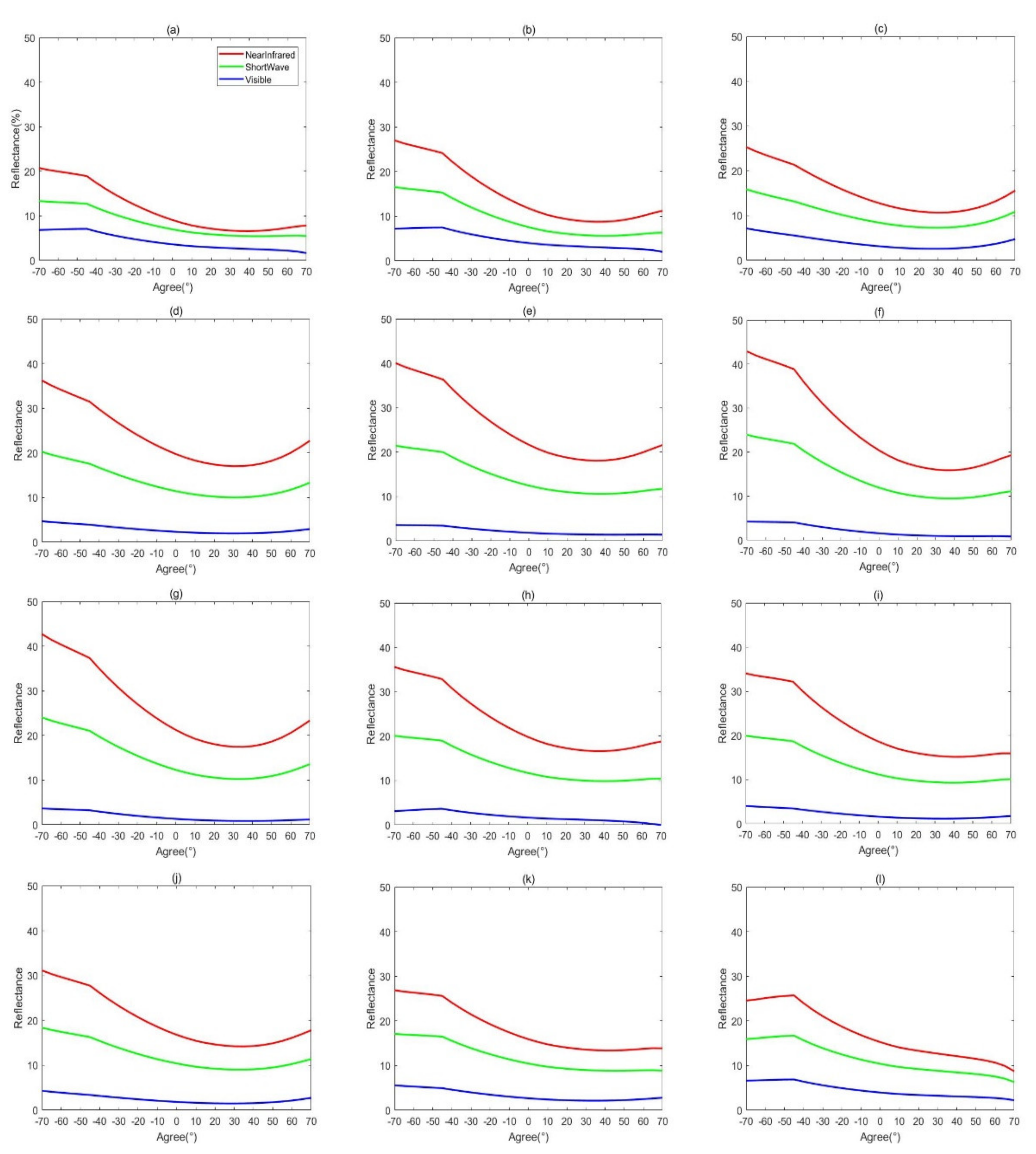
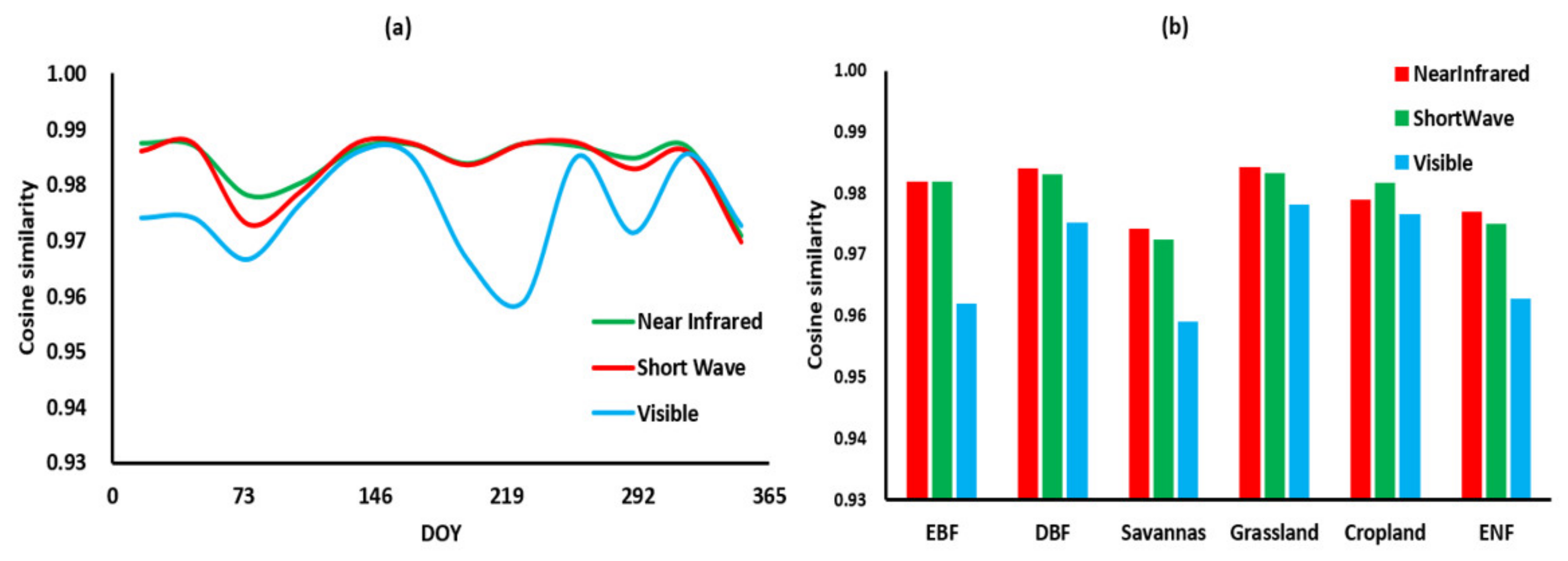
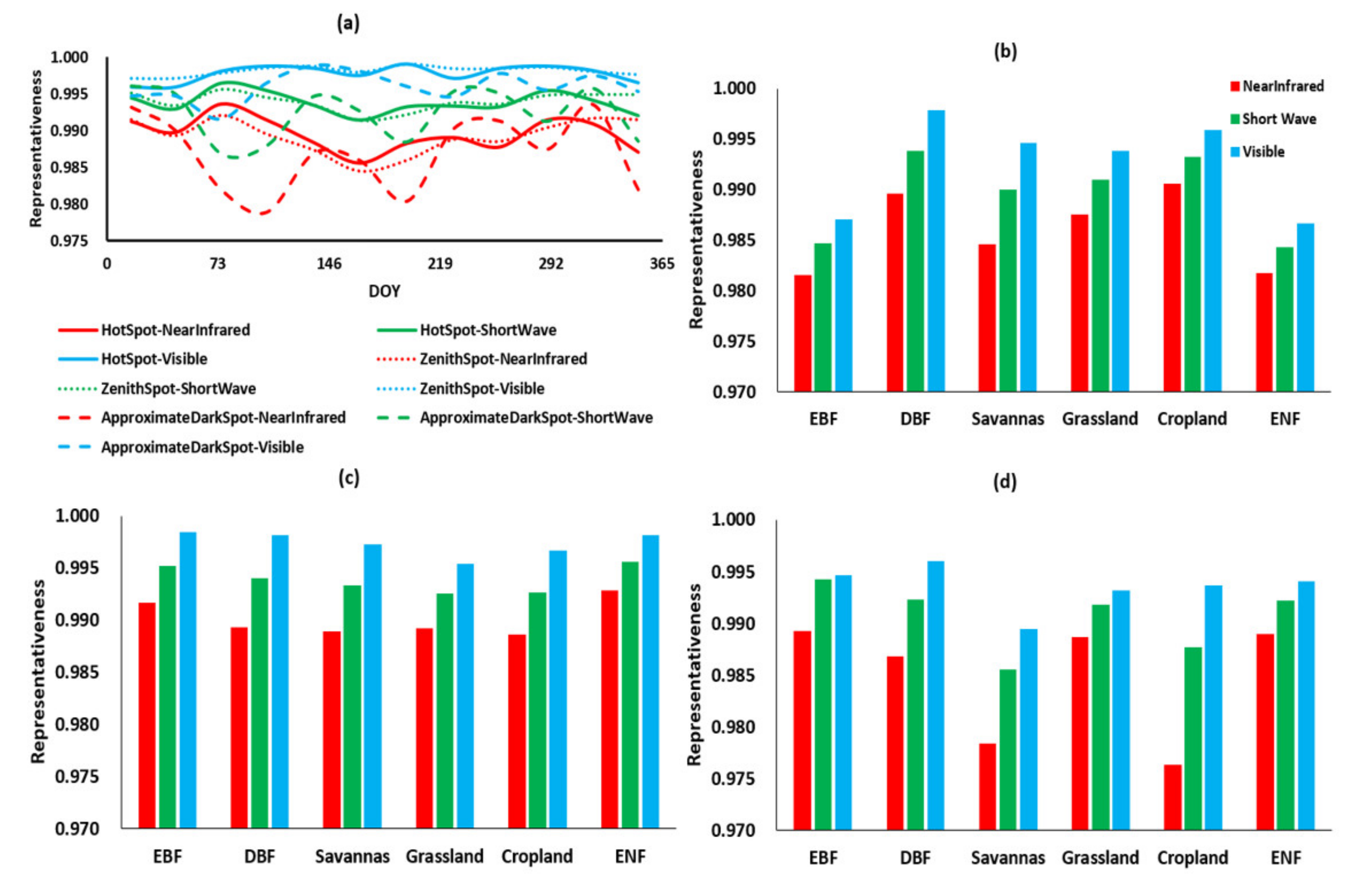


| Shape | Parameter | Data Mode | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Bell | P1 | 0.269 | 0.197 | 0.368 | 0.269 | 0.269 |
| P2 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | |
| P3 | 0.050 | 0.050 | 0.050 | 0.080 | 0.110 | |
| Bowl | P1 | 0.215 | 0.197 | 0.368 | 0.215 | 0.215 |
| P2 | 0.157 | 0.157 | 0.157 | 0.211 | 0.265 | |
| P3 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | |
| Item | Bell | Bowl | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |
| AFX | 0.745 | 0.652 | 0.814 | 0.592 | 0.438 | 1.125 | 1.137 | 1.073 | 1.173 | 1.220 |
| ANIF | 1.204 | 1.343 | 1.131 | 1.472 | 2.173 | 1.033 | 1.036 | 1.019 | 1.043 | 1.053 |
| ANIX | 1.685 | 2.153 | 1.440 | 2.582 | 4.934 | 1.343 | 1.377 | 1.194 | 1.462 | 1.587 |
| F1(%/°) | 0.151 | 0.151 | 0.151 | 0.243 | 0.335 | −0.165 | −0.165 | −0.165 | −0.224 | −0.282 |
| F2(%/°) | −0.234 | −0.234 | −0.234 | −0.374 | −0.514 | −0.154 | −0.154 | −0.154 | −0.203 | −0.253 |
| F3(%/°) | −0.134 | −0.134 | −0.134 | −0.213 | −0.293 | −0.116 | −0.116 | −0.116 | −0.155 | −0.193 |
| F4(%/°) | −0.076 | −0.076 | −0.076 | −0.121 | −0.166 | −0.064 | −0.064 | −0.064 | −0.084 | −0.105 |
| F5(%/°) | −0.084 | −0.084 | −0.084 | −0.134 | −0.185 | 0.025 | 0.025 | 0.025 | 0.034 | 0.044 |
| F6(%/°) | −0.261 | −0.261 | −0.261 | −0.418 | −0.576 | 0.198 | 0.198 | 0.198 | 0.270 | 0.342 |
| D1(°) | 158.214 | 158.214 | 158.214 | 145.833 | 134.295 | 179.375 | 179.375 | 179.375 | 178.885 | 178.423 |
| D2(°) | 176.730 | 176.730 | 176.730 | 174.877 | 173.137 | 177.005 | 177.005 | 177.005 | 176.045 | 175.105 |
| D3(°) | 170.185 | 170.185 | 170.185 | 164.939 | 160.507 | 170.202 | 170.202 | 170.202 | 166.856 | 163.647 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Huang, J.; Fan, H.; Duan, J.; Ma, X. The Description and Application of BRDF Based on Shape Vectors for Typical Landcovers. Sustainability 2022, 14, 11883. https://doi.org/10.3390/su141911883
Yang J, Huang J, Fan H, Duan J, Ma X. The Description and Application of BRDF Based on Shape Vectors for Typical Landcovers. Sustainability. 2022; 14(19):11883. https://doi.org/10.3390/su141911883
Chicago/Turabian StyleYang, Jian, Jiapeng Huang, Hongdong Fan, Junbo Duan, and Xianwei Ma. 2022. "The Description and Application of BRDF Based on Shape Vectors for Typical Landcovers" Sustainability 14, no. 19: 11883. https://doi.org/10.3390/su141911883
APA StyleYang, J., Huang, J., Fan, H., Duan, J., & Ma, X. (2022). The Description and Application of BRDF Based on Shape Vectors for Typical Landcovers. Sustainability, 14(19), 11883. https://doi.org/10.3390/su141911883






