Predicting Monthly Runoff of the Upper Yangtze River Based on Multiple Machine Learning Models
Abstract
1. Introduction
2. Methods
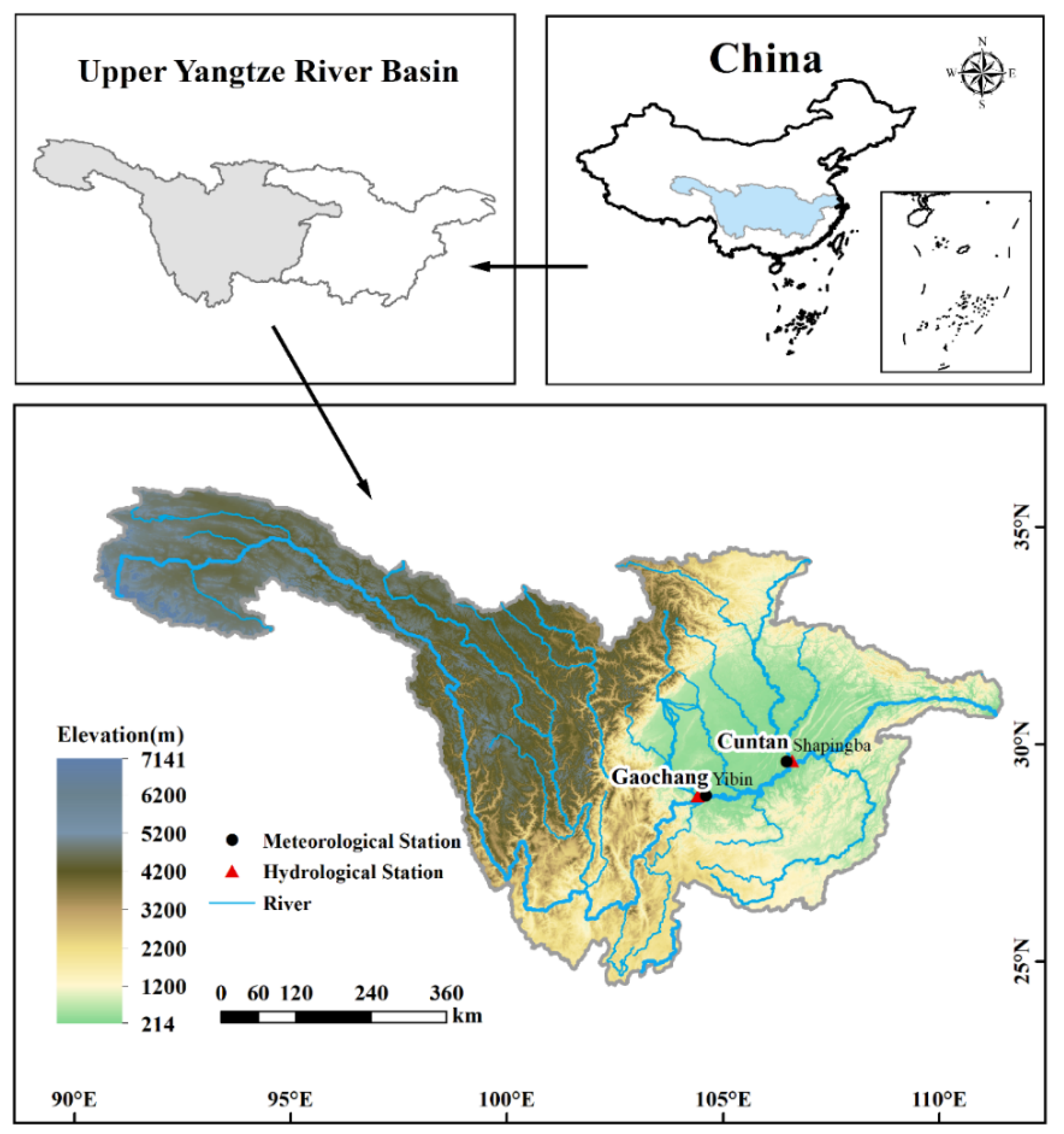
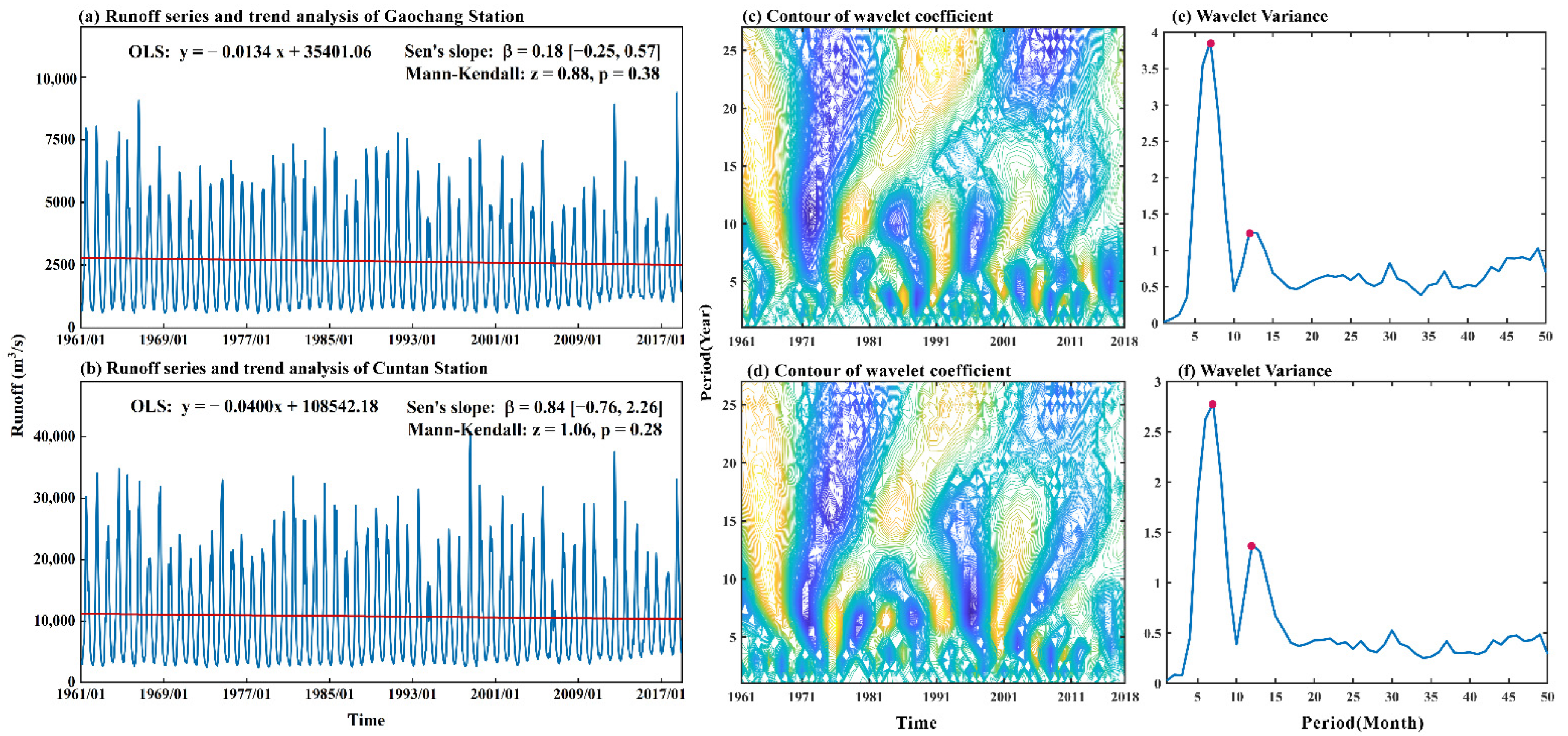
2.1. Study Area and Data
2.2. Variable Selection
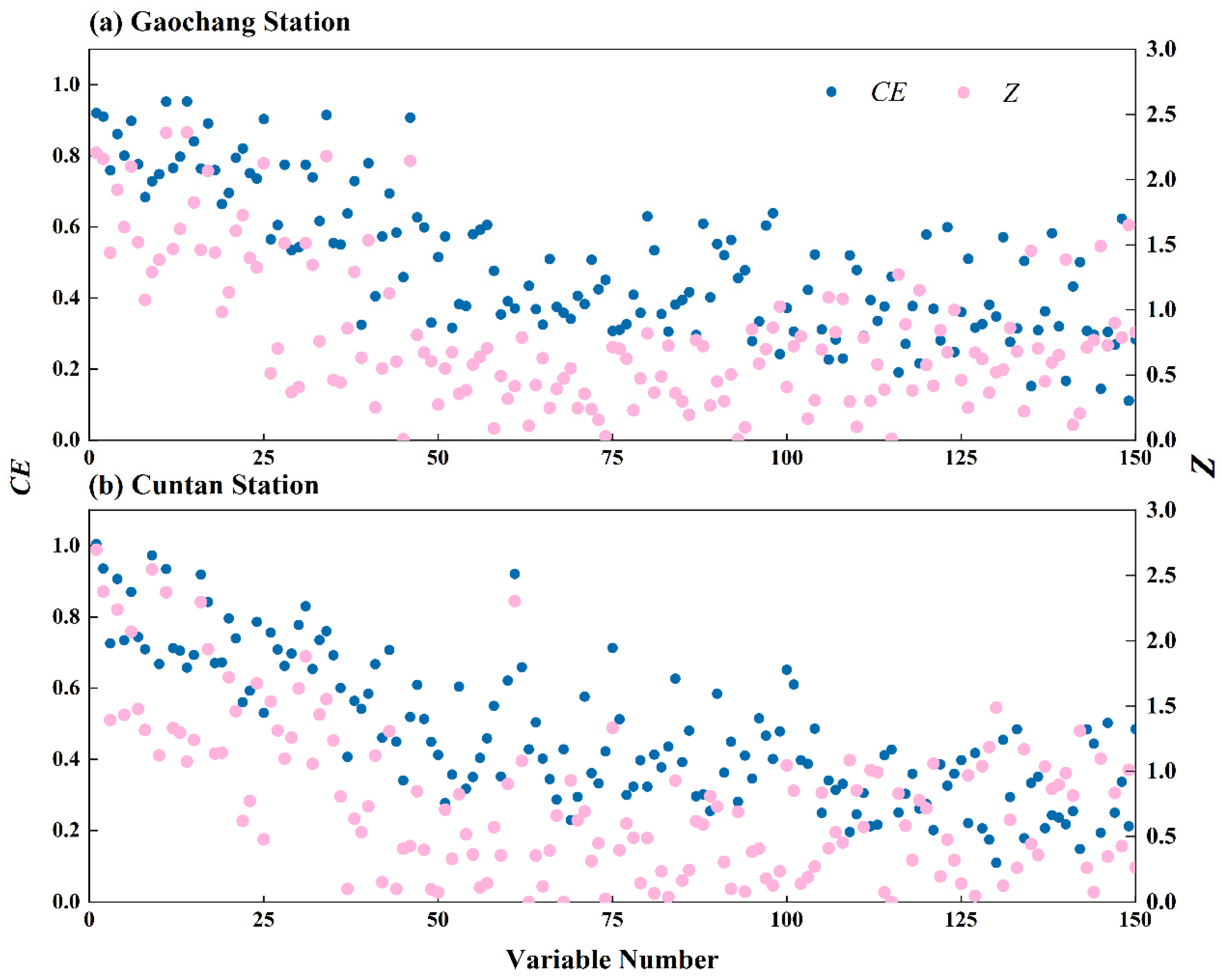
2.2.1. Pearson’s Correlation Coefficient
2.2.2. Stepwise Regression
2.2.3. Copula Entropy
2.3. Prediction Models
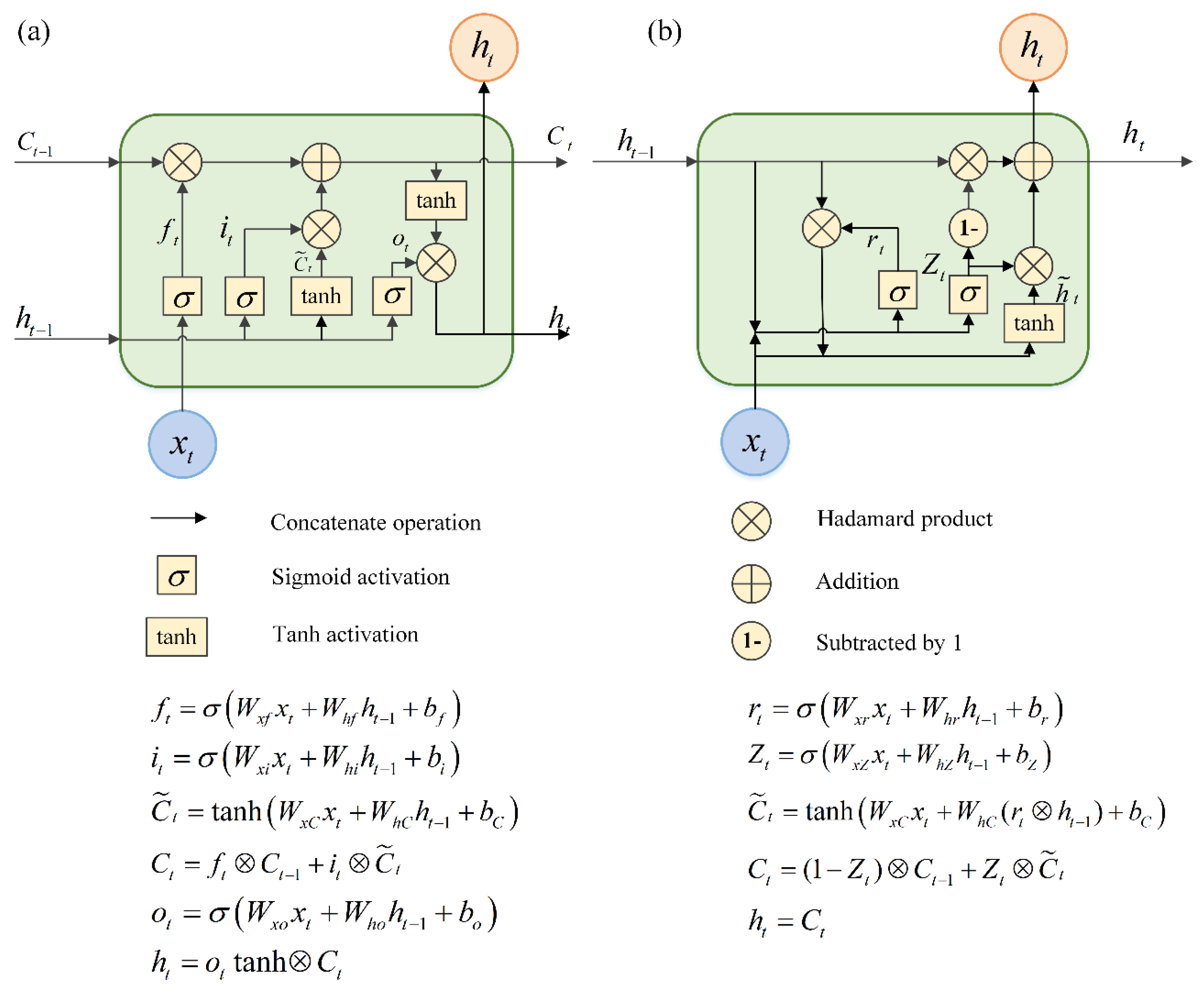
2.3.1. Long Short-Term Memory (LSTM)
2.3.2. Gate Recurrent Unit (GRU)
2.3.3. Gradient Boosted Decision Tree (GBDT)
2.3.4. Random Forest (RF)
2.3.5. Support Vector Regression (SVR)
2.4. Metrics of Performance Evaluation
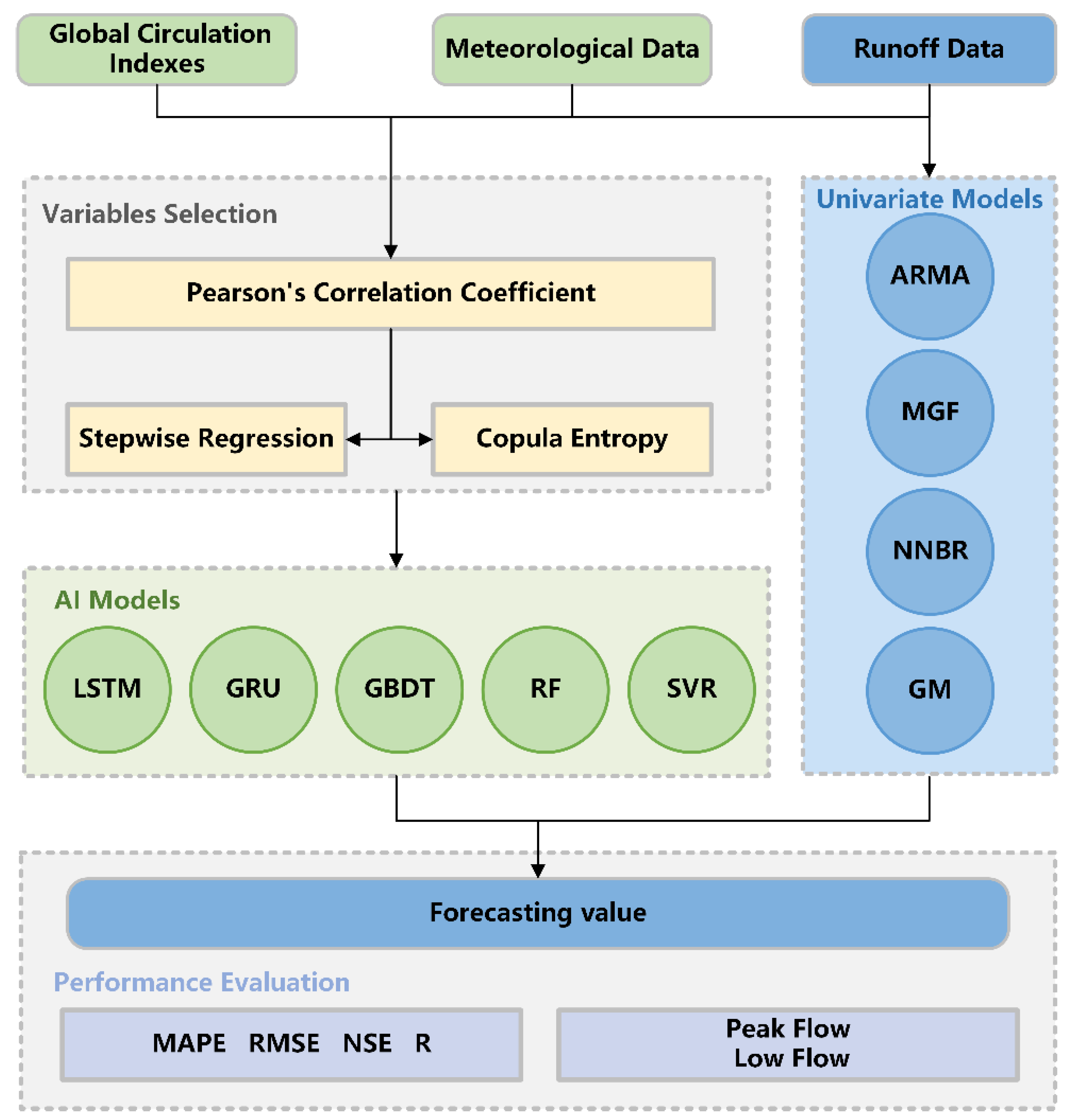
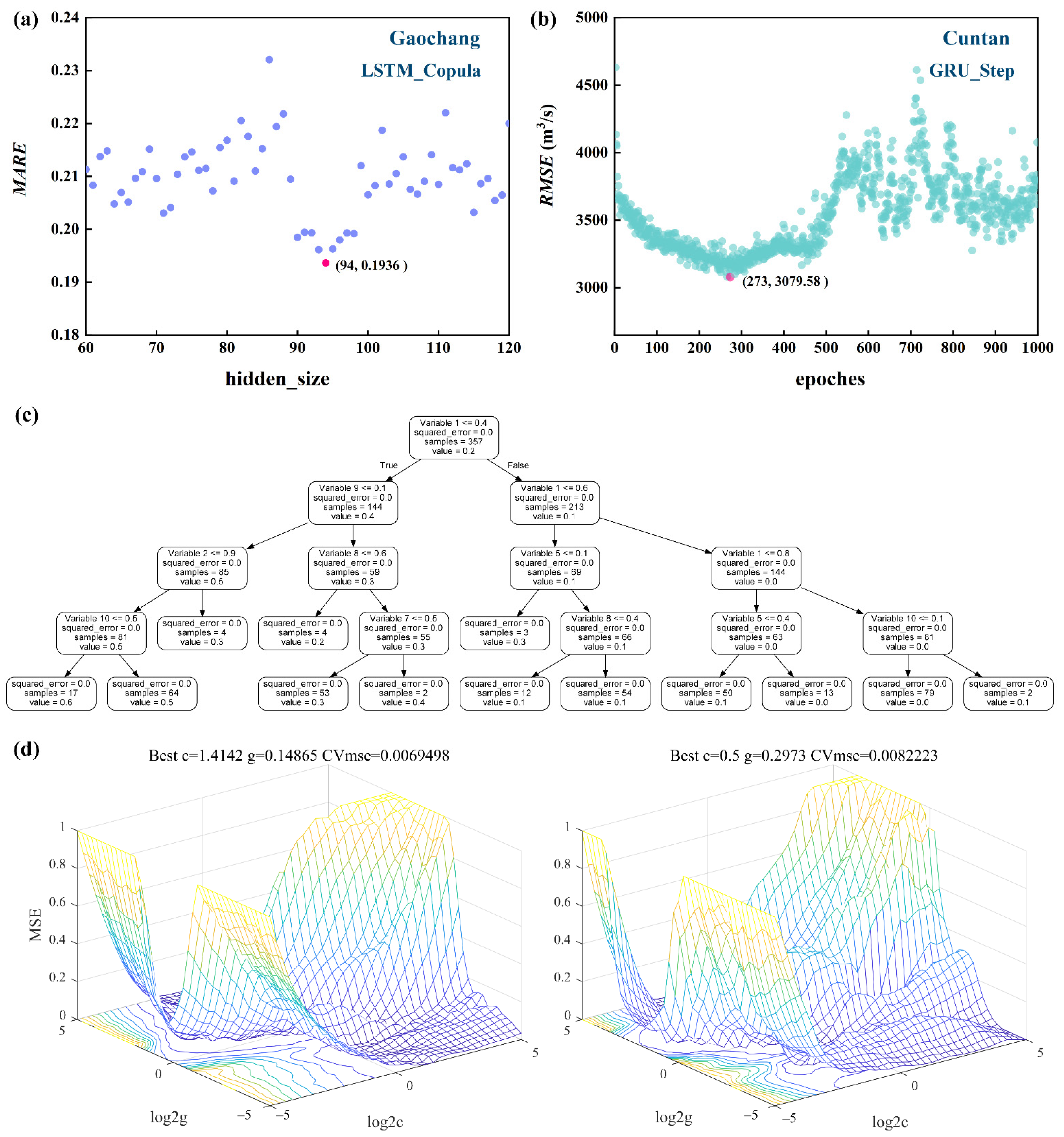
2.5. Model Calculation Scheme
3. Results
3.1. Variable Selection
3.2. Model Structure and Parameter Selection
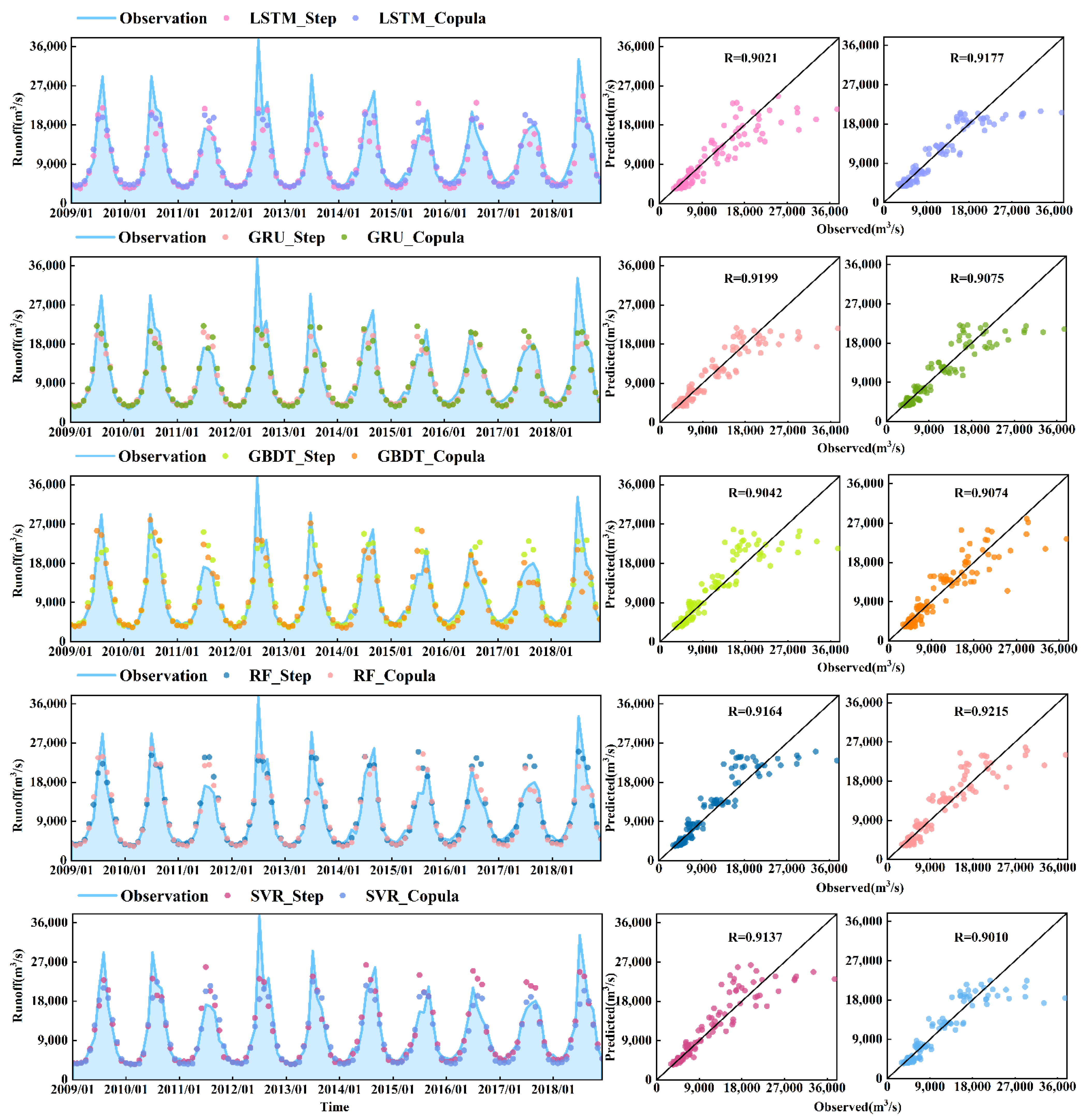
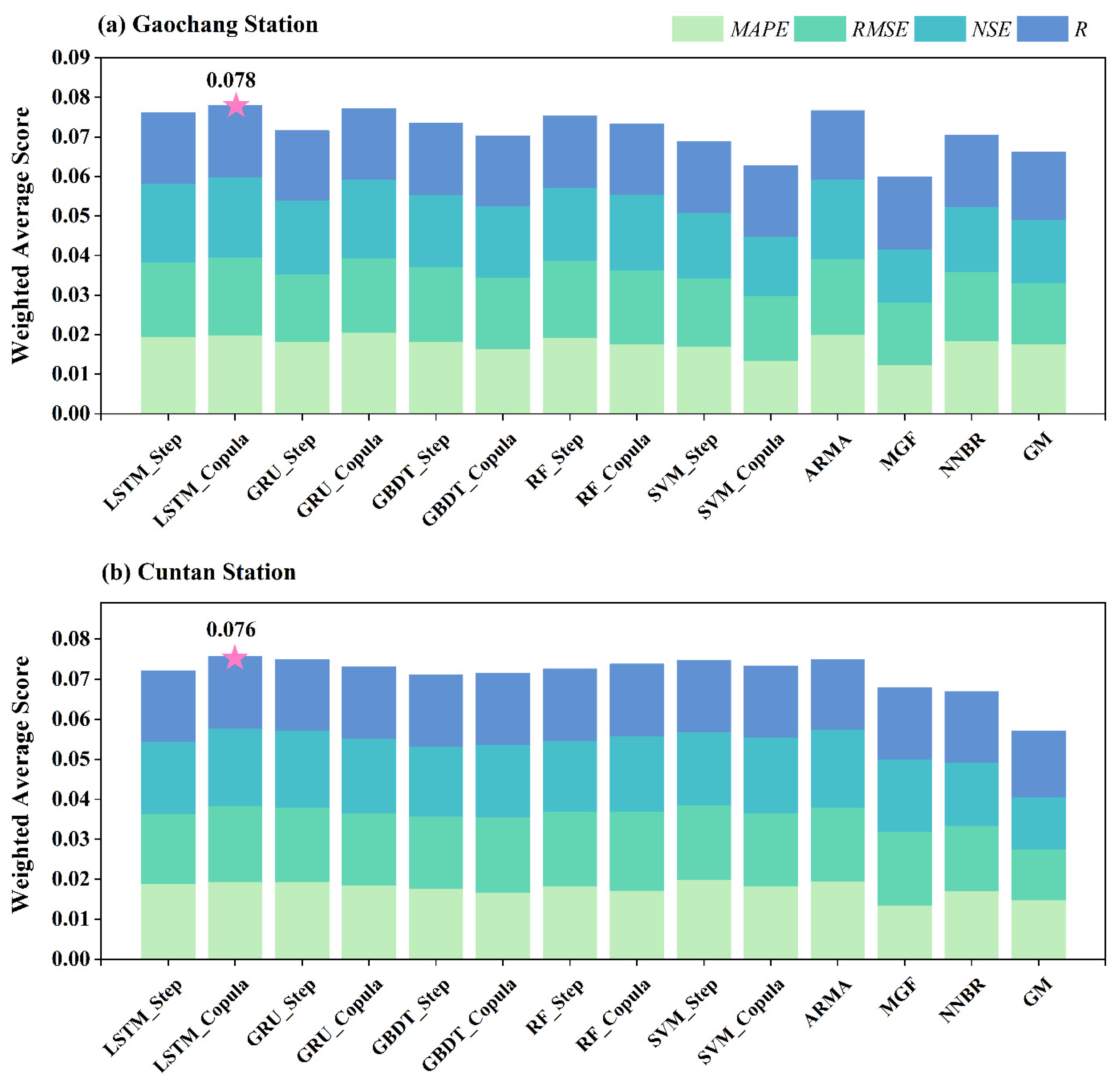
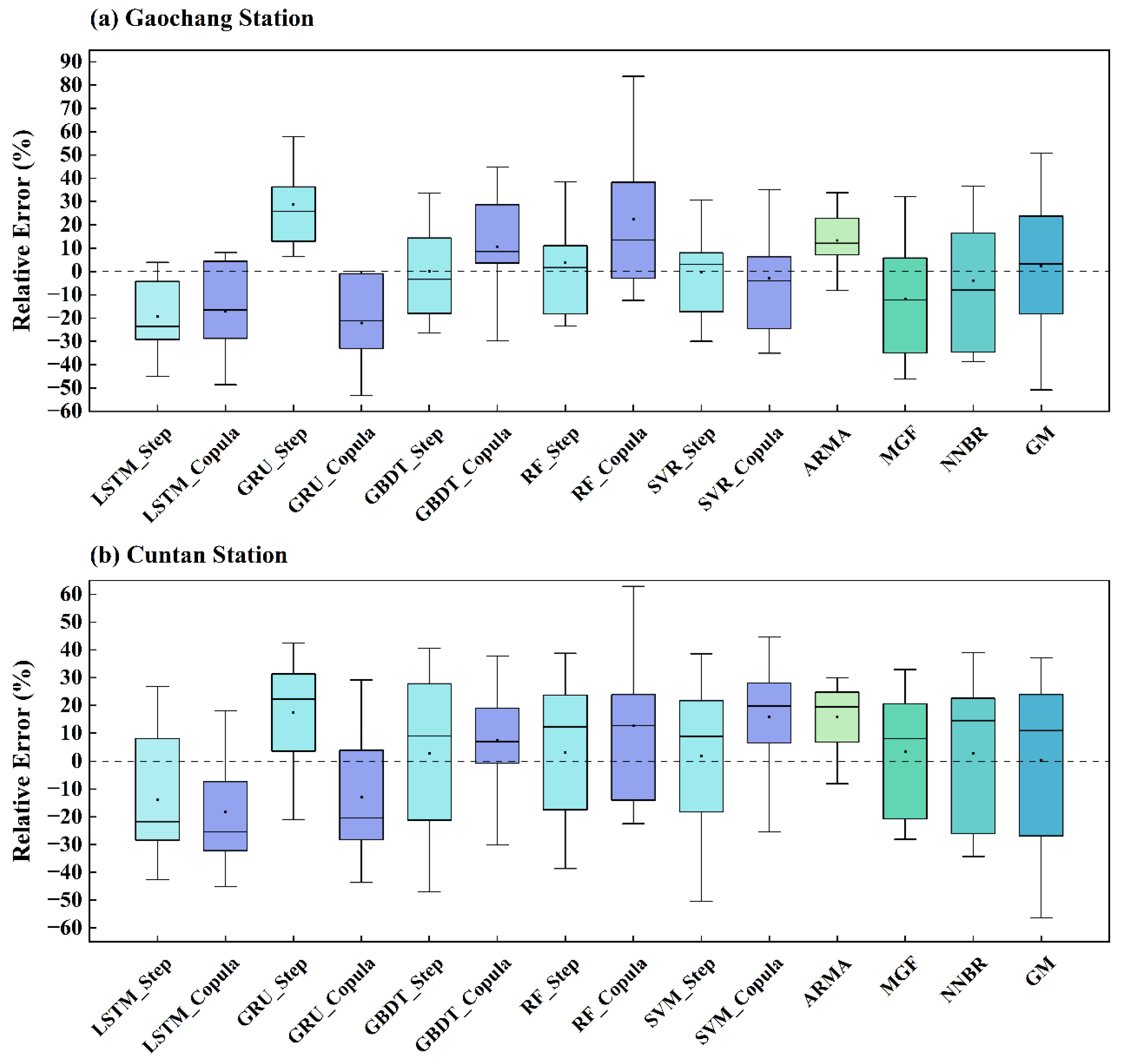
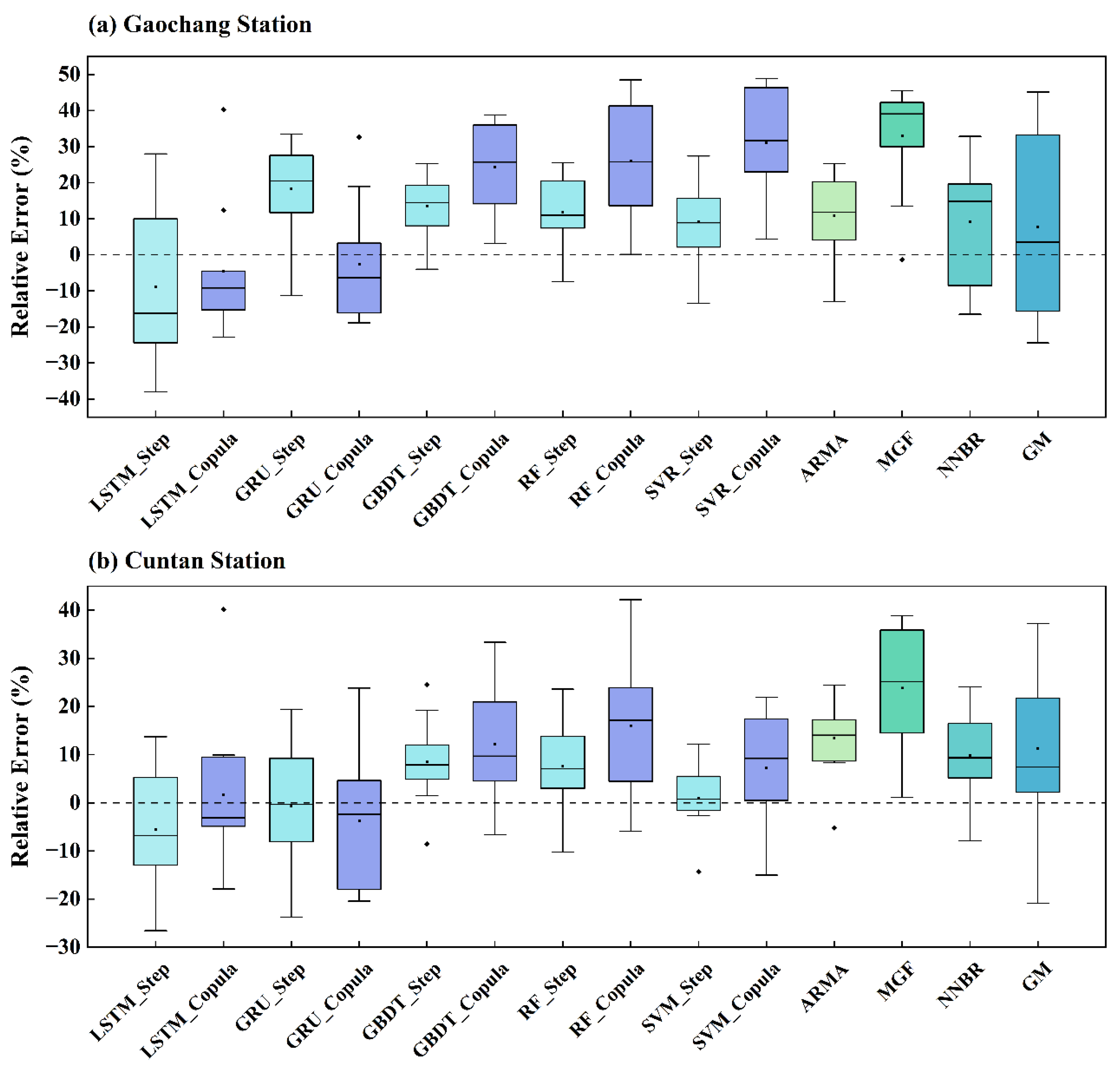
3.3. Comparison of Various Models’ Performance
3.4. Accuracy of Peak Flow and Low Flow Forecasts
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arora, A.; Arabameri, A.; Pandey, M.; Siddiqui, M.A.; Shukla, U.K.; Dieu Tien, B.; Mishra, V.N.; Bhardwaj, A. Optimization of state-of-the-art fuzzy-metaheuristic ANFIS-based machine learning models for flood susceptibility prediction mapping in the Middle Ganga Plain, India. Sci. Total Environ. 2021, 750, 141565. [Google Scholar] [CrossRef] [PubMed]
- Tabari, H. Extreme value analysis dilemma for climate change impact assessment on global flood and extreme precipitation. J. Hydrol. 2021, 593, 16. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.-w. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Lu, P.Y.; Lin, K.R.; Xu, C.Y.; Lan, T.; Liu, Z.Y.; He, Y.H. An integrated framework of input determination for ensemble forecasts of monthly estuarine saltwater intrusion. J. Hydrol. 2021, 598, 126225. [Google Scholar] [CrossRef]
- Feng, Z.-k.; Niu, W.-j.; Tang, Z.-y.; Jiang, Z.-q.; Xu, Y.; Liu, Y.; Zhang, H.-r. Monthly runoff time series prediction by variational mode decomposition and support vector machine based on quantum-behaved particle swarm optimization. J. Hydrol. 2020, 583, 124627. [Google Scholar] [CrossRef]
- Samantaray, S.; Das, S.S.; Sahoo, A.; Satapathy, D.P. Monthly runoff prediction at Baitarani river basin by support vector machine based on Salp swarm algorithm. Ain Shams Eng. J. 2022, 13, 101732. [Google Scholar] [CrossRef]
- Deb, P.; Kiem, A.S.; Willgoose, G. Mechanisms influencing non-stationarity in rainfall-runoff relationships in southeast Australia. J. Hydrol. 2019, 571, 749–764. [Google Scholar] [CrossRef]
- Xu, W.; Chen, J.; Zhang, X.J. Scale Effects of the Monthly Streamflow Prediction Using a State-of-the-art Deep Learning Model. Water Resour. Manag. 2022, 36, 3069–3625. [Google Scholar] [CrossRef]
- Zhang, F.; Kang, Y.; Cheng, X.; Chen, P.; Song, S. A Hybrid Model Integrating Elman Neural Network with Variational Mode Decomposition and Box–Cox Transformation for Monthly Runoff Time Series Prediction. Water Resour. Manag. 2022, 36, 3673–3697. [Google Scholar] [CrossRef]
- Ren, Y.; Zeng, S.; Liu, J.; Tang, Z.; Hua, X.; Li, Z.; Song, J.; Xia, J. Mid- to Long-Term Runoff Prediction Based on Deep Learning at Different Time Scales in the Upper Yangtze River Basin. Water 2022, 14, 1692. [Google Scholar] [CrossRef]
- Ai, P.; Song, Y.; Xiong, C.; Chen, B.; Yue, Z. A novel medium- and long-term runoff combined forecasting model based on different lag periods. J. Hydroinform. 2022, 24, 367–387. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2019, 569, 387–408. [Google Scholar] [CrossRef]
- Moosavi, V.; Gheisoori Fard, Z.; Vafakhah, M. Which one is more important in daily runoff forecasting using data driven models: Input data, model type, preprocessing or data length? J. Hydrol. 2022, 606, 127429. [Google Scholar] [CrossRef]
- Lall, U.; Sharma, A. A nearest neighbor bootstrap for resampling hydrologic time series. Water Resour. Res. 1996, 32, 679–693. [Google Scholar] [CrossRef]
- Mao, M.; Chirwa, E.C. Application of grey model GM (1, 1) to vehicle fatality risk estimation. Technol. Forecast. Soc. Chang. 2006, 73, 588–605. [Google Scholar] [CrossRef]
- McLeod, A.I.; Li, W.K. Diagnostic checking ARMA time series models using squared-residual autocorrelations. J. Time Ser. Anal. 1983, 4, 269–273. [Google Scholar] [CrossRef]
- Slay, J.C.; Solomon, J. A mean generating function. Two-Year Coll. Math. J. 1981, 12, 27–29. [Google Scholar] [CrossRef]
- Somu, N.; MR, G.R.; Ramamritham, K. A hybrid model for building energy consumption forecasting using long short term memory networks. Appl. Energy 2020, 261, 114131. [Google Scholar] [CrossRef]
- Chen, X.; Parajka, J.; Széles, B.; Strauss, P.; Blöschl, G. Controls on event runoff coefficients and recession coefficients for different runoff generation mechanisms identified by three regression methods. J. Hydrol. Hydromech. 2020, 68, 155–169. [Google Scholar] [CrossRef]
- Bojang, P.O.; Yang, T.-C.; Pham, Q.B.; Yu, P.-S. Linking Singular Spectrum Analysis and Machine Learning for Monthly Rainfall Forecasting. Appl. Sci. 2020, 10, 3224. [Google Scholar] [CrossRef]
- Niu, W.-j.; Feng, Z.-k.; Xu, Y.-s.; Feng, B.-f.; Min, Y.-w. Improving Prediction Accuracy of Hydrologic Time Series by Least-Squares Support Vector Machine Using Decomposition Reconstruction and Swarm Intelligence. J. Hydrol. Eng. 2021, 26, 04021030. [Google Scholar] [CrossRef]
- Abbasi, M.; Farokhnia, A.; Bahreinimotlagh, M.; Roozbahani, R. A hybrid of Random Forest and Deep Auto-Encoder with support vector regression methods for accuracy improvement and uncertainty reduction of long-term streamflow prediction. J. Hydrol. 2021, 597, 125717. [Google Scholar] [CrossRef]
- Cheng, Q.P.; Zuo, X.A.; Zhong, F.L.; Gao, L.; Xiao, S.C. Runoff variation characteristics, association with large-scale circulation and dominant causes in the Heihe River Basin, Northwest China. Sci. Total Environ. 2019, 688, 361–379. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, M.L.; Chen, J.; Zhong, P.A.; Wu, X.F.; Wu, S.Q. Multiscale attribution analysis for assessing effects of changing environment on runoff: Case study of the Upstream Yangtze River in China. J. Water Clim. Chang. 2021, 12, 627–646. [Google Scholar] [CrossRef]
- Tao, L.Z.; He, X.G.; Li, J.J.; Yang, D. A multiscale long short-term memory model with attention mechanism for improving monthly precipitation prediction. J. Hydrol. 2021, 602, 126815. [Google Scholar] [CrossRef]
- May, R.J.; Maier, H.R.; Dandy, G.C.; Fernando, T. Non-linear variable selection for artificial neural networks using partial mutual information. Environ. Model. Softw. 2008, 23, 1312–1326. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.P.; Liu, Y.R.; Gao, P.P. A MCMC-based maximum entropy copula method for bivariate drought risk analysis of the Amu Darya River Basin. J. Hydrol. 2020, 590, 125502. [Google Scholar] [CrossRef]
- Ma, J.; Sun, Z. Mutual Information Is Copula Entropy. Tsinghua Sci. Technol. 2011, 16, 51–54. [Google Scholar] [CrossRef]
- Singh, V.P.; Zhang, L. Copula-entropy theory for multivariate stochastic modeling in water engineering. Geosci. Lett. 2018, 5, 1–17. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Integrating Entropy and Copula Theories for Hydrologic Modeling and Analysis. Entropy 2015, 17, 2253–2280. [Google Scholar] [CrossRef]
- AghaKouchak, A. Entropy-Copula in Hydrology and Climatology. J. Hydrometeorol. 2014, 15, 2176–2189. [Google Scholar] [CrossRef]
- Qin, P.; Xu, H.; Liu, M.; Du, L.; Xiao, C.; Liu, L.; Tarroja, B. Climate change impacts on Three Gorges Reservoir impoundment and hydropower generation. J. Hydrol. 2020, 580, 123922. [Google Scholar] [CrossRef]
- Niu, X. Key Technologies of the Hydraulic Structures of the Three Gorges Project. Engineering 2016, 2, 340–349. [Google Scholar] [CrossRef]
- Xiong, L.H.; Guo, S.L. Trend test and change-point detection for the annual discharge series of the Yangtze River at the Yichang hydrological station. Hydrol. Sci. J.-J. Des. Sci. Hydrol. 2004, 49, 99–112. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhong, P.-a.; Wang, M.; Xu, B.; Chen, J. Changes identification of the Three Gorges reservoir inflow and the driving factors quantification. Quat. Int. 2018, 475, 28–41. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, G.; Huang, F.; Qin, H.; Wang, B.; Yi, L. Directed graph deep neural network for multi-step daily streamflow forecasting. J. Hydrol. 2022, 607, 127515. [Google Scholar] [CrossRef]
- Xu, J. Trends in suspended sediment grain size in the upper Yangtze River and its tributaries, as influenced by human activities. Hydrol. Sci. J.-J. Des. Sci. Hydrol. 2007, 52, 777–792. [Google Scholar] [CrossRef][Green Version]
- Zhang, X.; Zheng, Z.; Wang, K. Prediction of runoff in the upper Yangtze River based on CEEMDAN-NAR model. Water Supply 2021, 21, 3307–3318. [Google Scholar] [CrossRef]
- Yang, X.L.; Yu, X.H.; Wang, Y.Q.; Liu, Y.; Zhang, M.R.; Ren, L.L.; Yuan, F.; Jiang, S.H. Estimating the response of hydrological regimes to future projections of precipitation and temperature over the upper Yangtze River. Atmos. Res. 2019, 230, 104627. [Google Scholar] [CrossRef]
- Luo, K.S.; Li, Y.Z. Assessing rainwater harvesting potential in a humid and semi-humid region based on a hydrological model. J. Hydrol. Reg. Stud. 2021, 37, 100912. [Google Scholar] [CrossRef]
- Chen, J.; Finlayson, B.L.; Wei, T.Y.; Sun, Q.L.; Webber, M.; Li, M.T.; Chen, Z.Y. Changes in monthly flows in the Yangtze River, China—With special reference to the Three Gorges Dam. J. Hydrol. 2016, 536, 293–301. [Google Scholar] [CrossRef]
- Libiseller, C.; Grimvall, A. Performance of partial Mann-Kendall tests for trend detection in the presence of covariates. Environmetrics 2002, 13, 71–84. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Aljoda, A.; Jain, S. Uncertainties and risks in reservoir operations under changing hydroclimatic conditions. J. Water Clim. Chang. 2021, 12, 1708–1723. [Google Scholar] [CrossRef]
- Erdem, O.; Ceyhan, E.; Varli, Y. A new correlation coefficient for bivariate time-series data. Phys. A Stat. Mech. Its Appl. 2014, 414, 274–284. [Google Scholar] [CrossRef]
- Sharma, A.; Luk, K.; Cordery, I.; Lall, U. Seasonal to interannual rainfall probabilistic forecasts for improved water supply management: Part 2—Predictor identification of quarterly rainfall using ocean-atmosphere information. J. Hydrol. 2000, 239, 240–248. [Google Scholar] [CrossRef]
- Gao, S.; Huang, Y.; Zhang, S.; Han, J.; Wang, G.; Zhang, M.; Lin, Q. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. J. Hydrol. 2020, 589, 125188. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Muhammad Adnan, R. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2018, 270, 654–669. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Zheng, Y.X.; Yue, Q.M.; Liu, Y.; Yu, J.S. Regional characteristics’ impact on the performances of the gated recurrent unit on streamflow forecasting. Water Supply 2022, 22, 4142–4158. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Liu, Y.; Yue, Q.M.; Zheng, Y.X.; Yao, X.L.; Yu, J.S. Impact of Input Filtering and Architecture Selection Strategies on GRU Runoff Forecasting: A Case Study in the Wei River Basin, Shaanxi, China. Water 2020, 12, 3532. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, Y.; Wang, H.; Jiang, Z. Depth prediction of urban flood under different rainfall return periods based on deep learning and data warehouse. Sci. Total Environ. 2020, 716, 137077. [Google Scholar] [CrossRef]
- Yang, T.T.; Asanjan, A.A.; Welles, E.; Gao, X.G.; Sorooshian, S.; Liu, X.M. Developing reservoir monthly inflow forecasts using artificial intelligence and climate phenomenon information. Water Resour. Res. 2017, 53, 2786–2812. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Parisouj, P.; Mohebzadeh, H.; Lee, T. Employing Machine Learning Algorithms for Streamflow Prediction: A Case Study of Four River Basins with Different Climatic Zones in the United States. Water Resour. Manag. 2020, 34, 4113–4131. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.; Van Griensven, A.; Van Liew, M.W. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Wang, W.-c.; Chau, K.-w.; Qiu, L.; Chen, Y.-b. Improving forecasting accuracy of medium and long-term runoff using artificial neural network based on EEMD decomposition. Environ. Res. 2015, 139, 46–54. [Google Scholar] [CrossRef]
- Li, Y.H.; Wang, T.H.; Yang, D.W.; Tang, L.H.; Yang, K.; Liu, Z.W. Linkage between anomalies of pre-summer thawing of frozen soil over the Tibetan Plateau and summer precipitation in East Asia. Environ. Res. Lett. 2021, 16, 114030. [Google Scholar] [CrossRef]
- Lei, Y.H.; Shi, J.C.; Xiong, C.A.; Ji, D. Tracking the Atmospheric-Terrestrial Water Cycle over the Tibetan Plateau Based on ERA5 and GRACE. J. Clim. 2021, 34, 6459–6471. [Google Scholar] [CrossRef]
- Ma, T.T.; Wu, G.X.; Liu, Y.M.; Mao, J.Y. Abnormal warm sea-surface temperature in the Indian Ocean, active potential vorticity over the Tibetan Plateau, and severe flooding along the Yangtze River in summer 2020. Q. J. R. Meteorol. Soc. 2022, 148, 1001–1019. [Google Scholar] [CrossRef]
- Wang, Y.; Ye, A.; Peng, D.; Miao, C.; Di, Z.; Gong, W. Spatiotemporal variations in water conservation function of the Tibetan Plateau under climate change based on InVEST model. J. Hydrol. Reg. Stud. 2022, 41, 101064. [Google Scholar] [CrossRef]
- Ding, Y.H.; Liu, Y.Y.; Hu, Z.Z. The Record-breaking Meiyu in 2020 and Associated Atmospheric Circulation and Tropical SST Anomalies. Adv. Atmos. Sci. 2021, 38, 1980–1993. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, R.H.; Yang, S.; Li, W.H.; Wen, M. Quasi-Biweekly Oscillation of the South Asian High and Its Role in Connecting the Indian and East Asian Summer Rainfalls. Geophys. Res. Lett. 2019, 46, 14742–14750. [Google Scholar] [CrossRef]
- Zhou, Z.Q.; Xie, S.P.; Zhang, R.H. Historic Yangtze flooding of 2020 tied to extreme Indian Ocean conditions. Proc. Natl. Acad. Sci. USA 2021, 118, e2022255118. [Google Scholar] [CrossRef]
- Takaya, Y.; Ishikawa, I.; Kobayashi, C.; Endo, H.; Ose, T. Enhanced Meiyu-Baiu Rainfall in Early Summer 2020: Aftermath of the 2019 Super IOD Event. Geophys. Res. Lett. 2020, 47, e2020GL090671. [Google Scholar] [CrossRef]
- Feng, Z.-k.; Niu, W.-j. Hybrid artificial neural network and cooperation search algorithm for nonlinear river flow time series forecasting in humid and semi-humid regions. Knowl. Based Syst. 2021, 211, 106580. [Google Scholar] [CrossRef]
- Niu, W.-j.; Feng, Z.-k. Evaluating the performances of several artificial intelligence methods in forecasting daily streamflow time series for sustainable water resources management. Sustain. Cities Soc. 2021, 64, 102562. [Google Scholar] [CrossRef]
- Pham, B.T.; Le, L.M.; Le, T.T.; Bui, K.T.T.; Le, V.M.; Ly, H.B.; Prakash, I. Development of advanced artificial intelligence models for daily rainfall prediction. Atmos. Res. 2020, 237, 15. [Google Scholar] [CrossRef]
- Tiyasha; Tung, T.M.; Yaseen, Z.M. A survey on river water quality modelling using artificial intelligence models: 2000–2020. J. Hydrol. 2020, 585, 62. [Google Scholar]
- Wang, Z.Y.; Srinivasan, R.S. A review of artificial intelligence based building energy use prediction: Contrasting the capabilities of single and ensemble prediction models. Renew. Sust. Energ. Rev. 2017, 75, 796–808. [Google Scholar] [CrossRef]
- Meng, E.H.; Huang, S.Z.; Huang, Q.; Fang, W.; Wu, L.Z.; Wang, L. A robust method for non-stationary streamflow prediction based on improved EMD-SVM model. J. Hydrol. 2019, 568, 462–478. [Google Scholar] [CrossRef]
- Yoosefdoost, I.; Khashei-Siuki, A.; Tabari, H.; Mohammadrezapour, O. Runoff Simulation Under Future Climate Change Conditions: Performance Comparison of Data-Mining Algorithms and Conceptual Models. Water Resour. Manag. 2022, 36, 1191–1215. [Google Scholar] [CrossRef]
- Demir, V. Enhancing monthly lake levels forecasting using heuristic regression techniques with periodicity data component: Application of Lake Michigan. Theor. Appl. Climatol. 2022, 143, 915–929. [Google Scholar] [CrossRef]
- Rathnayake, N.; Rathnayake, U.; Tuan Linh, D.; Hoshino, Y. A Cascaded Adaptive Network-Based Fuzzy Inference System for Hydropower Forecasting. Sensors 2022, 22, 2905. [Google Scholar] [CrossRef]
- Rathnayake, N.; Dang, T.L.; Hoshino, Y. A Novel Optimization Algorithm: Cascaded Adaptive Neuro-Fuzzy Inference System. Int. J. Fuzzy Syst. 2021, 23, 1955–1971. [Google Scholar] [CrossRef]
- Chaudhari, S.; Mithal, V.; Polatkan, G.; Ramanath, R. An Attentive Survey of Attention Models. Acm Trans. Intell. Syst. Technol. 2021, 12, 1–32. [Google Scholar] [CrossRef]

| Station | Stepwise Regression | Copula Entropy | ||
|---|---|---|---|---|
| Variables | Lag (Month) | Variables | Lag (Month) | |
| Gaochang | Average Temperature | 7 | Maximum Temperature | 1 |
| Runoff | 12 | East Asian Trough Intensity Index | 6 | |
| Northern Hemisphere Polar Vortex Central Intensity Index | 1 | Average Temperature | 7 | |
| Maximum Temperature | 6 | Daylight Hours | 2 | |
| North American Subtropical High Area Index | 12 | Maximum Temperature | 7 | |
| Runoff | 1 | Runoff | 6 | |
| Relative Humidity | 1 | Daylight Hours | 1 | |
| Tibet Plateau Region 1 Index | 5 | East Asian Trough Intensity Index | 12 | |
| Asia Polar Vortex Area Index | 1 | Average Temperature | 1 | |
| Indian Ocean Warm Pool Strength Index | 9 | Runoff | 12 | |
| Cuntan | Maximum Temperature | 7 | Maximum Temperature | 7 |
| Runoff | 12 | Maximum Temperature | 1 | |
| Northern Hemisphere Polar Vortex Intensity Index | 2 | Average Temperature | 7 | |
| Runoff | 1 | East Asian Trough Intensity Index | 7 | |
| North American Subtropical High Intensity Index | 12 | Runoff | 6 | |
| Atlantic-European Polar Vortex Intensity Index | 7 | Average Temperature | 1 | |
| Daylight Hours | 12 | Runoff | 12 | |
| Asia Polar Vortex Intensity Index | 6 | East Asian Trough Intensity Index | 1 | |
| Eurasian Zonal Circulation Index | 9 | Daylight Hours | 8 | |
| Air Pressure | 3 | Daylight Hours | 2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhang, L.; Zeng, S.; Tang, Z.; Liu, L.; Zhang, Q.; Tang, Z.; Hua, X. Predicting Monthly Runoff of the Upper Yangtze River Based on Multiple Machine Learning Models. Sustainability 2022, 14, 11149. https://doi.org/10.3390/su141811149
Li X, Zhang L, Zeng S, Tang Z, Liu L, Zhang Q, Tang Z, Hua X. Predicting Monthly Runoff of the Upper Yangtze River Based on Multiple Machine Learning Models. Sustainability. 2022; 14(18):11149. https://doi.org/10.3390/su141811149
Chicago/Turabian StyleLi, Xiao, Liping Zhang, Sidong Zeng, Zhenyu Tang, Lina Liu, Qin Zhang, Zhengyang Tang, and Xiaojun Hua. 2022. "Predicting Monthly Runoff of the Upper Yangtze River Based on Multiple Machine Learning Models" Sustainability 14, no. 18: 11149. https://doi.org/10.3390/su141811149
APA StyleLi, X., Zhang, L., Zeng, S., Tang, Z., Liu, L., Zhang, Q., Tang, Z., & Hua, X. (2022). Predicting Monthly Runoff of the Upper Yangtze River Based on Multiple Machine Learning Models. Sustainability, 14(18), 11149. https://doi.org/10.3390/su141811149








