Research on Mining Maximum Subsidence Prediction Based on Genetic Algorithm Combined with XGBoost Model
Abstract
:1. Introduction
2. Methodology
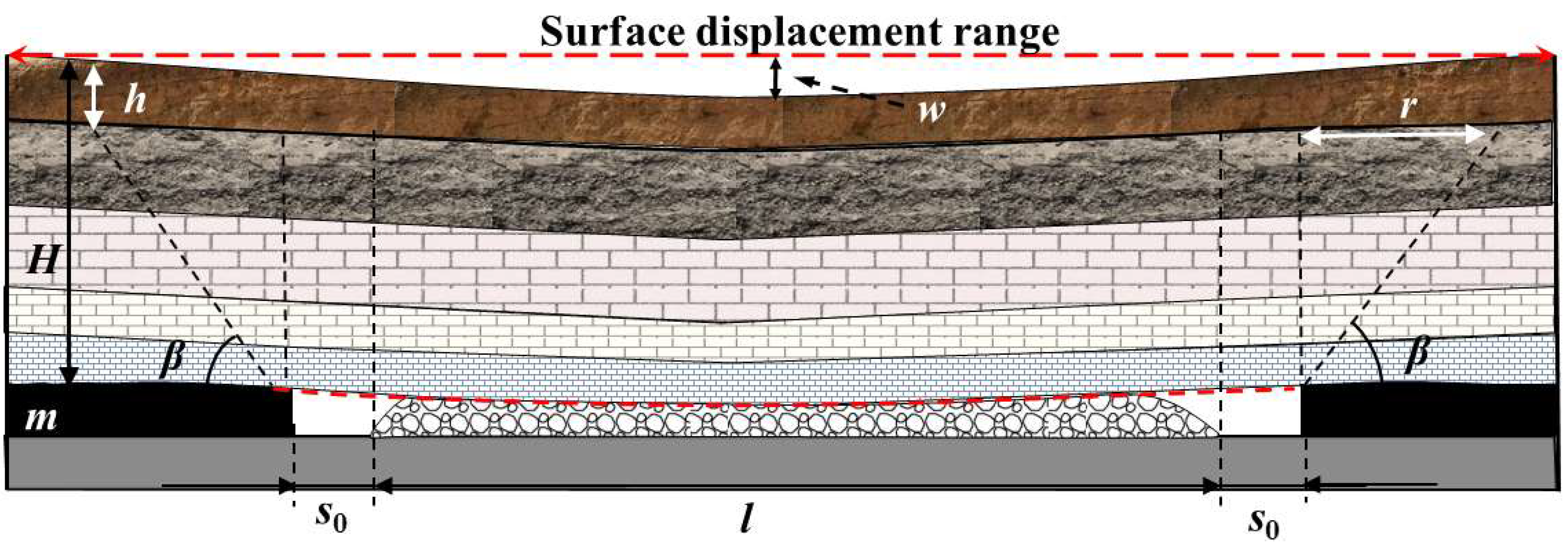
2.1. Model of Mining Subsidence
2.2. Extreme Gradient Boosting (XGBoost)
2.3. Genetic Algorithm (GA)
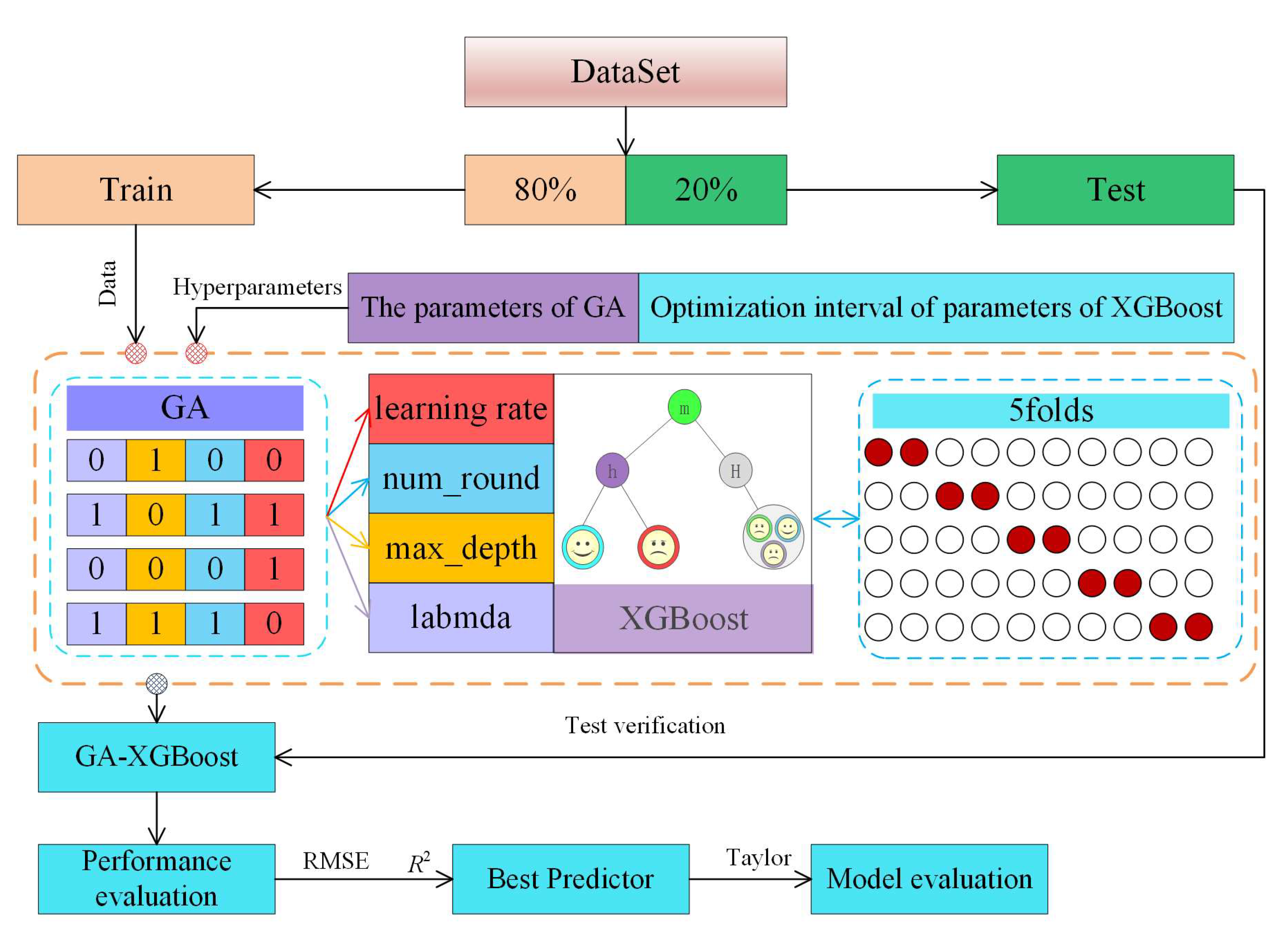
2.4. The Combined Model of GA-XGBoost
3. Materials
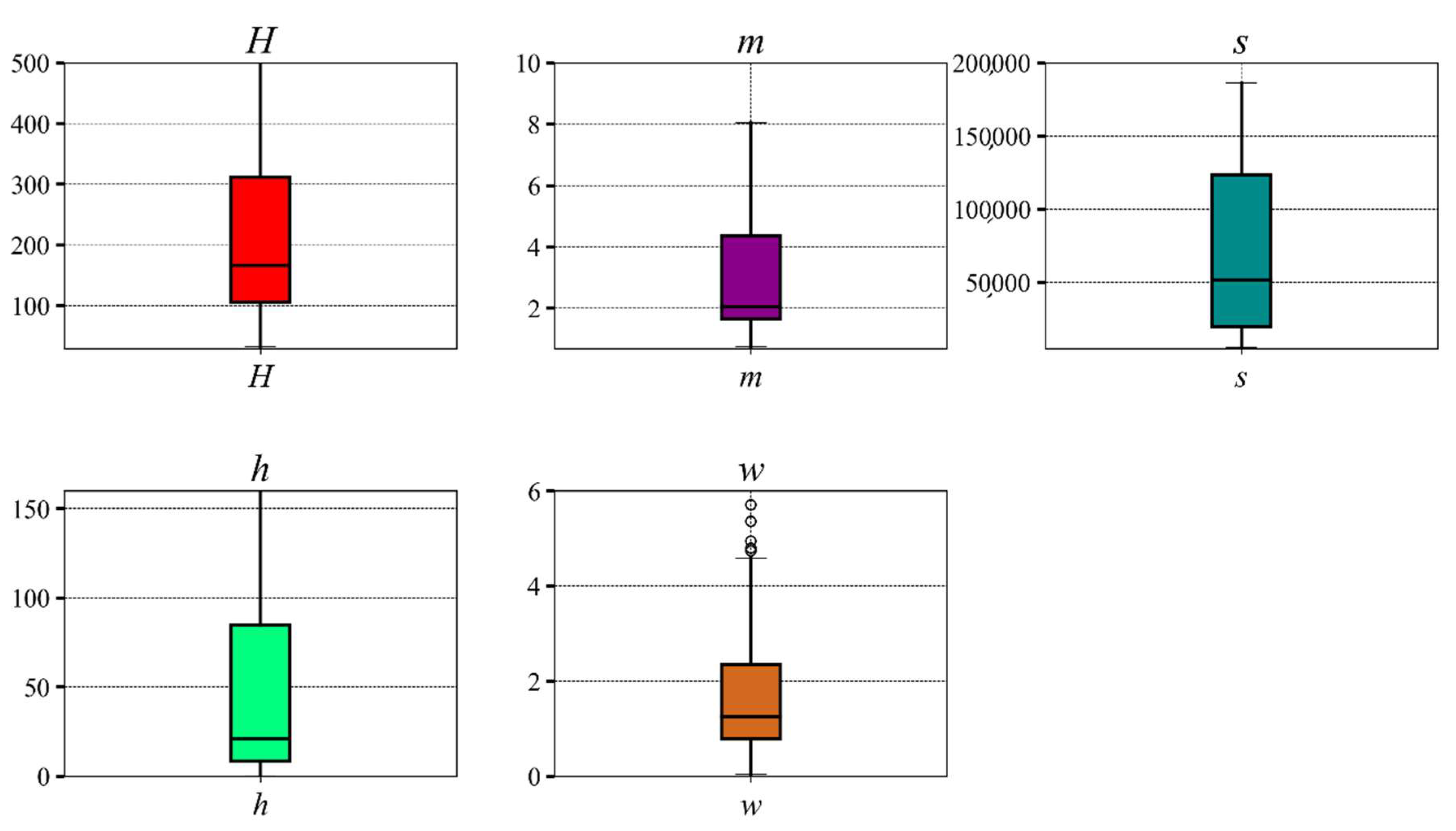
3.1. Data Set
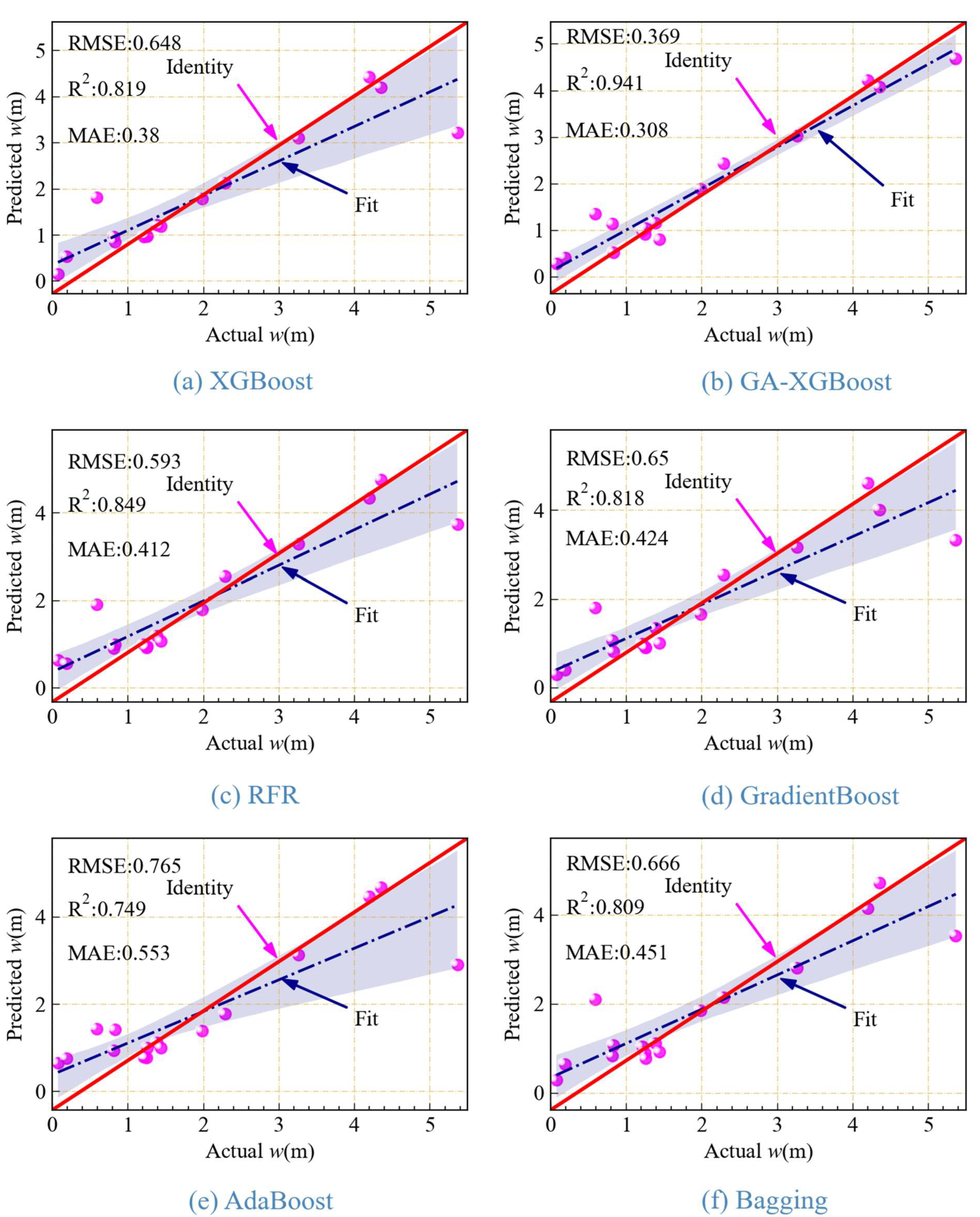
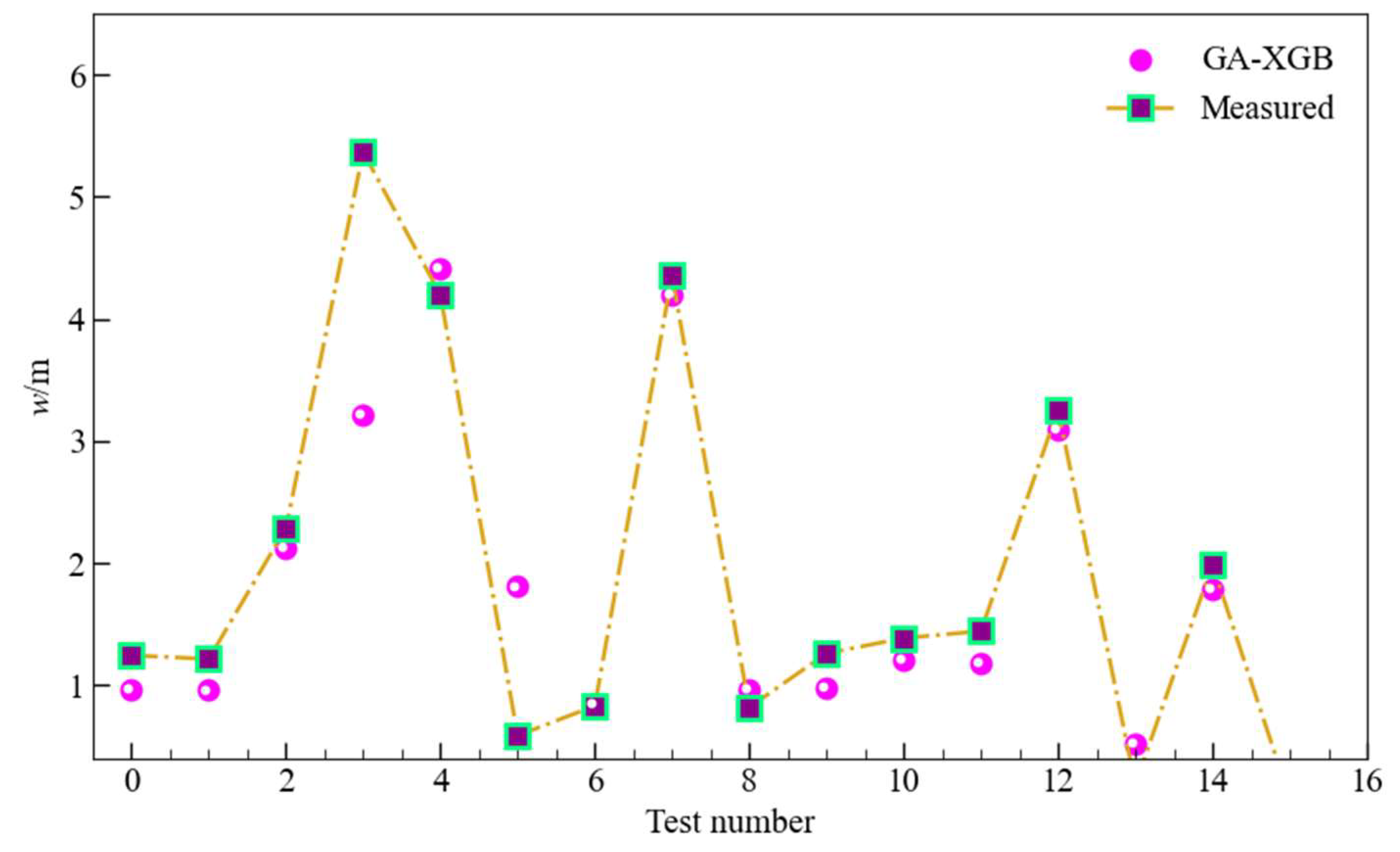
3.2. Model Verification and Evaluation
3.3. Results and Discussion
4. Conclusions
- (1)
- The prediction accuracy of the GA-XGBoost model is higher than that of a single integrated algorithm model such as XGBoost, RFR, Gradient Boost, etc., indicating that it is feasible to use the GA algorithm to optimize the hyperparameters of XGBoost to improve the prediction performance of the model. It is feasible to combine traditional machine learning models with intelligent algorithms to predict mining subsidence.
- (2)
- The essence of GA-XGBoost is to use the search ability of GA to realize the self-adaptation and self-optimization of the XGBoost model, thereby improving the prediction performance. With the continuous enrichment and accumulation of mine data sets, the application scenarios of this model will be more extensive, and more influencing factors can be considered such as: key strata, old empty areas, coal seam dip, dip change rate, thickness change rate, etc. The complex mining area has application value. It can supplement the prediction methods and theories in the field of mine subsidence and provide auxiliary support for the formulation and optimization of relevant mining plans and control measures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, J.-X.; Tang, F.-Q.; Zhao, J.-Y.; Yan, Z.-C. Review of study on mining subsidence and ground surface damage in loess mining area. J. Xi’an Univ. Sci. Technol. 2019, 39, 8. [Google Scholar]
- Dinar, A.; Esteban, E.; Calvo, E.; Herrera, G.; Teatini, P.; Tomas, R.; Li, Y.; Ezquerro, P.; Albiac, J. We lose ground: Global assessment of land subsidence impact extent. Sci. Total Environ. 2021, 786, 147415. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; An, S.; Zhou, D.; Zhan, S.; Gao, Y. Whole basin modeling and parameter inversion of mining subsidence based on UAV photogrammetry technology. Saf. Coal Mines 2022, 53, 179–186. [Google Scholar]
- Zheng, L.; Zhu, L.; Wang, W.; Guo, L.; Chen, B. Land Subsidence Related to Coal Mining in China Revealed by L-band InSAR Analysis. Int. J. Environ. Res. Public Health 2020, 17, 1170. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.-J. Caving and subsidence characteristics and reclamation technology of shallow coal seam mining in the Yellow River Valley. Coal Eng. 2021, 53, 140–144. [Google Scholar]
- Yan, Y.; Yan, W.; Liu, J.; Guo, J. The Prediction Model of Super Large Subsidence in High Water Table Coal Mining Areas Covered with Thick Unconsolidated Layer. Geofluids 2021, 2021, 5520548. [Google Scholar] [CrossRef]
- Zhu, X.-J. Study on Strata Movement Mechanism in Backfill-Strip Mining. Diploma Thesis, China University of Mining and Technology, Beijing, China, 2016. [Google Scholar]
- Deng, W.-N. Data Processing Method of Mining Subsidence Simulation Based on FISH Language. Coal Min. Technol. 2016, 21, 15–17. [Google Scholar]
- Sikora, P.; Wesolowski, M. Numerical assessment of the influence of former mining activities and plasticity of rock mass on deformations of terrain surface. Int. J. Min. Sci. Technol. 2021, 31, 209–214. [Google Scholar] [CrossRef]
- Li, X.; Guo, W.; Zhao, G. Study on influence of compression characteristics of super-thick alluvium on mining subsidence. China Saf. Sci. J. 2018, 28, 135–141. [Google Scholar]
- Niu, Y.; Xu, L.; Zhang, K.; Ye, W.; Zhang, J.; Jiang, B. Study on the Predicted Parameters of Probability Integral Method Based on GA-BP Neural Network. Met. Mine 2019, 10, 93–100. [Google Scholar]
- Xing, X.; Zhu, Y.; Yuan, Z.; Xiao, L.; Liu, B. Predicting mining-induced dynamic deformations for drilling solution rock salt mine based on probability integral method and weibull temporal function. Int. J. Remote Sens. 2021, 42, 639–671. [Google Scholar] [CrossRef]
- Xu, J.-Y. Research on Calculation Model of Mining Subsidence Prediction Parameters Based on Convolutional Neural Network. Diploma Thesis, Liaoning Technical University, Fuxin, China, 2021. [Google Scholar]
- Feng, T.; Wang, C.; Zhang, J. Prediction of Surface Settlement of Foundation Pit Based on ABC-BP Model. J. Hebei Univ. Eng. Nat. Sci. Ed. 2020, 37, 7–12. [Google Scholar]
- Xu, K. Deformation Prediction of Diaphragm Wall of Deep Foundation Pit based on BP Neural Network Improved by Genetic Algorithm. Fly Ash Compr. Util. 2021, 35, 6–11. [Google Scholar]
- Pan, H.; Zhao, Y.; Zhang, W.; Bai, Y.; Han, Y. Prediction of surface subsidence with improved BP neural network based on Adaboost. Coal Sci. Technol. 2019, 47, 161–167. [Google Scholar]
- Sui, L.C.; Ma, F.; Chen, N. Mining Subsidence Prediction by Combining Support Vector Machine Regression and Interferometric Synthetic Aperture Radar Data. ISPRS Int. J. Geo-Inf. 2020, 9, 390. [Google Scholar] [CrossRef]
- Abidin, H.Z.; Djaja, R.; Darmawan, D.; Hadi, S.; Akbar, A.; Rajiyowiryono, H.; Sudibyo, Y.; Meilano, I.; Kasuma, M.A.; Kahar, J.; et al. Land subsidence of Jakarta (Indonesia) and its geodetic monitoring system. Nat. Hazards 2001, 23, 365–387. [Google Scholar] [CrossRef]
- Wang, X.-Y. The Prediction of Mining Subsidence in Mountain Area Based on BP Neural. Diploma Thesis, Taiyuan University of Technology, Taiyuan, China, 2010. [Google Scholar]
- Zhou, J.; Shi, X.; Du, K.; Qiu, X.; Li, X.; Mitri, H.S. Feasibility of Random-Forest Approach for Prediction of Ground Settlements Induced by the Construction of a Shield-Driven Tunnel. Int. J. Geomech. 2017, 17, 04016129. [Google Scholar] [CrossRef]
- Rahmati, O.; Golkarian, A.; Biggs, T.; Keesstra, S.; Mohammadi, F.; Daliakopoulos, I.N. Land subsidence hazard modeling: Machine learning to identify predictors and the role of human activities. J. Environ. Manag. 2019, 236, 466–480. [Google Scholar] [CrossRef]
- Shi, L.; Gong, H.; Chen, B.; Zhou, C. Land Subsidence Prediction Induced by Multiple Factors Using Machine Learning Method. Remote Sens. 2020, 12, 4044. [Google Scholar] [CrossRef]
- Mao, W. Mining Subsidence Prediction Method Based on Genetic BP Neural Network Model. Met. Mine 2016, 45, 164. [Google Scholar]
- Wei, T.; Wang, L.; Li, N.; Chi, S.S.; Jiang, C. Inverse Method of the Parameters of Probability Integral Method Based on Quantum Genetic Algorithm. Met. Mine 2018, 8, 118–122. [Google Scholar]
- Qian, M.; Shi, P.; Xu, J. Mine Pressure and Strata Control; China University of Mining and Technology Press: Beijing, China, 2010. [Google Scholar]
- Deng, K.; Tan, Z.; Jiang, Y.; Dai, H.Y.; Shi, Y. Deformation Monitoring and Subsidence Engineering; China University of Mining and Technology Press: Beijing, China, 2014. [Google Scholar]
- Sun, J. Design of Enterprise Credit Rating Prediction Scheme Based on Improved XGBoost Algorithm. Diploma Thesis, Shanghai Normal University, Shanghai, China, 2021. [Google Scholar]
- Lei, D. Prediction and Analysis of Passenger Flow Sent by a Railway Bureau Based on XGBOOST Algorithm. Diploma Thesis, Southwest Jiaotong University, Chengdu, China, 2020. [Google Scholar]
- Wu, M.-T.; Chen, Q.-S.; Qi, C.-C. Slope safety, stability evaluation, and protective measures based on machine learning. Chin. J. Eng. 2022, 44, 180–188. [Google Scholar]
- Liu, W.-X. Research on Optimization of A Company’s Workshop Layout Based on Genetic Algorithm. Diploma Thesis, China University of Mining and Technology, Beijing, China, 2021. [Google Scholar]
- Gu, X.-L. Application Research of Flexible Job-shop Scheduling Problem Based on Improved Genetic Algorithm. Diploma Thesis, Dalian Jiaotong University, Dalian, China, 2020. [Google Scholar]
- Luo, C.-H. Research on Voltage Optimization Method of Distribution Network Based on Parallel Improved Genetic Algorithm. Diploma Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar]
- Sheng, Y.-H. Study on Surface Movement of Coal Seam Group in Loess Mountain Area. Diploma Thesis, Xi’an University of Science and Technology, Xi’an, China, 2020. [Google Scholar]
- Zhao, Y. Research on Prediction of Surface Subsidence Based on the Adaboost Improved BP Neural Network. Diploma Thesis, Xi’an University of Science and Technology, Xi’an, China, 2019. [Google Scholar]
- Xing, L.; Yuan, X.-T.; Zhang, P. Mining subsidence prediction based on Adaboost-PSO-BP model. Coal Eng. 2020, 52, 141–144. [Google Scholar]
- Yin, Y. Study on Hyper-Spectral Models for Predicting Black Soil Organic Matter Content. Diploma Thesis, Jilin University, Changchun, China, 2015. [Google Scholar]
- Zhou, J.; Qiu, Y.-G.; Khandelwal, M.; Zhu, S.; Zhang, X. Developing a hybrid model of Jaya algorithm-based extreme gradient boosting machine to estimate blast-induced ground vibrations. Int. J. Rock Mech. Min. Sci. 2021, 145, 104856. [Google Scholar] [CrossRef]
- Wang, X.; Qin, J.; Zhang, Q.; Chen, W.J.; Chen, X.L. Mining method optimization of Gu Mountain stay ore based on AHP-TOPSIS evaluation model. J. Cent. South Univ. Sci. Technol. 2013, 44, 1131–1137. [Google Scholar]
- Ganesh, S.; Ramakrishnan, S.K.; Palani, V.; Sundaram, M.; Sankaranarayanan, N.; Ganesan, S.P. Investigation on the mechanical properties of ramie/kenaf fibers under various parameters using GRA and TOPSIS methods. Polym. Compos. 2022, 43, 130–143. [Google Scholar] [CrossRef]
- Jiang, W.; Chen, H. Assessment and projection of changes in temperature extremes over the mid-high latitudes of Asia based on CMIP6 models. Trans. Atmos. Sci. 2021, 44, 12. [Google Scholar]

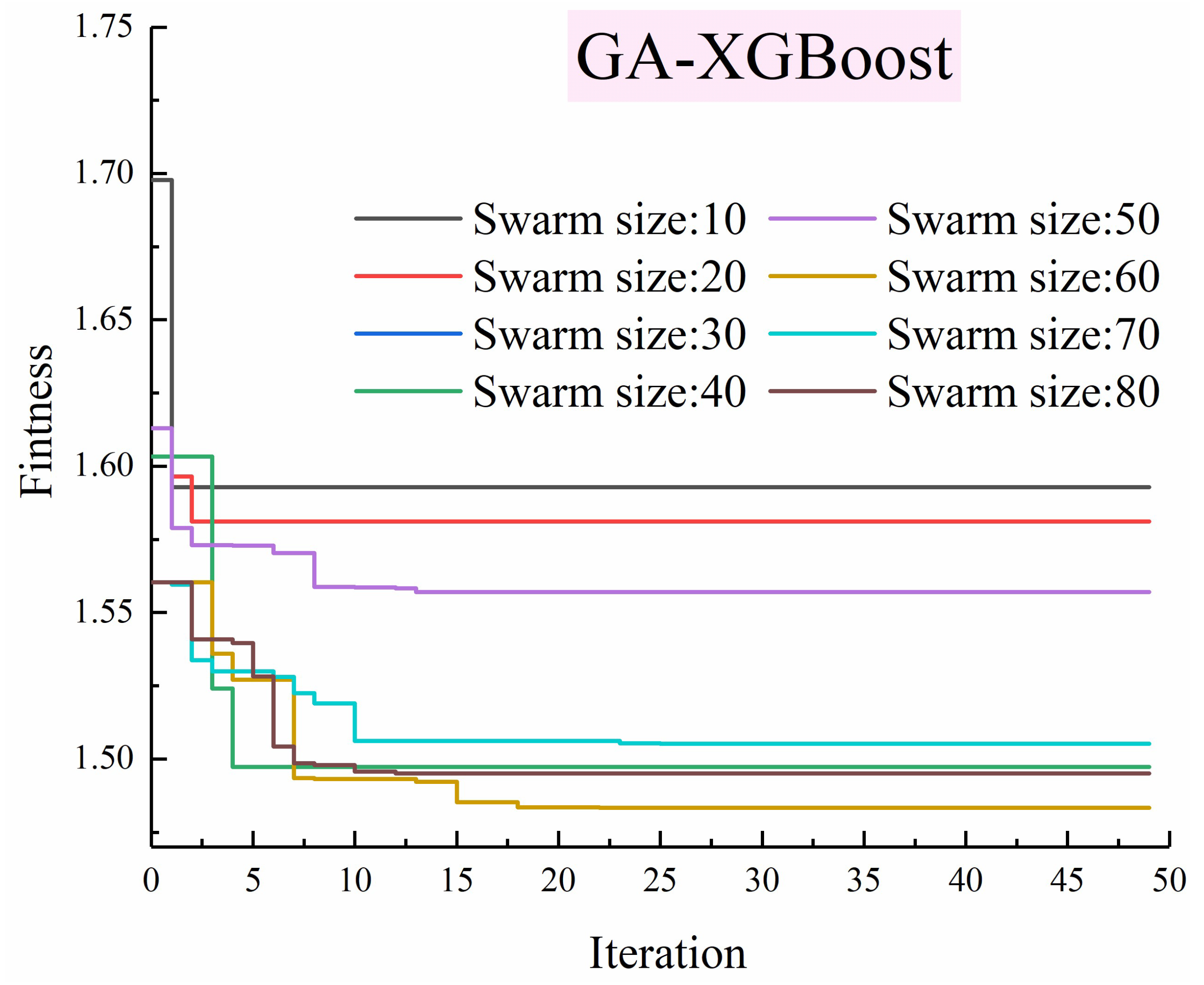

| Swarm Size | RMSE | R2 | MAE | Score | Rank |
|---|---|---|---|---|---|
| 10 | 0.462 | 0.908 | 0.394 | 0.017 | 7 |
| 20 | 0.407 | 0.928 | 0.312 | 0.150 | 4 |
| 30 | 0.386 | 0.935 | 0.287 | 0.193 | 2 |
| 40 | 0.369 | 0.942 | 0.308 | 0.200 | 1 |
| 50 | 0.413 | 0.926 | 0.319 | 0.138 | 5 |
| 60 | 0.405 | 0.929 | 0.347 | 0.129 | 6 |
| 70 | 0.471 | 0.904 | 0.392 | 0.002 | 8 |
| 80 | 0.398 | 0.931 | 0.299 | 0.170 | 3 |
| Model | RMSE | R2 | MAE | Score | Rank |
|---|---|---|---|---|---|
| XGBoost | 0.648 | 0.819 | 0.38 | 0.171 | 5 |
| GA-XGBoost | 0.369 | 0.941 | 0.308 | 0.371 | 1 |
| RFR | 0.593 | 0.849 | 0.412 | 0.189 | 3 |
| GradientBoost | 0.65 | 0.818 | 0.424 | 0.147 | 2 |
| AdaBoost | 0.765 | 0.749 | 0.553 | 0.000 | 6 |
| Bagging | 0.666 | 0.809 | 0.451 | 0.122 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Z.; Cao, M.; Wang, C.; Yu, N.; Qing, H. Research on Mining Maximum Subsidence Prediction Based on Genetic Algorithm Combined with XGBoost Model. Sustainability 2022, 14, 10421. https://doi.org/10.3390/su141610421
Gu Z, Cao M, Wang C, Yu N, Qing H. Research on Mining Maximum Subsidence Prediction Based on Genetic Algorithm Combined with XGBoost Model. Sustainability. 2022; 14(16):10421. https://doi.org/10.3390/su141610421
Chicago/Turabian StyleGu, Zhongyuan, Miaocong Cao, Chunguang Wang, Na Yu, and Hongyu Qing. 2022. "Research on Mining Maximum Subsidence Prediction Based on Genetic Algorithm Combined with XGBoost Model" Sustainability 14, no. 16: 10421. https://doi.org/10.3390/su141610421
APA StyleGu, Z., Cao, M., Wang, C., Yu, N., & Qing, H. (2022). Research on Mining Maximum Subsidence Prediction Based on Genetic Algorithm Combined with XGBoost Model. Sustainability, 14(16), 10421. https://doi.org/10.3390/su141610421





