A Study on Safety Evaluation of Pedestrian Flows Based on Partial Impact Dynamics by Real-Time Data in Subway Stations

Abstract

With the rapid development of urban rail transit, the scientific assurance of pedestrian safety has become an important issue. Orderly behavior is a crucial factor affecting pedestrian safety. Therefore, in-depth research into pedestrian behavior is needed. This study carries out an evaluation of safety in pedestrian flows by establishing a new force model based on real-time data. In this model, we consider the microscopic characteristics of pedestrians and define four force influence mechanisms for simulating pedestrian behavior. Compared with existing models, this model incorporates partial impact dynamics to make it applicable to the particular environment of subway stations. Through the validation of real-world data, it is demonstrated that the model can accurately describe pedestrian behavior and better reproduce the characteristics of pedestrians. The influence of pedestrians and of environmental factors on the model are also discussed. Using our model, we propose a risk evaluation system based on pedestrian volatility. By using real-time pedestrian information from subway stations, the potential risk to pedestrians can be discerned and assessed in advance. This research advances the management of pedestrian safety and provides a framework for studying behavior models and for safety evaluation.

1. Introduction

The first passenger transport subway offering large-capacity, electric-powered rail transit was launched in 1863 in London, England, marking the birth of urban rail transit as a public passenger transport system guided by a track structure within a city or metropolitan area. The subway quickly became a new power in urban rail transportation because of advantages such as speed, large capacity, and environmental protection [1]. As urbanization accelerates, more cities continue to acquire subway networks, and such services have a standard for measuring the development of urban transportation [2]. Increasing numbers of people choose it as a means of daily travel. In China, as of 2021, 48 cities have opened urban rail transit, with 223 subway operating lines and 7664.0 km of operational route [3]. The rail transit systems of cities, including all related facilities that serve urban passenger traffic, have recently progressed towards heavier passenger flows and higher passenger density [4]. As an example, in 2021, the rail transit system in Shanghai had a network operating mileage of 831 km, with an average daily passenger volume of 7,745,100, and now leads the world in the scale of its subway network [3].

Subway stations are confined underground areas and gathering places for high-density crowds, with safety hazards and risks everywhere [5]. Factors affecting safety in stations include people (pedestrians), the environment (natural disasters, terrorist attacks), equipment (damage to electrical equipment, traffic accidents), management (staff control of the station), and layout (geometrical and functional characteristics of stations) [6]. Among these, pedestrians are the active subjects of stations, and their behaviors have uncontrollable characteristics, including randomness and uncertainty [7,8]. The behavior of pedestrians is closely related to their safety. Safety exercises consider whether or not pedestrians follow specific rules, resulting in orderly behaviors such as queuing, showing courtesy, and strolling; or disorderly behaviors such as crowding, trampling and panic. Accidents caused by disorderly pedestrian behavior have serious consequences, directly leading to economic losses and serious injuries [7]. In recent times, accidents in subway stations caused by disorderly pedestrian behavior have occurred repeatedly.

Table 1. Recent accidents involving pedestrians at subway stations worldwide.

Year	Place	Description	Consequence
2019	Mexico City, Mexico	an escalator did not stop in time, resulting in congestion of passengers at the elevator entrance	two people were slightly injured
2018	Rome, Italy	pedestrians disrupted the operation of an escalator	a severe stampede injured thirty people
2018	London, England	staff handled a suspicious package and caused a small explosion, and people crowded in panic	a chaotic situation resulted in five injuries
2017	Shenzhen, China	a passenger collapsed, resulting in pedestrians crowding and rushing each other	pedestrians were thrown into a significant panic
2017	Mumbai, India	at the peak of passenger flow, people were crowded and pushed	22 personal deaths were caused

summarizes recent accidents involving disorderly behavior of pedestrians at subway stations worldwide. It can be readily understood that orderly pedestrian behavior improves the efficiency of pedestrian behavior in everyday travel and also ensures an optimal response to situations of risk, including evacuation situations. It thus represents an essential factor affecting pedestrian safety.

In response to the kind of safety problems at subway stations described above, safety management measures have been introduced, such as security checks for pedestrians [9] and supervision using video surveillance [10]. However, such management measures do not fundamentally address the issue of pedestrian safety and cannot identify potential risks in advance [11]. With the frequent occurrence of pedestrian accidents in subway stations, scholars have gradually recognized that understanding pedestrian behavior is crucial to improving their safety [12,13]. For this reason, many studies have attempted to explore the impact of pedestrian behavior on safety. Liu et al. [14] analyzed pedestrian behavior at both motivation and decision levels to enhance the safety and orderliness of pedestrians in an evacuation scenario. Through experiments, the study summarized the path selection behaviors of pedestrians during their escape. In pedestrian–vehicle interactions, Rasouli et al. [15] described pedestrians’ crossing behavior from two perspectives: the way pedestrians communicate with drivers, and the related influencing factors. The study sought to avoid collisions by characterizing the behaviors of pedestrians. Moussaid et al. [12] pointed out that simple pedestrian behavior can produce a risk of crowd disasters, and that understanding pedestrian dynamics ensures the safety of mass activities, thus laying the foundation for realistic models of pedestrian behaviors.

To characterize pedestrian behavior, scholars have developed pedestrian models [16], including macroscopic models (fluid-dynamic) [17,18], microscopic models (cellular automata) [19], a lattice gas model [20]), and hybrid models (heuristics) [12]. Helbing proposed the social force model (SFM) [21], which became the foundation of continuous microscopic pedestrian models. The SFM considers personal psychology in its consideration of force and demonstrates that pedestrian behavior results from the interaction between individuals and forces. Although the SFM is effective for simulation in generic scenarios, it lacks specificity for particular systems, making it challenging for the model to be fully applied for operational usage in a specific environment [22]. However, in practical applications, the pedestrian model often needs to be applied to different traffic scenarios, so scholars have tried to improve the SFM. Guo et al. [23] considered the resistance in the social force resulting from the operation of pedestrian crossings and added the force on pedestrians generated by the green light countdown. The results show that an enhanced SFM promotes pedestrian safety at signal crossings by analyzing the behavioral characteristics of pedestrians. Han et al. [24] proposed a message transfer mechanism to modify the SFM, reproducing pedestrians’ behavior in an emergency evacuation. The revised model avoided collisions between pedestrians and enabled them to choose the appropriate direction during the escape. On the other hand, Charitha et al. [25] calibrated the SFM for mixed traffic of personal mobility vehicles and pedestrians by experimentally collecting data, thus reflecting the potential of the SFM to simulate mixed traffic.

Simulation is a powerful way to verify pedestrian behaviors and models [26], providing data support for safety evaluation. Some pedestrian simulation software (PTV Viswalk [27], Anylogic [28], Legion [29]) has become available, greatly facilitating scholars’ exploration of pedestrian behaviors [26]. Krivda et al. [30] used PTV Viswalk to analyze pedestrian activities in different areas, thereby improving the functionality of traffic nodes. Zeng et al. [31] designed an intelligent passenger organization system using Anylogic to deal with unexpected accidents in stations. Chen et al. [32] carried out model calibration using Legion to identify measures for alleviating congestion in stations.

In summary, many articles point to the research efforts needed for further exploring pedestrian behaviors, so that models that improve their safety can be developed. However, behavioral models of pedestrian behaviors in subway stations are relatively scarce, and few studies have evaluated pedestrian safety from the perspective of pedestrian behavior and models. This study establishes a method of safety evaluation for pedestrian flow in subway stations. We construct a pedestrian behavior model based on characteristics analysis and evaluates pedestrian risk. We argue that the construction of the pedestrian model is based on the study of actual pedestrian behavior characteristics. The core of pedestrian behavior results from the joint action of individuals and the environment. Therefore, analyzing the microscopic features of pedestrian behavior should be used as the basis for determining pedestrian behavior logic. Concerning the SFM, because it is essential to consider different forces when determining the influence of the environments on pedestrians, we define partial impact dynamics within the model. We assess the effect of various factors upon pedestrian behavior by improving the original force structure and introducing new forces. Through the pedestrian model, we explore the influence of pedestrian behavior volatility upon their safety. Using real-time data, we judge and assess potential risks for pedestrians. Our study verifies the effectiveness of the pedestrian model through simulations and case studies and provides a reference basis for scientifically securing the safety of pedestrians.

2. Methodology and Models

2.1. Characteristics Analysis

Pedestrian flow is random and flexible, and the characteristics of pedestrians are different in various traffic environments. To manage the safety of pedestrians, it is essential to analyze their behaviors in specific environments. This paper describes the characteristics of pedestrians in subway stations, which form the basis for construction of the behavior model.

Hoogendoorn et al. [33] established normative pedestrian behavior theory with strategic, tactical, and operational levels, illustrating the microscopic nature and psychological characteristics of pedestrian behaviors. On the pedestrian behavioral levels, the behavior of higher levels determines that of lower levels, whereupon lower-level behaviors feedback upon higher levels for further influence. This study applies pedestrian behavior theory to analyze the characteristics of pedestrian behavior and develop an analysis of pedestrian behavioral levels in subway stations.

1. Strategic level. Behavior on the strategic levels refers to the intention made by pedestrians according to their needs which is the internal motivation to generate movement [33]. Generally, pedestrians in subway stations have a specific purpose such as making a ride, transferring between trains, or purchasing tickets. Compared with pedestrian flow in other scenarios, pedestrians in subway stations have more definite destinations or target behaviors. Therefore, we assume that pedestrians have pre-defined origins and destinations in subway stations; that is, they have definite OD (O-Origin, D-Destination). Note that if pedestrians are at an intermediate station on their journey, they too have a definite OD (origin and destination of transfer) [34].

2. Tactical level. The tactical level includes the behaviors that pedestrians make to achieve the goals set at the strategic level, which are affected by external and personal factors [33]. The input to the tactical level is the behavior of the strategy level; that is, the definite OD of pedestrians in subway stations. Specifically, pedestrians have already defined their origins and destinations and now need to perform route choice behavior at the tactical level. The factors that influence pedestrians’ route choice behaviors are summarized as: economy (charges, operating expenses), time (travel time, queue time), environment (congestion, queue length), and individual (age, personal habits) [35]. We assume that time factors influence pedestrians’ route choice behavior in subway stations because they are driven by a definite OD. Some scholars [36,37] similarly choose the shortest travel time to constrain the route choice behavior of pedestrians. Therefore, on the tactical level, we define the behavior of pedestrians as choosing the route that minimizes travel time.

3. Operational level. The operational level is the specific behavior of pedestrians that is performed to achieve targets based on the tactical level [33]. The decisions made at tactical levels serve as the inputs for pedestrians’ operational levels and determine their walking behaviors. The fact that pedestrians at subway stations choose the route with the shortest time makes pedestrians willing to ignore unimportant factors to achieve their goals. For example, pedestrian flow in subway stations is high during peak hours, and it is common for pedestrians to crowd each other [38]. Typically, pedestrians expect to keep a certain spatial distance from others [39]. However, in subway stations, pedestrians are willing to tolerate mutual crowding to reach their destinations quickly, and the space required for individuals can be compressed. The tolerance of squeezing behavior among pedestrians in subways is much greater than in other traffic settings such as intersections and pedestrian crossings. Moreover, pedestrians in subway stations are less sensitive to avoiding obstacles than in other scenarios and are reluctant to avoid such barriers in advance. Some scholars [38,40] also claim that pedestrians choose to ignore secondary factors to achieve their primary target. Thus, the behavior at the operational level includes high tolerance of pedestrian contact and low sensitivity behavior with regard to obstacles.

2.2. Behavior Model

2.2.1. Social Force Model

The social force model (SFM) assumes that the force on pedestrian $i$ is $F_i$, consisting of self-driven and interaction forces. In the model, the influence on pedestrian $i$ is the force acting on itself, other pedestrians, and the environment together, and the equation is shown in Equation (1):

$$F_i=m_i\frac{d{v}_i}{dt}=f_{will}+{\displaystyle \sum }_{j\left(\ne i\right)}{f}_{ij}+{\displaystyle \sum }_W{f}_{iw}$$

(1)

$$f_{will}=m_i\frac{v_i^0\left(t\right)e_i^0\left(t\right)-v_i\left(t\right)}{{\tau }_i},$$

(2)

$f_{will}$ is the self-driving force of pedestrians. Within this, $m_i$ is the mass of pedestrian $i$; $v_i^0\left(t\right)$ and $v_i\left(t\right)$ are the desired speed and actual velocity of pedestrian $i$; $e_i^0\left(t\right)$ is the direction of the desired speed; and ${\tau }_i$ is the characteristic time.

$$f_{ij}=\left\{A_i\exp \left[\frac{r_{ij}-d_{ij}}{B_i}\right]+kg\left(r_{ij}-d_{ij}\right)\right\}{n}_{ij}+ҡg\left(r_{ij}-d_{ij}\right)\Delta v_{ji}{t}_{ij},$$

(3)

$f_{ij}$ is the interaction force between pedestrians, where $A_i\exp \left[\frac{r_{ij}-d_{ij}}{B_i}\right]n_{ij}$ is the repulsive interaction force between pedestrians; $kg\left(r_{ij}-d_{ij}\right)n_{ij}$ is the body force; and $ҡg\left(r_{ij}-d_{ij}\right)\Delta v_{ji}{t}_{ij}$ is the sliding friction force.

Here, $A_i,B_i, k, ҡ$ are constants; $r_{ij}$ is the sum of the model radii of pedestrians $i$ and $j$; $d_{ij}$ is the distance between pedestrians’ centers of mass; $n_{ij}$ and $t_{ij}$ represent the direction vector and tangential direction vector between pedestrians, and $\Delta v_{ji}$ is the tangential velocity difference between pedestrians. Specifically, $g\left(x\right)$ is a segmentation function, where $g\left(x\right)=x$, if there is body contact between pedestrians; otherwise, $g\left(x\right)=0$.

$$f_{iw}=\left\{A_i\exp \left[\frac{r_i-d_{iw}}{B_i}\right]+kg\left(r_i-d_{iw}\right)\right\}{n}_{iw}-ҡg\left(r_i-d_{iw}\right)\left(v_i·t_{iw}\right)t_{iw}$$

(4)

$f_{iw}$ is the interaction force between pedestrians and walls, and $r_i$ is the radius of pedestrian $i$; $d_{iw}$ is the distance between pedestrians and walls; and $n_{iw}$ and $t_{iw}$ are the direction vector and tangential direction vectors pointing to pedestrians from walls.

The SFM aims at a generalized traffic scenario without absolute applicability to specific environments. In this study, to study the safety of pedestrian flow in subway stations, we need to construct an SFM that conforms to the characteristics of this specific setting. We shall now define the following four mechanisms of force influence that constrain social forces to simulate the behavior of pedestrians in subway stations. Our task involves changing the structure of forces and adding new forces. Therefore, we define this improved model of social forces as the Partial Impact Social Force Model (PI-SFM).

2.2.2. Self-Driving Force

Pedestrians in subway stations have the characteristics of definite OD, which is essentially the pedestrian psychological drive for OD. So, the self-driving force should account for a more significant proportion of the social force. This study introduces the OD factor, ${\omega }_i\left(t\right)$, to correct the desired speed of pedestrians, where ${\omega }_i\left(t\right)ϵ\left(0,1\right)$. Specifically, a better use of OD factors denotes pedestrians’ higher purposeful and desired speed. It is assumed that influences related to ${\omega }_i\left(t\right)$ include: the pedestrian’s personal characteristics and requirements ${\omega }_1$ (the urgency of the pedestrians’ need to reach their destination, which is a constant); the surrounding environment ${\omega }_2$ (the distance from the pedestrians’ positions to their destinations, which is a constant); and the duration of stay within subway stations ${\omega }_3\left(t\right)$ (which is a function of time $t$). All the above influences are positively correlated with ${\omega }_i\left(t\right)$. The improved equations for the self-driving force and desired speed are expressed in Equations (5)–(7):

$${\omega }_i\left(t\right)={\omega }_1{\omega }_2{\omega }_3\left(t\right),$$

(5)

$$v_i^{0S}\left(t\right)={\omega }_i\left(t\right)v_{i,1}\left(t\right)+\left[1-{\omega }_i\left(t\right)\right]v_{i,2}\left(t\right),$$

(6)

$$f_{will}^S=m_i\frac{v_i^{0S}\left(t\right)e_i^0\left(t\right)-v_i\left(t\right)}{{\tau }_i},$$

(7)

Here, ${\omega }_i\left(t\right)$ is set to 0.6; $v_i^{0S}\left(t\right)$ is the improved value of desired speed; $v_{i,1}\left(t\right)$ is the speed of pedestrians in an emergency, which takes the value $2 \mathrm{m}/\mathrm{s}$ [41]; and $v_{i,2}\left(t\right)$ is the speed of pedestrians in the absence of an emergency, which takes the value $1 \mathrm{m}/\mathrm{s}$ [41].

2.2.3. Force on Pedestrians

In the SFM, the interaction force between pedestrians consists of repulsive interaction force, body force, and sliding friction force. Generally, the repulsive interaction force is described as the social interaction force (SIF), while the body and sliding friction forces are defined as physical interaction forces (PIFs). The high purposefulness of pedestrians in subway stations results in high levels of tolerance for otherwise inappropriate behavior such as close physical contact and squeezing between themselves and others. This is reflected in our model by decreasing the required repulsive distance between pedestrians, which reduces the SIF between them. Hence the weight of SIF in social forces ought to be appropriately reduced. The study sets the threshold of the pedestrians’ squeeze. We assume that the SIF will be triggered only when the distance between pedestrians exceeds the threshold. The equation of interaction force between pedestrians is shown in Equation (8):

$$f_{ij}^S=\{\begin{array}{c}0, r_{ij}\le d_{ij} \\ f_{ij}^{physic}, r_{ij}-2S_{max}<d_{ij}<r_{ij},\\ f_{ij}^{social}+f_{ij}^{physic}, d_{ij}\le r_{ij}-2S_{max}\end{array}$$

(8)

Here, $S_{max}$ is the threshold of the pedestrians’ squeeze and is set to $0.2r_{ij}$ [42]. The mechanism of the improved interaction forces is as follows: if the distance is less than the sum of the pedestrians’ radius but does not reach the threshold, there are only PIFs between pedestrians; when the distance exceeds the threshold of the pedestrians’ squeeze, there are both PIFs and SIF; otherwise, there are neither PIFs nor SIF.

2.2.4. Force on Obstacles

The definite OD of pedestrians in subway stations makes them less sensitive to obstacles. Pedestrians do not focus on the position of obstacles and perform avoidance behaviors too early when walking. Hence, the role of the interaction force between pedestrians and obstacles in the social force is appropriately decreased. This study applies the concept of “respect area” [39] to the interaction force, being defined as the space needed by the pedestrian’s personal psychology, as shown in Figure 1. We assume that the interaction force is triggered only when the obstacle enters the respect area. Otherwise, there is no force between pedestrians and obstacles. The interaction force is then simplified to relate to the distance between pedestrians and obstacles. The improved equation for the interaction force between pedestrians and obstacles is expressed in Equations (9)–(11):

$$D_{Ri}=R_F·r_i,$$

(9)

$$d_{safe}=2D_{Ri},$$

(10)

$$f_{iw}^S=\{\begin{array}{c}0, d_{iw}\ge d_{safe} \\ \frac{d_{safe}-d_{iw}}{d_{iw}}\left(r_i-d_{iw}\right)n_{iw}, d_{iw}<d_{safe}\end{array},$$

(11)

Here, $D_{Ri}$ is the respect spacing; $R_F$ is the respect factor and set as 0.7 [39]; and $d_{safe}$ is the safe distance between pedestrians and obstacles.

2.2.5. Force on Signs

Indicator signs in subway stations have a guiding effect on pedestrians, who determine the location of targets and their direction according to the signs. Therefore, the force upon pedestrians is also influenced by the interaction force of indication signs as well as the social force. The study analogizes the coulomb force $F=k\frac{q_1{q}_2}{r^3\overrightarrow{r}}$ and defines the interaction force between pedestrians and indicator signs as a function related to magnetic pole strength and distance. We set the OD factor ${\omega }_i\left(t\right)$ to characterize the magnitude of the magnetic pole strength $q_1·q_2$ because the stronger the pedestrians’ purpose, the more the interaction force of indication signs increases. The equation for the interaction force between pedestrians and indicator signs is in Equation (12):

$$f_{is}^S=\frac{{\omega }_i\left(t\right)}{d_{is}·n_{is}},$$

(12)

where, $d_{is}$ is the distance between pedestrians and signs; and $n_{is}$ is the direction vector between pedestrians and signs.

In summary, the PI-SFM developed in this study is expressed in Equation (13):

$$F_i^S=f_{will}^S+f_{ij}^S+f_{iw}^S+f_{is}^S.$$

(13)

2.3. Risk Evaluation

Our study considers pedestrian characteristics and models of pedestrian behaviors in subway stations, from which we analyze the factors related to pedestrian safety. We perform a risk evaluation of pedestrians to standardize and systematize safety management. We use the analytic hierarchy process (AHP) to evaluate the risk to pedestrians. AHP is an assessment method applied to complex decision systems with multiple indicators, from qualitative to quantitative analysis [43].

The characteristic of pedestrians with definite OD is proposed in this paper. In terms of specific detail, the safety of pedestrians is reflected in the smooth completion (without other disturbances) of behaviors in the definite OD, which means the reaching of a destination at the desired speed in the expected time. However, pedestrian behavior is bound to be disturbed by the external environment. In addition, the movement of pedestrians generates unavoidable fluctuations with possible impacts upon safety and reliability. Therefore, we explore the influence of pedestrian fluctuations on risk and propose the risk factors of changes.

A data-driven approach helps to scientifically assess the safety of pedestrian flows. Pedestrians themselves provide a large amount of dynamic data in their walking behaviors. Real-time information characterizes pedestrian behavior and can also reflect fluctuations in behavior. By acquiring and integrating pedestrian information, managers can facilitate the behavioral trends of pedestrians and make advance judgments about risks. This study therefore assesses pedestrian risk based on data-driven approach, and constructs an evaluation of risk to pedestrians based on AHP, as follows:

1. Construction of hierarchical structure. We construct a three-level structure model consisting of target level, criterion level, and element level. The fluctuation of pedestrians is mainly caused by the interference of external environments [44]. After being disturbed, pedestrians’ behavior fluctuates in temporal and spatial dimensions. The movement time and speed provide valuable information for behavior analysis [45] and reflect the degree of interference. Similarly, travel distance and crowd density intuitively describe the behavior state and reflect the influence of interference on pedestrian behavior [46]. Therefore, we choose movement time and speed to represent the temporal fluctuation, while travel distance and crowd density show the spatial fluctuation. We define the element level factors as indicators describing the pedestrian fluctuation (FI) acquired by dynamic information of pedestrians in stations. Figure 2 shows the hierarchy of risk evaluation.

2. Calculation of elements’ weights. In the hierarchical structure, it is necessary to determine the importance of different elements in the target. In addition, the elements’ weights are determined by the calculation of the comparative judgment matrix. AHP introduces the numbers from 1–9 as the scale to characterize the relative importance of two elements for the target, enabling the construction of a comparative judgment matrix. The study quantifies the extent of FI for risk evaluation, and

Table 2. Comparative judgment matrix.

	Temporal Fluctuation	Spatial Fluctuation
Temporal fluctuation	1	2
Spatial fluctuation	1/2	1
	T	V
T	1	2
V	1/2	1
	S	P
S	1	4
P	1/4	1

Note: $a_{ij}=1$ means that element $i$ is equally important as $j$, and so on (more significant numbers indicate that factor $i$ is more important), $a_{ij}=9$ means that element $i$ is more important than $j$. The values of 2, 4, 6 and 8 are intermediate values between adjacent cases.

gives comparative judgment matrices for temporal and spatial FI, respectively. Subsequently, we adopt the square root method to calculate the comparative judgment matrix of FI and obtain element weights. The square root method is commonly used to calculate the relative importance of elements through the judgment matrix. The calculation steps are as follows: (1) multiply the elements of the judgment matrix by rows to obtain a new vector; (2) take each component of the new vector to the n power; (3) normalize the obtained vector to be the weight vector. The equation for weight calculation is shown in (14). Figure 2 shows the symbols and weights of FI.

$$P_i=\frac{\sqrt[n]{{{\displaystyle \prod }}_{j=1}^n{a}_{ij},}}{{{\displaystyle \prod }}_{i=1}^n\sqrt[n]{{{\displaystyle \prod }}_{j=1}^n{a}_{ij},}}, i=1,2,\cdots ,n,$$

(14)

where, $a_{ij}$ is the relative importance of element $i$ and element $j$; and $P_i={\left(P_1, P_2,\cdots ,P_n\right)}^T$ is the weight occupied by element $i$. The matrix formed by $a_{ij}$ is the judgment matrix $A{\left(a_{ij}\right)}_{n\times n}$, where n is the number of elements.

3. Quantitative analysis of elements. We assign values to FI and evaluates the risk to pedestrians on a quantitative level. We use numbers 1–5 to indicate levels of FI risk in descending order, so that higher quantitative values represent higher levels of risk.

Table 3. Quantification of FI for the risk evaluation.

	5	4	3	2	1
T	serious delay	high delay	obvious delay	a little delay	no delay
V	severe fluctuations	high fluctuations	obvious fluctuations	a little fluctuation	no fluctuations
S	serious deviation	high deviation	obvious deviation	a little deviation	no deviation
P	severe congestion	high congestion	obvious congestion	a little congestion	no congestion

shows the quantification of FI for the risk evaluation.

Definition and statement:

• The delay of movement time is the difference between the actual movement time of pedestrians and the ideal time, representing the efficiency of behaviors.
• The fluctuation of movement speed is the difference between the actual movement speed of pedestrians and their average speed, which denotes speed uniformity.
• The offset of travel distance is the difference between the actual walking path of pedestrians and the shortest possible path and indicates the fluctuation of trajectory.
• The crowd density is the number of pedestrians per unit area, expressing the objective environment during movement.

From Table 3, we can see that the risk to pedestrians is highest when they experience severe delays in movement time, variable movement speed, many pedestrian detours, winding walking trajectories, and high flow. Therefore, the quantitative analysis of elements provides a basis for quantifying risk evaluation.

4. Rating evaluation of risk. We introduce the indicator of fluctuation risk index (FRI) to evaluate the risk of pedestrians. The FRI measures pedestrian risk from the temporal/spatial fluctuations dimension, and takes values in the range [1,5]. The equation is given in Equation (15). Specifically, a larger FRI shows a higher risk to pedestrians, when different levels of safety measures need to be taken to ensure their safety. We divide the risk rating into five classes.

Table 4. Reference form for safety evaluation.

Risk Level	Color	FRI	Risk Evaluation
Level 1	blue	1–2	Basic security, no need to take measures
Level 2	green	2–3	General risk, take certain safety measures
Level 3	yellow	3–3.5	Moderate risk, safety measures should be taken
Level 4	orange	3.5–4	High risk, take safety measures as soon as possible
Level 5	red	4–5	High risk, take immediate safety measures

identifies the relationship between FRI and risk levels and establishes a reference form for safety evaluation.

$$FRI=0.444T+0.222V+0.2667S+0.0667P.$$

(15)

In summary, managers first acquire real-time dynamic data, including movement time, speed, travel distance, and crowd density, when assessing the risk of pedestrians in a subway station. Then, the FRI is obtained by determination of quantitative values and weights of the risk factors. Finally, managers consult the reference form’s and take safety measures appropriate to the risk level.

2.4. Overall

Our study considers the safety evaluation for pedestrian flow in subway stations, and the data flow chart of our research is shown in Figure 3. We elaborate on the characteristics of pedestrians on three levels based on the behavior theory. Applying these features, we define the partial impact dynamics in terms of four aspects and constrains the behavior model of pedestrians. Subsequently, the pedestrian risk is assessed using AHP based on real-time data. This method enables a practical judgment of pedestrian risks and helps appropriate decision-makers to take safety measures in advance.

3. Experiments and Results

3.1. Simulations

We carry out a simulation of the PI-SFM using Python to explore its performance. To verify the superiority of the PI-SFM, we compare the simulation with the original SFM. The simulation shows 30 pedestrians moving toward the exit in a room with dimensions of $20 \mathrm{m}\times 20 \mathrm{m}$ and an exit width of $2 \mathrm{m}$. The two models (SFM and PI-SFM, respectively) are applied in the scenario. We set the exit of the room as the destination of the pedestrians, the walls of the room as the obstacles, and the location of indicating signs at the entrance. At the beginning of the simulation, pedestrians are randomly distributed in any position in the room, and the simulation ends when all pedestrians leave the room. The scenario details are shown in Figure 4.

Table 5. Parameters of the two models.

Symbol	Description	Value
$m_i$	mass of the pedestrian	$80 \mathrm{kg}$
$r_i$	the radius of the pedestrian model	$U\left(0.39, 0.51\right)$
${\tau }_i$	characteristic time	$0.5 \mathrm{s}$
$A_i$	coefficient of repulsive interaction force	$2000 \mathrm{N}$
$B_i$	coefficient of repulsive interaction force	$0.08 \mathrm{m}$
$k$	coefficient of body force	$1.2\times {10}^5 \mathrm{kg}/{\mathrm{s}}^2$
$ҡ$	coefficient of sliding friction force	$2.4\times {10}^{5 }\mathrm{kg}/\left(\mathrm{m}·\mathrm{s}\right)$

gives descriptions and values of parameters in the two models.

3.1.1. Model Validation

This study validates the PI-SFM, both in the presentation of figures and the analysis of results. In general, pedestrian behavior exhibits self-organization phenomena. Self-organization is the macroscopic performance of the microscopic characteristics of individuals [47], expressed as the total of non-linear behaviors that pedestrians perform to reach their destinations. At bottlenecks (doors, elevators, etc.), pedestrians exhibit aggregation and stagnation behaviors due to a sudden decrease in the flow speed. They pass through such bottlenecks sequentially, in a similar way to the typical self-organization of a “ticking hour glass” [48]. Figure 4 presents a set of figures on the evolution of pedestrian behavior over time based on the PI-SFM. It can be observed from the figure that pedestrians continuously gather at the exit and pass through the entrance in turn, which shows that the PI-SFM simulates the self-organization of pedestrian flow well, therefore proving its correctness.

We can now provide comparisons of outputs to demonstrate the rationality and effectiveness of the PI-SFM. We calculate the indicators describing the pedestrian fluctuation (FI), including average pedestrian movement time, movement speed, travel distance, and exit density. We also determine a series of measures to reflect the optimization of the PI-SFM.

Table 6. Values of measures in the two models.

Measure	Unit	SFM	PI-SFM
Average movement time, $\overline{t}$	$\mathrm{s}$	43.23	31.78
Average movement speed, $\overline{v\left(t\right)}$	$\mathrm{m}/\mathrm{s}$	1.12	1.46
Average travel distance, $\overline{s}$	$\mathrm{m}$	48.42	46.40
Exit density, $\rho$	$\mathrm{people}/{\mathrm{m}}^2$	0.83	2.13
Variance of movement speed, $var\left(v\left(t\right)\right)$	$\mathrm{m}/\mathrm{s}$	0.55	0.32
Average self-driving force, $\overline{f_{will}}$	$\mathrm{N}$	22.47	30.09
The coefficient of correlation between speed and self-driving force, $\mu$	-	0.46	0.73

summarizes the values of measures in the two models, and we subsequently analyze the improvements achieved by the PI-SFM.

1. Verification of improved self-driving force. The PI-SFM considers the pedestrian characteristic of definite OD, making the self-driving force an essential factor driving pedestrians to move. As can be seen in Table 6, the average self-driving force of the PI-SFM is significantly higher than that of the SFM, suggesting that the PI-SFM better accounts for the self-driving force. Because the PI-SFM incorporates the OD factor affecting pedestrian speed, the correlation between speed and self-driving force is enhanced from weak to vigorous, reflecting the positive effect of self-driving force on speed. We also observe an increase in mean movement speed, but a decrease in the variance of pedestrian speed. The change in the measure of speed indicates that a strong self-driving force drives pedestrians to move toward their destinations with high speed and low-fluctuation walking behavior. Figure 5 shows the two models’ pedestrian-behavior range simultaneously. The range of pedestrian behavior is defined as the area covered by all pedestrians, showing in the red circles in Figure 5. It can be seen intuitively that the behavior range of the PI-SFM is significantly smaller than that of the SFM. In the PI-SFM, pedestrians tend to move closer to their destinations, being driven by the self-driving force. The number of pedestrians at the exit has increased, showing a gathering state. Therefore, it is clear that the improvement described in this paper with respect to self-driving force is reasonable and more consistent with the characteristics of pedestrians in subway stations.

2. Verification of improved force on pedestrians. The PI-SFM takes advantage of subway pedestrians’ high tolerance of mutual crowding. From Table 6, it can be seen that the exit density of the PI-SFM is noticeably higher than that of the SFM. We find that the PI-SFM allows for a moderate squeeze between pedestrians, reducing the required space for pedestrians and enabling adequate utilization of the area. Meanwhile, average movement times and travel distances are also reduced accordingly, due to the reduced spatial requirement. Figure 6a,b present simulations of pedestrians at the exit for both models. For purposes of comparison, we recall that the PI-SFM allows for contact between pedestrians. Figure 6c shows congregation of pedestrians at the exit in the PI-SFM simulation. A comparison of the two models indicates that the PI-SFM better simulates the crowding behavior on pedestrians, which results from the characteristics of the pedestrians. Hence, this study offers a reasonable assessment of the improvement of force on pedestrians.

3. Verification of improved force on obstacles. The PI-SFM better reflects how pedestrians are affected by obstacles with the need to make minor detours. Table 6 shows that the movement times and travel distances of the PI-SFM are effectively reduced compared to the SFM because it weakens the role of forces with respect to obstacles and shortens the detour distance of pedestrians. In the PI-SFM, pedestrians can reach their destination with a shorter walking distance and lower movement time, and their detour distance in the event of obstacles is effectively reduced. Figure 6d depicts the pedestrian contact with the wall at the exit for the PI-SFM, thereby reproducing the phenomenon of fewer detours to blocks. It can be readily appreciated that this improvement in modelling concerning the avoidance of obstacles is reasonable.

4. Verification of improved force on signs. The PI-SFM includes the attraction of indication signs to pedestrians, which prompts them to have a definite orientation to their destinations. In the simulation, we set the indication signs at the goal’s location to highlight the characteristic of pedestrians having a definite OD so that the uniqueness of pedestrian behaviors in subway stations can be manifested. The position of the sign means the pedestrians have a clear destination target to aim for. Both the self-driving force and the force on signs direct pedestrians to their destinations in the PI-SFM, driving pedestrians to move toward their goal with a firm intention. Figure 5 depicts the phenomenon of pedestrians converging upon their shared destination under the guidance of signs. Therefore, the average movement speed is improved, the movement time is reduced, and the force on signs is improved.

3.1.2. Sensitivity Analysis

This study also explores the sensitivity of the PI-SFM. Figure 7 shows the sensitivity of four performance measures (average movement speed, time, travel distance, and exit density) to the OD factor ${\omega }_i\left(t\right)$ and the force on signs $f_{sign}$.

The sensitivity of measures to the OD factor is shown in Figure 7a,b. The average movement speed increases and movement time declines with increases in the value of the OD factor. On the other hand, the OD factor has a minimal effect on average travel distance and exit density. The change in the measures is more apparent when the OD factor is less than 0.5, while it is small when the OD factor exceeds 0.8 because pedestrian behavior is close to the optimal state in the latter case. Therefore, the OD factor expresses the pedestrian expectations concerning destinations and optimizes walking behavior by acting upon movement speed.

Figure 7c,d show the variation of measures with the force on signs, where $f$ is the value of the force taken for the purposes of this study, and the remaining values are expressed as multiples of $f$. Similarly, the average movement time decreases as the force on signs increases. However, the force on signs exerts a more significant impact on the average travel distance and a more negligible impact on the average movement speed, indicating that the force optimizes walking behaviors by reducing the travel distances of pedestrians. Therefore, clear signs shorten pedestrians’ walking distances and delay times, which is conducive to orderly behavior and reduces risks to pedestrians in subway stations.

3.2. Case Study

We carried out a simplified experiment in an actual subway station. The experiment was conducted at the Wuyi Square subway station in Changsha, Hunan, China, the largest interchange station in Changsha, which has high pedestrian flows. Within the Wuyi Square station, we selected an $8 \mathrm{m}\times 8 \mathrm{m}$ square as the survey area (with a $1 \mathrm{m}\times 1 \mathrm{m}$ column), where the destination was set as the turnstile ($1 \mathrm{m}$ in width) at the edge of the square. The sign was located at the goal (an erected instruction sign was placed at the turnstile). Figure 8a depicts an overhead view of the survey area, (b) shows the layout of the concourse level in the station. We tracked the behavior of 30 pedestrians walking in the same direction during the morning rush hour (7:00 am to 8:00 am) and recorded the time it took them to move through the survey area (arrival at the turnstile) and the number of steps they took. The study also counted the number of pedestrians in the survey area. The statistical results of the actual experiments are recorded in

Table 7. Measures in the actual experiment and the simulation.

	Movement Speed	Movement Time	Travel Distance	Area Density
Real experiment	1.26	8.93	11.26	2.11
SFM	1.36	10.31	13.89	0.77
PI-SFM	1.29	8.20	10.57	2.65

.

We applied both the SFM and the PI-SFM to simulate pedestrian behavior in the survey area of the above subway station. Figure 8a reproduces the computer simulation of the survey area. We then compared the outputs of the simulations for four performance measures (pedestrian movement speed, movement time, travel distance, and area density) with data from the experiment in the actual station. Table 7 summarizes the measurements of the real-life experiment and the computer simulations.

As can be seen in Table 7, the outputs of the PI-SFM are closer to the actual experiment results than the SFM. The PI-SFM effectively reproduces the movement of pedestrians in the subway station, indicating that it is consistent with the behavioral characteristics of real pedestrians. Specifically, the pedestrians of the PI-SFM have high movement speed because both the strong self-driving force and the force on signs drive them to rush. The PI-SFM corrects the forces on obstacles by reducing pedestrians’ detour distances and time delays of pedestrians, resulting in savings in average movement time and travel distance. The area density of the PI-SFM is significantly higher than that of the SFM, reflecting the ability of a given area to bear more pedestrians in busy periods, thus demonstrating the improvement in the forces on pedestrians. Figure 9 compares the simulation results of the two models simultaneously. We find that pedestrians in the PI-SFM are closer to obstacles and converge upon their destination, effectively reducing the range of movement. The PI-SFM truly reflects the actual movement of pedestrians in subway stations, which is guided by signs to move towards the target. The case study shows that the behavior model constructed and described in this paper matches the actual walking behaviors of pedestrians very well.

In addition, we evaluated the risk to pedestrians in the Wuyi Square subway station. Using Formula (15), we obtained a value of 2.26 for the pedestrians’ fluctuating risk index (FRI). Following Table 4, we determined that the pedestrian risk was Level 2, meaning that specific safety measures could be taken. The method here described allows managers to identify and assess dangers to pedestrians in advance on a scientific basis, thus facilitating timely interventions and avoiding accidents.

3.3. Discussion

This study explores the behaviors and models of pedestrians in subway stations and achieves a scientific evaluation of their safety. The normative behavior theory is applied to the behavior analysis of pedestrians, and their unique behavior characteristics are assumed. We define four dynamic influence mechanisms to constrain social forces and thereby better reproduce pedestrian behavior. The new force model describes pedestrian behavior as dynamics of partial influence. According to our simulation and real-world experimental data, the validity and advancement of the model in simulating pedestrian behavior are verified. Furthermore, we establish an evaluation system for pedestrian safety, using the fluctuation of pedestrians to identify risks and hidden dangers in advance.

Our work is based on previous advanced research. Many studies [13,14,15] have shown that pedestrian behavior has an important relationship with safety. This study establishes a force model to describe the behavior of pedestrians and systematically evaluate their safety levels. In some studies, scholars have defined the force model so as to explore pedestrians’ behavior in different settings, such as intersections and public places [23,24,25]. The mechanism which is the subject of this study was implemented in the scenario of a subway station and obtained excellent results.

4. Conclusions

In this study, we sought to evaluate the safety of pedestrians to improve their security scientifically, in the particular circumstances of subway stations. Our conclusions can be summarized as follows:

• Based on normative pedestrian behavior theory, we elaborate on pedestrian behavior at the strategic, tactical, and operational levels, principally by incorporating the characteristics of pedestrians with a definite OD.
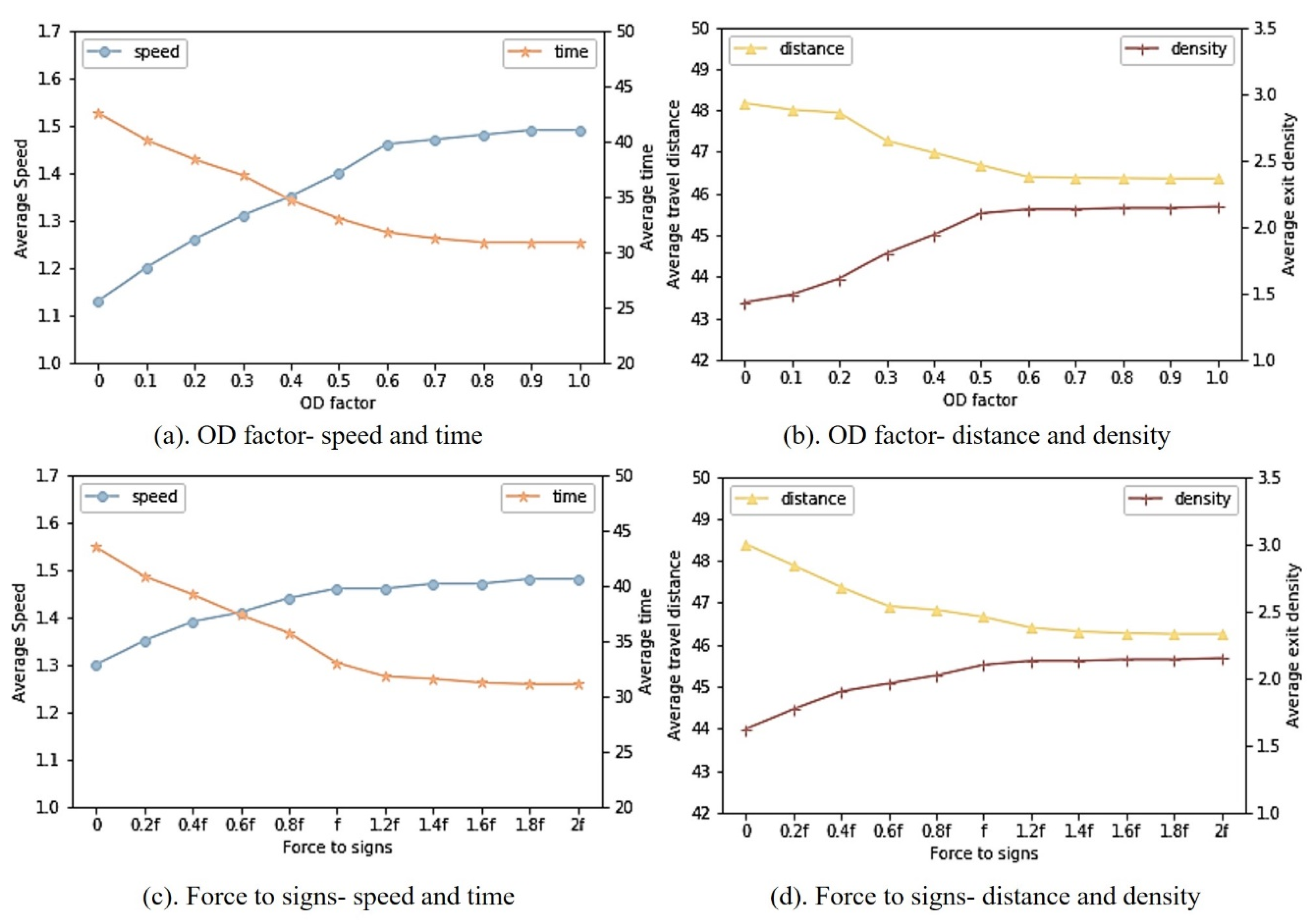
• We propose a force model with partial impact (PI-SFM) based on a consideration of the influence of forces in the existing SFM. Four force influence mechanisms are defined to constrain the social forces and so describe the behavior of pedestrians in subway stations, namely, self-driven forces, forces on pedestrians, forces on walls, and forces on signs.
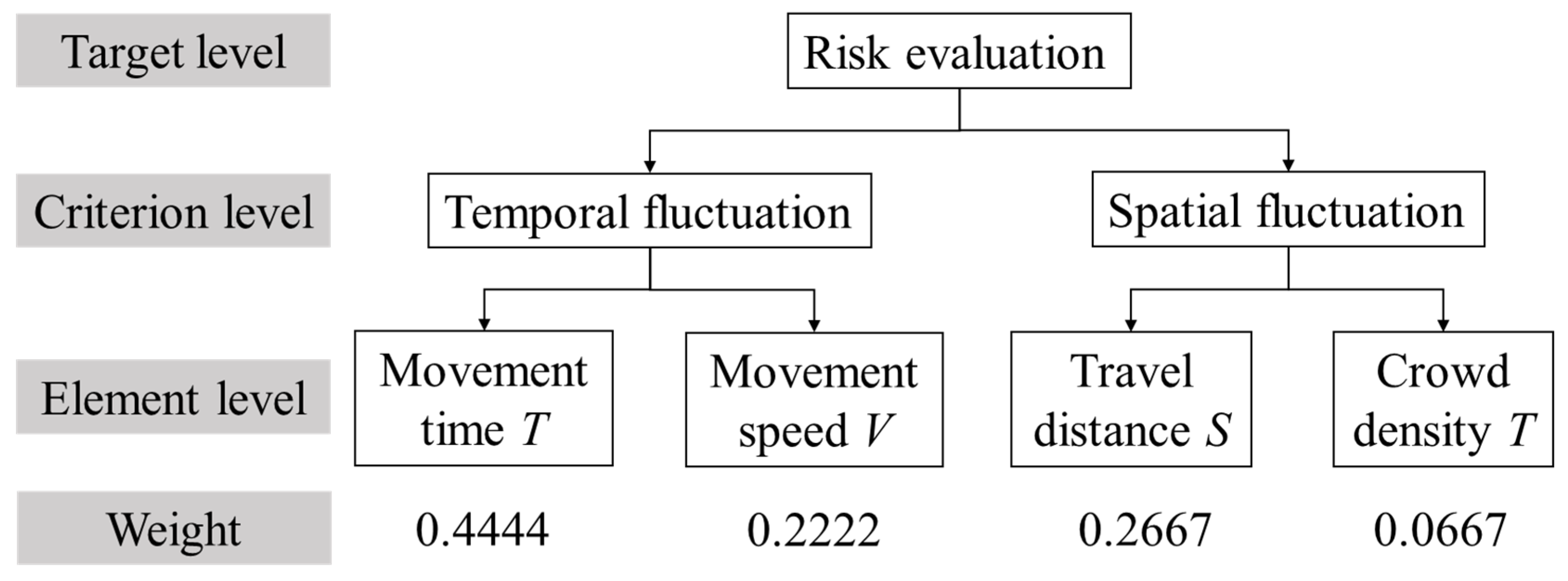
• We use real-time dynamic data to evaluate the risk to pedestrians. The influencing factors of pedestrian volatility are speed, time, distance, and crowd density. A hierarchical evaluation of pedestrian risk was achieved based on the proposed FRI.

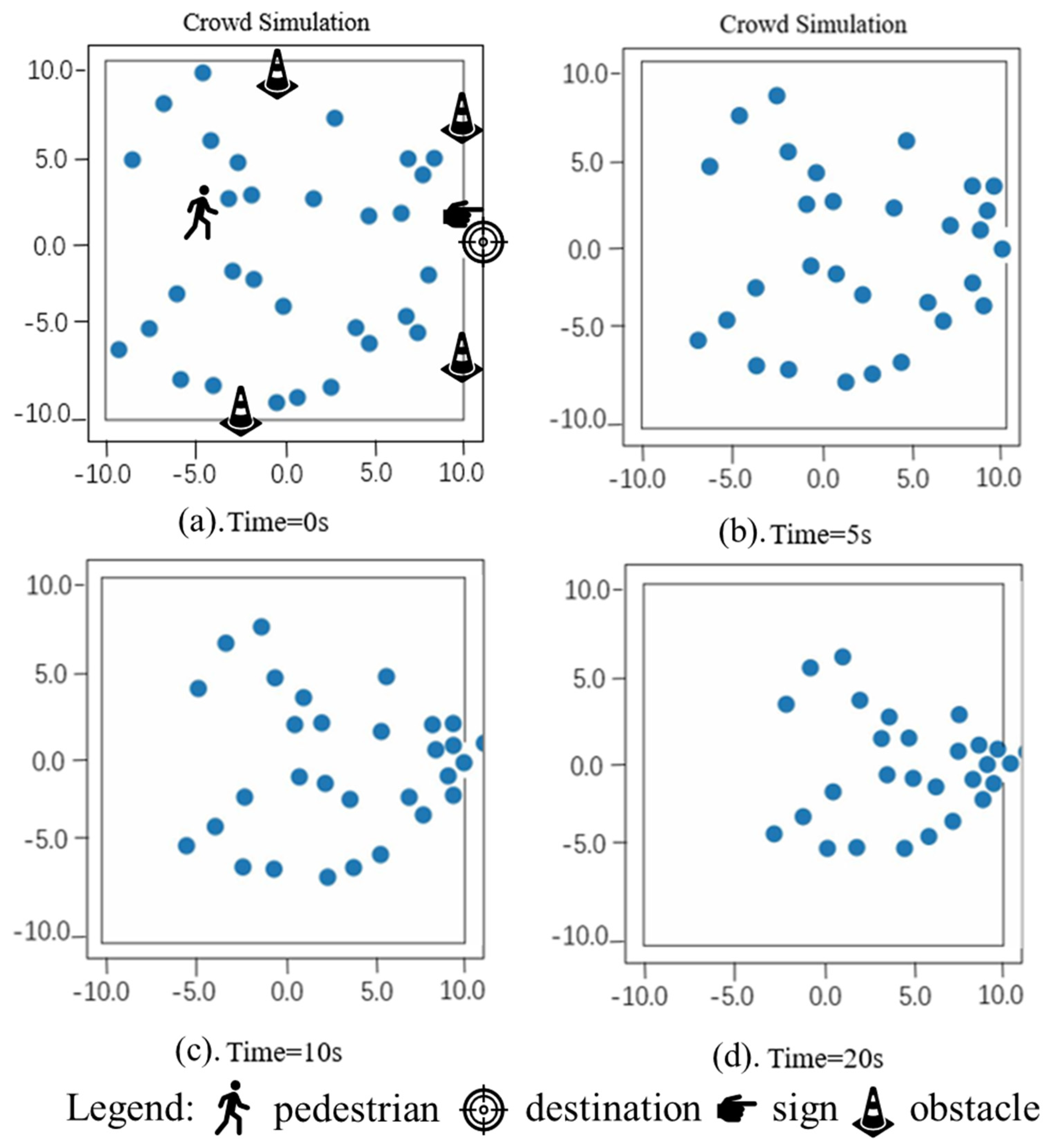
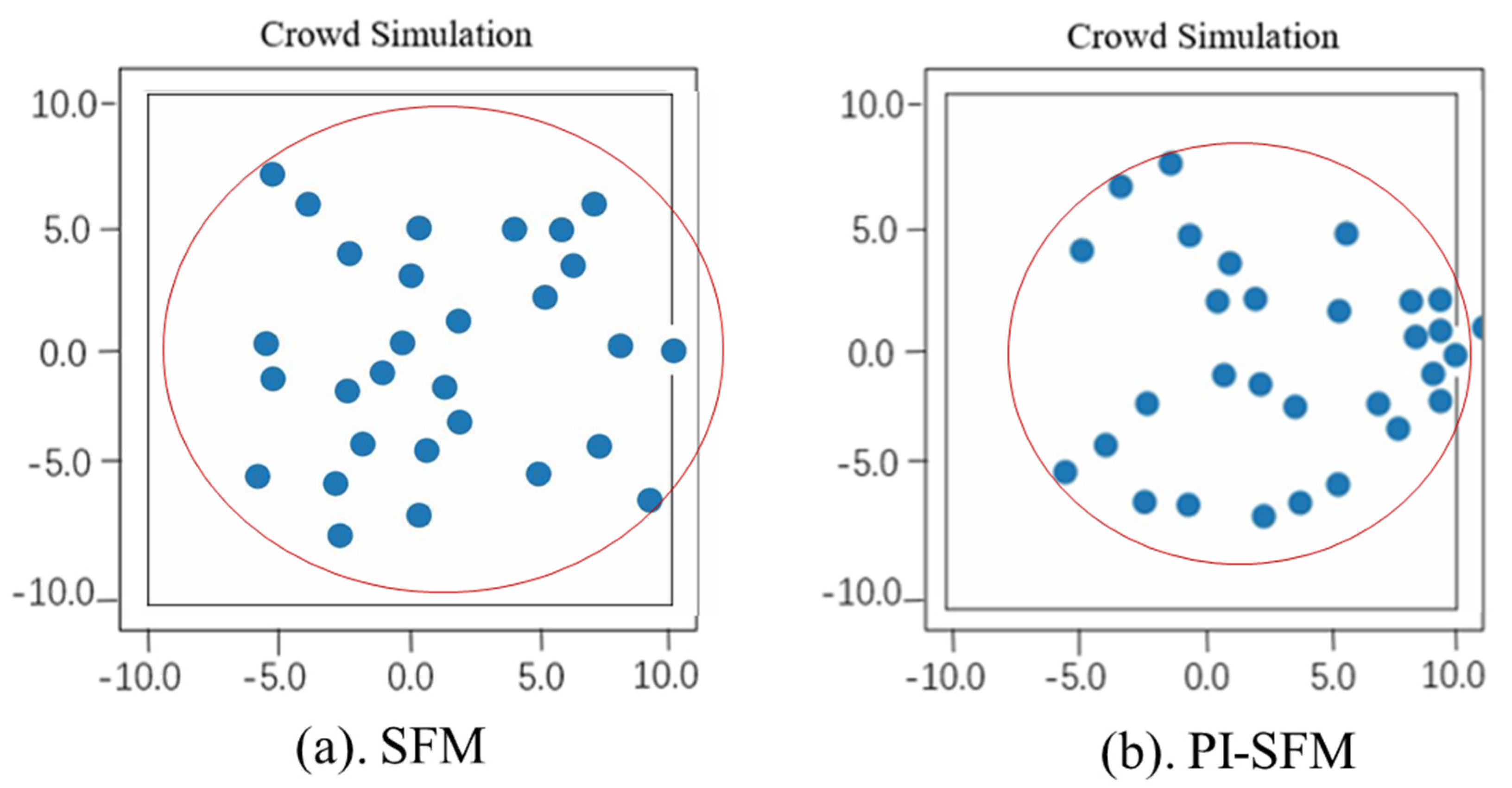
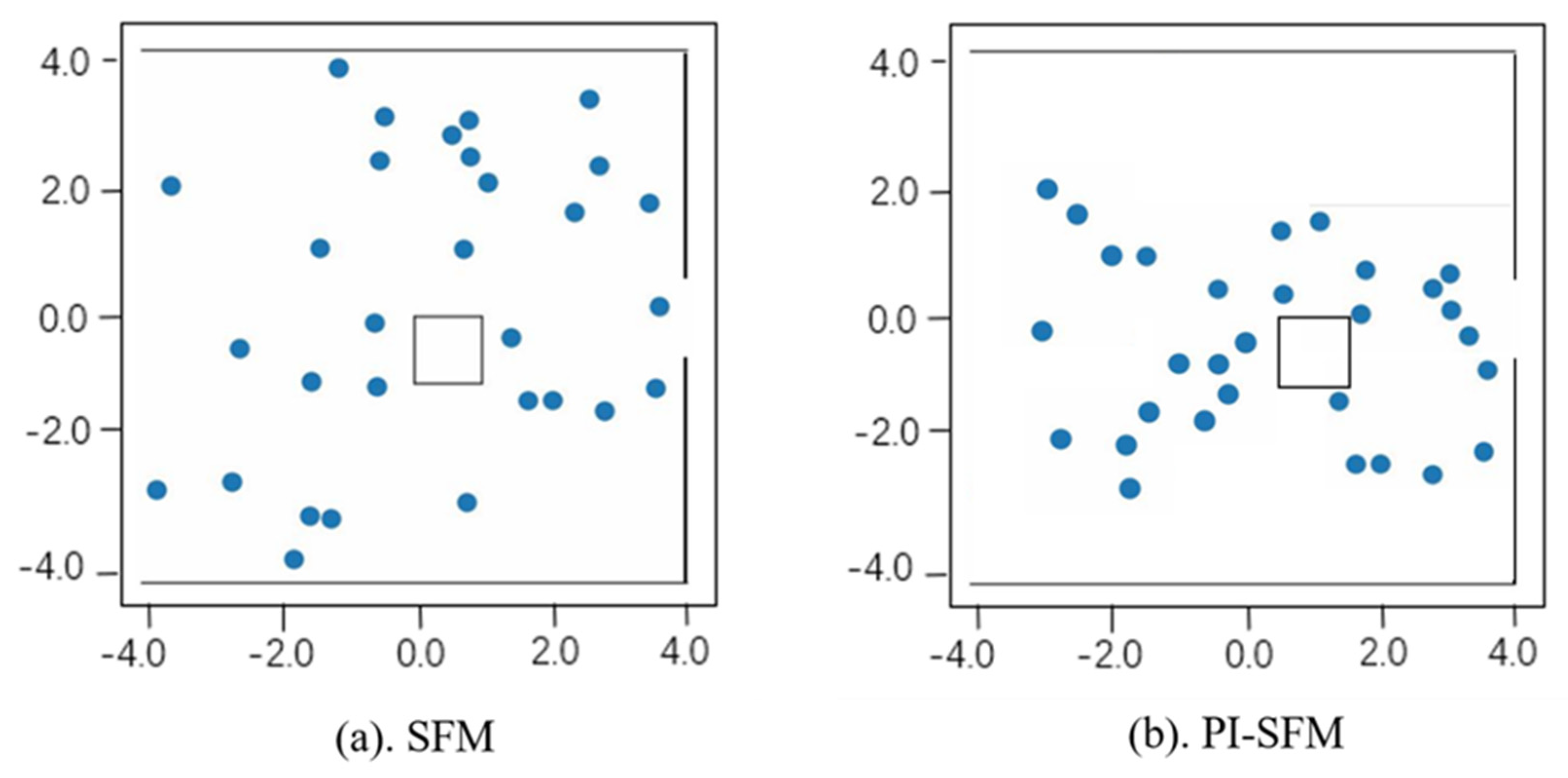
We conducted simulations using PI-SFM and verified the rationality of the designed force influence mechanism by comparing these results with those of SFM. Further, the behavioral characteristics of pedestrians were analyzed with evidence from actual subway station case experiments, which demonstrated the accurate description of pedestrian behavior produced by PI-SFM. In addition, the model was found to reproduce the microscopic behavior of pedestrians better than SFM, including contact behavior between pedestrians and behavior concerning the avoidance of obstacles. We conclude, therefore, that the PI-SFM model is more applicable to the simulation of pedestrian behavior in subway stations. The simulation and evaluation of pedestrian behavior by PI-SFM captures the actual movement characteristics of pedestrians in subway stations, which can effectively determine potential risks to pedestrians and help managers take safety measures. Our research provides a theoretical framework for future evaluation of pedestrian safety.

We also provide some strategic suggestions for the improvement of pedestrian safety, which can be summarized as follows: For traffic operators, we suggest that they set up corresponding signs in subway stations to indicate each traffic facility’s specific location (including direction and distance). Signs give passengers clear guidance, improve traffic operation efficiency and ensure pedestrians’ safety. We further suggest that traffic management agencies identify potential risks in advance by obtaining real-time dynamic information. Early judgment of hidden dangers helps decision-makers adopt corresponding safety measures in time, avoiding the occurrence of dangers and protecting people’s lives.

Our study has some limitations. The experiments used for model validation were subject to data bias and simplification of content due to the impact of the COVID-19 pandemic. The size and specificity of the situation may limit the applicability of PI-SFM, which remains to be verified in future work. We plan to conduct more complicated experiments in subway stations, by expanding the experimental area, increasing the number of pedestrians, and adding obstacles. Experiments under different conditions of pedestrian flow should also be conducted to illustrate the stability of the model. In terms of risk evaluation, the study mainly considered the impact of pedestrian volatility upon their safety, proposing four dimensions of indicators. It will be a challenge for such a system to evaluate pedestrians’ risk comprehensively, and so we seek to construct a multi-indicator evaluation system based on a data-driven approach.