Evaluation of Interaction between Bridge Infrastructure Resilience Factors against Seismic Hazard
Abstract
:1. Introduction
- (i)
- To assess the interplay among the resilience parameters of bridge infrastructure against any seismic event
- (ii)
- To find the effectiveness of the rough DEMATEL technique
- (iii)
- To compare the rough and crisp DEMATEL approaches
2. Rough DEMATEL Method
3. Case Study
3.1. Factor Selection
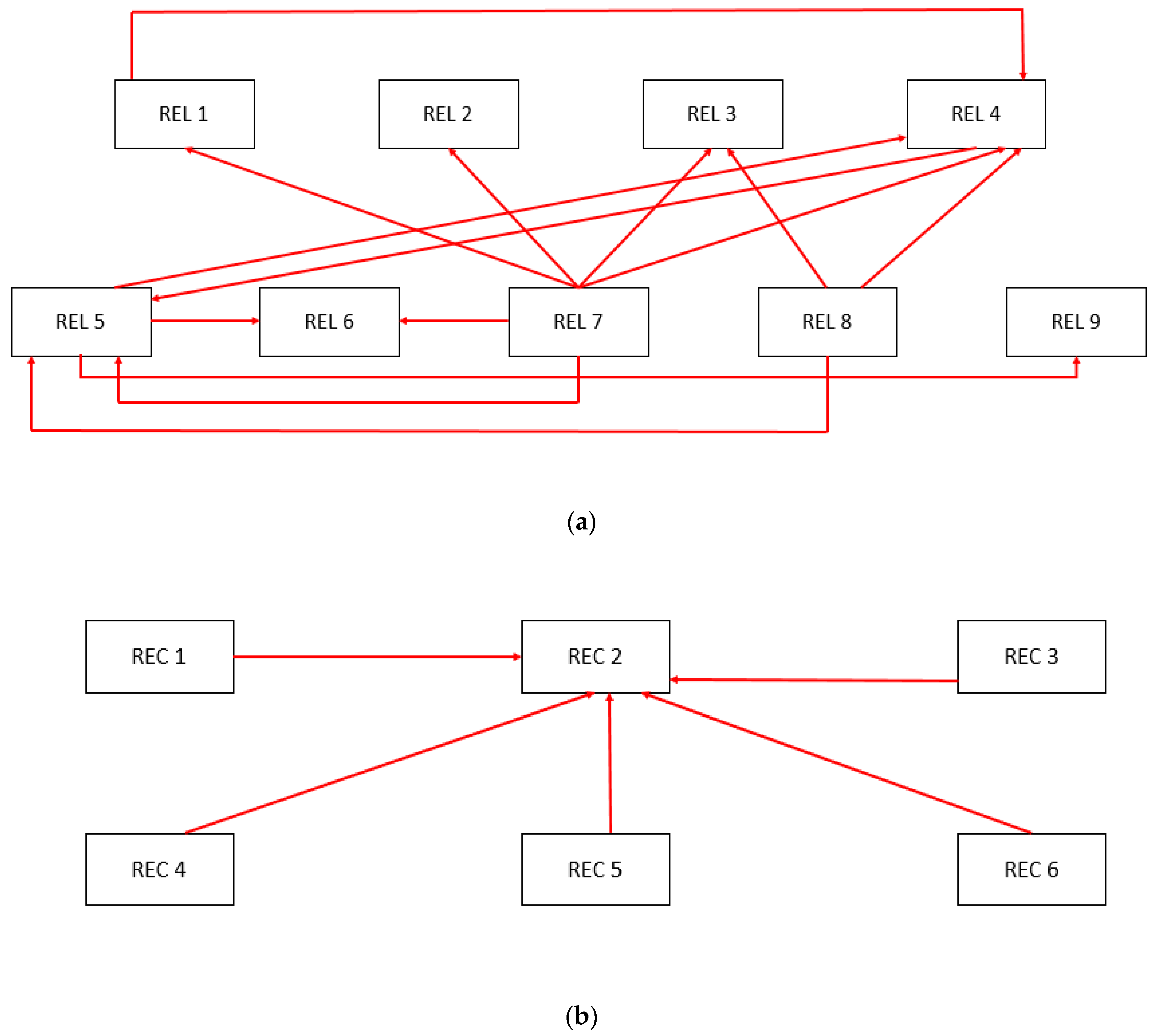
3.2. Causal and Relationship Diagram by Crisp DEMATEL
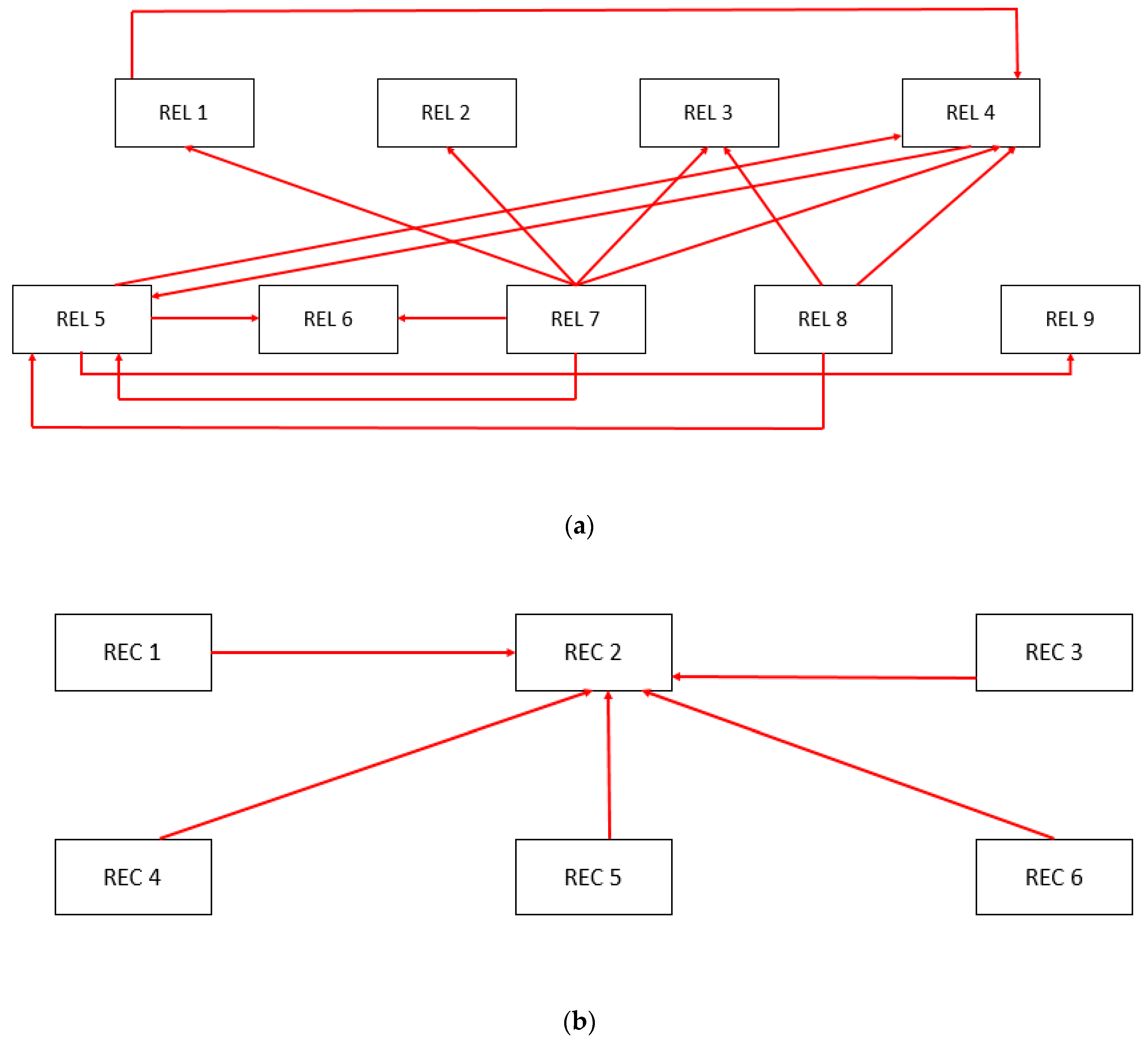
3.3. Causal and Relationship Diagram by Rough DEMATEL
4. Results and Discussion
5. Conclusions
- Crucial bridge resilience parameters and their interrelationships were identified.
- The bridge resilience indexes were evaluated by comparing the results from two well-established multi-criteria decision-making tools.
- Assistance to the stakeholders and policymakers was provided for preparing for future unforeseeable scenarios and hazards from the determinations of the study.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Topic of the Study | Factors of Resilience | Reference |
|---|---|---|
| Resilience assessment of housing infrastructure against flood | Reliability Recovery | [14] |
| Resilience assessment of urban transportation systems | Resistance Re-building of critical functionality Re-stabilization of critical functionality Reconfiguration after recovery | [28] |
| Seismic resilience assessment using fuzzy sets theory | Target functionality Residual functionality Recovery time Idle time interval | [29] |
| Structural resilience against natural hazards | Preparedness Management Risk analysis | [26] |
| Review paper on civil infrastructure resilience | Risk assessment Disasters risk management Water supply Water resources Climate change Economic and social resources Strategic planning Decision making Sustainable development | [25] |
| Resilience assessment of single system to interdependent systems | Damage propagation Disasters prevention Assessment and recovery | [30] |
| REL1 | REL2 | REL3 | REL4 | REL5 | REL6 | REL7 | REL8 | REL9 | |
| REL1 | 1,1,1,1,1 | 5,4,5,5,5 | 2,2,3,4,2 | 4,4,4,5,5 | 1,4,2,4,1 | 2,4,2,4,2 | 1,1,1,1,1 | 3,1,3,1,1 | 3,5,1,1,1 |
| REL2 | 4,4,4,2,4 | 1,1,1,1,1 | 2,2,4,3,3 | 2,3,2,4,2 | 2,4,2,4,2 | 1,3,3,4,2 | 1,1,1,1,1 | 2,1,2,1,1 | 4,4,1,2,4 |
| REL3 | 3,2,3,3,2 | 2,2,2,4,2 | 1,1,1,1,1 | 4,2,4,4,3 | 3,4,3,5,4 | 3,4,3,4,3 | 2,1,1,1,1 | 1,1,1,1,1 | 3,3,3,2,3 |
| REL4 | 4,4,5,4,4 | 2,2,1,4,2 | 4,3,4,4,3 | 1,1,1,1,1 | 3,4,5,4,5 | 3,4,2,4,4 | 1,1,1,1,1 | 1,1,2,1,1 | 4,4,3,4,4 |
| REL5 | 4,4,2,4,3 | 4,4,3,4,3 | 3,3,4,4,3 | 4,4,2,4,4 | 1,1,1,1,1 | 4,4,4,5,4 | 1,1,1,1,1 | 1,1,1,1,1 | 5,5,4,4,5 |
| REL6 | 2,2,2,1,2 | 3,2,1,1,3 | 2,4,2,2,2 | 3,2,1,3,3 | 3,3,1,5,3 | 1,1,1,1,1 | 2,1,1,1,1 | 1,1,1,1,1 | 3,3,4,1,3 |
| REL7 | 4,4,5,2,4 | 3,3,3,2,4 | 5,5,5,4,5 | 5,4,5,2,4 | 4,4,5,3,4 | 3,4,3,3,4 | 1,1,1,1,1 | 4,4,4,1,4 | 1,3,1,1,1 |
| REL8 | 4,4,4,1,4 | 4,3,3,1,4 | 5,3,5,1,5 | 5,5,4,1,5 | 3,3,5,1,4 | 3,3,4,1,3 | 2,3,3,1,2 | 1,1,1,1,1 | 1,3,1,1,3 |
| REL9 | 3,3,3,1,4 | 3,3,3,1,4 | 4,3,4,1,4 | 3,4,3,1,4 | 4,4,4,1,4 | 4,2,4,1,4 | 1,1,1,1,2 | 1,1,1,1,2 | 1,1,1,1,1 |
| REC1 | REC2 | REC3 | REC4 | REC5 | REC6 | |
| REC1 | 1,1,1,1,1 | 4,4,4,4,5 | 4,4,4,4,4 | 2,2,4,4,2 | 1,1,1,5,1 | 1,1,1,5,1 |
| REC2 | 1,1,1,4,2 | 1,1,1,1,1 | 5,4,5,4,5 | 4,4,4,4,2 | 3,2,4,5,2 | 2,2,3,5,2 |
| REC3 | 3,3,4,4,2 | 5,5,5,4,5 | 1,1,1,1,1 | 1,1,1,4,1 | 3,3,3,5,1 | 1,1,4,5,1 |
| REC4 | 2,4,3,4,4 | 4,4,4,4,4 | 5,2,2,4,5 | 1,1,1,1,1 | 3,3,2,5,3 | 3,3,1,5,3 |
| REC5 | 4,4,4,5,4 | 5,5,5,5,5 | 2,2,2,5,2 | 2,3,2,5,2 | 1,1,1,1,1 | 3,3,3,3,3 |
| REC6 | 3,3,3,5,3 | 4,4,4,5,4 | 1,1,1,5,1 | 2,2,2,5,2 | 3,3,4,3,3 | 1,1,1,1,1 |
| REL1 | REL2 | REL3 | REL4 | REL5 | REL6 | REL7 | REL8 | REL9 | |
| REL1 | 0.035 | 0.167 | 0.090 | 0.153 | 0.083 | 0.097 | 0.035 | 0.063 | 0.076 |
| REL2 | 0.125 | 0.035 | 0.097 | 0.090 | 0.097 | 0.090 | 0.035 | 0.049 | 0.104 |
| REL3 | 0.090 | 0.083 | 0.035 | 0.118 | 0.132 | 0.118 | 0.042 | 0.035 | 0.097 |
| REL4 | 0.146 | 0.076 | 0.125 | 0.035 | 0.146 | 0.118 | 0.035 | 0.042 | 0.132 |
| REL5 | 0.118 | 0.125 | 0.118 | 0.125 | 0.035 | 0.146 | 0.035 | 0.035 | 0.160 |
| REL6 | 0.063 | 0.069 | 0.083 | 0.083 | 0.104 | 0.035 | 0.042 | 0.035 | 0.097 |
| REL7 | 0.132 | 0.104 | 0.167 | 0.139 | 0.139 | 0.118 | 0.035 | 0.118 | 0.049 |
| REL8 | 0.118 | 0.104 | 0.132 | 0.139 | 0.111 | 0.097 | 0.076 | 0.035 | 0.063 |
| REL9 | 0.097 | 0.097 | 0.111 | 0.104 | 0.118 | 0.104 | 0.042 | 0.042 | 0.035 |
| REC1 | REC2 | REC3 | REC4 | REC5 | REC6 | |
| REC1 | 0.054 | 0.226 | 0.215 | 0.151 | 0.097 | 0.097 |
| REC2 | 0.097 | 0.054 | 0.247 | 0.194 | 0.172 | 0.151 |
| REC3 | 0.172 | 0.258 | 0.054 | 0.086 | 0.161 | 0.129 |
| REC4 | 0.183 | 0.215 | 0.194 | 0.054 | 0.172 | 0.161 |
| REC5 | 0.226 | 0.269 | 0.140 | 0.151 | 0.054 | 0.161 |
| REC6 | 0.183 | 0.226 | 0.097 | 0.140 | 0.172 | 0.054 |
| REL1 | REL2 | REL3 | REL4 | REL5 | REL6 | REL7 | REL8 | REL9 | |
| REL1 | 0.415 | 0.513 | 0.468 | 0.540 | 0.478 | 0.480 | 0.184 | 0.233 | 0.440 |
| REL2 | 0.462 | 0.364 | 0.440 | 0.452 | 0.454 | 0.440 | 0.171 | 0.205 | 0.431 |
| REL3 | 0.444 | 0.420 | 0.395 | 0.488 | 0.499 | 0.479 | 0.182 | 0.197 | 0.440 |
| REL4 | 0.537 | 0.460 | 0.523 | 0.461 | 0.558 | 0.526 | 0.193 | 0.224 | 0.514 |
| REL5 | 0.526 | 0.512 | 0.529 | 0.555 | 0.472 | 0.562 | 0.199 | 0.224 | 0.551 |
| REL6 | 0.357 | 0.348 | 0.379 | 0.392 | 0.410 | 0.338 | 0.158 | 0.169 | 0.379 |
| REL7 | 0.605 | 0.555 | 0.641 | 0.639 | 0.634 | 0.604 | 0.225 | 0.334 | 0.509 |
| REL8 | 0.534 | 0.500 | 0.550 | 0.577 | 0.548 | 0.525 | 0.241 | 0.228 | 0.466 |
| REL9 | 0.450 | 0.433 | 0.465 | 0.476 | 0.487 | 0.466 | 0.182 | 0.204 | 0.380 |
| REC1 | REC2 | REC3 | REC4 | REC5 | REC6 | |
| REC1 | 1.421 | 2.055 | 1.704 | 1.371 | 1.393 | 1.278 |
| REC2 | 1.598 | 2.079 | 1.857 | 1.515 | 1.576 | 1.433 |
| REC3 | 1.562 | 2.128 | 1.600 | 1.352 | 1.478 | 1.335 |
| REC4 | 1.752 | 2.334 | 1.914 | 1.474 | 1.655 | 1.515 |
| REC5 | 1.814 | 2.414 | 1.907 | 1.593 | 1.576 | 1.540 |
| REC6 | 1.597 | 2.133 | 1.668 | 1.420 | 1.509 | 1.286 |
| REL1 | REL2 | REL3 | REL4 | REL5 | REL6 | REL7 | REL8 | REL9 | |
| REL1 | (0.031, 0.031) | (0.145, 0.155) | (0.068, 0.096) | (0.130, 0.145) | (0.051, 0.101) | (0.072, 0.103) | (0.031, 0.031) | (0.041, 0.071) | (0.042, 0.098) |
| REL2 | (0.103, 0.123) | (0.031, 0.031) | (0.074, 0.102) | (0.068, 0.096) | (0.072, 0.103) | (0.060, 0.102) | (0.031, 0.031) | (0.036, 0.051) | (0.072, 0.116) |
| REL3 | (0.074, 0.089) | (0.065, 0.085) | (0.031, 0.031) | (0.092, 0.120) | (0.105, 0.133) | (0.099, 0.114) | (0.032, 0.042) | (0.031, 0.031) | (0.082, 0.093) |
| REL4 | (0.127, 0.137) | (0.053, 0.086) | (0.105, 0.120) | (0.031, 0.031) | (0.117, 0.145) | (0.092, 0.120) | (0.031, 0.031) | (0.032, 0.042) | (0.114, 0.124) |
| REL5 | (0.092, 0.120) | (0.105, 0.120) | (0.099, 0.114) | (0.103, 0.123) | (0.031, 0.031) | (0.127, 0.137) | (0.031, 0.031) | (0.031, 0.031) | (0.137, 0.152) |
| REL6 | (0.051, 0.061) | (0.046, 0.079) | (0.065, 0.085) | (0.060, 0.088) | (0.072, 0.116) | (0.031, 0.031) | (0.032, 0.042) | (0.031, 0.031) | (0.071, 0.104) |
| REL7 | (0.102, 0.135) | (0.083, 0.105) | (0.145, 0.155) | (0.104, 0.144) | (0.114, 0.136) | (0.099, 0.114) | (0.031, 0.031) | (0.091, 0.121) | (0.033, 0.054) |
| REL8 | (0.091, 0.121) | (0.073, 0.113) | (0.090, 0.146) | (0.097, 0.149) | (0.073, 0.127) | (0.071, 0.104) | (0.054, 0.082) | (0.031, 0.031) | (0.041, 0.071) |
| REL9 | (0.071, 0.104) | (0.071, 0.104) | (0.079, 0.119) | (0.073, 0.113) | (0.091, 0.121) | (0.072, 0.116) | (0.032, 0.042) | (0.032, 0.042) | (0.031, 0.031) |
| REC1 | REC2 | REC3 | REC4 | REC5 | REC6 | |
| REC1 | (0.048, 0.048) | (0.195, 0.211) | (0.193, 0.193) | (0.112, 0.158) | (0.056, 0.118) | (0.056, 0.118) |
| REC2 | (0.058, 0.120) | (0.048, 0.048) | (0.211, 0.234) | (0.158, 0.189) | (0.119, 0.192) | (0.107, 0.168) |
| REC3 | (0.133, 0.176) | (0.224, 0.240) | (0.048, 0.048) | (0.054, 0.100) | (0.111, 0.179) | (0.069, 0.161) |
| REC4 | (0.142, 0.185) | (0.193, 0.193) | (0.134, 0.211) | (0.048, 0.048) | (0.130, 0.181) | (0.111, 0.179) |
| REC5 | (0.195, 0.211) | (0.242, 0.242) | (0.102, 0.149) | (0.107, 0.168) | (0.048, 0.048) | (0.145, 0.145) |
| REC6 | (0.149, 0.180) | (0.195, 0.211) | (0.056, 0.118) | (0.102, 0.149) | (0.147, 0.162) | (0.048, 0.048) |
| REL1 | REL2 | REL3 | REL4 | REL5 | REL6 | REL7 | REL8 | REL9 | |
| REL1 | (0.168, 0.458) | (0.260, 0.557) | (0.198, 0.528) | (0.259, 0.593) | (0.183, 0.567) | (0.201, 0.544) | (0.085, 0.196) | (0.101, 0.264) | (0.166, 0.520) |
| REL2 | (0.219, 0.502) | (0.145, 0.409) | (0.190, 0.494) | (0.191, 0.510) | (0.188, 0.526) | (0.178, 0.504) | (0.080, 0.181) | (0.090, 0.229) | (0.180, 0.497) |
| REL3 | (0.206, 0.465) | (0.187, 0.451) | (0.163, 0.420) | (0.225, 0.522) | (0.233, 0.545) | (0.229, 0.508) | (0.086, 0.188) | (0.091, 0.206) | (0.206, 0.470) |
| REL4 | (0.271, 0.552) | (0.197, 0.499) | (0.251, 0.549) | (0.189, 0.491) | (0.261, 0.606) | (0.242, 0.561) | (0.093, 0.195) | (0.101, 0.237) | (0.250, 0.544) |
| REL5 | (0.249, 0.544) | (0.248, 0.534) | (0.253, 0.550) | (0.261, 0.581) | (0.190, 0.510) | (0.279, 0.582) | (0.096, 0.198) | (0.103, 0.230) | (0.278, 0.574) |
| REL6 | (0.153, 0.393) | (0.140, 0.399) | (0.165, 0.423) | (0.164, 0.443) | (0.171, 0.477) | (0.133, 0.381) | (0.074, 0.170) | (0.077, 0.184) | (0.164, 0.432) |
| REL7 | (0.276, 0.643) | (0.244, 0.601) | (0.315, 0.675) | (0.283, 0.694) | (0.284, 0.699) | (0.273, 0.648) | (0.103, 0.232) | (0.170, 0.356) | (0.197, 0.566) |
| REL8 | (0.227, 0.603) | (0.199, 0.581) | (0.224, 0.638) | (0.236, 0.667) | (0.207, 0.659) | (0.206, 0.610) | (0.110, 0.268) | (0.094, 0.257) | (0.167, 0.555) |
| REL9 | (0.191, 0.503) | (0.182, 0.492) | (0.197, 0.526) | (0.196, 0.543) | (0.208, 0.563) | (0.192, 0.535) | (0.082, 0.198) | (0.087, 0.228) | (0.144, 0.437) |
| REC1 | REC2 | REC3 | REC4 | REC5 | REC6 | |
| REC1 | (0.309, 1.781) | (0.584, 2.319) | (0.492, 2.019) | (0.342, 1.730) | (0.295, 1.816) | (0.264, 1.703) |
| REC2 | (0.352, 2.051) | (0.489, 2.424) | (0.518, 2.256) | (0.397, 1.933) | (0.373, 2.071) | (0.329, 1.925) |
| REC3 | (0.382, 1.994) | (0.601, 2.466) | (0.356, 1.995) | (0.290, 1.776) | (0.338, 1.962) | (0.274, 1.828) |
| REC4 | (0.442, 2.174) | (0.648, 2.639) | (0.484, 2.316) | (0.321, 1.877) | (0.399, 2.130) | (0.349, 1.998) |
| REC5 | (0.515, 2.133) | (0.731, 2.602) | (0.493, 2.207) | (0.406, 1.933) | (0.348, 1.954) | (0.402, 1.916) |
| REC6 | (0.427, 1.935) | (0.616, 2.364) | (0.392, 1.995) | (0.358, 1.759) | (0.394, 1.887) | (0.276, 1.669) |
Appendix B
Appendix B.1. Crisp DEMATEL Approach
Appendix B.2. Sample Calculation of Rough Number
References
- Cartes, P.C.; Echaveguren Navarro, T.; Giné, A.C.; Binet, E.A. A cost-benefit approach to recover the performance of roads affected by natural disasters. Int. J. Disaster Risk Reduct. 2021, 53, 102014. [Google Scholar] [CrossRef]
- Kilanitis, I.; Sextos, A. Integrated seismic risk and resilience assessment of roadway networks in earthquake prone areas. Bull. Earthq. Eng. 2019, 17, 181–210. [Google Scholar] [CrossRef]
- Didier, M.; Baumberger, S.; Tobler, R.; Esposito, S.; Ghosh, S.; Stojadinovic, B. Seismic Resilience of Water Distribution and Cellular Communication Systems after the 2015 Gorkha Earthquake. J. Struct. Eng. 2018, 144, 04018043. [Google Scholar] [CrossRef]
- Gardoni, P.; Murphy, C. Society-based design: Promoting societal well-being by designing sustainable and resilient infrastructure. Sustain. Resilient Infrastruct. 2020, 5, 4–19. [Google Scholar] [CrossRef]
- Mahmoud, H.; Chulahwat, A. Spatial and Temporal Quantification of Community Resilience: Gotham City under Attack. Comput.-Aided Civ. Infrastruct. Eng. 2017, 33, 353–372. [Google Scholar] [CrossRef]
- Hosseini, S.; Barker, K. Modeling infrastructure resilience using Bayesian networks: A case study of inland waterway ports. Comput. Ind. Eng. 2016, 93, 252–266. [Google Scholar] [CrossRef]
- Nasiopoulos, G.; Mantadakis, N.; Pitilakis, D.; Argyroudis, S.; Mitoulis, S. Resilience of bridges subjected to earthquakes: A case study on a portfolio of road bridges. In Proceedings of the International Conference on Natural Hazards and Infrastructure, Chania, Greece, 23–26 June 2019. [Google Scholar]
- Zhang, Z.; Wei, H.-H. Modeling Interaction of Emergency Inspection Routing and Restoration Scheduling for Postdisaster Resilience of Highway–Bridge Networks. J. Infrastruct. Syst. 2021, 27, 04020046. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Nasiopoulos, G.; Mantadakis, N.; Mitoulis, S.A. Cost-based resilience assessment of bridges subjected to earthquakes. Int. J. Disaster Resil. Built Environ. 2021, 12, 209–222. [Google Scholar] [CrossRef]
- Patel, D.A.; Lad, V.H.; Chauhan, K.A.; Patel, K.A. Development of Bridge Resilience Index Using Multicriteria Decision-Making Techniques. J. Bridge Eng. 2020, 25, 04020090. [Google Scholar] [CrossRef]
- Abunyewah, M.; Gajendran, T.; Maund, K.; Okyere, S.A. Linking information provision to behavioural intentions: Moderating and mediating effects of message clarity and source credibility. Int. J. Disaster Resil. Built Environ. 2020, 11, 100–118. [Google Scholar] [CrossRef]
- Firouzi Jahantigh, F.; Jannat, F. Analyzing the sequence and interrelations of Natech disasters in Urban areas using interpretive structural modelling (ISM). Int. J. Disaster Resil. Built Environ. 2019, 10, 392–407. [Google Scholar] [CrossRef]
- Wu, H.H.; Chang, S.Y. A case study of using DEMATEL method to identify critical factors in green supply chain management. Appl. Math. Comput. 2015, 256, 394–403. [Google Scholar] [CrossRef]
- Sen, M.K.; Dutta, S.; Kabir, G. Evaluation of interaction between housing infrastructure resilience factors against flood hazard based on rough DEMATEL approach. Int. J. Disaster Resil. Built Environ. 2021, 12, 555–575. [Google Scholar] [CrossRef]
- Song, W.; Cao, J. A rough DEMATEL-based approach for evaluating interaction between requirements of product-service system. Comput. Ind. Eng. 2017, 110, 353–363. [Google Scholar] [CrossRef]
- Khan, M.S.A.; Kabir, G.; Billah, M.; Dutta, S. Bridge Infrastructure Resilience Analysis Against Seismic Hazard Using Best-Worst Methods. In Proceedings of the Second International Workshop on Best-Worst Method, Online, 10–11 June 2021; Volume 1, pp. 95–109. [Google Scholar]
- Vishwanath, B.S.; Banerjee, S. Life-Cycle Resilience of Aging Bridges under Earthquakes. J. Bridge Eng. 2019, 24, 04019106. [Google Scholar] [CrossRef]
- Zheng, Y.; Dong, Y.; Li, Y. Resilience and life-cycle performance of smart bridges with shape memory alloy (SMA)-cable-based bearings. Constr. Build. Mater. 2018, 158, 389–400. [Google Scholar] [CrossRef]
- Billah, A.M.; Alam, M.S. Seismic fragility assessment of multi-span concrete highway bridges in British Columbia considering soil–structure interaction. Can. J. Civ. Eng. 2021, 48, 39–51. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M. Probabilistic Time-Dependent Multihazard Life-Cycle Assessment and Resilience of Bridges Considering Climate Change. J. Perform. Constr. Facil. 2016, 30, 04016034. [Google Scholar] [CrossRef]
- Mitchell, D.; Paultre, P.; Tinawi, R.; Saatcioglu, M.; Tremblay, R.; Elwood, K.; Adams, J.; DeVall, R. Evolution of seismic design provisions in the National building code of Canada. Can. J. Civ. Eng. 2010, 37, 1157–1170. [Google Scholar] [CrossRef]
- Shekhar, S.; Ghosh, J.; Ghosh, S. Impact of Design Code Evolution on Failure Mechanism and Seismic Fragility of Highway Bridge Piers. J. Bridge Eng. 2020, 25, 04019140. [Google Scholar] [CrossRef]
- Tavares, D.H.; Padgett, J.E.; Paultre, P. Fragility curves of typical as-built highway bridges in eastern Canada. Eng. Struct. 2012, 40, 107–118. [Google Scholar] [CrossRef]
- Kaviani, P.; Zareian, F.; Taciroglu, E. Seismic behavior of reinforced concrete bridges with skew-angled seat-type abutments. Eng. Struct. 2012, 45, 137–150. [Google Scholar] [CrossRef]
- Gay, L.F.; Sinha, S.K. Resilience of civil infrastructure systems: Literature review for improved asset management. Int. J. Crit. Infrastruct. 2013, 9, 330–350. [Google Scholar] [CrossRef]
- Mebarki, A.; Jerez, S.; Prodhomme, G.; Reimeringer, M. Natural hazards, vulnerability and structural resilience: Tsunamis and industrial tanks. Geomat. Nat. Hazards Risk 2016, 7, 5–17. [Google Scholar] [CrossRef]
- Ouyang, M.; Wang, Z. Resilience assessment of interdependent infrastructure systems: With a focus on joint restoration modeling and analysis. Reliab. Eng. Syst. Saf. 2015, 141, 74–82. [Google Scholar] [CrossRef]
- Tang, J.; Heinimann, H.; Han, K.; Luo, H.; Zhong, B. Evaluating resilience in urban transportation systems for sustainability: A systems-based Bayesian network model. Transp. Res. Part C Emerg. Technol. 2020, 121, 102840. [Google Scholar] [CrossRef]
- Andrić, J.M.; Lu, D.G. Fuzzy methods for prediction of seismic resilience of bridges. Int. J. Disaster Risk Reduct. 2017, 22, 458–468. [Google Scholar] [CrossRef]
- Chang, L.; Peng, F.; Ouyang, Y.; Elnashai, A.S.; Spencer, B.F. Bridge Seismic Retrofit Program Planning to Maximize Postearthquake Transportation Network Capacity. J. Infrastruct. Syst. 2012, 18, 75–88. [Google Scholar] [CrossRef]
| Reliability | Parameters | Description | Reference |
| Foundation (REL 1) Abutment (REL 2) Bearing (REL 3) Piers (REL 4) Girder (REL 5) In-span joint (REL 6) | These are the major structural components that are individually and in combination responsible for achieving the reliability of earthquake-resilient bridge infrastructure. | [17,18,19] | |
| Age (REL 7) | Since a newly constructed structure performs better than an aged structure, the age of the structure is crucial for structural reliability. | [17,20] | |
| Design Period (REL 8) | The design philosophy of the bridges has changed over time in terms of seismic considerations. | [21,22] | |
| Bridge geometry (REL 9) | Bridge geometry is a significant component of earthquake resilience because particular designs, such as skewed bridges, are more sensitive than straight bridges regarding seismic resilience. | [23,24] | |
| Recovery | Structural Monitoring (REC 1) | Constant monitoring is essential to continuously provide the status of bridges and thus determine complications at the proper time and perform quick recovery measures. | [25,26] |
| Maintenance (REC 2) | Regular and proper maintenance programs make a bridge more capable of securing speedy recuperation. | [26] | |
| Degree of damage (REC 3) | The pace of recovery is proportional to the degree of damage since the greater the extent of damage, the slower the recovery pace. | [27] | |
| Structural Importance (REC 4) | A significant determinant for decision-makers is whether spending resources on bridge rehabilitation is worthwhile. | [25] | |
| Availability of Resources (REC 5) | The availability of construction materials has a significant impact on the pace of recovery. | [14] | |
| Approachability (REC 6) | Bridge infrastructure recovery requires special tools and instruments; hence, obstacles in accessing the location affect the recovery process. | [14] |
| Decision Makers | Profile | Experience (Years) | Roll in Work/Designation |
|---|---|---|---|
| DM 1 | PhD. P. Eng. | 11 | Assistant Professor, Structural Engineering Dept. and Former Bridge Design Engineer |
| DM 2 | MSc. P. Eng. | 31 | Senior Principal Engineer (Transport infrastructure) |
| DM 3 | MSc. | 11 | Bridge Project Manager, Govt. Transport Institution |
| DM 4 | MSc. | 10 | Bridge Project Manager, Govt. Transport Institution |
| DM 5 | MSc. | 10 | Researcher, Bridge Engineering and Former Bridge Design Engineer, Govt. Transport Institution |
| Reliability Factors | Recovery Factors | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | D | R | D + R | D − R | Parameter | D | R | D + R | D − R |
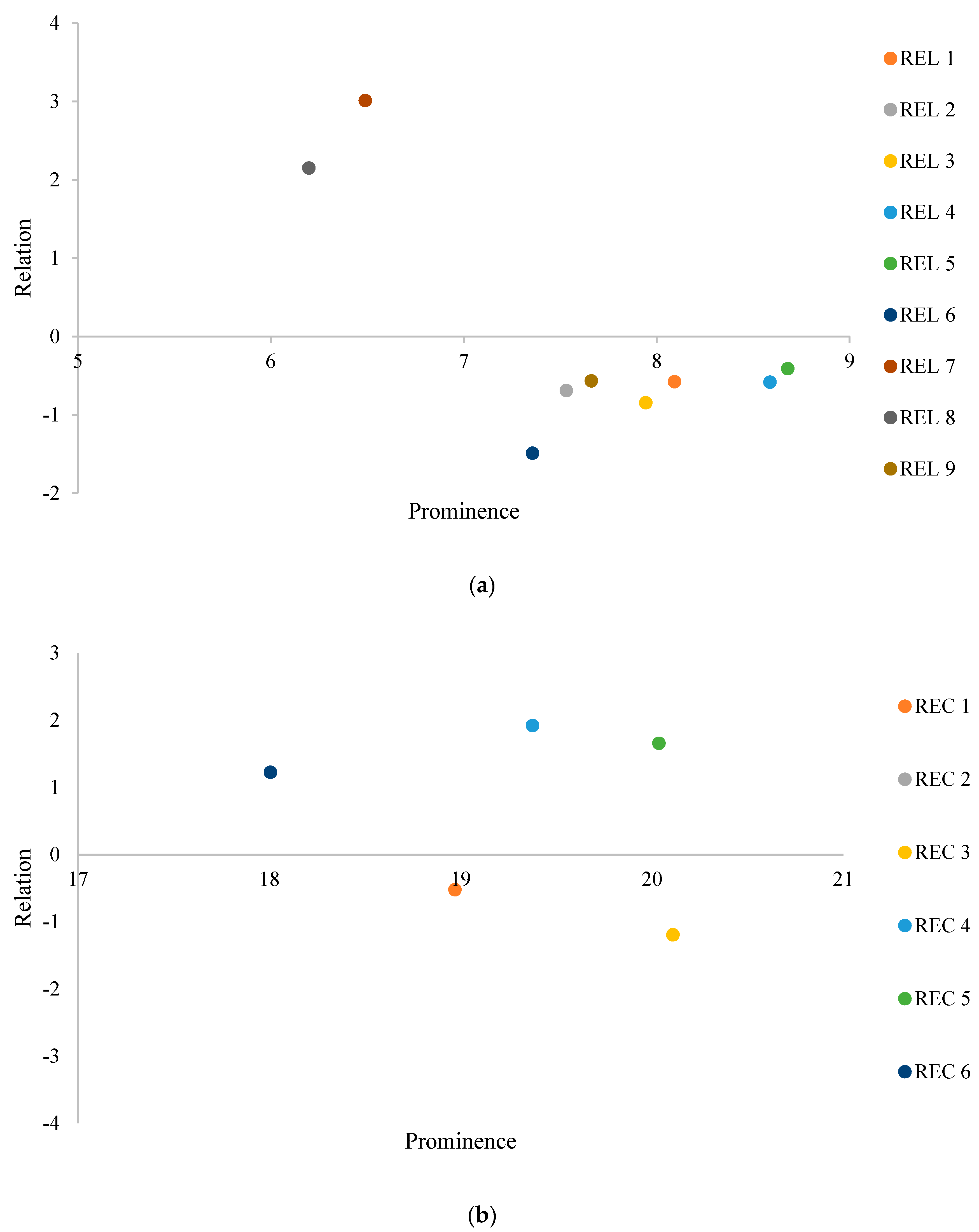
| REL1 | 3.76 | 4.33 | 8.09 | −0.58 | REC1 | 9.22 | 9.75 | 18.97 | −0.52 |
| REL2 | 3.42 | 4.11 | 7.53 | −0.69 | REC2 | 10.06 | 13.15 | 23.21 | −3.08 |
| REL3 | 3.55 | 4.39 | 7.94 | −0.84 | REC3 | 9.46 | 10.65 | 20.11 | −1.19 |
| REL4 | 4.00 | 4.59 | 8.59 | −0.58 | REC4 | 10.65 | 8.73 | 19.38 | 1.92 |
| REL5 | 4.13 | 4.55 | 8.68 | −0.41 | REC5 | 10.85 | 9.19 | 20.04 | 1.66 |
| REL6 | 2.93 | 4.42 | 7.36 | −1.49 | REC6 | 9.62 | 8.39 | 18.01 | 1.23 |
| REL7 | 4.75 | 1.74 | 6.49 | 3.01 | |||||
| REL8 | 4.17 | 2.02 | 6.20 | 2.15 | |||||
| REL9 | 3.55 | 4.11 | 7.66 | −0.57 | |||||
| Reliability Factors | Recovery Factors | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | D | R | D + R | D − R | Parameter | D | R | D + R | D − R |
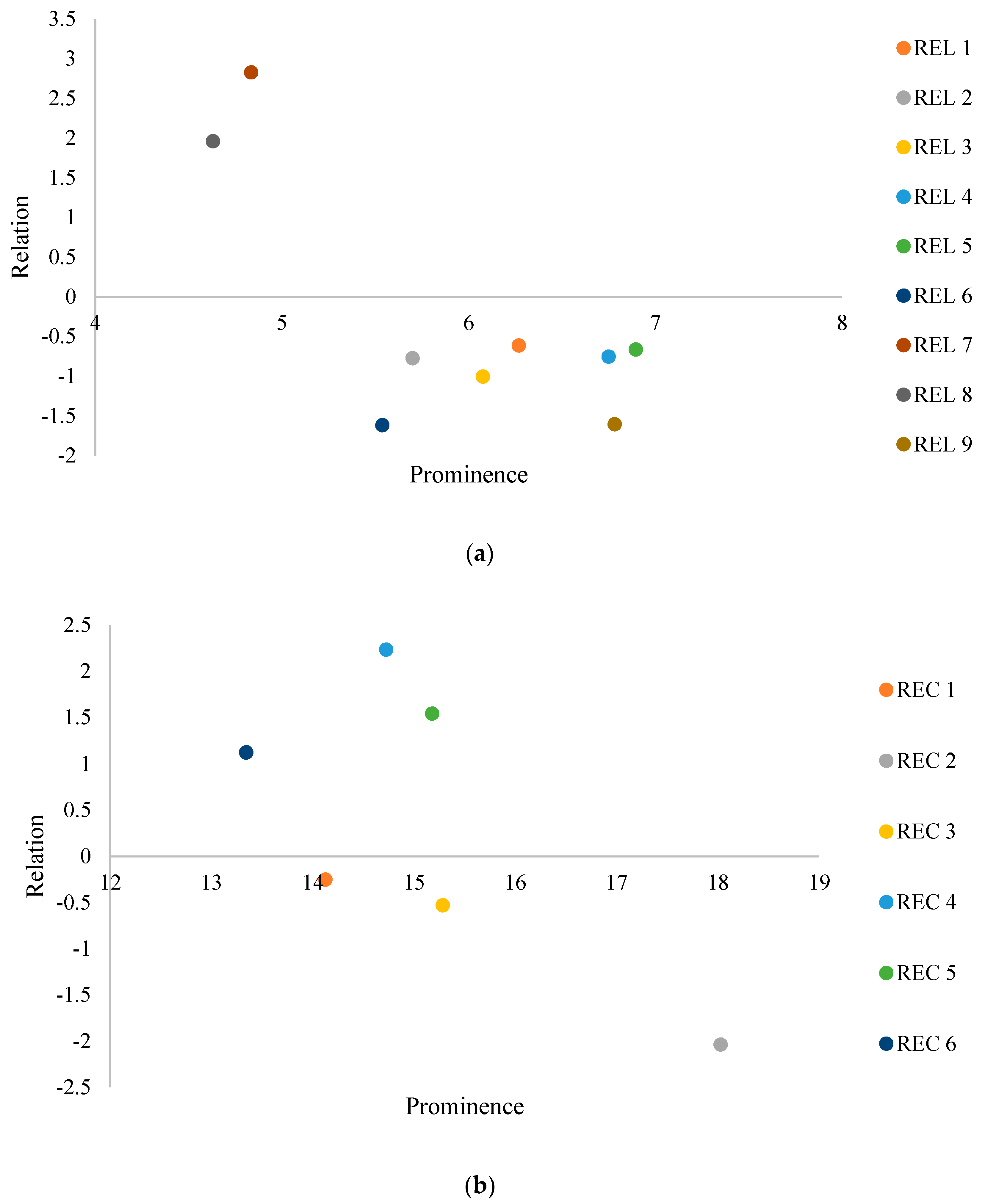
| REL1 | 2.83 | 3.44 | 6.27 | −0.61 | REC1 | 6.94 | 7.19 | 14.12 | −0.25 |
| REL2 | 2.46 | 3.24 | 5.70 | −0.77 | REC2 | 8.00 | 10.03 | 18.03 | −2.04 |
| REL3 | 2.54 | 3.54 | 6.08 | −1.01 | REC3 | 7.38 | 7.91 | 15.28 | −0.53 |
| REL4 | 3.00 | 3.75 | 6.75 | −0.75 | REC4 | 8.48 | 6.25 | 14.72 | 2.23 |
| REL5 | 3.12 | 3.78 | 6.90 | −0.66 | REC5 | 8.36 | 6.82 | 15.18 | 1.54 |
| REL6 | 1.96 | 3.58 | 5.54 | −1.62 | REC6 | 7.23 | 6.11 | 13.34 | 1.12 |
| REL7 | 3.83 | 1.01 | 4.84 | 2.82 | |||||
| REL8 | 3.29 | 1.34 | 4.63 | 1.96 | |||||
| REL9 | 2.59 | 4.20 | 6.78 | −1.61 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Román, Á.F.G.; Khan, M.S.A.; Kabir, G.; Billah, M.; Dutta, S. Evaluation of Interaction between Bridge Infrastructure Resilience Factors against Seismic Hazard. Sustainability 2022, 14, 10277. https://doi.org/10.3390/su141610277
Román ÁFG, Khan MSA, Kabir G, Billah M, Dutta S. Evaluation of Interaction between Bridge Infrastructure Resilience Factors against Seismic Hazard. Sustainability. 2022; 14(16):10277. https://doi.org/10.3390/su141610277
Chicago/Turabian StyleRomán, Ángel Francisco Galaviz, Md Saiful Arif Khan, Golam Kabir, Muntasir Billah, and Subhrajit Dutta. 2022. "Evaluation of Interaction between Bridge Infrastructure Resilience Factors against Seismic Hazard" Sustainability 14, no. 16: 10277. https://doi.org/10.3390/su141610277
APA StyleRomán, Á. F. G., Khan, M. S. A., Kabir, G., Billah, M., & Dutta, S. (2022). Evaluation of Interaction between Bridge Infrastructure Resilience Factors against Seismic Hazard. Sustainability, 14(16), 10277. https://doi.org/10.3390/su141610277







