Is COVID-19 Herd Immunity Influenced by Population Densities of Cities?

Abstract

The objective of the current study is to compare between densely and sparsely populated cities in the context of herd immunity against the SARS-CoV-2 virus. The sample refers to 46 (45) densely populated (sparsely populated) Israeli cities and towns, whose population density is below (above) the median of 2388 $\frac{persons}{sq.km}$, covering above $64.3\%$ of the entire Israeli population. Findings suggest, on the one hand, a higher projected scope of morbidity per 10,000 persons in sparsely populated cities with zero prevalence of vaccination (37.79 vs. 17.61 cases per 10,000 persons). On the other hand, the outcomes propose a steeper drop in the scope of COVID-19 morbidity with higher vaccination rates in sparsely populated cities. Findings suggest that in terms of vaccination campaigns, below 60–70 percent vaccination rates, more efforts should be invested in sparsely populated cities. If, however, the 70 percent threshold is achieved, a further reduction in the scope of morbidity would require a higher (lower) rate of vaccination in densely populated (sparsely populated) cities.

1. Introduction

Previous literature demonstrates that the urbanization process, proxied by high population densities, have both advantages and disadvantages in the context of the COVID-19 pandemic. On the one hand, higher densities facilitate provision of services for citizens in-need at the time of social distancing orders [1]. Compact areas have superior health and educational systems that are more prepared to handle pandemics, leading to higher rates of recovery and lower rates of mortality [2,3]. Also, denser environments facilitate human connections with neighbors, families, and friends, while they are sheltering in place [3]. On the other hand, in the United States, population density alone explains 57–76% of the variation (R-squared) in the spread of the COVID-19 pandemic [4]. This may be explained by the assumption that denser environments facilitate elevated interactions among people, which, in turn, raise the prospects of higher morbidity [3].

The objective of the current study is twofold. The first objective is to investigate the impact of vaccination rates on the scope of COVID-19 morbidity and compare between sparsely and densely populated cities. The second objective is to estimate the threshold required to reach herd immunity in sparsely and densely populated cities. This is defined as the threshold vaccination rate required to support the null hypothesis of zero scope of morbidity.

The sample refers to 91 Israeli cities and towns (covering above $64.3\%$ of the entire Israeli population), where the number of active COVID-19 cases per 10,000 persons ≥ 0. The two types of cities are defined based on the median population density of 2388 $\frac{persons }{sq.km}$ where densely-populated (sparsely-populated) cities are above (below) the median.

Findings suggest, on the one hand, a higher projected scope of morbidity per 10,000 persons in sparsely populated cities with zero prevalence of vaccination (37.79 vs. 17.61 cases per 10,000 persons). On the other hand, the outcomes propose a steeper drop in the scope of COVID-19 morbidity with higher vaccination rates in sparsely populated cities. The intersection point between the two lines is given at a vaccination rate of 70 percent, and a 6.69 cases per 10,000 persons. Starting from a vaccination rate of 60 percent, the null hypothesis that projected scope of morbidity per 10,000 persons is equal in sparsely and densely populated cities cannot be rejected. These findings are further corroborated by statistical tests. In sparsely (densely) populated cities, starting from a vaccination rate of 75 percent (85 percent), the null hypothesis of zero cases per 10,000 persons cannot be rejected.

The contributions of the article are threefold:

(1)

Many studies stress the lack of knowledge and the limited understanding of the factors influencing herd immunity (e.g., [5,6,7,8,9,10,11]). Neagu (2020) [9], for example, states that: “information on the long-term immune response against SARS-CoV-2 is yet scarce.” (Abstract). Avoidance of further spread of the pandemic and investigation of the efficiency of COVID-19 vaccination might prove to be especially important from a public policy perspective.

(2)

We attempt to address an unexplored question, as to whether instead of a country level, COVID-19 herd immunity can evolve at a city level.

(3)

We propose and apply a new methodology to estimate herd immunity in cities, which makes use of population density. Based on the median population density in the sample, we classify cities according to sparsely vs. densely populated municipalities, and examine the impact of population density on the formation of herd immunity.

The remainder of this article is organized as follows: Section 2 gives descriptive statistics and methodology; Section 3, the results; and Section 4 and Section 5 provide a discussion, conclusion, and summary.

2. Materials and Methods

2.1. Descriptive Statistics

This research is based on information obtained from the Israeli Ministry of Health [12] and the Israeli Central Bureau of Statistics [13]. A grid of the two files are given at a city level, on which the two files were merged.

Table 1. Descriptive statistics.

(a) Description of Variables
Variable	Description
$Cases\_per\_{\mathrm{10,000}}_t$	COVID-19 active cases divided by the population of the city and multiplied by 10,000.
$Population\_densit{y}_t$	Population density measured as $\frac{persons}{sq.km}$.
$Median\_densit{y}_t$	1 = Above or equal to the median population density; 0 = otherwise.
$Second\_Vaccinatio{n}_t$	Percent of vaccinated persons in the city multiplied by 100.
(b) Active Cases ≥ 0.
Variable	Obs	Mean	Median	Std. Dev.	Min	Max
$Cases\_per\_{\mathrm{10,000}}_t$	91	10.54396	5.0	15.43522	0	85.4
$Population\_densit{y}_t$	91	3711.9780	2388	4037.0320	67	26,512
$Median\_densit{y}_t$	91	0.4945	0.0000	0.5027	0	1
$Second\_Vaccinatio{n}_t$	91	57.3662	61.76	15.4098	18.22	80.21

Notes: The table refers to $t=1,2,3,\cdots ,91$ Israeli cities and towns (covering above 5,928,628 persons consisting of above $64.3\%=\frac{\mathrm{5,928,628}}{\mathrm{9,217,000}}$ of the entire Israeli population), where the number of active COVID-19 cases per 10,000 persons ≥ 0.

reports on the descriptive statistics of the variables subsequently incorporated in the regression analysis. The table refers to 91 Israeli cities and towns (covering more than 5.9 million people ($64.3\%=\frac{5,928,628}{9,217,000}$ of the entire Israeli population), where the number of active COVID-19 cases per 10,000 persons ≥ 0.

The mean number of COVID-19 active cases per 10,000 persons is 10.5 and the median is 5.0. The implication is right-tailed distribution (skewness of 2.527), where in a few (many) cities the active COVID-19 cases per 10,000 persons is high (low). The null hypothesis of symmetrical distribution is clearly rejected (adjusted calculated Chi² with two degrees of freedom of 47.72, compared to the 1% critical Chi², with two degrees of freedom of 9.21). Consequently, the right-tailed distribution is validated statistically. The standard deviation is 15.435 and the 99% confidence interval is (6.286, 14.802). Finally, the minimum number of cases per 10,000 persons is zero (no active cases) and the maximum is 85.4 active cases per 10,000 persons.

The mean population density is 3712 $\frac{persons }{sq.km}$ and the median is 2388 $\frac{persons }{sq.km}$. Once again, the implication is right tailed distribution (skewness of 2.829), where a few cities are densely populated, and many cities are sparsely populated. Again, given that the null hypothesis of symmetrical distribution is clearly rejected (adjusted calculated Chi² with two degrees of freedom of 55.96, compared to the 1% critical Chi² with two degrees of freedom of 9.21), this conclusion is validated statistically. The standard deviation is 15.435 and the 99% confidence interval is (2598, 4826). Finally, the minimum population density is 67 $\frac{persons }{sq.km}$ (Mizpe Ramon in the Negev desert) and the maximum is 26,512 $\frac{persons }{sq.km}$ (the ultra-Orthodox city of Bnei Berak).

Referring to the variable median density, which equals 1 if the population density of the city is above or equal to the median population density (2388 $\frac{persons }{sq.km}$); 0 = otherwise, as anticipated, the null hypothesis of equality of the mean to 0.5 cannot be rejected. The calculated t-value with 90 degrees of freedom is minus 0.1043 and the corresponding p-value is 0.9172.

Finally, the mean percent of persons who were vaccinated twice is 57.37, and the median is 61.76. This indicates left-tailed distribution (skewness of minus 1.112), where in many (few) cities, the percent of vaccinated population is high (low). The null hypothesis of symmetrical distribution is clearly rejected (adjusted calculated Chi² with two degrees of freedom of 13.12, compared to the 1% critical Chi² with two degrees of freedom of 9.21). Consequently, the left-tailed distribution is validated statistically. The standard deviation is 15.41 and the 99% confidence interval is (53.12, 61.62). Finally, the minimum percent of vaccinated persons is 18.22 and the maximum is 80.21.

2.2. Methods

Consider the following model consisting of two structural equations:

$$\begin{array}{c}Cases\_per\_{\mathrm{10,000}}_t\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\alpha }_0+{\alpha }_{1}Median\_densit{y}_t+{\alpha }_{2}Second\_Vaccinatio{n}_t\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\alpha }_{3}Median\_densit{y}_t\times Second\_Vaccinatio{n}_t+u_t\hfill \end{array}$$

(1)

$$u_t=\rho u_{t-1}+{\in }_t$$

(2)

where $t=1, 2, 3,\cdots , 91$ cities and towns are spatially organized from south to north based on longitudes and latitudes; $Cases\_per\_{\mathrm{10,000}}_t$ is the dependent variable (reflecting the scope of COVID-19 morbidity); $Median\_densit{y}_t$, $Second\_Vaccinatio{n}_t$ are the independent variables; ${\alpha }_0,{\alpha }_1,{\alpha }_2,\rho$ are parameters ($\rho$ is the first-order serial correlation); and ${\in }_t$ is the classical random disturbance term.

Equation (1) is well defined in the literature as an interaction model (e.g., [14] pp. 241–243, 290–305; [15] pp. 198–199). It divides the 91 cities into two equal groups based on the variable $Median\_densit{y}_t$. A densely populated city ($Median\_densit{y}_t=1$) is defined as a city with a population density above or equal to the median. A sparsely populated city ($Median\_densit{y}_t=0$) is defined as a city with a population density below the median. Consequently, Equation (1) may be split into two equations:

$$Median\_densit{y}_t=0:Cases\_per\_{\mathrm{10,000}}_t={\alpha }_0+{\alpha }_{2}Second\_Vaccinatio{n}_t+u_t$$

$$\begin{array}{c}Median\_densit{y}_t=1:Cases\_per\_{\mathrm{10,000}}_t\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left({\alpha }_0+{\alpha }_1\right)+({\alpha }_2+{\alpha }_3) Second\_Vaccinatio{n}_t+u_t\hfill \end{array}$$

The implication is that ${\alpha }_1$ is the constant-term difference between densely and sparsely populated cities (i.e., the difference in projected COVID-19 morbidity between sparsely and densely populated cities with zero rate of vaccination). ${\alpha }_3$ is the slope difference between densely and sparsely populated cities (i.e., the difference in projected COVID-19 morbidity between sparsely and densely populated cities following a one percent increase in the vaccination rate).

Referring to the meaning of the parameters in Equation (1):

Derivation of $Cases\_per\_{\mathrm{10,000}}_t$ with respect to $Median\_densit{y}_t$ gives $\frac{\partial Cases\_per\_{\mathrm{10,000}}_t}{\partial Median\_densit{y}_t}={\alpha }_1+{\alpha }_{3}Second\_Vaccinatio{n}_t$. The implication is that for a city where 30 percent of the population received the second vaccination, a shift from a sparsely populated to a densely populated city is associated with a change of ${\alpha }_1+{\alpha }_3\times 30$ in the projected prevalence of COVID-19 morbidity. For a city where 50 percent of the population received the second vaccination, a shift from a sparsely populated to a densely populated city is associated with a change of ${\alpha }_1+{\alpha }_3\times 50$ in the projected prevalence of morbidity.

Derivation of $Cases\_per\_{\mathrm{10,000}}_t$ with respect to $Second\_Vaccinatio{n}_t$ gives $\frac{\partial Cases\_per\_{\mathrm{10,000}}_t}{\partial Second\_Vaccinatio{n}_t}={\alpha }_1+{\alpha }_{3}Median\_densit{y}_t$. The implication is that for a densely populated city, a one unit increase in the vaccination rate is associated with a change of ${\alpha }_1+{\alpha }_3$ in the projected prevalence of morbidity. For a sparsely populated city, a one unit increase in the vaccination rate is associated with a change of ${\alpha }_1$ in the projected prevalence of morbidity.

Equation (2) gives the specification of the first-order serial correlation (AR (1)). This is a standard model in time series analysis. One of the classical assumptions of the regression model states the lack of first order serial correlation, namely, for Equation (2) $\rho =0$. Usually, in time series analysis $\rho \ne 0$. If this is the case, Prais-Winsten regression is the best way to correct this problem ([16], [17] pp. 188–192, [18]).

3. Results

Table 2. Regression Analysis.

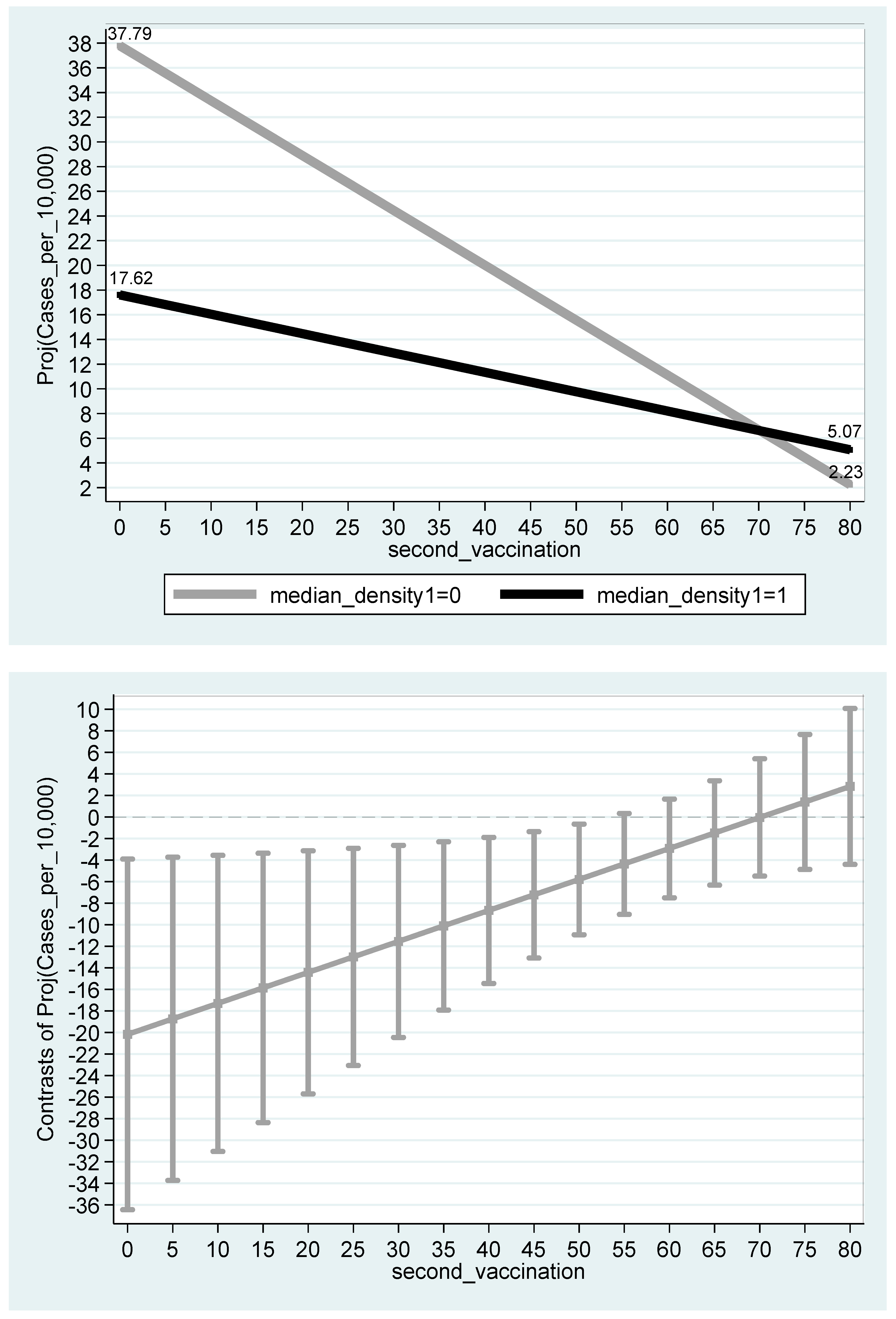
	(1)
Variables	$Cases\_per\_{\mathrm{10,000}}_t$
Constant	37.79 ***
	(8.96 × 10−9)
$Median\_densit{y}_t$	−20.17 **
	(0.0171)
$Second\_Vaccinatio{n}_t$	−0.444 ***
	(1.90 × 10−5)
$Median\_densit{y}_t\times Second\_Vaccinatio{n}_t$	0.288 **
	(0.0364)
Observations	91
R-squared	0.219

Notes: Based on Prais-Winsten regression for spatial autocorrelation. p-values are given in parentheses. ** p < 0.05; *** p < 0.01.

reports regression outcomes, based on Prais-Winsten regression for spatial autocorrelation. To obtain estimation outcomes, we employed Stata 16.1 software package. Figure 1 (top) describes the projected scope of COVID-19 morbidity vs. the percent of vaccinated persons for densely populated (equal to or above the median population density of 2388 $\frac{persons }{sq.km}$) and sparsely populated (below the median population density of 2388 $\frac{persons }{sq.km}$) cities and towns.

The outcomes show that for both city density types, the projected scope of morbidity drops with a higher level of vaccination. Yet, the pace of the decline is attenuated in densely populated cities. While the anticipated drop in sparsely populated cities is from 37.79 COVID-19 cases for zero percent of vaccination to 2.23 cases per 10,000 persons, the equivalent figures for densely populated cities are from 17.61 to 5.07 COVID-19 cases, respectively. The intersection point between the two lines is given at a vaccination rate of 70 percent, and the scope of morbidity at the intersection point is 6.69 cases per 10,000 persons. (This intersection point is calculated as follows: The estimated equation in Table 1 is: $proj\left(Cases\_per\_\mathrm{10,000}\right)=37.79-20.17\times Median\_density-0.444\times Second\_vaccination+0.288\times Median\_density\times Second\_vaccination$. Substitution of $Median\_density=1$ yields: (1)$proj\left(Cases\_per\_\mathrm{10,000}\right)=17.62-0.156\times Second\_vaccination$ (the regression line for 46 densely populated cities). Substitution of $Median\_density=0$ gives: (2) $proj\left(Cases\_per\_\mathrm{10,000}\right)=37.79-0.444\times Second\_vaccination$ (the regression line for 46 sparsely populated cities). Solving the system of Equations (1) and (2) yields (70.035, 6.6945)).

The bottom part of the figure provides the projected differences between densely and sparsely populated cities for each level of vaccination, and their 95% confidence intervals. As the bottom figure demonstrates, up to 50 percent vaccination, the projected difference is statistically significant at the 5% level.

Finally, Figure 2 gives the projected scope of COVID-19 morbidity vs. the percent of vaccinated persons for densely populated and sparsely populated cities separately, with 95% confidence interval for each projected value. According to our proposed definition of herd immunity, this is achieved for vaccination rates where the null hypothesis of zero cases per 10,000 persons cannot be rejected. As can be seen from the figure, it further corroborates our previous findings. In sparsely populated cities, starting from a vaccination rate of 75 percent, the null hypothesis of zero cases per 10,000 persons cannot be rejected. In contrast, for densely populated cities, the vaccination threshold required to support the conclusion of zero cases per 10,000 persons is removed to 85 percent.

4. Discussion

The concept of herd immunity is used to describe the threshold of immune individuals that will lead to a decrease in disease incidence [19]. Herd immunity is considered a dynamic concept that may vary from one disease to another, and from one region to another [20,21,22]. Kalish et al. (2020) [21] estimated ratios of between 1.8 and 12.2 for different regions of the U.S. as of the summer of 2020, with recent estimates closer to 4.

Table 3. Values of herd immunity thresholds (HITs) of well-known infectious diseases.

Disease	Transmission	HIT	Reference Number
Measles	Aerosol	92–94%	[23,24]
Chickenpox (varicella)	Aerosol	90–92%	[25]
Mumps	Respiratory droplets	90–92%	[26]
Rubella	Respiratory droplets	83–86%	[27,28,29]
Polio	Fecal–oral route	80–86%	[27,28,29]
Pertussis	Respiratory droplets	82%	[30,31]
COVID-19 (Delta variant)	Respiratory droplets and aerosol	80%	[22,32,33]
Smallpox	Respiratory droplets	71–83%	[34,35]
COVID-19 (Alpha variant)	Respiratory droplets and aerosol	75–80%	[36]
HIV/AIDS	Body fluids	50–80%	[31]
COVID-19 (ancestral strain)	Respiratory droplets and aerosol [37]	65% (58–71%)	[38]
SARS	Respiratory droplets	50–75%	[39]
Diphtheria	Saliva	62% (41–77%)	[40]
Ebola (2014 outbreak)	Body fluids	44% (31–44%)	[41,42]
Influenza (2009 pandemic strain)	Respiratory droplets	37% (25–51%)	[43]
Influenza (seasonal strains)	Respiratory droplets	23% (17–29%)	[44]
Andes hantavirus	Respiratory droplets and body fluids	16% (0–36%)	[37]

See the reference list.

reports the herd immunity required to reduce the level of infection in different diseases. As can be seen from the appendix, at the lowest end, the required proportion of immune persons to generate herd immunity against Andes hantavirus and influenza (seasonal strains) are only 16% and 23%, respectively. At the opposite extreme, the thresholds against chickenpox (varicella) and measles are 90–94% of the population. In that respect, COVID-19 is closer to the upper threshold, with 75–80% threshold for the Alpha variant, 58–71% threshold for the ancestral strain, and 80% threshold for the Delta variant.

5. Conclusions

Previous literature demonstrates that population density is a powerful predictor of the spread of the COVID-19 pandemic. In the United States population, density alone accounts for 57% of the variation (R-squared) and up to 76% in spatial models that account for first order serial autocorrelation [4]. On the other hand, Hamidi et al. (2020) [3] suggest that after controlling for metropolitan size and other confounding variables, county density leads to significantly lower infection rates and lower death rates. This outcome may be explained on the grounds that dense areas have better infrastructure to more effectively put in place measures that foster social distancing, thus reducing actual rates of infection. Density also could make it easier to provide services for citizens in-need at the time of social distancing orders [1]. Compact areas have superior health and educational systems that are more prepared to handle pandemics, leading to higher rates of recovery and lower rates of mortality [2]. Dye (2008) [2] suggests that the low urbanization rates at the beginning of the 19th century (only 10 to 15% of the European population living in urban areas in 1800, compared to 70% of the European population today) may be associated with poor living and health conditions and subsequent spread of pandemics (cholera, dysentery, measles, plague, smallpox, tuberculosis, typhus, and other infections exacerbated by undernourishment), and high rates of infant mortality imposing “urban penalties”. However, by the turn of the 20th century, the picture was gradually reversed. Urban health was typically improving faster than rural health in the industrialized world, and towns and cities grew faster than their hinterlands.

Also, it is possible that denser environments make it easier for people to stay somewhat connected with neighbors, families, and friends, while they are sheltering in place [3].

The objective of the current study is to compare between densely- and sparsely populated cities in the context of herd immunity against the SARS-CoV-2 virus. The sample refers to 91 Israeli cities and towns (covering above $64.3\%$ of the entire Israeli population), where the number of active COVID-19 cases per 10,000 persons ≥0. The two types of cities are defined based on the median population density of 2388 $\frac{persons }{sq.km}$ where densely-populated (sparsely-populated) cities are above (below) the median.

Findings suggest, on the one hand, a higher projected scope of morbidity per 10,000 persons in sparsely populated cities with zero prevalence of vaccination (37.79 vs. 17.61 cases per 10,000 persons). On the other hand, the outcomes propose a steeper drop in the scope of COVID-19 morbidity with higher vaccination rates in sparsely populated cities. The intersection point, between densely and sparsely populated cities, is starting from a vaccination rate of 60 percent; one cannot reject the null hypothesis that projected scope of morbidity per 10,000 persons is equal in sparsely and densely populated cities. Findings are further corroborated by statistical tests. In sparsely (densely) populated cities, starting from a vaccination rate of 75 percent (85 percent), the null hypothesis of zero cases per 10,000 persons cannot be rejected.

These outcomes may be explained as a game between two opposing forces. On the one hand, unlike most of the 19th century [2], the premium associated with denser cities is better health services and health literacy, which, in turn, reduces the scope of morbidity [3]. On the other hand, crowded cities are characterized by more interactions among people, which, in turn elevates the scope of morbidity [4].

Public policy repercussions of the study suggest that below 60–70 percent vaccination rates, more efforts should be invested in promoting vaccination campaigns in sparsely populated cities. Moreover, given the lack of ability to change population densities in the short term, an effort to reach herd immunity against the SAR-CoV-2 virus (reduce the scope of morbidity below the intersection point of 6.69 cases per 10,000 persons), would require higher vaccination rates in densely populated cities. Specifically, if the objective function is to lower the scope of morbidity to 3 cases per 10,000 persons, the required vaccination rate is 93.71 percent (78.36 percent) in densely populated (sparsely-populated) cities. (This may be calculated as follows. Footnote 2 demonstrates that the regression line for the 46 densely populated cities is: (1) $proj\left(Cases\_per\_\mathrm{10,000}\right)=17.62-0.156\times Second\_vaccination$ and the regression line for the 45 sparsley-populated cities is: (2) $proj\left(Cases\_per\_\mathrm{10,000}\right)=37.79-0.444\times Second\_vaccination$. Substitution of $proj\left(Cases\_per\_\mathrm{10,000}\right)=3$ in Equation (1) yields: $second\_vaccination=\frac{14.62}{0.156}=93.71$ percent. Substitution of $proj\left(Cases\_per\_\mathrm{10,000}\right)=3$ in Equation (2) gives: $Second\_vaccination=\frac{34.79}{0.444}=78.36$ percent.).

The limitations of our study are the following: As different mutations evolve over time and space, one cannot predict future levels of herd immunity thresholds; consequently, COVID-19 is not yet fully investigated. In addition, it is possible to explore herd immunity in the context of mortality. Finally, herd immunity is influenced from many confounders, including population structure, population density, and differences in contact rates across demographic groups [10]. The focus of the current study is population densities as a measure for sparsely/densely populated cities. However, future research should incorporate additional confounders.