Concentration-Temporal Multilevel Calibration of Low-Cost PM2.5 Sensors
Abstract
:1. Introduction
2. Materials and Methods
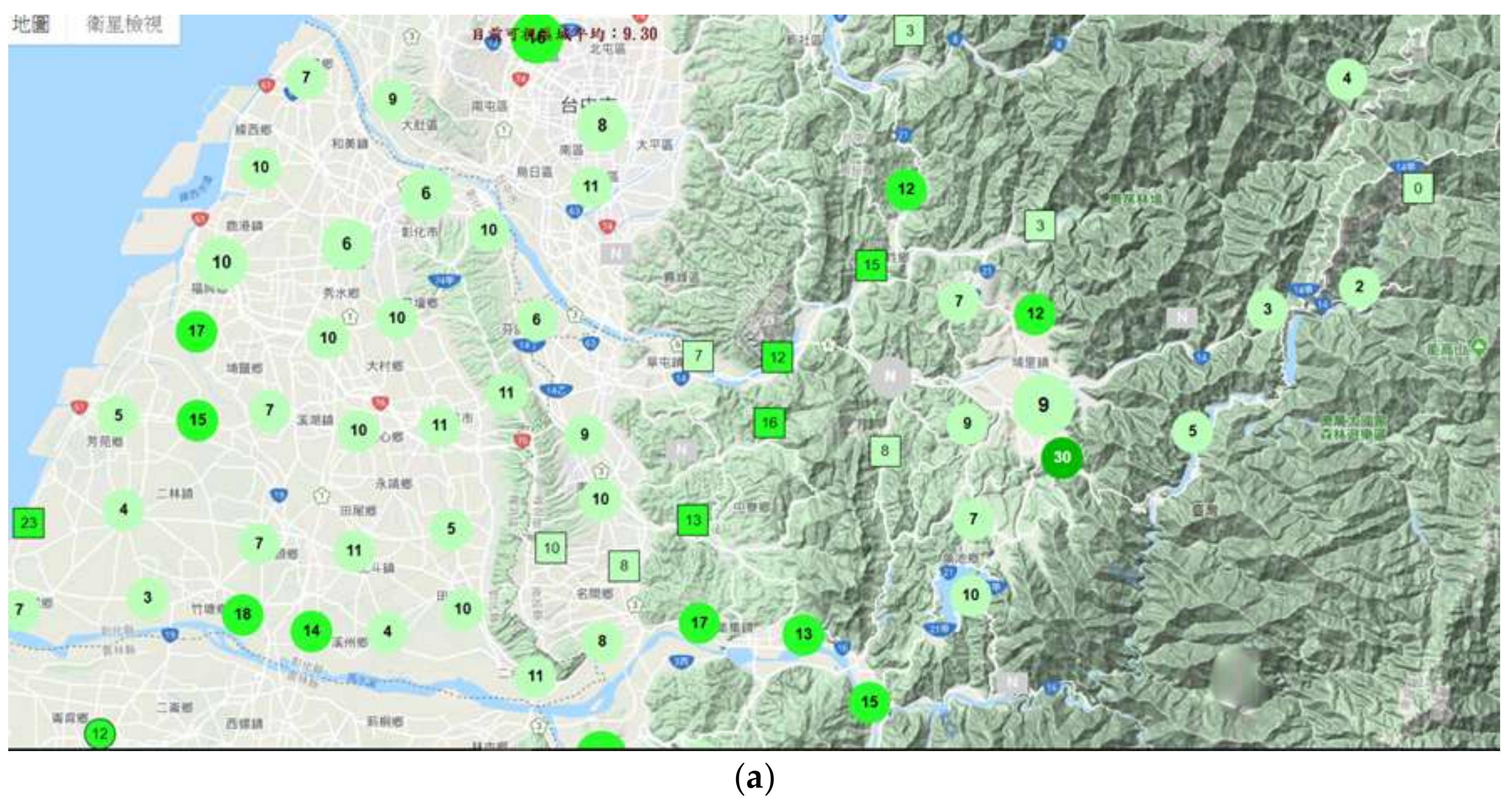
2.1. Deployment of PM2.5 Sensor IoT
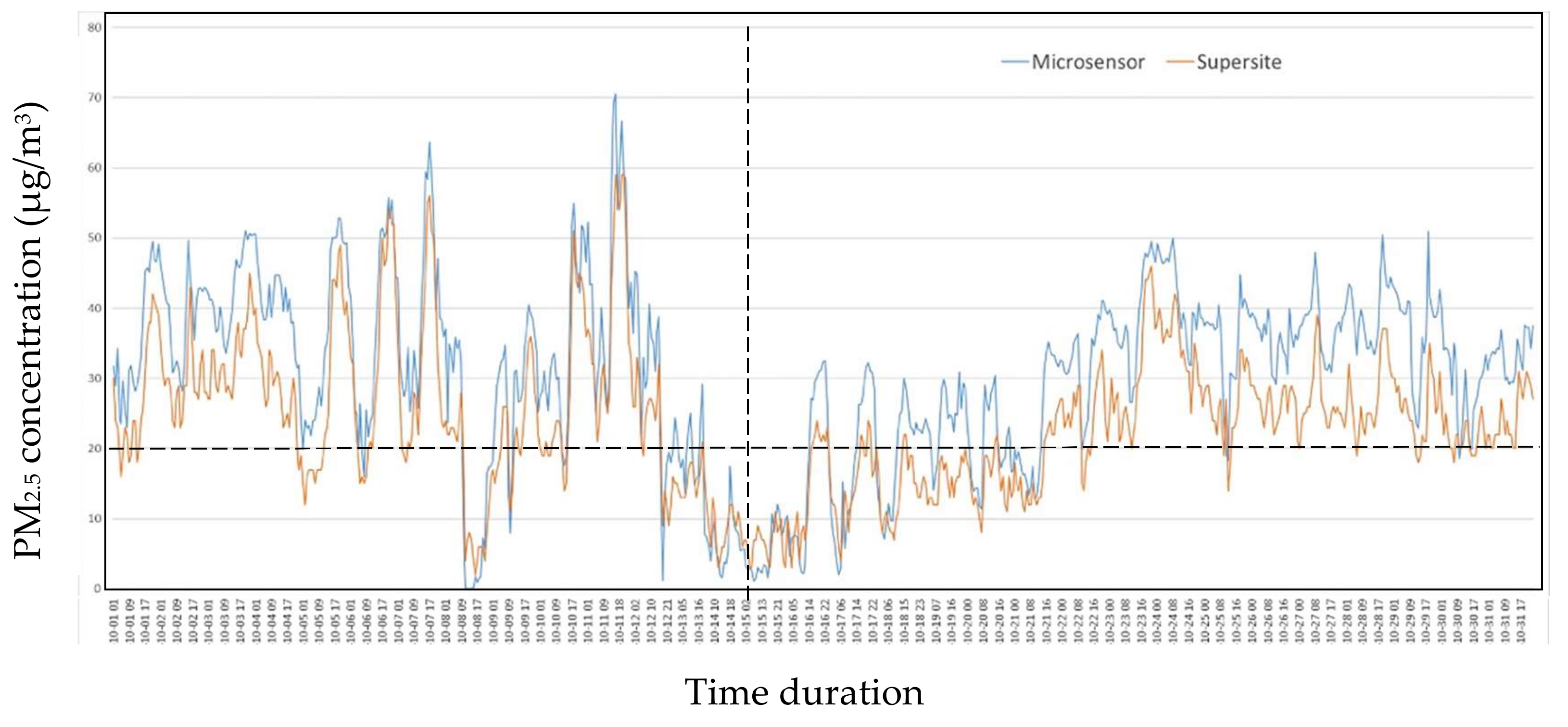
2.2. Field Study
2.3. Concentration-Temporal Multilevel Calibration Model
2.4. Performance Indicators
3. Results
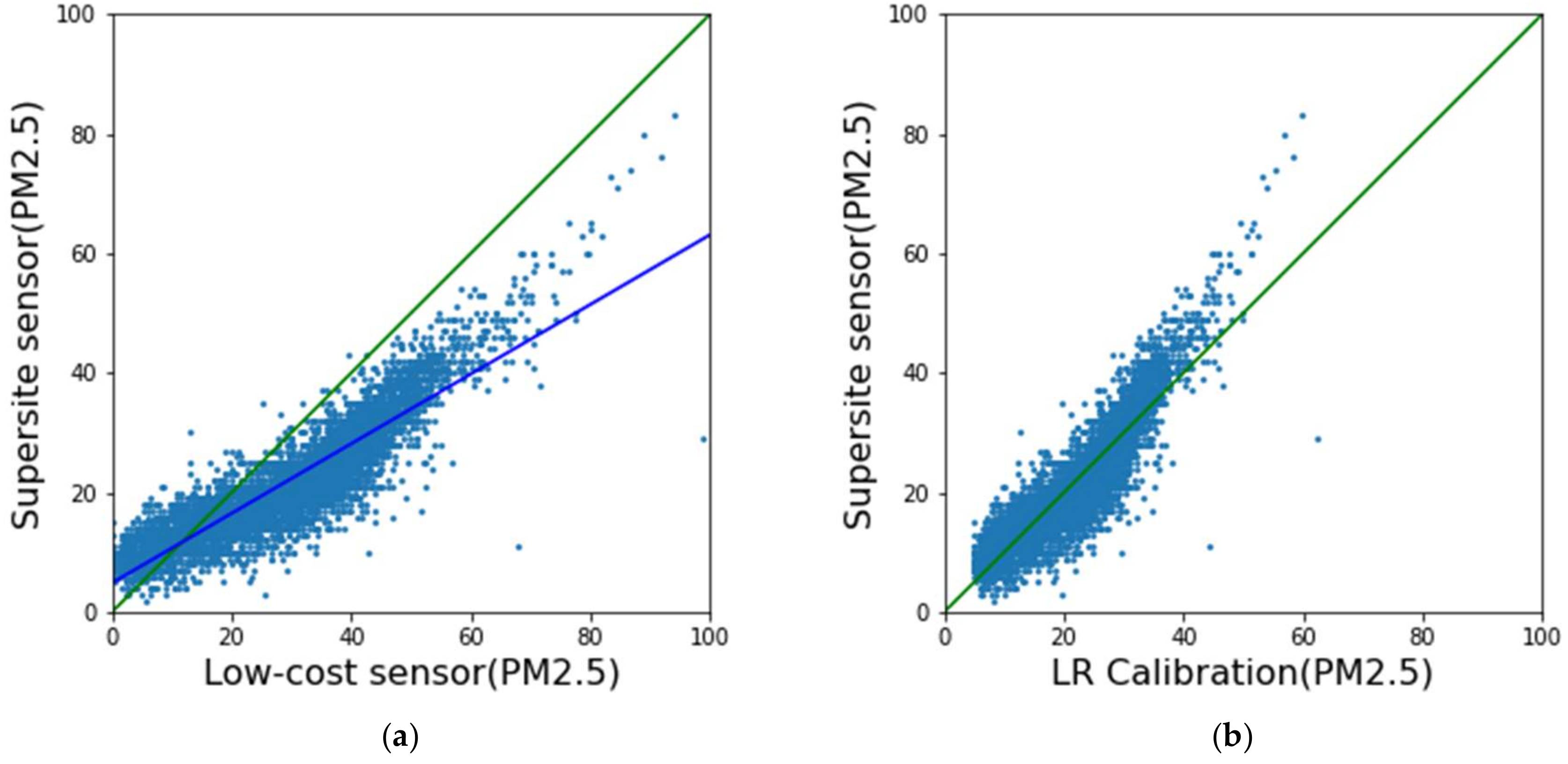
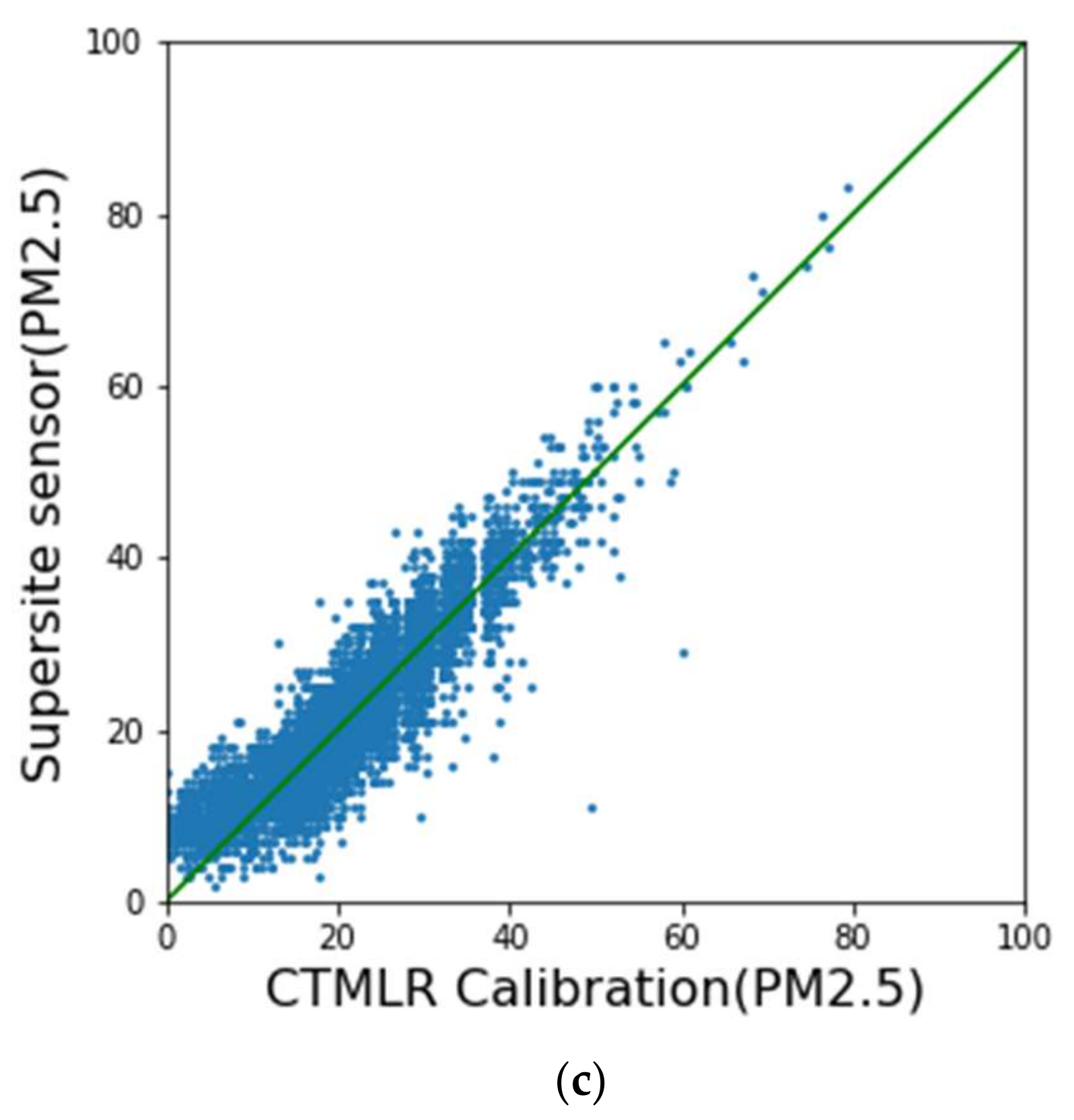
3.1. Validation of CTMLR Calibration
3.2. Comparison with Other Calibration Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, C.; He, J.; Wu, L.; Jin, T.; Chen, X.; Li, R.; Ren, P.; Zhang, L.; Mao, H. Health burden attributable to ambient PM2.5 in China. Environ. Pollut. 2017, 223, 575–586. [Google Scholar] [CrossRef] [PubMed]
- Day, R.F. Developing the Local PM2.5 Monitoring System and the Volunteer Program for Air Protection; Technical Report EPA024 105025; Environmental Protection Administration, Executive Yuan, R.O.C.: Taipei, Taiwan, 2017. [Google Scholar]
- Manikonda, A.; Zíková, N.; Hopke, P.K.; Ferro, A.R. Laboratory assessment of low-cost PM monitors. J. Aerosol Sci. 2016, 102, 29–40. [Google Scholar] [CrossRef]
- Sayahi, T.; Butterfield, A.; Kelly, K. Long-term field evaluation of the Plantower PMS low-cost particulate matter sensors. Environ. Pollut. 2019, 245, 932–940. [Google Scholar] [CrossRef] [PubMed]
- Jayaratne, R.; Liu, X.; Ahn, K.-H.; Asumadu-Sakyi, A.; Fisher, G.; Gao, J.; Mabon, A.; Mazaheri, M.; Mullins, B.; Nyaku, M. Low-cost PM2. 5 sensors: An assessment of their suitability for various applications. Aerosol Air Qual. Res. 2020, 20, 520–532. [Google Scholar]
- Chen, L.J.; Ho, Y.H.; Lee, H.C.; Wu, H.C.; Liu, H.M.; Hsieh, H.H.; Huang, Y.T.; Lung, S.C.C. An open framework for participatory PM2.5 monitoring in smart cities. IEEE Access 2017, 5, 14441–14454. [Google Scholar] [CrossRef]
- Jiao, W.; Hagler, G.; Williams, R.; Sharpe, R.; Brown, R.; Garver, D.; Judge, R.; Caudill, M.; Rickard, J.; Davis, M. Community Air Sensor Network (CAIRSENSE) project: Evaluation of low-cost sensor performance in a suburban environment in the southeastern United States. Atmos. Meas. Tech. 2016, 9, 5281–5292. [Google Scholar] [CrossRef] [PubMed]
- Morawska, L.; Thai, P.K.; Liu, X.; Asumadu-Sakyi, A.; Ayoko, G.; Bartonova, A.; Bedini, A.; Chai, F.; Christensen, B.; Dunbabin, M. Applications of low-cost sensing technologies for air quality monitoring and exposure assessment: How far have they gone? Environ. Int. 2018, 116, 286–299. [Google Scholar] [CrossRef] [PubMed]
- English, P.; Richardson, M.; Garzón-Galvis, C. From crowdsourcing to extreme citizen science: Participatory research for environmental health. Annu. Rev. Public Health 2018, 39, 335–350. [Google Scholar] [CrossRef] [PubMed]
- Yin, P.Y.; Tsai, C.C.; Day, R.F.; Tung, C.Y.; Bhanu, B. Ensemble learning of model hyperparameters and spatiotemporal data for calibration of low-cost PM2.5 sensors. Math. Biosci. Eng. 2019, 16, 6858–6873. [Google Scholar] [CrossRef] [PubMed]
- Castell, N.; Dauge, F.R.; Schneider, P.; Vogt, M.; Lerner, U.; Fishbain, B.; Broday, D.; Bartonova, A. Can commercial low-cost sensor platforms contribute to air quality monitoring and exposure estimates? Environ. Int. 2017, 99, 293–302. [Google Scholar] [CrossRef] [PubMed]
- Kelly, K.; Whitaker, J.; Petty, A.; Widmer, C.; Dybwad, A.; Sleeth, D.; Martin, R.; Butterfield, A. Ambient and laboratory evaluation of a low-cost particulate matter sensor. Environ. Pollut. 2017, 221, 491–500. [Google Scholar] [CrossRef] [PubMed]
- Yin, Q.; Wang, J.; Hu, M.; Wong, H. Estimation of daily PM2.5 concentration and its relationship with meteorological conditions in Beijing. J. Environ. Sci. 2016, 48, 161–168. [Google Scholar] [CrossRef] [PubMed]
- Baker, K.R.; Foley, K.M. A nonlinear regression model estimating single source concentrations of primary and secondarily formed PM2.5. Atmos. Environ. 2011, 45, 3758–3767. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks IV, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD2016), San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Joe, S.; Kuo, F.Y. Remark on algorithm 659: Implementing Sobol’s quasirandom sequence generator. ACM Trans. Math. Softw. (TOMS) 2003, 1, 49–57. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]



| Indicators | Temporal | Concentration (µg/m3) | |||||
|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | LR | ||
| R2 | month | 79% | 79% | 79% | 79% | 79% | 78% |
| season | 80% | 80% | 80% | 80% | 80% | 78% | |
| year | 82.81% | 82.85% | 82.87% | 82.7% | 82.6% | 80% | |
| RMSE | month | 4.99 | 4.9 | 4.9 | 4.9 | 4.9 | 5.0 |
| season | 4.8 | 4.8 | 4.8 | 4.8 | 4.8 | 5.0 | |
| year | 4.51 | 4.503 | 4.502 | 4.52 | 4.53 | 4.7 | |
| NME | month | 0.22 | 0.22 | 0.21 | 0.22 | 0.22 | 0.22 |
| season | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.22 | |
| year | 0.1939 | 0.1938 | 0.1937 | 0.194 | 0.196 | 0.20 | |
| Indicators | Temporal | Concentration (µg/m3) | |||||
|---|---|---|---|---|---|---|---|
| 15 | 16 | 17 | 18 | 19 | 20 | ||
| R2 | month | 79% | 79% | 79% | 80% | 79% | 79% |
| season | 80% | 80% | 80% | 80% | 80% | 80% | |
| year | 82.873% | 82.868% | 82.82% | 82.80% | 82.80% | 82.76% | |
| RMSE | month | 4.9 | 5.0 | 5.0 | 4.9 | 4.9 | 4.9 |
| season | 4.8 | 4.8 | 4.8 | 4.8 | 4.8 | 4.8 | |
| year | 4.502 | 4.501 | 4.51 | 4.51 | 4.52 | 4.52 | |
| NME | month | 0.21 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 |
| season | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | |
| year | 0.1937 | 0.1936 | 0.194 | 0.195 | 0.195 | 0.195 | |
| Indicators | XGBoost Ensembles | ||
|---|---|---|---|
| Sobol | N&M | PSO | |
| R2 | 80% | 78% | 80% |
| RMSE | 5.7 | 5.8 | 5.7 |
| NME | 0.173 | 0.18 | 0.175 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Day, R.-F.; Yin, P.-Y.; Huang, Y.-C.T.; Wang, C.-Y.; Tsai, C.-C.; Yu, C.-H. Concentration-Temporal Multilevel Calibration of Low-Cost PM2.5 Sensors. Sustainability 2022, 14, 10015. https://doi.org/10.3390/su141610015
Day R-F, Yin P-Y, Huang Y-CT, Wang C-Y, Tsai C-C, Yu C-H. Concentration-Temporal Multilevel Calibration of Low-Cost PM2.5 Sensors. Sustainability. 2022; 14(16):10015. https://doi.org/10.3390/su141610015
Chicago/Turabian StyleDay, Rong-Fuh, Peng-Yeng Yin, Yuh-Chin T. Huang, Cheng-Yi Wang, Chih-Chun Tsai, and Cheng-Hsien Yu. 2022. "Concentration-Temporal Multilevel Calibration of Low-Cost PM2.5 Sensors" Sustainability 14, no. 16: 10015. https://doi.org/10.3390/su141610015
APA StyleDay, R.-F., Yin, P.-Y., Huang, Y.-C. T., Wang, C.-Y., Tsai, C.-C., & Yu, C.-H. (2022). Concentration-Temporal Multilevel Calibration of Low-Cost PM2.5 Sensors. Sustainability, 14(16), 10015. https://doi.org/10.3390/su141610015






