Highlighting the Probabilistic Behavior of Occupants’ Preferences in Energy Consumption by Integrating a Thermal Comfort Controller in a Tropical Climate
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Case Study
- Passive: Only natural ventilation through windows (either (1) open or (2) closed) was considered.
- Active: (3) Windows closed and air conditioning equipment turned on are considered.
2.2. Parametric and Sensibility Analysis
2.3. Simplified Thermal Model
2.4. Parametric Optimization
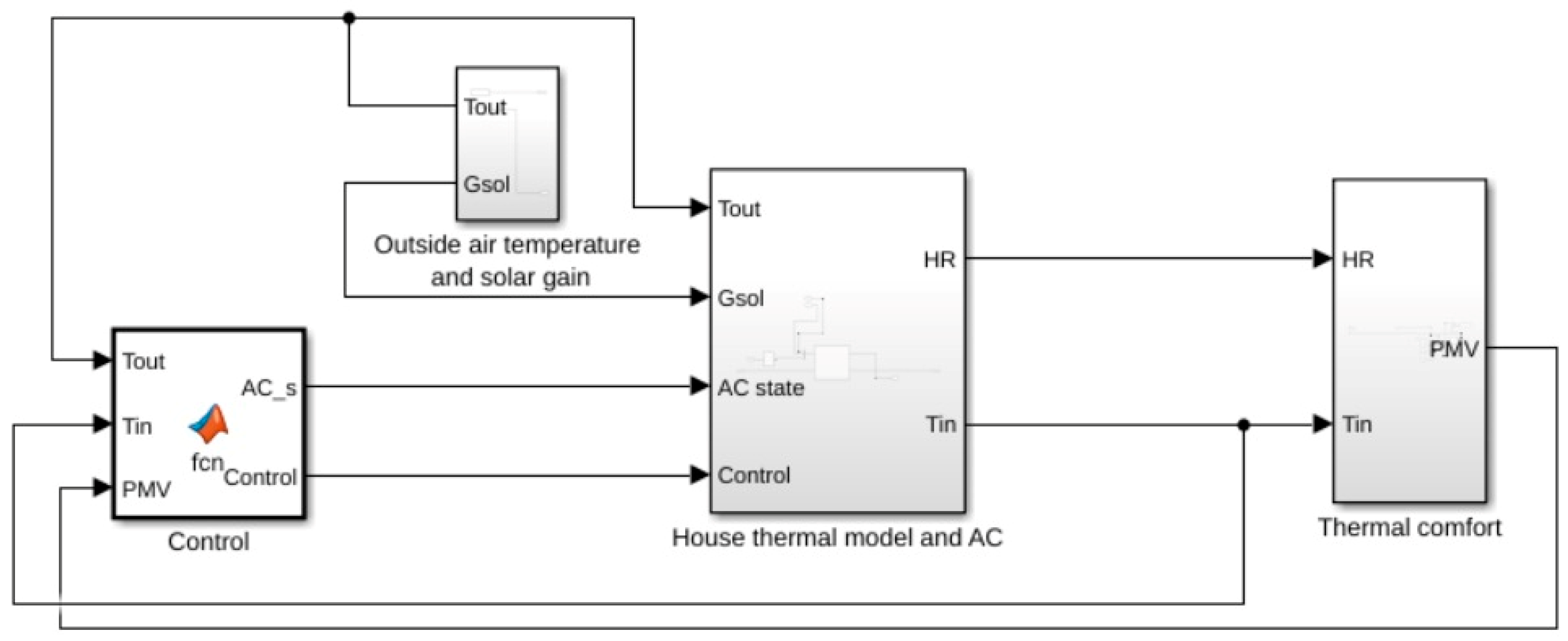
2.5. Simulation Case Selection and Controller Implementation
- Probabilistic scenario, developed by Kim et al. [44] in a study carried out in Australia, where the probability of executing an action with respect to a random number is evaluated, using Equations (5) and (6):where represents the probability, is the indoor temperature.
- Deterministic scenario: It considers a window opening and air conditioning hours obtained from a survey conducted by De León [45] in 33 Panamanian residences.
- Combined model #1: Deterministic and probabilistic scenarios are integrated, giving priority to the probabilistic method.
- Combined model #2: Deterministic and probabilistic scenarios are integrated, giving priority to the deterministic method.
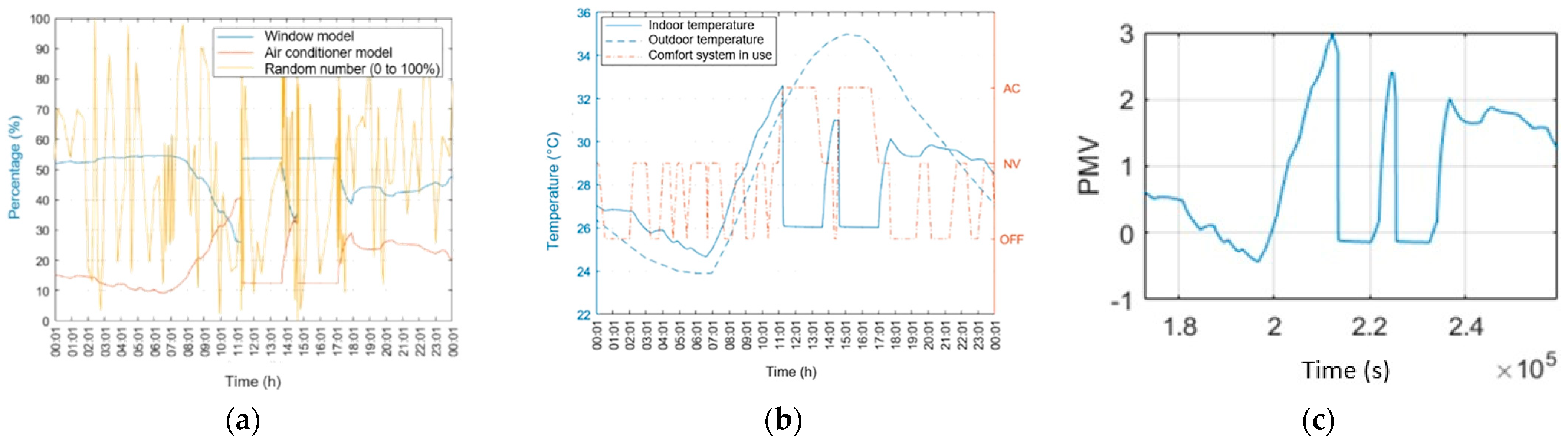
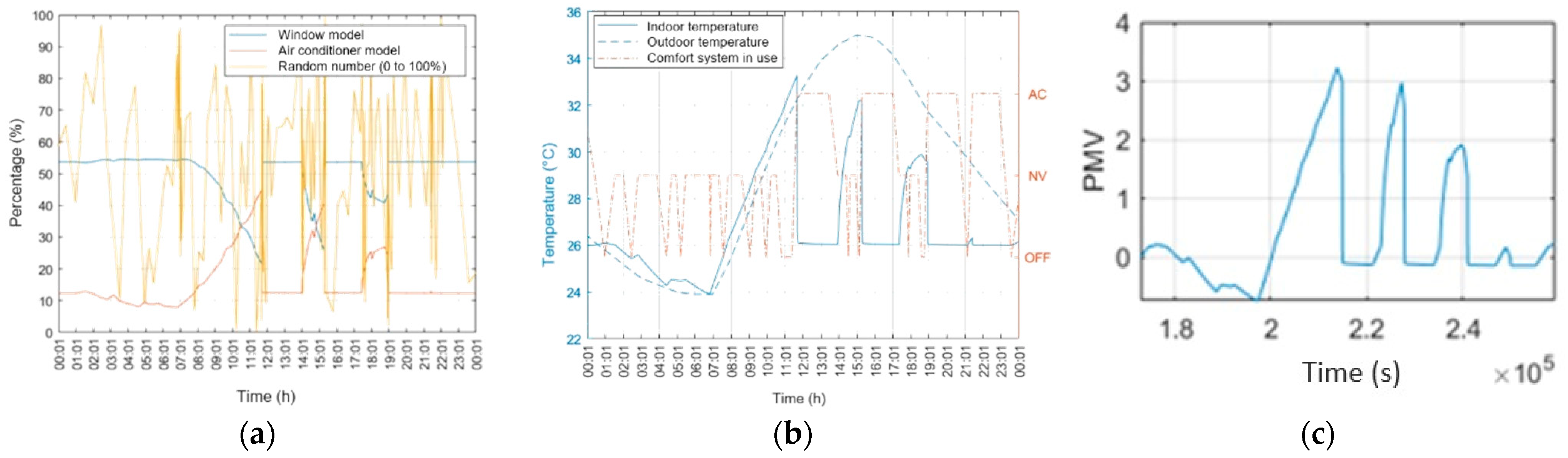
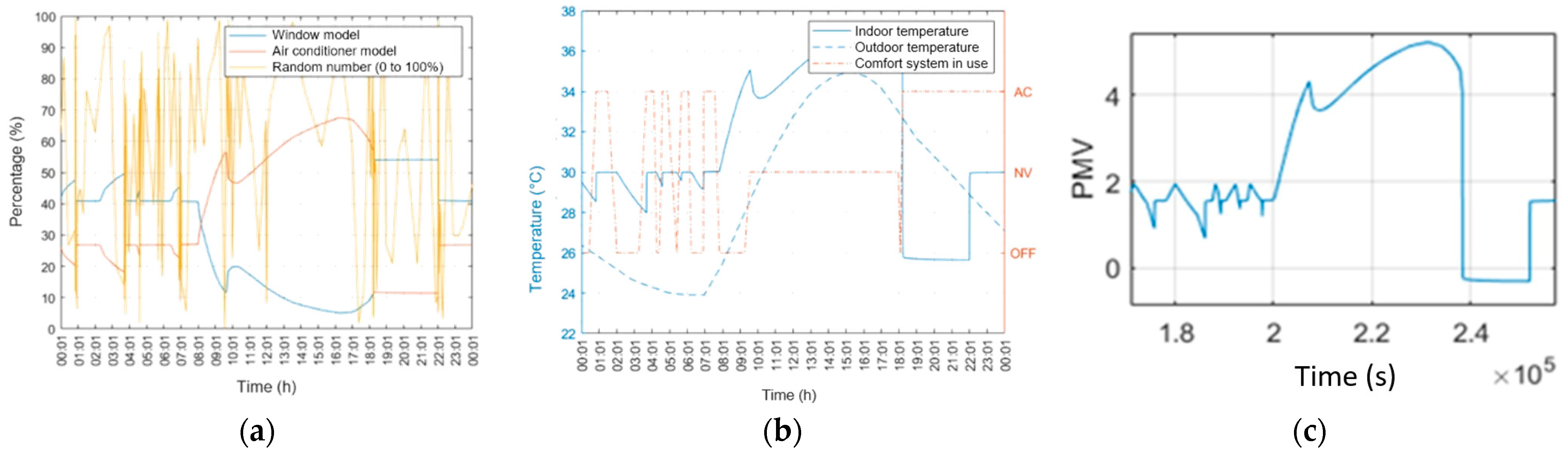
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| T | Temperature | %WWR | Window to Wall Ratio |
| PMV | Predicted mean vote | RC | Resistance–Capacitance |
| ePMV | Extension of the PMV | 4R3C | Four resistance three capacitance thermal model |
| BEM | Building Energy Modeling | 5R3C | Five resistance three capacitance thermal model |
| IoT | Internet of Things | R1 | Windows resistance |
| nZEB | Nearly zero energy building | R2 | External Ceilings and Walls resistance |
| PI | Proportional Integrative | R3 | Internal Ceilings and Walls resistance |
| BR1 | Bedroom 1 | R4 | Floor resistance |
| BR2 | Bedroom 2 | R5 | Air Conditioning resistance |
| CR | Control Room | GSol | Solar Gains |
| LR | Living Room | Tout | Outside Temperature |
| BES | Building Energy System | Tpp | Wall and Celling Temperature |
| U | Heat Transfer coefficient | Tia | Indoor air Temperature |
| HRmax | Maximum Relative Humidity | Tfloor | Floor Temperature |
| HRmin | Minimum Relative Humidity | C1 | Air Capacitance |
| ASHRAE | American Society of Heating, Refrigeration and Air-Conditioning Engineers | C2 | Ceilings and Walls capacitance |
| p | p value | C3 | Floor capacitance |
| met | Metabolic Rate | Tset | Air conditioning set point temperature |
| clo | Clothing Insulation | AC | Air Conditioning |
References
- O’Brien, W.; Wagner, A.; Schweiker, M.; Mahdavi, A.; Day, J.; Kjærgaard, M.B.; Carlucci, S.; Dong, B.; Tahmasebi, F.; Yan, D.; et al. Introducing IEA EBC annex 79: Key challenges and opportunities in the field of occupant-centric building design and operation. Build. Environ. 2020, 178, 106738. [Google Scholar] [CrossRef]
- International Energy Agency. Energy Efficiency 2019; International Energy Agency: Paris, France, 2019; p. 110. [Google Scholar]
- Wagner, A.; O’Brien, W.; Dong, B. Technical Report: Studying Occupant Behavior in Buildings: Methods and Challenges; International Energy Agency: Paris, France, 2017; Available online: http://www.annex66.org/sites/default/files/2018FinalReport/Annex%2066%20Deliverable%20-%20Occupant%20behavior%20study%20guidebook.pdf (accessed on 6 August 2021).
- D’Oca, S.; Chen, C.; Hong, T. Technical Report: An International Survey of Occupant Behavior in Workspaces; International Energy Agency: Paris, France, 2017; Available online: https://iea-ebc.org/Data/publications/EBC_Annex%2066_Occupant_Behavior_Survey.pdf (accessed on 15 August 2021).
- Yao, M.; Zhao, B. Factors affecting occupants’ interactions with windows in residential buildings in Beijing, China. Procedia Eng. 2017, 205, 3428–3434. [Google Scholar] [CrossRef]
- Fajilla, G.; Austin, M.C.; Mora, D.; de Simone, M. Assessment of probabilistic models to estimate the occupancy state in office buildings using indoor parameters and user-related variables. Energy Build. 2021, 246, 111105. [Google Scholar] [CrossRef]
- Mora, D.; Fajilla, G.; Austin, M.C.; de Simone, M. Occupancy patterns obtained by heuristic approaches: Cluster analysis and logical flowcharts. A case study in a university office. Energy Build. 2019, 186, 147–168. [Google Scholar] [CrossRef]
- Fabi, V.; Corgnati, S.; Andersen, R.; Filippi, M.; Olesen, B.W. Effect of occupant behaviour related influencing factors on final energy end uses in buildings. Proc. Climamed. 2011, 11, 1–17. [Google Scholar]
- D’Oca, S.; Chen, C.-F.; Hong, T.; Belafi, Z. Synthesizing building physics with social psychology: An interdisciplinary framework for context and occupant behavior in office buildings. Energy Res. Soc. Sci. 2017, 34, 240–251. [Google Scholar] [CrossRef]
- Carpino, C.; Mora, D.; Arcuri, N.; de Simone, M. Behavioral variables and occupancy patterns in the design and modeling of Nearly Zero Energy Buildings. Build. Simul. 2017, 10, 875–888. [Google Scholar] [CrossRef]
- Balbis-Morejón, M.; Rey-Hernández, J.M.; Amaris-Castilla, C.; Velasco-Gómez, E.; José-Alonso, J.F.S.; Rey-Martínez, F.J. Experimental study and analysis of thermal comfort in a university campus building in tropical climate. Sustainability 2020, 12, 8886. [Google Scholar] [CrossRef]
- Balbis-Morejon, M.; Noya-Sambrano, A. Thermal comfort evaluation in an educational building with air conditioning located in the warm tropical climate of Colombia. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 844. [Google Scholar] [CrossRef]
- De Dear, R.; Xiong, J.; Kim, J.; Cao, B. A review of adaptive thermal comfort research since 1998. Energy Build. 2020, 214, 109893. [Google Scholar] [CrossRef]
- Holopainen, R.; Tuomaala, P.; Hernandez, P.; Häkkinen, T.; Piira, K.; Piippo, J. Comfort assessment in the context of sustainable buildings: Comparison of simplified and detailed human thermal sensation methods. Build. Environ. 2014, 71, 60–70. [Google Scholar] [CrossRef]
- Enescu, D. A review of thermal comfort models and indicators for indoor environments. Renew. Sustain. Energy Rev. 2017, 79, 1353–1379. [Google Scholar] [CrossRef]
- Zhao, Q.; Lian, Z.; Lai, D. Thermal comfort models and their developments: A review. Energy Built Environ. 2021, 2, 21–33. [Google Scholar] [CrossRef]
- ASHRAE. ANSI/ASHRAE Standard 55-2017: Thermal Environmental Conditions for Human Occupancy; ASHRAE Inc.: Atlanta, GA, USA, 2017; Volume 2017, p. 66. [Google Scholar]
- Fanger, P.O.; Toftum, J. Extension of the PMV model to non-air-conditioned buildings in warm climates. Energy Build. 2002, 34, 533–536. [Google Scholar] [CrossRef]
- Aryal, A.; Becerik-Gerber, B. Thermal comfort modeling when personalized comfort systems are in use: Comparison of sensing and learning methods. Build. Environ. 2020, 185, 107316. [Google Scholar] [CrossRef]
- Lee, S.; Karava, P.; Bilionis, I. Inference of thermal preference profiles for personalized thermal environments with actual building occupants. Build. Environ. 2018, 148, 714–729. [Google Scholar] [CrossRef]
- Introduction|IEA-EBC Annex 66. Available online: http://www.annex66.org/ (accessed on 3 August 2022).
- Dong, B.; Lam, K. A real-time model predictive control for building heating and cooling systems based on the occupancy behavior pattern detection and local weather forecasting. Build. Simul. 2014, 7, 23. [Google Scholar] [CrossRef]
- IEA EBC Annex 79 Occupant Behaviour-Centric Building Design and Operation. Available online: https://annex79.iea-ebc.org/ (accessed on 3 August 2022).
- About IEA EBC Annex 79. Available online: https://annex79.iea-ebc.org/about (accessed on 18 May 2022).
- Bonte, M.; Perles, A.; Lartigue, B.; Thellier, F. An occupant behavior model based on artificial intelligence for energy building simulation. In Proceedings of the BS 2013: 13th Conference of the International Building Performance Simulation Association, Chambèry, France, 25–28 August 2013. [Google Scholar]
- Deng, Z.; Chen, Q. Artificial neural network models using thermal sensations and occupants’ behavior for predicting thermal comfort. Energy Build. 2018, 174, 587–602. [Google Scholar] [CrossRef]
- Irshad, K.; Khan, A.I.; Irfan, S.A.; Alam, M.M.; Almalawi, A.; Zahir, M.H. Utilizing Artificial Neural Network for Prediction of Occupants Thermal Comfort: A Case Study of a Test Room Fitted with a Thermoelectric Air-Conditioning System. IEEE Access 2020, 8, 99709–99728. [Google Scholar] [CrossRef]
- Zambrano, J.M.; Oberegger, U.F.; Salvalai, G. Towards integrating occupant behaviour modelling in simulation-aided building design: Reasons, challenges and solutions. Energy Build. 2021, 253, 111498. [Google Scholar] [CrossRef]
- Saralegui, U.; Anton, M.A.; Arbelaitz, O.; Muguerza, J. An IoT sensor network to model occupancy profiles for energy usage simulation tools. In Proceedings of the 2018 Global Internet of Things Summit (GIoTS), Bilbao, Spain, 4–7 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Khalil, M.; Esseghir, M.; Merghem-Boulahia, L. An IoT Environment for Estimating Occupants’ Thermal Comfort. In Proceedings of the 2020 IEEE 31st Annual International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, 31 August–3 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Abuimara, T. Roadmap for Occupant Modelling in Building Codes and Standards. Available online: https://www.academia.edu/36706133/Roadmap_for_Occupant_Modelling_in_Building_Codes_and_Standards (accessed on 18 May 2022).
- Barthelmes, V.M.; Becchio, C.; Corgnati, S.P. Occupant behavior lifestyles in a residential nearly zero energy building: Effect on energy use and thermal comfort. Sci. Technol. Built Environ. 2016, 22, 960–975. [Google Scholar] [CrossRef]
- D’Oca, S.; Fabi, V.; Corgnati, S.P.; Andersen, R.K. Effect of thermostat and window opening occupant behavior models on energy use in homes. Build. Simul. 2014, 7, 683–694. [Google Scholar] [CrossRef]
- Bavaresco, M.V.; Ghisi, E.; D’Oca, S.; Pisello, A.L. Triggering occupant behaviour for energy sustainability: Exploring subjective and comfort-related drivers in Brazilian offices. Energy Res. Soc. Sci. 2021, 74, 101959. [Google Scholar] [CrossRef]
- Sood, T.; Janssen, P.; Miller, C. Spacematch: Using Environmental Preferences to Match Occupants to Suitable Activity-Based Workspaces. Front. Built Environ. 2020, 6, 113. [Google Scholar] [CrossRef]
- Perera, D.W.U.; Skeie, N.O. Modeling and simulation of multi-room buildings. Modeling Identif. Control. 2016, 37, 99–111. [Google Scholar] [CrossRef][Green Version]
- Bagheri, A.; Feldheim, V.; Ioakimidis, C.S. On the Evolution and Application of the Thermal Network Method for Energy Assessments in Buildings. Energies 2018, 11, 890. [Google Scholar] [CrossRef]
- Attoue, N.; Shahrour, I.; Mroueh, H.; Younes, R. Determination of the Optimal Order of Grey-Box Models for Short-Time Prediction of Buildings’ Thermal Behavior. Buildings 2019, 9, 198. [Google Scholar] [CrossRef]
- Boodi, A.; Beddiar, K.; Amirat, Y.; Benbouzid, M. Simplified Building Thermal Model Development and Parameters Evaluation Using a Stochastic Approach. Energies 2020, 13, 2899. [Google Scholar] [CrossRef]
- Dimitriou, V.; Firth, S.K.; Hassan, T.M.; Kane, T.; Coleman, M. Data-driven Simple Thermal Models: The Importance of the Parameter Estimates. Energy Procedia 2015, 78, 2614–2619. [Google Scholar] [CrossRef]
- Belic, F.; Hocenski, Z.; Sliskovic, D. Thermal modeling of buildings with RC method and parameter estimation. In Proceedings of the 2016 International Conference on Smart Systems and Technologies (SST), Osijek, Croatia, 12–14 October 2016; pp. 19–25. [Google Scholar] [CrossRef]
- Hietaharju, P.; Ruusunen, M.; Leiviskä, K. A Dynamic Model for Indoor Temperature Prediction in Buildings. Energies 2018, 11, 1477. [Google Scholar] [CrossRef]
- Linear Grey-Box Model Estimation—MATLAB Greyest—MathWorks América Latina. Available online: https://la.mathworks.com/help/ident/ref/iddata.greyest.html (accessed on 30 May 2021).
- Kim, J.; Zhou, Y.; Raftery, P.; Brager, G. Personal comfort models: Predicting individuals’ thermal preference using occupant heating and cooling behavior and machine learning. Build. Environ. 2017, 129, 96–106. [Google Scholar] [CrossRef]
- De León, L.; Austin, M.C.; Carpino, C.; Mora, D. Towards Zero Energy Districts developments base on bioclimatic strategies: A Numerical Study in a Developing Country. In E3S Web of Conferences; ATI: Rome, Italy, 2021; Volume 312, p. 02017. [Google Scholar] [CrossRef]
- Boodi, A.; Beddiar, K.; Amirat, Y.; Benbouzid, M. Building Thermal-Network Models: A Comparative Analysis, Recommendations, and Perspectives. Energies 2022, 15, 1328. [Google Scholar] [CrossRef]
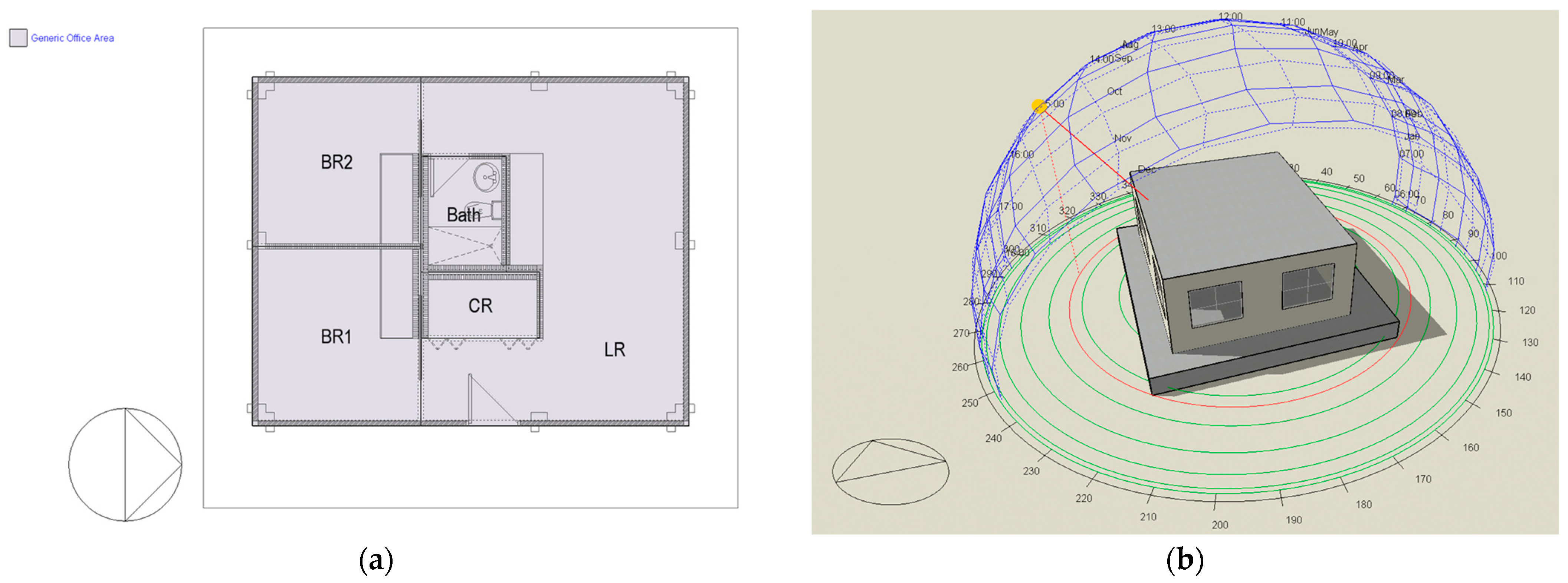
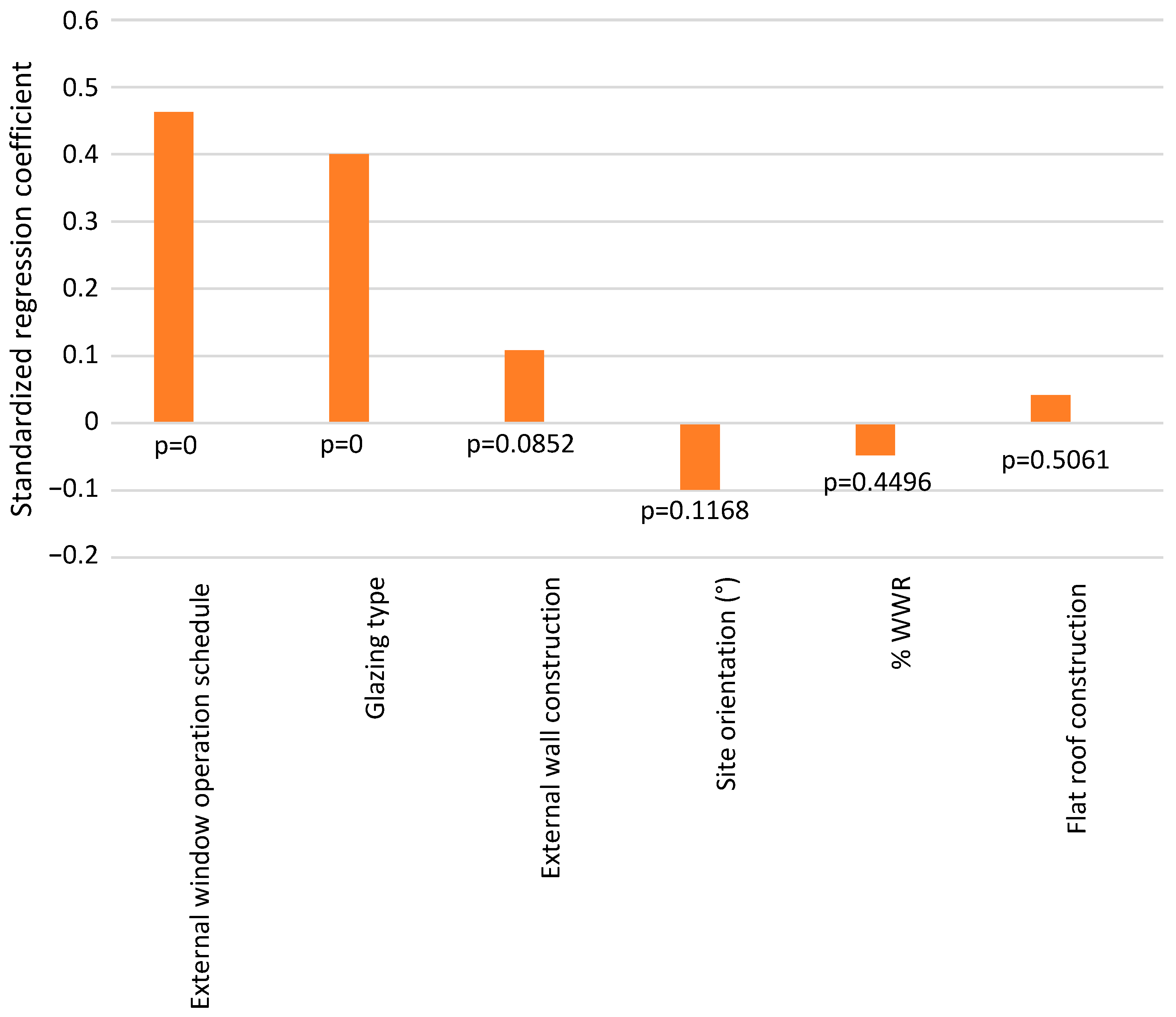
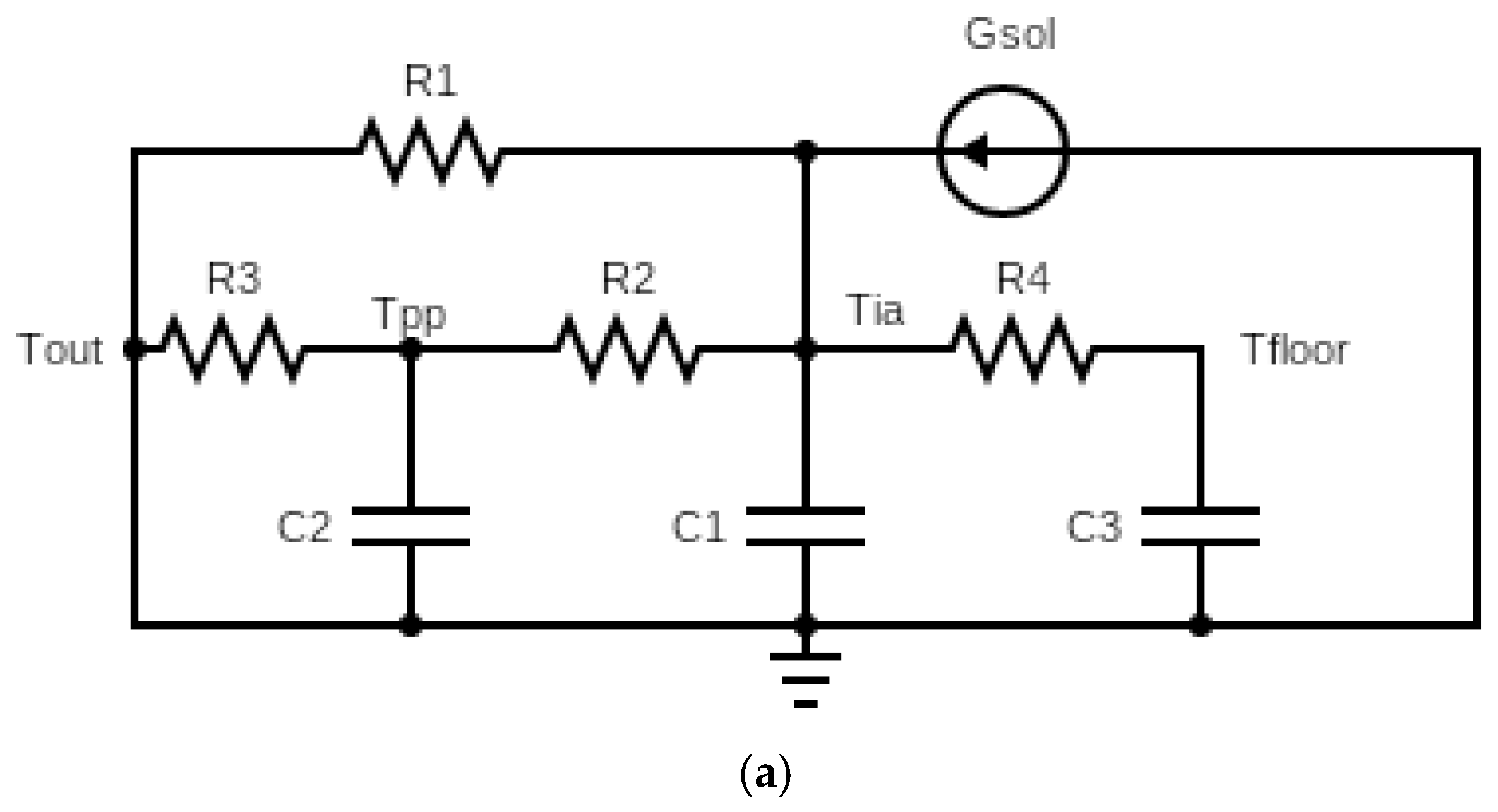
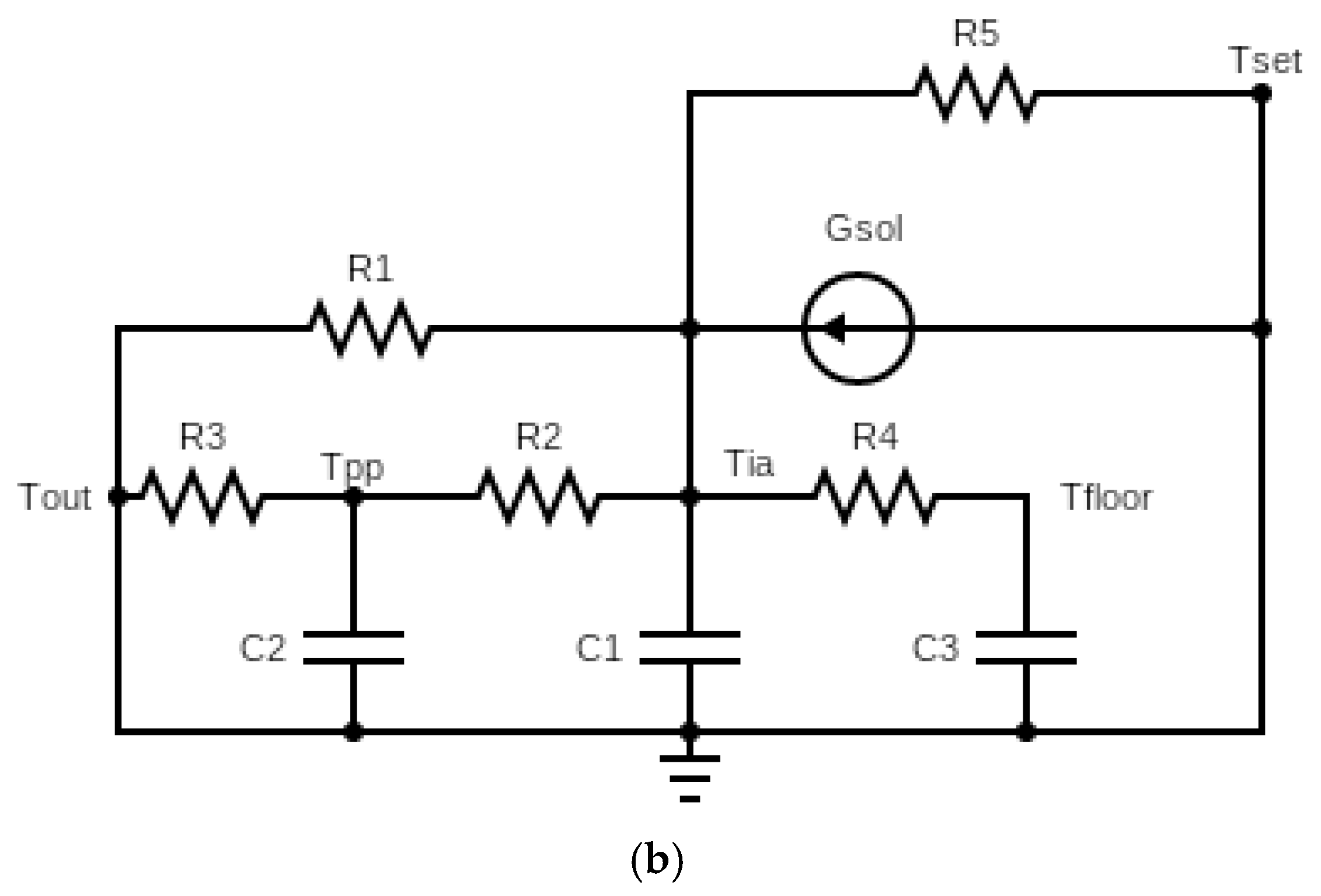

| Step | Procedure |
|---|---|
| 1 | Determination of the case study |
| 2 | Parametric and Sensibility Analysis to identify relevant variables |
| 3 | Formulation of thermal model that describes the case study (thermal resistance/capacitance model) |
| 4 | Simulation of the case performance to obtain the case’s thermal behavior |
| 5 | Parametric optimization by means of gray-box tools, training, and validation of the parameters |
| 6 | Determination of occupant decision-making scenarios |
| 7 | Determination of proportional and integrative values for each scenario |
| 8 | Integration of thermal model, occupant decision controller, and PMV calculation |
| Elements | Value | U (W/m2K) |
|---|---|---|
| Concrete block’s Base thickness | 150 mm | 2.533 |
| Concrete block’s wall thickness | 100 mm | 1.241 |
| Concrete block’s roof thickness | 280 mm | 0.719 |
| Concrete block’s ground thickness | 100 mm | 3.316 |
| Infiltration rate | 0.70 ach | - |
| Description | Value | U (W/m2K) |
|---|---|---|
| Wall to Window ratio | 30% | 3.779 |
| Window Height | 1.50 m | |
| Window spacing | 5 m | |
| Window sill’s height | 0.80 m | |
| Blinds | No blinds | |
| Openess percentage | 50% |
| Month | Tmax (°C) Hour | Tmin (°C) Hour | HRmax (%) Hour | HRmin (%) Hour | Wind Speed (m/s) | Wind Direction (°) |
|---|---|---|---|---|---|---|
| January 3 | 35 15:00 | 23.9 6:00 | 94 5:00 | 44 15:00 | 0.43 | 126 |
| February 20 | 34.6 15:00 | 22.2 6:00 | 93 6:00 | 40 15:00 | 2.77 | 85.77 |
| March 17 | 35.6 15:00 | 24.9 6:00 | 73 6:00 | 36 16:00 | 2.3 | 49 |
| April 11 | 35.3 15:00 | 24.8 6:00 | 82 24:00 | 44 16:00 | 1.75 | 87 |
| May 20 | 34.8 15:00 | 24.5 6:00 | 90 6:00 | 53 16:00 | 0.87 | 83.3 |
| June 23 | 32.8 15:00 | 23.4 6:00 | 94 6:00 | 58 15:00 | 0.45 | 108.25 |
| July 21 | 35.5 16:00 | 24.3 6:00 | 97 4:00 | 49 16:00 | 0.3 | 89.3 |
| August 19 | 34.7 15:00 | 24.1 6:00 | 95 5:00 | 52 15:00 | 3.9 | 188 |
| September 1 | 32.5 15:00 | 23 6:00 | 98 24:00 | 60 15:00 | 2.1 | 83 |
| October 20 | 32.5 15:00 | 23 6:00 | 96 6:00 | 62 14:00 | 2.33 | 90.67 |
| November 11 | 32.9 15:00 | 23.7 6:00 | 94 5:00 | 61 13:00 | 2.55 | 80 |
| December 16 | 34.3 15:00 | 24.6 6:00 | 94 7:00 | 50 16:00 | 4.2 | 34.5 |
| Passive Case: Closed Windows | |||||||
|---|---|---|---|---|---|---|---|
| JAN TO APRIL | MAY TO AUGUST | SEPT TO DEC | |||||
| Parameters | (K/W) | 5.69 × 10−3 | 6.09 × 10−3 | 7.26 × 10−3 | 7.25 × 10−3 | 5.35 × 10−3 | 6.93 × 10−3 |
| (K/W) | 4.47 × 10−4 | 6.67 × 10−4 | 1.27 × 10−3 | 8.69 × 10−4 | 6.76 × 10−4 | 1.68 × 10−3 | |
| (K/W) | 95 | 100 | 100 | 100 | 63 | 100 | |
| (K/W) | 8.11 | 5.81 | 6.15 | 5.44 | 11.12 | 6.76 | |
| (J/K) | 5.50 × 105 | 1.89 × 106 | 2.94 × 106 | 2.34 × 106 | 3.14 × 106 | 3.84 × 106 | |
| (J/K) | 5.98 × 106 | 4.66 × 106 | 2.63 × 106 | 3.82 × 106 | 3.75 × 106 | 2.28 × 106 | |
| (J/K) | 9.60 × 105 | 2.48 × 105 | 1.39 × 106 | 5.37 × 105 | 1.10 × 106 | 6.50 × 103 | |
| Training | Fit (1/3 of the data) | 80.73% | 84.09% | 85.60% | 87.99% | 79.55% | 82.70% |
| Error (°C) | 0.44 | 0.30 | 0.26 | 0.18 | 0.50 | 0.36 | |
| 365 Days Validation | Fit (all data) | 68.09% | 67.84% | 80.12% | 77.34% | 70.87% | 72.73% |
| Error (°C) | 1.15 | 1.01 | 0.62 | 0.66 | 1.49 | 0.76 | |
| Passive Case: Windows Opened at 50% | |||||||
|---|---|---|---|---|---|---|---|
| JAN TO APRIL | MAY TO AUGUST | SEPT TO DEC | |||||
| Parameters | (K/W) | 5.66 × 10−4 | 3.50 × 10−4 | 1.20 × 10−3 | 6.12 × 10−4 | 9.65 × 10−4 | 6.12 × 10−4 |
| (K/W) | 8.69 × 10−4 | 1.27 × 10−3 | 8.69 × 10−4 | 1.27× 10−3 | 8.69 × 10−4 | 1.27× 10−3 | |
| (K/W) | 100 | 100 | 100 | 100 | 100 | 100 | |
| (K/W) | 5.44 | 6.15 | 5.44 | 6.15 | 5.44 | 6.15 | |
| (J/K) | 2.34 × 106 | 2.94 × 106 | 2.34 × 106 | 2.94 × 106 | 2.34 × 106 | 2.94 × 106 | |
| (J/K) | 3.82 × 106 | 2.63 × 106 | 3.82 × 106 | 2.63 × 106 | 3.82 × 106 | 2.63 × 106 | |
| (J/K) | 5.37 × 105 | 1.39 × 106 | 5.37 × 105 | 1.39 × 106 | 5.37 × 105 | 1.39 × 106 | |
| Training | Fit (1/3 of the data) | 85.56% | 85.37% | 81.27% | 82.10% | 82.12% | 82.12% |
| Error (°C) | 0.21 | 0.21 | 0.25 | 0.22 | 0.22 | 0.22 | |
| 365 Days Validation | Fit (all data) | 76.27% | 76.91% | 70.67% | 76.01% | 73.08% | 76.01% |
| Error (°C) | 0.69 | 0.84 | 0.59 | 0.66 | 0.56 | 0.66 | |
| AIR CONDITIONING ON (ACTIVE CASE) | |||
|---|---|---|---|
| JANUARY 4TH 10 a.m.–12 p.m. | |||
| Parameters | (K/W) | 7.26 × 10−3 | 7.25 × 10−3 |
| (K/W) | 1.27 × 10−3 | 8.69 × 10−4 | |
| (K/W) | 100 | 100 | |
| (K/W) | 6.15 | 5.44 | |
| (K/W) | 100 | 100 | |
| (J/K) | 2.94 × 106 | 2.34 × 106 | |
| (J/K) | 2.63 × 106 | 3.82 × 106 | |
| (J/K) | 1.39 × 106 | 5.37 × 105 | |
| Training | Fit | 84.22% | 87.78% |
| Cost | 0.1576 | 0.0945 | |
| Parameter | R4C3: Passive, Closed Windows | R4C3: Passive, Open Windows (50%) | R5C3: Active, AC ON, Closed Windows |
|---|---|---|---|
| (K/W) | 7.25 × 10−3 | 1.20 × 10−3 | 7.25 × 10−3 |
| (K/W) | 8.69 × 10−4 | 8.69 × 10−4 | 8.69 × 10−4 |
| (K/W) | 100 | 100 | 100 |
| (K/W) | 5.44 | 5.44 | 5.44 |
| (K/W) | - | - | 100 |
| (J/K) | 2.34 × 106 | 2.34 × 106 | 2.34 × 106 |
| (J/K) | 3.82 × 106 | 3.82 × 106 | 3.82 × 106 |
| (J/K) | 5.37 × 105 | 5.37 × 105 | 5.37 × 105 |
| Controller Based on Scenario | P | I |
|---|---|---|
| Probabilistic scenario | 50 | −1.40 × 10−3 |
| Deterministic scenario | 50 | −6.88 × 10−4 |
| Combined model #1 | 50 | −1.40 × 10−3 |
| Combined model #2 | 50 | −1.05 × 10−4 |
| Month | Probabilistic Method’s Control System | Deterministic Method’s Control System | Combined Model #1′s Control System | Combined Model #2′s Control System |
|---|---|---|---|---|
| AC Energy Consumption (kWh) | ||||
| January | 219.7 | 155.2 | 319.4 | 209.8 |
| February | 207.8 | 153.0 | 330.5 | 200.9 |
| March | 259.7 | 175.5 | 375.3 | 235.8 |
| April | 243.3 | 169.6 | 356.9 | 226.0 |
| May | 190.6 | 155.4 | 298.4 | 203.6 |
| June | 141.8 | 128.7 | 222.3 | 178.1 |
| July | 176.8 | 169.9 | 299.7 | 189.9 |
| August | 162.0 | 152.8 | 285.5 | 176.6 |
| September | 142.5 | 122.4 | 246.3 | 167.9 |
| October | 125.5 | 135.9 | 221.9 | 183.4 |
| November | 121.7 | 111.9 | 174.2 | 156.4 |
| December | 193.5 | 144.2 | 316.3 | 201.8 |
| Annual | 2185.2 | 1774.7 | 3446.8 | 2330.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aversa, A.; Ballestero, L.; Chen Austin, M. Highlighting the Probabilistic Behavior of Occupants’ Preferences in Energy Consumption by Integrating a Thermal Comfort Controller in a Tropical Climate. Sustainability 2022, 14, 9591. https://doi.org/10.3390/su14159591
Aversa A, Ballestero L, Chen Austin M. Highlighting the Probabilistic Behavior of Occupants’ Preferences in Energy Consumption by Integrating a Thermal Comfort Controller in a Tropical Climate. Sustainability. 2022; 14(15):9591. https://doi.org/10.3390/su14159591
Chicago/Turabian StyleAversa, Alejandra, Luis Ballestero, and Miguel Chen Austin. 2022. "Highlighting the Probabilistic Behavior of Occupants’ Preferences in Energy Consumption by Integrating a Thermal Comfort Controller in a Tropical Climate" Sustainability 14, no. 15: 9591. https://doi.org/10.3390/su14159591
APA StyleAversa, A., Ballestero, L., & Chen Austin, M. (2022). Highlighting the Probabilistic Behavior of Occupants’ Preferences in Energy Consumption by Integrating a Thermal Comfort Controller in a Tropical Climate. Sustainability, 14(15), 9591. https://doi.org/10.3390/su14159591







