Optimal Speed Model of Urban Underwater Tunnel Based on CO2 Emissions Factor
Abstract
:1. Introduction
2. Basic Model of Velocity and Emissions
2.1. MEET
2.2. COPERT
3. Experiment
3.1. Test Plan
3.2. Test Road
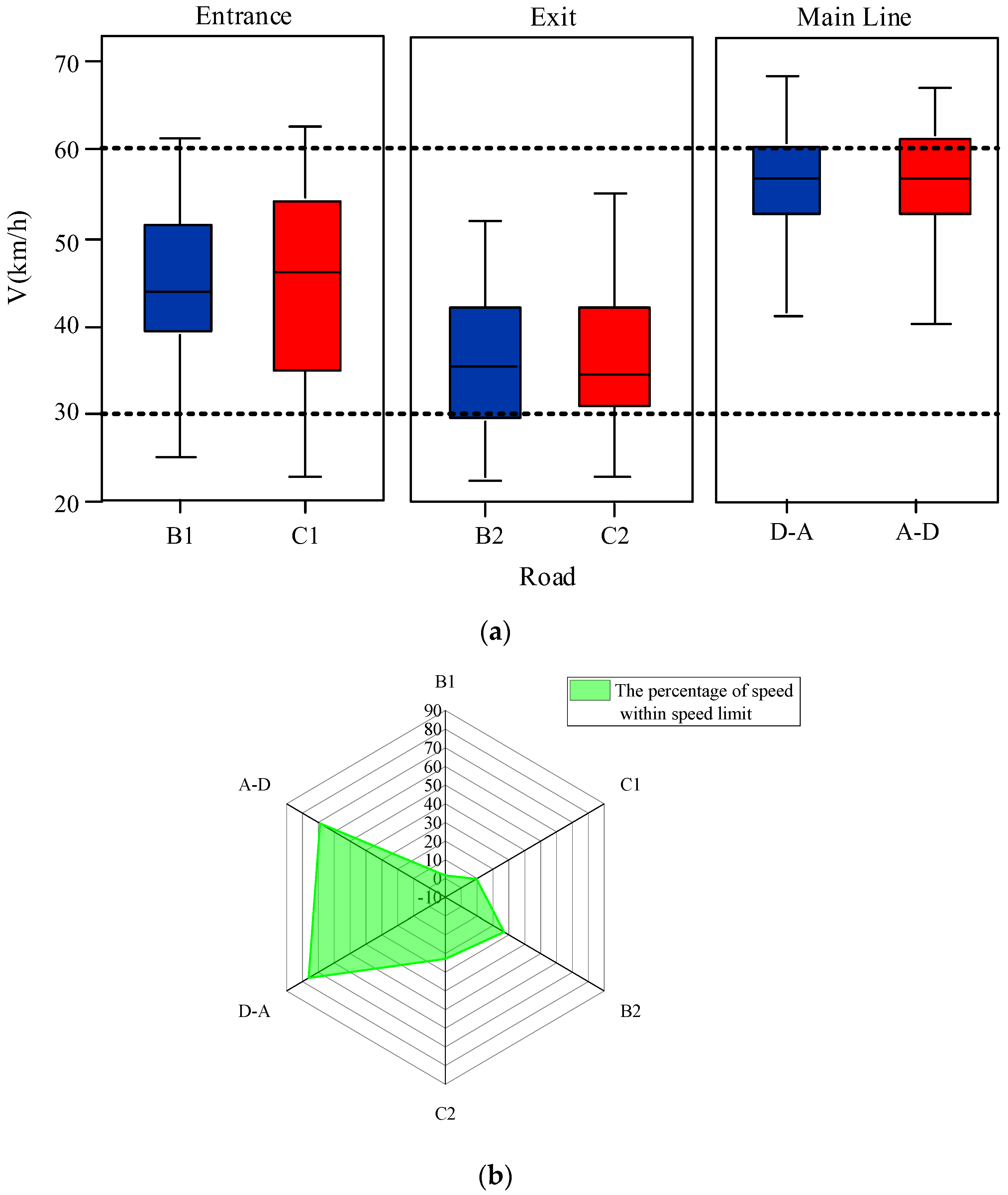
3.3. Speed Characteristics
4. Effective Model and Parameter Calculation
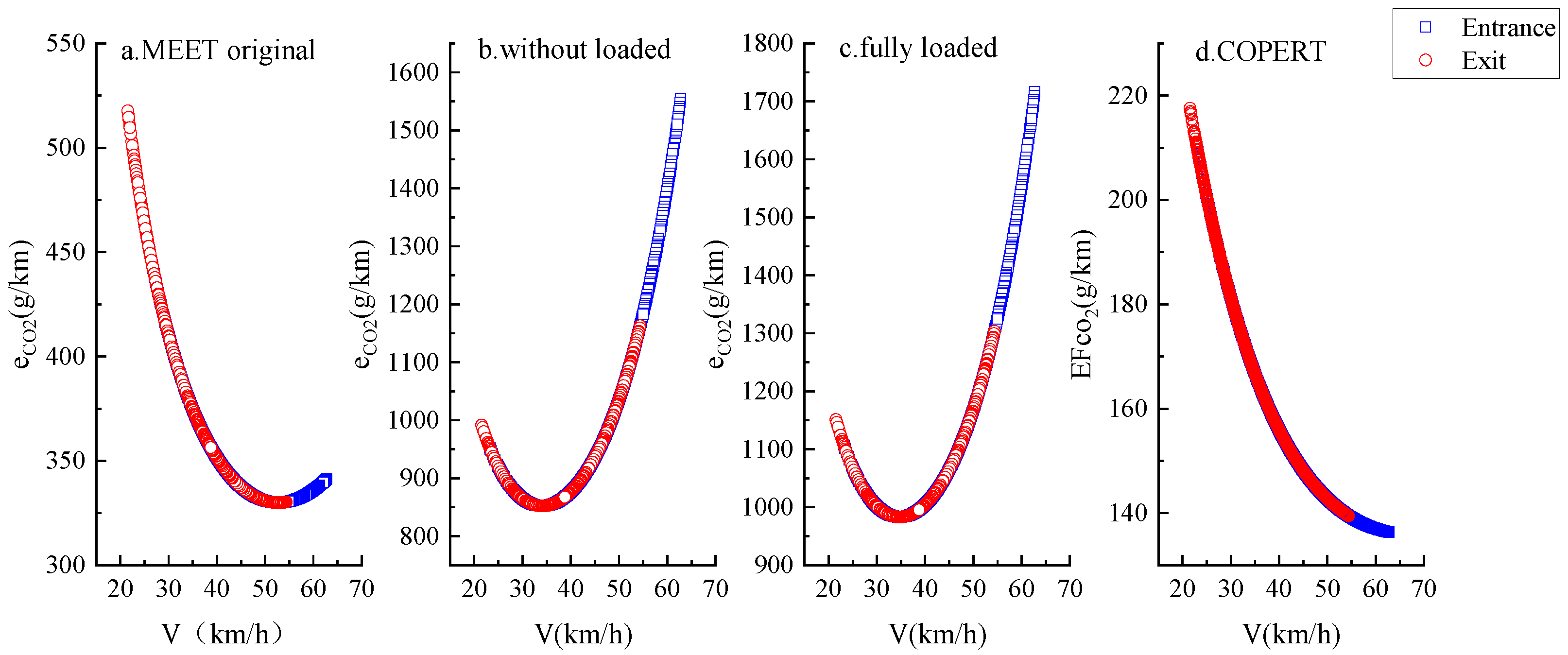
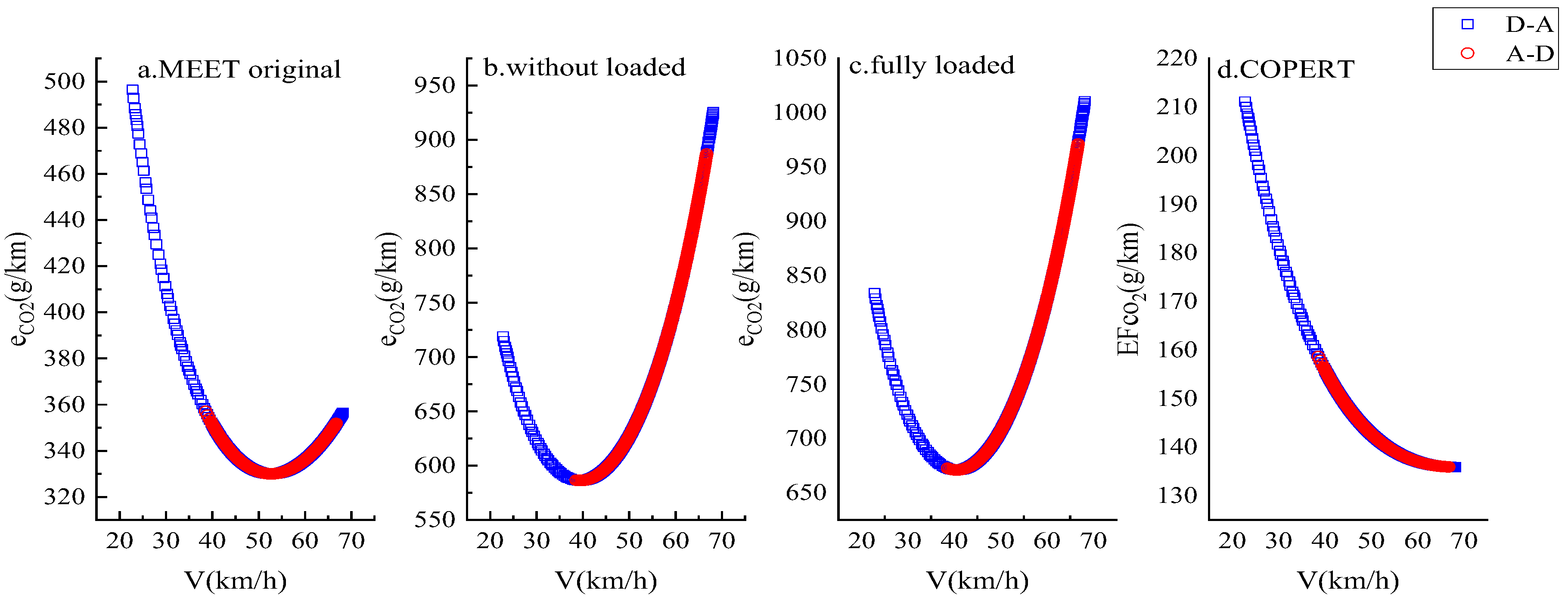
4.1. MEET Model of Urban Underwater Tunnel
4.2. COPERT Model of Urban Underwater Tunnel
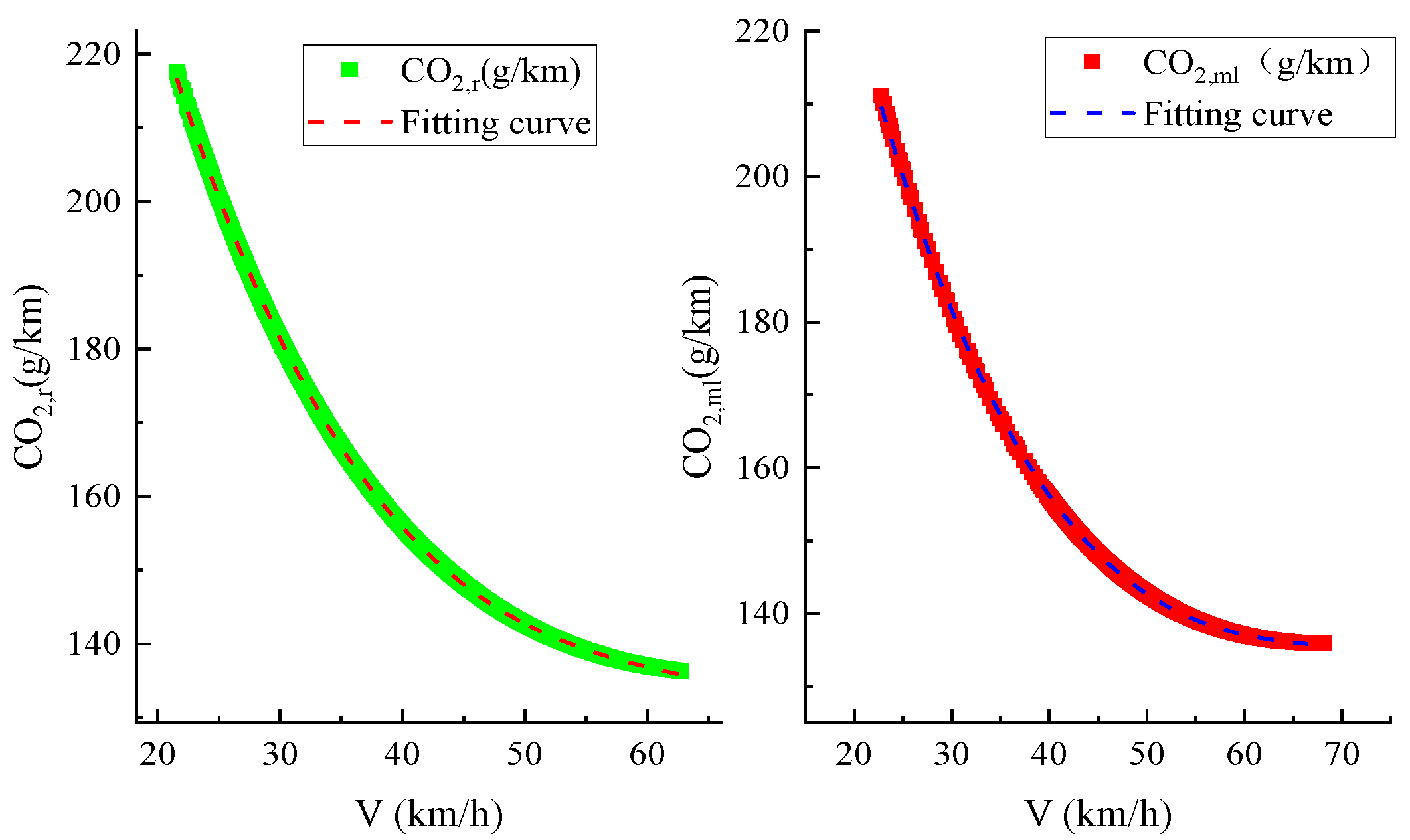
4.3. Fit Speed–CO2 Emissions Factor Model
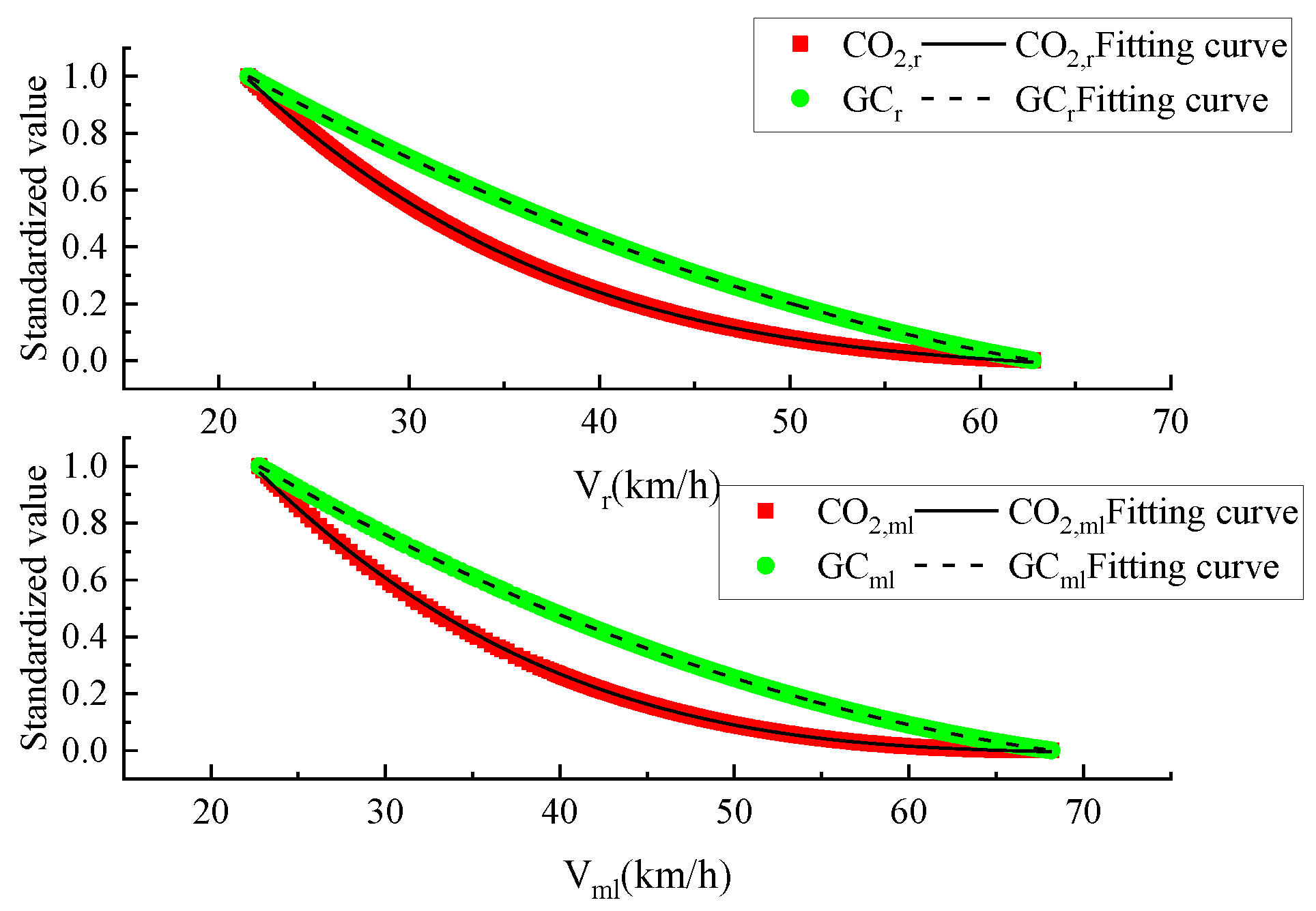
5. Gasoline Consumption and Optimal Driving Speed Model
6. Conclusions
- (1)
- Under the influence of the existing speed limit conditions, more than 70% of drivers on the ramp did not obey the speed limit rules, as well as 30% of drivers on the main lines;
- (2)
- Without considering the influence of road slope and vehicle load, there is a negative correlation between speed and CO2 emissions factor in MEET model. When affected by slope and load, these positive influence factors change the correlation of the original model, expand the size of CO2 emissions factor, and make the calculated values deviate from the actual size. It is only applicable to the research of parameter trend analysis, not applicable to further calculation research based on CO2 emissions factor;
- (3)
- COPERT model estimates CO2 emissions factor by calculating the gasoline consumption coefficient. When only considering the influence of gasoline consumption and speed parameters, the CO2 emissions factor is negatively correlated with speed. There are fewer variables in the model, and the parameters are more controllable and more in line with the actual situation;
- (4)
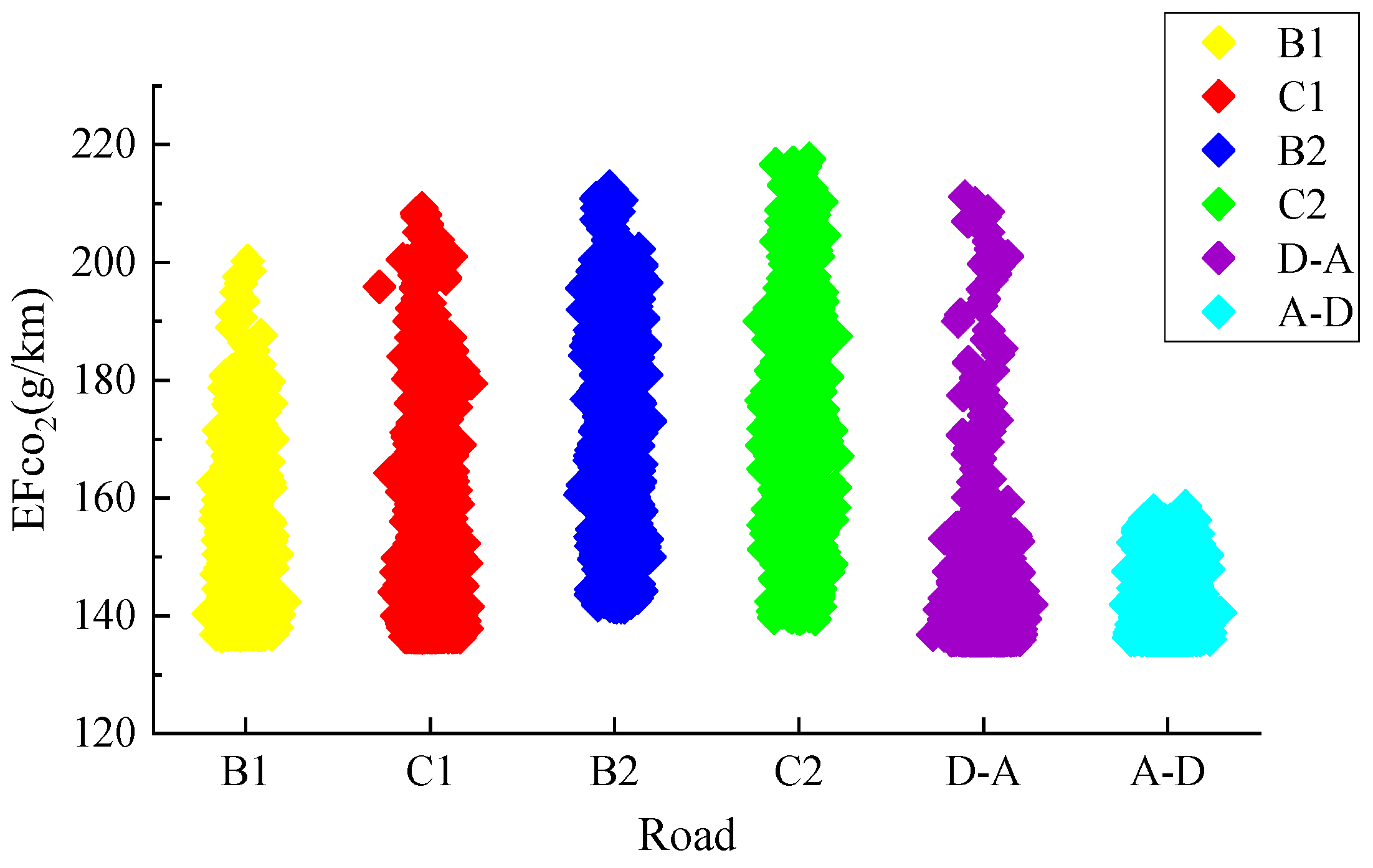
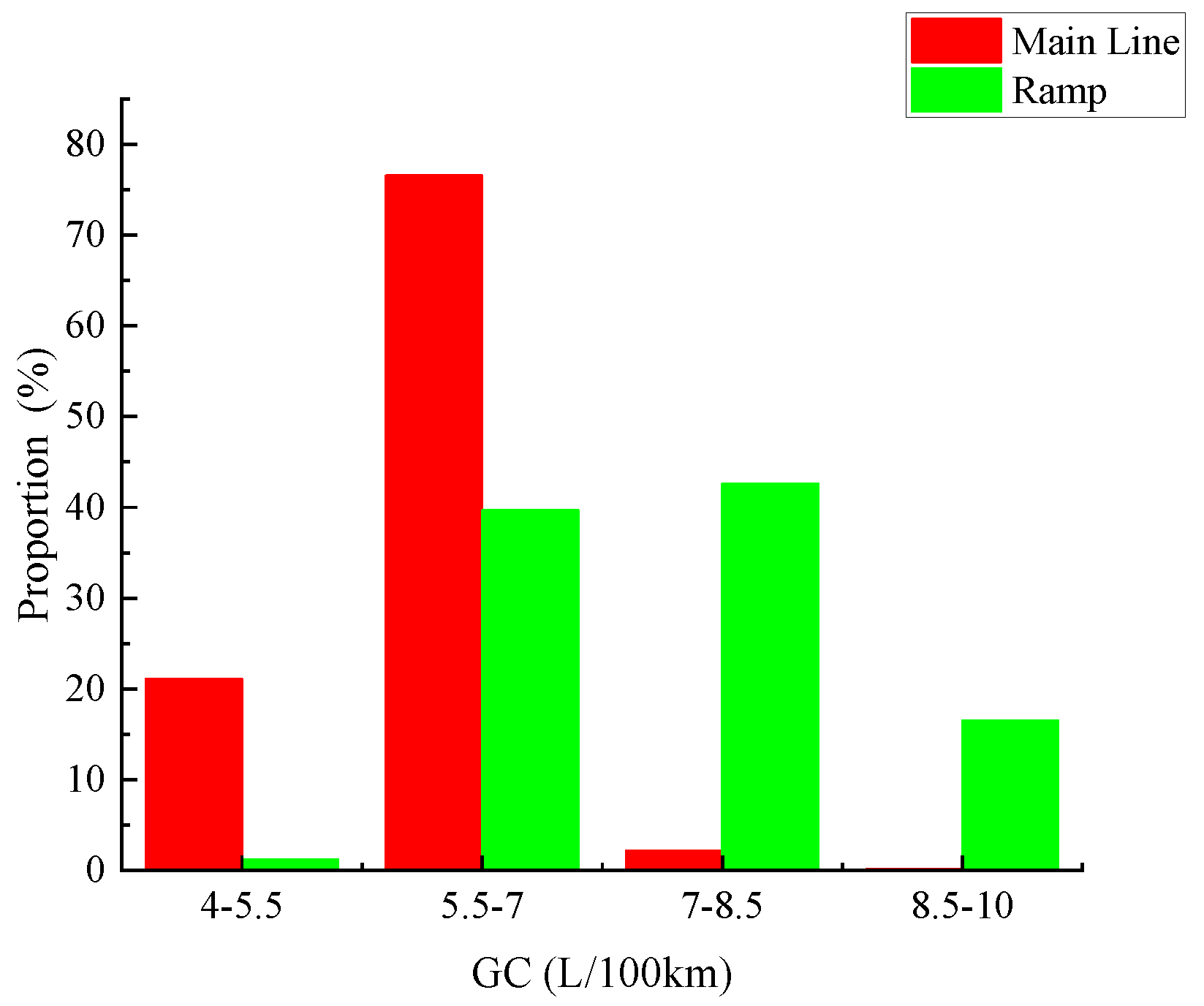
- The gasoline consumption distribution of vehicles at the ramp entrance and exit is mainly concentrated in the range of 7~8.5 L/100 km, while the main line is concentrated in the range of 5.5~7 L/100 km. By normalizing the gasoline consumption and CO2 emissions factor, the standardized fitting models at the ramp and the main line segment are obtained respectively;
- (5)
- Due to the highest proportion of CO2 emissions factor and the most sufficient fuel in the optimal driving speed range, the region of CO2, i > GCi in the standardized fitting model is selected to finally determine the limited speed applicable to the current urban underwater tunnel, with a ramp of 40 km/h, main line is 60 km/h.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vicente, F.; Marina, K.; Marilena, M.; Leonidas, N.; Stefan, H.; Panagiota, D. Road vehicle emission factors development: A review. Atmos. Environ. 2013, 70, 84–97. [Google Scholar] [CrossRef]
- Wang, X.; Liu, M.; Ci, Y.; Yang, Y. Effectiveness of driver’s bounded rationality and speed guidance on fuel-saving and emissions-reducing at a signalized intersection. J. Clean. Prod. 2021, 325, 129343. [Google Scholar] [CrossRef]
- Hyung-Wook, C.; Christopher Frey, H. Estimating diesel vehicle emission factors at constant and high speeds for short road segments. Transp. Res. Rec. 2010, 2158, 19–27. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, L.; Guo, J.; Cheng, Y.; He, W.; Song, G. Optimized adjustment of speed resolution and time alignment data for improving emissions estimations. Transp. Res. Rec. 2016, 2570, 77–86. [Google Scholar] [CrossRef]
- Wang, Y.; Xing, Z.; Zhang, H.; Wang, Y.; Du, K. On-road mileage-based emission factors of gaseous pollutants from bi-fuel taxi fleets in China: The influence of fuel type, vehicle speed, and accumulated mileage. Sci. Total Environ. 2022, 819, 151999. [Google Scholar] [CrossRef]
- Chandrashekar, C.; Chatterjee, P.; Pawar, D. Estimation of CO2 and CO emissions from auto-rickshaws in Indian heterogeneous traffic. Transp. Res. Part D: Transp. Environ. 2022, 104, 103202. [Google Scholar] [CrossRef]
- Vanatta, M.; Rathod, B.; Calzavara, J.; Courtright, T.; Sims, T.; Saint-Sernin, É.; Clack, H.; Jagger, P.; Craig, M. Emissions impacts of electrifying motorcycle taxis in Kampala, Uganda. Transp. Res. Part D: Transp. Environ. 2022, 104, 103193. [Google Scholar] [CrossRef]
- Ashik, F.; Rahman, M.H.; Kamruzzaman, M. Investigating the impacts of transit-oriented development on transport-related CO2 emissions. Transp. Res. Part D Transp. Environ. 2020, 105, 103227. [Google Scholar] [CrossRef]
- Jiao, F.; Du, Z.; Chen, G.; Zheng, H.; Tang, Z.; Wang, S. Entrance zone length of extra-long undersea tunnels based on vision adaptation. Tunn. Undergr. Space Technol. 2021, 113, 103970. [Google Scholar] [CrossRef]
- Jiao, F.; Du, Z.; Yiik, D.; He, S.; Xu, F.; Zheng, H. Self-explaining performance of visual guiding facilities in urban road tunnels based on speed perception. Tunn. Undergr. Space Technol. 2022, 122, 104371. [Google Scholar] [CrossRef]
- Yang, Y.; Du, Z.; Jiao, F.; Pan, F. Analysis of EEG Characteristics of drivers and driving safety in undersea tunnel. Int. J. Environ. Res. Public Health 2021, 18, 9810. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; He, K.; He, D.; Tang, Z.; Hao, J. A study on models of MOBILE source emission factors. Acta Sci. Circumstantiae 1997, 17, 89–94. [Google Scholar] [CrossRef]
- Shan, X.; Liu, H.; Zhang, X.; Chen, X.; Ye, J. Localization of light-duty vehicle emission factor estimation based on MOVES. J. Tongji Univ. (Nat. Sci.) 2021, 49, 1135–1143. [Google Scholar] [CrossRef]
- Arne, H. Comparing emission estimation models for rail freight transportation. Transp. Res. Part D Transp. Environ. 2020, 86, 102468. [Google Scholar] [CrossRef]
- Duan, Z. Research on the Peak Mechanism and Peak Comprehensive Judgment System of Carbon Emissions under the Evolution of Social Economic System. Ph.D. Thesis, Jilin University, Changchun, China, 2021. [Google Scholar] [CrossRef]
- Hickman, A. Methodology for Calculating Transport Emissions and Energy Consumption; European Commission: Luxembourg, 1999. [Google Scholar]
- Mansoureh, N.; Mahdi, A. Measurement, evaluation and minimization of CO2, NOx, and CO emissions in the open time dependent vehicle routing problem. Measurement 2016, 90, 443–452. [Google Scholar]
- Liu, C.; Shen, L.; Shen, H.; Lv, X.; Zhai, Y. Research on low-carbon time-dependent vehicle routing problem with traffic congestion avoidance approaches. Control. Decis. 2020, 35, 2486–2496. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, G.; Zhang, L.; Zhai, Z.; He, W.; Yu, L. How do errors occur when developing speed correction factors for emission modeling. Transp. Res. Part D Transp. Environ. 2021, 101, 103094. [Google Scholar] [CrossRef]
- Zhai, Z.; Xu, J.; Song, G.; Hatzopoulou, M. Comparative analysis of drive-cycles, speed limit violations, and emissions in two cities: Toronto and Beijing. Sci. Total Environ. 2022, 11, 152323. [Google Scholar] [CrossRef]
- Davison, J.; Bernard, Y.; Borken-Kleefeld, J.; Farren, N.J.; Hausberger, S.; Sjödin, Å.; Tate, J.E.; Vaughan, A.R.; Carslaw, D.C. Distance-based emission factors from vehicle emission remote sensing measurements. Sci. Total Environ. 2020, 739, 139688. [Google Scholar] [CrossRef]
- Xu, L.; Wang, L.; Liu, Y.; Song, G.; Li, C.; Zhai, Z. Calculation model of bus energy consumption and CO2 emission based on multi-source data. J. Transp. Syst. Eng. Inf. Technol. 2020, 20, 174–181. [Google Scholar] [CrossRef]
- He, Y.M. Estimating and Analyzing Spatiotemporal Patterns of Vehicle CO2 Emissions in Urban Road Based on GPS Data. Master’s Thesis, Chang’an University, Xian, China, 2020. [Google Scholar] [CrossRef]
- EMEP/EEA. Air Pollutant Emission Inventory Guidebook 2019; Publications Office of the European Union: Luxembourg, 2021; Available online: https://www.eea.europa.eu/publications/emep-eea-guidebook-2019 (accessed on 10 June 2022).
- Ali, M.; Kamal, M.; Tahir, A.; Atif, S. Fuel consumption monitoring through COPERT model—A case study for urban sustainability. Sustainability 2021, 13, 11614. [Google Scholar] [CrossRef]
- Ekström, M.; Sjödin, Å.; Andreasson, K. Evaluation of the COPERT III emission model with on-road optical remote sensing measurements. Atmos. Environ. 2004, 38, 6631–6641. [Google Scholar] [CrossRef]
- Xie, S.; Song, X.; Shen, X. Calculating vehicular emission factors with COPERTIII mode in China. Environ. Sci. 2006, 27, 3415–3419. [Google Scholar] [CrossRef]
- Wang, L.; Ji, H.; Wang, H. Research on driving speed range based on optimum carbon emission and fuel consumption optimization. Transp. Energy Conserv. Environ. Prot. 2020, 16, 4–8. [Google Scholar]


| Model Type | Author | Main Parameters of Calculation | Model Formula |
|---|---|---|---|
| MEET | Mansoureh et al. (2016) [17] | A, B, C | |
| Liu et al. (2020) [18] | A, B, C | ||
| Zhang et al. (2021) [19] | A, D, E | ||
| Zhai et al. (2022) [20] | A, F | ||
| Davison et al. (2020) [21] | A, F, G | ||
| Xu et al. (2020) [22] | A | ||
| COPERT | He et al. (2020) [23] | A |
| Gender | Number | Age Distribution | Average Age | Average Driving Age |
|---|---|---|---|---|
| Male | 13 | 24–40 | 28 | 8.6 |
| Female | 8 | 24–31 | 26.1 | 5.5 |
| Direction | Number | Driving Route |
|---|---|---|
| Entrance of the ramp | B1 | Jiefang Road–Qinyuan Road |
| C1 | Zhongshan Road–Qinyuan Road | |
| Exit of the ramp | B2 | Qinyuan Road–Jiefang Road |
| C2 | Qinyuan Road–Zhongshan Road | |
| Main line | A-D | Macao Road–Qinyuan Road |
| D-A | Qinyuan Road–Macao Road |
| Sig. | B1 | C1 | B2 | C2 | D–A | A–D |
|---|---|---|---|---|---|---|
| B1 | - | 0.000 | 0.053 | 0.000 | 0.000 | 0.000 |
| C1 | 0.000 | - | 0.000 | 0.000 | 0.000 | 0.000 |
| B2 | 0.053 | 0.000 | - | 0.027 | 0.000 | 0.000 |
| C2 | 0.000 | 0.000 | 0.027 | - | 0.000 | 0.000 |
| D-A | 0.000 | 0.000 | 0.000 | 0.000 | - | 0.000 |
| A-D | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | - |
| - | Entrance of the Ramp | Exit of the Ramp | Main Line | |||
|---|---|---|---|---|---|---|
| B1 | C1 | B2 | C2 | D–A | A–D | |
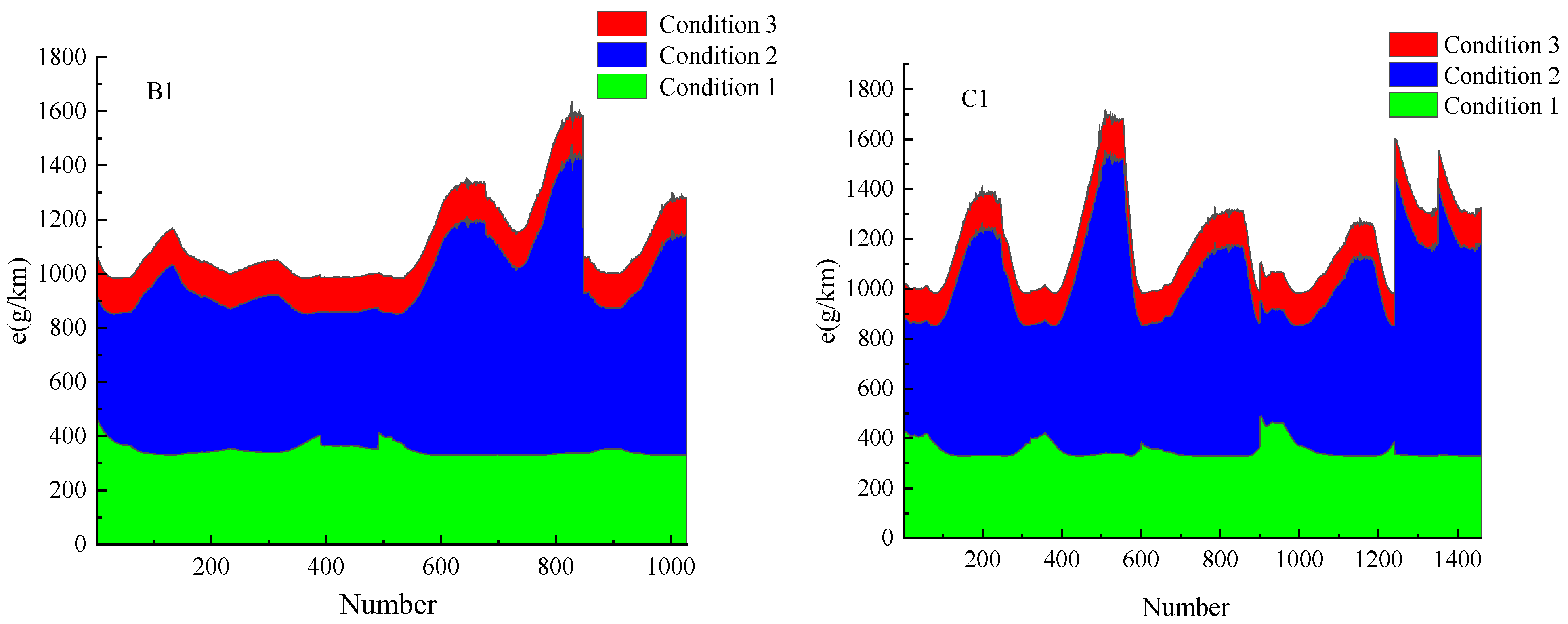
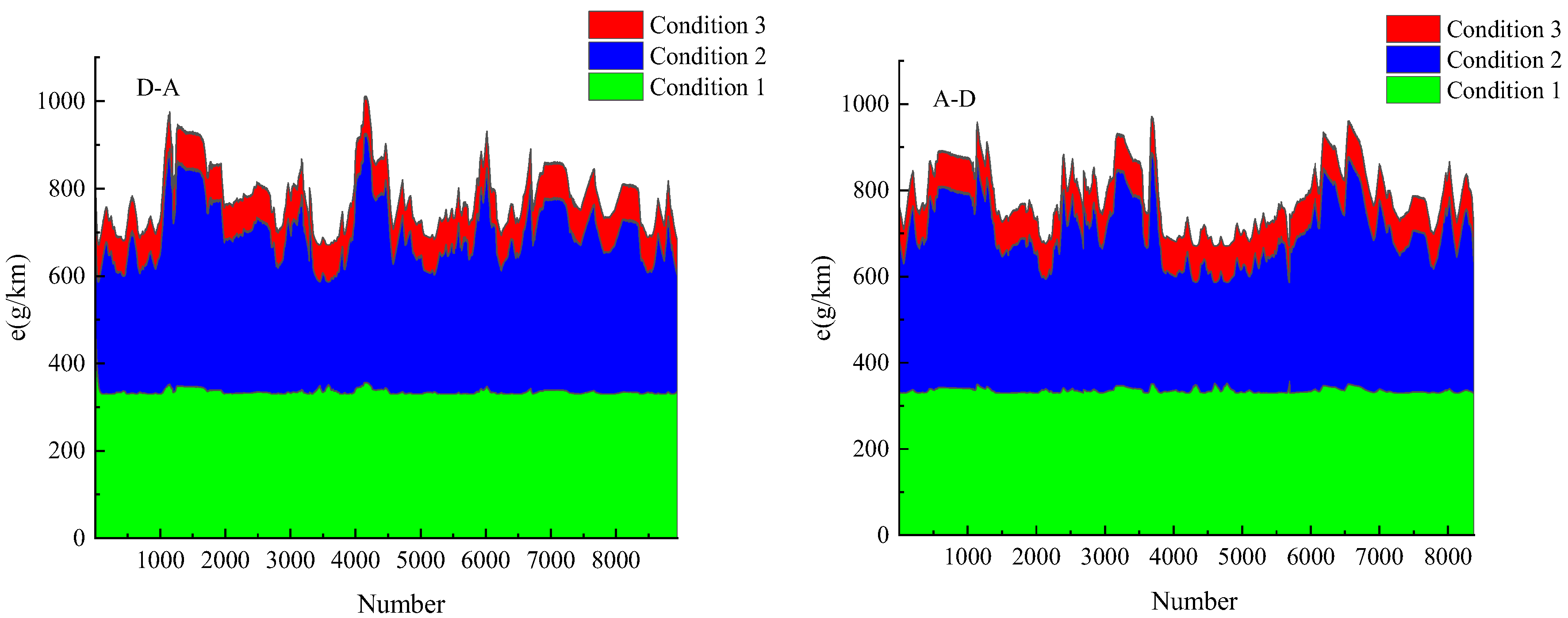
| Condition 1 | 347.41 | 351.90 | 382.59 | 381.00 | 335.13 | 335.56 |
| Condition 2 | 986.06 | 1059.07 | 894.39 | 891.51 | 780.82 | 787.42 |
| Condition 3 | 1119.37 | 1197.12 | 1028.30 | 1024.99 | 699.94 | 706.44 |
| — | a | b | c | d | R2 |
|---|---|---|---|---|---|
| Entrance of the ramp | −0.0008 | 0.1604 | −10.744 | 381.53 | 1 |
| Exit of the ramp | −0.0011 | 0.1943 | −12.035 | 397.42 | 1 |
| D-A | −0.0007 | 0.1393 | −9.848 | 369.69 | 0.99 |
| A-D | −0.0005 | 0.1127 | −8.3896 | 343.36 | 1 |
| The whole of the ramp | −0.0009 | 0.1689 | −11.1 | 386.3 | 1 |
| The whole of the main lane | −0.0007 | 0.1387 | −9.8068 | 368.77 | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Du, Z.; Jiao, F.; Zhang, S. Optimal Speed Model of Urban Underwater Tunnel Based on CO2 Emissions Factor. Sustainability 2022, 14, 9592. https://doi.org/10.3390/su14159592
Chen Y, Du Z, Jiao F, Zhang S. Optimal Speed Model of Urban Underwater Tunnel Based on CO2 Emissions Factor. Sustainability. 2022; 14(15):9592. https://doi.org/10.3390/su14159592
Chicago/Turabian StyleChen, Ying, Zhigang Du, Fangtong Jiao, and Shuyang Zhang. 2022. "Optimal Speed Model of Urban Underwater Tunnel Based on CO2 Emissions Factor" Sustainability 14, no. 15: 9592. https://doi.org/10.3390/su14159592
APA StyleChen, Y., Du, Z., Jiao, F., & Zhang, S. (2022). Optimal Speed Model of Urban Underwater Tunnel Based on CO2 Emissions Factor. Sustainability, 14(15), 9592. https://doi.org/10.3390/su14159592







