Spatiotemporal Evolution of Travel Pattern Using Smart Card Data
Abstract
:1. Introduction
- We built individual subway trip chains (i.e., the sequence of trips generated during the day, with the information of O-D times and locations) and explored individual travel patterns based on individual trip frequency.
- We proposed a user clustering scheme to unveil the distribution of trip frequency over the hour of the day for each user, employing the GMM with EM algorithm for clustering and integrated Pareto principle method to decide the number of clusters.
- We revealed the evolution of residents’ personal travel patterns from 2011 to 2017, as well as the spatial and temporal distribution of each cluster.
2. Methods
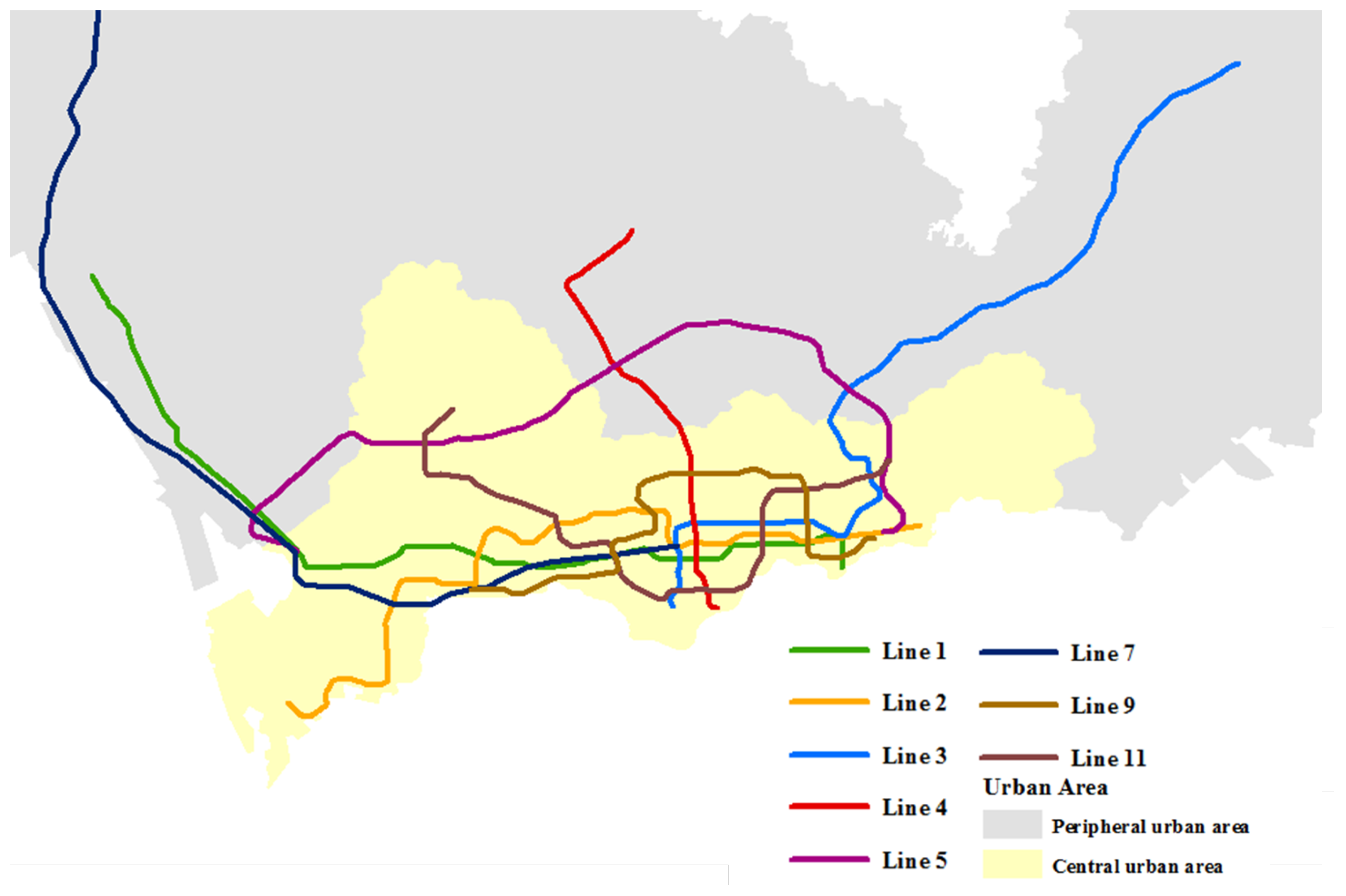
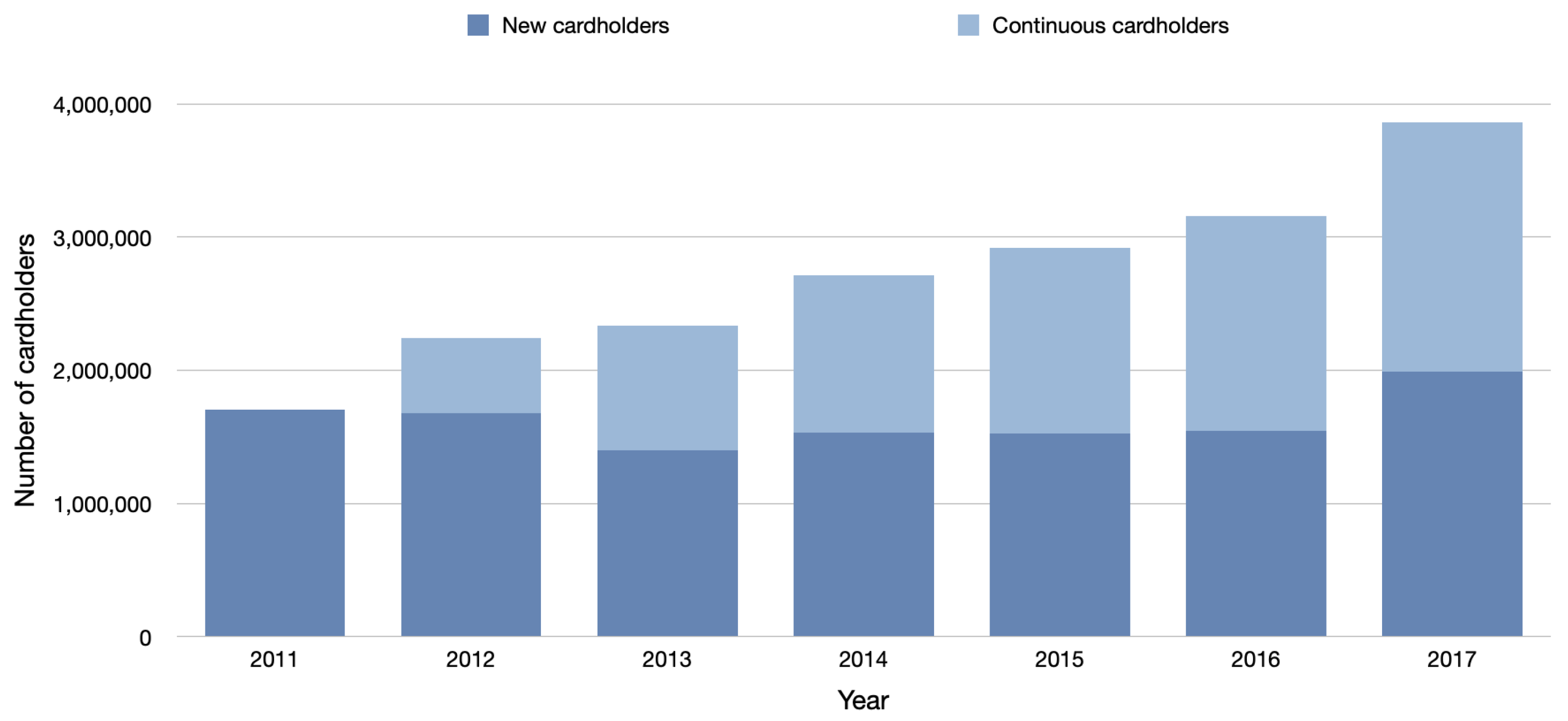
2.1. Data Source and Preliminary Analysis
2.2. Vector of Individual Trip Features
2.3. Gaussian Mixture Model
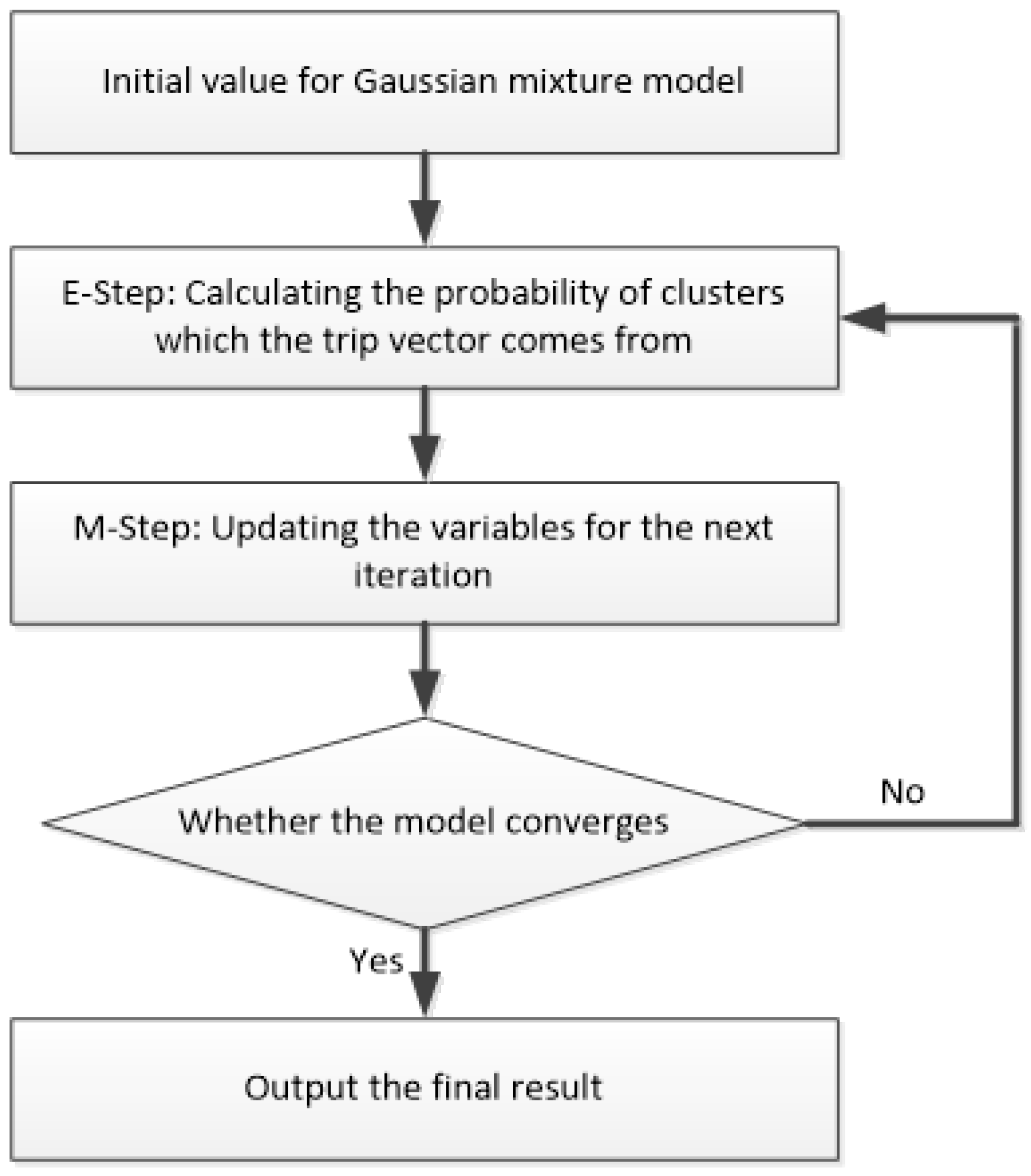
2.4. Expectation-Maximization Algorithm
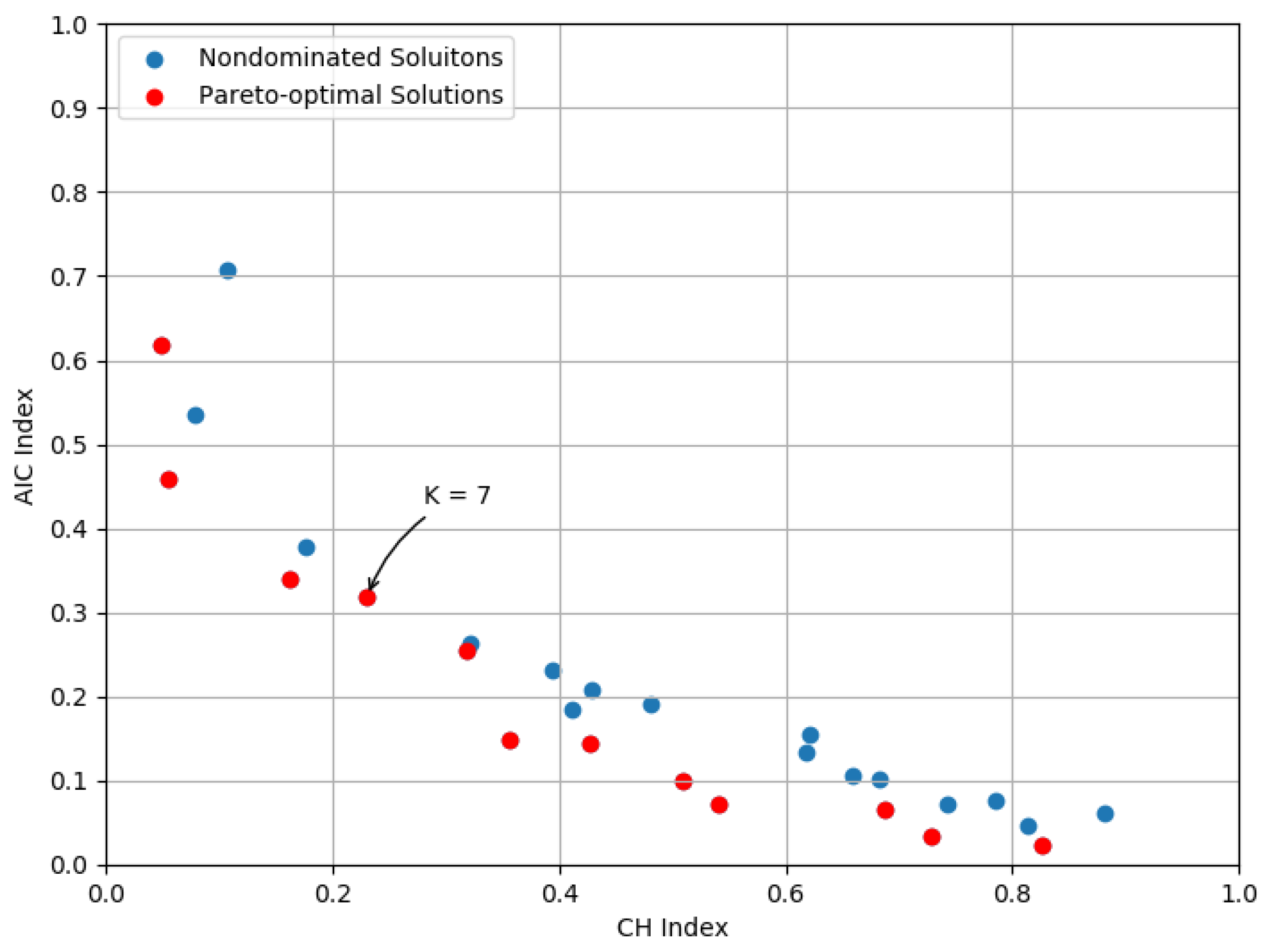
2.5. Parameter Choice
3. Results and Discussion
3.1. Clustering Results of Gaussian Mixture Model
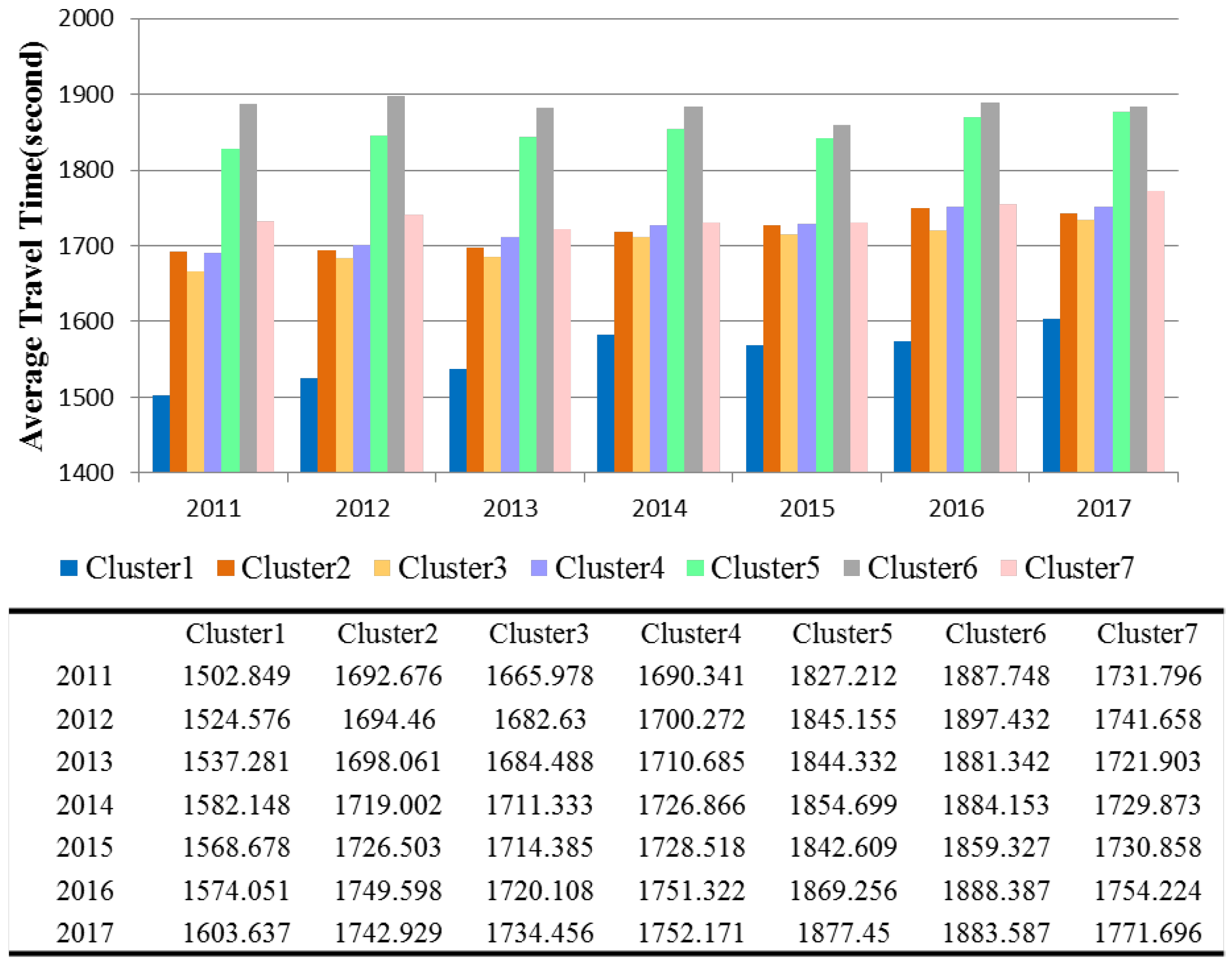
3.2. Passenger Structures and Travel Characteristics
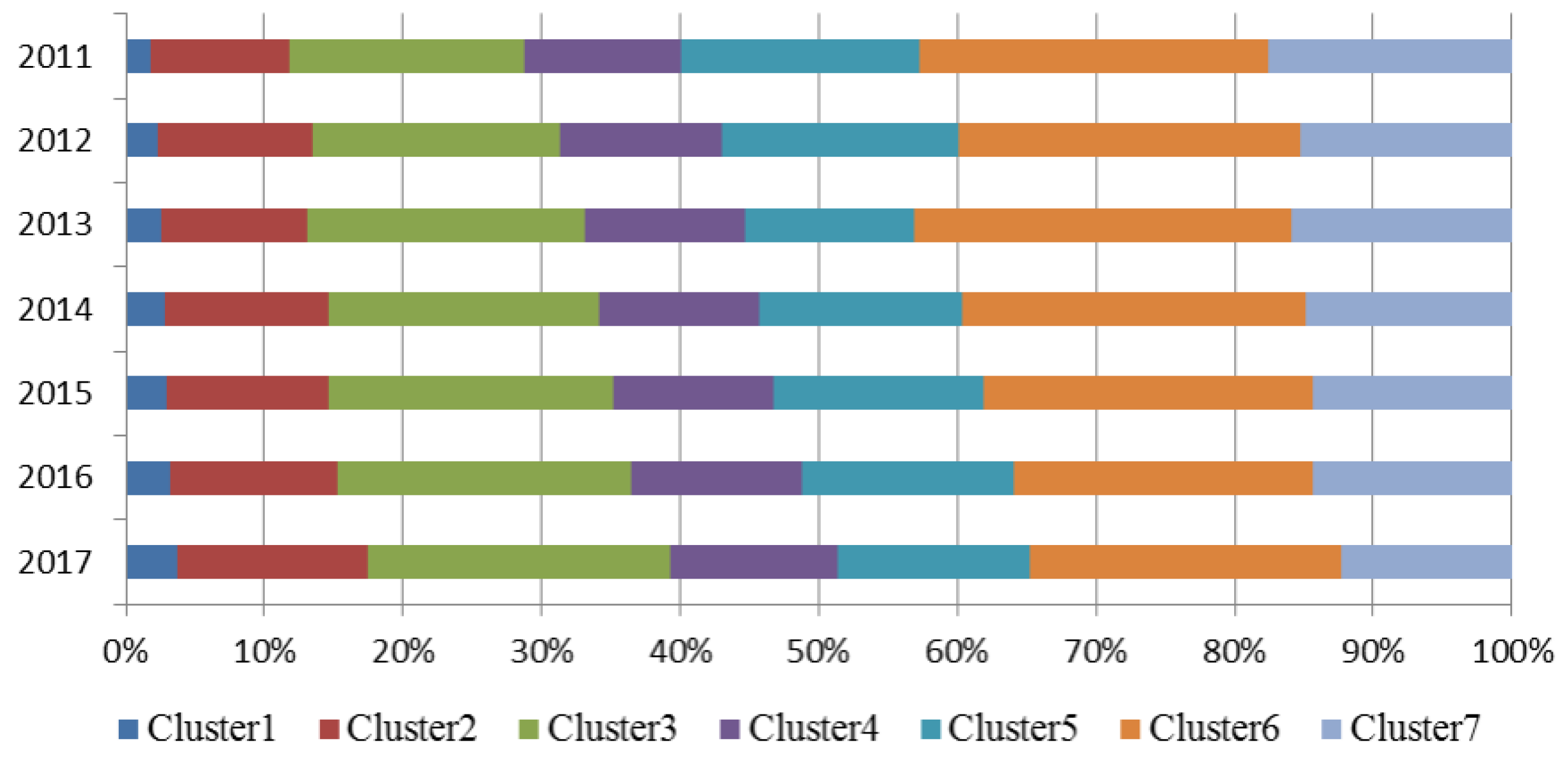
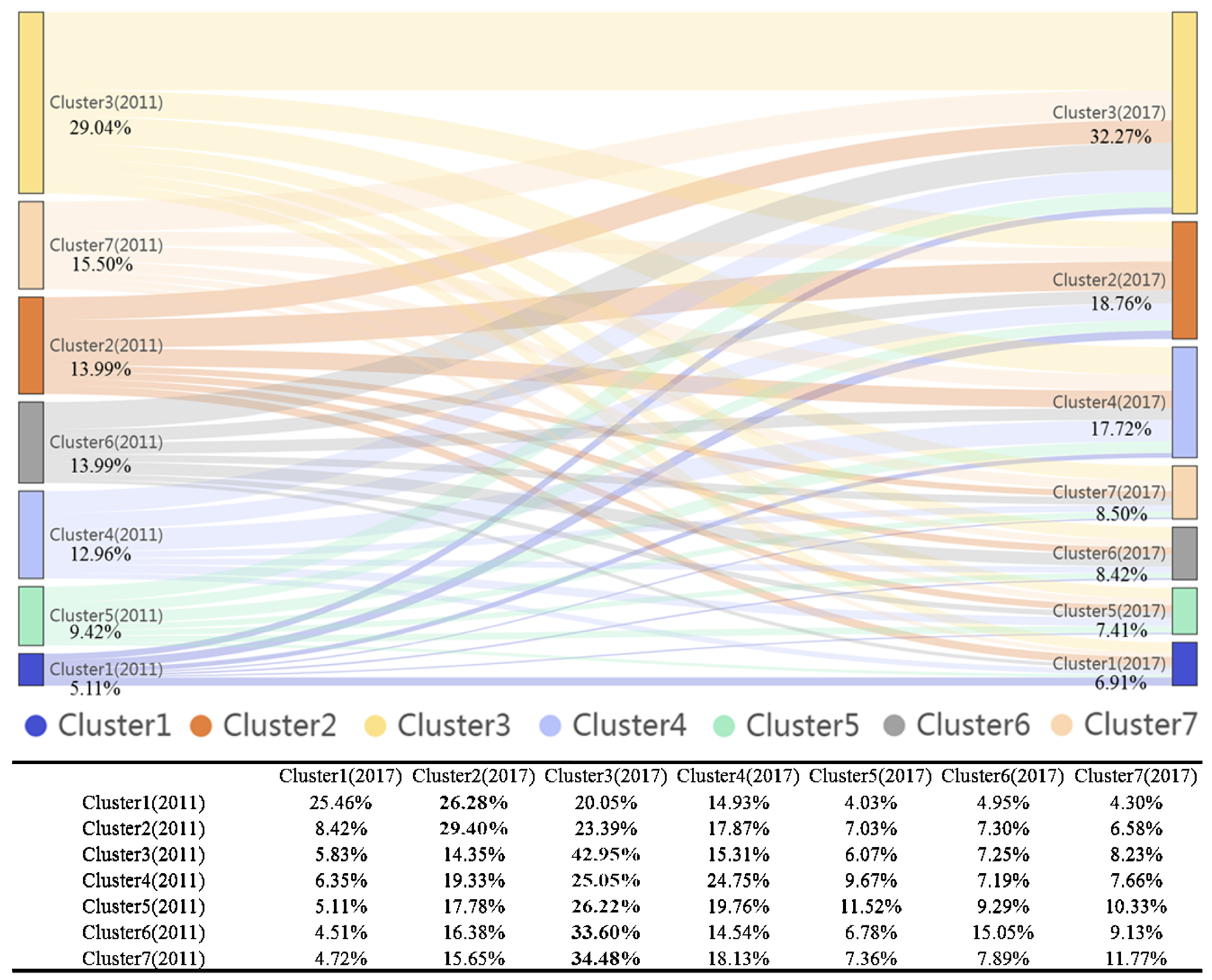
3.3. Spatio-Temporal Evolution of Cluster
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goulet-Langlois, G.; Koutsopoulos, H.N.; Zhao, J. Inferring patterns in the multi-week activity sequences of public transport users. Transp. Res. Part C Emerg. Technol. 2016, 64, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Tao, S.; Rohde, D.; Corcoran, J. Examining the spatial–temporal dynamics of bus passenger travel behaviour using smart card data and the flow-comap. J. Transp. Geogr. 2014, 41, 21–36. [Google Scholar] [CrossRef]
- Zhong, C.; Batty, M.; Manley, E.; Wang, J.; Wang, Z.; Chen, F.; Schmitt, G. Variability in regularity: Mining temporal mobility patterns in London, Singapore and Beijing using smart-card data. PLoS ONE 2016, 11, e0149222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, K.; Oh, K.; Lee, Y.K.; Kim, S.; Jung, J.Y. An analysis on movement patterns between zones using smart card data in subway networks. Int. J. Geogr. Inf. Sci. 2014, 28, 1781–1801. [Google Scholar] [CrossRef]
- Mohamed, K.; Côme, E.; Oukhellou, L.; Verleysen, M. Clustering smart card data for urban mobility analysis. IEEE Trans. Intell. Transp. Syst. 2016, 18, 712–728. [Google Scholar]
- Tu, W.; Cao, R.; Yue, Y.; Zhou, B.; Li, Q.; Li, Q. Spatial variations in urban public ridership derived from GPS trajectories and smart card data. J. Transp. Geogr. 2018, 69, 45–57. [Google Scholar] [CrossRef] [Green Version]
- Cheng, G.; Sun, S.; Zhou, L.; Wu, G.; Engineering, M. Using Smart Card Data of Metro Passengers to Unveil the Urban Spatial Structure: A Case Study of Xi’an, China. Math. Probl. Eng. 2021, 2021, 9176501. [Google Scholar] [CrossRef]
- Huang, J.; Levinson, D.; Wang, J.; Zhou, J.; Wang, Z.J. Tracking job and housing dynamics with smartcard data. Proc. Natl. Acad. Sci. USA 2018, 115, 12710–12715. [Google Scholar] [CrossRef] [Green Version]
- Long, Y.; Thill, J.C. Combining smart card data and household travel survey to analyze jobs-housing relationships in Beijing. Comput. Environ. Urban Syst. 2015, 53, 19–35. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Zhang, N.; Peng, H.; Huang, Y.; Zhang, Y. Spatiotemporal Heterogeneity Analysis of Influence Factor on Urban Rail Transit Station Ridership. J. Transp. Eng. Part A Syst. 2022, 148, 04021115. [Google Scholar] [CrossRef]
- Zhu, K.; Yin, H.; Qu, Y.; Wu, J. Measuring the Similarity of Metro Stations Based on the Passenger Visit Distribution. ISPRS Int. J. Geo-Inf. 2022, 11, 18. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, F.; Tu, L.; Xu, C.; Shen, D.; Tian, C.; Li, X.Y.; Li, Z. Estimation of passenger route choice pattern using smart card data for complex metro systems. IEEE Trans. Intell. Transp. Syst. 2016, 18, 790–801. [Google Scholar] [CrossRef]
- Kim, J.; Corcoran, J.; Papamanolis, M. Route choice stickiness of public transport passengers: Measuring habitual bus ridership behaviour using smart card data. Transp. Res. Part C Emerg. Technol. 2017, 83, 146–164. [Google Scholar] [CrossRef]
- Werner, C.M.; Brown, B.B.; Tribby, C.P.; Tharp, D.; Flick, K.; Miller, H.J.; Smith, K.R.; Jensen, W. Evaluating the attractiveness of a new light rail extension: Testing simple change and displacement change hypotheses. Transp. Policy 2016, 45, 15–23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chakour, V.; Eluru, N. Examining the influence of stop level infrastructure and built environment on bus ridership in Montreal. J. Transp. Geogr. 2016, 51, 205–217. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, D.; Li, Q.; Yue, Y.; Tu, W.; Cao, R. Impacts of weather on public transport ridership: Results from mining data from different sources. Transp. Res. Part C Emerg. Technol. 2017, 75, 17–29. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, X.; Sun, S.; Ma, X.; Lu, G. Forecasting short-term subway passenger flow under special events scenarios using multiscale radial basis function networks. Transp. Res. Part C Emerg. Technol. 2017, 77, 306–328. [Google Scholar] [CrossRef]
- Rodrigues, F.; Borysov, S.S.; Ribeiro, B.; Pereira, F.C. A Bayesian additive model for understanding public transport usage in special events. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 2113–2126. [Google Scholar] [CrossRef] [Green Version]
- Hörcher, D.; Graham, D.J.; Anderson, R.J. Crowding cost estimation with large scale smart card and vehicle location data. Transp. Res. Part B Methodol. 2017, 95, 105–125. [Google Scholar] [CrossRef]
- Long, Y.; Shen, Z. Profiling underprivileged residents with mid-term public transit smartcard data of Beijing. In Geospatial Analysis to Support Urban Planning in Beijing; Springer: Cham, Switzerland, 2015; pp. 169–192. [Google Scholar]
- Gao, Q.L.; Li, Q.Q.; Yue, Y.; Zhuang, Y.; Chen, Z.P.; Kong, H. Exploring changes in the spatial distribution of the low-to-moderate income group using transit smart card data. Comput. Environ. Urban Syst. 2018, 72, 68–77. [Google Scholar] [CrossRef]
- Briand, A.S.; Côme, E.; Trépanier, M.; Oukhellou, L. Analyzing year-to-year changes in public transport passenger behaviour using smart card data. Transp. Res. Part C Emerg. Technol. 2017, 79, 274–289. [Google Scholar] [CrossRef]
- Zhao, J.; Qu, Q.; Zhang, F.; Xu, C.; Liu, S. Spatio-temporal analysis of passenger travel patterns in massive smart card data. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3135–3146. [Google Scholar] [CrossRef]
- Ma, X.; Wu, Y.J.; Wang, Y.; Chen, F.; Liu, J. Mining smart card data for transit riders’ travel patterns. Transp. Res. Part C Emerg. Technol. 2013, 36, 1–12. [Google Scholar] [CrossRef]
- Morency, C.; Trépanier, M.; Agard, B. Analysing the variability of transit users behaviour with smart card data. In Proceedings of the 2006 IEEE Intelligent Transportation Systems Conference, Toronto, ON, Canada, 17–20 September 2006; pp. 44–49. [Google Scholar]
- Gong, Y.; Lin, Y.; Duan, Z. Exploring the spatiotemporal structure of dynamic urban space using metro smart card records. Comput. Environ. Urban Syst. 2017, 64, 169–183. [Google Scholar] [CrossRef]
- Bhaskar, A.; Chung, E. Passenger segmentation using smart card data. IEEE Trans. Intell. Transp. Syst. 2014, 16, 1537–1548. [Google Scholar]
- Kieu, L.M.; Bhaskar, A.; Chung, E. Mining temporal and spatial travel regularity for transit planning. In Proceedings of the Australasian Transport Research Forum 2013 Proceedings, Brisbane, Australia, 2–4 October 2013; pp. 1–12. [Google Scholar]
- Poussevin, M.; Tonnelier, E.; Baskiotis, N.; Guigue, V.; Gallinari, P. Mining ticketing logs for usage characterization with nonnegative matrix factorization. In Big Data Analytics in the Social and Ubiquitous Context; Springer: Cham, Switzerland, 2015; pp. 147–164. [Google Scholar]
- Lathia, N.; Smith, C.; Froehlich, J.; Capra, L. Individuals among commuters: Building personalised transport information services from fare collection systems. Pervasive Mob. Comput. 2013, 9, 643–664. [Google Scholar] [CrossRef]
- Xiong, H.; Wu, J.; Chen, J. K-means clustering versus validation measures: A data-distribution perspective. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2008, 39, 318–331. [Google Scholar] [CrossRef]
- Wang, W.T.; Wu, Y.L.; Tang, C.Y.; Hor, M.K. Adaptive density-based spatial clustering of applications with noise (DBSCAN) according to data. In Proceedings of the 2015 International Conference on Machine Learning and Cybernetics (ICMLC), Guangzhou, China, 12–15 July 2015; Volume 1, pp. 445–451. [Google Scholar]
- Greenspan, H.; Goldberger, J.; Mayer, A. Probabilistic space-time video modeling via piecewise GMM. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 384–396. [Google Scholar] [CrossRef] [PubMed]
- Toda, T.; Black, A.W.; Tokuda, K. Voice conversion based on maximum-likelihood estimation of spectral parameter trajectory. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 2222–2235. [Google Scholar] [CrossRef]
- Ahn, S.C.; Perez, M.F. GMM estimation of the number of latent factors: With application to international stock markets. J. Empir. Financ. 2010, 17, 783–802. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Axhausen, K.W. Understanding urban mobility patterns with a probabilistic tensor factorization framework. Transp. Res. Part B Methodol. 2016, 91, 511–524. [Google Scholar] [CrossRef]
- Ronchetti, E.; Trojani, F. Robust inference with GMM estimators. J. Econom. 2001, 101, 37–69. [Google Scholar] [CrossRef] [Green Version]
- Myronenko, A.; Song, X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Briand, A.S.; Côme, E.; El Mahrsi, M.K.; Oukhellou, L. A mixture model clustering approach for temporal passenger pattern characterization in public transport. Int. J. Data Sci. Anal. 2016, 1, 37–50. [Google Scholar] [CrossRef] [Green Version]
- Lee, E.H.; Lee, I.; Cho, S.H.; Kho, S.Y.; Kim, D.K. A travel behavior-based skip-stop strategy considering train choice behaviors based on smartcard data. Sustainability 2019, 11, 2791. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Wan, Z.; Zhan, S.; Tao, C.; Ran, X. Prediction of Geological Characteristic Using Gaussian Mixture Model. In Proceedings of the 75th EAGE Conference & Exhibition Incorporating SPE EUROPEC 2013, London, UK, 10–13 June 2013; p. cp-348. [Google Scholar]
- Zhao, Y.; Shrivastava, A.K.; Tsui, K.L. Regularized Gaussian mixture model for high-dimensional clustering. IEEE Trans. Cybern. 2018, 49, 3677–3688. [Google Scholar] [CrossRef] [PubMed]
- Lagrange, A.; Fauvel, M.; Grizonnet, M. Large-scale feature selection with Gaussian mixture models for the classification of high dimensional remote sensing images. IEEE Trans. Comput. Imaging 2017, 3, 230–242. [Google Scholar] [CrossRef] [Green Version]
- Pernkopf, F.; Bouchaffra, D. Genetic-based EM algorithm for learning Gaussian mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1344–1348. [Google Scholar] [CrossRef] [PubMed]
- McLachlan, G.J.; Rathnayake, S. On the number of components in a Gaussian mixture model. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 341–355. [Google Scholar] [CrossRef]
- Kim, I.Y.; De Weck, O.L. Adaptive weighted-sum method for bi-objective optimization: Pareto front generation. Struct. Multidiscip. Optim. 2005, 29, 149–158. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, M.; Huang, Z.; Zhao, T.; Zhang, Y.; Wei, H. Spatiotemporal Evolution of Travel Pattern Using Smart Card Data. Sustainability 2022, 14, 9564. https://doi.org/10.3390/su14159564
Lin M, Huang Z, Zhao T, Zhang Y, Wei H. Spatiotemporal Evolution of Travel Pattern Using Smart Card Data. Sustainability. 2022; 14(15):9564. https://doi.org/10.3390/su14159564
Chicago/Turabian StyleLin, Mu, Zhengdong Huang, Tianhong Zhao, Ying Zhang, and Heyi Wei. 2022. "Spatiotemporal Evolution of Travel Pattern Using Smart Card Data" Sustainability 14, no. 15: 9564. https://doi.org/10.3390/su14159564
APA StyleLin, M., Huang, Z., Zhao, T., Zhang, Y., & Wei, H. (2022). Spatiotemporal Evolution of Travel Pattern Using Smart Card Data. Sustainability, 14(15), 9564. https://doi.org/10.3390/su14159564






