Green Product Development and Order Strategies for Retailers

Abstract

In this study, we consider a green supply chain to encompass two competing retailers, whose market demands include a stochastic component and a deterministic component, and we assume that consumer returns exist. We use game theory to determine the optimal decisions that retailers could make regarding greenness level and purchase quantity in either competitive environments or monopoly environments, and we perform sensitivity analysis. We show that the optimal greenness level and the purchase quantity for the stochastic demand are both higher in a competitive environment than those in a monopoly environment when the consumer return rate is low; therefore, competition is more beneficial to the increasing of the greenness level of products and the market supply than monopoly environments. We also show that, in a competitive environment, the optimal greenness level, the purchase quantity for the stochastic demand, and the revenue of retailers increase as the retail price increases, or as the wholesale price, the greenness R&D investment cost coefficient, and the consumer return rate decrease, and that this finding remains true in a monopoly environment, except that the optimal greenness level is found to increase as the return rate increases in the case of a monopoly environment. Finally, we suggest that the government should break monopolies, encourage positive competition, support small- and medium-sized companies, and subsidize the green industry to increase the greenness level of products and market supplies.

1. Introduction

With the rapid development of the social economy the need for natural resources is increasing, and many of these resources have now been used exhaustively. The destruction of the ecological environment is also accelerating due to backward production technology and the lack awareness regarding environmental protection. In recent years, governments have attached great importance to the protection of the environment and the promotion of sustainable development. Against this background, green supply chain management, which considers resource consumption and environmental impacts, is gaining increasing interest among researchers and practitioners from the fields of both academia and industry regarding supply chain management [1,2]. Consequently, an increasing number of consumers are more interested in buying green products than traditional products. By manufacturing and selling green products, core members of supply chains can not only shape their own green image, but also gain greater market advantages. The term ‘green products’ refers to products that are harmless to the environment and beneficial for the regeneration and recycling of resources. Examples include the use of organic cotton to produce clothing, the use of recycled rubber to produce treads, and the development of clean dyeing processes in the clothing and footwear industries. However, the development and production of green products is more expensive for enterprises. Meanwhile, factors such as market competition, high demand uncertainty, and the consumer return rate greatly impact green operation decisions (e.g., the greenness level of products). Therefore, it is important to study the impact of factors such as market competition, demand uncertainty, and the consumer return rate on enterprises’ decision making regarding green operations.

Our study is related to those regarding product greenness decision-making problems in the green supply chain; many papers have been published concerning this problem, such as those by Nouira et al. [3], Liu et al. [4], Heydari et al. [5], Wang et al. [6], Liu et al. [7], and Zhang et al. [8]. However, when examining this problem, few of the existing studies focused on stochastic demand [4,9,10], among which even fewer studies considered competitive retailers, comparisons between competition and monopoly environments, or consumer returns. It is reasonable to assume that the market demand is stochastic and that consumer returns exist, and the comparative analysis of decisions made in the competitive environment and the monopoly environment is an interesting topic of research. In our work, firstly, we study green product development and order strategies for competitive retailers with stochastic demand and consumer returns, which could enrich the theory and methods used to address the product greenness decision-making problem in green supply chains and provide support for green product sellers and governments regarding operational decisions. Motivated by the above-mentioned research gap, our research objectives are to:

(1)

Establish the existence and uniqueness of pure strategy Nash equilibriums in the competitive environment and determine the optimal decisions in the monopoly environment.

(2)

Comparatively analyze the decisions of competitive retailers and monopoly retailers.

(3)

Study the impact of retail price, wholesale price, and greenness R&D investment cost coefficient on retailers’ decision making.

(4)

Provide suggestions for the development of the green supply chain.

As an extension of the work by Guo et al. [11], we assume the market demand to be stochastic instead of deterministic. We build models using game theory and optimization theory in the competitive environment and the monopoly environment, respectively. Consumer returns are considered in the model, and the retailers are required to decide the greenness level of products and the purchase quantity from suppliers. We obtain the following analytical results:

(1)

One pure strategy Nash equilibrium is established in the competitive environment, and one optimal solution is found in the monopoly environment.

(2)

The optimal greenness level and the purchase quantity for the stochastic demand are both found to be higher in the competitive environment than those in the monopoly environment when the consumer return rate is low.

(3)

As the retail price, the wholesale price, or the greenness R&D investment cost coefficient increases, the greenness level of the product and the supply for stochastic demand either increase or decrease together.

The rest of the paper is organized as follows: Section 2 shows the related literatures. Section 3 describes the problem and builds the model. In Section 4, we compare the decisions made in the competitive environment with those made in the monopoly environment and conduct sensitivity analyses. Section 5 provides a numerical analysis. Section 6 presents the discussion; we discuss our research implications from both theoretical perspectives and practical perspectives. Finally, in Section 7, we conclude our findings and present future extensions.

2. Literature Review

Our research is related to three streams of the literature: (1) literature concerning green strategies in supply chains, in which studies propose various green strategies to improve product greenness or increase supply chain members’ profits; (2) literature concerning consumer returns in supply chains, in which studies consider the consumer returns mechanism in their supply chain management; (3) literature concerning green supply chains with stochastic demand, in which studies assume the market demands are stochastic in a green supply chain.

2.1. Green Strategies in the Supply Chain

In this section of the literature, some studies focused on the coordination of green supply chains. Rao [12] empirically analyzed factors that can promote enterprises which make supply chains greener. Albino and Berardi [13] showed that the creation of greenness is correlated with a collaborative relationship between the supplier and the design team. Ghosh and Sha [14] studied a green supply chain containing a manufacturer and a retailer, and their research showed that collaboration between a manufacturer and a retailer is beneficial in improving green innovation, and that a higher level of greenness leads to higher retail prices. However, collaboration cannot increase the revenue of the manufacturer, therefore, retailers need to share revenue with manufacturers. Ghosh and Sha [15] examined the influence of a cost-sharing contract on the decision making of supply chain members related to product greenness, and they found that a cost-sharing contract leads to a higher level of greenness in products and revenues. However, Hong and Guo [16] studied product greenness and green efforts decision making, and found that cost-sharing contracts hurt the retailer’s revenue. Moreover, they discovered that the two-part tariff contract can achieve the highest product greenness compared with the price-only contract and the cost-sharing contract. Xin et al. [17] also confirmed the positive effect of the two-part tariff contract, and they found that both the revenue and cost-sharing contracts and the two-part tariff contract are better than the wholesale price-only contract, and that the two-part tariff contract could perform even better on coordinating the supply chain than other contracts they studied. Adhikari and Bisi [18] studied the coordination mechanism in green clothing supply chains in emerging economies by using green cost-sharing contracts and profit-sharing contracts, and they further analyzed the impact of supply chain members paying fair attention to green decision making and pricing decision making. Li et al. [19] explored the effects of three contracts and finally obtained that supply chain members prefer the revenue-sharing contract when the green marketing effort effect is low, but the cost-sharing contract when the green marketing effort effect is high.

Some studies have investigated problems in the competitive environment. Liu et al. [20] discussed the influence of consumers’ environmental awareness on a green competition game from two aspects: retailers and manufacturers. They found that the profits of enterprises that offer inferior green products tend to increase if the green competition level is low, and will tend to decrease if the competition level is high. Galbreth and Ghosh [21] constructed a green competition model composed of two asymmetric enterprises, and showed that if different consumers pay different levels of attention to greenness, then only when consumers’ green awareness is strong enough will the enhancement of consumers’ green awareness benefit both companies. Du et al. [22] studied the competition between the common product and the green product, and pointed out that whether to produce the green product or not depends on the cost, cannibalization, and competition degree. Zhu and He [23] studied greenness-related decision making under different supply chain structures; they discovered that price competition leads to a higher greenness level, and, on the contrary, greenness competition leads to a lower greenness level. Chen et al. [24] built a model consisting of two manufacturers and one retailer. In their model, horizontal competition existed between two manufacturers, and vertical competition existed between the manufacturers and the retailer. They found that a green manufacturer would benefit from the enhancement of environmental awareness, but would be inhibited by the increase in greening cost. Hong et al. [25] examined the pricing strategies for a green product that competes with a regular product with dual-product competition and an asymmetric information. They showed that the quality of the green product and the levels of consumers’ reference recognition and environmental awareness will impact the pricing of the green product, and that when the production cost of the green product is low, the manufacturer adopts a low-price, low-yield strategy under asymmetric information, by comparison with the strategies under symmetric information. Yang et al. [26] investigated two manufacturers with price and quality competition. They inferred that those manufacturers would make a greenness investment if the green sensitivity coefficient is low, that the manufacturer who makes a greenness investment would get more profit than its rival without a greenness investment, and that if both manufacturers make a greenness investment then the manufacturer who has a larger potential market share would receive more profit.

Other studies have considered multi-channels and government mandates in the green supply chain [27,28,29]. Khorshidvand et al. [29] built a model that contained one manufacturer, one distributor, and one retailer. The manufacturer and distributor had their own online channels to sell products; their research demonstrated that a centralized supply chain could optimally achieve Pareto, but that meanwhile, the manufacturer would face a huge loss. Gao et al. [30] established a green supply chain model in which an eco-label policy was considered; in their study, it was proven that an eco-label policy can have a positive effect on product greenness. Furthermore, Gao et al. [31] also showed that, in an eco-label policy environment, a higher green standard set by the government would lead to higher wholesale prices, retail prices, and direct sale prices. Yin et al. [32] considered government subsidies in their model, and found that tax policies and subsidies policies could improve product greenness under some mild conditions. Zhang et al. [33] studied the carbon emission regulation by the government, and showed that the increase of carbon tax is confirmed to have a significant effect on the abatement level and green technology investment of manufacturers. Meng et al. [34] analyzed a dual-channel supply chain with government subsidies, and argued that the increase of government subsidies would decrease the green product price and the regular product price and increase the manufacturer’s profit, but whether the retailer’s profit would increase or not depends on the specific amount of government subsidies.

2.2. Consumer Returns in Supply Chain

Many researchers have studied consumer returns in supply chain management. Su [35] examined the impact of both full return policies and partial return policies on supply chains. Shulman et al. [36] believed that heterogeneous consumers would only buy products after a trial. They studied the effect of consumer returns policies on retailers’ decisions regarding commodity pricing and replenishment. Shang et al. [37] assumed that strategic consumers would decide whether to use a probationary period for opportunistic short-term consumption, and they analyzed the impact of consumer returns policy on wardrobe service designs. Considering a green supply chain with two sales channels, Phadnis and Fine [38] discussed the impact of the product return rate and online return penalties on enterprise operations. However, the four above-mentioned studies did not consider the connection between consumer returns and the salvage value of products. Ulku and Hsuan [39] compared two products: a modular product with permission to return it, and a standard product without permission to return it. Their work revealed the advantages of modular products, and suggested that companies should sell products with permission to return them. Wang and Huang [40] examined whether retailers should implement return policies. The retail price, referral fee, and carbon reduction levels were decision variables in their study. Their results suggested that return policies would be implemented only when the salvage value of the product was high enough. Wang et al. [41] studied a manufacturer’s return policy, considering consumer environment awareness and environment quality improvement. They concluded that the environmental quality improvement effort and the environmental coefficient would increase if consumer environmental awareness strengthened. Furthermore, if consumer environmental awareness was weak, then the manufacturer would adopt a without-return policy; otherwise, the manufacturer would adopt a full-refund return policy. Zhang et al. [42] studied the impact of cross-channel return policies on decisions regarding green supply chains, and they came to the conclusion that cross-channel policies would increase the market demand of all the channels, and lead to higher optimal greenness level of products. Tang et al. [43] explored a Stackelberg game where the manufacturer was a leader and the retailer was a follower, and they found that the manufacturer could optimize the wholesale price and the transfer price to motivate the retailer to control return rate. Recently, Guo et al. [11] examined the effect of consumer returns on supply chain members’ greenness decisions, and they assumed the market demand to be deterministic.

2.3. Green Supply Chain with Stochastic Demand

The stochastic demand assumption is widely used in supply chain management problems, but most of the literature in the field of green supply chain management assume market demand to be deterministic. However, several studies have investigated green supply chains with stochastic demand. Lu et al. [44] made a hypothesis that manufacturers could be divided into ability-biased overconfident suppliers and precision-biased, overconfident suppliers. They assumed the market demand faced by these two kinds of suppliers to be stochastic, and Lu et al. [44] discovered that overconfident suppliers made more effort with regard to greenness than other suppliers. Raza et al. [45] studied a firm’s greening, pricing, and inventory decisions with environmental considerations and stochastic demand. In the study by Raza and Govindaluri [46], they analyzed market demand in two situations: full information with deterministic demand and stochastic demand, and partial information with stochastic demand. Both Wang et al. [47] and Qu et al. [48] investigated the supply chain containing one manufacturer and one retailer with stochastic demand. Wang et al. [47] examined the effect of risk aversion on supply chain members’ decisions, and they found that the centralized supply chain would result in a higher green degree of the product than decentralized supply chains. Qu et al. [48] studied the optimal strategy for a green supply chain considering shipping policy and default risk, and confirmed that government subsidies to manufacturers could improve social welfare, but that the effect of subsidies to retailers was on the opposite. Al-e-Hashem et al. [49] tried to use their model to minimize greenhouse gas emissions and supply chain costs, with the demand of each product being stochastic. The manufacturer played a Stackelberg leader role in the model of Wang and Choi [50], in which uniform distribution was used to formulate a stochastic demand variable. Wang and Choi [50] compared a decentralized supply chain and an integrated supply chain, and then they examined the decisions made by the manufacturer and the retailer under a revenue-sharing contract, a cost-sharing contract, and a two-part tariff contract. They found that revenue-sharing and two-part tariff contracts both helped to increase profitability and greenness. Recently, He [51] studied a jointly production and pricing optimization problem with a common product and a green product, and obtained the conditions required for enterprises to consider including green technology investment in their production.

In summary, in the related literature, most of previous studies focused on the supply chain which contained one manufacturer and one retailer, while some others considered the supply chain containing two manufacturers, and very few papers considered a supply chain containing two retailers, such as Guo et al. [11] and Galbreth and Ghosh [21]. Galbreth and Ghosh [21] assumed that the market demand was deterministic, and they focused on consumer attitudes toward sustainability, but not the greenness level of the product. Our work actually is an extension of the work of Guo et al. [11], but they also assumed that the demand was deterministic, while we assumed the demand is stochastic. Guo et al. [11] showed that the greenness level decreased as the consumer return rate increased if the parameter t was less than a threshold, and the conclusion is the opposite if the parameter t was larger than the threshold. However, according to our conclusions, in the case of stochastic demand, the impact of the consumer return rate on the greenness level of the product depends on the competitive or monopoly environment. In addition, most of the previous studies (such as Ghosh and Shah [15], Aslani and Heydari [27], and Wang et al. [47]) addressed monopolistic environments in a supply chain that contained a manufacturer and a retailer, and found that a monopoly entity containing a manufacturer and a retailer could lead to a higher greenness level of the product than a competitive environment in which a manufacturer and a retailer make decisions individually. In our work, we addressed monopolistic environments in a supply chain that contains two retailers; however, we found an opposite conclusion, that competitive retailers (each retailer makes decisions individually) can lead to a higher greenness level of the product than a monopoly entity containing two retailers if the consumer return rate is relatively low. Finally, many previous studies (such as Phadnis and Fine [38], and Zhang et al. [42]) considered the impact of the consumer return rate, but did not consider the connection between consumer returns and the salvage value of products, which is considered in our work.

In short, most studies in the literature assumed the market demand to be deterministic, and only a few studies considered stochastic demand, among which, even fewer studies considered competitive retailers, comparisons between competition and monopoly environments, or consumer returns. To supplement these research gaps, by considering stochastic demand and consumer returns, in our work, first, we studied the optimal decisions retailers could make regarding the greenness level of products and the purchase quantity from suppliers in either a competitive environment or a monopoly environment; we then comparatively analyzed the decisions made by competitive retailers and the monopoly retailer, and we provided suggestions to help raise the greenness level of products.

3. Model

This section presents the model analysis. First, we listed the complete notations in the back part.

To make the model clearer, Figure 1 displays the market structure and decision-making process of two retailers. The model considers two retailers (retailer 1 and retailer 2) in a green product market with stochastic demand. Retailer i (i = 1, 2) needs to choose the greenness level $b_i$ and purchase quantity $Q_i$ of the product to be sold, which is a static game with complete information. In order to reduce the complexity of the research problem, it is assumed that the two retailers are homogeneous. The market demand for green products consists of two parts: stochastic demand and deterministic demand. We referred to the demand function in Guo et al. [11], and supposed that the deterministic demand is affected by the greenness level of the product. The specific function can be expressed as: $D_i$ = ${\epsilon }_i$ + $\alpha$ + $b_i$ − $\gamma b_{3-i}$ = ${\epsilon }_i$ + $y_i$, i = 1, 2. ${\epsilon }_i$ is the stochastic part of the demand, and its probability density function is f(·), the cumulative distribution function is F(·), $\alpha$ represents the market size of the product, $\gamma$ is the sensitivity coefficient of demand to greenness level, and $0<\gamma <1$. The wholesale price of green products purchased by both retailers is $w$, and the retail price is $p$. According to Guo et al. [11], in order to make products more responsive to the consumers’ pursuit of greenness, retailers will also pay green investments for products, such as paying advertising fees, purchasing equipment, conducting production supervision and testing, etc. As assumed by Ghosh and Shah [14] and Huang et al. [1], here, we also assumed that the cost invested by retailers to improve the greenness level is a quadratic function of the greenness level; that is, the cost of retailer i (i = 1, 2) can be expressed as $\xi b_i^2/2$, and $\xi$ represents the R&D cost coefficient of the product greenness. Additionally, this is the first movement that retailer i spends $\xi b_i^2/2$ on greenness level investment in the whole process. Then, retailer i obtains the commodity from the supplier, and, if $Q_i$ cannot satisfy $D_i$, retailer i will suffer out-of-stock losses. The return rate of products sold by retailers is $\lambda$, and $0<\lambda <1$. The returned products cannot be sold again, and in addition, returned products and unsold products can only be disposed of by retailers in the recycling market, at which point the retailers recover the salvage value. The residual value is related to the greenness level; it can be expressed as: $t+k{b}_i$, where $t$ represents the residual value independent of the greenness level and $k$ represents the greenness level coefficient of the product residual value; the unit out-of-stock cost of both retailers is $s$. Finally, retailer i copes with the returned products and the unsold products, and receives the final income.

3.1. Model Contains Two Competitive Retailers

First, we studied a situation in which there are two competing retailers in the market; in this case, for i = 1, 2, the expected profit function of retailer i is:

$${\pi }_i^c=E\left\{\left[(1-\lambda )p+(t+k{b}_i)\lambda \right]\min (D_i,Q_i)-w{Q}_i+(t+k{b}_i){(Q_i-D_i)}^{+}-s{(D_i-Q_i)}^{+}-\xi b_i^2/2\right\}.$$

(1)

Similarly, in order to simplify the calculation, we followed Petruzzi and Dada [52], letting $Q_i$ = $y_i$ + $z_i$; where $y_i$ = $\alpha$ + $b_i$ − $\gamma b_{3-i}$, the purchase quantity $y_i$ can suffice the deterministic demand, and the purchase quantity $z_i$ can be used to satisfy the stochastic demand, so Equation (1) can be rewritten as follows:

$$\begin{array}{lll}{\pi }_i^c\hfill & =\hfill & E\{\left[(1-\lambda )p+(t+k{b}_i)\lambda \right]\left[y_i+z_i+{({\epsilon }_i-z_i)}^{-}\right]-w(y_i+z_i)\hfill \\ & & +(t+k{b}_i){(z_i-{\epsilon }_i)}^{+}-s{({\epsilon }_i-z_i)}^{+}-\xi b_i^2/2\}.\hfill \end{array}$$

(2)

Before proving the equilibrium decision of two retailers, the following Lemma is given (Zhao and Atkins [53]):

Lemma 1.

A bivariate function g (x₁, x₂) is jointly quasi-concave in two variables if and only if g (x₁, x₂) is quasi-concave, given mx₁ + x₂ = k for any real values m, k.

Proposition 1.

For i = 1, 2, let $N_i=\frac{[\lambda k+(1-\lambda )kF(z_i)][\lambda k+(1-\lambda )kF(z_i)-2k]}{(2\lambda k-\xi )f(z_i)}$; when s ≥ max (N₁, N₂), π_i^c is a jointly quasi-concave function of b_i and z_i. There is a pure strategy Nash equilibrium in the game between two competing retailers (b₁^c, z₁^c, b₂^c, z₂^c).

Proof of Proposition 1.

Through Lemma 1, let b_i = R − mz_i, and by substituting it into Equation (2), we could obtain:

$$\begin{array}{lll}{\pi }_i^c\hfill & =\hfill & E\{\left[(1-\lambda )p+(t+k(R-m{z}_i))\lambda \right][\alpha +R-m{z}_i-\gamma (R-m{z}_{3-i})+z_i+{({\epsilon }_i-z_i)}^{-}]\hfill \\ & & -w(\alpha +R-m{z}_i-\gamma (R-m{z}_{3-i})+z_i)+(t+k(R-m{z}_i)){(z_i-{\epsilon }_i)}^{+}-s{({\epsilon }_i-z_i)}^{+}\hfill \\ & & -\xi {(R-m{z}_i)}^2/2\}.\hfill \end{array}$$

As for the above equation, we could obtain the first-order condition and the second-order condition with respect to $z_i$:

$$\begin{array}{lll}\frac{d{\pi }_i^c}{d{z}_i}\hfill & =\hfill & -mk\lambda [\alpha +R-m{z}_i-\gamma (R-m{z}_{3-i})+z_i+E{({\epsilon }_i-z_i)}^{-}]+[1-m-F(z_i)]\hfill \\ & & \times \left\{(1-\lambda )p+\lambda [t+k(R-m{z}_i)]\right\}-w(1-m)-mkE{(z_i-{\epsilon }_i)}^{+}\hfill \\ & & +\left[t+k(R-m{z}_i)\right]F(z_i)+s\left[1-F(z_i)\right]+m\xi (R-m{z}_i),\hfill \end{array}$$

$$\frac{d^2{\pi }_i^c}{d{z}_i^c}=-2mk\lambda +m^2(2\lambda k-\xi )-2mk(1-\lambda )F(z_i)-(1-\lambda )\left[p-t-k(R-m{z}_i)\right]f(z_i)-sf(z_i).$$

Similarly to the proof of Proposition 2, it can be proven that, when $s\ge \max (N_1,N_2)$, ${\pi }_i^c$ is a joint quasi-concave function of $b_i$ and $z_i$. □

3.2. Model of the Monopoly Retailer

Next, we supposed that the two retailers belong to the same enterprise; that is, we considered the case of a monopoly retailer, and in this condition, the expected profit function of the monopoly retailer is:

$${\pi }^m=E\left\{{\displaystyle \sum _{i=1,2}\left\{\left[(1-\lambda )p+(t+k{b}_i)\lambda \right]\min (D_i,Q_i)-w{Q}_i+(t+k{b}_i){(Q_i-D_i)}^{+}-s{(D_i-Q_i)}^{+}-\xi b_i^2/2\right\}}\right\}.$$

(3)

In a similar way, Equation (3) can be rewritten as follows:

$$\begin{array}{lll}{\pi }^m\hfill & =\hfill & E\{{\displaystyle \sum _{i=1,2}\{\left[(1-\lambda )p+(t+k{b}_i)\lambda \right]\left[y_i+z_i+{({\epsilon }_i-z_i)}^{-}\right]-w(y_i+z_i)}\hfill \\ & & +(t+k{b}_i){(z_i-{\epsilon }_i)}^{+}-s{({\epsilon }_i-z_i)}^{+}-\xi b_i^2/2\}\}.\hfill \end{array}$$

(4)

Proposition 2.

When$\xi >2k\lambda (1+\gamma )$, and under the premise of $s<\frac{{\{k\lambda [1-F(z_1)]+kF(z_1)\}}^2}{(\xi -2k\lambda )f(z_1)}-\frac{(1-\lambda )f(z_1)[p-t-k{b}_1]}{f(z_1)}$,${\pi }^m$is a joint quasi-concave function ofb₁, b₂, z₁, andz₂, and the monopolistic retailers have optimal strategiesb₁^m, b₂^m, z₁^m, andz₂^mto maximize the expected profit.

Proof of Proposition 2.

For Equation (4), we obtained the first and second derivatives of $b_1$, $b_2$, $z_1$, and $z_2$. If the Hessen matrix H is negative, the monopolistic retailers have optimal strategies to maximize profits. As for the Hessen matrix H, it is easy to obtain the first-order sequential principal minor $\left|H_1\right|=2k\lambda -\xi <0$. For the second-order sequential principal minor $\left|H_2\right|=(2k\lambda -\xi +2\gamma k\lambda )(2k\lambda -\xi -2\gamma k\lambda )$, if $\xi >2k\lambda (1+\gamma )$, then

• $\left|H_2\right|>0$. For the third-order sequential principal minor

• $\left|H_3\right|=(\xi -2k\lambda ){\{k\lambda [1-F(z_1)]+kF(z_1)\}}^2-\{(1-\lambda )f(z_1)(p-t-k{b}_1)+sf(z_1)\}[{(2k\lambda -\xi )}^2-{(2\gamma k\lambda )}^2]$

, in order to make the third-order sequential principal minor less than 0, the following two conditions need to be implemented: $\xi >2k\lambda (1+\gamma )$, and $s<M_1=\frac{(\xi -2k\lambda ){\{k\lambda [1-F(z_1)]+kF(z_1)\}}^2}{f(z_1)[{(\xi -2k\lambda )}^2-{(2\gamma k\lambda )}^2]}-\frac{(1-\lambda )f(z_1)[p-t-k{b}_1]}{f(z_1)}$. The fourth-order principal minor $\begin{array}{lll}\left|A_4\right|\hfill & =\hfill & -{\{k\lambda [1-F(z_2)]+kF(z_2)\}}^2\{(2k\lambda -\xi )[(1-\lambda )f(z_1)(t+k{b}_1-p)-s]-k^2[\lambda +F(z_1)(1-\lambda )]\}\hfill \\ & & +[(1-\lambda )f(z_2)(t+k{b}_2-p)-sf(z_2)]k^2\{\lambda [1-F(z_1)]+F(z_1)\}(\xi -2k\lambda )[\lambda +F(z_1)(1-\lambda )]\hfill \\ & & -[(1-\lambda )f(z_2)(t+k{b}_2-p)-sf(z_2)][(1-\lambda )f(z_1)(p-t-k{b}_1)+sf(z_1)][{(\xi -2k\lambda )}^2-{(2\gamma k\lambda )}^2]\hfill \end{array}$. To make the fourth-order principal minor greater than 0, the following two conditions need to be implemented: $\xi >2k\lambda (1+\gamma )$, and $s<M_2=\frac{{\{k\lambda [1-F(z_1)]+kF(z_1)\}}^2}{(\xi -2k\lambda )f(z_1)}-\frac{(1-\lambda )f(z_1)[p-t-k{b}_1]}{f(z_1)}$. Because $M_2<M_1$, the condition of the negative definition of the Hessen matrix can be summarized as follows: $\xi >2k\lambda (1+\gamma )$, and $s<M_2$. □

4. Comparison and Analysis

In this section, we compared the optimal decisions ($b_i^c$, $z_i^c$) and ($b_i^m$, $z_i^m$) of competitive retailers and monopolistic retailers. For i = 1, 2, it is easy to obtain the following first-order partial derivatives:

$$\frac{\partial {\pi }_i^c}{\partial b_i}=(1-\lambda )p+t\lambda +\alpha k\lambda +(2\lambda k-\xi )b_i-\gamma k\lambda b_{3-i}+k\lambda z_i+kE[\lambda {({\epsilon }_i-z_i)}^{-}+{(z_i-{\epsilon }_i)}^{+}]-w,$$

(5)

$$\frac{\partial {\pi }_i^c}{\partial z_i}=[(1-\lambda )p+\lambda (t+k{b}_i)][1-F(z_i)]-w+(t+k{b}_i)F(z_i)+s[1-F(z_i)],$$

(6)

$$\begin{array}{lll}\frac{\partial {\pi }^m}{\partial b_i}\hfill & =\hfill & (1-\lambda )p+t\lambda +\alpha k\lambda +(2\lambda k-\xi )b_i+\gamma \lambda (p-t-k{b}_{3-i})-\gamma k\lambda b_{3-i}-\gamma (p-w)\hfill \\ \hfill & \hfill & +k\lambda z_i+kE[\lambda {({\epsilon }_i-z_i)}^{-}+{(z_i-{\epsilon }_i)}^{+}]-w,\hfill \end{array}$$

(7)

$$\frac{\partial {\pi }^m}{\partial z_i}=[(1-\lambda )p+\lambda (t+k{b}_i)][1-F(z_i)]-w+(t+k{b}_i)F(z_i)+s[1-F(z_i)].$$

(8)

From the above-mentioned first-order partial derivatives, the following relations can be further acquired:

$$\frac{{\partial }^2{\pi }_i^c}{\partial z_i^2}=\frac{{\partial }^2{\pi }^m}{\partial z_i^2}<0, \frac{{\partial }^2{\pi }_i^c}{\partial b_i^2}=\frac{{\partial }^2{\pi }^m}{\partial b_i^2}<0, \frac{{\partial }^2{\pi }_i^c}{\partial z_i\partial b_i}>0, \frac{{\partial }^2{\pi }^m}{\partial z_i\partial b_i}>0, \frac{{\partial }^2{\pi }_i^c}{\partial b_i\partial z_i}=\frac{{\partial }^2{\pi }^m}{\partial b_i\partial z_i}>0.$$

Finally, let $b_i\in [b^{\min },b^{\max }]$, ${\mathsf{\Delta }}_i=\gamma \lambda (p-t-k{b}_{3-i})-\gamma (p-w)$.

Proposition 3.

For i = 1, 2, when $\lambda \ge \frac{p-w}{p-t-k{b}^{\max }}$, then $b_i^c<b_i^m,z_i^c<z_i^m$; when $\lambda <\frac{p-w}{p-t-k{b}^{\min }}$, then $b_i^c\ge b_i^m,z_i^c\ge z_i^m$.

Proof ofProposition 3.

Owing to $\frac{\partial {\pi }^m}{\partial b_i}=\frac{\partial {\pi }_i^c}{\partial b_i}+{\mathsf{\Delta }}_i$, the result of the comparison depends on whether ${\mathsf{\Delta }}_i$ is positive or negative.

1.

When ${\mathsf{\Delta }}_i\ge 0$, the condition $\lambda \ge \frac{p-w}{p-t-k{b}^{\max }}$ needs to be established, and the following four situations are discussed:

(1)

$b_i^c\ge b_i^m,z_i^c<z_i^m$. This case is impossible, as if $\frac{\partial {\pi }_i^c}{\partial z_i}(b_i^c,z_i^c)=0$, as $\frac{{\partial }^2{\pi }_i^c}{\partial z_i^2}=\frac{{\partial }^2{\pi }^m}{\partial z_i^2}<0$ and $\frac{{\partial }^2{\pi }_i^c}{\partial z_i\partial b_i}=\frac{{\partial }^2{\pi }^m}{\partial z_i\partial b_i}>0$, then $\frac{\partial {\pi }^m}{\partial z_i}(b_i^m,z_i^m)<0$, which is contradictory to the fact that $\frac{\partial {\pi }_i^c}{\partial z_i}(b_i^c,z_i^c)=\frac{\partial {\pi }^m}{\partial z_i}(b_i^m,z_i^m)=0$.

(2)

$b_i^c<b_i^m,z_i^c\ge z_i^m$. This case is impossible, similar to the reasoning for case (1); in this case, if $\frac{\partial {\pi }_i^c}{\partial z_i}(b_i^c,z_i^c)=0$, then $\frac{\partial {\pi }^m}{\partial z_i}(b_i^m,z_i^m)>0$, which is also contradictory to the fact that $\frac{\partial {\pi }_i^c}{\partial z_i}(b_i^c,z_i^c)=\frac{\partial {\pi }^m}{\partial z_i}(b_i^m,z_i^m)=0$.

(3)

$b_i^c\ge b_i^m,z_i^c\ge z_i^m$. This case is impossible; note that $\frac{\partial {\pi }_i^c}{\partial b_i}(b_i^c,z_i^c)=0$, as ${\pi }_i^c$ is jointly quasi-concave in $b_i$ and $z_i$; therefore, $\frac{\partial {\pi }_i^c}{\partial b_i}(b_i^m,z_i^m)>0$, which leads to $\frac{\partial {\pi }^m}{\partial b_i}(b_i^m,z_i^m)=\frac{\partial {\pi }_i^c}{\partial b_i}(b_i^m,z_i^m)+{\mathsf{\Delta }}_i>0$. Obviously, this is a contradiction.

(4)

$b_i^c<b_i^m,z_i^c<z_i^m$. This case is possible, similar to the reasoning for case (3); we have $\frac{\partial {\pi }_i^c}{\partial b_i}(b_i^m,z_i^m)<0$, which can lead to $\frac{\partial {\pi }^m}{\partial b_i}(b_i^m,z_i^m)=\frac{\partial {\pi }_i^c}{\partial b_i}(b_i^m,z_i^m)+{\mathsf{\Delta }}_i=0$.

2.

When ${\mathsf{\Delta }}_i<0$, the condition $\lambda <\frac{p-w}{p-t-k{b}^{\min }}$ is required to be established, similarly to the proof in condition 1, and it is easy to prove that if ${\mathsf{\Delta }}_i<0$, then we will have $b_i^c\ge b_i^m,z_i^c\ge z_i^m$. □

According to Proposition 3, if the return rate is high ($\lambda \ge \frac{p-w}{p-t-k{b}^{\max }}$), then for i = 1, 2, $b_i^c<b_i^m,z_i^c<z_i^m$, and if the return rate is low ($\lambda <\frac{p-w}{p-t-k{b}^{\min }}$), then $b_i^m\le b_i^c,z_i^m\le z_i^c$. When the return rate is high, monopolistic retailers are more conducive to improving the greenness level of products and tend to increase the sales for deterministic demand and the supply for stochastic demand, which is disadvantageous to the protection of the ecological environment. However, within a reasonable range of values, $\frac{p-w}{p-t-k{b}^{\max }}$ is at least larger than 0.1 (for example, no matter what the values of other parameters are, when $p$ = 100, $w$ = 90, $\frac{p-w}{p-t-k{b}^{\max }}>0.1$), so the condition $\lambda \ge \frac{p-w}{p-t-k{b}^{\max }}$ is unreasonable, because it will require a high return rate, and in this case, the product cannot gain a foothold in the market. When the return rate is low, compared with monopolistic retailers, competitive retailers are more conducive to improving the greenness level of products, and at the same time, they tend to increase the sales for deterministic demand and the supply for stochastic demand. To sum up, governments should create a policy environment which facilitates increasing the degree of market competition, avoiding the formation of monopoly or oligopoly markets, and promoting the development of green supply chains.

Finally, we analyzed the influence of retail price $p$, wholesale price $w$, and greenness R&D investment cost coefficient $\xi$ on the decisions retailers make. According to Equations (5)–(8), we found: for i = 1, 2, $\frac{{\partial }^2{\pi }_i^c}{\partial b_i\partial p}=1-\lambda >0, \frac{{\partial }^2{\pi }_i^c}{\partial z_i\partial p}=(1-\lambda )[1-F(z_i)]>0$, $\frac{{\partial }^2{\pi }^m}{\partial b_i\partial p}=(1-\lambda )(1-\gamma )>0$, $\frac{{\partial }^2{\pi }^m}{\partial z_i\partial p}=(1-\lambda )[1-F(z_i)]>0$, $\frac{{\partial }^2{\pi }_i^c}{\partial b_i\partial w}=\frac{{\partial }^2{\pi }_i^c}{\partial z_i\partial w}=-1<0$, $\frac{{\partial }^2{\pi }^m}{\partial b_i\partial w}=\gamma -1<0$, $\frac{{\partial }^2{\pi }^m}{\partial z_i\partial w}=-1<0$, $\frac{{\partial }^2{\pi }_i^c}{\partial b_i\partial \xi }=\frac{{\partial }^2{\pi }^m}{\partial b_i\partial \xi }=-b_i<0$, $\frac{{\partial }^2{\pi }_i^c}{\partial z_i\partial \xi }=\frac{{\partial }^2{\pi }^m}{\partial z_i\partial \xi }=0$.

Proposition 4.

If the retail price p, wholesale price w, or greenness R&D investment cost coefficient ξ increases, the retailer’s optimal product greenness level and purchase quantity will either increase or decrease at the same time.

Proof of Proposition 4.

Here, we only proved the effects of $p$ on $b_i$ and $z_i$, and the effects of $w$ and $\xi$ on $b_i$ and $z_i$ can be proved in the same way; i = 1, 2. As to the competitive retailers’ model, because ${\partial }^2{\pi }_i^c/\partial b_i\partial p=1-\lambda >0, {\partial }^2{\pi }_i^c/\partial z_i\partial p=(1-\lambda )[1-F(z_i)]>0$, $\partial {\pi }_i^c/\partial b_i$ and $\partial {\pi }_i^c/\partial z_i$ will be larger than 0 as $p$ increases. When $p$ increases, there are four situations to be discussed:

1.

$b_i^c$ increases and $z_i^c$ decreases. Because ${\partial }^2{\pi }_i^c/\partial b_i^2<0$ and ${\partial }^2{\pi }_i^c/\partial b_i\partial z_i>0$, $\partial {\pi }_i^c/\partial b_i$ decreases because of the increase in $b_i^c$, so the reduction in $z_i^c$ will result in $\partial {\pi }_i^c/\partial b_i$ decreasing its value, and $\partial {\pi }_i^c/\partial b_i$ may reach a new equilibrium. Because ${\partial }^2{\pi }_i^c/\partial z_i^2<0$ and ${\partial }^2{\pi }_i^c/\partial z_i\partial b_i>0$, enlarging $b_i^c$ will cause the addition of $\partial {\pi }_i^c/\partial z_i$, the reduction in $z_i^c$ will also lead to enlargement of $\partial {\pi }_i^c/\partial z_i$, and it will make $\partial {\pi }_i^c/\partial z_i$ too big to reach a new equilibrium; therefore, this situation cannot be set up.

2.

$b_i^c$ decreases and $z_i^c$ increases. Because ${\partial }^2{\pi }_i^c/\partial b_i^2<0$ and ${\partial }^2{\pi }_i^c/\partial b_i\partial z_i>0$, $\partial {\pi }_i^c/\partial b_i$ will increase after $b_i^c$ decreases, and enlarging $z_i^c$ will also give rise to the increase in $\partial {\pi }_i^c/\partial b_i$, which will make it impossible to reach a new balance on account of the enlargement of $\partial {\pi }_i^c/\partial b_i$; in summary, this situation cannot be supported.

3.

$b_i^c$ increases and $z_i^c$ increases. Because ${\partial }^2{\pi }_i^c/\partial b_i^2<0$ and ${\partial }^2{\pi }_i^c/\partial b_i\partial z_i>0$, the addition of $b_i^c$ will reduce $\partial {\pi }_i^c/\partial b_i$, and increasing $z_i^c$ leads to the increase in $\partial {\pi }_i^c/\partial b_i$; $\partial {\pi }_i^c/\partial b_i$ may reach a new equilibrium. Because ${\partial }^2{\pi }_i^c/\partial z_i^2<0$ and ${\partial }^2{\pi }_i^c/\partial z_i\partial b_i>0$, if $b_i^c$ increases, $\partial {\pi }_i^c/\partial z_i$ will become larger, and the enlargement of $z_i^c$ will lead to the reduction in $\partial {\pi }_i^c/\partial z_i$; $\partial {\pi }_i^c/\partial z_i$ may reach a new equilibrium, meaning there is still potential for this situation to be supported.

4.

$b_i^c$ decreases and $z_i^c$ decreases. Because ${\partial }^2{\pi }_i^c/\partial b_i^2<0$ and ${\partial }^2{\pi }_i^c/\partial b_i\partial z_i>0$, the reduction in $b_i^c$ will cause the increase in $\partial {\pi }_i^c/\partial b_i$, and $\partial {\pi }_i^c/\partial b_i$ will become smaller after $z_i^c$ decreases its value, so $\partial {\pi }_i^c/\partial b_i$ may reach to a new equilibrium. Because ${\partial }^2{\pi }_i^c/\partial z_i^2<0$ and ${\partial }^2{\pi }_i^c/\partial z_i\partial b_i>0$, a diminution in $b_i^c$ will lead to a diminution in $\partial {\pi }_i^c/\partial z_i$, and if $z_i^c$ decreases its value, $\partial {\pi }_i^c/\partial z_i$ will get larger; $\partial {\pi }_i^c/\partial z_i$ may reach a new equilibrium, and this situation is likely to happen.

The proof of the monopolistic retailers’ model is similar to that of the competitive retailers’ model mentioned above. □

The specific values of b_i and z_i determine the purchase quantity for i = 1, 2. As we all know, when retailers believe that a market has good prospects, they will increase their investment in procuring products from suppliers; otherwise, they will reduce their purchase quantity to avoid potential market loss. Therefore, b_i and z_i are supposed to change their values in the same direction, either becoming larger or smaller. Specifically, no matter whether the retailers are in a competitive market or monopolistic market, if p increases, some retailers will decide to expand their purchase quantity so they will receive additional profits, but others may consider whether there will be a market bubble, so they will reduce their purchase quantity. The same reasoning applies to wholesale price w and greenness R&D investment cost coefficient $\xi$. If $w$ increases, some retailers might believe this to foreshadow an increase in retail price $p$, so they will aim to improve $b_i$ and increase $z_i$. However, some retailers are conservative, recognizing the price increase as a signal for future revenue loss; therefore, they will opt for a lower greenness level and less purchase quantity for stochastic demand. Similarly, when $\xi$ increases, some retailers will only be concerned about putting more money into greenness investment, and they will curtail their budget for purchasing commodities. Meanwhile, other retailers may consider products with a high greenness level to have obvious advantages in market competition, and thus, it is inevitable that they would choose to increase $b_i$ and $z_i$.

According to Proposition 4, as the retail price $p$, the wholesale price $w$, or the greenness R&D investment cost coefficient $\xi$ increases, the optimal product greenness level and purchase quantity of retailers will either increase or decrease at the same time; however, there is no analytical theoretical result to support whether these two factors increase or decrease; thus, this remains to be studied in numerical experiments.

5. Numerical Results

In Section 2, Section 3 and Section 4, we jointly optimized the revenues of retailers with two decision variables in both the competitive environment and the monopoly environment, and obtained some analytical solutions by comparison and sensitivity analysis. Those analytical solutions are presented in Propositions 1–4, which will always be true no matter what parameter values are taken and what distribution ${\epsilon }_i$ (i = 1, 2) follows. To further study the influence of the retail price $p$, the wholesale price $w$, the greenness R&D investment cost coefficient $\xi$, and the return rate $\lambda$ on retailers’ decisions, as well as the expected revenue of retailers, we performed some numerical experiments in this section. Without a loss of generality, let $p$ = 50, $w$ = 30, $\lambda$ = 0.03, $t$ = 0.2, $k$ = 0.3, $\alpha$ = 100, $\xi$ = 10, $\gamma$ = 0.5, and $s$ = 10, and assume that the market demand faced by each retailer obeys a uniform distribution with a range (20, 120). When studying the retail price $p$, we set its value range as (40, 60), and the value range of (14, 46) was set for the wholesale price $w$. Regarding the greenness R&D investment cost coefficient $\xi$, its value range was (2, 18), when in terms of return rate $\lambda$, the value range was (0.01, 0.2). The specific data on the sensitivity analysis are shown in Figure 2, Figure 3, Figure 4 and Figure 5.

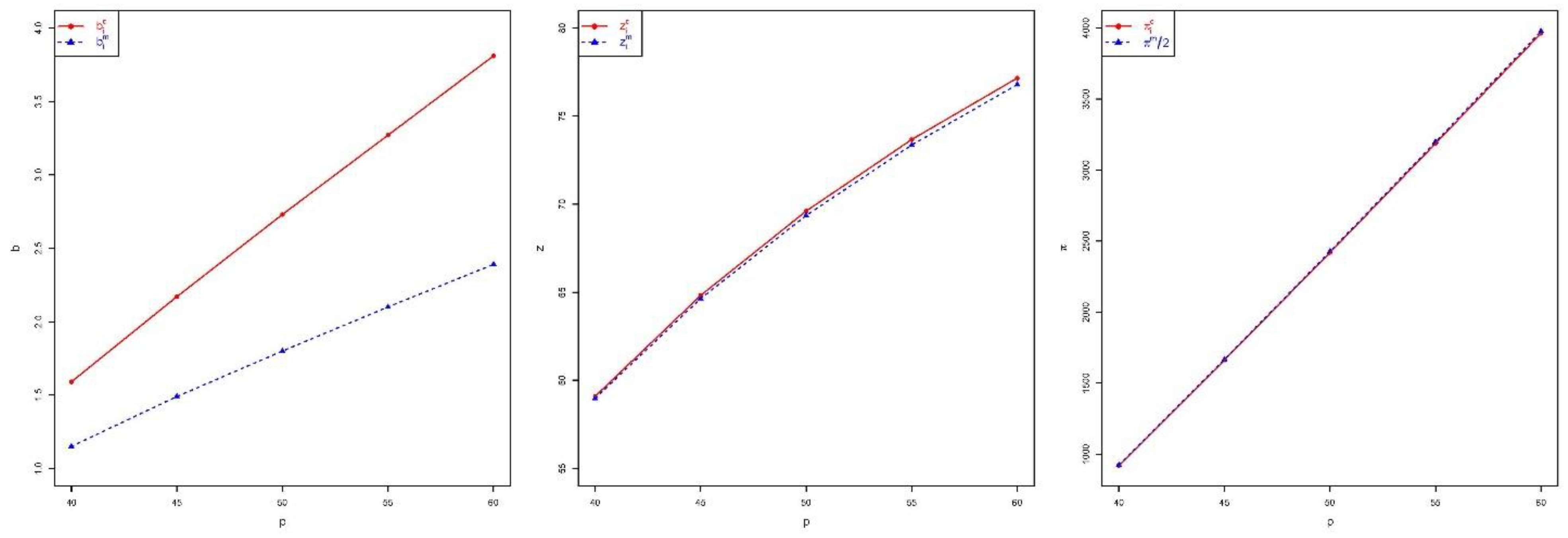
From Figure 2, it can be seen that the increase in retail price $p$ promotes both the greenness level and the purchase quantity for stochastic demand, which shows that most retailers think that when a retail price rises, they should expand their purchases in order to gain more revenue. In addition, we can also see from Figure 2 that the rise in retail price $p$ does have a significant positive effect on retailers’ earnings. Indeed, compared with dealing with returned products and unsold products, the revenue from the direct sale of products is the main source of income for retailers. Moreover, with the increase in retail price $p$, the difference between the greenness level under a competition environment and that under a monopoly environment increases, which shows that compared with a monopoly environment, the increase in retail price $p$ under a competition environment plays a more obvious role in the decision of retailers to increase greenness investment.

From Figure 3, it can be seen that an increase in wholesale price $w$ compresses the retailers’ profit space, and some retailers may consider this to be foreshadowing of a poor market, meaning retailers tend to reduce their greenness levels and decrease their supplies for stochastic demand. Consequently, the purchase quantity is reduced, and the retailers’ expected profit therefore drops. In addition, we found that as the wholesale price $w$ increases, the greenness level in the competitive scenario rapidly becomes close to that in the monopolistic scenario; a possible explanation for this is that the decrease in market investment makes different supply chain structures consistently exert small influences on retailers’ decisions.

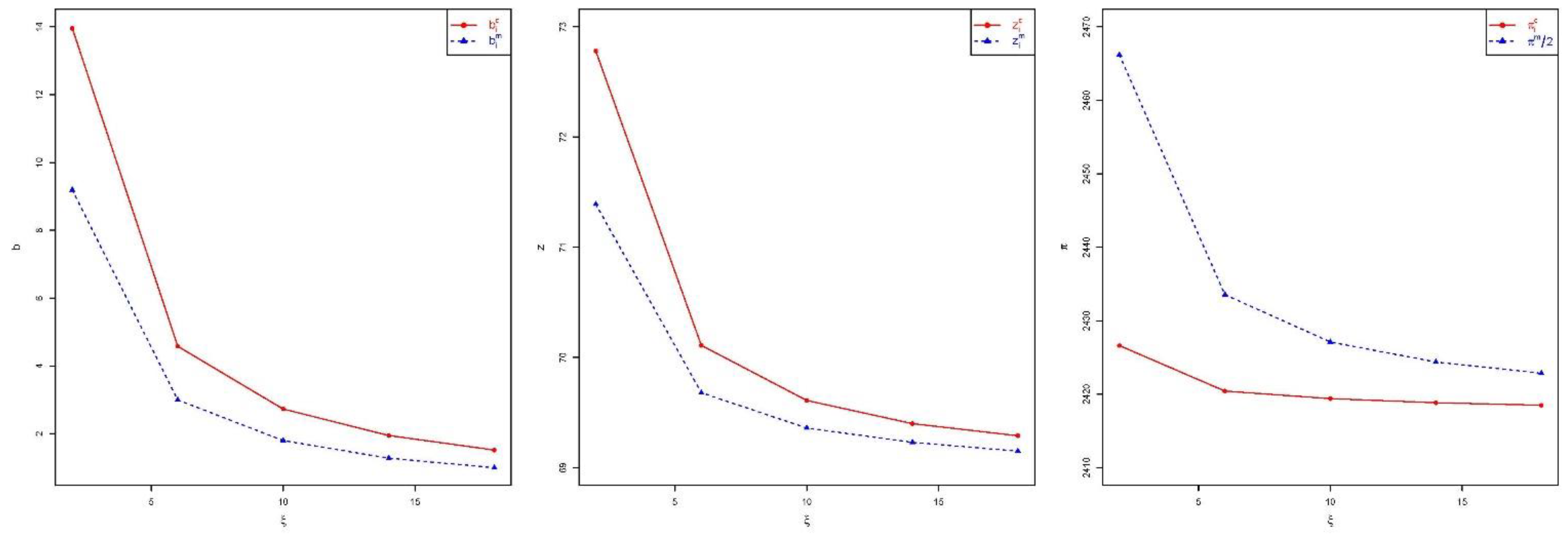
Figure 4 depicts the effects of the greenness coefficient $\xi$ on the greenness level, the purchase quantity for stochastic demand, and the retailers’ expected revenue. A larger greenness coefficient causes larger capital pressure from the retailers’ upfront greenness investment, while the benefit from the market demand caused by greater greenness is insufficient to offset the prior investment cost, so when the greenness coefficient $\xi$ increases, the retailers tend to lower product greenness levels to reduce costs, but lowering greenness levels causes some environmentally conscious consumers to leave the market, meaning retailers will predict that the market demand will become lower, and then they will reduce the purchase quantity for stochastic demand. Therefore, the total purchase quantity is reduced, and revenue declines. In addition, when the greenness coefficient $\xi$ is prone to variation, monopolistic retailers earn much more than competitive retailers, implying that such merchants are more likely to establish monopoly agreements if they believe the upfront greenness investment is generally unclear.

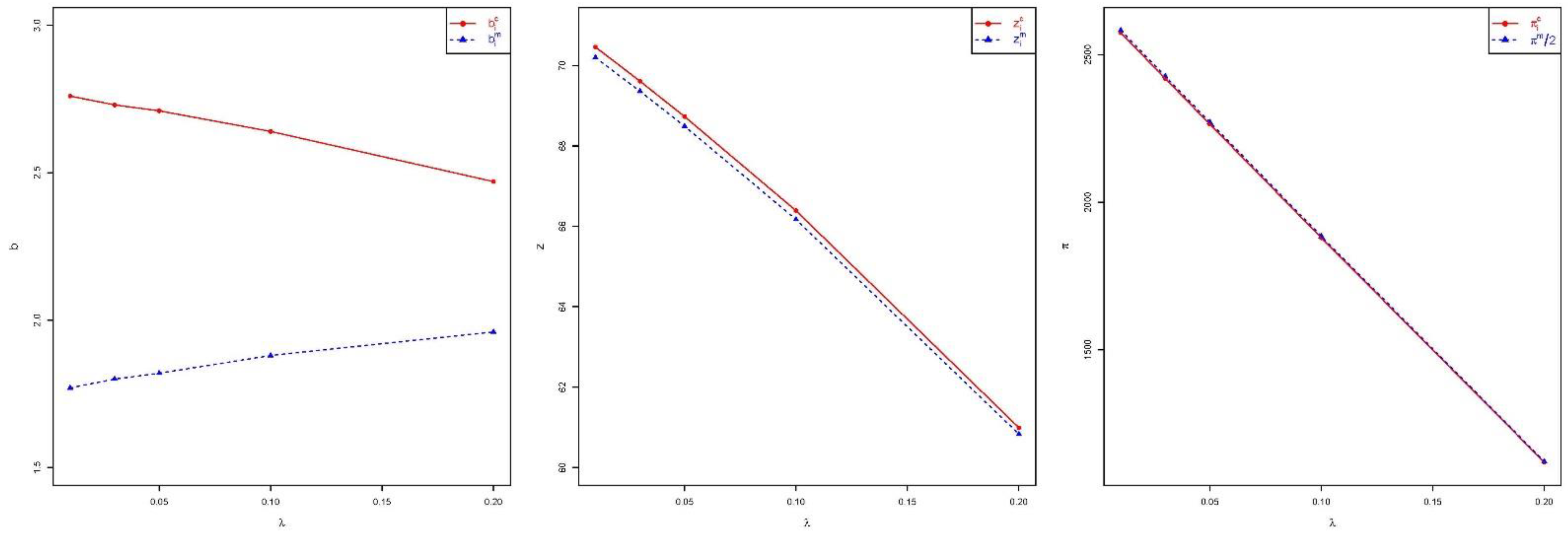
As shown in Figure 5, the return rate $\lambda$ has a decreasing effect on competitive retailers’ greenness level, but the effect on that of monopolistic retailers is conflicting. In addition, the increase in return rate $\lambda$ makes retailers decrease their purchase quantity for stochastic demand. In most cases, the salvage value of returned products is much lower than the retail price, so if the return rate increases, retailers will suffer revenue loss, but their reactions are not same. First, they will all decrease the purchase quantity for stochastic demand—this is a normal market reaction. However, competitive retailers may lower the greenness level because of vital competition, while monopolistic retailers have partners, which leads to stronger market resistance, meaning they will still try to improve product greenness level to attract consumers who have environmental awareness.

In addition to the observations and discussions above, from Figure 2, Figure 3, Figure 4 and Figure 5, the product greenness level and the purchase quantity for the stochastic demand of competitive retailers are both higher than those of the monopolistic retailer, and this validates Proposition 3. In addition, we see that the revenue of competitive retailers is almost same as the revenue of the monopolistic retailer when the retail price, wholesale price, or return rate changes. This finding implies that monopolistic retailers are not likely to compete again if the retail price, wholesale price, or return rate changes readily. Moreover, we discovered that the greenness R&D investment cost coefficient, compared to the other three factors, has the greatest effect on the greenness level. Therefore, to improve the product greenness, it is necessary to improve the input–output ratio of the greenness investment.

6. Discussion

In this section, we discuss our main contributions from a theoretical perspective and a practical perspective.

6.1. Theoretical Implications

In this subsection, we discuss the theoretical implications obtained from our analytical and numerical results.

In the literature, most studies optimized the revenue or utility of a supply chain member with one decision variable; in our work, we jointly optimized the revenue of retailers with two decision variables. By optimizing the revenues, we found that both the greenness level of the product and the purchase quantity for stochastic demand in the competitive environment were higher than those in the monopolistic environment if the return rate $\lambda <\frac{p-w}{p-t-k{b}^{\min }}$. Using a realistic situation, it was easy to confirm that the above condition can always be held. Therefore, competitive retailers are generally more willing to set a high greenness level of products, and also supply more than a monopoly retailer.

Furthermore, we observed that in the competitive environment, the optimal greenness level, the purchase quantity for the stochastic demand, and the revenue of retailers increase as the retail price $p$ increases or the wholesale price $w$, the greenness R&D investment cost coefficient $\xi$, and the consumer return rate $\lambda$ decrease, and this finding remains true in the monopoly environment, except that the optimal greenness level increases as the return rate $\lambda$ increases in the case of the monopoly environment. The sensitivity analysis of the greenness level of the product was partially different from that of Guo et al. [11]. Guo et al. [11] found that as the return rate increases, whether the greenness level of the product increases or decreases depends on the basic salvage value of the returned product. However, in our work, we found that in the competitive environment, as the return rate increases, the optimal greenness level will decrease, while in the monopoly environment, the result is the opposite.

In summary, from a theoretical point of view, in this paper, we apply game theory to green supply chain management, construct a game expansion model including two retailers, discuss the comparison of retailers’ optimal decisions under different situations, expand the research field and methods of the green supply chain, and further analyze the importance of green supply chain management in enterprises.

6.2. Practical Implications

Based on our results, we obtained some important practical implications for green supply chain management. We compared the expected revenue of competitive retailers with that of the monopoly retailer; it is clear that there is little difference between the revenues of competitive retailers and the monopoly retailer no matter how the retail price $p$, the wholesale price $w$, or the return rate $\lambda$ changes. Therefore, in reality, there is no motivation for most original monopolistic retailers to tear up monopoly agreements with their market partners, as this would not bring benefit to them and could cause unpredictable consequences. In addition, we observed that the expected revenue of the monopoly retailer is obviously higher than that of competitive retailers. Thus, if the prophase investment in product greenness is hard to accurately assess, it is very likely that retailers will reach monopoly agreements which are disadvantageous to improving product greenness. Furthermore, from the sensitivity analysis, as the retail price increases, the optimal greenness levels and the difference between the optimal greenness levels in the monopoly environment and the competitive environment become larger, which means that the increase of the retail price has a more positive impact on competitive retailers. Therefore, when the retail price increases, in this case, it is inferred that consumers will buy green products from competitive retailers, rather than the monopoly retailer. It is also observed that as the wholesale price increases, the optimal greenness levels and the difference between the optimal greenness levels in the monopoly environment and the competitive environment become smaller; therefore, suppliers are supposed to make efforts (e.g., improve production technology) on reducing production cost, so that they can set a lower wholesale price to improve the greenness level of the product. Meanwhile, as the wholesale price decreases, competitive retailers have more advantages than the monopoly retailer on improving the greenness level of the product. In addition, retailers are encouraged to improve the technology to decrease the R&D cost coefficient of the product greenness, and control the consumer return rate at a low level by offering better after-sales service, to increase the greenness level of the product.

For governments, it is necessary to improve greenness in supply chains. As such, governments may issue policies to conduct the level of competition in markets. Specifically, for the existing monopoly or oligopoly markets with green products, in addition to creating an environment to support small- and medium-sized enterprises, governments can also guide monopoly or oligopoly corporations to split themselves into more subsidiaries to increase the degree of competition among subsidiaries. Meanwhile, the anti-monopoly mechanism should be strengthened to avoid damage to the development of green supply chains and the social welfare of consumers because of monopolies. Finally, governments can also offer financial subsidies or tax-preferential policies to reduce the financial pressure on enterprises whose commodities include green products, especially small- and medium-sized companies.

In summary, from a practical point of view, under the premise of promoting traditional economic growth, resources will have to be consumed, the environment will worsen, and the balance of the ecosystem will be destroyed; therefore, the development of green supply chains is a general trend that must be realized. Based on the game theory, in this paper, we construct an enterprise game model of green supply chains and obtain and analyze the equilibrium result of the game. Thus, we can propose corresponding policy suggestions for the development of green supply chains.

7. Conclusions

In this paper, we analyzed the optimal decisions of two retailers in a green supply chain with stochastic demand and consumer returns. We compared the decisions and revenues of retailers in the competitive environment and the monopoly environment, and we examined the effects of the retail price, the wholesale price, the consumer return rate, and the greenness R&D investment cost coefficient on the decisions and expected revenues of retailers.

Previous studies, such as those by Ghosh and Shah [14] and Aslani and Heydari [27], showed that a centralized supply chain tends to have products with a higher greenness level than decentralized supply chains. In our work, we found that if the consumer return rate is relatively low, then competitive retailers aim to set a higher greenness level for products and provide more products than the monopoly retailer, which is contrary to the results in Ghosh and Shah [14] and Aslani and Heydari [27]. However, if the consumer return rate is relatively high (i.e., $\lambda \ge \frac{p-w}{p-t-k{b}^{\max }}$), then the results are the opposite, although this kind of situation does not happen very often. Therefore, in general, competition is more beneficial than monopoly in increasing the greenness level of products and providing more products to consumers.

The numerical experiments also showed that in the competitive environment, the optimal greenness level, the purchase quantity for the stochastic demand, and the revenue of retailers increase as the retail price increases or the wholesale price, the greenness R&D investment cost coefficient, and the consumer return rate decrease, and this finding remains true in the monopoly environment, except that the optimal greenness level increases as the return rate increases in the case of the monopoly environment.

Although stochastic demand and consumer returns were taken into account in our model, as well as a comparison of the competitive scenario and the monopolistic scenario, some further aspects can be considered in future research. First, more generally, based on the present model, we could consider applying an opaque selling mechanism to the sale of green products. Second, we think it would be interesting to add an extra selling channel between retailers and customers, so that a future study could compare the decisions made in different channels. Third, as this paper does not add a manufacturer into the game, the effect of a manufacturer should be assessed correctly, so that we may consider adding a manufacturer to construct a two-stage game model in the future.