Dominance Tracking Index for Measuring Pension Fund Performance with Respect to the Benchmark

Abstract

This paper focuses on the performance of Lithuanian life-cycle second-pillar pension funds. Every such fund first specifies its benchmark and then attempts to follow the benchmark in some way. This is a form of regulation, meaning that every such fund is somehow regulated and controlled by the central bank authorities. The goal of this paper is twofold: (i) to analyse the returns of the pension funds with respect to their benchmarks and (ii) to determine whether less strict regulation leads to a better outperformance of the fund with respect to the benchmark. In order to achieve this, we introduced a new performance measure called the dominance-tracking index, which combines the ideas of almost stochastic dominance relations and tracking errors. While the tracking error and its modifications measure the strength of the regulation, almost stochastic dominance provides information about preferences between the funds and their benchmarks. Therefore, the new index was constructed in such a way as to take into account both approaches. The empirical section of the study then presents the results separately for the considered pension managers and participants’ age groups as usual in the life-cycle pension funds analysis. Finally, by taking into account various periods, we studied the effects of the COVID-19 crisis.

1. Introduction

As most states can no longer fund pensions using state pension provision systems, the importance of pension funds has been growing. This change has built on changes in pension systems that have been taking place since 1981 [1,2,3]. During the financial crisis, pension funds, in addition to severe losses, led to a paradigm shift in terms of the depreciation of assets, the subsequent low interest rate environment, and the changing demographics of pension fund participants. These changes led not only to lower benefits but also to an increased discount value of pension fund liabilities [4,5,6]. US and European pension funds have been left with funding gaps as the current discounted value of accrued pensions has far exceeded the value of invested contributions by fund participants [7,8]. Research shows that US pension fund assets halved between 2007 and 2009 and that the funding gap for US state-sponsored pension plans in 2008 was USD 3.23 trillion [9]. Comparatively, the findings of Laboul [7] show that the liabilities of corporate pension funds in OECD countries in 2008 and 2009 were, on average, 25% higher than their assets. Such developments led both pension funds and regulators in both the US and Europe to restore the financial adequacy of pension funds, leading most OECD countries to reform their pension systems between 2009 and 2013 [10]. The European Union does not impose any limitations on pension fund participants when deciding on their investment strategy. Research conducted in Lithuania [11,12,13,14,15] showed that, according to appropriate investment strategy and risk fundamentals, most pension fund participants tend to select incorrect pension funds. Therefore, in order to protect pension fund participants and their funds, regulators made a mandatory switch to life-cycle pension funds [16]. The role of regulators, in both practice and research, is becoming increasingly important, as new mechanisms are implemented to protect stakeholders and promote financial stability [11,17]. Both regulatory and self-imposed restrictions might limit investment opportunities through prohibited short sales, imposed maximum asset weights, or limited absolute or relative risk. Naturally, limitations could lead to inefficient portfolios, which could be improved without taking on any additional risks [17].

The global financial crisis and the ongoing COVID-19 pandemic have both raised scientific questions about how and to what extent regulators and supervisors should influence pension fund investment strategies and regulate pension fund managers’ decision-making ability. The growing liabilities of pension funds due to a longer life expectancy, as well as historically low interest rates, threaten the sustainability of pension plans, meaning the challenge of implementing risk regulation without overly restricting investment is particularly relevant today [18]. It is important to note that the European Union does not regulate member state pension fund systems, although specific aspects are regulated by European regulation on fund management. Each country locally decides upon its pension system’s set-up, which tends to consist of three pillars. Analysing the research revealing the importance of regulators for the investment strategies of pension funds, it is observed that different pension funds managed by companies operating under the same market conditions show different performance results [6,12,19,20]. Therefore, questions are raised regarding whether the actual performance of pension funds differs depending on the investment strategy and how to compare the performance of pension funds if publicly available data show only simple statistical descriptive information and if the historical performance of individual funds and historical rates of return cannot be used for future forecasting. In such a case, the only rational way to choose a pension fund is purely random [15,21]. Finding answers to these questions is difficult, as most studies focus solely on observed pension fund underperformance, which occurs due to changes in regulation, while only a limited amount of research on the performance benchmark and tracking error exists. The creation of a new performance measure would enable us to determine whether less strict regulation leads to a better fund performance with respect to the benchmark.

This paper analyses the performance on Lithuanian life-cycle second-pillar funds with respect to their benchmark strategies. All of the pension managers must declare their individual benchmark strategy and then follow it. Some deviations from the benchmark are allowed, meaning that the pension managers may try to outperform the benchmark. Therefore, we analyse both the strength of the benchmark replication and the benchmark outperformance. Whereas the former is measured by a tracking error [22] (or its modification), the latter is modelled by almost stochastic dominance [23]. The smaller the tracking error, the more strongly the fund will follow its benchmark. Similarly, the smaller the coefficient of almost stochastic dominance, the stronger the preference between the fund and its benchmark; in other words, more investors prefer the fund to its benchmark. In this paper, we considered three types of tracking error measures and two orders of almost stochastic dominance (first- and second-order). Our goal is to analyse the returns of the funds with respect to the returns of their benchmarks and to determine whether the less strict replication of the benchmark (more freedom in investment strategy) leads to a better outperformance, i.e., stronger almost stochastic dominance between the fund and its benchmark. Finally, we introduced a new measure of pension fund performance, namely the dominance-tracking index, that combines the two approaches. The index takes values between 0 and 1. The higher the value, the better the fund follows and outperforms the benchmark. In the ideal case, when the return of the fund is always higher than the return of the benchmark, the index takes a value of 1. On the other hand, the index is equal to 0 if the fund is dominated by the benchmark, i.e., all pension participants prefer the benchmark to the fund. In the empirical part of the paper, we provide a deep analysis with respect to various age groups of participants, various pension managers and various time periods. This allows us to compare the pension managers with each other, study the effect of aging and analyse the robustness of our results with respect to the COVID-19 crisies.

The rest of the paper is structured as follows. Section 2 provides a literature review, followed by basic information regarding Lithuanian second-pillar pension funds (Section 3) and descriptive statistics of the funds’ returns (Section 4). New modifications of the tracking error, as well as the dominance-tracking index, are then introduced in Section 5. Finally, the results are summarised in Section 6 and the paper is concluded in Section 7.

2. Literature Review

As the pension fund sector is developing rapidly across the globe, regulators are constantly being exposed to new challenges that must be managed in order to maintain stability. The ever-changing environment and the global recession only complicate the work of these institutions, which must respond quickly to emerging risks and make every effort to eliminate or at least reduce those risks. For these reasons, traditional supervision is increasingly being replaced by new requirements that focus on a comprehensive risk assessment. Such an approach is geared towards effective control, which would enable the identification of uncertainties in the activities of pension funds, focusing on the most problematic areas, analysing the environment, detecting and assessing warning signals in a timely manner, distributing supervisory intensity and involving the regulated entities. As the outlook for pension funds should be long term, it is important that fund managers are able to increase the value of their portfolios by successfully investing in selected asset classes. Significant differences between European and US pension funds exist because the former specifies the maximum proportion of the asset class that an individual fund can hold, whereas, in the latter, funds very rarely operate as balanced funds containing multiple asset classes [11]. Some countries choose not only to restrict the investment freedom of fund managers but to fully ban investment in certain assets. OECD countries set limits or even impose a total ban on investing in real estate, private equity or loans. Direct investment in real estate is not allowed in Lithuania, Japan (except for the Mutual Aid Associations), Italy, Mexico, Poland, Hong Kong, Albania, Turkey, Croatia, India and Armenia [10]. Greece has relatively strict investment restrictions—Greek public pension funds can invest up to 23% in risky assets, and they are not allowed to invest outside Greece [17]. Such a regulatory and supervisory strategy is ambiguous: on the one hand, it ensures a minimum amount of investment in risk classes, but, on the other hand, it limits the maximum possible return on investment.

Regulatory constraints force pension funds to hold inefficient portfolios. For instance, as shown in [17], inefficient portfolio returns are consistently lower than average real wage growth. Boon et al. [18] elaborate on this, noting that stricter funding requirements lead to a decline in risky investment in assets, which is most pronounced during the financial crisis. The authors base their claims on a study that assesses the impact of various regulatory requirements on the investment risk of pension plans and demonstrates that the regulation of pension funds in the U.S., Canada and the Netherlands is a key factor in shaping asset allocation. Given the negative impact of the financial crisis on pension fund performance, Ambachtsheer [24] proposed a model to address people’s behavioural and longevity risk issues by automatically involving employees in pension accumulation and using auto-investment mechanisms to actively change individual contribution rates depending on asset deficit or surplus, as well as linking the investment policies of individual pension participants to their age. The author argues that the model using the autopilot feature would automatically adjust premium rates and investment policies to address behavioural and risk issues. The so-called ‘autopilot’ mechanisms can be used to implement a life-cycle investment policy, which ensures the safe conversion of retirement savings into annuities. The importance of life-cycle pension funds has been highlighted by other researchers, such as Choi et al. [25], Bovenberg et al. [26], Kooreman and Prast [27], who observed that individuals when selecting a pension fund face two main questions: how much to save and how accumulated financial assets should be invested. Participants engaged in pension plans rarely rebalance their portfolios or change the distribution of their contributions throughout their life-cycle [28]. Other research shows that only a small proportion of the population in countries such as the US and Italy directly own shares [26,27]. There is ample evidence that it is difficult for individuals to make the right savings and investment decisions, and much research raises the question of how to address this issue. One potential solution is the aforementioned life-cycle pension funds, which are managed by professionals. De la Torre Torres et al. [29] analysed Mexican public pension funds or SIEFORE, which are public funds that work as life-cycle mutual funds, and studied the lack of alpha generation. The research defined contribution pension funds and compared the performance of each fund against that of their life-cycle profile peers. The authors found that there was underperformance caused by underlying management costs and, more specifically, due to a homogeneous performance that they suggested to be induced by the actual investment policy. Consequently, the problem of homogeneous results in the management of life-cycle funds may also occur in the results of pension funds operating in Lithuania, where it becomes even more difficult to compare the results of funds.

The importance of comparing pension funds is emphasised not only by researchers but also by pension fund managers on the management side of pension funds, who argue that pension funds seek to compare administrative and investment costs with other pension funds, but there is no benchmark to identify what sort of management costs are large and which are small. Still, pension funds argue that benchmarking should become standard, but many funds do not want information to be widely available, as benchmarking might work against pension fund managers by limiting their ability to raise funds [30]. If pension funds discuss the creation of a standard benchmark, then, on the consumer side, the choice of a pension fund with a benchmark and tracking error becomes particularly relevant. However, as mentioned earlier, a research gap exists and only a limited number of studies that address the application of different types of benchmarks can be identified.

Bovenberg et al. [26] analysed the optimal saving and investment proportion throughout the life-cycle of an investor. The study begins by specifying a simple benchmark model, where optimal saving and investing conditions are evaluated from the perspective of an individual. The authors augmented this model by including human capital, additional risk factors, preferences and, finally, various constraints to replicate optimal individual decision making. The study discusses how collective pension schemes may work towards relieving prominent market inefficiencies and highlights how collective pension fund systems can work by risk sharing across generations and the transfer of surpluses and deficits over time. Meanwhile, Rubilar-Maturana et al. [5] applied a benchmark method using passive indices and an alternate instrument when analysing the performance of pension funds in Chile. The authors found that the Chilean market showed signs of asymmetric information between pension fund participants, thus creating extraordinary earnings to a degree that can be characterised as an oligopoly market. The findings indicate market inefficiencies in reporting comparable pension fund results and suggest possible solutions. Herteliu et al. [31] analysed Italian pension funds and their self-declared benchmarks, which, in fact, are market indexes. The key focus was on testing whether individual investments made according to a benchmark can be analysed as a portfolio of benchmarks.The findings suggested that the actual performance of pension funds is well below the performance of declared benchmarks, presumably due to constraints imposed by the regulator. Furthermore, Vitali et al. [32] and Anna Maria D’Arcangelis et al. [33] analysed investment style features in Italian pension funds and demonstrated that the fund network is dense and diverse. In addition, using community detection algorithms, it was determined that many funds have similar characteristics. In particular, the network of benchmarks was relatively homogeneous, used by groups of pension funds and disassortative. The addition of weights did not cause any significant changes in the centrality measure but did merge communities. The authors concluded that the structure of the Italian network of pension funds, irrespective of the weights, seems to provide sufficient information to identify similarities in investment styles. Broeders and de Haan [34] decomposed investment returns for Dutch pension funds based on market timing, selection of stocks and asset allocation. They connected the choice of a specific benchmark with pension fund managers’ investment risk and strategy. The results show that the distribution of assets explains approximately 39% of return variance, whereas the timing, selected benchmark and asset selection explain 9%, 11% and 16%, respectively. In all evaluated funds, the allocation between assets explains, on average, 19% of the fluctuations of returns, whereas the choice of a benchmark can explain 33% of the cross-sectional returns. Dopierala and Mosionek-Schweda [20] assessed the impact of open pension fund reforms in Poland in terms of fund management style, risk profile and investment preferences. The study analysed whether the removal of an internal benchmark has any effect on eliminating or reducing pension fund manager herd behaviour. The findings suggest that highly regulated funds may slightly outperform unregulated competitors and passive benchmarks. A restriction on investment in treasury bills increased both the risk and return volatility. However, it also increased the market competition and reduced herd behaviour tendencies.

Lee and Shim [35] evaluated the fiscal sustainability of the benchmark pension system in Korea. They estimated a lifetime pension deficit, which is the difference between the contributions and received benefits throughout an individual’s lifetime. The system is expected to run a deficit of approximately USD 22,000 per every individual’s lifetime and is unlikely to cover the deficit with current pension fund returns. For a balanced pension system to run, social welfare should be reduced by as much as 2.06%, the contribution rate should be 20.3% and the average replacement rate should be 66.4%. An increase in pension benefits, combined with an increase in pension contributions, could reduce income inequality due to the progressiveness of pension benefits and the proportionality of pension contributions.

3. Overview of Pension Funds in Lithuania

The European Union does not regulate member state pension fund systems, though specific aspects are governed by European regulation on fund management. Each country locally decides upon its pension system’s set-up, which most commonly consists of three pillars [36]. In Lithuania, the first pillar is mandatory; it ensures the base pension level and is purely managed by the local authority. The second pillar is mandatory as well, but it includes a combination of personal and state participation, which are then invested into particular private pension funds. These funds operate on a life-cycle basis [22]. This means that all employed persons by default are included in the second pillar of pension scheme, with the opportunity to opt out. More specifically, the inclusion in the life-cycle private funds is automatically organised. However, those who have reached the age of 40 will no longer have the possibility to leave the second pillar. Every participant can choose only one pension fund from those that are suitable for their age group. The use of savings in the second pillar is generally limited: the beneficiary can receive a payout only when a certain age is reached in the form of a one-off payment or annuity (if the balance is more than a set threshold). At the end of 2021, there were 40 second pillar funds operating in Lithuania: 35 target group funds and 5 asset preservation funds. The funds were managed by five fund managers: four fund management companies and one life insurance company. The total value of assets under management in the specified time amounted to almost EUR 5.91 billion. Almost 1.388 million participants were actively participating. The biggest pension fund managers were UAB ‘Swedbank investicijų valdymas’ (37.94%), ‘UAB SEB investicijų valdymas’ (26.17%) and ‘UAGDPB’ ‘Aviva Lietuva’ (14.40%) [37]. Participation in the third pillar is completely optional and is mostly supported indirectly via tax cuts. The third pillar fund set-up or management is not regulated as heavily as the second pillar (e.g., it does not have to follow a life-cycle investment strategy) and assets can be freely disposed.

A key document describing pension fund management is the prospectus, which is approved by the governing body, which, in the case of Lithuania, is the Bank of Lithuania. The prospectus defines key information about a fund’s management, including pricing, investment strategy and asset re-allocation principles. Adjustments in the allocation of a fund’s assets are defined by two strategies: strategic asset allocation, which defines key markets and asset allocation principles and is normally reviewed once per year; and tactical asset allocation, which defines particular sectors and is normally reviewed once per month. Typically, this would not lead to any drastic adjustments because pension funds follow a long-term investment strategy that ignores short-term adjustments.

The investment strategy of the pension fund must be based on the strategic allocation of pension assets that, according to the pension fund manager, aims to ensure an optimal ratio of risky to less risky asset classes throughout the whole accumulation period. This is carried out by taking into account the regulation and typical average investor factors, such as the total contribution sum, currently accumulated amount, the remaining duration of participation, most commonly selected types of pension benefits and longevity.

• In determining the optimal ratio of risky to less risky asset classes, a pension accumulation company must be able to substantiate why the selected investment strategy is appropriate in the opinion of the pension accumulation company and provide modelling assumptions and results upon request. The company may use calculations performed by itself or third parties and/or expert judgment for this purpose.
• A pension accumulation company that has determined the ratio of the share of risky and less risky assets in the portfolio must comply with it. The company is considered to not be following the chosen pension fund investment strategy when the share of risky and less risky assets in the pension fund investment portfolio of the target group of pension fund participants deviates by more than 10 percentage points from the established proportion.
• In order to limit the investment risk, the pension accumulation company must establish indicators and criteria that would be used to monitor the compliance of the pension fund’s investments with the chosen investment strategy (benchmark). For this purpose, the pension accumulation company must determine the scope of active investment management of the pension fund of the target group of pension fund participants, limiting the size of the benchmark tracking error and the limits of possible deviations.

Risky assets may include such asset classes as equities, commodities, private equity, venture capital, infrastructure (investing in equities), real estate funds and high-risk hedge funds. Less risky asset classes may include government, corporate bonds and other forms of loans, various asset-backed bonds, cash, money market instruments, infrastructure (investing in debt securities), financial instruments linked to insurance risk and lower-risk hedge funds.

According to the benchmark specified in the strategy for that year, the investments of the pension fund are re-balanced at the beginning of the year. Depending on the market forecasts, the company may perform or start re-balancing at the end of the previous year and/or at the beginning of the year. Other decisions, taking into account the markets and economic forecasts, are implemented on a continuous basis, within the tolerances set out in the strategy. Risks to be considered are as follows: securities selection and price risk; asset allocation risk; interest rate risk; markets and credit risk; exchange rate risk; inflation risk. In order to better manage the risk of the pension fund or its part, the pension fund may invest in the following derivative financial instruments transactions: forward transactions (forward transactions in the sale or purchase of currency, interest rates, shares, bonds, stock indices and other forward transactions); futures (futures on the sale or purchase of currency, interest rates, shares, bonds, stock indices and other futures); interest rate, currency, insolvency risk, stock or stock index swaps; options to buy or sell securities, currencies or financial instruments; and other financial derivatives. The investment strategy of the pension fund and its implementation and suitability shall be reviewed and evaluated at least once every three years.

Sustainability in investments is becoming an integral part of every fund manager’s decision-making process, and pension funds are no exception [38]. Though sustainability is not mandatory when managing pension funds, the disclosure of the portfolio set-up is still regulated. Part of the EU’s sustainability regulation framework is Sustainable Financial Disclosure Regulation (SFDR, see [39]), which ensures that every financial firm, including fund managers, is comprehensively disclosing how sustainable they really are.

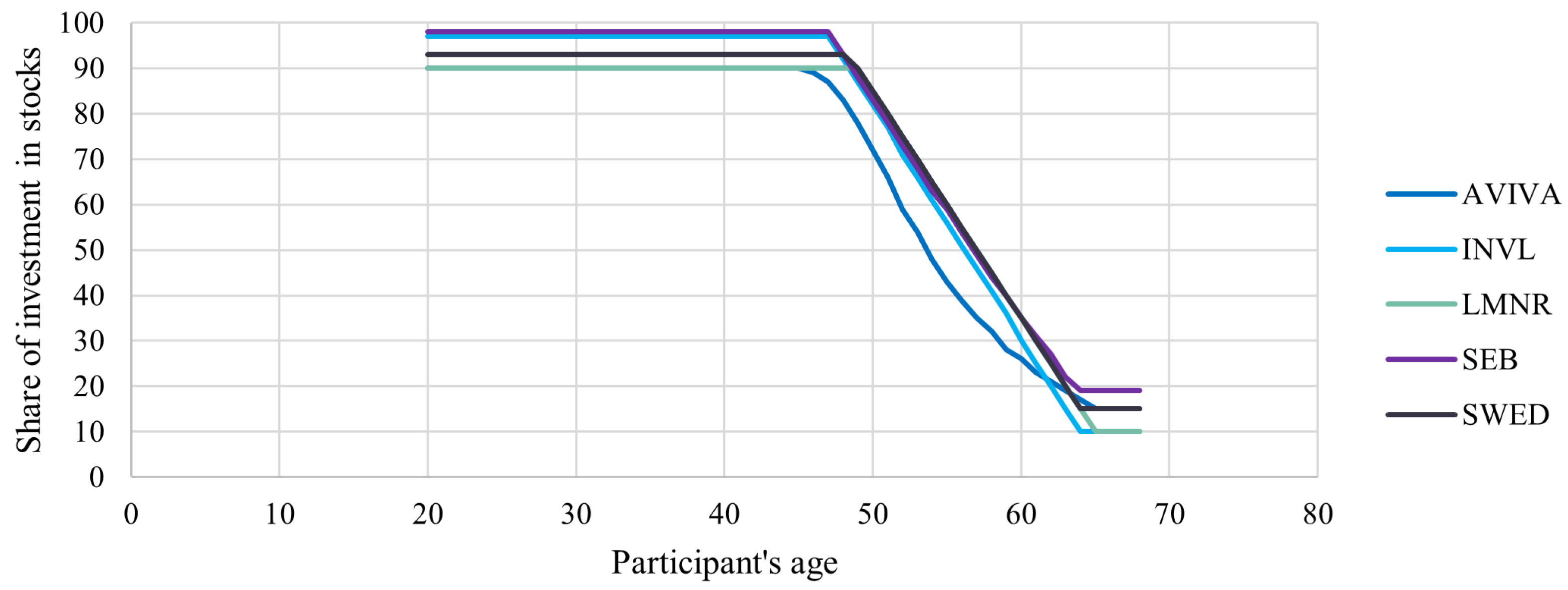
During the period analysed, the Lithuanian second pillar consists of five pension accumulation companies (managers): ‘Aviva Lietuva’(AVIVA), ‘INVL Asset Management’ (INVL), ‘Luminor investicijų valdymas’ (LMNR), ‘SEB investicijų valdymas’ (SEB) and ‘Swedbank investicijų valdymas’ (SWED). Each pension fund manager has individual strategy on how to manage their life-cycle funds in terms of share of investments in stocks and participant’s age (see Figure 1).

As defined in regulation, all pension funds must have a pre-defined benchmark, which would enable actual and potential investors to properly assess the pension fund performance. The pension fund benchmark composition must be selected according to the particular investment strategy set by the pension fund manager and then approved by the regulator. To ensure that the benchmark appropriately represents a given pension fund’s performance, the regulation requires the correlation between the benchmark and the pension fund performance, throughout a six-month period, to be no lower than 0.7. In addition to correlation tracking, pension funds are required to report the annualised tracking error, which is calculated by taking the average of monthly differences between the asset value and benchmark value changes.

When compiling a benchmark, pension fund managers are free to select a combination of indexes and their weights in order to appropriately represent their investment strategy and asset value changes. By comparing the benchmark composition between observed pension funds in

Table 1. The composition of pension fund benchmarks.

Manager	Index	Typical Year of Birth
		96–02	89–95	82–88	75–81	68–74	61–67	54–60
AVIVA	MSCI World Daily Net Total Return	90%	90%	90%	90%	80%	45%	15%
	Bloomberg Series-E Euro Govt 1-5 Yr Bond	10%	10%	10%	10%	20%	55%	85%
INVL	MSCI World Daily Net Total Return	89%	89%	89%	89%	70%	37%	9%
	MSCI Emerging Markets Index (USD)	8%	8%	8%	8%	6%	3%	1%
	ECB ESTR OIS Index	3%	3%	3%	3%	3%	3%	3%
	Bloomberg Series-E Euro Govt 5-7 Yr Bond	0%	0%	0%	0%	4%	12%	22%
	Bloomberg EuroAgg Treasury 5-7 Year TR Index	0%	0%	0%	0%	4%	12%	22%
	JPM EMBI Global Diversified Europe	0%	0%	0%	0%	4%	12%	22%
	JPM Corporate EMBI Broad Europe	0%	0%	0%	0%	4%	10%	10%
	JPM EMBI Global Hedged Europe	0%	0%	0%	0%	4%	10%	10%
LMNR	MSCI World Daily Net Total Return	63%	63%	63%	63%	56%	32%	7%
	MSCI Emerging Markets Index	27%	27%	27%	27%	24%	14%	3%
	Bloomberg Series-E Euro Govt 3-5 Yr Bond	6%	6%	6%	6%	12%	33%	54%
	Bloomberg EM Sovereign + Quasi Sovereign TR	3%	3%	3%	3%	6%	17%	27%
	Bloomberg Liquidity Screened Euro HY Index	1%	1%	1%	1%	2%	6%	9%
SEB	MSCI World Daily Net Total Return	83%	83%	83%	83%	66%	38%	16%
	MSCI Emerging Markets Index (EUR)	15%	15%	15%	15%	12%	7%	3%
	Bloomberg Euro Treasury 1-10yr A3 or better	2%	2%	2%	2%	5%	23%	45%
	Bloomberg Euro Aggregate Corporate	0%	0%	0%	0%	12%	24%	27%
	Bloomberg Global HY (EUR Hedged)	0%	0%	0%	0%	2%	3%	3%
	S&P European Leveraged Loan Index	0%	0%	0%	0%	1%	2%	2%
	JPM EMBI Global Unhedged Euro	0%	0%	0%	0%	1%	2%	2%
	JPM EMBI Global Diversified Hedged EUR	0%	0%	0%	0%	2%	3%	4%
SWED	MSCI World Daily Net Total Return	97%	97%	97%	97%	80%	45%	15%
	Bloomberg Euro Government Index	2%	2%	2%	2%	10%	28%	43%
	Bloomberg Euro-Aggregate corporates Index	1%	1%	1%	1%	4%	11%	17%
	JPM EMBI Global Diversified Europe	1%	1%	1%	1%	6%	17%	26%

Note: Stock indices are in bold, bond indices are in italic.

, we notice that the selection of used indexes is different across all observed fund managers. Though there are no differences in index selection for individual pension funds that are managed by the same managers, in such cases, only index weights differ.

4. Descriptive Statistics of Pension Funds

The historical net asset values observed on a daily basis were collected from the websites of pension accumulation companies (PACs), namely ‘Aviva Lietuva’(AVIVA),‘INVL Asset Management’(INVL), ‘Luminor investiciju valdymas’(LUMINOR), ‘SEB investiciju valdymas’ (SEB) and ‘Swedbank investiciju valdymas’ (SWED), for the period between January 2019 and May 2021. As each PAC manages seven pension funds of different age groups, a data set of 35 PFs was composed. 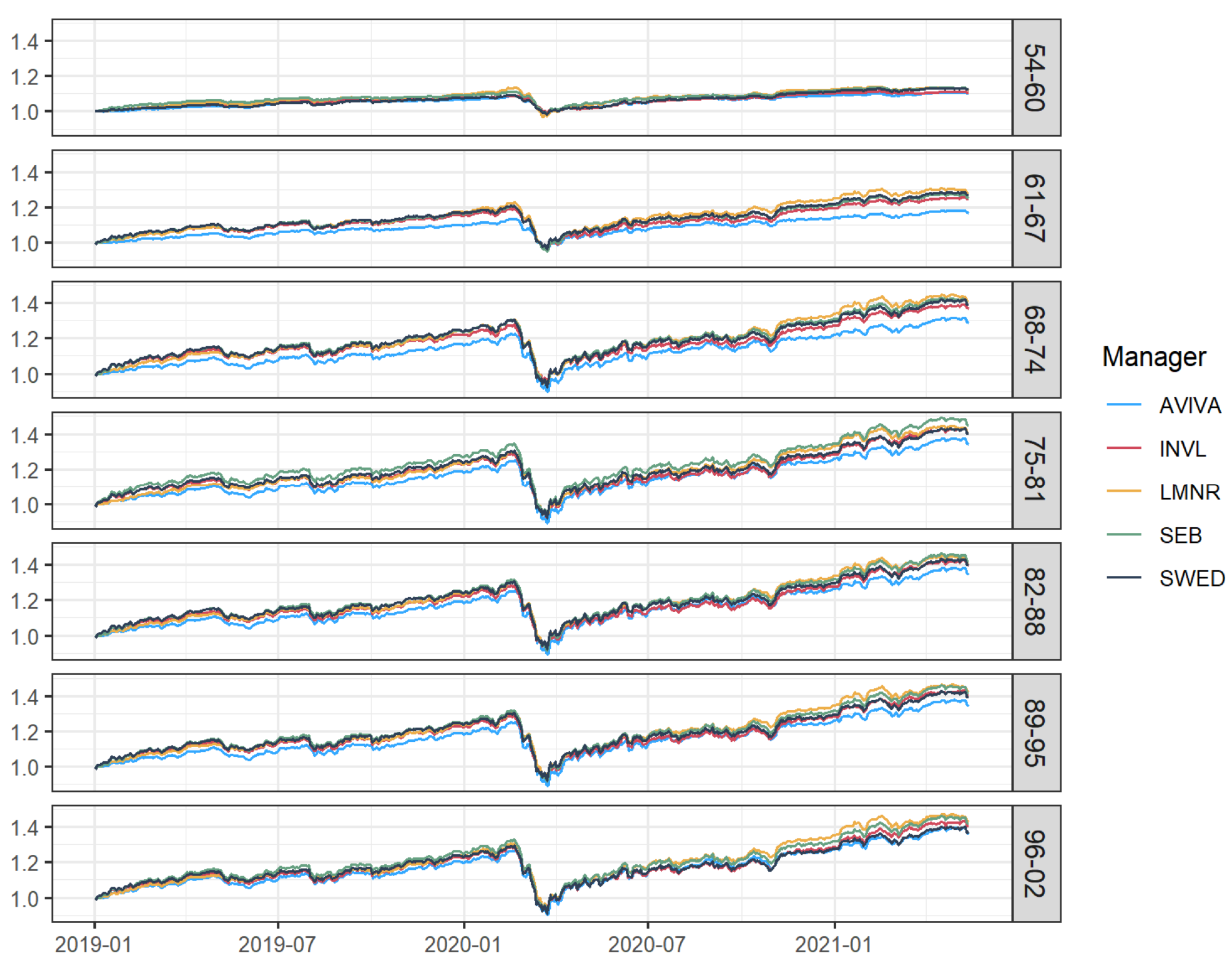Figure 2 illustrates the fluctuations in PFs’ net asset value over the considered time period.

As seen in Figure 2, all PFs demonstrated a growth with a varying slope until the onset of the COVID-19 crisis, during which, the funds experienced a maximum drawdown ranging from 8.7% to 31.01%. The recovery period was sufficiently long so that all funds achieved the value that they had before the crisis or even higher. In each age group, we can observe that AVIVA funds were outperformed by other funds, while the performance of the funds managed by other PACs varies depending on age group. From this figure, we can clearly observe the impact of the COVID-19 crisis on the PFs’ performance. Thus, in further analysis, the whole period will be additionally split into two periods on the date of 1 March 2020: before crisis, denoted as A, and the COVID-19 period, denoted as B. To be more precise, we considered three different periods:

• Period A (1 January 2019–28 February 2020, pre-COVID-19);
• Period B (1 March 2020–13 May 2021, COVID-19);
• Entire period (A + B) from 1 January 2019 to 13 May 2021.

The Kruskal–Wallis test by ranks was applied to test whether the PFs’ returns originate from the same distribution. This was carried out separately for periods A, B and A + B. The results show that, at the 0.05 significance level, no pension fund experienced a significant difference in sample distribution.

On the basis of the observed net asset value, the daily returns of PFs were calculated as the main variable. To quantify the expected reward and risk of PFs, the descriptive statistics and risk measures, such as historical 95% value-at-risk (VaR) and historical 95% expected shortfall (ES), as well as the Sharpe performance ratio with a risk-free rate of return of 0%, were estimated for all funds. Additionally, the Spearman correlation coefficient (Cor) between PF and its benchmark was estimated. The results are presented in

Table 2. Statistics and risk measures for daily returns of pension funds for entire period.

PF	Min	Mean	StDev	Skewness	VaR	ES	Sharpe	Cor
AVIVA.96–02	−0.0496	0.00056	0.0091	−0.5660	0.0138	0.0239	0.0614	0.2790
INVL.96–02	−0.0805	0.00062	0.0104	−1.2856	0.0146	0.0274	0.0600	0.8255
LMNR.96–02	−0.0428	0.00063	0.0072	−1.1425	0.0100	0.0195	0.0877	0.5701
SEB.96–02	−0.0778	0.00064	0.0097	−1.5062	0.0132	0.0254	0.0658	0.7256
SWED.96–02	−0.0862	0.00059	0.0108	−1.1610	0.0146	0.0284	0.0548	0.8322
AVIVA.89–95	−0.0484	0.00053	0.0089	−0.6965	0.0144	0.0236	0.0597	0.2862
INVL.89–95	−0.0808	0.00062	0.0104	−1.3551	0.0145	0.0274	0.0600	0.8321
LMNR.89–95	−0.0453	0.00062	0.0071	−1.2613	0.0094	0.0192	0.0873	0.5781
SEB.89–95	−0.0766	0.00063	0.0094	−1.5238	0.0126	0.0246	0.0669	0.7063
SWED.89–95	−0.0830	0.00062	0.0106	−1.1562	0.0145	0.0281	0.0580	0.8345
AVIVA.82–88	−0.0483	0.00054	0.0089	−0.6838	0.0143	0.0234	0.0608	0.2903
INVL.82–88	−0.0798	0.00062	0.0103	−1.3675	0.0144	0.0272	0.0600	0.8301
LMNR.82–88	−0.0473	0.00060	0.0071	−1.3695	0.0095	0.0190	0.0857	0.5955
SEB.82–88	−0.0760	0.00063	0.0094	−1.5160	0.0126	0.0244	0.0676	0.7001
SWED.82–88	−0.0828	0.00063	0.0106	−1.1619	0.0146	0.0280	0.0592	0.8349
AVIVA.75–81	−0.0486	0.00053	0.0088	−0.7146	0.0148	0.0234	0.0602	0.2897
INVL.75–81	−0.0794	0.00062	0.0103	−1.3687	0.0144	0.0271	0.0609	0.8293
LMNR.75–81	−0.0473	0.00060	0.0071	−1.3806	0.0097	0.0191	0.0851	0.6012
SEB.75–81	−0.0762	0.00067	0.0093	−1.5374	0.0125	0.0243	0.0714	0.6993
SWED.75–81	−0.0831	0.00063	0.0106	−1.1666	0.0146	0.0281	0.0591	0.8351
AVIVA.68–74	−0.0443	0.00046	0.0078	−0.8207	0.0125	0.0209	0.0584	0.2889
INVL.68–74	−0.0717	0.00057	0.0091	−1.4953	0.0123	0.0240	0.0629	0.8332
LMNR.68–74	−0.0477	0.00060	0.0070	−1.4167	0.0095	0.0190	0.0855	0.6050
SEB.68–74	−0.0683	0.00059	0.0085	−1.5169	0.0122	0.0222	0.0695	0.6877
SWED.68–74	−0.0830	0.00061	0.0105	−1.2097	0.0144	0.0279	0.0583	0.8364
AVIVA.61–67	−0.0226	0.00027	0.0041	−0.9224	0.0067	0.0111	0.0657	0.2772
INVL.61–67	−0.0528	0.00039	0.0060	−2.0619	0.0075	0.0160	0.0646	0.8397
LMNR.61–67	−0.0388	0.00043	0.0051	−1.6690	0.0064	0.0137	0.0844	0.6291
SEB.61–67	−0.0468	0.00039	0.0055	−1.7517	0.0078	0.0144	0.0722	0.4446
SWED.61–67	−0.0537	0.00042	0.0066	−1.4604	0.0089	0.0176	0.0642	0.8385
AVIVA.54–60	−0.0126	0.00016	0.0021	−1.3794	0.0033	0.0059	0.0765	0.2764
INVL.54–60	−0.0220	0.00017	0.0022	−3.1725	0.0025	0.0057	0.0784	0.8311
LMNR.54–60	−0.0296	0.00020	0.0032	−2.7661	0.0035	0.0083	0.0636	0.7332
SEB.54–60	−0.0250	0.00020	0.0025	−2.5064	0.0033	0.0066	0.0804	0.4529
SWED.54–60	−0.0229	0.00020	0.0027	−1.9100	0.0035	0.0073	0.0743	0.7806

.

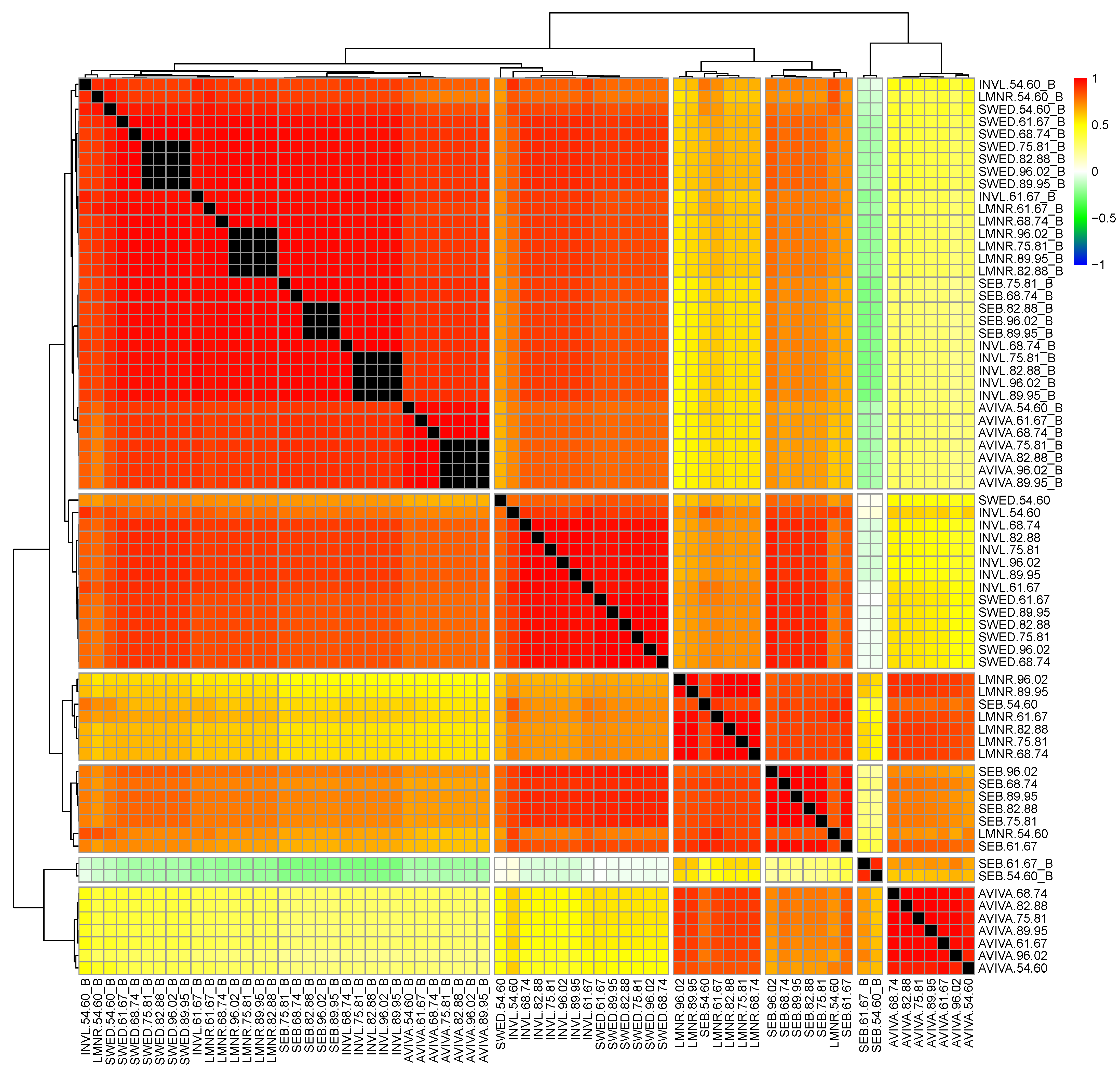
Table 2 shows that, on the basis of descriptive statistics and risk measures, the funds of five age groups (96–02, 89–95, 82–88, 75–81, 68–74) demonstrated very similar results, except for AVIVA funds. However, on closer inspection, it could be revealed that the most balanced reward-to-risk performance is observed for LMNR funds, which is well reflected by the best fit of Sharpe ratio. In particular, the risk, which lies in the left-tail of distribution, herein described as minimum, VaR and ES, was well managed by LMNR. Comparatively, SEB funds outperformed LMNR funds in terms of mean return, but their risk measures were slightly worse. Interestingly, the performance of INVL and SWED funds were observed as being very similar, demonstrating a comparatively high risk undertaken together with the expected return, which is, in terms of the Sharpe ratio, very similar to AVIVA funds. In contrast, AVIVA funds demonstrated good risk management, but the risk was not particularly well offset by a sufficient expected mean return, which may be a result of non-successful earnings from investments in equities. Considering the pension funds of the 61–67 and 54–60 are groups, we observed a different view, which is expected given that the investment portfolio is automatically adjusted to a lower risk as the desired retirement date approaches. Here, we can observe lower expected returns accompanied by lower risk estimates, such as standard deviation, minimum, VaR and ES. In general, their performance in terms of the Sharpe ratio is even better than was observed for some pension funds investing primarily in equities. This may be the consequence of the COVID-19 pandemic, which caused huge swings in the equity market in 2020. Focusing on skewness, it can be seen that all funds resulted in a negative value, indicating a fatter or longer tail on the left side of the return distribution, which might be easily related to the COVID-19 crisis. Finally, the correlation coefficient reveals the relation between PFs’ performance and their benchmarks. Interestingly, the correlation coefficients are very similar for the funds of the same manager. More specifically, all INVL and SWED funds demonstrated the strongest relation with their benchmarks, whereas AVIVA funds produced the smallest values. Comparatively, LMNR funds and their benchmarks were modestly correlated. In particular, the funds managed by SEB exclusively resulted in different correlations ranging from 0.4529 to 0.7256, which increases in line with the number of stocks included in the investment portfolio. The graphical illustration of daily returns is depicted in Figure 3.

The visual representation of daily returns in Figure 3 reveals that the deviation in returns is much larger for pension funds of the 68–74 to 96–02 age groups, which is an expected result because of dominating investments in stocks. Comparing the managers in between, we can observe that LMNR funds are more consistent, except for the 54–60 age group. The largest uncertainty is observed for the funds managed by SWED and INVL, with many observations distributed in the left side of the distribution. Comparatively, AVIVA funds are slightly less extreme than others, especially on the negative side of the distribution, but they still indicated a long negative tail. The descriptive statistics of PF benchmarks is provided in Appendix A,

Table A1. Descriptive statistics and risk measures for daily arithmetic returns of PF benchmarks.

Benchmark	Min	Mean	StDev	Skewness	Kurtosis	VaR	ES	Sharpe
AVIVA.96–02_B	−0.11301	0.00065	0.01246	−1.53504	19.73369	−0.01680	−0.03140	0.05257
INVL.96–02_B	−0.11238	0.00070	0.01234	−2.08707	23.94028	−0.01520	−0.03140	0.05657
LMNR.96–02_B	−0.09024	0.00065	0.01091	−1.95484	20.29657	−0.01230	−0.02770	0.05970
SEB.96–02_B	−0.10383	0.00072	0.01230	−1.79486	20.89777	−0.01500	−0.03120	0.05825
SWED.96–02_B	−0.09234	0.00066	0.01048	−1.87101	20.02402	−0.01200	−0.02680	0.06284
AVIVA.89–95_B	−0.11301	0.00065	0.01246	−1.53504	19.73369	−0.01680	−0.03140	0.05257
INVL.89–95_B	−0.11238	0.00070	0.01234	−2.08707	23.94028	−0.01520	−0.03140	0.05657
LMNR.89–95_B	−0.09024	0.00065	0.01091	−1.95484	20.29659	−0.01230	−0.02770	0.05970
SEB.89–95_B	−0.10383	0.00072	0.01230	−1.79486	20.89777	−0.01500	−0.03120	0.05825
SWED.89–95_B	−0.09234	0.00066	0.01048	−1.87101	20.02402	−0.01200	−0.02680	0.06284
AVIVA.82–88_B	−0.11301	0.00065	0.01246	−1.53504	19.73369	−0.01680	−0.03140	0.05257
INVL.82–88_B	−0.11238	0.00070	0.01234	−2.08707	23.94028	−0.01520	−0.03140	0.05657
LMNR.82–88_B	−0.09024	0.00065	0.01091	−1.95484	20.29659	−0.01230	−0.02770	0.05970
SEB.82–88_B	−0.10383	0.00072	0.01230	−1.79486	20.89777	−0.01500	−0.03120	0.05825
SWED.82–88_B	−0.09234	0.00066	0.01048	−1.87101	20.02402	−0.01200	−0.02680	0.06284
AVIVA.75–81_B	−0.11301	0.00065	0.01246	−1.53504	19.73369	−0.01680	−0.03140	0.05257
INVL.75–81_B	−0.11238	0.00070	0.01234	−2.08707	23.94028	−0.01520	−0.03140	0.05657
LMNR.75–81_B	−0.09024	0.00065	0.01091	−1.95484	20.29660	−0.01230	−0.02770	0.05970
SEB.75–81_B	−0.10383	0.00076	0.01233	−1.77930	20.66059	−0.01500	−0.03120	0.06190
SWED.75–81_B	−0.09234	0.00066	0.01048	−1.87101	20.02402	−0.01200	−0.02680	0.06284
AVIVA.68–74_B	−0.09854	0.00058	0.01085	−1.55296	19.67217	−0.01500	−0.02730	0.05350
INVL.68–74_B	−0.10232	0.00064	0.01104	−2.24587	25.07505	−0.01330	−0.02810	0.05810
LMNR.68–74_B	−0.09024	0.00065	0.01087	−1.97678	20.58528	−0.01230	−0.02770	0.05982
SEB.68–74_B	−0.09350	0.00066	0.01104	−1.88301	20.67070	−0.01310	−0.02820	0.06010
SWED.68–74_B	−0.09234	0.00064	0.01042	−1.90574	20.52751	−0.01180	−0.02670	0.06169
AVIVA.61–67_B	−0.05150	0.00030	0.00553	−1.73075	20.94403	−0.00750	−0.01390	0.05476
INVL.61–67_B	−0.06940	0.00043	0.00696	−2.93139	30.41741	−0.00750	−0.01790	0.06188
LMNR.61–67_B	−0.06236	0.00045	0.00723	−2.51426	23.22411	−0.00800	−0.01860	0.06227
SEB.61–67_B	−0.06205	0.00046	0.00693	−2.48759	22.79667	−0.00790	−0.01800	0.06586
SWED.61–67_B	−0.06505	0.00044	0.00705	−2.26716	23.08609	−0.00770	−0.01810	0.06300
AVIVA.54–60_B	−0.02738	0.00016	0.00281	−2.03733	23.76313	−0.00360	−0.00700	0.05536
INVL.54–60_B	−0.02587	0.00018	0.00227	−4.78208	47.09297	−0.00190	−0.00570	0.07906
LMNR.54–60_B	−0.03449	0.00025	0.00381	−3.52112	29.42344	−0.00400	−0.00960	0.06672
SEB.54–60_B	−0.02695	0.00024	0.00284	−3.09442	26.10482	−0.00310	−0.00740	0.08595
SWED.54–60_B	−0.03321	0.00022	0.00330	−3.30894	30.57115	−0.00340	−0.00850	0.06791

.

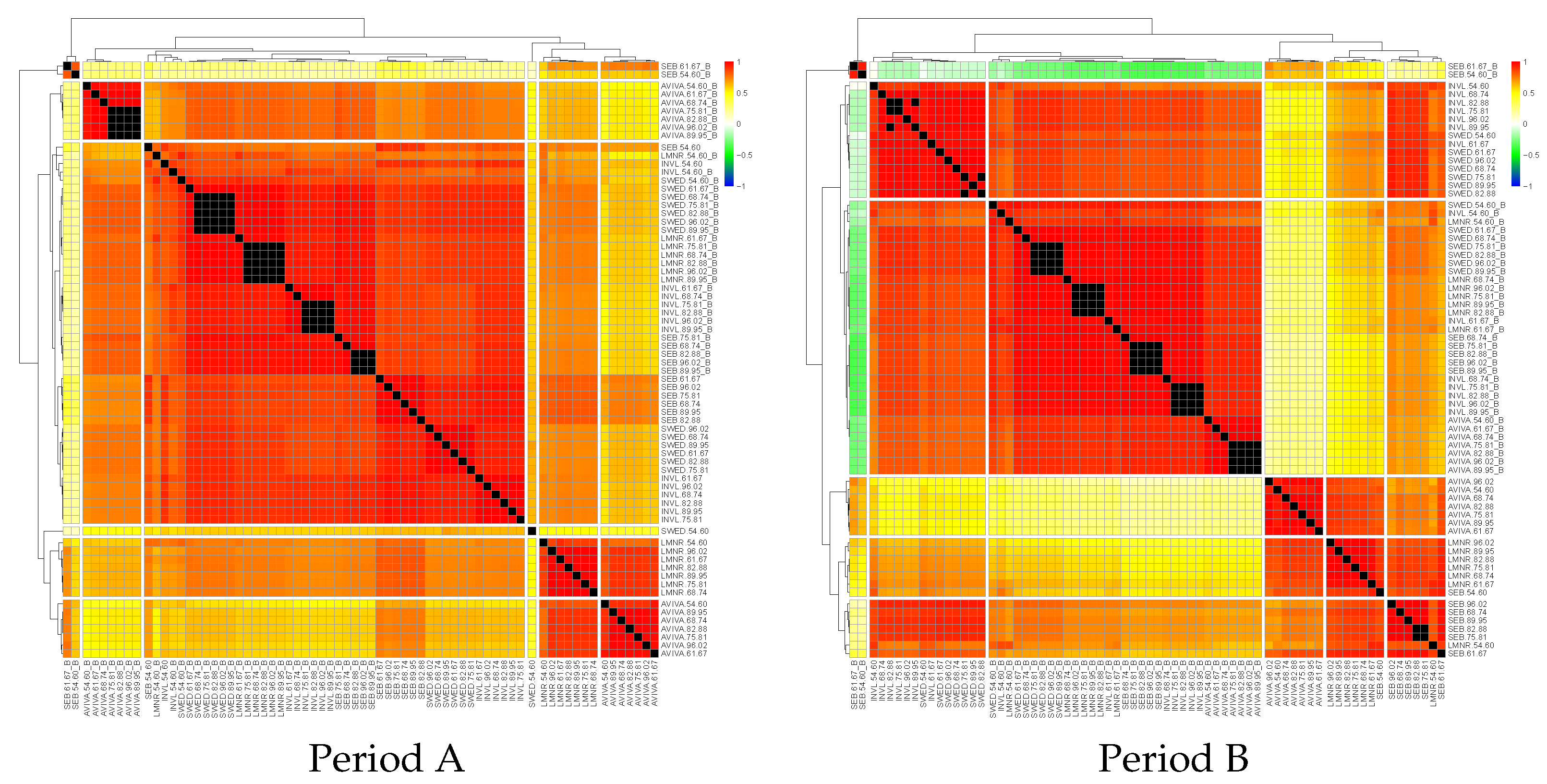
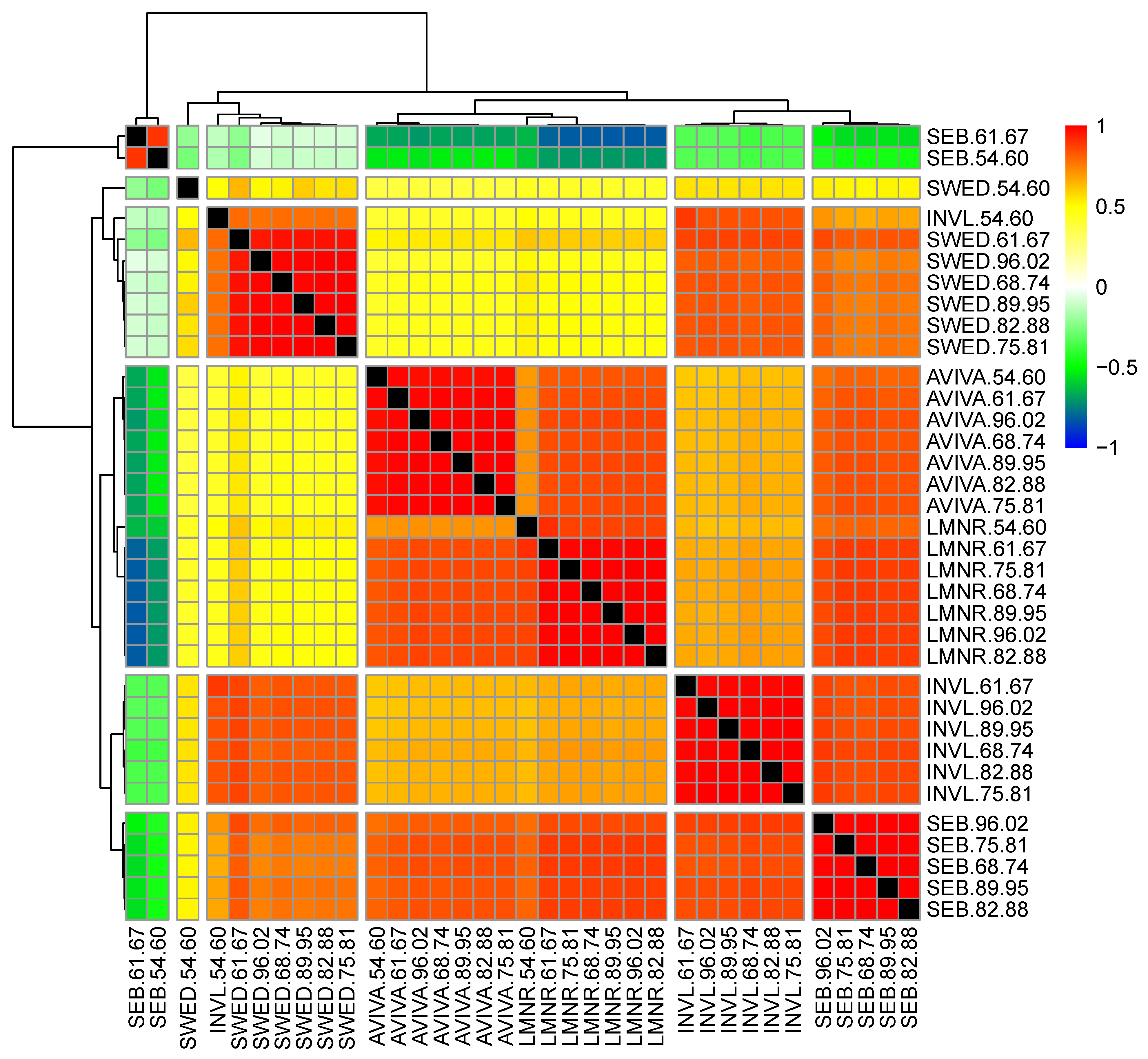
Correlations between PF values and benchmarks are provided in Figure 4.

From Figure 4 we can see that nearly all benchmarks are clustered to one cluster. This shows that benchmarks behave quite differently in comparison to their funds. Surprisingly, benchmarks of two SEB funds (61–67 and 54–60, the oldest age groups) are separated into very different clusters and exhibit weak or even negative correlations with other data sets observed. Moreover, as they correlate more strongly to AVIVA funds than to SEB or other data sets observed, we can state that they behave more similarly to AVIVA funds. INVL and SWED pension funds are clustered into the same cluster and exhibit very strong correlations. This cluster is relatively similar to the group of benchmark clusters. Such a close relation can be understood as similar behaviour to the fund’s value evolution and benchmark in the long term. The final two clusters include SEB and LMNR funds. The first cluster includes mainly SEB funds, with the exception of the oldest age group, which is substituted by the oldest group of the LMNR pension fund; conversely, the LMNR cluster involves mainly all LMNR funds with the exception of the oldest age group. These two clusters are quite strongly correlated with each other, but the LMNR cluster exhibits a weaker correlation to other clusters compared to the SEB cluster.

Now, we will turn to how correlations change over time, i.e., rolling from period A to period B. Such a transition is represented in Appendix A, Figure A1. In period A, the correlations are largely positive, varying from weak to very strong. However, in period B, the correlations landscape is more diverse. The correlations of two benchmarks from SEB (the 61–67 and 54–60 age groups) become negative with all other benchmarks and fund values of INVL and SWED managers. However, they remain weakly positively correlated to the SEB, AVIVA and LMNR pension funds. In general, correlations between benchmarks vary from very strong to perfect (this can be observed for the same manager), and the period has no influence on this result. However, correlations between fund values and benchmark values differ depending on the period and fund manager. For example, AVIVA funds exhibit an average or strong correlation with other funds and benchmarks in period A, but, in period B, their correlation with other benchmarks become very weak (close to 0), whereas the correlation with SEB funds becomes strong to very strong.

To summarise, it can be said that correlations between benchmark values are relatively stable (with the exception of two SEB funds) when the time window changes. However, correlations between funds and benchmarks vary over time.

5. Research Methodology

This section begins by first presenting the approach for measuring the pension funds’ performance with respect to their benchmarks in terms of almost stochastic dominance. Then, a relative upper semi-tracking error was developed, which was used to assess the strength of the benchmark replication.

5.1. First and Second Rules of Almost Stochastic Dominance

Almost stochastic dominance is a relaxation of stochastic dominance. Therefore, we first introduced some preliminaries of stochastic dominance, as presented in [23]. Depending on the assumptions on the pension system participant’s utility function $u\left(x\right)$, two different types of stochastic dominance relations were considered:

• First-order stochastic dominance (FSD)—no restriction on the participant’s utility, only non-satiation is assumed, i.e., $U_{FSD}=\{u\left(x\right):u^{\prime }\left(x\right)\ge 0\}$;
• Second-order stochastic dominance (SSD)—assumption of non-satiation and risk aversion is considered, such as $U_{SSD}=\{u\left(x\right)\in U_{FSD}:u^{″}\left(x\right)\le 0\}$.

SD rules were verified by performing pairwise comparisons. Given that, and considering pension investment options, we said that the fund i with cumulative distribution function of returns $F_i\left(x\right)$ dominates the fund j with cumulative distribution function of returns $F_j\left(x\right)$ by FSD for all $u\in U_{FSD}$ if and only if

$$[F_j\left(x\right)-F_i\left(x\right)]\ge 0$$

(1)

for any real number x, with at least one strong inequality. This means that, as long as the investor prefers having more wealth rather than less, the fund i is preferred to fund j.

With respect to SSD, the fund i with $F_i\left(x\right)$ dominates the fund j with $F_j\left(x\right)$ for all $u\in U_{SSD}$ if and only if

$${\int }_{-\infty }^x[F_j\left(t\right)-F_i\left(t\right)]\mathrm{d}t\ge 0$$

(2)

for any real number x, with at least one strong inequality. In this case, if the investor is risk averse, the dominating fund is preferred to the dominated one or the investor is indifferent about their choice. It is also true that $\mathrm{E}u\left(X_i\right)\ge$$\mathrm{E}u\left(X_j\right)$ for the pair of funds, where the fund i dominates the fund j for all $u\in U_{FSD}$ or $u\in U_{SSD}$. Moreover, in a set of considered funds, it is also possible to determine efficient funds if there is no other fund that dominates it. Notably, if no assumption about the theoretical distribution of returns is made, SD rules are applied to the empirical distribution of returns observed over some period.

Stochastic dominance is one of the most powerful tools for decision making under uncertainty. However, evidence shows that its application in practice is limited because it is highly restrictive in necessary and sufficient conditions. This means that a small violation area in the cumulative distribution function of returns may result in a failure to determine the dominating pension fund. According to [23], these conditions could be relaxed by the almost stochastic dominance, which is an extension of stochastic dominance. For this purpose, the subsets $U_{AFSD}\subset U_{FSD}$ and $U_{ASSD}\subset U_{SSD}$ were introduced for every $0<\epsilon ⩽0.5$ such as

$$U_{AFSD}\left(\epsilon \right)=\left\{u\in U_{FSD}:u^{\prime }\left(x\right)\le inf\left[u^{\prime }\left(x\right)\right]\left[\frac{1}{\epsilon }-1\right]\right\}$$

and

$$U_{ASSD}\left(\epsilon \right)=\left\{u\in U_{SSD}:-u^{″}\left(x\right)\le inf\left[-u^{″}\left(x\right)\right]\left[\frac{1}{\epsilon }-1\right]\right\}.$$

Notably, if $\epsilon =0$, then $U_{AFSD}=U_{FSD}$ and $U_{ASSD}=U_{SSD}$.

Then, the rules of almost stochastic dominance were specified as follows. Suppose that we have two functions $F_i\left(x\right)$ and $F_j\left(x\right)$ that cross and describe the cumulative distribution function of returns of fund i and fund j, respectively. The FSD violation range is defined as $s_1=\{x\in [a,b]:F_j\left(x\right)<F_i\left(x\right)\}$. Then, the fund i is said to dominate the fund j by $\epsilon$-AFSD for all $u\in U_{AFSD}$ if and only if

$${\int }_{s_1}\left[F_i\left(x\right)-F_j\left(x\right)\right]\mathrm{d}x\le \epsilon {\int }_a^b|F_i\left(x\right)-F_j\left(x\right)|\mathrm{d}x.$$

(3)

Now, let us introduce the SSD violation range as

$$s_2=\{x\in [a,b],x\in s_1:{\int }_a^x\left[F_j\left(t\right)-F_i\left(t\right)\right]\mathrm{d}t<0\}.$$

Considering all $u\in U_{ASSD}$, fund i with $F_i$ dominates fund j with $F_j$ by $\epsilon$-ASSD if and only if

$${\int }_{s_2}|F_j\left(x\right)-F_i\left(x\right)|\mathrm{d}x\le \epsilon {\int }_a^b|F_j\left(x\right)-F_i\left(x\right)|\mathrm{d}x.$$

(4)

Specifically, the maximal $\epsilon$ satisfying (3) or (4) shows the portion of FSD or SSD violations, respectively. It ranges in the interval $[0;1]$. Therefore, throughout this work, we refer to maximal $\epsilon$ satisfying (3) or (4) for measuring the strength of AFSD or ASSD, respectively, i.e., the smaller the value of $\epsilon$, the stronger the almost dominance of fund i to fund j. The case of $\epsilon =1$ means that fund j dominates fund i. If $0.5<\epsilon <1$, the violation of dominance between fund i and j is greater than that between fund j and i. In this case, one could say that fund j almost dominates fund i. However, in this paper, for the sake of the fund’s dominance comparison, we only considered one way in which almost dominance allows $\epsilon >0.5$, despite the fact that it is not consistent with the definition of $U_{AFSD}\left(\epsilon \right)$ and $U_{ASSD}\left(\epsilon \right).$

5.2. New Performance Index

As mentioned above, Bank of Lithuania [16] defines a tracking error as a statistical measure that shows the standard deviation of the difference between the change in fund unit value (unscaled) and change in benchmark unit value (unscaled). However, pension fund managers have an obligation to provide it in annual (by quarters) reports only [37]. This complicates statistical analysis and the decision-making process. To better understand how the behaviour of funds differs from benchmark behaviour over time, we defined tracking difference in the following way (similar to Jorion [40]).

Definition 1.

Tracking difference TD is the difference between the random return of the fund unit value and the random return of teh benchmark unit value. Hence, at a particular time moment$t\in [0,T]$, the tracking difference TD_t is defined as

$${TD}_t=R_t-B_t,$$

(5)

where $R_t$ stands for the return of the fund unit value and $B_t$ stands for the return of the benchmark unit value in time t.

Later in this paper, we use Definition 1 only when the tracking difference is mentioned. Following Bank of Lithuania [16], we first define the tracking error of the fund.

Definition 2.

Tracking error of a given fund is defined as the estimation of the standard deviation of the tracking difference; that is:

$$TE=\sqrt{\frac{1}{T}\sum _{t=1}^T{(T{D}_t-\overline{TD})}^2}$$

where

$$\overline{TD}=\frac{1}{T}\sum _{t=1}^T\left(T{D}_t\right).$$

Generalised tracking error expresses a violation of tracking distance from a threshold b in the following way:

$$GTE\left(b\right)=\sqrt{\frac{1}{T}\sum _{t=1}^T{(T{D}_t-b)}^2}$$

Since the positive tracking difference is desirable whereas the negative one is not, we focused on the absolute upper semi-tracking error, which is defined as the estimation of the second-order upper partial moment of the tracking difference. For the sake of comparison, the relative upper semi-tracking error is more useful.

Definition 3.

Absolute upper semi-tracking error of a given fund is defined as follows:

$$\mathrm{AUSTE}\left(b\right)=\sqrt{\frac{1}{T}\sum _{t=1}^{T}max{(T{D}_t-b,0)}^2}$$

and the relative upper semi-tracking error is given by:

$$\mathrm{RUSTE}\left(b\right)=\frac{\mathrm{AUSTE}\left(b\right)}{GTE\left(b\right)}$$

While AUSTE can be seen as a measure of the variability of ‘positive’ tracking differences in the absolute sense, RUSTE standardises it by the total variability expressed by TE. Hence, RUSTE depicts the percentage of ‘positive variability’ of the tracking difference. It always takes values between 0 and 1. Alternatively, one could consider a relative lower semi-tracking error (RLSTE) that focuses on ‘negative variability’. Since the square of a relative lower semi-tracking error is nothing other than $1-{\mathrm{RUSTE}}^2$, the minimisation of the RLSTE is equivalent to the maximisation of RUSTE. Thus, there is no need to consider both RLSTE and RUSTE. We therefore decided to focus on RUSTE because our final performance measure (dominance-tracking index) is the maximisation criterion. If the tracking difference is symmetrically distributed, then RUSTE $=\frac{\sqrt{2}}{2}\approx 0.7$. If $b=\overline{TD}$, the higher values of RUSTE indicate a right-skewed distribution—positive skewness—of the TD. Since the majority of investors prefer a higher to smaller skewness (skew lovers), we aimed for higher RUSTE values. If $b=0$, then RUSTE can be seen as a measure of the fund outperformance relative to its benchmark. In the ideal case, when the tracking difference is always positive, RUSTE = 1. Hence, the higher the RUSTE, the better the fund outperforms the benchmark. Moreover, following (4), we considered the ASSD parameter to be defined as:

$$\epsilon =\frac{{\int }_{s_2}|F_R\left(x\right)-F_B\left(x\right)|\mathrm{d}x}{{\int }_a^b|F_R\left(x\right)-F_B\left(x\right)|\mathrm{d}x}$$

(6)

where $F_R\left(x\right),F_B\left(x\right)$ is the cumulative distribution function of the fund and benchmark returns, respectively, and

$$s_2=\{x\in s_1:{\int }_a^x\left[F_B\left(t\right)-F_R\left(t\right)\right]\mathrm{d}t<0\}$$

$$s_1=\{x\in [a,b]:F_B\left(x\right)<F_R\left(x\right)\}.$$

The smaller the ASSD parameter, the stronger the ASSD relation. In the ideal case, $\epsilon =0$, which means that the return of the fund dominates the return of its benchmark. Combining the advantages of both approaches (stochastic dominance and tracking error), we propose a new performance index of pension funds.

Definition 4.

Dominance-tracking index of a given fund is defined as follows:

$$\mathrm{DTI}\left(b\right)=(1-\epsilon )\mathrm{RUSTE}\left(b\right),$$

where ε is given by (6).

This new index has the following properties:

• It takes values between 0 and 1;
• The higher the index, the better the outperformance is relative to the benchmark;
• Unlike the ASSD parameter $\epsilon$, the index may compare the outperformance even in the case where more than one fund dominates its benchmark with respect to SSD. In this case, $(1-\epsilon )=1$ and the best fund has the highest RUSTE;
• A higher ASSD parameter $\epsilon$ can be compensated by higher RUSTE;
• If the return of the fund is dominated by the return of its benchmark, that is, $\epsilon =1$, the index takes the worst value no matter how large the RUSTE is.

6. Results

In this section we present the results of the study. First, we describe historical tracking differences in returns for all pension funds separately and later by aggregating them according to the age group. We then compare how tracking differences vary depending on the period analysed. Secondly, we provide results of almost stochastic dominance between the pension fund and its benchmark, which is then entered into a RUSTE ratio. All of the results are obtained for the case $b=\overline{TD}$. Finally, we rank pension funds in terms of how well they track the benchmark over the entire period and periods before and after the beginning of the COVID-19 pandemic. The ranking is performed using the dominance-tracking index.

6.1. Tracking Differences in Returns

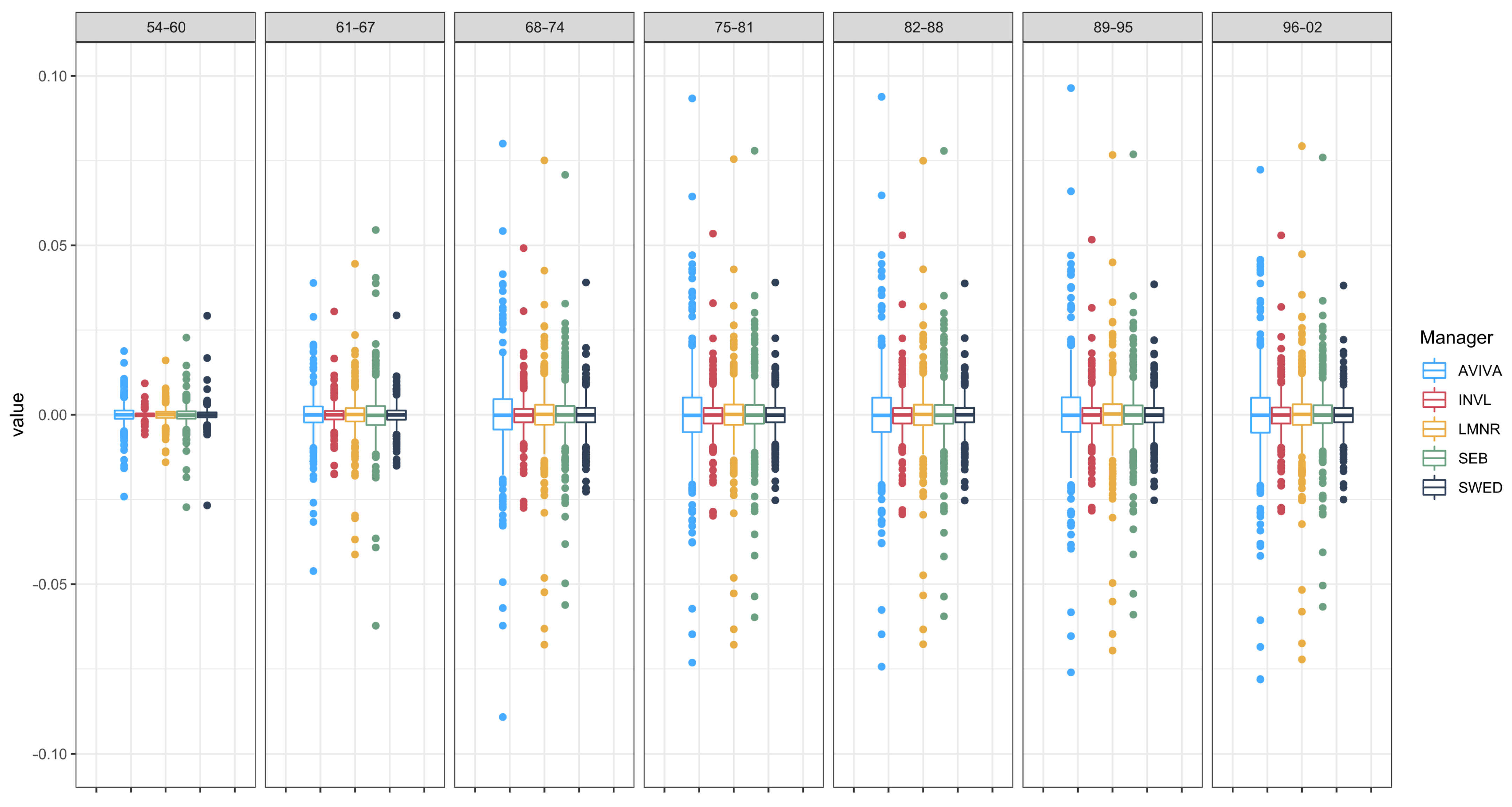
In

Table 3. Descriptive statistics of tracking difference for entire period (A + B).

Fund	Full Period
	Min	Max	Median	Mean	StDev	CoefVar	MAD
AVIVA.96–02	−0.111	0.102	−0.000118	−0.000096	0.014	−140.8	0.008
INVL.96–02	−0.029	0.053	−0.000039	−0.000073	0.006	−78.5	0.003
LMNR.96–02	−0.072	0.079	0.000135	−0.000022	0.009	−430.1	0.005
SEB.96–02	−0.057	0.076	−0.000053	−0.000081	0.008	−98.7	0.004
SWED.96–02	−0.025	0.038	−0.000145	−0.000069	0.005	−70.0	0.003
AVIVA.89–95	−0.103	0.096	−0.000129	−0.000121	0.013	−108.0	0.008
INVL.89–95	−0.028	0.052	−0.000033	−0.000075	0.006	−75.2	0.003
LMNR.89–95	−0.070	0.077	0.000237	−0.000031	0.009	−286.9	0.004
SEB.89–95	−0.059	0.077	−0.000032	−0.000086	0.008	−96.4	0.004
SWED.89–95	−0.025	0.039	−0.000057	−0.000043	0.005	−111.1	0.003
AVIVA.82–88	−0.101	0.094	−0.000177	−0.000115	0.013	−112.2	0.008
INVL.82–88	−0.029	0.053	−0.000020	−0.000081	0.006	−70.4	0.003
LMNR.82–88	−0.068	0.075	0.000126	−0.000047	0.009	−186.1	0.004
SEB.82–88	−0.059	0.078	−0.000085	−0.000084	0.008	−99.9	0.004
SWED.82–88	−0.025	0.039	0.000006	−0.000033	0.005	−146.9	0.003
AVIVA.75–81	−0.101	0.093	−0.000185	−0.000122	0.013	−105.1	0.008
INVL.75–81	−0.030	0.053	−0.000039	−0.000074	0.006	−78.1	0.003
LMNR.75–81	−0.068	0.075	0.000125	−0.000051	0.009	−170.6	0.004
SEB.75–81	−0.060	0.078	−0.000074	−0.000096	0.008	−87.4	0.004
SWED.75–81	−0.025	0.039	−0.000061	−0.000032	0.005	−151.8	0.003
AVIVA.68–74	−0.089	0.080	−0.000122	−0.000123	0.011	−90.7	0.007
INVL.68–74	−0.027	0.049	−0.000040	−0.000071	0.005	−72.1	0.003
LMNR.68–74	−0.068	0.075	0.000140	−0.000048	0.009	−180.5	0.004
SEB.68–74	−0.056	0.071	−0.000023	−0.000073	0.008	−105.7	0.004
SWED.68–74	−0.023	0.039	−0.000012	−0.000031	0.005	−150.5	0.003
AVIVA.61–67	−0.046	0.039	−0.000020	−0.000034	0.006	−171.0	0.003
INVL.61–67	−0.018	0.031	0.000000	−0.000044	0.003	−69.9	0.002
LMNR.61–67	−0.041	0.045	0.000077	−0.000021	0.005	−254.6	0.003
SEB.61–67	−0.062	0.055	−0.000154	−0.000062	0.007	−112.0	0.004
SWED.61–67	−0.015	0.029	−0.000017	−0.000021	0.003	−152.1	0.002
AVIVA.54–60	−0.024	0.019	0.000007	0.000009	0.003	348.7	0.002
INVL.54–60	−0.006	0.009	0.000035	−0.000005	0.001	−183.8	0.001
LMNR.54–60	−0.014	0.016	0.000030	−0.000054	0.002	−38.6	0.001
SEB.54–60	−0.027	0.023	−0.000050	−0.000044	0.003	−66.9	0.002
SWED.54–60	−0.027	0.029	−0.000046	−0.000022	0.002	−105.5	0.001

, we provide the descriptive statistics of the tracking difference in returns ($TD$).

Negative mean values indicate that the returns of funds are, on average, smaller than the returns of the benchmark for nearly all pension funds analysed (except for AVIVA.54–60). It is interesting to note, though, that such a statement is not true for medians because all LMNR funds have a positive median of tracking differences. Moreover, there are more funds with non-negative median tracking differences (INVL.61–67, INVL.54–60 and AVIVA.54–60). A non-negative median indicates that the fund value in more than 50% of observations outperforms the benchmark. 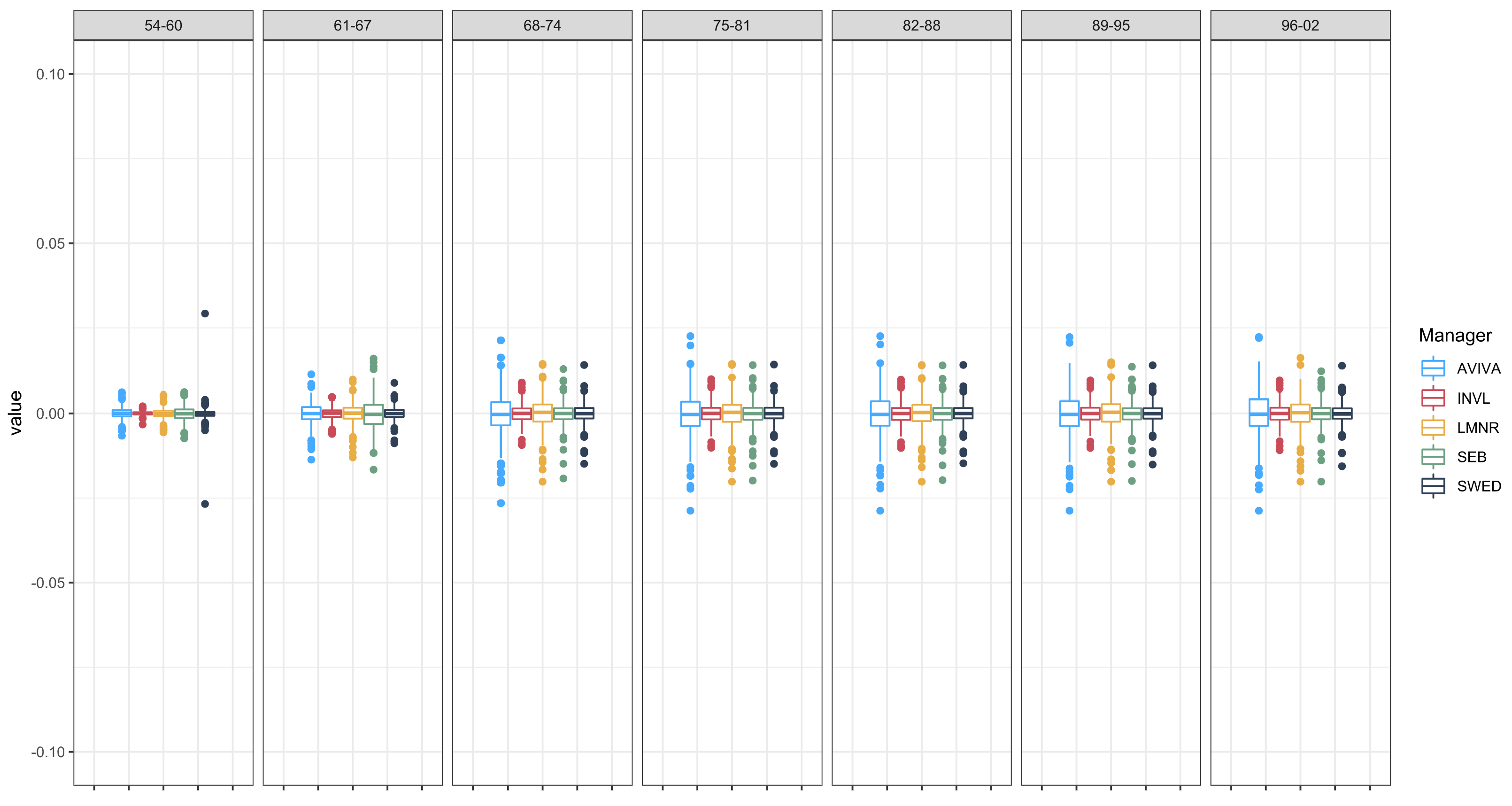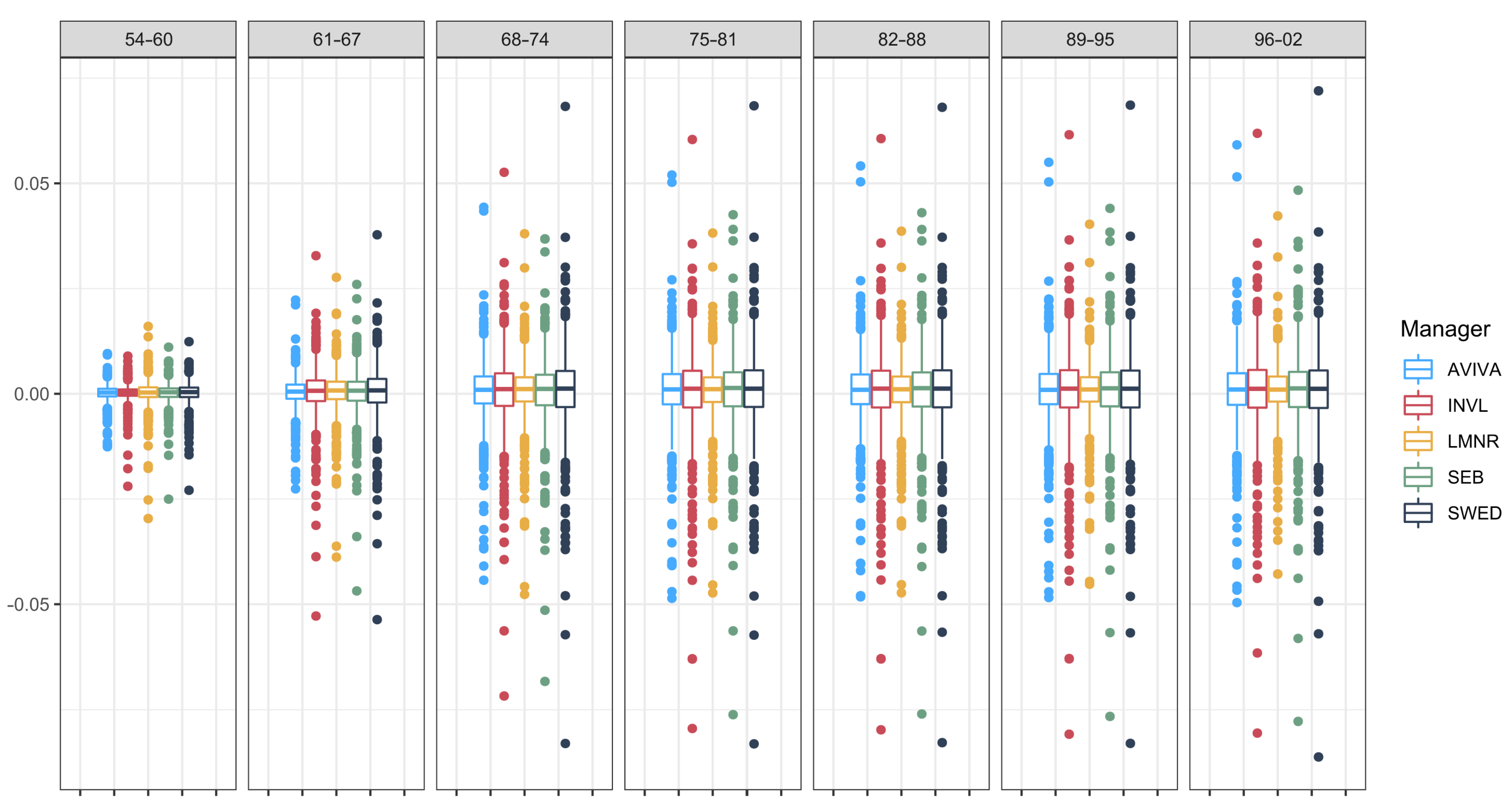In Figure 5, the distribution of tracking differences is provided for the entire period analysed and grouped according to the age of the pension system participant.

As one can see, the variability depends on the age group: it is relatively small for older participants and greater for younger participants. Additionally, in

Table 4. Descriptive statistics of tracking differences for each age group.

Age Group		96–02	89–95	82–88	75–81	68–74	61–67	54–60
Entire period (A + B)	Median	−0.000044	−0.000003	−0.000030	−0.000047	−0.000011	−0.000023	−0.000005
	Mean	−0.000068	−0.000071	−0.000072	−0.000075	−0.000069	−0.000036	−0.000023
	StDev	0.0083	0.0082	0.0081	0.0081	0.0075	0.0049	0.0023
	CoefVar	−163.6	−135.5	−123.1	−118.6	−119.9	−151.9	−9.2
	MAD	0.005	0.005	0.005	0.005	0.004	0.003	0.001
Period A	Median	−0.000030	−0.000002	−0.000002	−0.000009	0.000001	−0.000023	−0.000043
	Mean	−0.000067	−0.000075	−0.000076	−0.000081	−0.000074	−0.000058	−0.000061
	StDev	0.004	0.004	0.004	0.004	0.004	0.003	0.002
	CoefVar	−105.9	−103.7	−78.7	−70.1	−98.2	−51.2	−8.7
	MAD	0.003	0.003	0.003	0.003	0.003	0.002	0.001
Period B	Median	−0.000027	0.000029	−0.000005	−0.000062	−0.000038	0.000007	0.000040
	Mean	−0.000069	−0.000068	−0.000068	−0.000070	−0.000065	−0.000016	0.000013
	StDev	0.011	0.011	0.011	0.011	0.010	0.006	0.003
	CoefVar	−216.5	−190.1	−201.5	−191.5	−192.4	−737.4	−570.3
	MAD	0.006	0.006	0.006	0.006	0.006	0.003	0.001

, we provide the values for the median, mean, mean absolute deviation (MAD), standard deviation (StDev) and coefficient of variation (CoefVar) for each age group separately and in different considered periods.

It is clearly observable that the average tracking difference and average variability (StDev and MAD) decrease when participants of the pension system get older. This means that the fund tracks the benchmark better with age, which is in line with observations from Figure 5.

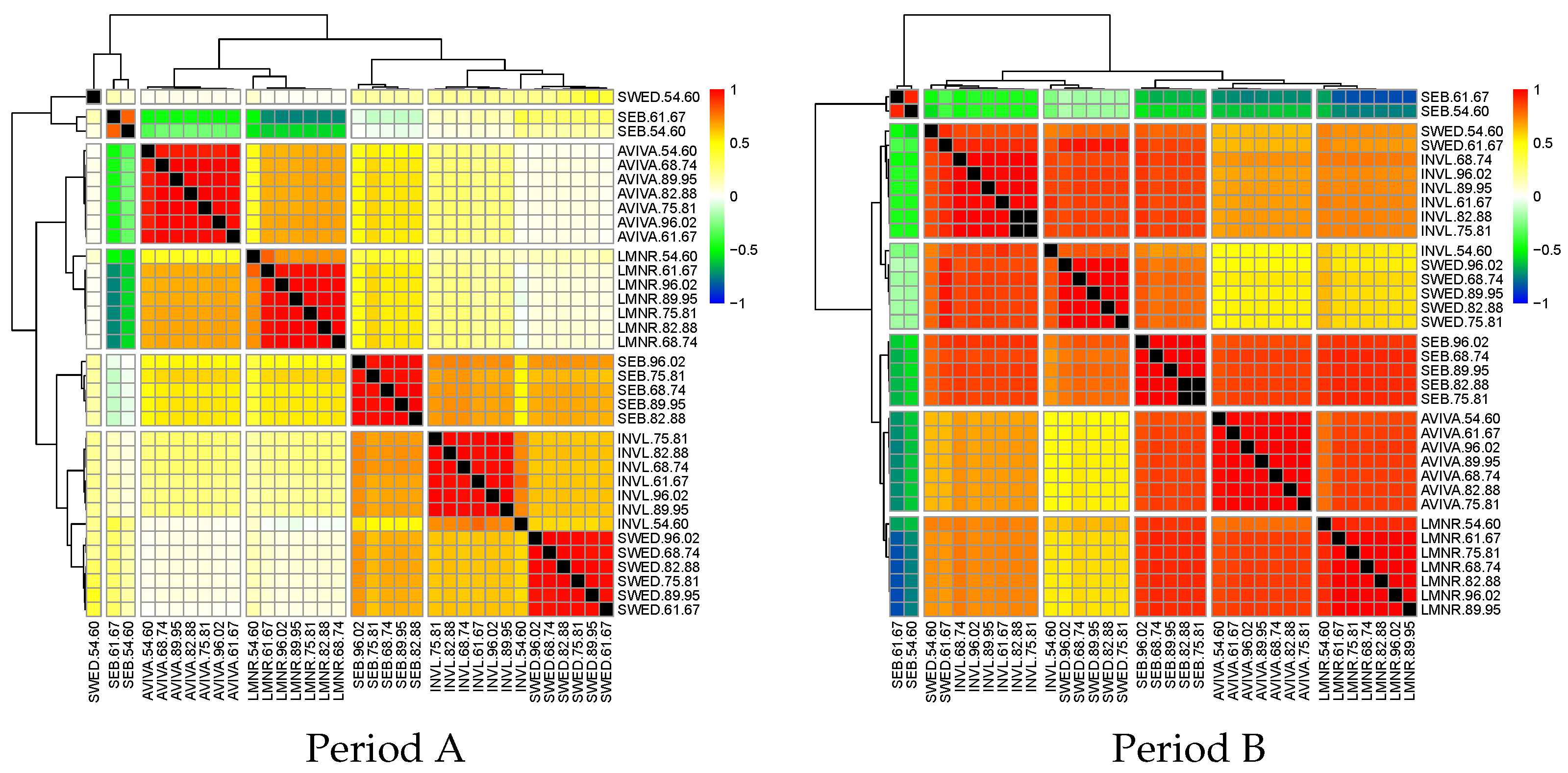
Now, let us investigate the correlations between tracking differences, which are provided in Figure 6.

From Figure 6, we can see that the tracking differences in SEB funds (the oldest age groups) behave quite differently, as their correlations are mainly negative. The strongest negative correlations are observed between the mentioned SEB funds and the LMNR funds. As expected, the tracking differences in the same manager correlate very strong (with the exception of SEB).

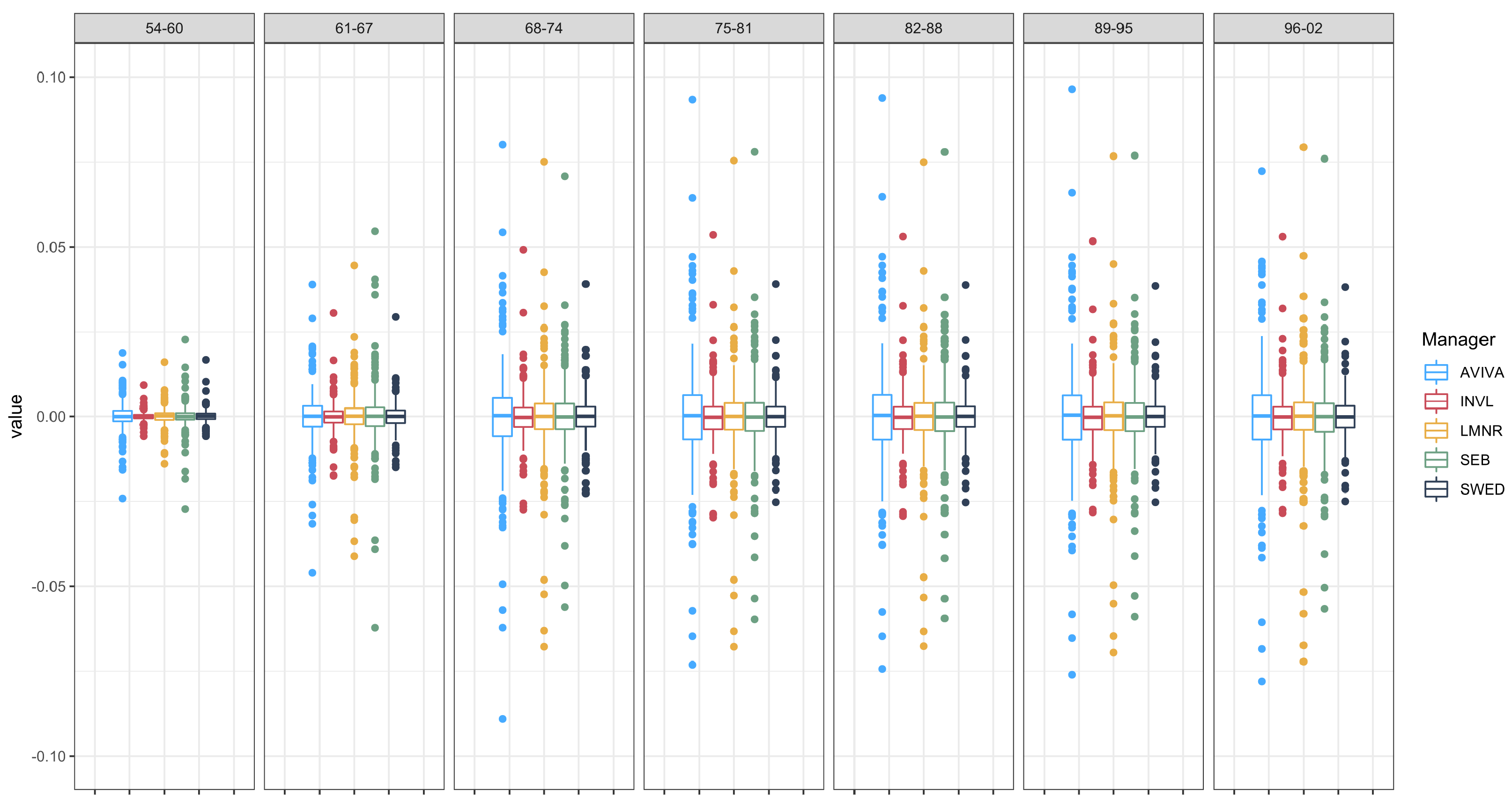
We continue with the investigation by tracking differences changes over time. The statistics of returns tracking differences in periods A and B are provided in Appendix A,

Table A2. Descriptive statistics of returns tracking error for pre-COVID-19 and COVID-19 period.

Fund	Period A							Period B
	Min	Max	Median	Mean	StDev	CoefVar	MAD	Min	Max	Median	Mean	StDev	CoefVar	MAD
AVIVA.96–02	−0.029	0.022	−0.00023	−0.00015	0.0066	−44.9	0.006	−0.111	0.102	0.00014	−0.00005	0.0179	−381.8	0.010
INVL.96–02	−0.011	0.009	0.00000	−0.00006	0.0030	−52.2	0.003	−0.029	0.053	−0.00015	−0.00009	0.0075	−84.3	0.005
LMNR.96–02	−0.020	0.016	0.00024	−0.00001	0.0045	−312.2	0.004	−0.072	0.079	0.00008	−0.00003	0.0123	−429.7	0.006
SEB.96–02	−0.020	0.012	−0.00003	−0.00004	0.0033	−80.5	0.002	−0.057	0.076	−0.00006	−0.00012	0.0107	−90.0	0.006
SWED.96–02	−0.016	0.014	−0.00015	−0.00007	0.0030	−39.7	0.002	−0.025	0.038	−0.00015	−0.00006	0.0061	−96.6	0.005
AVIVA.89–95	−0.029	0.022	−0.00028	−0.00020	0.0065	−32.5	0.005	−0.103	0.096	0.00036	−0.00005	0.0172	−377.3	0.010
INVL.89–95	−0.010	0.009	0.00000	−0.00005	0.0029	−53.1	0.003	−0.028	0.052	−0.00025	−0.00009	0.0074	−77.9	0.005
LMNR.89–95	−0.020	0.015	0.00033	−0.00001	0.0044	−311.8	0.004	−0.070	0.077	0.00020	−0.00005	0.0119	−247.2	0.006
SEB.89–95	−0.020	0.014	0.00000	−0.00006	0.0034	−55.9	0.003	−0.059	0.077	−0.00015	−0.00011	0.0111	−101.5	0.006
SWED.89–95	−0.015	0.014	−0.00006	−0.00005	0.0029	−65.4	0.002	−0.025	0.039	−0.00001	−0.00004	0.0061	−146.9	0.005
AVIVA.82–88	−0.029	0.023	−0.00028	−0.00019	0.0064	−33.2	0.005	−0.101	0.094	0.00029	−0.00004	0.0170	−435.3	0.010
INVL.82–88	−0.010	0.010	0.00000	−0.00006	0.0029	−47.1	0.003	−0.029	0.053	−0.00025	−0.00010	0.0075	−75.1	0.005
LMNR.82–88	−0.020	0.014	0.00029	−0.00002	0.0043	−181.0	0.004	−0.068	0.075	0.00007	−0.00007	0.0115	−166.0	0.006
SEB.82–88	−0.020	0.014	−0.00001	−0.00006	0.0034	−56.5	0.003	−0.059	0.078	−0.00016	−0.00011	0.0112	−106.4	0.006
SWED.82–88	−0.015	0.014	−0.00001	−0.00004	0.0029	−75.9	0.002	−0.025	0.039	0.00002	−0.00003	0.0061	−224.9	0.004
AVIVA.75–81	−0.029	0.023	−0.00030	−0.00020	0.0064	−31.8	0.005	−0.101	0.093	0.00018	−0.00005	0.0169	−374.3	0.010
INVL.75–81	−0.010	0.010	0.00002	−0.00004	0.0029	−66.6	0.002	−0.030	0.053	−0.00025	−0.00010	0.0075	−73.7	0.005
LMNR.75–81	−0.020	0.014	0.00032	−0.00003	0.0044	−133.4	0.004	−0.068	0.075	0.00000	−0.00007	0.0115	−166.7	0.006
SEB.75–81	−0.020	0.014	−0.00002	−0.00009	0.0035	−41.2	0.003	−0.060	0.078	−0.00019	−0.00011	0.0113	−106.1	0.006
SWED.75–81	−0.015	0.014	−0.00007	−0.00004	0.0029	−77.6	0.002	−0.025	0.039	−0.00005	−0.00003	0.0061	−236.6	0.004
AVIVA.68–74	−0.026	0.021	−0.00028	−0.00021	0.0059	−27.8	0.005	−0.089	0.080	0.00023	−0.00004	0.0146	−395.5	0.009
INVL.68–74	−0.009	0.009	0.00003	−0.00005	0.0027	−56.4	0.002	−0.027	0.049	−0.00030	−0.00009	0.0067	−71.3	0.004
LMNR.68–74	−0.020	0.014	0.00031	−0.00002	0.0044	−267.8	0.004	−0.068	0.075	0.00000	−0.00008	0.0114	−144.8	0.006
SEB.68–74	−0.019	0.013	0.00000	−0.00005	0.0033	−60.9	0.002	−0.056	0.071	−0.00015	−0.00009	0.0103	−112.8	0.006
SWED.68–74	−0.015	0.014	−0.00005	−0.00004	0.0029	−78.1	0.002	−0.023	0.039	0.00003	−0.00002	0.0059	−237.4	0.004
AVIVA.61–67	−0.014	0.011	−0.00003	−0.00007	0.0031	−47.7	0.003	−0.046	0.039	0.00005	0.00000	0.0075	−2279.4	0.004
INVL.61–67	−0.006	0.005	0.00011	−0.00004	0.0017	−44.7	0.001	−0.018	0.031	−0.00012	−0.00005	0.0040	−78.5	0.002
LMNR.61–67	−0.013	0.010	0.00008	−0.00004	0.0029	−76.0	0.002	−0.041	0.045	0.00007	0.00000	0.0070	−1616.2	0.003
SEB.61–67	−0.017	0.016	−0.00026	−0.00010	0.0046	−46.5	0.004	−0.062	0.055	0.00004	−0.00003	0.0086	−325.3	0.004
SWED.61–67	−0.009	0.009	−0.00003	−0.00005	0.0020	−41.1	0.002	−0.015	0.029	0.00000	0.00001	0.0039	612.5	0.003
AVIVA.54–60	−0.007	0.006	0.00005	0.00002	0.0016	84.7	0.001	−0.024	0.019	−0.00005	0.00000	0.0038	−1831.1	0.002
INVL.54–60	−0.003	0.002	0.00003	−0.00001	0.0006	−64.6	0.000	−0.006	0.009	0.00004	0.00000	0.0012	−975.3	0.001
LMNR.54–60	−0.006	0.005	−0.00011	−0.00012	0.0015	−12.6	0.001	−0.014	0.016	0.00015	0.00001	0.0025	271.1	0.002
SEB.54–60	−0.007	0.006	−0.00008	−0.00008	0.0022	−28.3	0.002	−0.027	0.023	−0.00003	−0.00001	0.0035	−345.8	0.001
SWED.54–60	−0.027	0.029	−0.00010	−0.00012	0.0026	−22.6	0.001	−0.006	0.017	0.00009	0.00007	0.0020	29.5	0.001

. A Kruskal–Wallis test confirmed that there are no significant differences between medians in periods A and B for all of the funds analysed. However, this cannot be said about the variability of tracking differences in periods A and B. According to a Fligner–Killeen test, variances are significantly different (with $p<0.05$) for nearly all funds when we compare variances in periods A and B. However, for SEB.61–67 and SEB.54–60, variances are equal in both time periods (A and B). This can also be seen from Figure A2 and Figure A3 provided in Appendix A. Finally, the correlations between tracking differences in periods A and B are provided in Appendix A, Figure A4). According to these results, there are no significant changes in correlation between nearly all funds of the same manager. Exceptions may be seen only in the 54–60 age group, where the correlation slightly increased, and for SEB managers, where correlations sharply decreased. Generally speaking, it may be said that correlations/relations between all tracking differences became stronger, which indicates that the pension funds market behaved similarly to how it did previously. Moreover, such an observation is in line with the findings of other studies (see [41] or [42]).

6.2. Almost Stochastic Dominance between Pension Fund and Benchmark

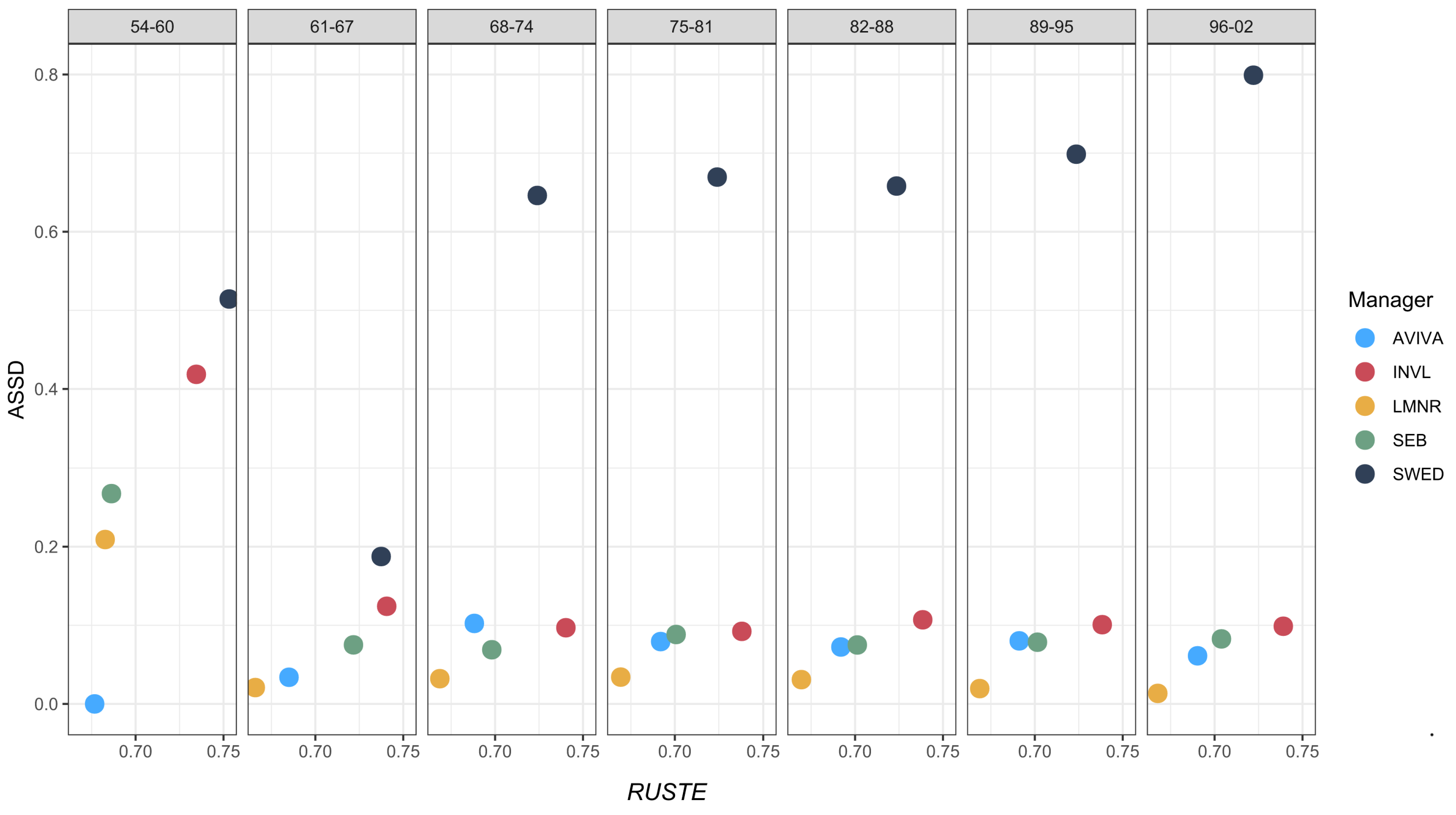
The analysis uses testing and stochastic dominance rules (see Section 5.1) to determine the PFs that dominated their benchmark. For this purpose, we first applied FSD using Equation (1), which resulted in no pairs satisfying this rule. After the SSD was tested using Equation (2), only one fund, i.e., AVIVA.54–60, was found, which dominated its benchmark. As stochastic dominance rules are highly restrictive in necessary and sufficient conditions, we proceeded with almost stochastic dominance rules. 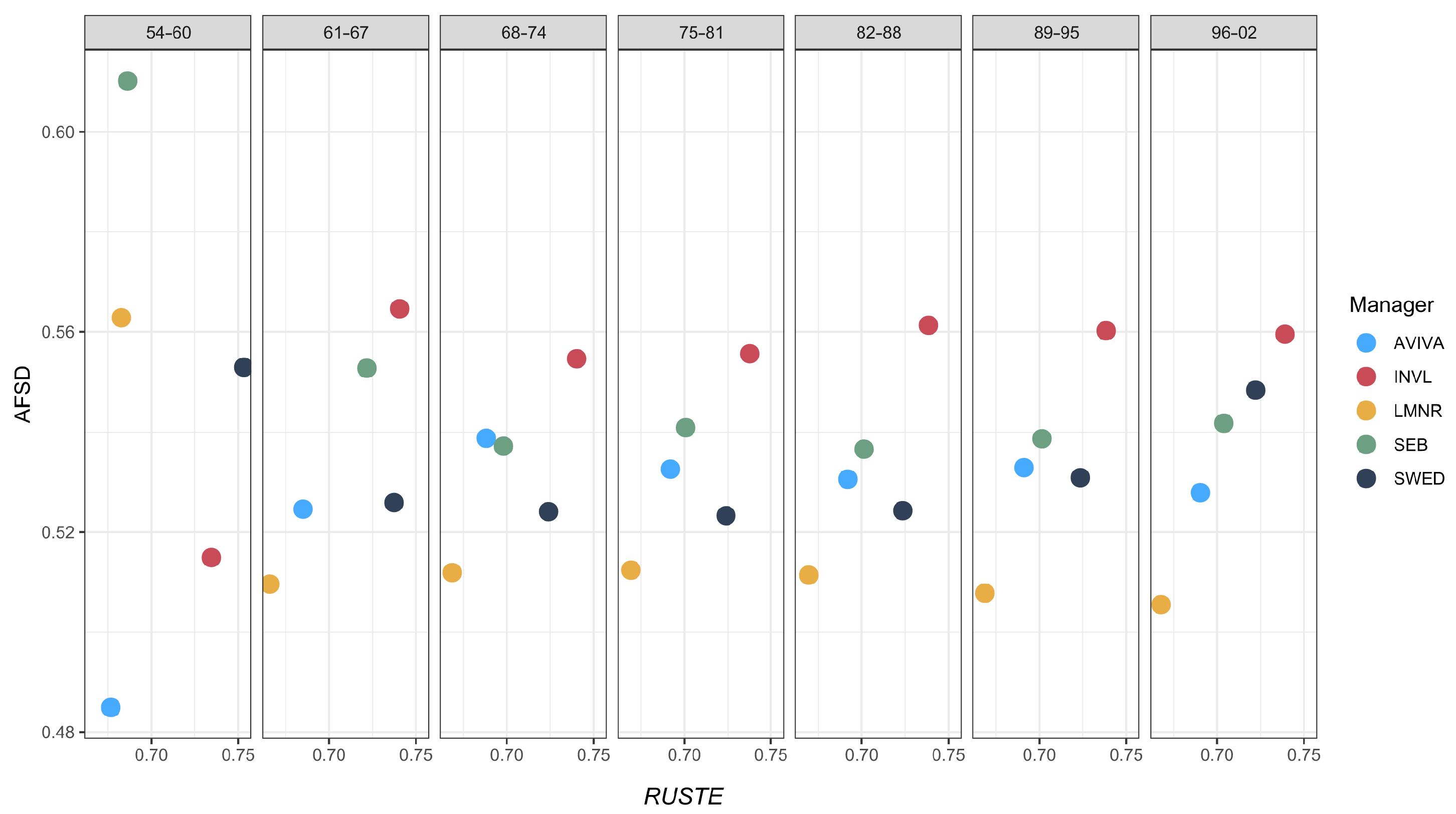In the following, Figure 7 demonstrates the values of ASSD obtained for each PF against the estimated RUSTE ratio.

Figure 7 reveals some interesting findings. First, the values of ASSD approaching 0 indicate a better dominance over the benchmark. From this perspective, we can observe that LMNR funds in all age groups, except 54–60, resulted in the lowest values of ASSD. Notably, AVIVA, SEB and INVL funds are comparatively close to LMNR funds. In contrast, SWED funds with ASSD greater than 0.5 suggest no almost second-order dominance with respect to their benchmark. In particular, the arrangement of funds belonging to the age group 54–60 exhibits different behaviour, whereby the AVIVA fund achieved 0, indicating a full SSD. This fund is then followed by LMNR, SEB, INVL and SWED. Another observation relates to each fund’s position against the ratio of SemiStDev to StDev. In most cases, with the exception of the SWED funds, smaller values of ASSD are observed for smaller values of RUSTE, and vice versa. Comparatively, the results of AFSD are provided in the Appendix B, Figure A5. It can be observed that AFSD values range around 0.5, indicating that there is no dominance with respect to the first rule of almost stochastic dominance. Now, the question is how the results of ASSD would differ as a consequence of the COVID-19 pandemic. Figure A6 in the Appendix B reveals that, in most cases, we observe the lower values of ASSD in period B compared to period A. This could suggest that PFs in general successfully recovered after the huge drop and even more often outperformed their benchmark. Specifically, LMNR funds suggested for individuals born in 1961 or later demonstrated an exceptionally stable performance, as the results from periods A and B coincide with the results observed for the entire period.

6.3. Analysis of DTI

In the table below, we can see the given values of DTI (within the age group) based on ASSD and the ranking (within the age group/overall) of funds for the entire period (A + B) and periods A (1 January 2019–28 February 2020) and B (1 March 2020–13 May 2021). The funds are grouped according to the birth years of the target participants.

According to the ranking based on the DTI ratio given in

Table 5. Values of DTI (within the age group) based on ASSD and ranking of funds for the entire period (A + B) and periods A and B. The funds are grouped according to the birth years of the target participants.

Fund	RUSTE			$1-\mathit{\epsilon }$			DTI Ratio			Rank
	A + B	A	B	A + B	A	B	A + B	A	B	A + B	A	B
AVIVA.96–02	0.690	0.679	0.690	0.9388	0.7417	0.9931	0.6481	0.5039	0.6857	3/16	2/11	2/13
INVL.96–02	0.739	0.691	0.746	0.9012	0.4821	0.9513	0.6660	0.3332	0.7094	1/5	3/21	1/4
LMNR.96–02	0.668	0.670	0.667	0.9866	0.9936	0.9898	0.6587	0.6656	0.6601	2/9	1/3	4/24
SEB.96–02	0.704	0.674	0.707	0.9173	0.3421	0.9453	0.6457	0.2305	0.6683	4/20	4/25	3/22
SWED.96–02	0.722	0.680	0.730	0.2009	0	0.3990	0.1451	0	0.2915	5/35	5/30	5/35
AVIVA.89–95	0.691	0.678	0.691	0.9198	0.6664	0.9935	0.6357	0.4521	0.6866	4/24	2/14	2/12
INVL.89–95	0.738	0.693	0.745	0.8992	0.5817	0.9469	0.6640	0.4031	0.7053	1/6	3/17	1/5
LMNR.89–95	0.669	0.671	0.668	0.9805	0.9938	0.9828	0.6556	0.6673	0.6565	2/10	1/2	4/26
SEB.89–95	0.702	0.677	0.704	0.9215	0.5875	0.9538	0.6464	0.3978	0.6711	3/18	4/18	3/21
SWED.89–95	0.724	0.682	0.732	0.3014	0	0.5624	0.2181	0	0.4117	5/34	5/30	5/34
AVIVA.82–88	0.692	0.680	0.692	0.9276	0.6816	0.9948	0.6419	0.4634	0.6883	4/21	2/12	2/10
INVL.82–88	0.738	0.697	0.744	0.8930	0.6427	0.9448	0.6594	0.4480	0.7032	1/8	3/15	1/8
LMNR.82–88	0.669	0.672	0.669	0.9691	0.9880	0.9749	0.6488	0.6635	0.6522	2/13	1/5	4/27
SEB.82–88	0.701	0.678	0.703	0.9250	0.5822	0.9567	0.6487	0.3944	0.6729	3/14	4/19	3/19
SWED.82–88	0.724	0.681	0.732	0.3419	0.0001	0.6361	0.2474	0.0001	0.4655	5/32	5/29	5/32
AVIVA.75–81	0.692	0.679	0.692	0.9207	0.6675	0.9937	0.6371	0.4532	0.6876	4/23	3/13	2/11
INVL.75–81	0.738	0.696	0.744	0.9077	0.7317	0.9433	0.6697	0.5095	0.7017	1/2	2/9	1/9
LMNR.75–81	0.669	0.672	0.668	0.9659	0.9814	0.9751	0.6464	0.6600	0.6518	2/19	1/6	4/28
SEB.75–81	0.701	0.670	0.703	0.9117	0.5143	0.9566	0.6389	0.3446	0.6727	3/22	4/20	3/20
SWED.75–81	0.724	0.681	0.732	0.3305	0	0.6266	0.2393	0	0.4589	5/33	5/30	5/33
AVIVA.68–74	0.688	0.676	0.688	0.8976	0.6012	0.9941	0.6177	0.4062	0.6840	4/25	3/16	2/14
INVL.68–74	0.740	0.699	0.747	0.9031	0.7628	0.9432	0.6685	0.5330	0.7042	1/3	2/8	1/7
LMNR.68–74	0.669	0.671	0.668	0.9679	0.9923	0.9707	0.6471	0.6654	0.6486	3/17	1/4	4/29
SEB.68–74	0.698	0.672	0.701	0.9311	0.4167	0.9622	0.6500	0.2799	0.6740	2/12	4/22	3/17
SWED.68–74	0.724	0.683	0.732	0.3539	0	0.6897	0.2562	0	0.5052	5/31	5/30	5/31
AVIVA.61–67	0.685	0.684	0.684	0.9661	0.7436	0.9992	0.6618	0.5084	0.6831	2/7	2/10	4/16
INVL.61–67	0.741	0.686	0.749	0.8758	0.3529	0.9415	0.6486	0.2422	0.7049	4/15	3/24	3/6
LMNR.61–67	0.666	0.663	0.665	0.9792	0.9600	0.9976	0.6520	0.6363	0.6636	3/11	1/7	5/23
SEB.61–67	0.722	0.727	0.719	0.9249	0.1332	0.9935	0.6675	0.0969	0.7143	1/4	4/27	2/3
SWED.61–67	0.737	0.682	0.749	0.8125	0.0038	1.0000	0.5992	0.0026	0.7485	5/26	5/28	1/2
AVIVA.54–60	0.677	0.690	0.674	1	0.9706	0.9994	0.6767	0.6702	0.6738	1/1	1/1	3/18
INVL.54–60	0.735	0.679	0.746	0.5814	0	0.7523	0.4271	0	0.5612	4/29	4/30	5/30
LMNR.54–60	0.683	0.665	0.684	0.7909	0.3855	0.9988	0.5399	0.2564	0.6834	2/27	2/23	2/15
SEB.54–60	0.686	0.714	0.674	0.7325	0.1395	0.9772	0.5027	0.0996	0.6585	3/28	3/26	4/25
SWED.54–60	0.753	0.732	0.782	0.4856	0	1.0000	0.3657	0	0.7820	5/30	4/30	1/1

, the best performance could be achieved if any investor pre-COVID-19 accumulated their pension in the AVIVA.54–60 fund and, after it, if they switched to the SWED.54–60 fund. However, bearing in mind that participants do not change their pension fund particularly often, the best choice would be to accumulate in the AVIVA.54–60 pension fund, as it has the highest rank in a long period and on average as well. It must be noted that INVL pension funds in general may be ranked on top (see

Table 6. Ranking of pension fund managers in different periods.

Fund Manager	Average Rank			Final Ranking
	A + B	A	B	A + B	A	B
AVIVA	16.7	11.0	13.4	3	2	2
INVL	9.7	17.7	9.9	1	3	1
LMNR	15.1	7.1	24.6	2	1	5
SEB	16.9	22.4	18.1	4	4	3
SWED	31.6	29.6	24.0	5	5	4

), as they have the greatest mean rank among all pension fund managers. The second rank could be assigned to LUMINOR funds. Third and fourth ranks according to our ratio could be assigned, respectively, to the AVIVA and SEB pension funds. The lowest rank can be assigned to SWED pension funds as they have a very low performance ranking (with some exceptions in recovery period B).

With regard to the age group performance, it must be noted that the group of 61–67 funds has the highest rank compared to other groups in the long term and after the COVID-19 period. However, during and pre-COVID-19, the best performance was observed in the 75–81 group, whereas the 61–67 group performed quite poorly in this period. Unsurprisingly, the 54–60 group performed poorly, but it was unexpected that the correlation between the age of the pension system participant and our ranking was weak.

7. Discussion

The role of regulators, in both practice and research, is becoming increasingly important as new mechanisms are starting to be implemented to protect stakeholders and promote financial stability. At the end of 2018, to protect pension fund participants and their holdings, the Bank of Lithuania regulated a mandatory switch to life-cycle pension funds. As the European Union does not regulate member state pension fund systems, each member state is free to locally decide upon the set-up of its pension system. As a number of research studies show, similar pension funds managed by different companies that are operating under the same conditions show different performance results. Most studies focus only on the observed pension fund’s under-performance that occurs due to reasons such as changes in regulation or strategic asset selection, whereas there exists only a limited amount of research on the performance benchmark or tracking error.

Different pension schemes face a number of risks to varying degrees. The historical data of the PF value show how PF managers were able to handle these risks. In this paper, the theory of stochastic dominance, serving as the basis for the research methodology, was used to estimate the PFs’ performance in relation to their benchmarks. Focusing on the first two SD rules, the dominance-tracking index (DTI) has been proposed as a way to include two aspects of risk assessment, i.e., the benchmark outperformance in terms of almost stochastic dominance and the strength of benchmark replication by measuring the tracking error.

According to DTI, funds can be ranked individually (overall ranking or within age group) or by using aggregation techniques, e.g., ranking PF managers. The first of these helps to determine which fund will be preferable among pension system participants at a particular age, whereas the second provides a long-term recommendation for passive pension system participants. Based on the results, the fund AVIVA.54 –60 should be the most favoured fund for all participants, as it outperforms and tracks the benchmark most effectively. However, the most favoured fund (and manager) differs depending on the age group. For young pension system participants, e.g., those born from 1968–2002, it is recommended that funds be chosen from the INVL manager. Comparatively, the most favoured fund for participants born from 61–67 is SEB.61–67, whereas, for the age group 54–60, AVIVA.54–60 is recommended. Notably, these findings are not robust at the time of the financial crisis (COVID-19). For instance, in period A, the fund AVIVA.54–60 tracks its benchmark best, but, in period B, the fund SWED.54–60 becomes a leader among all of the funds analysed. Regarding the age group, it must be noted that, for nearly all pension system participants (those born from 1961–2002), the LMNR funds are ranked as the best in period A. However, in period B, the landscape becomes similar to the results obtained for the entire period, where INVL funds have been on top. The only difference is that SWED funds from the age groups 61–67 and 54–60 occupy the dominant position.

As DTI is influenced by two determinants, let us consider them separately. The most interesting result from the SD analysis shows that all PF managers, except SWED, achieved an almost stochastic dominance of the second order (ASSD), roughly ranging in the interval (0; 0.1) for individuals born in 1961 or later, where the lower value indicates a superior dominance over the benchmark. Specifically, the lower values of ASSD are observed for a slightly smaller relative upper semi-tracking error (RUSTE) ratio, which could be related to a PF manager as a distinguishing feature. Another story could be told about PFs managed by SWED. Specifically, the results in terms of ASSD suggest that the performance of SWED funds is much worse with respect to benchmarks assigned to the PF. By contrast, conservative funds, covering the 54–60 age group, revealed an entirely different view in which the values of ASSD were considerably worse for all managers except for AVIVA, which resulted in a full SSD. Comparatively, the findings of the tracking error show that the observed values of RUSTE are more related to the PF manager than the age group of the PF, which is an unexpected outcome. More specifically, the greatest RUSTE is observed for the INVL and SWED funds, whereas the smallest is observed for the LMNR and AVIVA funds. This indicates how PF managers keep track of their benchmarks. Finally, after two approaches, i.e., almost stochastic dominance and tracking error, were combined together into DTI, it appeared that there is no clear leader among AVIVA, INVL, LMNR and SEB for the individuals born in 1961 or later, as their values of DTI are slightly larger than 0.6. In the meantime, SWED funds have managed to catch up with the other managers in the 61–67 age group. Among the conservative funds, the clear leader is the AVIVA fund, which outperformed its closest competitor by 25% in terms of DTI.

A closer inspection of Table 2 shows that 17 funds resulted in an average daily return of at least 0.0006, where the funds from different age groups (those born in 1975 or later) managed by SEB, LMNR, INVL and SWED could be identified. By contrast, the lowest profitability in terms of the average daily return is observed for conservative funds, with the smallest value estimated for the AVIVA fund, which has been identified as the dominating fund with respect to its benchmark. This contradiction between profitability and stochastic dominance with respect to the benchmark for some funds could be explained by the existing differences between benchmarks used by PF managers. In this context, we raise a key question/finding from our analysis: whether selecting the benchmark with some degree of freedom is an effective way to regulate a PF and report its results to the pension system’s participants. In other words, PF managers, by establishing more ambitious benchmarks, may present a distorted picture of the reality of its performance compared to some benchmark, and vice versa.

To conclude, DTI is a very useful measure for PF performance assessment because of how it tracks the benchmark. The suggested methodology in the paper could be easily generalised and applied in other regional markets. The main requirement is to select a benchmark for the assessment of the investment fund’s performance. One may choose a benchmark established by the fund manager (as is the case in Lithuania) or select another external benchmark, e.g., S&P 500. Nevertheless, DTI is not the best way to compare funds to each other and it does not measure systematic performance. Such issues could be solved by finding the best and the worst benchmarks existing in the market (in terms of SD) and then integrating them into a single multivariate ratio. Such a ratio could help a participant of a pension system to evaluate how their PF performs in comparison to other funds globally. From the computational perspective, DTI calculation includes the estimation of almost stochastic dominance and the calculation of the tracking error. As such, the main requirement for DTI application is to have a sufficient amount of historical data representing the PF value and benchmark evolution. For future research, the proposed methodology could be modified by including several benchmarks in the main formula.