Adaptive Control Strategy and Model of Gas-Drainage Parameters in Coal Seam

Abstract

For a long time, the serious mismatch between negative pressure and drainage parameters of underground gas drainage has been the main reason for the standing engineering problems in coal mines, such as low gas drainage concentration, fast decay, and low-utilization rate. Aiming at these problems, an innovative method by adding micro-frequency conversion drainage pumps and electronically controlled valves at the key nodes of the conventional pipe network system of gas drainage and the joint quantitative regulation of underground regulation facilities and surface drainage pumps based on the intrinsic correlation between the drainage parameters and negative pressure is proposed in this paper to solve the difficulty of how to regulate increasing pressure or resistance in the on-site gas-drainage system and to realize energy matching in the whole drainage system on demand. For this method, the study further defines the safety and efficiency criteria of gas drainage, proposes the adaptive control strategy of gas-drainage parameters, and establishes the adaptive control model based on particle swarm optimization. The model took the safety and efficiency criteria of gas drainage as the constraint conditions and the maximum gas-drainage flow or concentration as the objective function to adaptively adjust the operating conditions of drainage pumps, micro-frequency conversion drainage pumps, and electric control valves to realize the adaptive regulation of gas-drainage parameters. Finally, based on the adaptive control strategy and model of gas-drainage parameters, the numerical simulation research was carried out through Comsol with Matlab. The results show that the gas-drainage concentration and high-concentration drainage period can be increased many times, and the adaptive drainage parameters of valves and micro pumps can be adjusted intelligently, which provides a theoretical basis for the intelligent field implementation of gas.

1. Introduction

Gas disaster is a huge threat to the safety of the production of coal mines [1,2]. As a fundamental measure of gas-resource utilization and disaster prevention, gas drainage by boreholes has been widely applied in underground coal mines [3,4,5,6,7]. According to incomplete statistics, the gas-drainage system shows the serious “pathology” or “sub-health” operational characteristics. For example, in more than 75% of high-gas or coal-gas outburst mines in China, the concentration of gas drainage will decline to less than 10% in a short time [8,9,10,11]. The Safety Regulations in Coal Mine stipulates that when the concentration of gas drainage is less than 30%, it shall not be directly burned as gas. Especially when the gas concentration is between 5% and 16%, it may cause gas explosion accidents. In 2020, the amount of gas drainage was 12.8 billion cubic meters, but the utilization rate was only 44.8%, and most of the gas was directly discharged into the air after it was extracted, causing a serious waste of resources and greenhouse effect.

Negative pressure is a key factor affecting the concentration and flow of gas drainage. Whether the negative pressure is too large or too small, it will affect gas drainage [12,13]. Yang et al. [13] studied the correlation between the pure gas-flow rate and the negative pressure and proposed that the optimal negative pressure of the drilling hole was 40–45 kPa; Yin et al. [14] conducted a three-dimensional numerical simulation of gas drainage and believed that the influence of negative pressure on gas drainage was not obvious; Cheng et al. [15] carried out the research on the mechanism of negative pressure on gas drainage and its application in the utilization of gas resources. The study asserted that with the increase of drainage time, the effective of negative pressure gradually weakened, and reducing the negative pressure could effectively increase the gas concentration. Based on this, the technical measures of “grouping parallel” of drainage boreholes were proposed to reduce the negative pressure and improve the utilization of gas resources. The authors and some scholars believe that when the seal quality of boreholes is fixed, the negative pressure is positively correlated with the amount of air leakage from boreholes. The larger the negative pressure, the faster the gas drainage concentration decays, and it may even induce spontaneous combustion of coal or gas explosion; on the other hand, when the negative pressure is too small, the local resistance or the resistance along the way that exists in the borehole and the pipeline may not be overcome, which easily causes suffocation in pipelines and boreholes, and gas cannot be extracted out, or drainage efficiency becomes low [16,17,18].

In summary, gas drainage is a dynamic change process in coal mines. When the occurrence conditions of coal seam gas are different at diverse times and places, the required gas-drainage capacity and conditions are different, too. Therefore, the gas-drainage system should be dynamically regulated and coordinated through the setting of gas-drainage pump speed and valve opening at different locations of drainage pipeline so as to make the gas-drainage capacity and working environment provided by the gas-drainage system at each location match the actual demand. The connection structure of underground pipe network of gas drainage is a simple dendritic branch pipeline. Thus, the characteristic of the natural distribution of negative pressure is that the larger the negative pressure is along the drainage direction in the pipe network, which means that the negative pressure in the proximal area of the drainage pump is large, the smaller the negative pressure is in the remote area due to the loss of distance and local resistance. Therefore, the natural distribution of negative pressure makes it difficult to reasonably match the dynamic changes of the gas flow, concentration of the pipe network, and drainage characteristic parameters in the coal seam [10]. At present, the concentration and gas-flow regulation of the down-hole pipe network are mainly manually adjusted by experience, and the process is time-consuming, blind, and arbitrary, and the overall effect is not significant. The reason is largely due to the single monitoring means and low intelligence of the gas-drainage system, the manual regulation of gas-drainage parameters, the untimely and inaccurate system regulation, and the failure to regulate the gas-drainage parameters in real time according to the storage characteristics of coal gas and the dynamic changes of gas-drainage parameters, resulting in high energy consumption and low efficiency of the drainage system. In the context of this era, coal mine safety production needs to deeply integrate artificial intelligence, information control, and other technologies. The Guiding Opinions on Accelerating the Intelligent Development of Coal Mines issued by Order (2020) No. 283 of the Development and Reform Energy also clearly determines the direction of the intelligent development of coal mines. Intelligent drainage of gas is an inevitable trend in the development and utilization of coal mine gas resources.

2. Current Situation of Intelligent Gas Drainage

Intelligent gas drainage means to fully integrate information, automation, and intelligent technology into gas-drainage processes, and it could independently complete the gas-drainage operation with little or no human intervention. It can sense the working conditions of the system and the monitoring data of the drainage pipe network in real time, automatically analyze and evaluate the effect of gas drainage, and intelligently feed back and regulate the key devices according to the data change laws of negative pressure, flow, and concentration so as to achieve the goal of safe, efficient, and economic gas drainage [19].

Aiming at the regulation of gas-drainage parameters, many scholars have carried out in-depth research work from the aspects of surface pump transmission power, valve resistance increase in down-hole pipe network, and resistance optimization along the pipeline. Wang [20] proposed an early-warning system for automatic regulation of gas-drainage concentration, which realized the automatic adjustment of electric valves based on the principle of optimal negative pressure, and applied it on-site in the Jiulishan Mine of Coking Coal Group located in the eastern part of Jiaozuo Mining Area. In order to meet the automation needs of balancing the negative pressure of underground pumping, Li et al. [21] proposed the intelligent control system of the unattended gas-drainage pumping station based on WinCC to realize the automatic adjustment of the valve. Zhao [22] proposed an intelligent drainage method for coalbed methane based on fuzzy control of PLC, which regulates the flow of coalbed methane by adjusting the valve opening at different concentrations in the drainage pipeline. Li et al. [23] proposed the use of PLC as the core controller and the use of the hidden Markov model (HMM) to process and analyze the relevant data and adjust the opening position of the down-hole electric adjustment valve so as to make sure the gas-drainage concentration in the pipeline was always maintained within the scope of the drainage requirements. Ma et al. [24] carried out the research on the intelligent regulation model of gas drainage based on simple recurrent neural network (SimpleRNN) and model predictive control (MPC) and analyzed the influence of drainage pump and electronic control valve on negative pressure and how to automatically regulate the valve opening and pump power through the machine′s self-learning. Wang et al. [25] proposed a multi-objective optimization algorithm for the gas-drainage parameters in coal mine pipe network and realized the quantitative determination of the optimal pump speed, valve opening, and negative pressure of the drainage pipe network based on the steady-state model of pipeline gas flow. Zhou et al. [19] elaborated on the connotation and principle of intelligent gas drainage (Figure 1), established a parameter optimization model for a gas-drainage pipe network; clarified the adjustment indicators, constraints, and regulation strategies of target parameters; and provided a theoretical basis for the reasonable matching of negative pressure of a gas-drainage pipe network.

Not long ago, the authors established a gas–air binary gas transient flow model of a gas-drainage pipe network under active air leakage and revealed the dynamic evolution law of gas flow, concentration, and negative pressure in the pipe network and discussed the influence of negative pressure distribution characteristics and valve regulation on the drainage effect. Finally, it was concluded that the negative pressure would be gradually lost from close to far away from the drainage pump, and the natural distribution of negative pressure is difficult to reasonably match the gas flow and concentration of the pipe network as well as the dynamic changes of the characteristic parameters in the coal seam. By analyzing the existing negative pressure regulation mode of gas drainage, it was found that the above research is mainly aimed at the regulation of the surface drainage pump and valve, and it is difficult to increase the negative pressure of controlled branch or borehole fields by using valve control. If it is combined with a gas-drainage pump, it may cause excessive negative pressure of other branches and introduce new negative pressure-matching problems [10,26].

Focusing on the mismatch between the negative pressure of gas drainage, this paper studies the adaptive regulation mechanism and method of dynamic parameters of gas drainage in the underground drainage pipe network, which provides theoretical and technical support for the intelligent on-demand regulation of gas-drainage parameters.

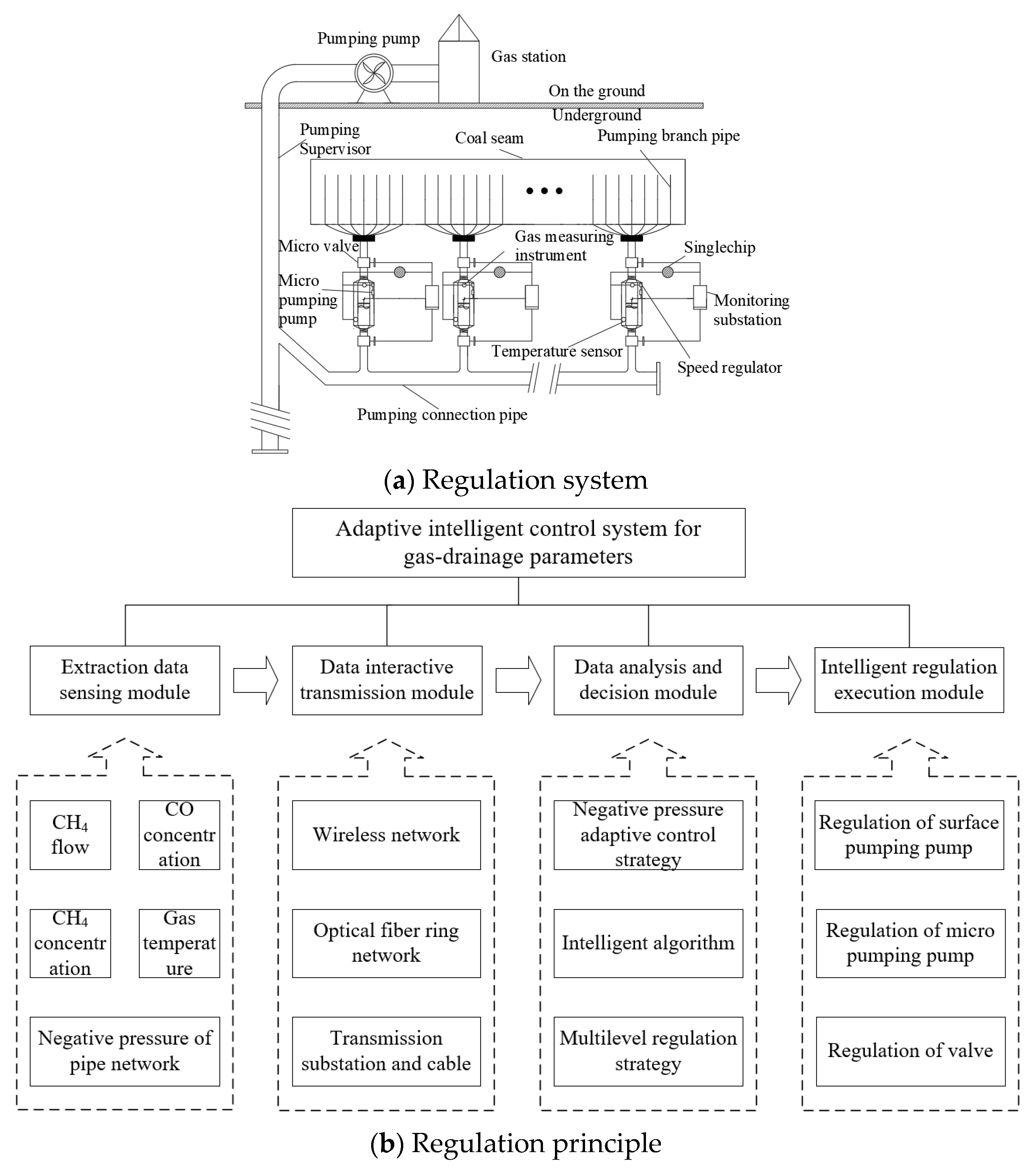
3. Adaptive Regulation Method and Strategy of Gas-Drainage Parameters

In view of the engineering problem that the negative pressure cannot match the dynamic changes of gas-drainage parameters on demand by only relying on the adjustment of valves and surface drainage pumps in the underground gas-drainage system and on the basis of the traditional use of the drainage pump (overall increase/decrease pressure) and electric control valve (increase/decrease resistance), it is proposed to install a micro-controllable drainage pump (local pressurization/decompression) at the key node or borehole field location of the drainage pipe network [27]. The system schematic is shown in Figure 2a. Based on the real-time calculation model of gas-drainage parameters in the pipe network, an artificial intelligence algorithm was used to study the dynamic matching relationship between the working parameters and the negative pressure of the pipe network, and an intelligent regulation algorithm of negative pressure was established to adapt the dynamic change of gas-drainage parameters in the pipe network. The algorithm realizes the intelligent regulation of negative pressure on demand and improves the safety, efficiency, and intelligence level. The schematic diagram of the regulation principle is shown in Figure 2b.

The adaptive control system of gas-drainage parameters is mainly composed of a small-diameter electronic control valve, large-diameter electronic control valve, comprehensive gas-measuring instrument, explosion-proof motor, frequency converter, micro-variable frequency drainage pump, etc. The comprehensive gas-measuring instrument is arranged at the entrance of each drainage area, which can monitor the negative pressure, flow, concentration, and other gas-drainage parameters in real time. The micro-variable frequency drainage pump and the small-diameter electronic control valve are also installed on the drainage connection pipe in turn as the regulatory element for the local drainage area to increase the resistance or pressure. One end of the single-chip microcomputer is connected to the comprehensive gas-measuring instrument, and the other end is connected to the frequency converter and the small-diameter electronic control valve. One end of the explosion-proof motor is connected to the frequency converter, the other end is connected to the miniature variable frequency drainage pump, and the single-chip is connected to a nearby substation. One end of the ring network switch is connected to the substation, the other end is connected to the monitoring center, the drainage connection pipe is connected to the drainage main pipe in turn, and the large-diameter electronic control valve and the comprehensive gas-measuring instrument are installed at the outlet of the main drainage pipe.

The main idea of adaptive intelligent regulation of drainage parameters is to lay corresponding sensors and negative pressure control devices in pumps, pipe networks, or borehole fields. Based on drainage safety-efficiency indicators, intelligent algorithms are used to adaptively adjust the working parameters of pumps, the electric control valve opening, and the micro-adjustable fan speed, and then, the negative pressure can self-adapt the characteristic parameters of gas drainage, thus improving the efficiency and safety of gas drainage.

The overall operation of the above-mentioned adaptive regulation ideas mainly relies on functional modules, such as drainage data sensing, data interaction and transmission, data analysis and decision, and intelligent regulation-execution modules:

(1) Drainage data sensing module: real-time obtaining of gas flow, gas concentration, and other parameters of pumps, pipe networks, and borehole fields.

(2) Data interaction and transmission module: realizing data transmission and interaction based on multi-source information interaction and transmission algorithm through wireless network, fiber optic ring network, transmission, etc.

(3) Data analysis and decision module: solving gas parameters of pipeline network in real time, automatically analyzing and evaluating gas-drainage effect; establishing adaptive adjustment algorithm of gas-drainage parameters to determine joint regulation scheme of drainage pumps, control valves, and micro fans; and issuing regulation commands with gas-drainage safety-efficiency index as the constraint.

(4) Intelligent regulation execution module: linkage regulating pump, control valve, and micro-motor based on the regulation command to achieve adaptive intelligent regulation of gas-drainage parameters and re-solving the information of the completed pipeline network parameters through the data interaction module and data analysis module to check the effectiveness of the execution effect in order to optimize the plan in time.

4. Adaptive Regulation Model and Criterion of Gas-Drainage Parameters

4.1. Pipe Network Flow Field Calculation Model

Based on the momentum equation, the continuity equation, and the solute diffusion equation for pipe flow, the transient flow-diffusion control equation for gas–air binary gases is [9]

$$\{\begin{array}{c}\frac{\partial \left(\rho \mathit{u}\right)}{\partial t\prime }+\rho \mathit{u}\nabla \mathit{u}=-\nabla p-f_{\mathrm{D}}\frac{\rho }{d_{\mathrm{h}}}\mathit{u}\left|\mathit{u}\right|+\mathit{F}\\ \frac{\partial \left(A\rho \right)}{\partial t\prime }+\nabla \left(A\rho \mathit{u}\right)=0\\ A\frac{\partial c_{{\mathrm{CH}}_4}}{\partial t\prime }+A\mathit{u}\nabla c_{{\mathrm{CH}}_4}=\nabla \left[A\left(D_{\mathrm{c}}+D_{\mathrm{a}}\right)\nabla c{\text{′}}_{{\mathrm{CH}}_4}\right]\end{array}$$

(1)

where $d_{\mathrm{h}}$ is the hydraulic diameter of pipeline, $c{\prime }_{{\mathrm{CH}}_4}$ is the ${\mathrm{CH}}_4$ molar concentration, u is the flow rate of gas, $D_{\mathrm{c}}$ is the diffusion coefficient, $D_{\mathrm{a}}$ is the gas-dispersion coefficient, ρ is the density of gas, $p$ is the pressure of gas, A is the cross-sectional area of pipeline, $f_{\mathrm{D}}$ is the Darcy friction coefficient, $F$ is the volume force term, and $t\prime$ is the time.

4.2. Regulation Criteria of Pipe Network Parameters

The principle of gas-drainage regulation is to seek the best negative pressure for drainage, that is, the on-demand matching of negative pressure for gas drainage. Taking the gas-drainage concentration and pure flow as the target constraints, the best negative pressure is to find the value corresponding to them under the target constraints.

In the process of gas drainage, it is first necessary to ensure that secondary disasters, such as spontaneous combustion of coal or gas explosion, are not triggered. That is, gas drainage needs to meet the following safety guidelines:

$$\{\begin{array}{c}T\le T_{\mathrm{L}}\\ c_{\mathrm{CO}}\le c_{\left(\mathrm{CO}\right)\mathrm{L}}\end{array}$$

(2)

where T is the temperature, c_CO is the CO gas concentration, and T_L and $c_{\left(\mathrm{CO}\right)\mathrm{L}}$ are, respectively, the critical values of the corresponding temperature and CO gas index. According to the relevant regulations on coal mine safety, $T_{\mathrm{L}}$ = 350 K, and $c_{\left(\mathrm{CO}\right)\mathrm{L}}$ = 24 ppm; once the $T$ or $c_{\mathrm{CO}}$ reaches critical value, the control valve should be immediately closed to stop drainage, and the causes should be checked and analyzed.

The healthy operation of gas drainage also needs to meet a certain gas concentration and flow value. That is, it needs to meet the following safety and efficiency criteria:

$$\{\begin{array}{c}{c}_{{\mathrm{CH}}_4}\ge c_{{(\mathrm{CH}}_4)\mathrm{L}}\\ Q_{{\mathrm{CH}}_4}\ge Q_{{(\mathrm{CH}}_4)\mathrm{L}}\end{array}$$

(3)

where $c_{{\mathrm{CH}}_4}$ and $Q_{{\mathrm{CH}}_4}$ are, respectively, the concentration and pure flow of gas drainage, and $c_{{(\mathrm{CH}}_4)\mathrm{L}}$ and $Q_{{(\mathrm{CH}}_4)\mathrm{L}}$ represent the critical concentration and pure flow rate of gas drainage, respectively. Under normal circumstances, the $c_{{(\mathrm{CH}}_4)\mathrm{L}}$ of borehole should not be less than 16%. The pure flow rate is taken according to the specific actual situation of the coal mine, and the flow standard stipulated by the Yangmei Group is that the pure gas flow of 100 m borehole should not be lower than 0.02 m³/min [28].

According to the principle of intelligent gas drainage, when the concentration or pure flow of gas drainage is less than the critical value, the corresponding maximum concentration or pure flow is used as the constraint conditions to seek the best negative pressure:

$$\{\begin{array}{c}{c}_{{\mathrm{CH}}_4}<c_{{(\mathrm{CH}}_4)\mathrm{L}}\\ Q_{{\mathrm{CH}}_4}<Q_{{(\mathrm{CH}}_4)\mathrm{L}}\end{array}\stackrel{\mathrm{Max}\left(c_{{\mathrm{CH}}_4}\right) or\mathrm{Max}( Q_{{\mathrm{CH}}_4})}{\to }f\left(p\right)$$

(4)

where $\mathrm{Max}(c_{{\mathrm{CH}}_4})$ and ${\mathrm{Max}(Q}_{{\mathrm{CH}}_4})$ are, respectively, the maximum CH₄ concentration and the pure flow maximum, and $f\left(p\right)$ is the adaptive control function of optimal negative pressure.

In summary, the adaptive regulation strategy of gas-drainage parameters (Figure 3) can be described as follows:

① Using CH₄ concentration, gas flow, negative pressure, CO concentration, and temperature sensors to monitor online the gas-drainage parameters of the pipe network or borehole field;

② If the gas temperature or CO concentration is greater than the safety threshold, it indicates that there is a hidden danger of drainage, so the relevant valves need to be closed immediately for inspection and treatment;

③ If the CH₄ concentration in the pipe network is greater than 30%, and the gas flow is too small, ${\mathrm{Max}(Q}_{{\mathrm{CH}}_4})$ needs to be taken as the goal of optimization and regulation. If the pure gas flow meets the requirements, it will no longer be regulated;

④ When the CH₄ concentration in the pipe network is less than 30%, $\mathrm{Max}(c_{{\mathrm{CH}}_4})$ needs to be taken as the goal of optimal regulation;

⑤ After this regulation, return to process ① for judgment;

⑥ When the concentration of CH₄ in the pipe network is less than 16%, the regulation is ended, and the drainage is stopped.

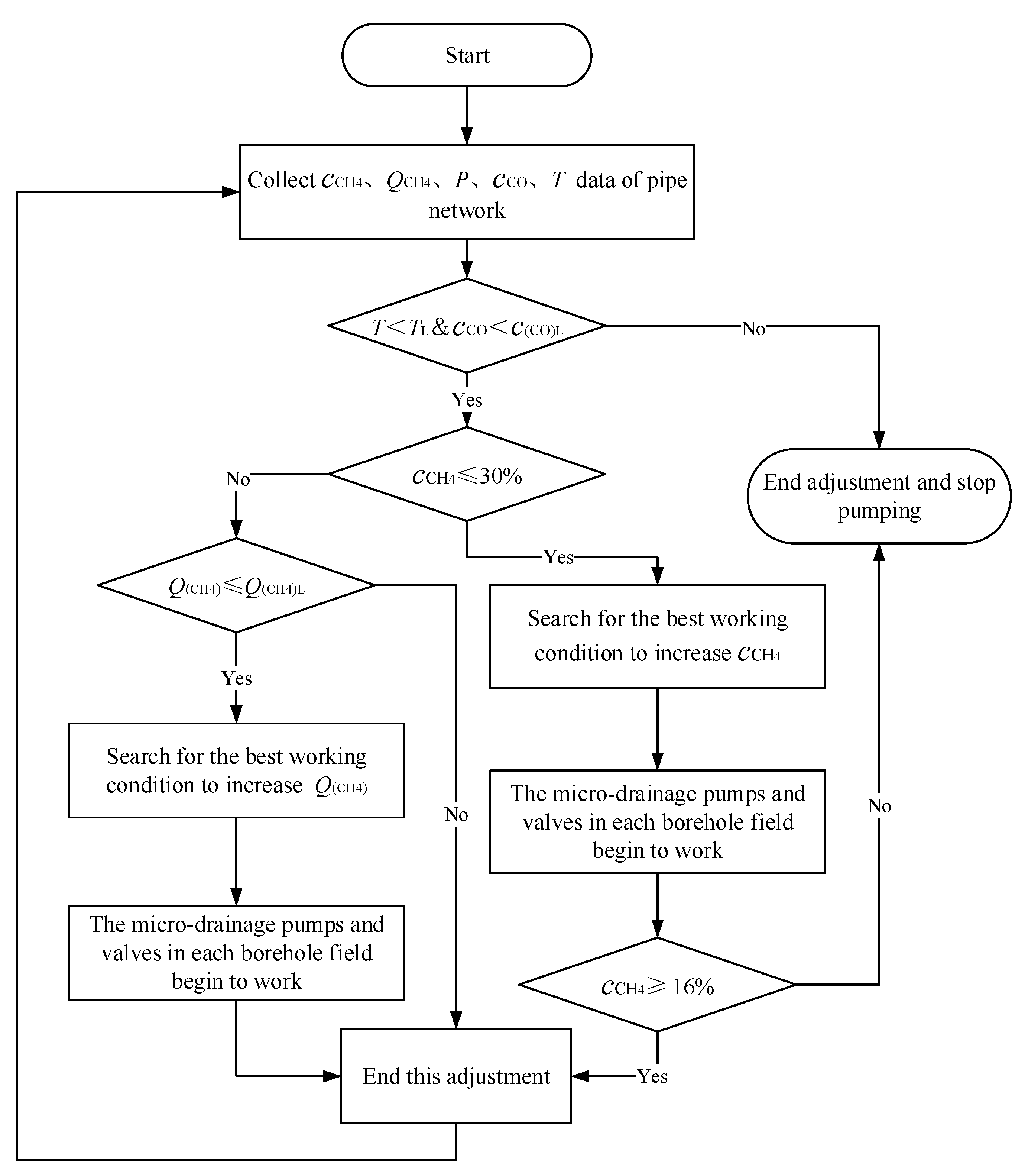
4.3. Adaptive Optimization Algorithm

Particle swarm optimization (PSO) is an intelligence optimization algorithm designed by simulating the predation behavior of birds [29] with the target of making all particles find the optimal solution in a multidimensional super-body. PSO has the advantages of fast iteration speed, simple structure, and fewer adjustment parameters, so it was selected as the optimal drainage condition optimization tool in this study. The main idea of optimization is to use PSO to iteratively search for the best valve opening or negative drainage pressure in the predetermined solution space after the system triggers the regulation mechanism and then upload the data to the regulation center as the regulation basis. Meanwhile, the micro-drainage pump and valve both affect the drainage effect through the change of negative pressure in the drainage pipeline. In the process of algorithm implementation, the negative pressure of the micro-drainage pump and valve opening are unified as the pressure drop $\mathsf{\Delta }P$ at their location in the pipeline. If the pressure drop is positive, it means that the valve opening is reduced. If the pressure drop is negative, it means that the micro-drainage pump is activated to increase the pumping negative pressure. Taking the regulation process of single borehole field as an example, the calculation flow of PSO is shown in Figure 4.

① Initialize population.

After triggering the regulation, PSO needs to determine the pressure-drop regulation range at the beginning and randomly assign the regulation scheme to each borehole field within the solution range. Each particle represents different regulation negative pressure. Then, the initial position of the particle $X_i$ and the selective range of the variation interval are revealed in Formula (5).

$$X_{\mathrm{i}}=\Delta P_{\mathrm{i}}$$

$$U_{\mathrm{i}}\le X_{\mathrm{i}}\le T_{\mathrm{i}}$$

(5)

where $i=\left(1,2,3.....N\right)$, $N$ is the selection of the number of particles, and the global optimization ability of PSO can be enhanced by increasing that. $U_i$ and $T_i$, respectively, represent the lower limit and upper limit of particles in the second particle swarm, which means the working condition range in which the pressure drop $\mathsf{\Delta }P$ can be regulated.

Fitness function, the basis of optimization, is established by the calculation model of pipe network flow field, which is used to evaluate the drainage effect of pipe network under this particle parameter. After comparing the fitness of all particles, the population history optimal position $GbestX$ and its fitness, which is called population history optimal solution $Gbest$, are recorded at this time, and the particle history optimal solution is initialized as Pb_X = X simultaneously.

② Start the iteration and update the particle swarm position.

The position of the particle with sequence number i is updated as

$$X_i^{k+1}=X_i^k+v_i^{k+1}$$

(6)

where k is the current number of iterations and speed $v_i^{k+1}$ is expressed by the formula as

$$v_i^{k+1}=w{v}_i^k+e_1{r}_1\left(Pb\_X_i^k-X_i^k\right) +e_2{r}_2\left(Gbest{X}^k-X_i^k\right)$$

(7)

where $w$ is the particle inertia factor, which indicates that the particle has the tendency to move in its own natural motion direction; $e_1$ and $e_2$ are the learning factor of particles representing the trend of particles approaching their best position in history and the best position in population history, which give the individual cognitive attributes and social attributes of particles, respectively; $r_1$ and $r_2$ are both two independent random parameters, which make the motion of particles more random and increase the possibility of global optimization.

In order to prevent the particles from skipping the optimal position directly due to too-large strides in the optimization process, the speed $v_{\mathrm{i}}$ of the particle needs to be limited as

$$v_{\min }\le v_{\mathrm{i}}\le v_{\max }$$

(8)

where $v_{min} and v_{max}$ represent the lower and upper limit of particle velocity, respectively.

③ Calculate the fitness of the particle at the current position and update $Gbest$, $GbestX$, and $\mathit{P}\mathit{b}\_\mathit{X}$ .

④ Determine the iteration result and decide whether to output the final result.

If the number of iterations ends, or the $Gbest$ meets the requirements at this iteration, jump out of the iteration and output the final result; otherwise, return to ② to continue the iterative calculation.

In addition, PSO does not set up a mutation process, so it is easy to fall into the local optimal solution, and finally, it cannot converge to the global optimal position. Therefore, the above classical PSO is improved, and the particle inertia factor $w$ in the velocity formula is changed from a fixed value to an alternating quantity with the number of iterations, i.e.,

$$w=w\_1-\left(w\_1-w\_2\right)*\left(k\right)/ger$$

(9)

where $w\_1 \mathrm{and} w\_2$ are the upper and lower limits of the inertia coefficient, respectively and $ger$ is the maximum number of iterations. In the early stage of iteration, the inertia factor $w$ is large; thus, the particles can move in the variable space at a large flight speed, which is beneficial in finding the global optimal value, and it is small in the later stage of iteration, which greatly improves the convergence of the algorithm.

5. Numerical Simulation of Gas-Drainage Adaptive Control

5.1. Physical Models and Boundaries

Figure 5a shows the simulation diagram of the intelligent gas-drainage system. The diameter of the main pipe is 600 m, the length of the transmission pipe from the ground to the underground is 600 m, and the length of the underground drainage main pipe is 600 m, which is connected with three borehole fields. Considering that 200 m is often used as an evaluation unit in engineering practice, we chose 200 m as the interval between adjacent borehole fields. The whole borehole field is abstractly simplified as a branch of pure gas-drainage pipeline and a branch of gas-leakage pipeline. Micro-drainage pumps and control valves are installed at each borehole field. The characteristic curve of the drainage pump is shown in Figure 5b.

A large number of surveys and field data shows that the gas-drainage volume will decline exponentially with time [25], such as

$$Q_{\mathrm{C}}=Q_{0}exp\left(-\beta ·t\right)$$

(10)

where $Q_{\mathrm{C}}$ is the gas amount emitted from the borehole, $Q_0$ is the initial gas flow of borehole, m³/s, $\beta$ is the CH₄ attenuation coefficient in the borehole, and t is the time.

The air leakage of the borehole is mainly caused by the lax sealing of borehole and the external air entering the borehole through cracks. The air leakage can be expressed as [10]

$$Q_{\mathrm{B}}=\frac{P_{\mathrm{amb}}-P_2}{R{\prime }_{\mathrm{i}}}$$

(11)

where $Q_{\mathrm{B}}$ is the amount of air leakage from the borehole; $P_{\mathrm{amb}}$ is the roadway atmospheric pressure, i.e., atmospheric pressure; $P_2$ is the inlet pressure of the branch pipe; and $R{\prime }_i$ is the air-leakage resistance coefficient of borehole i.

Since a borehole field is composed of n boreholes, the boundary conditions of gas flow and air flow at the inlet of drainage branch pipeline are obtained by combining Equations (10) and (11):

$$\{\begin{array}{c}{Q}_{{\mathrm{CH}}_4}=Q_{\mathrm{A}}·exp\left(-\beta ·t\right)\\ Q_{\mathrm{air}}=\frac{P_{\mathrm{amb}}-P_1}{R}\end{array}$$

(12)

where $Q_{{\mathrm{CH}}_4}$ is the gas pure flow emitted from the borehole field, m³/s; $Q_{\mathrm{A}}$ is the initial gas flow in the borehole field, m³/s; $Q_{\mathrm{air}}$ is the air leakage of the borehole field, m³/s; $P_1$ is the inlet pressure of the borehole field, Pa; and $R={(\sum _{i=1}^n{{R^{\prime }}_i}^{-1})}^{-1}$ is the air-leakage resistance coefficient of the borehole field, $\mathrm{Pa}\cdot \mathrm{s}\cdot {\mathrm{m}}^{-3}$.

Gas-concentration boundary of borehole field and borehole gas and air inlet:

$$\{\begin{array}{c}{c}_0=44.6\left(\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{/}{\mathrm{m}}^3\right)\\ c_1=0\left(\mathrm{m}\mathrm{o}\mathrm{l}\mathrm{/}{\mathrm{m}}^3\right)\end{array}$$

(13)

where $c_0 \mathrm{and} c_1$ are, respectively, expressed as the gas-concentration boundary conditions at the inlet of the branch pipe.

The operation characteristic curve of the gas-drainage pump at the outlet boundary of the pipe network can be expressed as

$$f\left(p_{\mathrm{sub}} ,Q_{\mathrm{sub}}\right)=0$$

(14)

where $p_{\mathrm{sub}}$ is the gas pressure at the inlet of the drainage pump, Pa; and $Q_{\mathrm{sub}}$ is the mixed gas flow at the inlet of the drainage pump, m³/s.

The pressure change $∆P$ caused by the valve has the following relationship with the valve loss coefficient [19]:

$$∆P=K\frac{\rho u^2}{2}$$

(15)

where K is the valve loss factor.

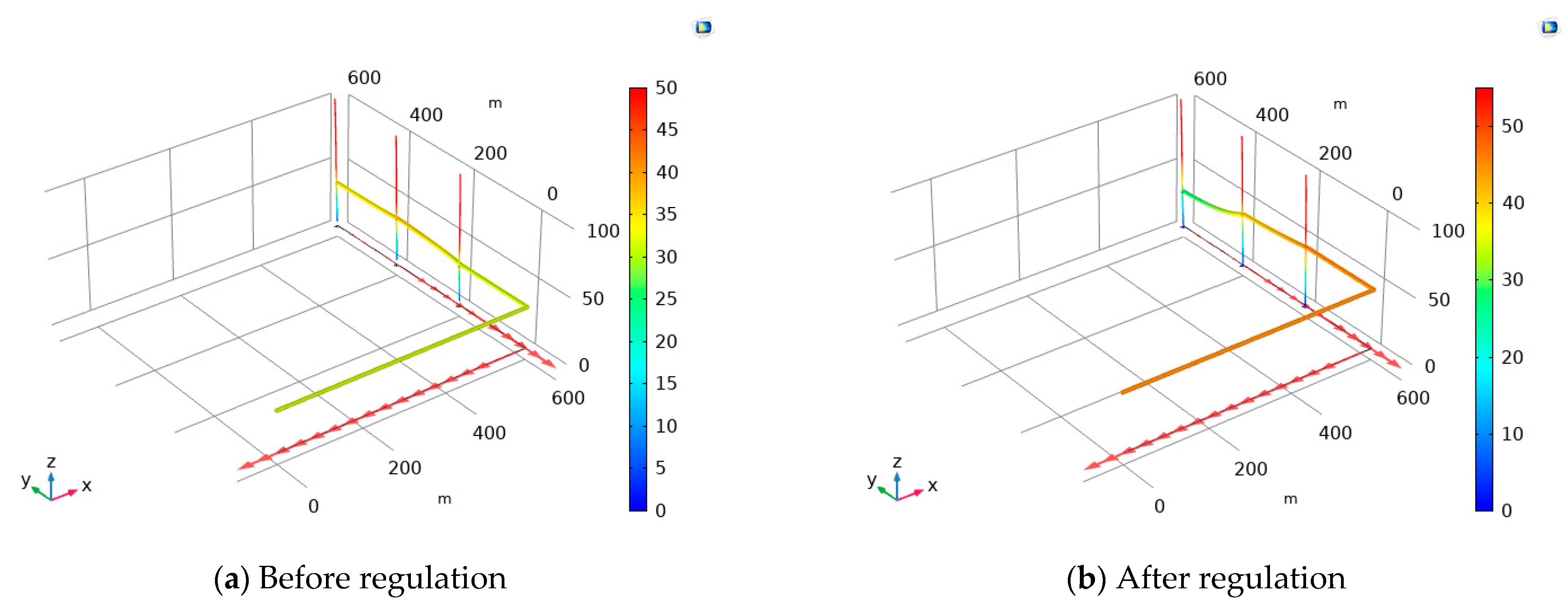
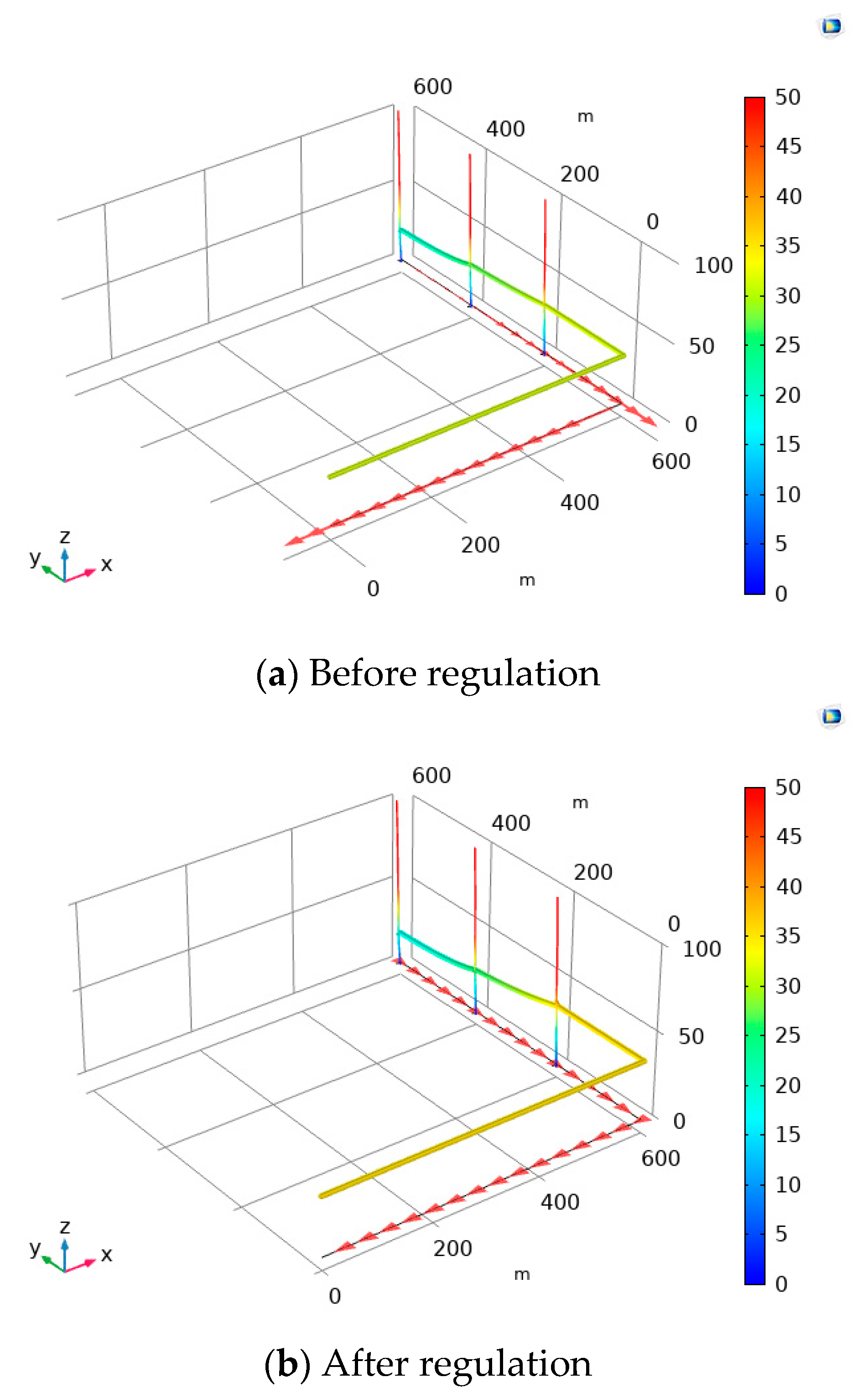
5.2. Numerical Calculation and Analysis

Model solving and particle PSO were implemented by Comsol with Matlab. The model was divided into 12,451 mesh vertices, with a maximum cell size of 0.1 m and a minimum cell size of 0.012 m. The regulatory threshold for gas concentration at the outlet of the pipe network was 30%, and it was set to stop regional pumping when the concentration is lower than 16%. The initial net gas flow of borehole field 1 was set to 0.12 m³/s, and gas attenuation coefficient ${\beta }_1$ was $0.005$ d⁻¹. The initial net gas flow of borehole field 2 was 0.155 m³/s, and the gas attenuation coefficient ${\beta }_2$ was $0.007 \mathrm{d}$ ⁻¹. The initial net gas flow of borehole field 3 was 0.13 m³/s, and the gas attenuation coefficient ${\beta }_3$ was $0.004$ d⁻¹. Air-leakage resistance coefficients of three borehole fields ($R_1,R_2,\mathrm{and} R_3$) were $\mathrm{100,000} \mathrm{Pa}\cdot \mathrm{s}\cdot {\mathrm{m}}^{-3}$. The other basic parameters of the model calculation are shown in

Table 1. Particle pipe network drainage parameters.

Parameter	Describe	Value
R	General gas constant, J/(mol·K)	8.314
T	Temperature, K	293.15
MCH4	Molar mass of CH4, kg/mol	0.016
MAir	Molar mass of air, kg/mol	0.029
e	Pipe surface roughness, m	1.7 × 10−4
μCH4	Dynamic viscosity of CH4, Pa·s	1.1 × 10−5
μAir	Dynamic viscosity of air, Pa·s	1.85 × 10−5
ρCH4	Density of CH4, kg/m3	0.717
ρAir	Density of air, kg/m3	1.29

.

The concentration calculation cloud map of the two adjustments is shown in Figure 6 and Figure 7. The geometric model is located on the XOY plane, and the Z-axis represents the gas concentration at this position. It can be seen that the concentration of the main pipeline has increased significantly after the adjustment. The gas concentration changes at the outlet of the pipe network before and after regulation are shown in Figure 8 and Figure 9, respectively.

As shown in Figure 8, when the gas concentration at the outlet of the pipe network decreased to 29.7%, lower than 30%, after 37 days of pumping, the maximum gas concentration was taken as the optimal solution target based on PSO, and the optimal valve loss coefficients of the three borehole fields were optimized to $K_1=3841,K_2=46,\mathrm{and}{K}_3=$ 0, and the negative pressure increment of the three borehole fields to control the pumping pump were $∆P_1=0,∆P_2=0,\mathrm{and}∆P_3=3000$. The gas concentration after regulation reached 42.7%, and the gas concentration increased by 13% as well compared with that before regulation.

The change curve of gas concentration in each borehole field before and after regulation is shown in Figure 9. In the first regulation, since borehole field 1 is closest to the main pumping pump, excessive negative pressure caused a large air leakage. The valve of borehole field 1 was regulated based on the adaptive regulation model. As a result, the valve loss coefficient was increased by 3841 compared with that before regulation, and the gas concentration was increased by 13%.

Borehole field 2 is slightly farther from the main drainage pump than borehole field 1, and thus, its negative pressure is smaller. Based on the adaptive regulation model, valve regulation is also selected for borehole field 2. The valve loss coefficient was increased by 46 compared with that before regulation, and the gas concentration was increased by 3%. Borehole field 3 is farthest from the main drainage pump, so there was insufficient negative pressure, which affected the gas flow. The drainage pump in borehole field 3 was regulated to overcome the resistance in the process of gas flow based on the adaptive control model. The micro-drainage pump was pressurized by 3000 Pa, but the increase of negative pressure caused the increase of air leakage, which reduced the gas concentration by 6%.

With the continuation of drainage, the working state of the valve and drainage pump remained unchanged after the first regulation, and the gas concentration continued to decline. When it reached 56 days, the gas concentration in the main pipeline was lower than 30% for the second time. At this time, based on the adaptive control strategy and model, taking the maximum gas concentration as the optimal solution goal, the optimal valve loss coefficient of the three borehole fields were ${\mathrm{K}}_1=5907$, ${\mathrm{K}}_2=0,$ and ${\mathrm{K}}_3=0$, and the negative pressure increase value of the three borehole fields to control the pumping pump were $∆{\mathrm{P}}_1=0$, $∆{\mathrm{P}}_2=1679,$ and $∆{\mathrm{P}}_3=5000$. The gas concentration after regulation increased to 35.8%, which was 6% higher than that before regulation.

In the second regulation, the adaptive regulation model regulated the valve of borehole field 1, so the negative pressure of borehole field 1 was still too high, and the gas leakage was too large. In order to reduce the gas leakage of borehole field1, the optimized valve loss coefficient was increased to 5907. At this time, the increase of valve loss coefficient reduced the gas leakage of borehole field 1, and the gas concentration of borehole field 1 was increased by 6%. Similarly, on the account of the adaptive control model, the pumping pump of borehole field 2 was regulated to overcome the flow resistance. The optimized valve loss coefficient was reduced to 0, and the negative pressure provided by the micro-pumping pump was increased by 1679 Pa, resulting in the increase of air leakage and the decrease of gas concentration by 2%. Based on the adaptive regulation model, the pumping pump of borehole field 3 was regulated, and the negative pressure increased to 5000 Pa, resulting in an increase in air leakage and a 6% reduction in gas concentration.

After 68 days of drainage, the gas concentration in the main pipeline was reduced to less than 30% for the third time. However, due to the continuous attenuation of the quantity of drainage, it was difficult to increase the gas-drainage concentration to more than 30% through intelligent regulation. In the later stage, it is necessary to further consider the pure amount of gas drainage as an optimization index for comprehensive intelligent regulation and control. When the gas concentration in the pipe network is lower than 16%, it can be considered to check the sealing quality of regional boreholes or close holes.

To summarize, after intelligent regulation, the gas concentration at the outlet of the pipe network increased significantly, and the drainage time with gas concentration above 30% was extended for 31 days. The valve-resistance coefficient, the increase of negative pressure in micro pump, and the increase of concentration increase at the outlet of pipe network of each borehole field after regulating twice are shown in the

Table 2. Parameter changes of each borehole field before and after regulation.

		Unregulated	First Regulation	Second Regulation
Time (d)		<37	37	56
Valve-resistance coefficient K and negative pressure increment of micro pump ∆P (Pa)	Borehole field 1	K1 = 0 ∆P1 = 0	K1 = 3841 ∆P1 = 0	K1 = 5907 ∆P1 = 0
	Borehole field 2	K2 = 0 ∆P2 = 0	K2 = 46 ∆P2 = 0	K2 = 0 ∆P2 = 1679
	Borehole field 3	K3 = 0 ∆P3 = 0	K3 = 0 ∆P3 = 3000	K3 = 0 ∆P3 = 5000
Concentration increase at outlet of pipe network (%)		0	13	6

below.

6. Conclusions

In view of the engineering problem that the conventional gas-drainage system cannot match the drainage negative pressure, an innovative gas-drainage system and an adaptive control model of gas drainage was proposed to realize the adaptive regulation of drainage parameters. The major conclusions are as follows:

(1) In order to solve the tough problem of adaptive matching on demand of the drainage energy in the whole pipe network, the innovative mode of installing micro-frequency conversion drainage pumps and electric control valves at the key nodes of the drainage pipe network was proposed.

(2) The safety-efficiency criteria and adaptive control strategy of gas drainage were put forward to maximize the drainage effect, and the operating conditions of the drainage pump, micro-frequency conversion drainage pump, and electric control valve were coordinated for adaptive regulation using a particle swarm intelligence algorithm.

(3) The numerical simulation research on the adaptive regulation of gas-drainage parameters was carried out, which realizes the multiple promotions of gas-drainage concentration and the significant extension of the high-concentration drainage period, providing a theoretical basis for the specific implementation of field engineering.