Experimental Study of the Fluctuating Wind Characteristics of Typhoon Jangmi Measured at the Top of a Building
Abstract
:1. Introduction
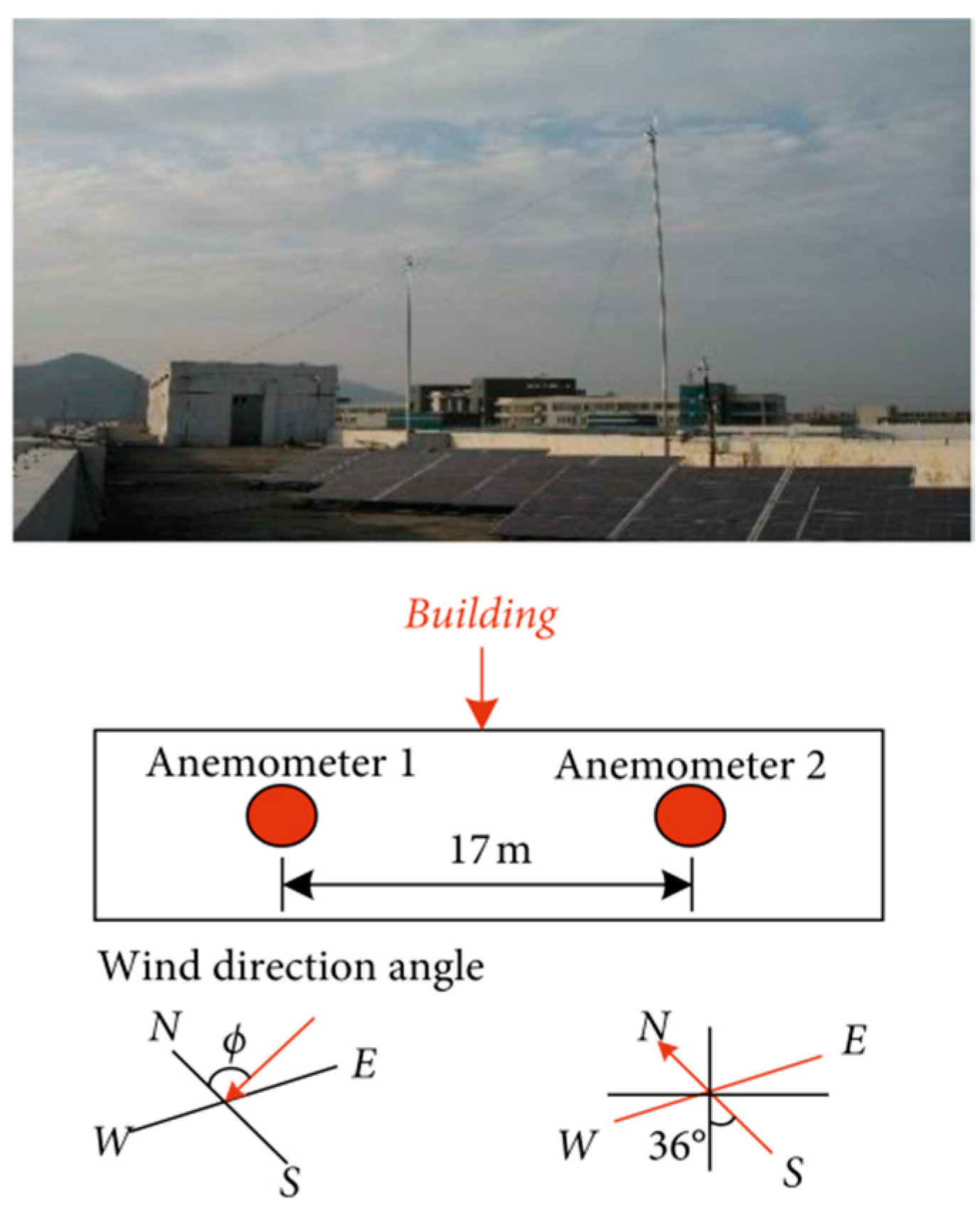
2. Typhoon Jangmi and Wind Speed Measurement
3. Research on the Wind Characteristics of the Typhoon
3.1. Mean Wind Speed and Direction
3.2. Turbulence Intensity
3.3. Gust Factor
3.4. Peak Factor
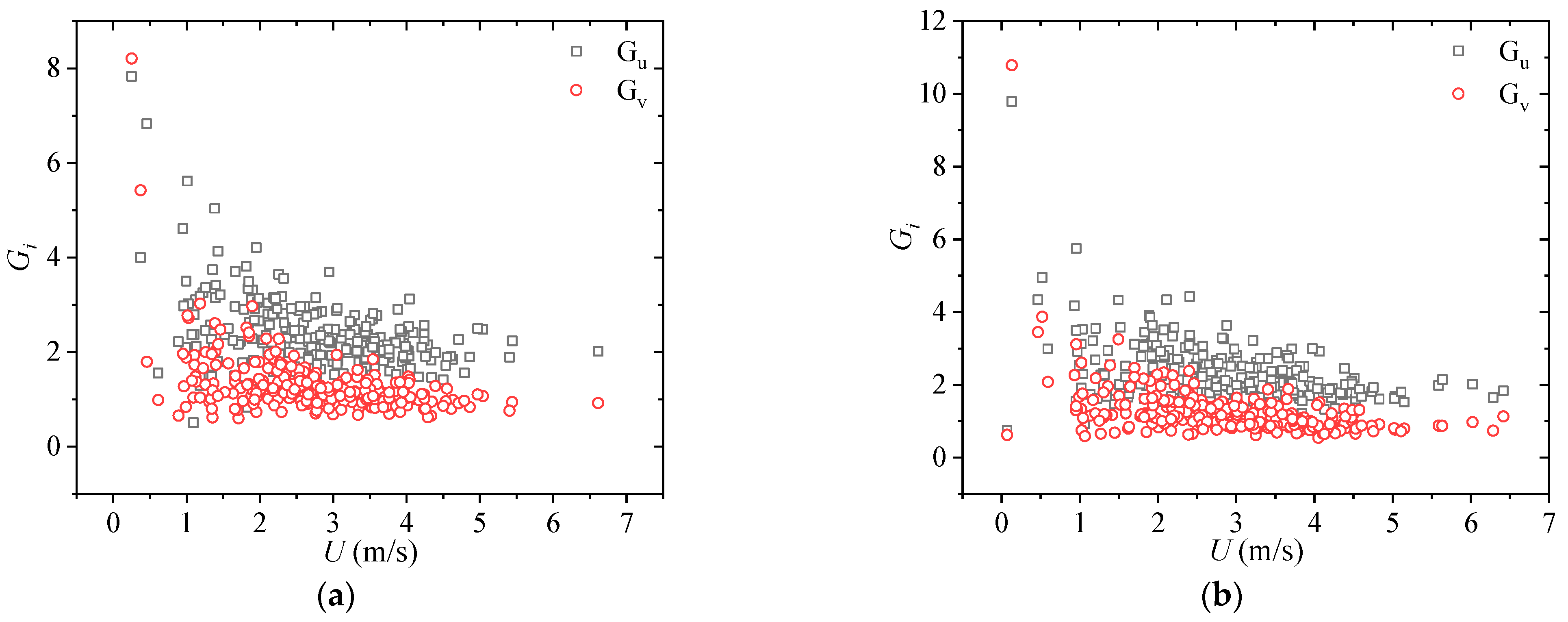
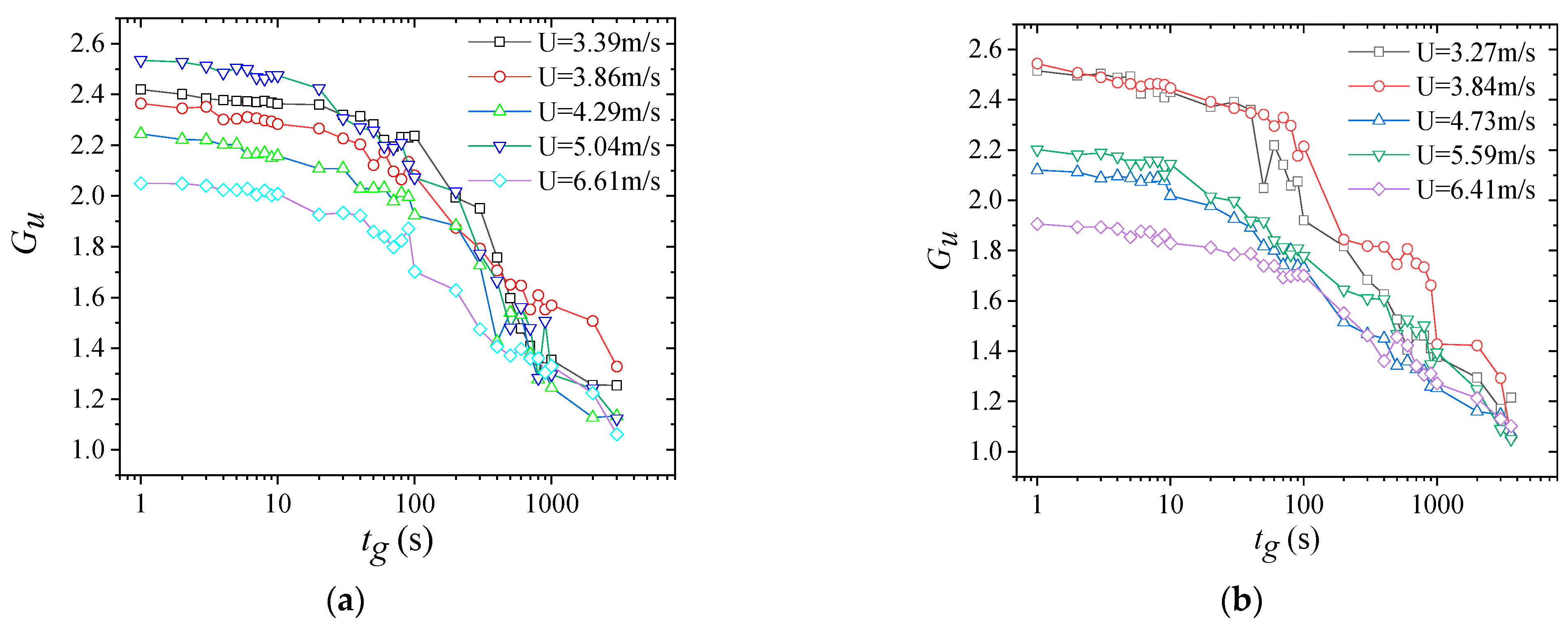
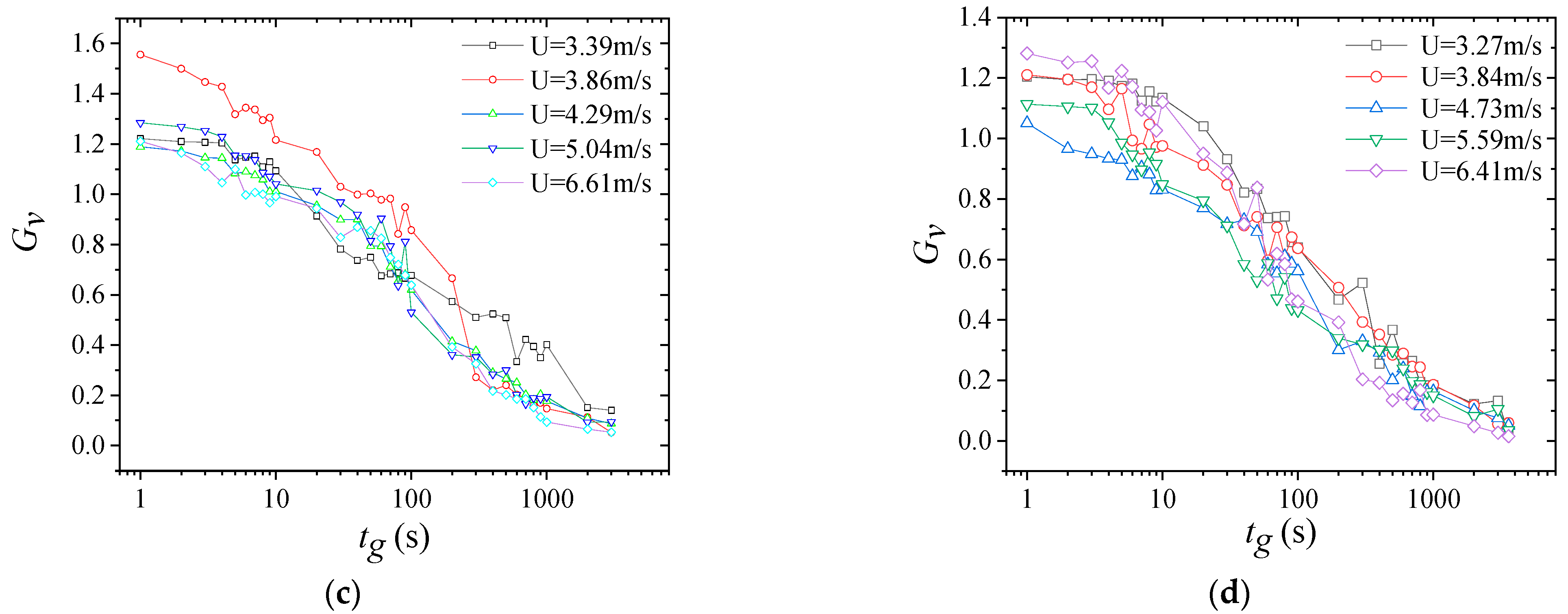
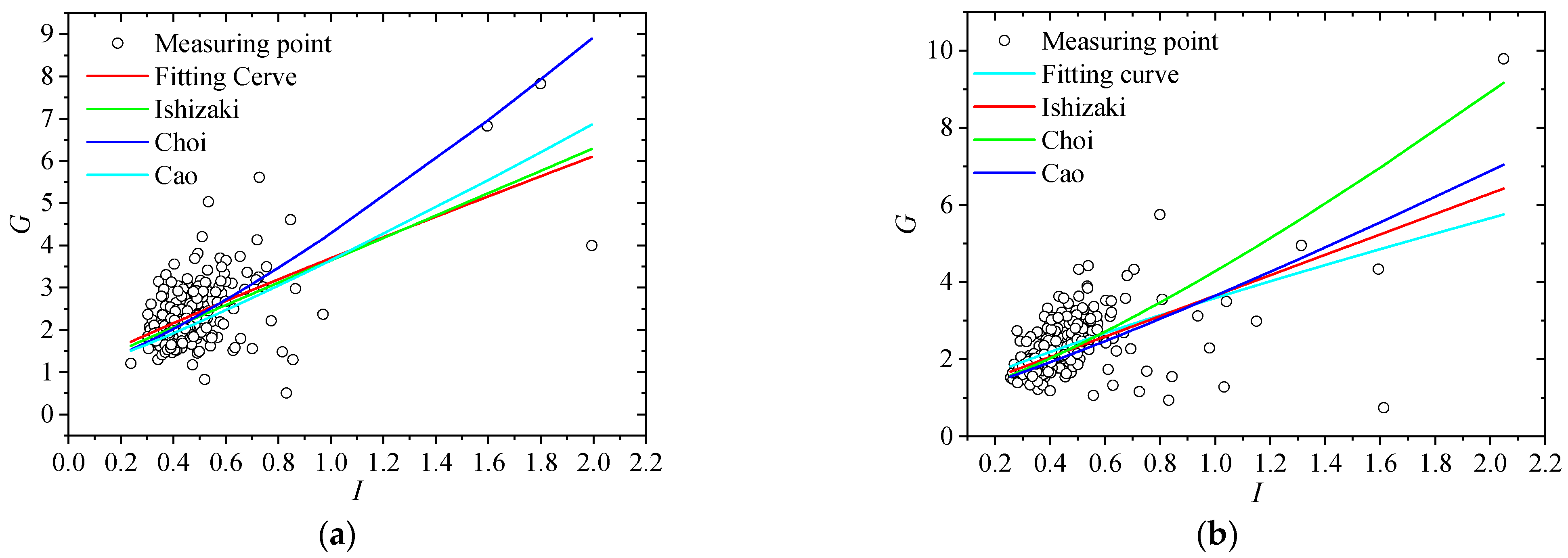
3.5. Gust Factor and Turbulence Intensity
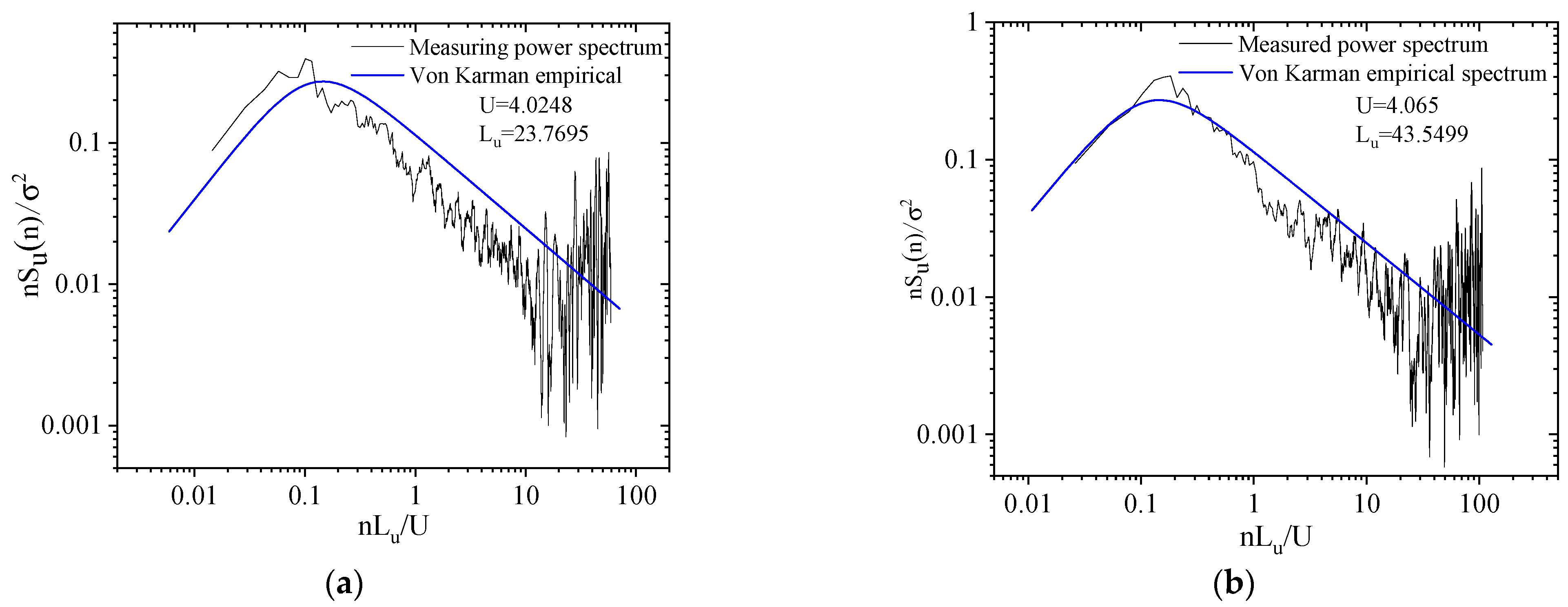
3.6. Power Spectrum
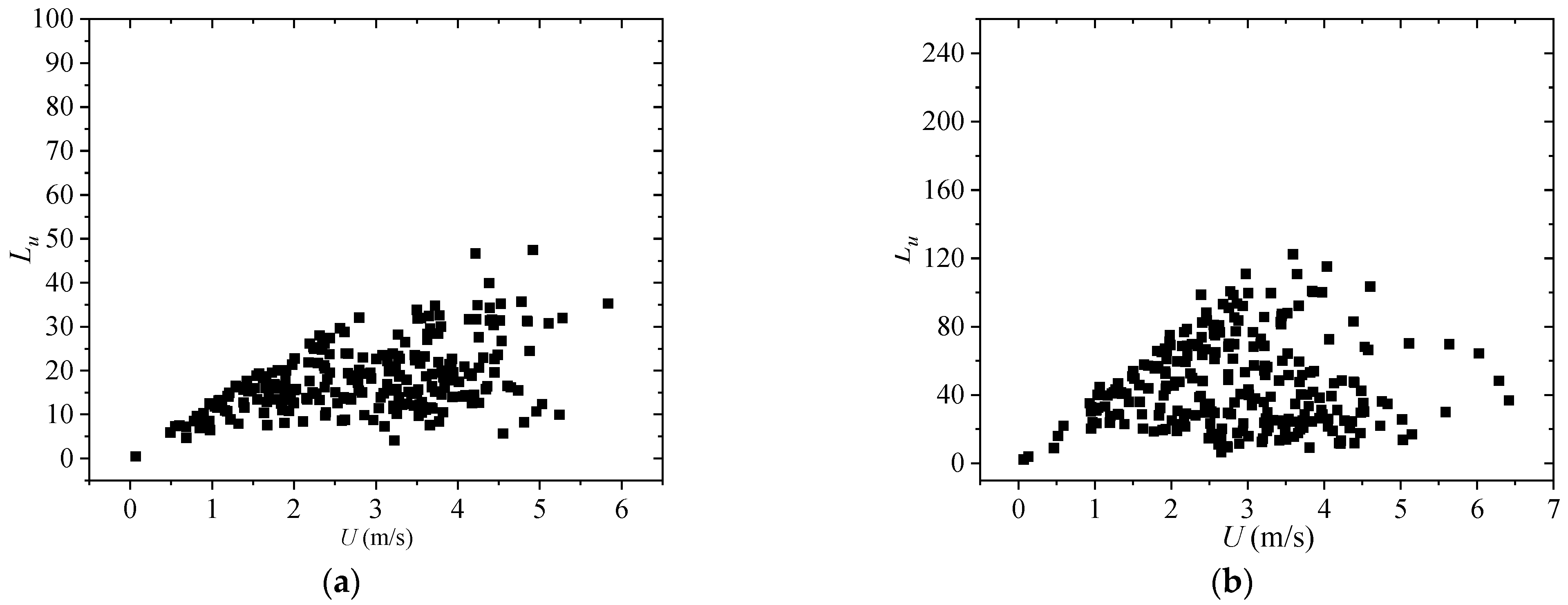
3.7. Turbulence Integral Scale
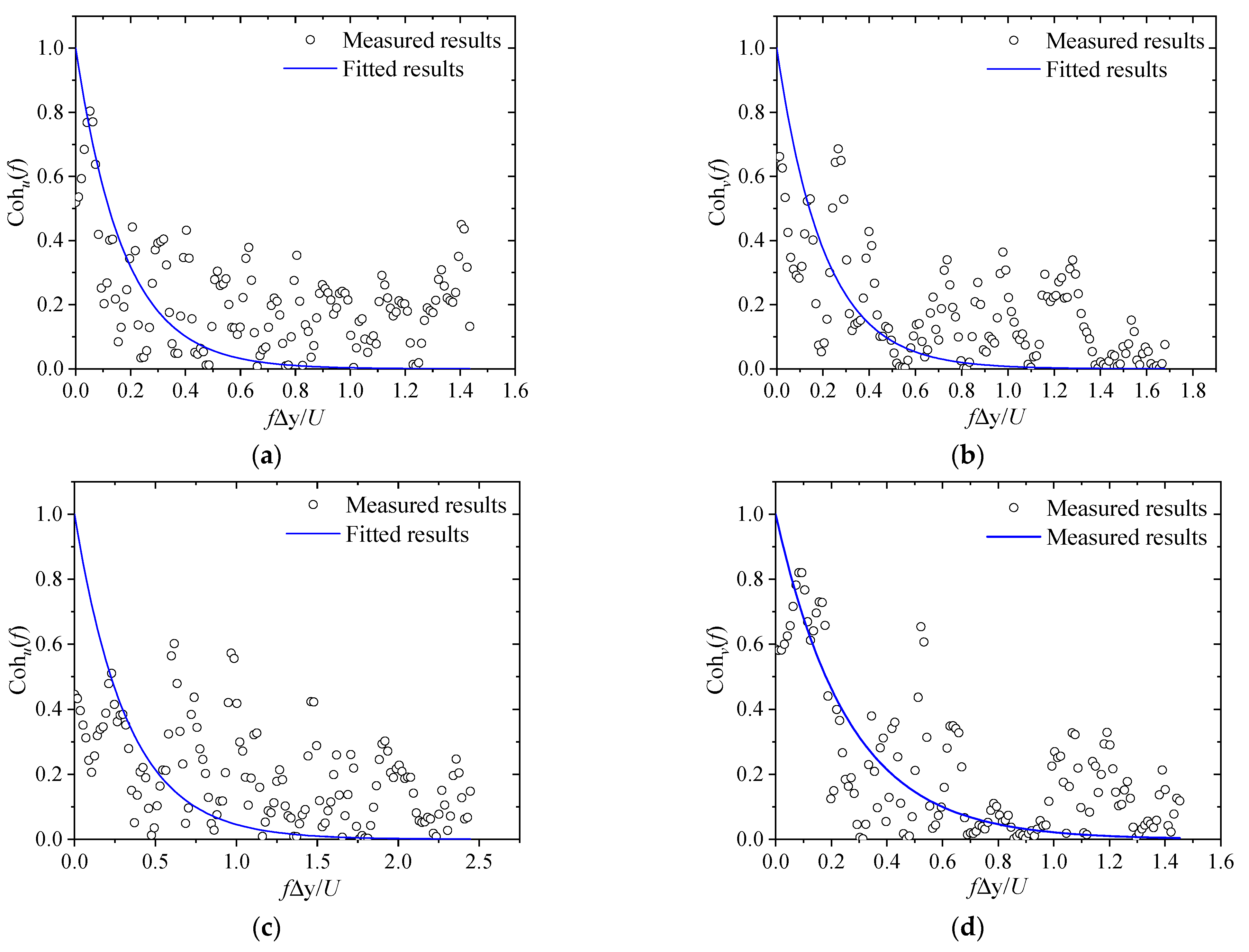
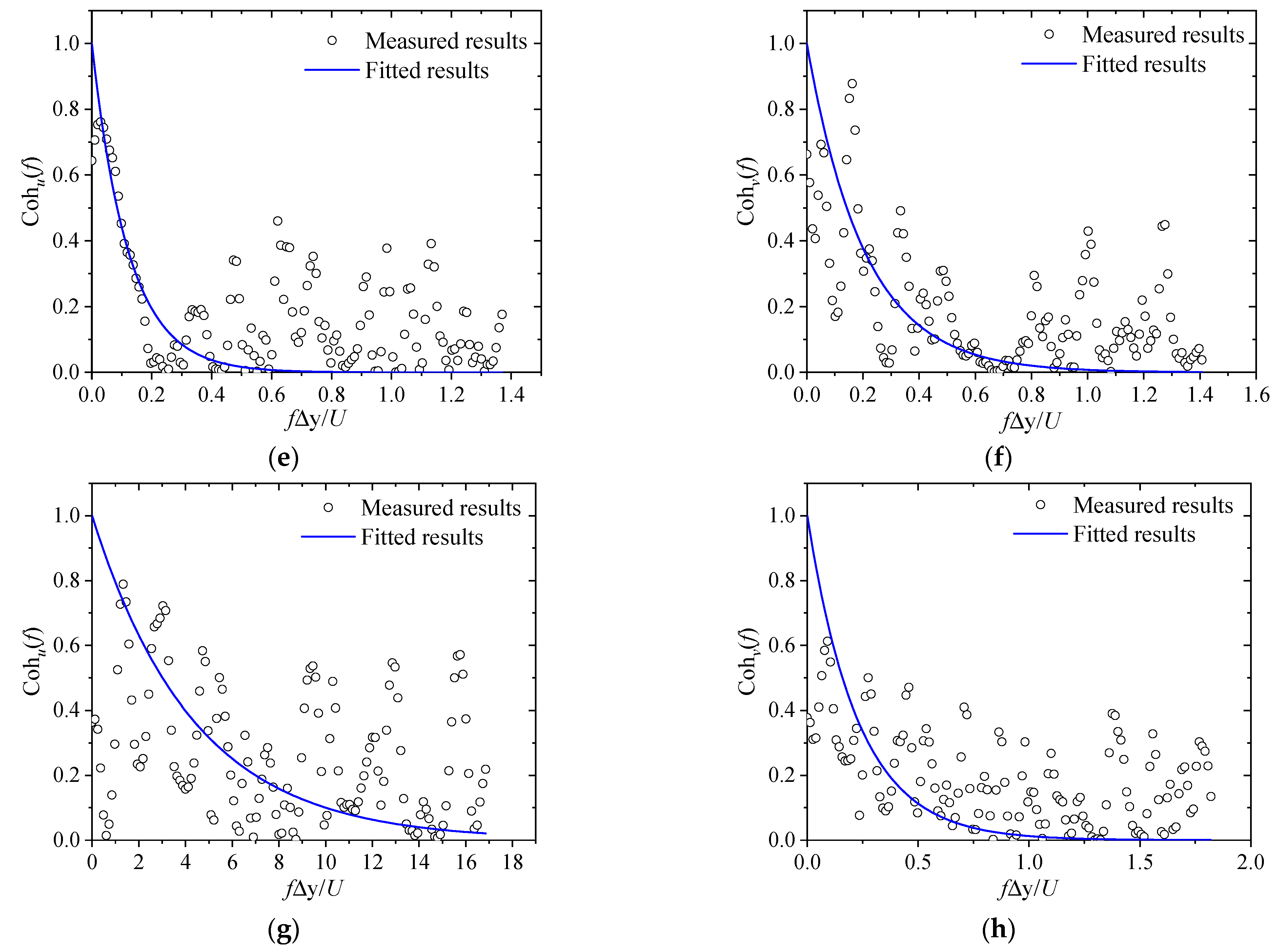
3.8. Coherence Analysis
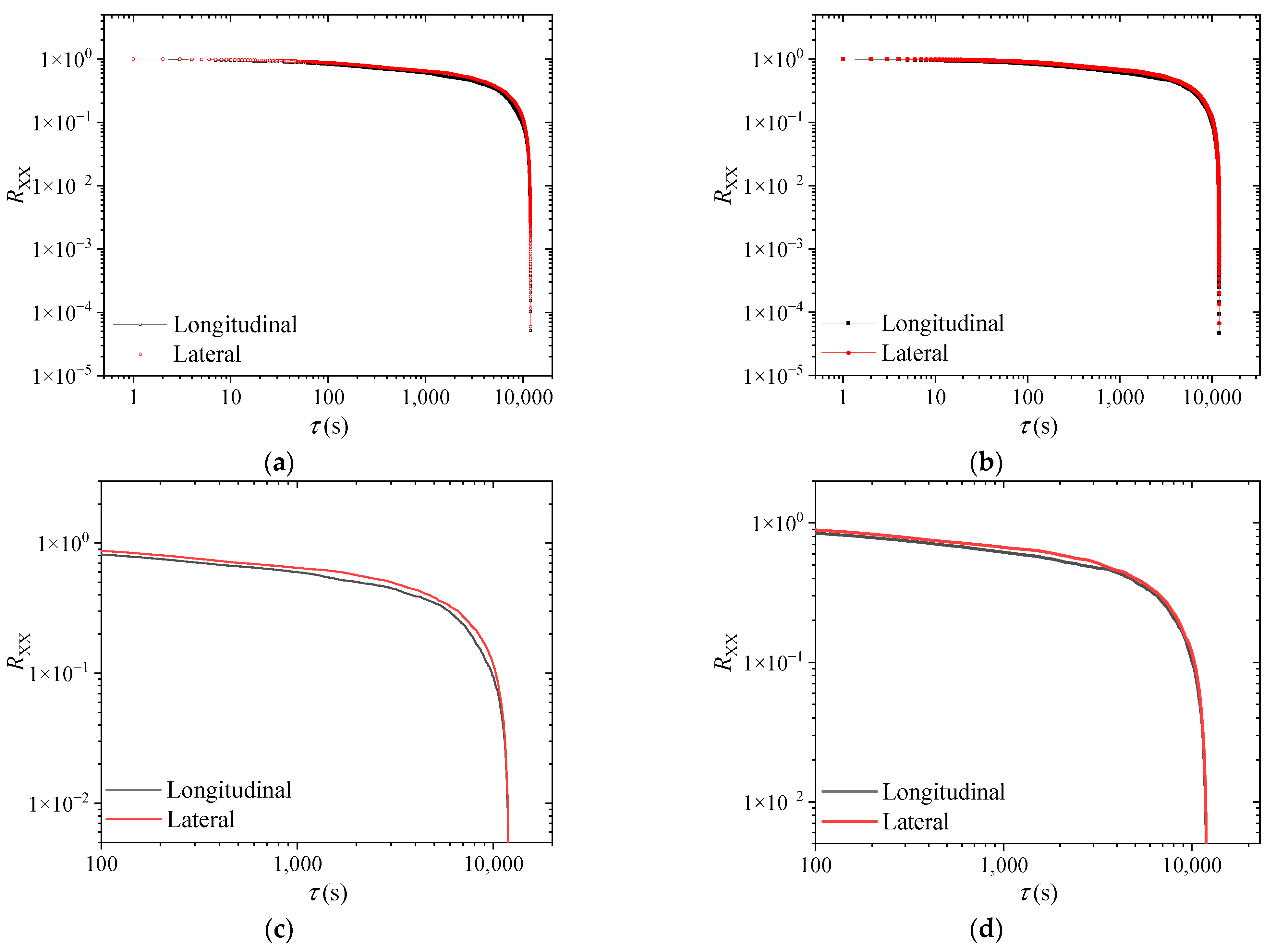
3.9. Autocorrelation Coefficient
4. Analysis of Wind Characteristics Based on Measured Data
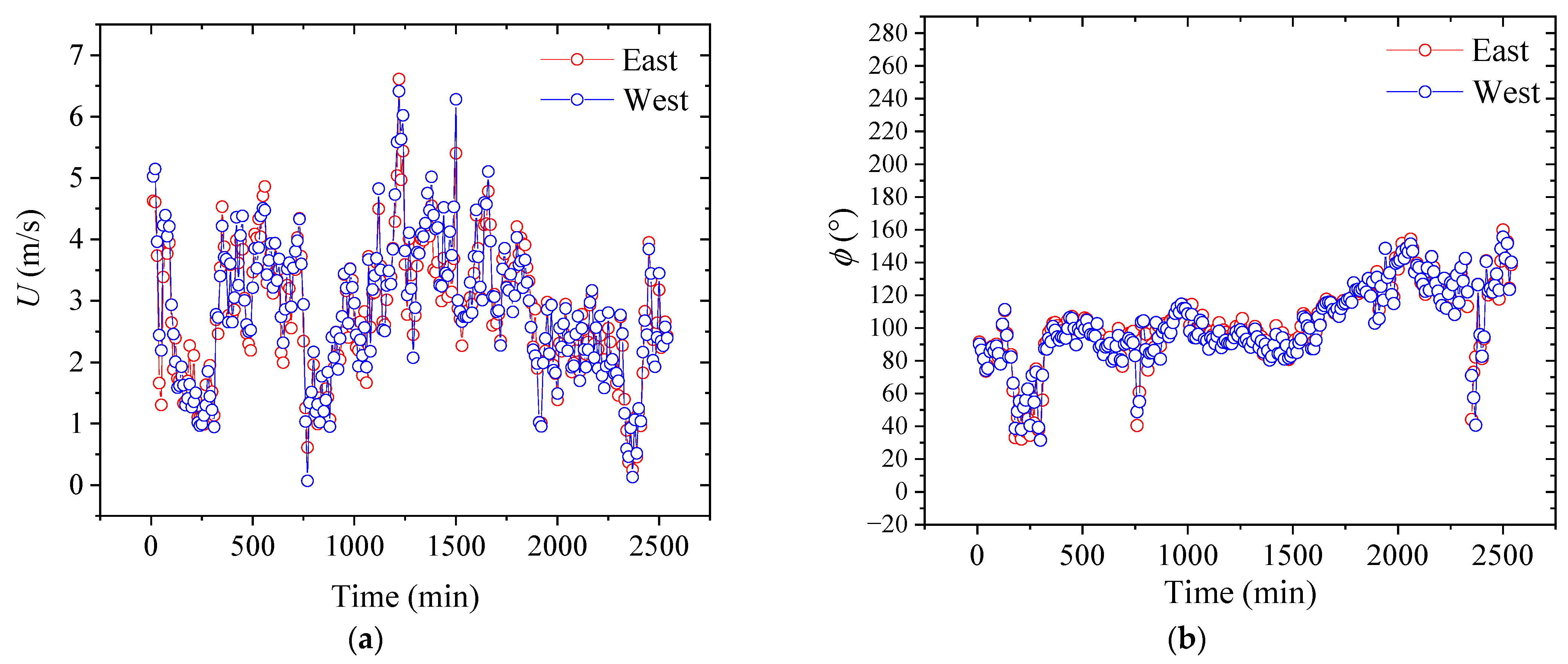
4.1. Mean Wind Speed and Direction
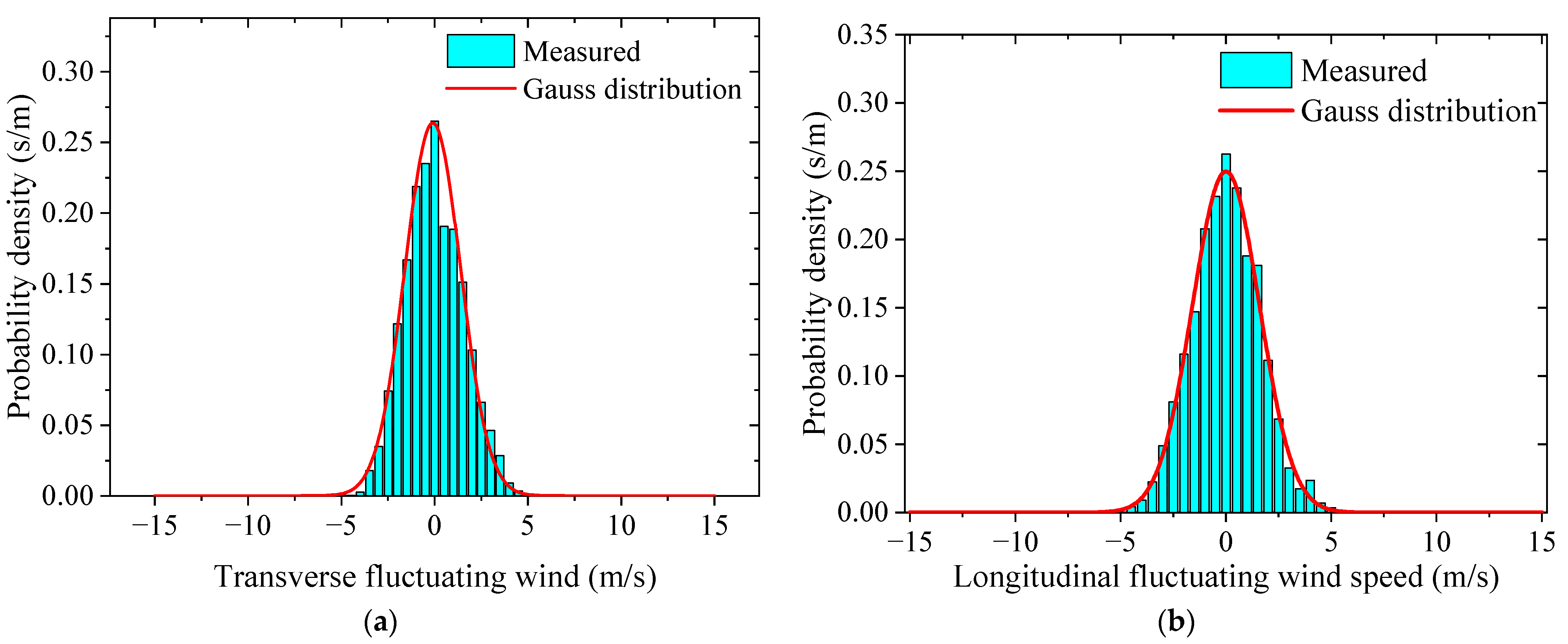
4.2. Probability Density Function
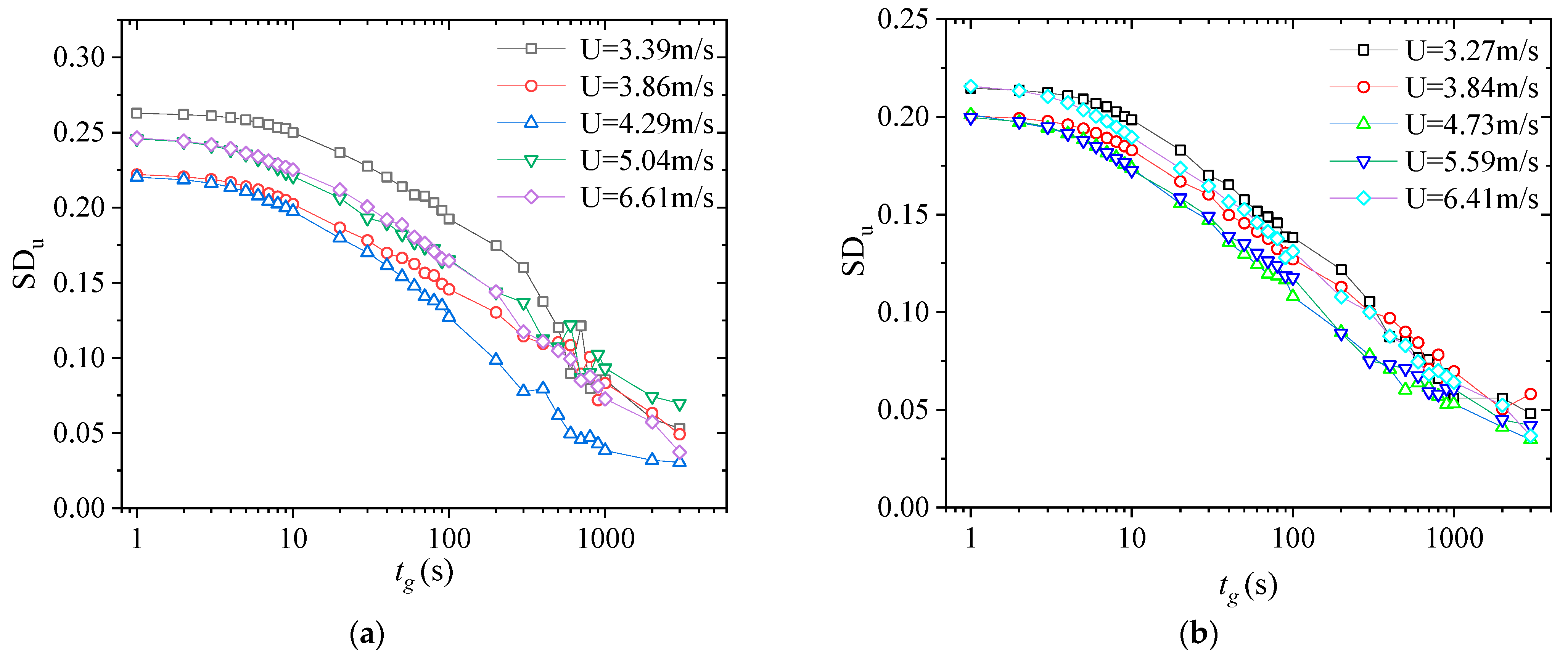
4.3. Turbulence Intensity
4.4. Gust Factor
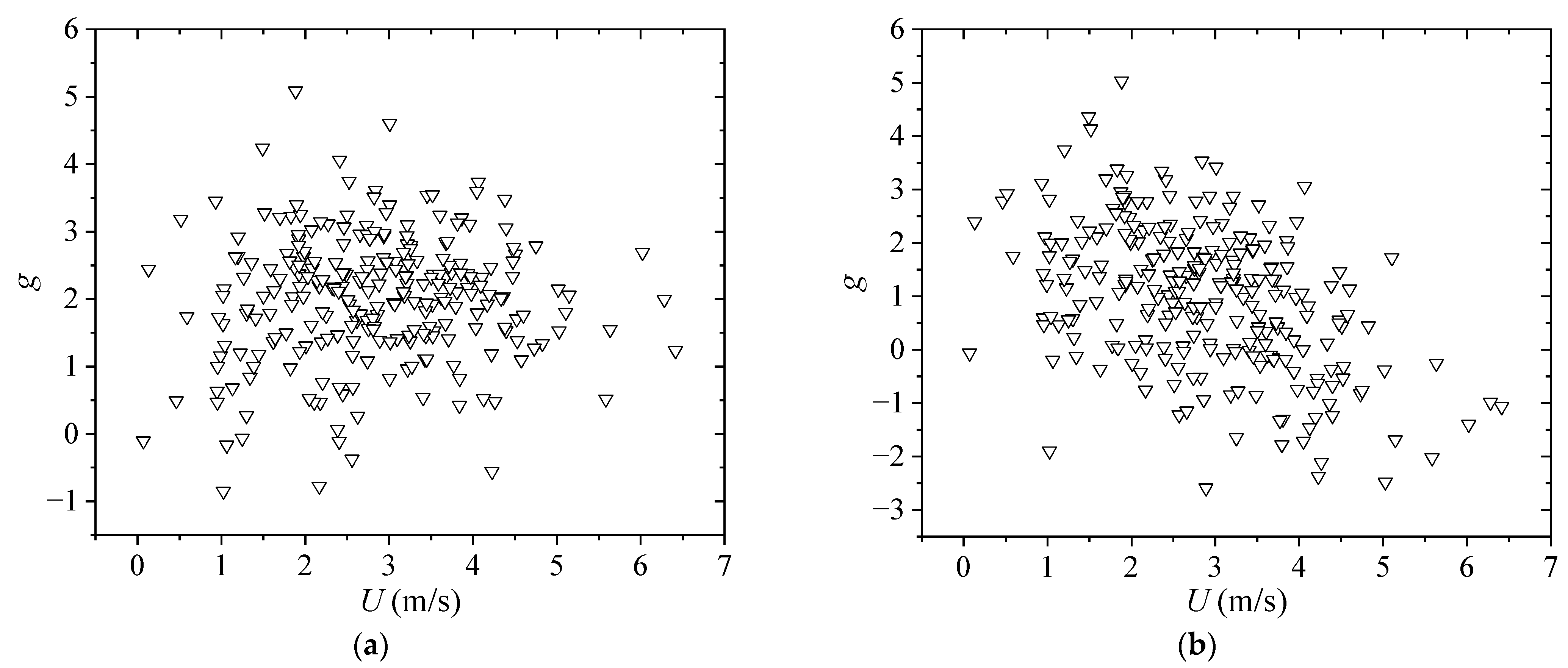
4.5. Peak Factor
4.6. Gust Factor and Turbulence Intensity
4.7. Power Spectrum
4.8. Turbulence Integral Scale
4.9. Coherence Analysis
4.10. Autocorrelation Coefficient
5. Conclusions
- During the landfall of Typhoon Jangmi in Wenzhou, its impact was complicated. The wind speed fluctuated irregularly, but overall, the wind speed decreased, though insignificantly. The wind direction, which is measured with an angle, gradually increased. The fluctuating wind speed components of Typhoon Jangmi at the east and west measuring stations tended to obey a Gaussian distribution and fit well with the Gaussian curve, which is consistent with the research findings of Cao [39];
- In low wind conditions, the turbulence intensity steadily reduced as the wind speed increased. As the wind speed continued to increase, this reduction rate dropped. At the east measuring point, the longitudinal and lateral turbulence intensities stabilized at about 0.5 and 0.25, respectively. At the west measuring point, the longitudinal and lateral turbulence intensities stabilized at 0.25. At these points, the curve between turbulence intensity and mean wind speed tended to level off, indicating that the turbulence intensity basically no longer changed with the mean wind speed. When the time interval was short, the decline curve of the turbulence intensity tended to level off; when the time interval was long, the decline curve of the turbulence intensity is steeper, and the steepness of the curve increased as the time interval became longer;
- The gust factor decreased with increasing mean wind speed. From the curves between the gust factor and the average wind speed, the distribution of gust factors at the east measurement site was relatively scattered, whereas gust factors at the west measuring point tended to cluster. The longitudinal and lateral gust factors decreased as the time interval increased for both east and west measurement stations, and the curve became unsmooth at the time intervals of 10, 100, and 1000 s. The gust factors under different wind speeds all approached 1.0 at the maximum time interval;
- The peak factor decreased, though insignificantly, with increasing mean wind speed, and the distribution of peak factors was greatly scattered. The maximum peak factors at the east and west measuring points both fell between 3.0 and 4.0. The gust factor increased as the peak factor increased, and the distribution of gust factors was relatively scattered;
- With increasing turbulence intensity, the gust factor became larger and exhibited a more scattered distribution. For the east measuring point, the fitting parameters of the fitted curve to the measured data were a = 0.5 and b = 0.97; for the west measuring point, the fitting parameters obtained were a = 0.49 and b = 0.9;
- The lateral fluctuating wind speed power spectrum and Von Karman’s empirical spectrum are in good agreement for the east and west measurement spots. The power spectrum of the longitudinal fluctuating wind speed is significantly lower than Von Karman’s empirical spectrum for the mid-band spectrum but is higher than Karman’s empirical spectrum for the high-band spectrum. The autocorrelation coefficient decreased with increasing τ over a 10 min interval.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fu, J.Y.; Wu, J.R.; Xu, A.; Li, Q.S.; Xiao, Y.Q. Full-scale measurements of wind effects on Guangzhou West Tower. Eng. Struct. 2012, 35, 120–139. [Google Scholar] [CrossRef]
- Wang, H.; Zong, Z.-H.; Li, A.-Q.; Tong, T.; Niu, J.; Deng, W.-P. Digital simulation of 3D turbulence wind field of Sutong Bridge based on measured wind spectra. J. Zhejiang Univ. Sci. A 2012, 13, 91–104. [Google Scholar] [CrossRef]
- Wang, B.; Hu, F.; Cheng, X. Wind gust and turbulence statistics of typhoons in South China. Acta Meteorol. Sin. 2011, 25, 113–127. [Google Scholar] [CrossRef]
- Song, L.; Pang, J.; Jiang, C.; Huang, H.; Qin, P. Field measurement and analysis of turbulence coherence for Typhoon Nuri at Macao Friendship Bridge. Sci. China Technol. Sci. 2010, 53, 2647–2657. [Google Scholar] [CrossRef]
- Shi, W.H.; Li, Z.N.; Zhang, C.X. Field measurements of strong wind characteristics near ground in Wenzhou district. J. Build. Struct. 2010, 31, 34–40. [Google Scholar]
- Wang, H.; Li, A.; Guo, T.; Xie, J. Field measurement on wind characteristic and buffeting response of the Runyang Suspension Bridge during typhoon Matsa. Sci. China Ser. E Technol. Sci. 2009, 52, 1354–1362. [Google Scholar] [CrossRef]
- Eaton, K.J.; Mayne J, R. The measurement of wind pressures on two-storey houses at Aylesbury. J. Wind Eng. Ind. Aerodyn. 1975, 1, 67–109. [Google Scholar] [CrossRef]
- Sparks, P.R.; Reid, G.T.; Reid, W.D.; Welsh, S.; Welsh, N. Wind conditions in Hurricane Hugo by measurement, inference, and experience. J. Wind Eng. Ind. Aerodyn. 1992, 41, 55–66. [Google Scholar] [CrossRef]
- Kato, N.; Ohkuma, T.; Kim, J.; Marukawa, H.; Niihori, Y. Full scale measurements of wind velocity in two urban areas using an ultrasonic anemometer. J. Wind Eng. Ind. Aerodyn. 1992, 41, 67–78. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Zhou, J.; Wang, Q.; Wang, X. Characteristics of Typhoon “Fung-Wong” Near Earth Pulsation. Shock. Vib. 2021, 2021, 9972981. [Google Scholar] [CrossRef]
- Zhao, L.; Cui, W.; Ge, Y. Measurement, modeling and simulation of wind turbulence in typhoon outer region. J. Wind Eng. Ind. Aerodyn. 2019, 195, 104021. [Google Scholar] [CrossRef]
- Yao, Y.; Wu, H.; Li, X.; Zhao, B.; Chen, B.; Yi, T. A review of the transmission tower-line system performance under typhoon in wind tunnel test. Wind Struct. Int. J. 2019, 29, 87–98. [Google Scholar]
- Kubota, T.; Miura, M.; Tominaga, Y.; Mochida, A. Wind tunnel tests on the relationship between building density and pedestrian-level wind velocity: Development of guidelines for realizing acceptable wind environment in residential neighborhoods. Build. Environ. 2008, 43, 1699–1708. [Google Scholar] [CrossRef]
- Lu, B.; Li Q, S. Investigation of the effects of wind veering and low-level jet on wind loads of super high-rise buildings by large eddy simulations. J. Wind Eng. Ind. Aerodyn. 2022, 227, 105056. [Google Scholar] [CrossRef]
- Ren, H.; Laima, S.; Chen, W.-L.; Zhang, B.; Guo, A.; Li, H. Numerical simulation and prediction of spatial wind field under complex terrain. J. Wind Eng. Ind. Aerodyn. 2018, 180, 49–65. [Google Scholar] [CrossRef]
- Huang, S.; Li, Q.; Xu, S. Numerical evaluation of wind effects on a tall steel building by CFD. J. Constr. Steel Res. 2007, 63, 612–627. [Google Scholar] [CrossRef]
- Feng, C.; Gu, M. Numerical simulation of wind veering effects on square-section super high-rise buildings under various wind directions. J. Build. Eng. 2021, 44, 102954. [Google Scholar] [CrossRef]
- Tao, T.; Wang, H.; Zhao, K. Efficient simulation of fully non-stationary random wind field based on reduced 2D hermite interpolation. Mech. Syst. Signal Processing 2021, 150, 107265. [Google Scholar] [CrossRef]
- Tao, T.; Shi, P.; Wang, H. Spectral modelling of typhoon winds considering nexus between longitudinal and lateral components. Renew. Energy 2020, 162, 2019–2030. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, M.; Huang, B.; Li, Y.; Yu, J.; Jiang, F. Wind Tunnel Test on Local Wind Field around the Bridge Tower of a Truss Girder. Adv. Civ. Eng. 2021, 2021, 8867668. [Google Scholar] [CrossRef]
- Li, Y.; Xu, X.; Zhang, M.; Xu, Y. Wind tunnel test and numerical simulation of wind characteristics at a bridge site in mountainous terrain. Adv. Struct. Eng. 2017, 20, 1223–1231. [Google Scholar] [CrossRef]
- Giorgio, D.; Omarini, S. A non-linear method to compute the buffeting response of a bridge validation of the model through wind tunnel tests. J. Wind Eng. Ind. Aerodyn. 2020, 201, 104163. [Google Scholar]
- Li, C.; Chen, Z.; Zhang, Z.; Cheung, J. Wind tunnel modeling of flow over mountainous valley terrain. Wind Struct. 2010, 13, 275. [Google Scholar] [CrossRef]
- Li, Y.; Hu, P.; Xu, X.; Qiu, J. Wind characteristics at bridge site in a deep-cutting gorge by wind tunnel test. J. Wind Eng. Ind. Aerodyn. 2017, 160, 30–46. [Google Scholar] [CrossRef]
- Argentini, T.; Ozkan, E.; Rocchi, D.; Rosa, L.; Zasso, A. Cross-wind effects on a vehicle crossing the wake of a bridge pylon. J. Wind Eng. Ind. Aerodyn. 2011, 99, 734–740. [Google Scholar] [CrossRef]
- Song, J.-L.; Li, J.-W.; Flay, R.G. Field measurements and wind tunnel investigation of wind characteristics at a bridge site in a Y-shaped valley. J. Wind Eng. Ind. Aerodyn. 2020, 202, 104199. [Google Scholar] [CrossRef]
- Zisis, I.; Stathopoulos, T. Wind load transfer mechanisms on a low wood building using full-scale load data. J. Wind. Eng. Ind. Aerodyn. 2012, 104–106, 65–75. [Google Scholar] [CrossRef]
- Li, Q.S.; Hu, S.Y. Monitoring of wind effects on an instrumented low-rise building during severe tropical storm. Wind Struct. 2015, 20, 469–488. [Google Scholar] [CrossRef]
- Li, Q.S.; Hu, S.Y.; Dai, Y.M.; He, Y.C. Field measurements of extreme pressures on a flat roof of a low-rise building during typhoons. J. Wind Eng. Ind. Aerodyn. 2012, 111, 14–29. [Google Scholar] [CrossRef]
- Li, J.; Hu, S.; Li, Q. Comparative study of full-scale and model-scale wind pressure measurements on a gable roof low-rise building. J. Wind Eng. Ind. Aerodyn. 2021, 208, 104448. [Google Scholar] [CrossRef]
- Wang, H.; Guo, T.; Tao, T.-Y.; Li, A.-Q. Study on Wind Characteristics of Runyang Suspension Bridge Based on Long-Term Monitored Data. Int. J. Struct. Stab. Dyn. 2016, 16, 1640019. [Google Scholar] [CrossRef]
- Wang, H.; Wu, T.; Tao, T.; Li, A.; Kareem, A. Measurements and analysis of non-stationary wind characteristics at Sutong Bridge in Typhoon Damrey. J. Wind Eng. Ind. Aerodyn. 2016, 151, 100–106. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Wang, H.; Xu, Z.; Zhang, Y.; Tao, T.; Mao, J. Monitoring-based analysis of wind-induced vibrations of ultra-long stay cables during an exceptional wind event. J. Wind Eng. Ind. Aerodyn. 2022, 221, 104883. [Google Scholar] [CrossRef]
- Pang, J.; Lin, Z.; Ge, Y. Field measurements of strong wind characteristics near ground in Pudong district. In Proceedings of the 9th National Conference on Atmospheric Environment and Pollution, Dalian, China, 16–19 October 2001; pp. 14–22. [Google Scholar]
- Peng, H.; Yin-tao, D.A.I.; Xu, W.A.N.G.; Ming, G.U. Field measurement on power spectra and coherence characteristics of near-ground wind in shanghai coastal area. Eng. Mech. 2014, 31, 126–133. [Google Scholar]
- Wang, Y.; Li, Y.; Fu, B.; Wang, X.; Zhang, C.; Fan, G. Characteristics of the Near-Ground Typhoon Morakot. Shock Vib. 2021, 2021, 9968586. [Google Scholar] [CrossRef]
- Ishizaki, H. Wind profiles, turbulence intensities and gust factors for design in typhoon-prone regions. J. Wind Eng. Ind. Aerodyn. 1983, 13, 55–66. [Google Scholar] [CrossRef]
- Choi, C. Wind Loading in Hong Kong: Commentary on the Code of Practice on Wind Effects Hong Kong, 1983; Hong Kong Institution of Engineers: Hong Kong, China, 1984. [Google Scholar]
- Cao, S.; Tamura, Y.; Kikuchi, N.; Saito, M.; Nakayama, I.; Matsuzaki, Y. Wind characteristics of a strong typhoon. J. Wind Eng. Ind. Aerodyn. 2009, 97, 11–21. [Google Scholar] [CrossRef]
- Von Kármán, T. Progress in the Statistical Theory of Turbulence. Proc. Natl. Acad. Sci. USA 1948, 34, 530–539. [Google Scholar] [CrossRef] [Green Version]
- Davenport, A.G. The spectrum of horizontal gustiness near the ground in high winds. Q. J. R. Meteorol. Soc. 1961, 87, 194–211. [Google Scholar] [CrossRef]
- Ashcroft, J. The relationship between the gust ratio, terrain roughness, gust duration and the hourly mean wind speed. J. Wind Eng. Ind. Aerodyn. 1994, 53, 331–355. [Google Scholar] [CrossRef]
- Krayer, W.R.; Marshall, R.D. Gust factors applied to hurricane winds. Bull. Am. Meteorol. Soc. 1992, 73, 613–618. [Google Scholar] [CrossRef] [Green Version]
- Durst, C.S. Wind speeds over short periods of time. Meteorol. Mag. 1960, 89, 181–186. [Google Scholar]
- Wang, X.; Huang, P.; Yu, X.-F.; Huang, C. Near ground wind characteristics during typhoon Meari: Turbulence intensities, gust factors, and peak factors. J. Cent. South Univ. 2017, 24, 2421–2430. [Google Scholar] [CrossRef]





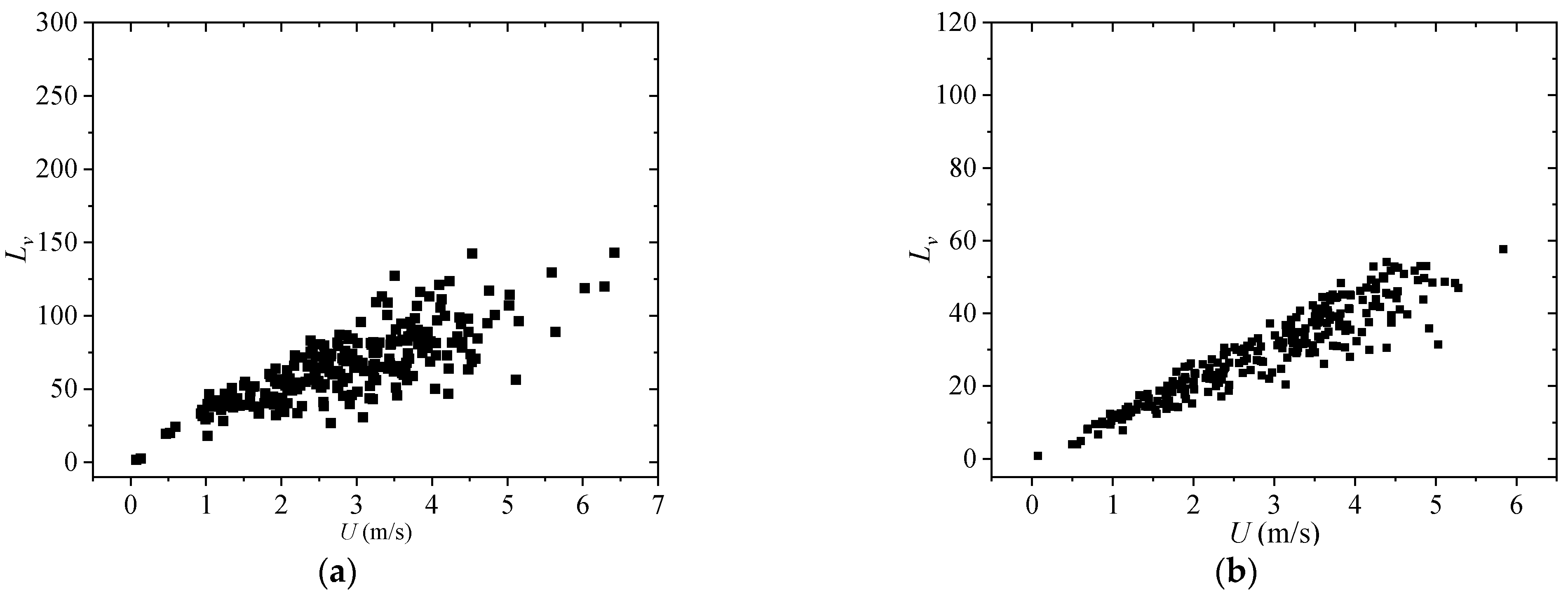
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, Y.; Qi, Q.; Zhang, C.; Wang, X.; Fan, G.; Fu, B. Experimental Study of the Fluctuating Wind Characteristics of Typhoon Jangmi Measured at the Top of a Building. Sustainability 2022, 14, 9266. https://doi.org/10.3390/su14159266
Wang Y, Li Y, Qi Q, Zhang C, Wang X, Fan G, Fu B. Experimental Study of the Fluctuating Wind Characteristics of Typhoon Jangmi Measured at the Top of a Building. Sustainability. 2022; 14(15):9266. https://doi.org/10.3390/su14159266
Chicago/Turabian StyleWang, Yanru, Yongguang Li, Qianqian Qi, Chuanxiong Zhang, Xu Wang, Guangyu Fan, and Bin Fu. 2022. "Experimental Study of the Fluctuating Wind Characteristics of Typhoon Jangmi Measured at the Top of a Building" Sustainability 14, no. 15: 9266. https://doi.org/10.3390/su14159266
APA StyleWang, Y., Li, Y., Qi, Q., Zhang, C., Wang, X., Fan, G., & Fu, B. (2022). Experimental Study of the Fluctuating Wind Characteristics of Typhoon Jangmi Measured at the Top of a Building. Sustainability, 14(15), 9266. https://doi.org/10.3390/su14159266







