Pattern and Dynamics of Teacher Emotions during Teaching: A Case Study of a Senior Secondary Mathematics Teacher

Abstract

Understanding the emotional dimension of classroom practices benefits sustainable education. However, the dynamic nature of teacher emotions during teaching remains understudied. To acquire an “in-depth” description of the emotional phenomena during teaching, a case study was adopted to examine the pattern and dynamics of a senior secondary mathematics teacher’s teaching-related emotions. Seven new mathematics lessons were observed and videotaped, and three video-stimulated, post-lesson teacher interviews were conducted. Based on appraisal theories of emotions, thematic analysis and content analysis were mainly used to analyse the data. The study revealed that the teacher most frequently experienced happiness/satisfaction as positive emotions and confusion/surprise as negative emotions. The emotions followed a three-stage process: perceptions, multilevel appraisals, and responses. The teacher most often perceived her students’ cognitive accuracy and adopted goal/need conduciveness/attainment, the discrepancy from expectations, and causal attribution as core appraisal dimensions. Teacher emotions in classrooms were also often hierarchical and cumulative, shifting from more negative at the beginning of a new semester to more positive at the middle of the semester. This study shed light on the dynamic development of teacher emotions, extending the theories and process models of emotions from the psychological field to educational research and facilitating teachers’ sustainable professional development.

1. Introduction

The importance of teacher emotions has attracted more and more attention over the past two decades. Teachers often experience multiple and intensive emotions during professional practices [1,2]. These emotions are closely associated with teachers’ cognition, instructional practices, and burnout [3,4,5]. The emotional nature of the teaching profession also probably influences teachers’ well-being and turnover rate, especially during the first five years of their careers [6]. Therefore, to facilitate teachers’ teaching and sustainable professional development, it is imperative to understand teacher emotions deeply.

Emotion is a dynamic process, changing with the individual’s appraisals, person-environment transactions, and time [7]. Nevertheless, existing research has often viewed teacher emotions as static entities and has seldom investigated the dynamic nature of teacher emotions from a microcosmic perspective [6,8,9]. Most studies have been conducted in Western countries and focused more on primary school or university teachers [10,11]. Little is known about the emotional processes experienced by senior secondary school mathematics teachers beyond mathematics anxiety in the context of China [3,12]. Compared with their Western counterparts, Chinese teachers are given higher social expectations and responsibilities [13], and classrooms in China place more emphasis on teachers’ role models, coherence, and students’ hard work [14]. Moreover, mathematics is compulsory in the national college entrance examination in China. This examination causes heavier pressure among senior secondary school teachers and students than primary and junior secondary ones. These differences probably shape mathematics teachers’ emotional experiences.

Teacher emotions also affect students’ emotions [15]. Although Chinese students often attained high mathematics achievement in international assessments, they exhibited higher levels of negative emotions and mathematics anxiety than their counterparts from Western countries [16,17]. Given that individual and collective well-being has become one of the education goals in the 21st century [18], an in-depth investigation of the origins and processes of mathematics teachers’ emotions during teaching may also help understand students’ emotions and facilitate their sustainable and lifelong learning.

Therefore, to address these research gaps and promote sustainable education, the present study aimed to explore how senior secondary school mathematics teacher emotions result from and change during classroom teaching in the context of China.

2. Literature Review and Theoretical Framework

2.1. Appraisal Theories and the Nature of Teacher Emotions

As one of the well-accepted theories on emotions, the appraisal theories define emotions as a process involving changes in five interactive components: (1) appraisals, (2) action tendencies, (3) physiological responses (e.g., heart rate), (4) expressive displays (e.g., facial expressions), and (5) subjective feelings (e.g., feeling positive) [19,20]. Based on the theories, two typical models of the emotional process have been proposed [7,21]. Fischer, Shaver, and Carnochan [21] suggested that the emotional process started with the detection of a notable change and ended with action, expression, and self-categorizing. The appraisal and action tendencies/physiological changes happened in the middle of the emotional process. Scherer and Moors [7] further refined the relationships among five components and emphasized a dynamic architecture of a multicomponent emotion process model. This model classifies the emotional process into three stages: elicitation, differentiation, and representation. Various triggers (e.g., event, behaviour, memory) and multilevel appraisals elicit differentiation in action tendencies, physiological responses, and motor expressions. The continuous variations are integrated and centrally represented as nonverbal feelings and then are categorized and labelled with emotion terms (e.g., anxiety) or dimensional descriptions (e.g., feeling good). The appraisal theories and emotion process models from the psychological field lay a solid foundation for this study and guide the development of theoretical framework.

Among the emotional process, the appraisal is considered as the central construct and refers to a process that detects and evaluates the significance of the environment for individuals’ well-being [20]. The process is multi-dimensional and hierarchical, involving a variety of appraisal dimensions occurring sequentially [22,23]. So far, four groups of stimulus evaluation checks (SECs) are well known and comprehensive [23]. The first SEC, namely relevance detection, evaluates whether a situation deserves further processing and encompasses novelty, intrinsic pleasantness, and goal/need pertinence as its most important criteria. The second SEC is implications/consequences, which include causal attribution, outcome probability, the discrepancy from expectation, goal/need conduciveness, and urgency. The third SEC is coping potential, which contains control, power, and adjustment. The fourth SEC is norm compatibility, which involves consistency with internal and external standards.

The characteristics of emotions are crucial for constructing and understanding the nature of teacher emotions. In line with the appraisal theories of emotions, a teacher with sequential appraisals may have different emotional reactions to the same event [1], and teacher emotions also probably vary with contexts or time [9,24]. Particularly, after analysing one million teachers’ online posts in three online forums of America, Chen, Shi, Zhang, and Qu [9] revealed the multi-dimensionality and dynamic nature of teachers’ emotions across contexts from their workplace to their personal lives and across three scales of time (i.e., calendar year, calendar month, and academic semesters). However, as Chen, Shi, Zhang, and Qu [9] indicated, they did not provide micro-level examinations of teachers’ appraisal processes at the individual level. Hence, it is essential to further investigate the pattern and dynamics of teacher emotions within a professional context, for example, in mathematics classrooms.

2.2. Teacher Emotions in Classrooms: Triggers and Appraisals

An increasing body of research has examined teacher emotions, suggesting that teachers frequently experience various emotions during teaching, with positive emotions being more often than negative ones [3]. In addition, enjoyment and satisfaction are experienced most frequently as positive emotions during teaching, while anxiety and anger are the most common negative emotions [2,25]. However, the existing studies were mainly conducted in Western countries [3,11] and seldom elaborate on the process nature of teacher emotions systematically (e.g., triggers and appraisals) [8,26].

2.2.1. Triggers of Teacher Emotions

Previous research literature indicates that triggers of teacher emotions during teaching can be categorized into two main groups: teachers’ teaching [3,27] and students’ behaviours [12,28,29].

So far, most studies classified students’ behaviours into four groups, namely achievement, motivation, social-emotional (e.g., discipline), and relational behaviours (i.e., teacher–student closeness), and tested their relationships with teacher emotions using a relatively large sample [30]. The social-emotional and relational behaviours were often found to be the most salient for teacher emotions [29,31]. Nevertheless, some results have yet come to an agreement, such as, the relations between students’ achievement behaviours and teacher emotions. Using questionnaires and lesson dairies and a sample of 237 primary and secondary school teachers in Germany, Frenzel, Goetz, Stephens, and Jacob [28] found that students’ motivation and discipline positively predicted teachers’ enjoyment and negatively predicted anger and anxiety. Discipline was the strongest predictor of anger and anxiety. However, only lesson dairies demonstrated significant relationships between students’ academic performance and the three emotions. By contrast, de Ruiter, Poorthuis, and Koomen [29] showed that students’ social-emotional and relational behaviours most often predicted 218 Dutch elementary teachers’ enjoyment and anger. Students’ achievement behaviours only predicted the teachers’ enjoyment, and students’ hostility or aggression towards the teacher as the relational behaviours was the only significant predictor of anxiety.

A few qualitative studies have also provided different insights into the categorization of students’ behaviours. Martínez-Sierra, Arellano-García, Hernández-Moreno, and Nava-Guzmán [26] demonstrated that a high school mathematics teacher’s diverse emotions in Mexican classrooms were mainly triggered by students’ independence, collaboration, and participation. Martínez-Sierra, Arellano-García, and Hernández-Moreno [12] identified the six most frequent triggers of secondary school mathematics teachers’ emotions, containing students’ achievement behaviours, learning, engagement/motivation, instructional effectiveness, teacher–student relationships, and parents’ or supervisors’ support.

2.2.2. Teacher Appraisals

Teacher appraisals in emotional processes have been studied from three major perspectives. First, based on the control-value theory that was initially developed by Pekrun [32] to examine students’ achievement emotions, most studies tested the relationships between the control/value appraisals and emotions among university teachers. For instance, Thies and Kordts-Freudinger [8] showed that the value and control appraisals accounted for large variances in 50 German university academics’ emotions. Moreover, the value appraisals predominantly predicted positive emotions, while the control appraisals were significantly associated with negative emotions.

Second, to verify the reciprocal model of Frenzel [30] and Frenzel et al. [33] on the causes and effects of teacher emotions that highlighted the appraisals of goal attainment, coping potential, accountability, and goal importance, some studies quantitatively examined the correlations between the appraisal dimensions and teacher emotions. For example, Frenzel, Fiedler, Marx, Reck, and Pekrun [33] substantiated that, among 244 German secondary teachers across different subjects, the goal attainment appraisal was most relevant to teachers’ enjoyment, anger, and anxiety, followed by goal importance appraisals.

Third, few research studies have employed the appraisal theories to explore the importance of additional appraisal dimensions for teacher emotions, such as discrepancy from expectations, norm appraisals, except for several studies [26,27]. Hagenauer and Volet [27] demonstrated that 15 pre-service Australian university teachers’ emotions during first-year teaching were mainly related to two appraisals: discrepancy from expectations of students’ engagement and coping potential. Martínez-Sierra, Arellano-García, Hernández-Moreno, and Nava-Guzmán [26] analysed the diverse emotions of a high school mathematics teacher in Mexican classrooms (e.g., satisfaction, disappointment) and unveiled goal and norm appraisals as the most important.

The literature review suggests that, although the existing studies have quantitatively examined the relationships between limited appraisal dimensions and teacher emotions, the key appraisal dimensions have not reached a consensus. There is also a paucity of empirical research on senior secondary teachers’ appraisals in mathematics education and in Asian cultural contexts. Emotions vary with individuals and contexts [20]. Particularly, Chinese mathematics classrooms highlight coherence, high expectation/achievement, and students’ effort [14,34]; senior secondary mathematics teachers and students have heavier pressure than their counterparts in lower grades, as they are faced with the national college entrance examination of mathematics. Therefore, it is essential to systematically explore the importance of various appraisal dimensions for senior secondary mathematics teacher emotions, drawing on the appraisal theories [29].

2.3. The Present Study

To address the research gaps and deeply understand the emotional phenomenon during teaching, this study aimed to explore the pattern and dynamic natures of senior secondary mathematics teachers’ teaching-related emotions in China. Specifically, this study sought to address the following three research questions:

(1)

What emotions do the senior secondary mathematics teachers experience during classroom teaching?

(2)

What patterns are the senior secondary mathematics teachers’ emotions characterized by during classroom teaching?

(3)

How do the senior secondary mathematics teachers’ emotions change during classroom teaching?

Drawing on the appraisal theories and the emotion process models [7,21,30], this study proposed a process model of teacher emotions in classrooms (see Figure 1). It characterized teacher emotions in classrooms in three stages: perceptions of classroom events, multilevel appraisals, and emotional responses. Teachers in classrooms perceive their instruction and students’ behaviours, and then interpret the events from four groups of dimensions (e.g., relevance detection) and finally show their emotional responses in four ways (e.g., expressive displays) and label their emotions.

3. Methodology

3.1. Sampling and Participants

This study, as part of a larger study, adopted a single case study approach. Its selection was mainly to acquire an “in-depth” description of the emotional phenomena during teaching and better answer the “how” research question [35]. Before data collection, approval from the research ethics committee was received, and all participants gave informed consent.

To obtain rich information about the research questions and ensure the potential representativeness of the case, three criteria were employed: (a) the participants’ emotions shared similar characteristics with those of most teacher-participants in a survey; (b) novice teachers; and (c) accessibility and willingness to participate in this study. Finally, Susie, a Grade 10 mathematics teacher with a 3-year teaching experience, was selected through purposive sampling. She experienced both positive and negative emotions during teaching, similar to most teachers in the larger study. The researchers also had access to Susie, and she was also willing to participate in this study.

When the data were collected, Susie was a 28-year-old female teacher with a postgraduate diploma and had a three-year teaching experience. She worked in a public high school in Shenzhen, Guangdong province of China. This school was newly established in 2012 and ranked top 20% of local public high schools in terms of students’ admission scores in the senior secondary school entrance examination (i.e., Zhongkao). During this study, Susie taught mathematics in two Grade 10 classes (Class A and B, around 15-year-old students) and was also the class teacher of Class A. Class A consisted of 50 students with mid-level academic achievement relative to their counterparts in the same school, based on Zhongkao scores.

3.2. Data Collection

To identify emotional patterns, trace changes in teacher emotions in the classroom, and triangulate the findings, multiple data were collected. Specifically, Susie’s seven regular lessons for teaching new content were observed and videotaped within two months (i.e., September and October) (see

Table 1. Information about lesson videotapes and video-stimulated interviews of Susie.

Type	Topic	Video/Observation	Interview
Pilot	Monotonicity of functions	Pilot	Pilot
Lesson 1	Maximum and minimum of functions	Yes	Nil
Lesson 2	Odd functions	Yes	Interview 1
Lesson 3	Functions and exponentiation	Yes	Nil
Lesson 4	Exponential functions and their properties I	Yes	Nil
Lesson 5	Exponential functions and their properties II	Yes	Nil
Lesson 6	Logarithm	Yes	Interview 2
Lesson 7	Logarithmic functions and their properties	Yes	Interview 3

).

Each lesson lasted around 45 min. Three video-stimulated, semi-structured interviews were conducted immediately after three classes, respectively. Specifically, after observing and videotaping each lesson, the researcher would invite the teacher to participate in an interview in a quiet library room. Susie chose to be interviewed after Lessons 2, 6, and 7, respectively. Lessons 4 and 5 were not selected because of Susie’s busy schedule. When Susie was quickly watching the classroom video from the beginning to the end, she tried to recall her emotional experiences. If a classroom situation involved her emotions, Susie would slow or pause the video and describe the classroom event and her emotions in detail.

Each interview lasted one to two hours. The interviews mainly included two core questions: (1) what emotions did you experience in this mathematics lesson? [26]; (2) why did you have this emotion at that time? In addition, because the researcher observed the significant changes in teacher emotions from Lesson 3 to Lessons 4, 5, and 6, an additional question was asked in Interview 2 after Lesson 6: why did this change occur during this period? Some probing questions and prompts were used to clarify incomplete or unclear responses and elicit more information.

3.3. Data Analysis Methods

The interviews, as the main data sources, were tape-recorded and transcribed verbatim. To examine the complexity of teacher emotions, thematic analysis was conducted with the interview data first, followed by content analysis. The thematic analysis could explore patterns within data and provide a purely qualitative and detailed account of data, while content analysis could offer quantitative counts of the codes [36].

A consecutive teaching episode involving one or a series of emotional processes was identified as a unit of analysis and abbreviated as an emotional teaching episode. An emotional teaching episode started when the teacher paused the video and talked about emotion-related content. The emotional teaching episode ended when the teacher used spoken words/phrases to indicate termination and turned to talk about emotions unrelated to the current teaching or emotions. The emotional teaching episode usually included everything, starting from triggering situations to immediate consequences of emotions.

The teacher’s emotional expressions in 7 lessons were also coded as positive and negative emotions, combining facial expressions and verbal language. After analysing the interview and video data, the researchers built the correspondences between the teacher’s self-report and the classroom videos. The content involved: (1) how did the teaching situations involve the teacher’s emotions; (2) how did the teacher display her emotions in classrooms when experiencing emotions.

3.4. Code Schemes

The process model in Figure 1 was regarded as an analytical framework and guided the development of coding schemes, together with the data. The code schemes were almost applied to each unit of analysis.

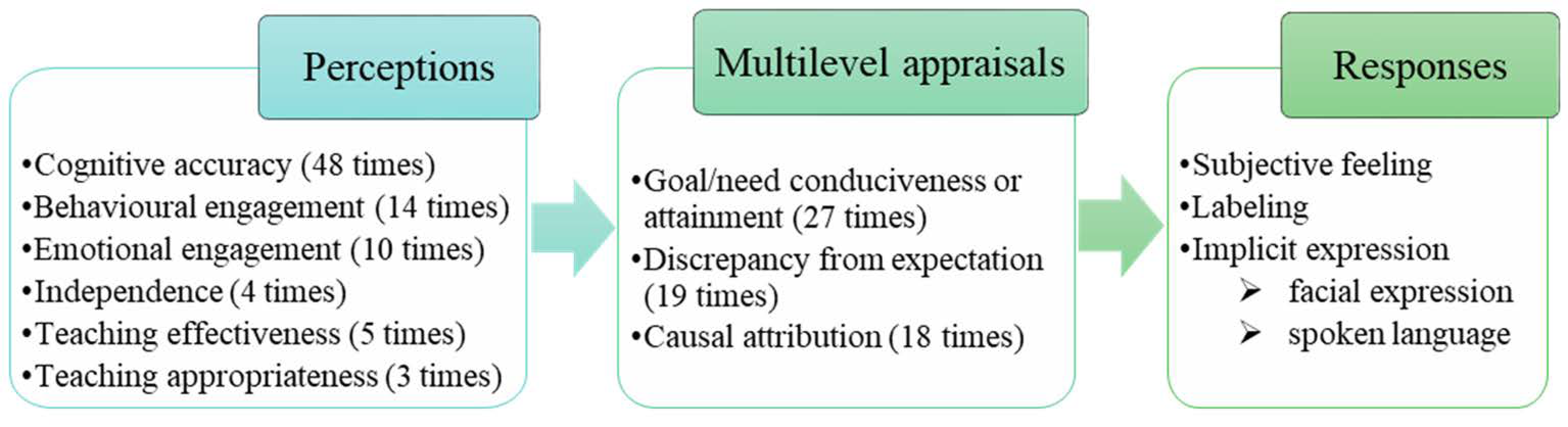
3.4.1. Teacher Perceptions

Four groups of codes emerged from the data: teacher instruction, students’ behaviours, classroom environment, and mathematics textbook (see

Table 2. Coding schemes of teacher perceptions.

Code	Descriptions	Examples
Cognitive accuracy	Students’ ideas are correct, or their language is standard/fluent.	T2 I think this child’s language is relatively standard.
Emotional engagement	Students’ positive or negative reactions to teachers: (1) students respond to the teacher quickly or in chorus; (2) students show their emotions.	T1 A lot of students responded quickly. T2 I didn’t know who said it, but I heard the sound, ‘Wow.’
Behavioural engagement	The act of taking part in academic activities.	T2 I saw the students nodding.
Independence	Students do something on their own.	T3 He supplemented it by himself.
Teaching effectiveness	Teaching makes students learn effectively or attains lesson objectives.	T3 Well, in this way, the composite functions were clear to all of us.
Teaching appropriateness	Teaching behaviours are appropriate or obey some rules or requirements.	T3 I saw my drawing at that time; oh, I did not graph well again.
Classroom environment	The physical environment of a classroom.	T2 The bell kept ringing until you pressed it. It was too loud to hear.
Mathematics textbook	It usually refers to the arrangement of mathematics content.	T2 I had a look at the textbook. It didn’t provide the tables of common logarithms and natural logarithms.

). Instruction was mainly perceived on its effectiveness and appropriateness. Students’ behaviours included four aspects: cognitive accuracy, emotional engagement, behavioural engagement, and independence.

3.4.2. Teacher Appraisals

In light of Scherer’s [23] SECs, the reciprocal model of Frenzel, Fiedler, Marx, Reck, and Pekrun [33], and the data in this study, nine appraisal dimensions of teacher emotions were identified: (1) novelty; (2) intrinsic pleasantness; (3) outcome probability; (4) causal attribution; (5) discrepancy from expectation; (6) goal/need conduciveness or attainment; (7) coping potential; (8) internal standard; (9) external standard (see

Table 3. Coding schemes of teacher appraisals.

Code	Descriptions	Examples
Novelty	Classroom event is sudden, unfamiliar, unpredictable, or not.	T1 In my previous teaching, I didn’t see the students respond so quickly.
Intrinsic pleasantness	The classroom event itself is (un)pleasant for the teacher.	T2 This child was actually very cute.
Causal attribution	Classroom event is caused by the teacher or students’ behaviours and caused un/intentionally.	T1 The person who answered this question was the commissary in charge of studies in our class.
Outcome probability	The consequences of the classroom event are predictable or not.	T1 I thought that it was not easy for the student to figure the problem out.
Discrepancy from expectation	The classroom event is (in)consistent with the teacher’s expectations.	T3 They unexpectedly proposed these (properties) by themselves.
Goal/need conduciveness/attainment	Consequences of the classroom event meet the teacher’s goal/need or not.	T1 He used appropriate language to remedy my embarrassment properly.
Coping potential	The teacher can control or has power over the consequences of the classroom event.	T3 Even if I erased them, I was not sure that I could graph better next time.
Internal standard	Classroom event is (in)congruent with the teacher’s standards and self-ideals.	T1 Doing exercises must be standardized, standardized.
External standard	Classroom event violates or follows socially or professionally accepted teaching habits/norms.	T3 The supplementary descriptions should be after the definition. The textbook presents this here directly.

).

3.4.3. Emotional Responses: Emotion Categories

In this study, four aspects provided by the teacher were used to label emotion categories: (1) emotion terms or phrases (e.g., happiness, worry), (2) dimensional descriptions (e.g., feeling good or bad), (3) descriptions of emotional processes (e.g., triggering situations, appraisals), and (4) verbal or facial expressions in classrooms [7,26]. Emotion terms used by the teacher were usually viewed as the corresponding emotion labels and were translated from Mandarin to English. The meanings of English and Mandarin emotion terms were double-checked during this translation process, based on the Cambridge Dictionary, Modern Chinese Dictionary, and existing literature. There were 22 types of emotions (see

Table 4. Code schemes of emotion categories.

English Code	Mandarin Terms	Examples
Satisfaction	manyi, tinghao, henhao, henbang	T3 On the whole, I was satisfied with it.
A sense of fulfilment	chongshigan	T2 After this whole lesson, I had a sense of fulfilment that did not appear in my previous classes.
A sense of accomplishment	chengjiugan	T2 I had a feeling of accomplishment.
Happiness	kaixin, xiyue	T1 Right, I was a bit happy at this time.
Amusement	haowan, lequ, xiaota, tingdou	T2 She used a word that amused me at that time.
Astonishment	jingxi, qiguai, jingqi	T3 Much to my astonishment, the students unexpectedly and independently proposed $x=1$ as a boundary.
Excitement	xingfen	T1 I felt excited now.
Pride	dese	T3 I thought it was very good, and I was proud of it.
Relaxation	qingsong	T2 So, I felt relatively relaxed in recent lessons.
Empathy	lijie	T1 I fully understood this kind of student behaviour.
Relief	bushi da wenti	T2 But when I thought about this thing again, actually, it was not a big problem.
Surprise	yiwai, jingya	T1 I felt surprised at that time.
Confusion	kunhuo, yihuo, yiwen	T1 I felt more confused at that time.
Sadness	shangxin	T1 I felt a bit of sadness later.
Disappointment	diluo, shiluo	T1 At this time … (I) felt very disappointed.
Helplessness	wuzhu	T2 I also felt helpless when I was teaching this.
Worry	danxin	T1 I was also worried about similar things occurring.
Anger	fapiqi	T2 I had felt happy; so, I did not lose my temper.
Annoyance	fan	T2 It was annoying; It was too loud to hear.
Shame	buhao yisi	T3 I was too ashamed to revise them.
Embarrassment	ganga	T1 He used proper words to remedy my embarrassment.
Guilt	zize	T2 I felt a bit guilty at that time.

).

3.4.4. Emotional Responses: Expressive Displays

Based on the teacher’s facial expressions and verbal language, teacher emotions in classrooms were coded as positive or negative emotions (see

Table 5. Expressive displays of teacher emotions.

Emotion	Facial Expressions or Spoken Language
Positive emotions	Eyes sparkle, mouth drawn back at corners, upper lip raised, laughing, smiling, grinning; praise, such as ‘very good’.
Negative emotions	Corner mouth depressed, inner corner eyebrows raised (sadness); eyebrows raised, mouth open, eyes open (surprise); lips compressed, a furrowed brow, eyes wide open, head erect (anger); negative language, such as ‘What’s wrong with you guys, in your head?’

).

3.5. Validity and Reliability

To guarantee the validity of this study, four strategies were employed: (1) prolonged engagement and persistent observation for around two months; (2) confidentiality; (3) triangulation among interviews, video, and observation; (4) detailed descriptions of results [37].

To enhance the reliability of this study, double-checking, constant comparison, and cross-check codes were adopted [37]. Two researchers independently coded transcripts of six emotional teaching episodes and one lesson video. After coding, the codes were compared, and disagreements were discussed. The percent agreement was about 94%, indicating good interrater consistency [37].

4. Results

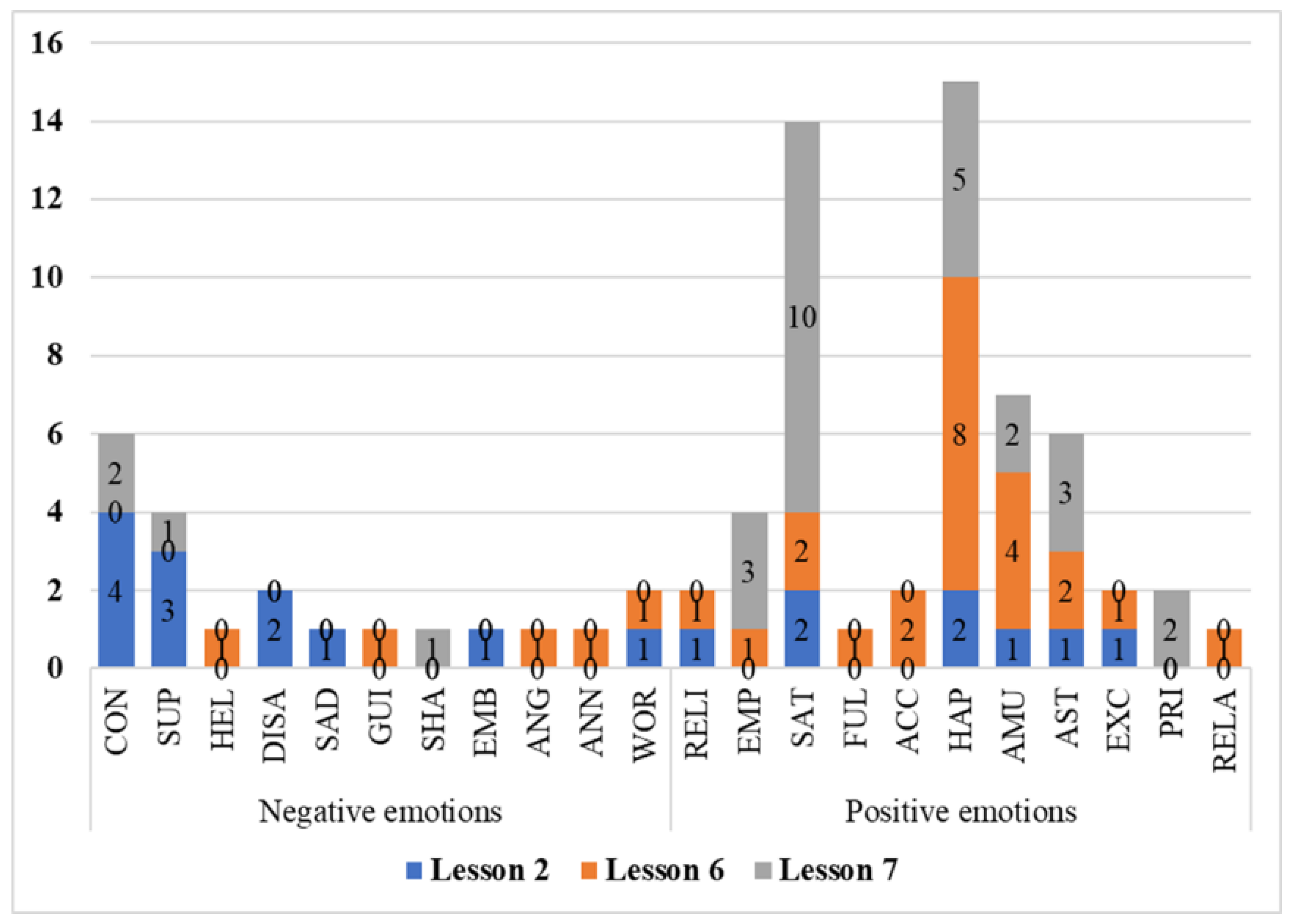
4.1. Emotion Categories Experienced in Classrooms

In total, 26 emotional teaching episodes were identified in the three lessons, with Lessons 2, 6, and 7 involving 5 (E2.1–E2.5), 11 (E6.1–E6.11), 10 (E7.1–E7.10) episodes, respectively.

During these episodes, 22 types of emotions were experienced 77 times (see Figure 2). Positive emotions were more frequent (56 times) than negative emotions (21 times). Happiness (15 times) and satisfaction (14 times) were triggered most frequently, followed by amusement (seven times) and astonishment (six times). Confusion (six times) and surprise (four times) were experienced most often as negative emotions by Susie. Shame (including embarrassment, guilt, shame, three times) and sadness (including disappointment and sadness, three times) were also more common than anger (including anger and annoyance, twice) and worry (twice).

4.2. Emotional Pattern: Perceptions, Appraisals, and Emotional Responses

An emotional process in classroom practice usually followed a three-stage pattern: perceptions, multilevel appraisals, and emotional responses. According to the results of data analysis, we refined the process model of teacher emotions in classrooms (see Figure 3).

The teacher’s perceptions of classroom events initially triggered an emotional process involving students’ behaviours, teacher instruction, mathematics textbooks, and the classroom environment. Among these, students’ cognitive accuracy was perceived most often (48 times). Behavioural engagement (14 times) and emotional engagement (10 times) ranked in the middle. Teaching effectiveness (five times) was perceived more often than students’ independence (four times) and teaching appropriateness (three times), followed by mathematics textbooks (twice) and classroom environments (once).

After this, teacher perceptions of an event were evaluated from nine dimensions: (1) novelty; (2) intrinsic pleasantness; (3) outcome probability; (4) the discrepancy from expectation; (5) goal/need conduciveness or attainment; (6) causal attribution; (7) coping potential; (8) internal standard; (9) external standard. Among these, the most frequent dimension was goal/need conduciveness or attainment (27 times), followed by discrepancy from expectation (19 times) and causal attribution (18 times).

Following the perceptions and appraisals, the teacher labelled her feelings and displayed her emotions selectively in the classroom through facial expressions or implicit language. For example, when Susie felt happy, she smiled and said ‘very good’ instead of specific emotional terms. When Susie was disappointed, she said, ‘after a holiday, you become stupid again. What is left in your mind?’

Two examples were given to elaborate on this emotional pattern.

4.2.1. Happiness

In E6.5, Susie asked students to show their answers to exercises about the transformation from exponentiations to logarithms ($2^3=8, 2^5=32, 2^{-1}=\frac{1}{2},{27}^{-\frac{1}{3}}=\frac{1}{3}$). The students gave the right answers:

T: Before I teach the property of operations, open page 64 of the textbook, page 64 … there are several exercises. We are going to invite students to answer them. The first one (2³ = 8), S2.

S2: The first one is log, regarding 2 as the base, 8 as the antilogarithm ($lo{g}_{2}8$).

T: Yeah, just say it in a nutshell, base 2 logarithm of 8, right? What does it equal?

S2: 3.

T: 3. Good, very good. Sit down. Sit down. Okay, the desk mate, next one ($2^5=32$)

…

T: It equals −1/3. It is very easy, right? Sit down, please. (E6.5_LT1)

Susie was experiencing happiness during this teaching episode:

Here, I was asking students to do exercises. I thought that the student’s language was standard. What he said was log, base $a$logarithm of $N$. I thought many things were related to teacher guidance … Regarding the accuracy and standardization of language, what I did for all these kids was much better than my previous teaching … I thought that boys are indolent. No matter writing or speaking, they often like omitting as much as possible. So, he based what he did on what I required, I thought it was good … As I told you before, in terms of language ability, they could acquire it when you train students gradually. I thought they were communicating with me in a rigorous way; hence, I felt pretty happy. (E6.5_1)

The excerpt above illustrates Susie’s perceptions of the accuracy of students’ answers, her appraisals, and her emotional responses. Susie perceived that the students were expressing their ideas with accurate language. She evaluated the perceptions from three dimensions: causal attribution, goal/need attainment, and discrepancy from expectation. First, Susie attributed the students’ rigorous language to her guidance. Second, Susie interpreted students’ use of standard language as goal accomplishment (i.e., improving students’ language ability). Third, in Susie’s expectation, boys were usually too lazy to use standard language, whereas they rigorously expressed their ideas. After these, Susie felt happy and expressed it by saying ‘very good’ and ‘it is so easy, right’ in the classroom, as shown in E6.5_LT1.

4.2.2. Shame

In E7.9, when Susie and her students were drawing graphs of two functions: $\mathrm{y}={\log }_{2}x$, $\mathrm{y}={\log }_{\frac{1}{2}}x$, Susie felt ashamed of her ugly graphs. Her narrative excerpt illuminates her perceptions of the classroom event, her appraisals, and her emotional responses:

When I took a close look at [the graphs], oh, so ugly. Yeah, when I saw my drawing at that time, oh, I did not graph well again. However, I was too ashamed to revise them because it was difficult to draw five points and connect them via a line. Even if I erased them, I was not sure that I could graph better next time … As always mentioned by teachers in our subject group, if the teachers do not organize their blackboard writing and language well, what can they instruct the students, right? (E7.9_1)

The excerpt suggests that Susie perceived the inappropriateness of her graphing and evaluated her perception from two aspects: external standards and coping potential. Teachers were socially required to have good blackboard writing as role models as an external standard. However, contrary to the external standard, Susie did not draw the graphs of functions well, and she also had no power to improve her drawing. Therefore, she felt ashamed of her ugly graphs. Susie labelled her shame but did not display it in the classroom.

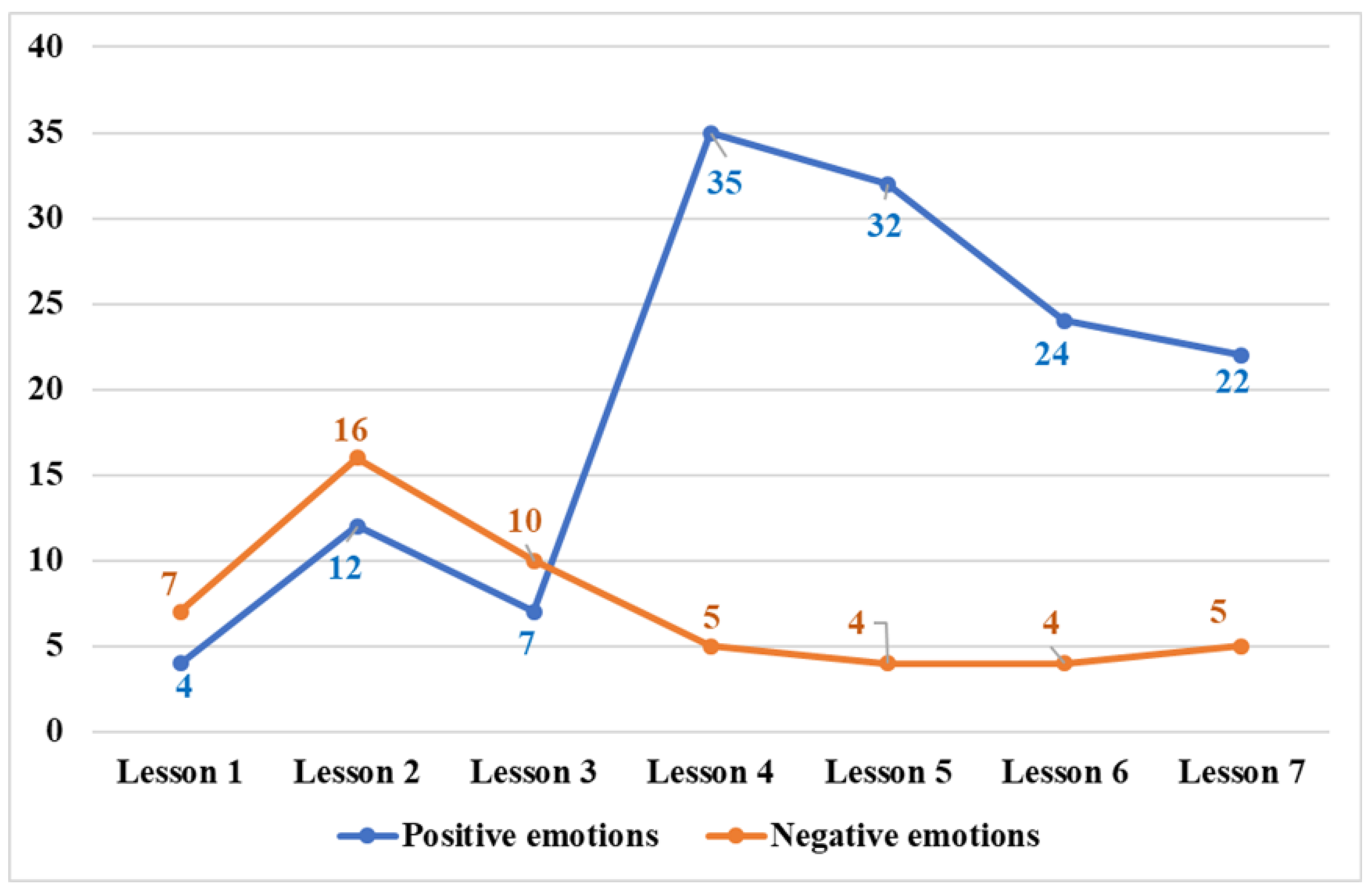
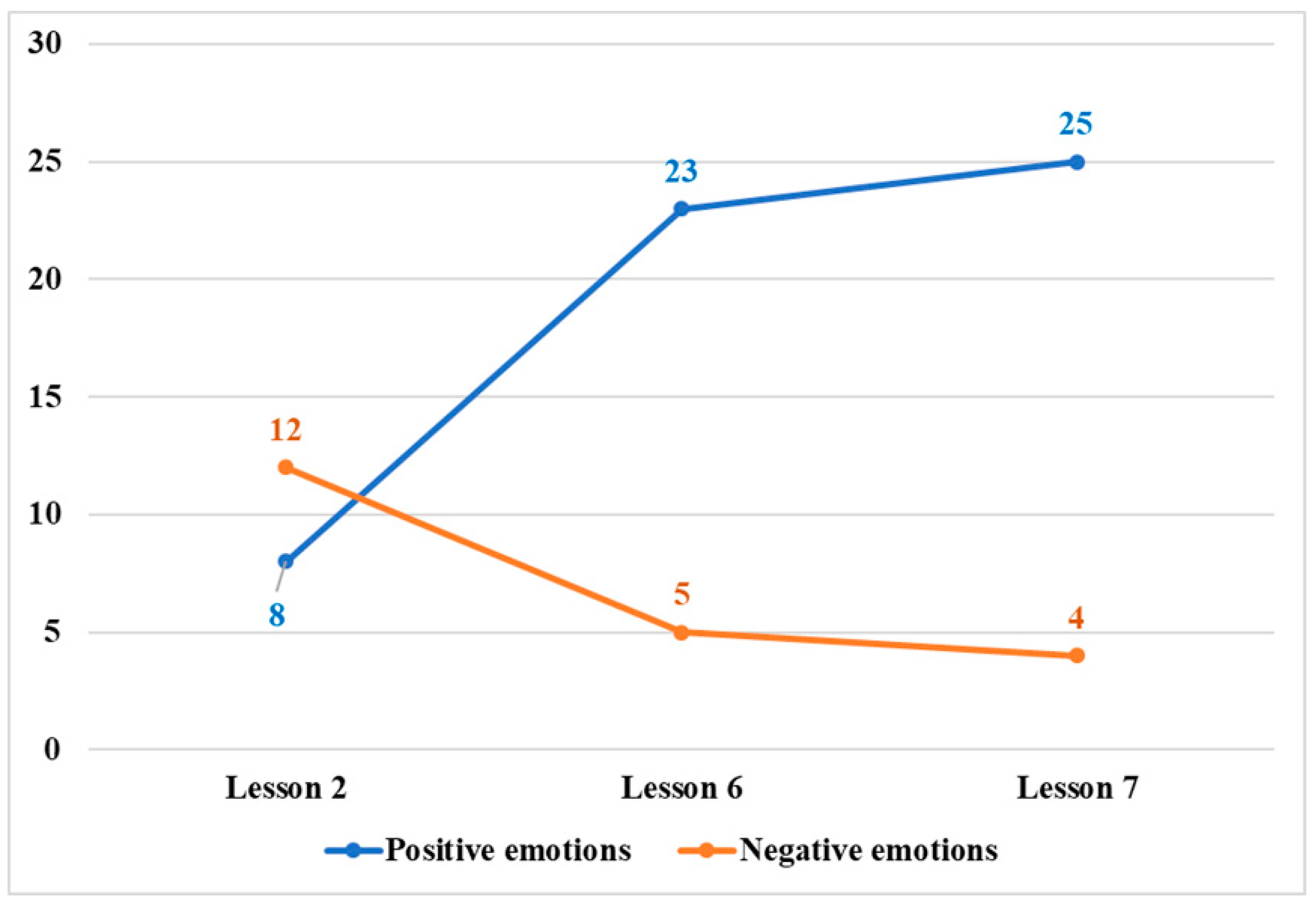
4.3. Emotional Dynamics in Mathematics Classrooms

4.3.1. Hierarchy and Accumulation of Teacher Emotions during Teaching

The teacher’s emotions during teaching followed a hierarchical and cumulative process, changing with the evolution of classroom practices and appraisals. Specifically, faced with the same classroom event, Susie experienced different parallel or sequential emotions because of hierarchical appraisal dimensions or reappraisals. Moreover, various emotions accumulated or intertwined as the classroom events proceeded. For instance, positive emotions gradually accumulated and reached a high intensity or a stable status. As Susie said, ‘I gradually felt happier and happier … Therefore, in recent lessons, I felt relatively relaxed … Indeed, it was. As I said, [emotion] is a cumulative and gradual process’ (E6.2_3). Susie’s happiness also weakened her anger towards students’ misbehaviours; for example, Susie said that ‘he did not do the allocated exercises until I corrected him … Because I was already happy at that time, I did not lose my temper towards him.’ (E6.9_1).

E2.1 was also detailed as an example to elaborate on these characteristics, which was about recalling previous knowledge of even functions. In E2.1, Susie experienced surprise, confusion, disappointment, and worry sequentially after different dimensional appraisals. Furthermore, surprise and confusion lasted for a period and became more and more intense, with the classroom practice proceeding. During this process, Susie tended to compress her lips and use implicit language to indicate her negative emotions. The teaching excerpt was presented as follows (see E2.1_LT1).

T: Let’s consider what we learned about evenness and oddness of functions in the lesson before the holidays.

(Pause for students’ thinking)

T: In terms of evenness and oddness, what knowledge did we learn? Think about it! S1.

S1: $f\left(x\right)=f\left(-x\right)$.

T: Only $f\left(x\right)=f\left(-x\right)$.What is it (The teacher tries to smile, lips then compress)?

(Pause for students’ thinking)

T: Hmm? This notation, what does it mean by $f\left(x\right)=f\left(-x\right)$that you said? Do you remember it?

T: Do you have the impression we discussed this symbol $f\left(x\right)=f\left(-x\right)$, right?

T: Well. Let’s think about it. What does this symbol describe? This equation is used for what, for who? (Lips compress)

T: Okay. Sit down. Please think about it. Okay, S2.

(S2 stands up)

T: What did we use it to do?

S2: To describe the definition of even functions.

T: Even function definition, isn’t it? Okay, we gave the definition of an even function. So how did we define even functions?

S2: For the function $f\left(x\right)$, if for any $x$in the domain, there exists $f\left(x\right)=f\left(-x\right).$

T: This is the even function, isn’t it? That’s too complicated to say. And if we were to memorize every concept that way, it would be too tedious, right? Extract the key information from this. What does an even function need to satisfy?

(The whole class is going to answer, S2 is thinking)

SS: The domain is symmetric about the origin.

T: Okay, let him summarize it! Can you sum it up? It’s so simple. Just extract the key information from it, isn’t it? (Lips compress)

T: Okay. Let’s help him refine it. What is it?

SS: For.

T: Domain?

SS: Symmetric about the origin.

T: Yeah, we required that for any $x$in the domain, isn’t it? Its function value is equal to the function value of its opposite number. Isn’t it? So here, we need to notice that any $x$has a minus $x$; it requires the domain to be symmetric about the origin.

(The teacher is writing on the blackboard)

T: This is the first one. Okay. After this domain is symmetric about the origin, we need to make a further requirement. There are a lot of functions whose domain is symmetric about the origin, isn’t it? But some of these functions are even, not all of them. So what functions are even? What do they need to meet? $f\left(x\right)=f\left(-x\right)$. Isn’t it? Yes, please have a seat.(E2.1_LT1)

As described above, Susie first asked a student, S1, to tell her what they learned in the previous lesson. However, S1 only gave a formula $f\left(-x\right)=f\left(x\right)$ without any explanation, even though Susie had repeatedly required the student to do so. Susie felt surprised and confused after evaluating the event from the perspectives of discrepancy from expectation and coping potential:

I experienced some emotional fluctuations here. Um, what were they? I felt very surprised at that time. When I asked a student Li, what surprised me? … I was asking what content we learned in the previous lesson. The first student stood up and only said a [formula]: $f\left(-x\right)=f\left(x\right)$. I said you gave me such abstract formula, what you wanted to express. She thought about it for a long time but said nothing. I was unsure whether she did not remember [the content] because of being shelved during the National Day holidays or she couldn’t express her ideas due to [poor] language organization ability. (E2.1_1)

Susie’s surprise and confusion were ongoing. Susie asked S2 to explain what $f\left(-x\right)=f\left(x\right)$ was used for. S2 gave a complete definition of the even functions but did not extract key points from it, as Susie required:

Then, I asked another student … what we taught [using the formula] … after he finished stating the concept, I asked him to extract [key information]. But he unexpectedly could not extract them. I felt [confused and surprised] again. Was the concept too difficult to understand? Or was the key information really very difficult? (E2.1_2)

The surprise and confusion of Susie were derived from discrepancies from expectations and low coping potential. Susie expected the student to be able to extract two key points from the definition of even functions; however, it was not the case. Meanwhile, Susie could not understand why the students performed poorly.

Student S2′s reactions also elicited Susie’s disappointment after she interpreted the situation as a failure of her teaching goal:

In fact, when I asked this question, I also had a bit of disappointment in addition to surprise. [I] felt, actually, we already taught this [i.e., even functions]. If he really internalized it as part of his own knowledge, there was no doubt that he could express his idea fluently in response to my question … so I felt a bit disappointed at that time. (E2.1_3)

Feeling surprised, confused, and disappointed, Susie turned to invite the whole class to describe the two key points. Most students responded to Susie’s question correctly, which made her even more confused about the former two students’ reactions:

Then, when I helped students to understand the information, most of the students did speak the two pieces of information out: the domain of functions and relational expression between two functional values (i.e., $f\left(-x\right)$, $f\left(x\right)$). Hence, I felt more confused at that time. (E2.1_4)

After experiencing more intense confusion, Susie started to worry that a similar situation would probably happen in the future:

Actually, abstract things are challenging to accept … If I ask other students, the same may be true. Even though their language expression ability is good in daily life, I was also worried about the appearance of similar situations. (E2.1_5)

The above excerpt indicates that Susie evaluated the teaching situation from the perspective of outcome probability. It could be predicted that other students with good language abilities would also make the same mistake. Therefore, Susie felt worried.

4.3.2. Emotional Changes in a New Semester

Susie’s emotions changed from being more negative at the beginning of the first semester in a new school year to more positive in the middle of the semester. Various data substantiated the result.

First, the classroom videos provided enough evidence of Susie’s emotional changes in the classroom (see Figure 4). In Lessons 1, 2, and 3, Susie exhibited negative emotions (e.g., frown) 7, 16, and 10 times, respectively, more often than positive emotions (4, 12, and 7 times, e.g., smiling). However, starting with Lesson 4, the frequency of displaying positive emotions (35, 32, 24, and 22 times) was much more than that of showing negative emotions (both around 4). In addition, laughs or smiling after Lesson 3 often lasted longer than in Lessons 1–3.

Second, Susie’s self-report of emotions in three lessons revealed that she became increasingly positive from Lesson 2 to Lesson 7 (see Figure 5). Susie reported positive emotions 8 times but negative emotions 12 times in Lesson 2. In contrast, in Lessons 6 and 7, Susie experienced far more positive emotions (23, 25 times) than negative emotions (5, 4 times).

Third, this changing trajectory in emotions was consistent with the researcher’s classroom observations. In Lesson 1, on 27 September 2017, Susie’s smiles or positive feelings were seldom perceived. Susie often showed a stern face, and the observer also felt a bit suppressed in the class. However, starting from Lesson 4, on 16 October 2017, the observer found that Susie began to smile in the classroom frequently, and the classroom climate became more obviously comfortable.

Fourth, noticing that Susie’s emotions in the classroom had become more positive, the researcher interviewed Susie about this. Susie admitted that she had become increasingly happy and smiled more frequently in her mathematics classrooms and explained why:

I also felt that I had smiled too many times in front of them recently [laughter]. I thought, previously, I had to spend a lot of energy dealing with their daily affairs, while recently, they caused me fewer troubles. Therefore, I think if a teacher spends a lot of time dealing with students’ problems every day, does he/she have enough energy to conduct classroom teaching with pleasure? I think it is challenging. Actually, I found that our class has gradually acquired a good learning atmosphere. In the beginning, it did not exist because the students were not used to the environment and probably paid less attention to learning … This is what I just observed recently. There is a sign of this, which I didn’t notice before. In addition, there is another thing. What is it? I got to know that there were some tests in some other subjects, and the teachers also informed me of the students’ grades. I found that their grades are good, and their performance is also good … I initially thought that students’ active performance was superficial, and they did not learn well in essence. However, they indeed learned well. I found that the phenomenon [active classroom performance] was identical to the learning outcome. (T2)

The excerpt above suggests that three changeable factors perceived by Susie contributed to her emotional changes in classrooms: (1) fewer class affairs or troubles to deal with; (2) a positive learning climate that had been established gradually; and (3) students’ more active engagement and good achievement.

5. Discussion

To improve the quality of teaching and the well-being of teachers and students, it is necessary to fully understand the emotional dimension of teaching. This study offers a snapshot of the complex and dynamic nature of a senior secondary school mathematics teacher’s emotions, combining teacher self-reporting with classroom videos and observations. Three main findings are summarized, which are worthy of discussion.

5.1. What Types of Emotions Are Frequent for the Senior Secondary Mathematics Teacher?

In response to the first research question, Susie experienced multiple emotions during classroom practices, with positive emotions being more frequent than negative emotions. Among all emotions, happiness and satisfaction were the most common. These findings align with previous studies [2,25], indicating that Chinese students’ higher level of negative emotions shown in previous studies [16,17] probably do not arise from teachers’ negative emotions in classrooms. One main reason for the results is that quality teacher–student interactions in the classroom may increase Susie’s positive emotions and decrease negative emotions [3]. Another possible explanation may relate to sociocultural factors, which, to some extent, determine which, when, where, and why emotions are experienced. The sociocultural factors are embodied by the emotional rules of teaching in China [13,38]. Teachers in China are expected to obey three emotional rules: teaching with passion, maintaining and displaying positive emotions, and hiding negative emotions [13]. Accordingly, Susie regulated her emotions in the classroom and reported comparatively high levels of positive emotions and low levels of negative emotions.

In terms of negative emotions, confusion and surprise were experienced most often. The results are similar to those obtained in the study of Martínez-Sierra, Arellano-García, Hernández-Moreno, and Nava-Guzmán [26] but differ from most existing studies, which found anxiety and anger to be the most frequent [2,25]. These differences are probably associated with teachers’ teaching experience. The teachers in the studies of Bahia, Freire, Amaral, and Teresa Estrela [25] and Uzuntiryaki-Kondakci, Kirbulut, Oktay, and Sarici [2] had rich teaching experience (almost more than 10 years). In contrast, the participant in Martínez-Sierra, Arellano-García, Hernández-Moreno, and Nava-Guzmán [26] and the teacher in the current study were novice teachers and only had a teaching experience of less than six years. In addition, Susie had just finished a cycle from Grade 10 to Grade 12 mathematics teaching. Susie’s existing knowledge possibly did not match incoming information, and she might also lack the abilities to understand the unexpected students’ reactions. Therefore, Susie had frequent confusion and surprise.

Shame and sadness were also experienced more frequently than anger, which is probably related to the teachers’ roles in Chinese culture. In China, teachers are given high expectations and responsibilities and compared to ‘silkworms’ and ‘candles’ who selflessly devote themselves [13]. In this sense, Chinese teachers are more likely to feel ashamed about their poor performance and feel sad toward students’ poor performance, rather than anger that is seen as incompatible with the professional role of a teacher. Another reason may be the good discipline in senior secondary classrooms. Compared with other primary and junior secondary students, senior secondary students have more explicit learning goals and stronger self-regulation abilities. Hence, senior secondary classrooms may feature fewer rule violations and misbehaviours, which have been found to be the primary sources of anger [1,28].

5.2. What Pattern Is Extracted from the Emotional Experiences?

This study proposed the process model of teacher emotions in classrooms (see Figure 3) and characterized the emotional process into three stages: perceptions, multilevel appraisals, and responses. The teacher selectively perceived the classroom event, evaluated it from multilevel dimensions, and then exhibited physical or verbal expressions. These findings are consistent with the appraisal theories and emotion process models in the psychological field [7,21], expanding the reciprocal model of Frenzel [30].

At the perception stage, the cognitive accuracy of students triggered mathematics teacher emotions most frequently, followed by students’ behavioural and emotional engagement and teaching effectiveness. These results align with existing research, verifying that teachers’ teaching and students’ behaviours mainly elicit teacher emotions [3,12]. These findings are also different from some Western studies, which proposed students’ social-emotional (e.g., discipline) and relational behaviours as the most important triggers [e.g., 28,29]. These differences are probably related to the examination culture in China. The senior secondary teachers and students are faced with the national college entrance examination, which is the most influential exam in China. As the ‘baton’ of teaching and the most important indicator of college entrance and school quality, this examination stresses the mathematics subject and high academic achievement. This led to the phenomenon that students put almost all their effort into learning instead of discipline violations and misbehaviours, and the teacher pays more attention to academic performance. Therefore, students’ cognitive accuracy was perceived most frequently.

At the appraisal stage, the classroom event was evaluated from nine appraisal dimensions: (1) goal/need conduciveness or attainment; (2) causal attribution; (3) discrepancy from expectation; (4) novelty; (5) intrinsic pleasantness; (6) outcome probability; (7) coping potential; (8) internal standard; and (9) external standard. One emotion was often a result of cumulative appraisals, which is in line with the study of Scherer [23]. Among the dimensions, the former three were the core appraisals dimensions, supported by Martínez-Sierra, Arellano-García, Hernández-Moreno, and Nava-Guzmán [26] and Hagenauer and Volet [27]. They found the goal/norm and discrepancy from expectation to be the most common appraisal type, respectively. The findings also extend the reciprocal model of Frenzel [30] and Frenzel, Fiedler, Marx, Reck, and Pekrun [33] by adding discrepancy from expectation and causal attribution dimensions as the core appraisals.

These core appraisal dimensions in this study may be explained by the features of mathematics education in China. First, teaching is a goal-directed behaviour, explaining why goal/need conduciveness or attainment is the core appraisal dimension. Second, Chinese teachers usually emphasize coherence more and have higher expectations for their students to succeed [14,34]. They carefully analyse students’ learning backgrounds before teaching and then design and deliver mathematics lessons in a coherent way. The teachers also communicate their expectations explicitly or implicitly to their students through classroom practice. Therefore, the teacher often compared her students’ learning with her expectations. Third, the role model of teachers is essential in the whole class teaching, while students are required to put in hard work and perseverance in their study in China [14]. Accordingly, the teacher was inclined to attribute students’ success or failure to her good model or her students’ effort.

At the emotional responses stage, Susie selectively expressed her emotions through facial expressions and implicit spoken language in the classroom instead of using emotional terms directly. This phenomenon is probably related to the mathematics subject and Chinese culture [13]. First of all, mathematics is a rational and objective subject, often excluding emotions in the mathematics classroom. Unlike for the teachers who teach humanities and social sciences subjects, the expression of emotions from mathematics teachers is more likely to be not considered professional. Next, emotions are regarded as conflicting with reason, and ‘face work’ and implicit and temperance expressions are emphasized in China. Hence, to maintain a suitable learning environment and the teacher’s dignity, the teacher usually controls the ways and frequency of emotional expressions.

5.3. How Do Mathematics Teacher Emotions Change in Classrooms?

Teacher emotions in the classroom constitute a hierarchical and cumulative process. Susie usually interpreted a classroom event from multilevel dimensions and experienced various emotions in sequence. As teaching proceeds, emotions of the same valence (positive or negative) accumulated gradually and reached a peak or a stable status. Sometimes, positive emotions also interacted with negative emotions. These findings align with the appraisal theories, educational research on emotional exhaustion [24], and neuroscientific research on emotions [22]. As Scherer [23] proposed, multidimensional appraisal results can yield sequential and cumulative effects on emotions.

In addition, teacher emotions changed from more negative at the beginning of the first semester in a new school year to more positive in the middle of the semester. This dynamic feature of teacher emotions in classrooms is in accordance with the findings of Chen, Shi, Zhang, and Qu [9] that teacher emotions in real-life events varied with three scales of time (i.e., calendar year, calendar month, and academic semesters). This result also corroborates the idea of Roth and Walshaw [39], who indicated that emotion changes in the course of activity and finally manifests positively. Susie explained that her emotions changed with the class characteristics, including: (1) fewer class affairs or troubles; (2) a more favorable learning climate; and (3) more active engagement and better academic performance of the whole class of students. Accordingly, Susie, as a class teacher, had more energy to focus on her teaching and was more likely to feel positive during teaching. A significant increase in positive emotions from Lesson 3 to Lesson 4 is mainly because the teacher became familiar with the students’ high scores in other subjects’ tests. The decreases in positive emotions from Lesson 4 to Lesson 6 are probably related to two reasons. First, as time passed, the effect of students’ good performance in other subjects on teacher emotions gradually reduced. Second, the teaching schedule possibly had an impact on teacher emotions. The teacher was probably more energetic on Monday and Tuesday (Lessons 4 and 5) than on Thursday (Lesson 6).

6. Conclusions and Implications

The present study offers insights into the patterns and dynamics of a novice mathematics teacher’s emotions during senior secondary teaching, providing theoretical, methodological, and practical implications for stakeholders.

6.1. Theoretical Implications

The most important contribution of this study is the proposal of the process model of mathematics teacher emotions in classrooms and identifying the dynamic features of teacher emotions across appraisals and time. These findings extend the theories and process model of emotions from the psychological field to educational research and enrich the research on teacher emotions. In addition, it complements the characteristics of multi-dimensionality and dynamics of teacher emotions proposed by Chen, Shi, Zhang, and Qu [9] through an in-depth qualitative analysis of an individual teacher’s appraisals within mathematics classrooms.

This study also offers rich information regarding Chinese mathematics teachers’ emotions, which could help better understand the similarities and differences between Western teachers and Chinese teachers. Both Western teachers and Chinese mathematics teachers probably experience positive emotions more frequently than negative ones during teaching, with happiness and satisfaction being the most common. It may be a universal emotional characteristic of teaching across different countries. Unlike Western teachers, Chinese mathematics teachers in senior secondary schools may perceive their students’ achievement behaviours more often than social-emotional ones (e.g., discipline). Apart from goal/need conduciveness or attainment emphasized in Western studies, Chinese mathematics teachers may also focus more on appraisals of discrepancy from expectations and causal attribution. These results imply that classrooms in distinct cultural contexts could be distinguished from not only a cognitive dimension but also an emotional aspect.

6.2. Methodological Implications

This study can also provide two methodological implications for future research on teacher emotions. First, the post-lesson, video-stimulated interviews have been identified in this study as a helpful method for examining dynamic and momentary teacher emotions. Interviews in previous research usually aim to recall the most impressive or striking emotions in teachers’ whole professional practices. However, emotions, as transient feelings, are extremely easy to forget, subject to reappraisal, and may become biased. The post-lesson, video-stimulated interviews can stimulate teachers’ recall of recent memories, scaffold fuller descriptions of teaching events and emotions, and reduce the influence of memory bias on the emotional processes.

Second, the process model of teacher emotions and relevant coding schemes may be useful tools for analyzing teacher emotions in future research. Although psychological research on emotions provides many insights into teacher emotions, there is a lack of powerful tools for analysing complex teacher emotions in educational settings. The process model and coding schemes elaborate on the entire emotional process and specific categories of possible constructs. Future research can use these as a reference to analyse data rigorously and understand the complexity of teacher emotions in classrooms.

6.3. Practical Implications

The patterns and dynamics of teacher emotions found in this study have three practical implications. First, this study supports teachers in understanding their emotions in classrooms and changing their attitudes towards emotions. Emotions are ubiquitous during mathematics teaching. Accordingly, mathematics teachers are suggested to recognize, embrace, and analyse their emotions instead of escaping.

Second, this study helps develop various strategies to tackle possible conflicts and regulate early career teachers’ emotions in classrooms, promoting teachers’ positive experiences, well-being, and sustainable professional development. Teacher emotions in classrooms involve three stages and change with teachers’ appraisals and time. Thus, teachers could pay attention to their emotions as early as possible and regulate their emotions in each stage (i.e., perceptions, appraisals). This study also indicates that fewer class affairs, good learning environments, and students’ active engagement benefit the teacher’s positive emotions. Hence, stakeholders can make efforts in these aspects to facilitate teachers’ professional well-being.

Third, this study could provide some theories and empirical evidence for teacher sustainable professional development. In some countries such as China and Portugal, pre-service or in-service teacher professional development programs seldom include an emotional dimension. This preparation is beneficially conducive to a less straining career, which improves the quality of teaching in schools and reduces teacher attrition.

6.4. Limitations and Future Research

The findings of this study should be interpreted with caution due to three research limitations, and future directions are suggested accordingly. First, this study examined one novice and female mathematics teacher’s emotions, limiting the possibility of generalizing the findings to a wide variety of other situations. Future research could expand the results to other subject teachers’ emotions and adopt questionnaires to promote the generalization of these findings. Second, although this study adopted multiple methods to collect data, some biases may exist due to emotion regulation and social desirability. Future research on teacher emotions can incorporate psychophysiological measurement techniques (e.g., electroencephalograph) to detect multiple components objectively [23]. Third, because of the limitation of Susie’s availability, we cannot interview her after lessons in the middle of the period. Although a variety of data showed Susie’s emotional changes in the new semester, future research can employ a longitudinal approach to investigate the dynamics of teacher emotions in a longer period (e.g., a whole school year).