Multistage Economic Scheduling Model of Micro-Energy Grids Considering Flexible Capacity Allocation
Abstract
:1. Introduction
1.1. Application Scenarios of Micro-Energy Grid
1.2. Construction of Micro-Energy Grid Optimization Scheduling Models
1.3. Operation Strategy of Micro-Energy Grids
- (1)
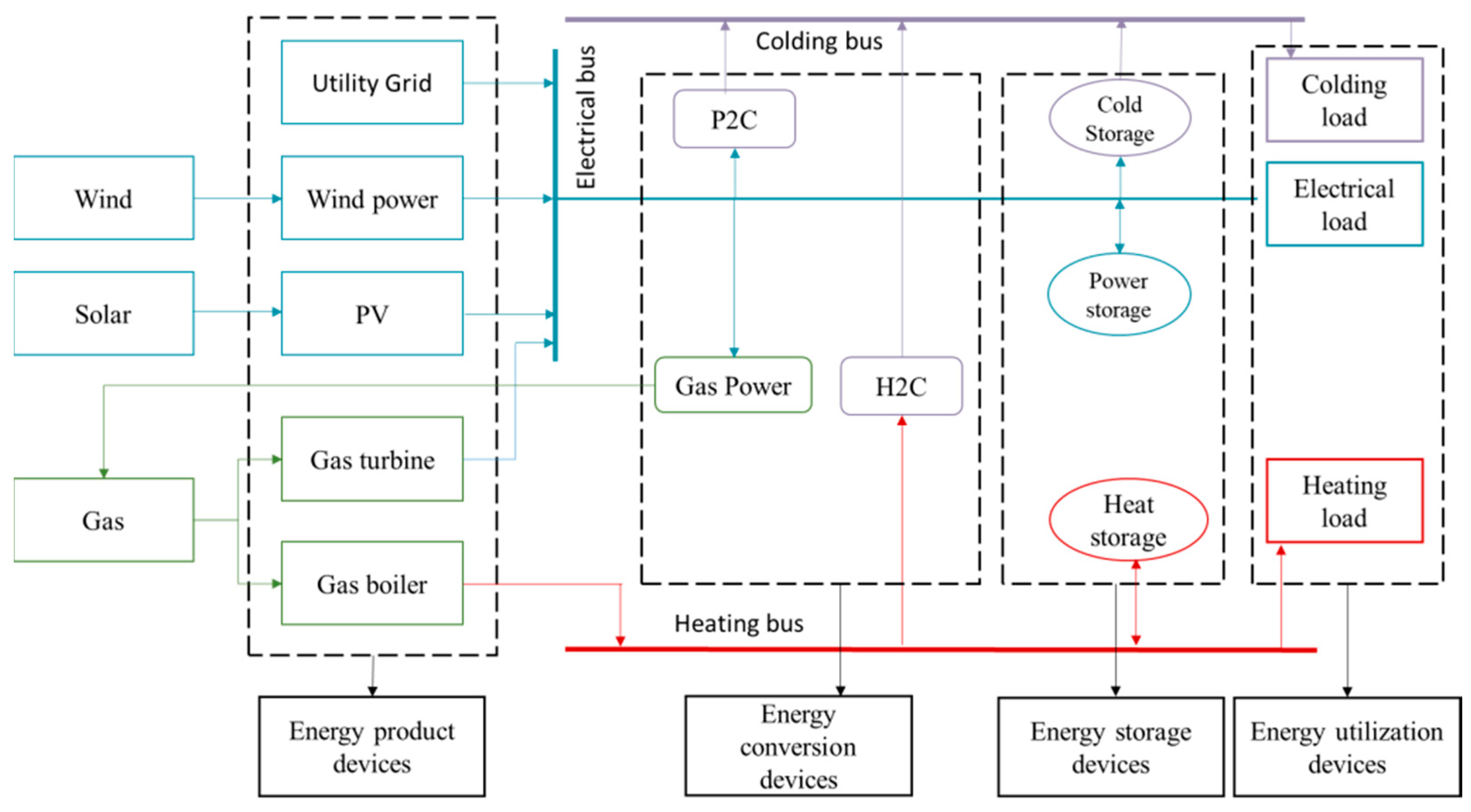
- Building a basic structural framework model of the micro-energy grid and explaining the mathematical model of the essential physical components;
- (2)
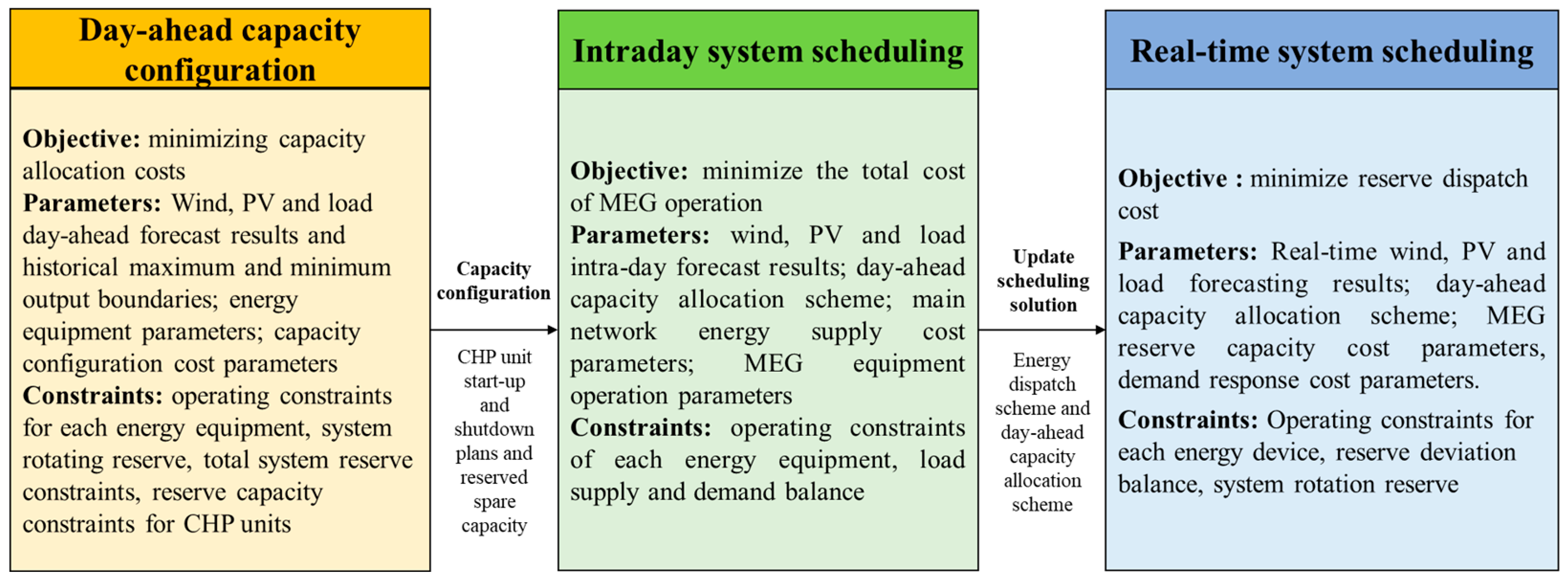
- Building a three-level scheduling optimization model for micro-energy grids, which is divided into three stages: (a) day-ahead capacity configuration; (b) intraday system scheduling; (c) real-time system scheduling.
- (3)
- Using the FCM-CCQ algorithm to describe the uncertainty of wind power and photovoltaics, the typical scenarios were obtained. The optimization calculation was carried out based on the typical scenarios.
- (4)
- Based on CVaR theory, the risk value of the micro-energy grid system participating in spot market transactions was evaluated.
2. The Three-Stage Collaborative Optimization Operation Mechanism for a Micro-Energy Grid
2.1. The Three-Stage Collaborative Optimization Framework of a Micro-Energy Grid
2.2. The Connection Mechanism of the Three Different Stage Models
3. Construction of a Three-Stage Scheduling Optimization Model for the Micro-Energy Grid
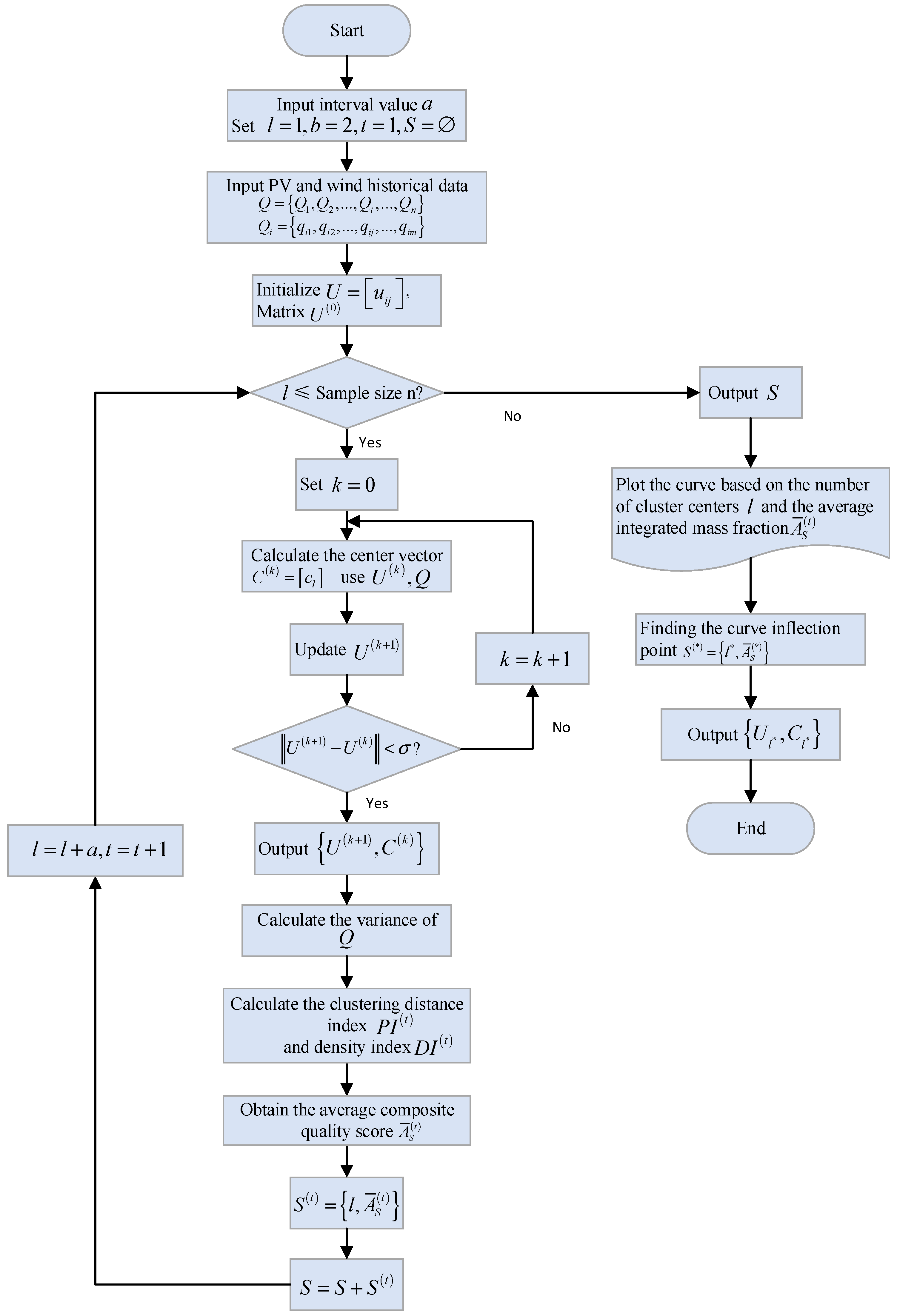
3.1. Uncertain Handling of Wind Power and Photovoltaic Output
3.2. The Construction of a Three-Stage Scheduling Optimization Model for Micro-Energy Grids
3.2.1. The First-Stage Model
- (1)
- The Objective functionIn the day-ahead capacity allocation, since the electricity transaction process is not involved, it is only necessary to control the total cost of the micro-energy grid in the day-ahead capacity allocation stage. Therefore, the target aims to minimize the day-ahead capacity allocation cost. The objective function is shown in Equation (1):It can be seen from the objective function that the total cost () can be divided into three parts: gas turbine capacity allocation cost (), energy storage capacity allocation cost (), and demand response capacity allocation cost (). Among them, the gas turbine capacity allocation cost includes the startup and shutdown cost of the unit, as well as the spare capacity cost.
- (2)
- System constraints
- (a)
- Gas turbinewhere and are, respectively, the maximum and minimum power of the gas turbine, while and are, respectively, the upper and lower reserves of the gas turbine. represents the actual gas turbine power.The functional relationship between the natural gas consumption and power generation of the gas turbine is shown in Equation (8):In the above formula, and are the gas-to-electricity conversion coefficients, is the power generation efficiency of the gas turbine, is the low calorific value of natural gas, and is a 0–1 variable: take 0 to mean gas turbine shutdown; take 1 to mean startup.In addition, the power output constraints and ramp rate constraints of the gas turbine need to be considered. The mathematical expressions are shown in Equations (9) and (10):where and , respectively, represent the upper and lower limits of the gas turbine output and , respectively, represent the boundary value of the gas turbine ramping power between every two time periods.Considering that the gas turbine also produces heat energy while generating electricity, and the thermoelectric power relationship curve is generally a nonlinear relationship, in order to facilitate the solution, this paper adopts the idea of piecewise linearization to linearize the thermoelectric power output relationship and convert it into a general mixed-integer programming problem [26]. The mathematical expressions are shown in Equations (11)–(14).where is the end point electric power value of each segment after the piecewise linearization of the thermoelectric curve; is a binary variable, indicating that the current operating state of the gas turbine is on the piecewise linear function of the segment; is the slope of the linear function of the segment; and represents the heat produced by the gas turbine.
- (b)
- Energy storage battery operation constraintsEquation (15) represents the state transition equation of the energy storage battery. represents the electrical energy stored by the energy storage battery in the time period . ,, and represent the charge and discharge efficiency of the energy storage battery and its self-discharge rate. and are the 0–1 state variables of the charging and discharging of the energy storage battery in the period , respectively; 0 means that the behavior does not occur, and 1 means that the behavior occurs. and are the corresponding charging and discharging power of the energy storage battery in the period.
- (c)
- Demand response capacity constraintswhere represents the actual demand response reserve capacity signed with the power user during the period, and represents the maximum corresponding capacity that the power user can bear.
- (d)
- Abandon wind power and photovoltaic output power constraintswhere and are the power generation of abandoned wind and photovoltaic, respectively, and are the predicted values of wind power and photovoltaic output, respectively.
- (e)
- System rotation reserve constraints:Reference [27] proposed that, in a distribution network with a high proportion of large-scale wind power, photovoltaics, and other highly volatile renewable energy units connected, the scheduling optimization model must consider the system spinning reserve constraints in the micro-energy grid. This constraint also needs to be considered. When there is a deviation in wind power and photovoltaic output, the reserved reserve capacity is enough to balance the deviation.
- (f)
- System total reserve constraints:In the day-ahead stage, the total system reserve should be reserved for the intraday scheduling operation stage to ensure that the basic load requirements of cooling, heating, and electricity are met.where , , and are the reserve coefficients of the cooling, heating, and electric load of the micro-energy grid, respectively.
3.2.2. The Second-Stage Model
- (1)
- The Objective functionThe second-stage model considers two objectives, and the specific indicators can be reflected in the total cost of system operation and the CO2 emissions of the micro-energy grid. However, due to the difference between the two target dimensions, this paper converts the CO2 emissions into penalty costs to measure the economy of the micro-energy grid operation. These two goals can be expressed together, as shown in Equations (27)–(31):where , , , and , respectively, represent the fuel cost of the gas turbine, the power interaction cost between the micro-energy grid and the main grid, the operation and maintenance cost of the micro-energy grid, and the CO2 emission penalty cost in the micro-energy grid. and represent the natural gas consumption of the gas turbine and gas boiler, respectively. refers to the real-time purchase cost of natural gas. and decibels indicate the purchase and sale of electricity. , , and represent the CO2 emission intensity coefficients of gas turbines, gas boilers, and electricity purchased from the grid, respectively. is the penalty coefficient. , , , , , , , , and represent the operation and maintenance costs per unit of electricity for gas turbines, electric refrigerators, waste heat boilers, gas boilers, batteries, heat storage tanks, ice storage machines, photovoltaics, and wind power, respectively.
- (2)
- System constraints
- (3)
- Subsection
- (a)
- Gas turbineCompared to the expression of the gas turbine in the first-stage model, more variables are added here. Among them, are the clearing results of the first stage, which are directly substituted here as boundary conditions.
- (b)
- Gas boilerwhere is the thermal power output of the gas boiler at time , and are the upper and lower limits of the output thermal power of the gas boiler, is the natural gas consumption of the gas boiler, is the energy conversion efficiency coefficient of the gas boiler.
- (c)
- Heat storage tankSimilar to the energy storage battery, the heat storage tank also has a thermal energy state transfer equation, charge/discharge power constraints, and charge and discharge state constraints, as shown in Equations (42)–(46):
- (d)
- Ice CoolerIn the same way, the operating constraints of the ice-cold storage machine are as follows:
- (e)
- Other energy conversion equipmentThe micro-energy grid also includes three types of equipment: electric cooling, gas heating, and thermal cooling. Electric refrigeration equipment converts electrical energy into cold energy, and gas heating generates thermal energy by burning natural gas. These energy conversion devices have different energy efficiencies when switching energy types. For simplicity, this paper uses the form of a matrix to represent the energy conversion process, as shown in Equation (52):where is the cooling power generated by the electric refrigeration at time t. is the thermal power generated by the gas boiler at time t. is the thermal power generated by the heating coil at time t. and , respectively, represent the electricity consumption of the electric refrigerator and the gas boiler at time t. represents the heat of the heating coil at time t. , , and represent the energy conversion efficiencies of the three devices.
- (f)
- Power balance constraintswhere represents the electric power consumed by the electric refrigerator at time t. represents the conversion coefficient of the electric refrigeration machine to cold. and represent the cooling power and charging power of the ice-cold storage machine at all times, respectively. , , and are the cooling load, heating load, and electrical load in the system at time t.
3.2.3. The Third-Stage Model
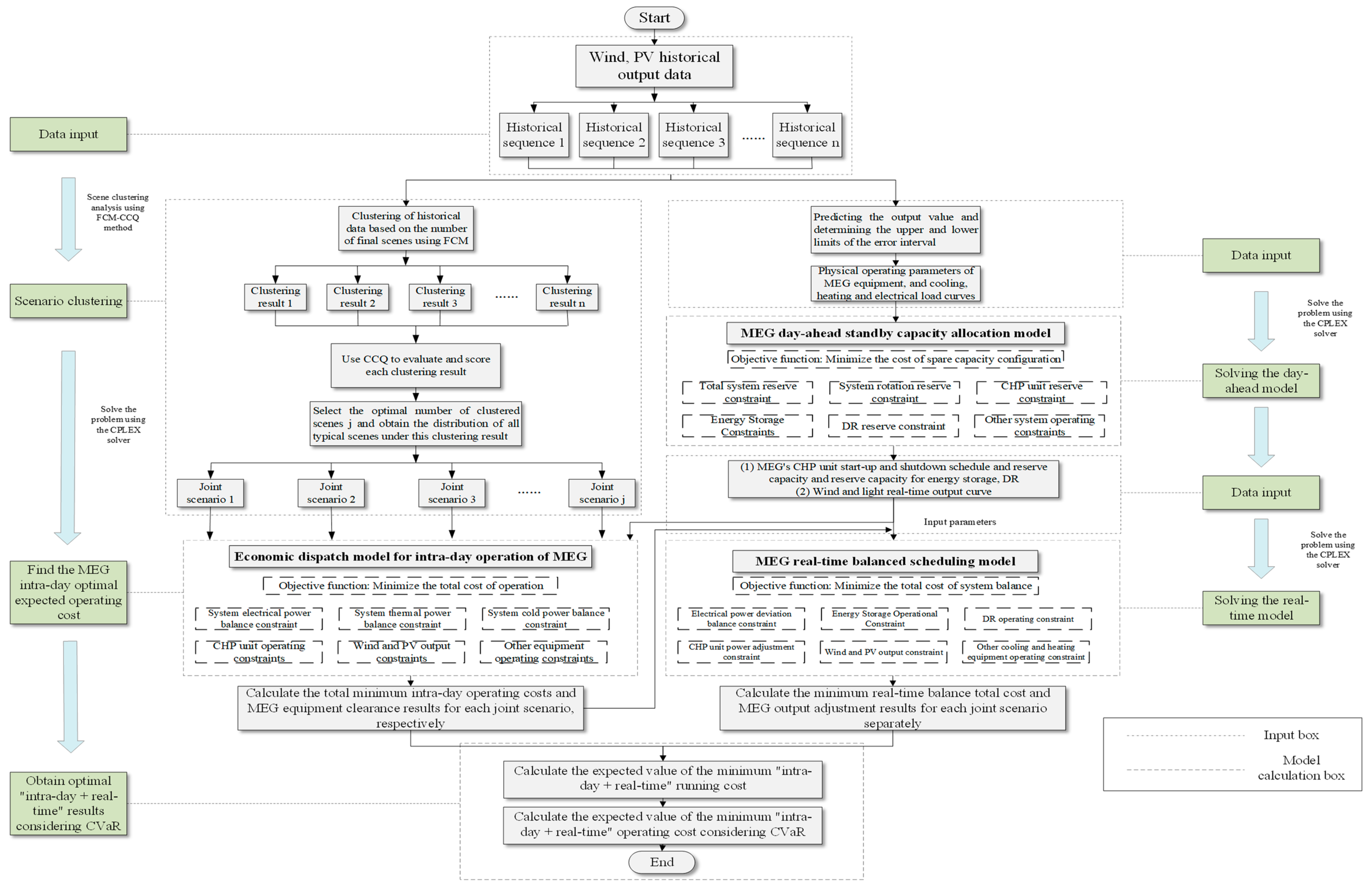
3.3. The Solution Method for the Three-Level Dispatch Optimization Model for the Micro-Energy Grid
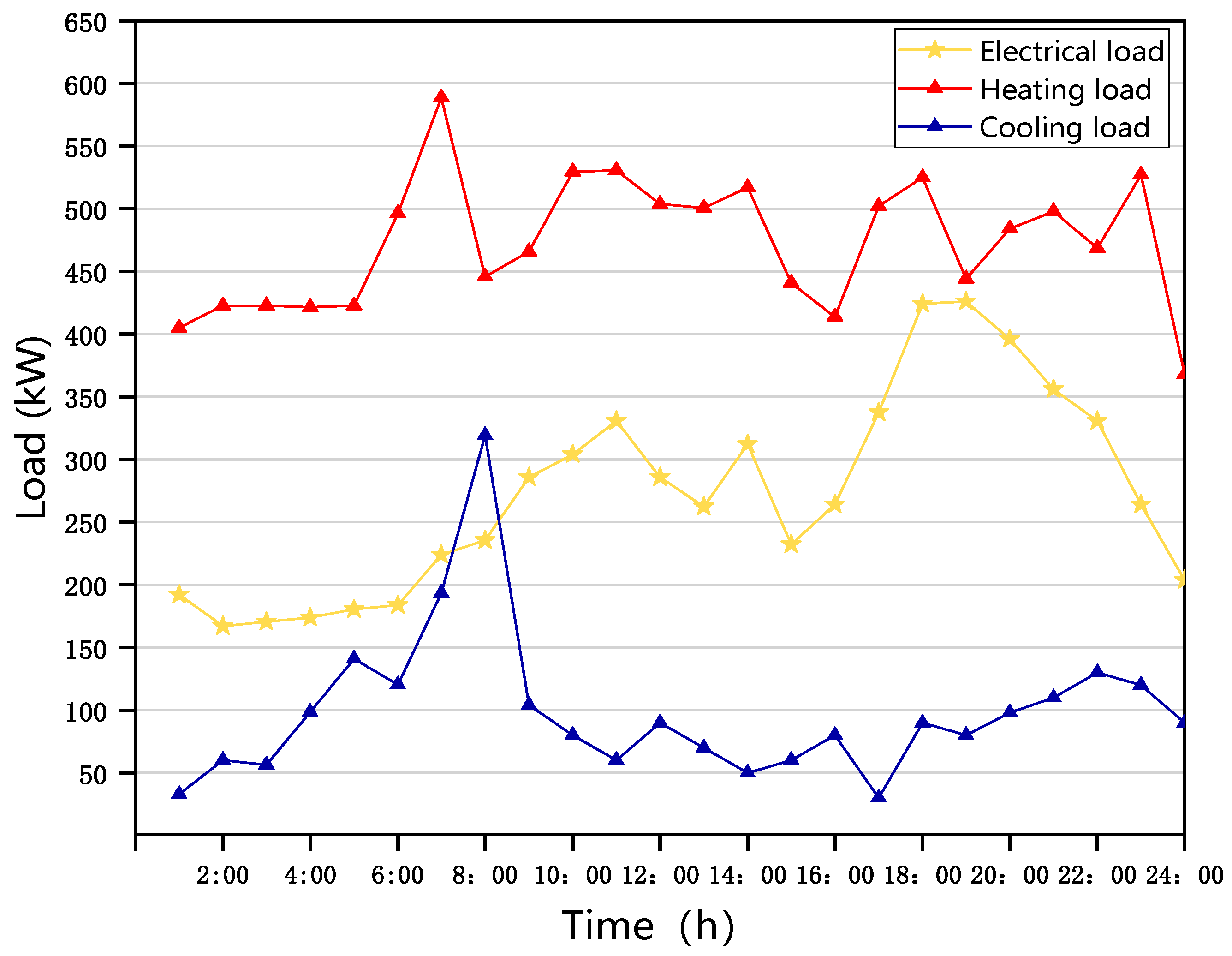
4. Example Analysis
4.1. Parameter Setting
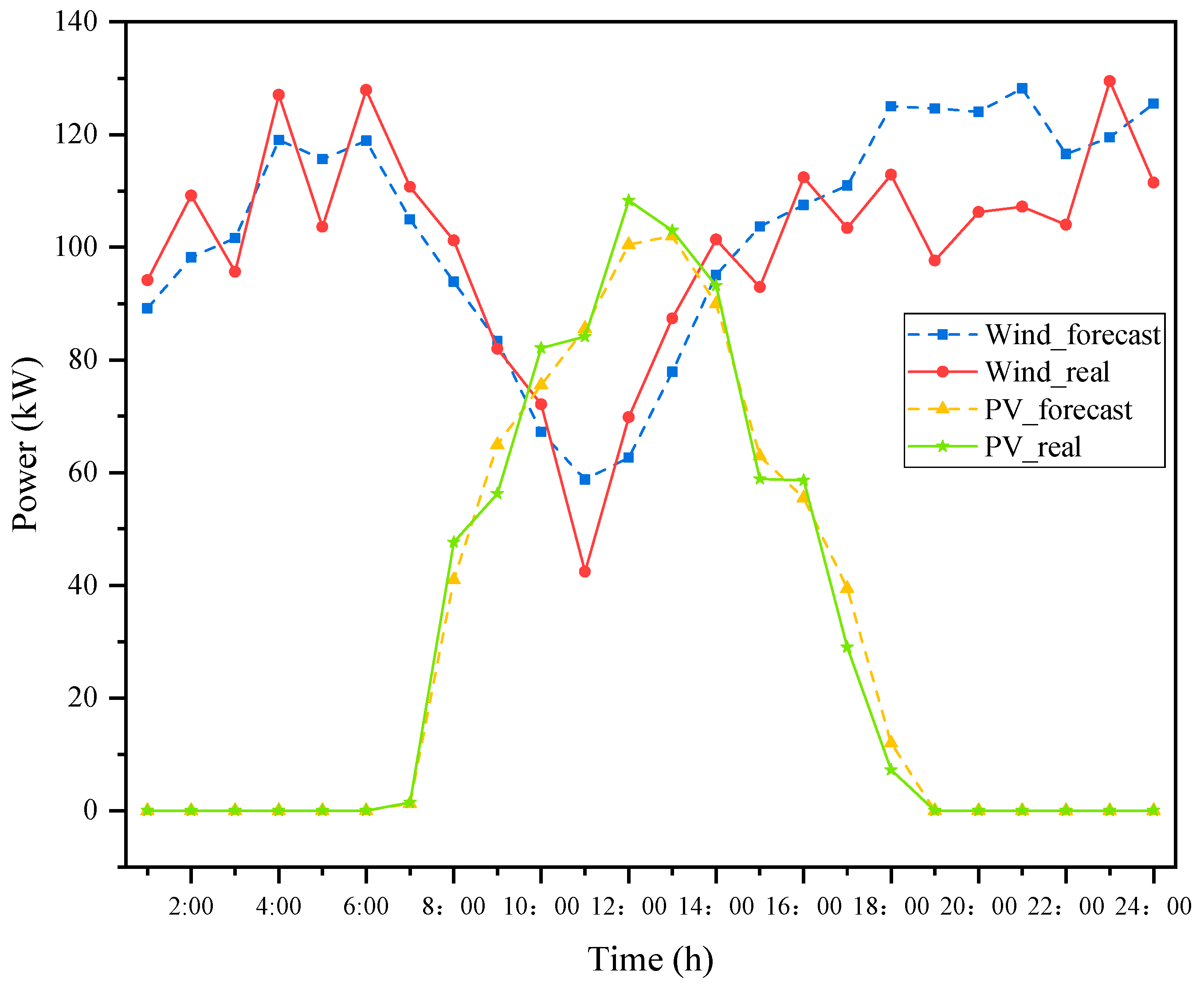
4.2. Analysis of Results of Clearing the Day before
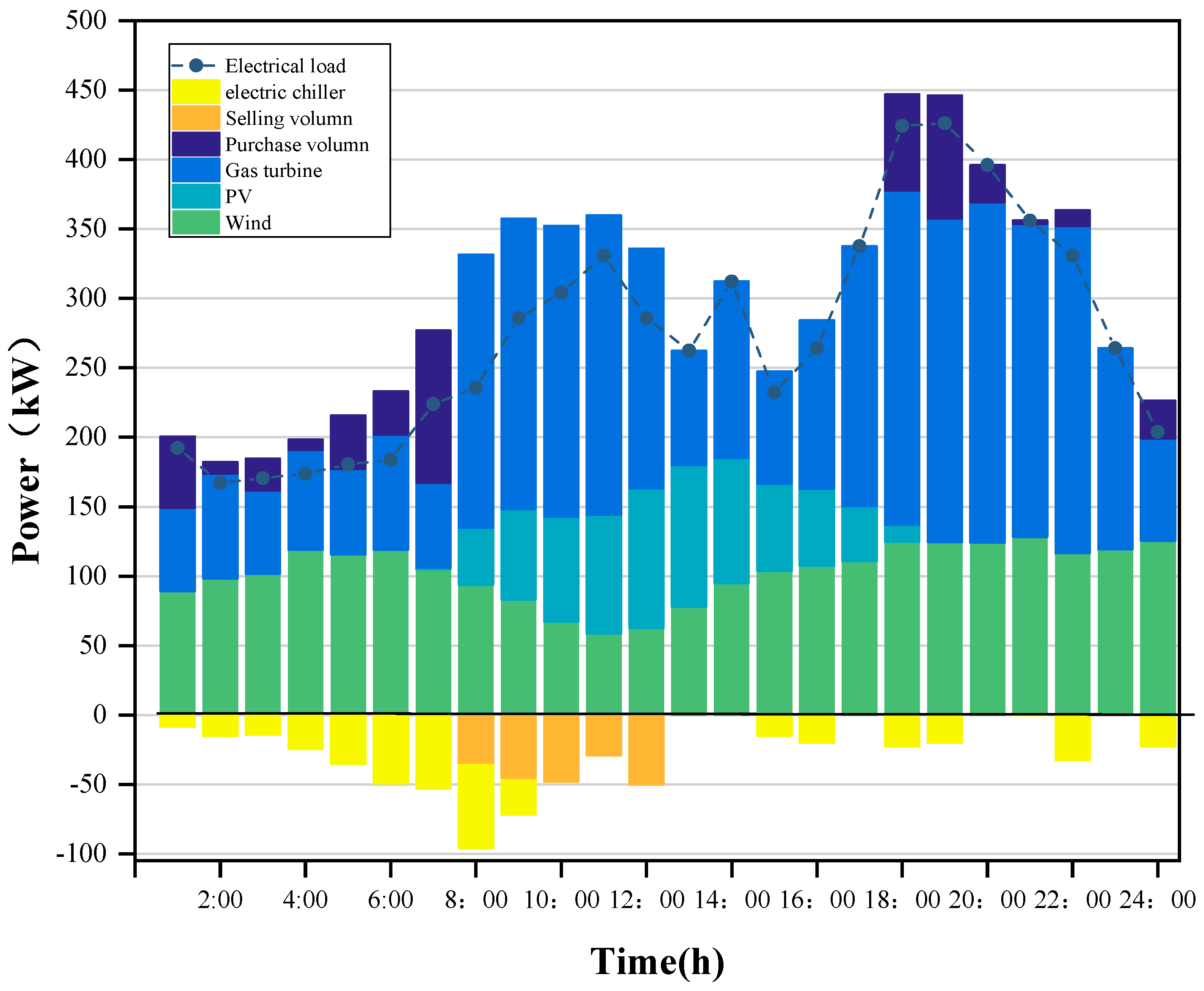
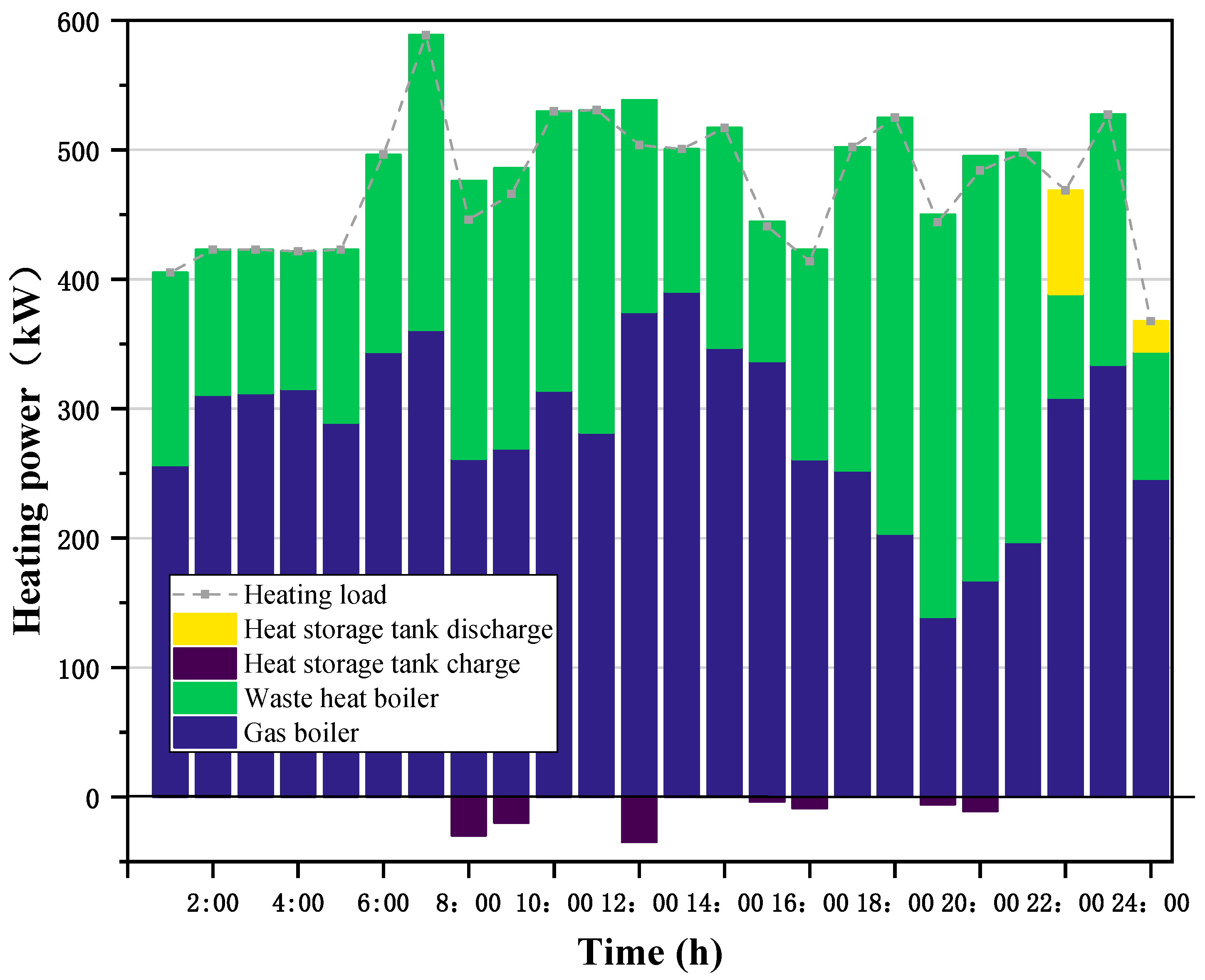
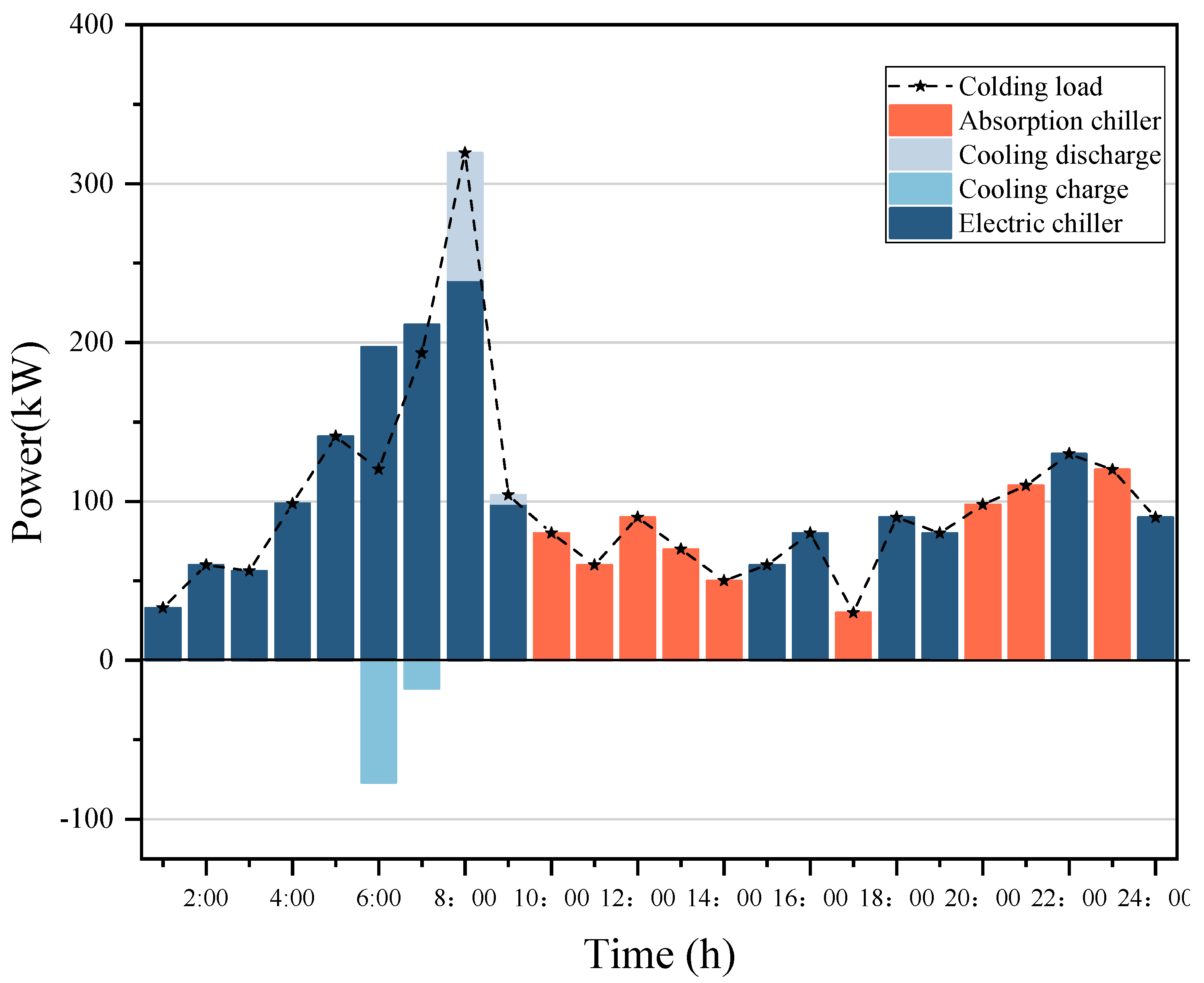
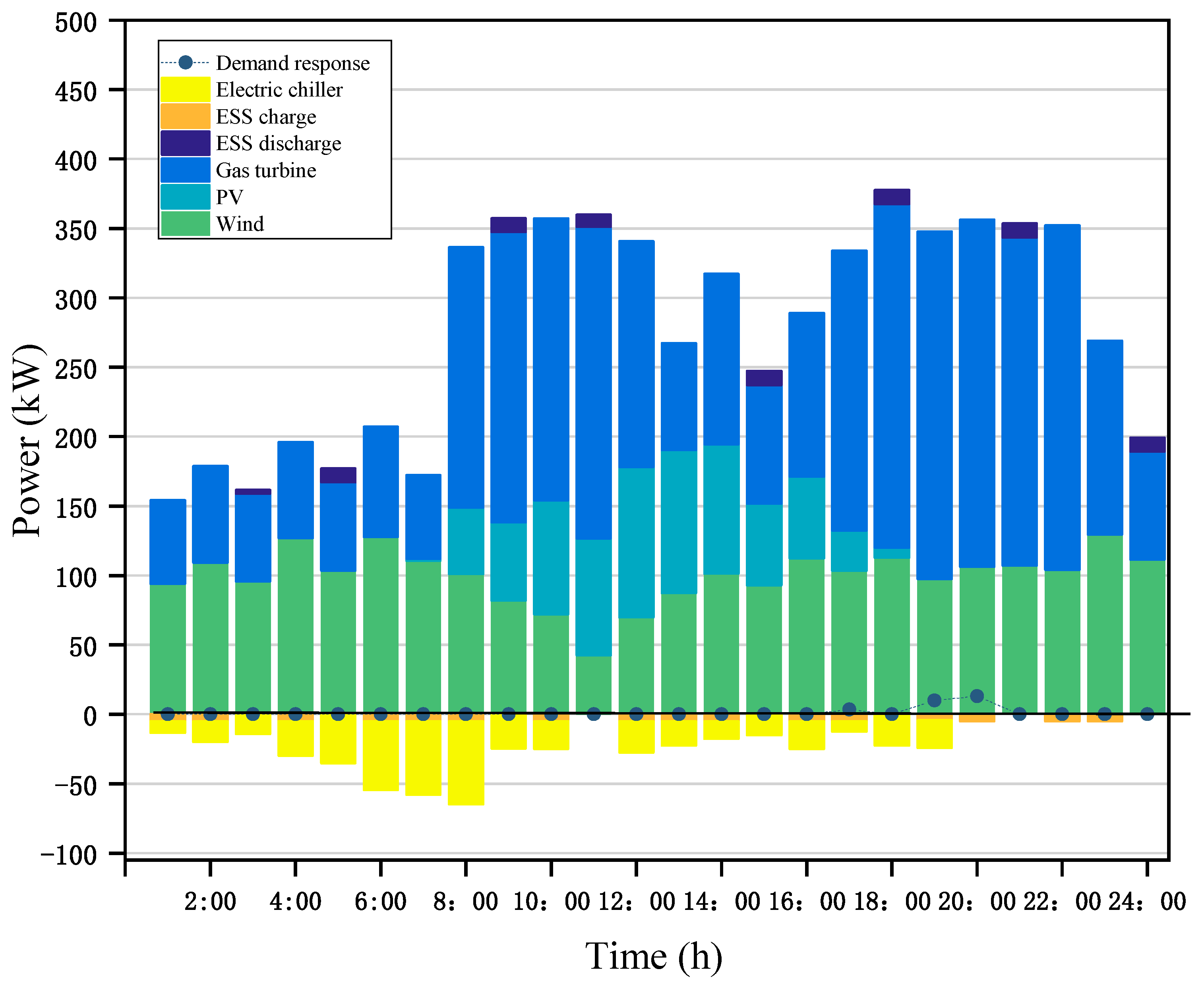
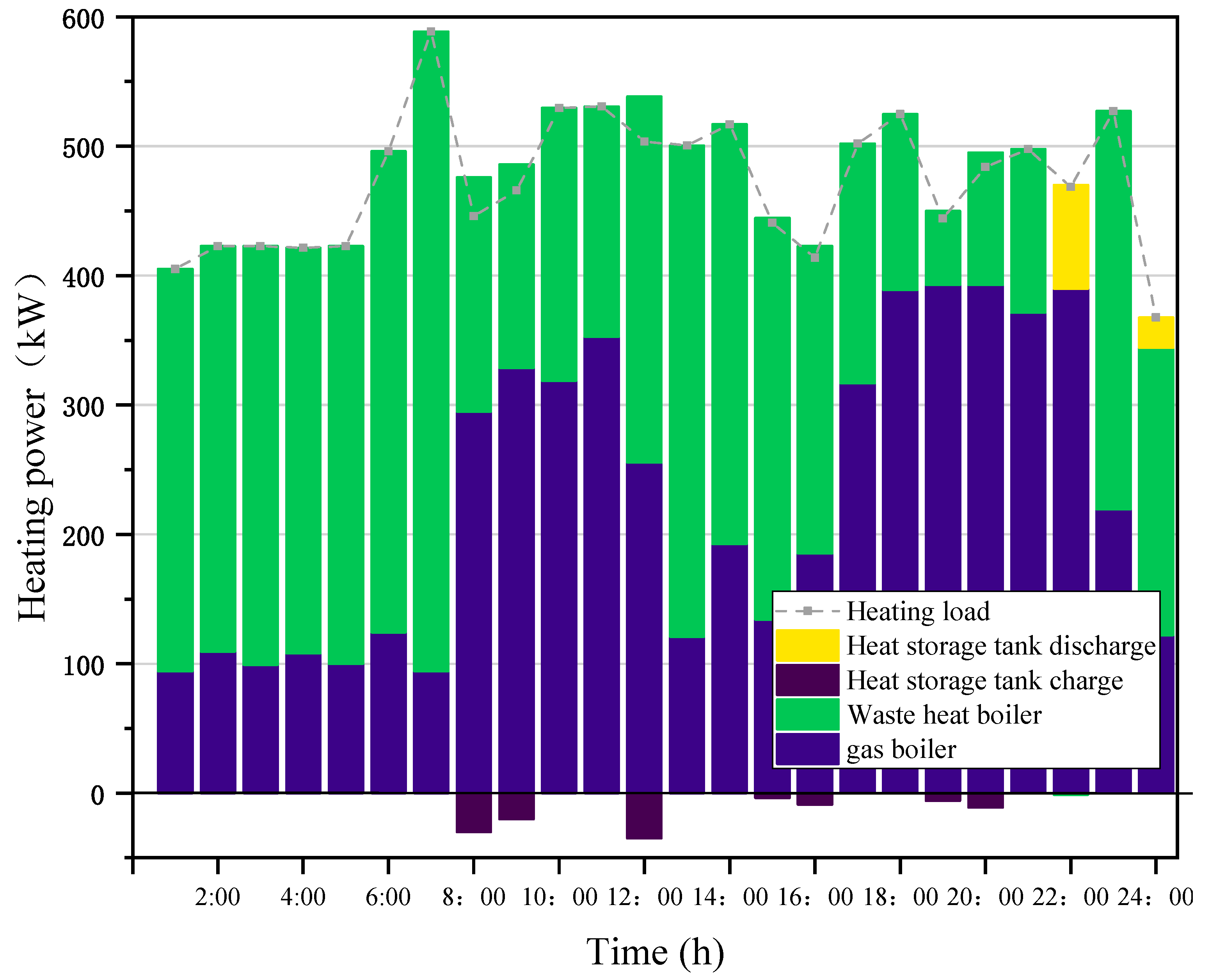
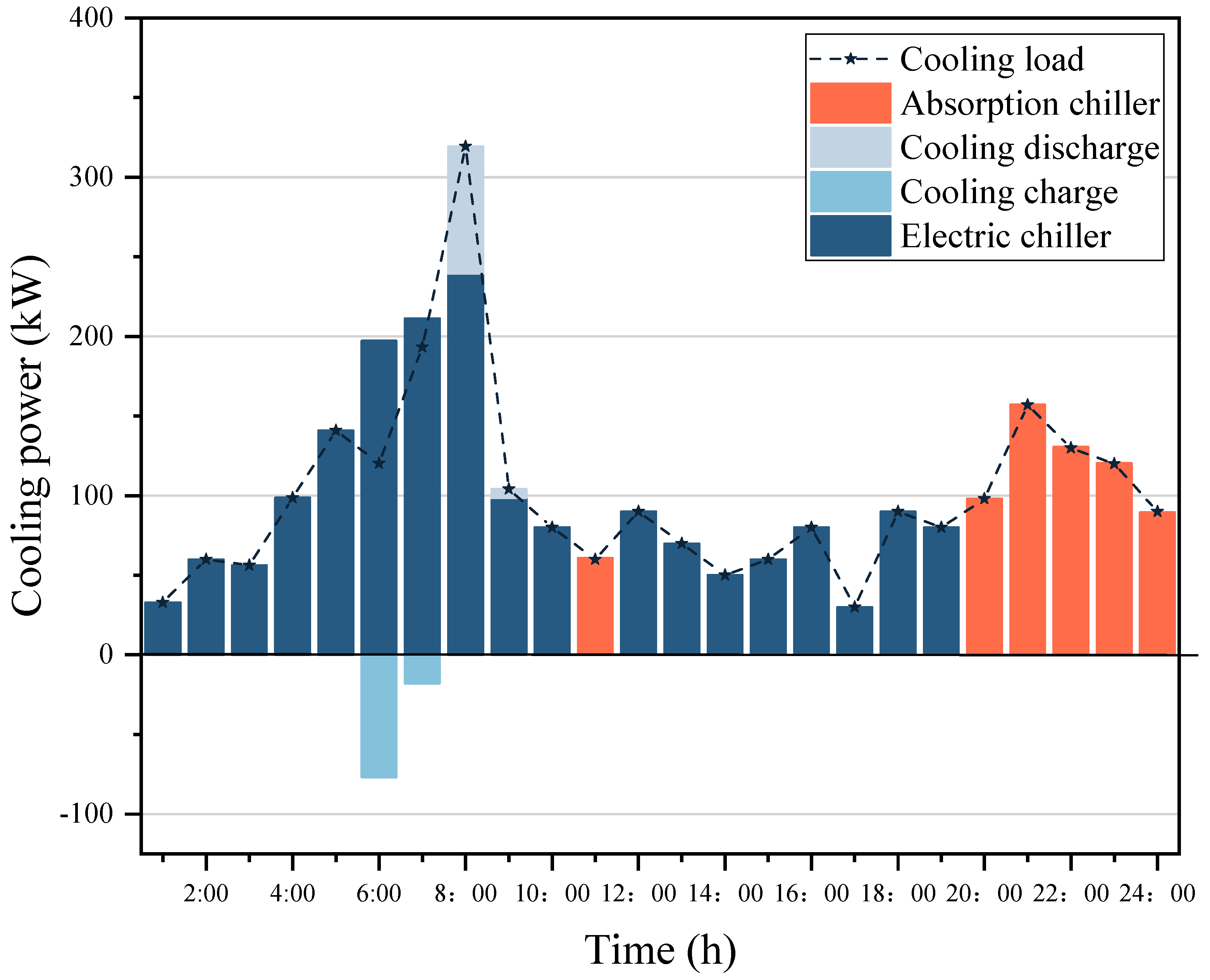
4.3. Analysis of Intraday Economic Dispatch Results
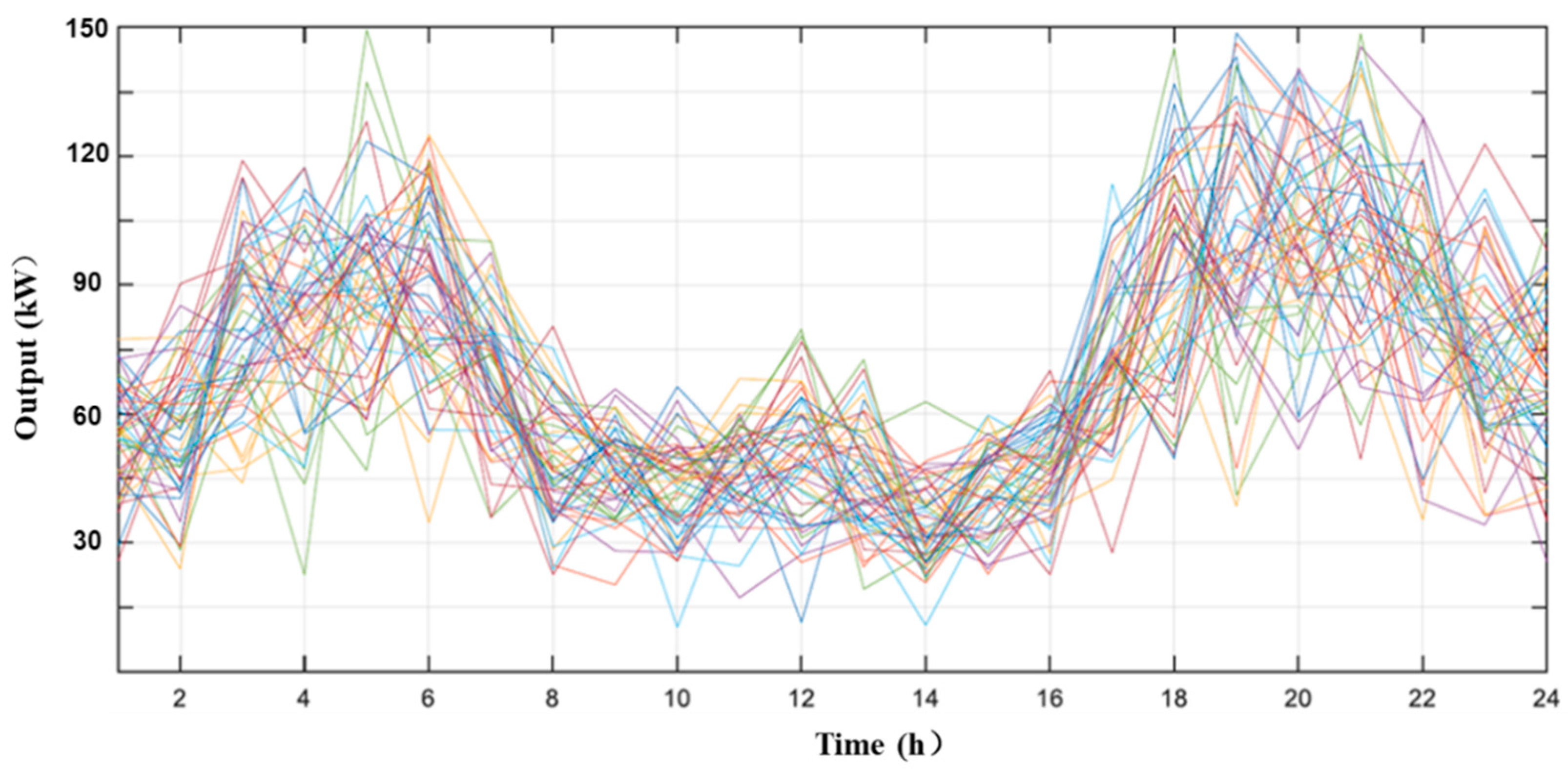
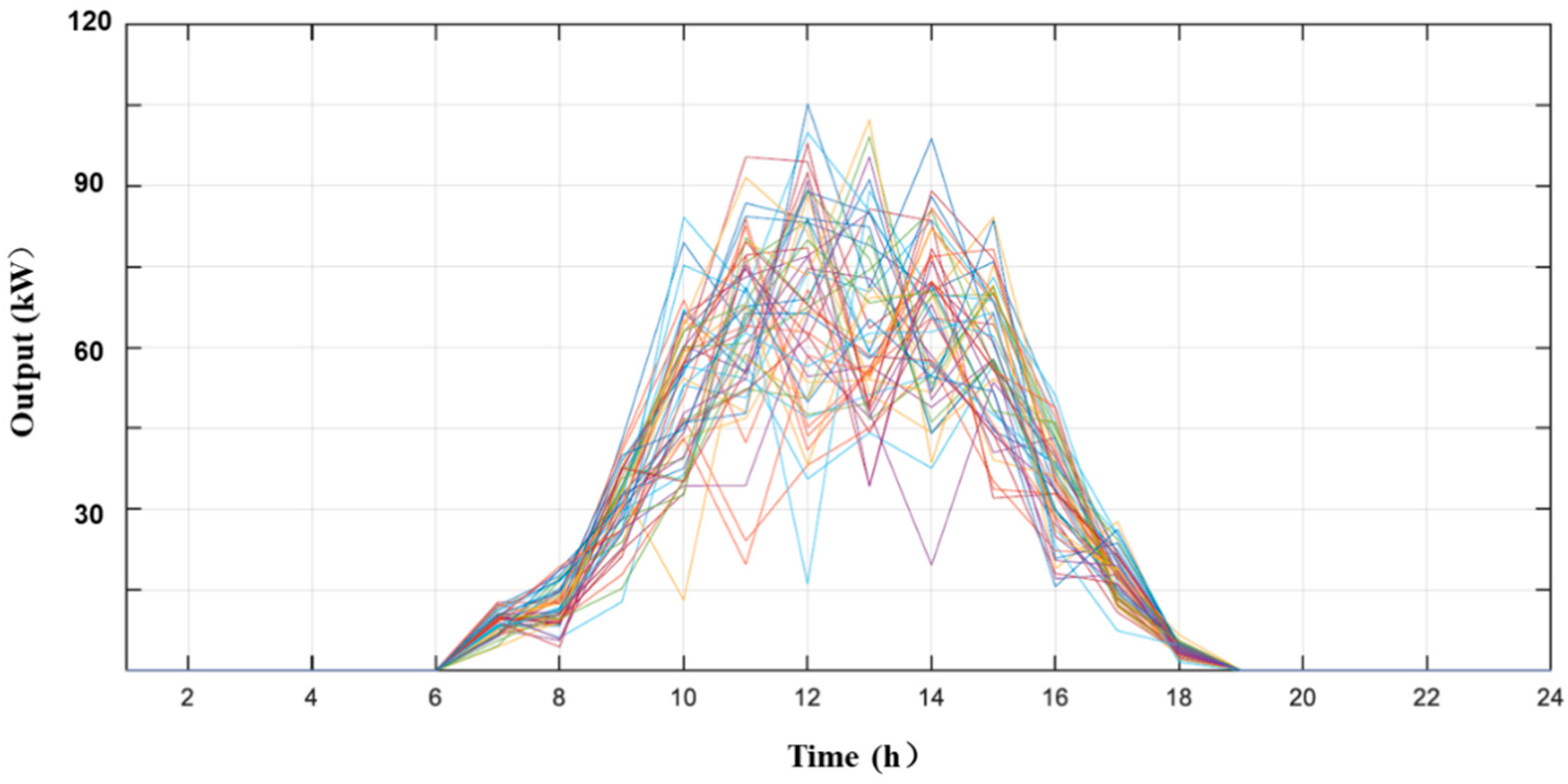
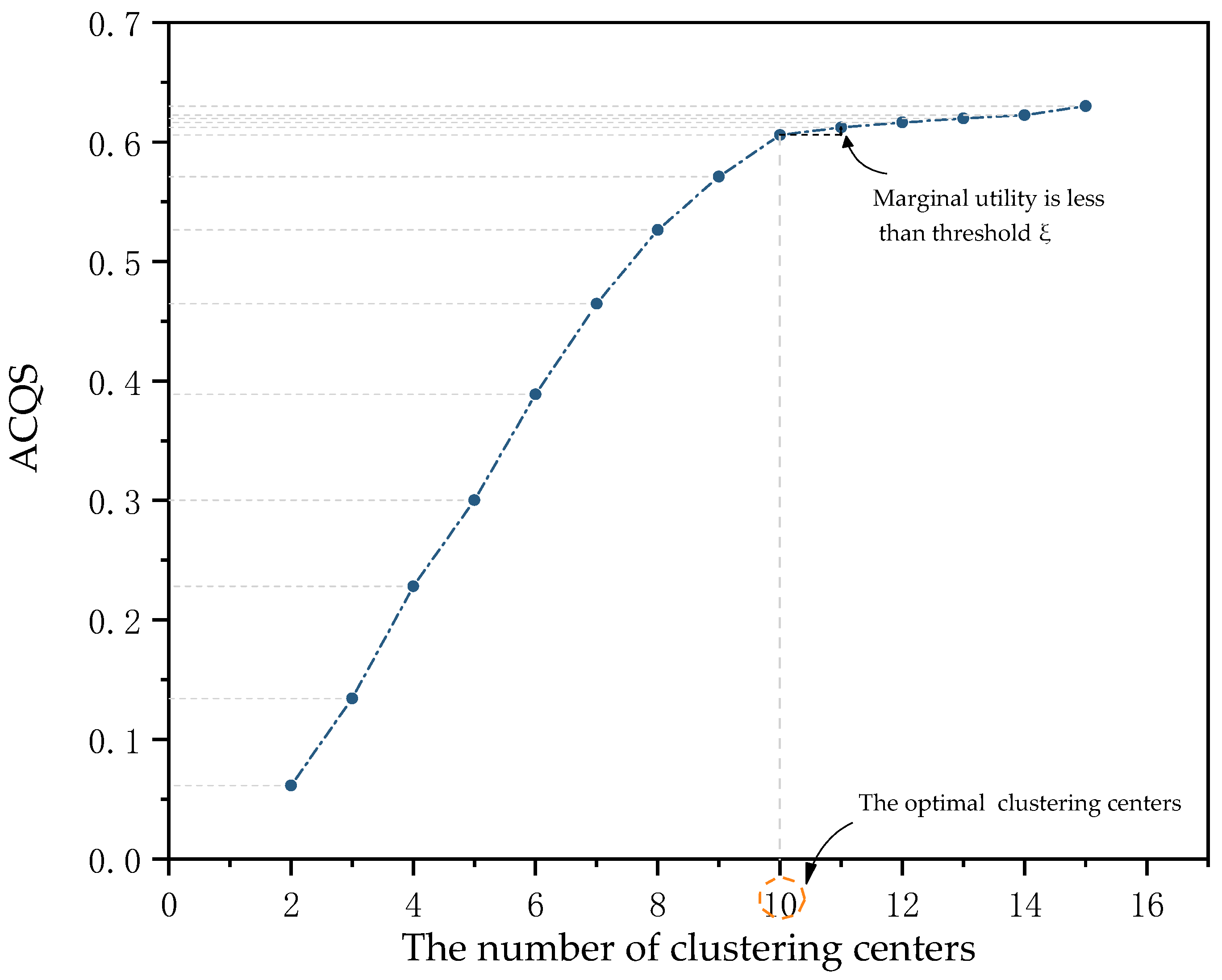
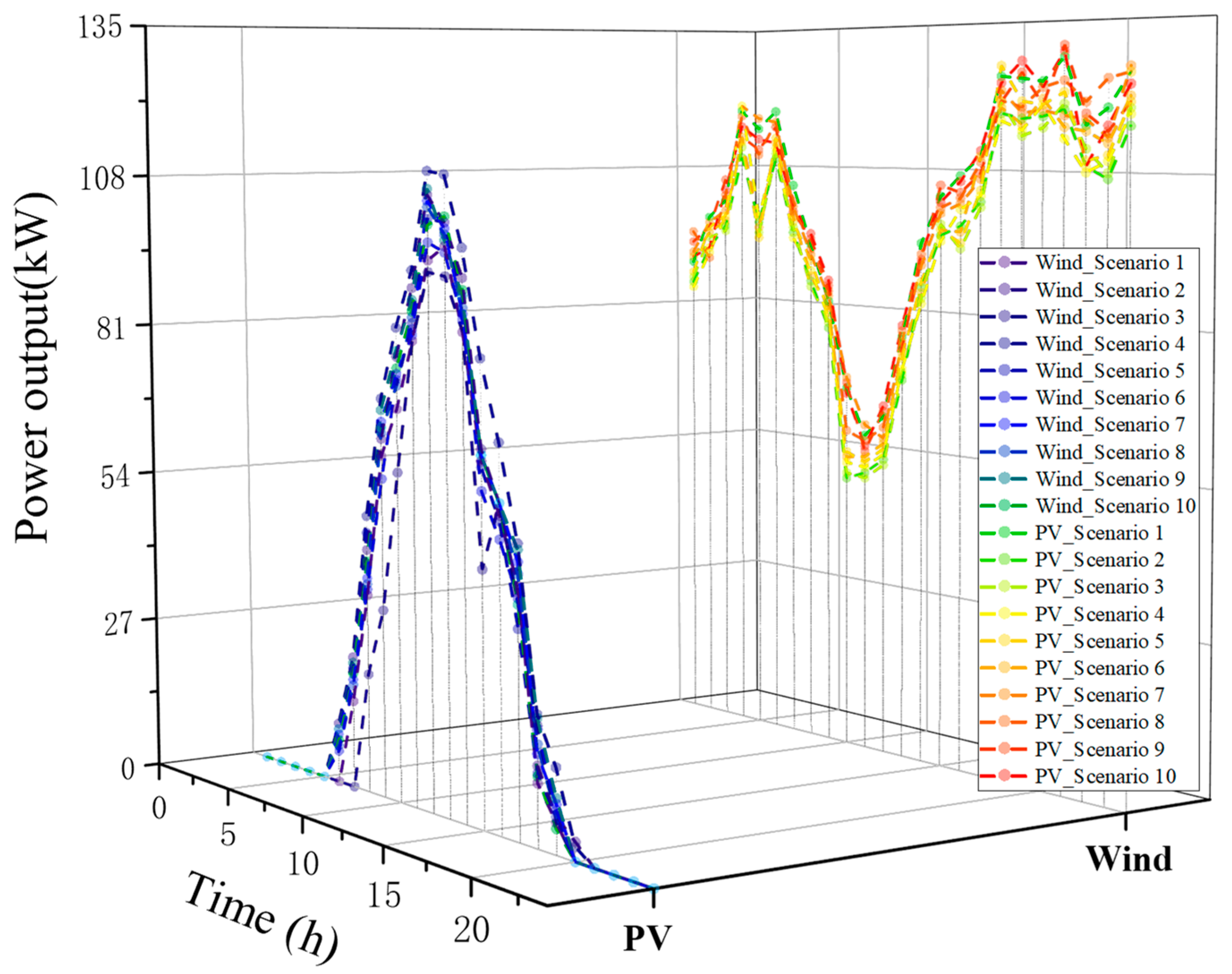
4.4. Analysis of Clustering Results
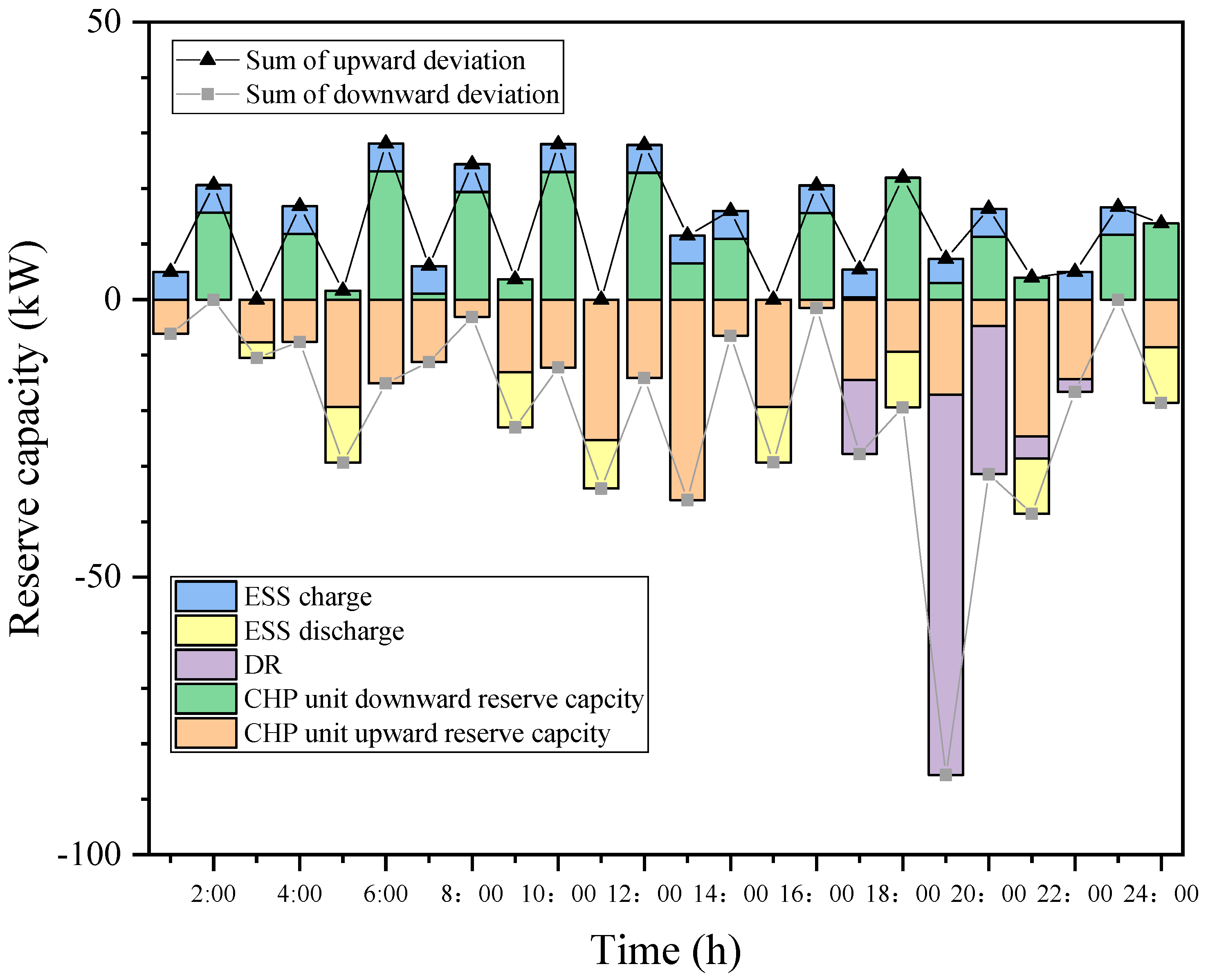
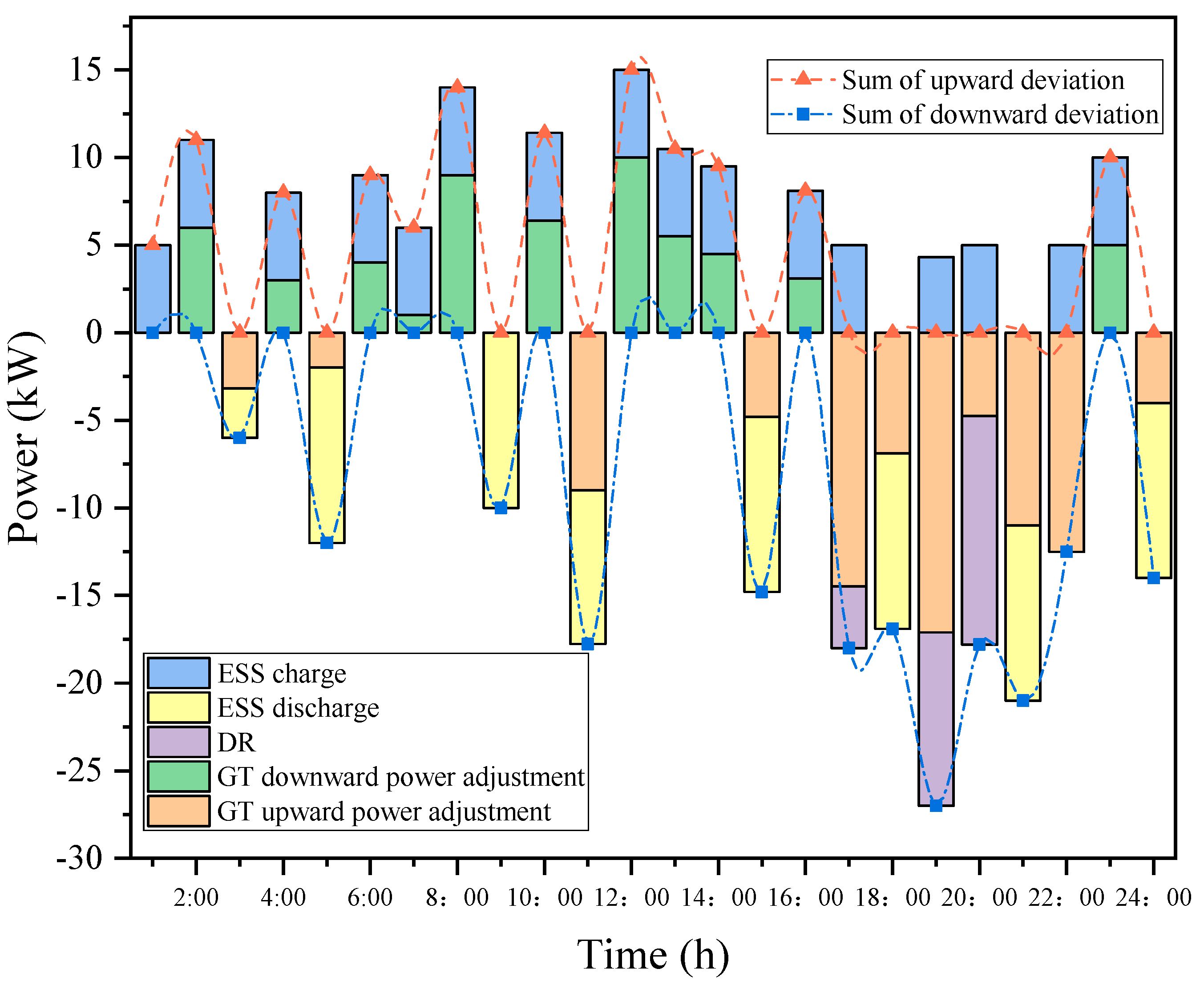
4.5. Analysis of Real-Time Stage-Clearing Results
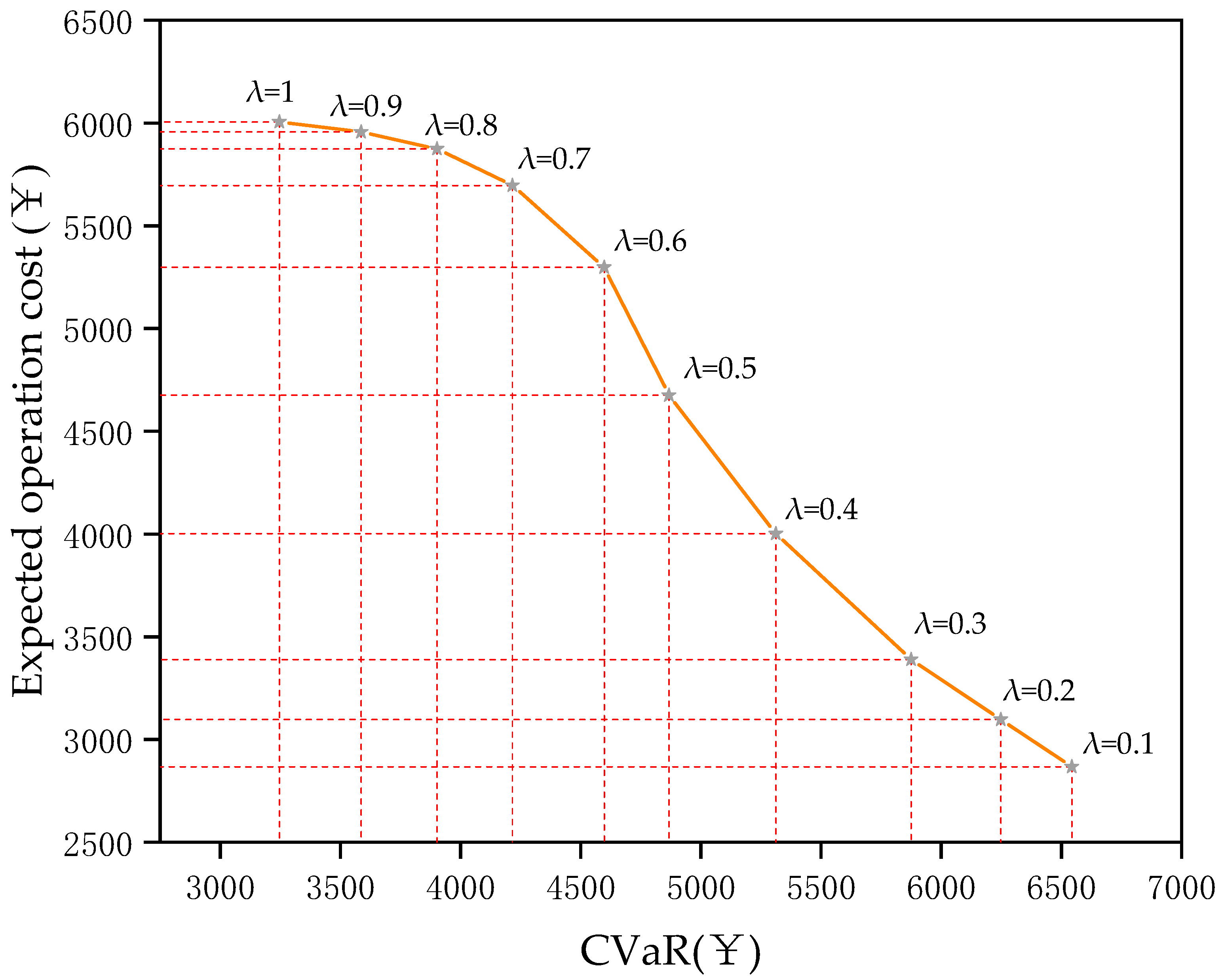
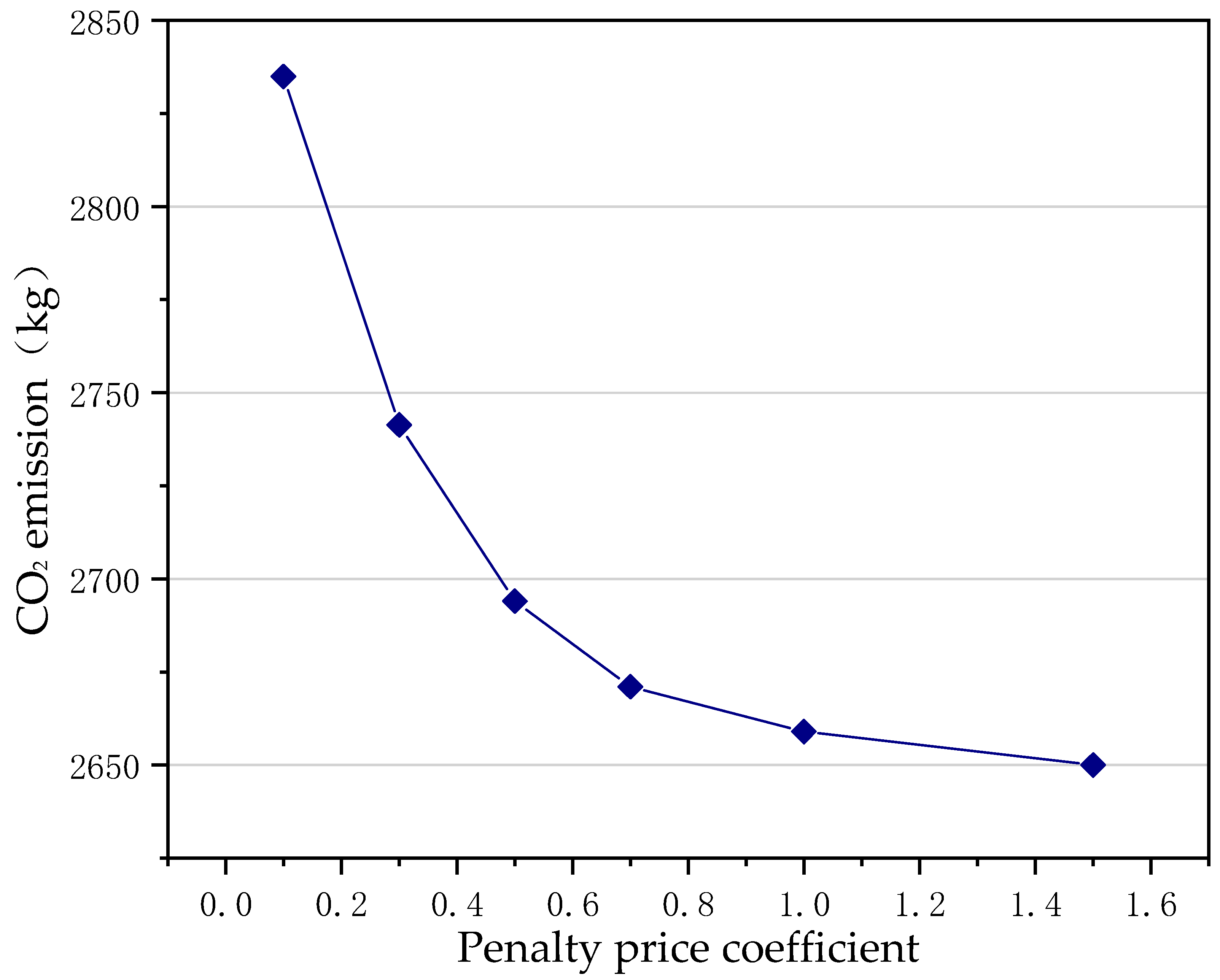
4.6. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CVaR | Conditional value at risk | The fuel cost of the gas turbine | |
| CCHP | Combined Cooling Heating and Power | The power interaction cost between the micro-energy grid and the main grid | |
| PV | Photovoltaic | The operation and maintenance cost of the micro-energy grid | |
| BESS | Battery energy storage system | The CO2 emission penalty cost in the micro-energy grid | |
| MT | Microturbine | The natural gas consumption of gas boiler | |
| GA | Genetic algorithm | The natural gas consumption of gas turbine | |
| CARIMA | Controlled autoregressive moving average | The real-time purchase cost price of natural gas | |
| RES | Renewable energy systems | The purchase of electricity | |
| ESS | Energy storage systems | The sale of electricity | |
| FCM-CCQ | Fuzzy c-means-clustering comprehensive quality | The CO2 emission intensity coefficients of gas turbine | |
| FCM | Fuzzy C-means | The CO2 emission intensity coefficients of gas boilers | |
| ACQS | Average comprehensive quality score | The CO2 emission intensity coefficients of electricity purchased from the grid | |
| The total cost | The penalty coefficient | ||
| Gas turbine capacity allocation cost | The operation and maintenance costs per unit of electricity for gas turbines | ||
| Energy storage capacity allocation cost | The operation and maintenance costs per unit of electricity for electric refrigerators | ||
| Demand response capacity allocation cost | The operation and maintenance costs per unit of electricity for waste heat boilers, | ||
| The maximum power of the gas turbine | The operation and maintenance costs per unit of electricity for gas boilers | ||
| The minimum power of the gas turbine | The operation and maintenance costs per unit of electricity for batteries | ||
| The upper reserves of the gas turbine | The operation and maintenance costs per unit of electricity for heat storage tanks | ||
| The lower reserves of the gas turbine | The operation and maintenance costs per unit of electricity for the ice storage machine | ||
| The actual gas turbine power | The operation and maintenance costs per unit of electricity for photovoltaic | ||
| The low calorific value of natural gas | The operation and maintenance costs per unit of electricity for wind power | ||
| The 0–1 variable | The thermal power output of the gas boiler at time t | ||
| The lower limits of the gas turbine output | The upper limits of the output thermal power of the gas boiler | ||
| The upper limits of the gas turbine output | The lower limits of the output thermal power of the gas boiler | ||
| Lower boundary value of gas turbine ramping power | The natural gas consumption of the gas boiler | ||
| Upper boundary value of gas turbine ramping power | The energy conversion efficiency coefficient of the gas boiler | ||
| The endpoint electric power value of each segment after the piecewise linearization of the thermoelectric curve | The cooling power generated by the electric refrigeration at time t | ||
| A binary variable | The thermal power generated by the gas boiler at time t | ||
| The slope of the linear function of the k segment | the thermal power generated by the heating coil at time t | ||
| The heat produced by the gas turbine | The electricity consumption of the electric refrigerator at time t | ||
| The electrical energy stored by the energy storage battery in the time period t | The electricity consumption of the gas boiler at time t | ||
| The charge efficiency of the energy storage battery | The heat of the heating coil at time t | ||
| The discharge efficiency of the energy storage battery | The electric power consumed by the electric refrigerator at time t | ||
| Its self-discharge rate | The conversion coefficient of the electric refrigeration machine to cold | ||
| The 0–1 state variables of the charging of the energy storage battery in the period t | The cooling power of the ice-cold storage machine at all times | ||
| The 0–1 state variables of the discharging of the energy storage battery in the period t | The charging power of the ice-cold storage machine at all times | ||
| The corresponding charging power of the energy storage battery in the period t | The cooling load in the system at the moment t | ||
| The corresponding discharging power of the energy storage battery in the period t | The heating load in the system at the moment t | ||
| The actual demand response reserve capacity signed with the power user during the period | The electrical load in the system at the moment t | ||
| The maximum corresponding capacity | The probability of scenario occurrence | ||
| The power generation of abandoned wind | The total cost function of intraday economic dispatch | ||
| The power generation of abandoned photovoltaic | The confidence level | ||
| The predicted values of wind power output | The weight coefficient | ||
| The predicted values of photovoltaic output | The joint scenario set in the micro-energy grid | ||
| The reserve coefficients of the cooling of the micro-energy grid | The k-th scenario | ||
| The reserve coefficients of the heating of the micro-energy grid | The probability of occurrence of the k-th scenario | ||
| The reserve coefficients of the electric load of the micro-energy grid |
References
- Ma, T.; Wu, J.; Hao, L. Energy flow modeling and optimal operation analysis of the micro energy grid based on energy hub. Energy Convers. Manag. 2017, 133, 292–306. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, M.; Wang, P.; Gu, J.; Zheng, W.; Dong, Y. Bi-stage stochastic model for optimal capacity and electric cooling ratio of CCHPs—A case study for a hotel. Energy Build. 2019, 194, 113–122. [Google Scholar] [CrossRef]
- Nami, H.; Anvari-Moghaddam, A.; Arabkoohsar, A. Application of CCHPs in a centralized domestic heating, cooling and power network—Thermodynamic and economic implications. Sustain. Cities Soc. 2020, 60, 102151. [Google Scholar] [CrossRef]
- Chen, C.; Xing, J.; Li, Q.; Liu, S.; Ma, J.; Chen, J.; Yang, L. Wasserstein distance-based distributionally robust optimal scheduling in rural microgrid considering the coordinated interaction among source-grid-load-storage. Energy Rep. 2021, 7, 60–66. [Google Scholar] [CrossRef]
- Dagdougui, Y.; Ouammi, A.; Benchrifa, R. Energy management-based predictive controller for a smart building powered by renewable energy. Sustainability 2020, 12, 4264. [Google Scholar] [CrossRef]
- Ullah, I.; Rasheed, M.B.; Alquthami, T.; Tayyaba, S. A residential load scheduling with the integration of on-site pv and energy storage systems in micro-grid. Sustainability 2019, 12, 184. [Google Scholar] [CrossRef] [Green Version]
- Ju, L.; Tan, Q.; Lin, H.; Mei, S.; Li, N.; Lu, Y.; Wang, Y. A two-stage optimal coordinated scheduling strategy for micro energy grid integrating intermittent renewable energy sources considering multi-energy flexible conversion. Energy 2020, 196, 117078. [Google Scholar] [CrossRef]
- An, S.; Wang, H.; Leng, X. Optimal operation of multi-micro energy grids under distribution network in Southwest China. Appl. Energy 2022, 309, 118461. [Google Scholar] [CrossRef]
- Qiu, J.; Zhao, J.; Yang, H.; Wang, D.; Dong, Z.Y. Planning of solar photovoltaics, battery energy storage system and gas micro turbine for coupled micro energy grids. Appl. Energy 2018, 219, 361–369. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, J.; Wang, W.; Zhang, M.; Jing, T. Integrated optimal dispatch of a rural micro energy-grid with multi-energy stream based on model predictive control. Energies 2018, 11, 3439. [Google Scholar] [CrossRef] [Green Version]
- Zidan, A.; Gabbar, H.A. DG mix and energy storage units for optimal planning of self-sufficient micro energy grids. Energies 2016, 9, 616. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Wang, Z.; Wang, H.; Zhang, H.; Yang, W.; Cao, R. Research on bi-level optimized operation strategy of microgrid cluster based on IABC algorithm. IEEE Access 2021, 9, 15520–15529. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, F.; Li, Y.; Wang, Y. An improved two-stage robust optimization model for CCHP-P2G microgrid system considering multi-energy operation under wind power outputs uncertainties. Energy 2021, 223, 120048. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, Z.; Zhu, Z.; Zhang, Z.; Qin, J.; Wang, H.; Yang, Z. A three-stage coordinated optimization scheduling strategy for a CCHP microgrid energy management system. Processes 2020, 8, 245. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wang, Y.; Huang, Y.; Li, F.; Zeng, M.; Li, J.; Zhang, F. Planning and operation method of the regional integrated energy system considering economy and environment. Energy 2019, 171, 731–750. [Google Scholar] [CrossRef]
- Amiri, S.; Honarvar, M. Providing an integrated Model for Planning and Scheduling Energy Hubs and preventive maintenance. Energy 2018, 163, 1093–1114. [Google Scholar] [CrossRef]
- Shariatkhah, M.H.; Haghifam, M.R.; Chicco, G.; Parsa-Moghaddam, M. Adequacy modeling and evaluation of multi-carrier energy systems to supply energy services from different infrastructures. Energy 2016, 109, 1095–1106. [Google Scholar] [CrossRef]
- Wang, J.; Liu, C.; Ton, D.; Zhou, Y.; Kim, J.; Vyas, A. Impact of plug-in hybrid electric vehicles on power systems with demand response and wind power. Energy Policy 2011, 39, 4016–4021. [Google Scholar] [CrossRef]
- Wang, Y.; Ai, X.; Tan, Z.; Yan, L.; Liu, S. Interactive dispatch modes and bidding strategy of multiple virtual power plants based on demand response and game theory. IEEE Trans. Smart Grid 2015, 7, 510–519. [Google Scholar] [CrossRef]
- Khodaei, A.; Bahramirad, S.; Shahidehpour, M. Microgrid planning under uncertainty. IEEE Trans. Power Syst. 2014, 30, 2417–2425. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, L.; Yang, Y.; Sun, W.; Zhao, H. A stochastic-robust coordinated optimization model for CCHP micro-grid considering multi-energy operation and power trading with electricity markets under uncertainties. Energy 2020, 198, 1172–1173. [Google Scholar] [CrossRef]
- Alavi, S.A.; Ahmadian, A.; Aliakbar-Golkar, M. Optimal probabilistic energy management in a typical micro-grid based-on robust optimization and point estimate method. Energy Convers. Manag. 2015, 95, 314–325. [Google Scholar] [CrossRef]
- Naz, A.; Javaid, N.; Rasheed, M.B.; Haseeb, A.; Alhussein, M.; Aurangzeb, K. Game theoretical energy management with storage capacity optimization and photo-voltaic cell generated power forecasting in micro grid. Sustainability 2019, 11, 2763. [Google Scholar] [CrossRef] [Green Version]
- Dong, J.; Zhang, Y.; Wang, Y.; Liu, Y. A Two-Stage Optimal Dispatching Model for Micro Energy Grid Considering the Dual Goals of Economy and Environmental Protection under CVaR. Sustainability 2021, 13, 10173. [Google Scholar] [CrossRef]
- Dong, J.; Yang, P.; Nie, S. Day-ahead scheduling model of the distributed small hydro-wind-energy storage power system based on two-stage stochastic robust optimization. Sustainability 2019, 11, 2829. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Yin, W.; Abdollahi, E.; Lahdelma, R.; Jiao, W. Modelling and optimization of CHP based district heating system with renewable energy production and energy storage. Appl. Energy 2015, 159, 401–421. [Google Scholar] [CrossRef]
- Munoz, C.; Sauma, E.; Contreras, J.; Aguado, J.; de La Torre, S. Impact of high wind power penetration on transmission network expansion planning. IET Gener. Transm. Distrib. 2012, 6, 1281–1291. [Google Scholar] [CrossRef]
- Ding, H.; Pinson, P.; Hu, Z.; Song, Y. Optimal offering and operating strategies for wind-storage systems with linear decision rules. IEEE Trans. Power Syst. 2016, 31, 4755–4764. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.; Wu, Z.; Li, Z.; Cai, H.; Li, B.; Gu, W. A two-stage optimization and control for CCHP microgrid energy management. Appl. Therm. Eng. 2017, 125, 513–522. [Google Scholar] [CrossRef]
| Gas Turbine Spare Capacity Cost | Demand Response Spare Capacity Compensation Costs | Cost of Energy Storage Backup Capacity | Total Reserve Capacity Cost | ||
|---|---|---|---|---|---|
| Up Spare Capacity Costs | Down Spare Capacity Costs | Discharge Capacity Cost | Charging Capacity Cost | ||
| 14,579.893 | 11,065.679 | 9181.017 | 2147.625 | 2379.639 | 39,353.854 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Wang, Y.; Nie, S.; Wang, Y.; Chen, Y. Multistage Economic Scheduling Model of Micro-Energy Grids Considering Flexible Capacity Allocation. Sustainability 2022, 14, 9013. https://doi.org/10.3390/su14159013
Liu H, Wang Y, Nie S, Wang Y, Chen Y. Multistage Economic Scheduling Model of Micro-Energy Grids Considering Flexible Capacity Allocation. Sustainability. 2022; 14(15):9013. https://doi.org/10.3390/su14159013
Chicago/Turabian StyleLiu, Hang, Yongcheng Wang, Shilin Nie, Yi Wang, and Yu Chen. 2022. "Multistage Economic Scheduling Model of Micro-Energy Grids Considering Flexible Capacity Allocation" Sustainability 14, no. 15: 9013. https://doi.org/10.3390/su14159013
APA StyleLiu, H., Wang, Y., Nie, S., Wang, Y., & Chen, Y. (2022). Multistage Economic Scheduling Model of Micro-Energy Grids Considering Flexible Capacity Allocation. Sustainability, 14(15), 9013. https://doi.org/10.3390/su14159013





