Comparative Study on Compressive and Flexural Properties of Concrete-Filled Steel Tubular Arch Joints
Abstract
:1. Introduction
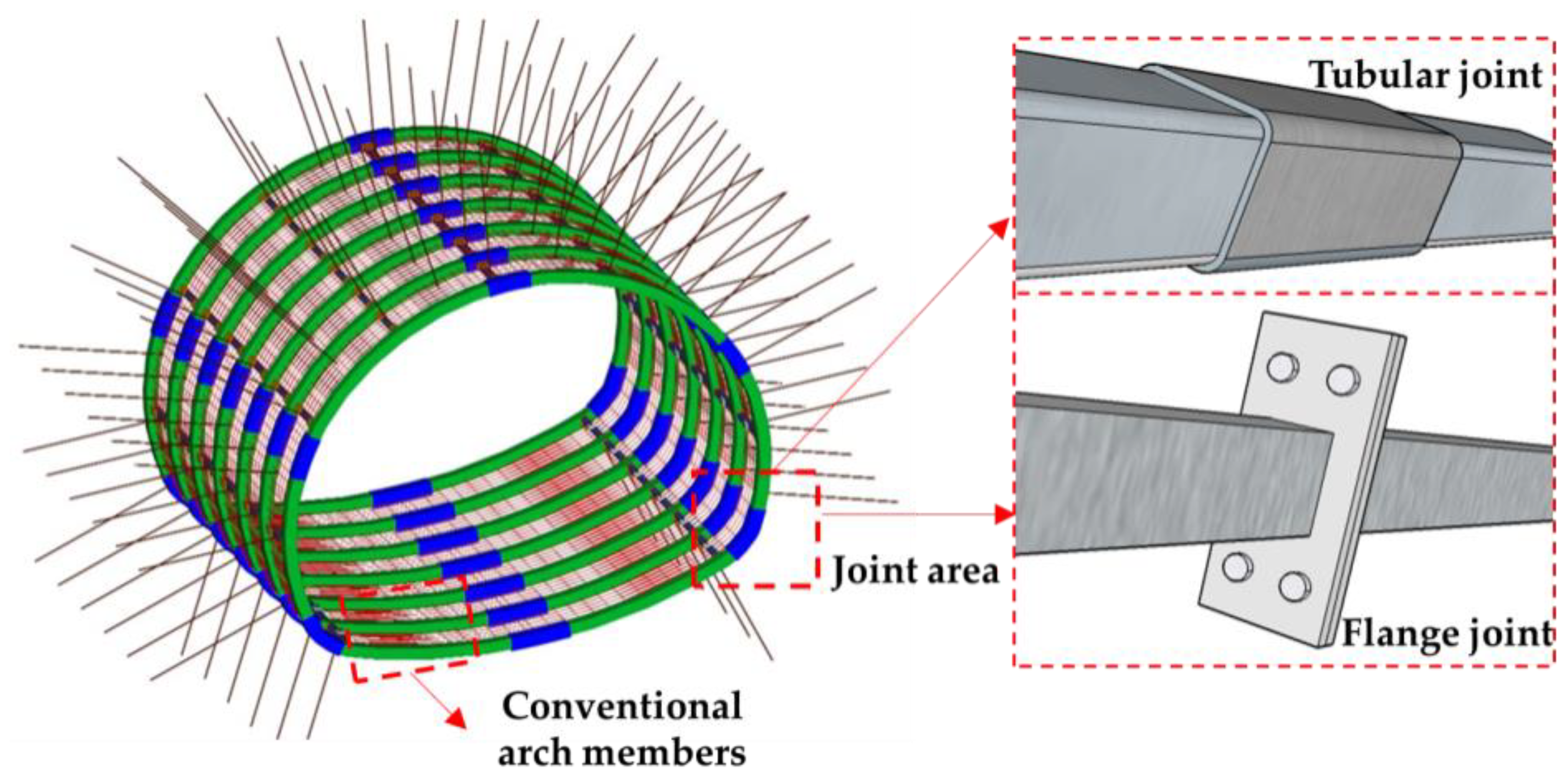
2. Joint Introduction and Typical Destruction Modes
2.1. Tubular Joints
2.2. Flange Joints
3. Laboratory Tests of Different Components
3.1. Overview of the Test
3.2. Analysis of Test Results
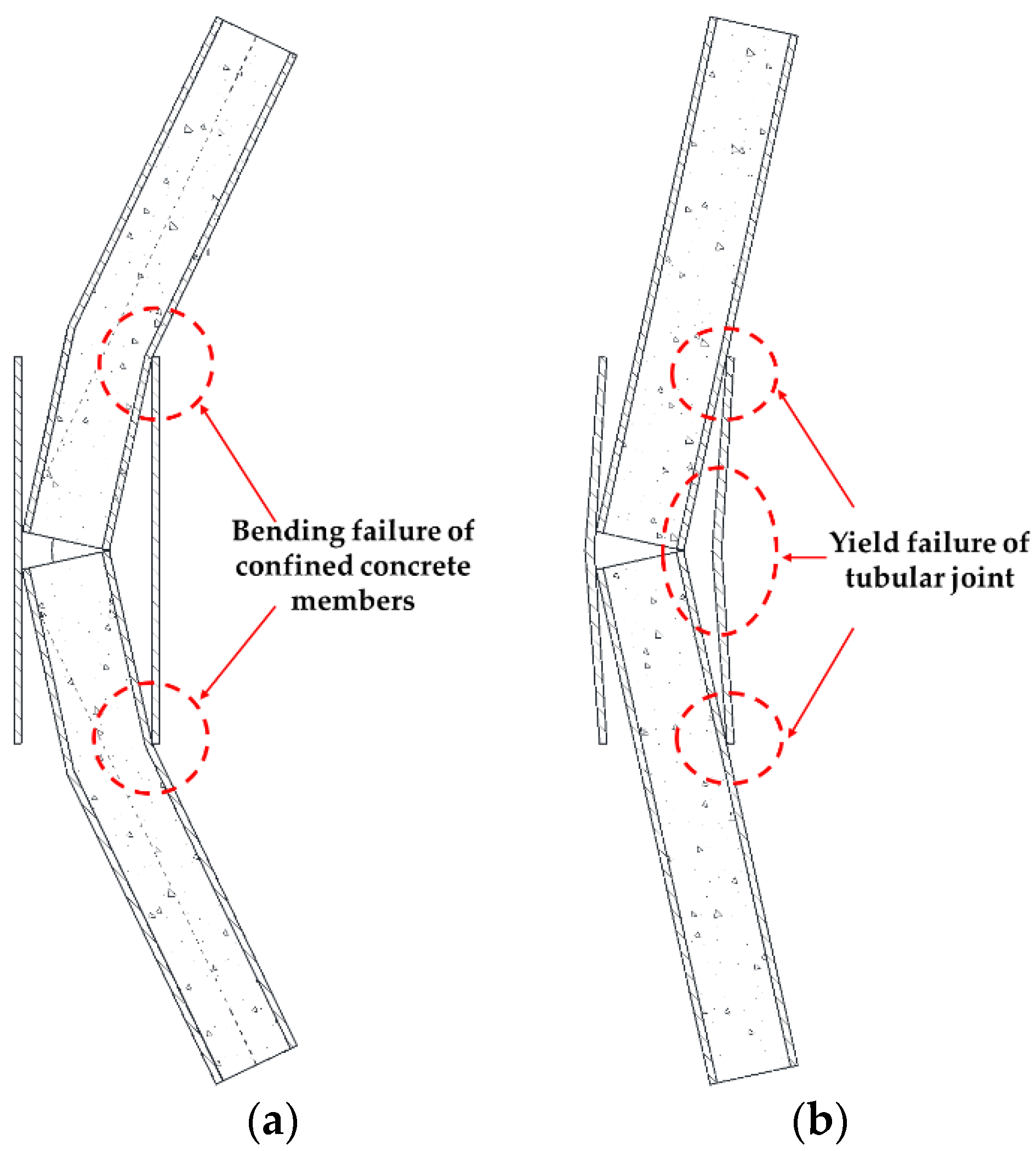
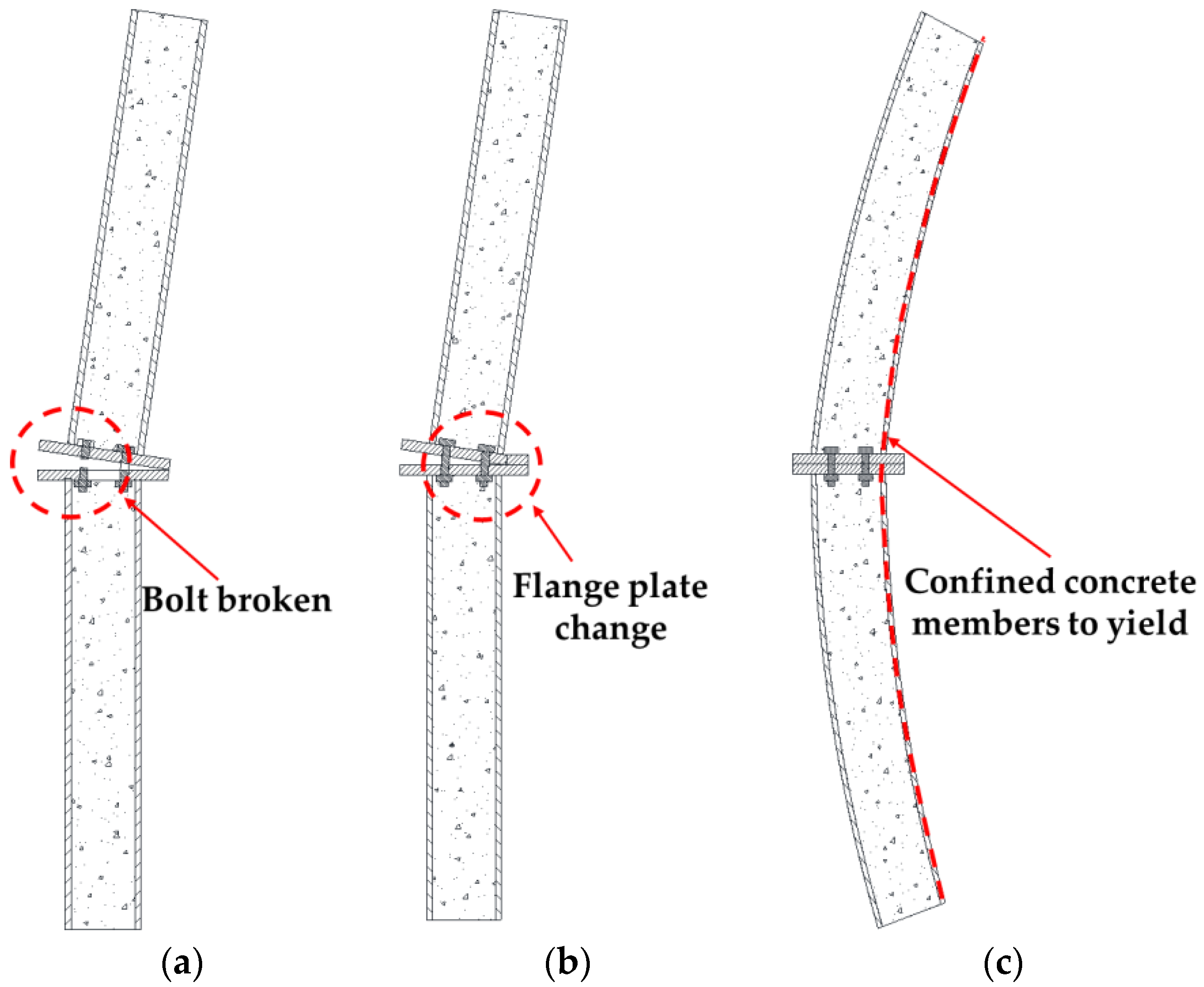
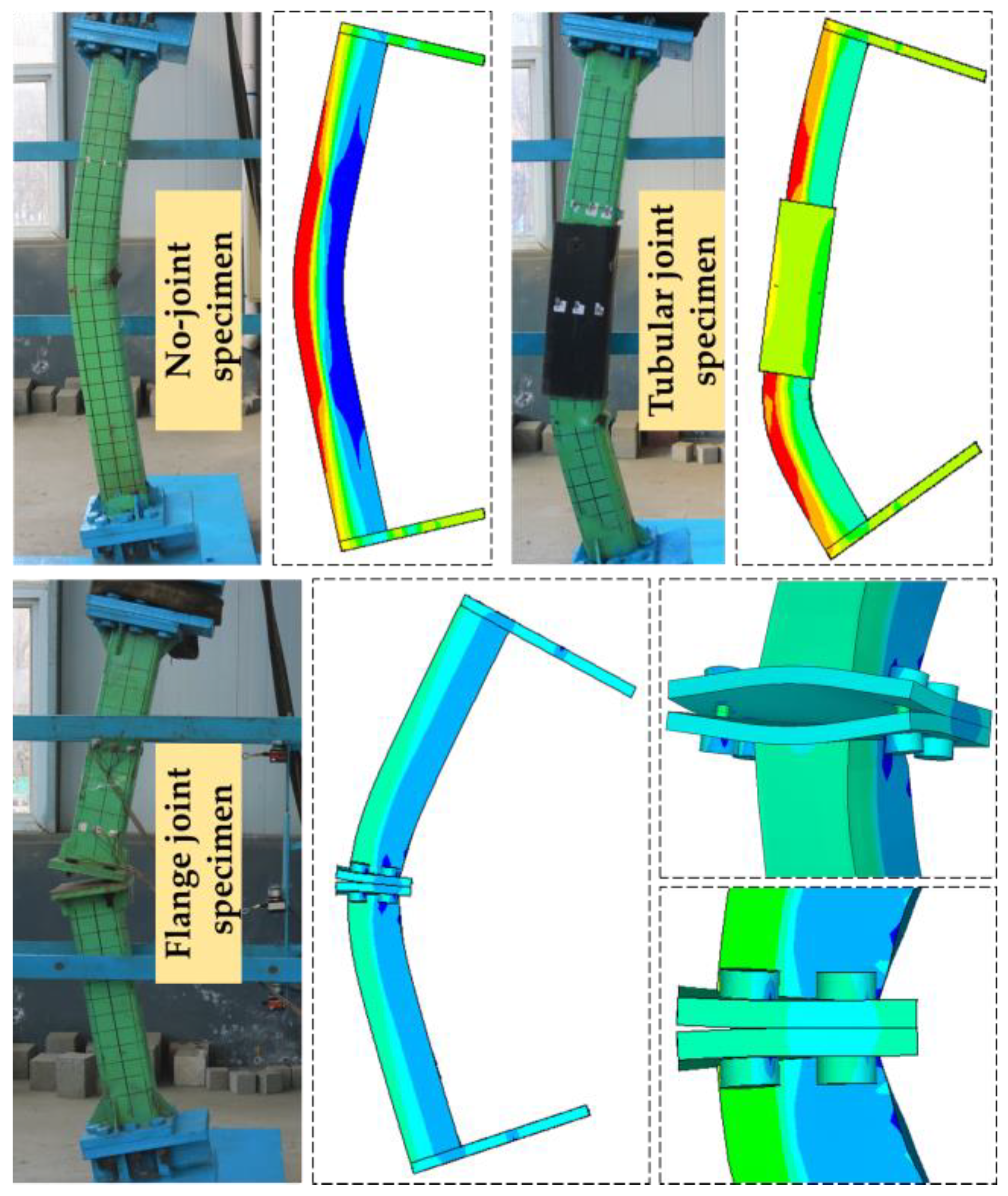
3.2.1. Experimental Phenomena
- ①
- The jointless components are bent uniformly, the steel tube in the pressure area of the midpoint section is bent, and the patent leather falls off after the ultimate load is reached.
- ②
- The failure form of the tubular joint component is closer to that of the jointless member, but the weak section is located at the junction between the two ends of the tubular and the CFST component, the steel tube bending, the patent leather shedding is obvious, and the deformation failure mode is consistent with the description of Section 2.1.
- ③
- During the test of the flange joint member, the bending appears to be polyline-shaped and the final failure form ends due to bolt pulling, the flange plate is not significantly deformed, and the failure mode is consistent with the description of Section 2.2.
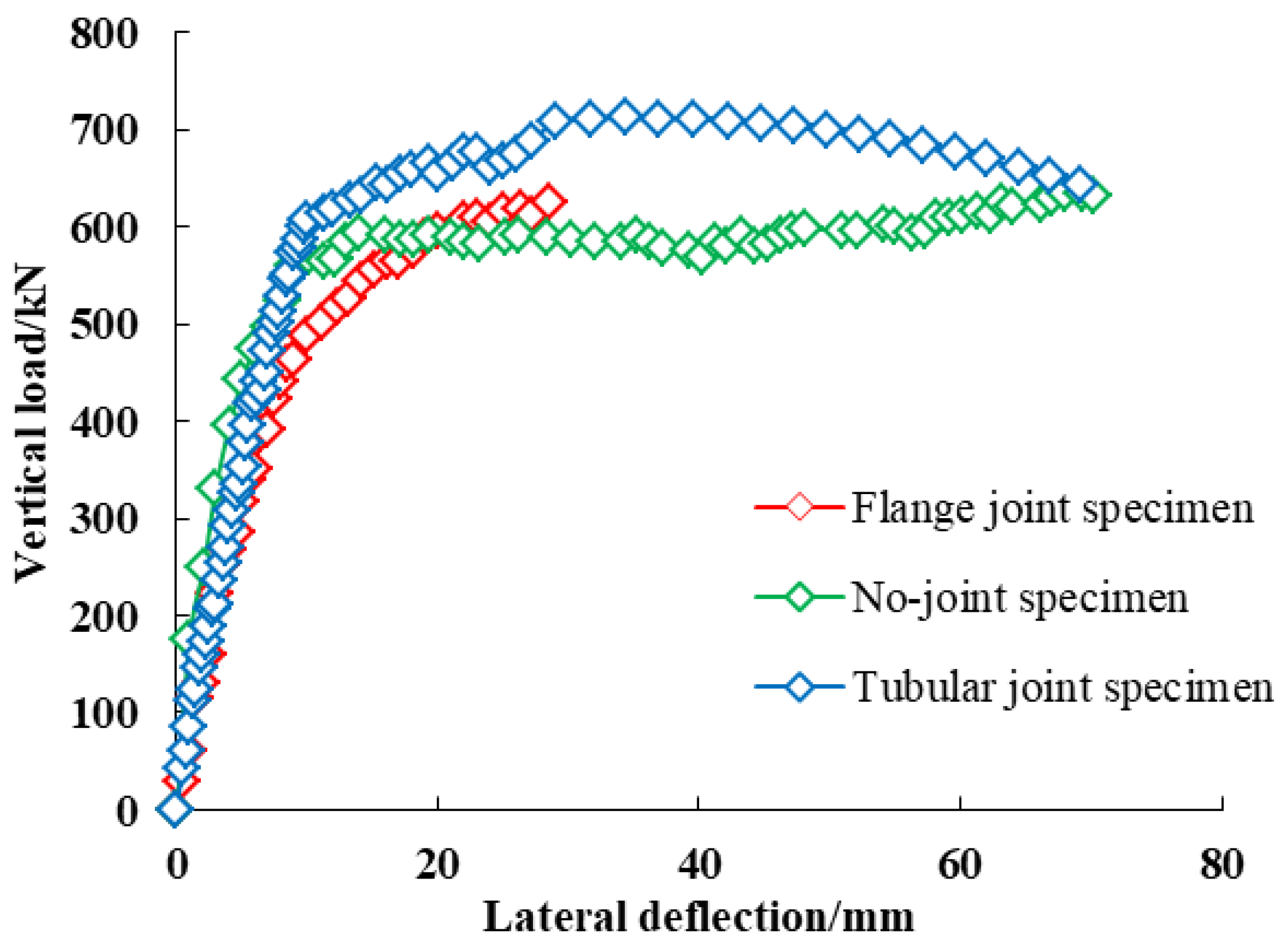
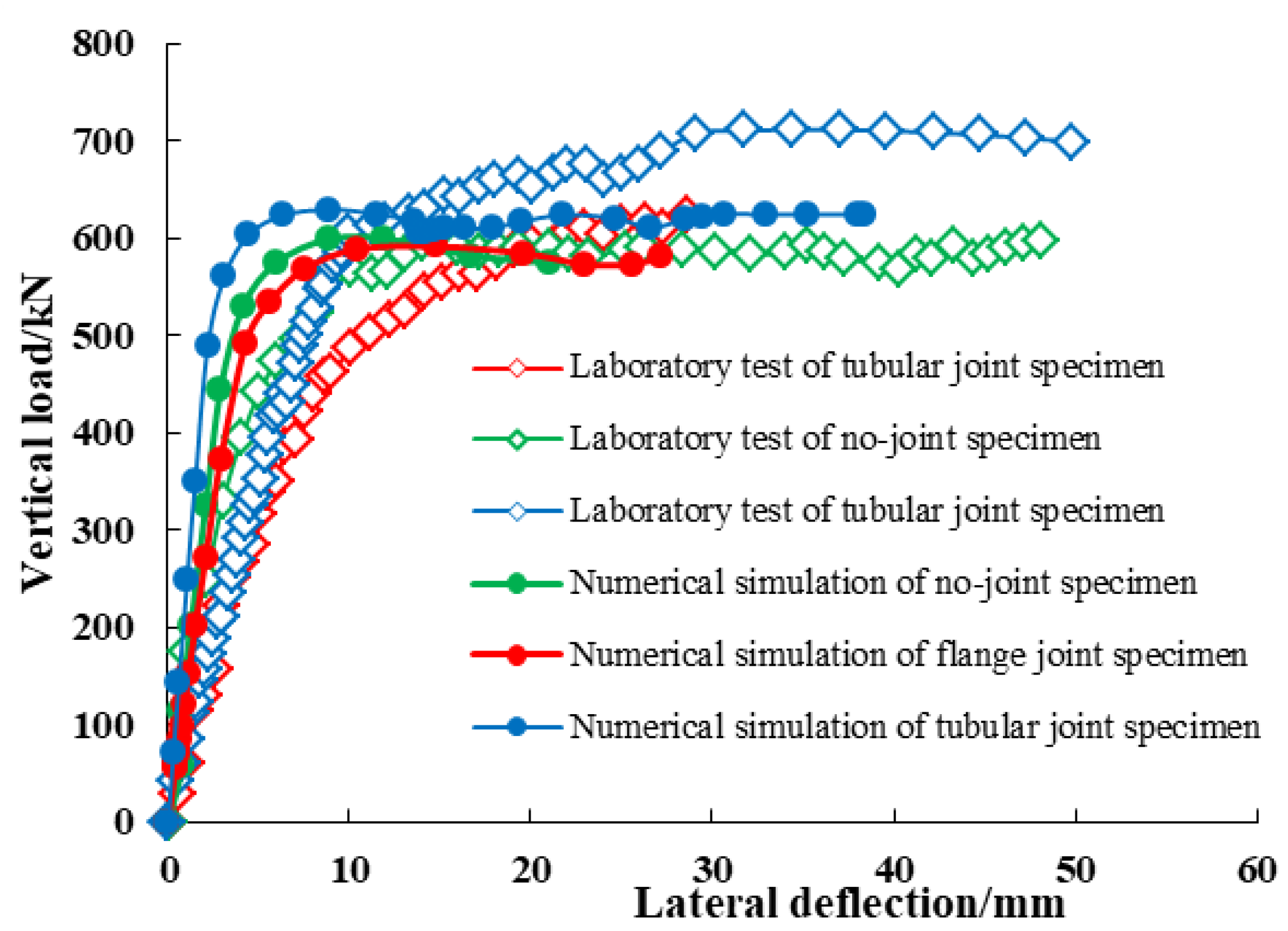
3.2.2. Load Deformation Curve
- ①
- The stiffness of the tubular joint and the no-joint member is similar, and after yielding, the strength of the tubular joint is significantly higher than that of the non-joint component; the stiffness of the flange joint is gradually reduced until the brittleness is destroyed.
- ②
- The ultimate bearing capacity of the jointless member in the specimen is 606.826 KN, which is not very different from the bearing capacity of the tubular joint specimen of 623.639 KN, of which the flange joint specimen is the smallest, with a bearing capacity of 544.92 KN.
- ③
- Due to bolt pulling, the flange joint shows typical brittle damage, resulting in instantaneous failure of the arch; no joint specimen and tubular specimen have better ductility, and the tubular joint has higher yield strength and ultimate strength due to the strengthening effect of the tubular joint.
4. Numerical Comparison Test of Mechanical Properties of Joint Bending
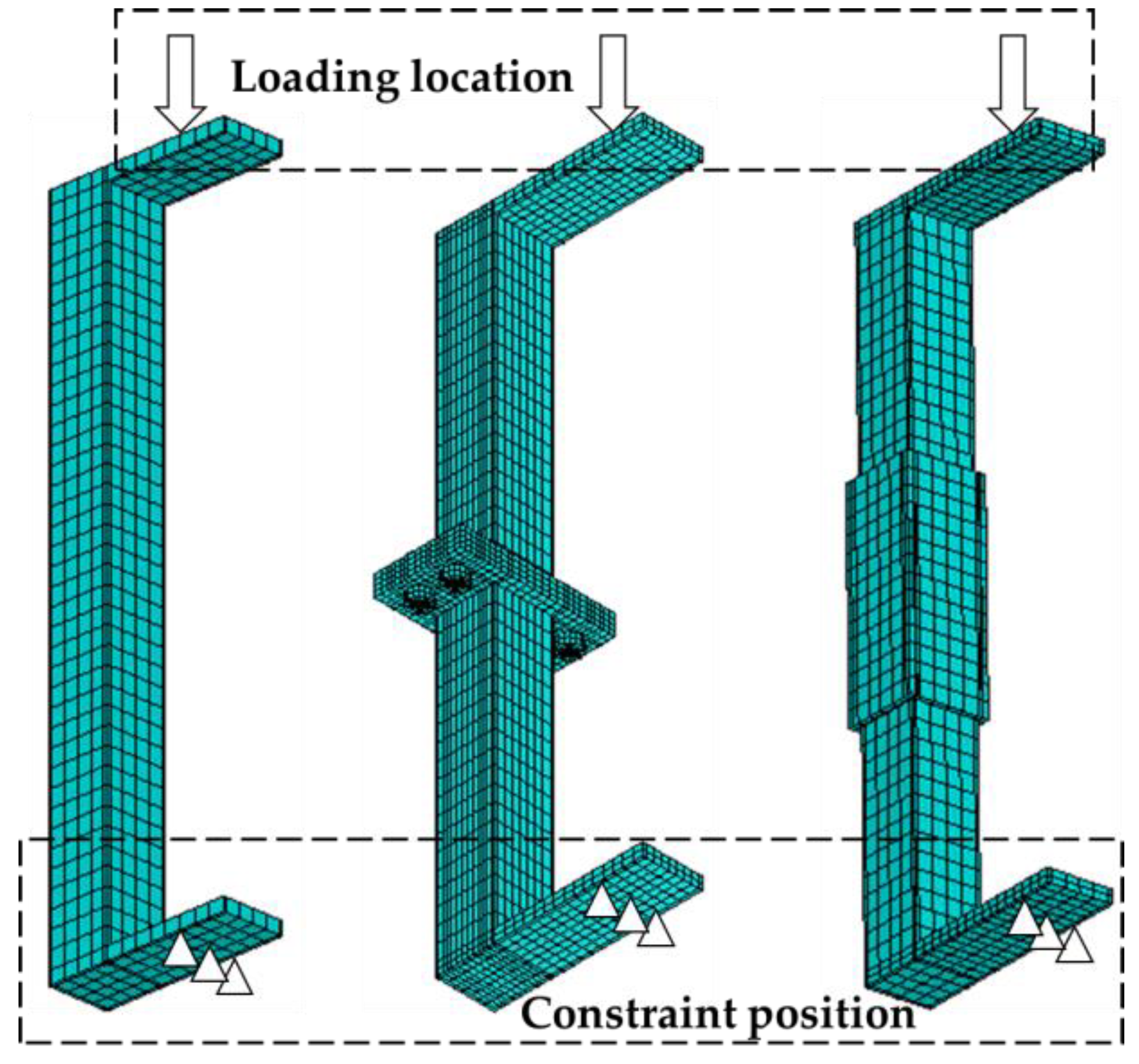
4.1. Simulation Scheme and Parameter Selection
4.2. Comparative Analysis of Test Results
- ①
- The joint specimen has essentially no obvious deformation before the load reaches the peak, and as the load gradually increases, the middle of the specimen slides to the left, and the test phenomenon and failure that form under the same loading conditions are consistent with the indoor test results, and the failure mode is smooth curve destruction.
- ②
- In the loading process of the tubular joint specimen, with the gradual increase in the load, due to the constraint of the tubular, the deformation of the concrete components of the steel pipe is limited, so that it bends and deforms around the upper edge of the tubular. At the same time, the tubular joint has undergone local deformation, and the steel pipe and tubular at the contact site have produced an obvious stress concentration, and the destruction phenomenon is consistent with the indoor test results.
- ③
- In the ultimate failure state of the flange joint, the bolt in the tension zone shrinks significantly. Overall, the deformation of the test piece joint area is small, and the overall deformation form is polyline-shaped.
5. Numerical Comparison Test of Mechanical Properties of Joint Bending
5.1. Test Protocol
5.2. Analysis of Test Results
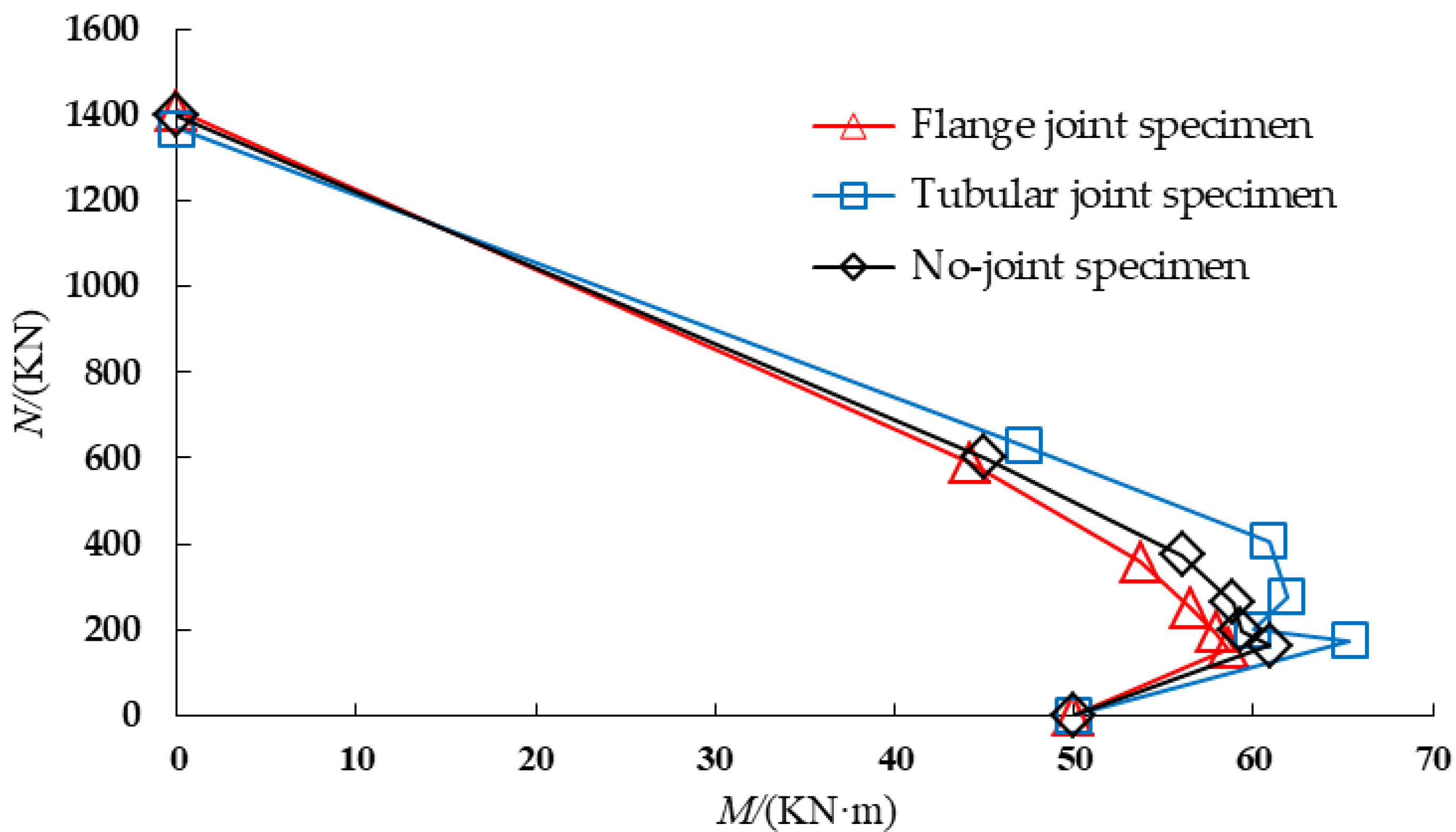
5.2.1. Tubular Joint Components
- ①
- The trend pattern of the NCJS specimen and the tubular joint specimen is consistent, and the distance between the tubular joint specimen curve and the intersection point of the M axis and the right vertex of the curve is larger than that of the NCJS specimen, which indicates that the bending-bearing capacity of the tubular joint under the action of axial force is greater than that of the NCJS specimen.
- ②
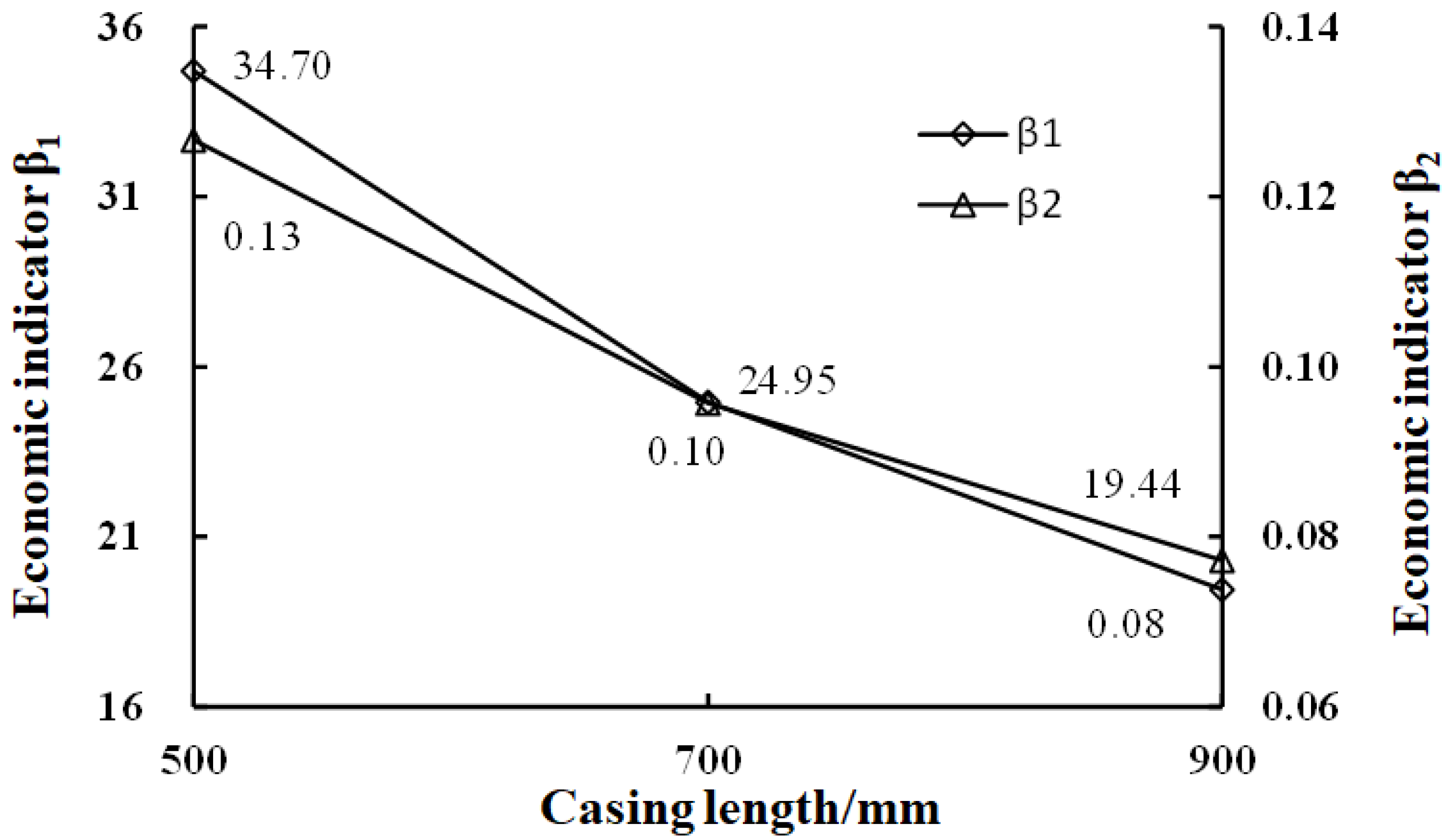
- The spacing of each curve decreases from basically unchanged to gradually increasing with a decrease in the N value, indicating that the length of the tubular joint has little impact on the axial pressure resistance of the bending specimen and has a significant impact on the bearing capacity of the bending resistance.
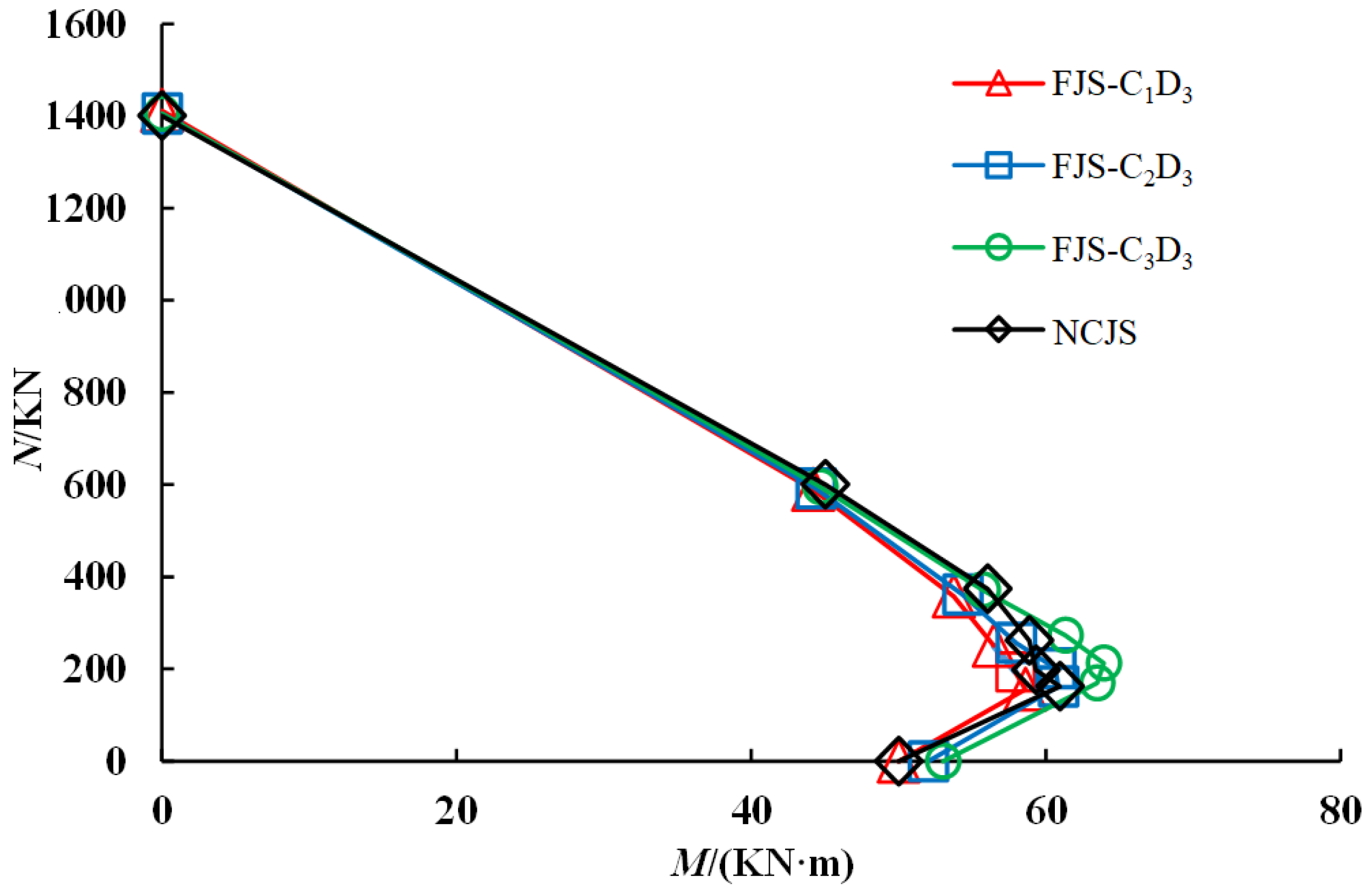
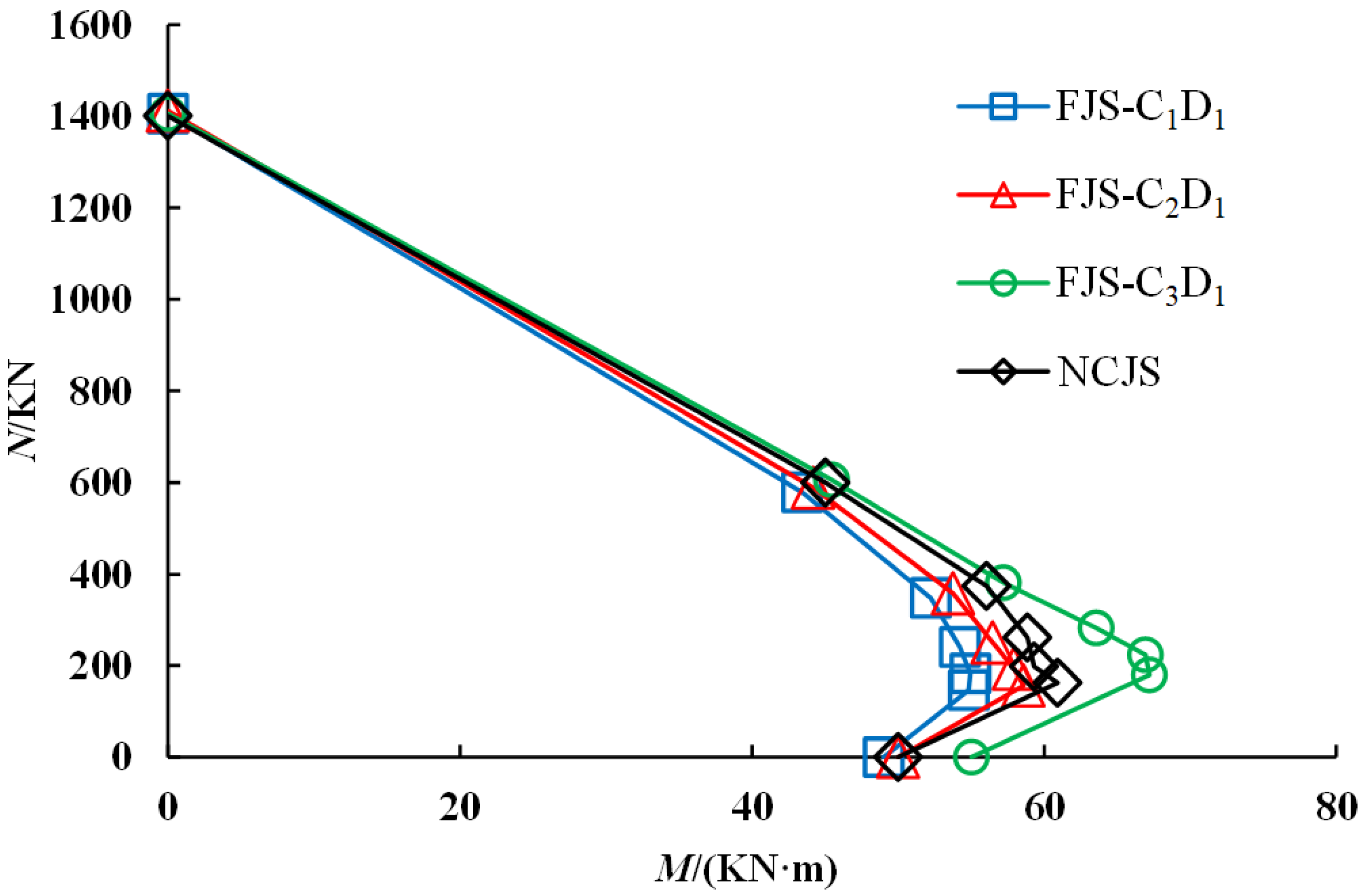
- ①
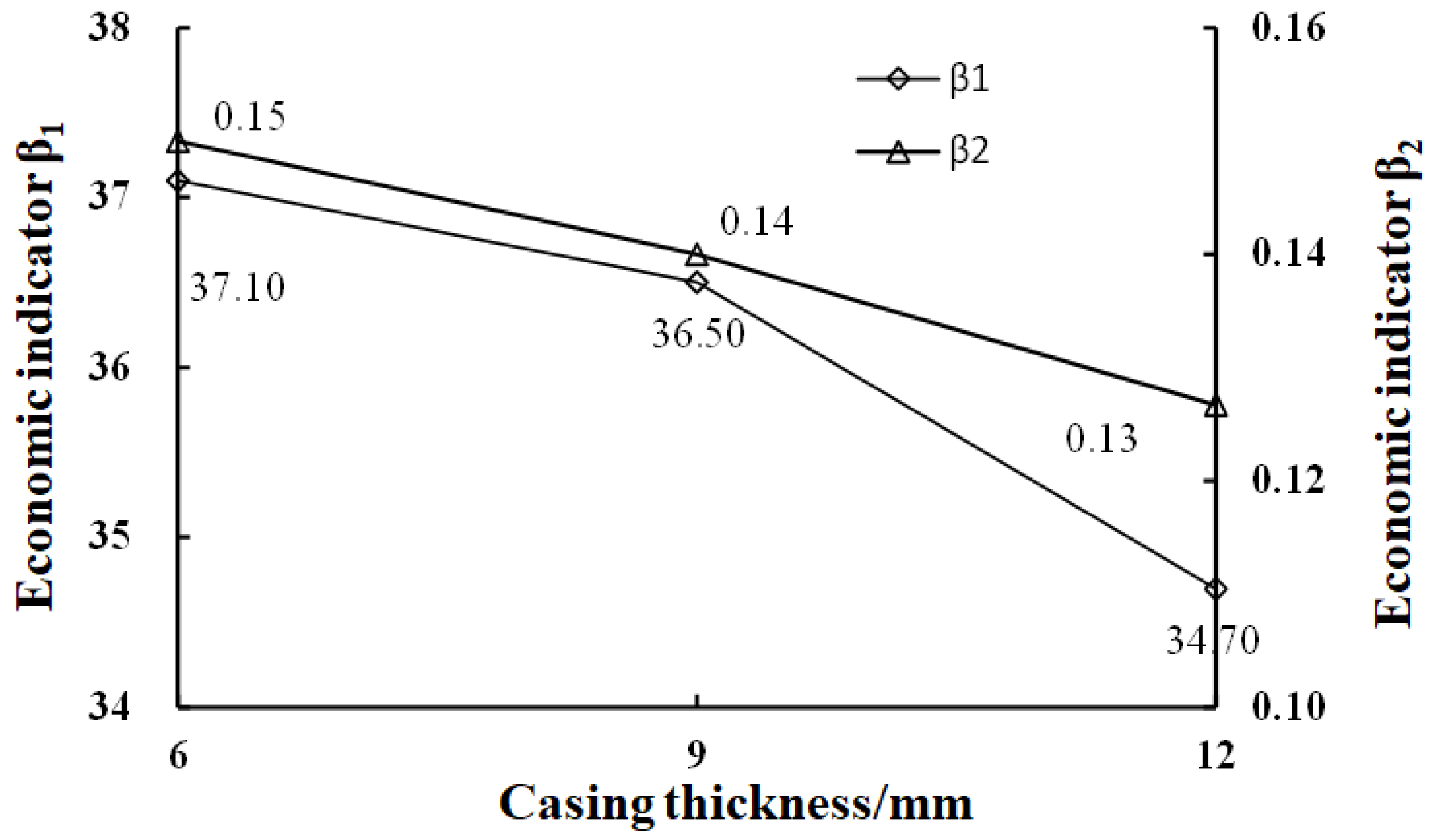
- The NCJS specimen is consistent with the trend pattern of the specimen of different tubular thicknesses, the influence of different tubular lengths is consistent, and the bending-bearing capacity of the tubular joint under the action of axial force is greater than that of the NCJS specimen.
- ②
- The spacing of each curve is basically the same, indicating that the wall thickness of the tubular joint has an impact on the bearing capacity of axial pressure and the bearing capacity of bending resistance, but it is not obvious.
5.2.2. Flange Joint Components
5.3. Design Recommendations
5.3.1. Joint Form Selection
5.3.2. Joint Parameter Design
6. Conclusions
- (1)
- The bending behavior of the no-joint specimen and the tubular joint specimen is similar, showing uniform curve deformation. The flange joint shows typical brittle damage due to bolt pulling, showing a polyline-shaped failure form. The ultimate bearing capacity of the n- joint component is 606.826 KN, which is not much different from the bearing capacity of the tubular joint specimen at 623.639 KN, and the flange joint specimen is the smallest, with a bearing capacity of 544.92 KN. The tubular joint has higher yield strength and limited strength due to the reinforcing action of the sleeve.
- (2)
- The M-N envelop curve under different joint parameters was obtained, the relationship between joint parameters and bending bearing performance was quantified, and the influence mechanism of joint parameters was clarified. Engineering design suggestions are proposed: The force transmission mechanism of the tubular joint is clear, of which the bearing capacity is high, and it can be applied to the deep roadway project of soft rock, high stress, and other complex geological conditions, with a length of 500 mm and a wall thickness of 9 mm. The tubular joint should be used as the preferred joint connection form for the CFST support arch.
- (3)
- This paper compares the strength of different types of joints and the no-joint component, which provides a reference for the relevant design. In the future, the quantitative analysis and evaluation of the joint strength and stiffness on the overall strength and stiffness of the arch should be carried out to establish a quantitative design method for concrete-filled steel tubular arch joints in underground engineering.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, M.C. Progress and challenges of soft rock engineering in depth. J. China Coal Soc. 2014, 39, 1409–1417. [Google Scholar]
- Wang, Q.Z.; Xie, W.B.; Jing, S.G. Instability mechanism and control technology of chamber group surrounding rock in complex structural area. J. Min. Saf. Eng. 2014, 31, 263–269. [Google Scholar]
- He, M.C.; Jing, H.H.; Sun, X.M. Mechanics of Soft Rock Engineering; Science Press: Beijing, China, 2002. [Google Scholar]
- Wang, L.; Wang, Q.; Huang, Y.B. Study on deformation mechanism and support technology of deep cross-measure roadway under high stress. J. Min. Saf. Eng. 2019, 36, 112–121. [Google Scholar]
- Meng, Q.; Han, L.J.; Zhang, F.E. Coupling support effect on high-stress deep soft rock roadway and its application. Rock Soil Mech. 2017, 38, 1424–1435. [Google Scholar]
- Hou, C.J. Key technology for surrounding rock control in deep roadway. J. China Univ. Min. Technol. 2017, 46, 970–978. [Google Scholar]
- Liao, W.; He, P.; Yan, D.M. Study on stress distribution law of steel arch frame for initial support of tunnel. J. China Railw. Soc. 2017, 39, 140–147. [Google Scholar]
- Yu, F.C.; Zhang, D.L.; Fang, Q. Experimental study on composite support characteristics of high strength reinforced grid concrete. J. Civ. Eng. 2015, 48, 104–111. [Google Scholar]
- Li, W.T.; Wang, Q.; Wang, D.C. Experimental study confined concrete on short columns under axial load of U-type arch centering and its application in mine. J. Min. Saf. Eng. 2014, 31, 1–9. [Google Scholar]
- Ellobody, E.; Young, B.; Lam, D. Behaviour of normal and high strength concrete-filled compact steel tube circular stub columns. Constr. Steel Res. 2006, 62, 706–715. [Google Scholar] [CrossRef]
- Hassan, M.M.; Mahmoud, A.A.; Serroe, M.H. Behavior of concrete-filled double skin steel tube beam-columns. Steel Compos. Struct. 2016, 22, 1141–1162. [Google Scholar] [CrossRef]
- Han, L.H.; Yang, Y.F. Study on axial bearing capacity of concrete-filled-steel-tube columns with rectangular section. China Civ. Eng. J. 2001, 34, 22–31. [Google Scholar]
- Li, X.W.; Zhao, J.H.; Zhu, T.D. Mechanics behavior of axially loaded short columns with concrete filled square steel tube. China J. Highw. Transp. 2006, 19, 77–81. [Google Scholar]
- Elremaily, A.; Azizinamini, A. Experimental behavior of steel beam to CFT column connections. J. Constr. Steel Res. 2001, 57, 1099–1119. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zhang, Y.; Shi, Y.J. Analysis of load capacity of new-style joints between cable and concrete-filled steel tube arch bridge. J. Archit. Civ. Eng. 2005, 22, 55–58. [Google Scholar]
- Zhu, T.; Liang, H.J.; Lu, Y.Y.; Li, W.J.; Zhang, H. Axial behaviour of slender concrete-filled steel tube square columns strengthened with square concrete-filled steel tube jackets. Adv. Struct. Eng. 2020, 23, 1074–1086. [Google Scholar] [CrossRef]
- Hanifehzadeh, M.; Aryan, H.; Gencturk, B.; Akyniyazov, D. Structural response of steel jacket-UHPC retrofitted reinforced concrete columns under blast loading. Materials 2021, 14, 1521. [Google Scholar] [CrossRef]
- Li, S.C.; Lu, W.; Wang, Q. Study on failure mechanism and mechanical properties of tubular joints of square steel confined concrete arch. Eng. Fail. Anal. 2018, 92, 539–552. [Google Scholar] [CrossRef]
- Gao, Y.F.; Wang, B.; Wang, J. Test on structural propertyand application of concrete-filled steel tube support of deep mine and soft rock roadway. Chin. J. Rock Mech. Eng. 2010, 29, 2604–2609. [Google Scholar]
- Zang, D.S.; Li, A.Q. Study on concrete-filled steel tube supports. Chin. J. Geotech. Eng. 2001, 23, 342–344. [Google Scholar]
- Sun, H.B. Study on Stability Bearing Mechanism and Key Technologies of Assembly Confined Concrete Support for Large Section Tunnel. Ph.D. Thesis, Shandong University, Jinan, China, 2019. [Google Scholar]
- Lu, W.; Sun, H.B. Study on support characteristic curve of primary support structures in underground excavation considering bond-slip behavior. Adv. Struct. Eng. 2021, 24, 497–508. [Google Scholar] [CrossRef]
- Hanl, H.; Yao, G.H.; Tao, Z. Performance of concrete-filled thin-walled steel tubes under pure torsion. Thin-Wall Struct. 2007, 45, 24–36. [Google Scholar]

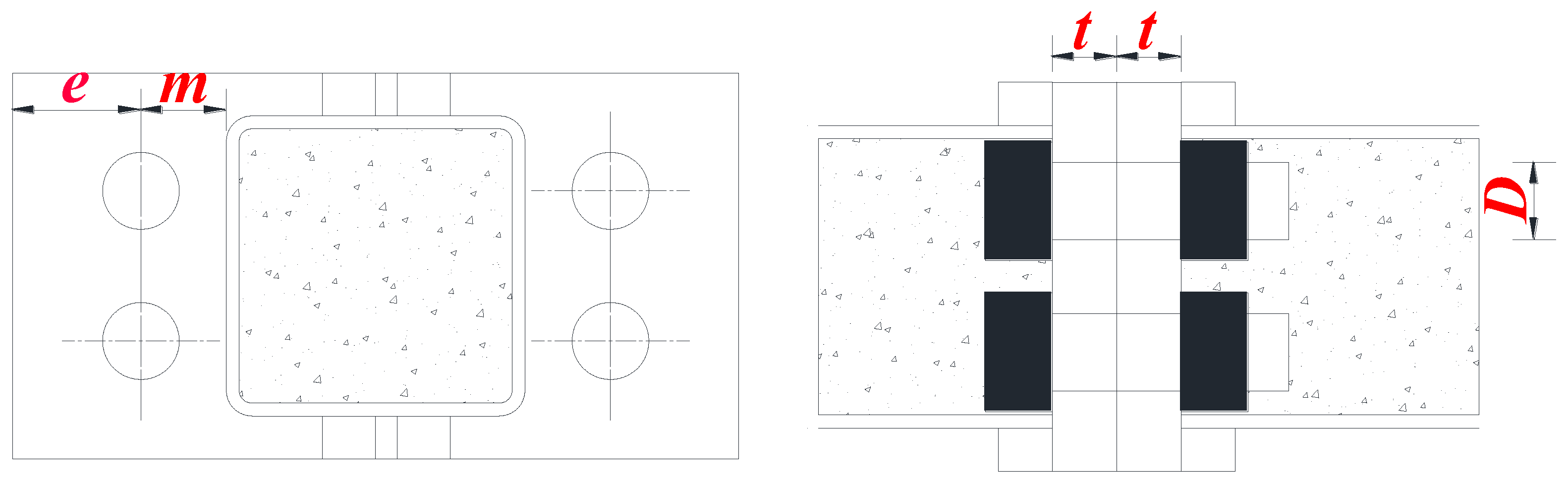
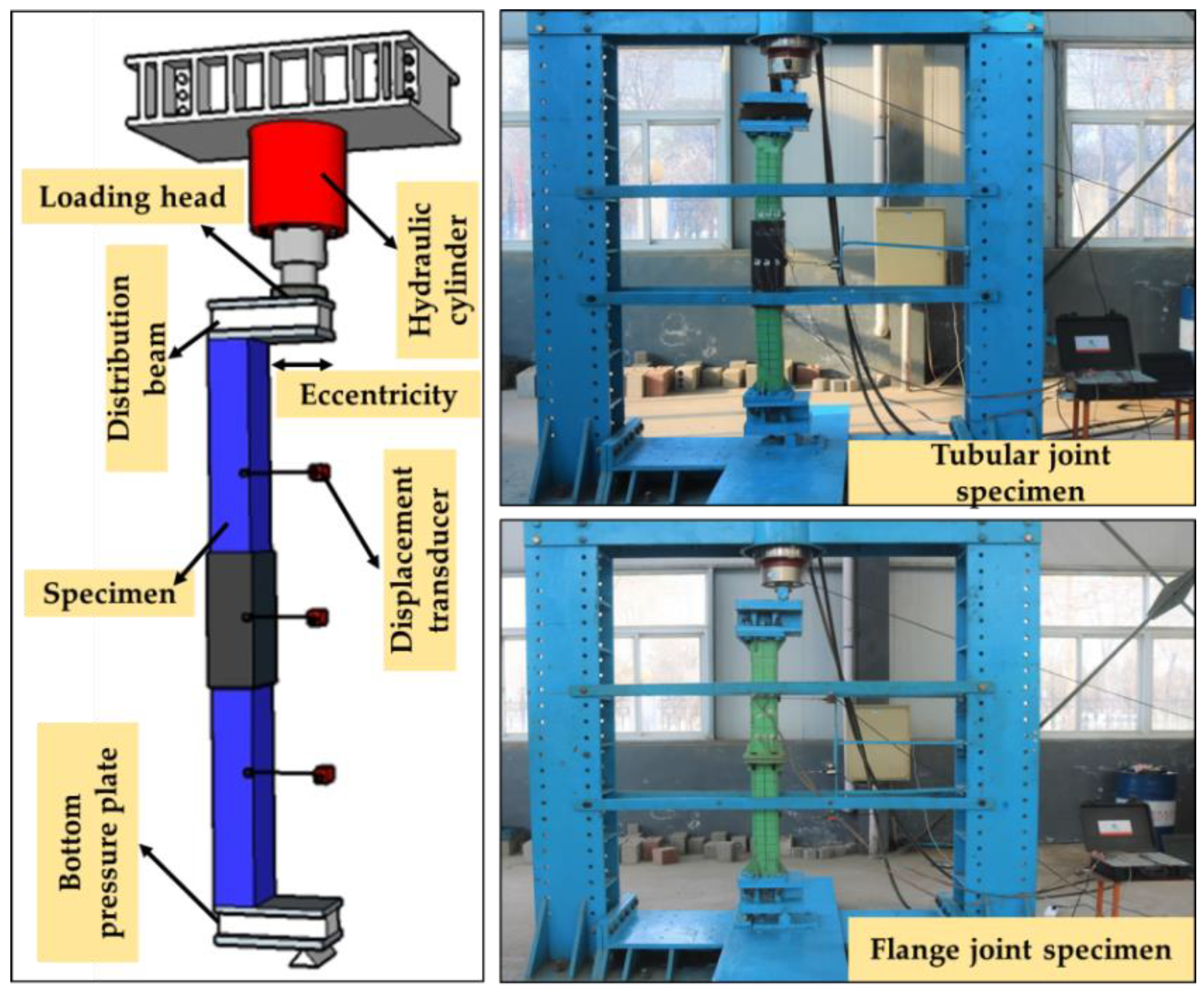




| Component Form | Arch Type | Tube Wall Thickness/mm | Tubular Length/mm | Core Concrete Strength/MPa |
|---|---|---|---|---|
| No joint specimen | CFST150-8 | 8 | 150 | C40 |
| Component Form | Arch Type | Tubular Wall Thickness/mm | Sleeve Width/mm | Tubular Length/mm | Specimen Length/mm |
|---|---|---|---|---|---|
| Tubular joint | CFST150-8 | 12 | 180 | 500 | 1500 |
| Component Form | Arch Type | Flange Thickness/mm | Bolt Diameter/mm | Specimen Length/mm |
|---|---|---|---|---|
| Flange connection | CFST150-8 | 25 | 22 | 1500 |
| Numbering | Parametric Variable | 1 | 2 | 3 |
|---|---|---|---|---|
| Ai | Tubular length/m | 0.5 | 0.7 | 0.9 |
| Bj | tubular wall thickness/mm | 6 | 9 | 12 |
| Cm | Bolt Diameter/mm | 22 | 24 | 26 |
| Scheme Number | Parameter 1 | Parameter 2 | Quantity | Eccentricity (E/d) |
|---|---|---|---|---|
| Ai | Tubular length/m | 0.5 | 0.7 | 0.9 |
| Bj | tubular wall thickness/mm | 6 | 9 | 12 |
| Cm | Bolt Diameter/mm | 22 | 24 | 26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Lu, W.; Wang, J.; Ren, Q.; Xu, X.; Han, D.; Li, X.; Yang, H.; Wei, L.; Liu, Y. Comparative Study on Compressive and Flexural Properties of Concrete-Filled Steel Tubular Arch Joints. Sustainability 2022, 14, 8916. https://doi.org/10.3390/su14148916
Sun H, Lu W, Wang J, Ren Q, Xu X, Han D, Li X, Yang H, Wei L, Liu Y. Comparative Study on Compressive and Flexural Properties of Concrete-Filled Steel Tubular Arch Joints. Sustainability. 2022; 14(14):8916. https://doi.org/10.3390/su14148916
Chicago/Turabian StyleSun, Huibin, Wei Lu, Jiancai Wang, Quangang Ren, Xin Xu, Debin Han, Xu Li, Huixiang Yang, Lianbang Wei, and Yan Liu. 2022. "Comparative Study on Compressive and Flexural Properties of Concrete-Filled Steel Tubular Arch Joints" Sustainability 14, no. 14: 8916. https://doi.org/10.3390/su14148916
APA StyleSun, H., Lu, W., Wang, J., Ren, Q., Xu, X., Han, D., Li, X., Yang, H., Wei, L., & Liu, Y. (2022). Comparative Study on Compressive and Flexural Properties of Concrete-Filled Steel Tubular Arch Joints. Sustainability, 14(14), 8916. https://doi.org/10.3390/su14148916





