Solar Photovoltaic Cell Parameter Identification Based on Improved Honey Badger Algorithm
Abstract
:1. Introduction
2. Photovoltaic Cell Model and Objective Function
2.1. Single Diode Model (SDM)
2.2. Double Diode Model (DDM)
2.3. Three Diode Model (TDM)
2.4. Objective Function
3. Improved Honey Badger Algorithm
3.1. Honey Badger Algorithm
3.2. Improved Honey Badger Algorithm
3.2.1. Spiral Exploration Mechanism
3.2.2. Density Factor of Quasi-Cosine Law Variation
3.2.3. Pinhole Imaging Strategy
3.2.4. IHBA Implementation Steps
3.2.5. Time Complexity Analysis of IHBA
4. Experimental Simulation and Result Analysis
4.1. Simulation Environment and Test Function
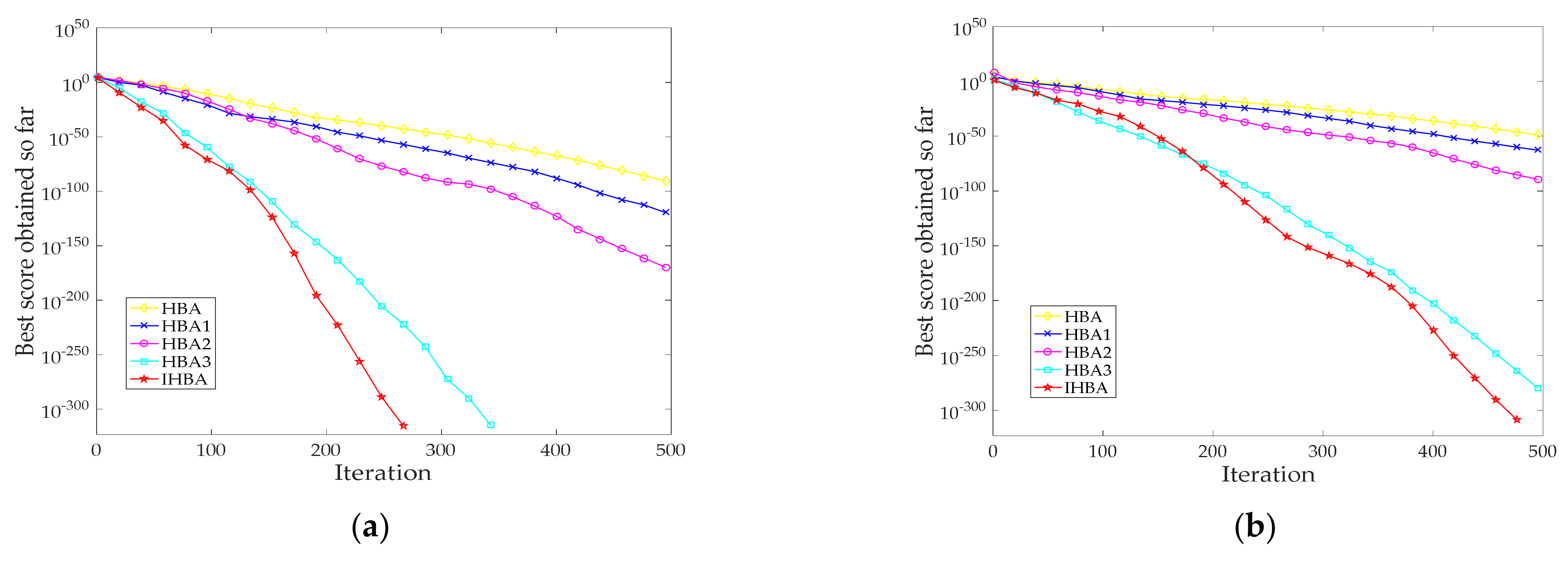
4.2. Optimization Comparison of Different Improvement Strategies
4.3. Comparison of Average Convergence Curves of Different Improvement Strategies
4.4. Comparison with Other New and Improved Algorithms
4.5. Wilcoxon Rank Sum Test
4.6. CEC2014 Test Function Optimization Comparison
5. Parameter Identification of Solar Photovoltaic Cell
5.1. Parameter Identification of SDM
5.2. Parameter Identification of DDM
5.3. Parameter Identification of TDM
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shahbaz, M.; Raghutla, C.; Chittedi, K.R.; Jiao, Z.; Vo, X.V. The effect of renewable energy consumption on economic growth: Evidence from the renewable energy country attractive index. Energy 2020, 207, 118162. [Google Scholar] [CrossRef]
- Adams, S.; Klobodu, E.K.M.; Apio, A. Renewable and non-renewable energy, regime type and economic growth. Renew. Energy 2018, 125, 755–767. [Google Scholar] [CrossRef]
- Güney, T. Renewable energy, non-renewable energy and sustainable development. Int. J. Sustain. Dev. World Ecol. 2019, 26, 389–397. [Google Scholar] [CrossRef]
- Ahmad, M.; Işık, C.; Jabeen, G.; Ali, T.; Ozturk, I.; Atchike, D.W. Heterogeneous links among urban concentration, non-renewable energy use intensity, economic development, and environmental emissions across regional development levels. Sci. Total Environ. 2021, 765, 144527. [Google Scholar] [CrossRef]
- Rasoulinezhad, E.; Saboori, B. Panel estimation for renewable and non-renewable energy consumption, economic growth, CO2 emissions, the composite trade intensity, and financial openness of the commonwealth of independent states. Environ. Sci. Pollut. Res. 2018, 25, 17354–17370. [Google Scholar] [CrossRef]
- Agrawal, S.; Soni, R. Renewable Energy: Sources, Importance and Prospects for Sustainable Future. Energy Cris. Chall. Solut. 2021, 131–150. [Google Scholar] [CrossRef]
- Xu, X.; Wei, Z.; Ji, Q.; Wang, C.; Gao, G. Global renewable energy development: Influencing factors, trend predictions and countermeasures. Resour. Policy 2019, 63, 101470. [Google Scholar] [CrossRef]
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strateg. Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Al-Shahri, O.A.; Ismail, F.B.; Hannan, M.A.; Lipu, M.S.H.; Al-Shetwi, A.Q.; Begum, R.A.; Al-Muhsen, N.F.O.; Soujeri, E. Solar photovoltaic energy optimization methods, challenges and issues: A comprehensive review. J. Clean. Prod. 2021, 284, 125465. [Google Scholar] [CrossRef]
- Benda, V.; Černá, L. PV cells and modules—State of the art, limits and trends. Heliyon 2020, 6, e05666. [Google Scholar] [CrossRef]
- Yıldıran, N.; Tacer, E. Identification of photovoltaic cell single diode discrete model parameters based on datasheet values. Sol. Energy 2016, 127, 175–183. [Google Scholar] [CrossRef]
- Hassan Hosseini, S.M.; Keymanesh, A.A. Design and construction of photovoltaic simulator based on dual-diode model. Sol. Energy 2016, 137, 594–607. [Google Scholar] [CrossRef]
- Ćalasan, M.; Abdel Aleem, S.H.E.; Zobaa, A.F. A new approach for parameters estimation of double and triple diode models of photovoltaic cells based on iterative Lambert W function. Sol. Energy 2021, 218, 392–412. [Google Scholar] [CrossRef]
- Lineykin, S.; Averbukh, M.; Kuperman, A. An improved approach to extract the single-diode equivalent circuit parameters of a photovoltaic cell/panel. Renew. Sustain. Energy Rev. 2014, 30, 282–289. [Google Scholar] [CrossRef]
- Pardhu, B.S.S.G.; Kota, V.R. Radial movement optimization based parameter extraction of double diode model of solar photovoltaic cell. Sol. Energy 2021, 213, 312–327. [Google Scholar] [CrossRef]
- Oliva, D.; Elaziz, M.A.; Elsheikh, A.H.; Ewees, A.A. A review on meta-heuristics methods for estimating parameters of solar cells. J. Power Sources 2019, 435, 126683. [Google Scholar] [CrossRef]
- Ben Hmamou, D.; Elyaqouti, M.; Arjdal, E.; Chaoufi, J.; Saadaoui, D.; Lidaighbi, S.; Aqel, R. Particle swarm optimization approach to determine all parameters of the photovoltaic cell. Mater. Today Proc. 2022, 52, 7–12. [Google Scholar] [CrossRef]
- Toledo, F.J.; Blanes, J.M.; Galiano, V. Two-Step Linear Least-Squares Method for Photovoltaic Single-Diode Model Parameters Extraction. IEEE Trans. Ind. Electron. 2018, 65, 6301–6308. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O.; Ekoh, E.E. Evaluation of numerical algorithms used in extracting the parameters of a single-diode photovoltaic model. Sustain. Energy Technol. Assess. 2016, 13, 51–59. [Google Scholar] [CrossRef]
- Chaibi, Y.; Allouhi, A.; Salhi, M. A simple iterative method to determine the electrical parameters of photovoltaic cell. J. Clean. Prod. 2020, 269, 122363. [Google Scholar] [CrossRef]
- Rasheed, M.; SuhaShihab; Alabdali, O.; Hassan, H.H. Parameters Extraction of a Single-Diode Model of Photovoltaic Cell Using False Position Iterative Method. J. Phys. Conf. Ser. 2021, 1879, 032113. [Google Scholar] [CrossRef]
- Çímen, M.E.; Garíp, Z.; Boz, A.F.; Karayel, D. Firefly Algorithm and Particle Swarm Optimization for photovoltaic parameters identification based on single model. In Proceedings of the 2018 2nd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 19–21 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Elazab, O.S.; Hasanien, H.M.; Alsaidan, I.; Abdelaziz, A.Y.; Muyeen, S.M. Parameter Estimation of Three Diode Photovoltaic Model Using Grasshopper Optimization Algorithm. Energies 2020, 13, 497. [Google Scholar] [CrossRef] [Green Version]
- Aydin, O.; Gozde, H.; Dursun, M.; Taplamacioglu, M.C. Comparative Parameter Estimation of Single Diode PV-Cell Model by Using Sine-Cosine Algorithm and Whale Optimization Algorithm. In Proceedings of the 2019 6th International Conference on Electrical and Electronics Engineering (ICEEE), Istanbul, Turkey, 16–17 April 2019; pp. 65–68. [Google Scholar] [CrossRef]
- Saxena, A.; Sharma, A.; Shekhawat, S. Parameter extraction of solar cell using intelligent grey wolf optimizer. Evol. Intell. 2022, 15, 167–183. [Google Scholar] [CrossRef]
- Kumar, C.; Raj, T.D.; Premkumar, M.; Raj, T.D. A new stochastic slime mould optimization algorithm for the estimation of solar photovoltaic cell parameters. Optik 2020, 223, 165277. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Han, E.; Ghadimi, N. Model identification of proton-exchange membrane fuel cells based on a hybrid convolutional neural network and extreme learning machine optimized by improved honey badger algorithm. Sustain. Energy Technol. Assess. 2022, 52, 102005. [Google Scholar] [CrossRef]
- Hosny, R.A.; Abd Elaziz, M.; Ali Ibrahim, R. Enhanced Feature Selection Based on Integration Containment Neighborhoods Rough Set Approximations and Binary Honey Badger Optimization. Comput. Intell. Neurosci. 2022, 2022, 3991870. [Google Scholar] [CrossRef]
- Ni, B.; Wang, S.; Ma, Y.; Li, G. An Optimized Extreme Learning Machine for Predicting Loan Default in Peer-to-peer Lending Based on an Enhanced Honey Badger Algorithm. In Proceedings of the 2022 7th International Conference on Control and Robotics Engineering (ICCRE), Beijing, China, 15–17 April 2022; pp. 139–146. [Google Scholar] [CrossRef]
- Fan, Q.; Chen, Z.; Li, Z.; Xia, Z.; Yu, J.; Wang, D. A new improved whale optimization algorithm with joint search mechanisms for high-dimensional global optimization problems. Eng. Comput. 2021, 37, 1851–1878. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K.; Mirjalili, S. An efficient equilibrium optimizer with mutation strategy for numerical optimization. Appl. Soft Comput. 2020, 96, 106542. [Google Scholar] [CrossRef]
- Chen, H.; Li, W.; Yang, X. A whale optimization algorithm with chaos mechanism based on quasi-opposition for global optimization problems. Expert Syst. Appl. 2020, 158, 113612. [Google Scholar] [CrossRef]
- Chen, H.; Yang, C.; Heidari, A.A.; Zhao, X. An efficient double adaptive random spare reinforced whale optimization algorithm. Expert Syst. Appl. 2020, 154, 113018. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft. Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Soft. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.L.; Dhiman, G. Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]











| Function | Name | Dim | Domain | Optimal Value |
|---|---|---|---|---|
| F1 | Sphere | 30/100/500 | [−100, 100] | 0 |
| F2 | Schwefel’ problem 2.22 | 30/100/500 | [−10, 10] | 0 |
| F3 | Schwefel’ problem 1.2 | 30/100/500 | [−100, 100] | 0 |
| F4 | Schwefel’ problem 2.21 | 30/100/500 | [−100, 100] | 0 |
| F5 | Step Function | 30/100/500 | [−100, 100] | 0 |
| F6 | Quartic Function | 30/100/500 | [−1.28, 1.28] | 0 |
| F7 | Generalized Rastrigin’s Function | 30/100/500 | [−5.12, 5.12] | 0 |
| F8 | Ackley’s Function | 30/100/500 | [−32, 32] | 0 |
| F9 | Ceneralized Criewank Function | 30/100/500 | [−600, 600] | 0 |
| F10 | Ceneralized Penalized Function 1 | 30/100/500 | [−50, 50] | 0 |
| F11 | Shekell’s Foxholes Function | 2 | [−65, 65] | 1 |
| F12 | Kowalik’s Function | 4 | [−5, 5] | 0.0003 |
| F13 | Six-Hump Camel-Back Function | 2 | [−5, 5] | −1.03 |
| F14 | Hatman’s Function1 | 3 | [0, 1] | −3.86 |
| F15 | Hatman’s Function2 | 6 | [0, 1] | −3.32 |
| F16 | Shekel’s Family 1 | 4 | [1, 10] | −10 |
| F17 | Shekel’s Family 2 | 4 | [1, 10] | −10 |
| F18 | Shekel’s Family 3 | 4 | [1, 10] | −10 |
| Function | Algorithm | Best | Worst | Mean | Std |
|---|---|---|---|---|---|
| F1 | HBA | 8.24 × 10−85 | 1.32 × 10−78 | 7.23 × 10−80 | 2.60 × 10−79 |
| HBA1 | 3.42 × 10−116 | 7.73 × 10−103 | 5.21 × 10−104 | 1.77 × 10−103 | |
| HBA2 | 8.05 × 10−158 | 2.81 × 10−141 | 1.00 × 10−142 | 5.13 × 10−142 | |
| HBA3 | 0.00 | 0.00 | 0.00 | 0.00 | |
| IHBA | 0.00 | 0.00 | 0.00 | 0.00 | |
| F2 | HBA | 8.92 × 10−46 | 8.76 × 10−43 | 1.66 × 10−43 | 1.66 × 10−43 |
| HBA1 | 7.12 × 10−59 | 4.02 × 10−53 | 5.24 × 10−54 | 5.24 × 10−54 | |
| HBA2 | 2.22 × 10−79 | 3.56 × 10−73 | 2.94 × 10−74 | 2.94 × 10−74 | |
| HBA3 | 3.02 × 10−295 | 9.06 × 10−274 | 3.05 × 10−275 | 3.05 × 10−275 | |
| IHBA | 0.00 | 1.61 × 10−319 | 5.37 × 10−321 | 5.37 × 10−321 | |
| F3 | HBA | 1.02 × 10−62 | 1.01 × 10−53 | 3.41 × 10−55 | 1.84 × 10−54 |
| HBA1 | 9.67 × 10−99 | 9.32 × 10−84 | 3.33 × 10−85 | 1.70 × 10−84 | |
| HBA2 | 1.14 × 10−138 | 1.87 × 10−126 | 7.51 × 10−128 | 3.46 × 10−127 | |
| HBA3 | 0.00 | 0.00 | 0.00 | 0.00 | |
| IHBA | 0.00 | 0.00 | 0.00 | 0.00 | |
| F4 | HBA | 3.91 × 10−33 | 2.73 × 10−31 | 4.39 × 10−32 | 5.83 × 10−32 |
| HBA1 | 2.04 × 10−55 | 1.32 × 10−45 | 9.14 × 10−47 | 3.24 × 10−46 | |
| HBA2 | 8.04 × 10−71 | 3.71 × 10−66 | 2.73 × 10−67 | 7.13 × 10−67 | |
| HBA3 | 2.16 × 10−269 | 8.49 × 10−254 | 3.41 × 10−255 | 0.00 | |
| IHBA | 0.00 | 2.07 × 10−321 | 6.90 × 10−323 | 0.00 | |
| F5 | HBA | 0.00 | 3.89 × 10−7 | 1.44 × 10−8 | 6.64 × 10−8 |
| HBA1 | 0.00 | 2.24 × 10−8 | 2.02 × 10−8 | 7.14 × 10−8 | |
| HBA2 | 0.00 | 2.24 × 10−8 | 3.12 × 10−9 | 6.04 × 10−9 | |
| HBA3 | 0.00 | 1.77 × 10−8 | 2.03 × 10−9 | 3.83 × 10−9 | |
| IHBA | 0.00 | 3.65 × 10−8 | 2.53 × 10−9 | 7.70 × 10−9 | |
| F6 | HBA | 8.56 × 10−5 | 2.28 × 10−3 | 8.38 × 10−4 | 5.95 × 10−4 |
| HBA1 | 4.66 × 10−5 | 1.93 × 10−3 | 5.21 × 10−4 | 5.95 × 10−4 | |
| HBA2 | 3.47 × 10−5 | 1.99 × 10−3 | 5.91 × 10−4 | 5.57 × 10−4 | |
| HBA3 | 3.88 × 10−6 | 2.55 × 10−4 | 6.71 × 10−5 | 6.12 × 10−5 | |
| IHBA | 4.55 × 10−6 | 3.30 × 10−4 | 8.60 × 10−5 | 7.35 × 10−5 | |
| F7 | HBA | 0.00 | 0.00 | 0.00 | 0.00 |
| HBA1 | 0.00 | 0.00 | 0.00 | 0.00 | |
| HBA2 | 0.00 | 0.00 | 0.00 | 0.00 | |
| HBA3 | 0.00 | 0.00 | 0.00 | 0.00 | |
| IHBA | 0.00 | 0.00 | 0.00 | 0.00 | |
| F8 | HBA | 8.88 × 10−16 | 2.00 × 10 | 1.46 × 10 | 8.98 |
| HBA1 | 8.88 × 10−16 | 1.55 × 10 | 5.15 × 10−1 | 2.82 | |
| HBA2 | 8.88 × 10−16 | 2.77 × 10−10 | 9.24 × 10−12 | 5.06 × 10−11 | |
| HBA3 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 0.00 | |
| IHBA | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 0.00 | |
| F9 | HBA | 0.00 | 0.00 | 0.00 | 0.00 |
| HBA1 | 0.00 | 0.00 | 0.00 | 0.00 | |
| HBA2 | 0.00 | 0.00 | 0.00 | 0.00 | |
| HBA3 | 0.00 | 0.00 | 0.00 | 0.00 | |
| IHBA | 0.00 | 0.00 | 0.00 | 0.00 | |
| F10 | HBA | 1.28 × 10−10 | 1.04 × 10−1 | 3.46 × 10−3 | 1.89 × 10−2 |
| HBA1 | 4.10 × 10−11 | 1.04 × 10−1 | 3.46 × 10−3 | 1.89 × 10−2 | |
| HBA2 | 2.13 × 10−10 | 1.04 × 10−1 | 3.47 × 10−3 | 1.89 × 10−2 | |
| HBA3 | 1.82 × 10−10 | 6.57 × 10−3 | 2.19 × 10−4 | 1.20 × 10−3 | |
| IHBA | 7.00 × 10−11 | 6.01 × 10−8 | 7.68 × 10−9 | 1.26 × 10−8 | |
| F11 | HBA | 9.98 × 10−1 | 1.08 × 10 | 2.18 | 2.10 |
| HBA1 | 9.98 × 10−1 | 3.97 | 1.46 | 9.64 × 10−1 | |
| HBA2 | 9.98 × 10−1 | 1.08 × 10 | 2.50 | 3.09 | |
| HBA3 | 9.98 × 10−1 | 1.08 × 10 | 1.88 | 2.49 | |
| IHBA | 9.98 × 10−1 | 5.93 | 1.82 | 1.42 | |
| F12 | HBA | 0.00 | 2.26 × 10−2 | 2.38 × 10−3 | 6.62 × 10−3 |
| HBA1 | 0.00 | 2.26 × 10−2 | 1.78 × 10−3 | 5.67 × 10−3 | |
| HBA2 | 0.00 | 2.26 × 10−2 | 2.21 × 10−3 | 6.41 × 10−3 | |
| HBA3 | 0.00 | 2.26 × 10−2 | 1.59 × 10−3 | 5.42 × 10−3 | |
| IHBA | 0.00 | 2.04 × 10−2 | 8.75 × 10−4 | 3.70 × 10−3 | |
| F13 | HBA | −1.03 | 0.00 | −3.44 × 10−12 | 4.95 × 10−12 |
| HBA1 | −1.03 | 0.00 | −3.44 × 10−12 | 4.95 × 10−12 | |
| HBA2 | −1.03 | 0.00 | −3.44 × 10−12 | 4.95 × 10−12 | |
| HBA3 | −1.03 | 0.00 | −3.44 × 10−12 | 4.95 × 10−12 | |
| IHBA | −1.03 | 0.00 | −3.44 × 10−12 | 4.95 × 10−12 | |
| F14 | HBA | −3.86 | −3.65 | −3.86 | −3.07 × 10−4 |
| HBA1 | 3.86 | −3.75 | 3.86 | −3.27 × 10−4 | |
| HBA2 | −3.86 | −3.75 | −3.86 | −3.27 × 10−4 | |
| HBA3 | −3.86 | −3.75 | −3.86 | −3.27 × 10−4 | |
| IHBA | −3.86 | −3.75 | −3.86 | −3.27 × 10−4 | |
| F15 | HBA | −3.20 | −3.20 | −3.20 | 1.56 × 10−2 |
| HBA1 | −3.20 | −3.20 | −3.20 | 1.56 × 10−2 | |
| HBA2 | −3.20 | −3.20 | −3.20 | 1.56 × 10−2 | |
| HBA3 | −3.32 | −3.30 | −3.32 | 1.58 × 10−2 | |
| IHBA | −3.32 | −3.32 | −3.32 | 1.58 × 10−2 | |
| F16 | HBA | −1.02 × 10 | −9.36 | −9.74 | 4.87 |
| HBA1 | −1.02 × 10 | −9.36 | −9.74 | 4.87 | |
| HBA2 | −1.02 × 10 | −1.02 × 10 | −1.02 × 10 | 4.71 | |
| HBA3 | −1.02 × 10 | −1.02 × 10 | −1.02 × 10 | 4.71 | |
| IHBA | −1.02 × 10 | −1.02 × 10 | −1.02 × 10 | 4.71 | |
| F17 | HBA | −9.24 | −8.21 | −8.68 | 4.99 |
| HBA1 | −9.79 | −9.24 | −9.38 | 4.16 | |
| HBA2 | −9.79 | −9.24 | −9.38 | 4.16 | |
| HBA3 | −9.79 | −9.24 | −9.38 | 4.16 | |
| IHBA | −1.04 × 10 | −1.04 × 10 | −1.04 × 10 | 3.89 | |
| F18 | HBA | −9.13 | −9.04 | −9.10 | 4.46 × 10−2 |
| HBA1 | −9.93 | −9.64 | −9.93 | 5.05 × 10−2 | |
| HBA2 | −9.93 | −9.64 | −9.93 | 5.05 × 10−2 | |
| HBA3 | −1.05 × 10 | −1.00 × 10 | −1.03 × 10 | 5.05 × 10−2 | |
| IHBA | −1.05 × 10 | −1.00 × 10 | −1.03 × 10 | 5.05 × 10−2 |
| Function | Algorithm | 30dim | 100dim | 500dim | |||
|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | ||
| F1 | JSWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| m-EO | 0.00 | 0.00 | 1.53 × 10−304 | 0.00 | 0.00 | 0.00 | |
| OBCWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| RDWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| IHBA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| F2 | JSWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| m-EO | 3.93 × 10−167 | 0.00 | 3.09 × 10−161 | 1.579 × 10−160 | 1.36 × 10−160 | 5.90 × 10−160 | |
| OBCWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| RDWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| IHBA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| F3 | JSWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| m-EO | 2.71 × 10−306 | 0.00 | 8.50 × 10−297 | 0.00 | 4.63 × 10−293 | 0.00 | |
| OBCWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| RDWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| IHBA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| F4 | JSWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| m-EO | 2.31 × 10−159 | 1.17 × 10−158 | 2.83 × 10−157 | 9.04 × 10−157 | 1.48 × 10−154 | 7.46 × 10−154 | |
| OBCWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| RDWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| IHBA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| F5 | JSWOA | 7.86 × 10−1 | 2.20 × 10−1 | 3.95 | 9.34 × 10−1 | 2.47 × 10 | 5.64 |
| m-EO | 9.23 × 10−5 | 4.18 × 10−5 | 5.28 × 10−3 | 4.241 × 10−3 | 4.92 × 10−2 | 5.50 × 10−2 | |
| OBCWOA | 3.87 × 10−1 | 2.10 × 10−1 | 4.41 | 1.33 | 4.36 × 10 | 9.22 | |
| RDWOA | - | - | - | - | - | - | |
| IHBA | 9.95 × 10−9 | 3.36 × 10−8 | 2.95 × 10−8 | 1.34 × 10−7 | 1.74 × 10−8 | 6.55 × 10−8 | |
| F6 | JSWOA | 7.63 × 10−5 | 7.12 × 10−5 | 6.90 × 10−5 | 5.53 × 10−5 | 1.02 × 10−4 | 8.16 × 10−5 |
| m-EO | 2.47 × 10−4 | 2.23 × 10−4 | 3.47 × 10−4 | 2.495 × 10−4 | 5.11 × 10−4 | 3.90 × 10−4 | |
| OBCWOA | 4.94 × 10−5 | 3.81 × 10−5 | 6.10 × 10−5 | 5.98 × 10−5 | 6.17 × 10−5 | 5.74 × 10−5 | |
| RDWOA | 1.30 × 10−5 | 1.23 × 10−5 | 1.00 × 10−5 | 1.39 × 10−5 | 6.94 × 10−6 | 4.48 × 10−6 | |
| IHBA | 6.24 × 10−5 | 4.48 × 10−5 | 5.38 × 10−5 | 4.79 × 10−5 | 5.35 × 10−5 | 7.61 × 10−5 | |
| F7 | JSWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| m-EO | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| OBCWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| RDWOA | 0.00 | 0.00 | 0.00 | 0.00 | 3.03 × 10−14 | 1.66 × 10−13 | |
| IHBA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| F8 | JSWOA | 8.88 × 10−16 | 0.00 | 8.88 × 10−16 | 0.00 | 8.88 × 10−16 | 0.00 |
| m-EO | 8.88 × 10−16 | 0.00 | 8.88 × 10−16 | 0.00 | 8.88 × 10−16 | 0.00 | |
| OBCWOA | 8.88 × 10−16 | 0.00 | 8.88 × 10−16 | 0.00 | 8.88 × 10−16 | 0.00 | |
| RDWOA | 8.88 × 10−16 | 0.00 | 8.88 × 10−16 | 0.00 | 8.88 × 10−16 | 0.00 | |
| IHBA | 8.88 × 10−16 | 0.00 | 8.88 × 10−16 | 0.00 | 8.88 × 10−16 | 0.00 | |
| F9 | JSWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| m-EO | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| OBCWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| RDWOA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| IHBA | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| F10 | JSWOA | 4.40 × 10−2 | 1.52 × 10−2 | 7.13 × 10−2 | 2.51 × 10−2 | 7.14 × 10−2 | 2.21 × 10−2 |
| m-EO | 6.25 × 10−6 | 3.92 × 10−6 | 2.18 × 10−5 | 1.781 × 10−5 | 1.98 × 10−5 | 2.25 × 10−5 | |
| OBCWOA | 2.41 × 10−2 | 1.38 × 10−2 | 6.43 × 10−2 | 3.33 × 10−2 | 5.87 × 10−1 | 1.18 × 10−1 | |
| RDWOA | 8.16 × 10−7 | 3.15 × 10−6 | 1.78 × 10−14 | 6.05 × 10−15 | 5.66 × 10−9 | 2.04 × 10−9 | |
| IHBA | 2.56 × 10−10 | 1.23 × 10−9 | 4.45 × 10−8 | 2.37 × 10−7 | 9.75 × 10−5 | 1.53 × 10−5 | |
| Function | Dim | Algorithm | Mean | Std | Function | Dim | Algorithm | Mean | Std |
|---|---|---|---|---|---|---|---|---|---|
| F11 | 2 | JSWOA | 7.01 | 5.19 | F15 | 6 | JSWOA | −3.14 | 1.19 × 10−1 |
| m-EO | −4.52 × 10−1 | 3.45 | m-EO | −3.28 | 6.46 × 10−2 | ||||
| OBCWOA | 3.89 | 4.18 | OBCWOA | −3.27 | 7.05 × 10−2 | ||||
| RDWOA | 9.98 × 10−1 | 2.08 × 10−16 | RDWOA | - | - | ||||
| IHBA | 1.32 | 3.02 | IHBA | −3.32 | 1.58 × 10−2 | ||||
| F12 | 4 | JSWOA | 4.96 × 10−4 | 1.84 × 10−4 | F16 | 4 | JSWOA | −1.01 × 10 | 6.07 × 10−3 |
| m-EO | 1.55 × 10−1 | 4.93 × 10−1 | m-EO | −9.33 | 2.23 | ||||
| OBCWOA | 3.82 × 10−4 | 2.05 × 10−4 | OBCWOA | −1.02 × 10 | 1.29 × 10−5 | ||||
| RDWOA | 3.08 × 10−4 | 1.24 × 10−7 | RDWOA | −1.02 × 10 | 1.02 × 10 | ||||
| IHBA | 8.23 × 10−4 | 7.08 × 10−4 | IHBA | −1.02 × 10 | 4.71 × 10−5 | ||||
| F13 | 2 | JSWOA | −1.02 | 1.09 × 10−2 | F17 | 4 | JSWOA | −1.04 × 10 | 5.83 × 10−3 |
| m-EO | −1.03 | 1.22 × 10−12 | m-EO | −1.01 × 10 | 1.35 | ||||
| OBCWOA | −1.03 | 3.09 × 10−11 | OBCWOA | - | - | ||||
| RDWOA | - | - | RDWOA | −1.04 × 10 | 2.30 × 10−5 | ||||
| IHBA | −1.03 | 0.95 × 10−12 | IHBA | −1.04 × 10 | 3.89 | ||||
| F14 | 3 | JSWOA | −3.85 | 1.63 × 10−2 | F18 | 4 | JSWOA | −1.05 × 10 | 3.64 × 10−3 |
| m-EO | −3.86 | 3.20 × 10−3 | m-EO | −1.04 × 10 | 9.87 × 10−1 | ||||
| OBCWOA | −3.86 | 4.70 × 10−8 | OBCWOA | - | - | ||||
| RDWOA | - | - | RDWOA | −1.05 × 10 | 3.13 × 10−15 | ||||
| IHBA | −3.86 | −3.27 × 10−9 | IHBA | −1.03 × 10 | 5.05 × 10−2 |
| Function | HBA | WOA | AOA | PSO | BOA | HBA1 | HBA2 | HBA3 |
|---|---|---|---|---|---|---|---|---|
| p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | |
| F1 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | NaN |
| F2 | 8.01 × 10−9 | 8.01 × 10−9 | NaN | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 |
| F3 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | NaN |
| F4 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 |
| F5 | 3.64 × 10−2 | 6.80 × 10−8 | 6.80 × 10−8 | 6.80 × 10−8 | 6.80 × 10−8 | 2.18 × 10−2 | 1.50 × 10−2 | 2.62 × 10−2 |
| F6 | 7.95 × 10−7 | 7.90 × 10−8 | 2.56 × 10−2 | 6.80 × 10−8 | 6.80 × 10−8 | 3.50 × 10−6 | 4.54 × 10−6 | 2.39 × 10−2 |
| F7 | NaN | NaN | NaN | 8.01 × 10−9 | 1.10 × 10−6 | NaN | NaN | NaN |
| F8 | 1.10 × 10−6 | 2.17 × 10−6 | NaN | 8.01 × 10−9 | 8.01 × 10−9 | NaN | 1.62 × 10−2 | NaN |
| F9 | NaN | 1.63 × 10−4 | 8.01 × 10−9 | 8.01 × 10−9 | 8.01 × 10−9 | NaN | NaN | NaN |
| F10 | 6.17 × 10−3 | 6.80 × 10−8 | 6.80 × 10−8 | 6.80 × 10−8 | 6.80 × 10−8 | 2.62 × 10−2 | 1.17 × 10−2 | 4.68 × 10−2 |
| F11 | 6.81 × 10−3 | 7.68 × 10−5 | 1.68 × 10−7 | 2.28 × 10−2 | 3.48 × 10−3 | 6.18 × 10−3 | 3.66 × 10−2 | 1.94 × 10−2 |
| F12 | 1.36 × 10−4 | 5.12 × 10−3 | 4.16 × 10−4 | 7.11 × 10−3 | 2.07 × 10−2 | 7.87 × 10−3 | 1.10 × 10−2 | 4.88 × 10−2 |
| F13 | 2.44 × 10−3 | 4.14 × 10−8 | 4.14 × 10−8 | 4.27 × 10−2 | 4.14 × 10−8 | 2.43 × 10−2 | 5.34 × 10−2 | 2.15 × 10−2 |
| F14 | 1.15 × 10−3 | 2.88 × 10−3 | 7.82 × 10−7 | 4.77 × 10−2 | 3.05 × 10−2 | 3.93 × 10−2 | 3.77 × 10−2 | 1.21 × 10−1 |
| F15 | 6.21 × 10−4 | 1.12 × 10−4 | 2.10 × 10−7 | 7.40 × 10−4 | 7.59 × 10−3 | 3.02 × 10−2 | 1.27 × 10−2 | 1.76 × 10−3 |
| F16 | 3.56 × 10−2 | 5.69 × 10−8 | 5.69 × 10−8 | 5.69 × 10−8 | 5.69 × 10−8 | 2.85 × 10−2 | 9.47 × 10−3 | 3.17 × 10−2 |
| F17 | 1.04 × 10−2 | 4.70 × 10−8 | 4.70 × 10−8 | 4.70 × 10−8 | 4.70 × 10−8 | 9.23 × 10−3 | 2.49 × 10−2 | 4.95 × 10−2 |
| F18 | 3.03 × 10−2 | 5.14 × 10−8 | 5.14 × 10−8 | 5.13 × 10−8 | 5.14 × 10−8 | 1.00 × 10−3 | 1.15 × 10−2 | 1.01 × 10−2 |
| +/=/− | 16/2/0 | 17/1/0 | 15/3/0 | 18/0/0 | 18/0/0 | 15/3/0 | 15/2/1 | 12/5/1 |
| Function | Type | Range | Optimal Value | Function | Type | Range | Optimal Value |
|---|---|---|---|---|---|---|---|
| CEC01 | UF | [−100, 100] | 100 | CEC16 | MF | [−100, 100] | 1600 |
| CEC02 | UF | [−100, 100] | 200 | CEC17 | HF | [−100, 100] | 1700 |
| CEC03 | UF | [−100, 100] | 300 | CEC18 | HF | [−100, 100] | 1800 |
| CEC04 | MF | [−100, 100] | 400 | CEC19 | HF | [−100, 100] | 1900 |
| CEC05 | MF | [−100, 100] | 500 | CEC20 | HF | [−100, 100] | 2000 |
| CEC06 | MF | [−100, 100] | 600 | CEC21 | HF | [−100, 100] | 2100 |
| CEC07 | MF | [−100, 100] | 700 | CEC22 | HF | [−100, 100] | 2200 |
| CEC08 | MF | [−100, 100] | 800 | CEC23 | CF | [−100, 100] | 2300 |
| CEC09 | MF | [−100, 100] | 900 | CEC24 | CF | [−100, 100] | 2400 |
| CEC 10 | MF | [−100, 100] | 1000 | CEC25 | CF | [−100, 100] | 2500 |
| CEC 11 | MF | [−100,100] | 1100 | CEC26 | CF | [−100, 100] | 2600 |
| CEC 12 | MF | [−100, 100] | 1200 | CEC27 | CF | [−100, 100] | 2700 |
| CEC13 | MF | [−100, 100] | 1300 | CEC28 | CF | [−100, 100] | 2800 |
| CEC14 | MF | [−100, 100] | 1400 | CEC29 | CF | [−100, 100] | 2900 |
| CEC15 | MF | [−100, 100] | 1500 | CEC30 | CF | [−100, 100] | 3000 |
| Function | Index | AOA | BOA | GWO | SCA | SMA | TSA | HBA | IHBA |
|---|---|---|---|---|---|---|---|---|---|
| CEC01 | Mean | 1.25 × 109 | 1.37 × 109 | 8.94 × 107 | 4.86 × 108 | 1.31 × 107 | 1.51 × 109 | 5.34 × 106 | 3.07 × 106 |
| Std | 3.54 × 108 | 4.55 × 108 | 6.82 × 107 | 1.25 × 108 | 7.30 × 106 | 2.16 × 108 | 3.54 × 106 | 1.76 × 106 | |
| CEC02 | Mean | 7.09 × 1010 | 6.36 × 1010 | 3.36 × 109 | 2.75 × 1010 | 1.74 × 105 | 6.68 × 1010 | 1.53 × 104 | 1.52 × 104 |
| Std | 9.24 × 109 | 1.09 × 1010 | 2.02 × 109 | 3.45 × 109 | 8.55 × 104 | 6.72 × 109 | 1.92 × 104 | 1.29 × 104 | |
| CEC03 | Mean | 8.09 × 104 | 7.89 × 104 | 5.34 × 104 | 7.78 × 104 | 1.07 × 104 | 8.51 × 104 | 1.18 × 104 | 5.25 × 103 |
| Std | 5.13 × 103 | 7.92 × 103 | 1.39 × 104 | 1.65 × 104 | 1.08 × 104 | 3.45 × 103 | 6.06 × 103 | 3.96 × 103 | |
| CEC04 | Mean | 1.08 × 104 | 1.55 × 104 | 7.22 × 102 | 2.93 × 103 | 5.44 × 102 | 1.23 × 104 | 5.24 × 102 | 5.21 × 102 |
| Std | 3.57 × 103 | 2.70 × 103 | 9.20 × 10 | 1.27 × 103 | 6.61 × 10 | 2.19 × 103 | 3.82 × 10 | 3.14 × 10 | |
| CEC05 | Mean | 5.21 × 102 | 5.21 × 102 | 5.21 × 102 | 5.21 × 102 | 5.21 × 102 | 5.21 × 102 | 5.21 × 102 | 5.21 × 102 |
| Std | 6.08 × 10−2 | 5.98 × 10−2 | 3.32 × 10−2 | 5.26 × 10−2 | 6.72 × 10−2 | 3.30 × 10−2 | 2.81 × 10−1 | 2.70 × 10−1 | |
| CEC06 | Mean | 6.38 × 102 | 6.38 × 102 | 6.17 × 102 | 6.38 × 102 | 6.18 × 102 | 6.43 × 102 | 6.23 × 102 | 6.29 × 102 |
| Std | 2.79 | 2.04 | 3.20 | 1.88 | 3.50 | 2.61 | 6.09 | 3.16 | |
| CEC07 | Mean | 1.40 × 103 | 1.48 × 103 | 7.32 × 102 | 9.52 × 102 | 7.01 × 102 | 1.35 × 103 | 7.03 × 102 | 7.00 × 102 |
| Std | 1.14 × 102 | 8.86 × 10 | 3.33 × 10 | 3.87 × 10 | 8.24 × 10−2 | 5.99 × 10 | 9.89 | 5.01 × 10−2 | |
| CEC08 | Mean | 1.15 × 103 | 1.13 × 103 | 9.03 × 102 | 1.08 × 103 | 8.72 × 102 | 1.14 × 103 | 9.02 × 102 | 9.37 × 102 |
| Std | 2.75 × 10 | 1.58 × 10 | 2.15 × 10 | 2.38 × 10 | 1.87 × 10 | 2.85 × 10 | 2.20 × 10 | 2.40 × 10 | |
| CEC09 | Mean | 1.22 × 103 | 1.25 × 103 | 1.02 × 103 | 1.21 × 103 | 1.04 × 103 | 1.25 × 103 | 1.03 × 103 | 1.07 × 103 |
| Std | 2.91 × 10 | 1.62 × 10 | 2.07 × 10 | 2.53 × 10 | 2.18 × 10 | 2.72 × 10 | 3.18 × 10 | 2.11 × 10 | |
| CEC10 | Mean | 7.30 × 103 | 8.82 × 103 | 3.74 × 103 | 7.91 × 103 | 2.53 × 103 | 8.91 × 103 | 3.85 × 103 | 4.48 × 103 |
| Std | 6.39 × 102 | 3.07 × 102 | 6.16 × 102 | 4.73 × 102 | 4.56 × 102 | 5.61 × 102 | 8.01 × 102 | 7.97 × 102 | |
| CEC11 | Mean | 8.11 × 103 | 9.06 × 103 | 5.08 × 103 | 8.78 × 103 | 4.91 × 103 | 9.34 × 103 | 5.19 × 103 | 4.88 × 103 |
| Std | 3.92 × 102 | 3.30 × 102 | 1.48 × 103 | 4.10 × 102 | 6.93 × 102 | 4.71 × 102 | 8.60 × 102 | 7.77 × 102 | |
| CEC12 | Mean | 1.20 × 103 | 1.20 × 103 | 1.20 × 103 | 1.20 × 103 | 1.20 × 103 | 1.20 × 103 | 1.20 × 103 | 1.20 × 103 |
| Std | 4.80 × 10−1 | 5.04 × 10−1 | 9.77 × 10−1 | 4.07 × 10−1 | 2.18 × 10−1 | 6.05 × 10−1 | 4.49 × 10−1 | 6.21 × 10−1 | |
| CEC13 | Mean | 1.31 × 103 | 1.31 × 103 | 1.30 × 103 | 1.30 × 103 | 1.30 × 103 | 1.31 × 103 | 1.30 × 103 | 1.30 × 103 |
| Std | 9.31 × 10−1 | 6.75 × 10−1 | 4.45 × 10−1 | 3.93 × 10−1 | 1.24 × 10−1 | 6.76 × 10−1 | 1.41 × 10−1 | 1.20 × 10−1 | |
| CEC14 | Mean | 1.65 × 103 | 1.70 × 103 | 1.41 × 103 | 1.48 × 103 | 1.40 × 103 | 1.65 × 103 | 1.40 × 103 | 1.40 × 103 |
| Std | 4.12 × 10 | 3.44 × 10 | 6.59 | 1.47 × 10 | 3.53 × 10−1 | 2.64 × 10 | 5.05 × 10−2 | 1.51 × 10−1 | |
| CEC15 | Mean | 3.77 × 105 | 3.45 × 105 | 1.67 × 103 | 3.79 × 104 | 1.54 × 103 | 1.78 × 105 | 1.54 × 103 | 1.52 × 103 |
| Std | 1.30 × 105 | 1.34 × 105 | 2.96 × 102 | 2.72 × 104 | 6.10 × 10 | 7.99 × 104 | 1.23 × 10 | 4.68 | |
| CEC16 | Mean | 1.61 × 103 | 1.61 × 103 | 1.61 × 103 | 1.61 × 103 | 1.61 × 103 | 1.61 × 103 | 1.61 × 103 | 1.61 × 103 |
| Std | 2.83 × 10−1 | 1.81 × 10−1 | 4.90 × 10−1 | 2.92 × 10−1 | 4.96 × 10−1 | 2.59 × 10−1 | 5.22 × 10−1 | 7.18 × 10−1 | |
| CEC17 | Mean | 1.26 × 108 | 1.44 × 108 | 3.06 × 106 | 1.77 × 107 | 2.63 × 106 | 1.26 × 108 | 3.16 × 105 | 2.97 × 105 |
| Std | 7.47 × 107 | 9.66 × 107 | 2.46 × 106 | 6.57 × 106 | 1.62 × 106 | 7.08 × 107 | 2.08 × 105 | 1.99 × 105 | |
| CEC18 | Mean | 4.72 × 109 | 4.66 × 109 | 1.73 × 107 | 4.05 × 108 | 3.26 × 104 | 3.57 × 109 | 6.61 × 104 | 6.26 × 103 |
| Std | 2.29 × 109 | 1.92 × 109 | 2.54 × 107 | 3.72 × 108 | 3.70 × 104 | 1.54 × 109 | 2.62 × 105 | 6.07 × 103 | |
| CEC19 | Mean | 2.32 × 103 | 2.42 × 103 | 1.96 × 103 | 2.05 × 103 | 1.92 × 103 | 2.26 × 103 | 1.93 × 103 | 1.92 × 103 |
| Std | 1.19 × 102 | 7.48 × 10 | 2.89 × 10 | 4.95 × 10 | 2.20 × 10 | 3.41 × 10 | 3.46 × 10 | 1.99 × 10 | |
| CEC20 | Mean | 2.22 × 105 | 3.47 × 105 | 3.96 × 104 | 5.76 × 104 | 3.65 × 104 | 2.86 × 105 | 1.75 × 104 | 1.73 × 104 |
| Std | 1.06 × 105 | 2.77 × 105 | 2.37 × 104 | 2.89 × 104 | 2.04 × 104 | 7.24 × 104 | 1.14 × 104 | 7.68 × 103 | |
| CEC21 | Mean | 5.15 × 107 | 3.23 × 107 | 1.23 × 106 | 4.10 × 106 | 9.50 × 105 | 4.34 × 107 | 1.65 × 105 | 1.29 × 105 |
| Std | 5.81 × 107 | 2.34 × 107 | 2.20 × 106 | 2.50 × 106 | 8.25 × 105 | 2.69 × 107 | 1.71 × 105 | 1.14 × 105 | |
| CEC22 | Mean | 1.17 × 104 | 2.42 × 104 | 2.67 × 103 | 3.40 × 103 | 2.90 × 103 | 1.38 × 104 | 2.95 × 103 | 2.95 × 103 |
| Std | 1.13 × 104 | 3.15 × 104 | 1.64 × 102 | 1.74 × 102 | 2.59 × 102 | 1.30 × 104 | 3.28 × 102 | 2.32 × 102 | |
| CEC23 | Mean | 2.50 × 103 | 2.50 × 103 | 2.64 × 103 | 2.72 × 103 | 2.50 × 103 | 2.52 × 103 | 2.57 × 103 | 2.50 × 103 |
| Std | 3.04 × 10−10 | 0.00 | 1.08 × 10 | 2.53 × 10 | 0.00 | 9.57 × 10 | 3.55 × 10 | 0.00 | |
| CEC24 | Mean | 2.60 × 103 | 2.60 × 103 | 2.60 × 103 | 2.63 × 103 | 2.60 × 103 | 2.60 × 103 | 2.60 × 103 | 2.60 × 103 |
| Std | 9.94 × 10−2 | 0.00 | 3.50 × 10−2 | 2.10 × 10 | 0.00 | 4.63 × 10−5 | 5.87 × 10−4 | 0.00 | |
| CEC25 | Mean | 2.70 × 103 | 2.70 × 103 | 2.71 × 103 | 2.74 × 103 | 2.70 × 103 | 2.70 × 103 | 2.70 × 103 | 2.70 × 103 |
| Std | 2.89 × 10−11 | 0.00 | 6.03 | 1.33 × 10 | 0.00 | 0.00 | 1.49 × 10−9 | 0.00 | |
| CEC26 | Mean | 2.80 × 103 | 2.79 × 103 | 2.74 × 103 | 2.70 × 103 | 2.70 × 103 | 2.79 × 103 | 2.71 × 103 | 2.78 × 103 |
| Std | 1.86 × 10 | 2.98 × 10 | 4.85 × 10 | 4.17 × 10−1 | 1.58 × 10−1 | 2.15 × 10 | 1.79 × 10 | 4.22 × 10 | |
| CEC27 | Mean | 4.09 × 103 | 3.51 × 103 | 3.43 × 103 | 3.75 × 103 | 2.90 × 103 | 4.75 × 103 | 3.22 × 103 | 2.90 × 103 |
| Std | 4.44 × 102 | 2.04 × 102 | 1.27 × 102 | 3.08 × 102 | 2.79 × 10−8 | 2.99 × 102 | 2.91 × 102 | 0.00 | |
| CEC28 | Mean | 5.11 × 103 | 5.54 × 103 | 4.00 × 103 | 5.89 × 103 | 3.00 × 103 | 1.15 × 104 | 3.76 × 103 | 3.00 × 103 |
| Std | 2.89 × 103 | 9.85 × 102 | 1.89 × 102 | 6.34 × 102 | 2.86 × 10−12 | 1.09 × 103 | 5.79 × 102 | 0.00 | |
| CEC29 | Mean | 4.95 × 108 | 3.10 × 103 | 2.23 × 106 | 4.36 × 107 | 9.32 × 105 | 4.39 × 108 | 9.43 × 107 | 5.81 × 105 |
| Std | 2.28 × 108 | 0.00 | 6.62 × 106 | 1.62 × 107 | 2.85 × 106 | 4.31 × 108 | 7.82 × 107 | 2.59 × 106 | |
| CEC30 | Mean | 5.72 × 106 | 3.20 × 103 | 1.04 × 105 | 7.35 × 105 | 1.56 × 104 | 6.71 × 106 | 4.38 × 105 | 2.17 × 105 |
| Std | 3.61 × 106 | 0.00 | 6.58 × 104 | 1.59 × 105 | 1.17 × 104 | 3.24 × 106 | 8.27 × 105 | 4.43 × 105 |
| Model Parameters | Range |
|---|---|
| Iph/A | [0, 1] |
| Isd1, Isd2, Isd3/μA | [0, 1] |
| A1, A2 | [1, 2] |
| A3 | [2, 5] |
| Rs/Ω | [0, 0.5] |
| Rsh/Ω | [0, 100] |
| Algorithm | Iph | Isd1 | A1 | Rs | Rsh | RMSE |
|---|---|---|---|---|---|---|
| HBA | 7.6003 × 10−1 | 4.2514 × 10−1 | 1.5018 | 3.3511 × 10−2 | 6.0306 × 10 | 3.8553 × 10−3 |
| WOA | 7.5951 × 10−1 | 5.9128 × 10−1 | 1.5164 | 2.9602 × 10−2 | 5.8346 × 10 | 9.4148 × 10−3 |
| SMA | 6.8771 × 10−1 | 5.7851 × 10−1 | 1.6169 | 5.6742 × 10−2 | 4.8681 × 10 | 1.9994 × 10−1 |
| PSO | 7.6189 × 10−1 | 8.0083 × 10−1 | 1.5746 | 2.7496 × 10−2 | 7.3965 × 10 | 6.4019 × 10−3 |
| SSA | 7.6019 × 10−1 | 4.1585 × 10−1 | 1.5042 | 3.5581 × 10−2 | 7.7523 × 10 | 1.2845 × 10−3 |
| GWO | 7.6252 × 10−1 | 6.2001 × 10−1 | 1.5389 | 3.0076 × 10−2 | 4.7638 × 10 | 7.1697 × 10−3 |
| BOA | 7.5872 × 10−1 | 6.4646 × 10−1 | 1.5378 | 3.0754 × 10−2 | 5.5493 × 10 | 1.9456 × 10−2 |
| IHBA | 7.6101 × 10−1 | 3.9445 × 10−1 | 1.4951 | 3.4789 × 10−2 | 5.5538 × 10 | 1.0272 × 10−3 |
| RMSE | Minimum | Maximum | Mean | Std |
|---|---|---|---|---|
| HBA | 9.8602 × 10−4 | 4.6014 × 10−2 | 2.7154 × 10−3 | 8.1932 × 10−3 |
| WOA | 1.0285 × 10−3 | 3.8245 × 10−2 | 5.4127 × 10−3 | 1.1131 × 10−2 |
| SMA | 7.7339 × 10−2 | 3.0085 × 10−1 | 2.0451 × 10−1 | 5.4230 × 10−2 |
| PSO | 1.2722 × 10−3 | 3.8151 × 10−2 | 1.4249 × 10−2 | 1.7193 × 10−2 |
| SSA | 9.8700 × 10−4 | 1.4847 × 10−3 | 1.2713 × 10−3 | 3.0391 × 10−4 |
| GWO | 1.1261 × 10−3 | 3.8169 × 10−2 | 6.1608 × 10−3 | 1.0272 × 10−2 |
| BOA | 4.7867 × 10−3 | 1.2368 × 10−1 | 1.9886 × 10−2 | 2.0707 × 10−2 |
| IHBA | 9.8262 × 10−4 | 1.4480 × 10−3 | 1.0836 × 10−3 | 3.7091 × 10−4 |
| Index | HBA | WOA | SMA | PSO | SSA | GWO | BOA | IHBA |
|---|---|---|---|---|---|---|---|---|
| Iph | 7.6081 × 10−1 | 7.6060 × 10−1 | 7.4359 × 10−1 | 7.6235 × 10−1 | 7.6080 × 10−1 | 7.6273 × 10−1 | 7.5591 × 10−1 | 7.6100 × 10−1 |
| Isd1 | 3.7332 × 10−1 | 5.5524 × 10−1 | 5.8655 × 10−1 | 8.5168 × 10−1 | 4.6367 × 10−1 | 6.4446 × 10−1 | 6.7507 × 10−1 | 3.6919 × 10−1 |
| Isd2 | 2.9999 × 10−1 | 5.0478 × 10−1 | 6.3973 × 10−1 | 3.6667 × 10−1 | 5.3711 × 10−1 | 3.0643 × 10−1 | 4.7833 × 10−1 | 4.0035 × 10−1 |
| A1 | 1.4935 | 1.5231 | 1.6267 | 1.5844 | 1.4926 | 1.5402 | 1.5511 | 1.4903 |
| A2 | 1.4041 | 1.5245 | 1.4515 | 1.5112 | 1.3425 | 1.3600 | 1.2564 | 1.3619 |
| Rs | 3.4893 × 10−2 | 3.0552 × 10−2 | 7.3144 × 10−2 | 2.5054 × 10−2 | 3.5916 × 10−2 | 2.8466 × 10−2 | 3.0321 × 10−2 | 3.4988 × 10−2 |
| Rsh | 5.9296 × 10 | 6.0604 × 10 | 5.0031 × 10 | 7.0622 × 10 | 6.9732 × 10 | 4.1533 × 10 | 5.7412 × 10 | 5.3916 × 10 |
| RMSE | 2.2968 × 10−3 | 6.8009 × 10−3 | 2.0474 × 10−1 | 1.0450 × 10−2 | 1.8936 × 10−3 | 8.8967 × 10−3 | 1.6850 × 10−2 | 1.2743 × 10−3 |
| RMSE | Minimum | Maximum | Mean | Std |
|---|---|---|---|---|
| HBA | 9.8602 × 10−4 | 4.6014 × 10−2 | 2.7154 × 10−3 | 8.1932 × 10−3 |
| WOA | 1.0285 × 10−3 | 3.8245 × 10−2 | 5.4127 × 10−3 | 1.1131 × 10−2 |
| SMA | 7.7339 × 10−2 | 3.0085 × 10−1 | 2.0451 × 10−1 | 5.4230 × 10−2 |
| PSO | 1.2722 × 10−3 | 3.8151 × 10−2 | 1.4249 × 10−2 | 1.7193 × 10−2 |
| SSA | 9.8700 × 10−4 | 1.4847 × 10−3 | 1.2713 × 10−3 | 3.3391 × 10−4 |
| GWO | 1.1261 × 10−3 | 3.8169 × 10−2 | 6.1608 × 10−3 | 1.0272 × 10−2 |
| BOA | 4.7867 × 10−3 | 1.2368 × 10−1 | 1.9886 × 10−2 | 2.0707 × 10−2 |
| IHBA | 9.8163 × 10−4 | 1.4480 × 10−3 | 1.0836 × 10−3 | 3.1091 × 10−4 |
| Index | HBA | WOA | SMA | PSO | SSA | GWO | BOA | IHBA |
|---|---|---|---|---|---|---|---|---|
| Iph | 7.6081 × 10−1 | 7.6090 × 10−1 | 7.2117 × 10−1 | 7.6309 × 10−1 | 7.6309 × 10−1 | 7.6309 × 10−1 | 7.6309 × 10−1 | 7.6309 × 10−1 |
| Isd1 | 3.9365 × 10−1 | 6.0423 × 10−1 | 5.4580 × 10−1 | 8.2321 × 10−1 | 8.2321 × 10−1 | 8.2321 × 10−1 | 8.2321 × 10−1 | 8.2321 × 10−1 |
| Isd2 | 5.3927 × 10−1 | 4.3814 × 10−1 | 4.8935 × 10−1 | 5.6667 × 10−1 | 5.6667 × 10−1 | 5.6667 × 10−1 | 5.6667 × 10−1 | 5.6667 × 10−1 |
| Isd3 | 5.6383 × 10−1 | 5.9062 × 10−1 | 5.0189 × 10−1 | 5.3360 × 10−1 | 5.3360 × 10−1 | 5.3360 × 10−1 | 5.3360 × 10−1 | 5.3360 × 10−1 |
| A1 | 1.4970 | 1.5352 | 1.5951 | 1.5771 | 1.5771 | 1.5771 | 1.5771 | 1.5771 |
| A2 | 1.5736 | 1.5708 | 1.5031 | 1.4333 | 1.4333 | 1.4333 | 1.4333 | 1.4333 |
| A3 | 4.0897 | 3.6015 | 3.6414 | 3.6986 | 3.6986 | 3.6986 | 3.6986 | 3.6986 |
| Rs | 3.4750 × 10−2 | 3.2910 × 10−2 | 5.4821 × 10−2 | 2.2278 × 10−2 | 2.2278 × 10−2 | 2.2278 × 10−2 | 2.2278 × 10−2 | 2.2278 × 10−2 |
| Rsh | 6.0829 × 10 | 6.1846 × 10 | 5.5039 × 10 | 5.9474 × 10 | 5.9474 × 10 | 5.9474 × 10 | 5.9474 × 10 | 5.9474 × 10 |
| RMSE | 3.7358 × 10−3 | 5.4162 × 10−3 | 1.9641 × 10−1 | 2.0756 × 10−3 | 1.2340 × 10−3 | 6.3537 × 10−3 | 1.4184 × 10−2 | 1.0291 × 10−3 |
| RMSE | Minimum | Maximum | Mean | Std |
|---|---|---|---|---|
| HBA | 9.8602 × 10−4 | 3.8151 × 10−2 | 2.2831 × 10−3 | 6.7797 × 10−3 |
| WOA | 9.9843 × 10−4 | 4.6014 × 10−2 | 8.5781 × 10−3 | 1.4332 × 10−2 |
| SMA | 8.3990 × 10−2 | 3.0677 × 10−1 | 2.1226 × 10−1 | 6.0214 × 10−2 |
| PSO | 9.8903 × 10−4 | 5.1840 × 10−3 | 2.0009 × 10−3 | 7.7885 × 10−4 |
| SSA | 9.8891 × 10−4 | 1.5074 × 10−3 | 1.2064 × 10−3 | 6.7854 × 10−3 |
| GWO | 1.1439 × 10−3 | 3.8121 × 10−2 | 6.3979 × 10−3 | 1.0433 × 10−2 |
| BOA | 4.3489 × 10−3 | 4.5074 × 10−2 | 1.6710 × 10−2 | 8.4708 × 10−3 |
| IHBA | 9.8015 × 10−4 | 3.8151 × 10−2 | 1.0049 × 10−3 | 2.0265 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, W.; He, Q.; Yang, L.; Jiao, H. Solar Photovoltaic Cell Parameter Identification Based on Improved Honey Badger Algorithm. Sustainability 2022, 14, 8897. https://doi.org/10.3390/su14148897
Lei W, He Q, Yang L, Jiao H. Solar Photovoltaic Cell Parameter Identification Based on Improved Honey Badger Algorithm. Sustainability. 2022; 14(14):8897. https://doi.org/10.3390/su14148897
Chicago/Turabian StyleLei, Wenjing, Qing He, Liu Yang, and Hongzan Jiao. 2022. "Solar Photovoltaic Cell Parameter Identification Based on Improved Honey Badger Algorithm" Sustainability 14, no. 14: 8897. https://doi.org/10.3390/su14148897
APA StyleLei, W., He, Q., Yang, L., & Jiao, H. (2022). Solar Photovoltaic Cell Parameter Identification Based on Improved Honey Badger Algorithm. Sustainability, 14(14), 8897. https://doi.org/10.3390/su14148897






