Spatio-Temporal Synergy between Urban Built-Up Areas and Poverty Transformation in Tibet
Abstract
:1. Introduction
2. Materials and Methods
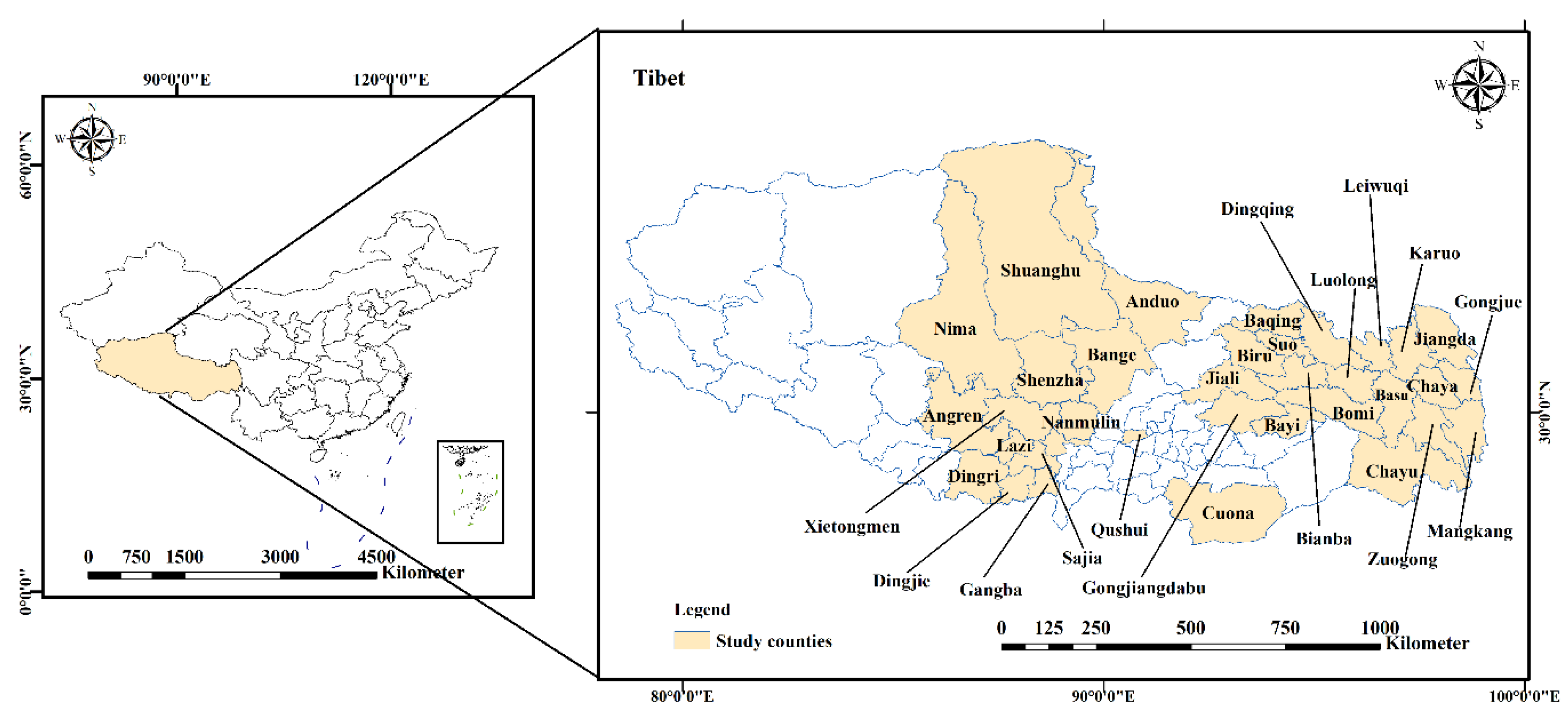
2.1. Study Areas and Data
2.2. Research Methodology
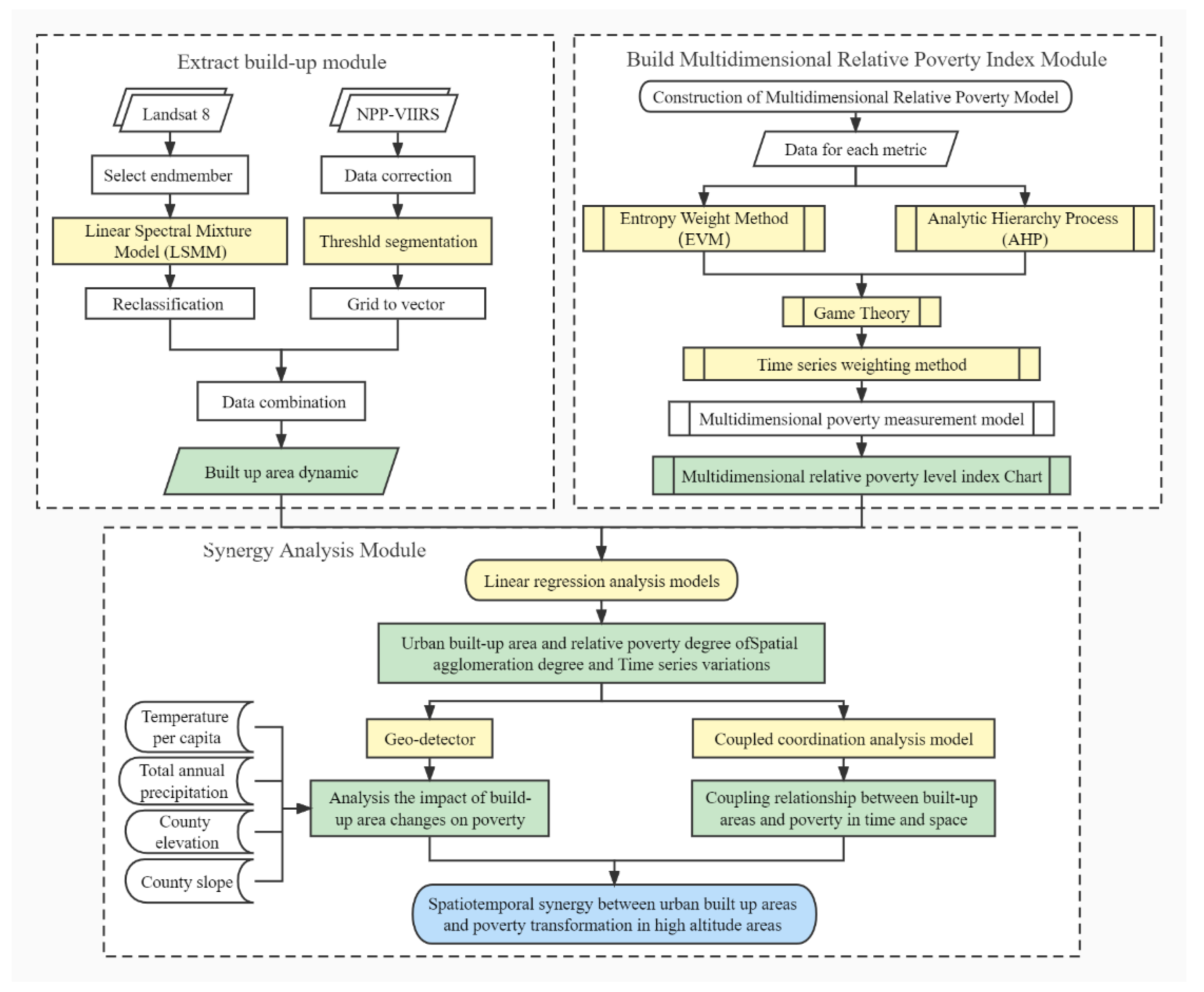
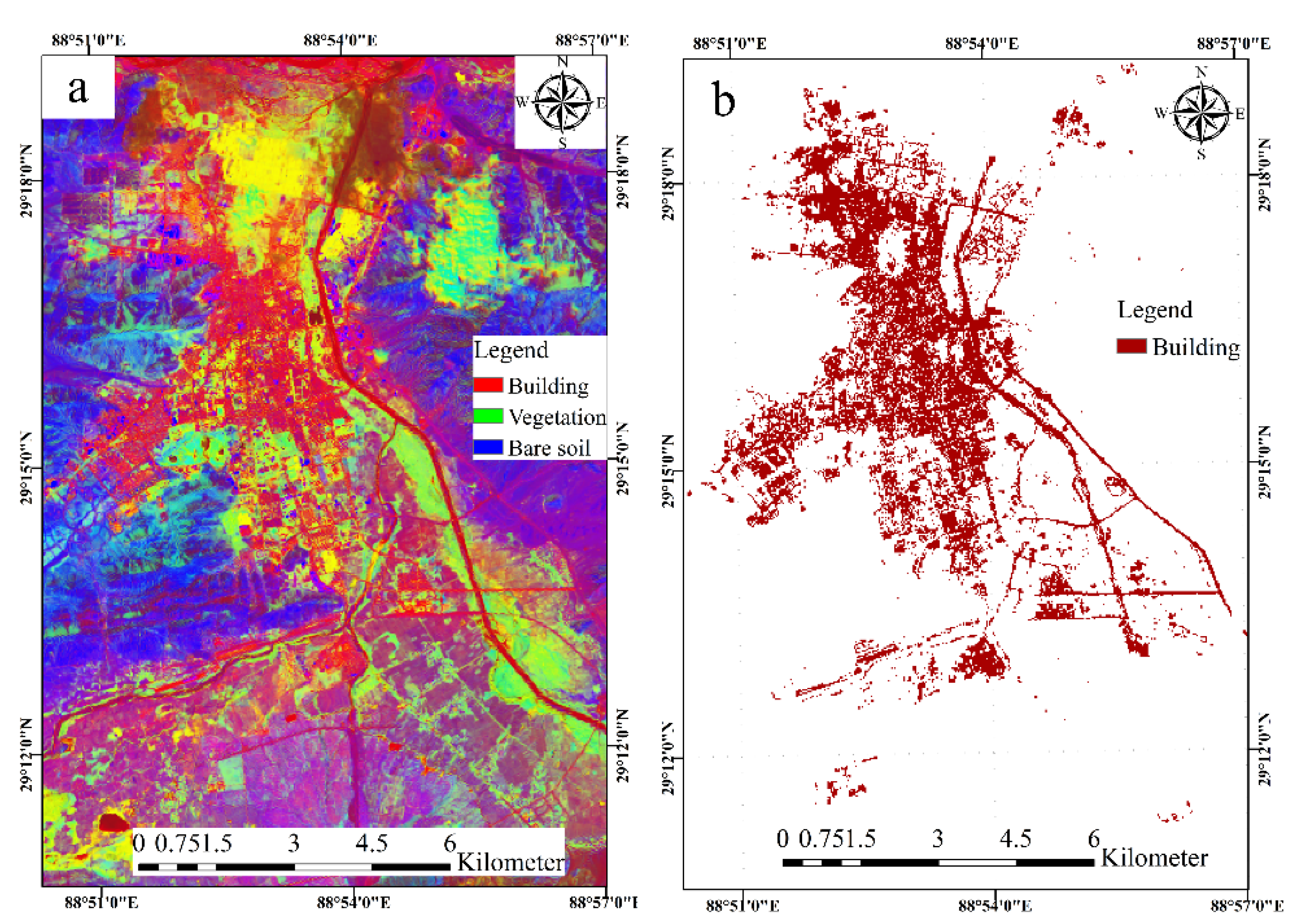
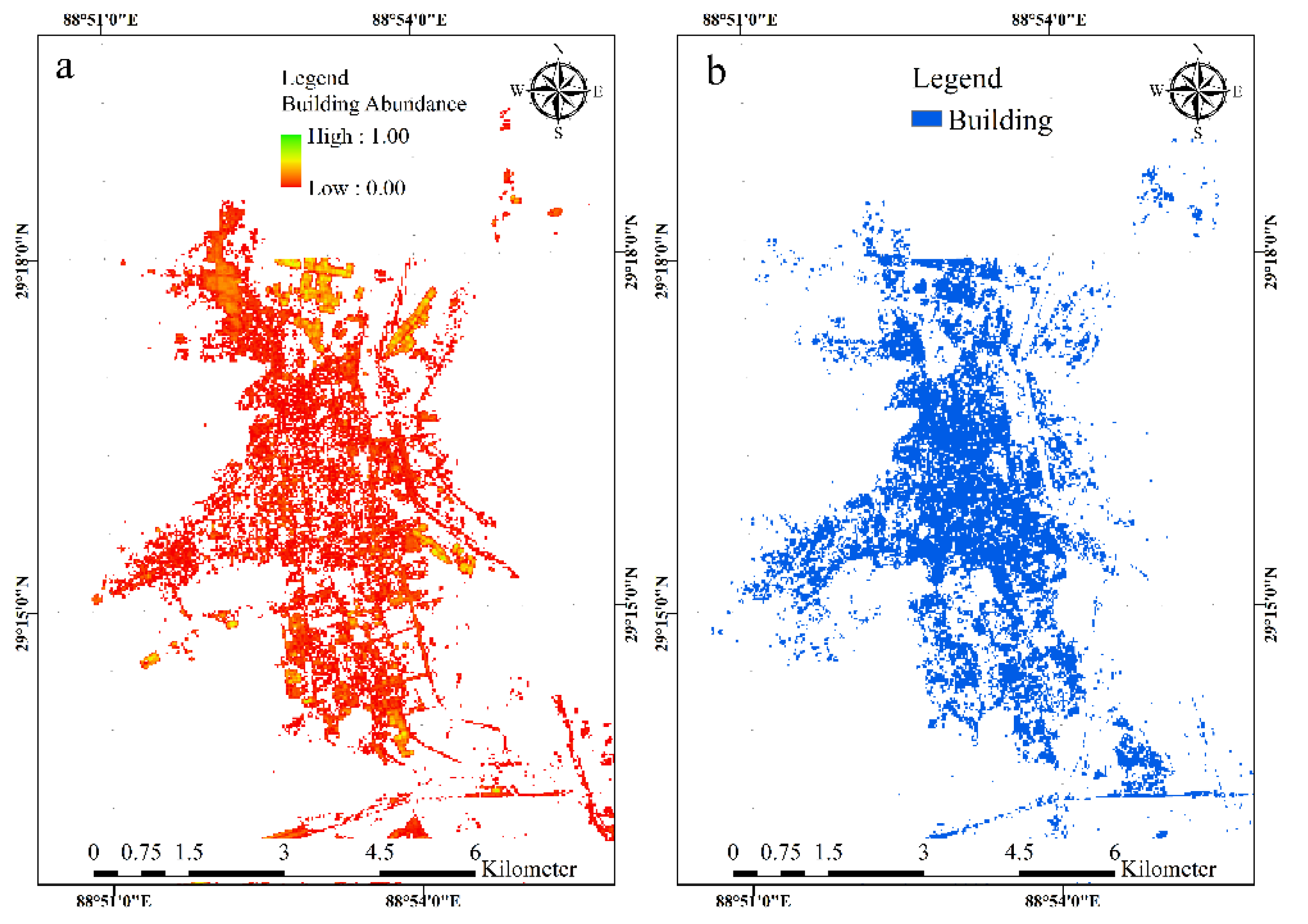
2.2.1. Urban Built-Up-Areas Extraction Module
- (1)
- Linear Spectral Mixture Model (LSMM)LSMM can obtain information on the abundance of substances in multispectral or hyperspectral images based on the spectral characteristics of the substance, solving the problem of feature mixing [33,34]. LSMM assumes that the reflectivity of each pixel in the image is a linear combination of the reflectivity of each substance in the pixel or the endmember spectrum [35,36]. This is expressed as:where is the spectral reflectance of the -th pixel in the band; is the spectral reflectance of the -th basic component in the band; is the abundance of the -th end element in the -th pixel; is the number of end elements; and is the residual error value.
- (2)
- Nighttime-lighting-threshold methodThe extraction of urban built-up areas with nighttime-lighting data focuses on obtaining the best threshold and segmenting the nighttime-lighting data with this threshold [37]. According to the accuracy, convenience, and automation of the method, the spatial-comparison method based on statistical data is selected in this paper, and the median interannual mean of the light values is taken as the threshold value for extraction, and the extracted area is corrected with the actual area until the difference between the two is minimized, at which point the threshold value is the best threshold value (Table 1).
2.2.2. Multidimensional Relative-Poverty-Construction Module
2.2.3. Analysis Module
- (1)
- Linear-regression modelThe linear-regression model was used to analyze the spatial-temporal-variation characteristics of urban built-up areas and multidimensional relative poverty. The regression slope is calculated using the least squares method.where, is the time variable, is the dependent variable representing the built-up area or relative poverty, and is the study period. > 0 represents an increasing trend; < 0 represents a decreasing trend.
- (2)
- Coupling-coordination-degree modelTo analyze the degree of interaction between built-up areas and relative-poverty levels in poor counties, a coupling-coordination-degree model of urban built-up areas and relative-poverty levels is constructed based on the concept of capacity coupling in physics [55,56]. The coupling-coordination degree is used to analyze the level of coordinated development of things, which can characterize whether the two systems are mutually reinforcing or constraining each other at different levels [57,58]. For a better presentation of the results, this paper refers to the study of related scholars and is combined with the actual situation of this study [59,60,61], the middle-index-segmentation method is used to classify the degree of coupled and coordinated development into six classes: serious imbalance (0–0.2), moderate imbalance (0.2–0.4), mild imbalance (0.4–0.5), primary coordination (0.5–0.6), moderate coordination (0.6–0.8), and good coordination (0.8–1.0). To calculate the coupling-coordination degree, the coupling degree is first calculated with the following equation:In Equation (12), is the coupling degree between the built-up area of the town and the relative-poverty level. The coupling-coordination degree is then presented with the following equation to define the system’s overall-development level of them, the coupling-coordination degree is then introduced with the following equation:In Equations (13) and (14), is the coupled-coordinated-development degree, is the integrated-development index of built-up area and relative-poverty level, α and are defined as the weight values of built-up area and relative-poverty level, respectively, and added together equal 1. Since built-up area and relative-poverty level are two independent systems, take , respectively.
- (3)
- Geographical detectorGeographical detector can explore the spatial heterogeneity of a single variable or detect whether the spatial distribution of two variables tends to be the same [62], and are widely used in regional spatial heterogeneity and the evolution of spatial patterns of geographic factors. The geographic detector has strong robustness and can identify the driving degree of the combination of two factors by q-value. Since the average altitude of Tibetan plateau is above 4000 m, and most of the deep-poverty areas are in areas with poor natural conditions and fragile ecological environment. Despite the previous adoption of various capital operation and anti-poverty measures, some of the population in the region still cannot get rid of poverty. Even if we ignore economic and social factors such as system, policy, education, and resources, the impact of natural geography on poverty is still a major problem that cannot be avoided. This paper selects the built-up area and four factors that can represent the physical geography to analysis the mutual driving effects of two factors on relative poverty as shown in Table 6. Referring to previous studies, the relative poverty is taken as the dependent variable (), while the independent variables are composed of the built-up area per capita (), temperature (), precipitation (), elevation (), and slope ().
3. Results
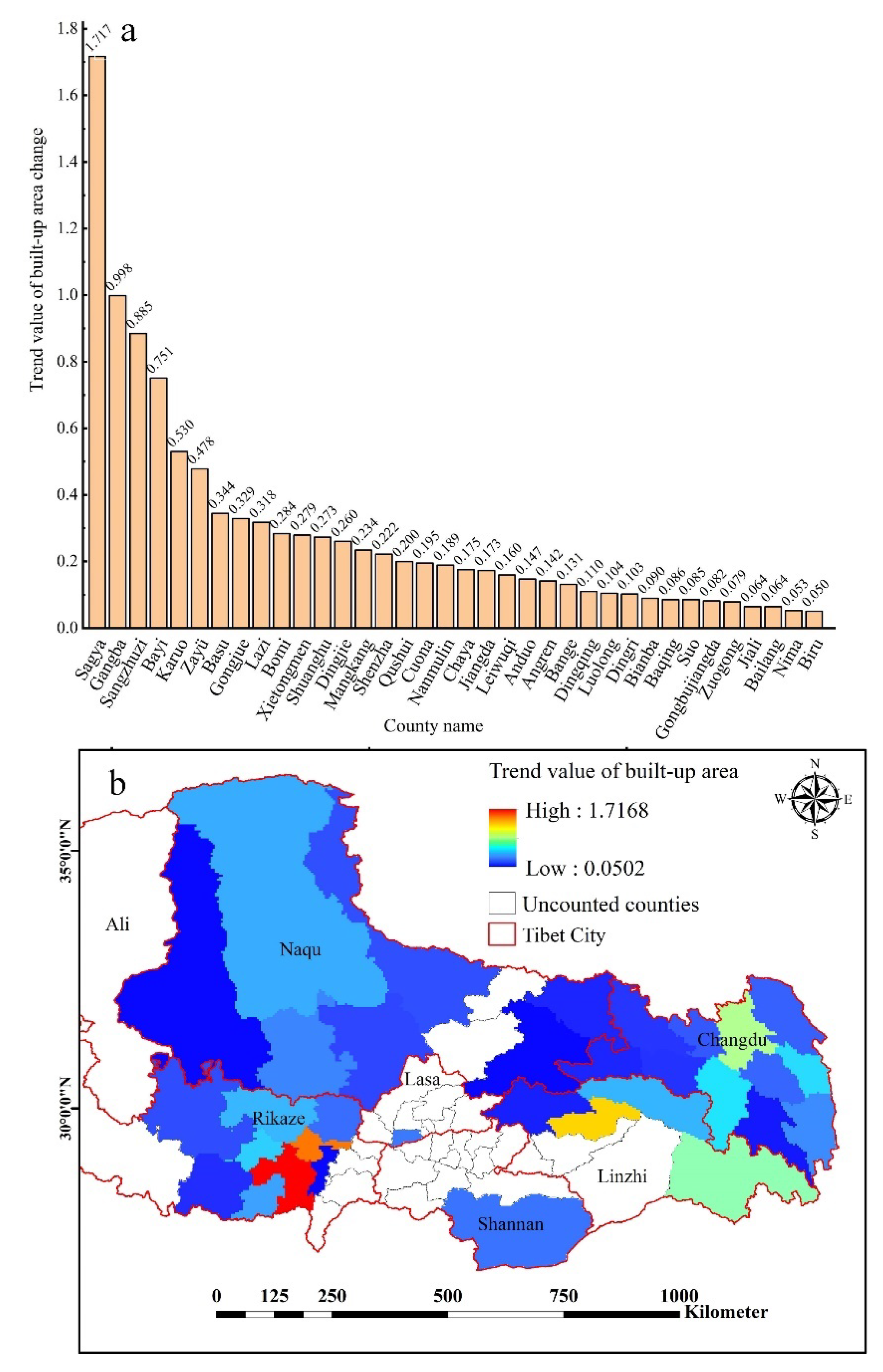
3.1. Evaluation of the Spatial and Temporal Patterns of Urban Built-Up Area
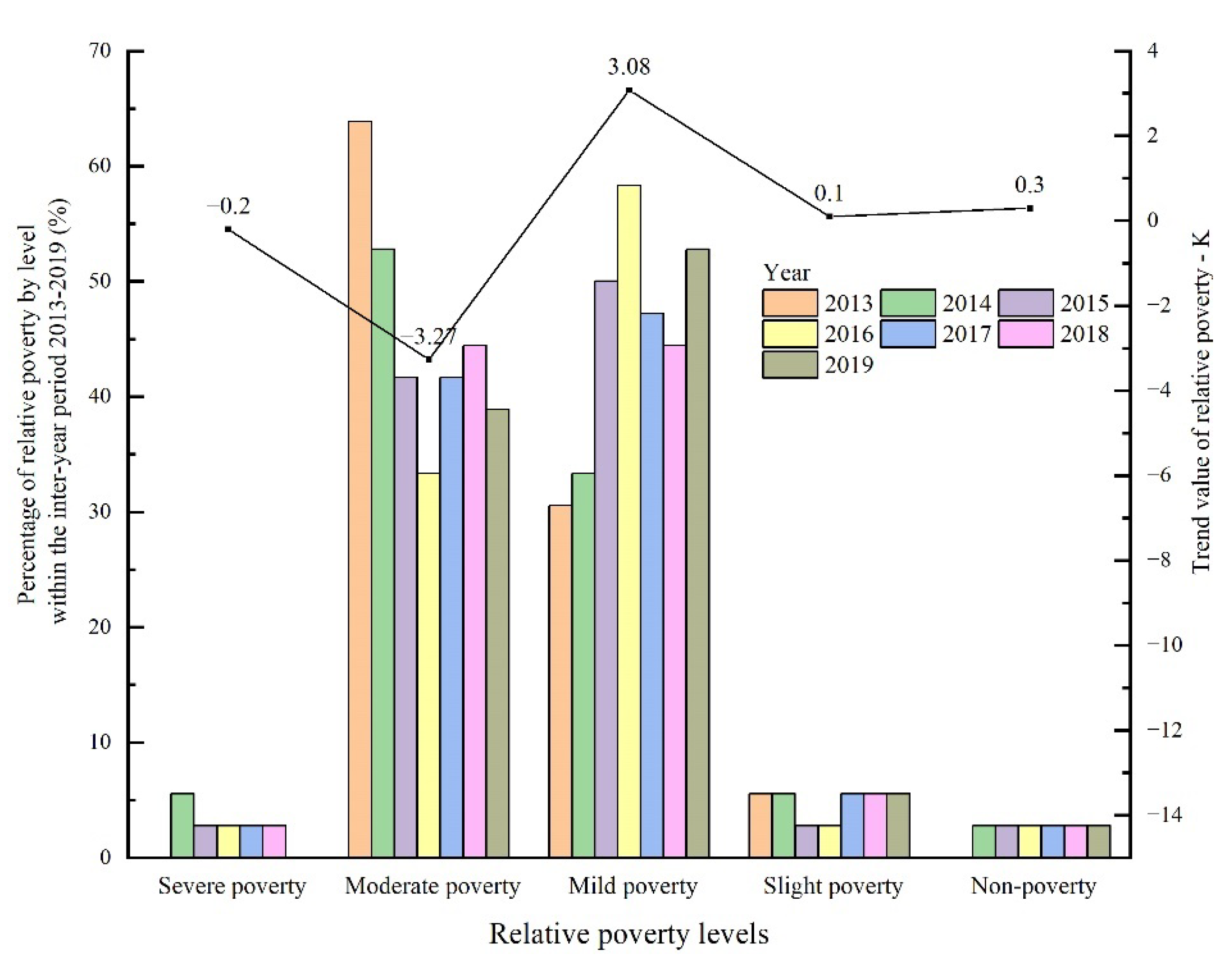
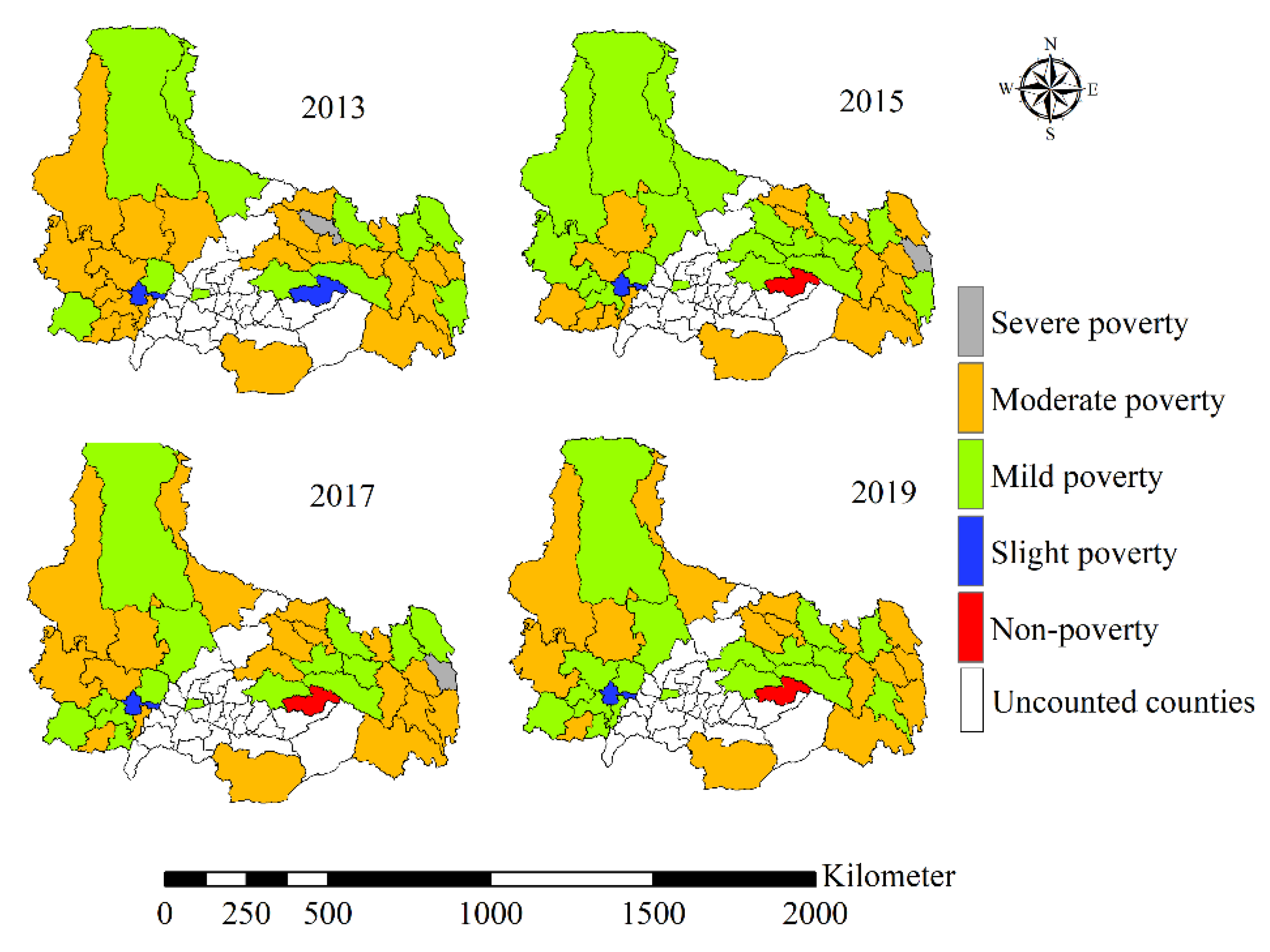
3.2. Spatial- and Temporal-Evolution Characteristics of Multidimensional Relative Poverty in Tibet
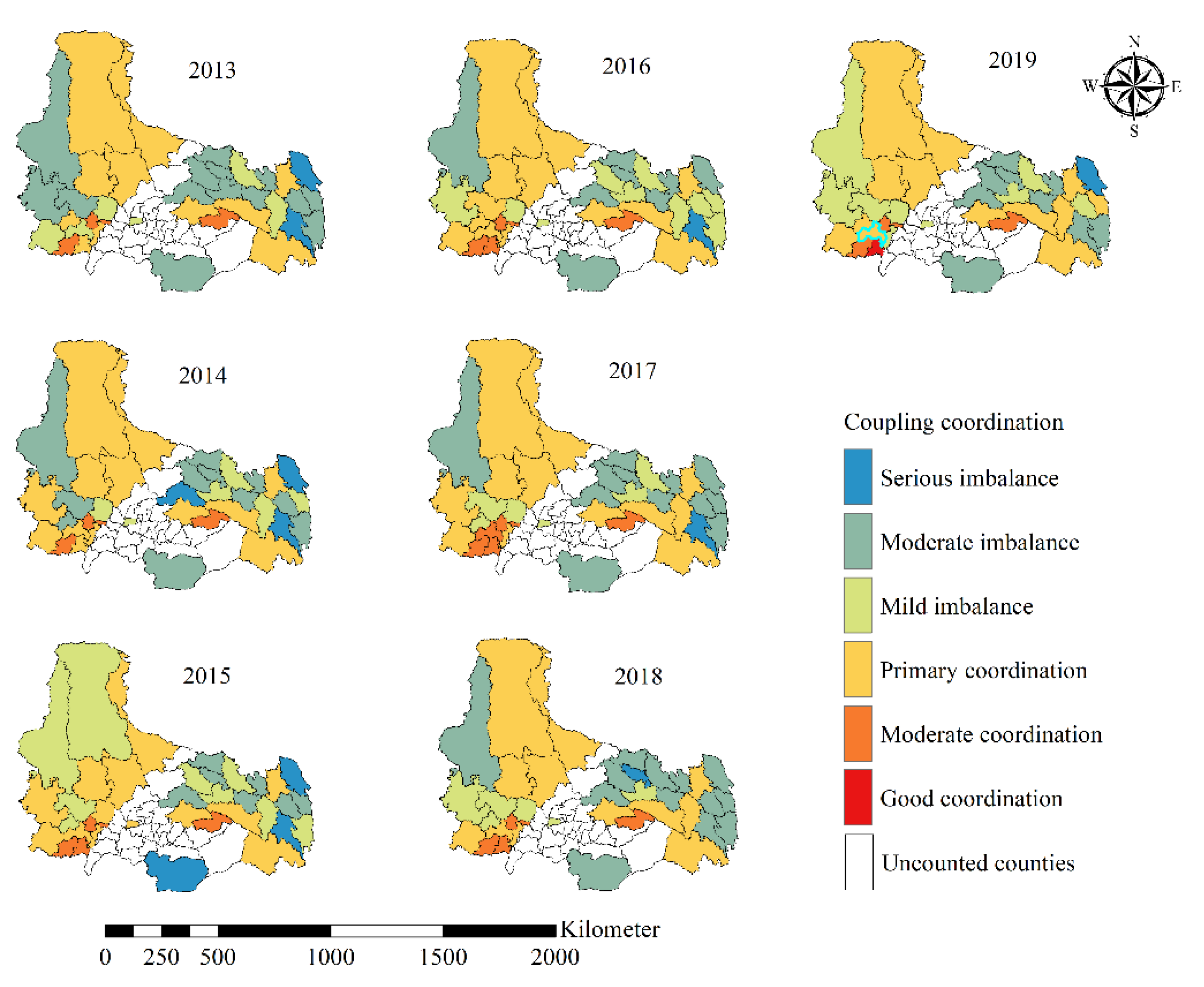
3.3. Spatio-Temporal Synergy between Urban Built-Up Area and Relative-Poverty Transformation
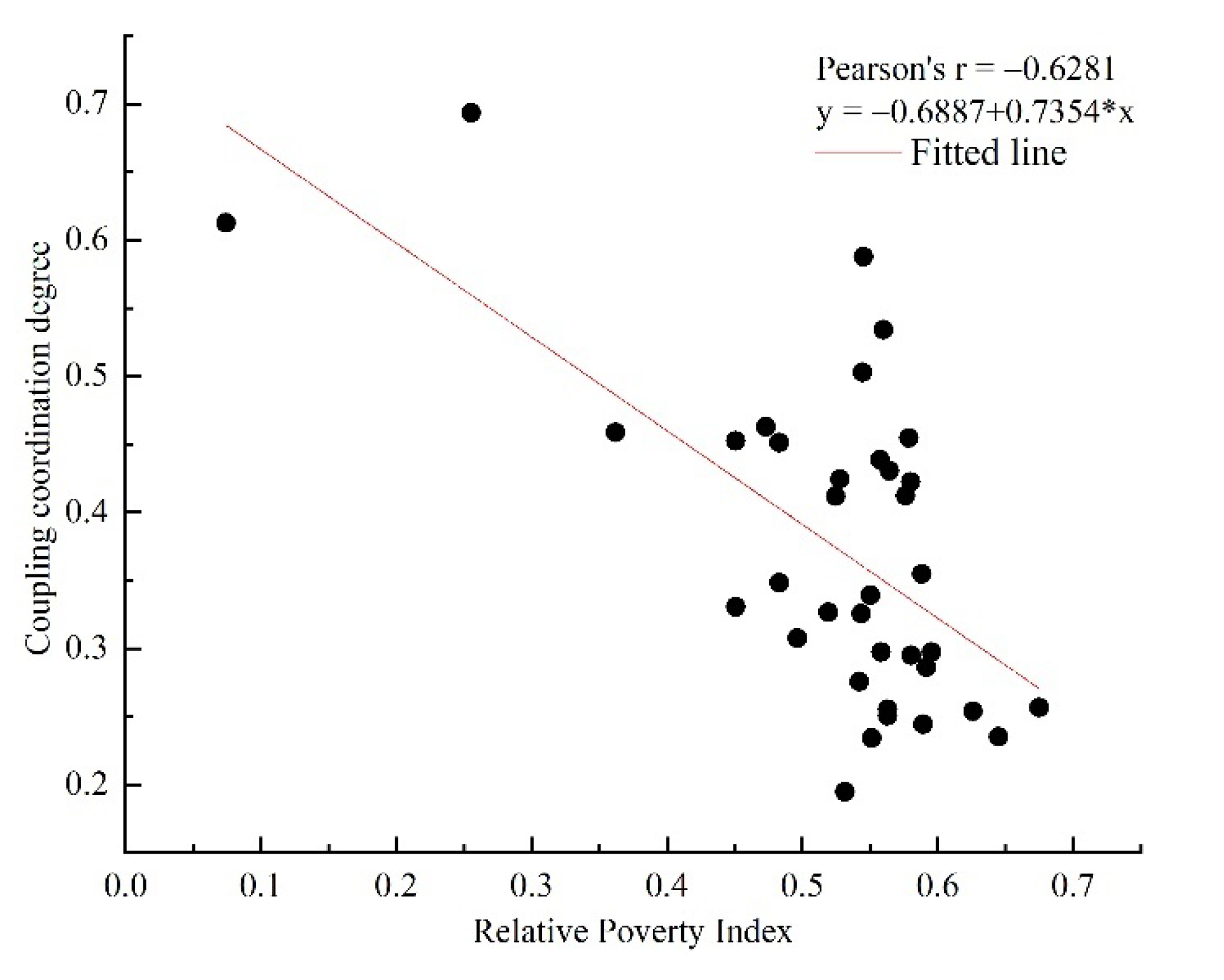
3.4. The Degree of Influence of the Association between Urban Built-up Area and Relative Poverty
4. Discussion
4.1. Combinatorial Weighting Method Based on Time-Series Weights
4.2. Comparison of Urban Built-Up Area Results and Product Data
4.3. Analysis of the Spatio-Temporal Synergy between Urban Built-Up Areas and Poverty Transformation
4.4. Research Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pezzulo, C.; Hornby, G.M.; Sorichetta, A.; Gaughan, A.E.; Linard, C.; Bird, T.J.; Kerr, D.; Lloyd, C.T.; Tatem, A.J. Sub-national mapping of population pyramids and dependency ratios in Africa and Asia. Sci. Data 2017, 4, 170089. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, K.; Chang, Z.; Chen, Z.; Wu, J.; Yu, B. Identifying and evaluating poverty using multisource remote sensing and point of interest (POI) data: A case study of Chongqing, China. J. Clean. Prod. 2020, 255, 120245. [Google Scholar] [CrossRef]
- Pan, J.; Hu, Y. Spatial Identification of Multi-dimensional Poverty in Rural China: A Perspective of Nighttime-Light Remote Sensing Data. J. Indian Soc. Remote 2018, 46, 1093–1111. [Google Scholar] [CrossRef]
- The Conference on Poverty Alleviation and Development Was Held in Beijing. Available online: http://www.gov.cn/xinwen/2020-12/31/content_5575691.htm (accessed on 26 March 2022).
- Jean, N.; Burke, M.; Xie, M.; Davis, W.M.; Lobell, D.B.; Ermon, S. Combining satellite imagery and machine learning to predict poverty. Science 2016, 353, 790–794. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Chen, Y.; Chi, Y.; Zhao, W.; Hu, Z.; Duan, F. Village-level multidimensional poverty measurement in China: Where and how. J. Geogr. Sci. 2018, 28, 1444–1466. [Google Scholar] [CrossRef] [Green Version]
- Tibet, R.G.O.U. Study on the Urban Poor Population in Tibet and Its Countermeasures. Tibet. Stud. 2001, 3, 14–27. [Google Scholar]
- Consolidate and Expand The Effectiveness of Poverty Alleviation and Relocation. Available online: https://news.gmw.cn/2020-12/18/content34473296.htm (accessed on 19 April 2022).
- Li, G.; Cai, Z.; Qian, Y.; Chen, F. Identifying Urban Poverty Using High-Resolution Satellite Imagery and Machine Learning Approaches: Implications for Housing Inequality. Land 2021, 10, 648. [Google Scholar] [CrossRef]
- Graesser, J.; Cheriyadat, A.; Vatsavai, R.R.; Chandola, V.; Long, J.; Bright, E. Image Based Characterization of Formal and Informal Neighborhoods in an Urban Landscape. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1164–1176. [Google Scholar] [CrossRef]
- Duque, J.C.; Patino, J.E.; Ruiz, L.A.; Pardo-Pascual, J.E. Measuring intra-urban poverty using land cover and texture metrics derived from remote sensing data. Landsc. Urban Plan. 2015, 135, 11–21. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Karácsonyi, D.; Liu, Z.; Wang, Y.; Wang, J. Spatio-temporal pattern and driving forces of construction land change in a poverty-stricken county of China and implications for poverty-alleviation-oriented land use policies. Land Use Policy 2019, 91, 104267. [Google Scholar] [CrossRef]
- Analysis of Urban Growth and Sprawl from Remote Sensing Data. Available online: https://link.springer.com/content/pdf/10.1007/978-3-642-05299-6.pdf (accessed on 23 June 2022).
- Randelli, F.; Martellozzo, F. Is rural tourism-induced built-up growth a threat for the sustainability of rural areas? The case study of Tuscany. Land Use Policy 2019, 86, 387–398. [Google Scholar] [CrossRef]
- Barbier, E.B.; Hochard, J.P. Poverty, rural population distribution and climate change. Environ. Dev. Econ. 2017, 23, 234–256. [Google Scholar] [CrossRef] [Green Version]
- Bossert, W.; Chakravarty, S.R.; D’Ambrosio, C. Multidimensional Poverty and Material Deprivation with Discrete Data. Rev. Income Wealth 2013, 59, 29–43. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Tan, Y.; Feng, S. Does reducing air pollution improve the progress of sustainable development in China? J. Clean. Prod. 2020, 272, 122759. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Sutton, P.C.; Ghosh, T.; Tuttle, B.T.; Baugh, K.E.; Bhaduri, B.; Bright, E. A global poverty map derived from satellite data. Comput. Geosci. 2009, 35, 1652–1660. [Google Scholar] [CrossRef]
- Oxford Poverty and Human Development Initiative. Global Multidimensional Poverty Index 2018: The Most Detailed Picture to Date of the World’s Poorest People; Oxford Poverty and Human Development Initiative (OPHI); University of Oxford, Queen Elizabeth House: Oxford, UK, 2018; pp. 1–4. [Google Scholar]
- Carr-Hill, R.A.; Chalmers-Dixon, P. The Public Health Observatory Handbook of Health Inequalities Measurement; South East Public Health Observatory: Oxford, UK, 2005; pp. 38–45. [Google Scholar]
- Zhao, X.; Yu, B.; Liu, Y.; Chen, Z.; Li, Q.; Wang, C.; Wu, J. Estimation of Poverty Using Random Forest Regression with Multi-Source Data: A Case Study in Bangladesh. Remote Sens. 2019, 11, 375. [Google Scholar] [CrossRef] [Green Version]
- Poverty Reduction and the Health Sector-the Health, Nutrition, and Population Network’s Chapter in the World Bank’s Poverty Reduction Strategy Sourcebook. Available online: https://documents1.worldbank.org/curated/en/936521468147314026/pdf/multi0page.pdf (accessed on 15 April 2022).
- Wang, W.; Cheng, H.; Zhang, L. Poverty assessment using DMSP/OLS night-time light satellite imagery at a provincial scale in China. Adv. Space Res. 2012, 49, 1253–1264. [Google Scholar] [CrossRef]
- Yang, C.; Yu, B.; Chen, Z.; Song, W.; Zhou, Y.; Li, X.; Wu, J. A Spatial-Socioeconomic Urban Development Status Curve from NPP-VIIRS Nighttime Light Data. Remote Sens. 2019, 11, 2398. [Google Scholar] [CrossRef] [Green Version]
- Yu, B.; Shi, K.; Hu, Y.; Huang, C.; Chen, Z.; Wu, J. Poverty Evaluation Using NPP-VIIRS Nighttime Light Composite Data at the County Level in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1217–1229. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, Y.; Claus, H.; Zeng, R.; Zhang, X.; Wang, J. Ecological and Environmental Issues Faced by a Developing Tibet. Environ. Sci. Technol. 2012, 46, 1979–1980. [Google Scholar] [CrossRef]
- Zhao, N.; Ghosh, T.; Samson, E.L. Mapping spatio-temporal changes of Chinese electric power consumption using night-time imagery. Int. J. Remote Sens. 2012, 33, 6304–6320. [Google Scholar] [CrossRef]
- He, X.; Zhou, C.; Zhang, J.; Yuan, X. Using Wavelet Transforms to Fuse Nighttime Light Data and POI Big Data to Extract Urban Built-Up Areas. Remote Sens. 2020, 12, 3887. [Google Scholar] [CrossRef]
- Hua, L.; Zhang, X.; Nie, Q.; Sun, F.; Tang, L. The Impacts of the Expansion of Urban Impervious Surfaces on Urban Heat Islands in a Coastal City in China. Sustainability 2020, 12, 475. [Google Scholar] [CrossRef] [Green Version]
- Hall, J.; Hossain, A.K.M.A. Mapping Urbanization and Evaluating Its Possible Impacts on Stream Water Quality in Chattanooga, Tennessee, Using GIS and Remote Sensing. Sustainability 2020, 12, 1980. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Tang, L.; Wang, H. An improved approach for monitoring urban built-up areas by combining NPP-VIIRS nighttime light, NDVI, NDWI, and NDBI. J. Clean. Prod. 2021, 328, 129488. [Google Scholar] [CrossRef]
- Weng, Q. Remote sensing of impervious surfaces in the urban areas: Requirements, methods, and trends. Remote Sens. Environ. 2012, 117, 34–49. [Google Scholar] [CrossRef]
- Su, Y.; Wang, D.; Zhao, S.; Shi, J.; Shi, Y.; Wei, D. Examining long-term natural vegetation dynamics in the Aral Sea Basin applying the linear spectral mixture model. PeerJ 2021, 9, e10747. [Google Scholar] [CrossRef]
- Small, S. The landsat ETM plus spectral mixing space. Remote Sens. Environ. 2004, 93, 1–17. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, L.; Chen, J.; Rao, Y.; Zhou, Y.; Chen, X. Assessing the impact of endmember variability on linear Spectral Mixture Analysis (LSMA): A theoretical and simulation analysis. Remote Sens. Environ. 2019, 235, 111471. [Google Scholar] [CrossRef]
- Wu, C.; Murray, A.T. Estimating impervious surface distribution by spectral mixture analysis. Remote Sens. Environ. 2003, 84, 493–505. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Lawrence, W.T.; Stutzer, D.C.; Elvidge, C.D. A technique for using composite DMSP/OLS “City Lights” satellite data to map urban area. Remote Sens. Environ. 1997, 61, 361–370. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, F.; Zhang, J.; Wang, Z. Fluctuation in the transformation of economic development and the coupling mechanism with the environmental quality of resource-based cities—A case study of Northeast China. Resour. Policy 2021, 72, 102128. [Google Scholar] [CrossRef]
- Yan, D.; Kong, Y.; Ren, X.; Shi, Y.; Chiang, S. The determinants of urban sustainability in Chinese resource-based cities: A panel quantile regression approach. Sci. Total Environ. 2019, 686, 1210–1219. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liu, J.; Tongsheng, L.I.; Zheng, R.; Fengqi, W.U. Analysis of the coupling relationship between ecological vulnerability and economic poverty in Qinling-Dabashan contiguous poor areas: A case study of Shanyang County in Shaanxi Province, China. Acta Ecol. Sin. 2019, 39, 3908–3917. [Google Scholar]
- Griggs, D.; Stafford-Smith, M.; Gaffney, O.; Rockström, J.; Öhman, M.C.; Shyamsundar, P.; Steffen, W.; Glaser, G.; Kanie, N.; Noble, I. Sustainable development goals for people and planet. Nature 2013, 495, 305–307. [Google Scholar] [CrossRef]
- Ren, Q.; Huang, Q.; He, C.; Tu, M.; Liang, X. The poverty dynamics in rural China during 2000–2014: A multi-scale analysis based on the poverty gap index. J. Geogr. Sci. 2018, 28, 1427–1443. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Xu, Y. A geographic identification of multidimensional poverty in rural China under the framework of sustainable livelihoods analysis. Appl. Geogr. 2016, 73, 62–76. [Google Scholar] [CrossRef]
- Wu, R.; Yang, D.; Dong, J.; Zhang, L.; Xia, F. Regional Inequality in China Based on NPP-VIIRS Night-Time Light Imagery. Remote Sens. 2018, 10, 240. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Dong, S.; Li, F.; Yang, Y.; Li, Y.; Li, Z. A circular economy system for breaking the development dilemma of ‘ecological Fragility–Economic poverty’ vicious circle: A CEEPS-SD analysis. J. Clean. Prod. 2019, 212, 381–392. [Google Scholar] [CrossRef]
- Padda, I.U.L.H.; Hameed, A. Estimating multidimensional poverty levels in rural Pakistan: A contribution to sustainable development policies. J. Clean. Prod. 2018, 197, 435–442. [Google Scholar] [CrossRef]
- Liu, X.; Han, L.; Zheng, J.; Li, X. Temporal-Spatial Characteristics and the Driving Mechanism of Multidimensional Comprehensive Poverty Degree in Poverty-Stricken Counties: A Case Study of Poor Counties in Deep Poverty-Stricken Areas of Southern Xinjiang. Econ. Geogr. 2019, 39, 165–174. [Google Scholar]
- Crentsil, A.O.; Asuman, D.; Fenny, A.P. Assessing the determinants and drivers of multidimensional energy poverty in Ghana. Energy Policy 2019, 133, 110884. [Google Scholar] [CrossRef]
- Chen, Q.; Liao, H.; Liu, Y.; Cai, J.; Ma, Y. Analysis of the Coupling Relationship Between Transportation Accessibility and Multidimensional Poverty at County Level in Chongqing. J. Southwest Univ. 2020, 42, 12–24. [Google Scholar]
- Xin, Y.; Wang, D.; Zhang, L.; Ma, Y.; Chen, X.; Wang, H.; Wang, H.; Wang, K.; Long, H.; Chai, H.; et al. Cooperative analysis of infrastructure perfection and residents’ living standards in poverty-stricken counties in Qinghai Province. Environ. Dev. Sustain. 2021, 24, 3687–3703. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020, 2020, 1–5. [Google Scholar] [CrossRef]
- Cheng, Q.Y. Structure entropy weight method to confirm the weight of evaluating index. Syst. Eng.-Theory Pract. 2010, 30, 1225–1228. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Piority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Gibbons, R. An Introduction to Applicable Game Theory. J. Econ. Perspect 1997, 1, 127–149. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Mao, Z.; Xian, L.; Liang, Z. A study on the coupling coordination between tourism and the low-carbon city. Asia Pac. J. Tour. Res. 2019, 24, 550–562. [Google Scholar] [CrossRef]
- Shi, T.; Yang, S.; Zhang, W.; Zhou, Q. Coupling coordination degree measurement and spatiotemporal heterogeneity between economic development and ecological environment ----Empirical evidence from tropical and subtropical regions of China. J. Clean. Prod. 2019, 244, 118739. [Google Scholar] [CrossRef]
- Cheng, X.; Long, R.; Chen, H.; Li, Q. Coupling coordination degree and spatial dynamic evolution of a regional green competitiveness system—A case study from China. Ecol. Indic. 2019, 104, 489–500. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, Z.; Li, G.; Zhuo, Y.; Xu, Z. Spatial-Temporal Evolution of Sustainable Urbanization Development: A Perspective of the Coupling Coordination Development Based on Population, Industry, and Built-Up Land Spatial Agglomeration. Sustainability 2018, 10, 1766. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Fang, C.; Mu, X.; Chen, D. Coupling and coordination analysis of urbanization and ecosystem service value in Beijing-Tianjin-Hebei urban agglomeration. Ecol. Indic. 2022, 137, 108782. [Google Scholar]
- Xiang, K.; Zhao, A.; Liu, H.; Zhang, X.; Zhang, A.; Tian, X.; Jin, Z. Spatiotemporal Evolution and Coupling Pattern Analysis of Urbanization and Ecological Environmental Quality of the Chinese Loess Plateau. Sustainability 2022, 14, 7236. [Google Scholar] [CrossRef]
- Caizhi, S.; Lin, C.; Liangshi, Z.; Wei, Z. Spatial-Temporal Coupling Between Rural Water Poverty and Economic Poverty in China. Resour. Sci. 2013, 35, 1991–2002. [Google Scholar]
- Zhao, R.; Zhan, L.; Yao, M.; Yang, L. A geographically weighted regression model augmented by Geodetector analysis and principal component analysis for the spatial distribution of PM2.5. Sustain. Cities Soc. 2020, 56, 102106. [Google Scholar] [CrossRef]
- Zhu, L.; Meng, J.; Zhu, L. Applying Geodetector to disentangle the contributions of natural and anthropogenic factors to NDVI variations in the middle reaches of the Heihe River Basin. Ecol. Indic. 2020, 117, 106545. [Google Scholar] [CrossRef]
- China’s Rural Poverty Alleviation and Development Outline (2011–2020). Available online: http://www.gov.cn/gongbao/content/2011/content_2020905.htm (accessed on 10 March 2022).
- Macharis, C.; Springael, J.; De Brucker, K.; Verbeke, A. PROMETHEE and AHP: The design of operational synergies in multicriteria analysis.: Strengthening promethee with ideas of AHP. Eur. J. Oper. Res. 2004, 153, 307–317. [Google Scholar] [CrossRef]
- Yin, S.; Li, J.; Liang, J.; Jia, K.; Yang, Z.; Wang, Y. Optimization of the Weighted Linear Combination Method for Agricultural Land Suitability Evaluation Considering Current Land Use and Regional Differences. Sustainability 2020, 12, 10134. [Google Scholar] [CrossRef]
- Koné, Y.A.; Konaté, J.; Maïga, O.Y.; Tembiné, H. Efficient Strategies Algorithms for Resource Allocation Problems. Algorithms 2020, 13, 270. [Google Scholar] [CrossRef]
- Sun, W.; Li, Y.; Wang, D.; Fan, J. The efficiencies and their changes of China’s resources-based cities employing DEA and Malmquist index models. J. Geogr. Sci. 2012, 22, 509–520. [Google Scholar] [CrossRef]
- Gan, G.-Y.; Lee, H.-S.; Tao, Y.-J.; Tu, C.-S. Selecting Suitable, Green Port Crane Equipment for International Commercial Ports. Sustainability 2021, 13, 6801. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.Y.; Wu, C.S.; Chen, X.D.; Gao, Y.; Xie, S.; Zhang, B. Development of a global 30 m impervious surface map using multisource and multitemporal remote sensing datasets with the Google Earth Engine platform. Earth Syst. Sci. Data 2020, 12, 1625–1648. [Google Scholar] [CrossRef]
- Aristondo, O.; Ciommi, M. The orness value for rank-dependent welfare functions and rank-dependent poverty measures. Fuzzy Sets Syst. 2017, 325, 114–136. [Google Scholar] [CrossRef]
- Shao, M. Tibet’s historic eradication of absolute poverty-written on the occasion of the 7th National Poverty Alleviation Day. New West 2020, 11, 19–21. [Google Scholar]
- Zhang, L.; Hou, X. Research on the Characteristics of Multidimensional Poverty and Targeted poverty alleviation in Tibet. Heilongjiang Natl. Ser. 2017, 3, 79–85. [Google Scholar]
- Wang, R.; Zhou, X.; Yang, S.; Xian, Y. The Study of Multidimensional Poverty Measurement and Spatial Distribution Characteristics of Poverty of Tibetan Counties. Tibet. Stud. 2017, 1, 60–70. [Google Scholar]
- Jiang, Y.; Zhu, C.; Zhang, J. Vulnerability and Multidimensionality of Poverty in Tibet—Case Studies of Famdo And Xigaze. Chin. J. Agric. Resour. Reg. Plan. 2020, 41, 92–101. [Google Scholar]

| Year | Threshold |
|---|---|
| 2013 | 0.2569 |
| 2014 | 0.1525 |
| 2015 | 0.3289 |
| 2016 | 0.3992 |
| 2017 | 0.1874 |
| 2018 | 0.3556 |
| 2019 | 0.1935 |
| Dimension | Orientation | Indicator | Description | AHP Weights | EVM Weights | GT Weights |
|---|---|---|---|---|---|---|
| Economic dimension | Economic development | Per capita Gross Domestic Product (GDP) (RMB) | Reflecting the macroeconomic situation of the region [44] | 0.1461 | 0.0844 | 0.0439 |
| Residents’ deposits (RMB) | Reflecting the economic sustainability of rural households [47] | 0.0962 | 0.0305 | 0.0603 | ||
| Investment and consumption | Per capita local budget income (RMB) | Measuring the revenue capacity and level of government [18] | 0.0273 | 0.0366 | 0.0231 | |
| Industrial structure | Second industrial output (RMB) | Reflecting the economic income of the county’s processing and manufacturing industry [42] | 0.0559 | 0.0461 | 0.1578 | |
| Output of the tertiary industry (RMB) | Reflecting the income of the county’s service economy | 0.0559 | 0.0426 | 0.0715 | ||
| Number of industries above scale (RMB) | The greater the number of factories, the greater the economic dynamics [43] | 0.0314 | 0.0414 | 0.0578 | ||
| Social dimension | Social security | Number of social service institutions (pcs) | Service coverage of the poor in favor of poverty reduction [16] | 0.0264 | 0.0552 | 0.0332 |
| Proportion of employed persons to total population (%) | Increasing the number of employed persons can improve people’s livelihood [42] | 0.0264 | 0.0708 | 0.1100 | ||
| Number of fixed telephone users (person) | Number of durable goods reflecting the poor [16] | 0.0121 | 0.0308 | 0.0595 | ||
| Number of street offices (pcs) | Service security for the poor energy [43] | 0.0121 | 0.2612 | 0.0328 | ||
| Infrastructure | Agricultural machinery power(w) | The higher the mechanical power, the lower the poverty level [48] | 0.0264 | 0.0381 | 0.0612 | |
| Per capita facility agriculture area (km2) | Increasing the area of facility agriculture and the efficiency of agricultural production [45] | 0.0664 | 0.0432 | 0.1018 | ||
| Health and medical community | Number of beds per capita in health institutions (berth) | Reflecting the level of medical care [42] | 0.0264 | 0.0365 | 0.0525 | |
| Educational level | Number of primary and secondary school students (person) | Reflecting Education Resources [43] | 0.1320 | 0.0411 | 0.0433 | |
| Natural dimension | Resource endowment | Per capita output of grain (kg) | The material resources of the population, which play a crucial role in the ability to withstand economic shocks at the population level [46] | 0.0629 | 0.0461 | 0.0862 |
| Per capita oil production (kg) | Same as above | 0.0629 | 0.0315 | 0.0439 | ||
| Per capita meat production (kg) | Same as above | 0.0629 | 0.0312 | 0.0603 | ||
| Total area of crop sowing per capita (km2) | Same as above | 0.0629 | 0.0314 | 0.0231 |
| Year | Time Series Weights |
|---|---|
| 2013 | 0.2025 |
| 2014 | 0.1625 |
| 2015 | 0.1530 |
| 2016 | 0.2592 |
| 2017 | 0.2228 |
| 2018 | 0.1954 |
| 2019 | 0.2025 |
| Scale | Meaning |
|---|---|
| 1 | Both factors have the same importance when compared |
| 3 | The former is slightly more important than the latter, when compared to the two factors |
| 5 | The former is significantly more important than the latter, when compared to the two factors |
| 7 | The former is more strongly important than the latter, when compared to the two factors |
| 9 | The former is more extremely important than the latter, when compared to the two factors |
| 2, 4, 6, 8 | The middle value of the above adjacent judgments |
| Countdown | If the ratio of the importance of factor i to factor j as then the ratio of the importance of factor j to factor i is |
| Dimension | Economic | Social | Natural | Weights |
|---|---|---|---|---|
| Economic | 1 | 1 | 2 | 0.4126 |
| Social | 1 | 1 | 0.3275 | |
| Natural | 1/2 | 1 | 1 | 0.2599 |
| Variables | Name | Meaning | Classification Criteria |
|---|---|---|---|
| Y | Relative poverty | The relative poverty of each county | Classification according to the natural discontinuity taxonomy |
| X1 | Built-up area per capita | Built-up area per capita of each county | |
| X2 | Temperature | The annual average temperature of each county | |
| X3 | Precipitation | The total annual precipitation of each county | |
| X4 | Elevation | The average elevation of each county based on the zoning statistics tool | |
| X5 | Slope | Calculation of slope from focus statistics |
| Interaction | Degree of the Relationship (q) |
|---|---|
| Temperature ∩ Precipitation | 0.2227 |
| Elevation ∩ Slope | 0.2440 |
| Built-up area per capita ∩ Temperature | 0.4870 |
| Built-up area per capita ∩ Precipitation | 0.5397 |
| Built-up area per capita ∩ Elevation | 0.5551 |
| Built-up area per capita ∩ Slope | 0.5460 |
| Precipitation ∩ Elevation | 0.2483 |
| Temperature ∩ Elevation | 0.2054 |
| Precipitation ∩ Slope | 0.0170 |
| Temperature ∩ Slope | 0.2328 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Li, J.; Wang, D.; Yue, J.; Yan, X. Spatio-Temporal Synergy between Urban Built-Up Areas and Poverty Transformation in Tibet. Sustainability 2022, 14, 8773. https://doi.org/10.3390/su14148773
Su Y, Li J, Wang D, Yue J, Yan X. Spatio-Temporal Synergy between Urban Built-Up Areas and Poverty Transformation in Tibet. Sustainability. 2022; 14(14):8773. https://doi.org/10.3390/su14148773
Chicago/Turabian StyleSu, Yiting, Jing Li, Dongchuan Wang, Jiabao Yue, and Xingguang Yan. 2022. "Spatio-Temporal Synergy between Urban Built-Up Areas and Poverty Transformation in Tibet" Sustainability 14, no. 14: 8773. https://doi.org/10.3390/su14148773
APA StyleSu, Y., Li, J., Wang, D., Yue, J., & Yan, X. (2022). Spatio-Temporal Synergy between Urban Built-Up Areas and Poverty Transformation in Tibet. Sustainability, 14(14), 8773. https://doi.org/10.3390/su14148773







