Experimental and Numerical Investigation of the Flow Behaviour of Fractured Granite under Extreme Temperature and Pressure Conditions
Abstract
:1. Introduction
2. Experimental Study
2.1. Sample Description
2.2. Experimental Procedure
3. Numerical Study
3.1. Model Development
3.2. Governing Equations
3.3. Model Input Parameters
4. Results and Discussions
4.1. Experimental Results on Flow Characteristics of Fractured Granite under High Temperatures
4.1.1. The Effect of Temperature on the Flow Rate of Fractured Granite
4.1.2. Applicability of Darcy Equation
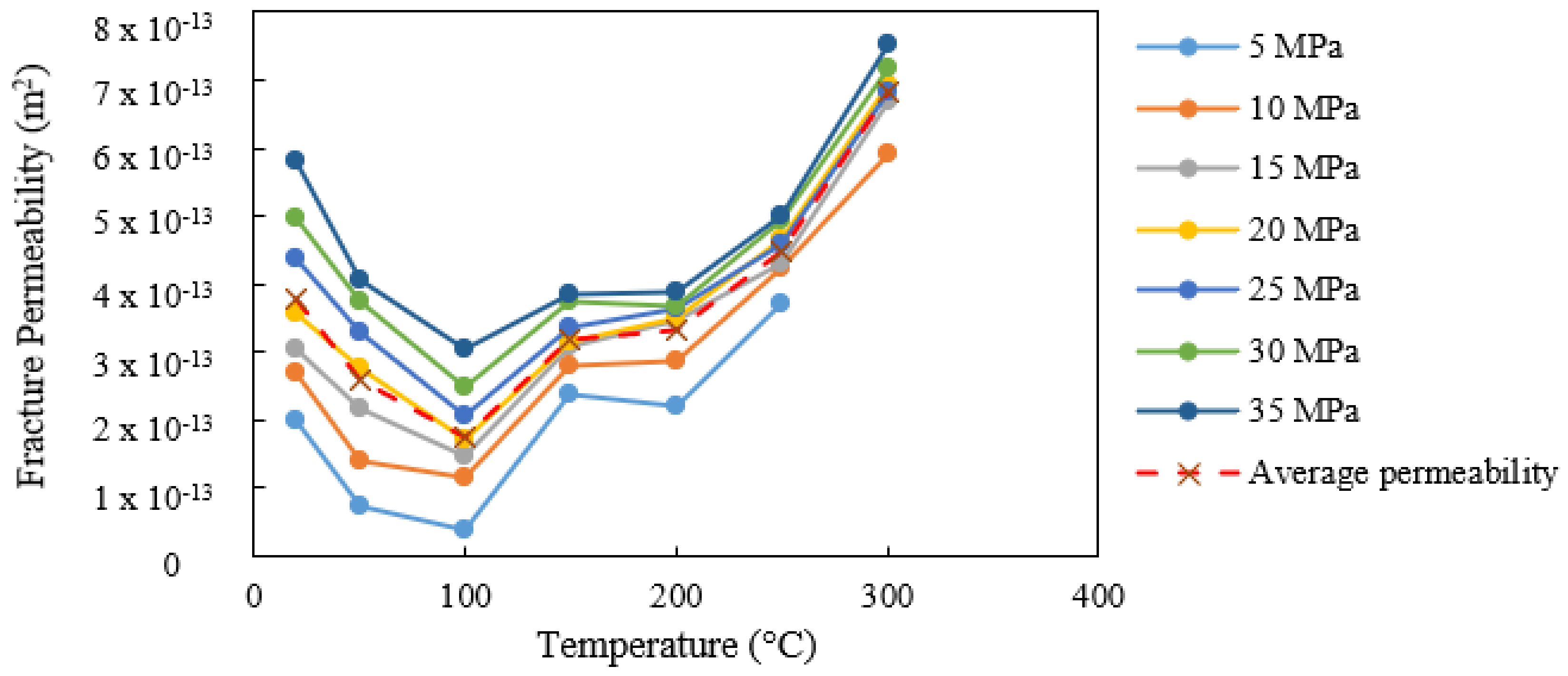
4.1.3. Temperature-Dependent Fracture Permeability
4.2. Numerical Simulations on Flow Characteristics of Fractured Granite under High Temperatures
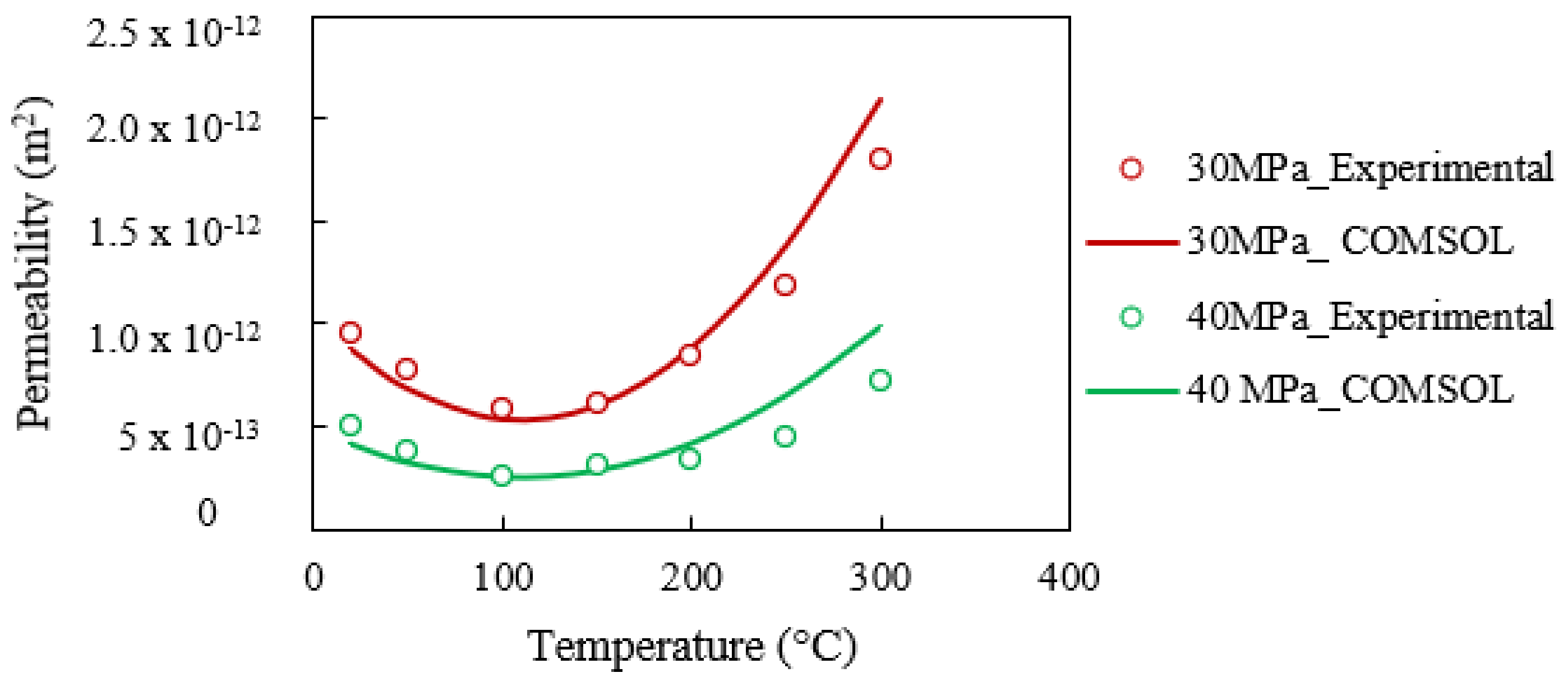
4.2.1. Model Validation
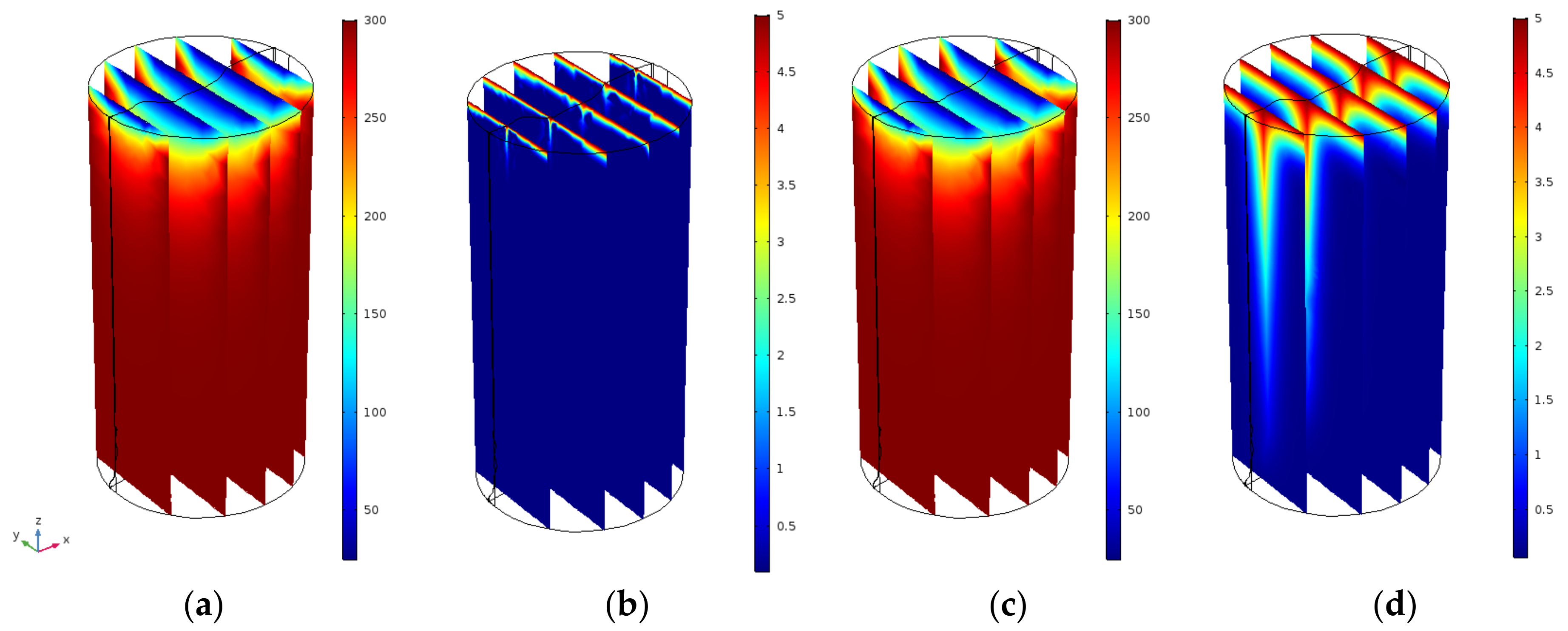
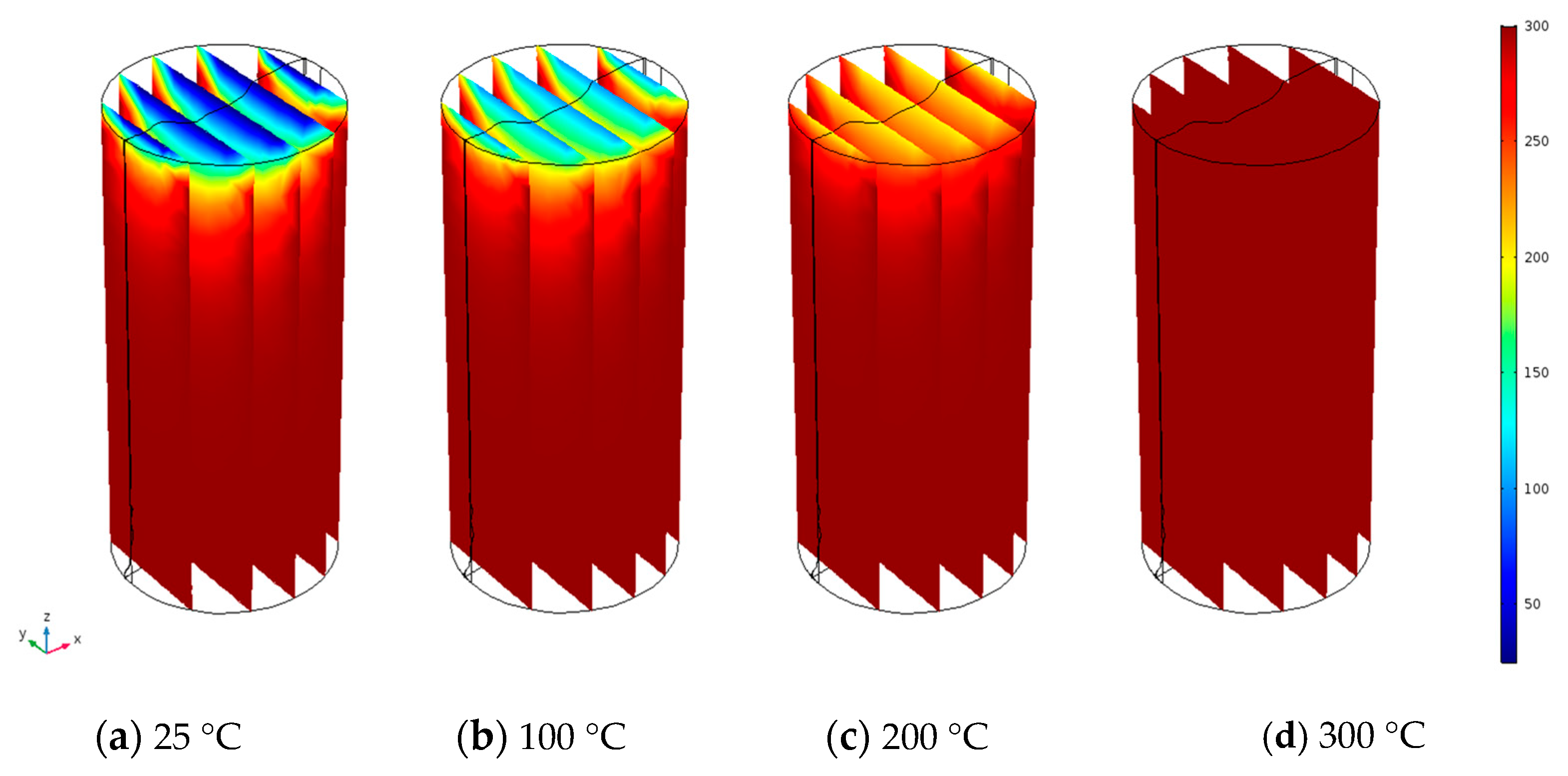
4.2.2. Pressure and Temperature Development on the Rock Matrix and the Fracture
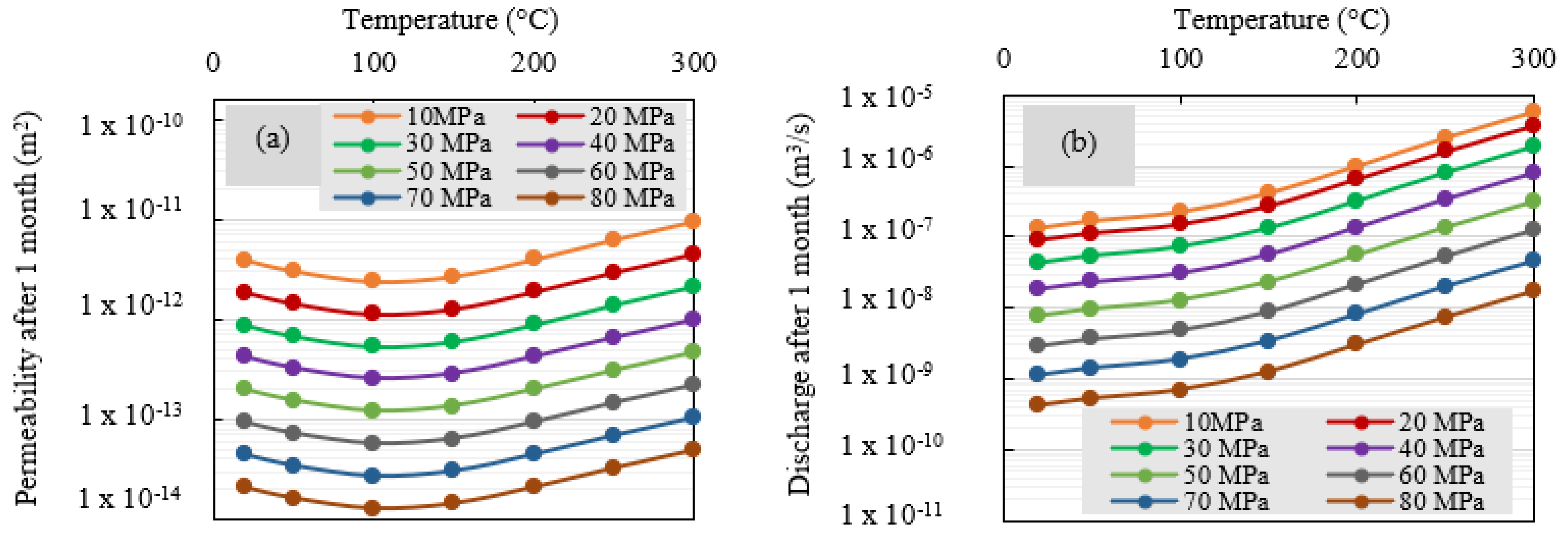
4.2.3. Predicted Flow Characteristics of Fractured Rocks under a Wide Range of Temperature and Stress Conditions
4.2.4. Effect of the Temperature of the Injection Fluid
4.2.5. Effect of Temperature on the Mechanical Characteristics of the Fractured Rocks
5. Conclusions
- Flow characteristics in fractured/porous media are significantly dependent on the properties of the fluid media, and therefore, the application of the relevant properties of the fluid media is an essential attribute for high-temperature conditions, since flow properties are significantly altered at higher temperatures.
- Both flow rate and fracture permeability non-linearly decrease with confining pressure due to the closure of the mechanically induced fracture under the larger effective stresses. Further, increasing the injection pressure results in a linear increment in fracture permeability due to opening the induced fracture.
- Increasing the temperature causes an initial reduction in granite’s fracture permeability up to 100° C due to the possible thermal expansion of the fracture, which attributes enhancement of the interlocking effect due to the thermal overclosure. A further increase in temperature causes enhancement of permeability-inducing thermal cracks, which results in enhancement of new flow paths in the rock matrix.
- It is essential to consider thermally induced damage to the material in the numerical simulations under non-isothermal conditions. In this regard, the temperature-dependent Young’s modulus and Poisson’s ratio, which can be determined from laboratory experiments, can be effectively utilised.
- Considering the reservoir-scale flow characteristics, closure of rock fractures can be expected at higher reservoir depths; however, both higher injection pressures and temperatures can enhance the flow characteristics of the deep geological reservoirs. Further, reservoir temperature and pressure are critical parameters when estimating the flow performance; thus, temperature-dependent circulation fluid properties should be incorporated into the analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Walsh, J.B. Effect of pore pressure and confining pressure on fracture permeability. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 429–435. [Google Scholar] [CrossRef]
- Blaisonneau, A.; Peter-Borie, M.; Gentier, S. Evolution of fracture permeability with respect to fluid/rock interactions under thermohydromechanical conditions: Development of experimental reactive percolation tests. Geotherm. Energy 2016, 4, 1. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Li, B.; Zhang, Y.; Zhang, S. Coupled thermo-hydro-mechanical-chemical modeling of water leak-off process during hydraulic fracturing in shale gas reservoirs. Energies 2017, 10, 1960. [Google Scholar] [CrossRef] [Green Version]
- Ghassemi, A.; Nygren, A.; Cheng, A. Effects of heat extraction on fracture aperture: A poro–thermoelastic analysis. Geothermics 2008, 37, 525–539. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, X.; Jeffrey, R.G.; Bunger, A.P.; Huddlestone-Holmes, C. Perturbation analysis for predicting the temperatures of water flowing through multiple parallel fractures in a rock mass. Int. J. Rock Mech. Min. Sci. 2015, 76, 162–173. [Google Scholar] [CrossRef]
- Izadi, G.; Elsworth, D. The influence of thermal-hydraulic-mechanical-and chemical effects on the evolution of permeability, seismicity and heat production in geothermal reservoirs. Geothermics 2015, 53, 385–395. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Zou, G.; Wang, Y.; Wang, Y.; Gao, T. Investigation of the temperature effect on rock permeability sensitivity. J. Pet. Sci. Eng. 2017, 156, 616–622. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, Y.; Guo, Q.; Tan, L.; Zhuang, Y.; Liu, M.; Zhang, C.; Xiang, W.; Rohn, J. Experimental investigation of the hydraulic and heat-transfer properties of artificially fractured granite. Sci. Rep. 2017, 7, 39882. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, N.; Kikuchi, T.; Ishibashi, T.; Tsuchiya, N. ν-X-type relative permeability curves for steam-water two-phase flows in fractured geothermal reservoirs. Geothermics 2017, 65, 269–279. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Z.; Sun, Z.; An, S.; Zhang, W.; Liu, P.; Yao, J.; Ma, J. Research on Stress Sensitivity of Fractured Carbonate Reservoirs Based on CT Technology. Energies 2017, 10, 1833. [Google Scholar] [CrossRef] [Green Version]
- Bandis, S.; Lumsden, A.; Barton, N. Fundamentals of rock joint deformation. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 249–268. [Google Scholar] [CrossRef]
- Barton, N.; Makurat, A. Hydro-thermo-mechanical over-closure of joints and rock masses and potential effects on the long term performance of nuclear waste repositories. In EUROCK; CRC Press: Liège, Belgium, 2006; pp. 445–450. [Google Scholar]
- Fang, Z.; Wu, W. Laboratory friction-permeability response of rock fractures: A review and new insights. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 15. [Google Scholar] [CrossRef]
- Olsson, R.; Barton, N. An improved model for hydromechanical coupling during shearing of rock joints. Int. J. Rock Mech. Min. Sci. 2001, 38, 317–329. [Google Scholar] [CrossRef]
- He, M.; Liu, R.; Xue, Y.; Feng, X.; Dang, F. Modeling of Navier–Stokes flow through sheared rough-walled granite fractures split after thermal treatment. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 96. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Qiao, L.; Liu, J.; Yang, J. The effects of hydro-mechanical coupling on hydraulic properties of fractured rock mass in unidirectional and radial flow configurations. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 87. [Google Scholar] [CrossRef]
- Moore, D.E.; Lockner, D.A.; Byerlee, J.D. Reduction of permeability in granite at elevated temperatures. Science 1994, 265, 1558–1561. [Google Scholar] [CrossRef] [Green Version]
- Bodvarsson, G. On the temperature of water flowing through fractures. J. Geophys. Res. 1969, 74, 1987–1992. [Google Scholar] [CrossRef]
- Fan, Z.; Parashar, R. Analytical solutions for a wellbore subjected to a non-isothermal fluid flux: Implications for optimizing injection rates, fracture reactivation, and EGS hydraulic stimulation. Rock Mech. Rock Eng. 2019, 52, 4715–4729. [Google Scholar] [CrossRef]
- Fan, Z.; Parashar, R.; Jin, Z.-H. Impact of convective cooling on pore pressure and stresses around a borehole subjected to a constant flux: Implications for hydraulic tests in an enhanced geothermal system reservoir. Interpretation 2020, 8, SG13–SG20. [Google Scholar] [CrossRef]
- Ghassemi, A. A review of some rock mechanics issues in geothermal reservoir development. Geotech. Geol. Eng. 2012, 30, 647–664. [Google Scholar] [CrossRef]
- Zeng, Y.-C.; Wu, N.-Y.; Su, Z.; Wang, X.-X.; Hu, J. Numerical simulation of heat production potential from hot dry rock by water circulating through a novel single vertical fracture at Desert Peak geothermal field. Energy 2013, 63, 268–282. [Google Scholar] [CrossRef]
- Hadgu, T.; Kalinina, E.; Lowry, T.S. Modeling of heat extraction from variably fractured porous media in Enhanced Geothermal Systems. Geothermics 2016, 61, 75–85. [Google Scholar] [CrossRef] [Green Version]
- Fu, P.; Hao, Y.; Walsh, S.D.; Carrigan, C.R. Thermal drawdown-induced flow channeling in fractured geothermal reservoirs. Rock Mech. Rock Eng. 2016, 49, 1001–1024. [Google Scholar] [CrossRef]
- Sanyal, S.K.; Butler, S.J.; Swenson, D.; Hardeman, B. Review of the state-of-the-art of numerical simulation of enhanced geothermal systems. In Proceedings of the World Geothermal Congress 2000, Tohoku, Kyushu, Japan, 28 May–10 June 2000; pp. 181–186. [Google Scholar]
- White, M.; Fu, P.; McClure, M.; Danko, G.; Elsworth, D.; Sonnenthal, E.; Kelkar, S.; Podgorney, R. A suite of benchmark and challenge problems for enhanced geothermal systems. Geomech. Geophys. Geo-Energy Geo-Resour. 2018, 4, 79–117. [Google Scholar] [CrossRef]
- Shao, S.; Ranjith, P.G.; Wasantha, P.L.P.; Chen, B.K. Experimental and numerical studies on the mechanical behaviour of Australian Strathbogie granite at high temperatures: An application to geothermal energy. Geothermics 2015, 54, 96–108. [Google Scholar] [CrossRef]
- Wanniarachchi, W.; Ranjith, P.; Perera, M.; Rathnaweera, T.; Zhang, C.; Zhang, D. An integrated approach to simulate fracture permeability and flow characteristics using regenerated rock fracture from 3-D scanning: A numerical study. J. Nat. Gas Sci. Eng. 2018, 53, 249–262. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Y.; Teng, Y.; Li, P.; Peng, S. Experiment study on the evolution of permeability and heat recovery efficiency in fractured granite with proppants. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 3. [Google Scholar] [CrossRef]
- COMSOL Multiphysics, v. 5.2.; COMSOL AB: Stockholm, Sweden, 2015.
- Phillips, G.; Clemens, J. Strathbogie batholith: Field-based subdivision of a large granitic intrusion in central Victoria, Australia. Appl. Earth Sci. 2013, 122, 36–55. [Google Scholar] [CrossRef]
- Kumari, W.G.P.; Ranjith, P.G.; Perera, M.S.A.; Chen, B.K.; Abdulagatov, I.M. Temperature-dependent mechanical behaviour of Australian Strathbogie granite with different cooling treatments. Eng. Geol. 2017, 229, 31–44. [Google Scholar] [CrossRef]
- Kumari, W.; Ranjith, P.; Perera, M.; Shao, S.; Chen, B.; Lashin, A.; Al Arifi, N.; Rathnaweera, T. Mechanical behaviour of Australian Strathbogie granite under in-situ stress and temperature conditions: An application to geothermal energy extraction. Geothermics 2017, 65, 44–59. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon: Exposition et Application. 1856. Available online: https://gallica.bnf.fr/ark:/12148/bpt6k624312.r=Les%20fontaines%20publiques%20de%20la%20ville%20de%20Dijon%20Exposition%20et%20application?rk=21459;2 (accessed on 7 June 2022).
- Witherspoon, P.A.; Wang, J.S.; Iwai, K.; Gale, J.E. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef] [Green Version]
- Rutqvist, J.; Wu, Y.-S.; Tsang, C.-F.; Bodvarsson, G. A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, and deformation in fractured porous rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 429–442. [Google Scholar] [CrossRef]
- Summers, R.; Winkler, K.; Byerlee, J. Permeability changes during the flow of water through Westerly Granite at temperatures of 100–400 C. J. Geophys. Res. Solid Earth 1978, 83, 339–344. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST reference fluid thermodynamic and transport properties–REFPROP. NIST Stand. Ref. Database 2002, 23, v7. [Google Scholar]
- O’Sullivan, M.J.; Pruess, K.; Lippmann, M.J. State of the art of geothermal reservoir simulation. Geothermics 2001, 30, 395–429. [Google Scholar] [CrossRef]
- Judy, J.; Maynes, D.; Webb, B. Characterization of frictional pressure drop for liquid flows through microchannels. Int. J. Heat Mass Transf. 2002, 45, 3477–3489. [Google Scholar] [CrossRef]
- Homand-Etienne, F.; Houpert, R. Thermally induced microcracking in granites: Characterization and analysis. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 125–134. [Google Scholar] [CrossRef]
- Johnson, B.; Gangi, A.; Handin, J. Thermal cracking of rock subjected to slow, uniform temperature changes. In Proceedings of the 19th US Symposium on Rock Mechanics (USRMS), Reno, NV, USA, 1–3 May 1978. [Google Scholar]
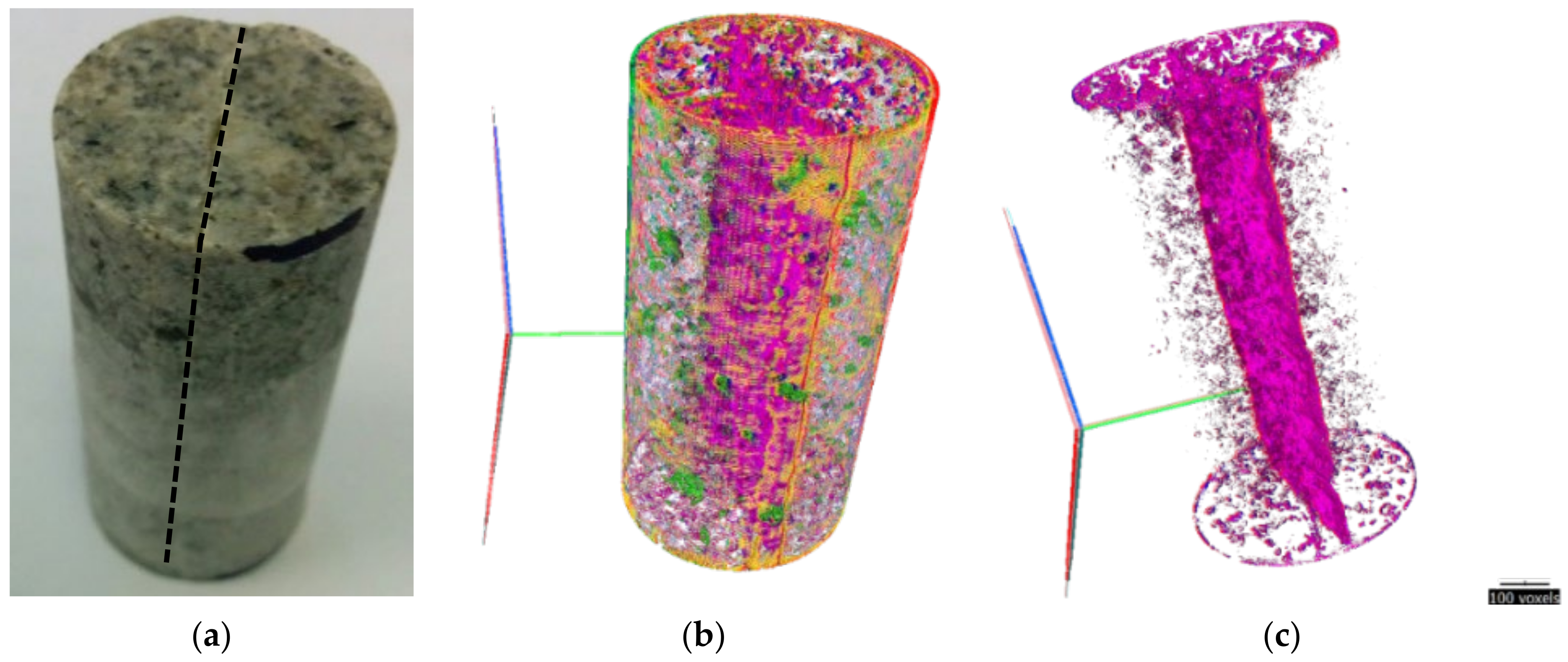

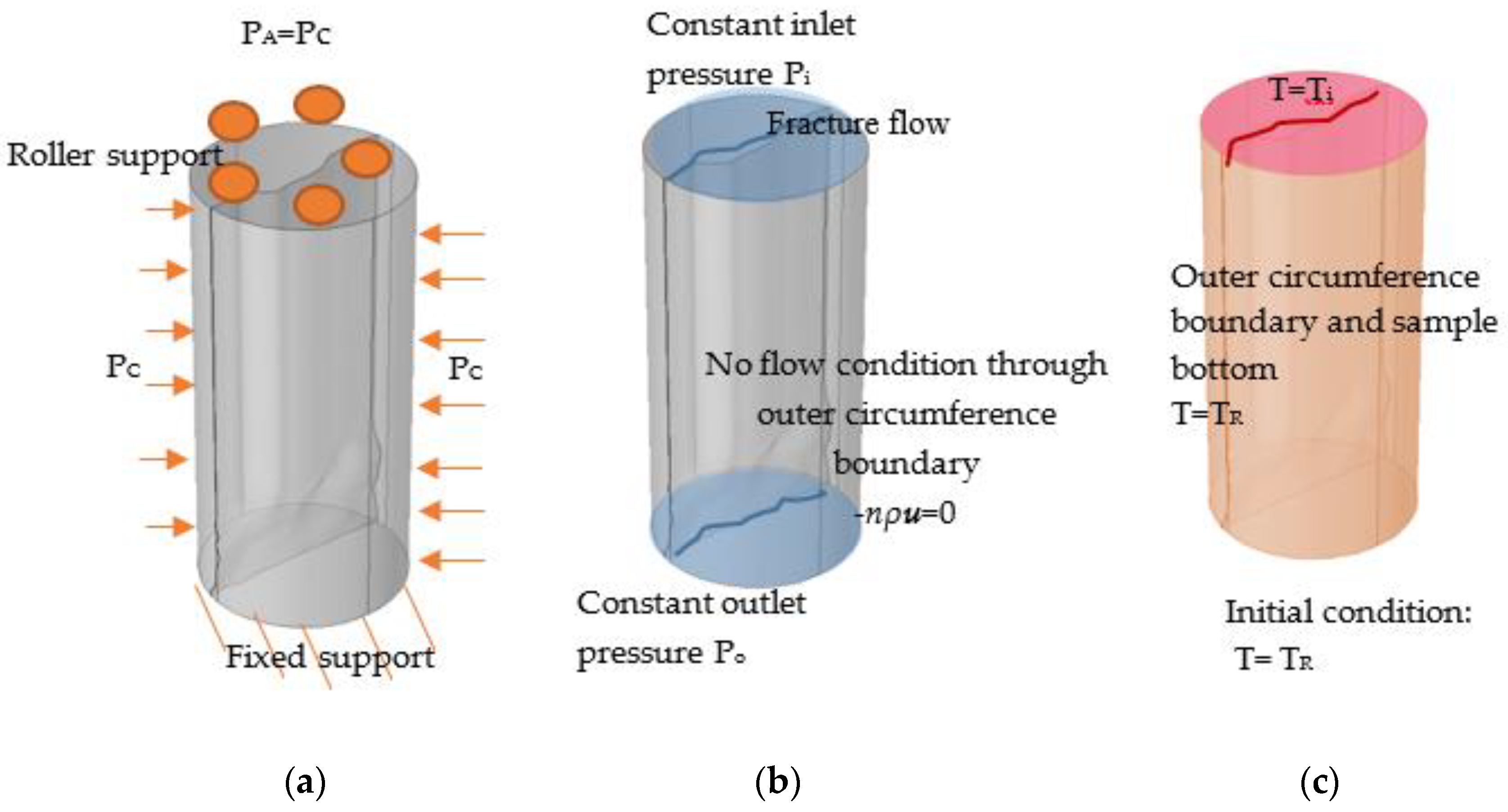
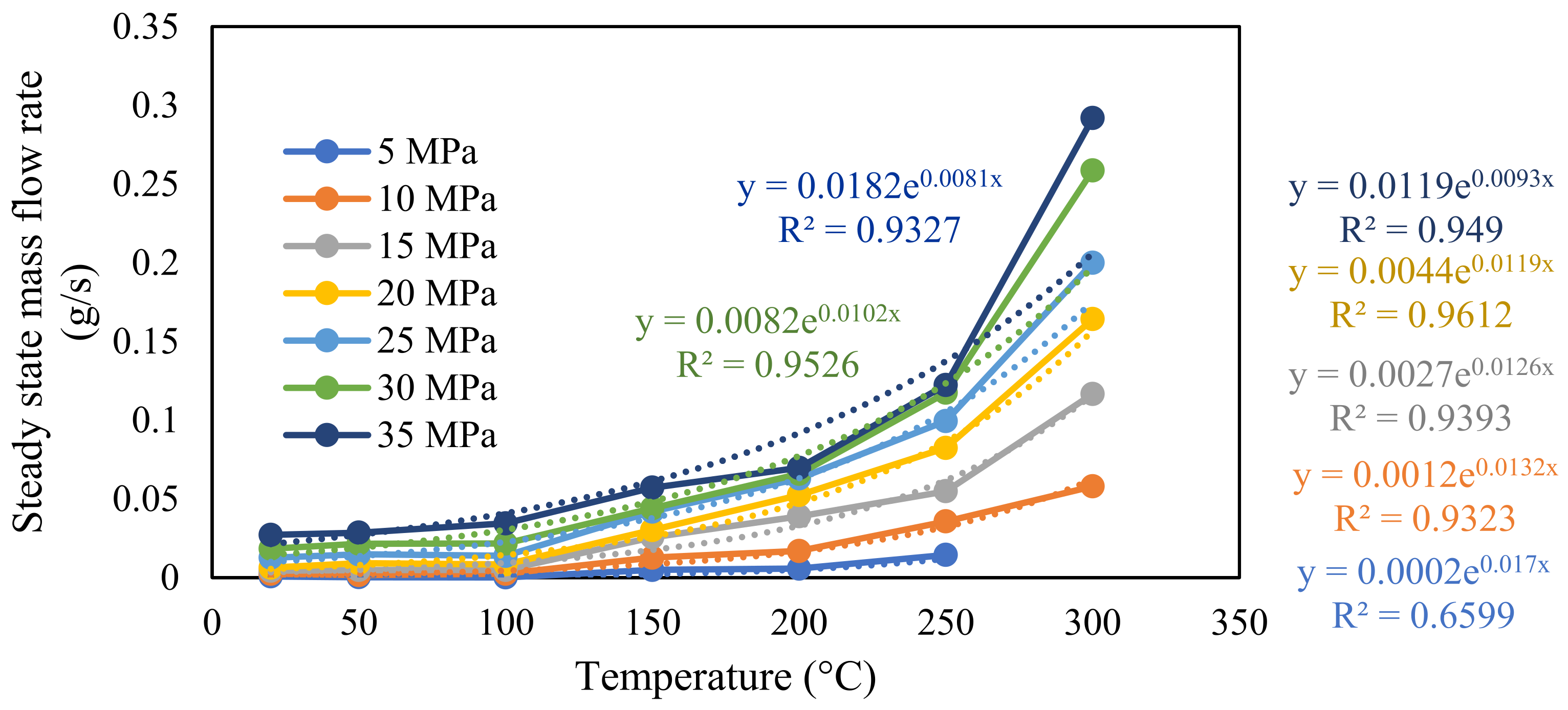
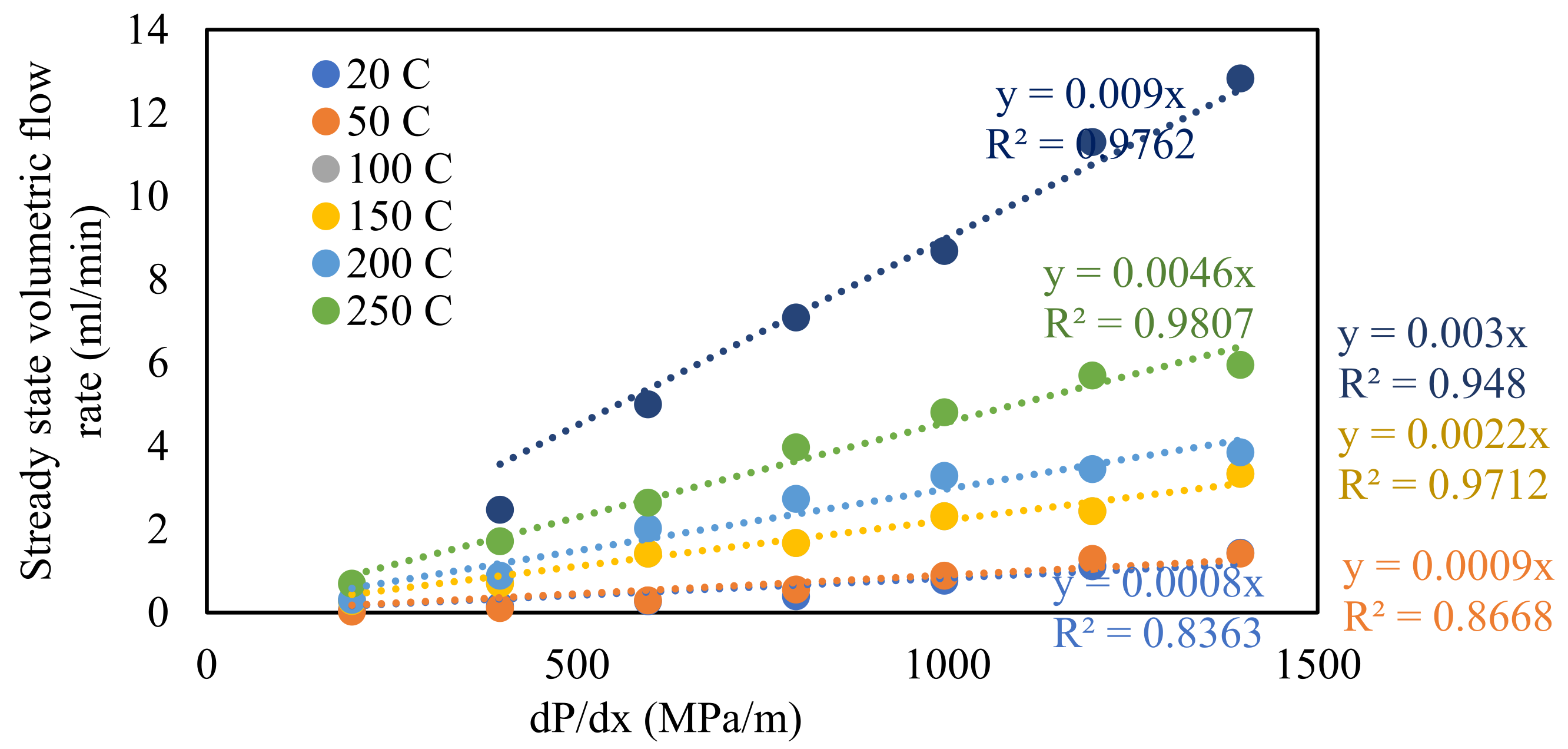


| Mineral | % Mass |
|---|---|
| Alpha quartz | 52 |
| K-feldspar | 23 |
| Sodic and intermediate plagioclase | 16 |
| Biotite—phlogopite | 4 |
| Clinochlore | 1 |
| Muscovite—sericite | 1 |
| Dolomite—ankerite | 1 |
| Talc, gypsum and clay minerals | 2 |
| Model Parameter | Value |
|---|---|
| Geometry | |
| Sample diameter (D) | 22.5 mm |
| Sample height (H) | 45 mm |
| Fracture | Parametric sweep with the corresponding coordinates obtained from CT images |
| Material properties of granite | |
| Density (ρ) | 2750 kg/m3 |
| Young’s modulus (E) | E(T) = E273(2 × 10−16 T6 − 9 × 10−13 T5 + 1 × 10−9 T4 − 1 × 10−6 T3 + 5 × 10−4 T2 − 0.1137 T + 11.189) GPa for 293 K–1073 K where E273 = 17.13 GPa |
| Poisson’s ratio (ν) | ν(T) = ν273(−4 × 10−16 T6 + 1 × 10−12 T5 − 2 × 10−9 T4 + 2 × 10−6 T3 − 6 × 10−4 T2 + 0.1305 T − 9.8608) for 293 K–1073 K where ν273 = 0.24 |
| Porosity | 0.01 |
| Matrix permeability | 5 × 10−20 m2 |
| Thermal conductivity (K) | 20 W/(m⋅K) |
| Heat capacity at constant pressure (Cp) | 300 J/(kg⋅K) |
| Coefficient of thermal expansion (α) | 5 × 10−6 K−1 |
| Material properties of water | |
| Density (ρw) | 838.466 + 1.401 T − 0.003 T2 + 3.718 × 10−7 T3 kg/m3 for 273 K–583 K |
| Dynamic viscosity (μw) | 1.380 − 0.021 T + 1.360 × 10−4 T2 − 4.645 × 10−7 T3 + 8.904 × 10−10 T4 − 9.079 × 1013 T5 + 3.846 × 10−16 T6 Pas for 273 K–413 K 0.004 − 2.10746715 × 10−5 T + 3.85772275 × 10−8 T2 − 2.39730284 × 10−11 T3 Pas for 413 K–583 K |
| Heat capacity at constant pressure (Cp) | 12010.15 − 80.407 T + 0.3108 T2 − 5.382 × 104 T3 + 3.625 × 10−7 T4 J/kgK for 413 K–583 K |
| Thermal conductivity (K) | −0.869 + 0.0089 T − 1.584 × 10−5 T2 + 7.9754 × 10−9 T3 W/mK for 413 K–583 K |
| Compressibility | 4.5 × 10−11 1/Pa |
| Boundary conditions (parametric sweep) | |
| Confining pressure (Pc) | 10–150 MPa |
| Vertical stress (PA) | PA = Pc |
| Injection pressure (Pi) | 5–140 MPa |
| Outlet pressure (Po) | 0.1 MPa |
| Rock temperature (TR) | 20–350 °C |
| Fluid temperature (Ti) | 20–350 °C |
| Calibration parameters | |
| Fracture permeability under the reference stress (1 MPa) (k0f) | 4 × 10−14 m2 |
| Constant for the non-linear stiffness of the fracture (ϑ) | 0.015 |
| Fracture aperture | 4 × 10−11 T2 − 3.1 × 10−8 T + 7.8 × 10−6 for 273 K–413 K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumari, W.G.P.; Ranjith, P.G. Experimental and Numerical Investigation of the Flow Behaviour of Fractured Granite under Extreme Temperature and Pressure Conditions. Sustainability 2022, 14, 8587. https://doi.org/10.3390/su14148587
Kumari WGP, Ranjith PG. Experimental and Numerical Investigation of the Flow Behaviour of Fractured Granite under Extreme Temperature and Pressure Conditions. Sustainability. 2022; 14(14):8587. https://doi.org/10.3390/su14148587
Chicago/Turabian StyleKumari, Wanniarachchige Gnamani Pabasara, and Pathegama Gamage Ranjith. 2022. "Experimental and Numerical Investigation of the Flow Behaviour of Fractured Granite under Extreme Temperature and Pressure Conditions" Sustainability 14, no. 14: 8587. https://doi.org/10.3390/su14148587
APA StyleKumari, W. G. P., & Ranjith, P. G. (2022). Experimental and Numerical Investigation of the Flow Behaviour of Fractured Granite under Extreme Temperature and Pressure Conditions. Sustainability, 14(14), 8587. https://doi.org/10.3390/su14148587







