Impacts of Fracture Roughness and Near-Wellbore Tortuosity on Proppant Transport within Hydraulic Fractures
Abstract
:1. Introduction
2. Model Buildup
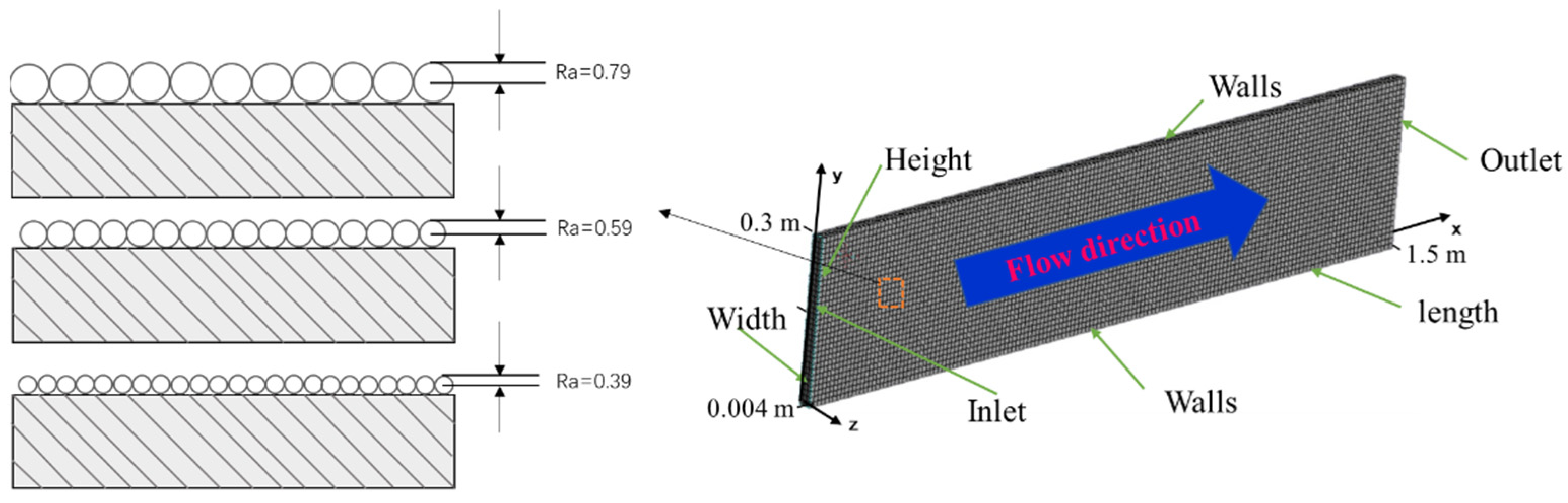
2.1. Experiment Setup
2.2. Simulation Setup
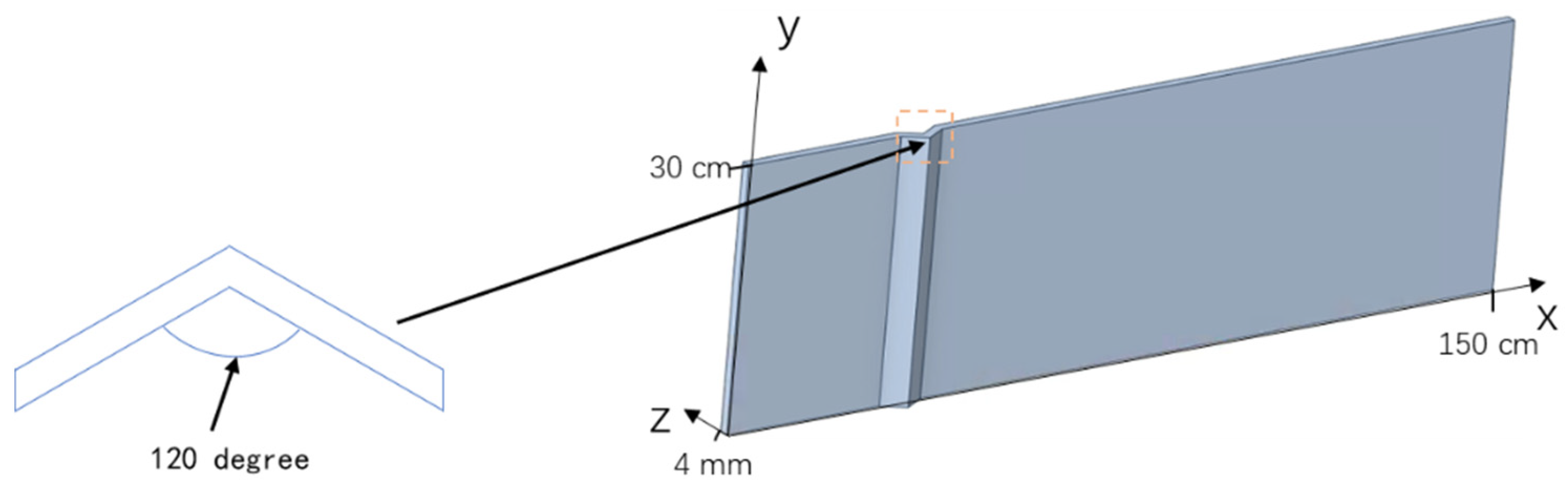
2.3. Rough and Tortuous Model Development
3. Results and Discussion
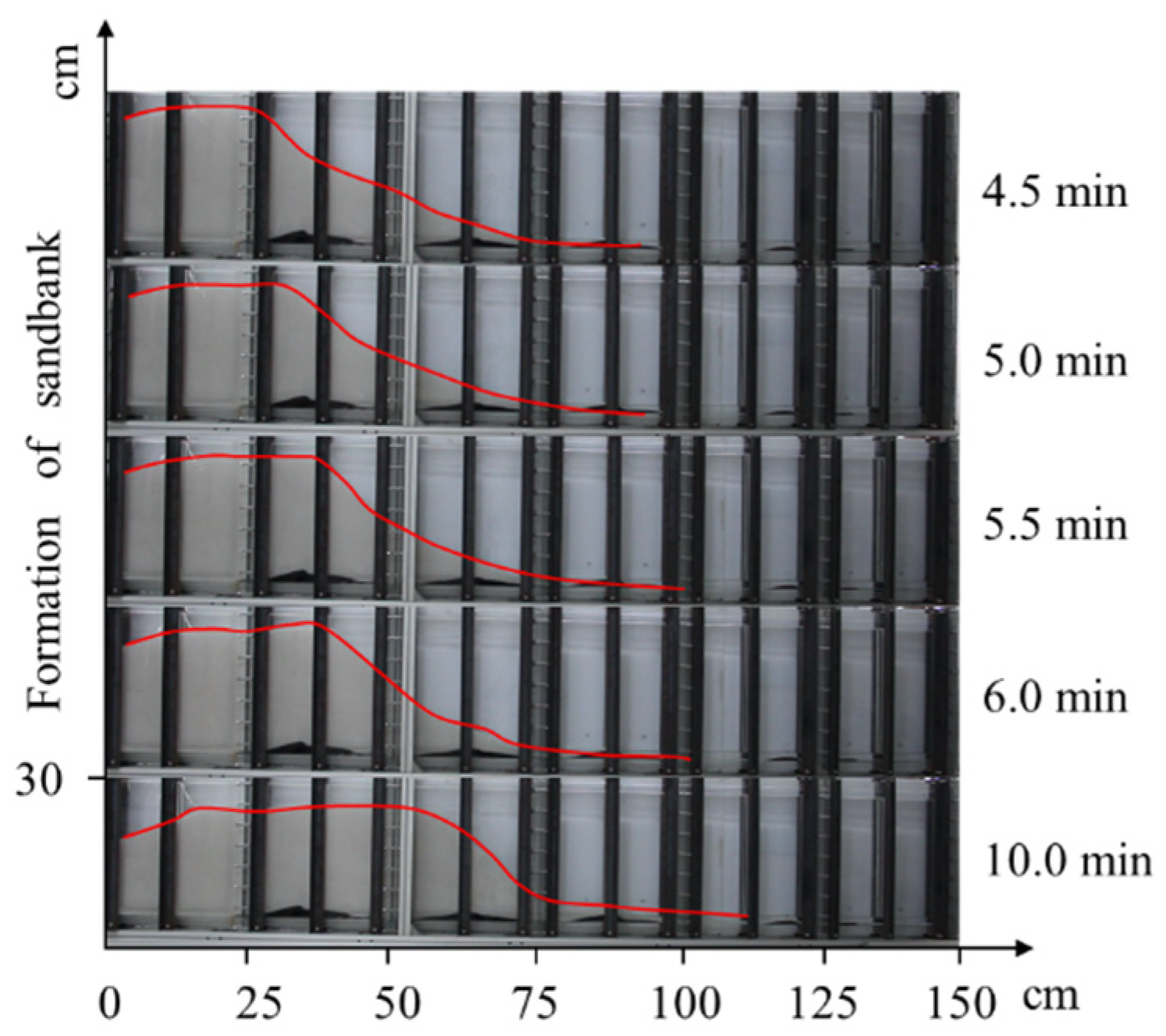
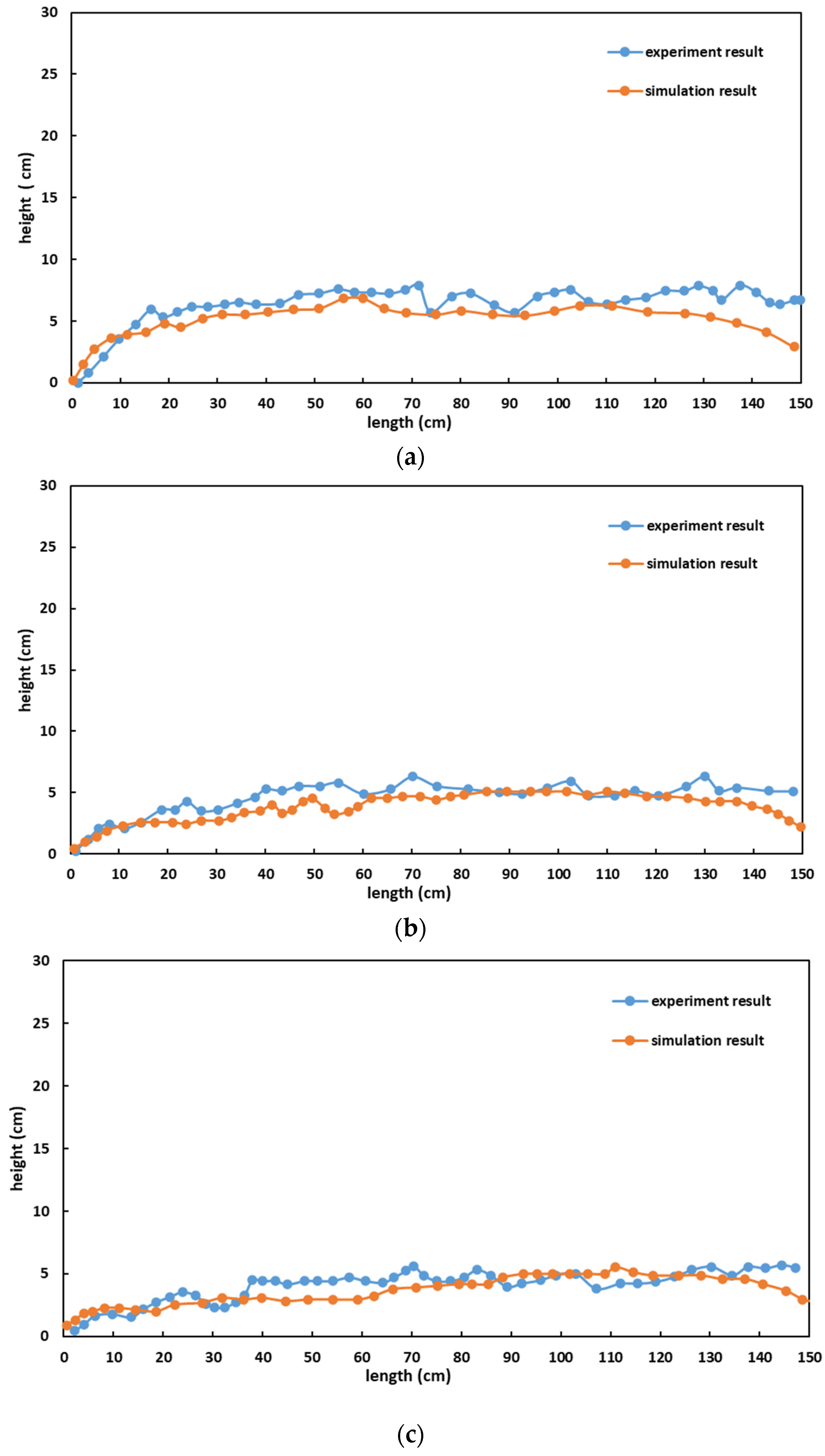
3.1. Validation of Numerical Model
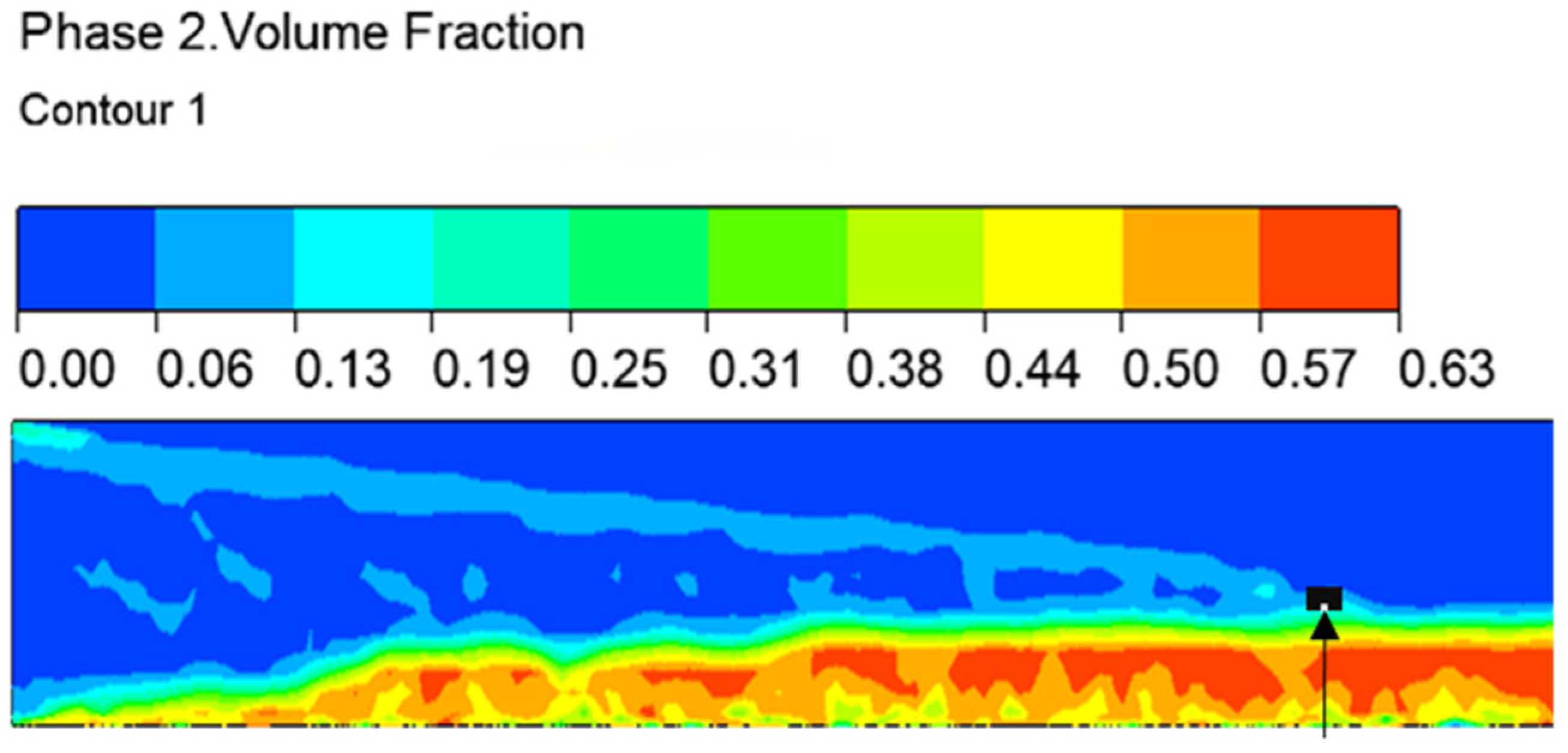
3.2. Sand Transport in Rough Fractures
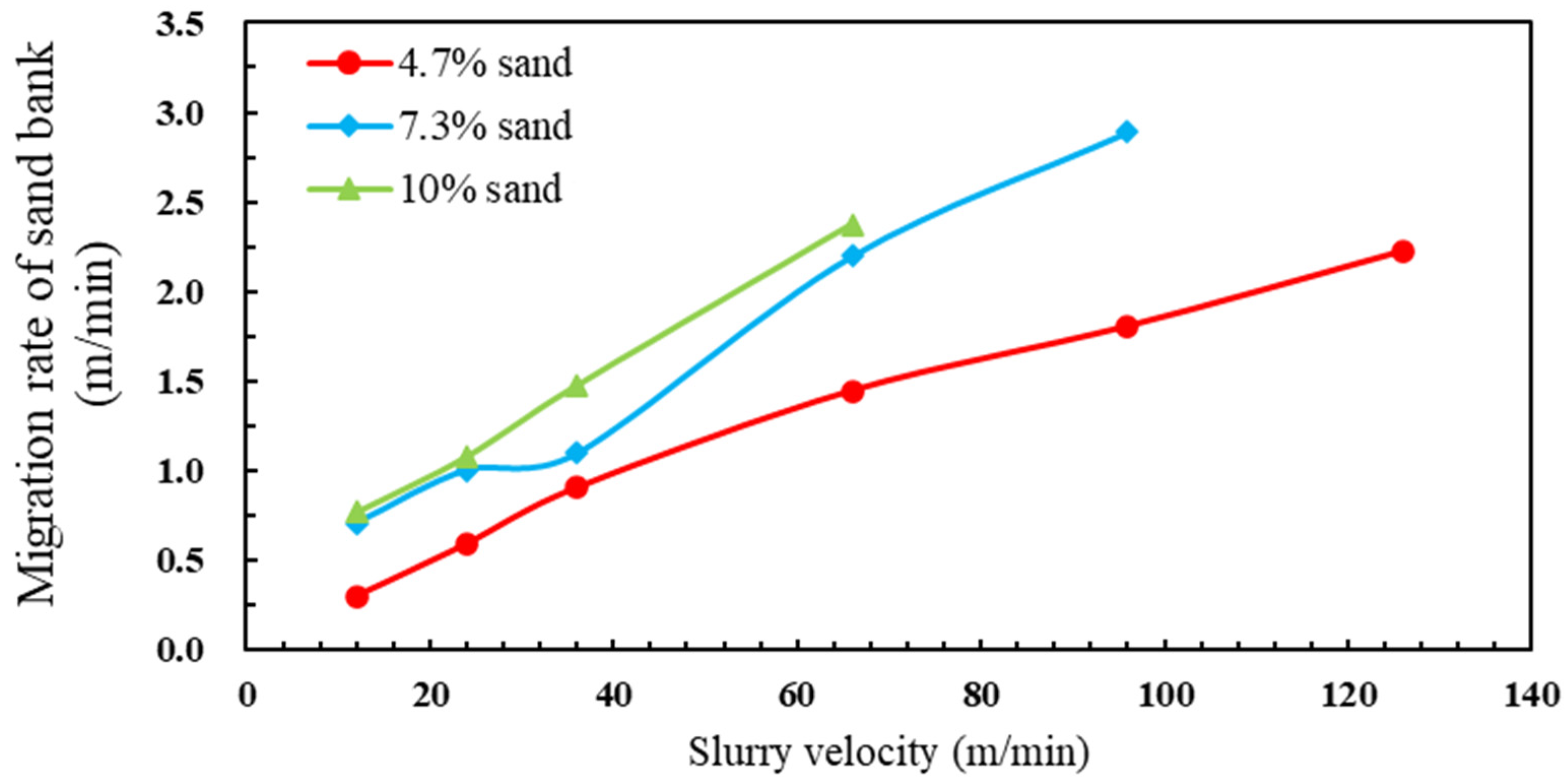
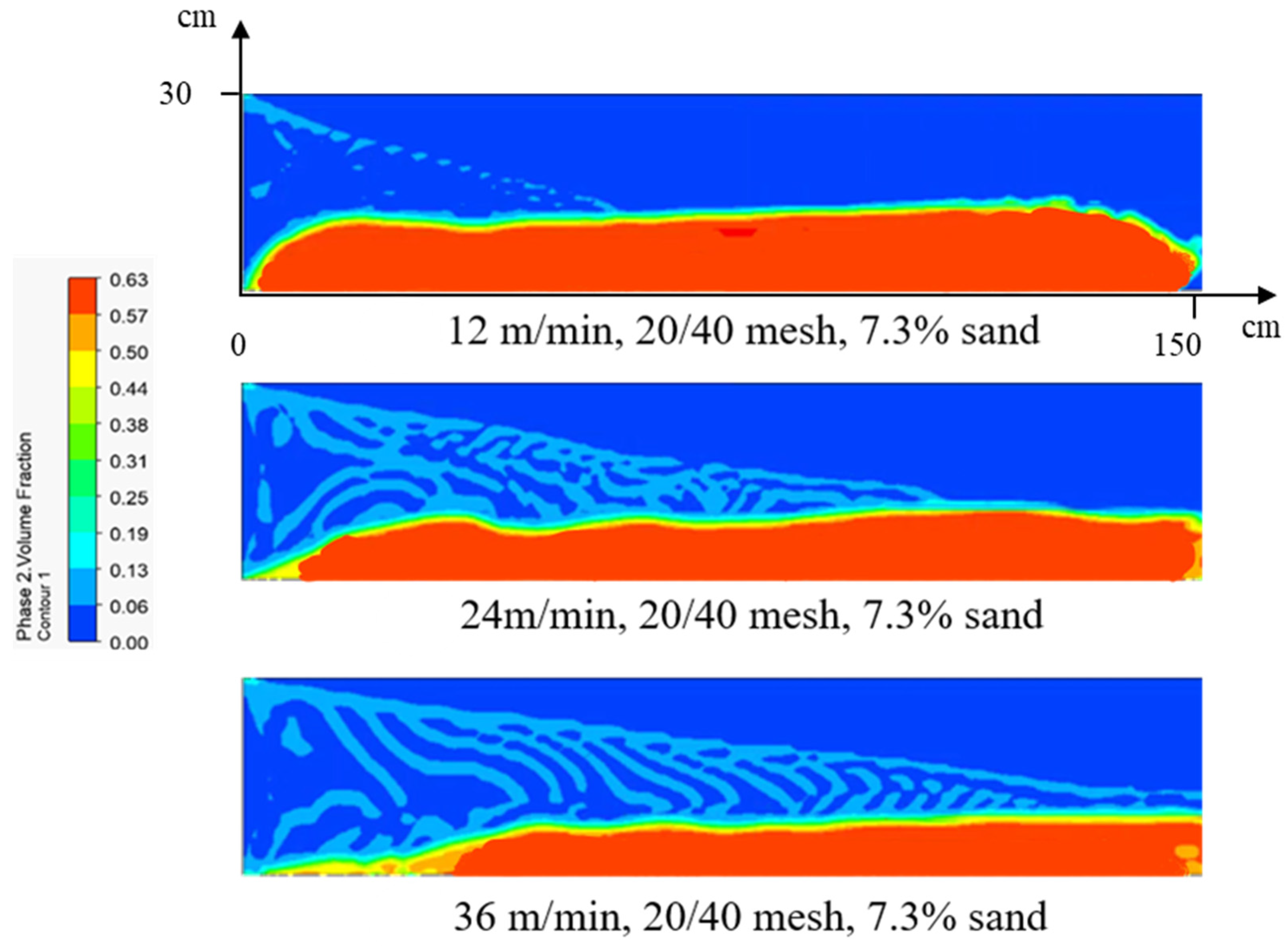
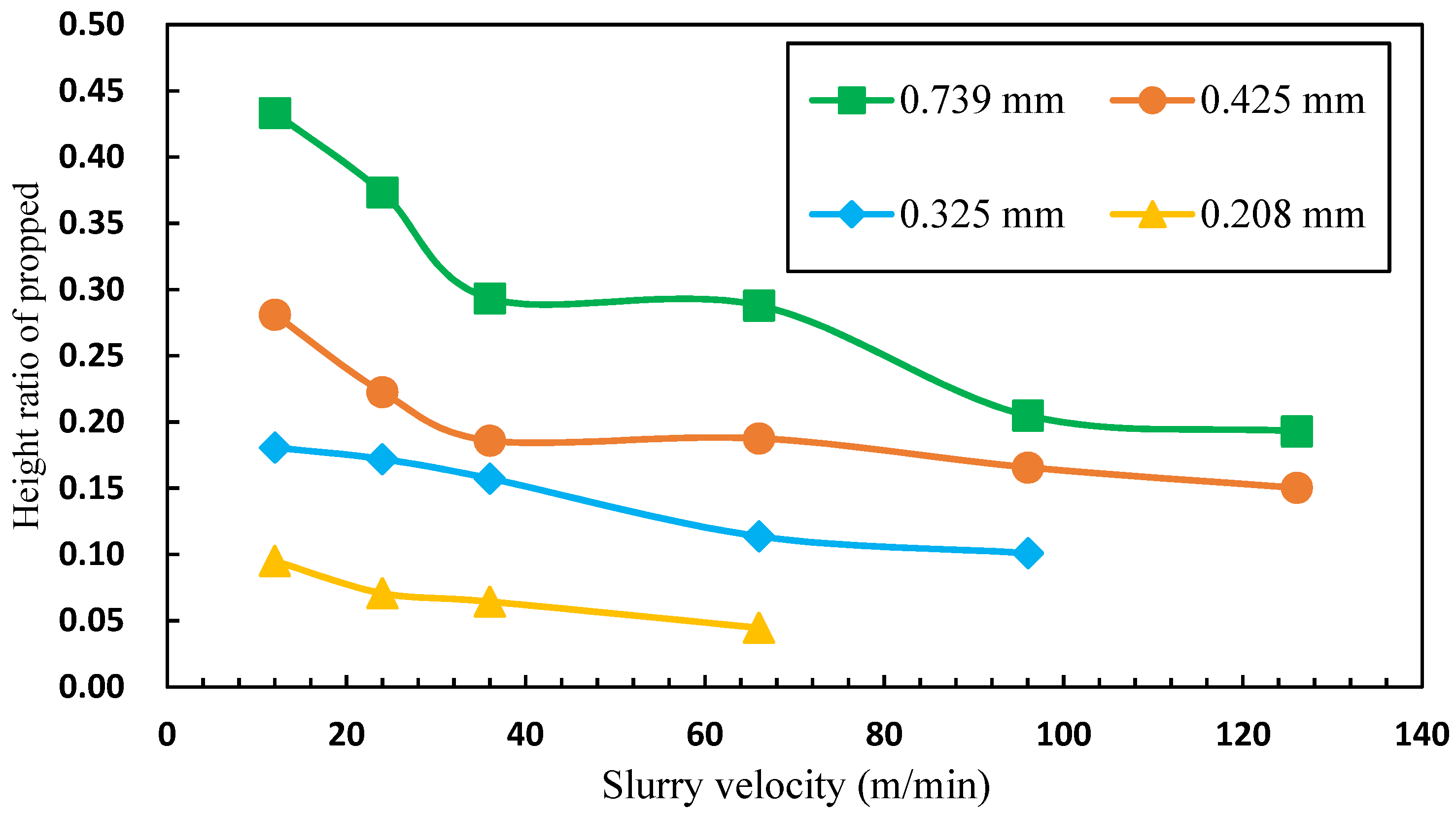
3.2.1. Effect of Slurry Velocity
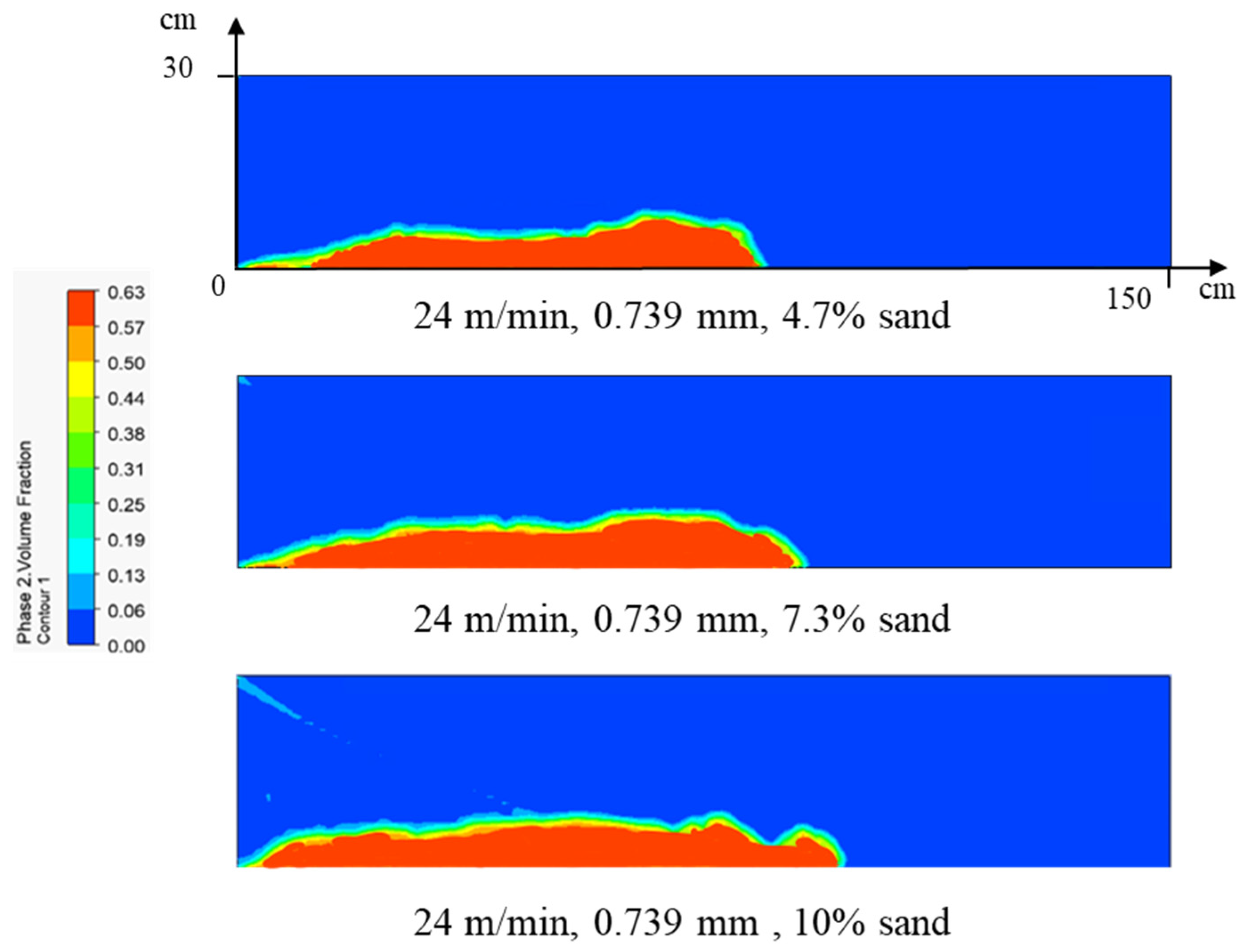
3.2.2. Effect of Sand Volume Fraction
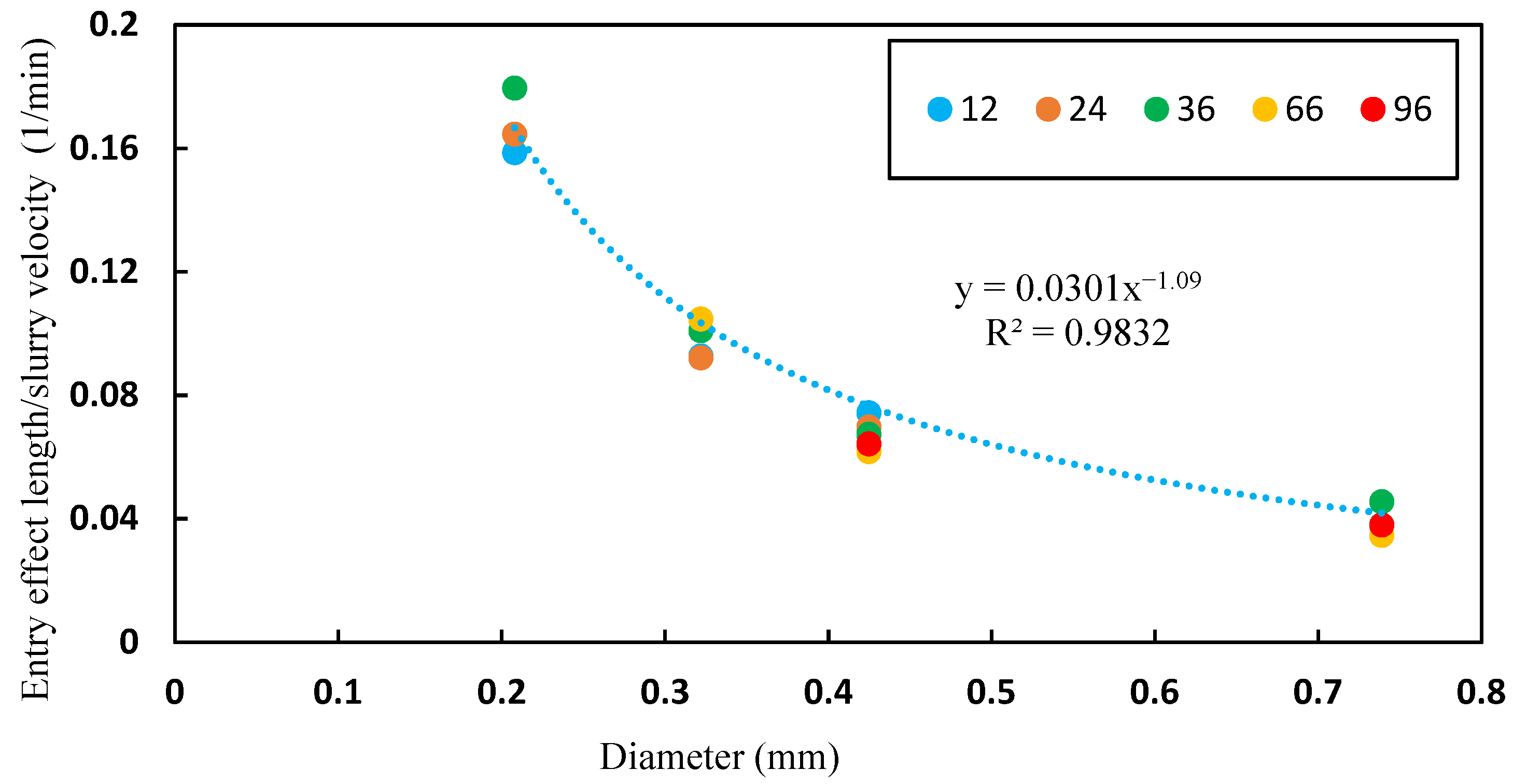
3.2.3. Effect of Sand Diameter
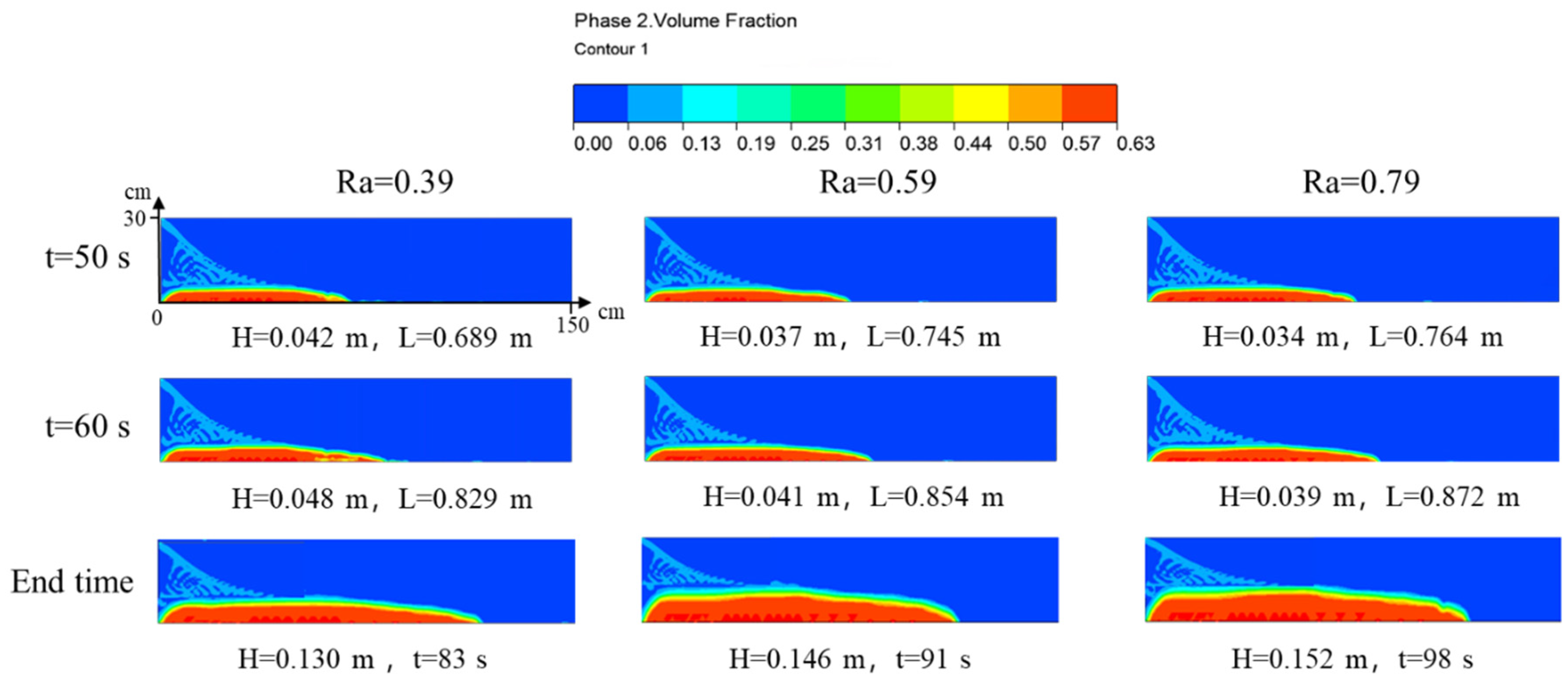
3.2.4. Effect of Surface Roughness
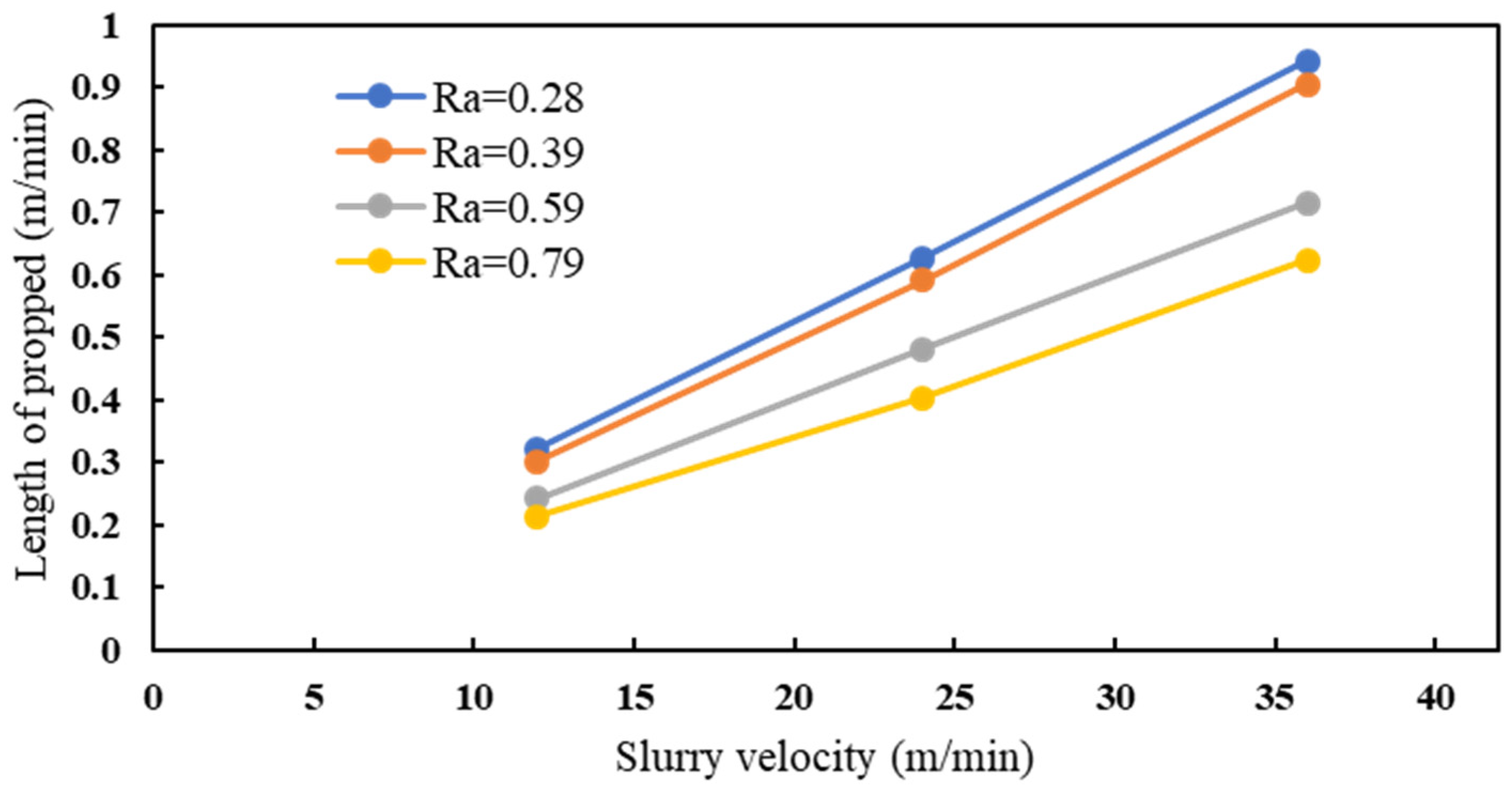
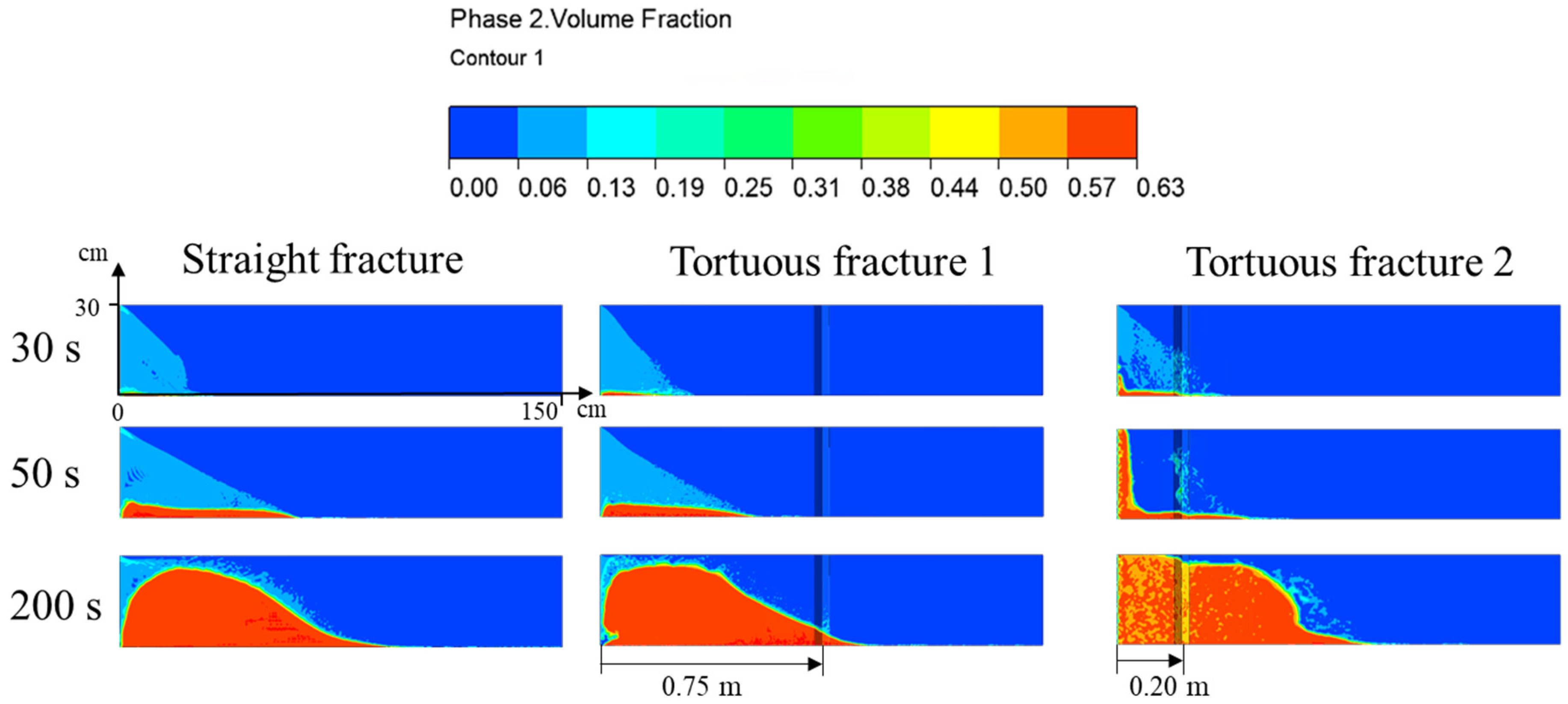
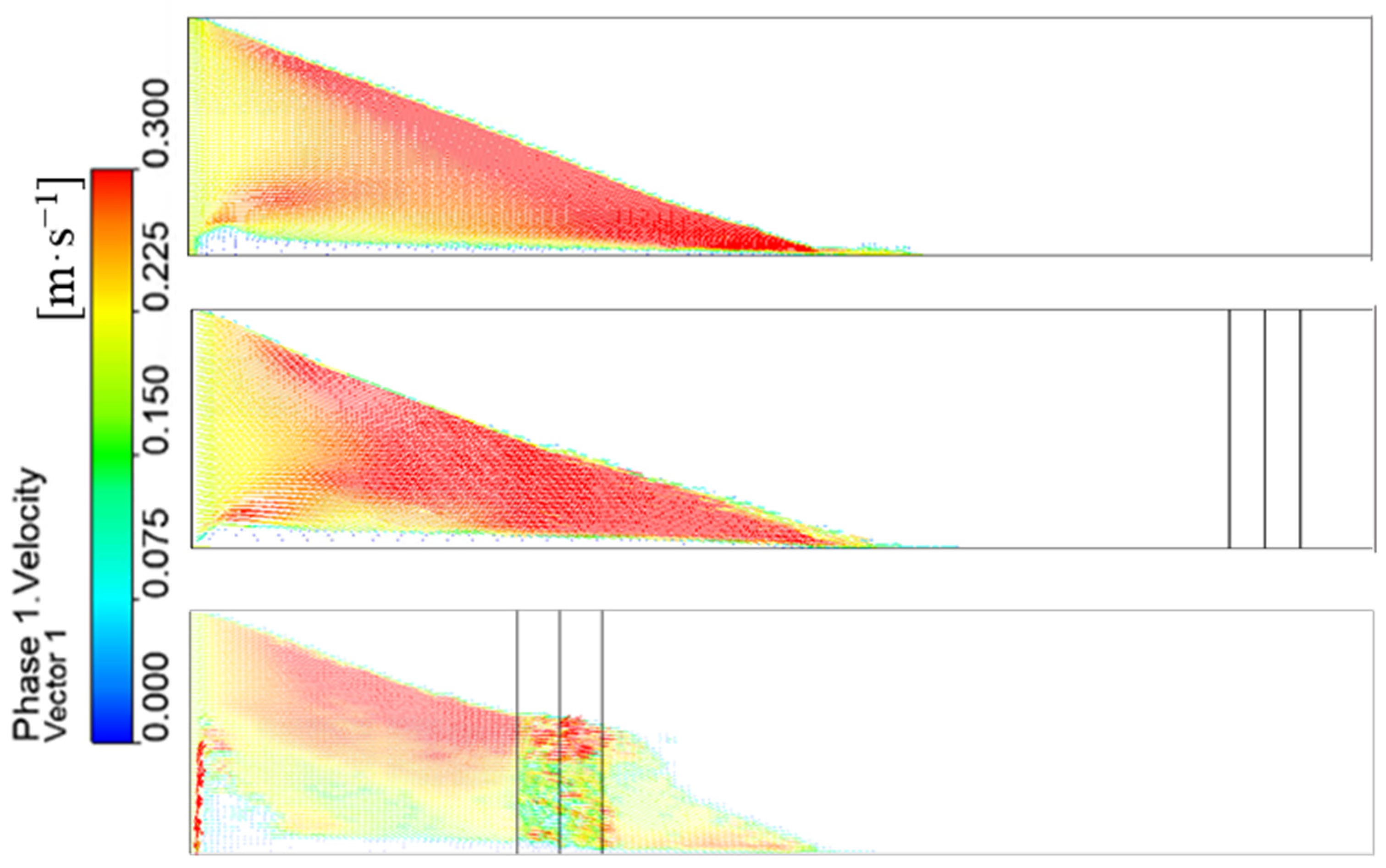
3.2.5. Effect of the Tortuous Fractures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| the stress tensors of the fluid | |
| the stress tensors of the solid | |
| the acceleration of gravity | |
| velocity of fluid | |
| velocity of solid | |
| granular temperature | |
| volume fraction of fluid | |
| volume fraction of solid | |
| density of the fluid | |
| density of the solid | |
| Cd | the drag coefficient |
| d | hydraulic diameter |
| ds | the diameter of the particle |
| g0 | radial distribution function |
| P | pressure of all the phases |
| Re | Reynolds number |
| Res | Reynolds number of solid |
| v | velocity |
| β | the Gidaspow drag force coefficient |
| μ | viscosity |
| μs,col | collisional viscosity |
| μs,fri | fractional viscosity |
| μs,kin | kinetic viscosity |
| μs | shear viscosity of solid |
| ρ | density |
References
- Hu, X.; Wu, K.; Song, X.; Yu, W.; Zuo, L.; Li, G.; Shen, Z. Development of a New Mathematical Model to Quantitatively Evaluate Equilibrium Height of Proppant Bed in Hydraulic Fractures for Slickwater Treatment. SPE J. 2018, 23, 2158–2174. [Google Scholar] [CrossRef]
- Yao, S.; Chang, C.; Hai, K.; Huang, H.; Li, H. A review of experimental studies on the proppant settling in hydraulic fractures. J. Pet. Sci. Eng. 2021, 208, 109211. [Google Scholar] [CrossRef]
- Kern, L.; Perkins, T.; Wyant, R. The Mechanics of Sand Movement in Fracturing. J. Pet. Technol. 1959, 11, 55–57. [Google Scholar] [CrossRef]
- Shrivastava, K.; Sharma, M.M. Proppant transport in complex fracture networks. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 23–25 January 2018. [Google Scholar] [CrossRef]
- Harrington, L.J.; Hannah, R.R.; Williams, D. Dynamic Experiments on Proppant Settling in Crosslinked Fracturing Fluids. In Proceedings of the SPE Annual Technical Conference and Exhibition, Las Vegas, NV, USA, 23–26 September 1979. [Google Scholar] [CrossRef]
- McMechan, D.E.; Shah, S.N. Static Proppant-Settling Characteristics of Non-Newtonian Fracturing Fluids in a Large-Scale Test Model. SPE Prod. Eng. 1991, 6, 305–312. [Google Scholar] [CrossRef]
- Gadde, P.B.; Liu, Y.; Norman, J.; Bonnecaze, R.; Sharma, M.M. Modeling Proppant Settling in Water-Fracs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 23–26 September 2004. [Google Scholar] [CrossRef]
- Maity, D.; Ciezobka, J. Digital Fracture Characterization at Hydraulic Fracturing Test Site HFTS-Midland: Fracture Clustering, Stress Effects and Lithologic Controls. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, Virtual, 3–6 May 2021. [Google Scholar] [CrossRef]
- Maity, D.; Ciezobka, J. An Interpretation of Proppant Transport within the Stimulated Rock Volume at the Hydraulic-Fracturing Test Site in the Permian Basin. SPE Reserv. Eval. Eng. 2019, 22, 477–491. [Google Scholar] [CrossRef]
- Patankar, N.; Joseph, D.; Wang, J.; Barree, R.; Conway, M.; Asadi, M. Power law correlations for sediment transport in pressure driven channel flows. Int. J. Multiph. Flow 2002, 28, 1269–1292. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Joseph, D.; Patankar, N.; Conway, M.; Barree, R. Bi-power law correlations for sediment transport in pressure driven channel flows. Int. J. Multiph. Flow 2003, 29, 475–494. [Google Scholar] [CrossRef]
- Dontsov, E.V.; Peirce, A.P. Slurry flow, gravitational settling and a proppant transport model for hydraulic fractures. J. Fluid Mech. 2014, 760, 567–590. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Ding, Y.; Yang, L.; Liu, Z.; Gao, R.; Wang, Z.; Mo, S. Numerical analysis of proppants transport in tortuous fractures of shale gas reservoirs after shear deformation. J. Nat. Gas Sci. Eng. 2020, 78, 103285. [Google Scholar] [CrossRef]
- Chun, T.; Li, Y.; Wu, K. Comprehensive experimental study of proppant transport in an inclined fracture. J. Pet. Sci. Eng. 2020, 184, 106523. [Google Scholar] [CrossRef]
- Chun, T.; Zhu, D.; Zhang, Z.; Mao, S.; Wu, K. Experimental Study of Proppant Transport in Complex Fractures with Horizontal Bedding Planes for Slickwater Fracturing. SPE Prod. Oper. 2021, 36, 83–96. [Google Scholar] [CrossRef]
- Fernández, M.E.; Pugnaloni, L.A.; Sánchez, M. Proppant transport in a planar fracture: Particle image velocimetry. J. Nat. Gas Sci. Eng. 2021, 89, 103860. [Google Scholar] [CrossRef]
- Zhang, J.; Dunn-Norman, S. Computational Fluid Dynamics (CFD) Modeling of Proppant Transport in A Plug and Perf Completion with Different Perforation Phasing. In Proceedings of the Unconventional Resources Technology Conference, Society of Petroleum Engineers, San Antonio, TX, USA, 20–22 July 2015. [Google Scholar] [CrossRef]
- Huang, H.; Babadagli, T.; Li, H.A.; Develi, K.; Wei, G. Effect of injection parameters on proppant transport in rough vertical fractures: An experimental analysis on visual models. J. Pet. Sci. Eng. 2019, 180, 380–395. [Google Scholar] [CrossRef]
- Basiuk, L.; Roschzttardtz, F.I.; Fernández, M.E.; Pugnaloni, L.A.; Sánchez, M. Proppant transport in scaled experiments: Effect of drainage configuration and fracture wall roughness. J. Pet. Sci. Eng. 2022, 208, 109433. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. Rock Eng. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Babadagli, T.; Ren, X.; Develi, K. Effects of fractal surface roughness and lithology on single and multiphase flow in a single fracture: An experimental investigation. Int. J. Multiph. Flow 2015, 68, 40–58. [Google Scholar] [CrossRef]
- Suri, Y.; Islam, S.Z.; Hossain, M. Effect of fracture roughness on the hydrodynamics of proppant transport in hydraulic fractures. J. Nat. Gas Sci. Eng. 2020, 80, 103401. [Google Scholar] [CrossRef]
- Baldini, M.; Carlevaro, C.M.; Pugnaloni, L.A.; Sánchez, M. Numerical simulation of proppant transport in a planar fracture. A study of perforation placement and injection strategy. Int. J. Multiph. Flow 2018, 109, 207–218. [Google Scholar] [CrossRef]
- Han, Y.; Cundall, P.A. LBM–DEM modeling of fluid–solid interaction in porous media. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 1391–1407. [Google Scholar] [CrossRef]
- Gale, J.F.W.; Elliott, S.J.; Laubach, S.E. Hydraulic Fractures in Core from Stimulated Reservoirs: Core Fracture Description of HFTS Slant Core, Midland Basin, West Texas. In Proceedings of the 6th Unconventional Resources Technology Conference American Association of Petroleum Geologists, Houston, TX, USA, 23–25 July 2018. [Google Scholar]
- Liu, Y.; Gadde, P.B.; Sharma, M.M. Proppant Placement Using Reverse-Hybrid Fracs. SPE Prod. Oper. 2007, 22, 348–356. [Google Scholar] [CrossRef]
- Menter, F. Zonal Two Equation kw Turbulence Models For Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Tong, S.; Mohanty, K.K. Proppant transport study in fractures with intersections. Fuel 2016, 181, 463–477. [Google Scholar] [CrossRef]
- Gidaspow, D.; Bezburuah, R.; Ding, J. Hydrodynamics of circulating fluidized beds, kinetic theory approach. In Proceedings of the 7th Engineering Foundation Conference on Fluidization, Gold Coast, Australia, 3–8 May 1992; pp. 75–82. [Google Scholar]
- Ogawa, S.; Umemura, A.; Oshima, N. On the equations of fully fluidized granular materials. J. Appl. Math. Phys. 1980, 31, 483–493. [Google Scholar] [CrossRef]
- Schaeffer, D.G. Instability in the evolution equations describing incompressible granular flow. J. Differ. Equ. 1987, 66, 19–50. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.; Ahmadi, G. A thermodynamical formulation for dispersed multiphase turbulent flows. Int. J. Multiph. Flow. 1990, 16, 323–351. [Google Scholar] [CrossRef]








| Volumetric Flow Rate (m3/min) | Fracture Height (m) | Fracture Width (mm) | Flow Rate (m/min) | Particle Reynolds Number | Fluid Reynolds Number | |
|---|---|---|---|---|---|---|
| Field Scale | 5–10 | 10–60 | 2–4 | 3.5–167 | 30–5337 | 457–21,929 |
| Lab Scale | 0.01–0.25 | 0.3 | 4 | 8.3–208 | 75–6590 | 1096–27,412 |
| Parameters | Values |
|---|---|
| Slurry velocity, m/min | 12, 24, 36 |
| Sand diameter, mm | 0.208, 0.325, 0.425, 0.739 |
| Fracture width, mm | 4 |
| Fluid viscosity, Pa·s | 0.001 |
| Real sand density, kg/m3 | 2600 |
| Sand bulk density, kg/m3 | 1500 |
| Volume fraction of sand | 7.3% |
| Parameters | Values |
|---|---|
| slurry velocity, m/min | 12, 24, 36, 66, 96, 126 |
| sand diameter, mm | 0.208, 0.325, 0.425, 0.739 |
| fracture width, mm | 4 |
| sand volume fraction | 4.7%, 7.3%, 10% |
| Ra (fracture roughness) | 0.39, 0.59, 0.79 |
| Straight Facture | Tortuous Facture 1 | Tortuous Facture 2 | |
|---|---|---|---|
| length, m | 1.5 | 1.5 | 1.5 |
| width, m | 0.004 | 0.004 | 0.004 |
| height, m | 0.3 | 0.3 | 0.3 |
| tortuous angle, degree | 120 | 120 | |
| tortuous length, m | 0.06 | 0.06 | |
| tortuous position, m | 0.75 | 0.2 | |
| tortuous width, m | 0.00346 | 0.00346 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Bai, B.; Wang, B.; Wei, D.; Liang, T. Impacts of Fracture Roughness and Near-Wellbore Tortuosity on Proppant Transport within Hydraulic Fractures. Sustainability 2022, 14, 8589. https://doi.org/10.3390/su14148589
Wang D, Bai B, Wang B, Wei D, Liang T. Impacts of Fracture Roughness and Near-Wellbore Tortuosity on Proppant Transport within Hydraulic Fractures. Sustainability. 2022; 14(14):8589. https://doi.org/10.3390/su14148589
Chicago/Turabian StyleWang, Di, Bingyang Bai, Bin Wang, Dongya Wei, and Tianbo Liang. 2022. "Impacts of Fracture Roughness and Near-Wellbore Tortuosity on Proppant Transport within Hydraulic Fractures" Sustainability 14, no. 14: 8589. https://doi.org/10.3390/su14148589
APA StyleWang, D., Bai, B., Wang, B., Wei, D., & Liang, T. (2022). Impacts of Fracture Roughness and Near-Wellbore Tortuosity on Proppant Transport within Hydraulic Fractures. Sustainability, 14(14), 8589. https://doi.org/10.3390/su14148589





