Design Methodology and Analysis of Five-Level LLC Resonant Converter for Battery Chargers
Abstract
:1. Introduction
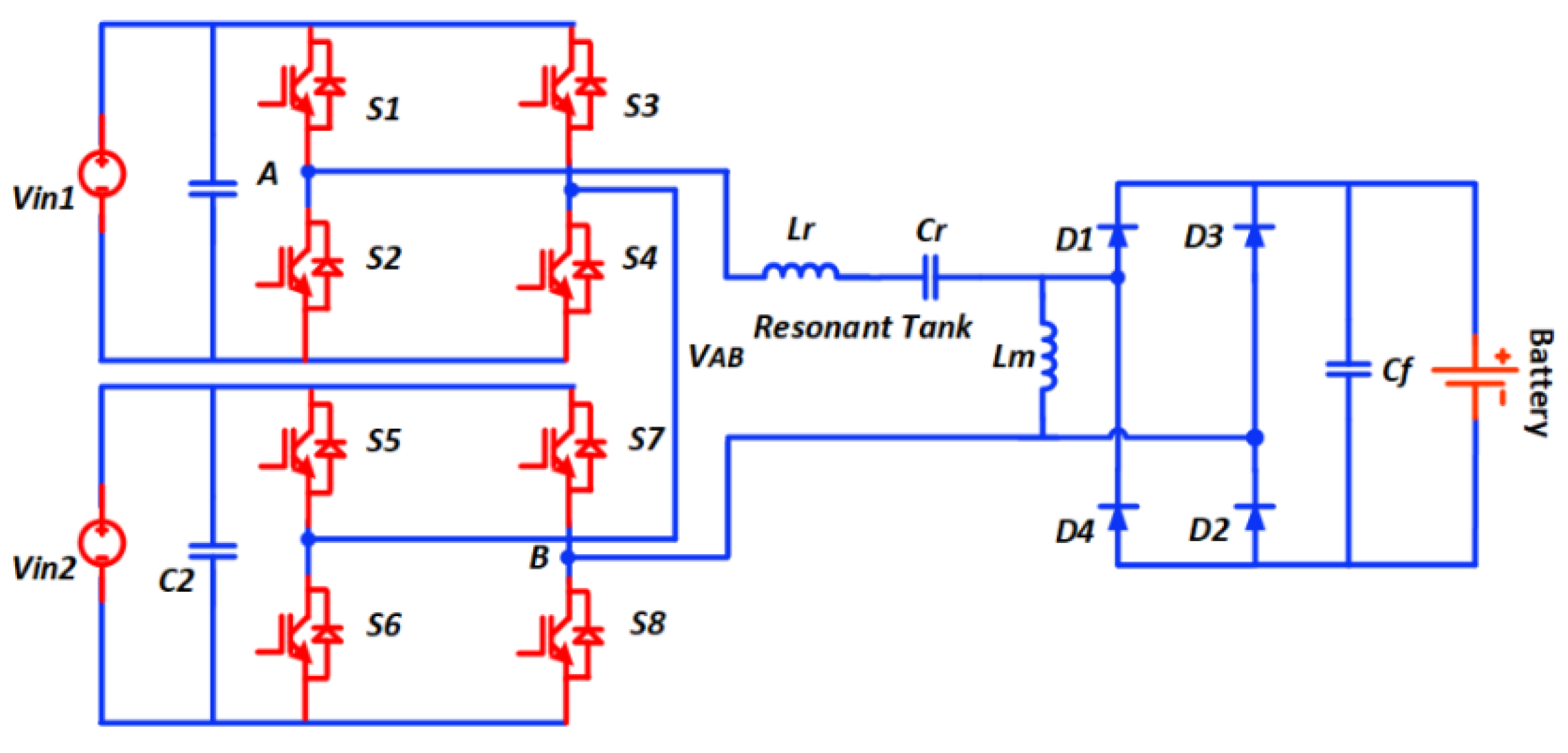
2. Proposed Topology
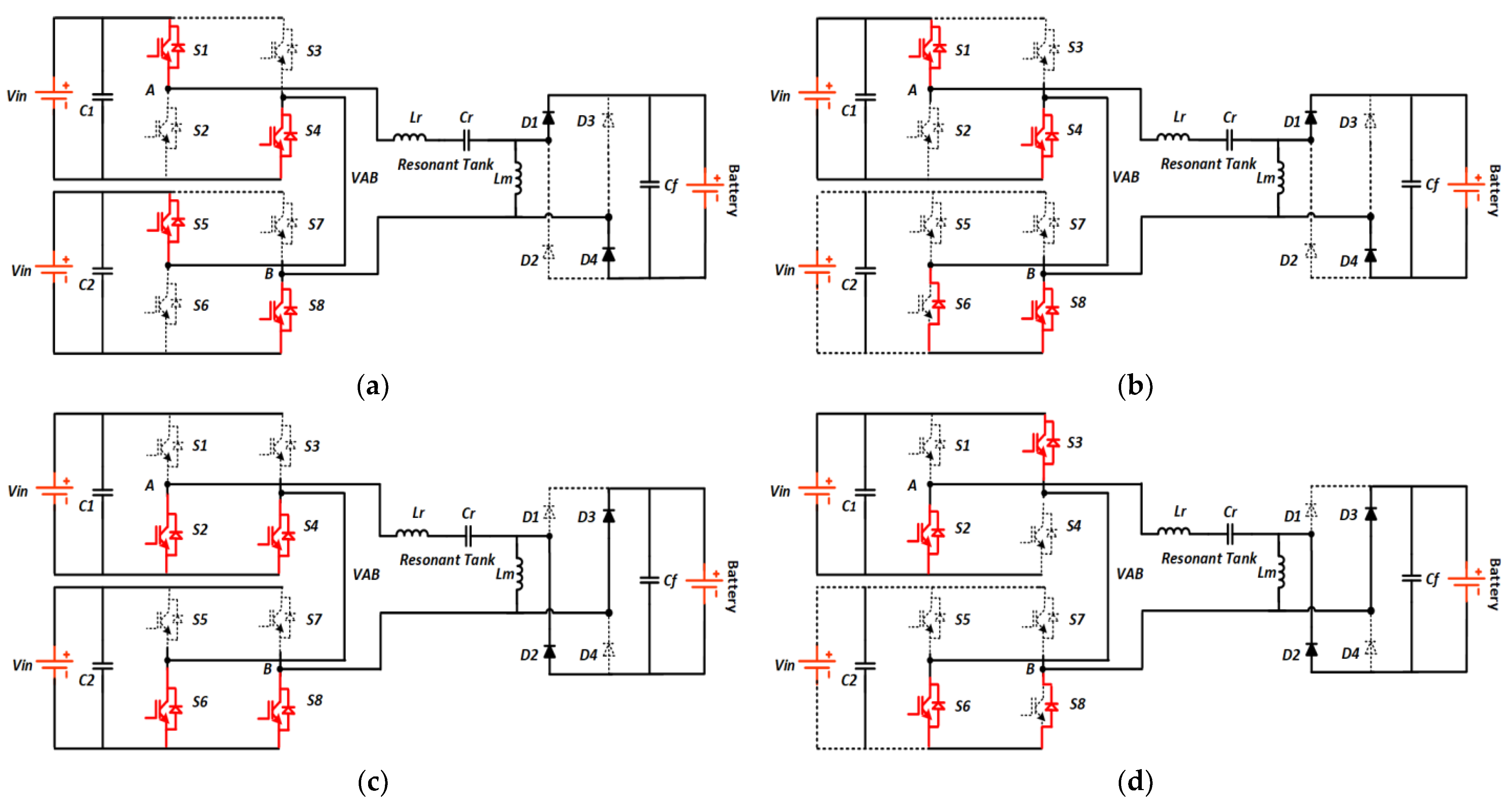
3. Modes of Operation
3.1. Mode1 (t0 < t < t1)
3.2. Mode2 (t1 < t < t2)
3.3. Mode3 (t2 < t < t3)
3.4. Mode4 (t3 < t < t4)
3.5. Mode5 (t4 < t < t5)
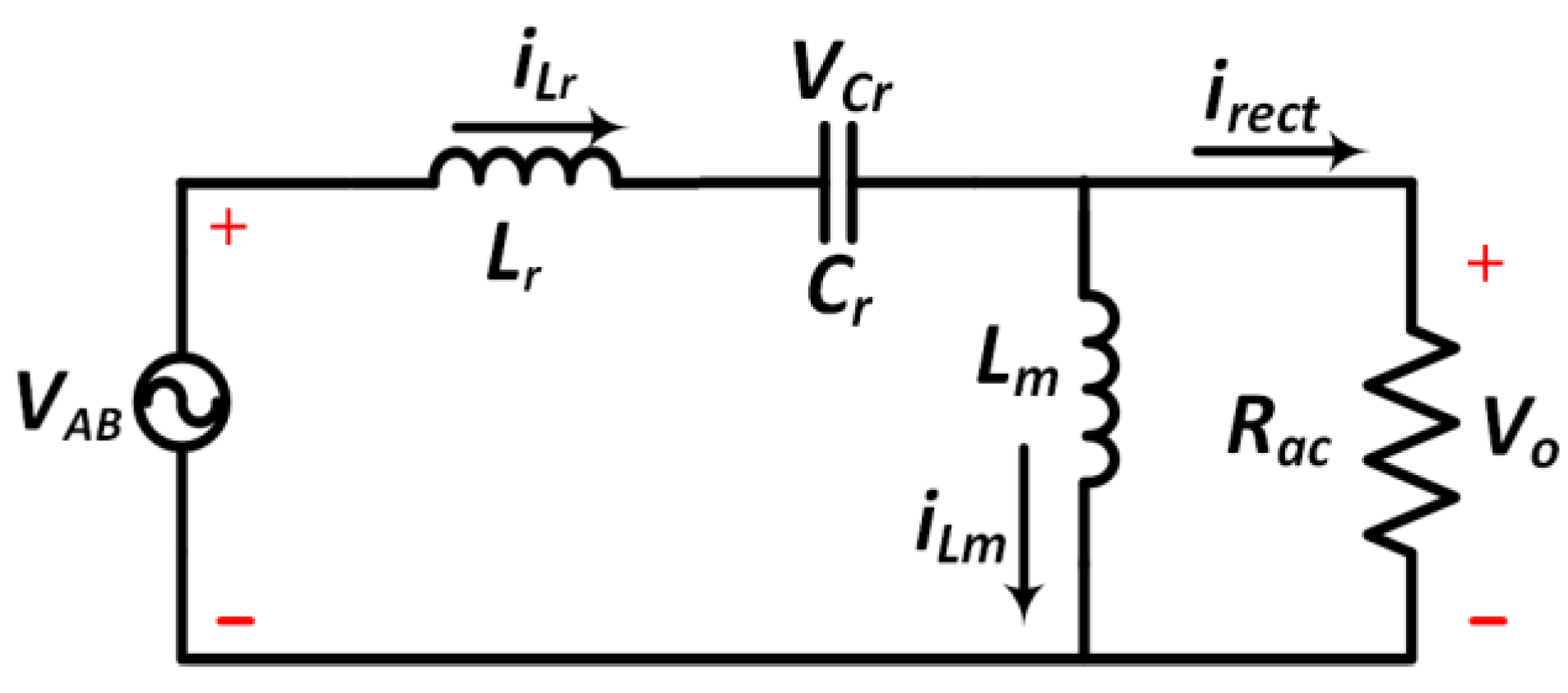
4. Design Consideration
Calculation of Components in Resonant Tank Circuit
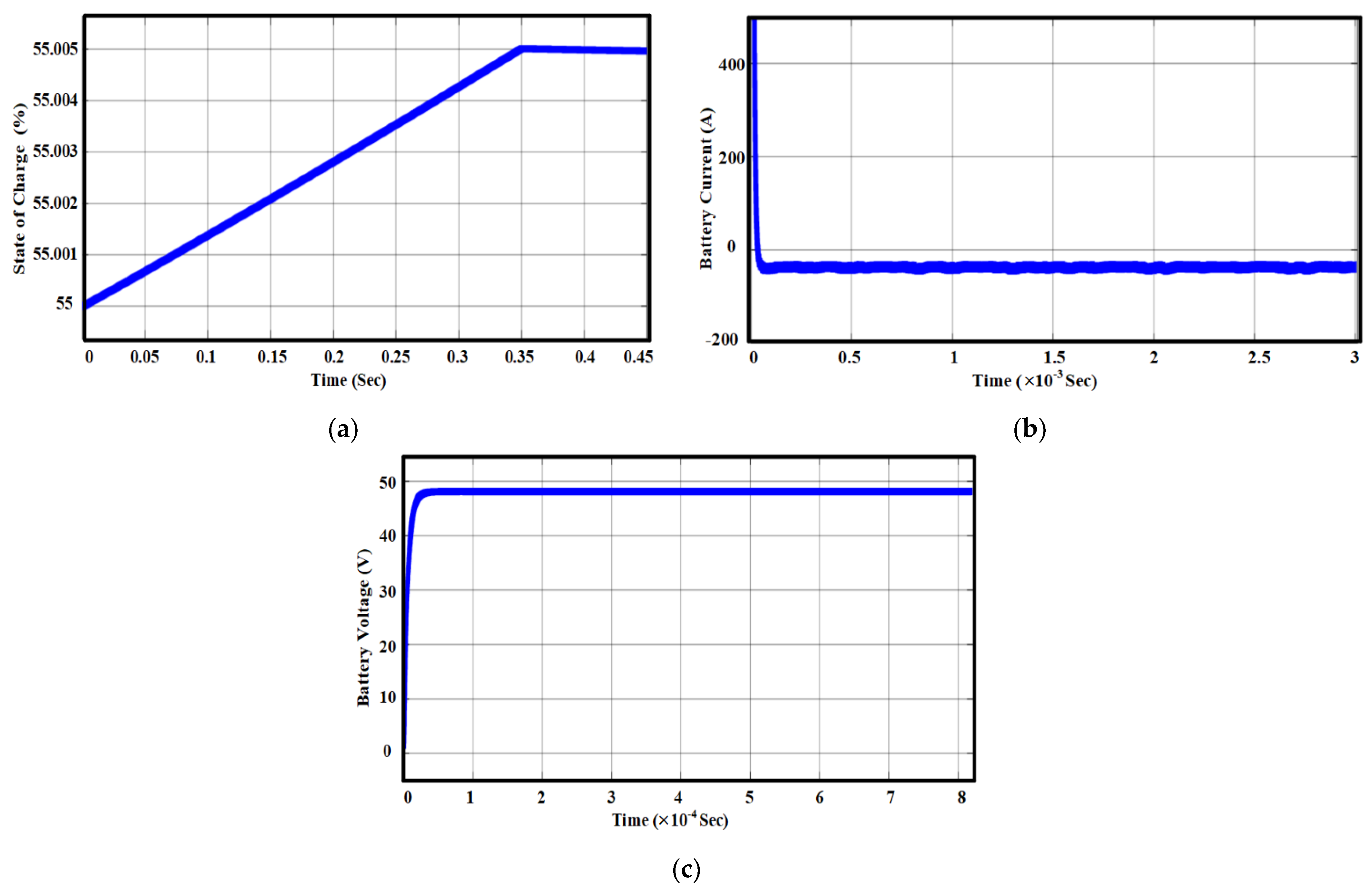
5. Simulation Results
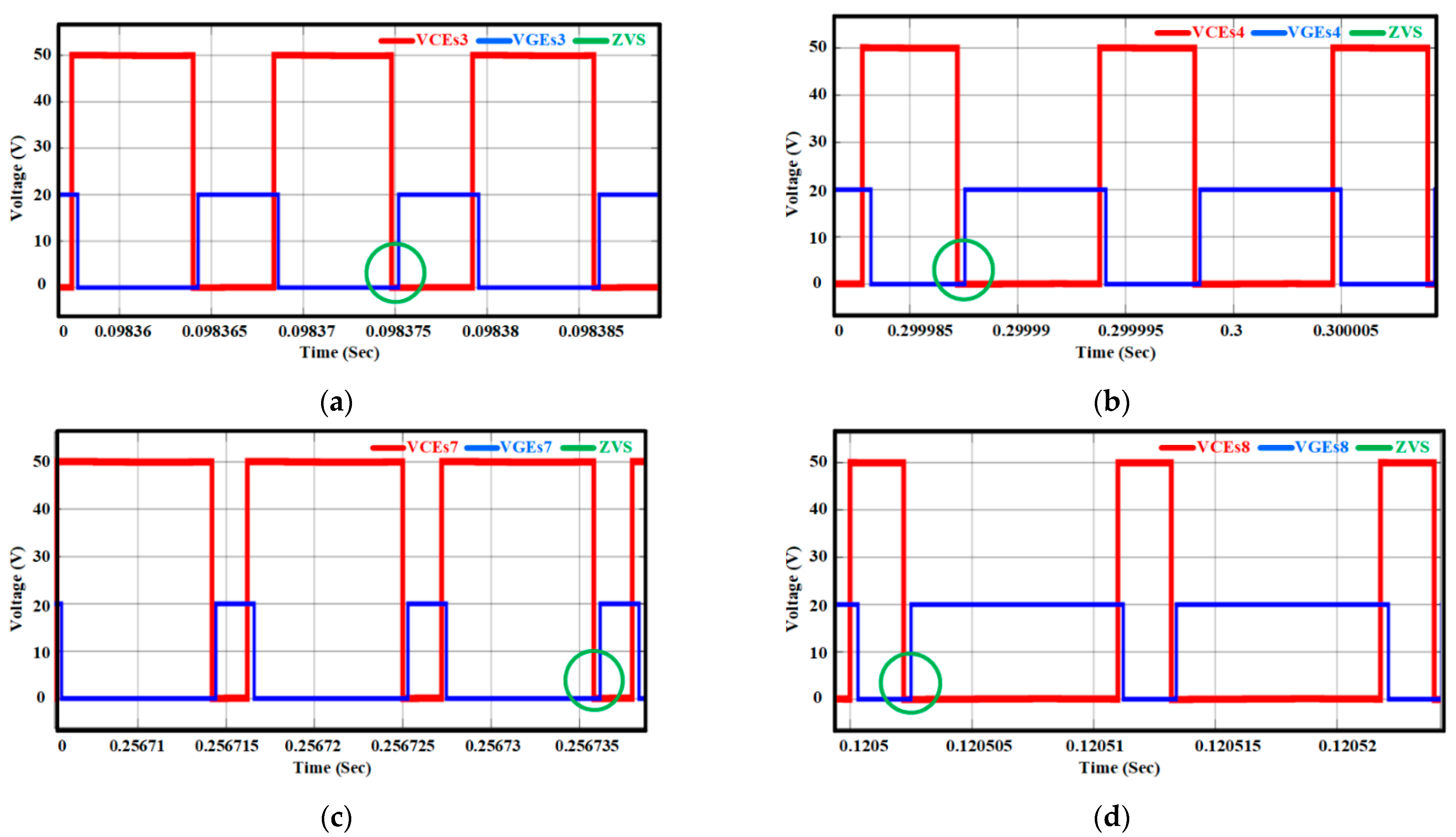
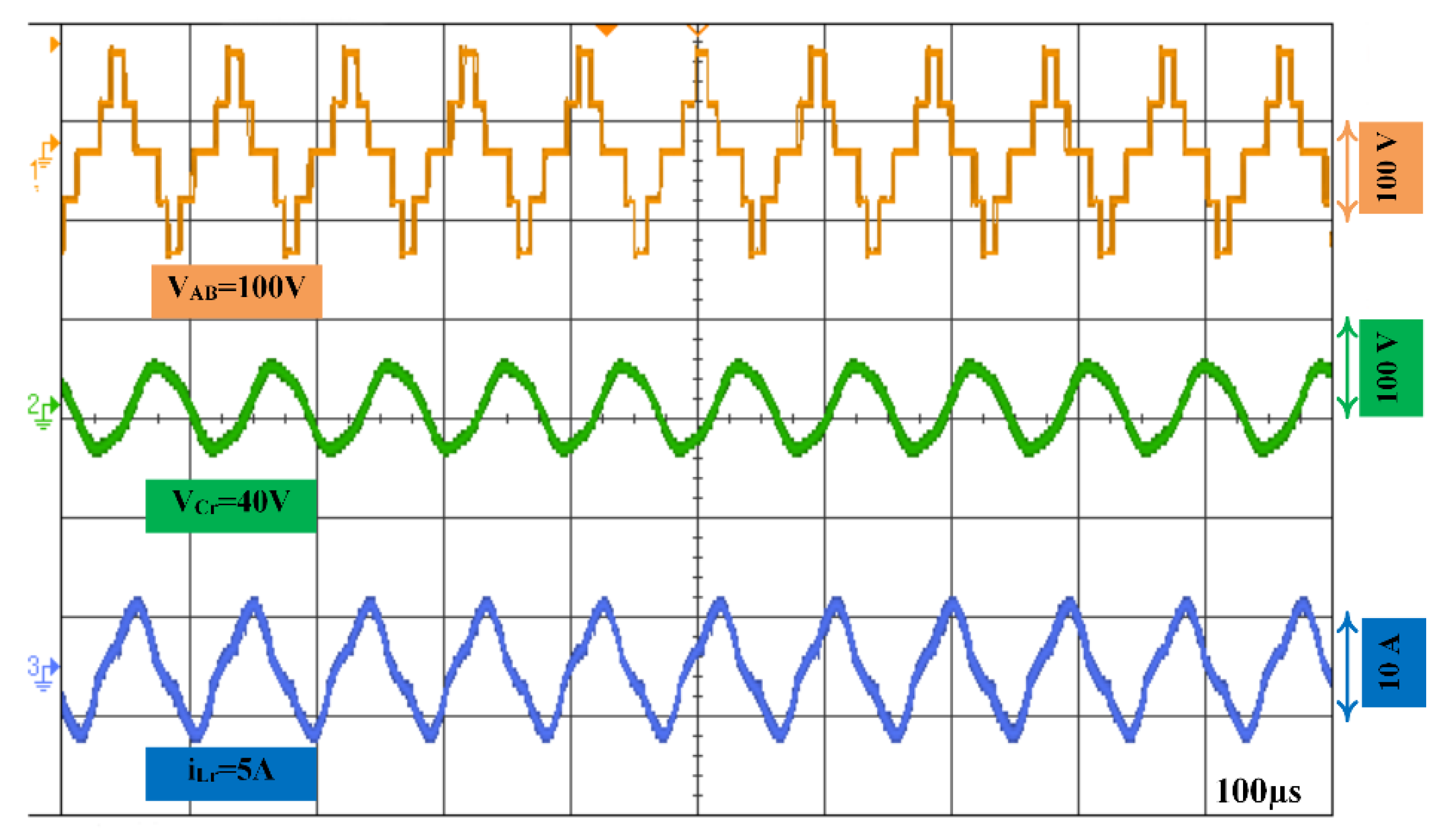
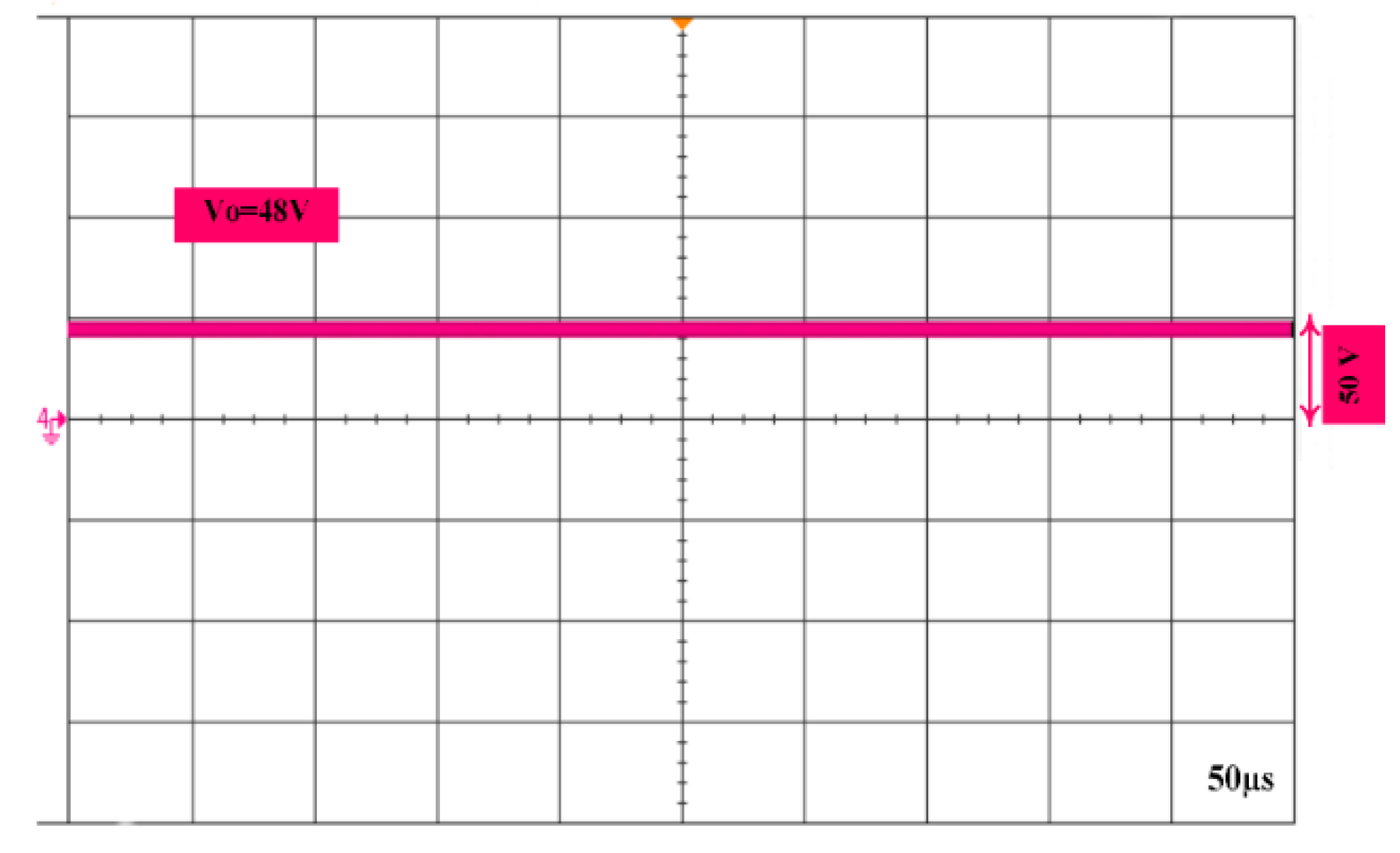
6. Experimental Results
7. Conclusions
8. Future Challenges
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Y.-E.; Hsiao, S.-L. Novel High-Efficiency Three-Port Bidirectional Step-Up/Step-Down DC–DC Converter for Photovoltaic Systems. Sustainability 2021, 13, 7913. [Google Scholar] [CrossRef]
- Alatai, S.; Salem, M.; Ishak, D.; Das, H.S.; Alhuyi Nazari, M.; Bughneda, A.; Kamarol, M. A Review on State-of-the-Art Power Converters: Bidirectional, Resonant, Multilevel Converters and Their Derivatives. Appl. Sci. 2021, 11, 10172. [Google Scholar] [CrossRef]
- Viswanathan, B. Chapter 7-Solar Energy: Fundamentals. Energy Sources Fundam. Chem. Convers. Processes Appl. 2017, 139–147. [Google Scholar] [CrossRef]
- Karthikeyan, V.; Gupta, R. Distributed power flow control using cascaded multilevel isolated bidirectional DC–DC converter with multi-phase shift modulation. IET Power Electron. 2019, 12, 2996–3003. [Google Scholar] [CrossRef]
- Hussan, M.R.; Sarwar, A.; Siddique, M.D.; Mekhilef, S.; Ahmad, S.; Sharaf, M.; Zaindin, M.; Firdausi, M. A novel switched-capacitor multilevel inverter topology for energy storage and smart grid applications. Electronics 2020, 9, 1703. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Y.; Wang, X. Resonant Converter for Battery Charging Applications With CC/CV Output Profiles. IEEE Access 2020, 8, 54879–54886. [Google Scholar] [CrossRef]
- Dhundhara, S.; Verma, Y.P.; Williams, A. Techno-economic analysis of the lithium-ion and lead-acid battery in microgrid systems. Energy Convers. Manag. 2018, 177, 122–142. [Google Scholar] [CrossRef]
- Al-Gabalawy, M.; Mahmoud, K.; Darwish, M.M.F.; Dawson, J.A.; Lehtonen, M.; Hosny, N.S. Reliable and Robust Observer for Simultaneously Estimating State-of-Charge and State-of-Health of LiFePO4 Batteries. Appl. Sci. 2021, 11, 3609. [Google Scholar] [CrossRef]
- Ali, E.S.; El-Sehiemy, R.A.; Abou El-Ela, A.A.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. An Effective Bi-Stage Method for Renewable Energy Sources Integration into Unbalanced Distribution Systems Considering Uncertainty. Processes 2021, 9, 471. [Google Scholar] [CrossRef]
- Bendary, A.F.; Abdelaziz, A.Y.; Ismail, M.M.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Proposed ANFIS Based Approach for Fault Tracking, Detection, Clearing and Rearrangement for Photovoltaic System. Sensors 2021, 21, 2269. [Google Scholar] [CrossRef] [PubMed]
- Abbas, A.S.; El-Sehiemy, R.A.; Abou El-Ela, A.; Ali, E.S.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Optimal Harmonic Mitigation in Distribution Systems with Inverter Based Distributed Generation. Appl. Sci. 2021, 11, 774. [Google Scholar] [CrossRef]
- Ryu, S.; Woo, D.; Kim, M.; Lee, B. Analysis and Design of Modified Half-Bridge Series-Resonant Inverter With DC-Link Neutral-Point-Clamped Cell. IEEE Trans. Power Electron. 2016, 31, 2282–2295. [Google Scholar] [CrossRef]
- Dominguez, A.; Barragan, L.A.; Artigas, J.I.; Otin, A.; Urriza, I.; Navarro, D. Reduced-Order Models of Series Resonant Inverters in Induction Heating Applications. IEEE Trans. Power Electron. 2017, 32, 2300–2311. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Chau, K.; Liu, C.; Lee, C.H. An overview of resonant circuits for wireless power transfer. Energies 2017, 10, 894. [Google Scholar] [CrossRef]
- Haga, H.; Kurokawa, F. Modulation method of a full-bridge three-level LLC resonant converter for battery charger of electrical vehicles. IEEE Trans. Power Electron. 2016, 32, 2498–2507. [Google Scholar] [CrossRef]
- Tang, X.; Li, Z.; Zhang, M. A Wide-Range Frequency Model for Dielectric Barrier Discharge Type Ozone Generators Powered by Series Resonant Inverters. IEEE Access 2019, 7, 124309–124314. [Google Scholar] [CrossRef]
- Salem, M.; Ramachandaramurthy, V.K.; Jusoh, A.; Padmanaban, S.; Kamarol, M.; Teh, J.; Ishak, D. Three-Phase Series Resonant DC-DC Boost Converter With Double LLC Resonant Tanks and Variable Frequency Control. IEEE Access 2020, 8, 22386–22399. [Google Scholar] [CrossRef]
- Maamar, A.E.T.; Helaimi, M.H.; Taleb, R.; Kermadi, M.; Mekhilef, S.; Wahyudie, A.; Rawa, M. Analysis and Small Signal Modeling of Five-Level Series Resonant Inverter. IEEE Access 2021, 9, 109384–109395. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mekhilef, S.; Shah, N.M.; Memon, M.A. Optimal design of a new cascaded multilevel inverter topology with reduced switch count. IEEE Access 2019, 7, 24498–24510. [Google Scholar] [CrossRef]
- Vemuganti, H.P.; Sreenivasarao, D.; Ganjikunta, S.K.; Suryawanshi, H.M.; Abu-Rub, H. A Survey on Reduced Switch Count Multilevel Inverters. IEEE Open J. Ind. Electron. Soc. 2021, 2, 80–111. [Google Scholar] [CrossRef]
- Rashid, M.H. Power Electronics Handbook; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Gadalla, A.S.; Yan, X.; Hasabelrasul, H. Performance of the battery energy storage systems based on cascaded H-bridge multilevel converter. J. Eng. 2019, 2019, 779–783. [Google Scholar] [CrossRef]
- Song, J.; Zhang, W.; Liang, H.; Jiang, J.; Yu, W. Fault-Tolerant Control for a Flexible Group Battery Energy Storage System Based on Cascaded Multilevel Converters. Energies 2018, 11, 171. [Google Scholar] [CrossRef] [Green Version]
- Agostini, E.; Barbi, I. Three-Phase Three-Level PWM DC–DC Converter. IEEE Trans. Power Electron. 2011, 26, 1847–1856. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mekhilef, S.; Shah, N.M.; Sarwar, A.; Memon, M.A. A new single-phase cascaded multilevel inverter topology with reduced number of switches and voltage stress. Int. Trans. Electr. Energy Syst. 2020, 30, e12191. [Google Scholar] [CrossRef]
- Dao, N.D.; Lee, D. Operation and Control Scheme of a Five-Level Hybrid Inverter for Medium-Voltage Motor Drives. IEEE Trans. Power Electron. 2018, 33, 10178–10187. [Google Scholar] [CrossRef]
- Ding, K.; Cheng, K.W.E.; Wang, S.X.; Wang, D.H.; Shi, Z. Five-level cascaded multilevel motor driver for electrical vehicle with battery charge management. In Proceedings of the 2008 Australasian Universities Power Engineering Conference, Sydney, Australia, 14–17 December 2008; pp. 1–6. [Google Scholar]
- Tolbert, L.A.; Fang Zheng, P.; Cunnyngham, T.; Chiasson, J.N. Charge balance control schemes for cascade multilevel converter in hybrid electric vehicles. IEEE Trans. Ind. Electron. 2002, 49, 1058–1064. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.-H.; Kim, M.-S.; Hussain Nengroo, S.; Kim, C.-H.; Kim, H.-J. LLC Resonant Converter for LEV (Light Electric Vehicle) Fast Chargers. Electronics 2019, 8, 362. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.; Luo, Q.; Du, X.; Altin, N.; Nasiri, A.; Alonso, J.M. A Dual Half-Bridge LLC Resonant Converter With Magnetic Control for Battery Charger Application. IEEE Trans. Power Electron. 2020, 35, 2196–2207. [Google Scholar] [CrossRef]
- Deng, J.; Li, S.; Hu, S.; Mi, C.C.; Ma, R. Design Methodology of LLC Resonant Converters for Electric Vehicle Battery Chargers. IEEE Trans. Veh. Technol. 2014, 63, 1581–1592. [Google Scholar] [CrossRef]
- Yilei, G.; Zhengyu, L.; Lijun, H.; Zhaoming, Q.; Guisong, H. Three-level LLC series resonant DC/DC converter. IEEE Trans. Power Electron. 2005, 20, 781–789. [Google Scholar] [CrossRef]
- Lee, I.; Moon, G. Analysis and Design of a Three-Level LLC Series Resonant Converter for High- and Wide-Input-Voltage Applications. IEEE Trans. Power Electron. 2012, 27, 2966–2979. [Google Scholar] [CrossRef]
- Zong, S.; Luo, Q.; Li, C.; Li, W.; He, X.; Su, S. Three-level frequency-doubling LLC resonant converter with high step-down ratio for high input voltage applications. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC, Fort Worth, TX, USA, 16–20 March 2014; pp. 14–19. [Google Scholar]
- Jin, F.; Liu, F.; Ruan, X.; Meng, X. Multi-phase multi-level LLC resonant converter with low voltage stress on the primary-side switches. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 4704–4710. [Google Scholar]
- Peter, A.K.; Mathew, J. A Single Phase, Single Stage AC-DC Multilevel LLC Resonant Converter With Power Factor Correction. IEEE Access 2021, 9, 70884–70895. [Google Scholar] [CrossRef]
- Kirshenboim, O.; Peretz, M.M. Combined Multilevel and Two-Phase Interleaved LLC Converter With Enhanced Power Processing Characteristics and Natural Current Sharing. IEEE Trans. Power Electron. 2018, 33, 5613–5620. [Google Scholar] [CrossRef]
- Chen, G.; Li, H.; Sun, X.; Wang, Y. A Method for Designing Resonant Tank of Half-Bridge Three-Level LLC Converter. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 2312–2316. [Google Scholar]
- Alatai, S.; Salem, M.; Ishak, D.; Kamarol, M.; Jamil, M.; Bughneda, A. Design and Analysis of Five-level cascaded LLC Resonant Converter. In Proceedings of the 2020 IEEE International Conference on Power and Energy (PECon), Penang, Malaysia, 7–8 December 2020; pp. 66–70. [Google Scholar]
- Deng, J.; Mi, C.C.; Ma, R.; Li, S. Design of LLC Resonant Converters Based on Operation-Mode Analysis for Level Two PHEV Battery Chargers. IEEE/ASME Trans. Mechatron. 2015, 20, 1595–1606. [Google Scholar] [CrossRef]
- Bughneda, A.; Salem, M.; Nazari, M.A.; Ishak, D.; Kamarol, M.; Alatai, S. Resonant Power Converters for Renewable Energy Applications: A Comprehensive Review. Front. Energy Res. 2022, 10, 846067. [Google Scholar] [CrossRef]
- Abdel-Rahman, S. Resonant LLC converter: Operation and design. Infineon Technol. N. Am. Corp 2012, 19, 1–19. [Google Scholar]
- Salem, M.; Jusoh, A.; Dahidah, M.; Ishak, D.; Richelli, A.; Alhamroni, I.; Kamarol, M. Improved topology of three-phase series resonant DC-DC boost converter with variable frequency control. Alex. Eng. J. 2022, 61, 1701–1713. [Google Scholar] [CrossRef]







| Parameter | Symbol | Value |
|---|---|---|
| Input voltage range | Vin,min~Vin,max | 60–140 V |
| Input voltage Nominal | Vin,nom | 100 V |
| Output voltage | Vb | 48 V |
| Output power | Pbat | 100 W |
| Resonant frequency | Fr1 | 100 kHz |
| Switching frequency | Fsw | 91–110 kHz |
| Parameter | Symbol | Calculated Value | Measured Value |
|---|---|---|---|
| Input voltage Nominal | Vin,nom | 100 V | 100 V |
| Resonant capacitances | cr | 218.5 nF | 215 nF |
| Resonant inductances | Lr | 11.5 µH | 12 µH |
| Magnetizing inductance | Lm | 34.7 µH | 35 µH |
| Equivalent load resistance | Rac | 18.67 Ω | 18.67 Ω |
| Output voltage | Vo | 48 V | 48 V |
| Component | Part Number |
|---|---|
| Active Switches (S1–S8) | GP35B60PD |
| Microcontroller | LAUNCHXL-F28379D LaunchPad |
| Magnetic ferrite core | ETD 34/17/11 |
| Resonant capacitor | KEMET R75 Film Capacitor |
| Diodes D1–D4 | MUR1560G |
| Topology | No of Switches | No of Rectifier | No of Transformer | Input Voltage V | Output Voltage V | Power Rated w | Swathing Frequency Range kHz | Modulation | Efficiency |
|---|---|---|---|---|---|---|---|---|---|
| Half-bridge LLC [6] | 2 | 8 | 1 | 200 | 100 | 200 | 100 | PWM 1 | 97% |
| Full bridge LLC [29] | 4 | 4 | 1 | 250–310 VAC | 25.6–33.6 | 1000 | 30–100 | PFM 2 | 96.4% |
| Dual Half-bridge LLC [30] | 2 | 8 | 2 | 340–380 | 120–160 | 320 | 100 | MC 3 | 95.5% |
| Full bridge LLC [31] | 4 | 4 | 1 | 400 | 250–450 | 3300 | 154.7–220 | - | 98.2% |
| Three level LLC [34] | 4 | 2 | 1 | 600 | 48 | 800 | 50 | PFM | 95.1% |
| Proposed | 8 | 4 | 0 | 100 | 48 | 100 | 91–110 | (PWM) (PFM) | 96.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alatai, S.; Salem, M.; Alhamrouni, I.; Ishak, D.; Bughneda, A.; Kamarol, M. Design Methodology and Analysis of Five-Level LLC Resonant Converter for Battery Chargers. Sustainability 2022, 14, 8255. https://doi.org/10.3390/su14148255
Alatai S, Salem M, Alhamrouni I, Ishak D, Bughneda A, Kamarol M. Design Methodology and Analysis of Five-Level LLC Resonant Converter for Battery Chargers. Sustainability. 2022; 14(14):8255. https://doi.org/10.3390/su14148255
Chicago/Turabian StyleAlatai, Salah, Mohamed Salem, Ibrahim Alhamrouni, Dahaman Ishak, Ali Bughneda, and Mohamad Kamarol. 2022. "Design Methodology and Analysis of Five-Level LLC Resonant Converter for Battery Chargers" Sustainability 14, no. 14: 8255. https://doi.org/10.3390/su14148255
APA StyleAlatai, S., Salem, M., Alhamrouni, I., Ishak, D., Bughneda, A., & Kamarol, M. (2022). Design Methodology and Analysis of Five-Level LLC Resonant Converter for Battery Chargers. Sustainability, 14(14), 8255. https://doi.org/10.3390/su14148255










