An Advanced and Robust Approach to Maximize Solar Photovoltaic Power Production

Abstract

The stochastic and erratic behavior of solar photovoltaic (SPV) is a challenge, especially due to changing meteorological conditions. During a partially irradiated SPV system, the performance of traditional maximum power point tracking (MPPT) controllers is unsatisfactory because of multiple peaks in the Power-Voltage curve. This work is an attempt to understand the performance uncertainties of the SPV system under different shading conditions and its mitigation. Here, a novel hybrid metaheuristic algorithm is proposed for the effective and efficient tracking of power. The algorithm is inspired by the movement of grey wolves and the swarming action of birds, and is thus known as the hybrid grey wolf optimizer (HGWO). The study focuses on the transient and steady-state performance of the proposed controller during different conditions. A comparative analysis of the proposed technique with incremental conductance and a particle swarm optimizer for different configurations is presented. Thus, the results are presented based on power extracted, shading loss, convergence factor and efficiency. The proposed HGWO–MPPT is found to be better as it has a maximum efficiency of 94.30% and a minimum convergence factor of 0.20 when compared with other techniques under varying conditions for different topologies. Furthermore, a practical assessment of the proposed controller on a 6.3 kW_p rooftop SPV system is also presented in the paper. Energy production is increased by 8.55% using the proposed approach to the practical system.

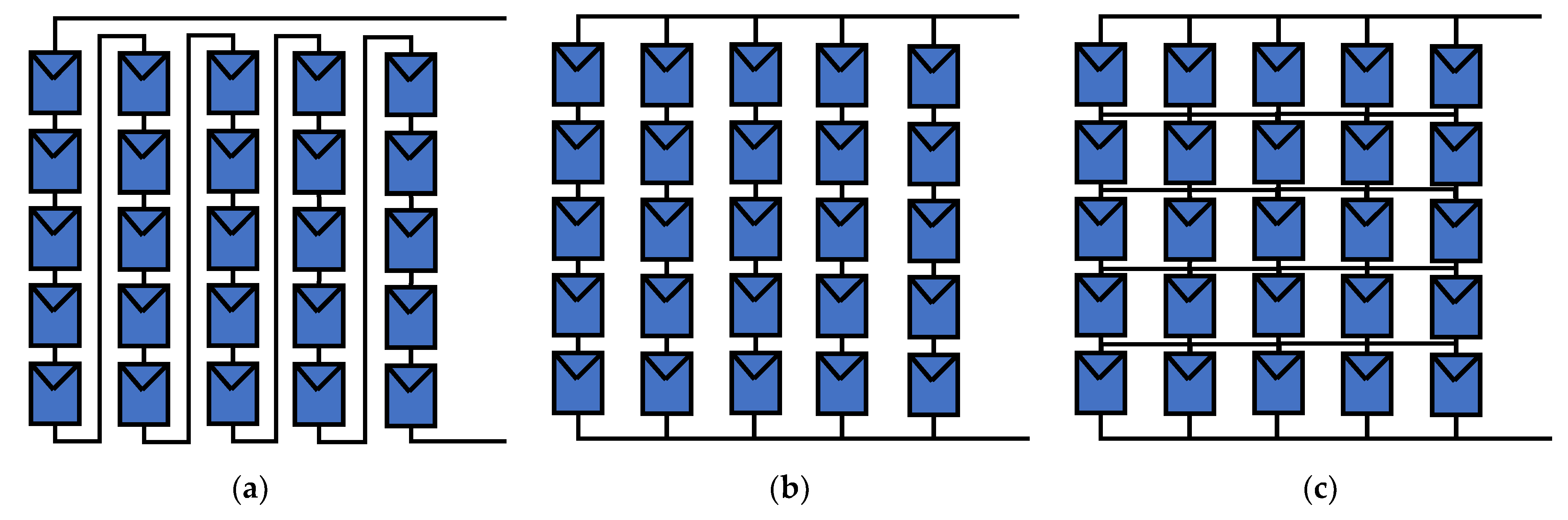
1. Introduction

The demand for cleaner production of energy is gaining importance to meet the exponentially rising energy demands of the population. Renewable energy is being considered as the key driving factor in addressing this issue in an eco-friendly and sustainable manner. These renewable energy technologies comprise of solar photovoltaics (SPV), wind energy conversion systems, geothermal energy, solar thermal and many more. Among these, SPV have been most widely adopted and have witnessed a rapid rise across the globe. Ease of maintenance, zero-emission energy production, promotion of research, and consumer-friendly government policies have been some of the major reasons for the booming SPV sector. The power generation from SPV in 2020 has been improved by 156 TWh, i.e., a 23% rise from 2019. SPV have a 3.1% share in the global electricity generation and is third behind hydropower and onshore wind. Estimated growth of 24–27% is predicted for the yearly average generation to reach the net-zero target of 6970 TWh by 2030 on the global level [1].

SPV technology has some issues to address, such as low conversion efficiency, variable power output from SPV systems and dependencies on various parameters. The output power of the SPV system, unlike fossil fuel energy, is dependent on different working conditions, i.e., temperature and irradiance. To make SPV systems work in an optimum operating range, a maximum power point tracking (MPPT) controller is designed for these varying meteorological conditions. Numerous MPPT techniques have already been documented and compared in the literature [2,3,4,5]. These methods effectively and efficiently track the maximum power that can be extracted from the SPV system and in return improve the return of interest on the investment. Partial shading conditions (PSC) is another important aspect that has to be considered while designing MPPT techniques [6]. PSC is when the entire SPV system has uneven irradiance, mainly due to clouds, nearby buildings, trees, etc.

Based on the location of the sensors and the type of sensors, there are different implementations of MPPT techniques, namely, SPV-side sensors, output sensors, additional irradiance/temperature sensors, additional current sensors, thermography camera arrangement and reduced sensor/sensor-less [7]. Another classification of the different MPPT techniques that can be implemented is: conventional algorithms, mathematical-based algorithms, hybrid algorithms, artificial intelligence-based and metaheuristic algorithms [8]. The conventional MPPT algorithms are the most simple and easy to implement. Some of the these MPPT algorithms are fractional open voltage, perturb and observe (P&O) [9,10] and incremental conductance (INC) [11,12]. These MPPT algorithms suffer from steady-state oscillations, drift conditions and low efficiency during PSCs.

PSCs cause multiple peaks in the I–V and P–V characteristics of the SPV. Among these multiple maximum power points (MPP), one is global MPP (GMPP) and others are local MPP (LMPP). The effectiveness and robustness of the MPPT is based on tracking and locating the GMPP. MPPT issues related to PSCs are discussed in [13]. According to the literature, each GMPPT method has different features, such as additional circuit requirement, complexity, tracking speed, convergence and number of sensors. Hence, these can be classified into three categories: segmental search techniques, soft computing techniques and two-stage methods [14]. Segmental search-based MPPT controllers are derived from the mathematical theories of a diving rectangle, center point iteration and Fibonacci techniques [15]. The basic principle of these methods is to initially select an exploration range and then it is reduced until GMPP is located. These are less complex, with easy implementation, but lack the accuracy of some of the advanced methods. The soft computing-based tracking algorithms show good performance but have issues of complexity and are difficult to implement without prior knowledge about the system. The MPPT controller utilized modern metaheuristic algorithms to compute GMPP, such as particle swarm optimizer (PSO) [16], firefly algorithm [17], ant colony optimization (ACO) [18], cuckoo search [19] and simulated annealing [20]. Further improvements were made to develop hybrid MPPT algorithms with enhanced performance under PSCs [21,22]. These MPPT algorithms utilized metaheuristic and artificial intelligence tools for comparatively better functioning and robust performance.

In recent years, various literature can be found on the hybrid MPPT, such as fuzzy logic–PSO [23], gravitational search–PSO [24], golden section–cuckoo search [25], fuzzy logic-based grasshopper [26], etc. Eltamaly presented a novel PSO approach to determine the optimal parameters for the tracking MPP in the case of PSC. This method utilized two nested PSO search loops to reduce convergence time and failure rate [27]. The effect of convergence rate and failure is further elaborated in [28]. The standard optimization-based controllers suffer from long conversion time, high failure rate and steady-state oscillations. Hence, modifications in PSO, cuckoo search and other optimization algorithms have been proposed in the literature to track effectively the MPP for rooftop SPV systems [29,30]. Enhanced GWO (EGWO)-based MPPT is discussed in [31], but with 4S and 2S2P configurations for performance analysis. The effectiveness and robustness of an MPPT controller can be determined when the designed technique is tested for a variety of the most commonly used PV configuration (such as series parallel) for varying shading patterns. The novelty of the proposed work is to develop a robust and efficient MPP tracking controller for different SPV configurations under varying irradiances.

In the literature, another solution is also presented for extracting the maximum performance from the SPV system. This solution is the rearrangement of the SPV panels, either physically or electrically. Reconfiguration of the PV arrays aims to distribute the shade so that each row gets the same amount of sunlight. Electronic array reconfiguration is a dynamic reconfiguration technique that utilizes sensors to determine partial shading and fault conditions, whereas in static array reconfiguration SPV systems fixed connections across modules are used according to their physical location, to redistribute the shade. Belhachat et al. presented a comprehensive review analysis for SPV array reconfiguration under PSCs [32]. The static reconfiguration strategies are considered a one time arrangement, as they use a preset interconnection idea to extract maximum power and smooth the P–V characteristic. The Lo Shu concept [33], chaotic baker map [34], grey wolf array reconfiguration [35], magic square [36] and shade dispersion array relocation are some of the latest techniques available in the literature. As in the case of dynamic array reconfiguration techniques [37], current injection [38], PSO-based electronic array reconfiguration [39], and direct power evaluation [40] are some of the latest works available in the literature.

Due to the advancement in recent years, bio-inspired algorithms have been deployed to improve the performance of the SPV system under different scenarios [41,42]. These algorithms have improved performance when compared with conventional methods such as P&O, INC, magic square, etc. However, there is a scope for further improvement on the following parameters, such as computational burden, precision and accuracy of the output, robustness, convergence rate and ease of implementation [43]. In addition to this, in the case of MPPT techniques, the tuning of parameters $({\mathrm{K}}_{\mathrm{p}}, {\mathrm{K}}_{\mathrm{i}}$ and ${\mathrm{K}}_{\mathrm{d}})$ for the controller is a trial-and-error method. Thus, it requires more time and ill-tuned parameters affect the optimal solution significantly. Furthermore, there is an issue of oscillation around MPP in the conventional MPPT controllers, and parameter tuning is required due to the indirect control of duty cycle to decide the step size for duty cycle update. Then, the update direction of duty cycle is dependent on the type of converter (i.e., from buck to boost). As in the case of modern metaheuristic techniques, PSO is the most widely incorporated technique, but it also has three tuning parameters: ${\mathrm{c}}_1, {\mathrm{c}}_2$ and $\mathrm{w}$ [44].

In the literature review, it was observed that different solar photovoltaic system configurations have been implemented to enhance power extraction from SPV panels. Furthermore, authors have also implemented optimization techniques for improving the tracking efficiency of the SPV system. However, there is still scope to study the performance of the SPV system with various configurations and modern metaheuristic techniques. In this paper, a modern computational intelligence-based hybrid algorithm is utilized for designing an MPPT controller. Figure 1 shows the schematic diagram of the proposed system with the proposed technique, designed and simulated in MATLAB-Simulink Environment for the 5 × 5 SPV system, as well as for the practical system of 6.3 kW. The MPPT controller is designed to improve the performance of the SPV system under PSCs. The performance of the hybrid metaheuristic MPPT controller is evaluated based on tracking efficiency, shading losses, speed of convergence, robustness to changing conditions and easy implementation. The proposed work aims to create sustainable buildings with integrated solar photovoltaic systems to meet the energy demand, by increasing the overall energy efficiency of the building.

2. Mathematical Modelling

The mathematical and numerical modelling of the solar photovoltaic system is presented in this section. This section also focusses on various configurations and partial shading conditions on the modelled SPV system.

2.1. SPV Array

The building blocks of the SPV system are cells, which act as an electrical transducer, converting light energy into electrical energy. There are numerous methods for modelling SPV cells, such as the single diode model, double diode model and various parameter estimation methods [45]. In the proposed work, a single diode model, as shown in Figure 2, is used for designing the 5 × 5 SPV system. The combination of multiple SPV cells in series and in parallel configure the desired SPV panel.

There are different methods for modeling of the SPV cell, such as the single diode model, double diode model, parameter estimation, among others. The modelling of the SPV cell is done considering the single diode model [46].

$$\mathrm{I}={\mathrm{I}}_{\mathrm{PH}}-{\mathrm{I}}_{\mathrm{o}}\left({\mathrm{e}}^{\frac{\mathrm{V}+{\mathrm{R}}_{\mathrm{s}}\mathrm{I}}{{\mathrm{nV}}_{\mathrm{t}}}}-1\right)-\frac{\mathrm{V}+{\mathrm{R}}_{\mathrm{s}}\mathrm{I}}{{\mathrm{R}}_{\mathrm{sh}}}$$

(1)

$${\mathrm{I}}_{\mathrm{PH}}=\frac{\mathrm{G}}{{\mathrm{G}}_{\mathrm{ref}}}{\mathrm{I}}_{\mathrm{sc}}+{\mathrm{K}}_{\mathrm{i}}\left({\mathrm{T}}_{\mathrm{c}}-{\mathrm{T}}_{\mathrm{ref}}\right)$$

(2)

$${\mathrm{I}}_{\mathrm{o}}=\frac{{\mathrm{I}}_{\mathrm{sc}}{\mathrm{e}}^{\left(\frac{{\mathrm{E}}_{\mathrm{go}}}{{\mathrm{V}}_{\mathrm{to}}}-\frac{{\mathrm{E}}_{\mathrm{g}}}{{\mathrm{V}}_{\mathrm{t}}}\right)}}{{\mathrm{e}}^{\frac{{\mathrm{V}}_{\mathrm{oc}}}{{\mathrm{nN}}_{\mathrm{s}}{\mathrm{V}}_{\mathrm{to}}}}-1}{\left(\frac{{\mathrm{T}}_{\mathrm{c}}}{{\mathrm{T}}_{\mathrm{ref}}}\right)}^3$$

(3)

The output current for the SPV array ${\mathrm{I}}_{\mathrm{PV}}$ is given as

$${\mathrm{I}}_{\mathrm{PV}}=\mathrm{p}·{\mathrm{I}}_{\mathrm{PH}}-\mathrm{p}·{\mathrm{I}}_{\mathrm{o}}\left({\mathrm{e}}^{\frac{\mathrm{V}+\frac{\mathrm{s}}{\mathrm{p}}{\mathrm{R}}_{\mathrm{s}}\mathrm{I}}{{\mathrm{nV}}_{\mathrm{t}}}}-1\right)-\frac{\mathrm{V}+\frac{\mathrm{s}}{\mathrm{p}}{\mathrm{R}}_{\mathrm{s}}\mathrm{I}}{\frac{\mathrm{s}}{\mathrm{p}}{\mathrm{R}}_{\mathrm{sh}}}$$

(4)

where ${\mathrm{I}}_{\mathrm{PH}}$ is the photogenerated controlled-current source, ${\mathrm{R}}_{\mathrm{s}}$ and ${\mathrm{R}}_{\mathrm{sh}}$ are the series and shunt resistance for power loss, ${\mathrm{I}}_{\mathrm{o}}$ is the reverse saturation current, $\mathrm{n}$ is the diode ideality factor and ${\mathrm{V}}_{\mathrm{t}}$ is thermal voltage. ${\mathrm{T}}_{\mathrm{ref}}$ and ${\mathrm{G}}_{\mathrm{ref}}$ are 25 deg. C and 1000 W/m², respectively. Whereas, ${\mathrm{T}}_{\mathrm{c}}$ is the temperature of the SPV cell and $\mathrm{G}$ is the irradiance incident on the plane of the SPV cell. ${\mathrm{I}}_{\mathrm{sc}}$ is the short-circuit current and ${\mathrm{K}}_{\mathrm{i}}$ is the temperature coefficient of the SPV cell. ${\mathrm{V}}_{\mathrm{to}}$ is thermal voltage at STC, ${\mathrm{E}}_{\mathrm{g}}$ and ${\mathrm{E}}_{\mathrm{go}}$ is the energy bandgap of the semiconductor and energy band at $\mathrm{T}=0 \mathrm{K}$. $\mathrm{s}$ is the number of SPV cells in series and $\mathrm{p}$ is the number of SPV cells in parallel.

2.2. Configuration/Topologies of the SPV System

Partial shading conditions are also known as mismatching conditions; under PSCs there are multiple MPP. This presence of MPP can further lead to the formulation of hot spots, reduced performance of the SPV system, increased mismatch power losses (MPL) and reduced system efficiency. To overcome this condition, different PV array topologies are considered for comparative analysis, as shown in Figure 3. The topologies considered for comparison with the proposed MPPT algorithm are series (S), Series–Parallel (SP), Total Cross Tied (TCT) and grey wolf–bridge linked TCT (GW–BLTCT) [35]. The PSCs considered for effective analysis of the performance of the SPV system are shown in Figure 4. The details of the SPV panel used in this work is presented in

Table 1. SPV Panel Description.

Specification	Data
Cell Type	Mono-crystalline
Cell Arrangement	144 [2 × (12 × 6)]
${\mathrm{P}}_{\mathrm{peak}}$	450 W
${\mathrm{I}}_{\mathrm{M}\mathrm{P}}$	11.12 A
${\mathrm{V}}_{\mathrm{M}\mathrm{P}}$	40.5 V
${\mathrm{I}}_{\mathrm{SC}}$	11.65 A
${\mathrm{V}}_{\mathrm{OC}}$	48.7 V
Operating Temperature	−40 °C to 85 °C
Power Tolerance	0 to 5 W

.

3. Methodology

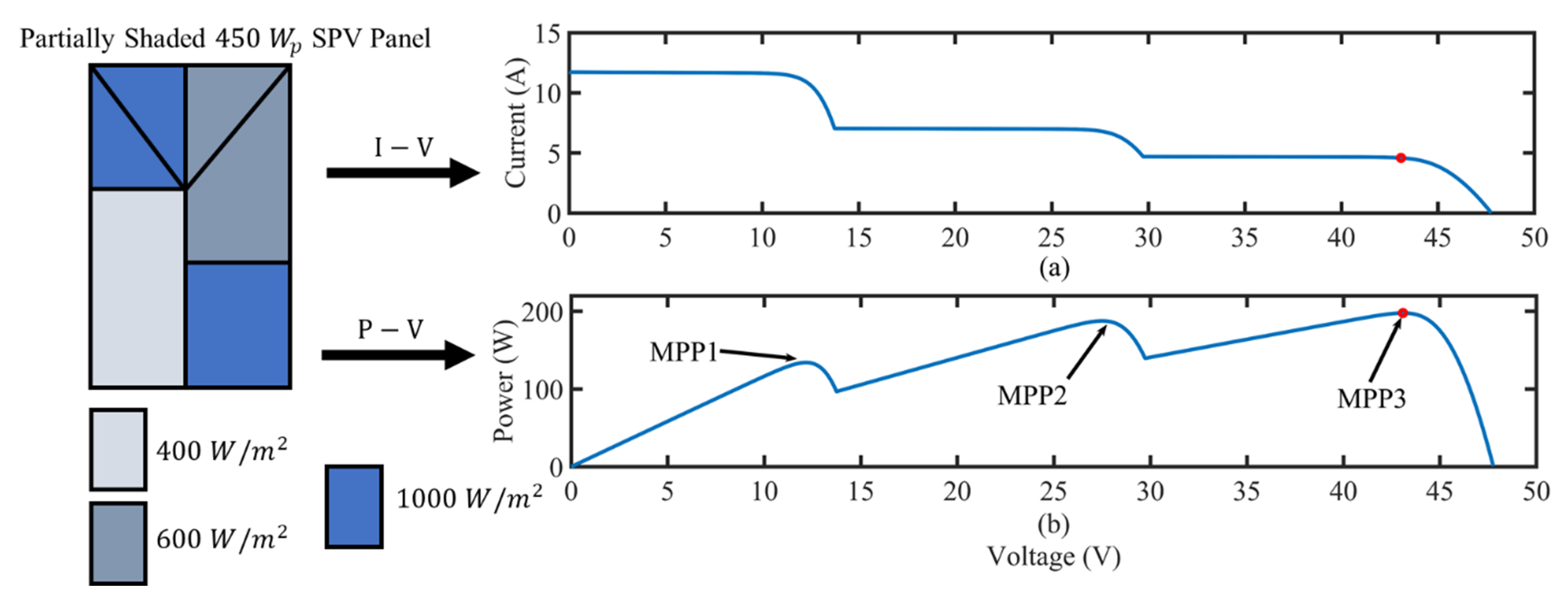
In this work, the problems arising due to improper shading of panels is addressed using a novel hybrid metaheuristic technique. This technique is designed to tune the MPPT controller for the SPV system. This hybrid metaheuristic technique is inspired from the movement of grey wolves while attacking their prey and the swarming action of birds in flight [47,48]. This proposed hybrid technique has been previously implemented for optimal sizing and location of energy resources in a distributed generation system. In this work, a hybrid grey wolf optimizer (HGWO)-based MPPT controller is presented for an effective and robust performance of the SPV system under PSCs. The characteristics of the SPV panel under PSCs utilized in this study is represented in Figure 5. Here, Figure 5a,b shows the I–V and P–V characteristics of a 450 W_p SPV panel during the uneven distribution of irradiance.

The maximum nominal power $\left({\mathrm{P}}_{\mathrm{n}\mathrm{m}\mathrm{p}}\right)$ that can be extracted from S, SP, TCT and GW–BLTCT under different PSCs (as shown in Figure 4) is given in

Table 2. Nominal Maximum Power $\left({\mathrm{P}}_{\mathrm{n}\mathrm{m}\mathrm{p}}\right)$ For Each Configuration Under Various Shading Scenarios.

Shading	Configuration of 5 × 5 SPV System
	S	SP	TCT	GWO–BLTCT
NS	11,250	11,250	11,250	11,250
CS	6645	8972	8972	9102
RS	6644	6644	6645	6877
DS	6277	7004	8570	8896
CNRS	5052	6096	7129	7262

. From Table 2 it can be noted that GW–BLTCT is comparatively better at performing topologies for the 5 × 5 SPV system under these scenarios. It is closely matched by TCT, but the only drawback of these two configurations is having skilled labor to perform these connections. SP is the most widely considered configuration across the world and for CS and RS, type of shade matches the performance of TCT. Whereas S configuration has major drawbacks in performance during PSCs, the SPV system has a voltage output of $\left(\mathrm{s}·{\mathrm{V}}_{\mathrm{oc}}\right)$, hence increasing the cost of the system and reducing the feasibility of the SPV system. The CNRS-type of shade has the most adverse impact on the performance of the SPV system. Hence, a comparative analysis of the proposed MPPT technique for SP, TCT and GW–BLTCT is presented in this work.

Hybrid Grey Wolf Optimizer-Based MPPT

From Figure 5 it is observed that the performance of the SPV panel is affected under varying irradiance conditions. It is observed that during partial shading of SPV panels, three different peaks occur in I–V and P–V curves. There are three different peaks because three different levels of irradiance occur on the SPV panel. These different peaks in power are MPP1, MPP2 and MPP3, among which maximum power points MPP1 and MPP2 are local MPPs, whereas MPP3 is the global maximum power point (GMPP), i.e., ≈198 W. To improve the performance of the SPV system under these varying conditions, implementation of a hybrid AI-based MPPT controller is proposed.

The application of intelligent meta-heuristic techniques to extract MPP is vital because of the numerous possibilities of shade dispersion. GWO is a modern nature-inspired optimization technique, capable of solving complex, nonlinear stochastic problems. This algorithm uses the movement of grey wolves encircling and targeting their prey. The algorithm uses randomly scattered particles in the search space known as wolves. These wolves are classified into four groups: alphas $\left(\mathsf{\alpha }\right)$, betas ($\mathsf{\beta }$), deltas $\left(\mathsf{\delta }\right)$ and omegas $(\mathsf{\omega }$). This classification is performed based on a hierarchical order, where the alphas are the lead pack of wolves with the least number, as shown in Figure 6. The betas follow the decision of the alphas; they are followed by the deltas and the remaining group of wolves are kept as omegas. The population of wolves increases from alphas to omegas. In optimization, the best solution is given by the alphas (best position) and the entire pack is driven by them. The major benefit of implementing HGWO-based MPPT are: (1) the method effectively converges to the best value in large search spaces, (2) the algorithm is robust and efficient, (3) the probability of getting stuck in local minima is reduced, and (4) the speed of convergence is higher than most of the hybrid meta-heuristic techniques. Here, PSO falls in local minima in high and complex dimensional space and, along with this, GWO suffers from low solving precision with a comparatively higher convergence rate for both. Hence, a hybrid technique considering the positives of PSO and GWO is proposed for MPP extraction. The exploitation and exploration of hybrid GWO are based on grey wolf optimization and particle swarm optimization, respectively. The modified governing Equations for the first three wolves are given by Equations (5) and (7). The velocity and position update Equation of PSO are shown by Equations (8) and (11).

In Figure 1, the SPV system is connected to a boost converter, where the switching pulses of the MOSFET of the boost converter is given by the proposed HGWO–MPPT algorithm. The voltage across the capacitor (V_dc) is converted in three-phase AC with the help of inverter gating pulses. Here, duty cycle ($\mathrm{d})$ is the grey wolf, and to find the optimal value of D is the main aim of the algorithm. During dynamic changing conditions, the current sensed by the HGWO–MPPT Algorithm changes with every change in irradiance. The proposed algorithm updates the optimum duty cycle value for the boost converter to extract maximum power at that instance. The robustness and versatility of the developed hybrid meta-heuristic MPPT algorithm, coupled with fast voltage and current sensors, are the key in avoiding the condition of ‘MPPT failure’ [49]. Figure 7 shows the flowchart for the proposed algorithm; it is divided into four stages:

Sensing phase: in this phase, the voltage $\left({\mathrm{V}}_{\mathrm{P}\mathrm{V}}\right)$ and current $\left({\mathrm{I}}_{\mathrm{P}\mathrm{V}}\right)$ from the SPV system is sensed, and the initialization of coefficient vectors for the GWO algorithm is done, where $\mathrm{q}$ is linearly decreased from 2 to 0 over the course of iterations and r1, r2 are random vectors in [8,11].

$$\mathrm{a}=2\mathrm{q}·\overrightarrow{{\mathrm{r}}_1}-\mathrm{q}.$$

(5)

$$\mathrm{c}=2·\overrightarrow{{\mathrm{r}}_2}$$

(6)

Encircling of Wolves: the initial values of wolves are done using (7) and (8) function and, moreover, the pack is formed.

$$\overrightarrow{{\mathrm{D}}_{\mathsf{\alpha }/\mathsf{\beta }/\mathsf{\delta }}}=|\mathrm{c}·\overrightarrow{{\mathrm{d}}_{\mathsf{\alpha }/\mathsf{\beta }/\mathsf{\delta }}}- \mathrm{d} \to \left(\mathrm{i}\right)$$

(7)

$$\mathrm{d} \to \left(\mathrm{i}+1\right)=\overrightarrow{{\mathrm{d}}_{\mathsf{\alpha }/\mathsf{\beta }/\mathsf{\delta }}}-\mathrm{a}·\overrightarrow{{\mathrm{D}}_{\mathsf{\alpha }/\mathsf{\beta }/\mathsf{\delta }}}$$

(8)

where $\overrightarrow{{\mathrm{d}}_{\mathsf{\alpha }}}, \overrightarrow{{\mathrm{d}}_{\mathsf{\beta }}}, \overrightarrow{{\mathrm{d}}_{\mathsf{\delta }}}$ are the position vectors of $\mathsf{\alpha }$, $\mathsf{\beta }$ and $\mathsf{\delta }$ wolves, respectively; $\overrightarrow{{\mathrm{D}}_{\mathsf{\alpha }}}$,$\overrightarrow{{\mathrm{D}}_{\mathsf{\beta }}}$,$\overrightarrow{{\mathrm{D}}_{\mathsf{\delta }}}$ define the encircling behavior of $\mathsf{\alpha }$, $\mathsf{\beta }$ and $\mathsf{\delta }$ wolves respectively. The below Equations (9) and (11) define the updated position vector of the wolf and is inspired from PSO particle updating.

$${\mathrm{d}}_{\mathsf{\alpha }/\mathsf{\beta }/\mathsf{\delta }}\left(\mathrm{i}+1\right)={\mathrm{d}}_{\mathsf{\alpha }/\mathsf{\beta }/\mathsf{\delta }}+\mathrm{v}\left(\mathrm{i}+1\right)$$

(9)

$${\mathrm{w}}_{\mathrm{pso}}\left(\mathrm{t}\right)={\mathrm{w}}_{\max }-\frac{\left({\mathrm{w}}_{\max }-{\mathrm{w}}_{\min }\right)}{\mathrm{T}}\ast \mathrm{t}$$

(10)

$$\mathrm{v}\left(\mathrm{i}+1\right)={\mathrm{w}}_{\mathrm{pso}}\left(\mathrm{t}\right)\ast {\mathrm{v}}_{\mathrm{i}}\left(\mathrm{t}\right)+{\mathrm{c}}_1·{\mathrm{r}}_{\mathrm{pso}1}\left({\mathrm{d}}_{\mathsf{\alpha }}-{\mathrm{d}}_{\mathsf{\alpha }}\left(\mathrm{i}\right)\right)+{\mathrm{c}}_2·{\mathrm{r}}_{\mathrm{pso}2}\left({\mathrm{d}}_{\mathsf{\beta }}-{\mathrm{d}}_{\mathsf{\beta }}\left(\mathrm{i}\right)\right)+{\mathrm{c}}_3·{\mathrm{r}}_{\mathrm{pso}3}\left({\mathrm{d}}_{\mathsf{\delta }}-{\mathrm{d}}_{\mathsf{\delta }}\left(\mathrm{i}\right)\right)$$

(11)

Evaluation Phase: during this phase, the objective function of the GWO-inspired MPPT algorithm is formulated in (12). This change in SPV power in consecutive iterations should be minimum.

$${\mathrm{P}}_{\mathrm{pv}}\left({\mathrm{D}}^{\mathrm{i}+1}\right)>{\mathrm{P}}_{\mathrm{pv}}\left({\mathrm{D}}^{\mathrm{i}}\right)$$

(12)

Termination Phase: this stage checks for changes in ${\mathrm{P}}_{\mathrm{pv}}$ due to changes in irradiance (presence of shade) and also evaluates the termination criteria, i.e., the maximum iterations. If these conditions are not met, then the whole process is reinitiated until the optimal duty cycles are obtained. Equations (5) and (11) present the mathematical modelling of the proposed HGWO technique and (12) defines the objective function for the problem of optimal MPPT.

4. Results and Discussion

The results and discussion section presents the performance analysis of the proposed hybrid intelligent HGWO MPPT controller under varying scenarios. This section is further divided into two subsections, first focusing on the simulation results for the 5 × 5 SPV system, and then testing HGWO MPPT on a practical 6.4 kW SPV system.

4.1. Simulation Results

The simulation work has been performed for a 5 × 5 system with 11.25 kW_p rating. The performance is analyzed on the basis of rise time $\left({\mathrm{t}}_{\mathrm{rs}}\right)$, settling time $\left({\mathrm{t}}_{\mathrm{st}}\right)$, maximum power extracted $\left({\mathrm{P}}_{\mathrm{mp}}\right)$, shading loss $\left({\mathrm{P}}_{\mathrm{sl}}\right)$, and efficiency $\left(\mathsf{\eta }\right)$. The above-mentioned parameters define the dynamic and steady-state performance of the MPPT controllers. On the basis of these parameters, the performance of the HGWO, PSO and INC MPPT controllers is assessed for three types of configurations of the SPV system (as mentioned in Section 3). In this work, the effectiveness and robustness in tracking MPP is addressed, as the MPPT techniques are tested for different shading conditions, as shown in Figure 4.

Table 3. Control parameters for the INC, PSO and HGWO algorithms.

Algorithms	Parameters
INC	${\mathrm{K}}_{\mathrm{p}}=$1.93, ${\mathrm{K}}_{\mathrm{i}}=$ 2.35
PSO	${\mathrm{w}}_{\mathrm{pso}}$$=0.83 \left(\mathrm{fixed}\right), {\mathrm{c}}_1$$=2, {\mathrm{c}}_2$$=2.4, {\mathrm{r}}_{\mathrm{pso}1}={\mathrm{r}}_{\mathrm{pso}2}$= rand (0,1)
HGWO	${\mathrm{w}}_{\mathrm{pso}}$$\mathrm{given} \mathrm{by} \mathrm{Equations}. 10 \left(\mathrm{variable}\right), {\mathrm{c}}_1$$=1.4, {\mathrm{c}}_2$$=1, {\mathrm{c}}_3$$=1, {\mathrm{r}}_{\mathrm{pso}1}={\mathrm{r}}_{\mathrm{pso}2}={\mathrm{r}}_{\mathrm{pso}3}$= rand (0, 1)
Common Parameters for Optimization Algorithms
Iterations	1000
Tolerance	10−3
Population Size	5
Sampling Time	10−5 s

presents the different control parameter values for the discussed MPPT algorithms. These values for PSO and HGWO were chosen by a trial-and-error method, such that, a common optimum value can suffice for the optimal performance for each scenario. Meanwhile, the values of ${\mathrm{K}}_{\mathrm{p}}$ and ${\mathrm{K}}_{\mathrm{i}}$ are the values of the proportional and integral controller for INC-based MPPT.

$${\mathrm{P}}_{\mathrm{sl}}={\mathrm{P}}_{\mathrm{nmp}}-{\mathrm{P}}_{\mathrm{mp}}$$

(13)

$$\mathsf{\eta }=\frac{{\mathrm{P}}_{\mathrm{mp}}}{{\mathrm{P}}_{\mathrm{nmp}}}$$

(14)

Scenario 1—No Shading (NS): During this scenario, as for all the configurations, ${\mathrm{P}}_{\mathrm{n}\mathrm{m}\mathrm{p}}$ is 11,250 W as a constant irradiance of 1000 $\mathrm{W}/{\mathrm{m}}^2$ is incident on each of the 25 panels. Since this scenario is also known as STC, the performance of the MPPTs for each of the configurations is similar and MPP from the controllers is also the same. The performance for no shading is presented in Figure 8 and

Table 4. Comparative performance analysis for scenario 1.

Configuration	MPPT	Performance Parameters
		${\mathbf{P}}_{\mathbf{m}\mathbf{p}} \left(\mathbf{W}\right)$	${\mathbf{P}}_{\mathbf{s}\mathbf{l}} \left(\mathbf{W}\right)$	$\mathsf{\eta } (\%)$	${\mathbf{t}}_{\mathbf{r}\mathbf{s}} \left(\mathbf{s}\right)$	${\mathbf{t}}_{\mathbf{s}\mathbf{t}} \left(\mathbf{s}\right)$
SP/TCT/GWOBLTCT	INC	10073	1177	89.54	0.04	0.14
	PSO	10685	565	94.97	0.03	0.06
	HGWO	10856	394	96.59	0.05	0.06

.

Scenario 2—Column Shading (CS): In this scenario, two columns, C4 and C5, of the 5 × 5 SPV system are shaded. The irradiance incident on the panels of columns C4 and C5 is 600 W/m² and 400 W/m², respectively. Figure 9 shows the performance of different MPPT controllers for each type of configuration. The proposed HGWO controller extracts the maximum power for each of the arrangements of the SPV system. The performance parameters for scenario 2 are presented in

Table 5. Comparative performance analysis for scenario 2.

Configuration	MPPT	Performance Parameters
		${\mathbf{P}}_{\mathbf{m}\mathbf{p}} \left(\mathbf{W}\right)$	${\mathbf{P}}_{\mathbf{s}\mathbf{l}} \left(\mathbf{W}\right)$	$\mathsf{\eta } (\%)$	${\mathbf{t}}_{\mathbf{r}\mathbf{s}} \left(\mathbf{s}\right)$	${\mathbf{t}}_{\mathbf{s}\mathbf{t}} \left(\mathbf{s}\right)$
SP	INC	7291	1681	81.26	0.03	0.10
	PSO	7425	1547	82.75	0.02	0.10
	HGWO	8256	716	92.02	0.08	0.12
TCT	INC	7339	1633	81.79	0.03	0.10
	PSO	7967	1005	88.80	0.02	0.10
	HGWO	8288	684	92.38	0.08	0.12
GWOBLTCT	INC	7567	1535	83.13	0.03	0.10
	PSO	8133	969	89.35	0.02	0.10
	HGWO	8561	541	94.06	0.07	0.08

.

Scenario 3—Row Shading (RS): In this scenario, two rows, R4 and R5, of the 5 × 5 SPV system are shaded. The irradiance incident on the panels of column R4 and R5 is 600 W/m² and 400 W/m², respectively. Figure 10 shows the performance of different MPPT controllers for each type of configuration. The performance parameters for scenario 2 are presented in

Table 6. Comparative performance analysis for scenario 3.

Configuration	MPPT	Performance Parameters
		${\mathbf{P}}_{\mathbf{m}\mathbf{p}} \left(\mathbf{W}\right)$	${\mathbf{P}}_{\mathbf{s}\mathbf{l}} \left(\mathbf{W}\right)$	$\mathsf{\eta } (\%)$	${\mathbf{t}}_{\mathbf{r}\mathbf{s}} \left(\mathbf{s}\right)$	${\mathbf{t}}_{\mathbf{st}} \left(\mathbf{s}\right)$
SP	INC	5695	949	85.72	0.03	0.18
	PSO	6227	417	93.72	0.03	0.16
	HGWO	6441	203	96.94	0.07	0.08
TCT	INC	5894	751	88.68	0.03	0.18
	PSO	6298	347	94.77	0.03	0.16
	HGWO	6488	157	97.65	0.07	0.08
GWOBLTCT	INC	6126	751	89.08	0.03	0.18
	PSO	6527	350	94.91	0.04	0.08
	HGWO	6738	139	97.98	0.07	0.08

. During the RS scenario, the steady-state response of the INC controller is not free from oscillations; similarly, PSO also has oscillations in tracking the power, whereas the MPP extracted from HGWO is free from oscillations and is more in comparable with PSO and INC. The GWOBLTCT-type of configuration of the PSO controller performs better than scenario 2.

Scenario 4—Diagonal Shading (DS): In this scenario, the primary diagonal of the 5 × 5 SPV system is partially shaded. The irradiance incident on the panels of the diagonal is 800 W/m², 600 W/m² and 400 W/m². Figure 11 shows the performance of different MPPT controllers for each type of configuration. The proposed HGWO controller has an average efficiency of 92.59% across all the topologies. This average efficiency in tracking the MPP is better in comparison to 76.74% for INC and 88.28% for PSO techniques. Here, PSO has irregular behavior in transient state and INC during steady-state. Both INC and PSO have fluctuations while trying to track the maximum power during DS-type of shade. The performance parameters for scenario 4 are presented in

Table 7. Comparative performance analysis for scenario 4.

Configuration	MPPT	Performance Parameters
		${\mathbf{P}}_{\mathbf{mp}} \left(\mathbf{W}\right)$	${\mathbf{P}}_{\mathbf{sl}} \left(\mathbf{W}\right)$	$\mathsf{\eta } (\%)$	${\mathbf{t}}_{\mathbf{rs}} \left(\mathbf{s}\right)$	${\mathbf{t}}_{\mathbf{st}} \left(\mathbf{s}\right)$
SP	INC	5267	1737	75.19	0.04	0.11
	PSO	6125	879	87.45	0.03	0.14
	HGWO	6347	657	90.61	0.07	0.08
TCT	INC	6651	1919	77.60	0.04	0.11
	PSO	7563	1007	88.21	0.03	0.14
	HGWO	7969	601	92.98	0.07	0.08
GWOBLTCT	INC	6887	2009	77.41	0.04	0.11
	PSO	7932	964	89.16	0.03	0.14
	HGWO	8377	519	94.16	0.07	0.08

.

Scenario 5—Corner Shading (CNRS): In this scenario, all the panels present in the corner of the 5 × 5 SPV system are partially shaded, as shown in Figure 4e. The irradiance incident on the panels of diagonal is 800 W/m², 600 W/m² and 400 W/m². Figure 12 shows the performance of different MPPT controllers for each type of configuration. During this scenario, the controllers INC, PSO and HGWO have an average efficiency of 78.34%, 90.33% and 92.05%. The proposed HGWO has comparatively better transient and steady characteristics of tracking MPP. INC still suffers from oscillations while trying to track the maximum power during CNRS-type of shade, whereas PSO performs significantly well under this challenging scenario. ${\mathrm{P}}_{\mathrm{m}{\mathrm{p}}_{\mathrm{pso}}}$ is better than INC and very close to ${\mathrm{P}}_{{\mathrm{mp}}_{\mathrm{hgwo}}}$. The performance parameters for scenario 5 are presented in

Table 8. Comparative performance analysis for scenario 5.

Configuration	MPPT	Performance Parameters
		${\mathbf{P}}_{\mathbf{mp}} \left(\mathbf{W}\right)$	${\mathbf{P}}_{\mathbf{sl}} \left(\mathbf{W}\right)$	$\mathsf{\eta } (\%)$	${\mathbf{t}}_{\mathbf{rs}} \left(\mathbf{s}\right)$	${\mathbf{t}}_{\mathbf{st}} \left(\mathbf{s}\right)$
SP	INC	4531	1565	74.32	0.06	0.10
	PSO	5439	657	89.22	0.02	0.06
	HGWO	5567	529	91.32	0.07	0.08
TCT	INC	5693	1436	79.85	0.06	0.10
	PSO	6403	726	89.81	0.02	0.06
	HGWO	6537	592	91.69	0.07	0.08
GWOBLTCT	INC	5871	1391	80.84	0.06	0.10
	PSO	6678	584	91.95	0.02	0.06
	HGWO	6764	498	93.14	0.07	0.08

.

A summarized analysis can be presented from the above study of the impact of different shades on the performance of MPPT techniques for different configurations.

Table 9. Overall performance comparison among various MPPT controllers.

MPPT	${\mathsf{\eta }}_{\mathbf{avg}} \left(\mathbf{\%}\right)$	${\mathbf{C}}_{\mathbf{f}}$
INC	82.90	2.45
PSO	91.01	2.78
GWO [50]	92.57	1.39
HGWO	94.30	0.20
IT-2 FL [51]	86.84	0.10
ANFIS [5]	91.67	0.32

presents a summary of the performance of different MPPT techniques on the basis of average efficiency and convergence factor $\left({\mathrm{C}}_{\mathrm{f}}\right)$. This convergence factor is an attempt to address the speed of convergence and the robustness of the MPPT controllers. It is given by Equation (15)

$${\mathrm{C}}_{\mathrm{f}}=\frac{{\mathrm{t}}_{\mathrm{st}}-{\mathrm{t}}_{\mathrm{rs}}}{{\mathrm{t}}_{\mathrm{rs}}}$$

(15)

From the different scenarios (i.e., 1–5), it was observed that the performance of the proposed HGWO-based MPPT technique was consistent and better for all the configurations. The dynamic and steady-state characteristics of PSO and INC were hampered. INC suffers from a drastic drop in the tracked power during sudden or low irradiance conditions whereas the performance of PSO–MPPT was affected due to various tuning parameters present in its design; this increases the computational time and complexity. Although in scenarios such as 3 and 4 PSO had better ${\mathrm{t}}_{\mathrm{rs}}$, due to higher computational time, ${\mathrm{t}}_{\mathrm{st}}$ was much higher, thus increasing the overall convergence and reducing the robustness to changing conditions. In addition, a single PSO MPPT was designed for different SPV system configurations subject to different shading. Thus, the exploitation and exploration factors ${\mathrm{c}}_1$ and ${\mathrm{c}}_2$ have values 2 and 2.4, i.e., ${\mathrm{c}}_1<{\mathrm{c}}_2$. Therefore, the initial response of PSO–MPPT is higher, but settles slowly at a lower value. Furthermore, Table 9 also compares the proposed HGWO–MPPT algorithm with Asymmetrical interval type-2 fuzzy logic control-based MPPT (IT-2 FL) and Adaptive neuro fuzzy inference system-based MPPT (ANFIS) presented in latest literature.

4.2. Practical Assessment

This section presents the results and elaborates the performance of the hybrid MPPT technique in real-time scenarios. The impact of changing irradiance and module temperature for the sunshine hours of the day is addressed in this analysis. The proposed HGWO-based MPPT controller is tested for the practical 6300 W_p SPV system. This system is a combination of fourteen 450 W_p SPV modules in a 7 × 2 arrangement on the rooftop of the Qassim University, KSA. This assessment is performed by collecting the data from the installed SPV system; this data includes irradiance incident on the system, module temperature, power and energy produced by the system. The recorded data for irradiance and temperature of a day are presented in Figure 13. These required data are collected through current sensors, voltage sensors, an irradiance meter and a wattmeter.

In Figure 14, the power and energy production corresponding to the irradiance and temperature for a day is presented. The installed rooftop system starts to produce power from 06:25 hrs until 17:55 hrs for a day in the month of October. The line graph in Figure 14 shows the energy production (Wh) from the SPV system and the area under the curve, i.e., the bar graphs depict the SPV power produced (W). It can be observed that the peak power is produced at 11:50 hrs. This peak SPV power using the HGWO–MPPT controller is recorded at 4896 W, whereas earlier it was 4661 W. Similarly, the total energy units recorded by the net meter was 31.55 kWh; this increased to 34.25 kWh for a day. The increase in SPV energy production was calculated to be 08.56% using the HGWO–MPPT controller. In Figure 14, a comparison is presented for energy and power production considering HGWO–MPPT and P&O MPPT (i.e., P_old and E_old is power and energy produced by the perturb and observe method). These values have been recorded in an online monitoring system for easier analysis.

5. Conclusions

In this work, performance analysis of a novel hybrid meta-heuristic MPPT controller is presented under various shading conditions. This hybrid MPPT controller is a combination of a grey wolf optimizer and particle swarm optimizer, and is known as HGWO–MPPT. Furthermore, testing of HGWO–MPPT is done in comparison with INC and PSO MPPT controllers. In addition, the study shows varying performance of the 5 × 5 SPV system with different configurations. Hence, each of the aforementioned MPPTs were tested for the following SPV topologies: SP, TCT, and GWOBLTCT. The proposed HGWO–MPPT algorithm performed better for all the shading scenarios and configurations considered. This comparison was performed considering ${\mathrm{P}}_{\mathrm{mp}}$, ${\mathrm{P}}_{\mathrm{sl}}$, $\mathsf{\eta }$, ${\mathrm{t}}_{\mathrm{rs}}$ and ${\mathrm{t}}_{\mathrm{st}}$. The HGWO–MPPT algorithm had better transient and steady-state dynamics in tracking the SPV power with high overall efficiency and minimum ${\mathrm{C}}_{\mathrm{f}}$, with values being 94.30% and 0.20, respectively. The presented MPPT controller was also tested for a 6300 Wp rooftop SPV system. The energy production for a single day improved by 08.56% using the HGWO–MPPT controller. The above results from the study establish that the developed MPPT algorithm is efficient and robust to changing meteorological conditions, as well as to different SPV configurations with high ${\mathrm{P}}_{\mathrm{mp}}$ and low ${\mathrm{P}}_{\mathrm{sl}}$. The above work helps in proposing more energy-efficient buildings with an integrated solar photovoltaic system.