Abstract
Traffic flow prediction can provide effective support for traffic management and control and plays an important role in the traffic system. Traffic flow has strong spatio-temporal characteristics, and existing traffic flow prediction models tend to extract long-term dependencies of traffic flow in the temporal and spatial dimensions individually, often ignoring the potential correlations existing between spatio-temporal information of traffic flow. In order to further improve the prediction accuracy, this paper proposes a coordinated attention-based spatio-temporal graph convolutional network (CVSTGCN) model for simultaneously and dynamically capturing the long-term dependencies existing between the spatio-temporal information of traffic flows. CVSTGCN is composed of a full convolutional network structure, which combines coordinate methods to specify the influence degrees of different feature information in different spatio-temporal dimensions, and the spatio-temporal information of different spatio-temporal dimensions by the graph convolutional network. In addition, the hard-swish activation function is introduced to replace the Rectified Linear Unit (ReLU) activation function in the prediction of traffic flow. Finally, evaluation experiments are conducted on two real datasets to demonstrate that the proposed model has the best prediction performance in both short-term and long-term forecasting.
1. Introduction
The advent of the era of big data, the development of data mining technology and vehicle communication technology [1] has brought new ideas to solve traffic problems and promoted better and faster development of intelligent transportation systems. Intelligent Transportation System (ITS) is used to effectively manage and control the transportation system network through massive traffic big data [2], all in a reasonable and effective way to reduce traffic congestion and improve transportation services. Traffic data are an important basis for ITS analysis and decision making. Real-time and accurate traffic data provides commuters, government agencies and the public with reasonable decisions.
With the continuous growth of car ownership, the growing number of vehicles in limited road resources will inevitably cause phenomena such as road space loading. Traffic flow prediction serves intelligent transportation system, which can effectively alleviate traffic congestion and other phenomena by using current and past moment traffic information (flow, speed and density, etc.) for predicting traffic flow in future moments. Real-time and accurate traffic flow forecasting is the primary goal, real-time forecasting data can provide road participants with sufficient decision-making time and make the best decision choice, while accurate forecasting data are a necessary condition for traffic flow forecasting, more accurate forecasting data can respond to more accurate traffic statuses to make more applicable decisions. Traffic flow can respond to the traffic state, traffic flow prediction helps the traffic department to perceive the traffic state in advance, to provide reference meaning for traffic planning and traffic management, to develop reasonable traffic deployment, to reach the purpose of relieving traffic congestion and reducing traffic accidents, and also to provide road participants with suitable travel routes to provide safe and high rate of travel. Traffic flow forecasting is usually bound by 30 min and divided into short-time traffic flow forecasting (up to 30 min) and long-time traffic flow forecasting (more than 30 min). Most forecasting methods, which achieve good performance in short-time traffic flow prediction problems, do not perform as well as expected in long-time prediction problems, which is mainly attributed to the uncertainty and complexity of traffic flow [3], and the nonlinear characteristics of traffic flow are amplified as the prediction time deepens, which affects the accuracy of the prediction.
At this stage, much literature, including [3,4,5,6,7], explore the complex nonlinear relationships of traffic flow from both time and space dimensions. A convolutional neural network is the main tool for traffic flow spatial information exploration. A traffic prediction model with traditional convolutional network as the main body can only extract local spatial information based on the limitation of grid data input, which cannot fully reflect the traffic variation of a complete road network, so graph convolutional networks gradually appear in the study of traffic problems, which we will introduce in detail in the following sections. With the continuous development of deep learning techniques, attention mechanisms are used to dynamically capture the long-term dependence of spatio-temporal information of traffic flow, based on the variability of traffic information in different spaces over time, for example, the traffic distribution in commercial and residential areas is not the same in the morning, midday and evening, and the potential correlation between such spatio-temporal information of traffic flow is often ignored, such as ASTGCN [4], IGAGCN [5], and MFDGCN [6] and other models capture the spatial dependence and temporal dependence of traffic information through two independent components, ignoring the dependence under the potential association of spatio-temporal information, and not specifying the degree of influence of multiple traffic flow characteristics in different spatio-temporal dimensions.
Based on the above existing problems, this paper proposes a novel deep learning network model (CVSTGCN) consisting of a fully convolutional network structure and collaboratively extracting spatio-temporal attention mechanisms for the purpose of improving traffic flow prediction accuracy. Firstly, in order to demonstrate the spatio-temporal characteristics of traffic flow information and the potential long-term dependence, we analyze the traffic flow information from two perspectives of time and space, respectively. Second, to fully explore the long-term dependencies of traffic flow information in the spatio-temporal dimension, we bring coordinated attention to the exploration of traffic flow spatio-temporal information inspired by channel attention in machine vision, which is used to dynamically capture the long-term dependencies (spatio-temporal attention weights) existing between traffic flow spatio-temporal information at the same time. Then, a combination of convolutional neural network and graph convolutional neural network is formed into CVSTGCN layer for interactive learning of spatio-temporal traffic flow information. The main contributions of the article are:
- Using Graph Convolutional Network (GCN) and attention mechanism, a traffic flow prediction model applicable to the generalization of global road network is proposed. By coordinating the attention mechanism, the potential correlation properties existing between the temporal and spatial dimensions are considered to quantify the dynamic dependencies of different time segments at different checkpoints; the influence degree of different feature information in different spatial and temporal dimensions is clarified by combining the coordinate method;
- Fully consider the influencing factors of traffic flow and analyze the spatio-temporal characteristics of traffic flow from several features, and select the traffic flow, average speed, and average occupancy as the learning objects of the model. In addition, in order to improve the flexibility and efficiency of the model, on the one hand, the long-term dependencies of the spatio-temporal dimension are learned with the help of convolutional networks, the graph structure information based on the spatial dimension is aggregated using graph convolutional networks, and the long-term dynamic dependencies based on the temporal dimension are aggregated using regular convolution; on the other hand, the hard-swish activation function is introduced into the traffic flow prediction, so that the model the prediction accuracy is further improved;
- The validity of our model is verified on two real datasets, and the excellent prediction performance of the proposed model is demonstrated by comparing other traffic flow prediction models, both in short-time and long-time prediction.
The rest of the paper is organized as follows. In Section 2, related work on traffic flow forecasting is discussed. Section 3 analyzes and defines the parameters related to traffic flow information and describes the proposed method in detail. In Section 4, two real traffic datasets are demonstrated and the experimental results are analyzed. Finally, it concludes with the research conclusions and outlook in Section 5.
2. Related Work
In recent years, statistical models based on data-driven methods and machine learning models are two representatives of the development process of traffic flow prediction [8]. Statistical models include Autoregressive Integrated Moving Average (ARIMA) models [9] and Kalman filter models [10], etc. ARIMA models were the first time-series models applied in the field of traffic flow forecasting and achieved considerable forecasting accuracy, after which a series of variants of ARIMA appeared in the study of traffic flow prediction, such as KARIMA [11], subset ARIMA [12], and seasonal ARIMA [13]. The system models relying on mathematical and statistical methods are static assumptions and do not capture the uncertainty (dynamics) and nonlinearity of traffic flow, while machine learning models overcome this aspect and can effectively capture the changing patterns of traffic flow by learning from historical traffic data, such as K-Nearest Neighbor (KNN) [14], SVR [15], and ANN [16] algorithmic models. In particular, artificial neural networks, based on the powerful self-learning ability and anti-interference ability of neural networks, have multiplied many efficient algorithmic models in the field of traffic prediction research and achieved a lot of results. The BP neural network [17] was the first neural network model applied in traffic flow prediction research, and then wavelet neural network (WNN) [18] and GA-BP [19] appeared along other derived network models. With continuous development, the emergence of deep learning models overcame the shortcomings of BP neural networks in dealing with complex problems such as slow convergence speed and high tendency to fall into local minima, and further promoted the accuracy of prediction in the research of traffic flow field. For example, Recurrent Neural Network (RNN) [20] iterates the traffic flow information of past moments through recurrent memory function, and its variants LSTM [21] and GRU [22] filter the information through a gating mechanism. In a recent study, Lu et al. [23] used the ability of ARMIA to capture linear features of time series combined with the ability of LSTM to capture nonlinear features of time series, mixed ARMIA and LSTM for traffic flow prediction by a dynamic weighting method. This proved that the hybrid model has better prediction performance. Huang et al. [24], in order to better exploit the potential periodicity of traffic flow, used the proposed time series decomposition (TSD) to decompose the traffic flow time series and combine with BiLSTM for traffic flow prediction.
Although most of the above studies researched traffic flow variation patterns in the temporal dimension, the spatial information is equally important for traffic flow variation in a complete traffic road network. As S.Narmadha et al. [25] found, weather-related factors are considered in traffic flow prediction, and the spatio-temporal characteristics of the road network input variables are captured using CNN and LSTM deep network models, respectively. The importance of the spatial information upstream and downstream of the target nodes is demonstrated, and the prediction model that also considers the spatio-temporal characteristics of the road network has a high prediction accuracy. The memory iteration and gating mechanism of the recurrent neural network model retains the sequence information of time segments, but its complex structure increases the training time and flexibility of the network, while the convolutional neural network has the features of simple structure, being flexible, versatile, and possessing fast training speed. Based on this, many scholars have predicted traffic flow using a network model with full convolution in recent years, such as Zhao et al. [26], who constructed a temporal convolutional network (TCN) by causal convolution, which obtained a larger sensory field with fewer parameters, not only reducing the computational cost of training but also obtaining better performance. Felix Rempe et al. [27] used deep convolutional neural networks (DCNNs) to accurately estimate spatio-temporal traffic speeds and reconstruct heterogeneous congestion types under sparse data on highways. Zhang et al. [28] proposed a new multi-task deep learning (MDL) framework for simultaneously predicting incoming and outgoing flows (node flows) as well as transition flows (edge flows) in spatio-temporal networks by capturing the spatio-temporal characteristics of traffic flows through a fully convolutional network (FCN) in order to more accurately capture the flow of traffic between regions. Most conventional convolutional methods are based on grid-based traffic data, which can only extract spatial information about upstream and downstream or local locations, while in a complete urban road network, the spatial information affecting the traffic flow changes to involve the whole network. For such topological road networks, recent works have applied graph convolutional networks (GCN) to traffic prediction, such as Zhao et al. [29] and Xu et al. [30], who combined GRU with GCN and RNN to capture the spatial information of road network topology through GCN. Lee et al. [31], to research traffic speed in future moments, combined three spatial dependencies of distance, direction, and location with a graph convolutional network to form a variety of different spatial graph elements, and used 1D convolution to extract temporal features to form a spatio-temporal convolutional block, which performed better in long-term prediction but did not perform as well as long-term prediction in short-term prediction. Chen et al. [32] used floating vehicle data as the basis and extracted traffic parameters of floating vehicle data through a grid model, combined with GCN to consider topological propagation patterns of intersections to construct a multi-task fusion deep learning (MFDL) model for predicting the passage time and speed of intersections at future moments.
The attention mechanism is a network approach to highlight important information about the learning object and has proven its effectiveness in many fields. Examples include natural language processing [33], image enhancement [34], and fault diagnosis [35]. In the research of traffic field, attention mechanism advances the drawback of existing models that tend to extract static spatio-temporal dependence information in traffic data, such as Guo et al. [4] who added attention mechanism to GCN and constructed a temporal attention block and spatial attention block for dynamically capturing long-term spatio-temporal dependence of traffic information, respectively. Later, An et al. [5] used the knowledge of information geometry to measure the distribution differences of data between nodes as a priori information to enhance the spatial attention matrix based on ASTGCN. Xu et al. [36] and Zheng et al. [37] embedded the transformer into the spatio-temporal prediction problem of traffic flow and proposed a spatial-temporal block ST (Spatial-Temporal Transformer) for dynamically capturing spatio-temporal information and long-term dependencies of traffic flows. The transformer [38] achieves efficient sequence learning through a highly parallel self-attentive mechanism, but the self-attentive mechanism is resource-intensive and is not a good choice in resource-limited situations due to the large amount of internal computation.
3. Methodology
3.1. Problem Analysis and Definition
3.1.1. Spatial and Temporal Characteristics of Traffic Flow
There are many factors affecting the traffic flow variation, such as traffic flow, vehicle speed, traffic density, headway or time distance and weather. Among them, traffic flow, vehicle speed and traffic density are the three main factors of traffic flow characteristics, referred to as the three elements of traffic flow, which serve for traffic system evaluation and traffic organization optimization. In this paper, the average occupancy is used instead of traffic density to reflect the traffic density during the observed time period. As shown in Figure 1, which shows the different characteristic information collected every 5 min on the same day, it can be seen that there is a strong correlation between the three. A large part of the speed of the vehicle in motion is influenced by the density of the traffic flow, the occupancy increases, the travel speed decreases; the occupancy decreases, the travel speed increases. The speed of traffic is lowest in the peak hours, and the corresponding low hours are the largest, and in the time dimension, it is negatively correlated with the change of traffic flow. There are many factors that affect the occupancy rate, such as the speed of the vehicle through the detector, the length of the body, etc. Fast speed, low occupancy rate; slow speed, high occupancy rate. Correspondingly from Figure 1, we can see that occupancy is positively correlated with traffic flow in the time dimension, and occupancy is high during peak hours and lower in the inverse time. In this paper, these three factors are chosen as the main basis for predicting traffic flow in future moments.
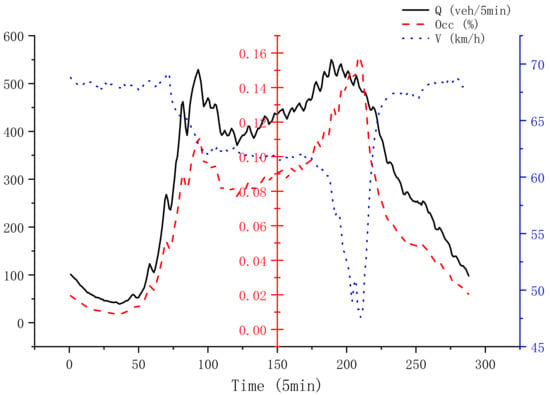
Figure 1.
Traffic flow (Q), Average speed (V), and Average Occupancy (Occ) Relationship Graph.
Traffic flow has strong spatial and temporal characteristics. The temporal characteristics are mainly reflected in the cyclical trend of traffic flow over time; the spatial characteristics are reflected in the changes of traffic flow in the road network with the changes of traffic information in adjacent road sections. Certain spatio-temporal correlations can be captured in parameters such as traffic flow, average speed and average occupancy, as shown in Figure 2a, which describes the trend of traffic flow for each day of the week, from which it can be seen that the traffic flow from Monday to Friday has an obvious change in the same trend in the process of low peak and peak shift, and the traffic flow at peak and low peak is also relatively close. There is some variability in the traffic flow on weekends compared to weekdays, which may be attributed to a change in travel patterns, but the overall trend of increase and decrease over time is still roughly the same. The spatial characteristics of the traffic flow are illustrated in Figure 2b, which depicts the traffic flow variation curves collected by three adjacent detectors during the same day time (where 314433, 3011042, and 3118593 denote the ID numbers of detectors, respectively), from which it can be seen that the increase or decrease in traffic flow in one road section will drive the increase or decrease in traffic flow in adjacent road sections, indicating that the traffic flow in adjacent road sections will affect each other. Similarly, the spatial correlation between the average speed and the average occupancy can be seen in Figure 2c,d, respectively. The correlation coefficient plotted in Figure 2d uses the average occupancy data of six adjacent detectors (D.1, D.2, D.3, D.4, D.5, and D.6) on the same day, and the scale on the right side shows the color shades corresponding to different correlation coefficients; the darker the color, the stronger the correlation. As can be seen from the figure, the correlation coefficient for each of the detector data reaches above 0.55, indicating that the average occupancy is correlated in the spatial dimension. In particular, several of the detector data have correlation coefficients reaching above 0.8, further highlighting the homogeneous trend of average occupancy in the traffic road network.
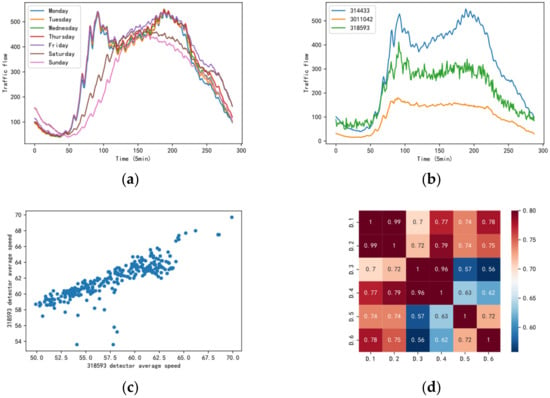
Figure 2.
Spatial and temporal characteristics analysis of traffic flow: (a) Daily traffic flow variation diagram; (b) traffic flow variation diagram at different detection points, (c) spatial relationship diagram of average speed; (d) spatial relationship diagram of average occupancy.
3.1.2. Definition of Road Traffic Flow on the Graph
A road traffic network is a topological structure graph composed of detectors as nodes and road connection sections between detectors as edges, denoted , where is the detection node and is the road connection between nodes. As shown in Figure 3a, a complete road network spatio-temporal graph, is composed of topological structure graphs at T moments. Where denotes the spatial topology graph at moment t. Each data node contains the traffic information vector at moment t. The graph information at moment t is denoted by , and this paper uses the adjacency matrix A to represent the connection of edge between nodes, and if edge exists, it is assigned a weight; if it does not exist, it is denoted by 0.
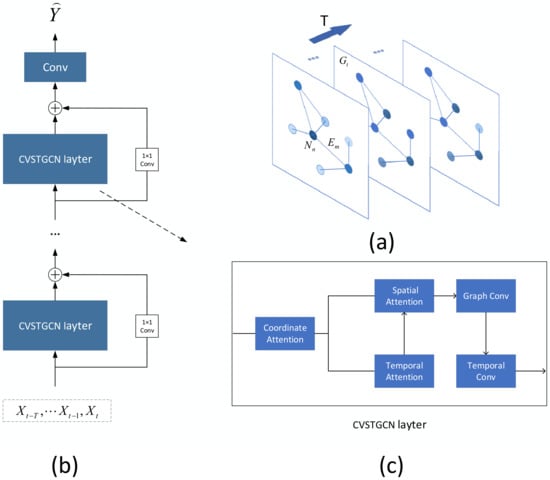
Figure 3.
(a) Representation of the topology of road information involving the temporal dimension; (b) is a CVSTGCN model framework consisting of multiple attentional spatio-temporal modules. The input of the model is the spatio-temporal information of the first T time steps, where is the output result of the model training, which is used to measure the model performance; (c) is the internal structure of a CVSTGCN layer. Temporal Convolution is composed of 1D convolution is used for interaction learning of temporal information.
3.2. Model Overview
In this section, based on the analysis and definition in the previous subsection, the general framework structure of the CVSTGCN model is outlined, and the principal methods involved in the prediction model are described in step-by-step detail, and suitable methods are selected to justify the traffic flow prediction model in the experimental section of the subsequent chapter.
The general framework structure of the proposed CVSTGCN model is shown in Figure 3, which first captures the long-term dependence of spatio-temporal information of traffic flow through the attention mechanism. Specifically, coordinated attention is applied to capture the attention matrix common to traffic information in the spatio-temporal dimension, after which the attention weights of traffic flow information in the temporal and spatial dimensions are further enhanced using the method in the literature [4], respectively. Secondly, the traffic flow information is learned interactively in spatial and temporal dimensions by graph convolutional network and temporal convolutional network to form a complete CVSTGCN layer, after which we improve the training performance of the model by the residual network structure to optimize the network for problems such as performance degradation or gradient disappearance due to the increase in depth to form a complete attentional spatio-temporal unit. The learning results are output by the Conv layer by stacking multiple attentional spatio-temporal unit blocks to fully learn the change pattern of input information.
3.2.1. Graph Convolutional Network (GCN)
Unlike conventional convolution, graph convolution faces a graph whose nodes’ neighbors are unordered and variable in size. Currently, graph convolution can be divided into graph convolution by spectral methods and graph convolution by spatial methods. The spectral method implements convolution by converting information on the graph into a spectral domain through the Graph Fourier transform, while the spatial method attempts to define convolution directly in the spatial domain, where the aggregate adjacency information represents the intermediate node. In this paper, we choose a graph convolution based on the spectral graph theory approach defined. The spectral approach [39] constructs the basis of the Graph Fourier transform with the help of the normalized Laplacian matrix , where is a real symmetric semi-positive definite matrix obtained from the adjacency matrix and the degree matrix of the graph, satisfying Equation (1), is a matrix unit consisting of eigenvectors of the eigenvalues of , satisfying Equations (2) and (3). The degree matrix is a diagonal matrix, where the diagonal elements , are unit matrices.
The operation of graph convolution can be defined as:
where denotes the filter that performs the convolution operation in the spectral domain and denotes the convolution operation of the graph convolution.
After the input information is convolved in the spectral domain, the convolved result is transformed back into the original spatial domain by an inverse Fourier transformation. However, the cost required to perform the decomposition of matrix eigenvalues in larger networks is expensive, constrained to a filter with Chebyshev polynomials of diagonal matrices [40], which can change the computational cost from to [39], is a very efficient way, which can be expressed as the definition as follows:
where are the coefficients of the Chebyshev polynomial, is the Laplace matrix constrained to (−1, 1), and the Chebyshev polynomial is (where, , ).
3.2.2. Coordinated Attention
Coordinated attention [41] is a kind of attention mechanism promoted on the base of SE [42] and CBAM [43], that is, the global dependencies of channel and spatial position information are considered at the same time, and their common feature is to tap the potential weight relationship between channel information with the help of pooling operations. Coordinated attention aggregates feature information along the horizontal and vertical directions, respectively, constituting two one-dimensional feature codes that capture the global dependency (weight) relationship of spatial location information by combining coordinates. In the study of spatio-temporal traffic information, we combine coordinated attention to capture the potential long-term dependencies in both the temporal and spatial dimensions. As shown in Figure 4, we pooled the input feature maps along two mutually perpendicular directions, respectively, to form two two-dimensional maps of convergent feature information, where the output of the nth node at moment t in the vertical direction is as follows:
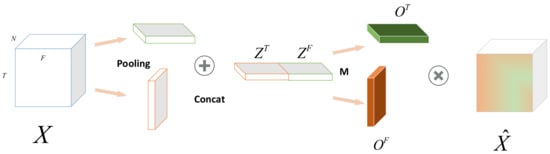
Figure 4.
Flow chart of coordinated attention.
Similarly, the output of node n at horizontal direction f is as follows:
In road traffic networks, the dependencies between nodes are not deterministic but change over time. To capture this highly dynamic correlation, we merge two feature mappings in the horizontal and vertical directions and perform a convolution operation (varying the channel number size) using a 1 × 1 convolution to enable cross-channel information to interact and tap potential spatial dependencies. The output of the convolution process is:
where, , , are nonlinear activation functions. has been applied in many large networks such as GoogleNet and ResNet through its own flexibility, and by controlling the number of channels to increase or decrease, the parameters of the model can be effectively controlled (there are fewer mapping parameters than full connections) based on achieving cross-channel information interaction, so that the network can be wide and deep enough. After that, we separate the feature tensor after the interaction by the original merged dimension and obtain two attention modules whose directions are perpendicular to each other by the Sigmoid activation function as follows:
With the above attention transformation, each attention block can capture not only the long-term dependence of spatial information, but also the long-term dependence of temporal and feature information along its own direction at the same time, and the importance of different feature information in different spatio-temporal dimensions can be clarified by combining the attention weights of relative vertical directions. Finally, the attention weights are combined with the input feature map to obtain the feature map of spatio-temporal information with long-term dependencies.
3.2.3. Activation Function
Activation functions are essential parts of deep learning models, they introduce nonlinear factors into the network models to make the network models learn more complex and deeper nonlinear relationships. They are also used to enhance the characterization ability of the network models. Currently, the common activation functions are Sigmoid, Tanh and ReLU, among which ReLU is the most widely and commonly used activation function. ReLU has the feature of no saturation compared with Sigmoid and Tanh, which avoids the risk of gradient disappearance in back propagation and improves the performance of the network model. In the field of traffic flow prediction ReLU is considered to be the universal activation function and few people have tried to improve the accuracy of traffic flow prediction from the perspective of the activation function. Based on the fact that ReLU is a zero-negative segmentation function, when the input value is negative, the gradient of neurons will become zero, which will cause some neurons to “die” and prevent the parameters from updating properly.
Traffic flow information involves several dimensions with different features, and the magnitude of these features are different, which can affect the comparative analysis of the data. When solved by the gradient descent method, this variability tends to affect the convergence speed of the model, and if the variability is large, it will make the model difficult to converge. Based on the uncertainty of traffic flow and the suddenness of external factors and traffic accidents, it tends to affect the extreme values of traffic flow data, such as the traffic flow in the free driving state, which tends to change according to the subjective consciousness of drivers; driving violations, weather factors, and sudden traffic accidents can make the traffic flow change greatly. Therefore, when processing traffic flow data, standardization is often chosen to resolve the difference in magnitude between features. The multidimensional traffic data are unified to the same scale by means and variances for effective analysis and learning. However, doing so can generate negative values for non-negative traffic data, further amplifying the disadvantage of “necrosis” of ReLU activation function neurons. Therefore, we try to find an alternative function to the ReLU activation function to further improve the prediction accuracy of traffic flow.
The Swish [44] activation function is a self-gated activation function, defined in Equation (11), whose structural simplicity and ReLU similarity make it often superior to the latter in deeper networks. As shown in Figure 5, its characteristics of smoothness, non-monotonicity, and unboundedness have proven its superior performance in research in the fields of image classification and machine translation. The nonlinear characteristics of the Swish activation function can further amplify the characteristics of traffic flow data nonlinearity, so that the network model more deeply learns nonlinear characteristics, and its unsaturated characteristics can also effectively avoid risks such as gradient disappearance, as well as its unboundedness which effectively overcomes the disadvantages of the ReLU activation function due to non-negative inputs, which further improves the characterization ability of the model while ensuring the learning efficiency of the network model. Based on the higher computational cost of the S-type function, this paper introduces Swish’s extension function hard-swish [45] to the research in the field of traffic flow to replace the role of the ReLU activation function, which is defined in Equation (12).
where s is the Sigmoid activation function and ReLU6 is a segmentation function that suppresses the output value of ReLU.
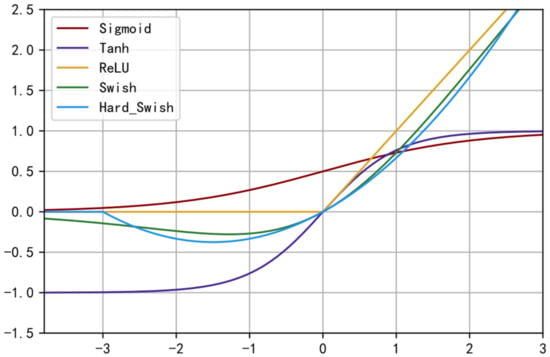
Figure 5.
Comparison of activation function curves.
4. Experiment
To verify the applicability of the model, this paper trains the network model with two real datasets and compares it with previous representative traffic flow prediction models to validate the performance of the proposed model in traffic flow prediction.
4.1. Datasets
The PEMS datasets is a relatively complete and comprehensive datasets for Californian freeways, which is divided into several detection zones, and the traffic data are counted by zones. In this paper, the datasets consisting of traffic flow, average speed, and average occupancy collected in zones D4 and D8 are selected to validate our model. The datasets consisting of 307 detectors with information aggregated every 5 min from January–February 2018 is selected for the D4 area, and the datasets consisting of 170 detectors with information aggregated every 5 min from June–August 2016 is selected for the D8 area.
4.2. Description of Evaluation Indicators and Parameter Settings
4.2.1. Evaluation Indicators
To facilitate comparison, the evaluation metrics MAE and RMSE, which are widely used in traffic flow forecasting, are chosen in this paper to evaluate our forecasting models, as follows:
where denotes the actual traffic flow collected at moment and denotes the traffic flow predicted by the model for moment .
4.2.2. Parameter Setting
In the experiments, six different traffic flow prediction models are chosen for comparison, which include (1) the Historical Average method (HA); (2) the Autoregressive Integrated Moving Average model (ARIMA); (3) two variants of recurrent neural networks, LSTM and GRU; and (4) the MSTGCN model without the attention mechanism and the ASTGCN model with the attention mechanism.
For fairness, the input time step of all models in this paper is set to the first 12 steps, i.e., the spatio-temporal information of the first 1 h is used as the learning object. In the proposed model, we choose a spectral convolutional network of order k = 3, the number of convolutional kernels is set to 64, and the mean square error (MSE) is chosen as the loss function of our model.
4.3. Experimental Results and Analysis
The validation results of the seven models on the two datasets are shown in Table 1 and Table 2, from which it can be seen that the CVSTGCN model proposed in this paper achieves the optimal prediction performance in all prediction time steps of the two datasets. The traditional model is not ideal for learning the nonlinear characteristics of traffic flow, and the model performance is getting worse as the number of prediction time steps and nodes increases. The deep learning model, however, has made great progress in traffic flow prediction based on its powerful self-learning ability and generalization ability, especially the prediction model that considers both temporal and spatial information, compared with the traditional prediction model that only considers temporal information LSTM and GRU show better prediction performance, which proves the importance of spatial information in traffic flow prediction.

Table 1.
Comparison of the prediction performance of different models on the PEME04 datasets (Some of the data results in the table are referenced from the literature [46]).

Table 2.
Comparison of the prediction performance of different models on the PEME08 datasets (Some of the data results in the table are referenced from the literature [46]).
It is noteworthy that the MSTGCN model has a significant increase in the long-term prediction error for the PEMS04 datasets with more detection nodes compared to the short- and medium-term prediction errors, which fully illustrate the importance of the attention mechanism in spatio-temporal traffic flow prediction, with the data structure and prediction time steps continually increasing, the uncertainty and nonlinear characteristics of traffic flow will also increase, and the attention mechanism can effectively extract the long-term dependence of spatio-temporal information of traffic flow, which suppresses the increase in such uncertainty and nonlinear characteristics and provides some help for the training learning of the prediction model.
The experimental results show that the CVSTGCN model proposed in this paper has the optimal prediction effect in the prediction of traffic flow and can effectively learn the nonlinear characteristics of traffic flow. As shown in Table 2, taking the validation results of PEMS08 datasets as an example, the MAE and RMSE values of CVSTGCN model compared with GRU model are reduced by 3.31 and 2.84 in short-time prediction and 3.58 and 1.94 in long-time prediction, respectively. This is because the CVSTGCN model involves spatial information of traffic flow based on temporal information, and through the spatio-temporal attention mechanism to learn the potential long-term dependence of traffic flow, which further improves the accuracy of prediction while increasing the learning efficiency. Compared with the best base model ASTGCN, the MAE and RMSE values are reduced by 0.37 and 0.56 in short-time prediction and 2.07 and 2.85 in long-time prediction, respectively. The coordinated attention mechanism, which takes into account the interaction between temporal dimension information and spatial dimension information, dynamically and collaboratively captures the long-term dependencies of traffic flow information in the spatio-temporal dimension, and fully considers the influence of different features in the spatio-temporal dimension.
Figure 6 shows the error distributions of the two prediction models for 12 prediction time steps on the two data sets, respectively. It can be intuitively seen that the overall prediction performance of the CVSTGCN model is better than that of the ASTGCN, where the quartile distance of the former is smaller than that of the latter, and the overall error distribution of the former is more concentrated, and the error growth of the former is lower than that of the latter as the prediction time step increases continuously.
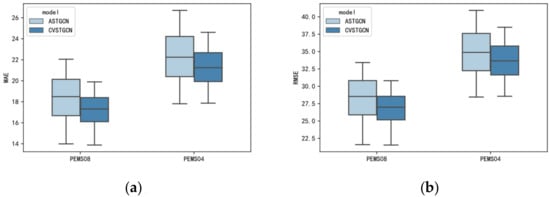
Figure 6.
Comparison of model prediction error distributions: (a) MAE values of the prediction models; (b) RMSE values of the prediction models.
Figure 7 shows the prediction results of two prediction models with attention mechanism (ASTGCN and CVSTGCN) compared with the real traffic values, and the prediction results of 30 min and 60 min are chosen to show the prediction performance of CVSTGCN more intuitively. For the nonlinearly varying traffic flow curves, both models can basically capture the trend of traffic flow and control the error within a certain range, while the gap between the prediction curve of the ASTGCN model and the target curve gradually increases as the prediction time step increases. In contrast, the prediction results of the CVSTGCN model are closer to the true values and maintain a good fit even at larger prediction time steps. This performance result indicates that the prediction models involving collaborative extraction of long-term dependencies of spatio-temporal information of traffic flows have better performance than those separately extracting long-term dependencies of spatio-temporal information of traffic flows, and from the side, it confirms that there is a certain potential connection between spatio-temporal information of traffic flows.
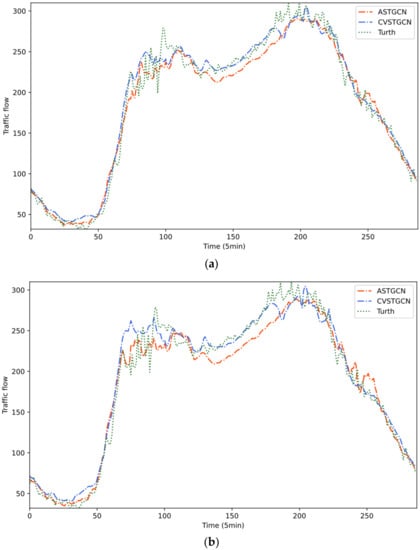
Figure 7.
Plot of predicted versus true values: (a) Prediction results for a prediction time step of 30 min; (b) prediction results for a prediction time step of 60 min.
To demonstrate the applicability of the hard-swish activation function in the field of traffic flow prediction, it is compared with the prediction results of the ReLU activation function. As shown in Figure 8, the prediction results of the CVSTGCN prediction model are plotted for the two activation functions at different prediction time steps on the two datasets, and it can be seen that the prediction error of the former is lower than that of the latter, especially on the datasets with larger prediction time intervals and more complex structures, hard-swish highlights a more excellent prediction performance.
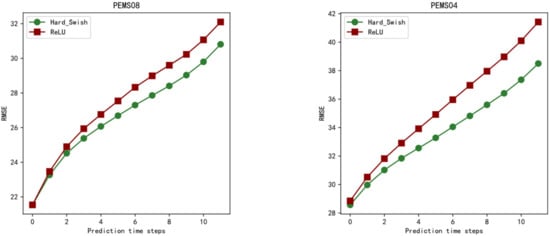
Figure 8.
REMS values for different activation functions.
5. Conclusions
In this paper, a spatio-temporal graph convolutional network model CVSTGCN based on coordinated attention is proposed for predicting traffic flow in future moments. The model is able to effectively extract the long-term dependencies of spatio-temporal information of traffic flow, determine the influence degree of different information features in different spatio-temporal dimensions, and introduce the hard-swish activation function into the prediction of traffic flow on the basis of considering the existence of potential correlations between spatio-temporal information of traffic flow. By comparing the results with other prediction models on real datasets, it is demonstrated that the prediction models extracting the long-term dependencies of spatio-temporal information of traffic flow by collaborative methods can effectively improve the prediction accuracy, and our proposed CVSTGCN prediction model shows the best prediction performance in both short-term and long-term prediction. In our future work, we will involve the study of traffic flow external factors, such as weather, distribution of cities, and population growth, to fully exploit the advantages of our model and further improve the prediction accuracy.
Author Contributions
Conceptualization, M.L. (Min Li) and M.L. (Mengshan Li); Methodology, M.L. (Min Li); Software, M.L. (Min Li) and M.L. (Mengshan Li); Validation, M.L. (Min Li), M.L. (Mengshan Li), D.L. and Z.L.; Formal analysis, M.L. (Mengshan Li) and J.L.; Investigation, M.L. (Mengshan Li) and D.L.; Data curation, M.L. (Mengshan Li); Writing—Original draft preparation, M.L. (Min Li) and M.L. (Mengshan Li); Writing—Review and editing, M.L. (Min Li) and D.L.; Supervision, J.L.; Project administration, B.L.; Funding acquisition, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Provincial Natural Science Foundation of Shandong (No. ZR2019MEE072) and the Shandong Taishan Scholars Construction Special Project (No. ts201712054) and the Hubei Natural Science Foundation Youth Project (No. 2020CFB320).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhu, J.; Easa, S.; Gao, K. Merging control strategies of connected and autonomous vehicles at freeway on-ramps: A comprehensive review. J. Intell. Connect. Veh. 2022, 5, 99–111. [Google Scholar] [CrossRef]
- Peled, I.; Lee, K.; Jiang, Y.; Dauwels, J.; Pereira, F.C. On the quality requirements of demand prediction for dynamic public transport. Commun. Transp. Res. 2021, 1, 100008. [Google Scholar] [CrossRef]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting. arXiv 2018. [Google Scholar] [CrossRef]
- Guo, S.; Lin, Y.; Feng, N.; Song, C.; Wan, H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 922–929. [Google Scholar] [CrossRef] [Green Version]
- An, J.; Guo, L.; Liu, W.; Fu, Z.; Ren, P.; Liu, X.; Tao, L.A. IGAGCN: Information geometry and attention-based spatiotemporal graph convolutional networks for traffic flow prediction. Neural Netw. 2021, 143, 355–367. [Google Scholar] [CrossRef] [PubMed]
- Cui, Z.; Zhang, J.; Noh, G.; Park, H.J. MFDGCN: Multi-Stage Spatio-Temporal Fusion Diffusion Graph Convolutional Network for Traffic Prediction. Appl. Sci. 2022, 12, 2688. [Google Scholar] [CrossRef]
- Liu, Y.; Lyu, C.; Zhang, Y.; Liu, Z.; Yu, W.; Qu, X. DeepTSP: Deep traffic state prediction model based on large-scale empirical data. Commun. Transp. Res. 2021, 1, 100012. [Google Scholar] [CrossRef]
- Ma, T.; Antoniou, C.; Toledo, T. Hybrid machine learning algorithm and statistical time series model for network-wide traffic forecast. Transp. Res. Part C Emerg. Technol. 2020, 111, 352–372. [Google Scholar] [CrossRef]
- Ahmaed, M.S.; Cook, A.R. Analysis of Freeway Traffic Time-Series Data by Using Box-Jenkins Technique. Transp. Res. Rec. 1979, 773, 1–9. [Google Scholar]
- Okutani, I.; Stephanedes, Y.J. Dynamic prediction of traffic volume through Kalman filtering theory. Transport. Res. B-Meth. 1984, 18, 1–11. [Google Scholar] [CrossRef]
- Voort, M.; Dougherty, M.; Watson, S. Combining kohonen maps with arima time series models to forecast traffic flow. Transp. Res. Part C Emerg. Technol. 1996, 4, 307–318. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Fambro, D. Application of Subset Autoregressive Integrated Moving Average Model for Short-Term Freeway Traffic Volume Forecasting. Transp. Res. Record. 1999, 1678, 179–188. [Google Scholar] [CrossRef]
- Williams, B.M.; Hoel, L.A. Modeling and Forecasting Vehicular Traffic Flow as a Seasonal ARIMA Process: Theoretical Basis and Empirical Results. J. Transp. Eng. 2003, 129, 664–672. [Google Scholar] [CrossRef] [Green Version]
- Chang, H.; Lee, Y.; Yoon, B.; Baek, S. Dynamic near-term traffic flow prediction: System-oriented approach based on past experiences. IET Intell. Transp. Syst. 2012, 6, 292–305. [Google Scholar] [CrossRef]
- Hu, W.; Yan, L.; Liu, K.; Wang, H. A Short-term Traffic Flow Forecasting Method Based on the Hybrid PSO-SVR. Neural Process. Lett. 2016, 43, 155–172. [Google Scholar] [CrossRef]
- Ghanim, M.S.; Muley, D.; Kharbeche, M. ANN-Based traffic volume prediction models in response to COVID-19 imposed measures. Sust. Cities Soc. 2022, 81, 103830. [Google Scholar] [CrossRef]
- Vythoulkas, P.C. Alternative approaches to short term traffic forecasting for use in driver information systems. In Proceedings of the Transportation and traffic theory proceedings of the 12th International Symposium on the Theory of Traffic Flow and Transportation, Berkeley, CA, USA, 21–23 July 1993; pp. 485–506. [Google Scholar]
- Du, W.; Zhang, Q.; Chen, Y.; Ye, Z. An Urban Short-term Traffic Flow Prediction Model Based on Wavelet Neural Network with Improved Whale Optimization Algorithm. Sust. Cities Soc. 2021, 69, 102858. [Google Scholar] [CrossRef]
- Peng, Y.; Xiang, W.; Dawson, K.A.; Indekeu, J.O.; Stanley, H.E.; Tsallis, C. Short-term traffic volume prediction using GA-BP based on wavelet denoising and phase space reconstruction. Phys. A 2020, 549, 123913. [Google Scholar] [CrossRef]
- Zou, Z.; Peng, H.; Liu, L.; Xiong, G.; Du, B.; Bhuiyan, M.Z.A.; Long, Y.; Li, D. Deep Convolutional Mesh RNN for Urban Traffic Passenger Flows Prediction. In Proceedings of the 2018 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Guangzhou, China, 8–12 October 2018; pp. 1305–1310. [Google Scholar]
- Zheng, Y.; Dong, C.; Dong, D.; Wang, S. Traffic Volume Prediction: A Fusion Deep Learning Model Considering Spatial–Temporal Correlation. Sustainability 2021, 13, 10595. [Google Scholar] [CrossRef]
- Zhang, D.; Kabuka, M.R. Combining Weather Condition Data to Predict Traffific Flow: A GRU Based Deep Learning Approach. IET Intell. Transp. Syst. 2018, 12, 578–585. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, Q.; Chen, G.; Seng, D. A combined method for short-term traffic flow prediction based on recurrent neural network. Alex. Eng. J. 2021, 60, 87–94. [Google Scholar] [CrossRef]
- Huang, H.; Chen, J.; Sun, R.; Wang, S. Short-term traffic prediction based on time series decomposition. Phys. A 2022, 585, 126441. [Google Scholar] [CrossRef]
- Narmadha, S.; Vijayakumar, V. Spatio-Temporal vehicle traffic flow prediction using multivariate CNN and LSTM model. Mater. Today Proc. 2021, 4, 249. [Google Scholar] [CrossRef]
- Zhao, W.; Gao, Y.; Ji, T.; Wan, X.; Ye, F.; Bai, G. Deep Temporal Convolutional Networks for Short-Term Traffic Flow Forecasting. IEEE Access 2019, 7, 114496–114507. [Google Scholar] [CrossRef]
- Rempe, F.; Franeck, P.; Bogenberger, K. On the estimation of traffic speeds with Deep Convolutional Neural Networks given probe data. Transp. Res. Part C Emerg. Technol. 2022, 134, 103448. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Sun, J.; Qi, D. Flow Prediction in Spatio-Temporal Networks Based on Multitask Deep Learning. IEEE Trans. Knowl. Data Eng. 2020, 32, 468–478. [Google Scholar] [CrossRef]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Li, H. T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction. IEEE. Trans. Intell. Transp. Syst. 2020, 21, 3848–3858. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Hou, L.; Zhang, Y.; Zhang, J. Passenger Flow Prediction of Scenic Spot Using a GCN–RNN Model. Sustainability 2022, 14, 3295. [Google Scholar] [CrossRef]
- Lee, K.; Rhee, W. DDP-GCN: Multi-graph convolutional network for spatiotemporal traffic forecasting. Transp. Res. Part C Emerg. Technol. 2022, 134, 103466. [Google Scholar] [CrossRef]
- Chen, D.; Yan, X.; Liu, X.; Wang, L.; Li, F.; Li, S. Multi-Task Fusion Deep Learning Model for Short-Term Intersection Operation Performance Forecasting. Remote Sens. 2021, 13, 1919. [Google Scholar] [CrossRef]
- Deng, H.; Ergu, D.; Liu, F.; Cai, Y.; Ma, B. Text sentiment analysis of fusion model based on attention mechanism. Procedia Comput. Sci. 2022, 199, 741–748. [Google Scholar] [CrossRef]
- Chen, Q.; Fan, J.; Chen, W. An improved image enhancement framework based on multiple attention mechanism. Displays 2021, 70, 102091. [Google Scholar] [CrossRef]
- Han, S.; Shao, H.; Huo, Z.; Yang, X.; Cheng, J. End-to-end chiller fault diagnosis using fused attention mechanism and dynamic cross-entropy under imbalanced datasets. Build Environ. 2022, 212, 108821. [Google Scholar] [CrossRef]
- Xu, M.; Dai, W.; Liu, C.; Gao, X.; Lin, W.; Qi, G.J.; Xiong, H. Spatial-Temporal Transformer Networks for Traffic Flow Forecasting. arXiv 2020. [Google Scholar] [CrossRef]
- Zheng, C.; Fan, X.; Wang, C.; Qi, J. GMAN: A Graph Multi-Attention Network for Traffic Prediction. arXiv 2019. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef] [Green Version]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. arXiv 2016. [Google Scholar] [CrossRef]
- Hou, Q.; Zhou, D.; Feng, J. Coordinate Attention for Efficient Mobile Network Design. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 13708–13717. [Google Scholar] [CrossRef]
- Jie, H.; Li, S.; Gang, S.; Albanie, S. Squeeze-and-Excitation Networks. arXiv 2017. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. arXiv 2018. [Google Scholar] [CrossRef]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Swish: A Self-Gated Activation Function. arXiv 2017. [Google Scholar] [CrossRef]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for MobileNetV3. arXiv 2019. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, H.-Y.; Qiu, Q.; Jian, Z.; Zhu, D.; Cheng, C.; He, L.; Liu, G.; Wen, X.; Hu, R. Augmented Multi-Component Recurrent Graph Convolutional Network for Traffic Flow Forecasting. ISPRS Int. J. Geo-Inf. 2022, 11, 88. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).