Improvement in Solar-Radiation Forecasting Based on Evolutionary KNEA Method and Numerical Weather Prediction
Abstract
:1. Introduction
2. Materials and Methods
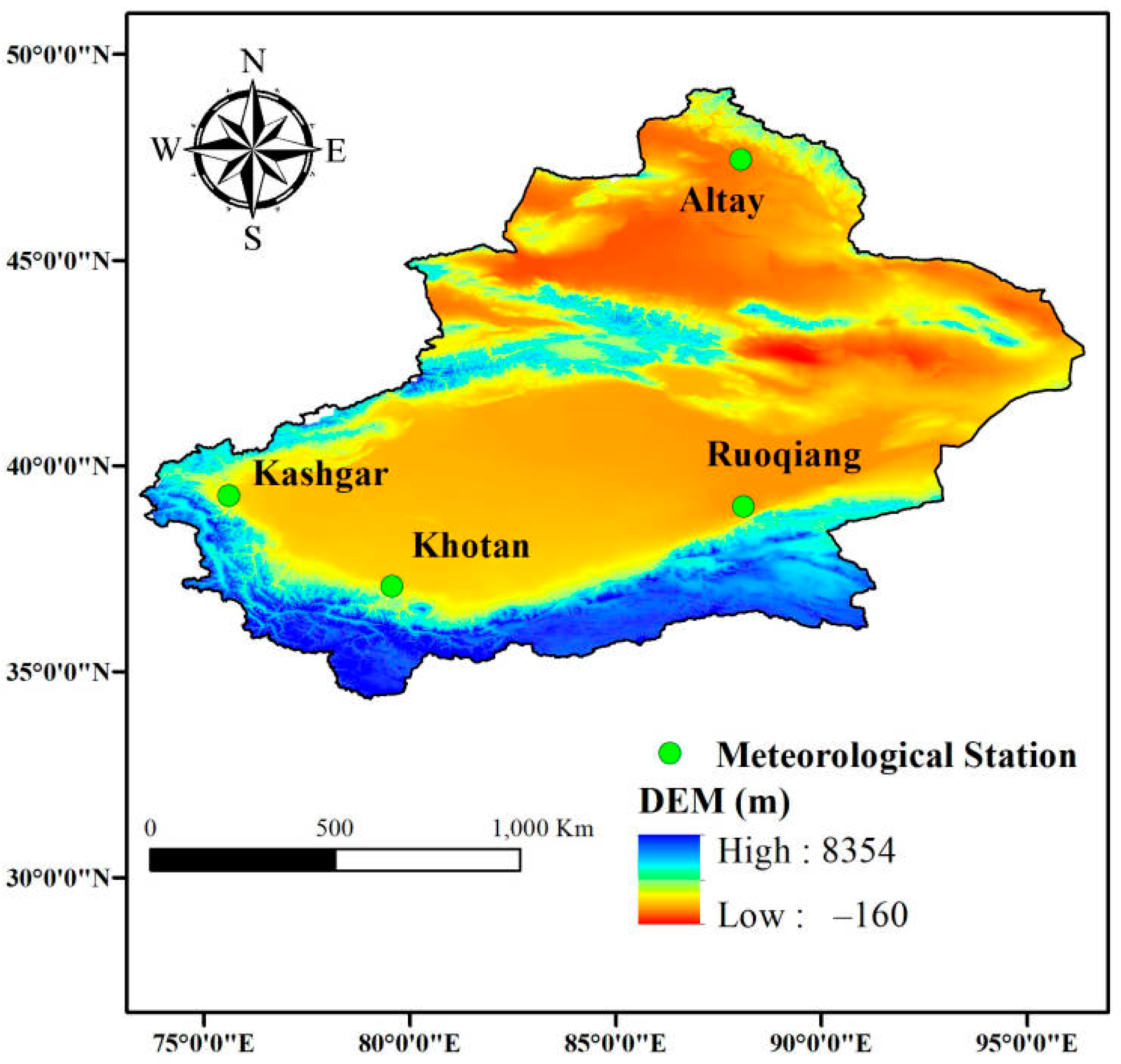
2.1. Study Region
2.2. Quantile Mapping (QM)
2.3. Equiratio Cumulative Distribution Function Matching (EDCDFm)
2.4. Machine-Learning Algorithms
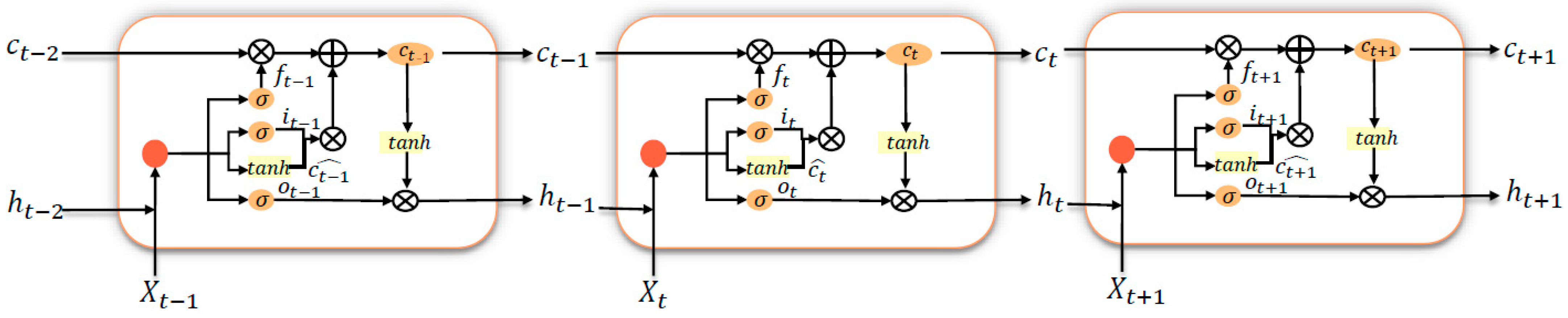
2.4.1. Long-Short Term Memory (LSTM)
2.4.2. Support Vector Machine (SVM)
2.4.3. Extreme Gradient Boosting (XGBoost)
2.4.4. Kernel-Based Nonliear Extension of Arps Decline (KNEA)
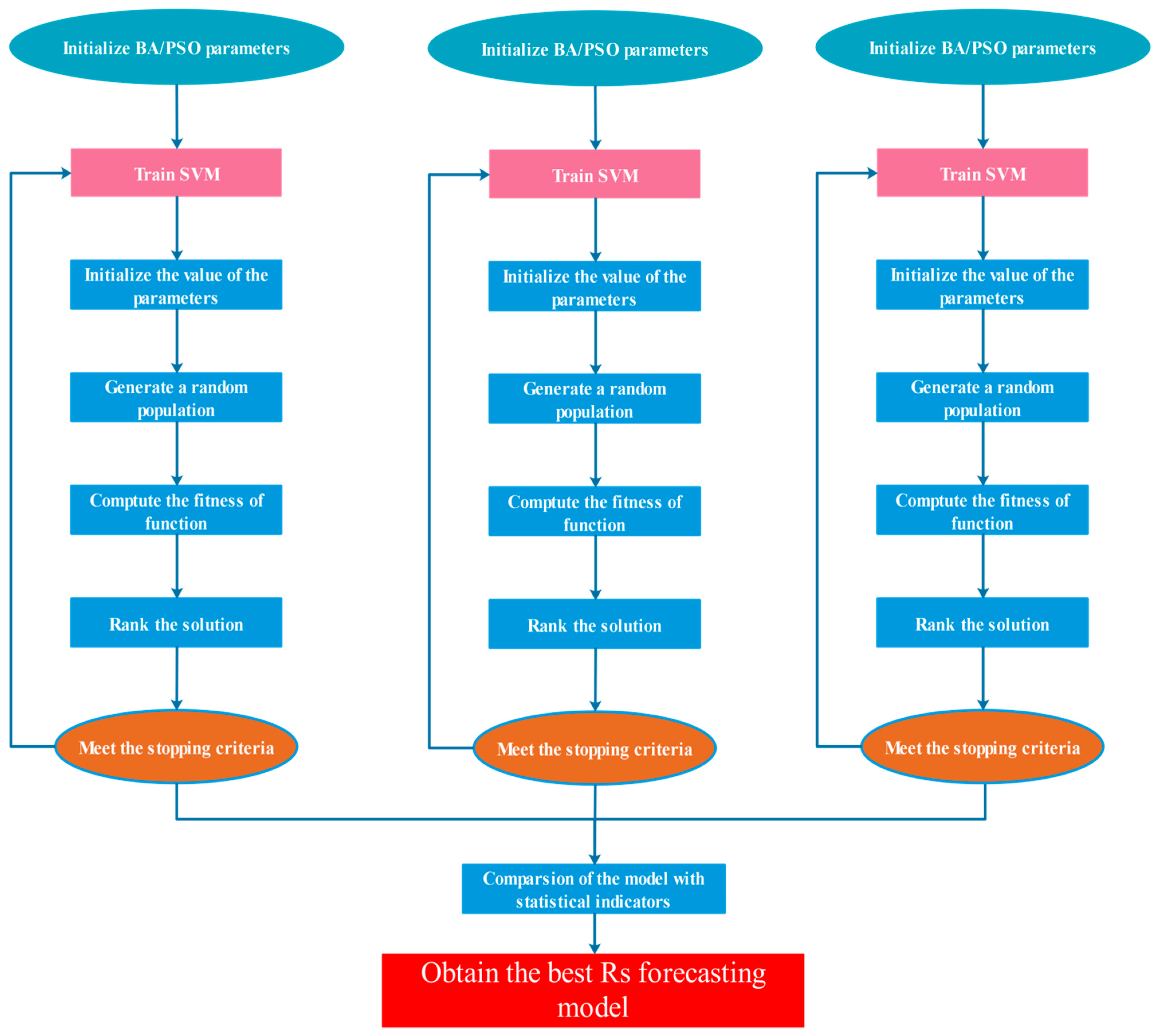
2.4.5. Bat Algorithm
2.4.6. Particle Swarm Optimization Algorithm (PSO)
2.5. Statistical Indicators
3. Results
3.1. Empirical Statistics Methods
3.2. Machine-Learning Methods
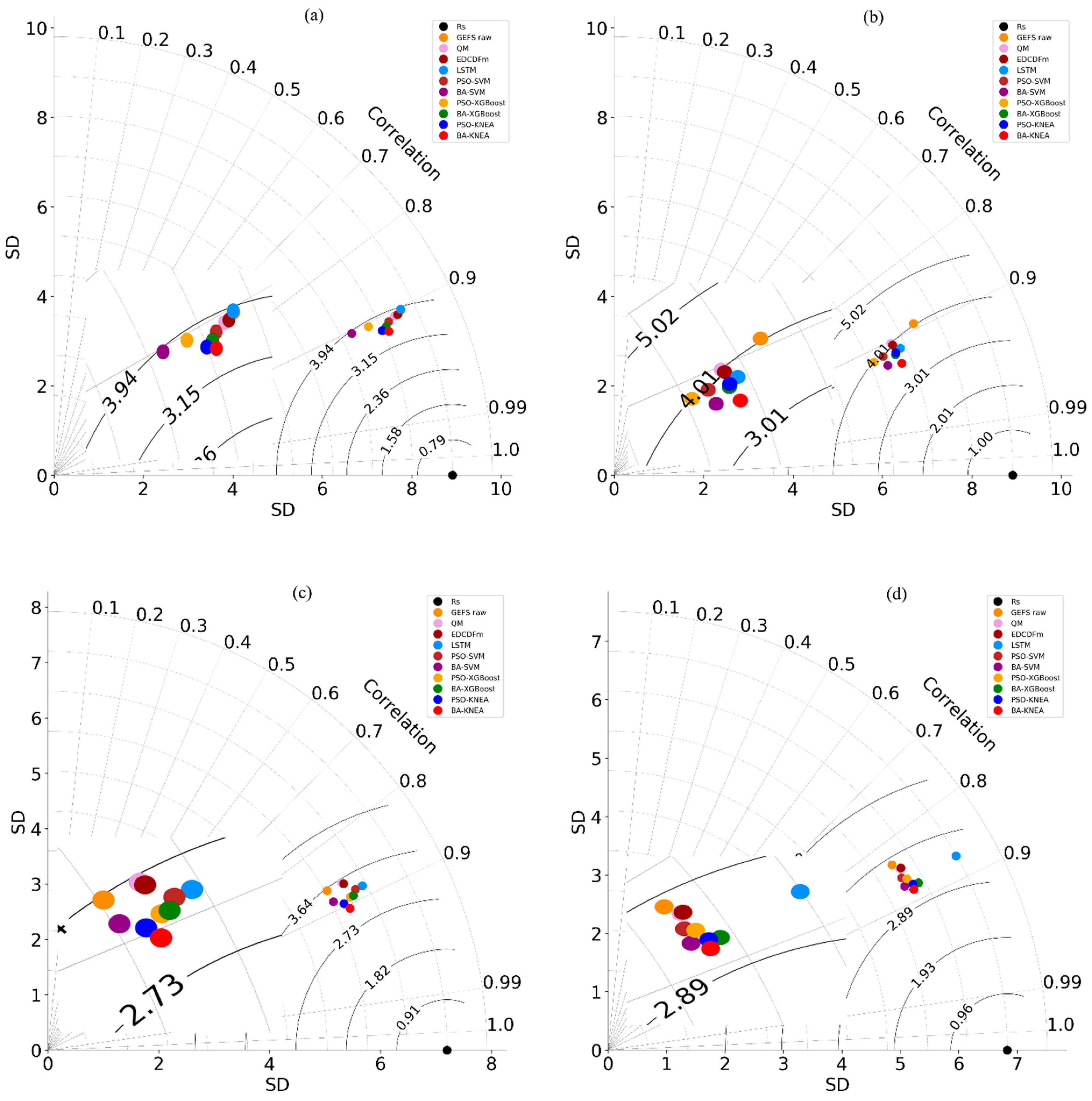
3.3. Comparison of Statistical Models and Machine-learning Models
3.4. BA-KNEA with Different Input Combinations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, P.; Tong, X.; Zhang, J.; Meng, P.; Li, J.; Zheng, J. Estimation of half-hourly diffuse solar radiation over a mixed plantation in north China. Renew. Energy 2020, 149, 1360–1369. [Google Scholar] [CrossRef]
- Demircan, C.; Bayrakçı, H.C.; Keçebaş, A. Machine learning-based improvement of empiric models for an accurate estimating process of global solar radiation. Sustain. Energy Technol. Assess. 2020, 37, 100574. [Google Scholar] [CrossRef]
- Chang, K.; Zhang, Q. Improvement of the hourly global solar model and solar radiation for air-conditioning design in China. Renew. Energy 2019, 138, 1232–1238. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Wang, M.; Wei, Z.; Sun, G. Application of functional deep belief network for estimating daily global solar radiation: A case study in China. Energy 2019, 191, 116502. [Google Scholar] [CrossRef]
- Rehman, S.; Mohandes, M. Artificial neural network estimation of global solar radiation using air temperature and relative humidity. Energy Policy 2008, 36, 571–576. [Google Scholar] [CrossRef] [Green Version]
- Quej, V.H.; Almorox, J.; Arnaldo, J.A.; Saito, L. ANFIS, SVM and ANN soft-computing techniques to estimate daily global solar radiation in a warm sub-humid environment. J. Atmos. Sol.-Terr. Phys. 2017, 155, 62–70. [Google Scholar] [CrossRef] [Green Version]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms. Appl. Energy 2019, 253, 113541. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M.; Adamowski, J.F.; Mi, J. Universally deployable extreme learning machines integrated with remotely sensed MODIS satellite predictors over Australia to forecast global solar radiation: A new approach. Renew. Sustain. Energy Rev. 2019, 104, 235–261. [Google Scholar] [CrossRef]
- Hassan, M.A.; Khalil, A.; Kaseb, S.; Kassem, M.A. Exploring the potential of tree-based ensemble methods in solar radiation modeling. Appl. Energy 2017, 203, 897–916. [Google Scholar] [CrossRef]
- Güçlü, Y.S.; Yeleğen, M.Ö.; Dabanlı, İ.; Şişman, E. Solar irradiation estimations and comparisons by ANFIS, Angström–Prescott and dependency models. Sol. Energy 2014, 109, 118–124. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Kamsin, A.; Lai, P.C.; Mansor, Z. Identifying the most significant input parameters for predicting global solar radiation using an ANFIS selection procedure. Renew. Sustain. Energy Rev. 2016, 63, 423–434. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Chen, Y.; Gong, D.; Hu, X. Development of data-driven models for prediction of daily global horizontal irradiance in northwest China. J. Clean. Prod. 2019, 223, 136–146. [Google Scholar] [CrossRef]
- Wu, L.; Huang, G.; Fan, J.; Zhang, F.; Wang, X.; Zeng, W. Potential of kernel-based nonlinear extension of Arps decline model and gradient boosting with categorical features support for predicting daily global solar radiation in humid regions. Energy Convers. Manag. 2019, 183, 280–295. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluating the effect of air pollution on global and diffuse solar radiation prediction using support vector machine modeling based on sunshine duration and air temperature. Renew. Sustain. Energy Rev. 2018, 94, 732–747. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Ma, X.; Zhou, H.; Zhang, F. Hybrid support vector machines with heuristic algorithms for prediction of daily diffuse solar radiation in air-polluted regions. Renew. Energy 2020, 145, 2034–2045. [Google Scholar] [CrossRef]
- Belaid, S.; Mellit, A. Prediction of daily and mean monthly global solar radiation using support vector machine in an arid climate. Energy Convers. Manag. 2016, 118, 105–118. [Google Scholar] [CrossRef]
- Urraca, R.; Martinez-de-Pison, E.; Sanz-Garcia, A.; Antonanzas, J.; Antonanzas-Torres, F. Estimation methods for global solar radiation: Case study evaluation of five different approaches in central Spain. Renew. Sustain. Energy Rev. 2017, 77, 1098–1113. [Google Scholar] [CrossRef]
- Álvarez-Alvarado, J.M.; Ríos-Moreno, J.G.; Obregón-Biosca, S.A.; Ronquillo-Lomelí, G.; Ventura-Ramos, E.; Trejo-Perea, M. Hybrid techniques to predict solar radiation using support vector machine and search optimization algorithms: A review. Appl. Sci. 2021, 11, 1044. [Google Scholar] [CrossRef]
- Dong, J.; Wu, L.; Liu, X.; Fan, C.; Leng, M.; Yang, Q. Simulation of daily diffuse solar radiation based on three machine learning models. Comput. Model. Eng. Sci. 2020, 123, 49–73. [Google Scholar] [CrossRef]
- Feng, Y.; Hao, W.; Li, H.; Cui, N.; Gong, D.; Gao, L. Machine learning models to quantify and map daily global solar radiation and photovoltaic power. Renew. Sustain. Energy Rev. 2020, 118, 109393. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Y.; Chen, Y.; Wang, D.; Wang, Y.; Zhu, Y. Comparison of support vector machine and copula-based nonlinear quantile regression for estimating the daily diffuse solar radiation: A case study in China. Renew. Energy 2020, 146, 1101–1112. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Huang, C.; Kuo, P. Multiple-input deep convolutional neural network model for short-term photovoltaic power forecasting. IEEE Access 2019, 7, 74822–74834. [Google Scholar] [CrossRef]
- Kaba, K.; Sarıgül, M.; Avcı, M.; Kandırmaz, H.M. Estimation of daily global solar radiation using deep learning model. Energy 2018, 162, 126–135. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.; Paoli, C.; Motte, L.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Sun, H.; Gui, D.; Yan, B.; Liu, Y.; Liao, W.; Zhu, Y.; Lu, C.; Zhao, N. Assessing the potential of random forest method for estimating solar radiation using air pollution index. Energy Convers. Manag. 2016, 119, 121–129. [Google Scholar] [CrossRef] [Green Version]
- Ibrahim, I.A.; Khatib, T. A novel hybrid model for hourly global solar radiation prediction using random forests technique and firefly algorithm. Energy Convers. Manag. 2017, 138, 413–425. [Google Scholar] [CrossRef]
- Prasad, R.; Ali, M.; Kwan, P.; Khan, H. Designing a multi-stage multivariate empirical mode decomposition coupled with ant colony optimization and random forest model to forecast monthly solar radiation. Appl. Energy 2019, 236, 778–792. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S.; Shlyaeva, A.; Bates, G.; Fredrick, S.; Pegion, P.; Sinsky, E.; Zhu, Y.; Tallapragada, V.; Guan, H.; et al. The Reanalysis for the Global Ensemble Forecast System, Version 12. Monthly. Weather Rev. 2022, 150, 59–79. [Google Scholar] [CrossRef]
- Fan, J.; Chen, B.; Wu, L.; Zhang, F.; Lu, X.; Xiang, Y. Evaluation and development of temperature-based empirical models for estimating daily global solar radiation in humid regions. Energy 2018, 144, 903–914. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, Y.; Hou, D.; Fu, B.; Li, W.; Guan, H.; Sinsky, E.; Kolczynski, W.; Xue, X.; Luo, Y.; et al. The Development of the NCEP Global Ensemble Forecast System Version 12. Weather Forecast. 2022, 37, 727. [Google Scholar] [CrossRef]
- Tallapragada, V. Recent updates to NCEP Global Modeling Systems: Implementation of FV3 based Global Forecast System (GFS v15. 1) and plans for implementation of Global Ensemble Forecast System (GEFSv12). In AGU Fall Meeting Abstracts; Astrophysics Data System: San Francisco, CA, USA, 2019; pp. A31C–A34C. [Google Scholar]
- Lee, T.; Singh, V.P. Statistical Downscaling for Hydrological and Environmental Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Maraun, D. Bias correction, quantile mapping, and downscaling: Revisiting the inflation issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Gao, Q.; Jiang, Z.; Li, L. Bias correction and projection of surface air temperature in LMDZ multiple simulation over central and eastern China. Adv. Clim. Chang. Res. 2018, 9, 81–92. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Yan, R.; Liao, J.; Yang, J.; Sun, W.; Nong, M.; Li, F. Multi-hour and multi-site air quality index forecasting in Beijing using CNN, LSTM, CNN-LSTM, and spatiotemporal clustering. Expert Syst. Appl. 2021, 169, 114513. [Google Scholar] [CrossRef]
- Ao, C.; Zeng, W.; Wu, L.; Qian, L.; Srivastava, A.K.; Gaiser, T. Time-delayed machine learning models for estimating groundwater depth in the Hetao Irrigation District, China. Agric. Water Manag. 2021, 255, 107032. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K. Xgboost: Extreme Gradient Boosting; R Package Vers. 0.4-2; Xgboost: Seattle, WA, USA, 2015; pp. 1–4. [Google Scholar]
- Ma, X.; Liu, Z. Predicting the oil production using the novel multivariate nonlinear model based on Arps decline model and kernel method. Neural Comput. Appl. 2018, 29, 579–591. [Google Scholar] [CrossRef]
- Lu, H.; Ma, X.; Huang, K.; Azimi, M. Prediction of offshore wind farm power using a novel two-stage model combining kernel-based nonlinear extension of the Arps decline model with a multi-objective grey wolf optimizer. Renew. Sustain. Energy Rev. 2020, 127, 109856. [Google Scholar] [CrossRef]
- Yang, X.; He, X. Bat algorithm: Literature review and applications. Int. J. Bio-Inspired Comput. 2013, 5, 141–149. [Google Scholar] [CrossRef] [Green Version]
- Cui, Y.; Jia, L.; Fan, W. Estimation of actual evapotranspiration and its components in an irrigated area by integrating the Shuttleworth-Wallace and surface temperature-vegetation index schemes using the particle swarm optimization algorithm. Agric. For. Meteorol. 2021, 307, 108488. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Erfani, S.M.; Rajasegarar, S.; Karunasekera, S.; Leckie, C. High-dimensional and large-scale anomaly detection using a linear one-class SVM with deep learning. Pattern Recognit. 2016, 58, 121–134. [Google Scholar] [CrossRef]
- Zang, H.; Liu, L.; Sun, L.; Cheng, L.; Wei, Z.; Sun, G. Short-term global horizontal irradiance forecasting based on a hybrid CNN-LSTM model with spatiotemporal correlations. Renew. Energy 2020, 160, 26–41. [Google Scholar] [CrossRef]
- Shin, D.; Ha, E.; Kim, T.; Kim, C. Short-term photovoltaic power generation predicting by input/output structure of weather forecast using deep learning. Soft Comput. 2021, 25, 771–783. [Google Scholar] [CrossRef]
- Hu, M.; Zhao, B.; Ao, X.; Cao, J.; Wang, Q.; Riffat, S.; Su, Y.; Pei, G. Applications of radiative sky cooling in solar energy systems: Progress, challenges, and prospects. Renew. Sustain. Energy Rev. 2022, 160, 112304. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, X.; Jia, Y.; Cui, N.; Hao, W.; Li, H.; Gong, D. High-resolution assessment of solar radiation and energy potential in China. Energy Convers. Manag. 2021, 240, 114265. [Google Scholar] [CrossRef]
- De Araujo, J.M.S. Performance comparison of solar radiation forecasting between WRF and LSTM in Gifu, Japan. Environ. Res. Commun. 2020, 2, 045002. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Y.; Wang, D.; Liu, X.; Wang, Y. A review on global solar radiation prediction with machine learning models in a comprehensive perspective. Energy Convers. Manag. 2021, 235, 113960. [Google Scholar] [CrossRef]
- Qiu, R.; Li, L.; Wu, L.; Agathokleous, E.; Liu, C.; Zhang, B.; Luo, Y.; Sun, S. Modeling daily global solar radiation using only temperature data: Past, development, and future. Renew. Sustain. Energy Rev. 2022, 163, 112511. [Google Scholar] [CrossRef]
- Makade, R.G.; Chakrabarti, S.; Jamil, B. Development of global solar radiation models: A comprehensive review and statistical analysis for Indian regions. J. Clean. Prod. 2021, 293, 126208. [Google Scholar] [CrossRef]
- Tao, H.; Ewees, A.A.; Al-Sulttani, A.O.; Beyaztas, U.; Hameed, M.M.; Salih, S.Q.; Armanuos, A.M.; Al-Ansari, N.; Voyant, C.; Shahid, S.; et al. Global solar radiation prediction over North Dakota using air temperature: Development of novel hybrid intelligence model. Energy Rep. 2021, 7, 136–157. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, N.; Feng, Y.; Gong, D.; Hu, X. Comparison of BP, PSO-BP and statistical models for predicting daily global solar radiation in arid Northwest China. Comput. Electron. Agric. 2019, 164, 104905. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S.S. Solar radiation prediction using Artificial Neural Network techniques: A review. Renew. Sustain. Energy Rev. 2014, 33, 772–781. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wu, L.; Zhang, F.; Bai, H.; Lu, X.; Xiang, Y. New combined models for estimating daily global solar radiation based on sunshine duration in humid regions: A case study in South China. Energy Convers. Manag. 2018, 156, 618–625. [Google Scholar] [CrossRef]



| Station | Period | Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sept. | Oct. | Nov. | Dec. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Altay | Train | 7 ± 2.7 | 11.1 ± 3.5 | 15.7 ± 4.8 | 20.3 ± 5.9 | 23.8 ± 7.5 | 25.3 ± 7.1 | 24.2 ± 7 | 21.3 ± 6.3 | 17 ± 5.7 | 10.2 ± 4.6 | 6.1 ± 3.1 | 5.3 ± 2.4 |
| Test | 6 ± 2.7 | 9.6 ± 3.6 | 15 ± 4.4 | 18.7 ± 5.9 | 22.5 ± 6.7 | 24.6 ± 5.6 | 23.7 ± 5.5 | 20.4 ± 5.1 | 15.9 ± 4.4 | 10 ± 4 | 6.1 ± 2.7 | 4.9 ± 2.3 | |
| Kashgar | Train | 8.3 ± 2.5 | 9.6 ± 3.8 | 13.8 ± 4.6 | 19 ± 5.8 | 22.3 ± 6.2 | 26.4 ± 5 | 25.2 ± 4.6 | 21.3 ± 5 | 17.3 ± 4.4 | 13.1 ± 3.2 | 8.3 ± 2.4 | 6.2 ± 1.9 |
| Test | 6.8 ± 2.4 | 9.1 ± 3.5 | 13 ± 4.7 | 17.2 ± 5.6 | 20.7 ± 6.1 | 24.7 ± 5 | 22.9 ± 5.6 | 19.7 ± 4.5 | 16.1 ± 4.1 | 12.3 ± 3.3 | 8.5 ± 2.5 | 6.4 ± 2 | |
| Ruoqiang | Train | 9.3 ± 2.5 | 10.9 ± 2.7 | 16 ± 4.3 | 20.1 ± 4.7 | 22.1 ± 5.9 | 22.9 ± 6.6 | 24.1 ± 6.7 | 21.9 ± 6.1 | 19 ± 3.5 | 14.8 ± 3.1 | 9.5 ± 2.7 | 8 ± 1.8 |
| Test | 8.6 ± 2.6 | 11.2 ± 2.8 | 15.4 ± 3.8 | 18.8 ± 5.2 | 21.8 ± 6 | 23 ± 5 | 21.5 ± 5.9 | 20.3 ± 5.5 | 17.9 ± 4 | 14.2 ± 2.8 | 10.6 ± 2.2 | 7.8 ± 1.9 | |
| Khotan | Train | 10.1 ± 2.5 | 11.6 ± 3.3 | 15.5 ± 4 | 19.8 ± 5.4 | 23.4 ± 5.8 | 23.9 ± 6 | 22.3 ± 6.3 | 20.1 ± 5.4 | 18.6 ± 4.8 | 16.3 ± 2.8 | 11.1 ± 2.3 | 8.8 ± 2.6 |
| Test | 9.1 ± 3 | 11.2 ± 3.8 | 15.2 ± 4.6 | 18.9 ± 5.2 | 21.5 ± 5.1 | 22.1 ± 5.4 | 21.3 ± 5.9 | 19.2 ± 4.6 | 16.2 ± 4.9 | 14.9 ± 2.8 | 10.8 ± 2.2 | 8.7 ± 1.7 |
| Model | Parameter Names | Range |
|---|---|---|
| SVM | Regularization coefficient | [0.01, 10,000] |
| Kernel parameter | [0.01, 10,000] | |
| XGBoost | Number of trees | [50, 1000] |
| Maximum tree depth | [2, 50] | |
| Learning rate | [0.01, 0.3] | |
| KNEA | Regularization coefficient | [0.1, 10,000] |
| Kernel parameter | [0.1, 10,000] |
| ID | 1 d | 2 d | 3 d | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | RMSE | MAE | NRMSE | R2 | RMSE | MAE | NRMSE | R2 | RMSE | MAE | NRMSE |
| 51076 Altay | ||||||||||||
| NWP | 0.816 | 3.939 | 3.120 | 0.250 | 0.766 | 4.313 | 3.417 | 0.274 | 0.745 | 4.582 | 3.482 | 0.292 |
| QM | 0.821 | 3.843 | 3.077 | 0.246 | 0.787 | 4.194 | 3.304 | 0.269 | 0.768 | 4.387 | 3.442 | 0.281 |
| EDCDFm | 0.820 | 3.838 | 3.071 | 0.246 | 0.788 | 4.189 | 3.301 | 0.268 | 0.768 | 4.384 | 3.437 | 0.281 |
| 51709 Kashgar | ||||||||||||
| NWP | 0.795 | 5.016 | 3.822 | 0.327 | 0.772 | 5.214 | 3.955 | 0.340 | 0.757 | 5.378 | 4.080 | 0.351 |
| QM | 0.816 | 3.460 | 2.633 | 0.217 | 0.792 | 3.707 | 2.798 | 0.233 | 0.776 | 3.862 | 2.943 | 0.243 |
| EDCDFm | 0.820 | 3.437 | 2.633 | 0.216 | 0.795 | 3.699 | 2.815 | 0.232 | 0.780 | 3.841 | 2.950 | 0.241 |
| 51777 Ruoqiang | ||||||||||||
| NWP | 0.753 | 4.547 | 3.102 | 0.280 | 0.726 | 4.859 | 3.312 | 0.299 | 0.697 | 5.156 | 3.478 | 0.317 |
| QM | 0.754 | 3.708 | 2.553 | 0.224 | 0.713 | 4.002 | 2.762 | 0.241 | 0.681 | 4.257 | 2.920 | 0.257 |
| EDCDFm | 0.758 | 3.632 | 2.499 | 0.219 | 0.719 | 3.912 | 2.709 | 0.236 | 0.688 | 4.138 | 2.864 | 0.250 |
| 51828 Khotan | ||||||||||||
| NWP | 0.701 | 4.822 | 3.398 | 0.296 | 0.668 | 5.127 | 3.628 | 0.315 | 0.650 | 5.354 | 3.788 | 0.329 |
| QM | 0.720 | 3.674 | 2.750 | 0.219 | 0.665 | 4.057 | 3.048 | 0.241 | 0.649 | 4.178 | 3.143 | 0.249 |
| EDCDFm | 0.721 | 3.637 | 2.733 | 0.216 | 0.669 | 4.012 | 3.044 | 0.239 | 0.652 | 4.145 | 3.151 | 0.247 |
| ID | 1 d | 2 d | 3 d | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | R2 | RMSE | MAE | NRMSE | R2 | RMSE | MAE | NRMSE | R2 | RMSE | MAE | NRMSE |
| 51076 Altay | ||||||||||||
| LSTM | 0.813 | 3.889 | 3.086 | 0.202 | 0.798 | 4.178 | 3.314 | 0.216 | 0.787 | 4.258 | 3.168 | 0.207 |
| PSO-SVM | 0.817 | 3.875 | 2.988 | 0.191 | 0.792 | 4.116 | 3.181 | 0.204 | 0.773 | 4.292 | 3.319 | 0.213 |
| BA-SVM | 0.837 | 3.627 | 2.854 | 0.183 | 0.811 | 3.91 | 3.032 | 0.194 | 0.793 | 4.091 | 3.174 | 0.203 |
| PSO-XGBoost | 0.816 | 3.917 | 3.118 | 0.2 | 0.79 | 4.178 | 3.28 | 0.21 | 0.773 | 4.33 | 3.403 | 0.218 |
| BA-XGBoost | 0.833 | 3.685 | 2.893 | 0.185 | 0.803 | 4.005 | 3.114 | 0.199 | 0.786 | 4.171 | 3.243 | 0.208 |
| PSO-KNEA | 0.826 | 3.723 | 2.903 | 0.186 | 0.794 | 4.053 | 3.088 | 0.198 | 0.77 | 4.281 | 3.268 | 0.209 |
| BA-KNEA | 0.844 | 3.552 | 2.785 | 0.178 | 0.819 | 3.839 | 2.98 | 0.191 | 0.803 | 4.002 | 3.105 | 0.199 |
| 51709 Kashgar | ||||||||||||
| LSTM | 0.834 | 3.485 | 2.81 | 0.177 | 0.808 | 3.735 | 2.75 | 0.173 | 0.799 | 3.908 | 3.033 | 0.191 |
| PSO-SVM | 0.838 | 3.436 | 2.641 | 0.166 | 0.809 | 3.735 | 2.863 | 0.18 | 0.789 | 3.824 | 2.886 | 0.181 |
| BA-SVM | 0.861 | 3.38 | 2.707 | 0.17 | 0.838 | 3.596 | 2.854 | 0.179 | 0.799 | 3.923 | 3.136 | 0.197 |
| PSO-XGBoost | 0.84 | 3.445 | 2.7 | 0.17 | 0.811 | 3.754 | 2.933 | 0.184 | 0.8 | 3.808 | 2.982 | 0.187 |
| BA-XGBoost | 0.845 | 3.345 | 2.55 | 0.16 | 0.819 | 3.661 | 2.775 | 0.174 | 0.808 | 3.677 | 2.796 | 0.176 |
| PSO-KNEA | 0.841 | 3.231 | 2.438 | 0.153 | 0.824 | 3.45 | 2.629 | 0.165 | 0.801 | 3.618 | 2.748 | 0.173 |
| BA-KNEA | 0.869 | 3.056 | 2.37 | 0.149 | 0.837 | 3.434 | 2.654 | 0.167 | 0.834 | 3.487 | 2.733 | 0.172 |
| 51777 Ruoqiang | ||||||||||||
| LSTM | 0.784 | 3.401 | 2.431 | 0.147 | 0.74 | 3.821 | 2.547 | 0.159 | 0.719 | 3.852 | 2.749 | 0.168 |
| PSO-SVM | 0.796 | 3.313 | 2.331 | 0.141 | 0.76 | 3.603 | 2.528 | 0.153 | 0.732 | 3.796 | 2.711 | 0.164 |
| BA-SVM | 0.803 | 3.266 | 2.296 | 0.139 | 0.764 | 3.592 | 2.542 | 0.153 | 0.733 | 3.811 | 2.693 | 0.163 |
| PSO-XGBoost | 0.787 | 3.423 | 2.429 | 0.147 | 0.75 | 3.688 | 2.614 | 0.158 | 0.731 | 3.822 | 2.746 | 0.166 |
| BA-XGBoost | 0.796 | 3.319 | 2.304 | 0.139 | 0.753 | 3.639 | 2.542 | 0.153 | 0.721 | 3.853 | 2.728 | 0.165 |
| PSO-KNEA | 0.785 | 3.552 | 2.41 | 0.145 | 0.739 | 3.86 | 2.6 | 0.157 | 0.717 | 4.069 | 2.736 | 0.165 |
| BA-KNEA | 0.819 | 3.123 | 2.196 | 0.133 | 0.791 | 3.354 | 2.387 | 0.144 | 0.752 | 3.674 | 2.624 | 0.158 |
| 51828 Khotan | ||||||||||||
| LSTM | 0.762 | 3.331 | 2.619 | 0.155 | 0.717 | 3.739 | 2.74 | 0.161 | 0.696 | 3.873 | 2.822 | 0.166 |
| PSO-SVM | 0.752 | 3.459 | 2.665 | 0.159 | 0.71 | 3.731 | 2.815 | 0.167 | 0.697 | 3.81 | 2.883 | 0.172 |
| BA-SVM | 0.771 | 3.384 | 2.664 | 0.159 | 0.737 | 3.755 | 2.968 | 0.177 | 0.704 | 3.969 | 3.116 | 0.185 |
| PSO-XGBoost | 0.755 | 3.32 | 2.621 | 0.151 | 0.723 | 3.885 | 3.003 | 0.179 | 0.703 | 3.991 | 3.197 | 0.189 |
| BA-XGBoost | 0.754 | 3.37 | 2.678 | 0.157 | 0.734 | 3.689 | 2.847 | 0.167 | 0.722 | 3.788 | 2.895 | 0.175 |
| PSO-KNEA | 0.743 | 3.506 | 2.587 | 0.154 | 0.689 | 3.834 | 2.8 | 0.167 | 0.671 | 3.929 | 2.899 | 0.172 |
| BA-KNEA | 0.783 | 3.227 | 2.509 | 0.149 | 0.754 | 3.483 | 2.676 | 0.159 | 0.737 | 3.576 | 2.732 | 0.163 |
| Model | 1 d | 2 d | 3 d |
|---|---|---|---|
| GEFS raw | 10 | 10 | 10 |
| QM | 9 | 9 | 9 |
| EDCDFm | 8 | 8 | 8 |
| LSTM | 6 | 6 | 6 |
| PSO-SVM | 5 | 5 | 5 |
| BA-SVM | 2 | 2 | 3 |
| PSO-XGBoost | 7 | 7 | 7 |
| BA-XGBoost | 3 | 3 | 2 |
| PSO-KNEA | 4 | 4 | 4 |
| BA-KNEA | 1 | 1 | 1 |
| ID | Input | 1 d | 2 d | 3 d | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | NRMSE | R2 | RMSE | MAE | NRMSE | R2 | RMSE | MAE | NRMSE | ||
| 51076 Altay | |||||||||||||
| 1 | Rsf | 0.824 | 3.778 | 3.019 | 0.193 | 0.789 | 4.139 | 3.23 | 0.207 | 0.771 | 4.312 | 3.382 | 0.217 |
| 2 | Rsf, RHf | 0.828 | 3.741 | 2.978 | 0.191 | 0.799 | 4.051 | 3.164 | 0.203 | 0.781 | 4.226 | 3.305 | 0.212 |
| 3 | Rsf, Tmaxf, Tminf | 0.832 | 3.687 | 2.913 | 0.187 | 0.805 | 3.983 | 3.079 | 0.197 | 0.787 | 4.178 | 3.269 | 0.209 |
| 4 | Rsf, Uf | 0.835 | 3.651 | 2.862 | 0.183 | 0.808 | 3.943 | 3.057 | 0.196 | 0.792 | 4.097 | 3.169 | 0.203 |
| 5 | Tmaxf, Tminf, Ra | 0.723 | 4.705 | 3.766 | 0.241 | 0.721 | 4.757 | 3.737 | 0.239 | 0.712 | 4.812 | 3.799 | 0.243 |
| 6 | All | 0.844 | 3.552 | 2.785 | 0.178 | 0.819 | 3.839 | 2.98 | 0.191 | 0.803 | 4.002 | 3.105 | 0.199 |
| 51709 Kashgar | |||||||||||||
| 1 | Rsf | 0.852 | 3.21 | 2.499 | 0.157 | 0.829 | 3.494 | 2.711 | 0.17 | 0.814 | 3.663 | 2.87 | 0.18 |
| 2 | Rsf, RHf | 0.859 | 3.23 | 2.551 | 0.16 | 0.84 | 3.456 | 2.705 | 0.17 | 0.823 | 3.632 | 2.869 | 0.18 |
| 3 | Rsf, Tmaxf, Tminf | 0.867 | 3.185 | 2.535 | 0.159 | 0.846 | 3.388 | 2.634 | 0.165 | 0.832 | 3.488 | 2.741 | 0.172 |
| 4 | Rsf, Uf | 0.87 | 3.223 | 2.55 | 0.16 | 0.841 | 3.464 | 2.701 | 0.17 | 0.826 | 3.502 | 2.705 | 0.17 |
| 5 | Tmaxf, Tminf, Ra | 0.796 | 3.958 | 3.09 | 0.194 | 0.785 | 3.809 | 2.93 | 0.184 | 0.776 | 3.838 | 2.954 | 0.186 |
| 6 | All | 0.869 | 3.056 | 2.37 | 0.149 | 0.837 | 3.434 | 2.654 | 0.167 | 0.834 | 3.487 | 2.733 | 0.172 |
| 51777 Ruoqiang | |||||||||||||
| 1 | Rsf | 0.789 | 3.403 | 2.352 | 0.142 | 0.755 | 3.64 | 2.504 | 0.151 | 0.73 | 3.818 | 2.663 | 0.161 |
| 2 | Rsf, RHf | 0.798 | 3.302 | 2.286 | 0.138 | 0.767 | 3.527 | 2.479 | 0.15 | 0.741 | 3.732 | 2.639 | 0.159 |
| 3 | Rsf, Tmaxf, Tminf | 0.811 | 3.199 | 2.296 | 0.139 | 0.782 | 3.467 | 2.467 | 0.149 | 0.756 | 3.649 | 2.616 | 0.158 |
| 4 | Rsf, Uf | 0.814 | 3.222 | 2.245 | 0.135 | 0.774 | 3.511 | 2.445 | 0.148 | 0.74 | 3.746 | 2.649 | 0.16 |
| 5 | Tmaxf, Tminf, Ra | 0.745 | 3.764 | 2.792 | 0.168 | 0.724 | 3.875 | 2.871 | 0.173 | 0.702 | 4.035 | 2.96 | 0.179 |
| 6 | All | 0.819 | 3.123 | 2.196 | 0.133 | 0.791 | 3.354 | 2.387 | 0.144 | 0.752 | 3.674 | 2.624 | 0.158 |
| 51828 Khotan | |||||||||||||
| 1 | Rsf | 0.747 | 3.44 | 2.607 | 0.155 | 0.694 | 3.787 | 2.827 | 0.168 | 0.671 | 3.948 | 2.998 | 0.178 |
| 2 | Rsf, RHf | 0.769 | 3.293 | 2.523 | 0.15 | 0.719 | 3.645 | 2.767 | 0.165 | 0.705 | 3.729 | 2.818 | 0.168 |
| 3 | Rsf, Tmaxf, Tminf | 0.782 | 3.236 | 2.5 | 0.149 | 0.751 | 3.564 | 2.771 | 0.165 | 0.731 | 3.678 | 2.833 | 0.169 |
| 4 | Rsf, Uf | 0.763 | 3.337 | 2.504 | 0.149 | 0.725 | 3.643 | 2.786 | 0.166 | 0.708 | 3.765 | 2.867 | 0.171 |
| 5 | Tmaxf, Tminf, Ra | 0.73 | 3.602 | 2.775 | 0.165 | 0.716 | 3.718 | 2.857 | 0.17 | 0.697 | 3.823 | 2.919 | 0.174 |
| 6 | All | 0.783 | 3.227 | 2.509 | 0.149 | 0.754 | 3.483 | 2.676 | 0.159 | 0.737 | 3.576 | 2.732 | 0.163 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, G.; Wu, L.; Liu, F.; Wang, Y.; Wu, S. Improvement in Solar-Radiation Forecasting Based on Evolutionary KNEA Method and Numerical Weather Prediction. Sustainability 2022, 14, 6824. https://doi.org/10.3390/su14116824
Duan G, Wu L, Liu F, Wang Y, Wu S. Improvement in Solar-Radiation Forecasting Based on Evolutionary KNEA Method and Numerical Weather Prediction. Sustainability. 2022; 14(11):6824. https://doi.org/10.3390/su14116824
Chicago/Turabian StyleDuan, Guosheng, Lifeng Wu, Fa Liu, Yicheng Wang, and Shaofei Wu. 2022. "Improvement in Solar-Radiation Forecasting Based on Evolutionary KNEA Method and Numerical Weather Prediction" Sustainability 14, no. 11: 6824. https://doi.org/10.3390/su14116824
APA StyleDuan, G., Wu, L., Liu, F., Wang, Y., & Wu, S. (2022). Improvement in Solar-Radiation Forecasting Based on Evolutionary KNEA Method and Numerical Weather Prediction. Sustainability, 14(11), 6824. https://doi.org/10.3390/su14116824






