Projection Matrix Models: A Suitable Approach for Predicting Sustainable Growth in Uneven-Aged and Mixed Hyrcanian Forests
Abstract
:1. Introduction
- Can individual-tree increment models and matrix models be combined to reliably estimate growth rate and allowable cut rate in uneven-aged mixed forests managed by single-selection silvicultural techniques in Hyrcanian forests?
- Are the total operated allowable cut (OAC) and estimated allowable cut (EAC) volumes for Hyrcanian forests consistent?
- How does the estimated volume from the developed individual tree increment/matrix model compare to the predicted volume according to the Hyrcanian forest plan?
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
- (A)
- Operated allowable cut (OAC): is the by volume of trees harvested in three compartments of 305, 306 and 309 according to forestry plan.
- (B)
- Predicted allowable cut (PAC): is the amount of tree harvesting predicted when formulating a forestry plan for the whole district.
- (C)
- Estimated allowable cut (EAC): is the amount of tree harvesting that has been obtained in the present study.
2.3. Projection Matrix Model and Determination of Harvest Rate
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Shi, Y.; Zhu, D.; Wang, W.; Liu, H.; Li, J.; Shi, N.; Ma, L.; Fu, S. Fine root biomass and morphology in a temperate forest are influenced more by the nitrogen treatment approach than the rate. Ecol. Indic. 2021, 130, 108031. [Google Scholar] [CrossRef]
- O’hara, K.L.; Hasenauer, H.; Kindermann, G. Sustainability in multi-aged stands: An analysis of long-term plenter systems. Forestry 2007, 80, 163–181. [Google Scholar] [CrossRef] [Green Version]
- Geng, M.; Ma, K.; Sun, Y.; Wo, X.; Wang, K. Changes of land use/cover and landscape in Zhalong wetland as “red-crowned cranes country”, Heilongjiang province, China. Glob. Nest J. 2020, 22, 477. [Google Scholar]
- Hamidi, S.K.; Zenner, E.K.; Bayat, M.; Fallah, A. Analysis of plot-level volume increment models developed from machine learning methods applied to an uneven-aged mixed forest. Ann. For. Sci. 2021, 78, 4. [Google Scholar] [CrossRef]
- Bayat, M.; Pukkala, T.; Namiranian, M.; Zobeiri, M. Productivity and optimal management of the uneven-aged hardwood forests of Hyrcania. Eur. J. For. Res. 2013, 132, 851–864. [Google Scholar] [CrossRef]
- Rayner, M.; Turner, B. Growth and yield modelling of Australian eucalypt forests I. Historical development. Aust. For. 1990, 53, 224–237. [Google Scholar] [CrossRef]
- Orrego, S.; Montes, C.; Restrepo, H.I.; Bullock, B.P.; Zapata, M. Modeling height growth for teak plantations in Colombia using the reducible stochastic differential equation approach. J. For. Res. 2021, 32, 1035–1045. [Google Scholar] [CrossRef]
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Solomon, D.S.; Hosmer, R.A.; Hayslett, H.T., Jr. A two-stage matrix model for predicting growth of forest stands in the Northeast. Can. J. For. Res. 1986, 16, 521–528. [Google Scholar] [CrossRef]
- Liang, J.; Picard, N. Matrix model of forest dynamics: An overview and outlook. For. Sci. 2013, 59, 359–378. [Google Scholar] [CrossRef]
- Ma, W.; Domke, G.M.; D’Amato, A.W.; Woodall, C.W.; Walters, B.F.; Deo, R.K. Using matrix models to estimate aboveground forest biomass dynamics in the eastern USA through various combinations of LiDAR, Landsat, and forest inventory data. Environ. Res. Lett. 2018, 13, 125004. [Google Scholar] [CrossRef]
- Lewis, E. On the Generation and Growth of a Population Mathematical Demography; Springer: Berlin/Heidelberg, Germany, 1942. [Google Scholar]
- Leslie, P.H. On the use of matrices in certain population mathematics. Biometrika 1945, 33, 183–212. [Google Scholar] [CrossRef]
- Usher, M. A matrix model for forest management. Biometrics 1969, 25, 309–315. [Google Scholar] [CrossRef]
- Keyfitz, N.; Caswell, H. Applied Mathematical Demography; Springer: Berlin/Heidelberg, Germany, 2005; Volume 47. [Google Scholar]
- Huenneke, L.F.; Marks, P. Stem dynamics of the shrub Alnus incana ssp. rugosa: Transition matrix models. Ecology 1987, 68, 1234–1242. [Google Scholar] [CrossRef]
- Manders, P. A transition matrix model of the population dynamics of the Clanwilliam cedar (Widdringtonia cedarbergensis) in natural stands subject to fire. For. Ecol. Manag. 1987, 20, 171–186. [Google Scholar] [CrossRef]
- Alvarez-Buylla, E.R.; Slatkin, M. Finding confidence limits on population growth rates: Three real examples revised. Ecology 1994, 75, 255–260. [Google Scholar] [CrossRef]
- Liang, J.; Buongiorno, J.; Monserud, R.A. Bootstrap simulation and response surface optimization of management regimes for Douglas-fir/western hemlock stands. For. Sci. 2006, 52, 579–594. [Google Scholar]
- Liang, J.; Zhou, M. A geospatial model of forest dynamics with controlled trend surface. Ecol. Model. 2010, 221, 2339–2352. [Google Scholar] [CrossRef]
- Synek, M.; Hrib, M. Analysing data sources’ suitability to support forest policy decision-making in the Czech Republic. Int. For. Rev. 2019, 21, 92–107. [Google Scholar] [CrossRef]
- Liang, J.; Zhou, M.; Verbyla, D.L.; Zhang, L.; Springsteen, A.L.; Malone, T. Mapping forest dynamics under climate change: A matrix model. For. Ecol. Manag. 2011, 262, 2250–2262. [Google Scholar] [CrossRef]
- Hoffmann, W.A. Fire and population dynamics of woody plants in a neotropical savanna: Matrix model projections. Ecology 1999, 80, 1354–1369. [Google Scholar] [CrossRef]
- Schmidt, I.B.; Mandle, L.; Ticktin, T.; Gaoue, O.G. What do matrix population models reveal about the sustainability of non-timber forest product harvest? J. Appl. Ecol. 2011, 48, 815–826. [Google Scholar] [CrossRef]
- Van der Werf, E.; Indrajaya, Y.; Mohren, F.; van Ierland, E.C. Logging damage and injured tree mortality in tropical forest management. Nat. Resour. Model. 2019, 32, e12210. [Google Scholar]
- Gourlet-Fleury, S.; Cornu, G.; Jésel, S.; Dessard, H.; Jourget, J.-G.; Blanc, L.; Picard, N. Using models to predict recovery and assess tree species vulnerability in logged tropical forests: A case study from French Guiana. For. Ecol. Manag. 2005, 209, 69–85. [Google Scholar] [CrossRef]
- Picard, N.; Franc, A. Aggregation of an individual-based space-dependent model of forest dynamics into distribution-based and space-independent models. Ecol. Model. 2001, 145, 69–84. [Google Scholar] [CrossRef]
- Verzelen, N.; Picard, N.; Gourlet-Fleury, S. Approximating spatial interactions in a model of forest dynamics as a means of understanding spatial patterns. Ecol. Complex. 2006, 3, 209–218. [Google Scholar] [CrossRef]
- Picard, N.; Bar-Hen, A.; Gourlet-Fleury, S. Estimator of upgrowth transition rates for size-classified matrix from small samples. Ecol. Model. 2007, 204, 59–69. [Google Scholar] [CrossRef]
- Van Nes, E.H.; Scheffer, M. A strategy to improve the contribution of complex simulation models to ecological theory. Ecol. Model. 2005, 185, 153–164. [Google Scholar] [CrossRef]
- Huston, M.; DeAngelis, D.; Post, W. New computer models unify ecological theory: Computer simulations show that many ecological patterns can be explained by interactions among individual organisms. BioScience 1988, 38, 682–691. [Google Scholar] [CrossRef]
- Grimm, V.; Railsback, S.F. Individual-based modeling and ecology. In Individual-Based Modeling and Ecology; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Grimm, V. Ten years of individual-based modelling in ecology: What have we learned and what could we learn in the future? Ecol. Model. 1999, 115, 129–148. [Google Scholar] [CrossRef]
- Haight, R.G. Evaluating the efficiency of even-aged and uneven-aged stand management. For. Sci. 1987, 33, 116–134. [Google Scholar]
- Haight, R.G.; Monserud, R.A. Optimizing any-aged management of mixed-species stands: II. Effects of decision criteria. For. Sci. 1990, 36, 125–144. [Google Scholar]
- Buongiorno, J.; Peyron, J.-L.; Houllier, F.; Bruciamacchie, M. Growth and management of mixed-species, uneven-aged forests in the French Jura: Implications for economic returns and tree diversity. For. Sci. 1995, 41, 397–429. [Google Scholar]
- Tahvonen, O.; Pukkala, T.; Laiho, O.; Lähde, E.; Niinimäki, S. Optimal management of uneven-aged Norway spruce stands. For. Ecol. Manag. 2010, 260, 106–115. [Google Scholar] [CrossRef]
- Sist, P.; Picard, N.; Gourlet-Fleury, S. Sustainable cutting cycle and yields in a lowland mixed dipterocarp forest of Borneo. Ann. For. Sci. 2003, 60, 803–814. [Google Scholar] [CrossRef]
- Hamidi, S.K.; Weiskittel, A.; Bayat, M.; Fallah, A. Development of individual tree growth and yield model across multiple contrasting species using nonparametric and parametric methods in the Hyrcanian forests of northern Iran. Eur. J. For. Res. 2021, 140, 421–434. [Google Scholar] [CrossRef]
- Bourque, C.P.-A.; Bayat, M.; Zhang, C. An assessment of height–diameter growth variation in an unmanaged Fagus orientalis-dominated forest. Eur. J. For. Res. 2019, 138, 607–621. [Google Scholar] [CrossRef]
- Bayat, M.; Burkhart, H.; Namiranian, M.; Hamidi, S.K.; Heidari, S.; Hassani, M. Assessing biotic and abiotic effects on biodiversity index using machine learning. Forests 2021, 12, 461. [Google Scholar] [CrossRef]
- Bourque, C.P.-A.; Bayat, M. Landscape variation in tree species richness in northern Iran forests. PLoS ONE 2015, 10, e0121172. [Google Scholar] [CrossRef]
- Bayat, M.; Bettinger, P.; Hassani, M.; Heidari, S. Ten-year estimation of Oriental beech (Fagus orientalis Lipsky) volume increment in natural forests: A comparison of an artificial neural networks model, multiple linear regression and actual increment. For. Int. J. For. Res. 2021, 94, 598–609. [Google Scholar] [CrossRef]
- López, I.; Ortuño, S.F.; Martín, Á.J.; Fullana, C. Estimating the sustainable harvesting and the stable diameter distribution of European beech with projection matrix models. Ann. For. Sci. 2007, 64, 593–599. [Google Scholar] [CrossRef] [Green Version]
- Torres, I.L.; Belda, C.F.; Pérez, S.O.; Fernández, A.M. Choosing Fagus sylvatica L. matrix model dimension by sensitivity analysis of the population growth rate with respect to the width of the diameter classes. Ecol. Model. 2008, 218, 307–314. [Google Scholar] [CrossRef]
- Salehnasab, A.; Bayat, M.; Namiranian, M.; Khaleghi, B.; Omid, M.; Masood Awan, H.U.; Al-Ansari, N.; Jaafari, A. Machine Learning for the Estimation of Diameter Increment in Mixed and Uneven-Aged Forests. Sustainability 2022, 14, 3386. [Google Scholar] [CrossRef]
- Amoli Kondori, A.; Marvi Mohajer, M.R.; Zobeiri, M.; Etemad, V. Natural regeneration of tree species in ralation to gap charactristics in natural beech (Fagus orientalis Lipsky) stand, north of Iran. Iran. J. For. Poplar Res. 2012, 20, 151–164. [Google Scholar]
- Sterba, H. Forest inventories and growth models to examine management strategies for forests in transition. Forestry 2002, 75, 411–418. [Google Scholar] [CrossRef]
- Mohadjer, M.M.; Zobeiri, M.; Etemad, V.; Gholami, M.J. Performing the single selection method at compartment level and necessity for full inventory of tree species (case study: Gorazbon district in Kheyroud forest). Iran. J. Nat. Resour. 2009, 61, 889–908. [Google Scholar]
- Bayat, M.; Bettinger, P.; Heidari, S.; Hamidi, S.K.; Jaafari, A. A Combination of Biotic and Abiotic Factors and Diversity Determine Productivity in Natural Deciduous Forests. Forests 2021, 12, 1450. [Google Scholar] [CrossRef]
- Van Gardingen, P.R.; Valle, D.; Thompson, I. Evaluation of yield regulation options for primary forest in Tapajos National Forest, Brazil. For. Ecol. Manag. 2006, 231, 184–195. [Google Scholar] [CrossRef]
- Okuda, T.; Suzuki, M.; Adachi, N.; Quah, E.S.; Hussein, N.A.; Manokaran, N. Effect of selective logging on canopy and stand structure and tree species composition in a lowland dipterocarp forest in peninsular Malaysia. For. Ecol. Manag. 2003, 175, 297–320. [Google Scholar] [CrossRef]
- Cannon, C.H.; Peart, D.R.; Leighton, M. Tree species diversity in commercially logged Bornean rainforest. Science 1998, 281, 1366–1368. [Google Scholar] [CrossRef] [Green Version]
- Ferry Slik, J.; Verburg, R.W.; KEßLER, P.J. Effects of fire and selective logging on the tree species composition of lowland dipterocarp forest in East Kalimantan, Indonesia. Biodivers. Conserv. 2002, 11, 85–98. [Google Scholar] [CrossRef]
- Bonnell, T.R.; Reyna-Hurtado, R.; Chapman, C.A. Post-logging recovery time is longer than expected in an East African tropical forest. For. Ecol. Manag. 2011, 261, 855–864. [Google Scholar] [CrossRef]
- Lindner, A.; Sattler, D. Biomass estimations in forests of different disturbance history in the Atlantic Forest of Rio de Janeiro, Brazil. New For. 2012, 43, 287–301. [Google Scholar] [CrossRef]
- Ghajar, I.; Najafi, A. Evaluation of harvesting methods for Sustainable Forest Management (SFM) using the Analytical Network Process (ANP). For. Policy Econ. 2012, 21, 81–91. [Google Scholar] [CrossRef]
- Chen, X.; Quan, Q.; Zhang, K.; Wei, J. Spatiotemporal characteristics and attribution of dry/wet conditions in the Weihe River Basin within a typical monsoon transition zone of East Asia over the recent 547 years. Environ. Model. Softw. 2021, 143, 105116. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, K.; Chao, L.; Li, D.; Tian, X.; Bao, H.; Chen, G.; Xia, Y. Exploring the utility of radar and satellite-sensed precipitation and their dynamic bias correction for integrated prediction of flood and landslide hazards. J. Hydrol. 2021, 603, 126964. [Google Scholar] [CrossRef]
- Zhao, X.; Xia, H.; Pan, L.; Song, H.; Niu, W.; Wang, R.; Li, R.; Bian, X.; Guo, Y.; Qin, Y. Drought monitoring over Yellow River basin from 2003–2019 using reconstructed MODIS land surface temperature in Google Earth Engine. Remote Sens. 2021, 13, 3748. [Google Scholar] [CrossRef]
- Zhang, K.; Ali, A.; Antonarakis, A.; Moghaddam, M.; Saatchi, S.; Tabatabaeenejad, A.; Chen, R.; Jaruwatanadilok, S.; Cuenca, R.; Crow, W.T. The sensitivity of North American terrestrial carbon fluxes to spatial and temporal variation in soil moisture: An analysis using radar-derived estimates of root-zone soil moisture. J. Geophys. Res. Biogeosci. 2019, 124, 3208–3231. [Google Scholar] [CrossRef]


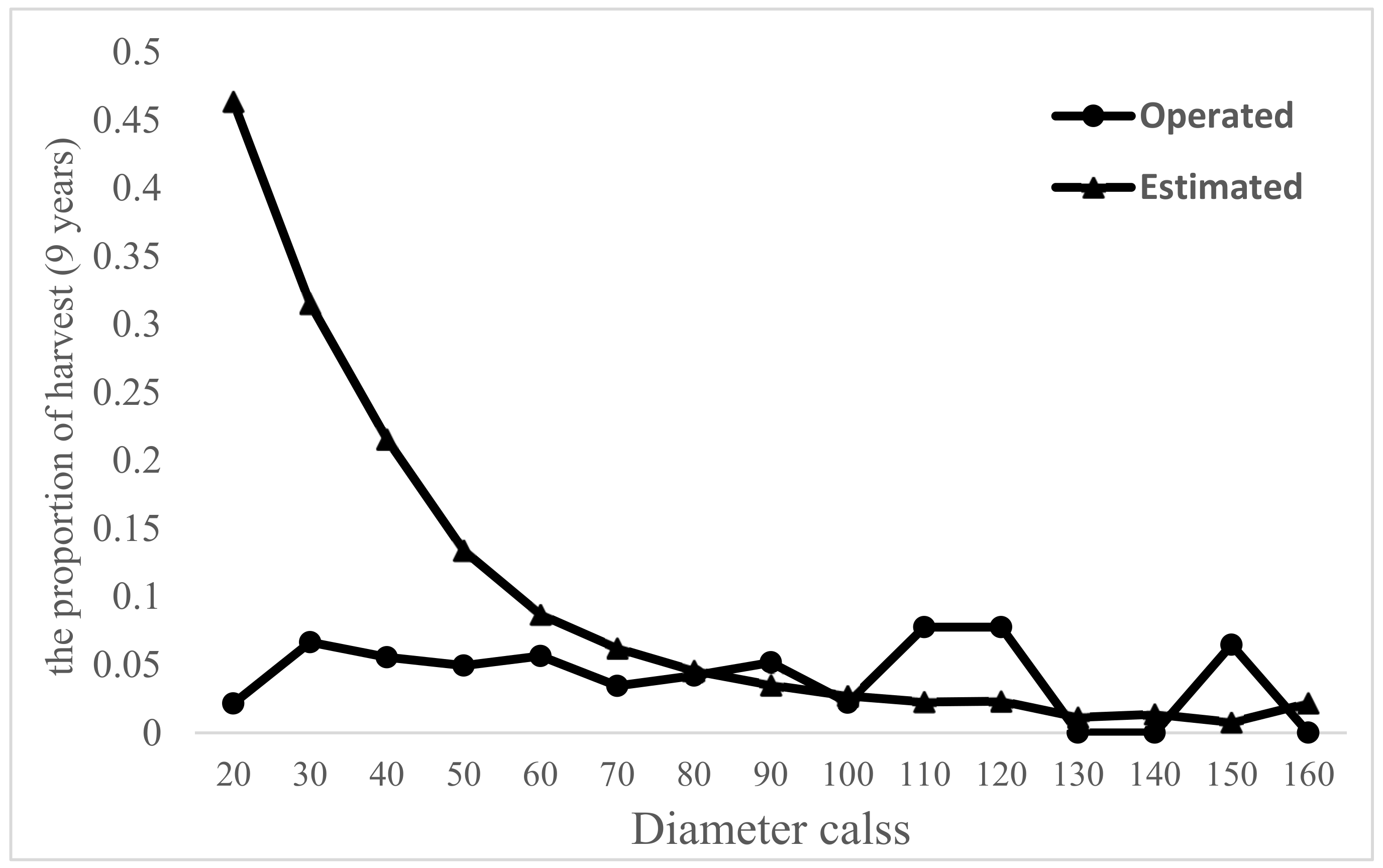
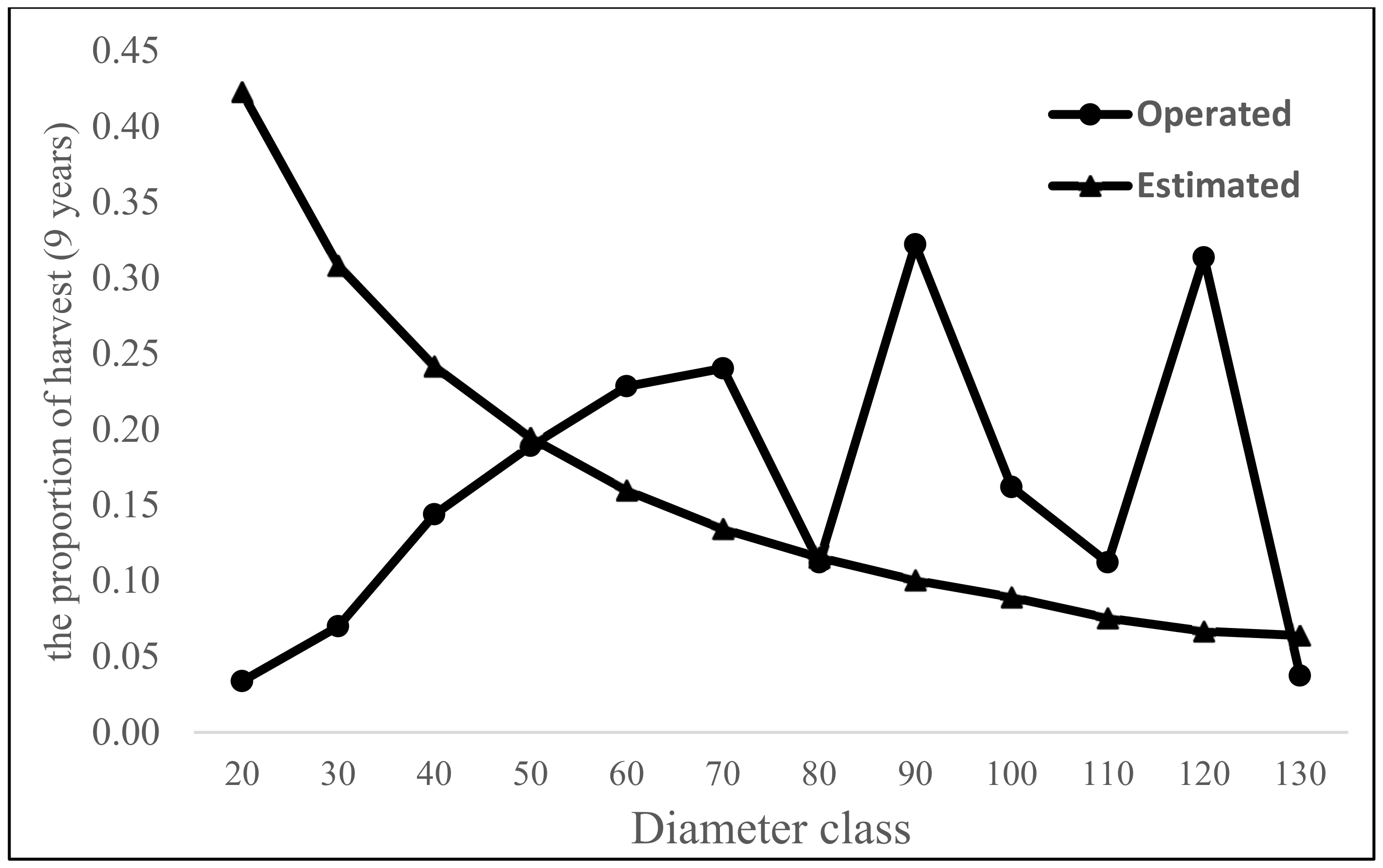

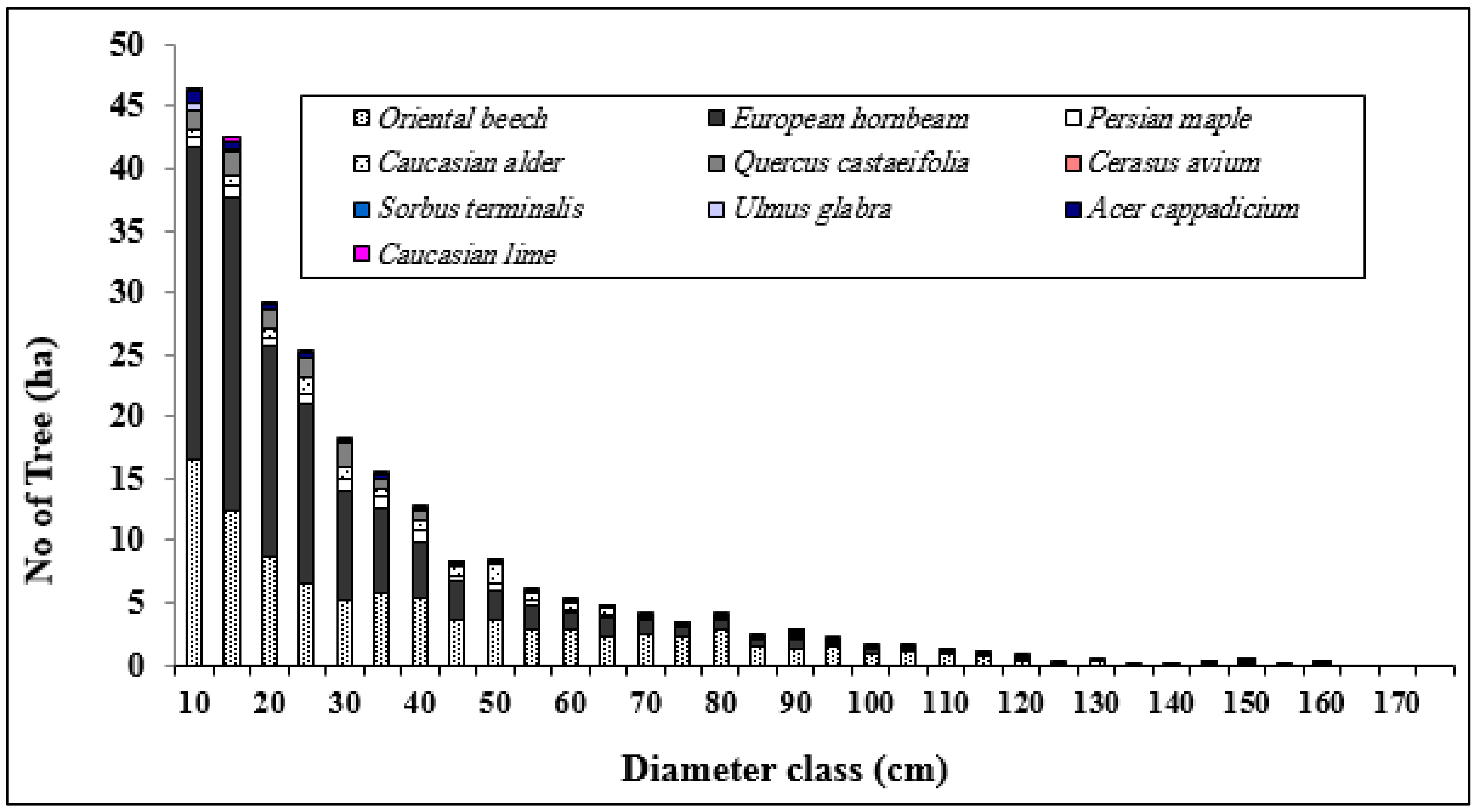

| Variable | Minimum | Maximum | Standard Deviation |
|---|---|---|---|
| Diameter (cm) | 7 | 188 | 24.7 |
| The mean of basal area at sample plot (m2) | 0.02 | 0.633 | 0.1 |
| The basal area of the largest tree (m2/ha) | 0 | 52 | 8.4 |
| Size diversity index of the sample plot | 0 | 2.468 | 0.314 |
| Shannon-Wiener index | 0 | 1.8 | 0.663 |
| Compartments Number | Number of Marked Trees in Compartments | Predicted Allowable Cut in Forestry Plan (m3) | |||||
|---|---|---|---|---|---|---|---|
| Beech | Hornbeam | Chestnut-Leaved Oak | Other Species | Total | Without Coefficient | With Coefficient 0.9 | |
| 305 | 73 | 97 | 0 | 7 | 177 | 600 | 540 |
| 306 | 16 | 216 | 0 | 10 | 246 | 520 | 468 |
| 309 | 81 | 237 | 0 | 9 | 327 | 1420 | 1278 |
| Total | 170 | 550 | 0 | 26 | 750 | 2536 | 2282.4 |
| Species Group | Compartment 305 | Compartment 306 | Compartment 309 | Total | ||||
|---|---|---|---|---|---|---|---|---|
| Volume | Volume with Coefficient 0.9 | Volume | Volume with Coefficient 0.9 | Volume | Volume with Coefficient 0.9 | Volume | Volume with Coefficient 0.9 | |
| Beech | 480.82 | 432.74 | 74.79 | 67.31 | 632.33 | 569.1 | 1187.94 | 1069.15 |
| Hornbeam | 296.75 | 267.7 | 586.35 | 527.72 | 865.34 | 778.8 | 1748.44 | 1573.6 |
| Chestnut-leaved oak | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Other species | 14.41 | 12.97 | 12.1 | 10.89 | 46.94 | 42.25 | 73.45 | 66.105 |
| Total | 791.98 | 712.78 | 673.24 | 605.916 | 1544.761 | 1390.15 | 3009.83 | 2708.847 |
| Pj | Unlogged Compartments | Logged Compartments (305, 306 and 309) | ||||||
|---|---|---|---|---|---|---|---|---|
| Beech | Hornbeam | Chestnut-Leaved Oak | Other Species | Beech | Hornbeam | Chestnut-Leaved Oak | Other Species | |
| P1 | 0.1564 | 0.1981 | 0.2278 | 0.2791 | 0.1433 | 0.1956 | 0.2152 | 0.2502 |
| P2 | 0.2119 | 0.2317 | 0.3070 | 0.3459 | 0.1834 | 0.2313 | 0.2951 | 0.3005 |
| P3 | 0.2418 | 0.2597 | 0.3597 | 0.3729 | 0.2456 | 0.2577 | 0.3587 | 0.3427 |
| P4 | 0.2787 | 0.2842 | 0.4111 | 0.3919 | 0.2785 | 0.2828 | 0.4087 | 0.3724 |
| P5 | 0.3174 | 0.3076 | 0.4602 | 0.4030 | 0.3352 | 0.3075 | 0.3895 | |
| P6 | 0.3311 | 0.3268 | 0.4712 | 0.4098 | 0.3610 | 0.3286 | 0.4053 | |
| P7 | 0.3343 | 0.3378 | 0.4678 | 0.4046 | 0.3846 | 0.3451 | 0.4088 | |
| P8 | 0.3382 | 0.3601 | 0.5097 | 0.3978 | 0.3929 | 0.3598 | 0.4051 | |
| P9 | 0.3556 | 0.3725 | 0.4985 | 0.3872 | 0.4000 | 0.3678 | 0.4075 | |
| P10 | 0.3298 | 0.3912 | 0.3779 | 0.3674 | 0.3977 | 0.3949 | ||
| P11 | 0.3293 | 0.3934 | 0.3427 | 0.2529 | 0.4128 | 0.3835 | ||
| P12 | 0.3257 | 0.3711 | 0.3113 | 0.2462 | ||||
| P13 | 0.3097 | 0.2949 | 0.2309 | |||||
| P14 | 0.2880 | 0.2787 | 0.2053 | |||||
| P15 | 0.2693 | 0.2525 | ||||||
| The Group of Compartments | Unlogged Compartments | Logged Compartments | ||||||
|---|---|---|---|---|---|---|---|---|
| Species Group | Beech | Hornbeam | Chestnut-Leaved Oak | Other Species | Beech | Hornbeam | Chestnut-Leaved Oak | Other Species |
| The largest right dominant eigenvalue | 1.062 | 1.079 | 1.113 | 1.074 | 1 | 0.91 | 1.121 | 1.083 |
| The nine-year harvest rate | 0.06 | 0.073 | 0.101 | 0.067 | 0 | - | 0.108 | 0.077 |
| Annual allowable cut (m3/ha) | 1.26 | 0.55 | 0.08 | 0.83 | 0 | - | 0.1 | 0.75 |
| Total of Nine-year allowable cut (m3) | 8237.26 | 3564.46 | 537.68 | 5433.52 | 0 | −830.57 | 78.62 | 533.835 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salehnasab, A.; Burkhart, H.E.; Bayat, M.; Khaleghi, B.; Heidari, S.; Masood Awan, H.U. Projection Matrix Models: A Suitable Approach for Predicting Sustainable Growth in Uneven-Aged and Mixed Hyrcanian Forests. Sustainability 2022, 14, 6777. https://doi.org/10.3390/su14116777
Salehnasab A, Burkhart HE, Bayat M, Khaleghi B, Heidari S, Masood Awan HU. Projection Matrix Models: A Suitable Approach for Predicting Sustainable Growth in Uneven-Aged and Mixed Hyrcanian Forests. Sustainability. 2022; 14(11):6777. https://doi.org/10.3390/su14116777
Chicago/Turabian StyleSalehnasab, Abotaleb, Harold E. Burkhart, Mahmoud Bayat, Bagher Khaleghi, Sahar Heidari, and Hafiz Umair Masood Awan. 2022. "Projection Matrix Models: A Suitable Approach for Predicting Sustainable Growth in Uneven-Aged and Mixed Hyrcanian Forests" Sustainability 14, no. 11: 6777. https://doi.org/10.3390/su14116777
APA StyleSalehnasab, A., Burkhart, H. E., Bayat, M., Khaleghi, B., Heidari, S., & Masood Awan, H. U. (2022). Projection Matrix Models: A Suitable Approach for Predicting Sustainable Growth in Uneven-Aged and Mixed Hyrcanian Forests. Sustainability, 14(11), 6777. https://doi.org/10.3390/su14116777






