Management Optimization of Electricity System with Sustainability Enhancement
Abstract
:1. Introduction
2. Modeling of Uncertainties
2.1. Modeling of Probable Load
2.2. Probabilistic Wind Modeling
2.3. Probabilistic Line Rating Modeling
3. Probabilistic Power Flow
4. Formulation of the Issue
4.1. Objective Functions
4.1.1. Overall Cost of Power Production
4.1.2. Probable Reliability Objective
5. Solution Method
5.1. Enhanced Particle Swarm Optimization
5.2. Islanding Prevention
5.3. Suggested Method
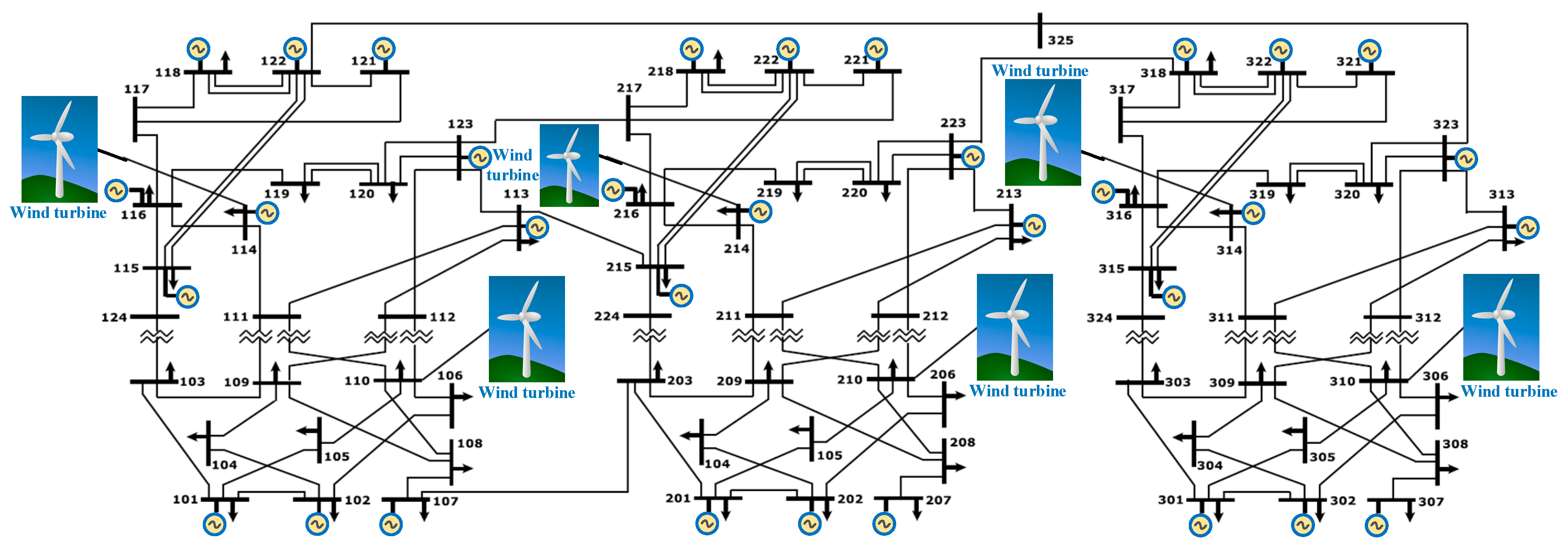
6. Test System and Scenarios
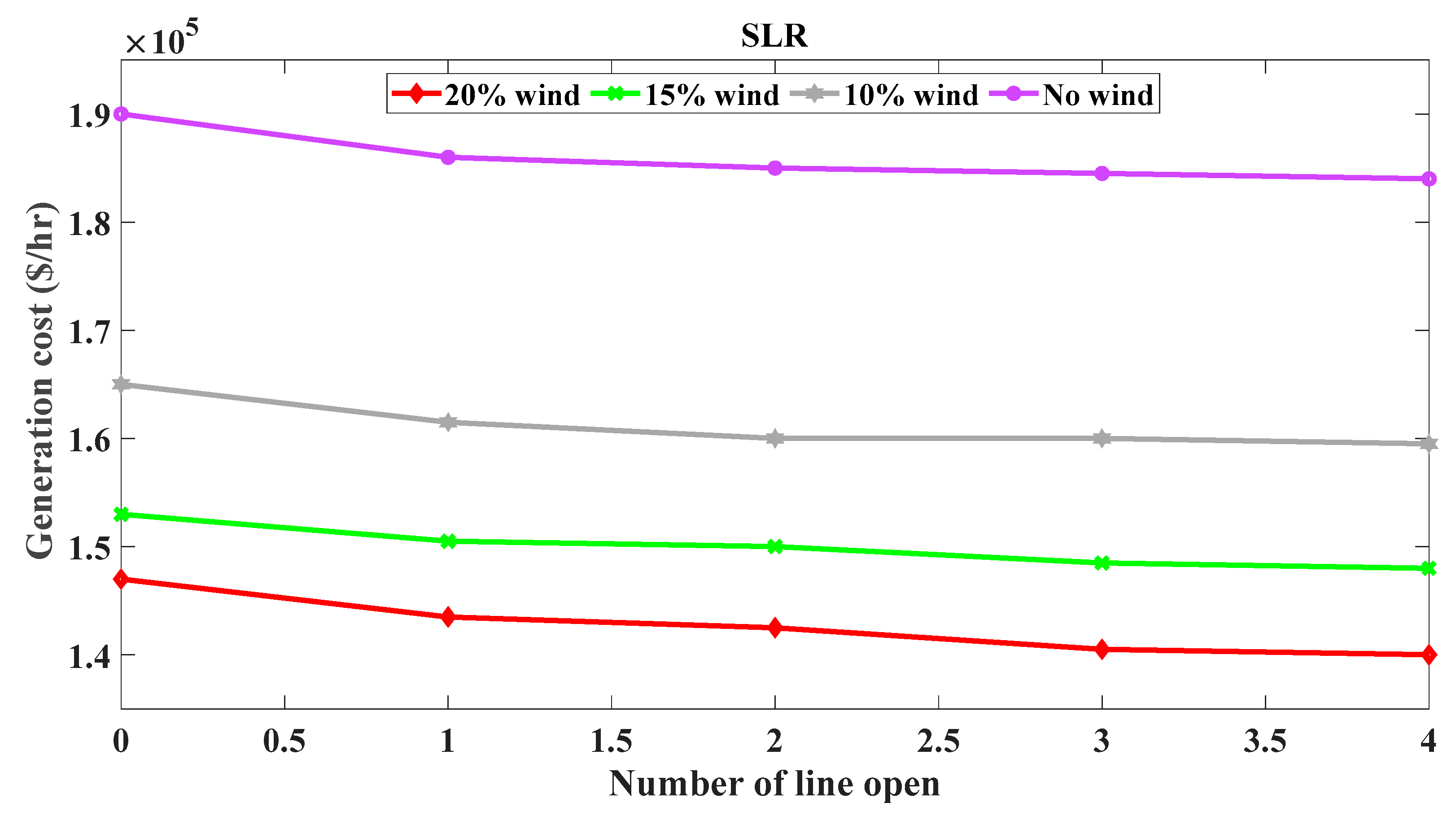
6.1. First Case Study: OTS with SLR
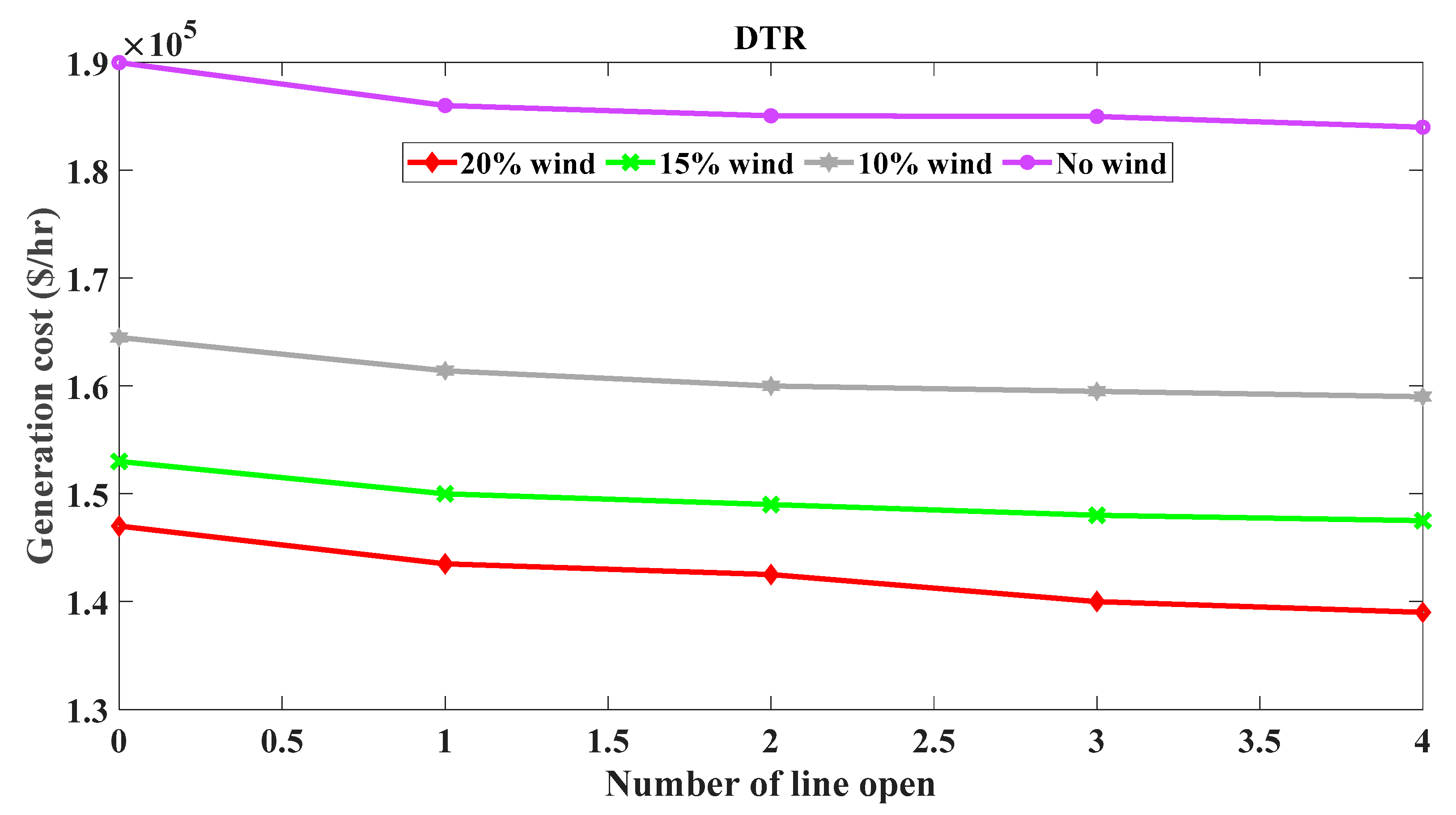
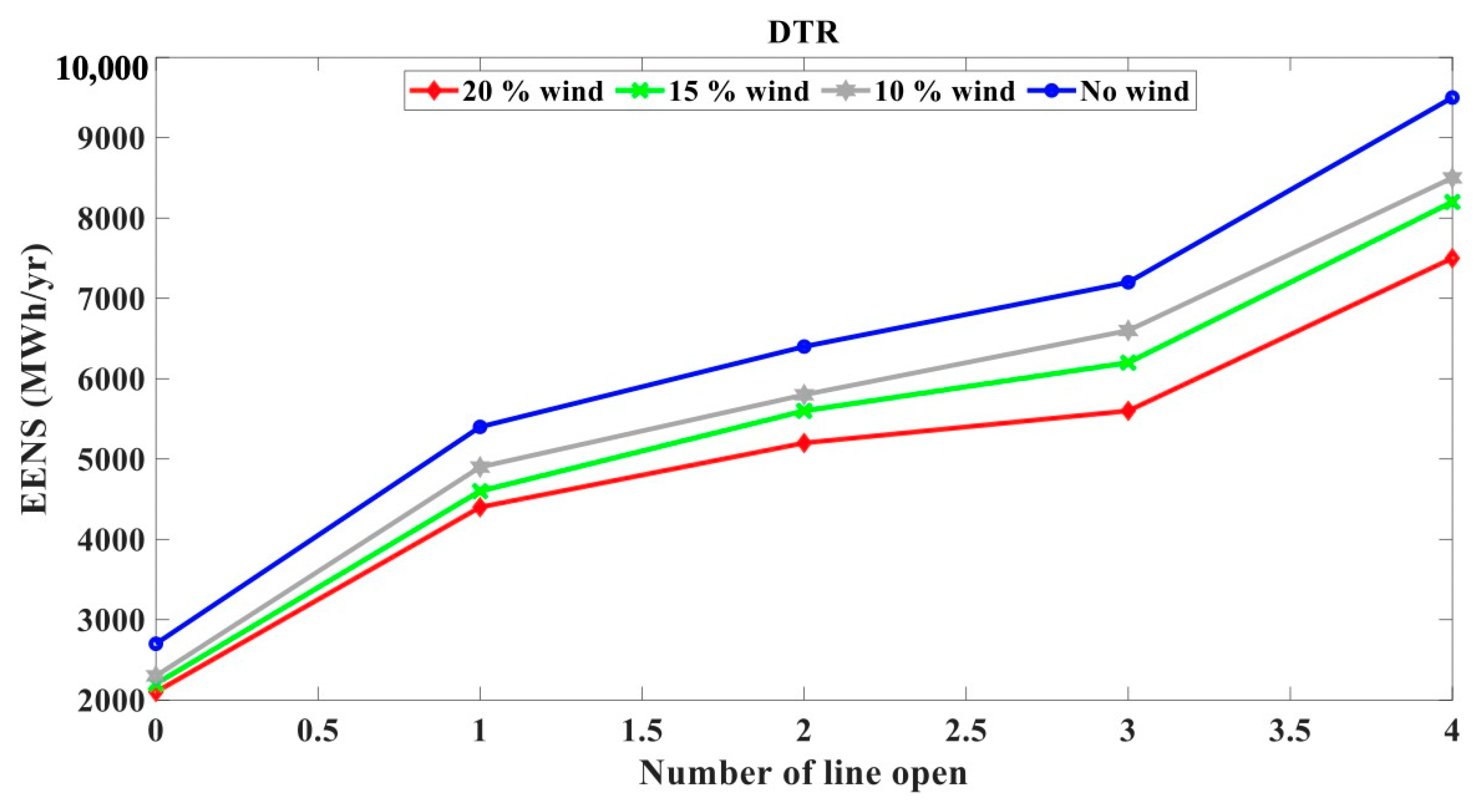
6.2. Case Study: OTS with DTR
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviation
| ACOPF | AC optimal power flow |
| CM | Congestion management |
| EENS | Expected energy not supplied |
| FACTs | Flexible AC-TS |
| LD | Load demand |
| MPSO | Modified particle swarm optimization |
| MOMPSO | Multi-objective MPSO |
| MCS | Monte Carlo simulation |
| NTO | Network topology optimization |
| OTS | Optimal transmission switching |
| PEM | points estimation method |
| PPF | Probabilistic power flow |
| PDFs | probability distribution functions |
| RO | Robust optimization |
| SOTS | Stochastic optimal transmission switching |
| SLRs | Static line ratings |
| SLR | Static line ratings |
| TL | Transmission lines |
| TN | Transmission network |
| WT | Wind turbine |
Appendix A
| Scale parameter c = 8.549 m/s; |
| Shape parameter k = 1.98; |
| V_i = 5 m/s; |
| V_r = 15 m/s; |
| V_o = 25 m/s; |
| and P_r = 1.5 MW. |
References
- Alnowibet, K.; Annuk, A.; Dampage, U.; Mohamed, M.A. Effective Energy Management via False Data Detection Scheme for the Interconnected Smart Energy Hub–Microgrid System under Stochastic Framework. Sustainability 2021, 13, 11836. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Mirjalili, S.; Dampage, U.; Salmen, S.H.; Al Obaid, S.; Annuk, A. A Cost-Efficient-Based Cooperative Allocation of Mining Devices and Renewable Resources Enhancing Blockchain Architecture. Sustainability 2021, 13, 10382. [Google Scholar] [CrossRef]
- Abhinav, R.; Pindoriya, N.M. Grid integration of wind turbine and battery energy storage system: Review and key challenges. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Dabbaghjamanesh, M.; Wang, B.; Kavousi-Fard, A.; Hatziargyriou, N.D.; Zhang, J. Blockchain-Based Stochastic Energy Management of Interconnected Microgrids Considering Incentive Price. IEEE Trans. Control Netw. Syst. 2021, 8, 1201–1211. [Google Scholar] [CrossRef]
- Aghajan-Eshkevari, S.; Sasan, A.; Morteza, N.; Mohammad, T.A.; Somayeh, A. “Charging and Discharging of Electric Vehicles in Power Systems: An Updated and Detailed Review of Methods”, Control Structures, Objectives, and Optimization Methodologies. Sustainability 2022, 14, 2137. [Google Scholar] [CrossRef]
- Shojaei, F.; Rastegar, M.; Dabbaghjamanesh, M. Simultaneous placement of tie-lines and distributed generations to optimize distribution system post-outage operations and minimize energy losses. CSEE J. Power Energy Syst. 2020, 7, 318–328. [Google Scholar]
- Dabbaghjamanesh, M.; Kavousi-Fard, A.; Dong, Z.Y. A Novel Distributed Cloud-Fog Based Framework for Energy Management of Networked Microgrids. IEEE Trans. Power Syst. 2020, 35, 2847–2862. [Google Scholar] [CrossRef]
- Putranto, L.M.; Irnawan, R.; Priyanto, A.; Isnandar, S.; Savitri, I. Transmission Expansion Planning for the Optimization of Renewable Energy Integration in the Sulawesi Electricity System. Sustainability 2021, 13, 10477. [Google Scholar] [CrossRef]
- Reusser, C.A.; Pérez, J.R. Evaluation of the emission impact of cold-ironing power systems, using a bi-directional power flow control strategy. Sustainability 2020, 13, 334. [Google Scholar] [CrossRef]
- Abdulwahid, A.H.; Wang, S. A Novel Method of Protection to Prevent Reverse Power Flow Based on Neuro-Fuzzy Networks for Smart Grid. Sustainability 2018, 10, 1059. [Google Scholar] [CrossRef] [Green Version]
- Salimi, A.A.; Karimi, A.; Noorizadeh, Y. Simultaneous operation of wind and pumped storage hydropower plants in a linearized security-constrained unit commitment model for high wind energy penetration. J. Energy Storage 2019, 22, 318–330. [Google Scholar] [CrossRef]
- Dehbozorgi, M.R.; Rastegar, M.; Dabbaghjamanesh, M. Decision tree-based classifiers for root-cause detection of equipment-related distribution power system outages. IET Gener. Transm. Distrib. 2020, 14, 5809–5815. [Google Scholar] [CrossRef]
- Shepero, M.; van der Meer, D.; Munkhammar, J.; Widén, J. Residential probabilistic load forecasting: A method using Gaussian process designed for electric load data. Appl. Energy 2018, 218, 159–172. [Google Scholar] [CrossRef]
- Teh, J.; Lai, C.-M. Reliability impacts of the dynamic thermal rating and battery energy storage systems on wind-integrated power networks. Sustain. Energy Grids Netw. 2019, 20, 100268. [Google Scholar] [CrossRef]
- Douglass, D.A.; Gentle, J.; Nguyen, H.; Chisholm, W.; Xu, C.; Goodwin, T.; Chen, H.; Nuthalapati, S.; Hurst, N.; Grant, I.; et al. A review of dynamic thermal line rating methods with forecasting. IEEE Trans. Power Deliv. 2019, 34, 2100–2109. [Google Scholar] [CrossRef]
- Zeng, L.; Xia, T.; Elsayed, S.; Ahmed, M.; Rezaei, M.; Jermsittiparsert, K.; Dampage, U.; Mohamed, M. A Novel Machine Learning-Based Framework for Optimal and Secure Operation of Static VAR Compensators in EAFs. Sustainability 2021, 13, 5777. [Google Scholar] [CrossRef]
- Lai, C.M.; Teh, J.; Cheng, Y.H. Fuzzy evaluation of transmission line end-of-life reliability model. In Proceedings of the 2019 International Automatic Control Conference (CACS), Keelung, Taiwan, 13–16 November 2019; pp. 1–4. [Google Scholar]
- Li, Y.; Hu, B.; Xie, K.; Wang, L.; Xiang, Y.; Xiao, R.; Kong, D. Day-Ahead Scheduling of Power System Incorporating Network Topology Optimization and Dynamic Thermal Rating. IEEE Access 2019, 7, 35287–35301. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Awwad, E.M.; El-Sherbeeny, A.M.; Nasr, E.A.; Ali, Z.M. Optimal scheduling of reconfigurable grids considering dynamic line rating constraint. IET Gener. Transm. Distrib. 2020, 14, 1862–1871. [Google Scholar] [CrossRef]
- Kazemi, B.; Kavousi-Fard, A.; Dabbaghjamanesh, M.; Karimi, M. IoT-Enabled Operation of Multi Energy Hubs Considering Electric Vehicles and Demand Response. 2022. IEEE Transactions on Intelligent Transportation Systems. Available online: https://osuva.uwasa.fi/handle/10024/13474 (accessed on 24 April 2022).
- Karimi, S.; Musilek, P.; Knight, A.M. Dynamic thermal rating of transmission lines: A review. Renew. Sustain. Energy Rev. 2018, 91, 600–612. [Google Scholar] [CrossRef]
- Rizwan, M.; Waseem, M.; Liaqat, R.; Sajjad, I.A.; Dampage, U.; Salmen, S.H.; Al Obaid, S.; Mohamed, M.A.; Annuk, A. SPSO Based Optimal Integration of DGs in Local Distribution Systems under Extreme Load Growth for Smart Cities. Electronics 2021, 10, 2542. [Google Scholar] [CrossRef]
- Luo, L.; Abdulkareem, S.S.; Rezvani, A.; Miveh, M.R.; Samad, S.; Aljojo, N.; Pazhoohesh, M. Optimal scheduling of a renewable based microgrid considering photovoltaic system and battery energy storage under uncertainty. J. Energy Storage 2020, 28, 101306. [Google Scholar] [CrossRef]
- Razmjouei, P.; Kavousi-Fard, A.; Dabbaghjamanesh, M.; Jin, T.; Su, W. Ultra-Lightweight Mutual Authentication in the Vehicle Based on Smart Contract Blockchain: Case of MITM Attack. IEEE Sens. J. 2020, 21, 15839–15848. [Google Scholar] [CrossRef]
- Zhang, L.; Shaby, B. Uniqueness and global optimality of the maximum likelihood estimator for the generalized extreme value distribution. arXiv 2020, arXiv:2008.06400. [Google Scholar] [CrossRef]
- Tajalli, S.Z.; Mardaneh, M.; Taherian-Fard, E.; Izadian, A.; Kavousi-Fard, A.; Dabbaghjamanesh, M.; Niknam, T. DoS-resilient distributed optimal scheduling in a fog supporting IIoT-based smart microgrid. IEEE Trans. Ind. Appl. 2020, 56, 2968–2977. [Google Scholar] [CrossRef]
- Ashkaboosi, M.; Ashkaboosi, F.; Nourani, S.M. The Interaction of Cybernetics and Contemporary Economic Graphic Art as. “Interactive Graphics”; University Library of Munich: Munich, Germany, 2016. [Google Scholar]
- Dabbaghjamanesh, M.; Zhang, J. Deep learning-based real-time switching of reconfigurable microgrids. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar]
- Ghaffari, S.; Ashkaboosi, M. Applying Hidden Markov Model Baby Cry Signal Recognition Based on Cybernetic Theory. IJEIR 2016, 5, 243–247. [Google Scholar]
- Dabbaghjamanesh, M.; Wang, B.; Kavousi-Fard, A.; Mehraeen, S.; Hatziargyriou, N.D.; Trakas, D.N.; Ferdowsi, F. A Novel Two-Stage Multi-Layer Constrained Spectral Clustering Strategy for Intentional Islanding of Power Grids. IEEE Trans. Power Deliv. 2019, 35, 560–570. [Google Scholar] [CrossRef]





| Variable | P | |||||||
|---|---|---|---|---|---|---|---|---|
| Value | 5 | 0.5 | 0.5 | 0.5 | 1 | 5 × 10−3 | 1 | 30 |
| Generator Unit | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Size (MW) | 12.00 | 20.00 | 50.00 | 76.00 | 100.00 | 155.00 | 197.00 | 350.00 | 400.00 |
| Fuel | Steam/Oil | CT/Oil | Hydro | Steam/Coal | Steam/Oil | Steam/Coal | Steam/Oil | Steam/Coal | Nuclear |
| 8.4 | 15.17 | 0 | 1.78 | 8.4 | 1.78 | 8.4 | 1.78 | 0.6 | |
| 85.5 | 149.56 | 0.1 | 17 | 67.95 | 14.71 | 74.75 | 14.96 | 22 |
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Wind penetration (0%) Lines open | - | [111–114] | [210,211]; [111–114] | [118–121]; [209–111]; [210,211] | [310,311]; [106–110]; [118–121]; [109–111] |
($/h) | 189,685 | 186,439 | 185,285 | 184,633 | 184,125 |
(Mwh/y) | |||||
| Wind penetration (10%) Lines open | - | [111–114] | [210,211]; [109–111] | [110–112]; [109–111]; [215,216] | [312–314]; [106–110]; [118–121]; [109–111] |
($/h) | 164,860 | 161,340 | 160,215 | 159,730 | 159,310 |
(Mwh/y) |
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Wind penetration (15%) Lines open | - | [109–111] | [210,211]; [114–111] | [118–121]; [109–108]; [210–205] | [310–305]; [106–110]; [118–117]; [109–111] |
($/h) | 189,685 | 186,439 | 185,285 | 184,633 | 184,125 |
(Mwh/y) | |||||
| Wind penetration (20%) Lines open | - | [119–114] | [210,211]; [109–103] | [118–121]; [109–108]; [210,211] | [311–314]; [106–110]; [218–222]; [109–104] |
($/h) | 164,820 | 143,620 | 142,510 | 140,715 | 140,030 |
(Mwh/y) |
| Generator Unit | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Size (MW) | 12.00 | 20.00 | 50.00 | 76.00 | 100.00 | 155.00 | 197.00 | 350.00 | 400.00 |
| Fuel kind | Oil/Steam | Oil/CT | Hydro | Coal/Steam | Oil/Steam | Coal/Steam | Oil/Steam | Coal/Steam | Nuclear |
| 8.4 | 15.17 | 0 | 1.78 | 8.4 | 1.78 | 8.4 | 1.78 | 0.6 | |
| 85.5 | 149.56 | 0.1 | 17 | 67.95 | 14.71 | 74.75 | 14.96 | 22 | |
| Change in output (Mw) | 4.5 | 0 | 0 | 29.74 | −17.37 | 0 | −98 | 81.13 | 0 |
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Wind penetration (0%) Lines open | - | [109–111] | [210,211]; [109–111] | [118–121]; [109–111]; [210,211] | [310,311]; [106–110]; [118–121]; [109–111] |
($/h) | 189,625 | 186,412 | 185,235 | 184,587 | 184,098 |
(Mwh/y) | |||||
| Wind penetration (10%) Lines open | - | [119–111] | [210,211]; [109–111] | [118–121]; [109–111]; [210,211] | [310,311]; [106–110]; [118–121]; [109–111] |
($/h) | 164,710 | 161,240 | 160,215 | 159,510 | 159,205 |
(Mwh/y) |
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Wind penetration (15%) Lines open | - | [109–111] | [210,211]; [114–111] | [118–121]; [109–108]; [210–205] | [310–305]; [106–110]; [118–117]; [109–111] |
($/h) | 153,101 | 150,05 | 149,520 | 148,490 | 147,850 |
(Mwh/y) | |||||
| Wind penetration (20%) Lines open | - | [119–114] | [210,211]; [109–103] | [118–121]; [109–108]; [210,211] | [311–314]; [106–110]; [218–222]; [109–104] |
($/h) | 141,520 | 140,320 | 137,210 | 134,415 | 131,830 |
(Mwh/y) |
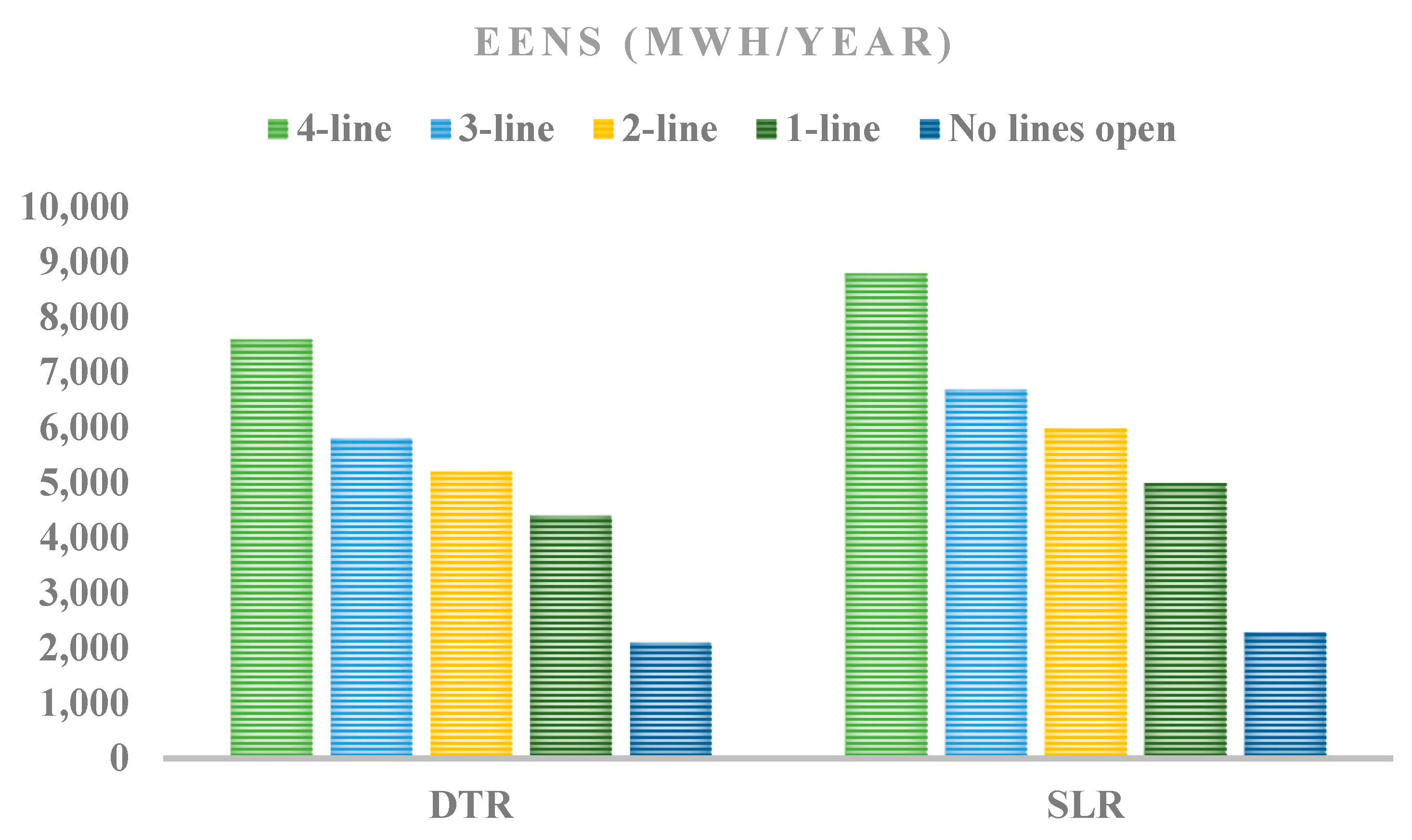
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| SLR Lines open | - | [109–111] | [210,211]; [114–111] | [118–121]; [109–108]; [210–205] | [310–305]; [106–110]; [118–117]; [109–111] |
($/h) | 146,820 | 143,620 | 142,510 | 140,715 | 140,030 |
(Mwh/y) | |||||
| DTR Lines open | - | [109–111] | [210,211]; [109–111] | [118–121]; [109–111]; [210,211] | [310,311]; [106–110]; [118–121]; [109–111] |
($/h) | 141,520 | 140,320 | 137,210 | 134,415 | 131,830 |
(Mwh/y) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, W.; Man Li, R.Y.; Sittihai, T. Management Optimization of Electricity System with Sustainability Enhancement. Sustainability 2022, 14, 6650. https://doi.org/10.3390/su14116650
Hou W, Man Li RY, Sittihai T. Management Optimization of Electricity System with Sustainability Enhancement. Sustainability. 2022; 14(11):6650. https://doi.org/10.3390/su14116650
Chicago/Turabian StyleHou, Wei, Rita Yi Man Li, and Thanawan Sittihai. 2022. "Management Optimization of Electricity System with Sustainability Enhancement" Sustainability 14, no. 11: 6650. https://doi.org/10.3390/su14116650
APA StyleHou, W., Man Li, R. Y., & Sittihai, T. (2022). Management Optimization of Electricity System with Sustainability Enhancement. Sustainability, 14(11), 6650. https://doi.org/10.3390/su14116650





