Spatiotemporal Distribution Characteristics and Influencing Factors Analysis of Reference Evapotranspiration in Beijing–Tianjin–Hebei Region from 1990 to 2019 under Climate Change
Abstract
:1. Introduction
2. Materials and Methods
2.1. Overview of the Study Area
2.2. Data Sources and Processing
2.3. FAO-56 Penman–Monteith Equation
2.4. Climate Tendency Rate
2.5. Mann-Kendall Trend Testing
2.6. Morlet Wavelet Analysis
2.7. Path Analysis
2.8. Sensitivity Analysis
2.9. Contribution Rate Analysis
2.10. Inverse Distance Weighted Interpolation
3. Results
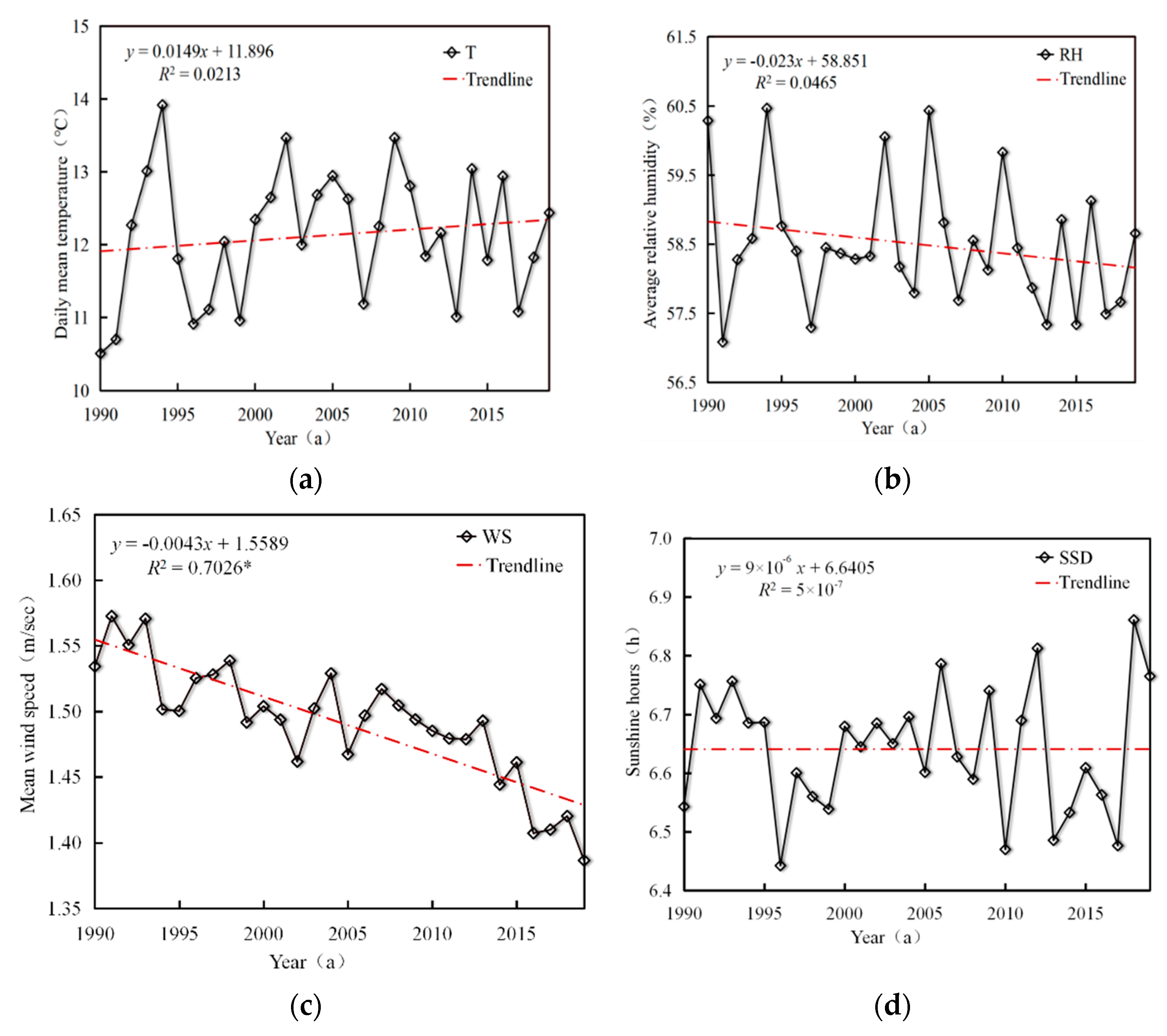
3.1. Temporal Variation of Meteorological Factors
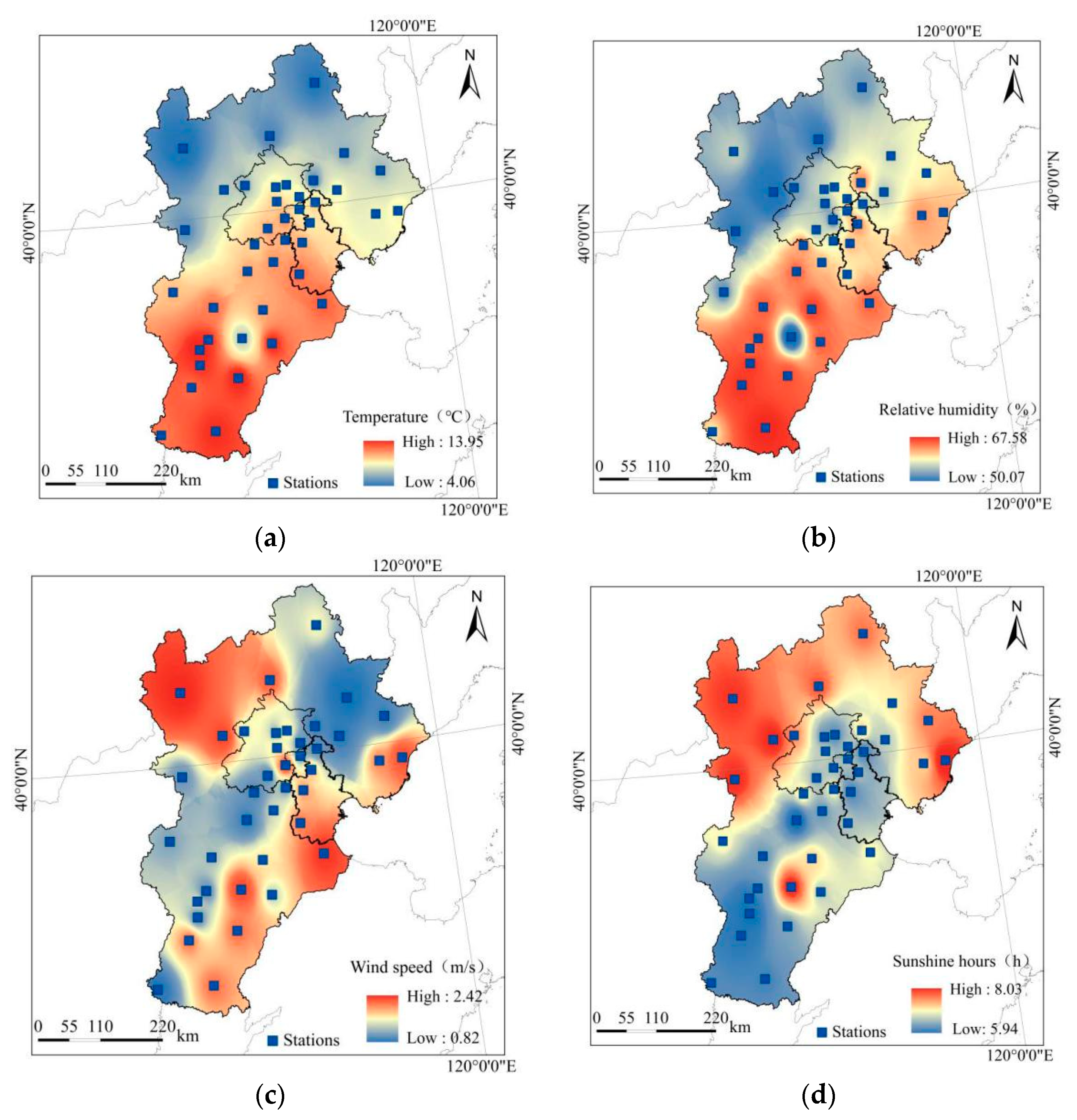
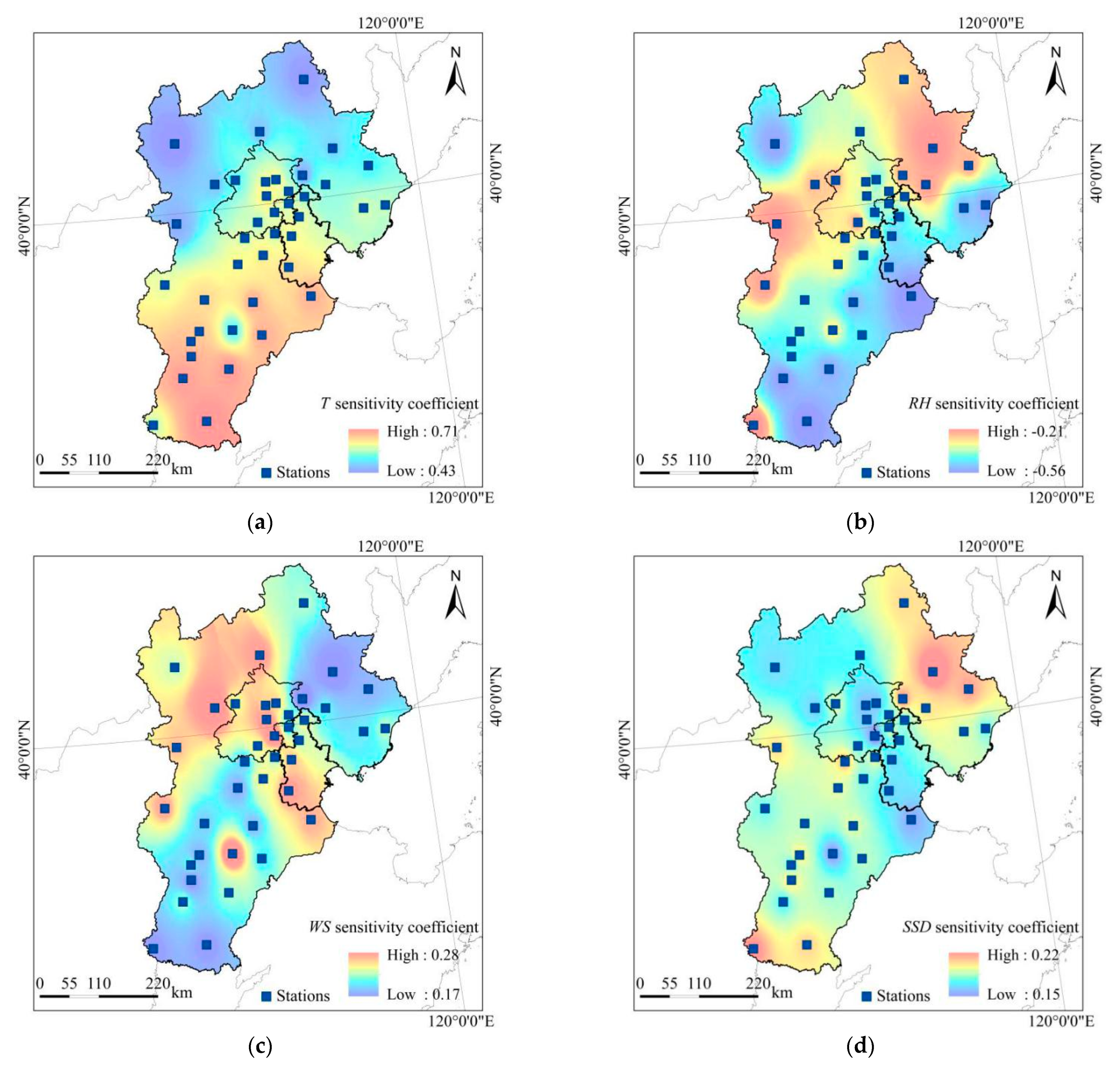
3.2. Spatial Distribution of Meteorological Factors
3.3. Temporal Variation of ET0
3.4. Spatial Distribution of ET0
3.5. The Trend Test of ET0
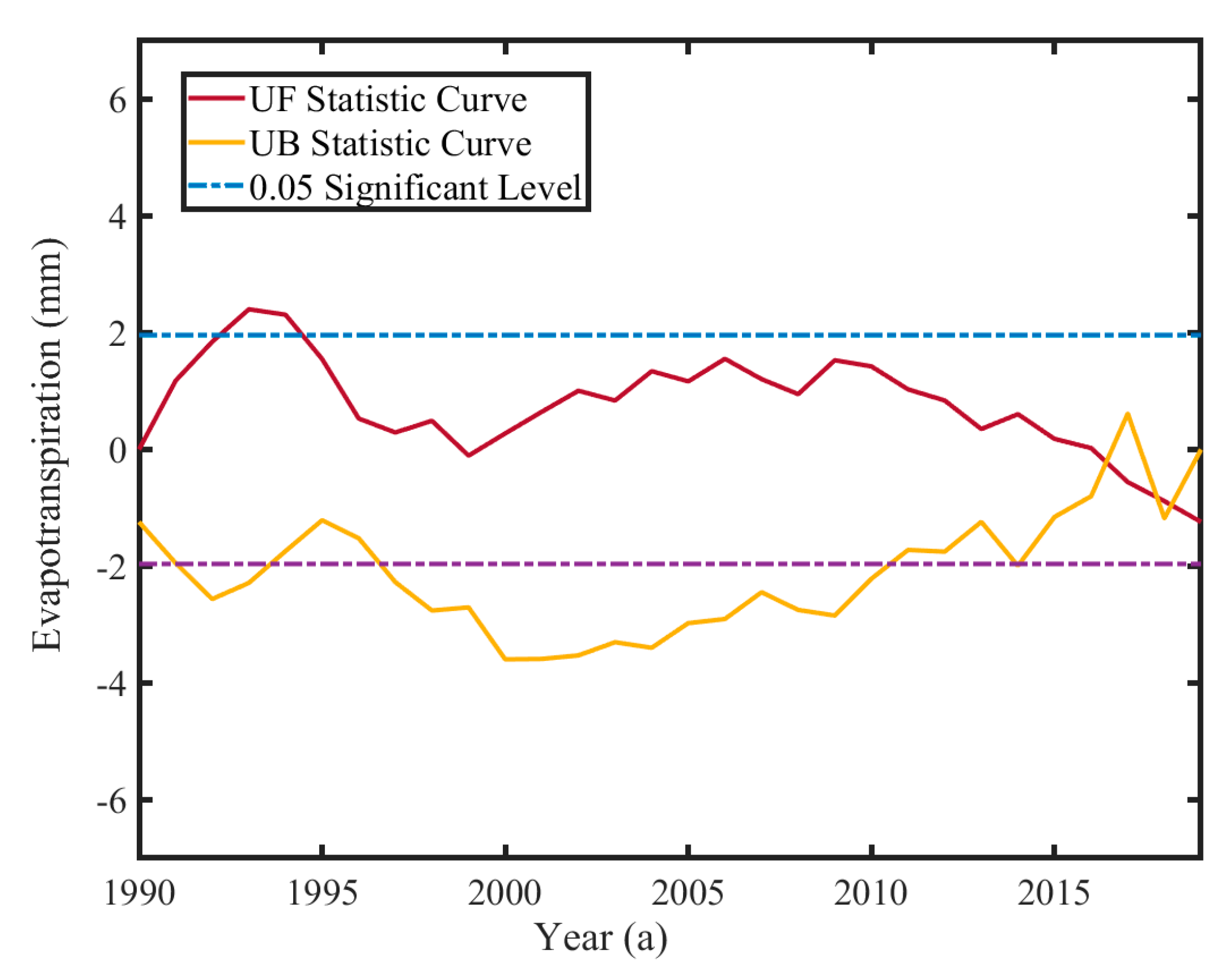
3.5.1. Mann-Kendall Trend Test
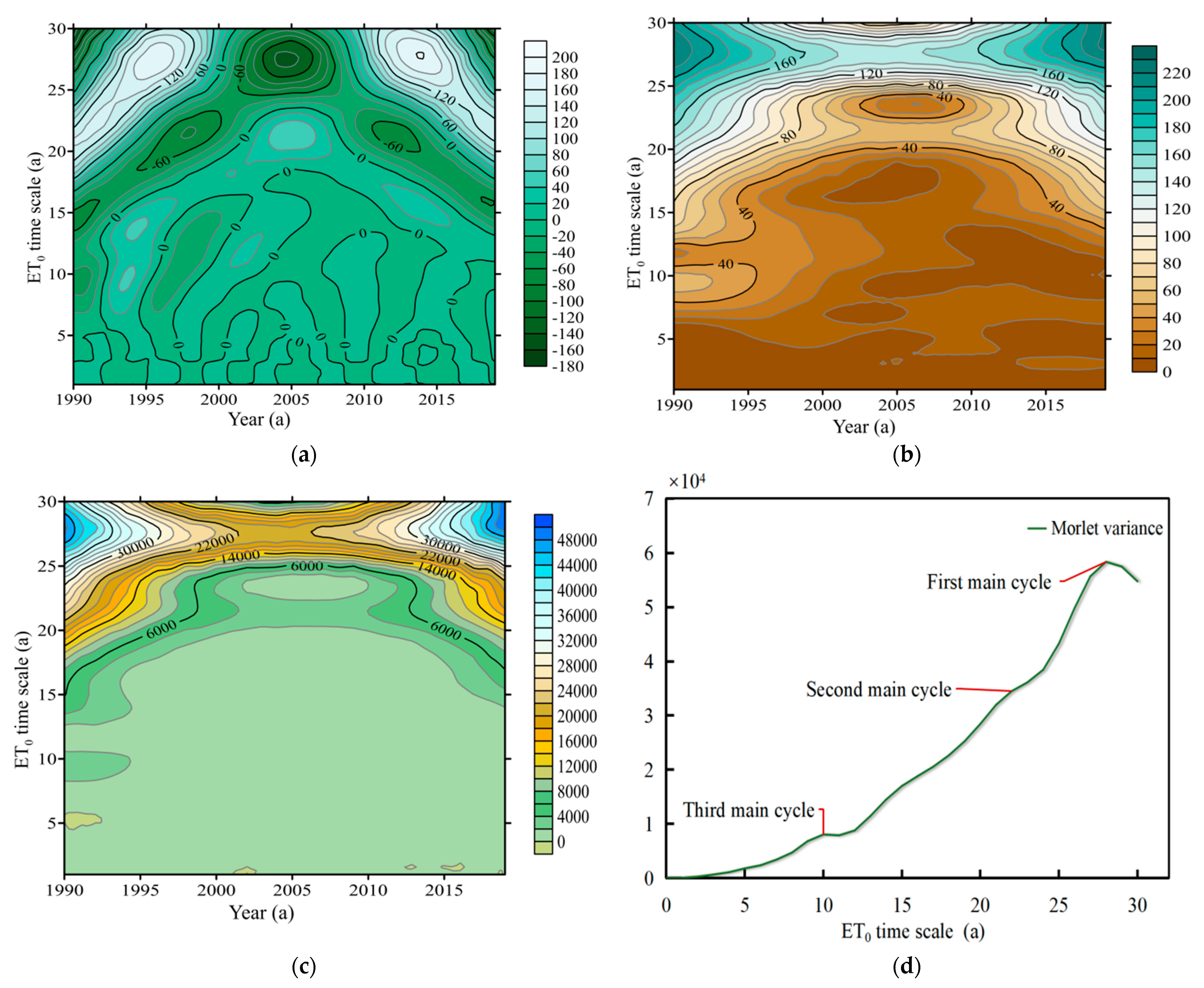
3.5.2. Morlet Wavelet Periodic Inspection
3.6. Effects of Meteorological Factors on ET0 Analysis
3.6.1. Path Analysis of Each Meteorological Factor on the Annual Average ET0
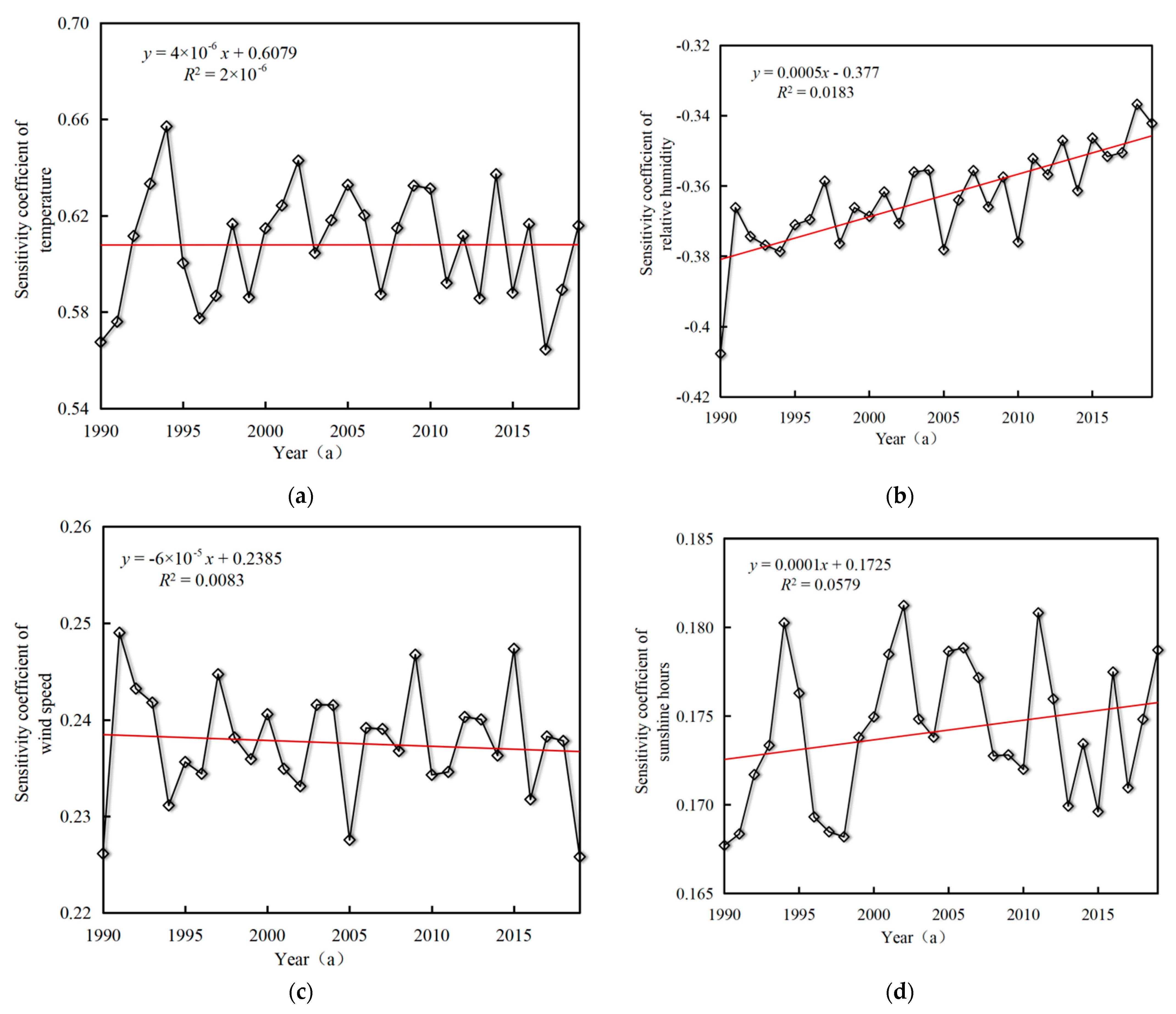
3.6.2. Sensitivity Analysis of Each Meteorological Factor on the Annual Average ET0
3.6.3. Contribution Rate Analysis between Meteorological Factors and ET0
4. Discussion
5. Conclusions
- (1)
- The average annual values for T, RH, WS, and SSD in the Beijing–Tianjin–Hebei region, from 1990 to 2019, were 12.1 °C, 58.5%, 1.49 m/s, and 6.6 h, respectively. The RH and WS showed an overall downward trend with time, while the T showed an upward trend, and the overall change in SSD was not large. Except for WS, the temporal variation trend of T, RH, and SSD were not significant. The spatial distribution of WS had latitudinal zonal characteristics, and T, RH, and SSD showed longitudinal variations.
- (2)
- In terms of time change, the annual average ET0 in the past 30 years has shown a downward trend, and the decline rate is −3.07 mm/10 a. The inter-annual highest value of ET0 was 1010.80 mm in 1993, and the lowest value was 896.24 mm in 1990. In terms of spatial distribution, the high-value areas of inter-annual ET0 are, mainly, distributed in southern Hebei, southeastern Beijing, and central and southern Tianjin, with relatively small values in the northern and northwestern regions of the Beijing–Tianjin–Hebei region.
- (3)
- The M-K trend test showed that the inter-annual ET0 in the Beijing–Tianjin–Hebei region changed abruptly in 2016, with a decrease of 9.71 mm. There is a main oscillation period of 22~28 a, during the evolution of ET0 from 1990 to 2019. There are three obvious cycles in the evolution of ET0, which correspond to the time scales of 10 a, 22 a, and 28 a, in order from small to large. The fluctuations of these three cycles control the variation characteristics of ET0, in the entire time domain.
- (4)
- The multi-year average ET0 in the Beijing–Tianjin–Hebei region was positively correlated with T, WS, and SSD, and negatively correlated with RH. The direct path coefficients of T and WS and ET0 are the highest, reaching 0.63 and 0.42, respectively. Combined with the results of path analysis, it is shown that WS and T are the dominant meteorological factors affecting the changes of ET0 in the Beijing–Tianjin–Hebei region. The comprehensive influence of SSD and RH is not high, and the contribution rate of each meteorological factor from high to low is WS > T > RH > SSD.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, K.; Awange, J.; Kuhn, M.; Zerihun, A. Irrigated agriculture potential of Australia’s northern territory inferred from spatial assessment of groundwater availability and crop evapotranspiration. Agric. Water Manag. 2022, 264, 107466. [Google Scholar] [CrossRef]
- Fernández-Pacheco, V.M.; Antuña-Yudego, E.; Carús-Candás, J.L.; Suárez-López, M.J.; Álvarez-Álvarez, E. An Evapotranspiration Evolution Model as a Function of Meteorological Variables: A CFD Model Approach. Sustainability 2022, 14, 3800. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, H.; Wang, C.; Li, W.; Chen, H.; Gong, S.X.; Krakauer, N.Y. Impacts of Climatic Change on Reference Crop Evapotranspiration across Different Climatic Zones of Ningxia at Multi-Time Scales from 1957 to 2018. Adv. Meteorol. 2020, 2020, 3156460. [Google Scholar] [CrossRef]
- Minhas, P.; Ramos, T.B.; Ben-Gal, A.; Pereira, L.S. Coping with salinity in irrigated agriculture: Crop evapotranspiration and water management issues. Agric. Water Manag. 2020, 227, 832–845. [Google Scholar] [CrossRef]
- Nouri, M.; Homaee, M. On modeling reference crop evapotranspiration under lack of reliable data over Iran. J. Hydrol. 2018, 566, 705–718. [Google Scholar] [CrossRef]
- Lu, X.; Zang, C.; Burenina, T. Study on the variation in evapotranspiration in different period of the Genhe River Basin in China. Phys. Chem. Earth 2020, 120, 102902. [Google Scholar] [CrossRef]
- Yao, N.; Li, L.; Feng, P.; Feng, H.; Liu, D.L.; Liu, Y.; Jiang, K.; Hu, X.; Li, Y. Projections of drought characteristics in China based on a standardized precipitation and evapotranspiration index and multiple GCMs. Sci. Total Environ. 2019, 704, 222–245. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Liu, Q.; Zhang, S.; Chen, X.; Ji, Y.; Liu, F.; Pulatov, A.; Feng, P. Response of wheat and maize growth-yields to meteorological and agricultural droughts based on standardized precipitation evapotranspiration indexes and soil moisture deficit indexes. Agric. Water Manag. 2022, 266, 566–589. [Google Scholar] [CrossRef]
- Nam, W.-H.; Hong, E.-M.; Choi, J.-Y. Has climate change already affected the spatial distribution and temporal trends of reference evapotranspiration in South Korea? Agric. Water Manag. 2015, 150, 129–138. [Google Scholar] [CrossRef]
- Liu, M.; Tian, H.; Yang, Q.; Yang, J.; Song, X.; Lohrenz, S.E.; Cai, W.-J. Long-term trends in evapotranspiration and runoff over the drainage basins of the Gulf of Mexico during 1901–2008. Water Resour. Res. 2013, 49, 1988–2012. [Google Scholar] [CrossRef]
- Prăvălie, R.; Piticar, A.; Rosca, B.; Sfîcă, L.; Bandoc, G.; Tiscovschi, A.; Patriche, C. Spatio-temporal changes of the climatic water balance in Romania as a response to precipitation and reference evapotranspiration trends during 1961–2013. Catena 2018, 172, 295–312. [Google Scholar] [CrossRef]
- Tang, Y.; Tang, Q. Variations and influencing factors of potential evapotranspiration in large Siberian river basins during 1975–2014. J. Hydrol. 2021, 598, 443–465. [Google Scholar] [CrossRef]
- Hu, X.; Chen, M.; Liu, D.; Li, D.; Jin, L.; Liu, S.; Cui, Y.; Dong, B.; Khan, S.; Luo, Y. Reference evapotranspiration change in Heilongjiang Province, China from 1951 to 2018: The role of climate change and rice area expansion. Agric. Water Manag. 2021, 253, 912–933. [Google Scholar] [CrossRef]
- Kang, T.; Li, Z.; Gao, Y. Spatiotemporal Variations of Reference Evapotranspiration and Its Determining Climatic Factors in the Taihang Mountains, China. Water 2021, 13, 3145. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, J.; Yang, Q.; Wang, G. Changing characteristics and attribution analysis of potential evapotranspiration in the Huang–Huai–Hai River Basin, China. Meteorol. Atmos. Physics. 2021, 133, 97–108. [Google Scholar] [CrossRef]
- Saeed, F.H.; Al-Khafaji, M.S.; Al-Faraj, F.A.M. Sensitivity of Irrigation Water Requirement to Climate Change in Arid and Semi-Arid Regions towards Sustainable Management of Water Resources. Sustainability 2021, 13, 13608. [Google Scholar] [CrossRef]
- Chen, L.-H.; Chen, J.; Chen, C. Effect of Environmental Measurement Uncertainty on Prediction of Evapotranspiration. Atmosphere 2018, 9, 400. [Google Scholar] [CrossRef] [Green Version]
- HeBei Statistical YearBook; National Bureau of statistics of the People’s Republic of China: Beijing, China. 2020. Available online: http://tjj.hebei.gov.cn/hetj/tjnj/2020/zk/indexch.htm (accessed on 5 July 2021).
- Li, W.; Song, H.; Dong, F.; Li, F. The high-quality development in Beijing-Tianjin-Hebei regions: Based on the perspective of comparison. Procedia Comput. Sci. 2022, 199, 1244–1251. [Google Scholar] [CrossRef]
- Wu, L.; Guo, X.; Chen, Y. Grey Relational Entropy Calculation and Fractional Prediction of Water and Economy in the Beijing-Tianjin-Hebei Region. J. Math. 2021, 2021, 260–271. [Google Scholar] [CrossRef]
- Liu, L.; Lei, Y.; Zhuang, M.; Ding, S. The impact of climate change on urban resilience in the Beijing-Tianjin-Hebei region. Sci. Total Environ. 2022, 827, 157–179. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Y.; Li, Q. High-Resolution PM2.5 Estimation Based on the Distributed Perception Deep Neural Network Model. Sustainability 2021, 13, 13985. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; pp. 15–64. [Google Scholar]
- Zhang, P.; Ma, W.; Hou, L.; Liu, F.; Zhang, Q. Study on the Spatial and Temporal Distribution of Irrigation Water Requirements for Major Crops in Shandong Province. Water 2022, 14, 1051. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, H.; Wang, C.; Li, W.; Chen, H.; Deng, C. Changes in reference evapotranspiration over Northwest China from 1957 to 2018: Variation characteristics, cause analysis and relationships with atmospheric circulation. Agric. Water Manag. 2020, 231, 958–971. [Google Scholar] [CrossRef]
- Wang, Q.; Meng, C.; Wang, C. Analog Continuous-Time Filter Designing for Morlet Wavelet Transform Using Constrained L2-Norm Approximation. IEEE Access 2020, 8, 121955–121968. [Google Scholar] [CrossRef]
- Abadi, B.; Kelboro, G. Farmers’ Contributions to Achieving Water Sustainability: A Meta-Analytic Path Analysis of Predicting Water Conservation Behavior. Sustainability 2022, 14, 279. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity Analysis for Importance Assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef]
- Kaoula, D.; Bouchair, A. The pinpointing of the most prominent parameters on the energy performance for optimal passive strategies in ecological buildings based on bioclimatic, sensitivity and uncertainty analyses. Int. J. Ambient. Energy 2022, 43, 685–712. [Google Scholar] [CrossRef]
- Elhadad, S.; Orban, Z. A Sensitivity Analysis for Thermal Performance of Building Envelope Design Parameters. Sustainability 2021, 13, 14018. [Google Scholar] [CrossRef]
- Ogunrinde, A.T.; Olasehinde, D.A.; Olotu, Y. Assessing the sensitivity of standardized precipitation evapotranspiration index to three potential evapotranspiration models in Nigeria. Sci. Afr. 2020, 8, e00431. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zheng, J.; Zhang, F. Medium-range forecasting of daily reference evapotranspiration across China using numerical weather prediction outputs downscaled by extreme gradient boosting. J. Hydrol. 2021, 126, 664–681. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2013: The Physical Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Zhao, F.; Ma, S.; Wu, Y.; Qiu, L.; Wang, W.; Lian, Y.; Chen, J.; Sivakumar, B. The role of climate change and vegetation greening on evapotranspiration variation in the Yellow River Basin, China. Agric. For. Meteorol. 2022, 316, 842–867. [Google Scholar] [CrossRef]
- Bi, Y.J.; Zhao, J.; Zhao, Y.; Xiao, W.H.; Meng, F.J. Spatial-temporal variation characteristics and attribution analysis of potential evapotranspiration in Beijing-Tianjin-Hebei region. Trans. CSAE. 2020, 36, 130–140, (In Chinese with English abstract). Available online: http://www.tcsae.org/nygcxb/article/abstract/20200515 (accessed on 5 July 2021).
- Han, J.; Wang, J.; Zhao, Y.; Wang, Q.; Zhang, B.; Li, H.; Zhai, J. Spatio-temporal variation of potential evapotranspiration and climatic drivers in the Jing-Jin-Ji region, North China. Agric. For. Meteorol. 2018, 256, 75–83. [Google Scholar] [CrossRef]







| Meteorological Factor | T (°C) | RH (%) | WS (m/s) | SSD (h) |
|---|---|---|---|---|
| Data range | −50~50 | 0~100 | 0~20 | 0~20 |
| Data accuracy | 0.1 | 1 | 0.1 | 0.1 |
| Factors | Coefficients | Direct Path Coefficients | Sum of Indirect Path Coefficients | Indirect Path Coefficients | Decision-Making Coefficients | |||
|---|---|---|---|---|---|---|---|---|
| T | RH | WS | SSD | |||||
| T | 0.856 | 0.630 | −0.287 | - | −0.200 | −0.090 | 0.003 | 0.340 |
| RH | −0.204 | −0.323 | 0.070 | 0.322 | - | −0.043 | −0.001 | −0.045 |
| WS | 0.212 | 0.418 | −0.100 | −0.135 | 0.033 | - | 0.005 | 0.318 |
| SSD | 0.405 | 0.008 | 0.2575 | 0.204 | 0.044 | 0.010 | - | 0.270 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Jing, D.; Han, Y.; Yu, J.; Lu, T.; Zhangzhong, L. Spatiotemporal Distribution Characteristics and Influencing Factors Analysis of Reference Evapotranspiration in Beijing–Tianjin–Hebei Region from 1990 to 2019 under Climate Change. Sustainability 2022, 14, 6277. https://doi.org/10.3390/su14106277
Liu Z, Jing D, Han Y, Yu J, Lu T, Zhangzhong L. Spatiotemporal Distribution Characteristics and Influencing Factors Analysis of Reference Evapotranspiration in Beijing–Tianjin–Hebei Region from 1990 to 2019 under Climate Change. Sustainability. 2022; 14(10):6277. https://doi.org/10.3390/su14106277
Chicago/Turabian StyleLiu, Zihan, Dong Jing, Yu Han, Jingxin Yu, Tiangang Lu, and Lili Zhangzhong. 2022. "Spatiotemporal Distribution Characteristics and Influencing Factors Analysis of Reference Evapotranspiration in Beijing–Tianjin–Hebei Region from 1990 to 2019 under Climate Change" Sustainability 14, no. 10: 6277. https://doi.org/10.3390/su14106277
APA StyleLiu, Z., Jing, D., Han, Y., Yu, J., Lu, T., & Zhangzhong, L. (2022). Spatiotemporal Distribution Characteristics and Influencing Factors Analysis of Reference Evapotranspiration in Beijing–Tianjin–Hebei Region from 1990 to 2019 under Climate Change. Sustainability, 14(10), 6277. https://doi.org/10.3390/su14106277








