Mechanical Characterization of Industrial Waste Materials as Mineral Fillers in Asphalt Mixes: Integrated Experimental and Machine Learning Analysis
Abstract
:1. Introduction
2. Materials and Experimental Investigation
2.1. Materials
2.1.1. Aggregate and Bitumen Properties
2.1.2. Mineral Filler
2.2. Designing and Testing of Asphalt Concrete
2.2.1. Sample Preparation and Determination of Marshall and Volumetric Properties
2.2.2. Rutting Resistance
2.2.3. Cracking Resistance
2.2.4. Moisture Susceptibility
2.2.5. Cantabro Abrasion Loss Test
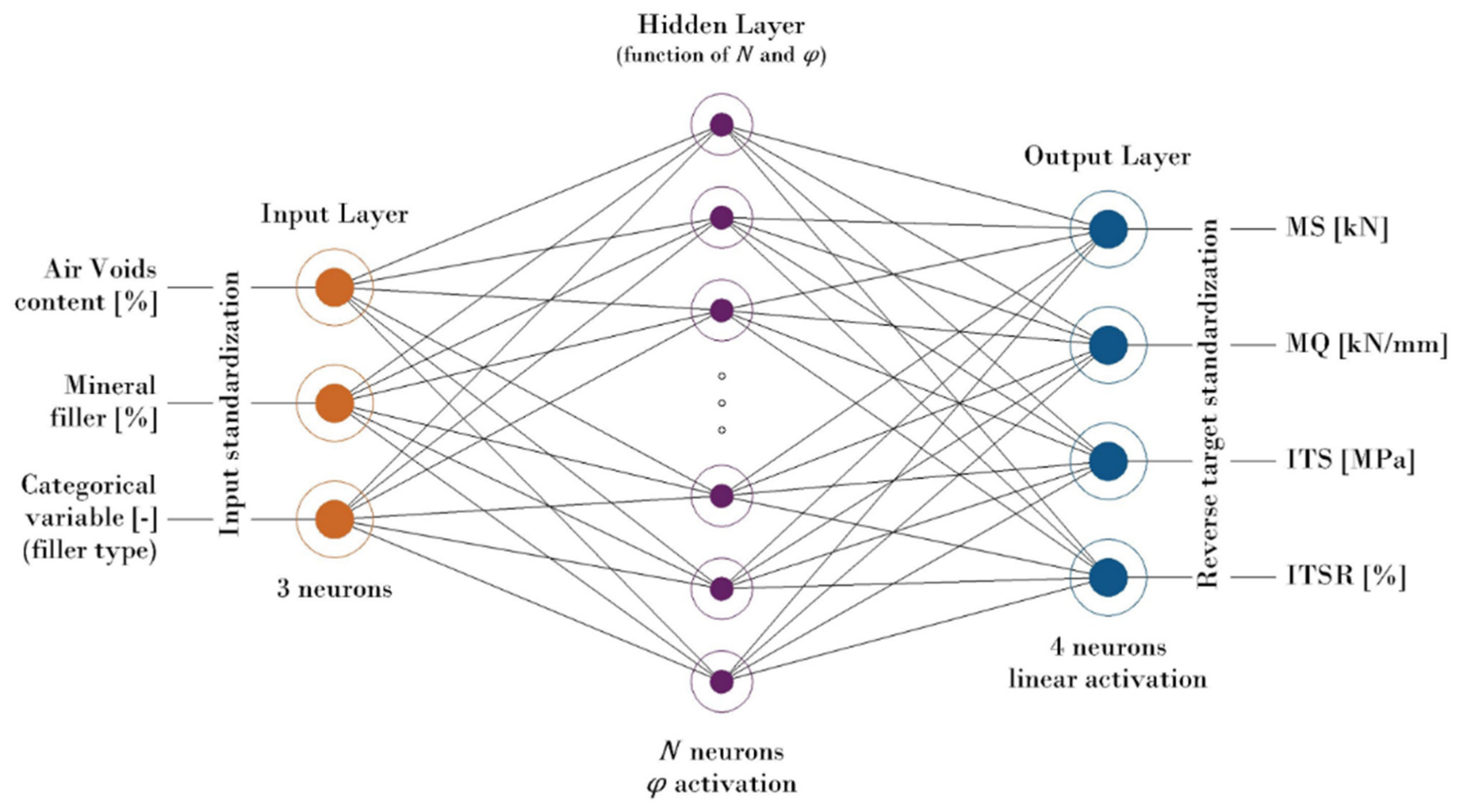
2.3. Theory of Machine Learning Modeling
2.3.1. Artificial and Shallow Neural Networks
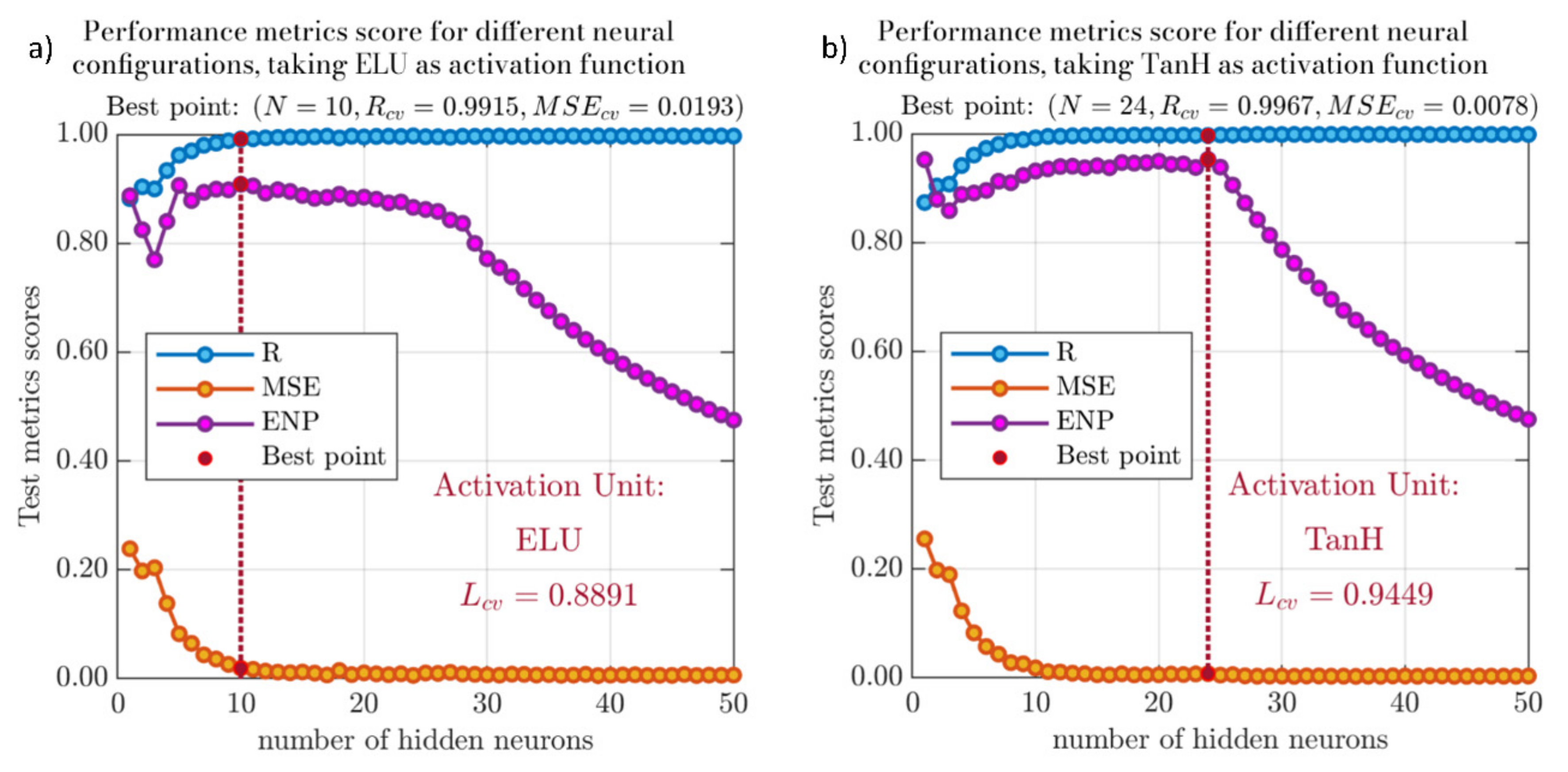
2.3.2. SNN Optimization
2.3.3. k-Fold Cross-Validation
2.3.4. Data Augmentation
3. Results and Discussion
3.1. Performance of Modified Asphalt Mixes
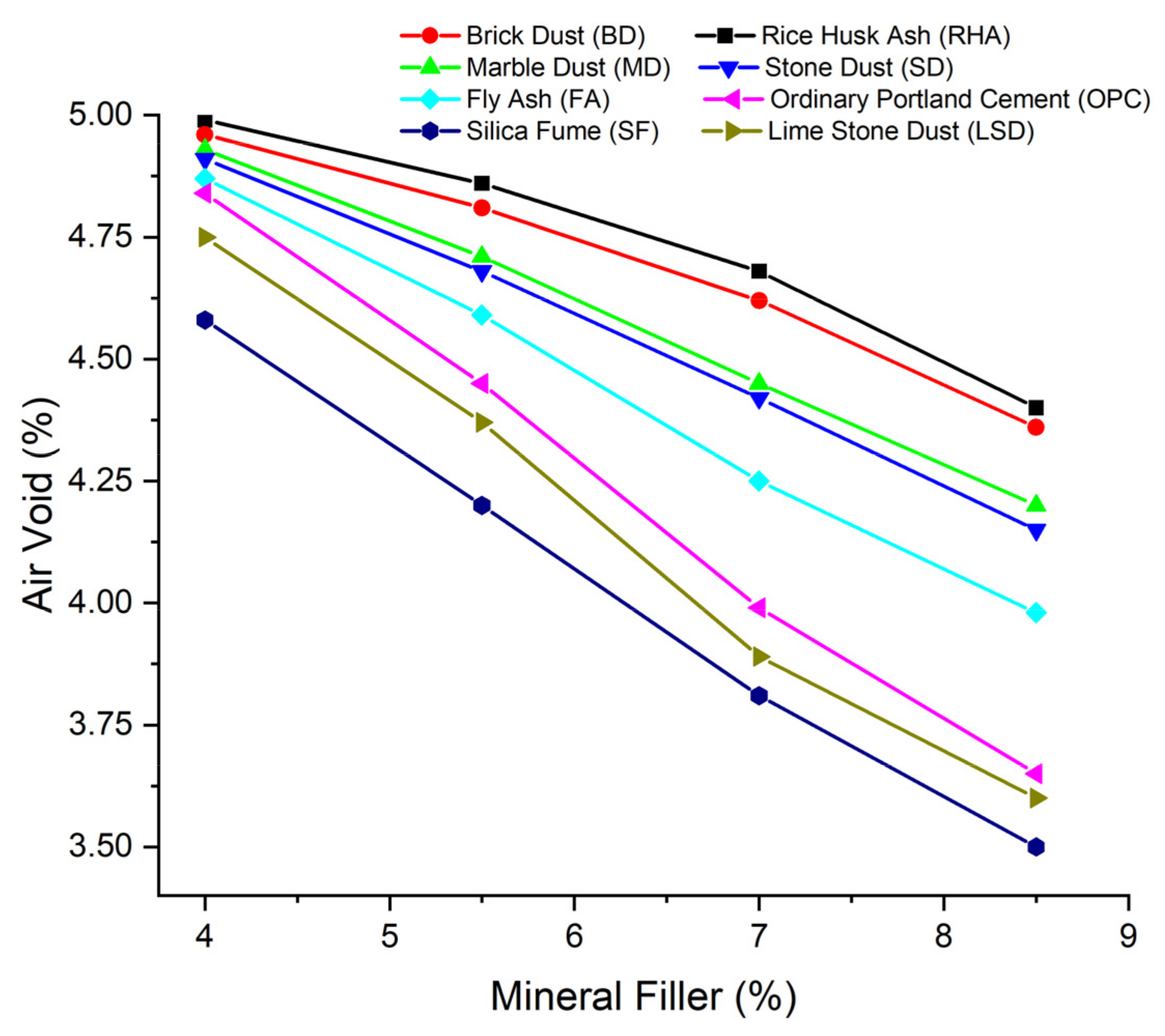
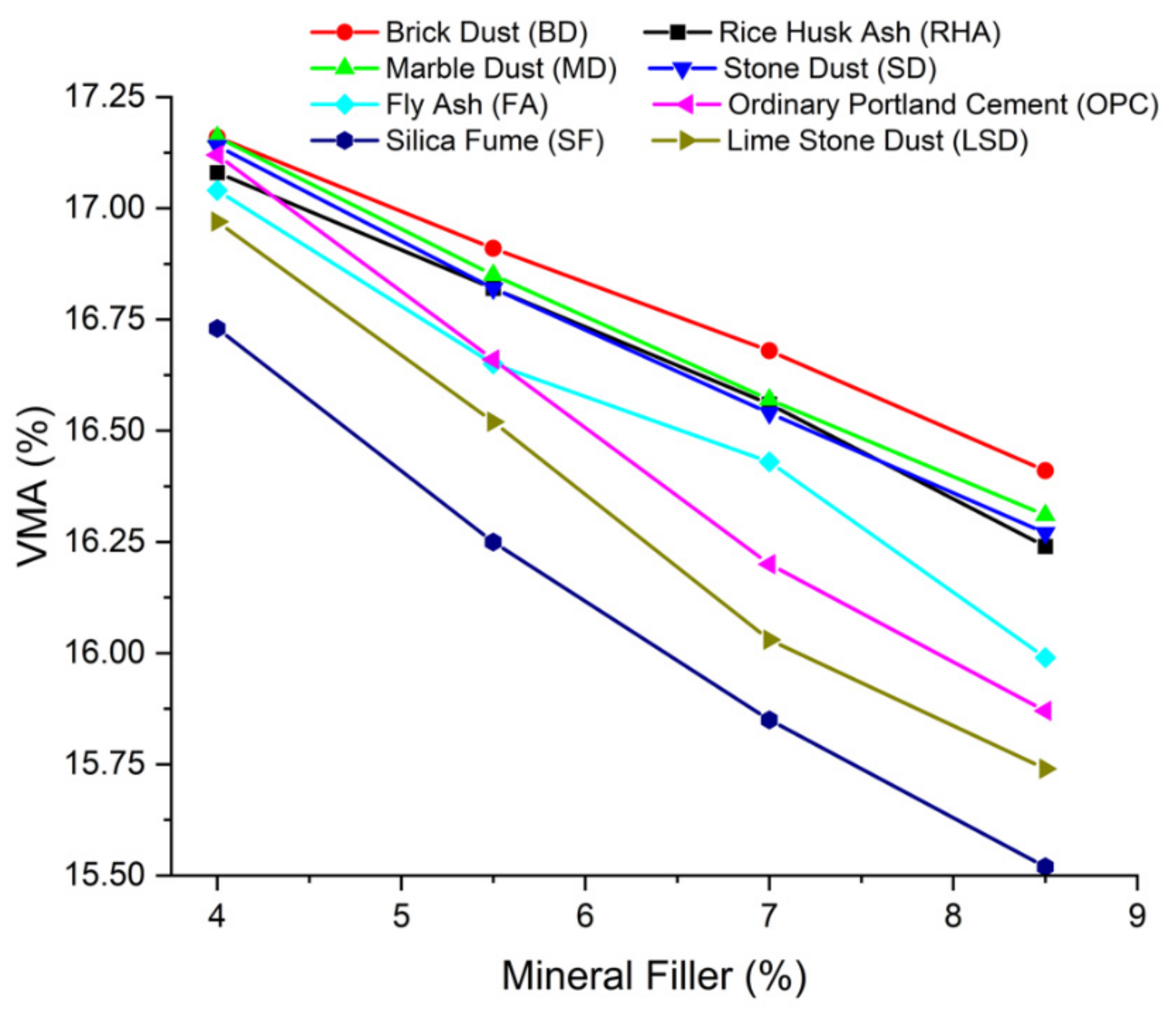
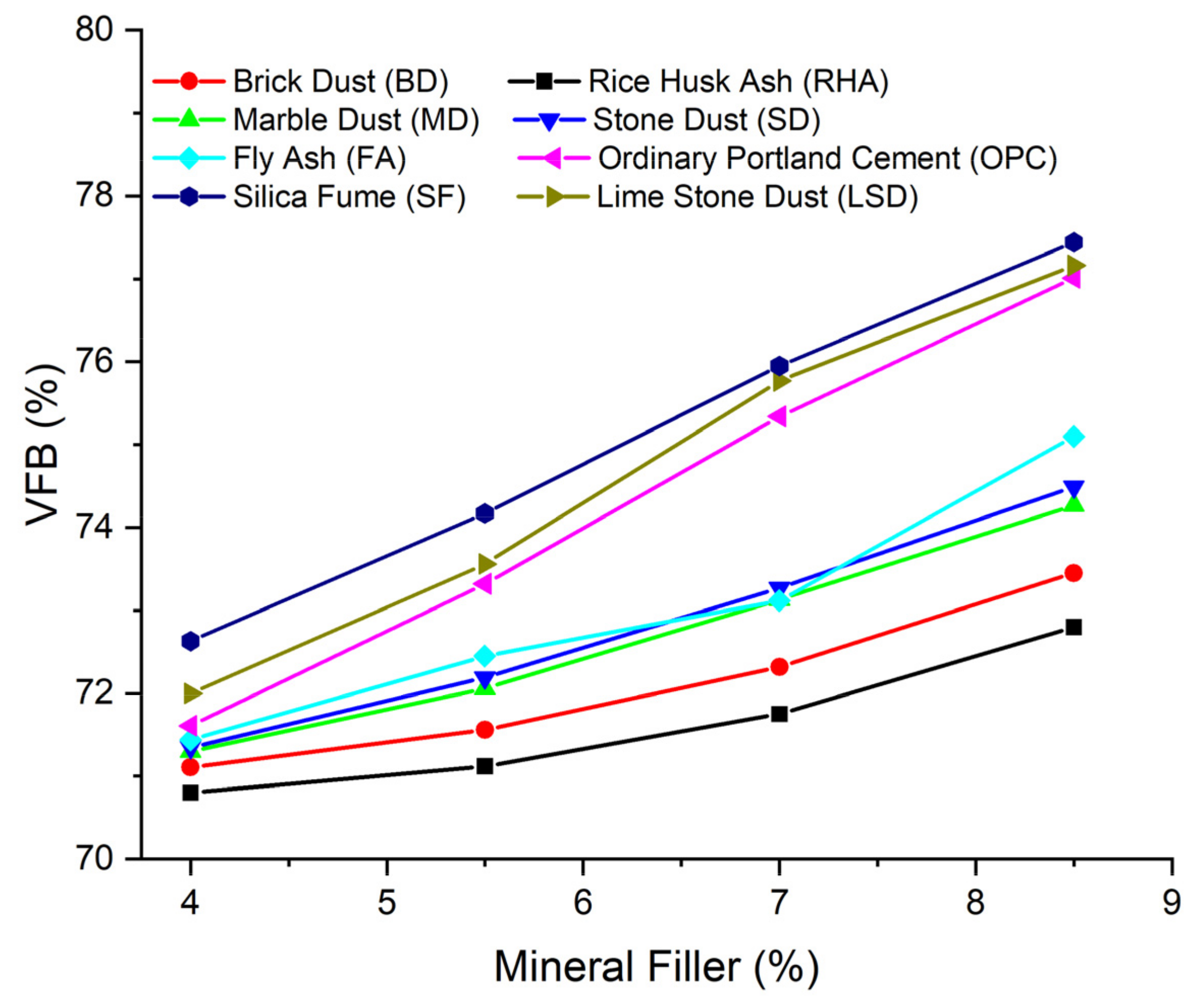
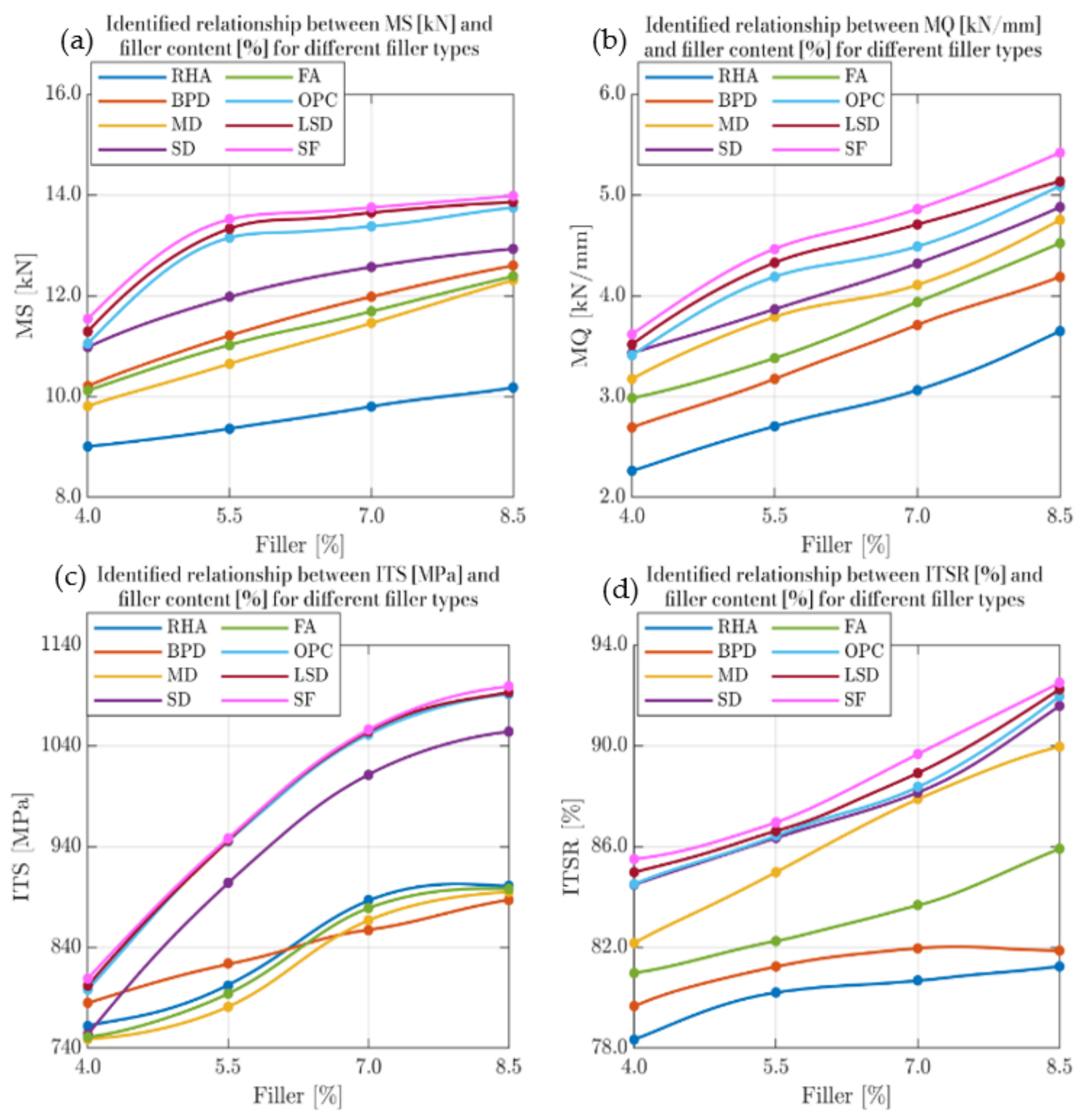
3.1.1. Marshall and Volumetric Properties
3.1.2. Cracking Resistance
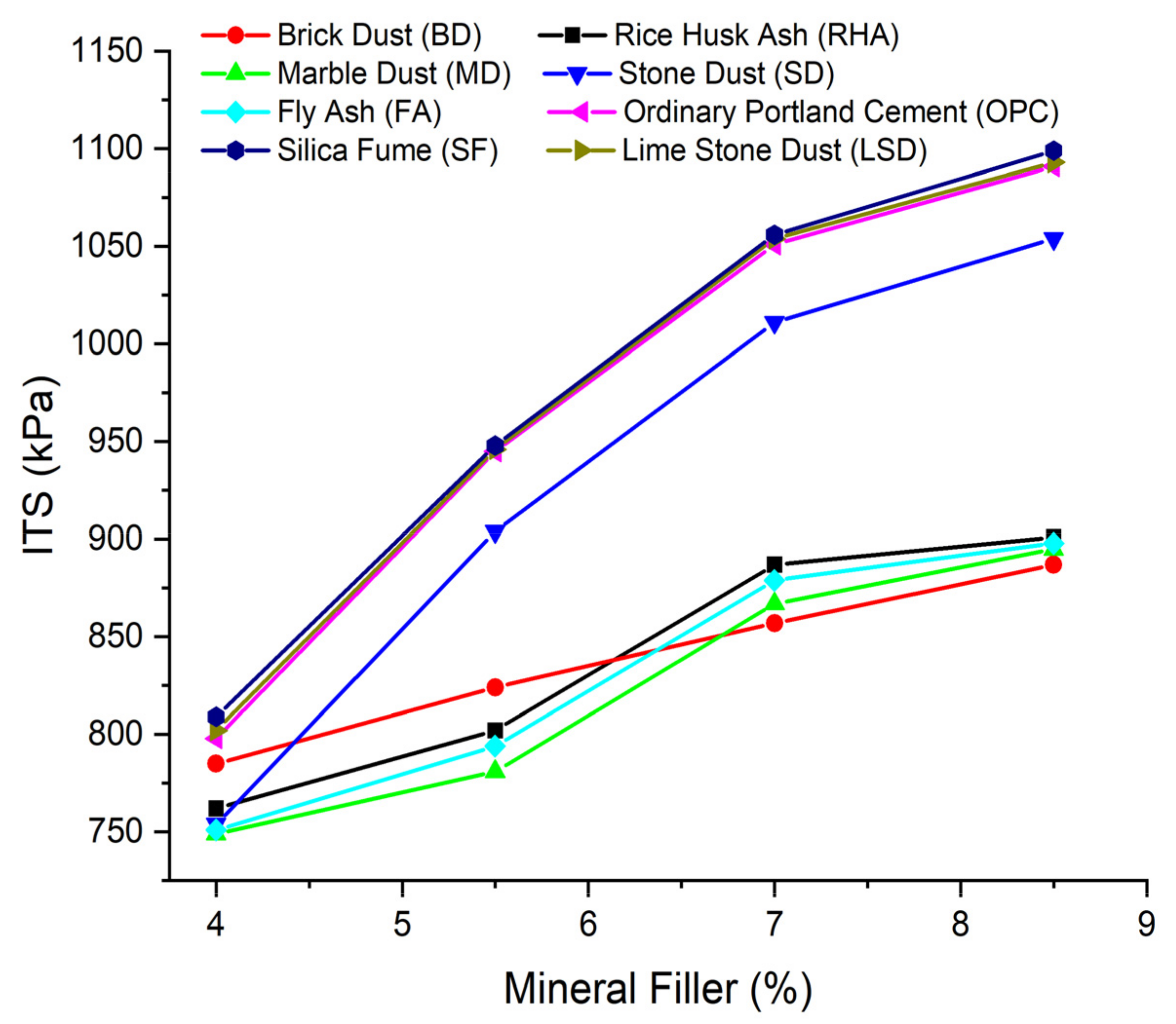
3.1.3. Moisture Susceptibility
3.1.4. Abrasion Loss
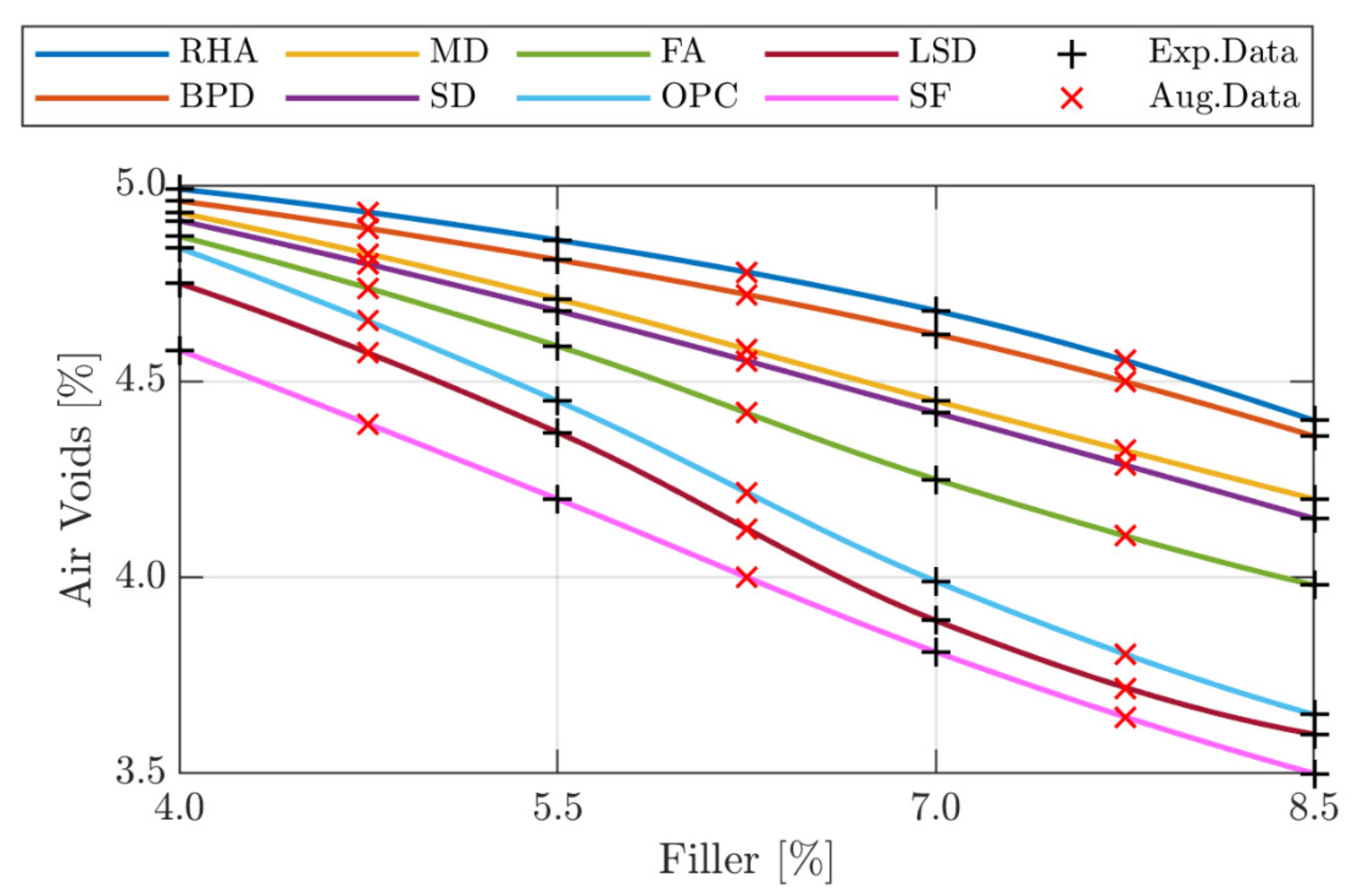
3.2. Numerical Discussion
4. Conclusions
- The chemical and physical properties of silica fume (SF), limestone dust (LSD), stone dust (SD), rice husk ash (RHA), fly ash (FA), brick dust (BD), and marble dust (MD) have been assessed, and it has been observed that all the fillers follow the required requisites of the Indian Standard. Therefore, these fillers can be used in asphalt concrete;
- The mechanical strength and moisture susceptibility tests on the waste-modified asphalt mixtures have shown satisfactory results with respect to the acceptance requisites, as per the MoRTH. Therefore, these mineral fillers can be effectively used for field applications. The acceptance requisite for mixtures made with modified bitumen (MS higher than 13 kN) is fully satisfied if the filler content is raised from 5.5% to 8.5% in case of LSD and SF, demonstrating the significant improvement to the mechanical response of the asphalt mixes given by the filler. It has been observed that LSD- and SF-modified asphalt mixtures have demonstrated superior performance, compared to the OPC-modified asphalt concretes;
- The LSD and SF can be identified as the best alternatives to the OPC in asphalt concrete, since the performances of these mixes were better than those of the OPC-modified asphalt concretes. The MS of SF (13.98 kN) and LSD (13.86 kN) was slightly higher, with respect to the asphalt mixtures made with OPC (13.74 kN). The calcium-based mineral filler performed extremely well due to its higher moisture resistance, though the other filler-modified mixtures also fulfilled the requirements of the MoRTH, since ITSR values greater than 75%, and MS values greater than 10 kN have been observed;
- Shallow neural networks have been successfully used to develop a predictive model of the main empirical and rational mechanical characteristics of ACs prepared with different filler types, namely, Marshall stability (kN), Marshall quotient (kN/mm), indirect tensile strength (kPa), and indirect tensile strength ratio (%);
- The results obtained from the implementation of the k-folds resampling and MAKIMA data-augmentation methods in the SNN’s learning process were fully satisfactory considering the small number of experimental observations available. The optimal SNN for the modeling problem in question receives as input a three-component features vector, the air voids content (%), the filler content (% by volume of the mix), along with the categorical variable distinguishing the filler type; such features are processed by a twenty-four-neuron hidden layer characterized by the hyperbolic tangent activation function;
- The optimal SNN model is a smooth regression of the experimental observations and is able to properly reproduce the physical behavior of asphalt concretes: as the percentage of filler by volume of the mix increases and, consequently, as the air voids content decreases, all mechanical features are improved, regardless of the type of filler used;
- The optimal model developed in this study admits solutions only along the univocal relationship existing between the filler content and air voids, as the type and content of bitumen, as well as the type of coarse aggregate, have been kept constant in the preparation of the investigated mixtures. Therefore, this SNN represents a modeling experience that, for the obtained results, encourages the development of an extensive model that can be applied to other types of mixtures and allow the optimal filler contents for each asphalt concrete in question to be properly identified.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- UNFCCC. The Paris Agreement. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement (accessed on 4 April 2022).
- UNFCCC. Action on Climate and SDGs. Available online: https://unfccc.int/topics/action-on-climate-and-sdgs/action-on-climate-and-sdgs (accessed on 4 April 2022).
- Choudhary, J.; Kumar, B.; Gupta, A. Utilization of Solid Waste Materials as Alternative Fillers in Asphalt Mixes: A Review. Constr. Build. Mater. 2020, 234, 117271. [Google Scholar] [CrossRef]
- Mohammadhosseini, H.; Tahir, M.M.; Mohd Sam, A.R.; Abdul Shukor Lim, N.H.; Samadi, M. Enhanced Performance for Aggressive Environments of Green Concrete Composites Reinforced with Waste Carpet Fibers and Palm Oil Fuel Ash. J. Clean. Prod. 2018, 185, 252–265. [Google Scholar] [CrossRef]
- Pasetto, M.; Baldo, N. Electric arc furnace steel slags in “high performance” asphalt mixes: A laboratory characterisation. In Proceedings of the MS Fall Extraction and Processing Division: Sohn International Symposium, San Diego, CA, USA, 27–31 August 2006. [Google Scholar]
- Pasetto, M.; Baldo, N. Comparative performance analysis of bituminous mixtures with EAF steel slags: A laboratory evaluation. In Proceedings of the 2008 Global Symposium on Recycling, Waste Treatment and Clean Technology, REWAS 2008, Cancun, Mexico, 12–15 October 2008; pp. 565–570. [Google Scholar]
- Pasetto, M.; Baldo, N. Recycling of steel slags in road foundations. Environ. Eng. Manag. J. 2010, 9, 773–777. [Google Scholar] [CrossRef]
- Kong, D.; Wu, S.; Chen, M.; Zhao, M.; Shu, B. Characteristics of Different Types of Basic Oxygen Furnace Slag Filler and its Influence on Properties of Asphalt Mastic. Materials 2019, 12, 4034. [Google Scholar] [CrossRef] [Green Version]
- Terrones-Saeta, J.M.; Suárez-Macías, J.; Iglesias-Godino, F.J.; Corpas-Iglesias, F.A. Evaluation of the Use of Electric Arc Furnace Slag and Ladle Furnace Slag in Stone Mastic Asphalt Mixes with Discarded Cellulose Fibers from the Papermaking Industry. Metals 2020, 10, 1548. [Google Scholar] [CrossRef]
- Kang, G.-O.; Kang, J.-G.; Kim, J.-Y.; Kim, Y.-S. Time-Dependent Strength Behavior, Expansion, Microstructural Properties, and Environmental Impact of Basic Oxygen Furnace Slag-Treated Marine-Dredged Clay in South Korea. Sustainability 2021, 13, 5026. [Google Scholar] [CrossRef]
- Gobetti, A.; Cornacchia, G.; Ramorino, G. Innovative Reuse of Electric Arc Furnace Slag as Filler for Different Polymer Matrixes. Minerals 2021, 11, 832. [Google Scholar] [CrossRef]
- Sas, W.; Dzięcioł, J.; Radzevičius, A.; Radziemska, M.; Dapkienė, M.; Šadzevičius, R.; Skominas, R.; Głuchowski, A. Geotechnical and Environmental Assessment of Blast Furnace Slag for Engineering Applications. Materials 2021, 14, 6029. [Google Scholar] [CrossRef]
- Dzięcioł, J.; Radziemska, M. Blast Furnace Slag, Post-Industrial Waste or Valuable Building Materials with Remediation Potential? Minerals 2022, 12, 478. [Google Scholar] [CrossRef]
- Huang, B.; Shu, X.; Chen, X. Effects of Mineral Fillers on Hot-Mix Asphalt Laboratory-Measured Properties. Int. J. Pavement Eng. 2007, 8, 1–9. [Google Scholar] [CrossRef]
- Vavrik, W.R.; Pine, W.J.; Carpenter, S.H. Aggregate Blending for Asphalt Mix Design Bailey Method. Transp. Res. Rec. 2002, 1789, 146–153. [Google Scholar] [CrossRef]
- Wang, H.; Al-Qadi, I.L.; Faheem, A.F.; Bahia, H.U.; Yang, S.H.; Reinke, G.H. Effect of Mineral Filler Characteristics on Asphalt Mastic and Mixture Rutting Potential. Transp. Res. Rec. 2011, 2208, 33–39. [Google Scholar] [CrossRef]
- Tiwari, N.; Satyam, N. Evaluation of Strength and Water Susceptibility Performance of Polypropylene Fiber-Reinforced and Silica Fume-Modified Hot Mix Asphalt. Adv. Civ. Eng. Mater. 2021, 10, 380–395. [Google Scholar] [CrossRef]
- Arabani, M.; Tahami, S.A.; Taghipoor, M. Laboratory Investigation of Hot Mix Asphalt Containing Waste Materials. Road Mater. Pavement Des. 2017, 18, 713–729. [Google Scholar] [CrossRef]
- Chandra, S.; Choudhary, R. Performance Characteristics of Bituminous Concrete with Industrial Wastes as Filler. J. Mater. Civ. Eng. 2013, 25, 1666–1673. [Google Scholar] [CrossRef]
- Woszuk, A.; Bandura, L.; Franus, W. Fly Ash as Low Cost and Environmentally Friendly Filler and Its Effect on the Properties of Mix Asphalt. J. Clean. Prod. 2019, 235, 493–502. [Google Scholar] [CrossRef]
- Xu, P.; Chen, Z.; Cai, J.; Pei, J.; Gao, J.; Zhang, J.; Zhang, J. The Effect of Retreated Coal Wastes as Filler on the Performance of Asphalt Mastics and Mixtures. Constr. Build. Mater. 2019, 203, 9–17. [Google Scholar] [CrossRef]
- Lukjan, A.; Iyaruk, A.; Somboon, C. Evaluation on Mechanical Deterioration of the Asphalt Mixtures Containing Waste Materials When Exposed to Corrosion Solutions. Int. J. Eng. Technol. 2022, 12, 130–144. [Google Scholar] [CrossRef]
- Choudhary, J.; Kumar, B.; Gupta, A. Feasible Utilization of Waste Limestone Sludge as Filler in Bituminous Concrete. Constr. Build. Mater. 2020, 239, 117781. [Google Scholar] [CrossRef]
- Kuity, A.; Jayaprakasan, S.; Das, A. Laboratory Investigation on Volume Proportioning Scheme of Mineral Fillers in Asphalt Mixture. Constr. Build. Mater. 2014, 68, 637–643. [Google Scholar] [CrossRef]
- Choudhary, J.; Kumar, B.; Gupta, A. Performance Evaluation of Bauxite Residue Modified Asphalt Concrete Mixes. Eur. J. Environ. Civ. Eng. 2019, 26, 978–994. [Google Scholar] [CrossRef]
- Modarres, A.; Alinia Bengar, P. Investigating the Indirect Tensile Stiffness, Toughness and Fatigue Life of Hot Mix Asphalt Containing Copper Slag Powder. Int. J. Pavement Eng. 2019, 20, 977–985. [Google Scholar] [CrossRef]
- Awed, A.M.; Tarbay, E.W.; El-Badawy, S.M.; Azam, A.M. Performance characteristics of asphalt mixtures with industrial waste/by-product materials as mineral fillers under static and cyclic loading. Road Mat. Pavement Des. 2022, 23, 335–357. [Google Scholar] [CrossRef]
- Hamedi, G.H.; Esmaeeli, M.R.; Najafi Moghaddam Gilani, V.; Hosseinian, S.M. The effect of aggregate-forming minerals on thermodynamic parameters using surface free energy concept and its relationship with the moisture susceptibility of asphalt mixtures. Adv. Civ. Eng. 2021, 2021, 8818681. [Google Scholar] [CrossRef]
- Sherre, T.K.; Liao, M.C. Characteristics of Recycled Mineral Fillers and Their Effects on the Mechanical Properties of Hot-Mix Asphalt When Used as Limestone Filler Replacements. J. Mater. Civ. Eng. 2022, 34, 04021395. [Google Scholar] [CrossRef]
- Sholevar, N.; Golroo, A.; Esfahani, S.R. Machine learning techniques for pavement condition evaluation. Autom. Constr. 2022, 136, 104190. [Google Scholar] [CrossRef]
- Hou, Y.; Li, Q.; Zhang, C.; Lu, G.; Ye, Z.; Chen, Y.; Wang, L.; Cao, D. The state-of-the-art review on applications of intrusive sensing, image processing techniques, and machine learning methods in pavement monitoring and analysis. Engineering 2021, 7, 845–856. [Google Scholar] [CrossRef]
- Pasetto, M.; Baldo, N. Numerical visco-elastoplastic constitutive modelization of creep recovery tests on hot mix asphalt. J. Traffic Transp. Eng. 2016, 3, 390–397. [Google Scholar] [CrossRef]
- De Oliveira Junior, M.; De Farias, M.M. A simple numerical methodology to simulate creep and recovery tests in HMA. Constr. Build. Mater. 2020, 262, 120793. [Google Scholar] [CrossRef]
- Cao, P.; Leng, Z.; Shi, F.; Zhou, C.; Tan, Z.; Wang, Z. A novel visco-elastic damage model for asphalt concrete and its numerical implementation. Constr. Build. Mater. 2020, 264, 120261. [Google Scholar] [CrossRef]
- Sun, B.; Hao, P.; Zhang, H.; Liu, J. Establishment and verification of a developed viscoelastic damage model and creep instability criterion for modified fine asphalt mortar. Mater. Struct. 2022, 55, 107. [Google Scholar] [CrossRef]
- Hoang, N.D.; Nguyen, Q.L. A novel method for asphalt pavement crack classification based on image processing and machine learning. Eng. Comput. 2019, 35, 487–498. [Google Scholar] [CrossRef]
- Fathi, A.; Mazari, M.; Saghafi, M.; Hosseini, A.; Kumar, S. Parametric study of pavement deterioration using machine learning algorithms. In Airfield and Highway Pavements 2019: Innovation and Sustainability in Highway and Airfield Pavement Technology; American Society of Civil Engineers: Reston, VA, USA, 2019; pp. 31–41. [Google Scholar]
- Majidifard, H.; Adu-Gyamfi, Y.; Buttlar, W.G. Deep machine learning approach to develop a new asphalt pavement condition index. Constr. Build. Mater. 2020, 247, 118513. [Google Scholar] [CrossRef]
- Marcelino, P.; De Lurdes Antunes, M.; Fortunato, E.; Gomes, M.C. Machine learning approach for pavement performance prediction. Int. J. Pavement Eng. 2021, 22, 341–354. [Google Scholar] [CrossRef]
- Zeiada, W.; Dabous, S.A.; Hamad, K.; Al-Ruzouq, R.; Khalil, M.A. Machine learning for pavement performance modelling in warm climate regions. Arab. J. Sci. Eng. 2020, 45, 4091–4109. [Google Scholar] [CrossRef]
- Gilani, V.N.M.; Hosseinian, S.M.; Behbahani, H.; Hamedi, G.H. Prediction and pareto-based multi-objective optimization of moisture and fatigue damages of asphalt mixtures modified with nano hydrated lime. Constr. Build. Mater. 2020, 261, 120509. [Google Scholar] [CrossRef]
- Behbahani, H.; Hamedi, G.H.; Gilani, V.N.M. Predictive model of modified asphalt mixtures with nano hydrated lime to increase resistance to moisture and fatigue damages by the use of deicing agents. Constr. Build. Mater. 2020, 265, 120353. [Google Scholar] [CrossRef]
- Tapkin, S.; Çevik, A.; Uşar, Ü. Prediction of Marshall Test Results for Polypropylene Modified Dense Bituminous Mixtures Using Neural Networks. Expert Syst. Appl. 2010, 37, 4660–4670. [Google Scholar] [CrossRef]
- Baldo, N.; Manthos, E.; Pasetto, M. Analysis of the Mechanical Behaviour of Asphalt Concretes Using Artificial Neural Networks. Adv. Civ. Eng. 2018, 2018, 1650945. [Google Scholar] [CrossRef] [Green Version]
- Ministry of Road Transport and Highways (MoRTH) India. Specifications for Road and Bridges Works V; Ministry of Transport, Department of Surface Transport: New Delhi, India, 2013; Volume 1. [Google Scholar]
- IS 8112-2013; Ordinary Portland Cement, 43 Grade—Specification. Bureau of Indian Standard: New Delhi, India, 2013.
- Kandhal, P.S.; Lynn, C.Y.; Parker, F. Characterization Tests for Mineral Fillers Related to Performance of Asphalt Paving Mixtures. Transp. Res. Rec. J. Transp. Res. Board 1998, 1638, 101–110. [Google Scholar] [CrossRef] [Green Version]
- Sousa, J.B.; Way, G.; Harvey, J.T.; Hines, M. Comparison of Mix Design Concepts. Transp. Res. Rec. 1995, 1492, 151–160. [Google Scholar]
- Xue, Y.; Hou, H.; Zhu, S.; Zha, J. Utilization of Municipal Solid Waste Incineration Ash in Stone Mastic Asphalt Mixture: Pavement Performance and Environmental Impact. Constr. Build. Mater. 2009, 23, 989–996. [Google Scholar] [CrossRef]
- Baldo, N.; Manthos, E.; Miani, M. Stiffness Modulus and Marshall Parameters of Hot Mix Asphalts: Laboratory Data Modeling by Artificial Neural Networks Characterized by Cross-Validation. Appl. Sci. 2019, 9, 3502. [Google Scholar] [CrossRef] [Green Version]
- Pasandín, A.R.; Pérez, I. Overview of Bituminous Mixtures Made with Recycled Concrete Aggregates. Constr. Build. Mater. 2015, 74, 151–161. [Google Scholar] [CrossRef] [Green Version]
- Salam Al-Ammari, M.A.; Jakarni, F.M.; Muniandy, R.; Hassim, S. The Effect of Aggregate and Compaction Method on the Physical Properties of Hot Mix Asphalt. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Selangor, Malaysia, 6–8 November 2019; Volume 512. [Google Scholar]
- Ozgan, E. Artificial Neural Network Based Modelling of the Marshall Stability of Asphalt Concrete. Expert Syst. Appl. 2011, 38, 6025–6030. [Google Scholar] [CrossRef]
- Zavrtanik, N.; Prosen, J.; Tušar, M.; Turk, G. The Use of Artificial Neural Networks for Modeling Air Void Content in Aggregate Mixture. Autom. Constr. 2016, 63, 155–161. [Google Scholar] [CrossRef]
- ASTM D6927-15; Standard Test Method for Marshall Stability and Flow of Asphalt Mixtures: Designation: D6927-15. ASTM International: West Conshohocken, PA, USA, 2015; Volume I.
- Zoorob, S.E.; Suparma, L.B. Laboratory Design and Investigation of the Properties of Continuously Graded Asphaltic Concrete Containing Recycled Plastics Aggregate Replacement (Plastiphalt). Cem. Concr. Compos. 2000, 22, 233–242. [Google Scholar] [CrossRef]
- ASTM D6931−17; Standard Test Method for Indirect Tensile (IDT) Strength of Asphalt Mixtures. ASTM International: West Conshohocken, PA, USA, 2017.
- Aschenbrener, T.; Mcgennis, R.B. Investigation of the Modified Lottman Test to Predict the Stripping Performance of Pavements in Colorado; Final Report; U.S. Department of Transportation Federal Highway of Administration: Washington, DC, USA, 1993.
- AASHTO(T-283); Standard Method of Test for Resistance of Compacted Asphalt Mixtures to Moisture Induced Damage. American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2014.
- TxDOT: Tex-245-F; Test Procedure for Cantabro Loss. Materials and Test Division Texas Department of Transportation: Austin, TX, USA, 2019.
- Widrow, B.; Hoff, M.E. Adaptive Switching Circuits; IRE WESCON Convention Record Part 4; Institute of Radio Engineers: New York, NY, USA, 1960. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. In Neurocomputing: Foundations of Research; Anderson, J.A., Rosenfeld, E., Eds.; The MIT Press: Cambridge, MA, USA, 1998; pp. 15–27. [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; De Jesus, O. Neural Network Design, 2nd ed.; PWS Publishing Co.: Worcester, UK, 2014; ISBN 1846283027. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training Feedforward Networks with the Marquardt Algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Akima, H. A Method of Bivariate Interpolation and Smooth Surface Fitting Based on Local Procedures. Commun. ACM 1974, 17, 18–20. [Google Scholar] [CrossRef]
- Oh, C.; Han, S.; Jeong, J. Time-Series Data Augmentation Based on Interpolation. Procedia Comput. Sci. 2020, 175, 64–71. [Google Scholar] [CrossRef]
- Kutuk-Sert, T. Stability Analyses of Submicron-Boron Mineral Prepared by Mechanical Milling Process in Concrete Roads. Constr. Build. Mater. 2016, 121, 255–264. [Google Scholar] [CrossRef]
- Smith, B.J. Low-Temperature and Dynamic Fatigue Toughening Mizchanisms in Asphalt Mastics and Mixtures. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2000. [Google Scholar]
- Dehghan, Z.; Modarres, A. Evaluating the Fatigue Properties of Hot Mix Asphalt Reinforced by Recycled PET Fibers Using 4-Point Bending Test. Constr. Build. Mater. 2017, 139, 384–393. [Google Scholar] [CrossRef]

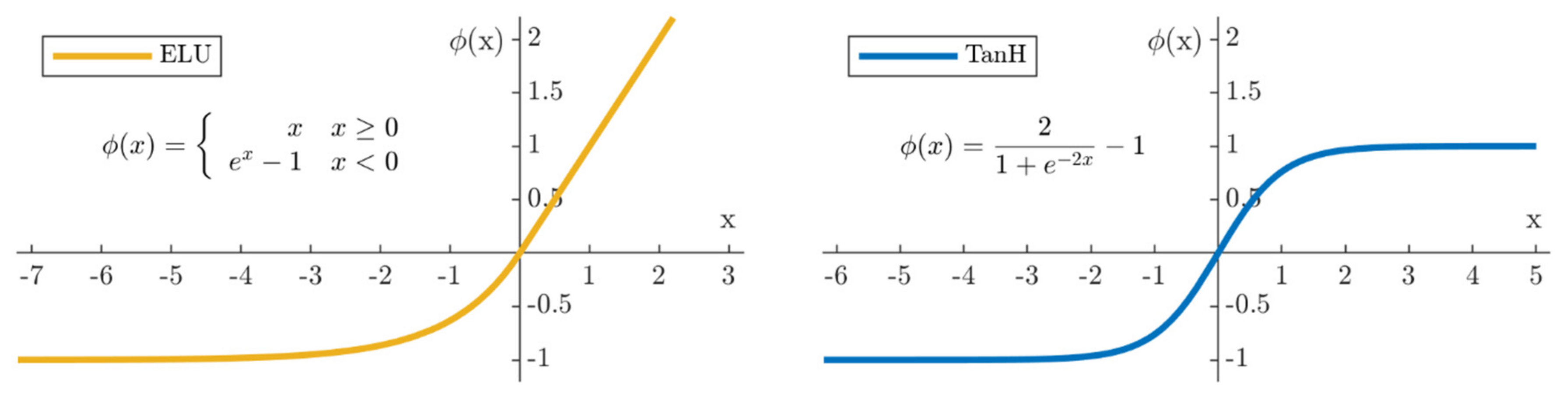




| Material | Test Parameters | Specified Limit (MoRTH) | Test Results | Test Method |
|---|---|---|---|---|
| Aggregate | Cleanliness (dust) (%) | Max 5 % | 3 | IS 2386 Part I |
| Bulk specific gravity (g/cm3) | 2–3 | 2.68 | IS 2386 Part III | |
| Percent wear by Los Angeles abrasion (%) | Max 35 % | 10.6 | IS 2386 Part IV | |
| Soundness loss by sodium sulphate solution (%) | Max 12% | 3.4 | IS 2386 Part V | |
| Soundness loss by magnesium sulphate solution (%) | Max 18% | 3.7 | IS 2386 Part V | |
| Flakiness and elongation index (%) | Max 35% | IS 2386 Part I | ||
| 20 mm | 27.93 | |||
| 10 mm | 32.13 | |||
| Impact strength (%) | Max 27% | IS 2386 Part IV | ||
| 20 mm | 4.15 | |||
| 10 mm | 5.91 | |||
| Water absorption (%) | Max 2% | 1.67 | IS 2386 Part III | |
| Bitumen | Absolute viscosity at 60 °C (poises) | 2400–3600 | 2855 | IS 1206 (P-2) |
| Kinematic viscosity at 135 °C (cSt), Min. | 350 | 392 | IS 1206 (P-3) | |
| Flash point Cleveland open cup, (°C), Min. | 250 | 304 | IS 1448 (P-69) | |
| Penetration at 25 °C, 100 gm, 5 sec, (1/10 mm), Min | 45 | 49 | IS 1203 | |
| Softening point (R&B), (°C), Min | 47 | 48 | IS 1205 | |
| Matter soluble in trichloroethylene, (% by mass), Min. | 99 | 99.45 | IS 1216 | |
| Viscosity ratio at 60 °C, Max | 4.0 | 1.3 | IS 1206 (P-2) | |
| Ductility at 25 °C, (cm) after TFOT min. | 40 | 75 | IS 1208 | |
| Specific gravity (gm/cc) | 0.97–1.02 | 0.987 | IS 1202 |
| Property | Type of Mineral Filler | |||||||
|---|---|---|---|---|---|---|---|---|
| OPC | LSD | FA | RHA | SD | MD | BPD | SF | |
| Specific gravity (g/cm3) | 3.04 | 2.65 | 2.32 | 2.02 | 2.69 | 2.695 | 2.56 | 2.2 |
| MBV (g/kg) | 3 | 3.75 | 3.86 | 4.72 | 3.67 | 4.45 | 6.25 | 3.85 |
| German filler (g) | 85 | 97 | 75 | 65 | 85 | 70 | 40 | 94 |
| Fineness modulus (FM) | 4.96 | 3.03 | 3.77 | 3.21 | 5.38 | 2.12 | 5.17 | 1.96 |
| Surface area (m2/g) | 1.75 | 2.70 | 2.193 | 2.31 | 2.701 | 4.372 | 2.688 | 16.45 |
| pH | 12.9 | 10.22 | 7.3 | 10.86 | 12.57 | 8.5 | 8.67 | 6.98 |
| SiO2 (%) | 21.43 | 0.48 | 48.24 | 89.67 | 82.37 | 0.6 | 39.55 | 93.5 |
| CaO (%) | 66.58 | 96.57 | 13.4 | 1.88 | 2.79 | 55.6 | 12.88 | 0.89 |
| Al2O3(%) | 3.01 | 0.41 | 24.15 | 1.62 | 8.23 | 0.4 | 15.71 | 0.08 |
| MgO(%) | 1.39 | 0.46 | 1.46 | 0.97 | 1.47 | 0.1 | 3.29 | 0.82 |
| Fe2O3(%) | 4.68 | 0.32 | 6.48 | 1.06 | 5.27 | 0.2 | 14.05 | 0.5 |
| Particle shape | Granules and sub-angular particles | Granular particles | Rounded | Honeycombed | Angular particles e | Sub-angular | Sub-angular particles | Spherically shaped |
| No. | Name of Equipment | Specification |
|---|---|---|
| 1. | Digital Marshall Stability Apparatus | Ref. standards—ASTMD 1559, ASTM D6927-06 Capacity—100 kN single speed Sample size—4″ and 6″ dia Load cell: 100 kN LVDT: 50 mm Maximum vertical clearance—470 mm Minimum vertical clearance—250 mm Horizontal clearance—265 mm Platen diameter—133 mm Platen travel—25 mm Platen speed—50.8 mm/min Rated power—375 W Dimension (l × w × h)—550 × 400 × 870 mm |
| 2. | Automatic Compactor for Bituminous Mixes | Ref. standards: ASTM D 5581:1996, ASTM D 6926-04 Weight of hammer—4.5 kg (4″ sample dia) and 10.2 kg (6″sample dia) Sample ejector: 4″ and 6″ sample dia Falling height: 457 mm Suitable for operation—440 V and 50 Hz Power supply—three-phase AC supply |
| 3. | Indirect Tensile Strength Test Machine | Ref. standard: ASTM D6931 Ram stroke—400 mm Ram speed range—50 to 70 mm/min Load cell—250 kN Deformation transducer—400 mm Clearance between columns—530 mm Electrical supply—three-phase 415 Volts 50 Hz Dimensions (W × D × H)—2100 × 616 × 2111 mm Working space required (W × D × H)—2300 × 1616 × 2300 mm |
| 4 | Los Angeles Abrasion Machine | Ref. Standard: AASHTO T 96, ASTM C535 Revolutions per minute—30–33 Drum diameter—700 mm Inside height—500 mm Electrical—220 V/50 Hz Product dimensions (W × D × H)—965 × 1016 × 1181 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiwari, N.; Baldo, N.; Satyam, N.; Miani, M. Mechanical Characterization of Industrial Waste Materials as Mineral Fillers in Asphalt Mixes: Integrated Experimental and Machine Learning Analysis. Sustainability 2022, 14, 5946. https://doi.org/10.3390/su14105946
Tiwari N, Baldo N, Satyam N, Miani M. Mechanical Characterization of Industrial Waste Materials as Mineral Fillers in Asphalt Mixes: Integrated Experimental and Machine Learning Analysis. Sustainability. 2022; 14(10):5946. https://doi.org/10.3390/su14105946
Chicago/Turabian StyleTiwari, Nitin, Nicola Baldo, Neelima Satyam, and Matteo Miani. 2022. "Mechanical Characterization of Industrial Waste Materials as Mineral Fillers in Asphalt Mixes: Integrated Experimental and Machine Learning Analysis" Sustainability 14, no. 10: 5946. https://doi.org/10.3390/su14105946
APA StyleTiwari, N., Baldo, N., Satyam, N., & Miani, M. (2022). Mechanical Characterization of Industrial Waste Materials as Mineral Fillers in Asphalt Mixes: Integrated Experimental and Machine Learning Analysis. Sustainability, 14(10), 5946. https://doi.org/10.3390/su14105946









