A Novel Neural Computing Model Applied to Estimate the Dynamic Modulus (DM) of Asphalt Mixtures by the Improved Beetle Antennae Search
Abstract
:1. Introduction
2. Materials and Methods
2.1. Raw Materials
2.2. Mix Design
2.3. Experimental Tests
2.3.1. Determination of the Dynamic Shear Modulus of the Asphalt Binders
2.3.2. Determination of the DM of the Asphalt Mixtures
2.4. Methods
2.4.1. Backpropagation Neural Network (BPNN)
2.4.2. Improved BAS Algorithm
Traditional BAS Algorithm
Improved BAS with Higher Searching Efficiency
| Algorithm 1. Pseudo-code of the MBAS algorithm [84] |
| Input Fitness function f(x^i), initial position of the beetle x^0, initial step-size δ^0, maximum iterations n, ratio of antennae length to step-size c, attenuation coefficient of step-size η |
| Output: Optimal position x_b, optimal fitness function value f_b. |
| FOR I = 1 to n |
| Generate random antennae direction b; |
| Calculate the antennae length d^i = c × δ^i; |
| Calculate the left-hand and right-hand positions x_l and x_r, respectively; |
| Calculate the fitness function value f(xl) and f(xr) at the left and right antennae position; |
| Calculate the next position x^i; |
| Calculate the fitness function value f(x^(i + 1) ) at next position x^(i + 1); |
| IF f(x^(i + 1)) < f_b |
| THEN Update x_b to x^(i + 1);⋯Update f_b to f(x^(i + 1) ); |
| END |
| Update step-size δ^(i + 1) using Equations (8) and (9); |
| IF |f (x^(i + 1)) − f (x^i)| < μ (fw − fb) |
| THEN Update step-size δ^(i + 1) using Levy flight according to Equation (9); |
| ELSE Update step-size δ^(i + 1) according to Equation (8) |
| END |
| i = i + 1; |
| END |
3. Results and Discussion
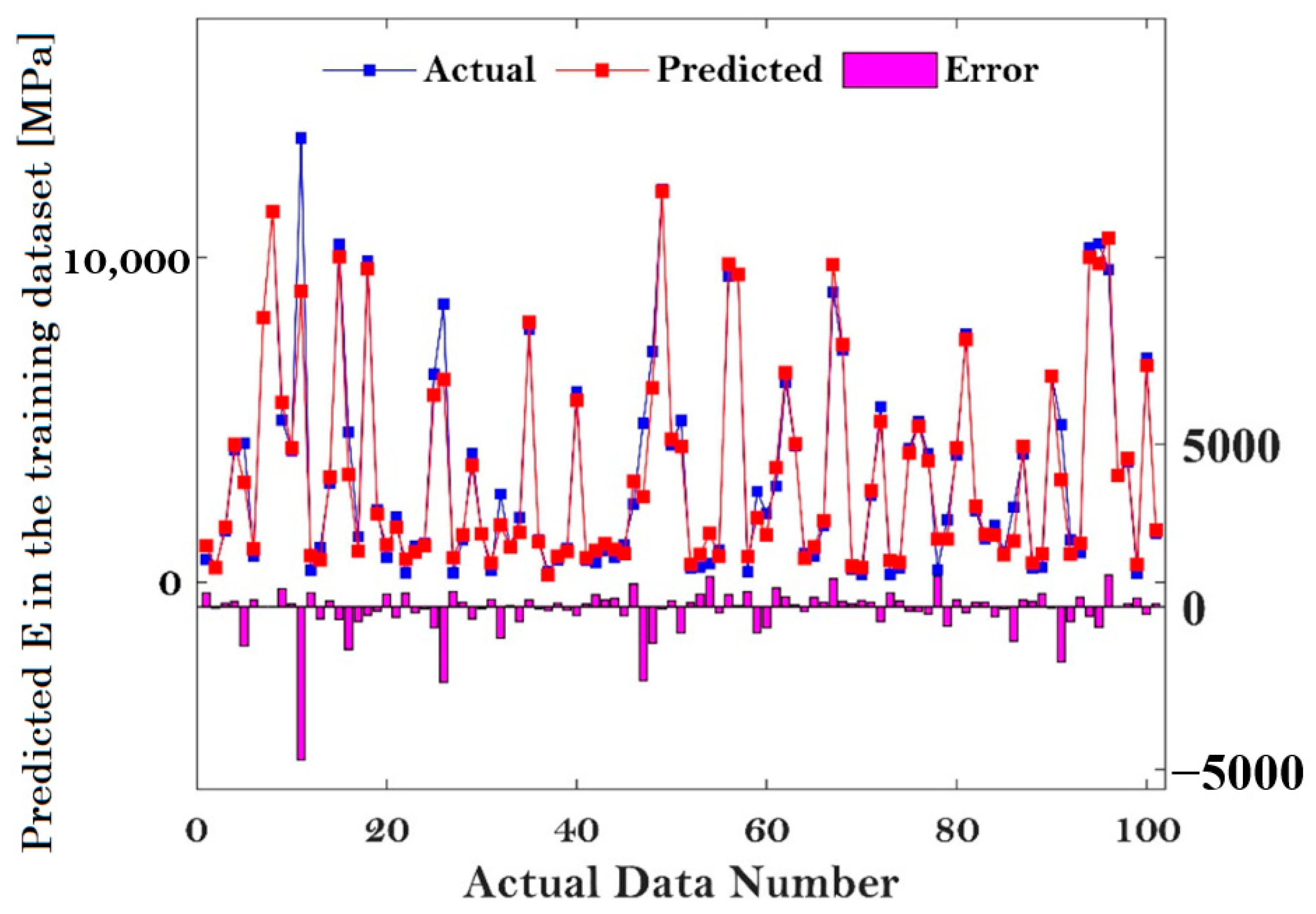
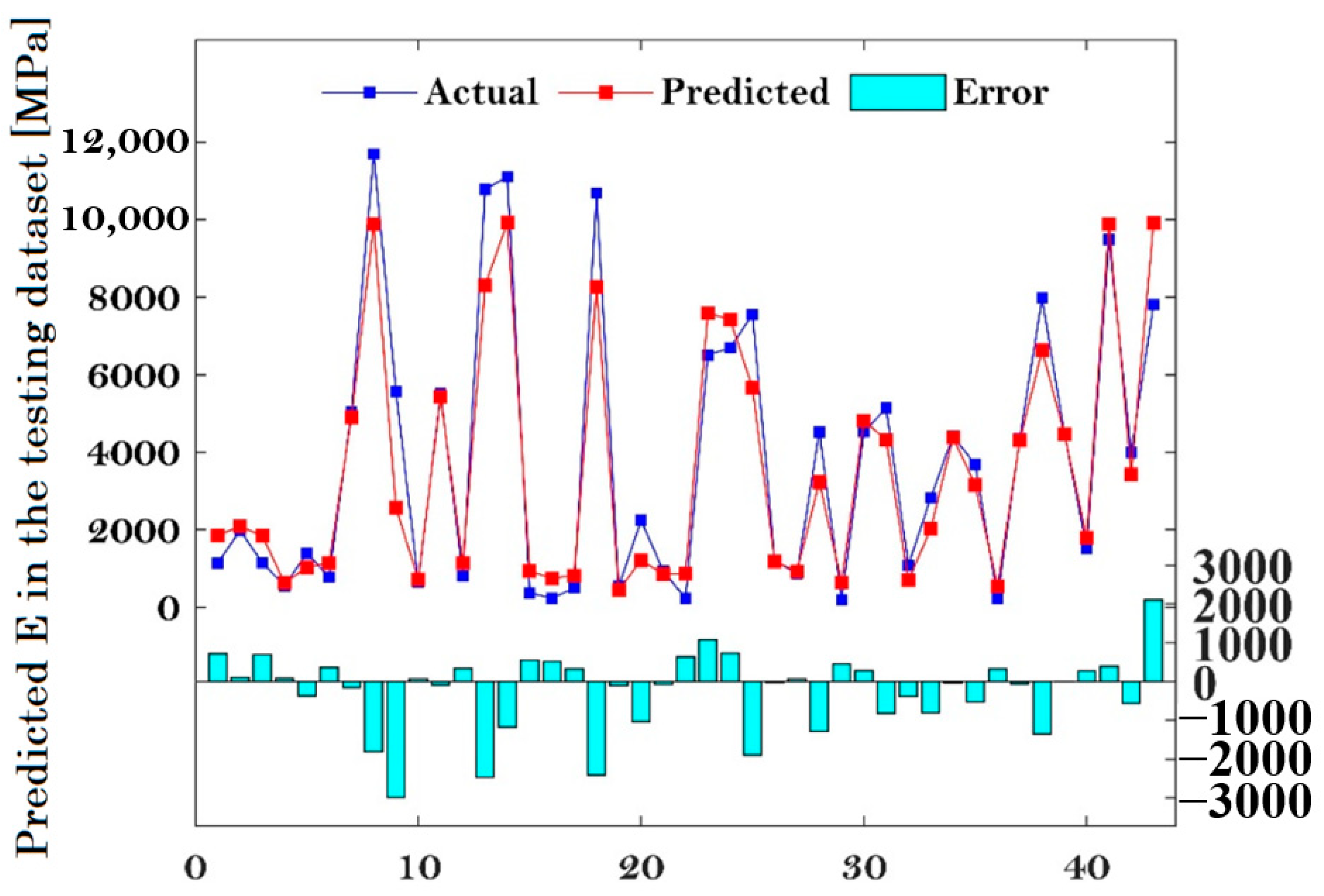
3.1. Testing Results and Dataset Description
3.2. Hyperparameter Tuning Results
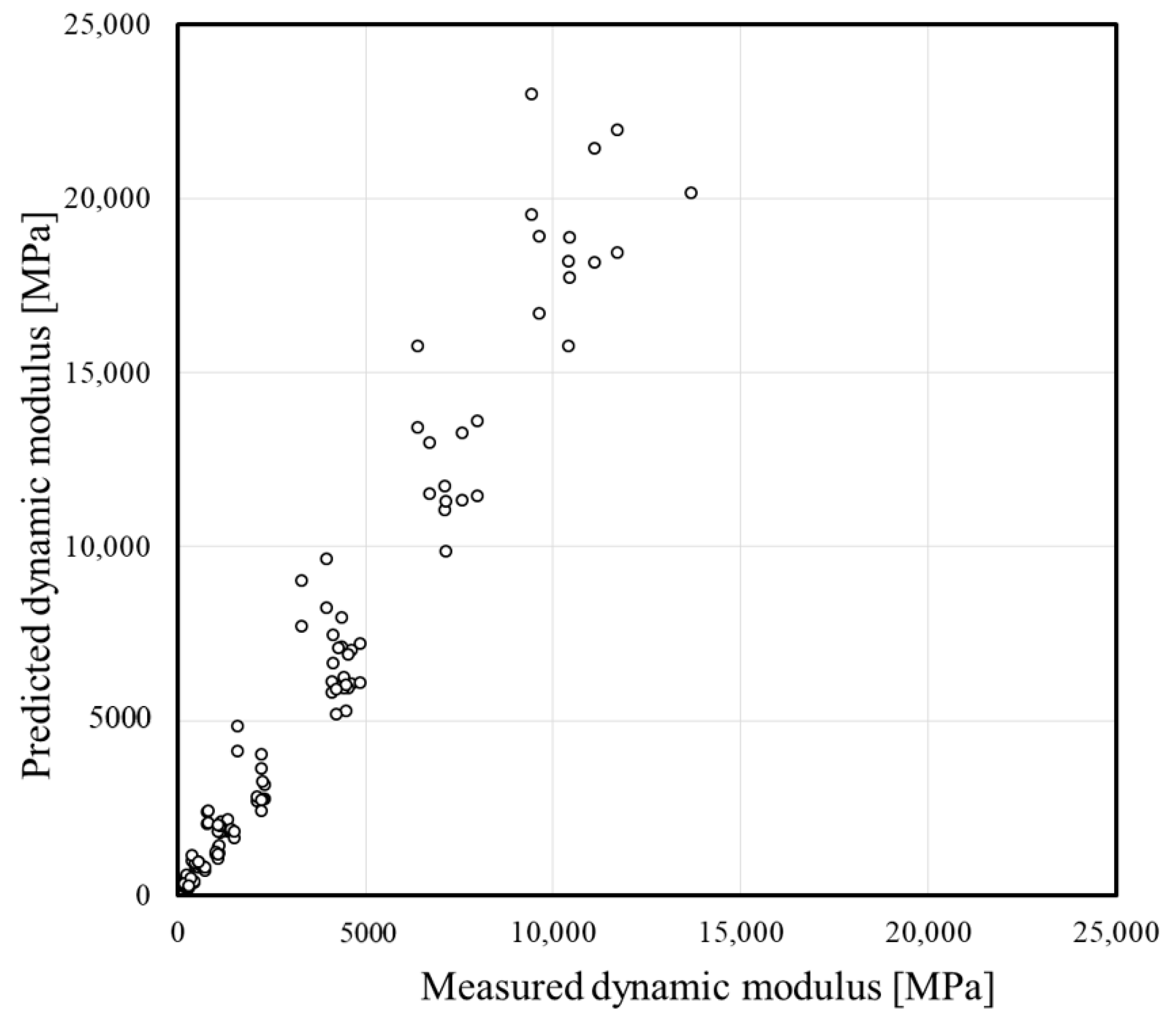
3.3. Predictive Performance of the Proposed Model
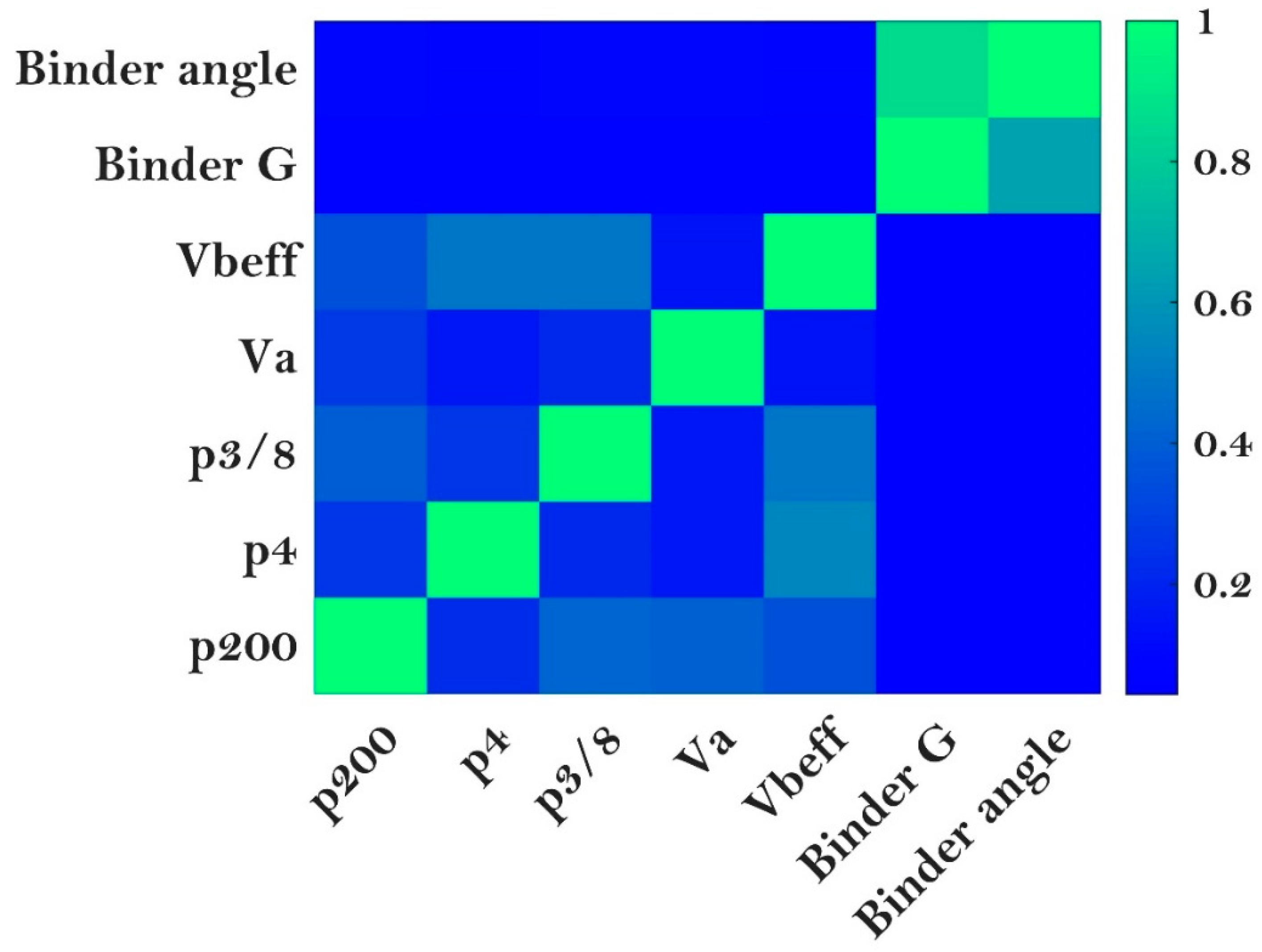
3.4. Importance of the Input Variables
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MEPDG | Mechanistic-Empirical Pavement Design Guide |
| BAS | Beetle antennae search |
| DM | Dynamic modulus |
| AASHTO | American Association of State Highway and Transportation Officials |
| PI | Penetration index |
| AI | Artificial intelligence |
| RC | Reinforced concrete |
| BPNN | Backpropagation neural network |
| Superpave | SUperior PERforming Asphalt PAVEments |
| Va | Air voids |
| DSR | Dynamic shear rheometer |
| RMSE | Root mean square error |
| R | Correlation coefficient |
References
- Walubita, L.F.; Zhang, J.; Das, G.; Hu, X.; Mushota, C.; Alvarez, A.E.; Scullion, T. Hot-mix asphalt permanent deformation evaluated by hamburg wheel tracking, dynamic modulus, and repeated load tests. Transp. Res. Rec. 2012, 2296, 46–56. [Google Scholar] [CrossRef]
- Lacroix, A.; Underwood, B.S.; Kim, Y.R. Reduced testing protocol for measuring the confined dynamic modulus of asphalt mixtures. Transp. Res. Rec. 2011, 2210, 20–29. [Google Scholar] [CrossRef]
- Kim, Y.R.; Seo, Y.; King, M.; Momen, M. Dynamic modulus testing of asphalt concrete in indirect tension mode. Transp. Res. Rec. 2004, 1891, 163–173. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, J.; Ren, J.; Chen, H. Anti-rutting performance of the damping asphalt mixtures (dams) made with a high content of asphalt rubber (ar). Constr. Build. Mater. 2021, 271, 121878. [Google Scholar] [CrossRef]
- Gu, L.; Chen, L.; Zhang, W.; Ma, H.; Ma, T. Mesostructural modeling of dynamic modulus and phase angle master curves of rubber modified asphalt mixture. Materials 2019, 12, 1667. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Velasquez, R.; Hoegh, K.; Yut, I.; Funk, N.; Cochran, G.; Marasteanu, M.; Khazanovich, L. Implementation of the Mepdg for New and Rehabilitated Pavement Structures for Design of Concrete and Asphalt Pavements in Minnesota. 2009. Available online: https://conservancy.umn.edu/handle/11299/150992 (accessed on 10 March 2022).
- Schwartz, C.W.; Li, R.; Kim, S.; Ceylan, H.; Gopalakrishnan, K. Sensitivity evaluation of mepdg performance prediction. Final. Rep. NCHRP Proj. 2011, 1, 47. [Google Scholar]
- Li, Q.; Xiao, D.X.; Wang, K.C.; Hall, K.D.; Qiu, Y. Mechanistic-empirical pavement design guide (mepdg): A bird’s-eye view. J. Mod. Transp. 2011, 19, 114–133. [Google Scholar] [CrossRef] [Green Version]
- Ji, R.; Siddiki, N.; Nantung, T.; Kim, D. Evaluation of resilient modulus of subgrade and base materials in indiana and its implementation in mepdg. Sci. World J. 2014, 2014, 372838. [Google Scholar] [CrossRef]
- El-Badawy, S.; Bayomy, F.; Awed, A. Performance of mepdg dynamic modulus predictive models for asphalt concrete mixtures: Local calibration for idaho. J. Mater. Civ. Eng. 2012, 24, 1412–1421. [Google Scholar] [CrossRef]
- Al-Qadi, I.L.; Xie, W.; Elseifi, M.A. Frequency determination from vehicular loading time pulse to predict appropriate complex modulus in mepdg. Asph. Paving Technol.-Proc. 2008, 77, 739. [Google Scholar]
- Bayomy, F.; El-Badawy, S.; Awed, A. Implementation of the Mepdg for Flexible Pavements in Idaho; Transportation Dept.: Boise, ID, USA, 2012. [Google Scholar]
- Huang, J.; Li, X.; Kumar, G.S.; Deng, Y.; Gong, M.; Dong, N. Rheological properties of bituminous binder modified with recycled waste toner. J. Clean. Prod. 2021, 317, 128415. [Google Scholar] [CrossRef]
- Zieliński, P. Indirect tensile test as a simple method for rut resistance evaluation of asphalt mixtures–polish experience. Road Mater. Pavement Des. 2020, 23, 112–128. [Google Scholar] [CrossRef]
- Zelelew, H.; Paugh, C.; Corrigan, M.; Belagutti, S.; Ramakrishnareddy, J. Laboratory evaluation of the mechanical properties of plant-produced warm-mix asphalt mixtures. Road Mater. Pavement Des. 2013, 14, 49–70. [Google Scholar] [CrossRef]
- Willis, J.R. Use of ground tire rubber in a dense-graded asphalt mixture on us 231 in alabama: A case study. In Airfield and Highway Pavement 2013: Sustainable and Efficient Pavements; 2013; pp. 1192–1201. Available online: https://ascelibrary.org/doi/abs/10.1061/9780784413005.100 (accessed on 10 March 2022).
- Wang, B.; Yang, J. Analysis of the dynamic responses of crcp and crcp+ ac under the vehicle loading by fem. In Pavements and Materials: Modeling, Testing, and Performance; 2009; pp. 131–139. Available online: https://ascelibrary.org/doi/abs/10.1061/41008(334)14 (accessed on 10 March 2022).
- Vancura, M.; MacDonald, K.; Khazanovich, L. Structural analysis of pervious concrete pavement. Transp. Res. Rec. 2011, 2226, 13–20. [Google Scholar] [CrossRef]
- Tian, Y.; Lee, J.; Nantung, T.; Haddock, J.E. Development of a mid-depth profile monitoring system for accelerated pavement testing. Constr. Build. Mater. 2017, 140, 1–9. [Google Scholar] [CrossRef]
- Siddharthan, R.; Norris, G.M.; Epps, J.A. Use of fwd data for pavement material characterization and performance. J. Transp. Eng. 1991, 117, 660–678. [Google Scholar] [CrossRef]
- Ren, J.; Yin, C. Investigating mechanical characteristics of aggregate structure for road materials. Int. J. Pavement Eng. 2022, 23, 372–386. [Google Scholar] [CrossRef] [Green Version]
- Ren, J.; Zhang, L.; Zhao, H.; Zhao, Z.; Wang, S. Determination of the fatigue equation for the cement-stabilized cold recycled mixtures with road construction waste materials based on data-driven. Int. J. Fatigue 2022, 158, 106765. [Google Scholar] [CrossRef]
- Ren, J.; Zhao, H.; Zhang, L.; Zhao, Z.; Xu, Y.; Cheng, Y.; Wang, M.; Chen, J.; Wang, J. Design optimization of cement grouting material based on adaptive boosting algorithm and simplicial homology global optimization. J. Build. Eng. 2022, 49, 104049. [Google Scholar] [CrossRef]
- Bressi, S.; Fiorentini, N.; Huang, J.; Losa, M. Crumb rubber modifier in road asphalt pavements: State of the art and statistics. Coatings 2019, 9, 384. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Fan, Y.; Huang, J.; Shah, S.P. Effect of nano-metakaolinite clay on the performance of cement-based materials at early curing age. Constr. Build. Mater. 2021, 291, 123107. [Google Scholar] [CrossRef]
- Xu, W.; Huang, X.; Yang, Z.; Zhou, M.; Huang, J. Developing hybrid machine learning models to determine the dynamic modulus (e*) of asphalt mixtures using parameters in witczak 1-40d model: A comparative study. Materials 2022, 15, 1791. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Huang, X.; Huang, J.; Yang, Z. Structural analysis of backfill highway subgrade on the lower bearing capacity foundation using the finite element method. Adv. Civ. Eng. 2021, 2021, 1690168. [Google Scholar] [CrossRef]
- Wang, Q.-A.; Zhang, J.; Huang, J. Simulation of the compressive strength of cemented tailing backfill through the use of firefly algorithm and random forest model. Shock Vib. 2021, 2021, 5536998. [Google Scholar] [CrossRef]
- Wang, Q.-A.; Zhang, C.; Ma, Z.-G.; Huang, J.; Ni, Y.-Q.; Zhang, C. Shm deformation monitoring for high-speed rail track slabs and bayesian change point detection for the measurements. Constr. Build. Mater. 2021, 300, 124337. [Google Scholar] [CrossRef]
- Ma, H.; Liu, J.; Zhang, J.; Huang, J. Estimating the compressive strength of cement-based materials with mining waste using support vector machine, decision tree, and random forest models. Adv. Civ. Eng. 2021, 2021, 6629466. [Google Scholar] [CrossRef]
- Liang, X.; Yu, X.; Chen, C.; Ding, G.; Huang, J. Towards the low-energy usage of high viscosity asphalt in porous asphalt pavements: A case study of warm-mix asphalt additives. Case Stud. Constr. Mater. 2022, 16, e00914. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, J.; Gao, Y. Intelligently predict the rock joint shear strength using the support vector regression and firefly algorithm. Lithosphere 2021, 2021, 2467126. [Google Scholar] [CrossRef]
- Zhong, X.; Zeng, X.; Rose, J. Shear modulus and damping ratio of rubber-modified asphalt mixes and unsaturated subgrade soils. J. Mater. Civ. Eng. 2002, 14, 496–502. [Google Scholar] [CrossRef]
- Phillips, C.; Hashash, Y.M. A simplified constitutive model to simultaneously match modulus reduction and damping soil curves for nonlinear site response analysis. In Geotechnical Earthquake Engineering and Soil Dynamics IV; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 1–10. [Google Scholar]
- Gao, Y.; Huang, J.; Li, M.; Dai, Z.; Jiang, R.; Zhang, J. Chemical modification of combusted coal gangue for u(vi) adsorption: Towards a waste control by waste strategy. Sustainability 2021, 13, 8421. [Google Scholar] [CrossRef]
- Yang, B.; Li, X.; Hou, Y.; Meier, A.; Cheng, X.; Choi, J.-H.; Wang, F.; Wang, H.; Wagner, A.; Yan, D. Non-invasive (non-contact) measurements of human thermal physiology signals and thermal comfort/discomfort poses-a review. Energy Build. 2020, 224, 110261. [Google Scholar] [CrossRef]
- Xie, S.; Yu, Z.; Lv, Z. Multi-disease prediction based on deep learning: A survey. Comput. Modeling Eng. Sci. 2021. Available online: https://search.bvsalud.org/global-literature-on-novel-coronavirus-2019-ncov/resource/fr/covidwho-1278935 (accessed on 10 March 2022).
- Wan, Z.; Dong, Y.; Yu, Z.; Lv, H.; Lv, Z. Semi-supervised support vector machine for digital twins based brain image fusion. Front. Neurosci. 2021, 15, 802. [Google Scholar] [CrossRef] [PubMed]
- Lv, Z.; Zhang, S.; Xiu, W. Solving the security problem of intelligent transportation system with deep learning. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4281–4290. [Google Scholar] [CrossRef]
- Lv, Z.; Qiao, L.; Cai, K.; Wang, Q. Big data analysis technology for electric vehicle networks in smart cities. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1807–1816. [Google Scholar] [CrossRef]
- Jahanbakht, M.; Xiang, W.; Hanzo, L.; Azghadi, M.R. Internet of underwater things and big marine data analytics—a comprehensive survey. IEEE Commun. Surv. Tutor. 2021, 23, 904–956. [Google Scholar] [CrossRef]
- Cheng, X.; Yang, B.; Hedman, A.; Olofsson, T.; Li, H.; Van Gool, L. Nidl: A pilot study of contactless measurement of skin temperature for intelligent building. Energy Build. 2019, 198, 340–352. [Google Scholar] [CrossRef]
- Cai, Z.; Zheng, X. A private and efficient mechanism for data uploading in smart cyber-physical systems. IEEE Trans. Netw. Sci. Eng. 2018, 7, 766–775. [Google Scholar] [CrossRef]
- Cai, Z.; He, Z. Trading private range counting over big iot data. In Proceedings of the 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS), Dallas, TX, USA, 7–10 July 2019; pp. 144–153. [Google Scholar]
- Huang, J.; Koopialipoor, M.; Armaghani, D.J. A combination of fuzzy delphi method and hybrid ann-based systems to forecast ground vibration resulting from blasting. Sci. Rep. 2020, 10, 19397. [Google Scholar] [CrossRef]
- Huang, J.; Asteris, P.G.; Pasha, S.M.K.; Mohammed, A.S.; Hasanipanah, M. A new auto-tuning model for predicting the rock fragmentation: A cat swarm optimization algorithm. Eng. Comput. 2020, pp. 1–12. Available online: https://link.springer.com/article/10.1007/s00366-020-01207-4 (accessed on 10 March 2022).
- Huang, J.; Leandri, P.; Cuciniello, G.; Losa, M. Mix design and laboratory characterisation of rubberised mixture used as damping layer in pavements. Int. J. Pavement Eng. 2021, 1–15. [Google Scholar] [CrossRef]
- Huang, J.; Alyousef, R.; Suhatril, M.; Baharom, S.; Alabduljabbar, H.; Alaskar, A.; Assilzadeh, H. Influence of porosity and cement grade on concrete mechanical properties. Adv. Concr. Constr. 2020, 10, 393–402. [Google Scholar]
- Huang, J.; Duan, T.; Lei, Y.; Hasanipanah, M. Finite element modeling for the antivibration pavement used to improve the slope stability of the open-pit mine. Shock Vib. 2020, 2020, 6650780. [Google Scholar]
- Ahmad, M.; Tang, X.-W.; Ahmad, F.; Pirhadi, N.; Wan, X.; Cheng, K. Probabilistic evaluation of cpt-based seismic soil liquefaction potential: Towards the integration of interpretive structural modeling and bayesian belief network. Math. Biosci. Eng. 2021, 18, 9233–9252. [Google Scholar] [CrossRef] [PubMed]
- Hoang, N.-D. Estimating punching shear capacity of steel fibre reinforced concrete slabs using sequential piecewise multiple linear regression and artificial neural network. Measurement 2019, 137, 58–70. [Google Scholar]
- Yang, H.; Koopialipoor, M.; Armaghani, D.J.; Gordan, B.; Khorami, M.; Tahir, M. Intelligent design of retaining wall structures under dynamic conditions. Steel Compos. Struct. 2019, 31, 629–640. [Google Scholar]
- Xu, C.; Gordan, B.; Koopialipoor, M.; Armaghani, D.J.; Tahir, M.; Zhang, X. Improving performance of retaining walls under dynamic conditions developing an optimized ann based on ant colony optimization technique. IEEE Access 2019, 7, 94692–94700. [Google Scholar] [CrossRef]
- Tang, D.; Gordan, B.; Koopialipoor, M.; Jahed Armaghani, D.; Tarinejad, R.; Thai Pham, B.; Huynh, V.V. Seepage analysis in short embankments using developing a metaheuristic method based on governing equations. Appl. Sci. 2020, 10, 1761. [Google Scholar]
- Sun, L.; Koopialipoor, M.; Armaghani, D.J.; Tarinejad, R.; Tahir, M. Applying a meta-heuristic algorithm to predict and optimize compressive strength of concrete samples. Eng. Comput. 2019, 37, 1133–1145. [Google Scholar] [CrossRef]
- Mohamad, E.T.; Armaghani, D.J.; Momeni, E.; Yazdavar, A.H.; Ebrahimi, M. Rock strength estimation: A pso-based bp approach. Neural Comput. Appl. 2018, 30, 1635–1646. [Google Scholar] [CrossRef]
- Mahdiyar, A.; Jahed Armaghani, D.; Koopialipoor, M.; Hedayat, A.; Abdullah, A.; Yahya, K. Practical risk assessment of ground vibrations resulting from blasting, using gene expression programming and monte carlo simulation techniques. Appl. Sci. 2020, 10, 472. [Google Scholar] [CrossRef] [Green Version]
- Koopialipoor, M.; Armaghani, D.J.; Haghighi, M.; Ghaleini, E.N. A neuro-genetic predictive model to approximate overbreak induced by drilling and blasting operation in tunnels. Bull. Eng. Geol. Environ. 2019, 78, 981–990. [Google Scholar] [CrossRef]
- Khandelwal, M.; Marto, A.; Fatemi, S.A.; Ghoroqi, M.; Armaghani, D.J.; Singh, T.; Tabrizi, O. Implementing an ann model optimized by genetic algorithm for estimating cohesion of limestone samples. Eng. Comput. 2018, 34, 307–317. [Google Scholar] [CrossRef]
- Huang, L.; Asteris, P.G.; Koopialipoor, M.; Armaghani, D.J.; Tahir, M. Invasive weed optimization technique-based ann to the prediction of rock tensile strength. Appl. Sci. 2019, 9, 5372. [Google Scholar] [CrossRef] [Green Version]
- Hasanipanah, M.; Shahnazar, A.; Amnieh, H.B.; Armaghani, D.J. Prediction of air-overpressure caused by mine blasting using a new hybrid pso–svr model. Eng. Comput. 2017, 33, 23–31. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Noorian-Bidgoli, M.; Armaghani, D.J.; Khamesi, H. Feasibility of pso-ann model for predicting surface settlement caused by tunneling. Eng. Comput. 2016, 32, 705–715. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Monjezi, M.; Shahnazar, A.; Armaghani, D.J.; Farazmand, A. Feasibility of indirect determination of blast induced ground vibration based on support vector machine. Measurement 2015, 75, 289–297. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Armaghani, D.J.; Amnieh, H.B.; Abd Majid, M.Z.; Tahir, M.M. Application of pso to develop a powerful equation for prediction of flyrock due to blasting. Neural Comput. Appl. 2017, 28, 1043–1050. [Google Scholar] [CrossRef]
- Hajihassani, M.; Armaghani, D.J.; Marto, A.; Mohamad, E.T. Ground vibration prediction in quarry blasting through an artificial neural network optimized by imperialist competitive algorithm. Bull. Eng. Geol. Environ. 2015, 74, 873–886. [Google Scholar] [CrossRef]
- Cai, M.; Koopialipoor, M.; Armaghani, D.J.; Thai Pham, B. Evaluating slope deformation of earth dams due to earthquake shaking using mars and gmdh techniques. Appl. Sci. 2020, 10, 1486. [Google Scholar] [CrossRef] [Green Version]
- Armaghani, D.J.; Raja, R.S.N.S.B.; Faizi, K.; Rashid, A.S.A. Developing a hybrid pso–ann model for estimating the ultimate bearing capacity of rock-socketed piles. Neural Comput. Appl. 2017, 28, 391–405. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Mohamad, E.T.; Narayanasamy, M.S.; Narita, N.; Yagiz, S. Development of hybrid intelligent models for predicting tbm penetration rate in hard rock condition. Tunn. Undergr. Space Technol. 2017, 63, 29–43. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Mirzaei, F.; Shariati, M.; Trung, N.T.; Shariati, M.; Trnavac, D. Hybrid ann-based techniques in predicting cohesion of sandy-soil combined with fiber. Geomech. Eng. 2020, 20, 191–205. [Google Scholar]
- Armaghani, D.J.; Koopialipoor, M.; Marto, A.; Yagiz, S. Application of several optimization techniques for estimating tbm advance rate in granitic rocks. J. Rock Mech. Geotech. Eng. 2019, 11, 779–789. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Koopialipoor, M.; Bahri, M.; Hasanipanah, M.; Tahir, M. A svr-gwo technique to minimize flyrock distance resulting from blasting. Bull. Eng. Geol. Environ. 2020, 79, 4369–4385. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Hasanipanah, M.; Mohamad, E.T. A combination of the ica-ann model to predict air-overpressure resulting from blasting. Eng. Comput. 2016, 32, 155–171. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Asteris, P.G. A comparative study of ann and anfis models for the prediction of cement-based mortar materials compressive strength. Neural Comput. Appl. 2021, 33, 4501–4532. [Google Scholar] [CrossRef]
- Wang, G.; Xu, X.; Yao, Y.; Tong, J. A novel bpnn-based method to overcome the gps outages for ins/gps system. IEEE Access 2019, 7, 82134–82143. [Google Scholar] [CrossRef]
- Samantaray, S.; Sahoo, A. Estimation of runoff through bpnn and svm in agalpur watershed. In Frontiers in Intelligent Computing: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 268–275. [Google Scholar]
- Hansen, L.K.; Salamon, P. Neural network ensembles. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 993–1001. [Google Scholar] [CrossRef] [Green Version]
- Granitto, P.M.; Verdes, P.F.; Ceccatto, H.A. Neural network ensembles: Evaluation of aggregation algorithms. Artif. Intell. 2005, 163, 139–162. [Google Scholar] [CrossRef] [Green Version]
- Ghaleini, E.N.; Koopialipoor, M.; Momenzadeh, M.; Sarafraz, M.E.; Mohamad, E.T.; Gordan, B. A combination of artificial bee colony and neural network for approximating the safety factor of retaining walls. Eng. Comput. 2019, 35, 647–658. [Google Scholar] [CrossRef]
- Getahun, M.A.; Shitote, S.M.; Gariy, Z.C.A. Artificial neural network based modelling approach for strength prediction of concrete incorporating agricultural and construction wastes. Constr. Build. Mater. 2018, 190, 517–525. [Google Scholar] [CrossRef]
- Erb, R.J. Introduction to backpropagation neural network computation. Pharm. Res. 1993, 10, 165–170. [Google Scholar] [CrossRef] [PubMed]
- Singh, D.; Zaman, M.; Commuri, S. Artificial neural network modeling for dynamic modulus of hot mix asphalt using aggregate shape properties. J. Mater. Civ. Eng. 2013, 25, 54–62. [Google Scholar] [CrossRef]
- Jiang, X.; Li, S. Bas: Beetle antennae search algorithm for optimization problems. arXiv 2017, arXiv:1710.10724. [Google Scholar] [CrossRef]
- Huang, J.; Duan, T.; Zhang, Y.; Liu, J.; Zhang, J.; Lei, Y. Predicting the permeability of pervious concrete based on the beetle antennae search algorithm and random forest model. Adv. Civ. Eng. 2020, 2020, 8863181. [Google Scholar] [CrossRef]
- Huang, J.; Shiva Kumar, G.; Ren, J.; Zhang, J.; Sun, Y. Accurately predicting dynamic modulus of asphalt mixtures in low-temperature regions using hybrid artificial intelligence model. Constr. Build. Mater. 2021, 297, 123655. [Google Scholar] [CrossRef]
- Dai, Z.; Li, H.; Zhao, W.; Wang, X.; Wang, H.; Zhou, H.; Yang, B. Multi-modified effects of varying admixtures on the mechanical properties of pervious concrete based on optimum design of gradation and cement-aggregate ratio. Constr. Build. Mater. 2020, 233, 117178. [Google Scholar] [CrossRef]
- Samareh-Mousavi, S.S.; Taheri-Behrooz, F. A novel creep-fatigue stiffness degradation model for composite materials. Compos. Struct. 2020, 237, 111955. [Google Scholar] [CrossRef]
- Kamal, M.; Rumman, R.; Manzur, T.; Noor, M.; Bari, M. A novel durability based concrete mix design using supplementary cementitious materials and modified aggregate band gradation. Int. J. Civ. Eng. 2020, 19, 39–50. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Hagan, P.; Mitra, R.; Hebblewhite, B. Numerical Investigation of Asperity Degradation in the Direct Shear Test of Rock Joints. In Proceedings of the ISRM International Symposium-EUROCK 2013, OnePetro, Wroclaw, Poland, 23–26 September 2013. [Google Scholar]
- American Association of State Highway and Transportation Officials. Standard Method of Test for Determining Dynamic Modulus of Hot-Mix Asphalt Concrete Mixtures; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2011. [Google Scholar]
- Oreta, A.W.; Kawashima, K. Neural network modeling of confined compressive strength and strain of circular concrete columns. J. Struct. Eng. 2003, 129, 554–561. [Google Scholar] [CrossRef]





| Basic Properties | Binder 1 | Binder 2 | Aggregates | |
|---|---|---|---|---|
| Binder-index properties of asphalt | Penetration @ 25 °C (0.1 mm) | 92.0 | 75.1 | - |
| Penetration index (PI) | −1.17 | 0.2 | - | |
| Softening point (°C) | 44.0 | 52.5 | - | |
| Viscosity @ 135 °C (Pa∙s) | 0.363 | 1.3 | - | |
| Physical properties of aggregate | LA abrasion value (%) | - | - | 23.0 |
| Aggregate impact value (%) | - | - | 22.0 | |
| Water absorption (%) | - | - | 0.14 | |
| Combined elongation and flakiness indices (%) | - | - | 28.0 | |
| Soundness, magnesium sulfate solution (%) | - | - | 0.4 | |
| Asphalt Mixtures | Nominal Aggregate Size (mm) | Binder Content (%) | Va (%) |
|---|---|---|---|
| Asphalt Mixture-1 | 19 | 4.5 | 4.0 |
| Asphalt Mixture-2 | 19 | 4.4 | 4.0 |
| Asphalt Mixture-3 | 19 | 4.8 | 4.0 |
| Asphalt Mixture-4 | 19 | 5.0 | 4.0 |
| Asphalt Mixture-5 | 12.5 | 5.0 | 4.0 |
| Asphalt Mixture-6 | 12.5 | 5.3 | 4.0 |
| Asphalt Mixture-7 | 12.5 | 5.5 | 4.0 |
| Asphalt Mixture-8 | 12.5 | 5.4 | 4.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Zhou, M.; Sabri, M.M.S.; Yuan, H. A Novel Neural Computing Model Applied to Estimate the Dynamic Modulus (DM) of Asphalt Mixtures by the Improved Beetle Antennae Search. Sustainability 2022, 14, 5938. https://doi.org/10.3390/su14105938
Huang J, Zhou M, Sabri MMS, Yuan H. A Novel Neural Computing Model Applied to Estimate the Dynamic Modulus (DM) of Asphalt Mixtures by the Improved Beetle Antennae Search. Sustainability. 2022; 14(10):5938. https://doi.org/10.3390/su14105938
Chicago/Turabian StyleHuang, Jiandong, Mengmeng Zhou, Mohanad Muayad Sabri Sabri, and Hongwei Yuan. 2022. "A Novel Neural Computing Model Applied to Estimate the Dynamic Modulus (DM) of Asphalt Mixtures by the Improved Beetle Antennae Search" Sustainability 14, no. 10: 5938. https://doi.org/10.3390/su14105938
APA StyleHuang, J., Zhou, M., Sabri, M. M. S., & Yuan, H. (2022). A Novel Neural Computing Model Applied to Estimate the Dynamic Modulus (DM) of Asphalt Mixtures by the Improved Beetle Antennae Search. Sustainability, 14(10), 5938. https://doi.org/10.3390/su14105938







