Evaluation of Transport and Location Policies to Realize the Carbon-Free Urban Society
Abstract
:1. Introduction
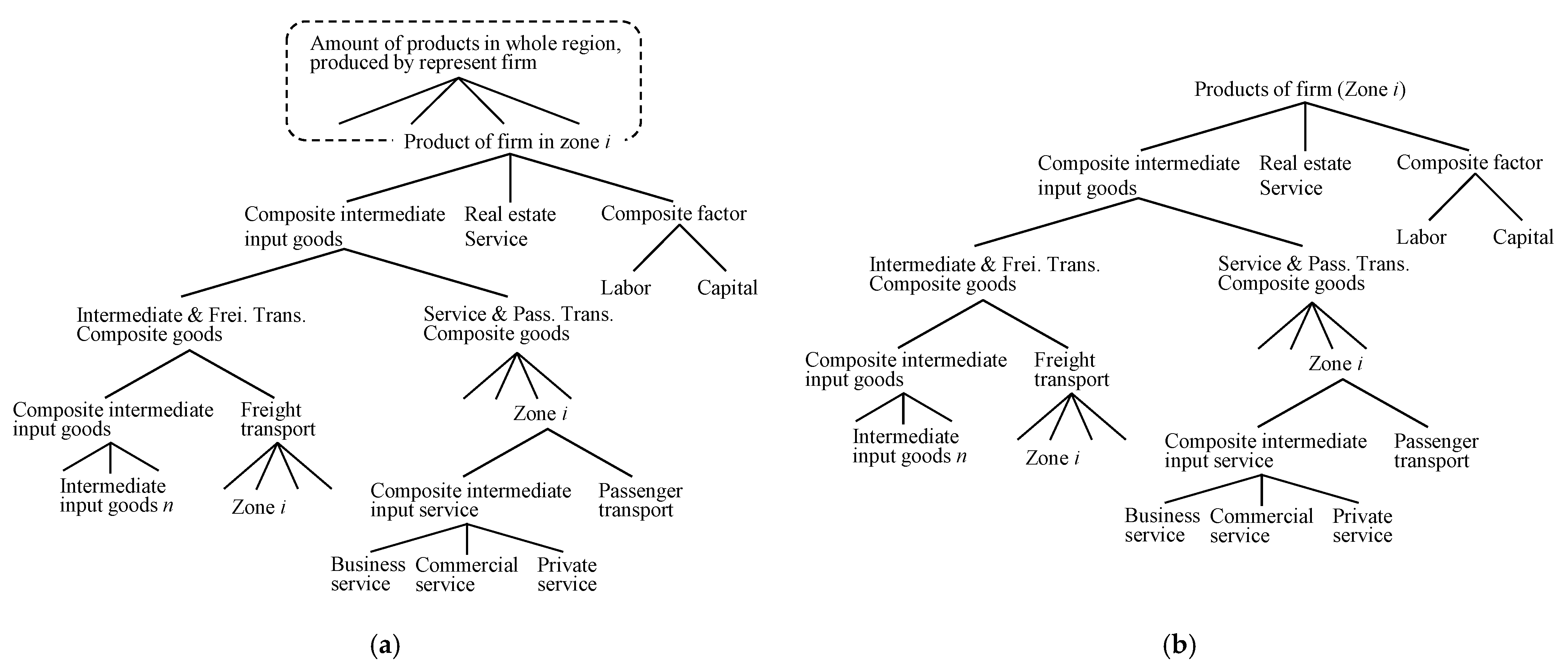
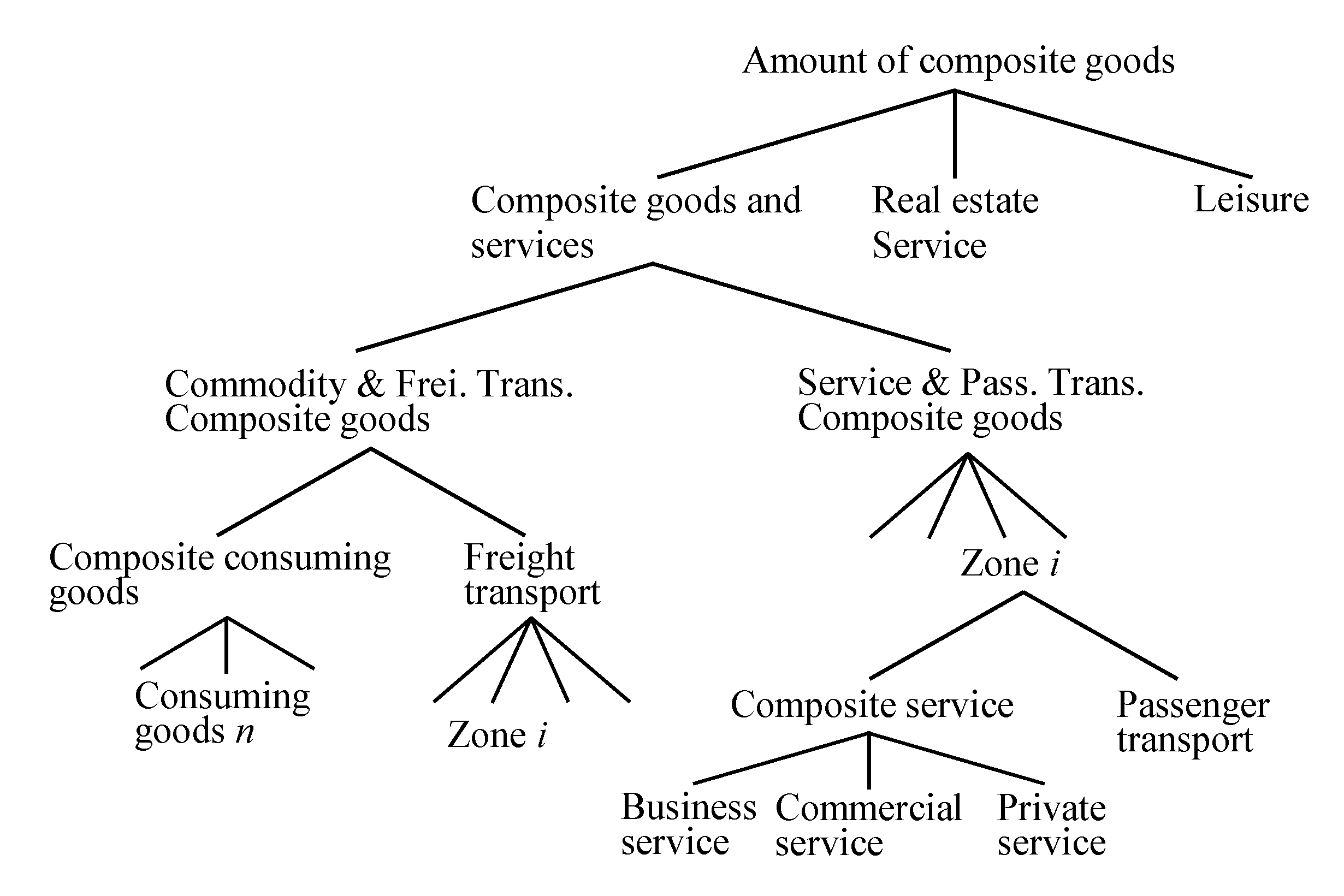
2. Structure of the CGEUE Model
2.1. Concept of Modelling
2.2. Assumption of the CGEUE Model
2.3. Formulation of the CGEUE Model
2.3.1. Firm’s Behavior
2.3.2. Household’s Behavior
2.3.3. Real Estate Firm’s Behavior
2.3.4. Transport Firm’s Behavior
2.4. Market Equilibrium Conditions
2.5. Definition of Benefit
3. Numerical Results
3.1. Outline of Numerical Simulation
- The policy for converting fossil fuel vehicles to electric vehicles;
- 2.
- The policy for improving public transport;
- 3.
- The environmental tax policy;
- 4.
- The policy for making city compact.
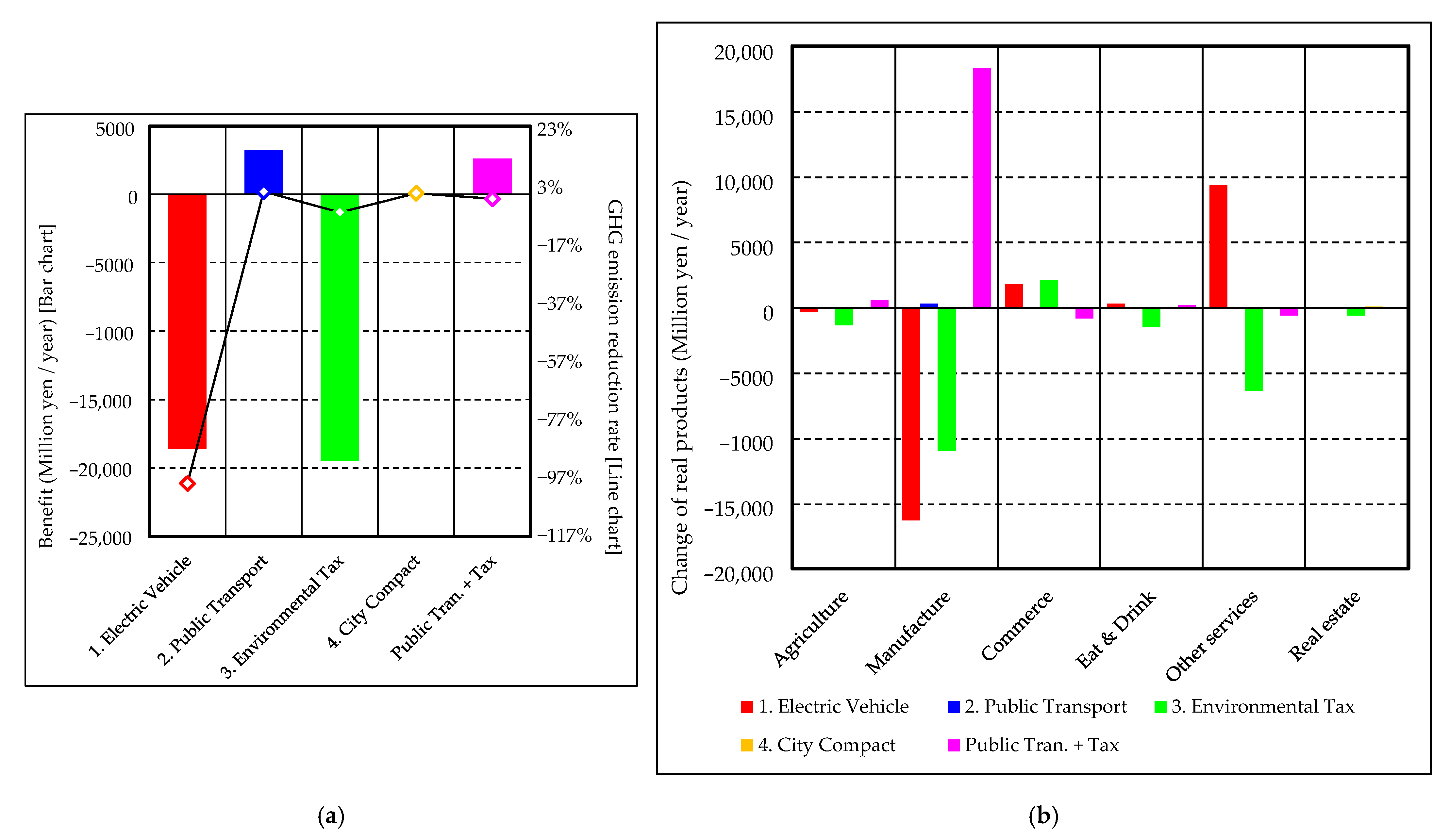
3.2. Results of Policies
3.2.1. Results of the Entire Simulation
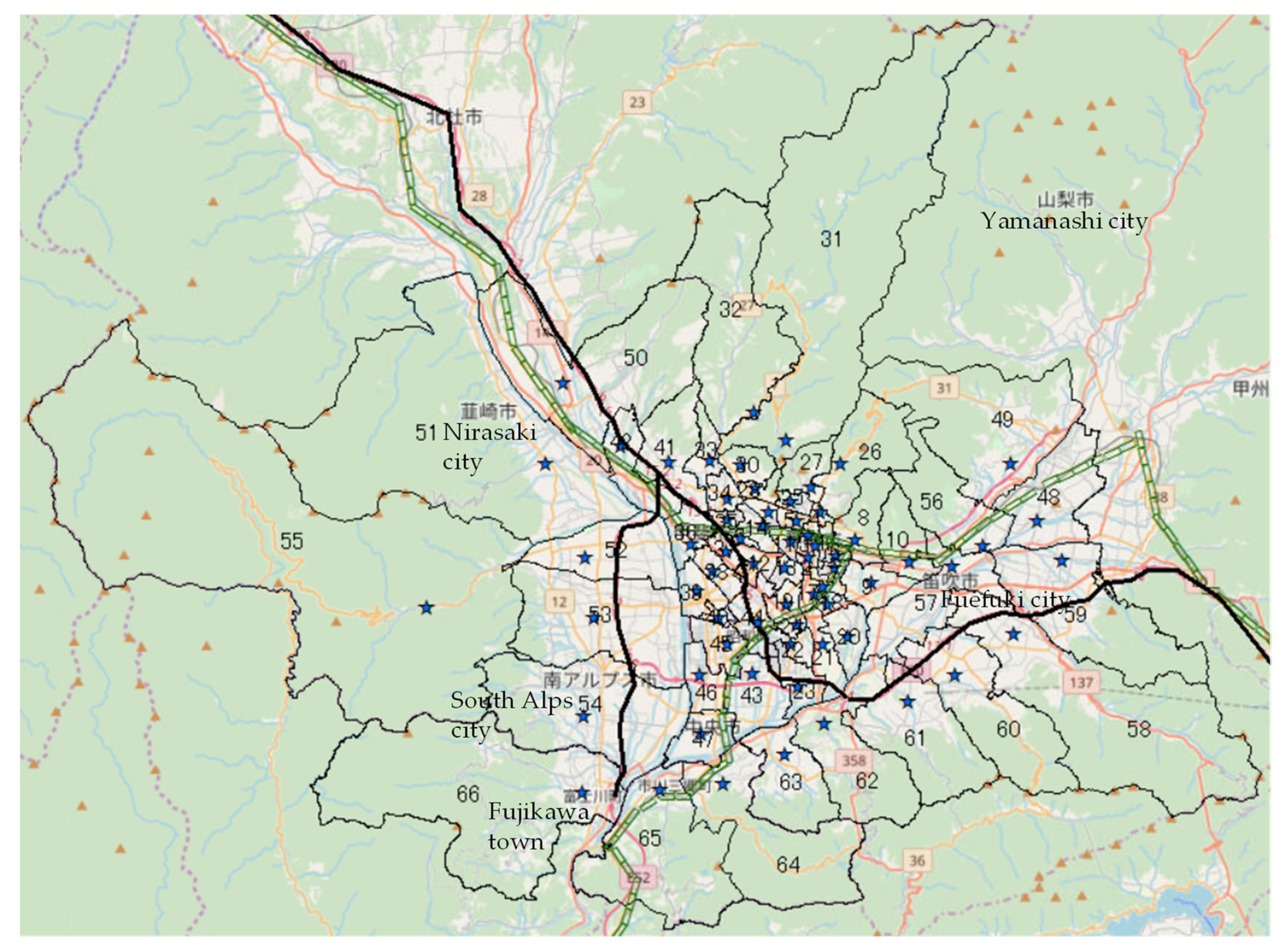
3.2.2. Results of Policies for Each Zone
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ministry of Economy, Trade and Industry. Japan’s 2050 Carbon Neutral Goal, METI Reports 2021. 2021. Available online: https://www.meti.go.jp/english/policy/energy_environment/global_warming/roadmap/report/20201111.html (accessed on 5 December 2021).
- Muto, S.; Ueda, T.; Morisugi, H. The national economic evaluation of polices to regulate external diseconomies caused by automobiles. In Proceedings of the World Transport Research: Selected Proceedings of the 8th World Conference on Transport Research, Antwerp, Belgium, 12–17 July 1998; Volume 3, pp. 583–596. [Google Scholar]
- Muto, S.; Morisugi, H.; Ueda, T. Measuring market damage of automobile related carbon tax by dynamic computable general equilibrium model. In Proceedings of the ERSA the 43rd European Congress, Jyväskylä, Finland, 27–30 August 2003; Volume 43, p. 257. [Google Scholar]
- Wegener, M. Overview of land-use transport models. In Transport Geography and Spatial Systems; Handbook 5 of the Handbook in Transport; Hensher, D.A., Button, K., Eds.; Pergamon/Elsevier Science: Kidlington, UK, 2004; pp. 99, 127–146. [Google Scholar]
- Ueda, T.; Tsutsumi, M.; Muto, S.; Yamasaki, K. Unified computable urban economic model. Ann. Reg. Sci. 2013, 50, 341–362. [Google Scholar] [CrossRef] [Green Version]
- Muto, S.; Ueda, T.; Yamaguchi, K.; Yamasaki, K. Evaluation of environmental pollutions occurred by transport infrastructure project at Tokyo Metropolitan Area. In Proceedings of the 10th World Conference on Transport Research, Istanbul, Turkey, 4–8 July 2004; p. 1152. [Google Scholar]
- Zhang, R.; Matsushima, K.; Kobayashi, K. Land use, transport and carbon emissions: A Computable Urban Economic model for Changzhou, China. Rev. Urban Reginal Dev. Stud. 2016, 28, 162–181. [Google Scholar] [CrossRef]
- Thorpe, S.G. Automobile-related environmental policies in a spatial model: Lessons from theory. J. Reg. Anal. Policy 1999, 29, 56–73. [Google Scholar]
- Alonso, W. Location and Land Use; Harvard University Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Unteroberdoerster, O. Trade and transboundary pollution: Spatial separation reconsidered. J. Environ. Econ. Manag. 2001, 41, 269–285. [Google Scholar] [CrossRef]
- Krugman, P. Increasing returns and economic geography. J. Political Econ. 1991, 99, 483–499. [Google Scholar] [CrossRef]
- Anas, A.; Xu, R. Congestion, land use, and job dispersion: A general equilibrium model. J. Urban Econ. 1999, 45, 451–473. [Google Scholar] [CrossRef]
- Robson, E.N.; Wijayaratna, K.P.; Dixit, V.V. A review of computable general equilibrium models for transport and their applications in appraisal. Transp. Res. Part A 2018, 116, 31–53. [Google Scholar] [CrossRef]
- Anas, A.; Liu, Y. A regional economy, land use, and transportation model (RELU-TRAN): Formulation, algorithm design, and testing. J. Reg. Sci. 2007, 47, 415–455. [Google Scholar] [CrossRef]
- Robson, E.N.; Dixit, V.V. A general equilibrium framework for integrated assessment of transport and economic impacts. Netw. Spat. Econ. 2017, 17, 989–1013. [Google Scholar] [CrossRef]
- Muto, S.; Ito, T. Construction of computable general equilibrium model considered location equilibrium to evaluate environmental projects on urban transport. J. Stud. Reg. Sci. 2006, 36, 503–512. [Google Scholar] [CrossRef] [Green Version]
- Muto, S.; Madhu, S.K. Integrated model of CGE and CUE modeling for evaluation of urban transport projects. In Proceedings of the 2018 Joint 10th International Conference on Soft Computing and Intelligent Systems (SCIS) and 19th International Symposium on Advanced Intelligent Systems (ISIS), Toyama, Japan, 5–8 December 2018; pp. 19–26. [Google Scholar]
- Muto, S.; Takagi, A.; Ueda, T. The benefit evaluation of transport network improvement with Computable Urban Economic model. In Proceedings of the 9th World Congress on Transport Research, Seoul, Korea, 22–27 July 2001; p. 6218. [Google Scholar]
- Gavanas, N.; Pozoukidou, G.; Verani, E. Integration of LUTI models into sustainable urban mobility plans (SUMPs). Eur. J. Environ. Sci. 2016, 6, 11–17. [Google Scholar] [CrossRef] [Green Version]
- Anas, A. Residential Location Markets and Urban Transportation; Academic Press: London, UK, 1982. [Google Scholar]
- Anas, A. Discrete Choice Theory and the General Equilibrium of Employment, Housing and Travel Networks in a Lowry-type Model of the Urban Economy. Environ. Plan. A 1984, 16, 1489–1502. [Google Scholar] [CrossRef]
- Ministry of Economy, Trade and Industry. Green Growth Strategy through Achieving Carbon Neutrality in 2050, METI. 2021. Available online: https://www.meti.go.jp/english/policy/energy_environment/global_warming/ggs2050/index.html (accessed on 8 December 2021).



| 1 | Agriculture | Industrial sector |
| 2 | Manufacture | |
| 3 | Commerce | |
| 4 | Eating and drinking services | |
| 5 | Public services | |
| 6 | Business and personal services | |
| 7 | Petroleum refinery products | |
| 8 | Electricity | |
| 9 | Water supply | |
| 10 | Real estate services | |
| 11 | Railway transport | Industrial sector |
| 12 | Road passenger transport | |
| 13 | Self-transport (passenger) | |
| 14 | Road freight transport | |
| 15 | Self transport (freight) | |
| 1 | Household | Final demand sector |
| 2 | Government | |
| 3 | Public investment | |
| 4 | Private investment |
| 1 | Fujigawa | Kofu city | 24 | Ookuni | Kofu city | 46 | Tatomi North | Chuo city |
| 2 | Aioi | 25 | Kitashin | 47 | Tatomi South | |||
| 3 | Kasuga | 26 | Aikawa | 48 | Yamanashi South | Yamanashi city | ||
| 4 | Shinkonya | 27 | Yumura | 49 | Yamanashi North | |||
| 5 | Shiobe | 28 | Tsukahara | 50 | Nirasaki east | Nirasaki city | ||
| 6 | Takumi | 29 | Chiduka | 51 | Nirasaki west | |||
| 7 | Azuma | 30 | Haguro | 52 | Hatta | South Alps city | ||
| 8 | Satogaki | 31 | Chiyoda | 53 | Shirane | |||
| 9 | Tamao | 32 | Shikishima North | Kai city | 54 | Ogasawara | ||
| 10 | Kouun | 33 | Shikishima | 55 | Ashiyasu | |||
| 11 | Anakiri | Central-North | 56 | Kasugai | Fuefuki city | |||
| 12 | Kugawa | 34 | Shikishima Central | 57 | Isawa | |||
| 13 | Ishida | 35 | Shikishima South | 58 | Misaka | |||
| 14 | Ikeda | 36 | Ryuo | 59 | Ichimiya | |||
| 15 | Shinden | 37 | Tomitake Shinden | 60 | Yatsushiro | |||
| 16 | Yuda | 38 | Shinohara | 61 | Sakaigawa | |||
| 17 | Ise | 39 | Nishiyahata | 62 | Nakamiti | Kofu city | ||
| 18 | Sumiyoshi | 40 | Tamagawa | 63 | Toyotomi | Chuo city | ||
| 19 | Kokubo | 41 | Futaba North | 64 | Mitama | Ichikawamisato | ||
| 20 | Kose | 42 | Futaba West | 65 | Ichikawadaimon | town | ||
| 21 | Yamashiro | 43 | Tamaho | Chuo city | 66 | Masuho | Fujikawa town | |
| 22 | Oosato | 44 | Saijo | Showa town | 67 | Oshikoshi | Showa town | |
| 23 | Horinouchi | 45 | Jouei |
| Benefit | Reduction Rate | Change of Real Products (Million Yen/Year) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Million Yen/Year) | of GHGs (%) | Railway Trans. | Road Pass. Trans. | Self-Trans. Pass. | Road Frei. Trans. | Self-Trans. Frei. | Agricultue | Manufacture | Commerce | Eat & Drink | Other Services | Real Estate | |
| 1.Electric vehicle | −18,630 | −98.92% | 15 | −574 | −10,919 | −9189 | 11,924 | −319 | −16,241 | 1804 | 311 | 9391 | 36 |
| 2.Public transport | 3221 | 0.60% | 23 | 2590 | −7 | 6 | 4 | 6 | 343 | −43 | −21 | 36 | 19 |
| 3.Environmental tax | −19,479 | −6.48% | −3 | −231 | −4656 | −1901 | −2050 | −1321 | −10,937 | 2147 | −1420 | −6319 | −577 |
| 4.City compact | −1 | 0.0016% | 0 | 0 | 1 | 1 | 1 | 0 | 38 | 15 | 4 | 55 | 107 |
| Public Tran. + Tax | 2623 | −1.83% | 25 | 2458 | −1727 | −842 | −758 | 608 | 18,358 | −808 | 251 | −582 | 67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muto, S.; Toyama, H.; Takai, A. Evaluation of Transport and Location Policies to Realize the Carbon-Free Urban Society. Sustainability 2022, 14, 14. https://doi.org/10.3390/su14010014
Muto S, Toyama H, Takai A. Evaluation of Transport and Location Policies to Realize the Carbon-Free Urban Society. Sustainability. 2022; 14(1):14. https://doi.org/10.3390/su14010014
Chicago/Turabian StyleMuto, Shinichi, Hiroto Toyama, and Akina Takai. 2022. "Evaluation of Transport and Location Policies to Realize the Carbon-Free Urban Society" Sustainability 14, no. 1: 14. https://doi.org/10.3390/su14010014
APA StyleMuto, S., Toyama, H., & Takai, A. (2022). Evaluation of Transport and Location Policies to Realize the Carbon-Free Urban Society. Sustainability, 14(1), 14. https://doi.org/10.3390/su14010014





