Multi-Domain and Multi-Material Topology Optimization in Design and Strengthening of Innovative Sustainable Structures
Abstract
1. Introduction
2. Sub-Domain Based Multi-Material Topology Optimization
3. Cellular Automata Rules for Topology Optimization
4. Multi-Domain and Multi-Material Topology Optimization
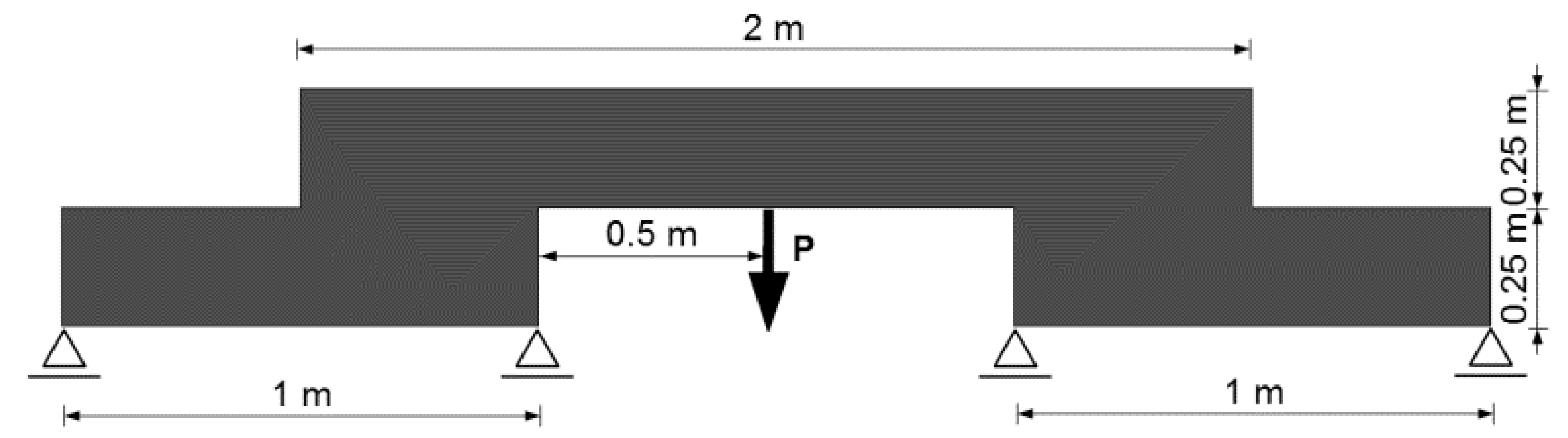
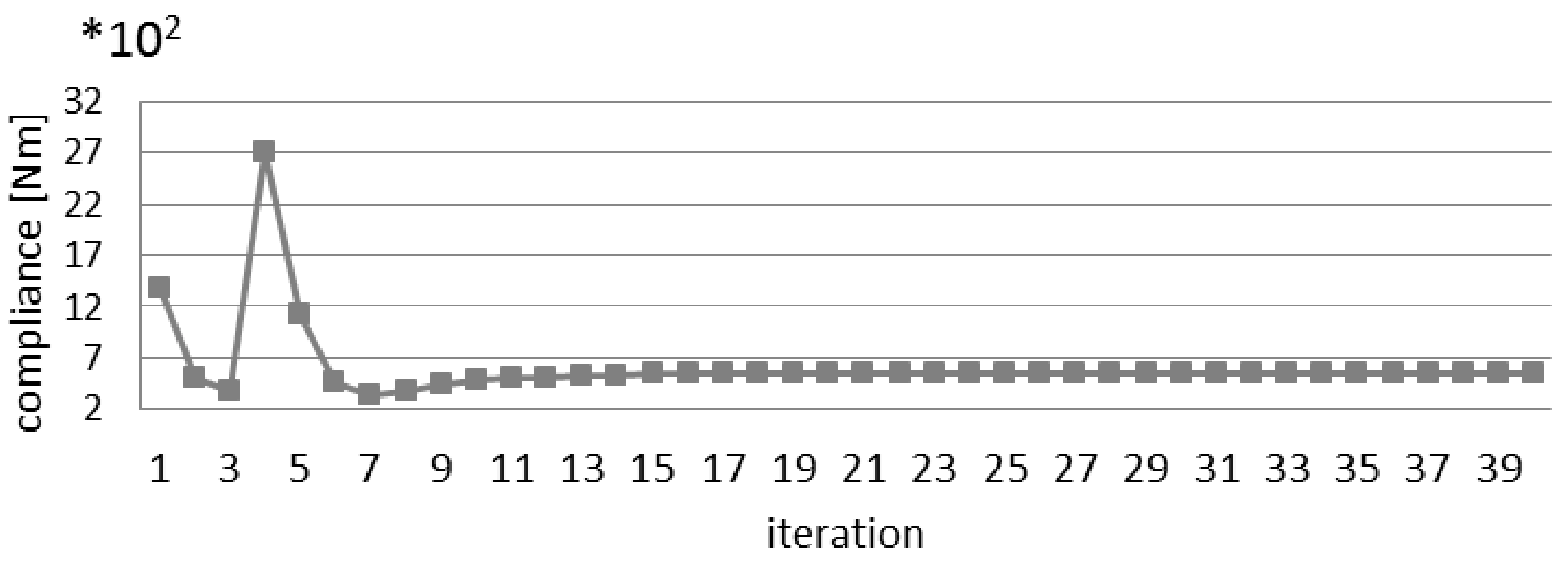
4.1. Example 1—Support Structure
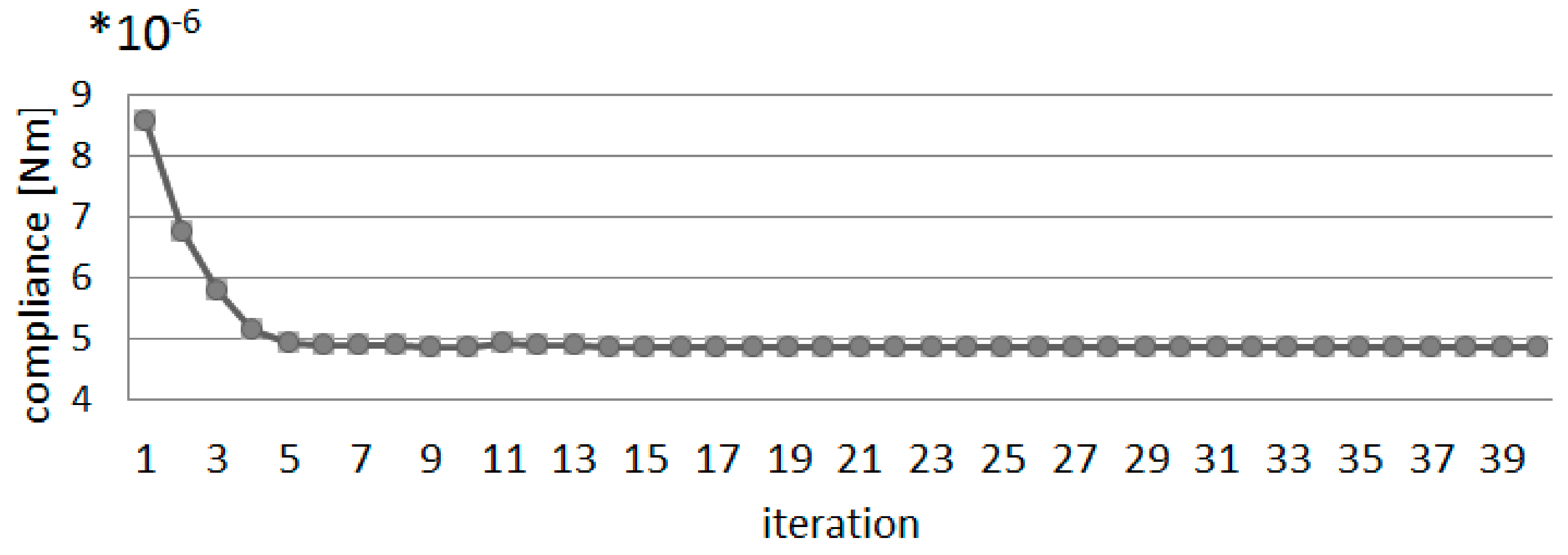
4.1.1. Topology Optimization of Uni-Material Structure under External Load
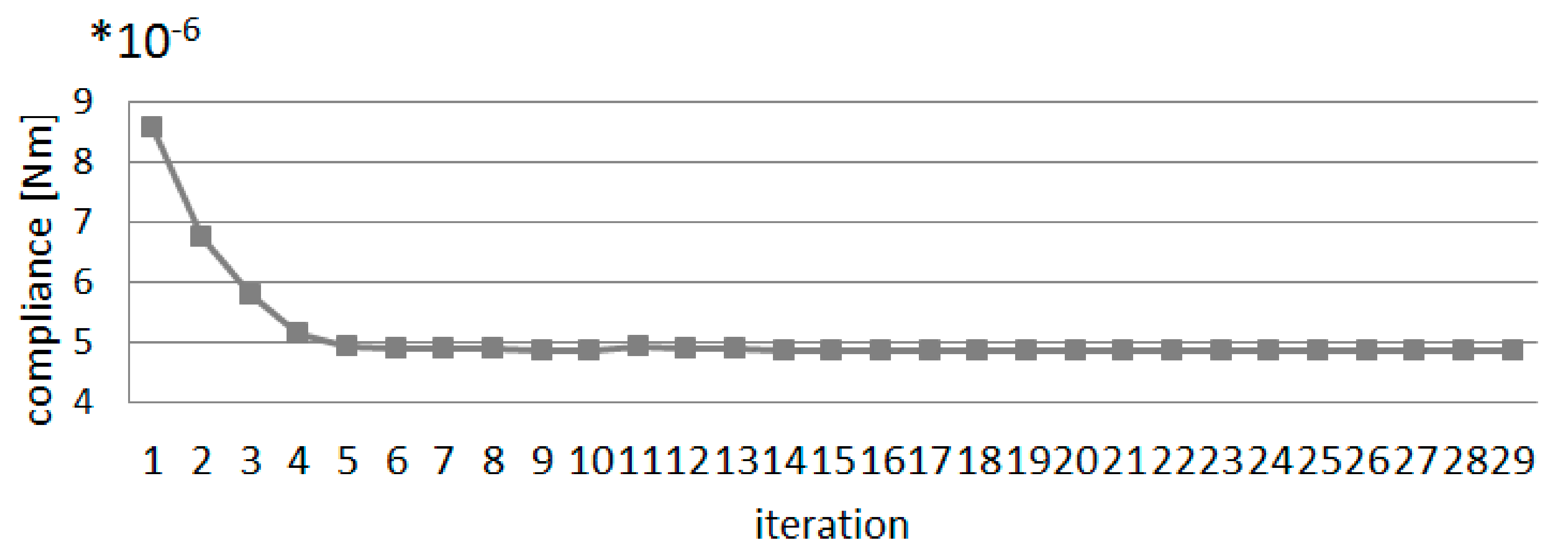
4.1.2. Topology Optimization of Multi-Material Structure under External Load
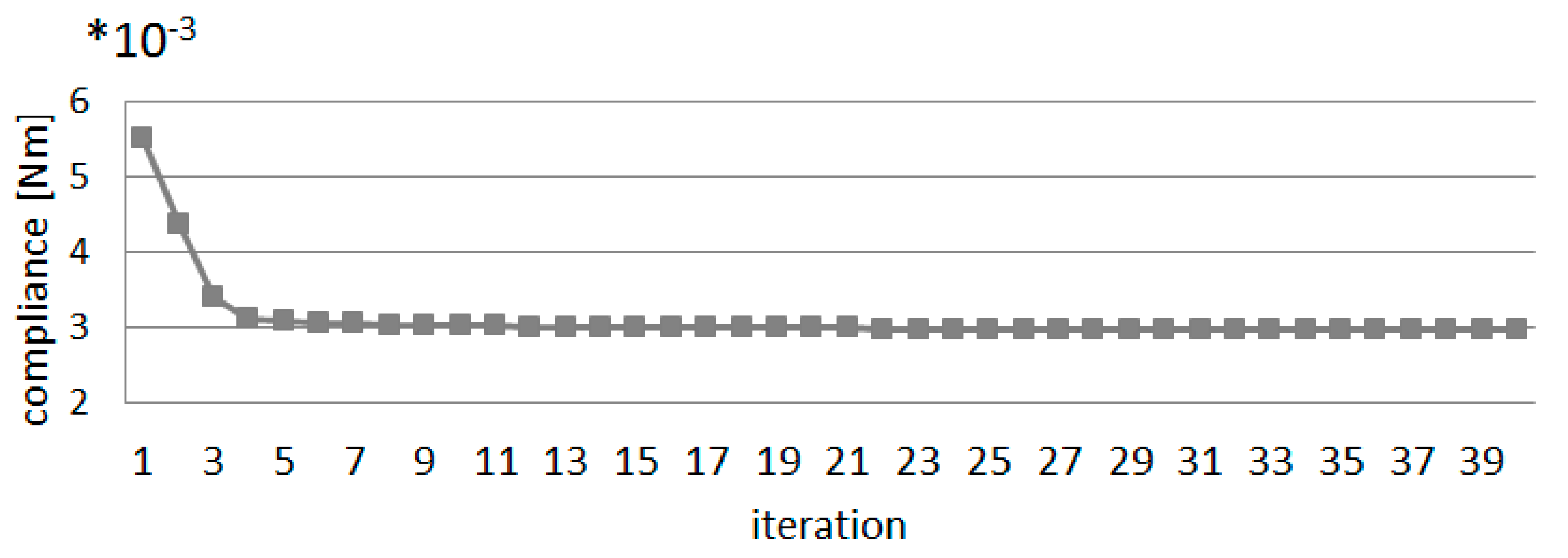
4.1.3. Topology Optimization of Multi-Material Structure under External Load and the Self-Weight
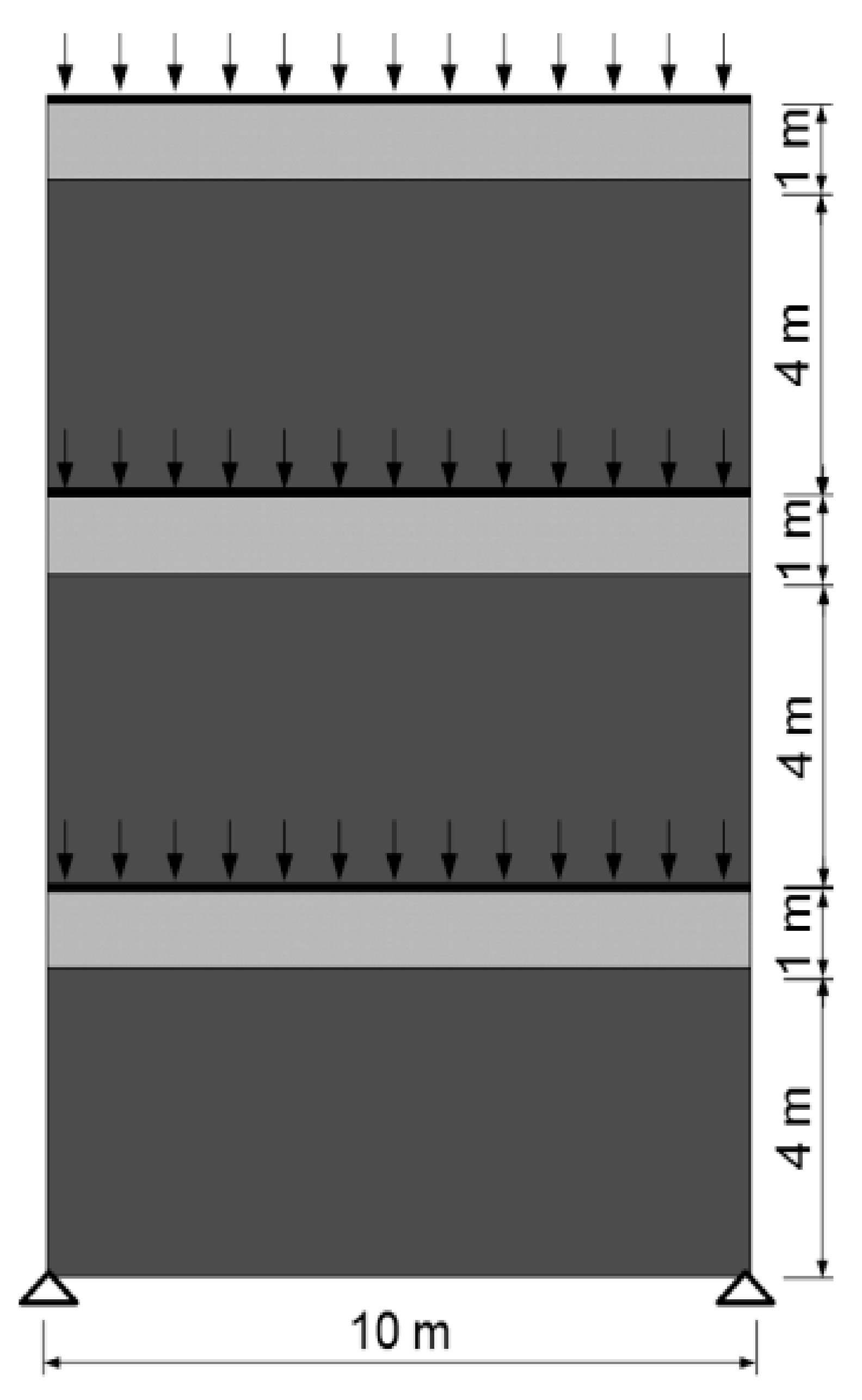
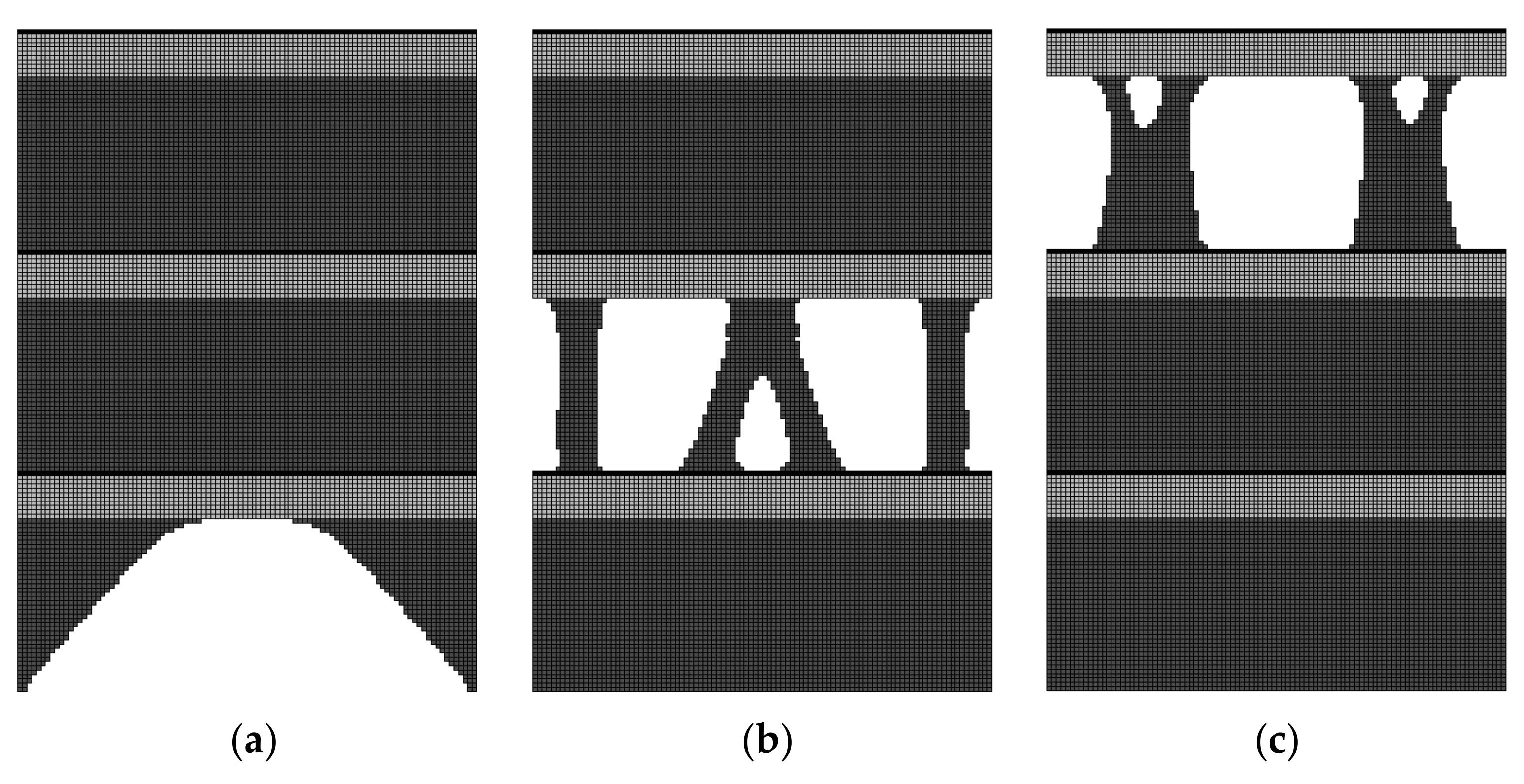
4.2. Example 2—Multi-Layer Structure
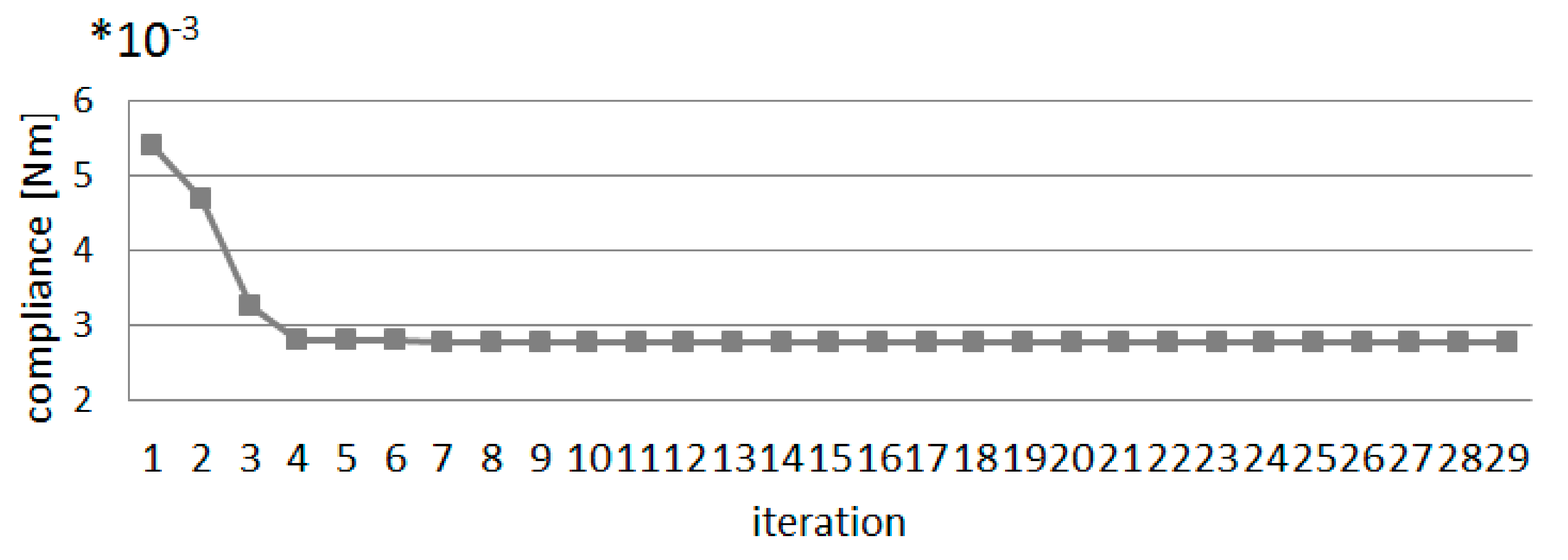
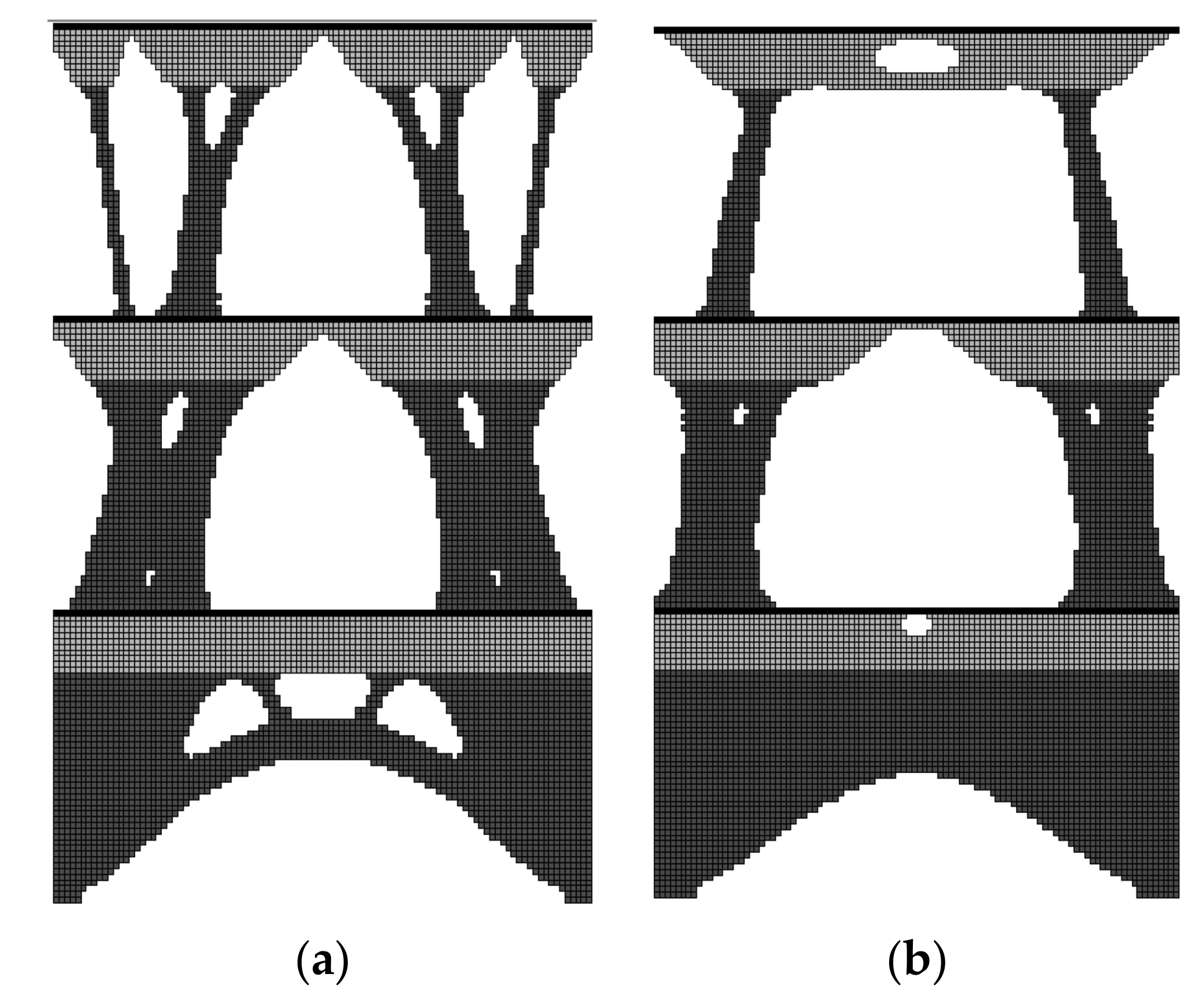
4.2.1. Topology Optimization of Multi-Material Multi-Layer Structure under External Load and Self-Weight
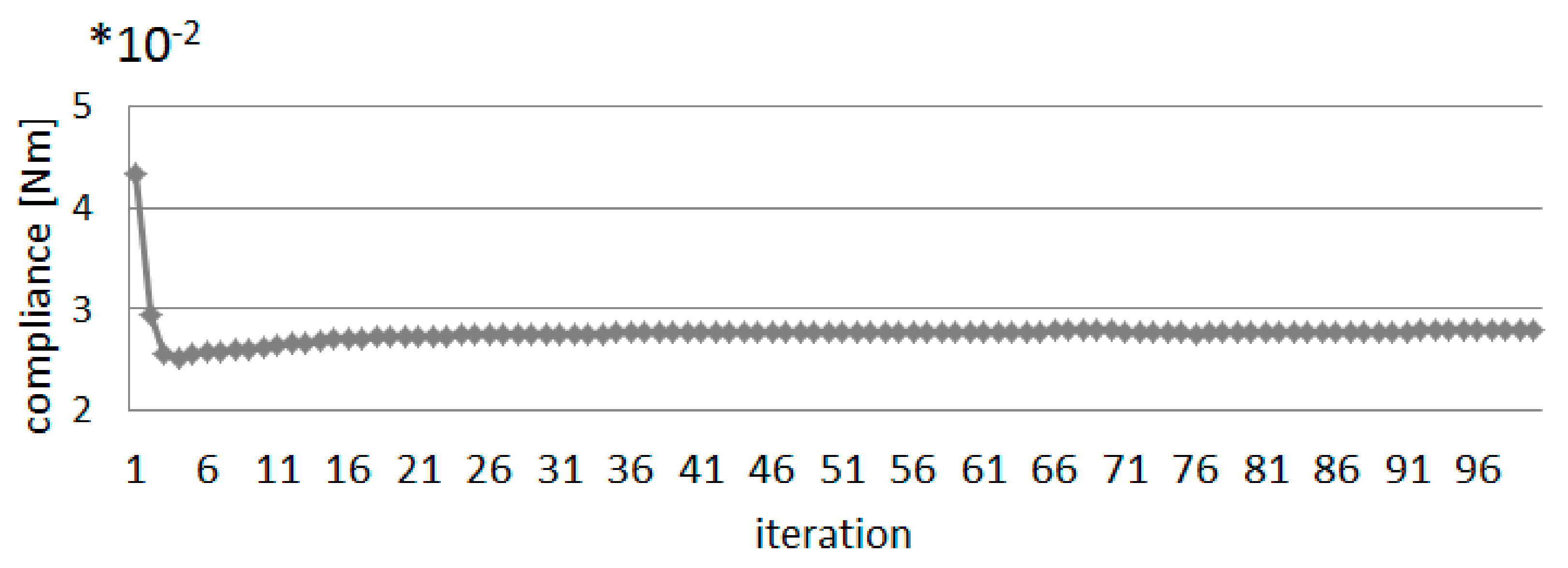
4.2.2. Topology Optimization of Multi-Material Multi-Layer Structure under External Load and Self-Weight—Design of the Reinforcement
5. Topology Optimization Techniques Adapted to Strengthening and Retrofitting of Civil Structures
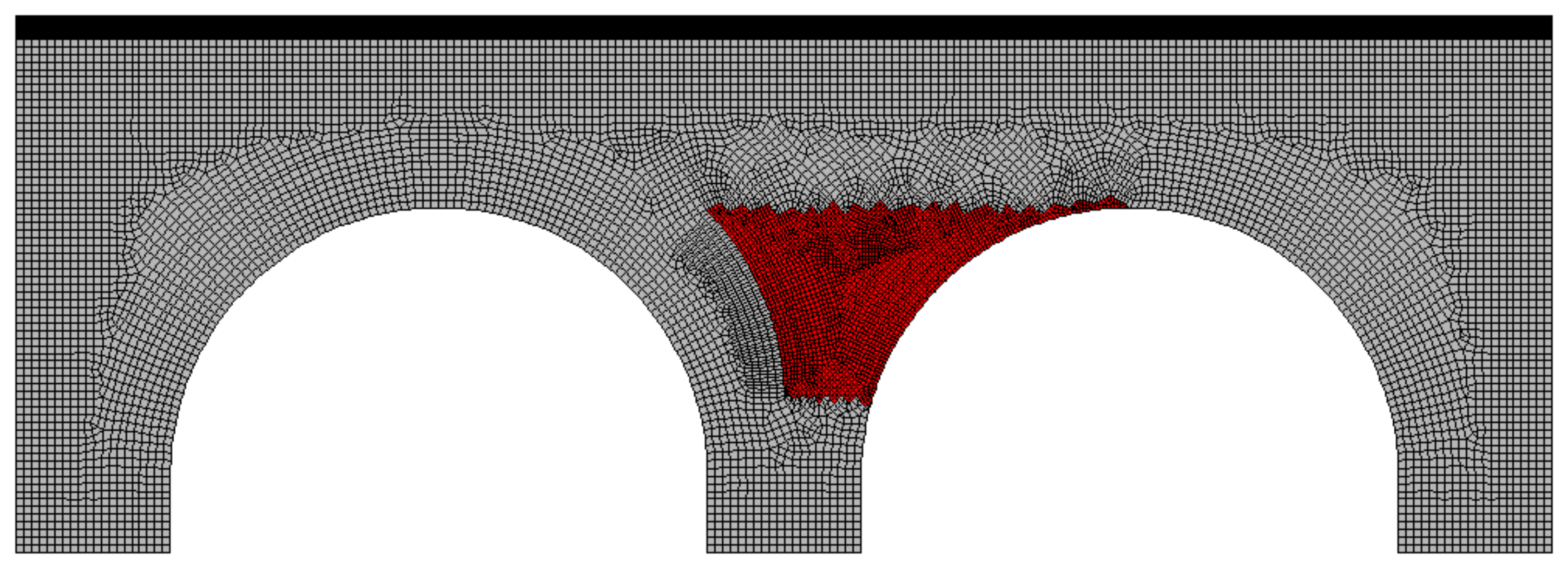
5.1. Strengthening of Structures Suffering from the Effects of Material Degradation
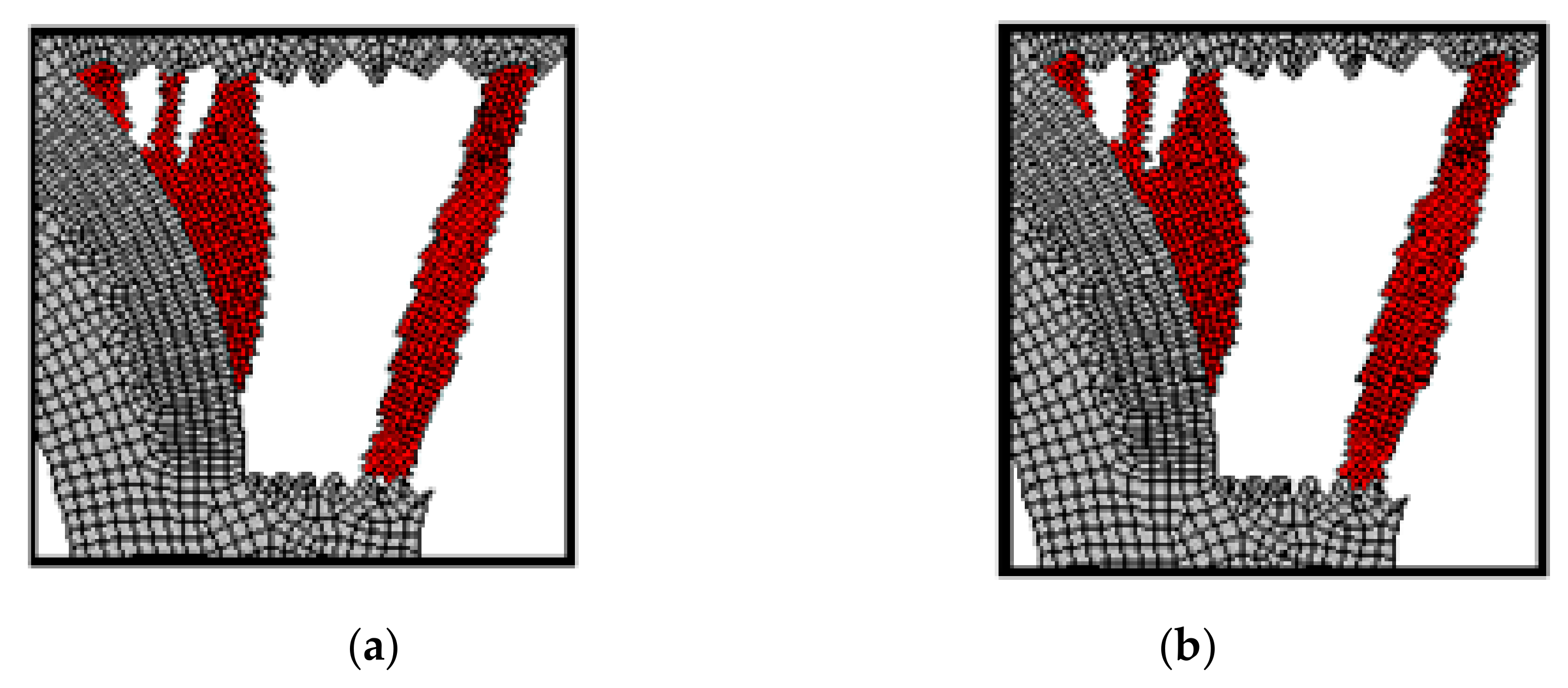
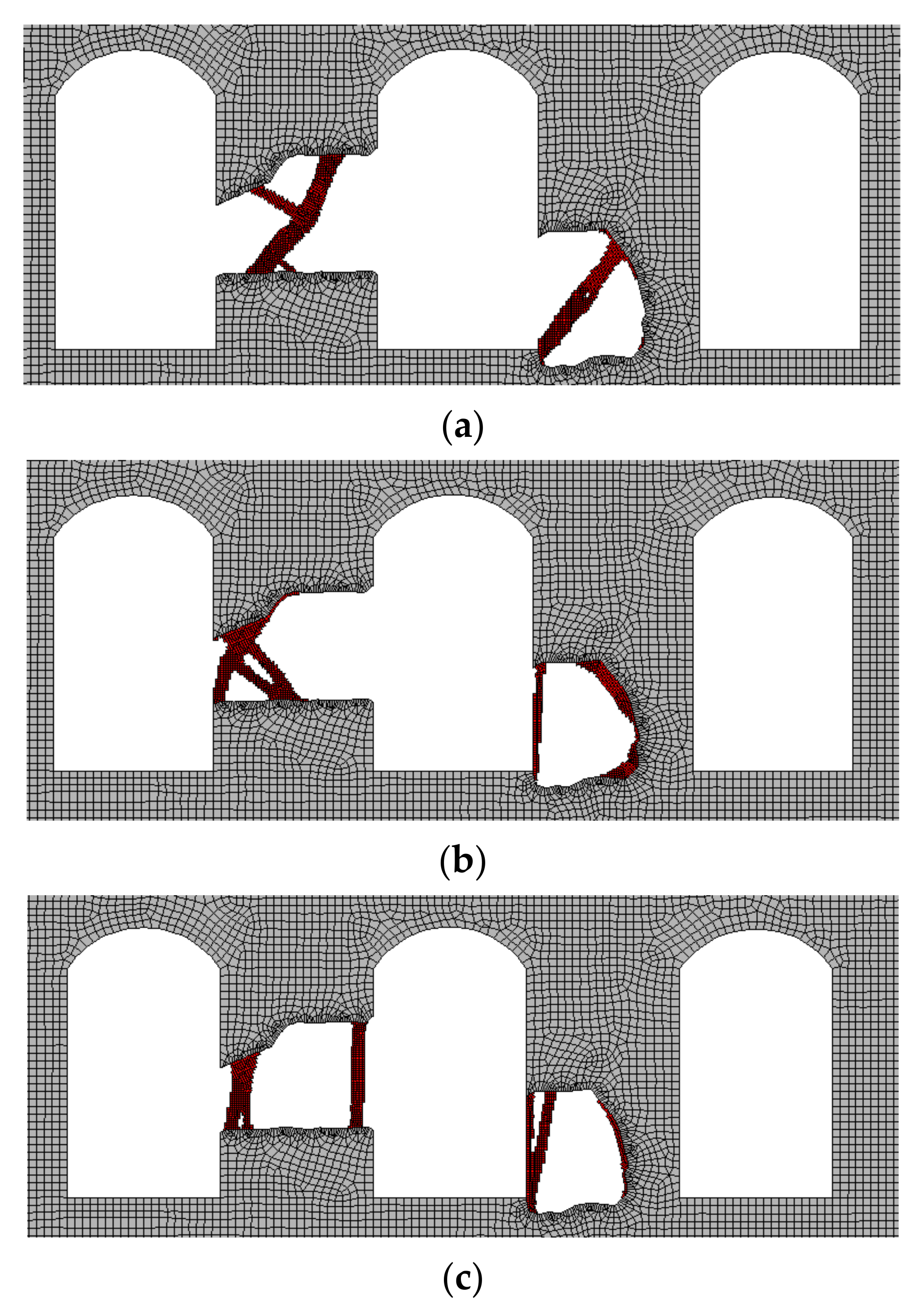
5.2. Strengthening of Structures Suffering from the Structural Damage—The Multiple-Load Case
5.3. Strengthening of the Multi-Material 3D Structures
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bendsoe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 line topology optimization code written in MATLAB. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schvenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in Matlab using 88 lines of code. Struct. Multidiscip. Optim. 2011, 4, 1–16. [Google Scholar] [CrossRef]
- Liu, K.; Tovar, A. An efficient 3D topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2014, 50, 1175–1196. [Google Scholar] [CrossRef]
- Xie, X.M.; Steven, G.P. Evolutionary Structural Optimisation; Springer: Berlin, Germany, 1997. [Google Scholar]
- Querin, Q.M.; Steven, G.P.; Xie, Y.M. Evolutionary structural optimization using a bi-directional algorithm. Eng. Comput. 1998, 15, 1034–1048. [Google Scholar] [CrossRef]
- Kane, C.; Jouve, F.; Schoenauer, M. Structural topology optimization in linear and nonlinear elasticity using genetic algorithms. In Proceedings of the 21st ASME Design Automatic Conference, Boston, MA, USA, 17–20 September 1995; pp. 1–8. [Google Scholar]
- Balamurugan, R.; Ramakrishnan, C.; Singh, N. Performance evaluation of a two stage adaptive genetic algorithm in structural topology optimization. Appl. Soft Comput. 2008, 8, 1607–1624. [Google Scholar] [CrossRef]
- Kaveh, A.; Hassani, B.; Shojaee, S.; Tavakkoli, S.M. Structural topology optimization using ant colony methodology. Eng. Struct. 2008, 30, 2559–2565. [Google Scholar] [CrossRef]
- Kobayashi, M.H. On a biologically inspired topology optimization method. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 787–802. [Google Scholar] [CrossRef]
- Chang, S.Y.; Youn, S.K. Material cloud method for topology optimization. Numer. Methods Eng. 2006, 65, 1585–1607. [Google Scholar] [CrossRef]
- Eschenauer, H.A.; Kobelev, V.V.; Schumacher, A. Bubble method for topology and shape optimization of structures. Struct. Optim. 1993, 8, 42–51. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, X.; Guo, D. A level set method for structural topology optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246. [Google Scholar] [CrossRef]
- Allaire, G.; Jouve, F.; Toader, A.M. Structural optimization using sensitivity analysis and a level-set method. J. Comput. Phys. 2004, 194, 363–393. [Google Scholar] [CrossRef]
- Otomori, M.; Yamada, T.; Izui, K.; Nishiwaki, S. Matlab code for a level set-based topology optimization method using a reaction diffusion equation. Struct. Multidiscip. Optim. 2015, 51, 1159–1172. [Google Scholar] [CrossRef]
- Wei, P.; Li, Z.; Li, X.; Wang, M.Y. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions. Struct. Multidiscip. Optim. 2018, 58, 831–849. [Google Scholar] [CrossRef]
- Biyikli, E.; To, A.C. Proportional topology optimization: A new non-sensitivity method for solving stress constrained and minimum compliance problems and its implementation in Matlab. PLoS ONE 2015, 10, e0145041. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, W.S.; Zhong, W.L. Doing topology optimization explicitly and geometrically—A new moving morphable components based framework. J. Appl. Mech. 2014, 81, 081009. [Google Scholar] [CrossRef]
- Zhang, W.; Yuan, J.; Zhang, J.; Guo, X. A new topology optimization approach based on Moving Morphable Components (MMC) and the ersatz material model. Struct. Multidiscip. Optim. 2016, 53, 1243–1260. [Google Scholar] [CrossRef]
- Gao, J.; Xue, H.; Gao, L.; Luo, Z. Topology optimization for auxetic metamaterials based on isogeometric analysis. Comput. Methods Appl. Mech. Engrg. 2019, 352, 211–236. [Google Scholar] [CrossRef]
- Xu, J.; Gao, L.; Xiao, M.; Xu, J.; Li, H. Isogeometric topology optimization for rational design of ultra-lightweight architected materials. Int. J. Mech. Sci. 2020, 166, 105103. [Google Scholar] [CrossRef]
- Gao, J.; Xiao, M.; Gao, L.; Yan, J.; Yan, W. Isogeometric topology optimization for computational design of re-entrant and chiral auxetic composites. Comput. Methods Appl. Mech. Engrg. 2020, 362, 112876. [Google Scholar] [CrossRef]
- Gao, J.; Luo, Z.; Xiao, M.; Gao, L.; Li, P. A NURBS-based Multi-Material Interpolation (N-MMI) for isogeometric topology optimization of structures. Appl. Math. Model. 2020, 81, 818–843. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Deaton, J.D.; Grandhi, R.V. A survey of structural and multidisciplinary continuum topology optimization: Post 2000. Struct. Multidiscip. Optim. 2014, 49, 1–38. [Google Scholar] [CrossRef]
- Sajjad Zargham, S.; Thomas Arthur Ward, T.A.; Rahizar Ramli, R.; Irfan Anjum Badruddin, I.A. Topology optimization: A review for structural designs under vibration problems. Struct. Multidiscip. Optim. 2016, 53, 1157–1177. [Google Scholar] [CrossRef]
- Liu, J.; Gaynor, A.T.; Chen, S.; Kang, Z.; Suresh, K.; Takezawa, A.; Li, L.; Kato, J.; Tang, J.; Wang, C.C.L.; et al. Current and future trends in topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 2018, 57, 2457–2483. [Google Scholar] [CrossRef]
- Wu, J.; Wu, L. Revised level set-based method for topology optimization and its applications in bridge construction. Open Civ. Eng. J. 2017, 11, 153–166. [Google Scholar] [CrossRef][Green Version]
- Xie, Y.; Zuo, Z.; Huang, X.; Black, T.; Felicetti, P. Application of topological optimization technology to bridge design. Struct. Eng. Int. 2014, 24, 185–191. [Google Scholar]
- Beghini, L.; Beghini, A.; Katz, N.; Baker, W.; Paulino, G. Connecting architecture and engineering through structural topology optimization. Eng. Struct. 2014, 59, 716–726. [Google Scholar] [CrossRef]
- Kingman, J.; Tsavdaridis, K.; Toropov, V. Applications of topology optimization in structural engineering: High-rise buildings and steel components. Jordan J. Civ. Eng. 2015, 9, 335–357. [Google Scholar]
- Dapogny, C.; Faure, A.; Michailidis, G.; Allaire, G.; Couvelas, A.; Estevez, R. Geometric constraints for shape and topology optimization in architectural design. Comput. Mech. 2017, 59, 933–965. [Google Scholar] [CrossRef]
- Aage, N.; Amir, O.; Clausen, A.; Hadar, L.; Maier, D.; Sondergaard, A. Advanced topology optimization methods for conceptual architectural design. In Advances in Architectural Geometry; Block, P., Knippers, J., Mitra, N., Wang, W., Eds.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Syngellakis, S. (Ed.) Retrofitting of Heritage Structures. Design and Evaluation of Strengthening Technique; WIT Press: Southampton, UK, 2016; p. 62. [Google Scholar]
- Costa, A.; Arêde, A.; Varum, H. (Eds.) Strengthening and Retrofitting of Existing Structures; Springer: Singapore, 2018. [Google Scholar]
- Bel Hadj Ali, N.; Rhode-Barbarigos, L.; Pascual Albi, A.A.; Smith, I.F.C. Design optimization and dynamic analysis of a tensegrity-based footbridge. Eng. Struct. 2010, 32, 3650–3659. [Google Scholar] [CrossRef]
- Montuori, R.; Skelton, R.E. Globally stable tensegrity compressive structures for arbitrary complexity. Compos. Struct. 2017, 179, 682–694. [Google Scholar] [CrossRef]
- Rozvany, G.I.N. Optimal plastic design: Allowance for self-weight. J. Eng. Mech. Div. 1977, 103, 1165–1170. [Google Scholar] [CrossRef]
- Bruyneel, M.; Duysinx, P. Note on topology optimization of continuum structures including self-weight. Struct. Multidiscip. Optim. 2005, 29, 245–256. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, S.; Xiong, Z. Topology optimization of 3d structures with design-dependent loads. Acta Mech. Sin. 2010, 26, 767–775. [Google Scholar] [CrossRef]
- Chen, B.C.; Kikuchi, N. Topology optimization with design-dependent loads. Finite Elem. Anal. Des. 2001, 37, 57–70. [Google Scholar] [CrossRef]
- Zhou, M.; Rozvany, G.I.N. The COC algorithm, Part II: Topological, geometry and generalized shape optimization. Comput. Methods Appl. Mech. Eng. 1991, 89, 197–224. [Google Scholar] [CrossRef]
- Felix, L.; Gomes, A.; Suleman, A. Wing topology optimization with self-weight loading. In Proceedings of the 10th World Congress on Structural and Multidisciplinary Optimization, Orlando, FL, USA, 19–24 May 2013; Furnish, M.D., Ed.; [Google Scholar]
- Tajs-Zielińska, K.; Bochenek, B. Topology Optimization—Engineering Contribution to Architectural Design. Iop Conf. Ser. Mater. Sci. Eng. 2017, 245, 082057. [Google Scholar] [CrossRef]
- Peraza-Hernandez, E.A.; Hartl, D.J.; Malak, R.J., Jr.; Lagoudas, D.C. Origami-inspired active structures: A synthesis and review. Smart Mater. Struct. 2014, 23, 094001. [Google Scholar] [CrossRef]
- Farzampour, A.; Khatibinia, M.; Mansouri, I. Shape optimization of butterfly-shaped shear links using Grey Wolf algorithm. Ing. Sism. 2019, 36, 27–41. [Google Scholar]
- Tajs-Zielińska, K.; Bochenek, B. CARMA—Cellular Automata with Refined Mesh Adaptation—The Easy Way of Generation of Structural Topologies. Appl. Sci. 2020, 10, 3691. [Google Scholar] [CrossRef]
- Bochenek, B.; Tajs-Zielińska, K. Novel local rules of cellular automata applied to topology and size optimization. Eng. Optim. 2012, 44, 23–35. [Google Scholar] [CrossRef]
- Tajs-Zielinska, K.; Bochenek, B. Novel Topology Optimization Techniques Adapted to Strengthening of Civil Structures Suffering from the Effects of Material Degradation. Iop Conf. Ser. Mater. Sci. Eng. 2019, 471, 052010. [Google Scholar] [CrossRef]





















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tajs-Zielińska, K.; Bochenek, B. Multi-Domain and Multi-Material Topology Optimization in Design and Strengthening of Innovative Sustainable Structures. Sustainability 2021, 13, 3435. https://doi.org/10.3390/su13063435
Tajs-Zielińska K, Bochenek B. Multi-Domain and Multi-Material Topology Optimization in Design and Strengthening of Innovative Sustainable Structures. Sustainability. 2021; 13(6):3435. https://doi.org/10.3390/su13063435
Chicago/Turabian StyleTajs-Zielińska, Katarzyna, and Bogdan Bochenek. 2021. "Multi-Domain and Multi-Material Topology Optimization in Design and Strengthening of Innovative Sustainable Structures" Sustainability 13, no. 6: 3435. https://doi.org/10.3390/su13063435
APA StyleTajs-Zielińska, K., & Bochenek, B. (2021). Multi-Domain and Multi-Material Topology Optimization in Design and Strengthening of Innovative Sustainable Structures. Sustainability, 13(6), 3435. https://doi.org/10.3390/su13063435





