Synthesizing Multi-Layer Perceptron Network with Ant Lion Biogeography-Based Dragonfly Algorithm Evolutionary Strategy Invasive Weed and League Champion Optimization Hybrid Algorithms in Predicting Heating Load in Residential Buildings
Abstract
1. Introduction
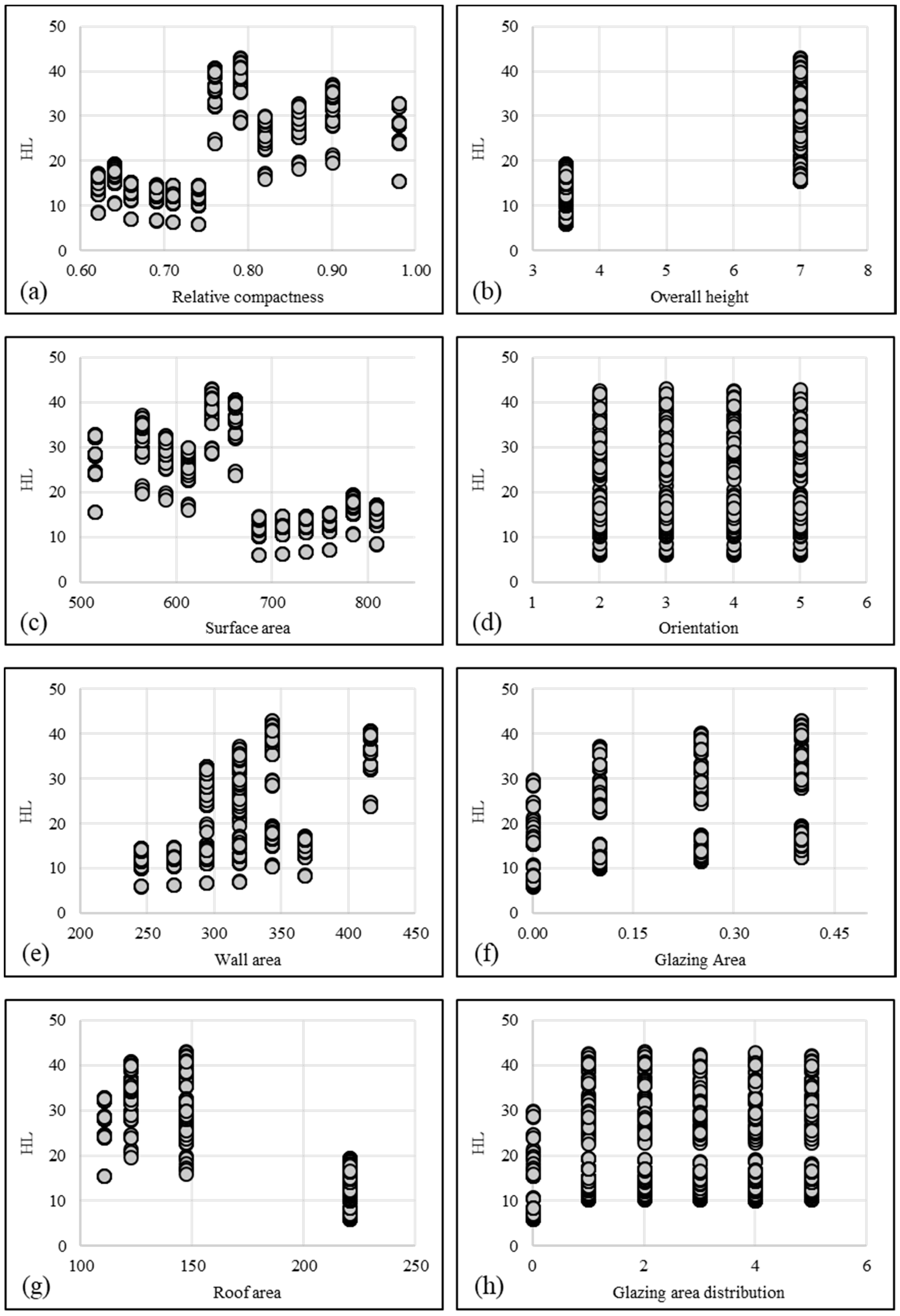
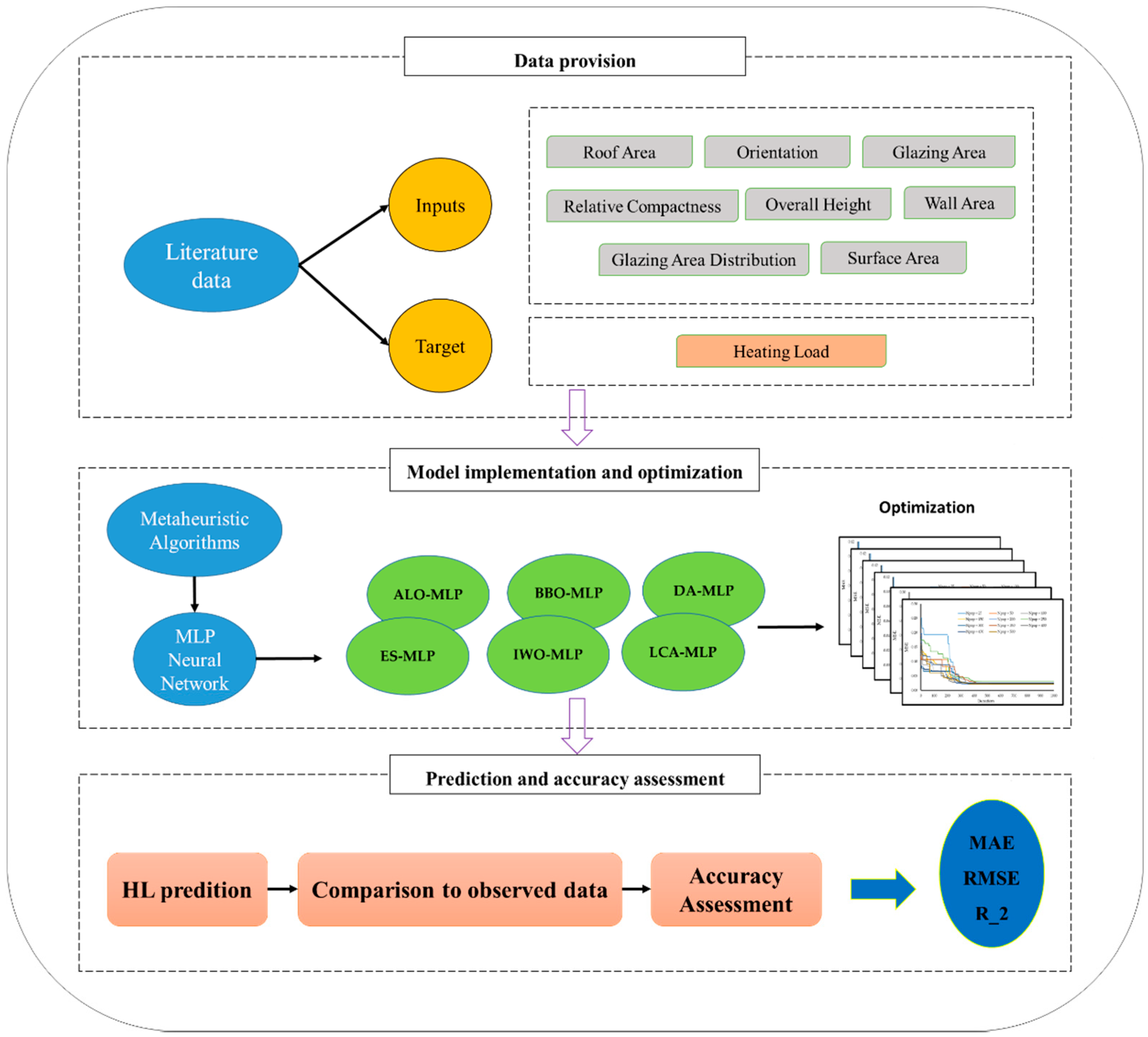
2. Data Provision and Analysis
3. Methodology
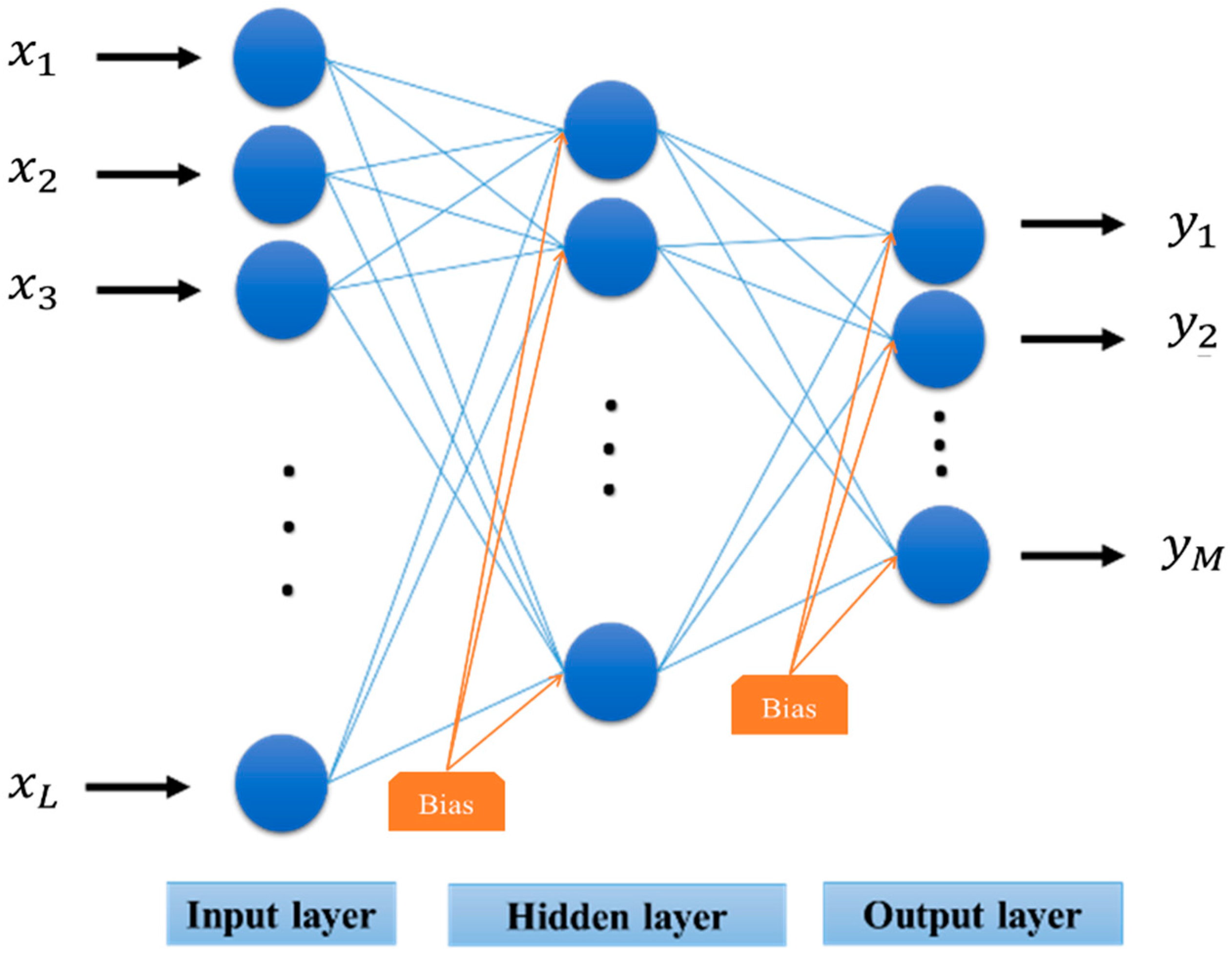
3.1. Artificial Neural Network
3.2. Swarm-Based Metaheuristic Ideas
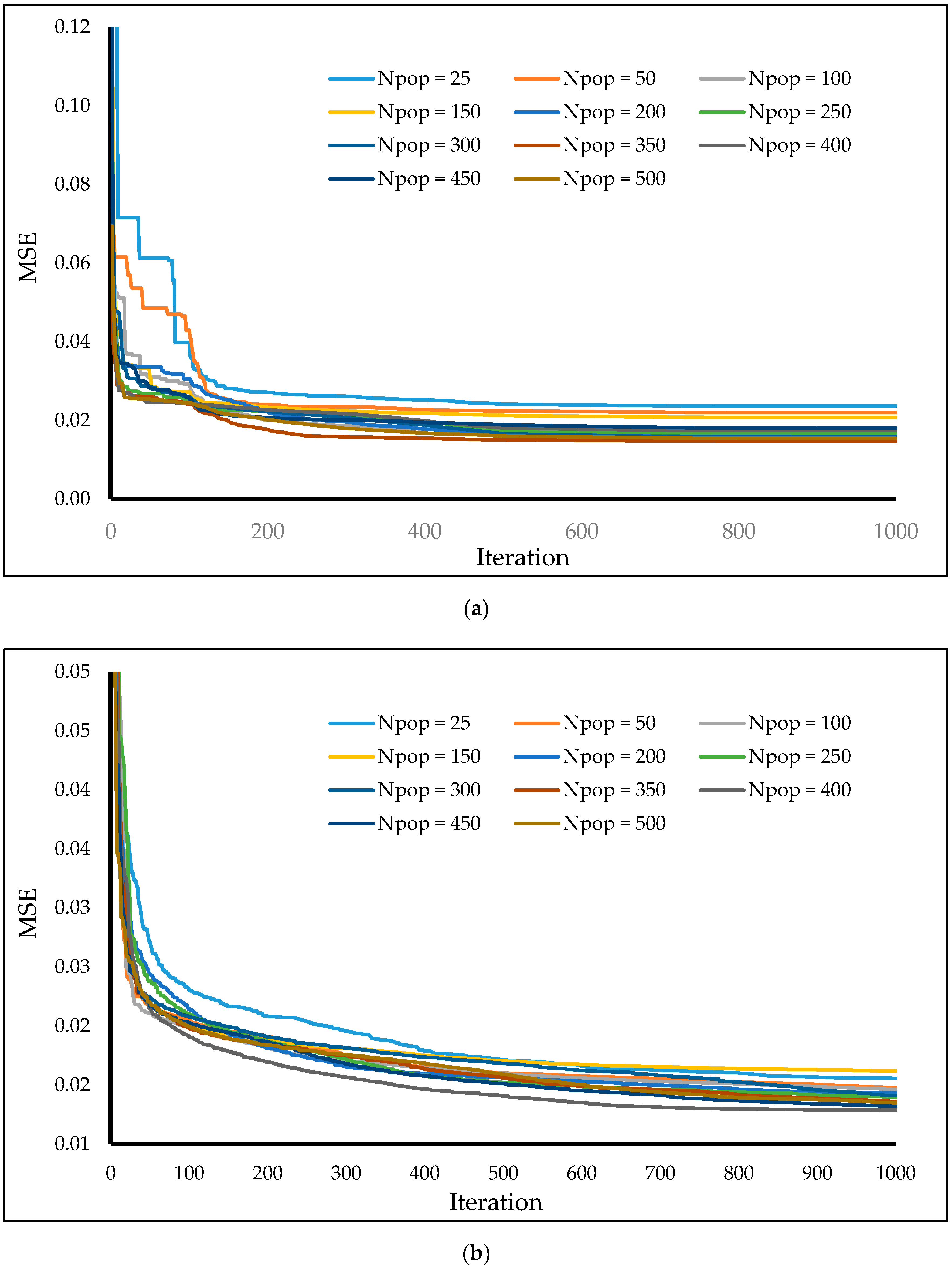
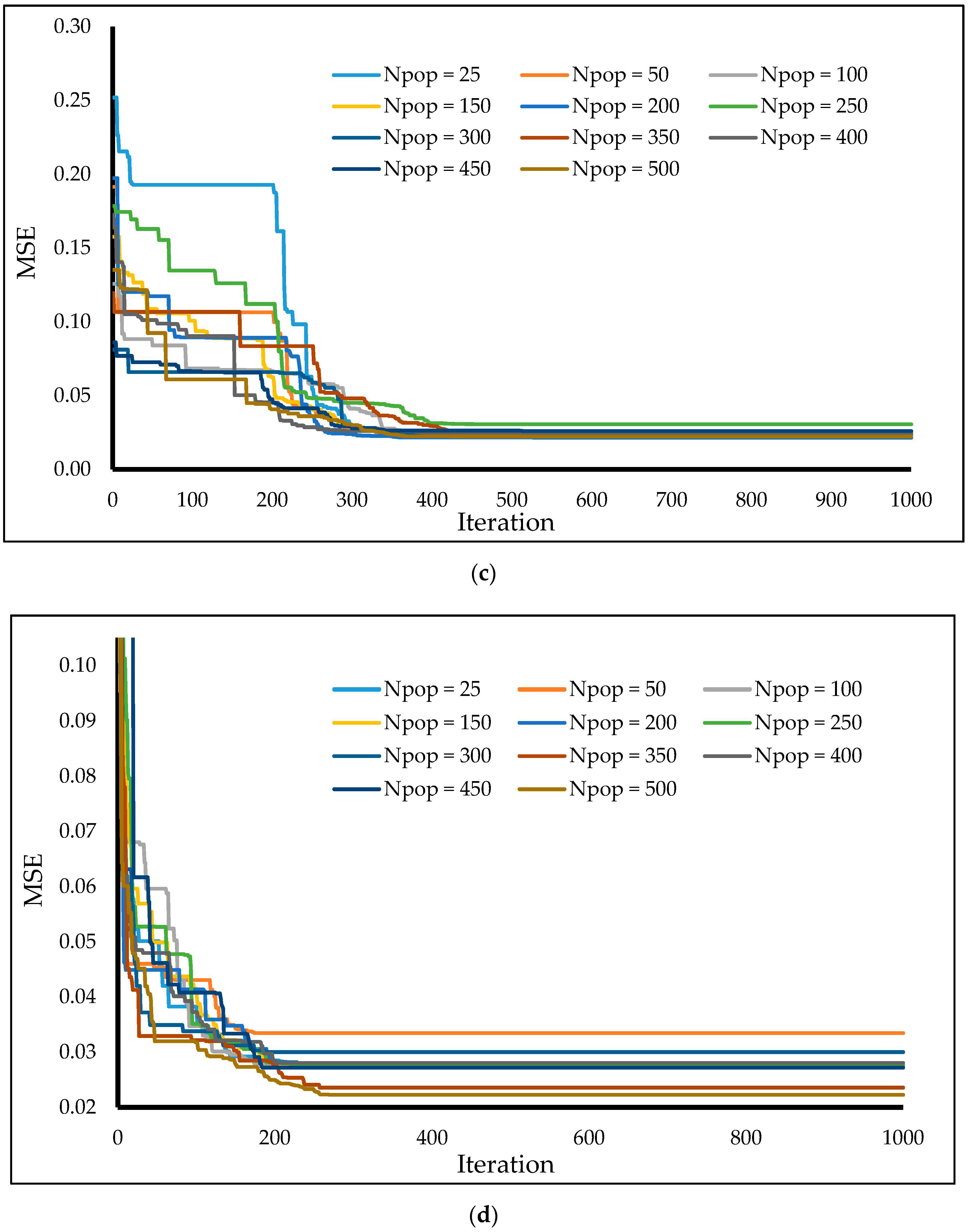
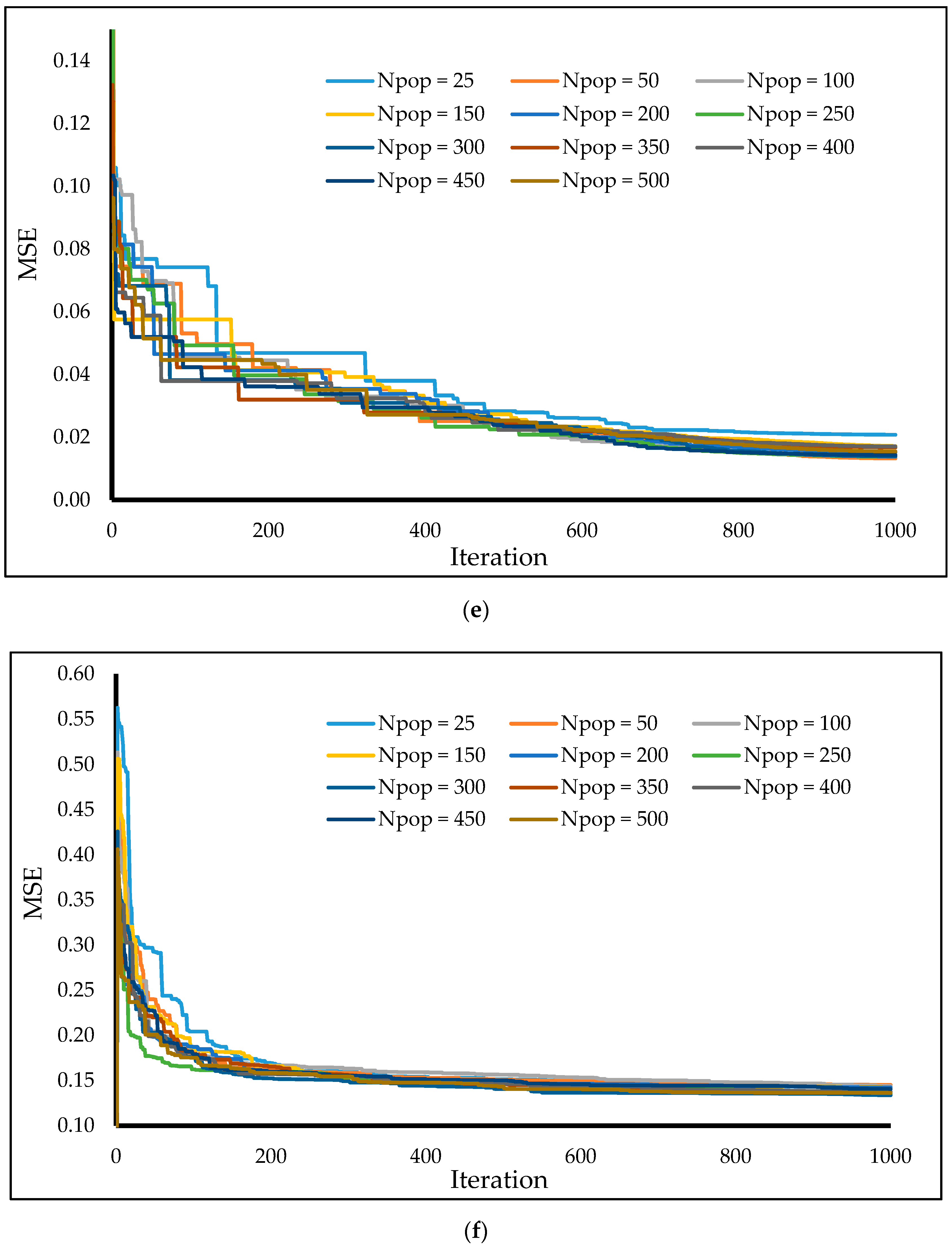
3.3. Hybridization Process and Sensitivity Analysis
4. Results and Discussion
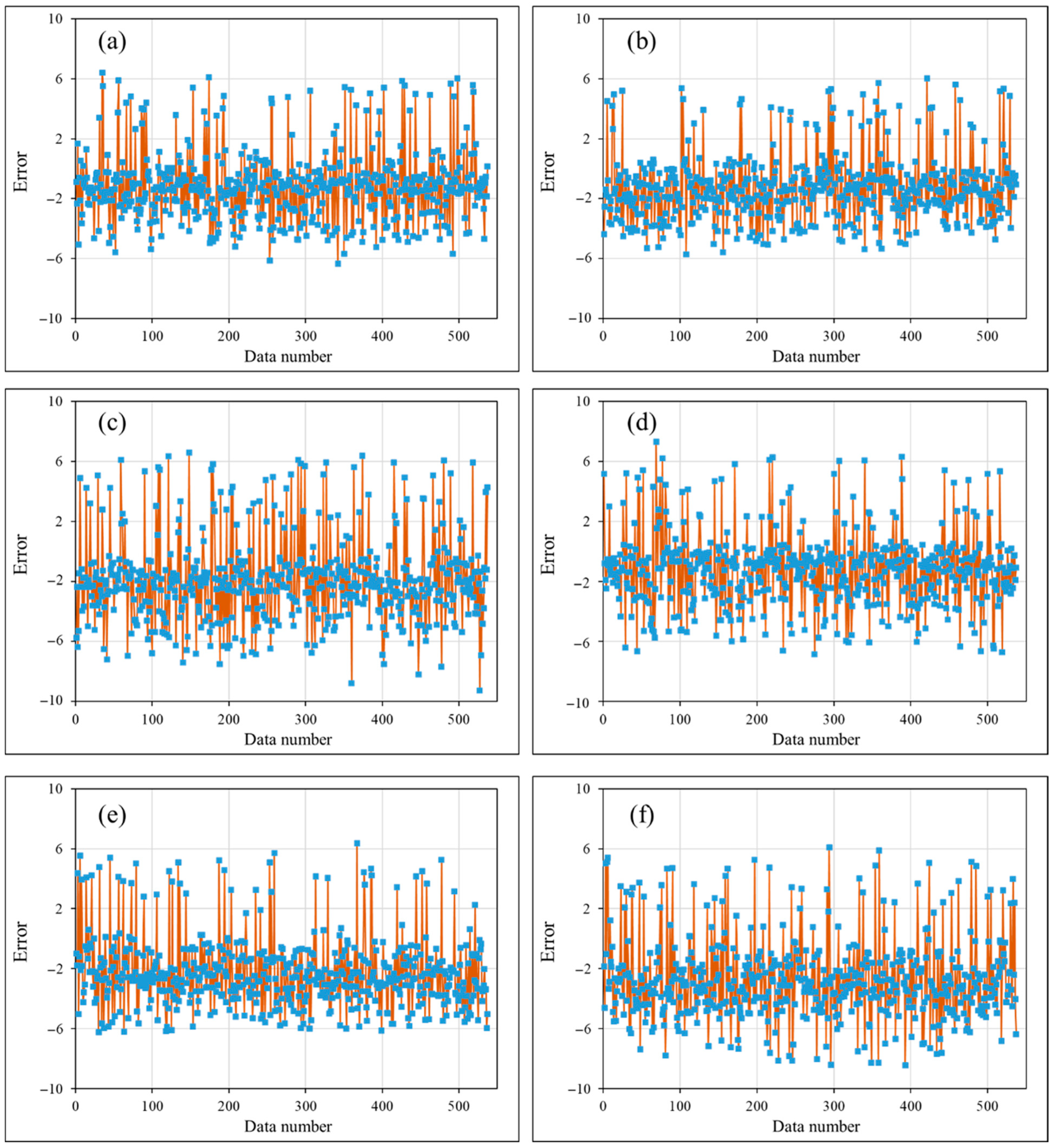
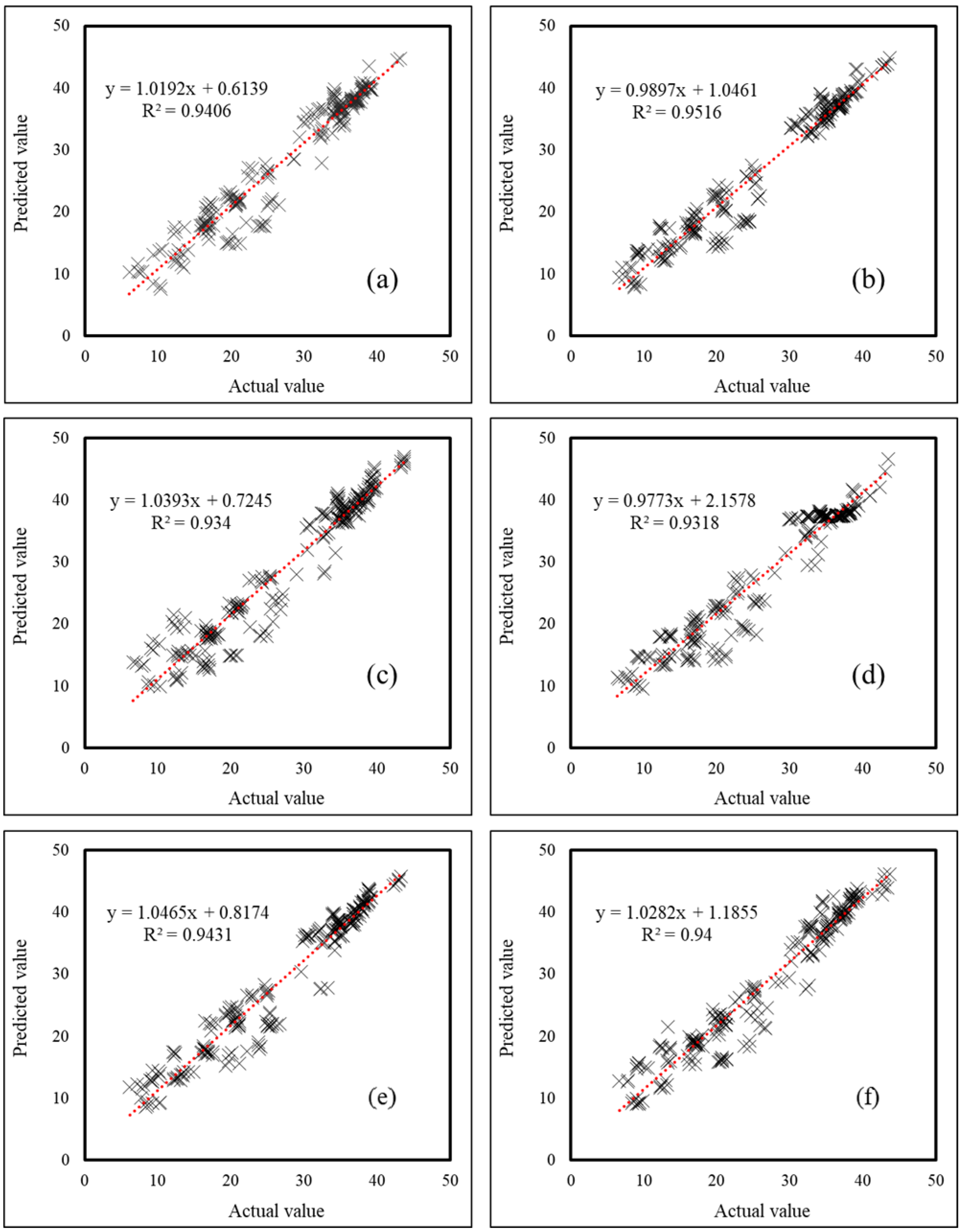
4.1. Statistical Accuracy Assessment
4.2. Training Results
4.3. Validation Results
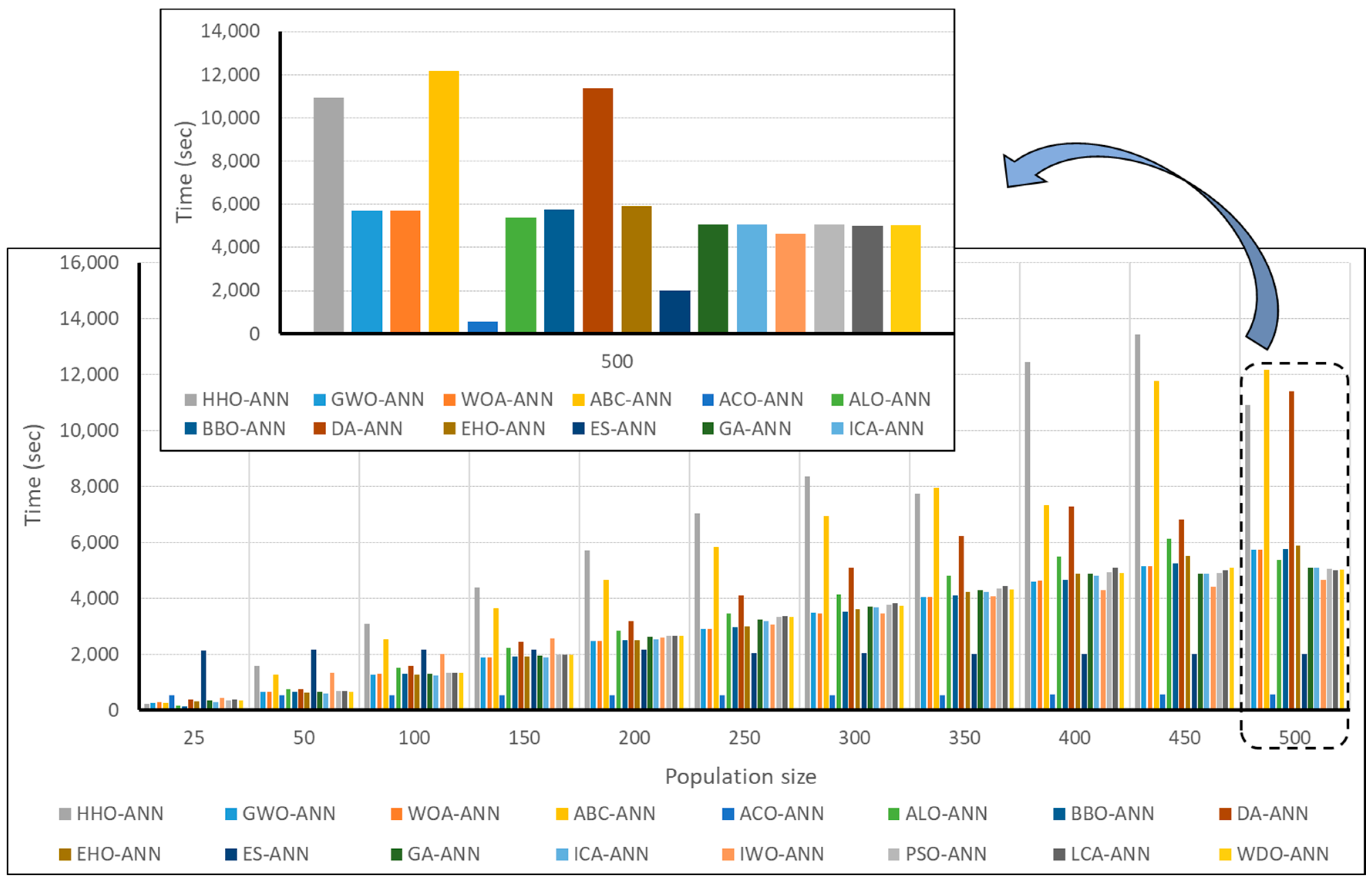
4.4. Score-Based Comparison and Time Efficiency
4.5. Presenting the HL Predictive Equation
4.6. Further Discussion and Future Works
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. Key World Energy Statistics; International Energy Agency: Paris, France, 2015. [Google Scholar]
- McQuiston, F.C.; Parker, J.D.; Spitler, J.D. Heating, Ventilating, and Air Conditioning: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Turhan, C.; Kazanasmaz, T.; Uygun, I.E.; Ekmen, K.E.; Akkurt, G.G. Comparative study of a building energy performance software (KEP-IYTE-ESS) and ANN-based building heat load estimation. Energy Build. 2014, 85, 115–125. [Google Scholar] [CrossRef]
- Catalina, T.; Iordache, V.; Caracaleanu, B. Multiple regression model for fast prediction of the heating energy demand. Energy Build. 2013, 57, 302–312. [Google Scholar] [CrossRef]
- Geysen, D.; De Somer, O.; Johansson, C.; Brage, J.; Vanhoudt, D. Operational thermal load forecasting in district heating networks using machine learning and expert advice. Energy Build. 2018, 162, 144–153. [Google Scholar] [CrossRef]
- Liu, S.; Chan, F.T.; Ran, W. Decision making for the selection of cloud vendor: An improved approach under group decision-making with integrated weights and objective/subjective attributes. Expert Syst. Appl. 2016, 55, 37–47. [Google Scholar] [CrossRef]
- Tian, P.; Lu, H.; Feng, W.; Guan, Y.; Xue, Y. Large decrease in streamflow and sediment load of Qinghai–Tibetan Plateau driven by future climate change: A case study in Lhasa River Basin. Catena 2020, 187, 104340. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, J.; Wu, J.; Shi, W.; Ji, D.; Wang, X.; Zhao, X. Constraints Hindering the Development of High-Rise Modular Buildings. Appl. Sci. 2020, 10, 7159. [Google Scholar] [CrossRef]
- Liu, S.; Yu, W.; Chan, F.T.S.; Niu, B. A variable weight-based hybrid approach for multi-attribute group decision making under interval-valued intuitionistic fuzzy sets. Int. J. Intell. Syst. 2021, 36, 1015–1052. [Google Scholar] [CrossRef]
- Liu, Z.; Shao, J.; Xu, W.; Chen, H.; Zhang, Y. An extreme learning machine approach for slope stability evaluation and prediction. Nat. Hazards 2014, 73, 787–804. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Osuch, M.; Napiorkowski, M.J.; Rowinski, P.M.; Napiórkowski, J.J. Comparing large number of metaheuristics for artificial neural networks training to predict water temperature in a natural river. Comput. Geosci. 2014, 64, 136–151. [Google Scholar] [CrossRef]
- Liu, J.; Wu, C.; Wu, G.; Wang, X. A novel differential search algorithm and applications for structure design. Appl. Math. Comput. 2015, 268, 246–269. [Google Scholar] [CrossRef]
- Feng, S.; Lu, H.; Tian, P.; Xue, Y.; Lu, J.; Tang, M.; Feng, W. Analysis of microplastics in a remote region of the Tibetan Plateau: Implications for natural environmental response to human activities. Sci. Total. Environ. 2020, 739, 140087. [Google Scholar] [CrossRef]
- Fu, X.; Fortino, G.; Pace, P.; Aloi, G.; Li, W. Environment-fusion multipath routing protocol for wireless sensor networks. Inf. Fusion 2020, 53, 4–19. [Google Scholar] [CrossRef]
- Han, X.; Zhang, D.; Yan, J.; Zhao, S.; Liu, J. Process development of flue gas desulphurization wastewater treatment in coal-fired power plants towards zero liquid discharge: Energetic, economic and environmental analyses. J. Clean. Prod. 2020, 261, 121144. [Google Scholar] [CrossRef]
- He, L.; Chen, Y.; Zhao, H.; Tian, P.; Xue, Y.; Chen, L. Game-based analysis of energy-water nexus for identifying environmental impacts during Shale gas operations under stochastic input. Sci. Total. Environ. 2018, 627, 1585–1601. [Google Scholar] [CrossRef]
- He, L.; Shen, J.; Zhang, Y. Ecological vulnerability assessment for ecological conservation and environmental management. J. Environ. Manag. 2018, 206, 1115–1125. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Wang, X. An environmental assessment model of construction and demolition waste based on system dynamics: A case study in Guangzhou. Environ. Sci. Pollut. Res. 2019, 27, 37237–37259. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Y.; Wang, Q.; Liu, C.; Zhi, Q.; Cao, J. Changes in air quality related to the control of coronavirus in China: Implications for traffic and industrial emissions. Sci. Total. Environ. 2020, 731, 139133. [Google Scholar] [CrossRef]
- Liu, L.; Li, J.; Yue, F.; Yan, X.; Wang, F.; Bloszies, S.; Wang, Y. Effects of arbuscular mycorrhizal inoculation and biochar amendment on maize growth, cadmium uptake and soil cadmium speciation in Cd-contaminated soil. Chemosphere 2018, 194, 495–503. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Liu, J.; Yao, J.; Kou, J.; Li, Z.; Wu, T.; Zhang, K.; Zhang, L.; Sun, H. Adsorption behaviors of shale oil in kerogen slit by molecular simulation. Chem. Eng. J. 2020, 387, 124054. [Google Scholar] [CrossRef]
- Liu, J.; Yi, Y.; Wang, X. Exploring factors influencing construction waste reduction: A structural equation modeling approach. J. Clean. Prod. 2020, 276, 123185. [Google Scholar] [CrossRef]
- Sun, L.; Li, C.; Zhang, C.; Liang, T.; Zhao, Z. The Strain Transfer Mechanism of Fiber Bragg Grating Sensor for Extra Large Strain Monitoring. Sensors 2019, 19, 1851. [Google Scholar] [CrossRef] [PubMed]
- Su, Z.; Liu, E.; Xu, Y.; Xie, P.; Shang, C.; Zhu, Q. Flow field and noise characteristics of manifold in natural gas transportation station. Oil Gas Sci. Technol. Rev. IFP 2019, 74, 70. [Google Scholar] [CrossRef]
- Liu, E.; Lv, L.; Yi, Y.; Xie, P. Research on the Steady Operation Optimization Model of Natural Gas Pipeline Considering the Combined Operation of Air Coolers and Compressors. IEEE Access 2019, 7, 83251–83265. [Google Scholar] [CrossRef]
- Keshtegar, B.; Heddam, S.; Sebbar, A.; Zhu, S.-P.; Trung, N.-T. SVR-RSM: A hybrid heuristic method for modeling monthly pan evaporation. Environ. Sci. Pollut. Res. 2019, 26, 35807–35826. [Google Scholar] [CrossRef] [PubMed]
- Ghaemi, A.; Rezaie-Balf, M.; Adamowski, J.; Kisi, O.; Quilty, J. On the applicability of maximum overlap discrete wavelet transform integrated with MARS and M5 model tree for monthly pan evaporation prediction. Agric. For. Meteorol. 2019, 278, 107647. [Google Scholar] [CrossRef]
- Kisi, O.; Heddam, S. Evaporation modelling by heuristic regression approaches using only temperature data. Hydrol. Sci. J. 2019, 64, 653–672. [Google Scholar] [CrossRef]
- Roy, D.K.; Barzegar, R.; Quilty, J.; Adamowski, J. Using ensembles of adaptive neuro-fuzzy inference system and optimization algorithms to predict reference evapotranspiration in subtropical climatic zones. J. Hydrol. 2020, 591, 125509. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, D.; Liu, Y.; Li, F.; Cai, J.; Du, L. Multi-scale evapotranspiration of summer maize and the controlling meteorological factors in north China. Agric. For. Meteorol. 2016, 216, 1–12. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Li, Z.; Zhu, Y.; Wang, J.; Yu, Z. Geographically weighted regression based methods for merging satellite and gauge precipitation. J. Hydrol. 2018, 558, 275–289. [Google Scholar] [CrossRef]
- Chen, Y.; He, L.; Guan, Y.; Lu, H.; Li, J. Life cycle assessment of greenhouse gas emissions and water-energy optimization for shale gas supply chain planning based on multi-level approach: Case study in Barnett, Marcellus, Fayetteville, and Haynesville shales. Energy Convers. Manag. 2017, 134, 382–398. [Google Scholar] [CrossRef]
- He, L.; Chen, Y.; Li, J. A three-level framework for balancing the tradeoffs among the energy, water, and air-emission implications within the life-cycle shale gas supply chains. Resour. Conserv. Recycl. 2018, 133, 206–228. [Google Scholar] [CrossRef]
- Lu, H.; Tian, P.; He, L. Evaluating the global potential of aquifer thermal energy storage and determining the potential worldwide hotspots driven by socio-economic, geo-hydrologic and climatic conditions. Renew. Sustain. Energy Rev. 2019, 112, 788–796. [Google Scholar] [CrossRef]
- Wu, C.; Wu, P.; Wang, J.; Jiang, R.; Chen, M.; Wang, X. Critical review of data-driven decision-making in bridge operation and maintenance. Struct. Infrastruct. Eng. 2020, 1–24. [Google Scholar] [CrossRef]
- Zhu, L.; Kong, L.; Zhang, C. Numerical Study on Hysteretic Behaviour of Horizontal-Connection and Energy-Dissipation Structures Developed for Prefabricated Shear Walls. Appl. Sci. 2020, 10, 1240. [Google Scholar] [CrossRef]
- Zhao, X.; Ye, Y.; Ma, J.; Shi, P.; Chen, H. Construction of electric vehicle driving cycle for studying electric vehicle energy consumption and equivalent emissions. Environ. Sci. Pollut. Res. 2020, 27, 37395–37409. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, T.; Sharma, B.K.; Nie, H. Optimization and mechanism studies on cell disruption and phosphorus recovery from microalgae with magnesium modified hydrochar in assisted hydrothermal system. Sci. Total. Environ. 2019, 646, 1140–1154. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, X.; Fan, X.; Tsang, D.C.; Li, G.; Shen, Y. Corn waste valorization to generate activated hydrochar to recover ammonium nitrogen from compost leachate by hydrothermal assisted pretreatment. J. Environ. Manag. 2019, 236, 108–117. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Lu, H.; Yan, P. Coupling system dynamics analysis and risk aversion programming for optimizing the mixed noise-driven shale gas-water supply chains. J. Clean. Prod. 2021, 278, 123209. [Google Scholar] [CrossRef]
- Cheng, X.; He, L.; Lu, H.; Chen, Y.; Ren, L. Optimal water resources management and system benefit for the Marcellus shale-gas reservoir in Pennsylvania and West Virginia. J. Hydrol. 2016, 540, 412–422. [Google Scholar] [CrossRef]
- Li, L.-L.; Liu, Y.-W.; Tseng, M.-L.; Lin, G.-Q.; Ali, M.H. Reducing environmental pollution and fuel consumption using optimization algorithm to develop combined cooling heating and power system operation strategies. J. Clean. Prod. 2020, 247, 119082. [Google Scholar] [CrossRef]
- Qian, J.; Feng, S.; Tao, T.; Hu, Y.; Li, Y.; Chen, Q.; Zuo, C. Deep-learning-enabled geometric constraints and phase unwrapping for single-shot absolute 3D shape measurement. APL Photon 2020, 5, 46105. [Google Scholar] [CrossRef]
- Quan, Q.; Hao, Z.; Huang, X.; Lei, J. Research on water temperature prediction based on improved support vector regression. Neural Comput. Appl. 2020, 1–10. [Google Scholar] [CrossRef]
- Yang, M.; Sowmya, A. An Underwater Color Image Quality Evaluation Metric. IEEE Trans. Image Process. 2015, 24, 6062–6071. [Google Scholar] [CrossRef]
- Cao, B.; Fan, S.; Zhao, J.; Yang, P.; Muhammad, K.; Tanveer, M. Quantum-enhanced multiobjective large-scale optimization via parallelism. Swarm Evol. Comput. 2020, 57, 100697. [Google Scholar] [CrossRef]
- Qian, J.M.; Feng, S.; Li, Y.; Tao, T.; Han, J.; Chen, Q.; Zuo, C. Single-shot absolute 3D shape measurement with deep-learning-based color fringe projection profilometry. Opt. Lett. 2020, 45, 1842–1845. [Google Scholar] [CrossRef]
- Lyu, Z.; Chai, J.; Xu, Z.; Qin, Y.; Cao, J. A Comprehensive Review on Reasons for Tailings Dam Failures Based on Case History. Adv. Civ. Eng. 2019, 2019, 1–18. [Google Scholar] [CrossRef]
- Feng, W.; Lu, H.; Yao, T.; Yu, Q. Drought characteristics and its elevation dependence in the Qinghai–Tibet plateau during the last half-century. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef]
- Yan, J.; Pu, W.; Zhou, S.; Liu, H.; Bao, Z. Collaborative detection and power allocation framework for target tracking in multiple radar system. Inf. Fusion 2020, 55, 173–183. [Google Scholar] [CrossRef]
- Xiong, Z.; Tang, Z.; Chen, X.; Zhang, X.-M.; Zhang, K.; Ye, C. Research on Image Retrieval Algorithm Based on Combination of Color and Shape Features. J. Signal Process. Syst. 2019, 1–8. [Google Scholar] [CrossRef]
- Zhu, Q. Research on Road Traffic Situation Awareness System Based on Image Big Data. IEEE Intell. Syst. 2019, 35, 18–26. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J.; Shou, W.; Ngo, T.; Sadick, A.-M.; Wang, X. Computer Vision Techniques in Construction: A Critical Review. Arch. Comput. Methods Eng. 2020, 1–15. [Google Scholar] [CrossRef]
- Sun, L.; Yang, Z.; Jin, Q.; Yan, W. Effect of Axial Compression Ratio on Seismic Behavior of GFRP Reinforced Concrete Columns. Int. J. Struct. Stab. Dyn. 2020, 20, 2040004. [Google Scholar] [CrossRef]
- Chao, M.; Kai, C.; Zhang, Z. Research on tobacco foreign body detection device based on machine vision. Trans. Inst. Meas. Control. 2020, 42, 2857–2871. [Google Scholar] [CrossRef]
- Liu, D.; Wang, S.; Huang, D.; Deng, G.; Zeng, F.; Chen, H. Medical image classification using spatial adjacent histogram based on adaptive local binary patterns. Comput. Biol. Med. 2016, 72, 185–200. [Google Scholar] [CrossRef] [PubMed]
- Abedini, M.; Mutalib, A.A.; Zhang, C.; Mehrmashhadi, J.; Raman, S.N.; Alipour, R.; Momeni, T.; Mussa, M.H. Large deflection behavior effect in reinforced concrete columns exposed to extreme dynamic loads. Front. Struct. Civ. Eng. 2020, 14, 532–553. [Google Scholar] [CrossRef]
- Yang, C.; Gao, F.; Dong, M. Energy Efficiency Modeling of Integrated Energy System in Coastal Areas. J. Coast. Res. 2020, 103, 995–1001. [Google Scholar] [CrossRef]
- Xiong, Z.; Xiao, N.; Xu, F.; Zhang, X.; Xu, Q.; Zhang, K.; Ye, C. An Equivalent Exchange Based Data Forwarding Incentive Scheme for Socially Aware Networks. J. Signal Process. Syst. 2020, 1–15. [Google Scholar] [CrossRef]
- Abedini, M.; Zhang, C. Performance Assessment of Concrete and Steel Material Models in LS-DYNA for Enhanced Numerical Simulation, A State of the Art Review. Arch. Comput. Methods Eng. 2020, 1–22. [Google Scholar] [CrossRef]
- Mou, B.; Li, X.; Bai, Y.; Wang, L. Shear Behavior of Panel Zones in Steel Beam-to-Column Connections with Unequal Depth of Outer Annular Stiffener. J. Struct. Eng. 2019, 145, 4018247. [Google Scholar] [CrossRef]
- Mou, B.; Zhao, F.; Qiao, Q.; Wang, L.; Li, H.; He, B.; Hao, Z. Flexural behavior of beam to column joints with or without an overlying concrete slab. Eng. Struct. 2019, 199, 109616. [Google Scholar] [CrossRef]
- Gholipour, G.; Zhang, C.; Mousavi, A.A. Numerical analysis of axially loaded RC columns subjected to the combination of impact and blast loads. Eng. Struct. 2020, 219, 110924. [Google Scholar] [CrossRef]
- Zhang, H.; Qu, S.; Li, H.; Luo, J.; Xu, W. A Moving Shadow Elimination Method Based on Fusion of Multi-Feature. IEEE Access 2020, 8, 63971–63982. [Google Scholar] [CrossRef]
- Yang, W.; Pudasainee, D.; Gupta, R.; Li, W.; Wang, B.; Sun, L. An overview of inorganic particulate matter emission from coal/biomass/MSW combustion: Sampling and measurement, formation, distribution, inorganic composition and influencing factors. Fuel Process. Technol. 2020, 213, 106657. [Google Scholar] [CrossRef]
- Zhang, C.-W.; Ou, J.-P.; Zhang, J.-Q. Parameter optimization and analysis of a vehicle suspension system controlled by magnetorheological fluid dampers. Struct. Control. Health Monit. 2006, 13, 885–896. [Google Scholar] [CrossRef]
- Yue, H.; Wang, H.; Chen, H.; Cai, K.; Jin, Y. Automatic detection of feather defects using Lie group and fuzzy Fisher criterion for shuttlecock production. Mech. Syst. Signal Process. 2020, 141, 106690. [Google Scholar] [CrossRef]
- Zhu, G.; Wang, S.; Sun, L.; Ge, W.; Zhang, X. Output Feedback Adaptive Dynamic Surface Sliding-Mode Control for Quadrotor UAVs with Tracking Error Constraints. Complexity 2020, 2020, 8537198. [Google Scholar] [CrossRef]
- Xiong, Q.; Zhang, X.; Wang, W.-F.; Gu, Y. A Parallel Algorithm Framework for Feature Extraction of EEG Signals on MPI. Comput. Math. Methods Med. 2020, 2020, 9812019. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Liu, B. A review on the recent developments of sequence-based protein feature extraction methods. Curr. Bioinform. 2019, 14, 190–199. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, M.; Wang, D.; Zhou, P.; Tao, D. Top-k Feature Selection Framework Using Robust 0-1 Integer Programming. IEEE Trans. Neural Netw. Learn. Syst. 2020, 1–15. [Google Scholar] [CrossRef]
- Zhao, X.; Li, D.; Yang, B.; Chen, H.; Yang, X.; Yu, C.; Liu, S. A two-stage feature selection method with its application. Comput. Electr. Eng. 2015, 47, 114–125. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, J.; Lv, Z.; Gu, Y.; Yang, P.; Halgamuge, S.K. Multiobjective Evolution of Fuzzy Rough Neural Network via Distributed Parallelism for Stock Prediction. IEEE Trans. Fuzzy Syst. 2020, 28, 939–952. [Google Scholar] [CrossRef]
- Shi, K.; Wang, J.; Tang, Y.; Zhong, S. Reliable asynchronous sampled-data filtering of T–S fuzzy uncertain delayed neural networks with stochastic switched topologies. Fuzzy Sets Syst. 2020, 381, 1–25. [Google Scholar] [CrossRef]
- Shi, K.; Wang, J.; Zhong, S.; Tang, Y.; Cheng, J. Non-fragile memory filtering of T-S fuzzy delayed neural networks based on switched fuzzy sampled-data control. Fuzzy Sets Syst. 2020, 394, 40–64. [Google Scholar] [CrossRef]
- Yang, S.; Deng, B.; Wang, J.; Li, H.; Lu, M.; Che, Y.; Wei, X.; Loparo, K.A. Scalable Digital Neuromorphic Architecture for Large-Scale Biophysically Meaningful Neural Network With Multi-Compartment Neurons. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 148–162. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Lv, Z.; Qiao, L. Deep belief network and linear perceptron based cognitive computing for collaborative robots. Appl. Soft Comput. 2020, 92, 106300. [Google Scholar] [CrossRef]
- Adeli, H. Neural Networks in Civil Engineering: 1989–2000. Comput. Civ. Infrastruct. Eng. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Xu, M.; Li, T.; Wang, Z.; Deng, X.; Yang, R.; Guan, Z. Reducing Complexity of HEVC: A Deep Learning Approach. IEEE Trans. Image Process. 2018, 27, 5044–5059. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Xu, M.; Zhu, C.; Yang, R.; Wang, Z.; Guan, Z. A Deep Learning Approach for Multi-Frame In-Loop Filter of HEVC. IEEE Trans. Image Process. 2019, 28, 5663–5678. [Google Scholar] [CrossRef] [PubMed]
- Qiu, T.; Shi, X.; Wang, J.; Li, Y.; Qu, S.; Cheng, Q.; Cui, T.; Sui, S. Deep Learning: A Rapid and Efficient Route to Automatic Metasurface Design. Adv. Sci. 2019, 6, 1900128. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.-L.; Wang, G.; Ma, C.; Cai, Z.-N.; Liu, W.-B.; Wang, S.-J. An efficient hybrid kernel extreme learning machine approach for early diagnosis of Parkinson׳s disease. Neurocomputing 2016, 184, 131–144. [Google Scholar] [CrossRef]
- Hu, L.; Hong, G.; Ma, J.; Wang, X.; Chen, H. An efficient machine learning approach for diagnosis of paraquat-poisoned patients. Comput. Biol. Med. 2015, 59, 116–124. [Google Scholar] [CrossRef]
- Wang, S.-J.; Chen, H.-L.; Yan, W.-J.; Chen, Y.-H.; Fu, X. Face Recognition and Micro-expression Recognition Based on Discriminant Tensor Subspace Analysis Plus Extreme Learning Machine. Neural Process. Lett. 2013, 39, 25–43. [Google Scholar] [CrossRef]
- Xia, J.; Chen, H.; Li, Q.; Zhou, M.; Chen, L.; Cai, Z.; Fang, Y.; Zhou, H. Ultrasound-based differentiation of malignant and benign thyroid Nodules: An extreme learning machine approach. Comput. Methods Progr. Biomed. 2017, 147, 37–49. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Meng, Q.; Cai, J.; Yoshino, H.; Mochida, A. Applying support vector machine to predict hourly cooling load in the building. Appl. Energy 2009, 86, 2249–2256. [Google Scholar] [CrossRef]
- Urdaneta, S.; Zapata, E.; Contreras, J. Fuzzy Model for Estimation of Energy Performance of Residential Buildings. Int. J. Appl. Eng. Res. 2017, 12, 2766–2771. [Google Scholar]
- Fan, C.; Xiao, F.; Zhao, Y. A short-term building cooling load prediction method using deep learning algorithms. Appl. Energy 2017, 195, 222–233. [Google Scholar] [CrossRef]
- Xie, L. The Heat load Prediction Model based on BP Neural Network-markov Model. Procedia Comput. Sci. 2017, 107, 296–300. [Google Scholar] [CrossRef]
- Chou, J.-S.; Bui, D.-K. Modeling heating and cooling loads by artificial intelligence for energy-efficient building design. Energy Build. 2014, 82, 437–446. [Google Scholar] [CrossRef]
- Roy, S.S.; Roy, R.; Balas, V.E. Estimating heating load in buildings using multivariate adaptive regression splines, extreme learning machine, a hybrid model of MARS and ELM. Renew. Sustain. Energy Rev. 2018, 82, 4256–4268. [Google Scholar] [CrossRef]
- Sholahudin, S.; Han, H. Simplified dynamic neural network model to predict heating load of a building using Taguchi method. Energy 2016, 115, 1672–1678. [Google Scholar] [CrossRef]
- Tsanas, A.; Xifara, A. Accurate quantitative estimation of energy performance of residential buildings using statistical machine learning tools. Energy Build. 2012, 49, 560–567. [Google Scholar] [CrossRef]
- Gao, W.; Alsarraf, J.; Moayedi, H.; Shahsavar, A.; Nguyen, H. Comprehensive preference learning and feature validity for designing energy-efficient residential buildings using machine learning paradigms. Appl. Soft Comput. 2019, 84, 105748. [Google Scholar] [CrossRef]
- Nilashi, M.; Dalvi-Esfahani, M.; Ibrahim, O.; Bagherifard, K.; Mardani, A.; Zakuan, N. A soft computing method for the prediction of energy performance of residential buildings. Measurement 2017, 109, 268–280. [Google Scholar] [CrossRef]
- Moayedi, H.; Hayati, S. Artificial intelligence design charts for predicting friction capacity of driven pile in clay. Neural Comput. Appl. 2019, 31, 7429–7445. [Google Scholar] [CrossRef]
- Fu, X.; Pace, P.; Aloi, G.; Yang, L.; Fortino, G. Topology optimization against cascading failures on wireless sensor networks using a memetic algorithm. Comput. Netw. 2020, 177, 107327. [Google Scholar] [CrossRef]
- Moayedi, H.; Nguyen, H.; Foong, L.K. Nonlinear evolutionary swarm intelligence of grasshopper optimization algorithm and gray wolf optimization for weight adjustment of neural network. Eng. Comput. 2019, 1–11. [Google Scholar] [CrossRef]
- Amar, M.N.; Zeraibi, N. A combined support vector regression with firefly algorithm for prediction of bottom hole pressure. SN Appl. Sci. 2020, 2, 1–12. [Google Scholar]
- Le, L.T.; Nguyen, H.; Dou, J.; Zhou, J. A Comparative Study of PSO-ANN, GA-ANN, ICA-ANN, and ABC-ANN in Estimating the Heating Load of Buildings’ Energy Efficiency for Smart City Planning. Appl. Sci. 2019, 9, 2630. [Google Scholar] [CrossRef]
- Cao, B.; Dong, W.; Lv, Z.; Gu, Y.; Singh, S.; Kumar, P. Hybrid Microgrid Many-Objective Sizing Optimization With Fuzzy Decision. IEEE Trans. Fuzzy Syst. 2020, 28, 2702–2710. [Google Scholar] [CrossRef]
- Cao, B.; Wang, X.; Zhang, W.; Song, H.; Lv, Z. A Many-Objective Optimization Model of Industrial Internet of Things Based on Private Blockchain. IEEE Netw. 2020, 34, 78–83. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, J.; Yang, P.; Gu, Y.; Muhammad, K.; Rodrigues, J.J.P.C.; De Albuquerque, V.H.C. Multiobjective 3-D Topology Optimization of Next-Generation Wireless Data Center Network. IEEE Trans. Ind. Informatics 2020, 16, 3597–3605. [Google Scholar] [CrossRef]
- Qu, S.; Han, Y.; Wu, Z.; Raza, H. Consensus Modeling with Asymmetric Cost Based on Data-Driven Robust Optimization. Group Decis. Negot. 2020, 1–38. [Google Scholar] [CrossRef]
- Roberts, A.; Marsh, A. ECOTECT: Environmental Prediction in Architectural Education; Cardiff University: Cardiff, UK, 2001. [Google Scholar]
- McCulloch, W.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity (1943). Ideas That Creat. Future 2021, 5, 79–88. [Google Scholar] [CrossRef]
- Seyedashraf, O.; Mehrabi, M.; Akhtari, A.A. Novel approach for dam break flow modeling using computational intelligence. J. Hydrol. 2018, 559, 1028–1038. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Mosallanezhad, M.; Rashid, A.S.A.; Pradhan, B. Modification of landslide susceptibility mapping using optimized PSO-ANN technique. Eng. Comput. 2019, 35, 967–984. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Orr, M.J. Introduction to Radial Basis Function Networks; Technical Report; Center for Cognitive Science, University of Edinburgh: Edinburgh, UK, 1996. [Google Scholar]
- Specht, D. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- El-Bakry, M. Feed forward neural networks modeling for K–P interactions. Chaos Solitons Fractals 2003, 18, 995–1000. [Google Scholar] [CrossRef]
- Cigizoglu, H.K.; Kişi, Ö. Flow prediction by three back propagation techniques using k-fold partitioning of neural network training data. Hydrol. Res. 2005, 36, 49–64. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Let a biogeography-based optimizer train your multi-layer perceptron. Inf. Sci. 2014, 269, 188–209. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Schwefel, H.-P.P. Evolution and Optimum Seeking: The Sixth Generation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Mehrabian, A.; Lucas, C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006, 1, 355–366. [Google Scholar] [CrossRef]
- Kashan, A.H. League Championship Algorithm: A New Algorithm for Numerical Function Optimization. In Proceedings of the 2009 International Conference of Soft Computing and Pattern Recognition, Malacca, Malaysia, 4–7 December 2009; IEEE: New York, NY, USA, 2009; pp. 43–48. [Google Scholar]
- Spoljaric, T.; Pavic, I. Performance analysis of an ant lion optimizer in tuning generators’ excitation controls in multi machine power system. In Proceedings of the 2018 41st International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 21–25 May 2018; IEEE: New York, NY, USA, 2018; pp. 1040–1045. [Google Scholar]
- Kose, U. An Ant-Lion Optimizer-Trained Artificial Neural Network System for Chaotic Electroencephalogram (EEG) Prediction. Appl. Sci. 2018, 8, 1613. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chattopadhyay, P.K. Solving complex economic load dispatch problems using biogeography-based optimization. Expert Syst. Appl. 2010, 37, 3605–3615. [Google Scholar] [CrossRef]
- Vanishree, J.; Ramesh, V. Optimization of size and cost of static var compensator using dragonfly algorithm for voltage profile improvement in power transmission systems. Int. J. Renew. Energy Res. 2018, 8, 56–66. [Google Scholar]
- Yuan, C.; Moayedi, H. The performance of six neural-evolutionary classification techniques combined with multi-layer perception in two-layered cohesive slope stability analysis and failure recognition. Eng. Comput. 2020, 36, 1705–1714. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Akbari, E.; Vahed, A.A. Solving non-linear, non-smooth and non-convex optimal power flow problems using chaotic invasive weed optimization algorithms based on chaos. Energy 2014, 73, 340–353. [Google Scholar] [CrossRef]
- Kashan, A.H. League Championship Algorithm (LCA): An algorithm for global optimization inspired by sport championships. Appl. Soft Comput. 2014, 16, 171–200. [Google Scholar] [CrossRef]
- Kashan, A.H. An efficient algorithm for constrained global optimization and application to mechanical engineering design: League championship algorithm (LCA). Comput. Des. 2011, 43, 1769–1792. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report; Citeseer Technical Report-tr06; Erciyes University, Engineering Faculty, Computer Engineering Department Kayseri Turkey: Kayseri, Turkey, 2005. [Google Scholar]
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed optimization by ant colonies. In Proceedings of the First European Conference on Artificial Life, Paris, France, 11 December 1991; MIT Press: Cambridge, MA, USA, 1992; pp. 134–142. [Google Scholar]
- Wang, G.-G.; Deb, S.; Coelho, L.D.S. Elephant herding optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI), Bali, Indonesia, 7–9 December 2015; IEEE: New York, NY, USA, 2015; pp. 1–5. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Bayraktar, Z.; Komurcu, M.; Werner, D.H. Wind Driven Optimization (WDO): A novel nature-inspired optimization algorithm and its application to electromagnetics. In Proceedings of the 2010 IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010; IEEE: New York, NY, USA, 2010; pp. 1–4. [Google Scholar]
- Deng, H.; Fannon, D.; Eckelman, M.J. Predictive modeling for US commercial building energy use: A comparison of existing statistical and machine learning algorithms using CBECS microdata. Energy Build. 2018, 163, 34–43. [Google Scholar] [CrossRef]
| Ensemble Models | Network Results | |||||
|---|---|---|---|---|---|---|
| Training Phase | Testing Phase | |||||
| RMSE | MAE | R2 | RMSE | MAE | R2 | |
| ALO-MLP | 2.6054 | 2.0992 | 0.9539 | 2.7162 | 2.1865 | 0.9406 |
| BBO-MLP | 2.5359 | 2.0846 | 0.9596 | 2.4807 | 1.8284 | 0.9516 |
| DA-MLP | 3.4314 | 2.9402 | 0.9222 | 3.3998 | 2.8713 | 0.9340 |
| ES-MLP | 2.7146 | 2.0848 | 0.9357 | 3.0958 | 2.5072 | 0.9318 |
| IWO-MLP | 3.2506 | 2.8709 | 0.9547 | 3.3524 | 2.9702 | 0.9431 |
| LCA-MLP | 3.8297 | 3.4091 | 0.9386 | 3.2954 | 2.7807 | 0.9400 |
| Models | Scores | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Training | Testing | |||||||||
| RMSE | MAE | R2 | Overall Score | Rank | RMSE | MAE | R2 | Overall Score | Rank | |
| ALO-MLP | 5 | 4 | 4 | 13 | 2 | 5 | 5 | 4 | 14 | 2 |
| BBO-MLP | 6 | 6 | 6 | 18 | 1 | 6 | 6 | 6 | 18 | 1 |
| DA-MLP | 2 | 2 | 1 | 5 | 5 | 1 | 2 | 2 | 5 | 6 |
| ES-MLP | 4 | 5 | 2 | 11 | 3 | 4 | 4 | 1 | 9 | 3 |
| IWO-MLP | 3 | 3 | 5 | 11 | 3 | 2 | 1 | 5 | 8 | 5 |
| LCA-MLP | 1 | 1 | 3 | 5 | 5 | 3 | 3 | 3 | 9 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moayedi, H.; Mosavi, A. Synthesizing Multi-Layer Perceptron Network with Ant Lion Biogeography-Based Dragonfly Algorithm Evolutionary Strategy Invasive Weed and League Champion Optimization Hybrid Algorithms in Predicting Heating Load in Residential Buildings. Sustainability 2021, 13, 3198. https://doi.org/10.3390/su13063198
Moayedi H, Mosavi A. Synthesizing Multi-Layer Perceptron Network with Ant Lion Biogeography-Based Dragonfly Algorithm Evolutionary Strategy Invasive Weed and League Champion Optimization Hybrid Algorithms in Predicting Heating Load in Residential Buildings. Sustainability. 2021; 13(6):3198. https://doi.org/10.3390/su13063198
Chicago/Turabian StyleMoayedi, Hossein, and Amir Mosavi. 2021. "Synthesizing Multi-Layer Perceptron Network with Ant Lion Biogeography-Based Dragonfly Algorithm Evolutionary Strategy Invasive Weed and League Champion Optimization Hybrid Algorithms in Predicting Heating Load in Residential Buildings" Sustainability 13, no. 6: 3198. https://doi.org/10.3390/su13063198
APA StyleMoayedi, H., & Mosavi, A. (2021). Synthesizing Multi-Layer Perceptron Network with Ant Lion Biogeography-Based Dragonfly Algorithm Evolutionary Strategy Invasive Weed and League Champion Optimization Hybrid Algorithms in Predicting Heating Load in Residential Buildings. Sustainability, 13(6), 3198. https://doi.org/10.3390/su13063198







