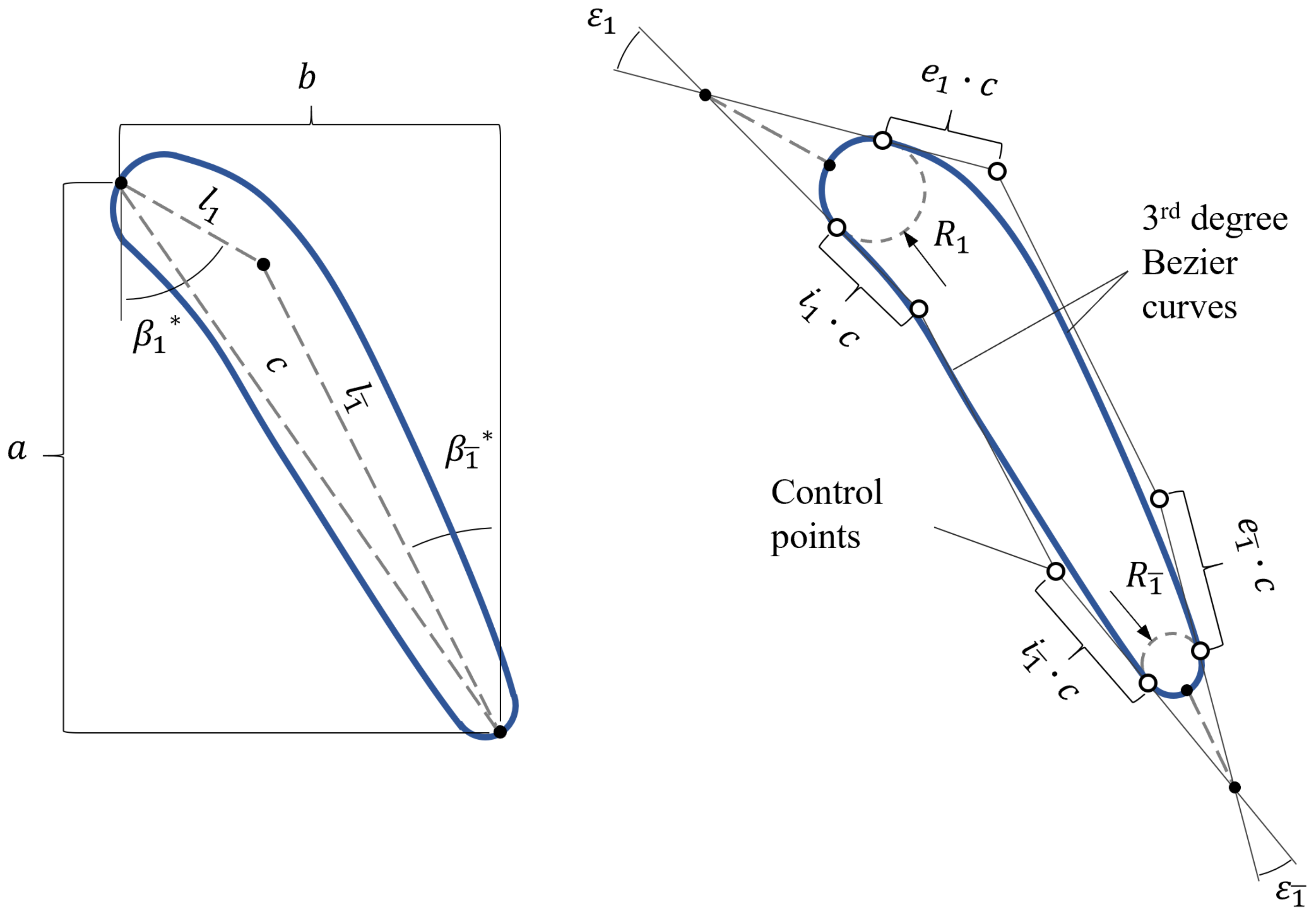
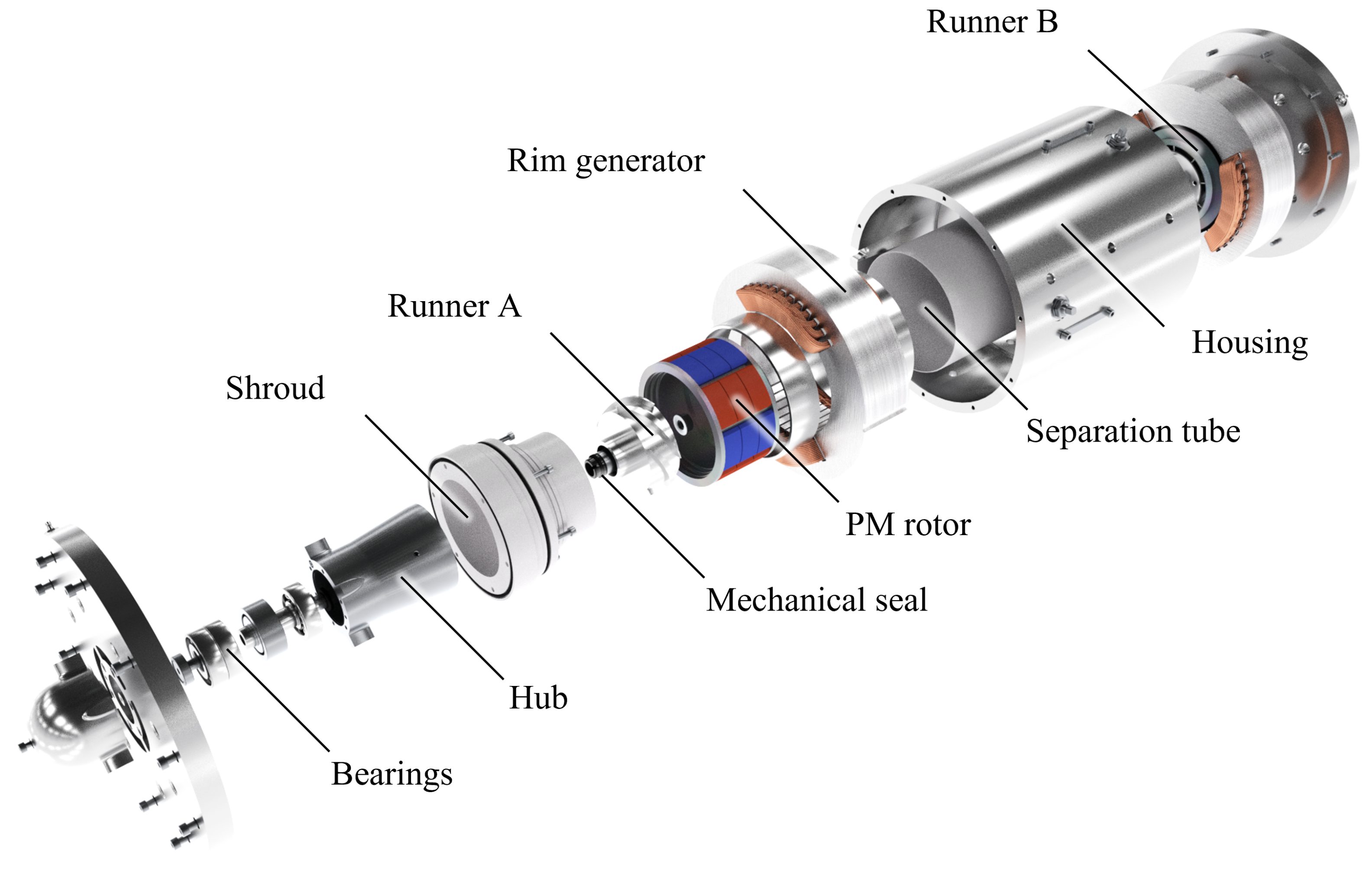
1. Introduction
Among today’s renewable energy sources, hydropower remains one of the most important suppliers of electricity, meeting over 15% of the global needs. In hydrologically and topographically predestined countries, hydropower constitutes even the bulk of electricity production. In Switzerland, hydropower covers more than 57% of the electricity demand [
1]. Thereby, small hydropower (SHP) facilities with a gross capacity below 10 MW constitute about 10% of the Swiss hydroelectric capacity. Globally, energy strategies are evolving towards clean and sustainable technologies that also drives the expansion of SHP [
2]. In Switzerland, the installed SHP energy production of about 3.4 TWh/year is planned to be increased by up to 770 GWh/year before 2050. Micro-hydropower (MHP), referring to power units below 500 kW, can contribute to a noticeable extent to the SHP mix. Particularly, the field of water treatment and distribution infrastructures hides a considerable MHP potential [
3]. However, different main issues are identified such as variations in flows or turbine efficiency and the necessity of further risk assessments and evaluations of long-term reliability of MHP installations. Therefore, energy recovery in the water industry using MHP remains an active area of research, considering the various technical and economical complexities. In Swiss drinking water supply systems, more than 100 GWh/year are already exploited by hundreds of drinking water turbines, thus, about 50% of the estimated potential [
4]. Since 2008, a Swiss electricity supply act is in force providing compensatory feed-in remuneration for renewable energies. The newly introduced feed-in tariffs are encouraging MHP exploitation in lower power ranges. Nevertheless, many drinking water facilities with a power potential of a few kW still remain untapped due to the lack of profitable solutions.
One of the most installed hydraulic machines for energy recovery from water distribution systems is the Pump as Turbine (PAT) [
5] which represents an economically interesting solution since small pumps are generally produced in series. Extensive research is dedicated to PATs and their implementation in real-world water distribution systems, for example [
6]. Recent studies present methodologies to overcome major obstacles for practical applications of PATs such as the lack of performance data [
7,
8]. Moreover, several technical solutions have been developed to adapt small pumps into small PATs, and variable speed drives may give them one degree of freedom. A recent case study shows that the adoption of PATs in collective irrigation systems is a viable solution to improve their economic and environmental impacts [
9]. The latter research reveals a substantial cost decrease of 74% in the electro-mechanical equipment compared to site-specific designed turbines, whereas the electricity production is decreased by only 19%. To increase the sustainability of water distribution systems, special attention is dedicated to management strategies that minimize the overall energy input, inter alia, by integration of MHP technologies [
10]. To point out one result of the proposed management strategies, it is found that a set of independent District Metered Areas locally increase the hydraulic energy (compared to widely open water distribution systems) that favors the installation of energy recovery devices at these locations. To facilitate the function extension of water supply networks to energy production, harmony search algorithms are proposed to optimize the planning of such schemes [
11].
In the case of facilities with strong hydraulic variations, the development of adapted low power hydroelectric technologies with additional degrees of freedom may provide more operational flexibility. In comparison, the speed coefficient—discharge coefficient characteristic of a PAT with variable speed is typically clustered on only one S-shaped curve [
12] whilst for a counter-rotating micro-turbine with one additional degree of freedom it may cover a large area [
13]. Moreover, with specific turbine-oriented hydraulic design, efficiency can be optimized. Low head tubular propeller turbines point out one example of this research field [
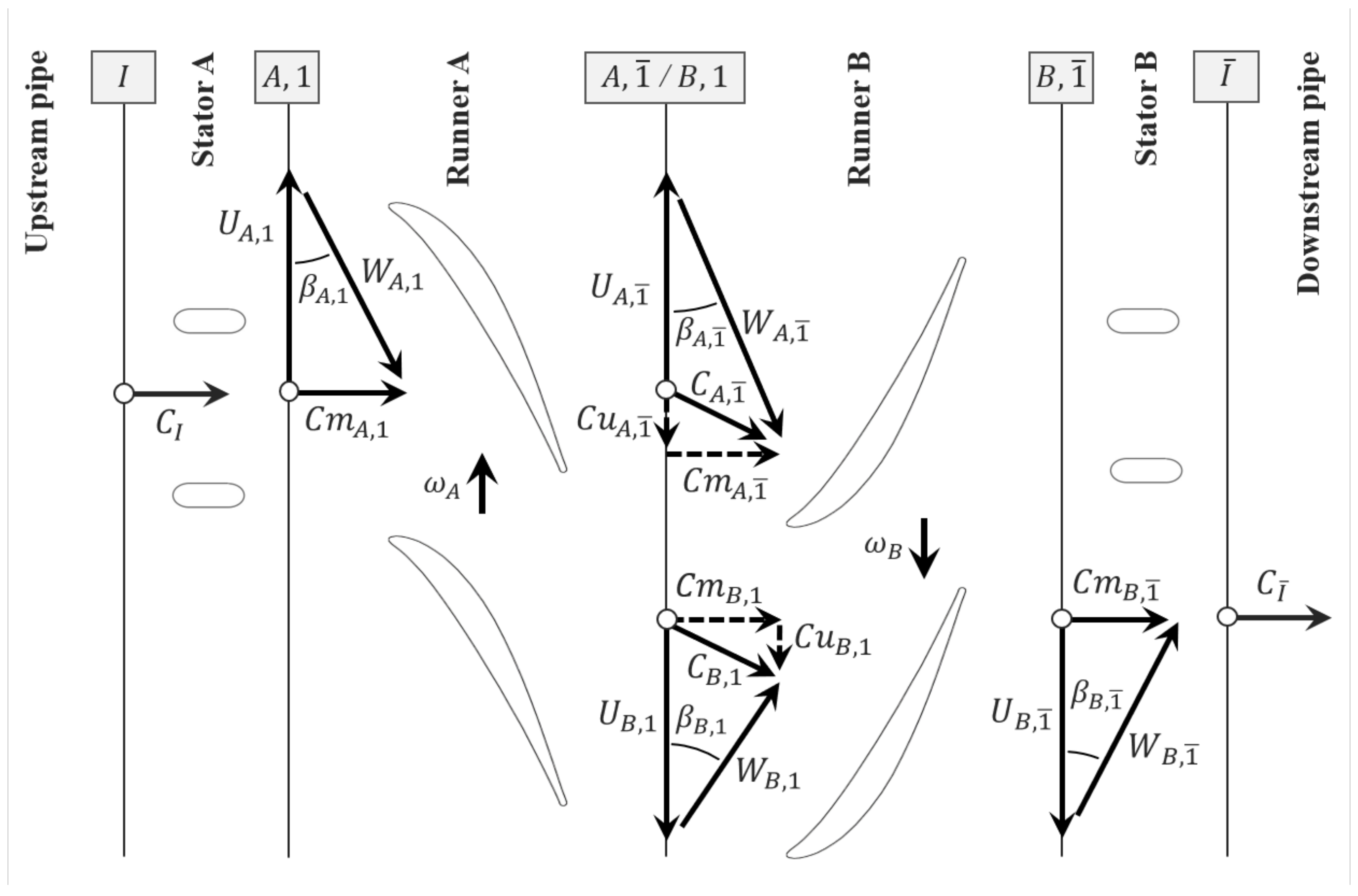
14]. In the perspective of developing a more flexible micro-hydroelectric system for drinking water facilities, HES-SO Valais-Wallis and EPFL-LMH have initiated the DuoTurbo project, focusing on an output power range between 5 kW and 25 kW. A counter-rotating microturbine forms the core element of the new energy recovery station. One stage of this microturbine consists of two axial counter-rotating runners. One early prototype of this specific turbine design was realized at EPFL-LMH using an elbowed pipe system with external electrical generators. Preliminary CFD simulations of this prototype were carried out [
15] showing hydraulic efficiencies over 80% for an output power of 2.65 kW. Numerical and experimental methodologies to evaluate the performance and flow features of such type of turbine, involving Laser Doppler Velocimetry, were presented by [
16,
17]. The experimental validations including losses from the blade tip radial clearance still showed reasonable hydraulic efficiencies above 60%. The integration of a counter-rotating microturbine into water utility networks, considering analytical hill chart models to maximize energy recovery, was presented by [
18]. Further, virtual Energy Recovery Station models were analyzed to simulate the energy recovery on a given installation site [
19]. A custom runner design strategy [
20] is thereby considered to maximize the electricity production at each potential water network. A second prototype with a more compact “bulb” configuration, comprising in-line electrical generators, was later built at HES-SO Valais-Wallis for ongoing developments. Finally, an even more compact DuoTurbo mechanical concepts with more powerful custom rim generators was developed that facilitates the integration into existing water pipelines. To investigate the new hydro-mechanical and electrical concepts, a DuoTurbo laboratory prototype was built in collaboration with industrial partners and extensively tested on the hydraulic test rig of the HES-SO Valais-Wallis [
21,
22]. Several mechanical solutions concerning the runner bearings and labyrinth seals were investigated to build a first DuoTurbo product prototype in 2018 [
23]. Finally, in May 2019, the first DuoTurbo pilot was commissioned at a drinking water network in Savièse, VS Switzerland. The pilot enables long term monitoring and collection of hydraulic, mechanical and electrical parameters and is therefore essential for advanced system validation.
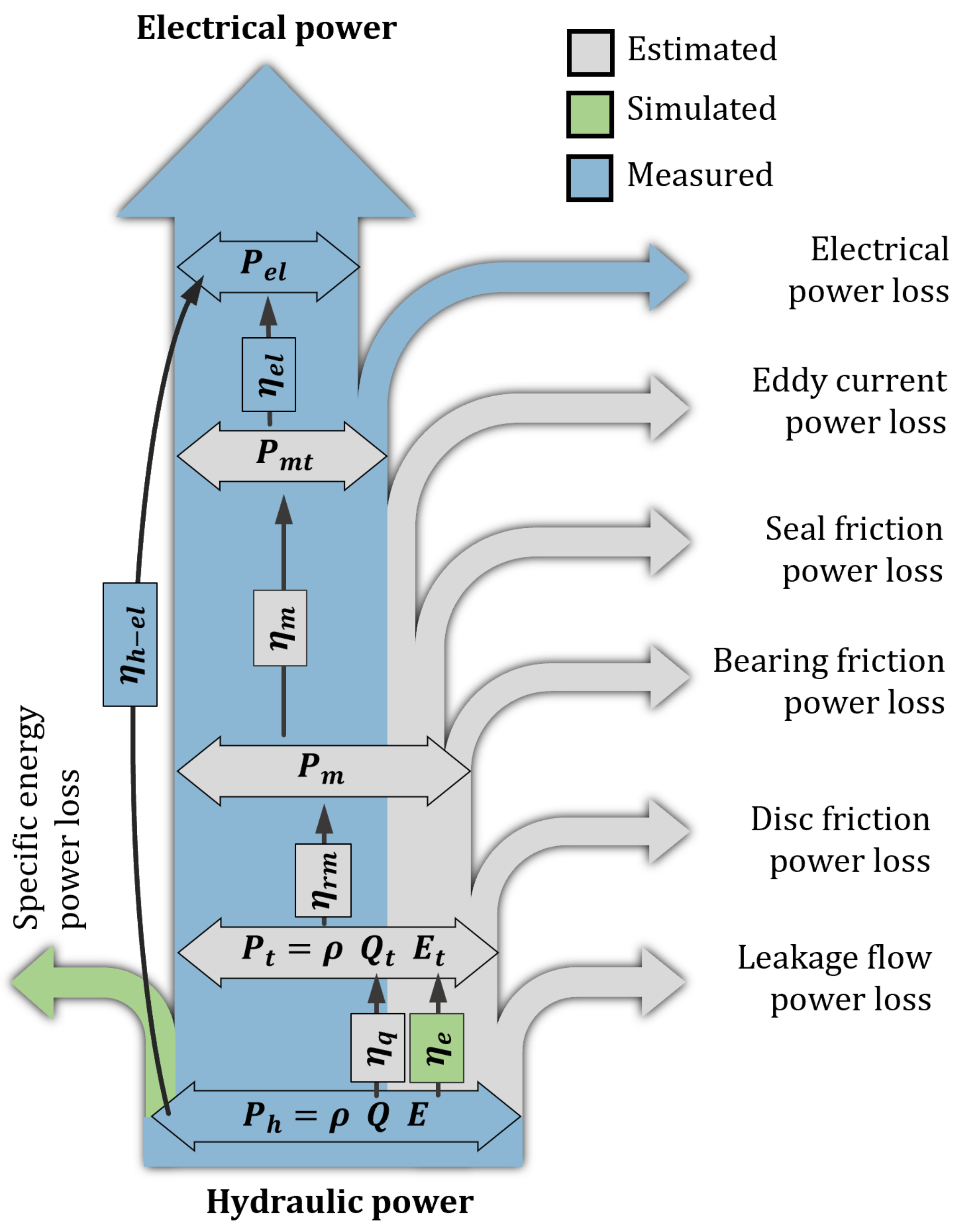
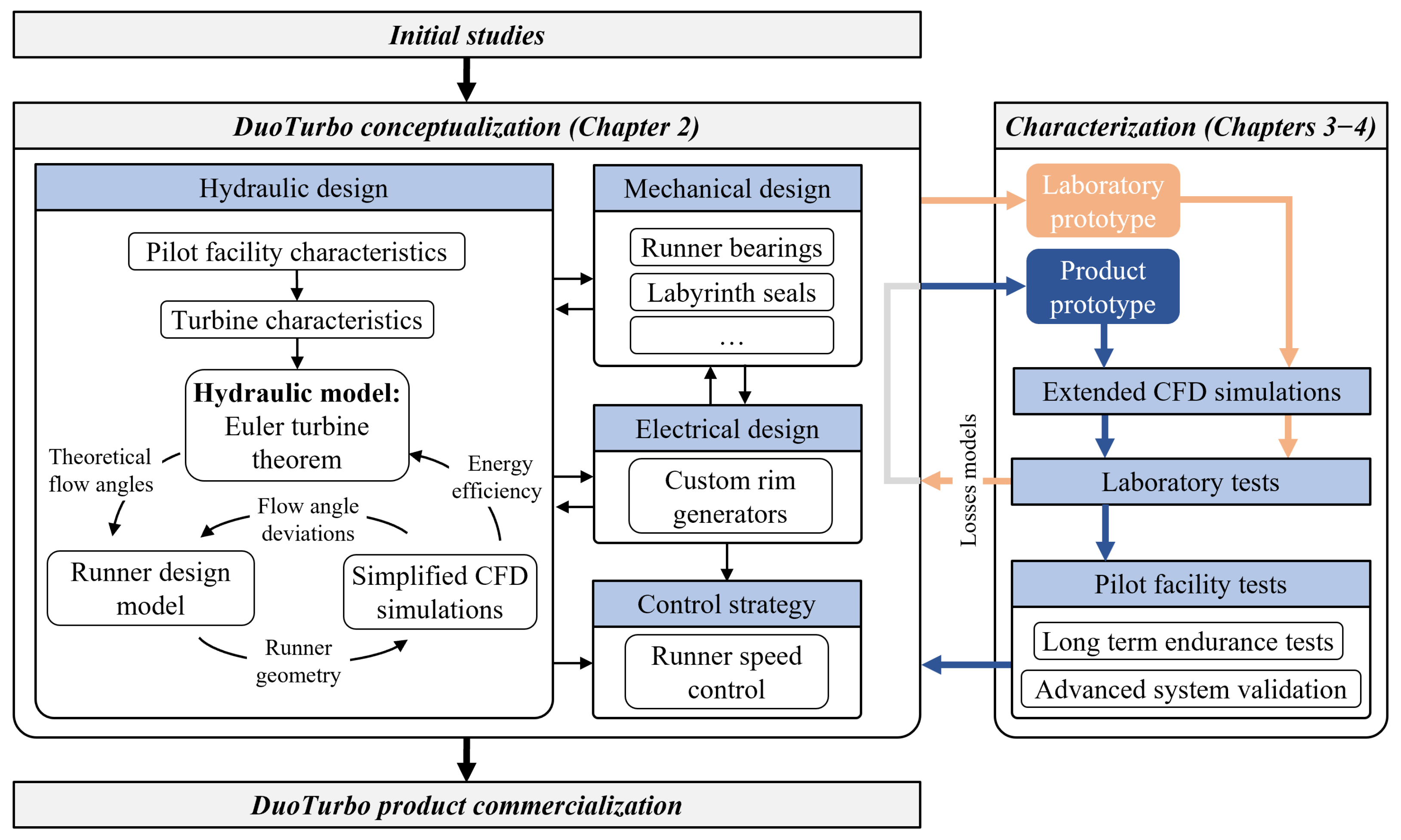
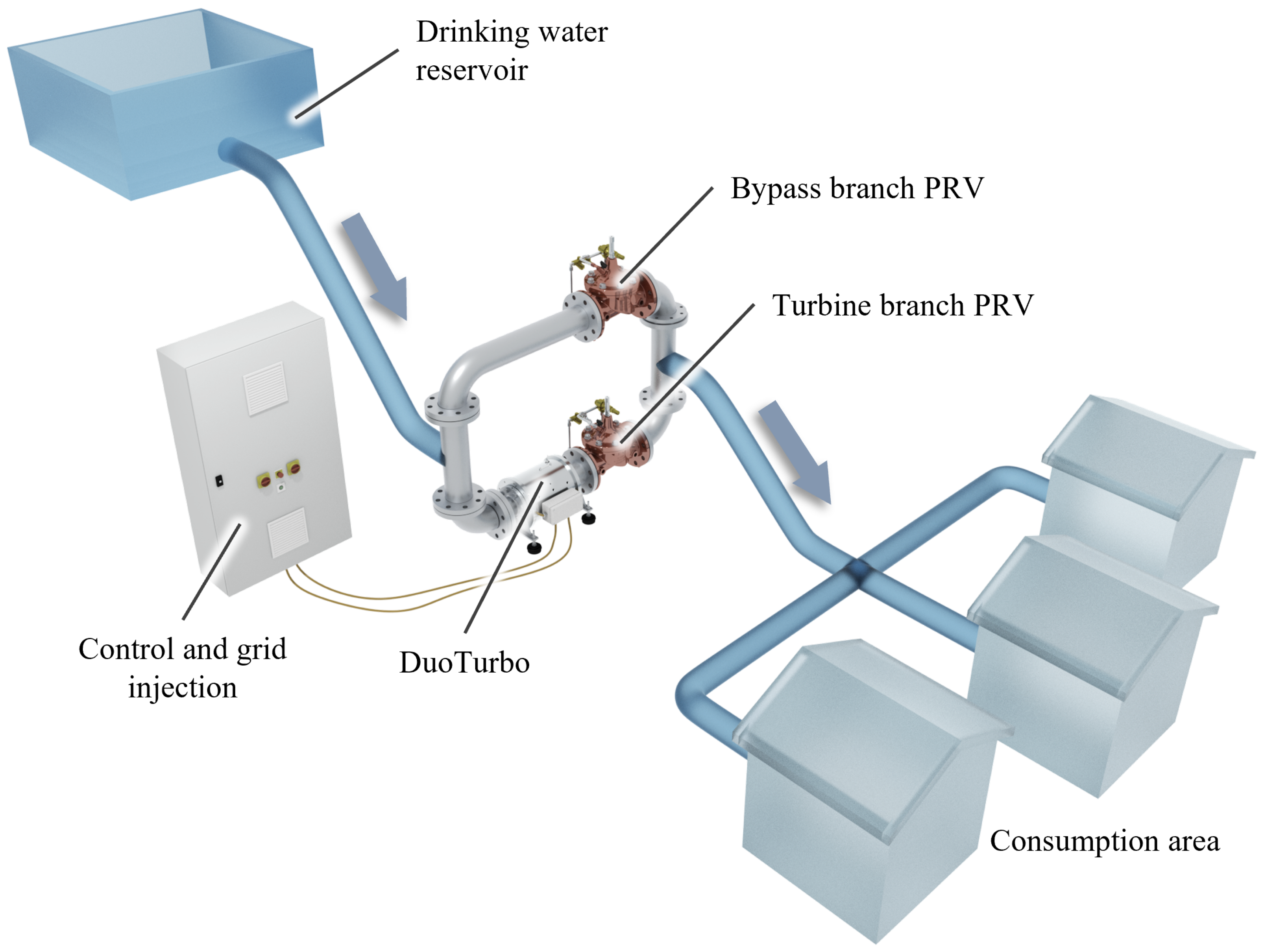
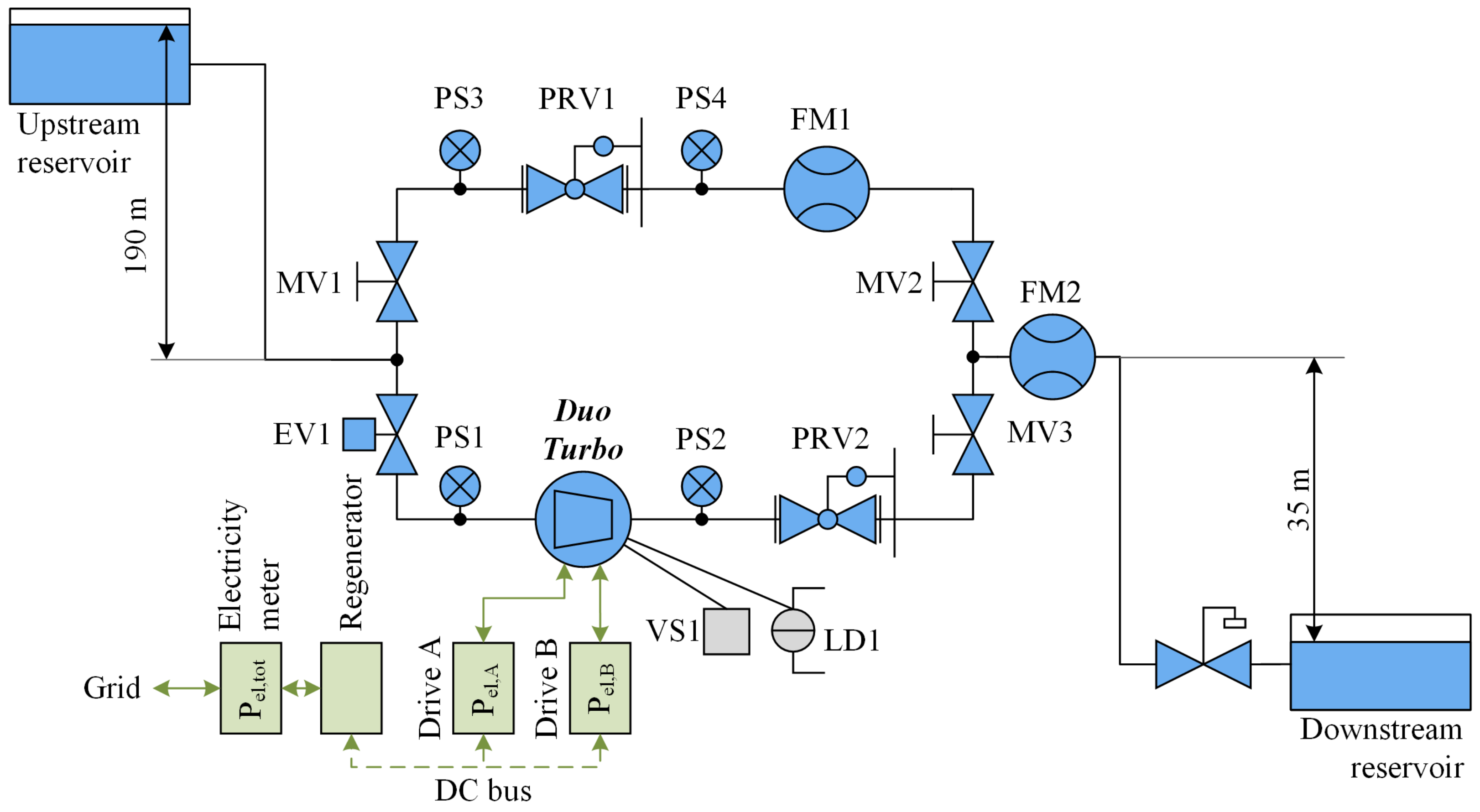
The aim of this paper is to point out the main technical aspects of the developed DuoTurbo product prototype and to demonstrate its reliability operating in a real drinking water network. First, the hydraulic, mechanical and electrical concepts are presented (see
Figure 1). Then, numerical and experimental methods used for the system characterization, including the monitoring of the pilot facility, are explained. This paper only deals with the product prototype, as highlighted in dark blue in
Figure 1. The corresponding numerical results, laboratory test results and long-term measurement data from the DuoTurbo pilot facility are then presented and discussed.
5. Conclusions
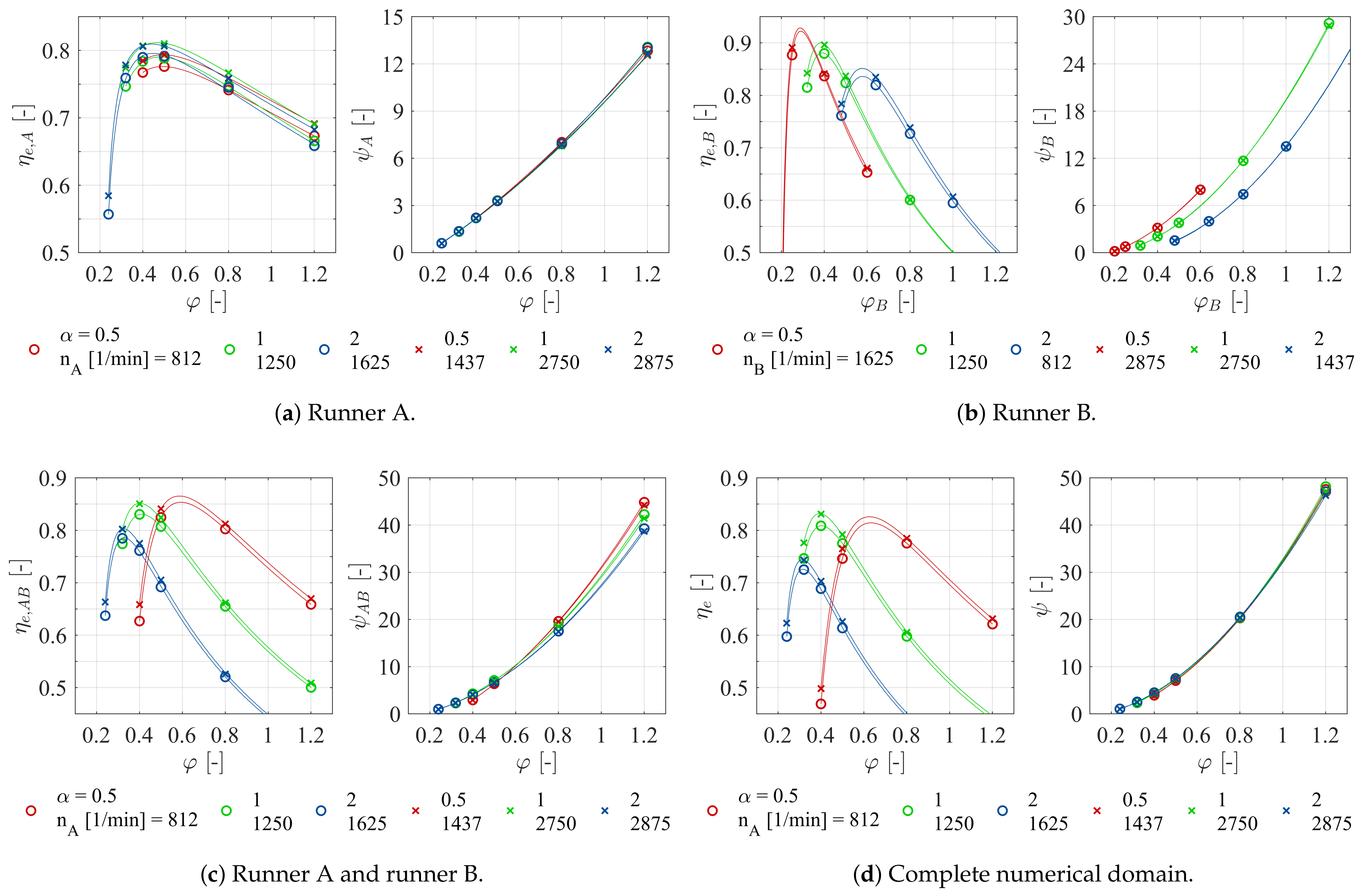
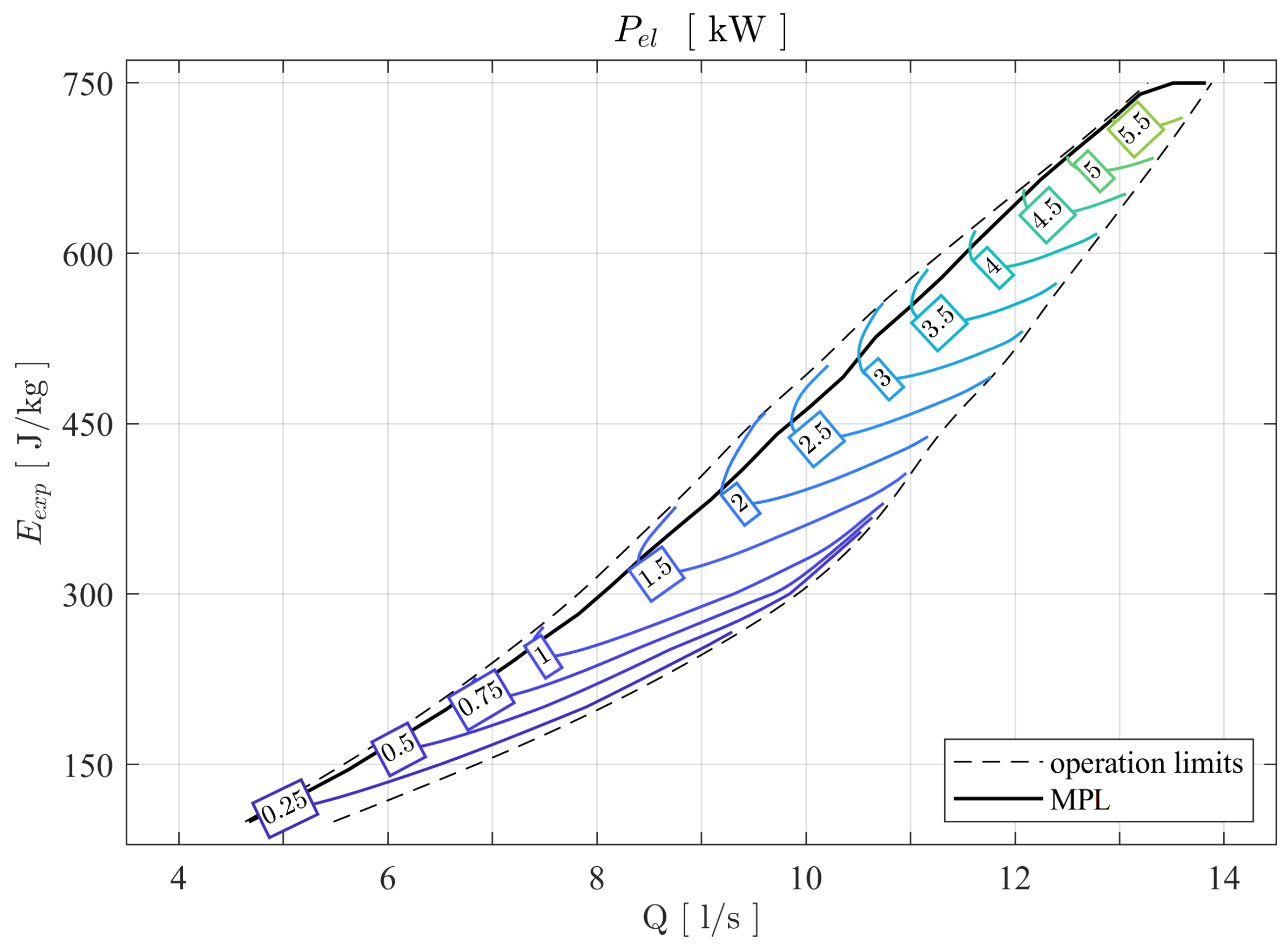
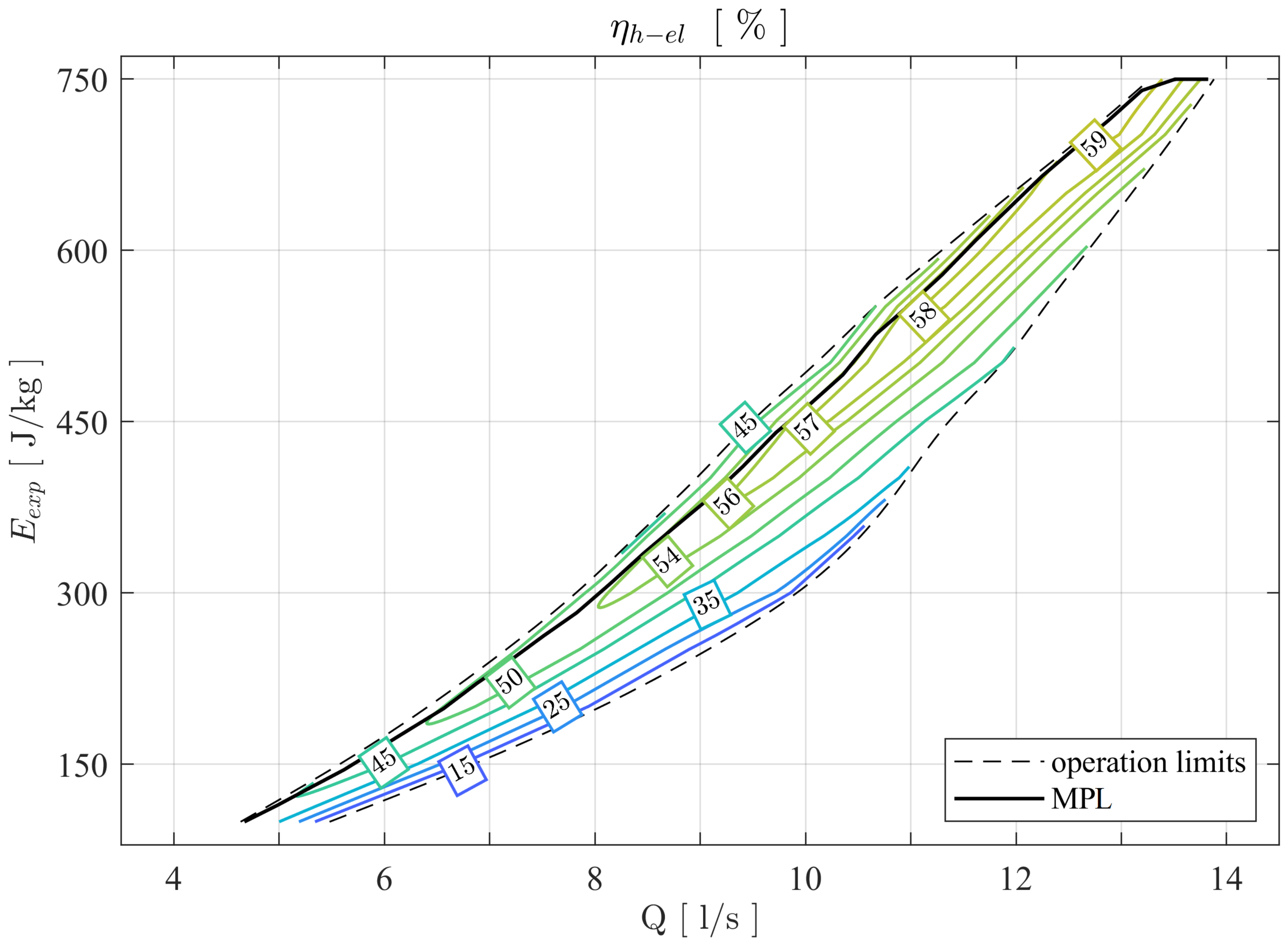
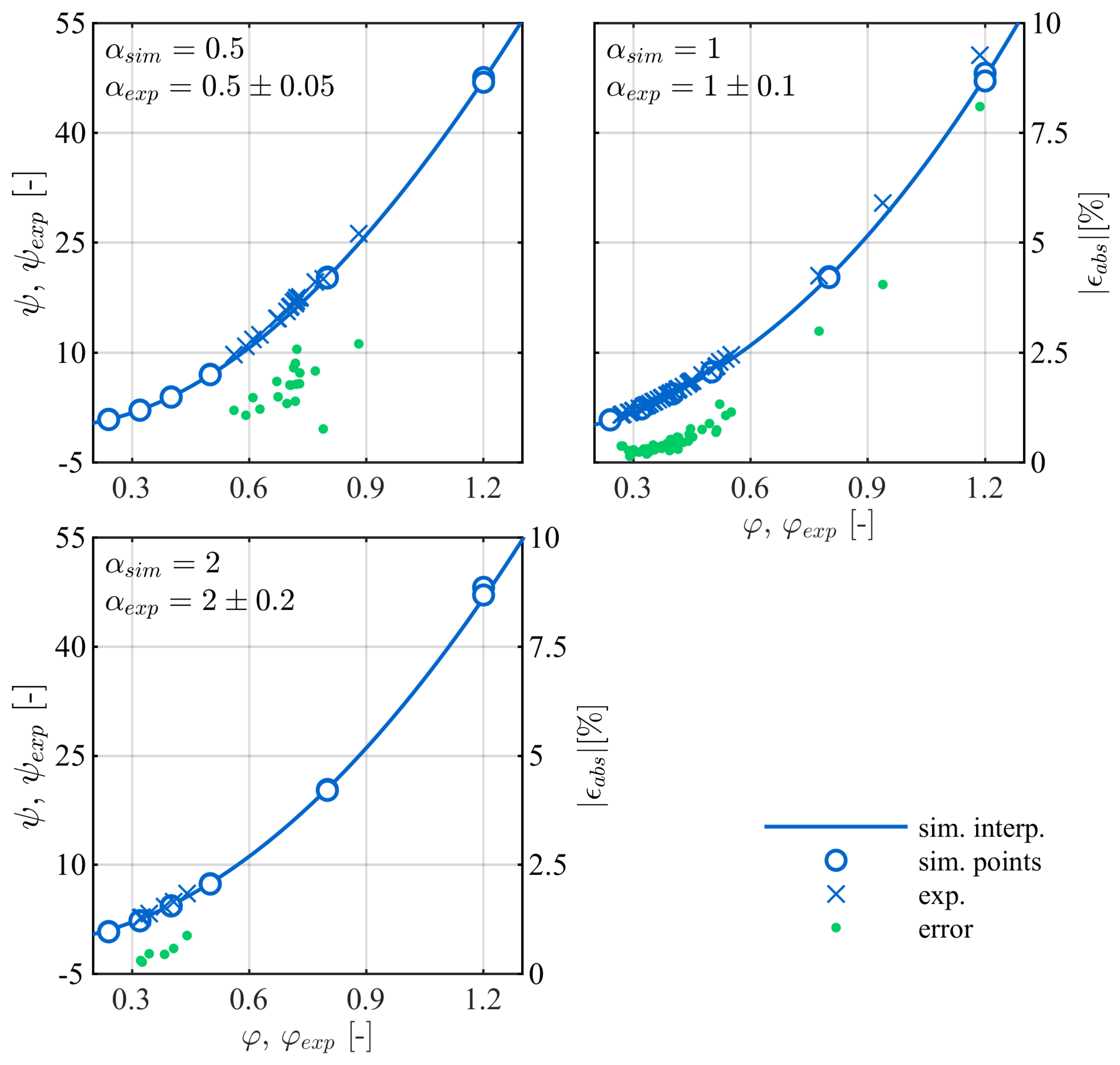
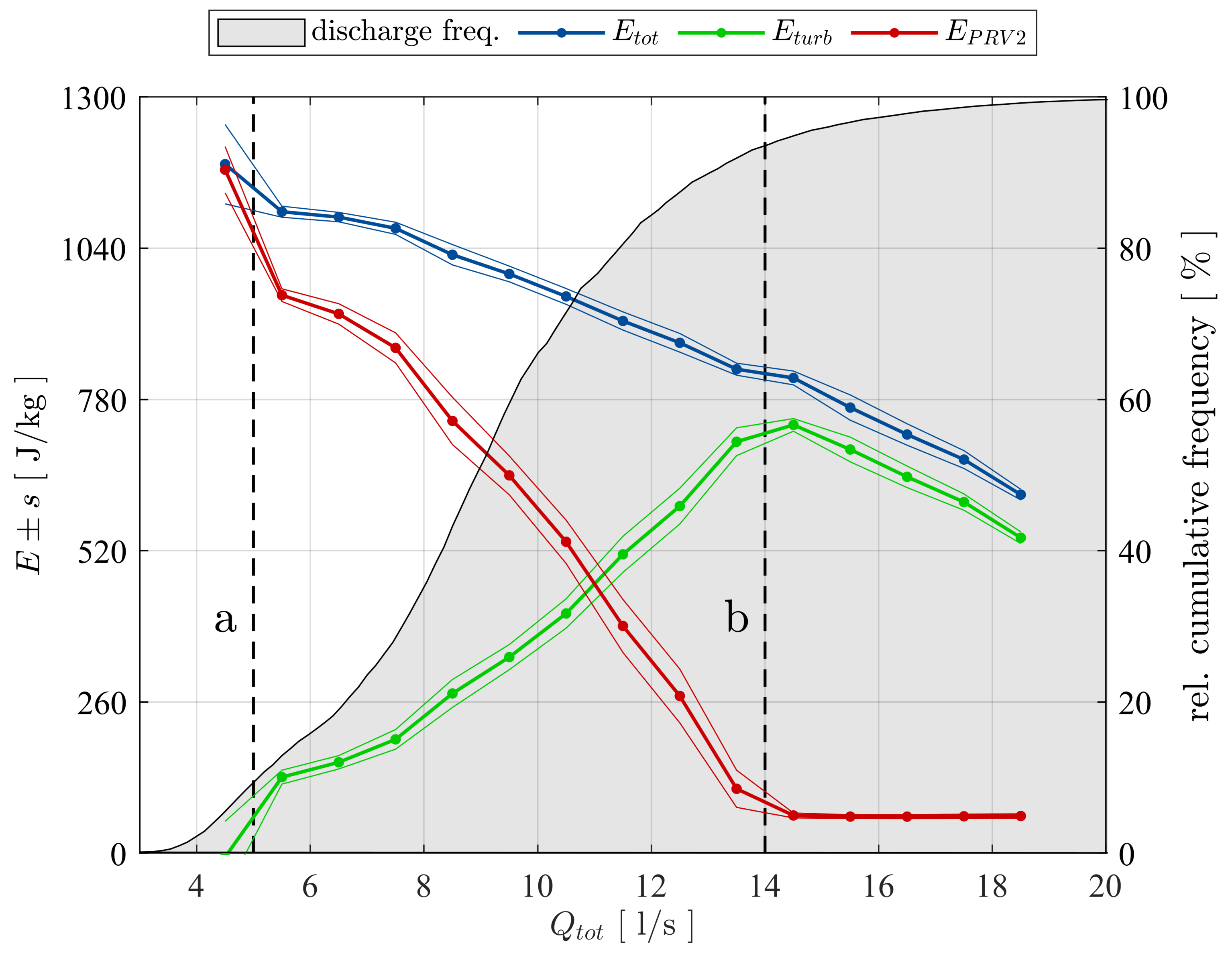
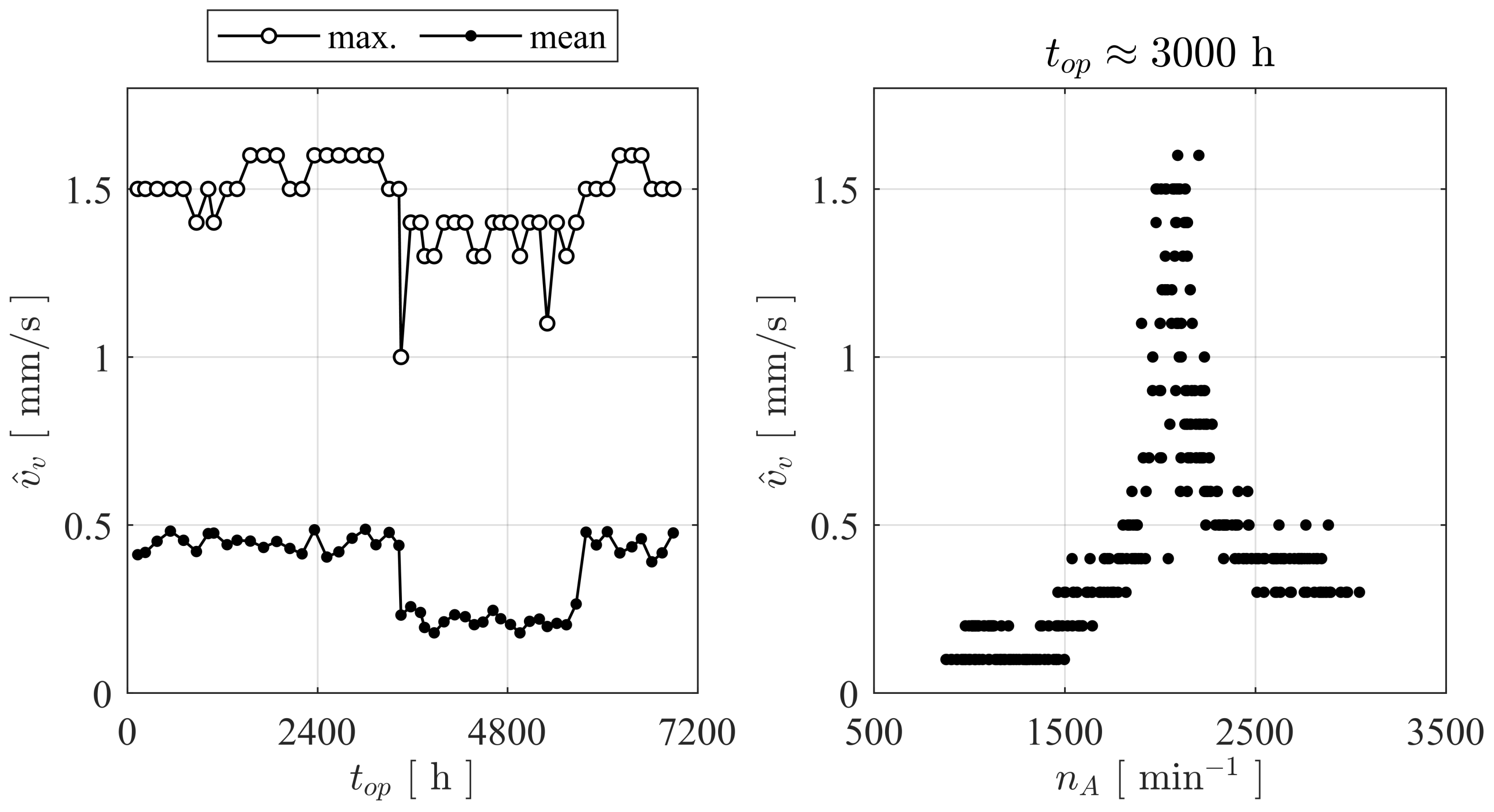
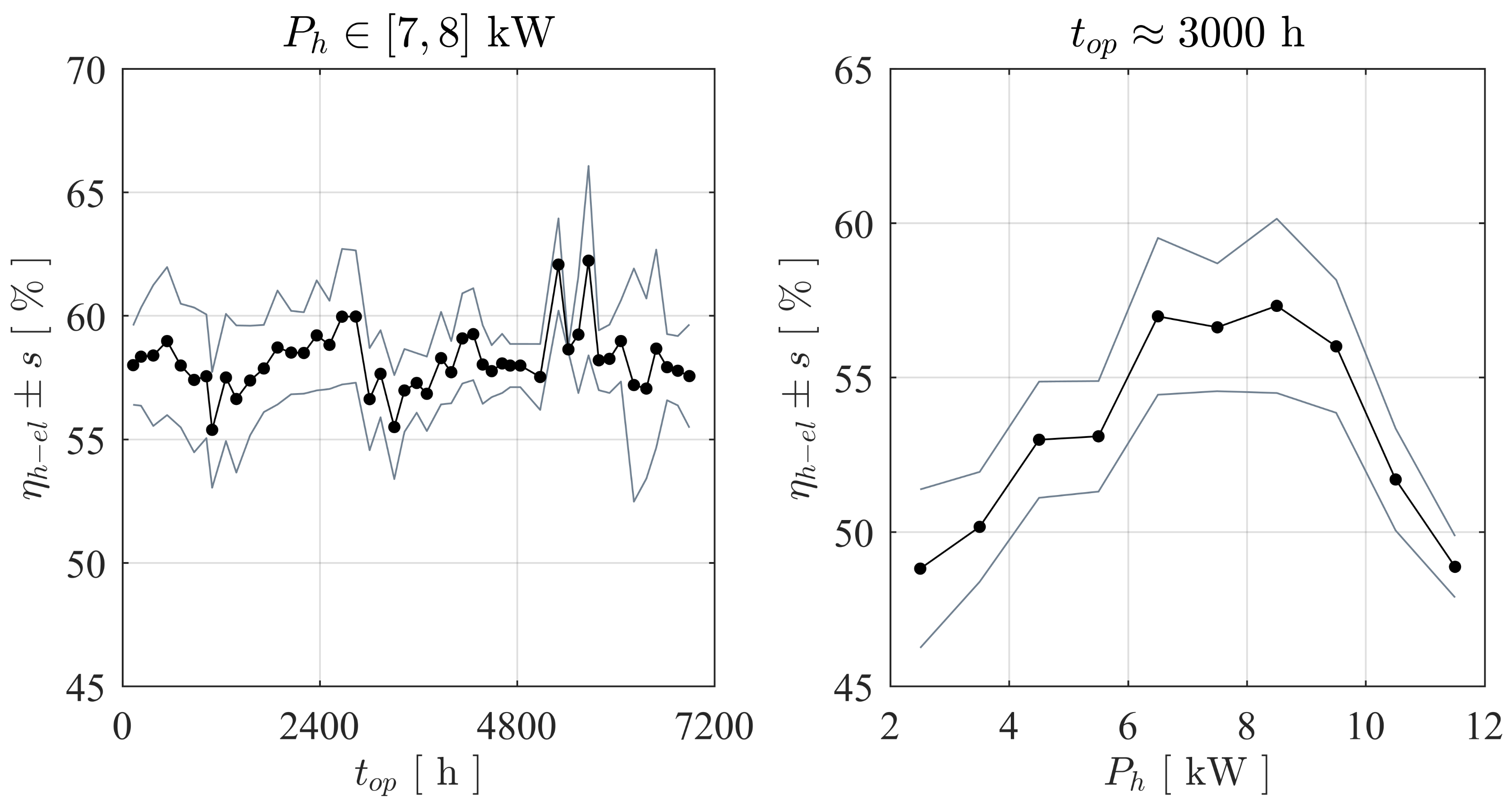
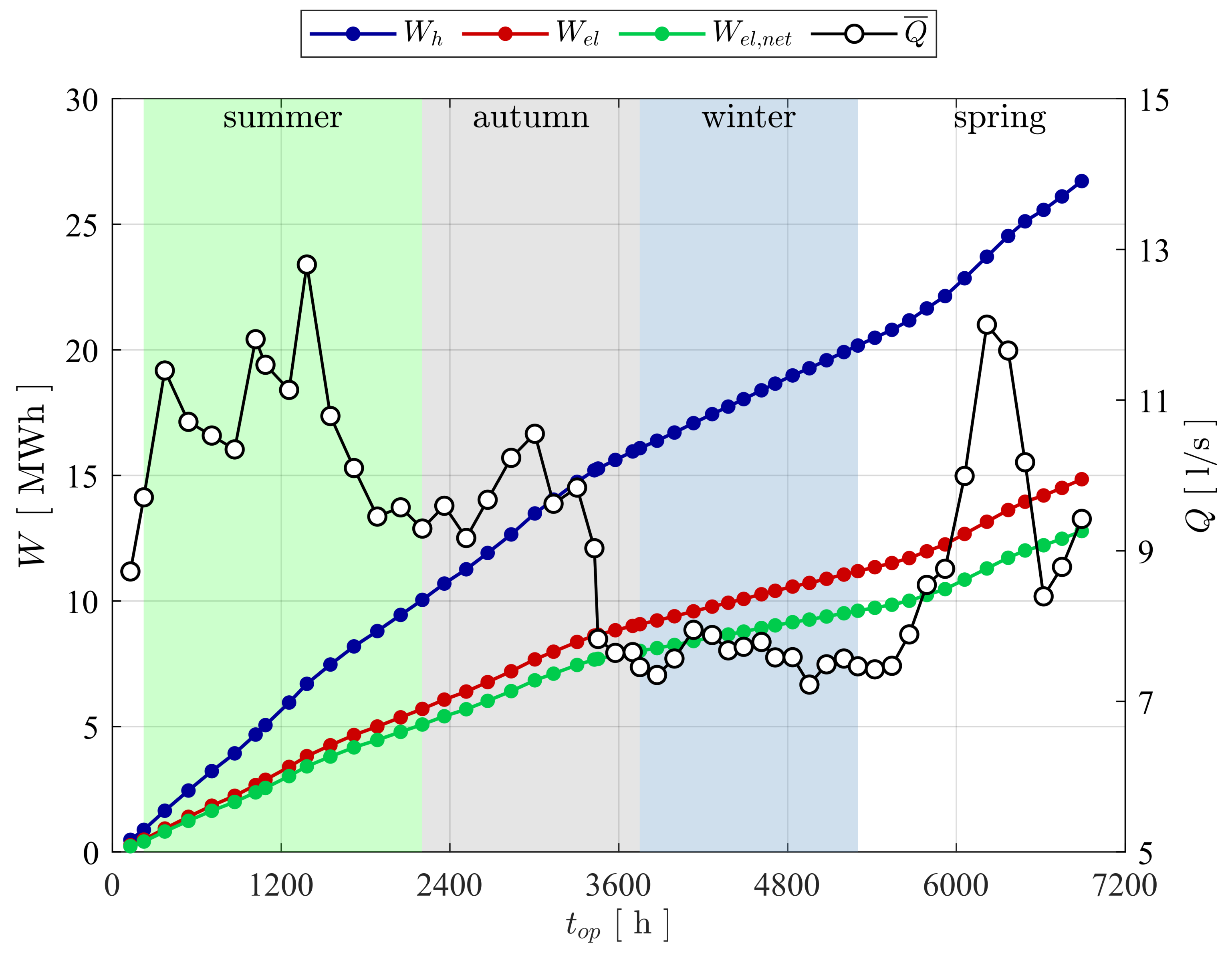
The drinking water industry hides a considerable hydraulic energy potential that remains mostly unexploited for gross capacities of a few kW. In this context, the DuoTurbo research project was initiated to provide a complementary solution for energetic exploitation of drinking water networks in the power range between 5 kW and 25 kW. A new hydroelectric system with a counter-rotating microturbine is developed and installed for long term tests at a drinking water facility. The counter-rotating architecture with particular variable speed rim generators enables a compact design, reaching relatively high specific energy values with extended operational flexibility compared to single degree of freedom solutions. The present study provides an overview of the different technical concepts and methodologies applied for the development of a product prototype with advanced technology readiness level. The particular double rotor hydraulic design is developed and characterized by steady state CFD RANS simulations. The numerical investigations point out the significance of the speed ratio of the system that allows for an extension of the high efficiency range facing important variations of the discharge coefficient. No significant offsets between the characteristic lines of each simulated speed ratio in the plane are observed considering the complete turbine domain. This result indicates the limitations on hydraulic flexibility of a fixed geometry hydraulic concept. Despite the currently very low specific speed value of about 16, an energy efficiency greater than 83% could numerically be revealed. This indicates an increased capability of double rotor axial designs handling low specific speed regimes compared to single rotor solutions. The specific speed range of the DuoTurbo turbine could be increased to more than 135 according to typical axial flow designs. Thus, the design range of the DuoTurbo turbine is considerable. In a complementary development step, advanced laboratory tests are performed on a hydraulic test rig to validate the design methodology and to reveal the final characteristics of the product prototype. The tests are conducted at several constant heads between 10 m and 80 m while varying the rotational speeds of each runner to capture the entire characteristics and hydroelectric efficiency of the system. A peak hydroelectric efficiency of 59% is measured that lets estimate a still relatively high amount of power losses from labyrinth leakage flow, disc friction and mechanical friction. The measured energy coefficients and discharge coefficients are then compared to the steady state RANS simulation results, showing a maximum absolute error of almost 8% in the high energy coefficient range, but displaying fair agreements close to BEP conditions with absolute errors widely far below 5%. The hydraulic design procedure is therefore considered reasonably accurate. For the final step of the system validation, a DuoTurbo pilot was commissioned in May 2019 at a pressure reducing station of a drinking water supply network. A complete year of operation counting more than 6’890 operating hours is monitored that confirms the functioning, stability and reliability of the system to a large extend. The vibration level on the turbine housing as well as the hydroelectric efficiency do not show significant deviation trends during the long-term endurance testing. The demonstration of the system in operational environment at pre-commercial state is validated that can be attributed to a technology readiness level of 7. This state includes briefly the in-field operation of the demonstrator adaptable to different operational environments and the verification of the expected efficiency and system stability under long-term real-time operational conditions. The present work demonstrates the technological capability of a counter-rotating micro turbine to recover hydraulic energy from existing water facilities in the power range of a few kW. Subsequent to the endurance tests, research on the required commercialization steps to transform the DuoTurbo concept into a viable MHP solution would typically be addressed. The further steps would also require the broadening and fine tuning of the hydraulic, mechanical and electrical designs along with system scaling considerations in order to target a wide range of potential drinking water networks.