Junction Management for Connected and Automated Vehicles: Intersection or Roundabout?
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions
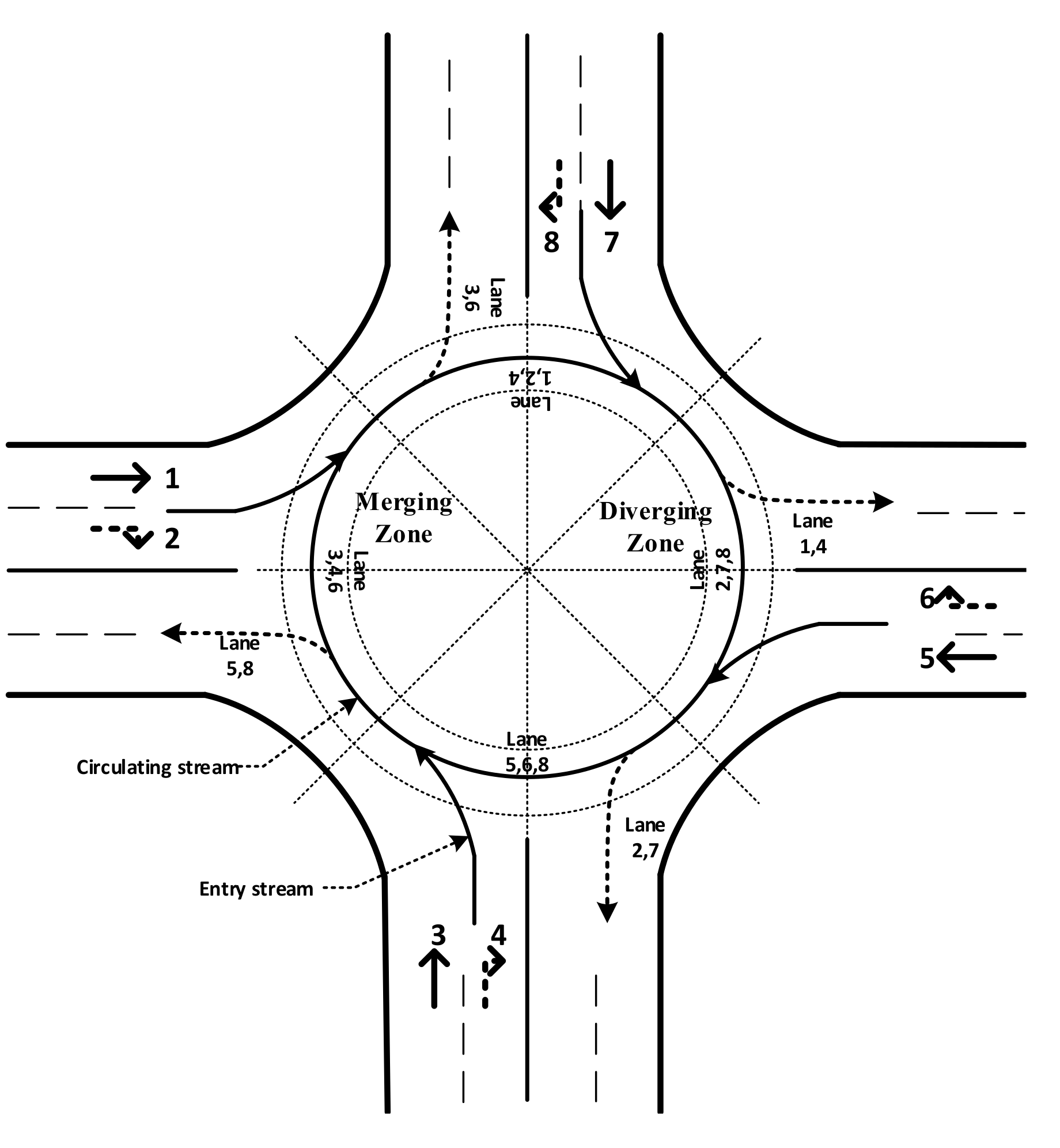
2. Preliminaries
- The communication capabilities of CAVs are perfectly operated, without any malfunctions.
- Lane changing is not allowed within the junction area, and vehicles strictly follow the traffic rules determined by the organization of the junction.
- The arrival process of vehicles on each stream is a Poison process with parameter and independent of each other.
- The difference between is not distinguished in this paper and a general distribution with expectation for is assumed. The distribution of is determined by the CACC policies with expectation . Empirically, .
- Gap acceptance of CAVs is determined by the advanced control systems.
3. Capacity
3.1. Signalized Intersection (I-Signal)
3.2. Intersection Using FCFS Policy (I-FCFS)
3.3. Roundabout Using FCFS Policy (R-FCFS)
3.4. Roundabout Using Major-Minor Policy (R-MM)
3.5. Capacity Comparison
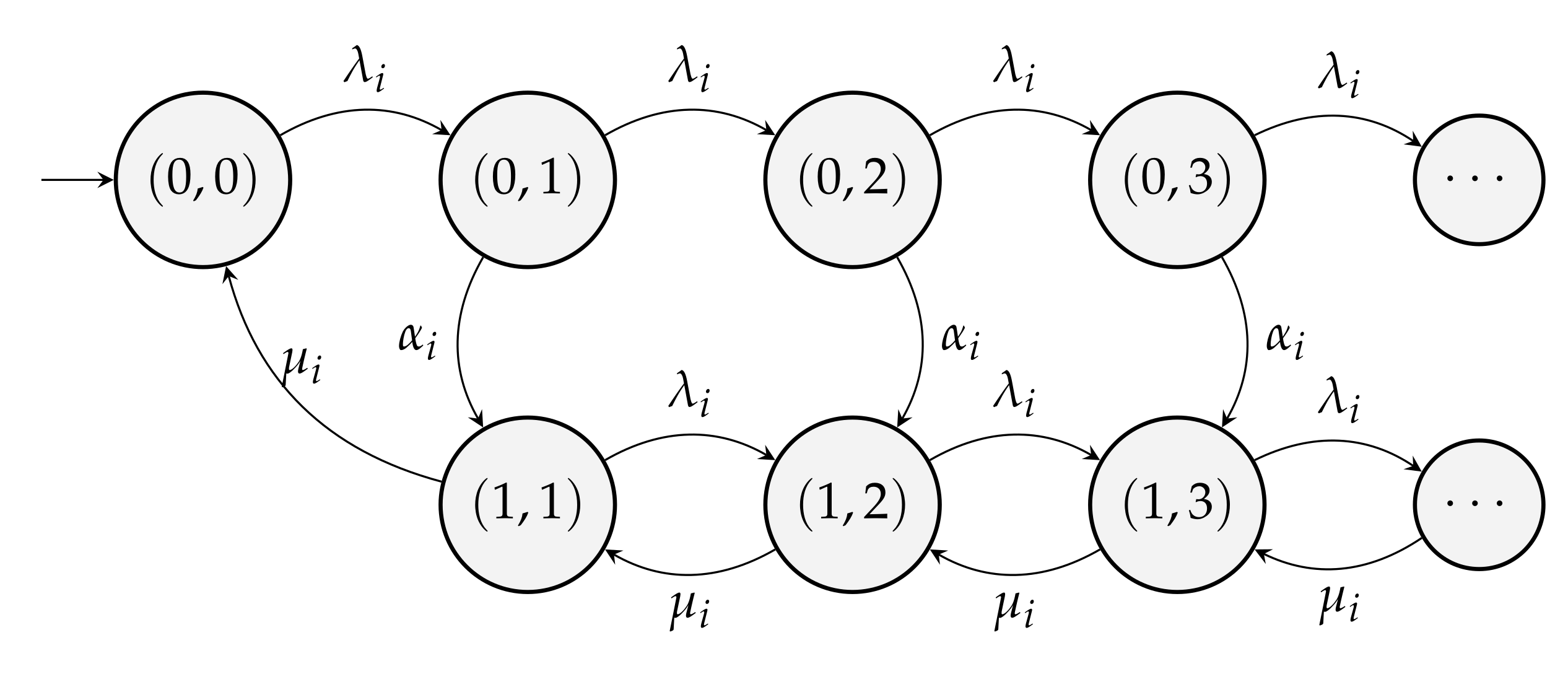
4. Delay
4.1. Delay Formulation
4.2. Delay Comparison
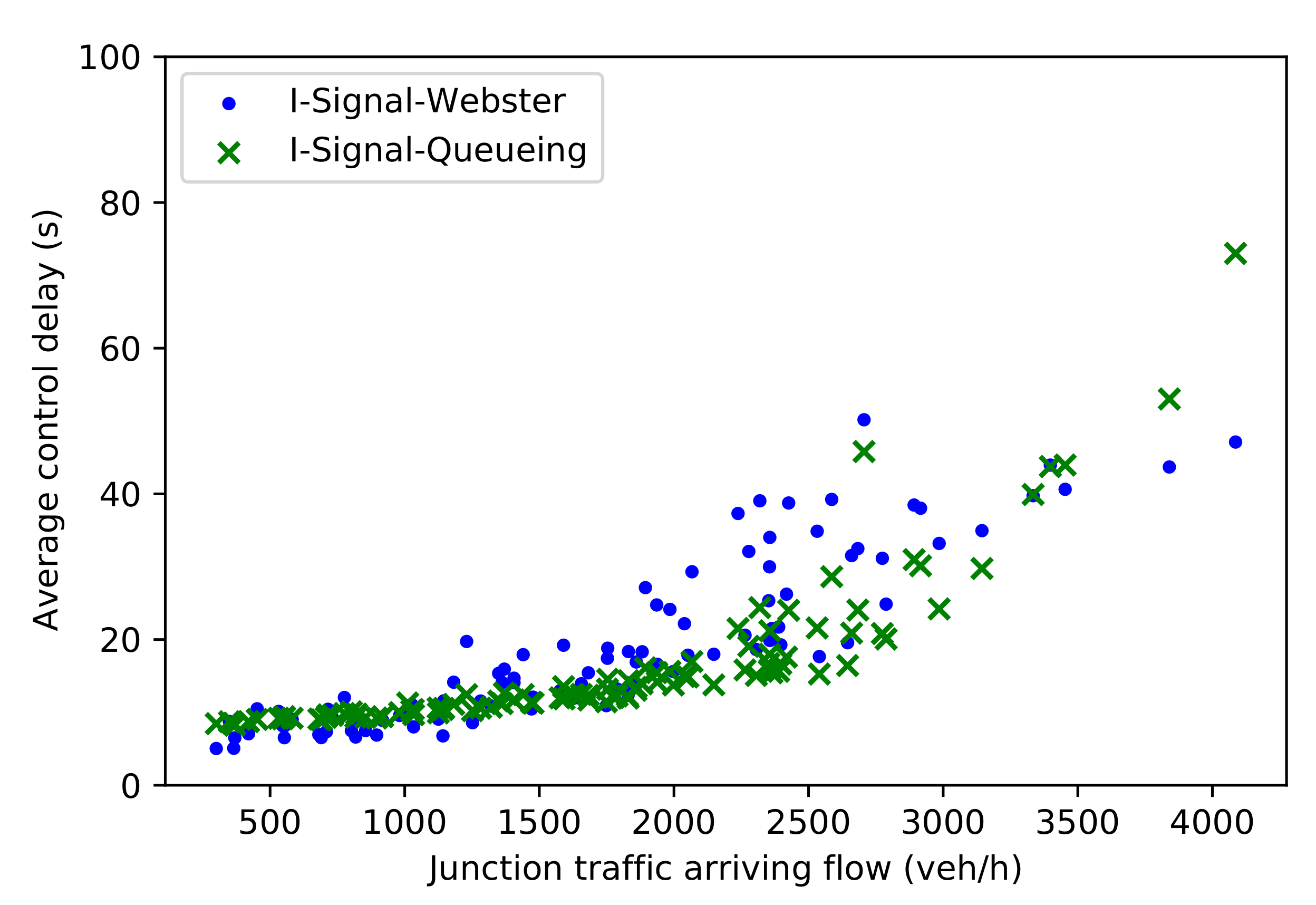
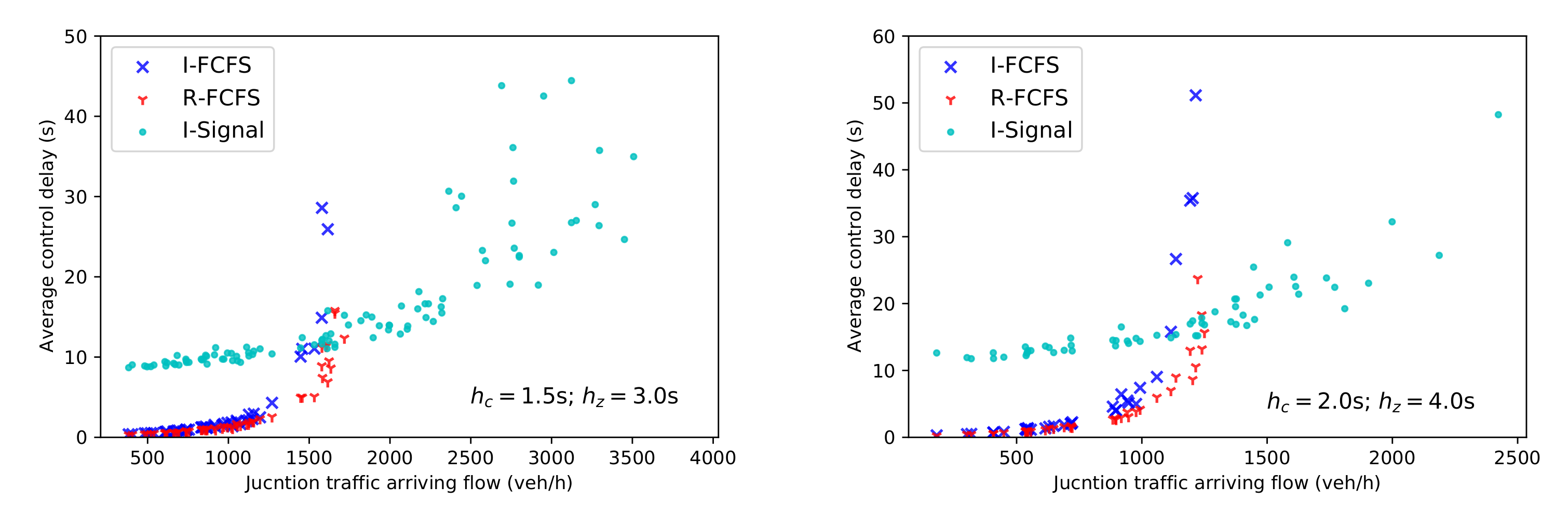
4.2.1. Signal vs. Signal-Free Strategies
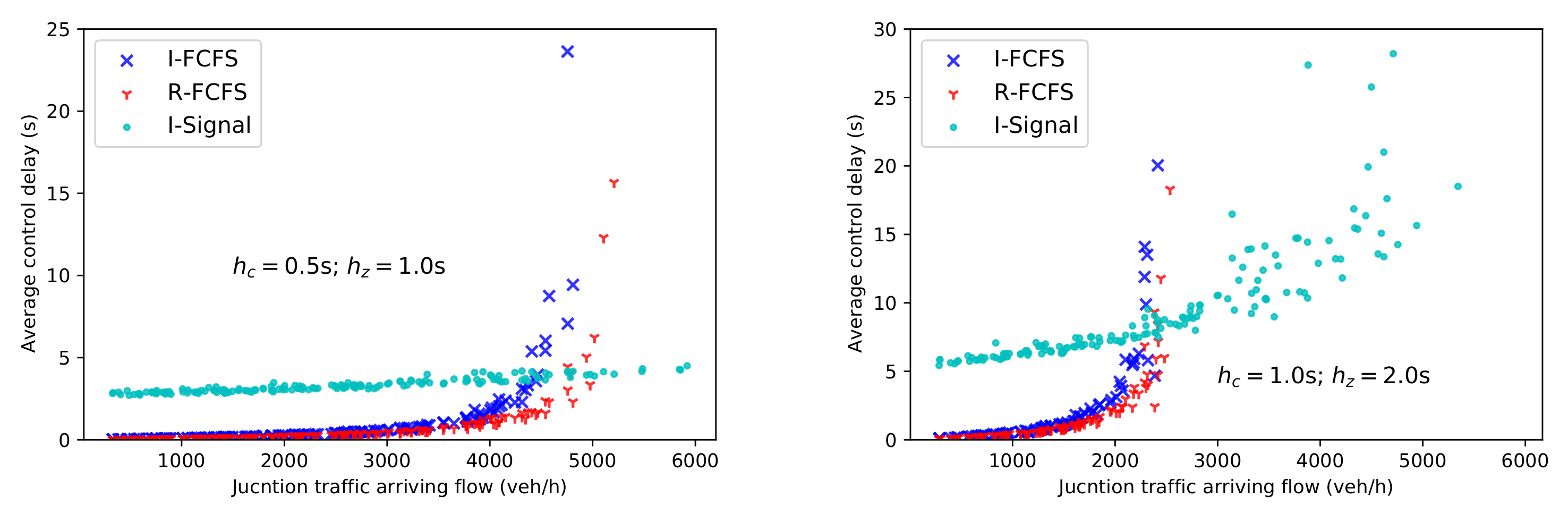
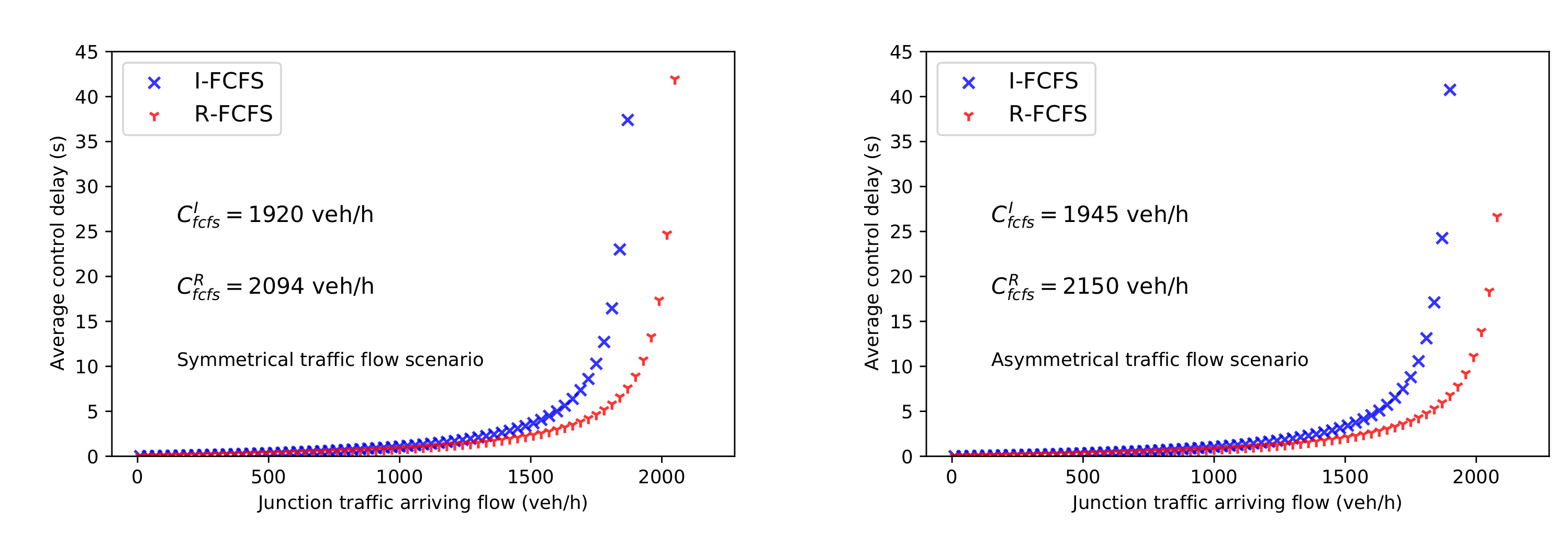
4.2.2. R-FCFS vs. I-FCFS
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Taiebat, M.; Brown, A.L.; Safford, H.R.; Qu, S.; Xu, M. A review on energy, environmental, and sustainability implications of connected and automated vehicles. Environ. Sci. Technol. 2018, 52, 11449–11465. [Google Scholar] [CrossRef]
- Azmat, M.; Kummer, S. Potential applications of unmanned ground and aerial vehicles to mitigate challenges of transport and logistics-related critical success factors in the humanitarian supply chain. Asian J. Sustain. Soc. Responsib. 2020, 5, 3. [Google Scholar] [CrossRef] [Green Version]
- Fagnant, D.J.; Kockelman, K. Preparing a nation for autonomous vehicles: Opportunities, barriers and policy recommendations. Transp. Res. Part A Policy Pract. 2015, 77, 167–181. [Google Scholar] [CrossRef]
- Wintersberger, S.; Azmat, M.; Kummer, S. Are we ready to ride autonomous vehicles? A Pilot Study on Austrian Consumers’ Perspective. Logistics 2019, 3, 20. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Englund, C. Cooperative intersection management: A survey. IEEE Trans. Intell. Transp. Syst. 2016, 17, 570–586. [Google Scholar] [CrossRef]
- Dresner, K.; Stone, P. Multiagent traffic management: A reservation-based intersection control mechanism. In Third International Joint Conference on Autonomous Agents and Multiagent Systems-Volume 3; IEEE Computer Society: Los Alamitos, CA, USA, 2004; pp. 530–537. [Google Scholar]
- Kimber, R. The Traffic Capacity of Roundabouts, TRRL Laboratory Report 942; Transport and Road Research Laboratory: Crowthorne, UK, 1980. [Google Scholar]
- Veith, G. Guide to Road Design: Part 4A: Unsignalised and Signalised Intersections; Technical Report; Austroads: Sydney, Australia, 2010. [Google Scholar]
- HCM. Highway Capacity Manual, 6th ed.; Transportation Research Board: Washington, DC, USA, 2016. [Google Scholar]
- Mauro, R.; Pompigna, A. State of the art and computational aspects of time-dependent waiting models for non-signalised intersections. J. Traffic Transp. Eng. (Engl. Ed.) 2020, 7, 808–831. [Google Scholar] [CrossRef]
- Pompigna, A.; Guerrieri, M.; Mauro, R. New Extensions and Applications of the Modified Chumanov Model for Calculating Entry Capacity of Single-Lane Roundabouts. Sustainability 2020, 12, 6122. [Google Scholar] [CrossRef]
- Molina-Masegosa, R.; Gozalvez, J. LTE-V for sidelink 5G V2X vehicular communications: A new 5G technology for short-range vehicle-to-everything communications. IEEE Veh. Technol. Mag. 2017, 12, 30–39. [Google Scholar] [CrossRef]
- Van Arem, B.; Van Driel, C.J.; Visser, R. The impact of cooperative adaptive cruise control on traffic-flow characteristics. IEEE Trans. Intell. Transp. Syst. 2006, 7, 429–436. [Google Scholar] [CrossRef] [Green Version]
- Makridis, M.; Mattas, K.; Ciuffo, B.; Raposo, M.A.; Thiel, C. Assessing the impact of connected and automated vehicles. A freeway scenario. In Advanced Microsystems for Automotive Applications 2017; Springer: Cham, Switzerland, 2018; pp. 213–225. [Google Scholar]
- Zhou, J.; Zhu, F. Analytical analysis of the effect of maximum platoon size of connected and automated vehicles. Transp. Res. Part C Emerg. Technol. 2021, 122, 102882. [Google Scholar] [CrossRef]
- Azmat, M.; Kummer, S.; Moura, L.T.; Gennaro, F.D.; Moser, R. Future outlook of highway operations with implementation of innovative technologies like AV, CV, IoT and Big Data. Logistics 2019, 3, 15. [Google Scholar] [CrossRef] [Green Version]
- Malikopoulos, A.A.; Cassandras, C.G.; Zhang, Y.J. A decentralized energy-optimal control framework for connected automated vehicles at signal-free intersections. Automatica 2018, 93, 244–256. [Google Scholar] [CrossRef] [Green Version]
- Dresner, K.; Stone, P. A multiagent approach to autonomous intersection management. J. Artif. Intell. Res. 2008, 31, 591–656. [Google Scholar] [CrossRef] [Green Version]
- Hausknecht, M.; Au, T.C.; Stone, P. Autonomous intersection management: Multi-intersection optimization. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 4581–4586. [Google Scholar]
- Fajardo, D.; Au, T.C.; Waller, S.; Stone, P.; Yang, D. Automated intersection control: Performance of future innovation versus current traffic signal control. Transp. Res. Rec. J. Transp. Res. Board 2011, 2259, 223–232. [Google Scholar] [CrossRef] [Green Version]
- Mauro, R.; Cattani, M. Functional and economic evaluations for choosing road intersection layout. PROMET-Traffic Transp. 2012, 24, 441–448. [Google Scholar] [CrossRef] [Green Version]
- NYSDOT. NYSDOT’s Web Site Dedicated to Modern Roundabouts. 2018. Available online: https://www.dot.ny.gov/main/roundabouts (accessed on 20 August 2019).
- Zhu, F.; Ukkusuri, S.V. A linear programming formulation for autonomous intersection control within a dynamic traffic assignment and connected vehicle environment. Transp. Res. Part C Emerg. Technol. 2015, 55, 363–378. [Google Scholar] [CrossRef]
- Sun, W.; Zheng, J.; Liu, H.X. A capacity maximization scheme for intersection management with automated vehicles. Transp. Res. Procedia 2017, 23, 121–136. [Google Scholar] [CrossRef]
- Mirheli, A.; Hajibabai, L.; Hajbabaie, A. Development of a signal-head-free intersection control logic in a fully connected and autonomous vehicle environment. Transp. Res. Part C Emerg. Technol. 2018, 92, 412–425. [Google Scholar] [CrossRef]
- Levin, M.W.; Fritz, H.; Boyles, S.D. On optimizing Reservation-Based intersection controls. IEEE Trans. Intell. Transp. Syst. 2017, 18, 505–515. [Google Scholar] [CrossRef]
- Zohdy, I.H.; Rakha, H.A. Intersection management via vehicle connectivity: The intersection cooperative adaptive cruise control system concept. J. Intell. Transp. Syst. 2016, 20, 17–32. [Google Scholar] [CrossRef]
- Nor, M.H.B.M.; Namerikawa, T. Merging of Connected and Automated Vehicles at Roundabout Using Model Predictive Control. In Proceedings of the 2018 57th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Nara, Japan, 11–14 September 2018; pp. 272–277. [Google Scholar]
- Debada, E.G.; Gillet, D. Virtual Vehicle-Based Cooperative Maneuver Planning for Connected Automated Vehicles at Single-Lane Roundabouts. IEEE Intell. Transp. Syst. Mag. 2018, 10, 35–46. [Google Scholar] [CrossRef]
- Zhao, L.; Malikopoulos, A.; Rios-Torres, J. Optimal control of connected and automated vehicles at roundabouts: An investigation in a mixed-traffic environment. IFAC-PapersOnLine 2018, 51, 73–78. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Xue, K. A new traffic-signal control for modern roundabouts: Method and application. IEEE Trans. Intell. Transp. Syst. 2004, 5, 282–287. [Google Scholar] [CrossRef]
- Lioris, J.; Pedarsani, R.; Tascikaraoglu, F.Y.; Varaiya, P. Platoons of connected vehicles can double throughput in urban roads. Transp. Res. Part C Emerg. Technol. 2017, 77, 292–305. [Google Scholar] [CrossRef] [Green Version]
- Heidemann, D.; Wegmann, H. Queueing at unsignalized intersections. Transp. Res. Part B Methodol. 1997, 31, 239–263. [Google Scholar] [CrossRef]
- Little, J.D.; Graves, S.C. Little’s law. In Building Intuition; Springer: Boston, MA, USA, 2008; pp. 81–100. [Google Scholar]
- Medhi, J. Stochastic Models in Queueing Theory; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Simchi-Levi, D.; Trick, M.A. Introduction to Little’s Law as Viewed on Its 50th Anniversary. Oper. Res. 2011, 59, 535. [Google Scholar] [CrossRef]
- Wu, N. A universal procedure for capacity determination at unsignalized (priority-controlled) intersections. Transp. Res. Part B Methodol. 2001, 35, 593–623. [Google Scholar] [CrossRef]
- Boon, M.A.; Mandjes, M.; Núñez-Queija, R. Congestion analysis of unsignalized intersections: The impact of impatience and Markov platooning. Eur. J. Oper. Res. 2019, 273, 1026–1035. [Google Scholar]
- Tanner, J. A theoretical analysis of delays at an uncontrolled intersection. Biometrika 1962, 49, 163–170. [Google Scholar] [CrossRef]
- Wu, N. Impedance Effects for Streams of Higher Ranks at unsignalized intersections. In Proceedings of the Third International Symposium on Highway Capacity, Copenhagen, Denmark, 22–26 June 1998; pp. 1137–1154. [Google Scholar]
- Abhishek, A.; Mandjes, M.; Boon, M.; Núñez-Queija, R. Congestion analysis of unsignalized intersections. In Proceedings of the 2016 8th International Conference on Communication Systems and Networks (COMSNETS), Bangalore, India, 5–10 January 2016. [Google Scholar]
- Gandhi, A.; Doroudi, S.; Harchol-Balter, M.; Scheller-Wolf, A. Exact analysis of the M/M/k/setup class of Markov chains via recursive renewal reward. In ACM SIGMETRICS Performance Evaluation Review; ACM: New York, NY, USA, 2013; Volume 41, pp. 153–166. [Google Scholar]
- Webster, F.V. Traffic Signal Settings; Technical Report; Transportation Research Board: Washington, DC, USA, 1958. [Google Scholar]
- Ghiasi, A.; Hussain, O.; Qian, Z.S.; Li, X. A mixed traffic capacity analysis and lane management model for connected automated vehicles: A Markov chain method. Transp. Res. Part B Methodol. 2017, 106, 266–292. [Google Scholar] [CrossRef]
- Dresner, K.M. Autonomous Intersection Management; Technical Report; University of Texas at Austin Austin United States: Austin, TX, USA, 2009. [Google Scholar]
- Levin, M.W.; Boyles, S.D.; Patel, R. Paradoxes of reservation-based intersection controls in traffic networks. Transp. Res. Part A Policy Pract. 2016, 90, 14–25. [Google Scholar] [CrossRef]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flötteröd, Y.P.; Hilbrich, R.; Lücken, L.; Rummel, J.; Wagner, P.; Wießner, E. Microscopic Traffic Simulation using SUMO. In Proceedings of the 21st IEEE International Conference on Intelligent Transportation Systems, Maui, HI, USA, 4–7 November 2018. [Google Scholar]
- Milanés, V.; Shladover, S.E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data. Transp. Res. Part C Emerg. Technol. 2014, 48, 285–300. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Li, S.; Shamo, D.E. A platoon-based traffic signal timing algorithm for major–minor intersection types. Transp. Res. Part B Methodol. 2006, 40, 543–562. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, H.; Zhu, F. DCL-AIM: Decentralized coordination learning of autonomous intersection management for connected and automated vehicles. Transp. Res. Part C Emerg. Technol. 2019, 103, 246–260. [Google Scholar] [CrossRef]
- Yu, C.; Sun, W.; Liu, H.X.; Yang, X. Managing connected and automated vehicles at isolated intersections: From reservation-to optimization-based methods. Transp. Res. Part B Methodol. 2019, 122, 416–435. [Google Scholar] [CrossRef]
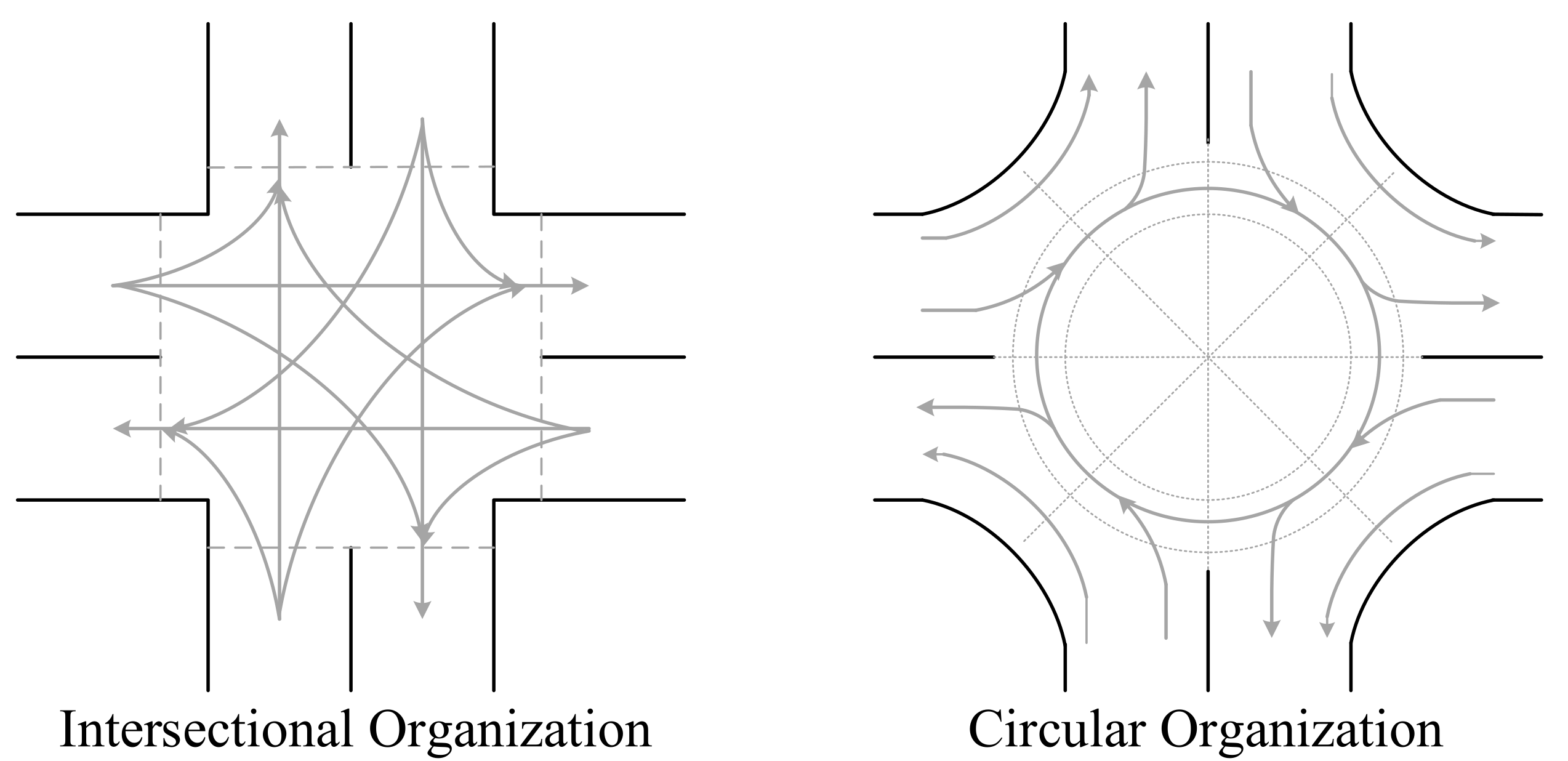
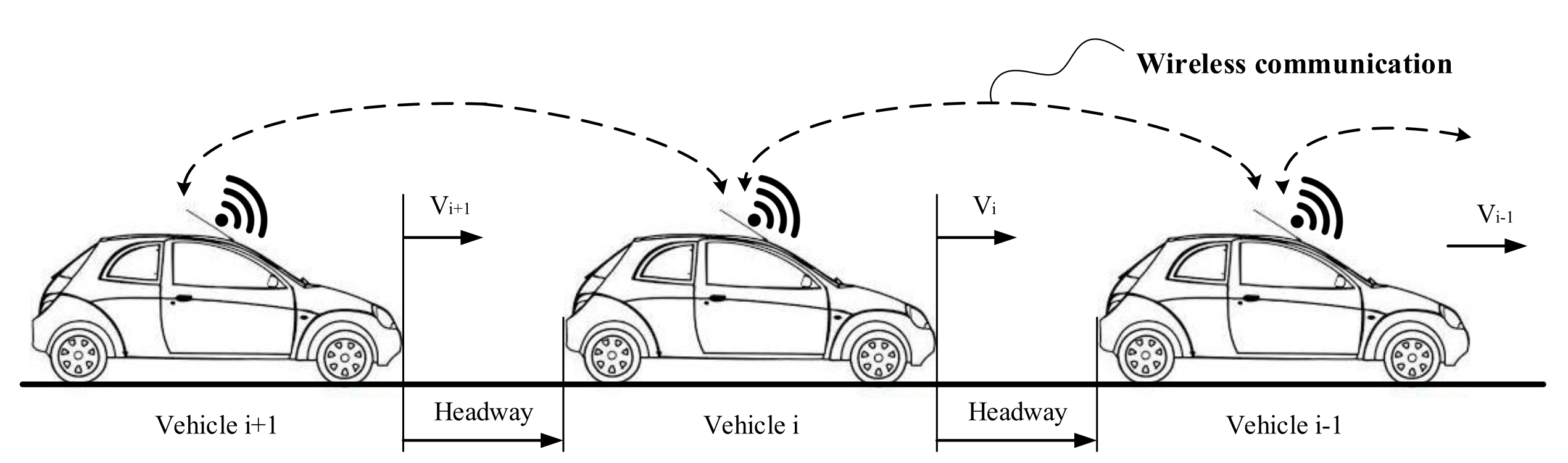
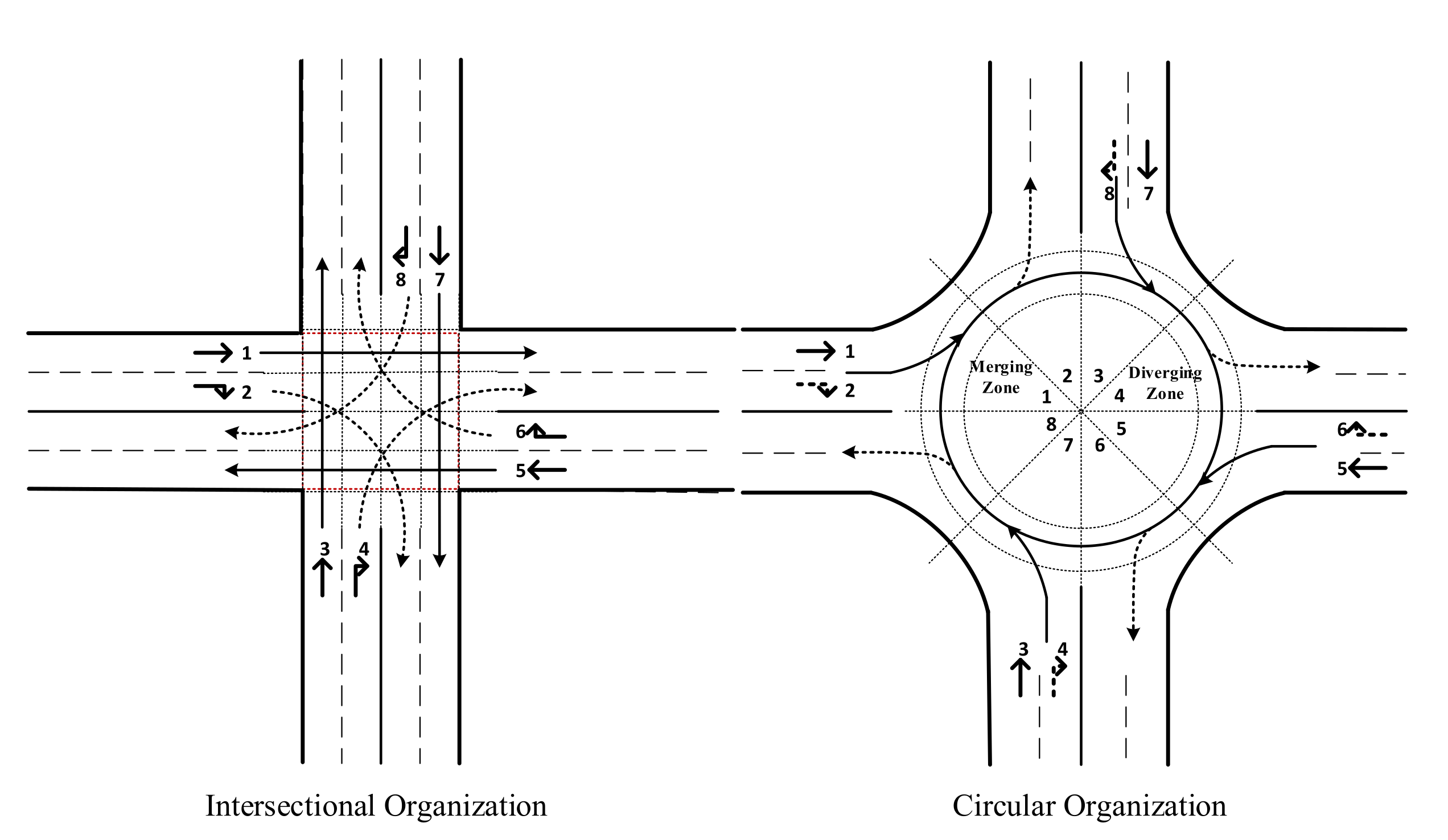
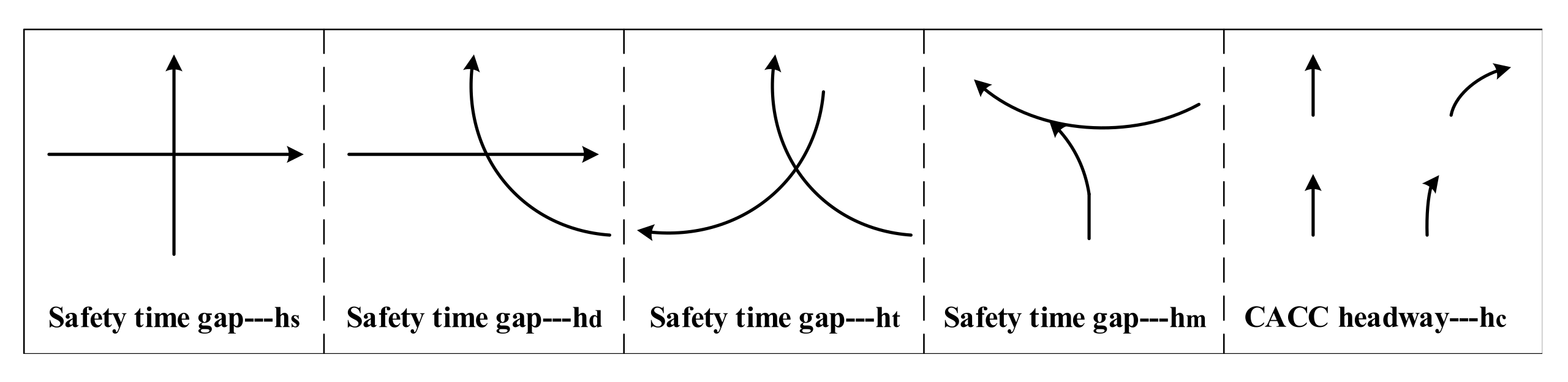
| Set | Description |
|---|---|
| L | set of lanes (streams) |
| set of non-conflicting streams of stream i | |
| set of conflicting streams of stream i | |
| E | set of entry approaches |
| Variable | Description |
| C | capacity of a control strategy |
| D | average control delay |
| signal cycle time (s) | |
| total loss time in signal control (s) | |
| total green time in signal control (s) | |
| an arbitrary CAV | |
| headway of CACC (s) | |
| safety time gap between two vehicles from conflicting streams (s) | |
| base/saturation flow rate of a stream () | |
| vehicle arrival rate of stream i () | |
| the sum of the arrival rate in stream group g | |
| the maximum arrival rate in stream group g | |
| the sum of | |
| the sum of | |
| service rate of a queueing system | |
| X | service time |
| W | mean waiting time of a queueing system |
| Stream i | Conflicting Stream Set |
|---|---|
| 1 | 3 6 7 8 |
| 2 | 3 4 5 8 |
| 3 | 1 2 5 8 |
| 4 | 2 5 6 7 |
| 5 | 2 3 4 7 |
| 6 | 1 4 7 8 |
| 7 | 1 4 5 6 |
| 8 | 1 2 3 6 |
| Entry Stream | Circulating Stream | |
|---|---|---|
| superimposed of stream | 1 2 | 3 4 6 |
| superimposed of stream | 3 4 | 5 6 8 |
| superimposed of stream | 5 6 | 2 7 8 |
| superimposed of stream | 7 8 | 1 2 4 |
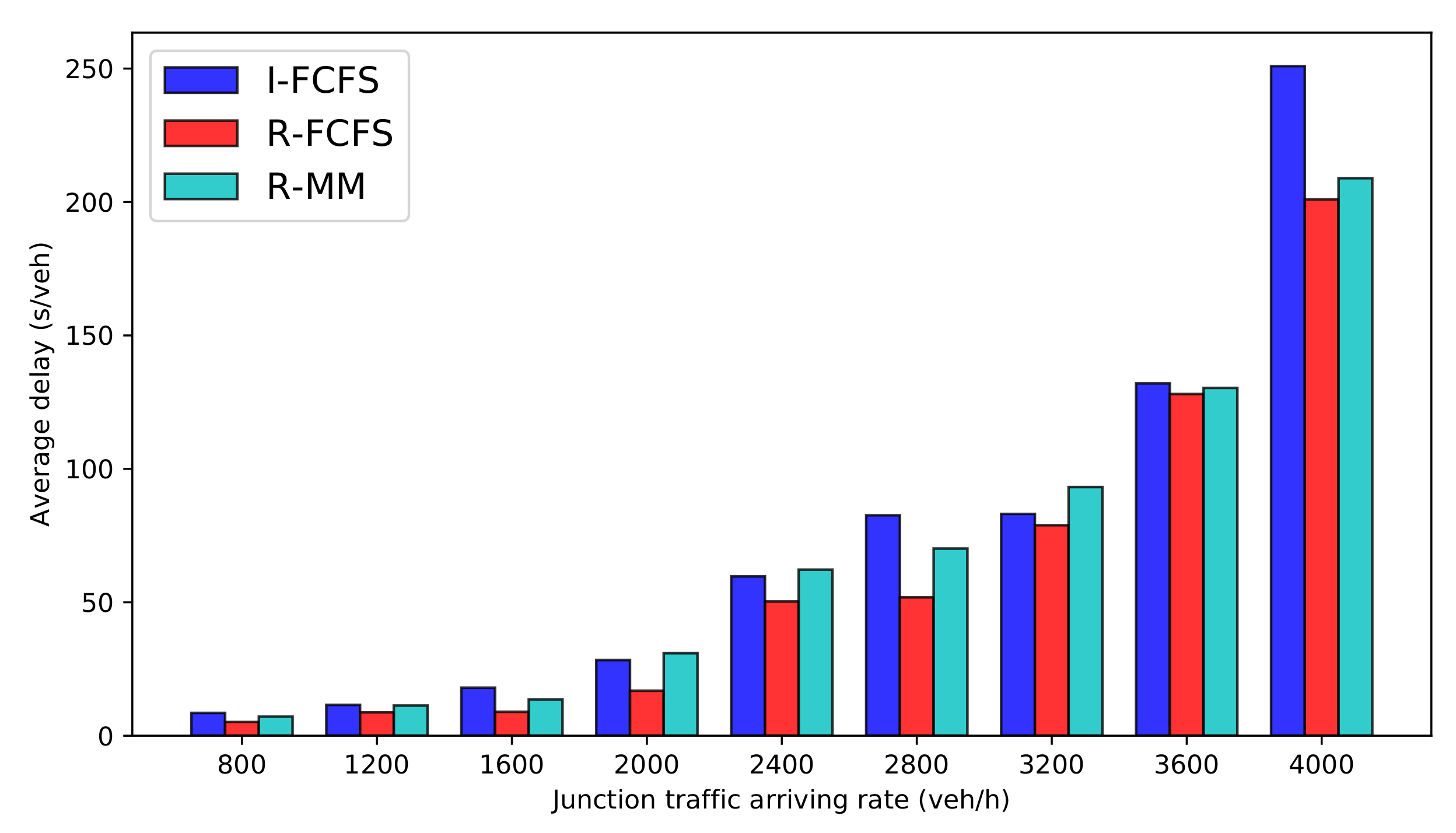
| Junction Traffic Arriving Rate | I-FCFS | R-FCFS | R-MM |
|---|---|---|---|
| 800 veh/h | 8.55 | 5.13 | 7.16 |
| 1200 veh/h | 11.53 | 8.75 | 11.32 |
| 1600 veh/h | 18.01 | 8.94 | 13.54 |
| 2000 veh/h | 28.34 | 16.86 | 30.9 |
| 2400 veh/h | 59.70 | 50.29 | 62.21 |
| 2800 veh/h | 82.59 | 51.84 | 70.12 |
| 3200 veh/h | 83.11 | 78.87 | 93.17 |
| 3600 veh/h | 132.01 | 128.06 | 130.33 |
| 4000 veh/h | 250.92 | 201.00 | 208.92 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Zhu, F. Junction Management for Connected and Automated Vehicles: Intersection or Roundabout? Sustainability 2021, 13, 9482. https://doi.org/10.3390/su13169482
Wu Y, Zhu F. Junction Management for Connected and Automated Vehicles: Intersection or Roundabout? Sustainability. 2021; 13(16):9482. https://doi.org/10.3390/su13169482
Chicago/Turabian StyleWu, Yuanyuan, and Feng Zhu. 2021. "Junction Management for Connected and Automated Vehicles: Intersection or Roundabout?" Sustainability 13, no. 16: 9482. https://doi.org/10.3390/su13169482
APA StyleWu, Y., & Zhu, F. (2021). Junction Management for Connected and Automated Vehicles: Intersection or Roundabout? Sustainability, 13(16), 9482. https://doi.org/10.3390/su13169482






